Estimating global biomass and biogeochemical cycling of marine fish with and without fishing

The global biomass of fish in the ocean leaves a significant imprint on ocean biogeochemistry and the biological pump.

Abstract

The biomass and biogeochemical roles of fish in the ocean are ecologically important but poorly known. Here, we use a data-constrained marine ecosystem model to provide a first-order estimate of the historical reduction of fish biomass due to fishing and the associated change in biogeochemical cycling rates. The pre-exploitation global biomass of exploited fish (10 g to 100 kg) was 3.3 ± 0.5 Gt, cycling roughly 2% of global primary production (9.4 ± 1.6 Gt year⁻¹) and producing 10% of surface biological export. Particulate organic matter produced by exploited fish drove roughly 10% of the oxygen consumption and biological carbon storage at depth. By the 1990s, biomass and cycling rates had been reduced by nearly half, suggesting that the biogeochemical impact of fisheries has been comparable to that of anthropogenic climate change. Our results highlight the importance of developing a better mechanistic understanding of how fish alter ocean biogeochemistry.

INTRODUCTION

Fish have not typically been considered as a dynamic component of global ocean biogeochemistry. Instead, the dominant biogeochemical paradigm has focused on the interactions between phytoplankton, zooplankton, and bacteria (1). Yet, in recent years, there has been a growing appreciation for the potential role of fish, which is becoming increasingly important in light of marked alterations caused by fishing, habitat degradation, warming, deoxygenation, and acidification (2–5). Fish and other consumers can exert control on marine food webs via top-down interactions (6, 7) and affect nutrient dynamics by storing, redistributing, and releasing carbon and nutrients within and across ecosystems (8–10). But while the biogeochemical role of fish has been documented in a variety of environments, most notably freshwater and coral reef ecosystems (8, 10), few studies have highlighted the role of fish on the ocean’s biological pump and seawater chemistry (11–14), and the influence of fish has only begun to be represented in Earth system models (15, 16).

Assessing the importance of fish in ocean biogeochemistry has primarily been hindered by a lack of knowledge regarding their abundance, distribution, and metabolic rates (17), properties that have changed markedly over the past century and remain uncertain (14, 18–21). Historically, the development of fisheries was accompanied by rapid and substantial biomass declines (5, 22, 23), most of which occurred without direct scientific observation. In many regions, industrial fisheries exploited ecosystems that had already been affected by traditional fishing, resulting in uncertain baselines (24). Climate change is now causing additional declines, although these remain much smaller than the direct fishing-related reductions for the species targeted by fisheries (25, 26). Fishing has been shown to have a substantial impact on ocean carbon fluxes by diminishing the flux of sinking fish carcasses (27), but this does not capture the full impact of fish on the long-term biogeochemical state of the ocean, which also includes respiration by fish and production of sinking fecal pellets, which are integrated over the multicentennial time scale of ocean circulation.

The animal biomass that existed before major human disturbances is a natural starting point from which the role of fish on ocean biogeochemistry can be evaluated. By providing estimates of carrying capacity that approximate pre-exploitation fish biomass, scientific stock assessments (28) can shed light on these quantities, in particular in data-rich regions. Likewise, analysis of historical records (24) and sedimentary proxies (29) has allowed reconstruction of fish populations for periods that predate modern fisheries. These efforts have been complemented by numerical models, which allow for extrapolation of sparse observations to entire ecosystems on large scales, coupling ecosystem dynamics to spatially varying environmental drivers (18, 30, 31).

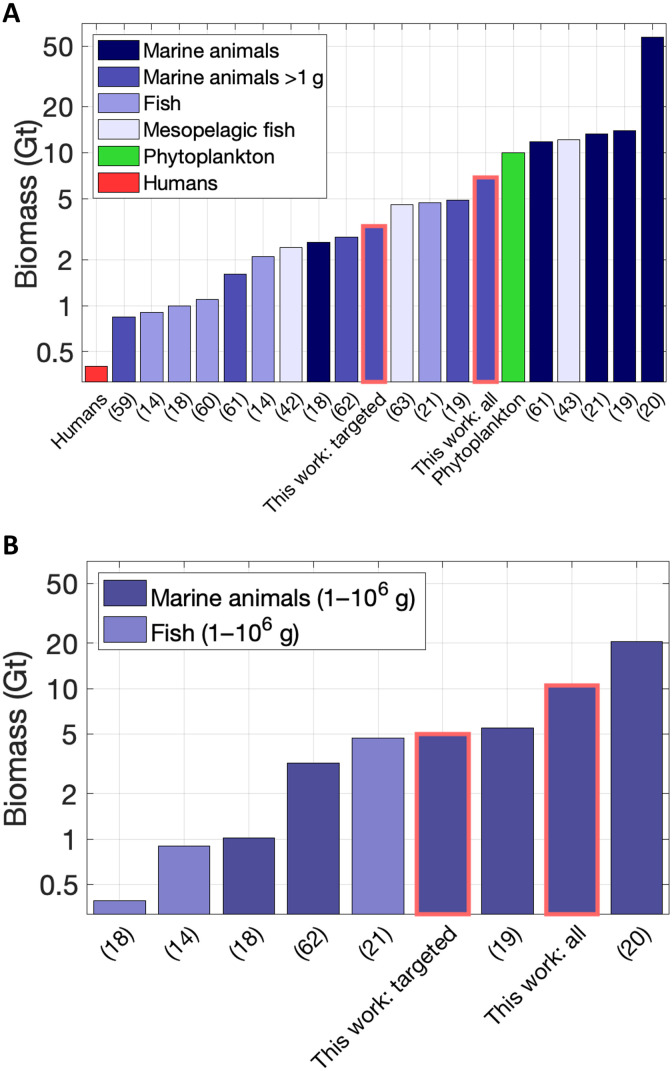
However, large uncertainties remain, as shown by the wide range of estimates of global fish biomass, mostly from numerical models, which range from less than 1 Gt to more than 50 Gt (Fig. 1A). While discrepancies can partly be explained by differences in the definition of fish and the size classes considered, we find a similar range even when comparing the same size classes and taxonomic groups (Fig. 1B and section S1). These discrepancies reflect variability in model formulations, ranging from application of ecological theory (18, 20) to intricate food web models (31), compounded by the scarcity of observations available to constrain models at the global scale. The persistent uncertainty has prompted a call for new, unified approaches and models that combine diverse constraints to provide more robust estimates of the global biomass and biogeochemical cycling rates of fish (17).

Fig. 1. Estimates of the biomass of fish and other consumers in the ocean.

We include both (A) the biomass originally reported in the papers and (B) an estimate of the same biomass rescaled to the range between 1 g and 1000 kg, a typical range for marine fish and other consumers, applying a conversion factor based on size-spectrum theory, as described in section S1. Note that, going from (A) to (B), biomass estimates could increase or decrease, depending on whether the original size range is smaller or larger than 1 g and 1000 kg, respectively. The complete list of values and the corresponding references are listed in table S1. The values reported as “this work” (highlighted in red) reflect fish biomass in the absence of fishing. Note the logarithmic scale on the vertical axis.

Here, we take advantage of records of the intense removal of wild fish by fisheries to better constrain the dynamics of global fish communities and their role for biogeochemistry. We use historical reconstructions of fish catch and stock assessments (28, 32), in combination with a biological-economic model (33, 34), to infer the biomass, metabolic rate, and biogeochemical importance of fish targeted by fisheries, their spatial distribution in the global ocean, and their historical change (Materials and Methods). Because the relationship between catch and biomass is complex (35) and has been subject to debate (36), we use complementary diagnostics to calibrate the dynamical model, forcing an interpretation of the data that is consistent across sources and with ecological theory. The combined use of catch reconstructions and stock assessments offers a global, long-term perspective on marine ecosystems that is not available from other sources.

The model resolves a globally gridded, size-structured ecosystem that depends on local water temperature and primary production (33) and is coupled to an economic model that simulates dynamically interactive fish catches (34). We include targeted invertebrates (e.g., squid) as “fish” due to their ecological similarities with true fish, but note that the fraction of total catch from invertebrates is only around 10% (32). Although the model does simulate variable recruitment, our analysis considers only the sizes larger than plankton (>10 g), because the mortality rates of ichthyoplankton are large, variable, and poorly constrained. Thus, our estimates do not include larval fish, which can functionally be described as zooplankton.

We carry out the model calibration by producing a large ensemble of simulations and objectively selecting model variants with catch histories and catch-to-biomass (C:B) ratios that are in best agreement with observations (34). Our most important constraints come from the relatively unambiguous characteristics of catch peaks at global, large marine ecosystem (LME) and individual stock levels (Materials and Methods and fig. S1) (37, 38).

We focus on reconstructing ocean fish biomass in the absence of fisheries, which, for simplicity, we refer to as “preindustrial biomass,” analogous to the preindustrial state that is widely used in climate research. Note that several additional drivers have likely altered fish biomass over the historical period in a way that we do not assess here. These include anthropogenic climate change (3, 25, 26), pollution and habitat degradation (39), and early defaunation (4, 5, 40), such as the marked early reduction in anadromous fish species (9) and marine mammals (41). Thus, the term preindustrial should be considered to reflect the ocean state in the absence of fishing rather than in the absence of human activities.

Our approach necessarily makes many assumptions, and the nature of the available data constraints requires a number of simplifications (summarized in table S6). For example, the data used here reflect environmental conditions during years of peak harvest (1960s to early 2000s) overprinted by natural variability. Our use of LME catch data to constrain the fish biomass means that the model explicitly represents only those species exploited by fisheries, a factor that we highlight by referring throughout to “targeted species.” Our high seas estimates and extensions to nontargeted species assume that the overall fish biomass, including species that are not currently exploited, can be predicted by the same environmental dependences as for targeted species in LMEs. This strategy is based on an assumption that there is no fundamental bioenergetic difference between the portion of the ecosystem that we choose to exploit and that we do not, an assumption that bears future exploration (42, 43). Our analysis also ignores other potential environmental factors such as iron limitation (44). Last, while we estimate parameter uncertainty using an ensemble of simulations, we cannot quantify structural model uncertainty, which requires using an ensemble of models based on different architectures (26). We hope that our estimates can be improved by addressing these issues through future work.

RESULTS

Model verification

Our ensemble reproduces realistic peak catches spanning more than three orders of magnitude, across LMEs encompassing the range of temperatures and productivity found over most of the ocean (fig. S2). Peak catches are reasonably well correlated between the ensemble and observational reconstructions (Pearson correlation coefficient R = 0.56, P < 10⁻⁴). The remaining variability (fig. S2A) is not surprising, given uncertainties in the catch data (32) and the model simplifications, and suggests an important role for management. For example, the model overestimates fish catch in a cluster of warm-water LMEs along the Australian shelf (left side of fig. S2A), where stringent quota-based regulations limited fishing effort (37). The ensemble also produces C:B ratios in line with observations (Materials and Methods and fig. S2, B to D), with an average value of 0.21 ± 0.11 year⁻¹ as compared to 0.22 ± 0.20 year⁻¹ in stock assessment data (28), indicating that it simulates realistic fish production rates.

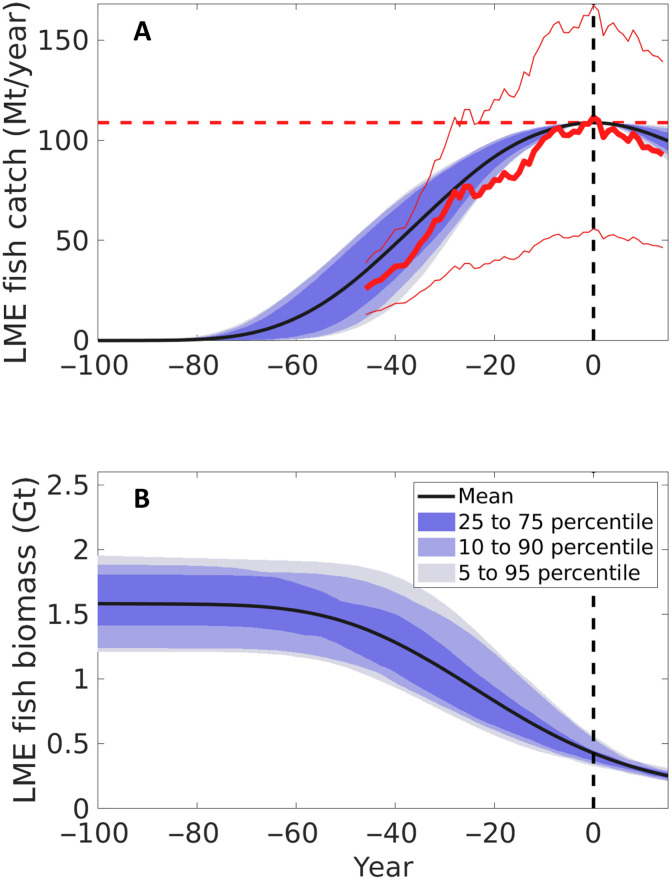
When forced by a continuous expansion of technology, the model reproduces a trajectory of development, peak, and decline of global fisheries that parallels observations of global fish catch, biomass, and effort (Fig. 2) (23, 32, 45, 46). The preindustrial fish biomass can then be estimated by backtracking the biomass trajectory to the beginning of the simulations, i.e., in the absence of fish catches (Fig. 2B).

Fig. 2. Estimated temporal evolution of fish catch and biomass.

(A) Fish catch integrated over large marine ecosystems (LMEs) (Mt year⁻¹). The thick red line indicates the Sea Around Us Project (SAUP) (32) catch summed over LME, and the thin red lines indicate the 50% uncertainty on the SAUP estimates. The thick and thin solid red lines show the central estimate and the range of catch from SAUP reconstructions, respectively, and the horizontal dashed line shows the global peak catch over LME from SAUP (109 Mt year⁻¹). (B) Global fish biomass (Gt) from the optimized ensemble of simulations. In each panel, in (A) and (B), the solid black line shows the mean of the ensemble of simulations, and the three blue shadings include 50% (25 to 75%), 80% (10 to 90%), and 90% (5 to 95%) of the model results. All model simulations and the SAUP catch have been aligned so that the global peak catch occurs at time t = 0 (vertical dashed line).

Estimated global preindustrial biomass and losses due to fishing

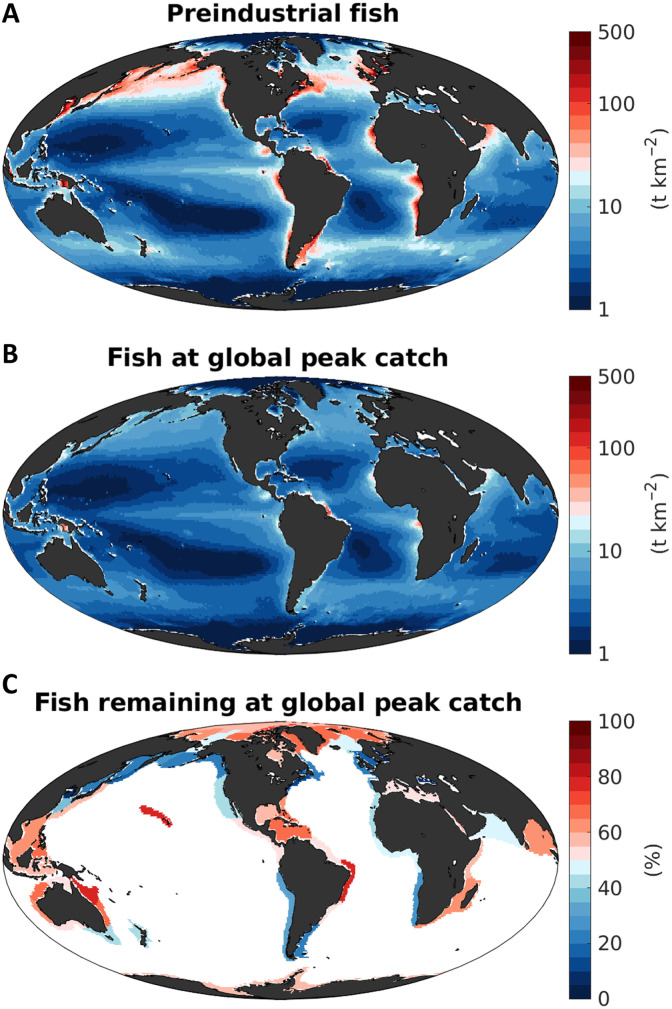
In the absence of fishing, we obtain a global biomass for targeted fish from 10 g to 100 kg of 3.3 ± 0.5 Gt (Table 1). About half of this preindustrial biomass (1.6 ± 0.2 Gt) is found within LMEs, which, despite covering only 20% of the ocean surface, include the most productive areas of the ocean. The largest preindustrial biomass densities are found within coastal regions and marginal seas with expansive continental shelves, extending further into the open ocean in the productive mid and high latitudes (Fig. 3A). Preindustrial biomass density is much lower in the vast oligotrophic areas of the ocean’s subtropical gyres, reflecting a combination of low primary production and dissipation of energy by small organisms (47).

Table 1. Ensemble model estimates of biomass (Gt) and cycling rates (Gt year⁻¹) of fish targeted by fisheries.

All values represent means from the optimized ensemble and have been spatially integrated (biomass and cycling rates) or averaged [cycling rates relative to net primary production (NPP)] over LME regions (i.e., excluding the high seas) and over the global ocean. Preindustrial ocean (top rows) refers to the ocean in the absence of fishing; peak catch (bottom rows) refers to the year when maximum catch is reached, considering each LME independently.

	LME			Global
	Biomass (Gt)	Cycling rate (Gt year−1)	% of NPP*	Biomass (Gt)	Cycling rate (Gt year−1)	% of NPP*
	Preindustrial ocean
Commercial	1.6 ± 0.2	4.3 ± 0.7	1.0 ± 0.2	3.3 ± 0.5	9.4 ± 1.6	1.1 ± 0.2
Total	3.3 ± 1.6	8.5 ± 3.4	2.0 ± 08	6.9 ± 3.6	18.9 ± 7.8	2.2 ± 0.9
	Peak catch †
Commercial	0.6 ± 0.2	2.5 ± 0.4	0.7 ± 0.1	1.1 ± 0.2	5.5 ± 0.9	0.7 ± 0.1

*Ratios of cycling rates to NPP were calculated at each model grid point and then spatially averaged.

†Values determined at the time of the global peak catch integrated over LME regions in the model.

Fig. 3. Estimated biomass of fish targeted by fisheries (size range of 10 g to 100 kg) and its historical reduction.

(A) Preindustrial biomass of targeted fish (t km⁻²). (B) Biomass of targeted fish (t km⁻²) at the time of global peak catch. (C) Fraction (%) of biomass remaining at the time of the global peak catch, relative to the preindustrial biomass, averaged over every LME. All maps are based on means from the optimized ensemble of simulations.

By the time of the global peak catch, the simulated biomass has decreased to 47 ± 20% of the preindustrial values averaged over LMEs (Fig. 3, B and C), falling within the range suggested by reconstructions of global stock depletions for the past century (46). The model indicates that stronger biomass depletions (approximately 20% of fish remaining) occur in high-biomass, cold-water regions, and weaker depletions (approximately 60% remaining) in less productive, low-biomass ecosystems (Fig. 3C). This pattern reflects the progression of model fisheries from initially profitable, biomass-rich but slow-growing ecosystems, mostly located in high latitudes, to ecosystems with less initial biomass but faster growth rates, mostly located in the tropics and subtropics (38). While the open-access dynamic omits important social aspects of fisheries, such as management, which played a role in the development of real-world fisheries, it nonetheless captures the main progression of observed catches (23, 38).

Biogeochemical role of targeted fish in the ocean

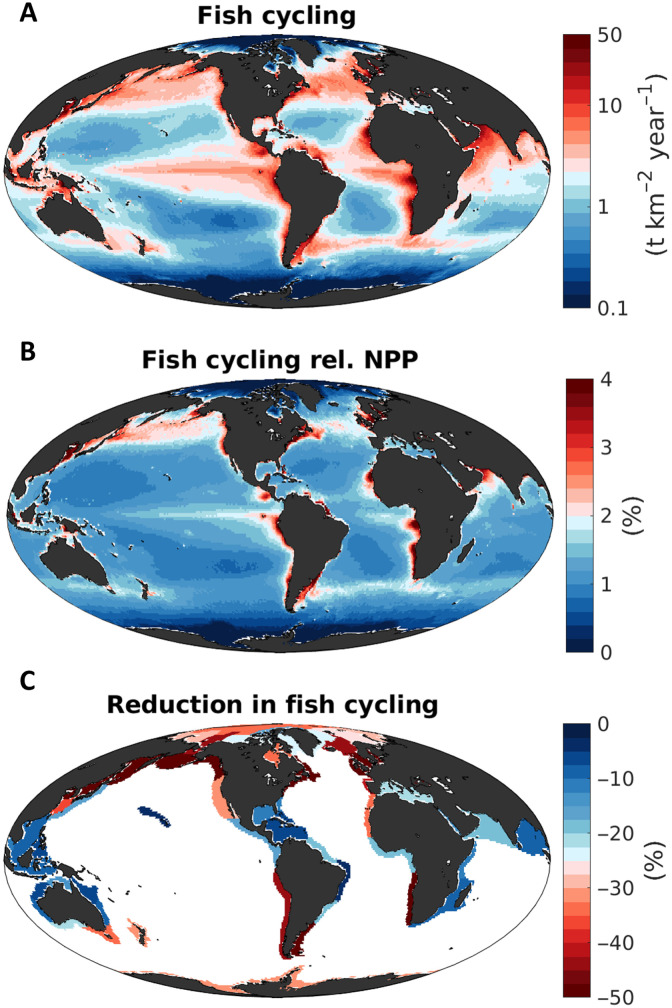
We estimate the biogeochemical impact of fish by considering the rate at which energy, in the form of biomass, passes through the fish community, and refer to it as the biomass cycling rate. The model indicates that targeted fish were responsible for cycling biomass at a globally integrated rate of 9.4 ± 1.6 Gt year⁻¹, with about half of this cycling (4.3 ± 0.7 Gt year⁻¹) occurring in LMEs (Table 1). The fraction of primary production consumed by targeted fish was approximately 2% when globally integrated, 1.1 ± 0.2% when globally averaged, and 1.0 ± 0.2% when averaged locally over LMEs, reflecting the high trophic level position of fish in the marine food web. This flow represents biomass that passes through fish and is returned to the environment, as a combination of dissolved and particulate forms, and reflects gross metabolic demand plus egestion. This metabolic demand is strongly correlated with biomass: More abundant fish populations require larger amounts of energy. Thus, regions hosting abundant fish stocks (Fig. 3A) also cycle large amounts of biomass (Fig. 4A).

Fig. 4. Estimated biomass cycling rate, and its historical reduction, for fish targeted by fisheries (size range of 10 g to 100 kg).

(A) Biomass cycling rate (t km⁻² year⁻¹) by targeted fish in the preindustrial state (i.e., in the absence of fishing). (B) Biomass cycling rate of targeted fish, relative to net primary production (%). (C) Reduction (%) of the biomass cycling rate by targeted fish at the time of the global peak catch, averaged over LMEs. All maps are based on means from the optimized ensemble of simulations.

As with biomass, the fraction of primary production that is cycled through fish also shows distinctive regional patterns (Fig. 4B). In relatively cold, productive ecosystems, targeted fish processed up to 4% of the energy fixed by phytoplankton, compared to values of less than 1% in oligotrophic regions. These regional patterns can be explained by a combination of primary production and temperature effects (fig. S3). Where productivity is high, a larger portion of photosynthesis is cycled through fish. This dependence is further modulated by temperature; colder regions show a greater utilization of net primary production by fish (fig. S3). This dependence reflects structural assumptions of the model regarding the response of trophic webs and energy transfer under different environmental conditions (37, 47), as constrained by the model optimization. Nutrient and chlorophyll-rich low-temperature waters tend to host larger phytoplankton cells at the base of the food web compared to warm, oligotrophic waters (48). In the model, this results in relatively short food webs, where primary production is more efficiently transferred to fish and other consumers before being dissipated (37, 47).

At peak catch, driven by the widespread reduction of biomass, the cycling rate of targeted fish declines to 5.5 ± 0.9 Gt year⁻¹ globally and 2.5 ± 0.4 Gt year⁻¹ over LMEs, corresponding to a reduction from the unfished level of approximately 40% when spatially averaged, similar to the biomass decline (around 50%). The reduction of fish cycling at the time of global peak catch is more pronounced in cold, high-latitude LMEs compared to less productive low-latitude regions, to a similar degree, or even stronger than the biomass reduction, suggesting potential nonlinear interactions between biomass depletion and temperature (Fig. 4C).

Roughly one-fifth of the biomass ingested by fish returns to the environment as fecal pellets (49), an important source of large organic particles from the surface ocean (11). For the unfished ocean, this implies a fecal flux of 1.9 Gt year⁻¹, roughly one order of magnitude larger than the sinking carcass flux estimated in (27). Relative to a satellite-based estimate of the total particle export (48), the overall contribution of targeted fish remains small, on average, around 2%. However, because fish fecal pellets sink at speeds that are orders of magnitude faster than small particles (up to approximately 1000 m day⁻¹) (11), the expected contribution of fish-produced fecal pellets becomes increasingly significant at depth. An idealized calculation based on a data-constrained representation of marine particle flux (section S6 and table S5) (50) suggests that, at a depth of 200 m, the upper boundary of the ocean’s mesopelagic zone, fish fecal pellets will be twice as important as at the base of the euphotic zone. This amplification rises to a fivefold increase at 1000 m, a horizon below which exported carbon and nutrients would be sequestered for hundreds to thousands of years (51). At these depths, our simple calculation suggests that fish fecal pellets from targeted species could contribute approximately 10% of the total global sinking particle flux (table S5).

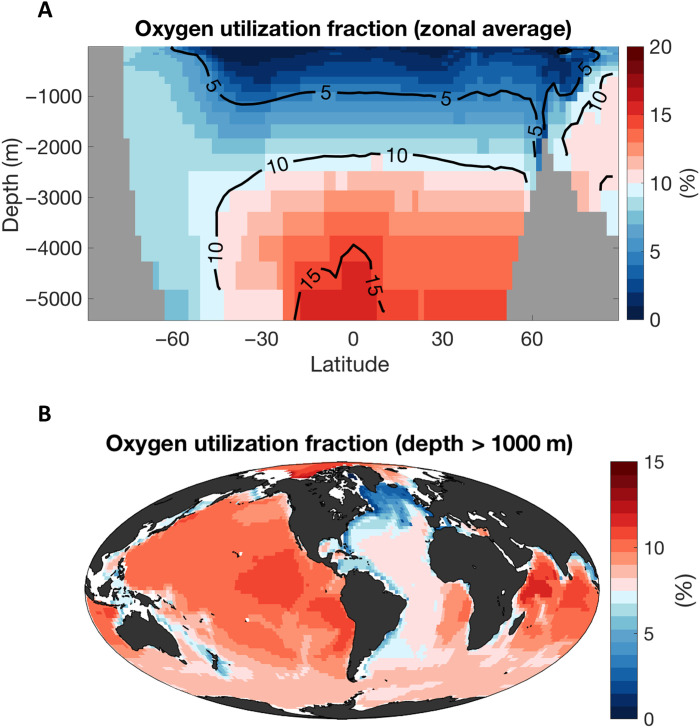
We use an ocean circulation inverse model (52), and a simple representation of the sinking and degradation of organic particles, to illustrate the imprint of fish-produced fecal pellets on seawater chemistry (Fig. 5 and Materials and Methods). Decomposition of fast-sinking particles preferentially occurs in the abyssal ocean, where the respiration of fish-produced particles could reach up to 20% of the total oxygen utilization (Fig. 5A). This oxygen deficit accumulates along the pathway of the deep ocean circulation, increasing from the North Atlantic to the North Pacific (Fig. 5B), and is further modulated by the patterns of surface export (48). This respiration is accompanied by an accumulation of inorganic nutrients and carbon at depth, which, based on our model, would contribute approximately 10% of the biological nutrient and carbon sequestration below 1000 m depth, consistent with the idealized calculation presented above. The total carbon sequestration by fish-produced particles is approximately 100 GtC, or about 10% of the total deep carbon sequestration by the biological pump (51). The sequestration time of fish-produced fecal pellets is approximately 600 years, making it one of the most efficient natural carbon sequestration mechanisms in the ocean (51).

Fig. 5. Illustration of the impact of fish cycling on ocean biogeochemistry.

The two panels show estimates of the dissolved oxygen utilization caused by the decomposition of sinking organic particles produced by targeted fish and other consumers as a fraction (%) of the dissolved oxygen utilization caused by remineralization of all sinking particles. The estimate reflects fish cycling rate in the unfished ocean (Fig. 4A). Details of the calculation are provided in section S7. (A) Zonal average. (B) Average for the deep ocean (all depths are greater than 1000 m).

Extrapolation to nontargeted fish

The results discussed above focus on targeted fish, which are explicitly simulated by the model and constrained with catch and biomass observations. We also extrapolate the results to the sum of targeted and nontargeted species by carrying out a set of simulations that approximate the whole spectrum of animals within the model size range (10 g to 100 kg; see section S4). Targeted fish are assumed to have access to a fraction of the total photosynthetic energy transferred across food webs, estimated as 0.58 ± 0.22 (Materials and Methods). The remaining energy is implicitly transferred to nontargeted consumers in the same size range, assuming that they are identical to targeted fish in terms of their bioenergetics. By repeating the simulations with this fraction set to 1, the biomass and metabolic rates are thereby extrapolated to the sum of targeted and nontargeted species (section S4).

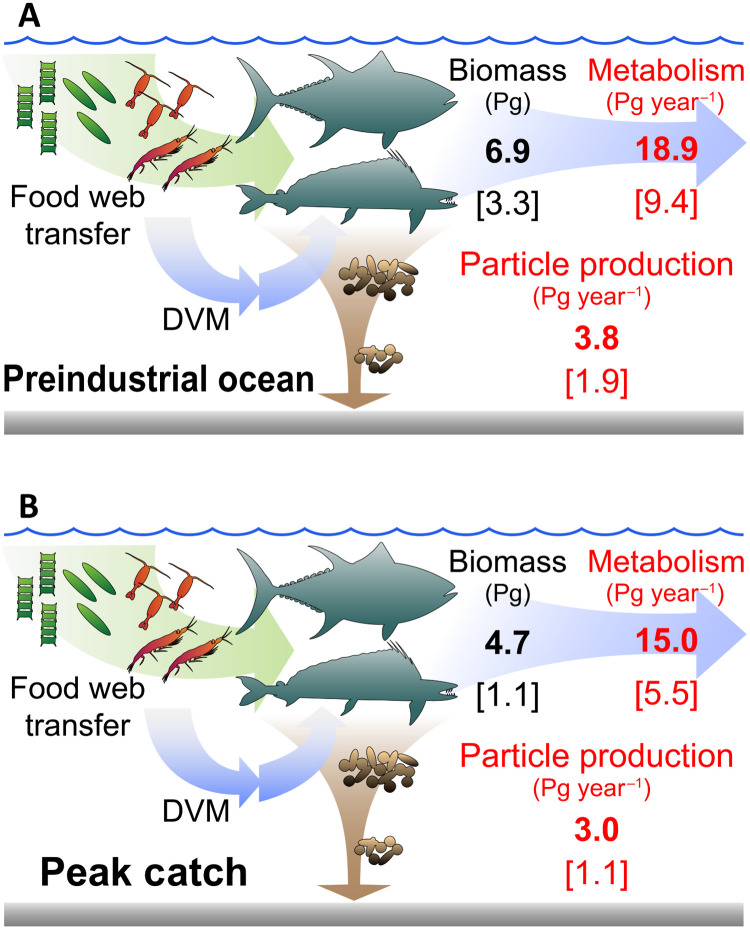
The results of these additional simulations suggest that the total animal biomass and cycling rates in the unfished ocean were roughly twofold those of targeted species (Table 1 and Fig. 6). While this extrapolation is weakly constrained (section S4), it suggests a preindustrial global biomass of consumers between 10 g and 100 kg of 3.3 ± 1.7 Gt over LME regions and 6.9 ± 3.6 Gt globally (Fig. 6). Together, this animal biomass would have cycled organic matter at rates of 8.5 ± 3.4 and 18.9 ± 7.8 Gt year⁻¹, representing approximately 4% of primary production when integrated globally, 2.0 ± 0.8% when averaged globally, and 2.2 ± 0.9% when averaged over LMEs.

Fig. 6. Summary of simulated fish biomass, metabolism, and biogeochemical impacts.

(A) Preindustrial ocean (i.e., in the absence of fishing). (B) Ocean at the time of the global peak catch. In both panels, numbers in black show fish biomass in Pg; in red biomass cycling processes in Pg year⁻¹, for all fish in bold, and for targeted fish in brackets (size range of 10 g to 100 kg for both groups). Processes affecting ocean biogeochemistry consist of respiration, production of sinking particles, and diel vertical migrations (DVMs), all included in the metabolism term. Total metabolism and particle production are explicitly quantified in this paper, but not DVM. See also Table 1 for numerical values.

DISCUSSION

When extrapolated to the size range between 1 g and 1000 kg (section S1), our results indicate a preindustrial biomass of 5.0 Gt for targeted fish and 10.5 Gt for the sum of all fish (Fig. 1B). While this is on the high end of previous estimates, it lies within the published range of 5 to 20 Gt from recent global models (19, 20) and meta-analyses (21) for the biomass of fish and other consumers in the ocean (Fig. 1B).

Although the biomass directly cycled by 10 g to 100 kg fish in the absence of fishing (18.9 Gt year⁻¹) is only about 4% of the total biomass generated by phytoplankton (53), fish have a significant potential to modify the fluxes of carbon and nutrients in the ocean (Figs. 5 and 6), by forming fast-sinking fecal pellets (11), or via horizontal (9) and vertical migrations (13, 16).

For example, our estimate suggests that fish feces are an important and efficient component of particle export, the biogeochemical significance of which would be expected to increase with depth. Because fish fecal pellets sink much faster and further than smaller particles such as phytoplankton aggregates and zooplankton fecal pellets (11), they could account for more than 20% (considering targeted and nontargeted species) of the deep ocean respiration and carbon sequestration driven by the ocean’s biological pump. This contribution is comparable in magnitude to other secondary export processes such as particle subduction and downward mixing, diel vertical migrations, and ontogenetic zooplankton migrations and could be important for closing the deep ocean carbon budget (51). In addition, if we consider that this export may have been altered by more than 30% in response to fishing pressures, the resulting effect on the biological pump would rival in magnitude estimates of climate change impacts (54).

Furthermore, the magnitude of fish-mediated fluxes is sufficient to alter the sensitive balance of oxygen in the deep sea. We estimate that respiration of fecal pellets produced by targeted fish is responsible for an average of about 20 mmol m⁻³ oxygen utilization below 2000 m, corresponding to about 10 to 15% of the total oxygen utilization at these depths. If the flux of fish fecal pellets had simply been reduced proportionally to the fish cycling rate reduction estimated here, it would imply a sizable reduction of respiration in the deep ocean. While this form of oxygen utilization is not dominant at those depths, even for the unfished ocean, it is still an important shift to consider, for example, in the deep Pacific Ocean, where the accumulated effect of respiration drives oxygen concentrations close or even below the thresholds for hypoxia (55). In this and comparable hypoxic regions, oxygen declines of few tens of mmol m⁻³ are sufficient to limit the habitat of marine organisms, requiring specific adaptations to life at low oxygen (55). Consequently, any process increasing available oxygen would strongly influence the ecology in these regions.

Changes in oxygen of this magnitude are also significant when compared to observed deep ocean deoxygenation, on the order of a few mmol m⁻³ over the past century (2). These reconstructions indicate that the contribution from global warming can only explain half of the observed oxygen loss (3), requiring a significant component due to unresolved biological processes (2). While a causal link between fisheries and deoxygenation cannot be firmly established yet (15), our results suggest that the magnitude of fish-mediated export makes it an integral part of oceanic oxygen regulation so that changes in fish populations would be expected to drive change in ocean oxygen concentrations of a similar magnitude to those recently observed. That is, deoxygenation changes could be larger than appreciated, as the drop in fish biomass (and thus respiration) may have masked a substantial fraction of the effect. However, we caution that the possibility for trophic cascades and shifts between communities (including phytoplankton and zooplankton) could lead to nontrivial patterns of change (15).

Our results provide a first-order quantification of global fish biomass and metabolism and their decline caused by fisheries. Generating this quantification required making several simplifying assumptions regarding the marine ecosystem, leading to a number of important caveats and uncertainties (table S6). While acknowledging these necessary simplifications, we estimate that, at the time of global peak catch, the simulated biomass of targeted fish was reduced to less than half of its unfished state, and the cycling rate by about 40% over LMEs, with marked reductions in productive, cold-water ecosystems. These estimates are likely to underestimate the total change, because they do not include the detrimental effects of habitat degradation (4) and climate change (3), the latter of which has probably contributed an additional 4 to 5% fish biomass decline over the past century (25, 26).

While classical fisheries science would argue that this level of biomass change is close to desired for achieving maximum sustainable yields (56), this overlooks the broader ecosystem implications of that degree of biomass change. Biogeochemistry is just one ecosystem process potentially affected by such change but should be considered among the consequences of rebuilding marine fisheries and ecosystems (56, 57). Evaluating the signature of fisheries on ocean biogeochemistry is a complex problem that requires a better characterization of the impacts of fish on productivity and particle export (15–17), and of the ecosystem changes that follow the depletion, for example, changes in size structure and trophic cascades (7). Nonetheless, it is likely that changes in biomass and cycling rate caused by fisheries would reverberate through the food web to alter carbon, nutrient, and oxygen cycles relative to the unfished ocean (15), given the tight stoichiometric relationships between these elements. While a number of challenges remain (table S6), global ecosystem models will be essential to quantifying interactions between fisheries and biogeochemistry and should aim at representing fish and other consumers as integral components of Earth system cycles. Recent marine ecosystem model intercomparison and ensemble analyses are promising steps in this direction (26). Given the large change in global fish communities that has resulted from industrial fishing and early defaunation (40), and the emerging effect of additional stressors such as ocean warming (25), the development of a better understanding of these biogeochemical implications is an urgent undertaking.

MATERIALS AND METHODS

Model description and experimental design

We use the BiOeconomic mArine Trophic Size-spectrum (BOATS) model (33, 34), which consists of a size-based representation of fish ecology and life history, coupled to an “open-access” economic model of fishing effort. BOATS represents all targeted species with individual mass between 10 g and 100 kg, as three continuous, independent size spectra with different asymptotic sizes, which provide a rough representation of fish diversity and are directly comparable to size-dependent catch reconstructions (32). While these species include invertebrates (e.g., mollusks and crustaceans), they are dominated by fish, and we simply refer to them as fish in the paper. The model is implemented on a global, two-dimensional grid at 1° spatial resolution and is forced with monthly climatological temperatures and satellite-derived primary productivity from observations representative of the 1990s to 2000s period (34). We use the same forcings for simulations with and without fishing. Thus, our estimate of preindustrial fish biomass (i.e., in the absence of fishing) does not include the impacts of anthropogenic climate change, which has been estimated to be relatively minor for the historical period (25, 26).

Biological and ecological processes (e.g., growth, mortality, reproduction, and recruitment) are parameterized on the basis of relationships that draw from macroecological theory and observations (33). The ecological model is coupled to a representation of fishing effort and catches based on the open-access Gordon-Schaefer fishery economics model (section S2) (34), which reasonably approximates to the dynamics of fisheries under weak regulation, up to the time of the global peak catch in the 1990s (23, 38). Because our focus is on the difference between fished and unfished biomasses, rather than details of the historical transient, we simply use a single, high rate of technological progress of 7% year⁻¹ throughout the simulations, on the higher range of observational estimates (23). Note that the hindcasts likely underestimate catches in the early decades of the simulations (Fig. 2A), primarily because preindustrial artisanal and subsistence fisheries are not explicitly represented.

Among the model parameters, we define the fraction of primary production that is potentially available to targeted fish, ϕ_π, as the energy input to the base of the food web that can ultimately support targeted species, and the vast majority of which is implicitly respired by zooplankton and bacteria (section S2.2). As default, we set the value of ϕ_π equal to 1, but we reassess it as part of the model optimization procedure.

A summary of the model rationale, equations, and parameters is presented in section S2. A summary of model assumptions and limitations is presented in table S6.

Observational constraints

We use two observational datasets to constrain model catch and biomass at the global scale. The first is the Sea Around Us Project database (SAUP) 2010 release (32), which contains reconstruction of global annual catches based on Food and Agriculture Organization (FAO) data, encompassing industrial, artisanal, and recreational fisheries, as well as bycatches. The SAUP database spans the ocean exclusive economic zones from 1950s to 2010, providing a global, long-term perspective on fish catches. The second dataset is the RAM Legacy Database version 4.3 (28), which contains a synthesis of more than a thousand stock assessments from the global ocean, including biomass and catch data.

We aggregate and analyze the SAUP data at the scale of 66 LMEs, which provide ecologically consistent, regional-scale spatial units that can be directly compared with spatially integrated model output. Following previous studies (37), we further consider the peak catches as the average of the largest 5 years of catches in each LME.

Biomass estimates are only available for scientifically assessed stocks and represent only a fraction of the targeted fish biomass in the ocean. To overcome this limitation, we use the stock assessments in the RAM database to define the C:B ratio at the scale of LMEs.

The C:B ratio is computed from the general total catch (the variable “TCbest”) and general total biomass (the variable “TBbest”) reported by the RAM Legacy Database (28). We combine these ratios with the global SAUP catch data to constrain the model fish biomass. That is, a model with a realistic representation of fish catches and C:B ratios would also produce a realistic representation of fish biomass. We recognize that C:B ratios vary by species, environmental conditions, and level of exploitation. To minimize the effects of these sources of variability, we select C:B ratios for available stocks at the time of maximum catch, which tend to reflect the inherent productivity of stocks [e.g., (37)], and aggregate them over LMEs, where environmental conditions tend to be more uniform than at the global scale. Accordingly, we determine the C:B ratio at peak catch for 25 LMEs from 292 stocks by calculating the total catch and dividing it by the total biomass in each LME, and taking the average over the highest 5 years of catch. Using the total catch and biomass from each LME ensures that the resulting C:B ratios are representative of the overall LME productivity, rather than reflecting individual stocks. The list of LME used, the number of stocks, and the corresponding average C:B ratios are summarized in table S4.

Monte Carlo approach and optimized ensemble

Without posterior constraints, the range of model parameters produces model solutions that span several orders of magnitude for the globally integrated fish biomass and catch (34). Following previous work (23, 33), we adopt a Bayesian Monte Carlo approach to select a set of model parameters (“optimized ensemble”) producing solutions that best agree with observational estimates of fish catch and biomass at the scale of LMEs. The approach is schematically shown in fig. S1 and is summarized by the following steps:

1) We start from an initial set of N = 10,000 simulations (“Monte Carlo ensemble”), with parameters randomly assigned based on ranges drawn from the literature. Details of this Monte Carlo ensemble are presented in (34, 23) and are summarized in section S3. Although we use the same Monte Carlo ensemble, the selection of optimized members (described below) differs from the two prior works, leading to a new, larger ensemble that spans a broader range of parameters.

2) For each simulation in the Monte Carlo ensemble, we calculate the global peak catch as the average of the five largest annual catches integrated over LMEs. On the basis of these peak catches, we estimate the fraction of primary production potentially available to fish (ϕ_π) that would produce in each simulation a global peak catch equal to the SAUP estimate, 110 Mt year⁻¹, summed over LMEs (32). We then exclude all the runs that would require more energy than potentially available from net primary production to sustain the global fish catch (i.e., all the runs for which ϕ_π > 1). This leaves us with N = 962 simulations.

3) To preserve a realistic partitioning of fish captures by size, we constrain the catch for fish in the medium and large size groups to be in the observed range relative to fish in the small group (34). This reduces the number of runs to N = 618.

4) To ensure that global catches are supported by realistic rates of fish biomass production, we compare the model C:B ratios averaged over 25 LMEs to the observational estimate from the RAM database (28). We do so by only retaining runs for which a Kolmogorov-Smirnoff test indicates a probability greater than 50% that the model C:B ratios follow the same distribution as observations. This selection leaves N = 66 runs.

5) To ensure that the selected runs reflect geographical patterns of observed catches across a range of temperatures and productivities, we select model solutions that produce similar peak catch at the scale of LMEs as the SAUP reconstructions. Specifically, we calculate the Pearson correlation coefficient R between modeled and observed peak catches for each LME and take all solutions with R > 0.60 as our optimized ensemble. This leaves us with N = 31 solutions, with average ϕ_π of 0.58 ± 0.22 and average C:B ratio over LME of 0.21 ± 0.11 year⁻¹.

We finally rerun the optimized ensemble for 200 years without catches to reach an equilibrium representative of the biomass of targeted fish in the absence of fishing, followed by a continuous 220-year increase of catchability at a rate of 7% year⁻¹, mimicking the historical progression of global fisheries (23). In each of these runs, the fraction of primary production potentially available to fish, ϕ_π, is set to the value required to produce the global catch of 110 Mt year⁻¹ from SAUP (section S4). To obtain an approximate estimate of the biomass of all consumers (that is, both targeted and nontargeted species), we also run a second instance of this optimized ensemble, where we set ϕ_π = 1 in each run. For this second set of simulations, we assume that targeted and nontargeted consumers follow the same dynamics and together represent all consumers within the model size range of 10 g to 100 kg.

Model diagnostics

We focus our analysis on the biomass of fish, both in the unfished state and at the time of the global peak catch. We further calculate the metabolic demand of fish and compare it to the net primary production that ultimately sustains it. We use the new biomass production rate and the trophic efficiency from the model (see section S5) and determine the biomass ingested by fish, and returned directly to the environment as a combination of organic (e.g., fecal pellets and excretion) and inorganic (respiration) fluxes, but not retained within the fish size spectrum. We express this cycling rate in units of wet biomass processed per unit area per unit time (i.e., t km⁻² year⁻¹). As a proxy of the particle production by fish, we assume that about 20% of the biomass cycling rate is returned to the environment as fecal pellets (49). Assuming a constant carbon content of organic matter of 10 gC/cWB (18), we compare these quantities to biogeochemical rates expressed in carbon units, such as generation of new biomass from photosynthesis and export of organic matter from the upper ocean as particles, which we take from existing satellite-based estimates (48).

Oxygen utilization due to fish-produced particles

We use an ocean inverse circulation model (52) to estimate the impact of remineralization of fish-produced fecal pellets in the ocean interior. The ocean inverse circulation model provides a data-based estimate of ocean transport, which we use to solve for the steady-state distribution of dissolved biogeochemical tracers (i.e., oxygen and carbon) resulting from remineralization of organic matter in the ocean interior. We assume that remineralization is mainly driven by the flux of organic particles produced in the euphotic zone (here set equal to 74 m, the depth of the second model layer, and close to the global average) but acknowledge that this neglects a portion of remineralization that is driven by other mechanisms such as dissolved organic matter and vertically migrating organisms (51). Below the euphotic zone, particles sink and decompose, following a remineralization profile described by a power-law equation (section S6) (50). We specify the total surface particle export flux from a satellite-based observational synthesis (48) and assume that these particles remineralize with a power-law exponent equal to −0.7, a representative value for the ocean (50). The export of fish-produced particles is estimated based on the mean fish egestion from the optimized ensemble. We assume that fish-produced particles are formed above the euphotic depth (a conservative assumption), and sink with a velocity 10 times larger than the bulk sinking speed of all particles, consistent with observations (11). We represent this rapid sinking by imposing a power-law exponent for fish particle flux equal to −0.07 (section S6). We then use the ocean circulation inverse model to solve separately for the three-dimensional steady-state concentration of dissolved inorganic carbon resulting from (i) the remineralization of all particles and (ii) the remineralization of fish-produced particles (details on the model equations and solution are discussed in section S7). The results (Fig. 5) are presented as the oxygen utilization resulting from this remineralization, which is calculated by using a typical stoichiometric ratio of oxygen to carbon of −150:106 (58).

Supplementary Materials

This PDF file includes:

Sections S1 to S9

Tables S1 to S6

Figs. S1 to S4

References

Other Supplementary Material for this manuscript includes the following:

Data file S1