A comparison of ten polygenic score methods for psychiatric disorders applied across multiple cohorts

Abstract

Background:

Polygenic scores (PGSs), which assess the genetic risk of individuals for a disease, are calculated as a weighted count of risk alleles identified in genome-wide association studies (GWASs). PGS methods differ in which DNA variants are included and the weights assigned to them; some require an independent tuning sample to help inform these choices. PGSs are evaluated in independent target cohorts with known disease status. Variability between target cohorts is observed in applications to real data sets, which could reflect a number of factors, e.g., phenotype definition or technical factors.

Methods:

The Psychiatric Genomics Consortium working groups for schizophrenia (SCZ) and major depressive disorder (MDD) bring together many independently collected case-control cohorts. We used these resources (31K SCZ cases, 41K controls; 248K MDD cases, 563K controls) in repeated application of leave-one-cohort-out meta-analyses, each used to calculate and evaluate PGS in the left-out (target) cohort. Ten PGS methods (the baseline PC+T method and nine methods that model genetic architecture more formally: SBLUP, LDpred2-Inf, LDpred-funct, LDpred2, Lassosum, PRS-CS, PRS-CS-auto, SBayesR, MegaPRS) are compared.

Results:

Compared to PC+T, the other nine methods give higher prediction statistics, MegaPRS, LDPred2 and SBayesR significantly so, up to 9.2% variance in liability for SCZ across 30 target cohorts, an increase of 44%. For MDD across 26 target cohorts these statistics were 3.5% and 59%, respectively.

Conclusions:

Although the methods that more formally model genetic architecture have similar performance, MegaPRS, LDpred2, and SBayesR rank highest in most comparison and are recommended in applications to psychiatric disorders.

Introduction

Polygenic scores (PGSs), which assess the genetic risk of individuals for a disease(1, 2), are calculated as a weighted count of genetic risk alleles in the genome of an individual, with the risk alleles and their weights derived from the results of genome-wide association studies (GWAS)(3). PGS can be calculated for any trait or disease with sufficiently powered GWAS (‘discovery samples’), and accuracy of PGS applied in independent GWAS ‘target samples’ will increase as discovery sample size increases. Since genetic factors only capture the genetic contribution to risk and since PGS only capture part of the genetic risk, PGS cannot be diagnostically accurate risk predictors (see review(4)). Nonetheless, for many common complex genetic disorders, such as cancers(5, 6) and heart disease(7, 8), there is increasing interest in evaluating PGS for early disease detection, prevention and intervention(9–11).

There are now many methods to calculate PGSs, and the methods differ in terms of two key criteria: which DNA variants to include and what weights to allocate to them. Here, for simplicity, we assume the DNA variants are single nucleotide polymorphisms, SNPs, but other DNA variants tested for association with a trait can be used. While stringent thresholds are set to declare significance for association of individual SNPs in GWAS, PGSs are robust to inclusion of some false positives. Hence, the maximum prediction from PGSs tested in target samples may include nominally associated SNPs. The optimum method to decide which SNPs to select and what weights to allocate them, may differ between traits depending on the sample size of the discovery GWAS and on the genetic architecture of the trait (the number, frequencies and effect sizes of causal variants), particularly given the linkage disequilibrium (LD) correlation structure between SNPs. Often, when new PGS methods are introduced, comparisons are made between a limited set of methods using simulated data, together with application to some real data examples. However, it can be difficult to compare across the new methods, particularly because in real data there can be variability in PGS evaluation statistics between target cohorts, not encountered in idealised simulations. The reasons for this variability are usually unknown and not simple to identify (12) but could reflect a number of factors such as phenotype definition, ascertainment strategies of cases and controls, cohort-specific ancestry within the broad classification of ancestry defined by the GWAS discovery samples (e.g., European), or technical artefacts in genotype generation.

Here, we compare ten PGS methods (PC+T(3, 13), SBLUP(14), LDpred2-Inf(15), LDpred2(15), LDpred-funct(16), Lassosum(17), PRS-CS(18), PRS-CS-auto(18) and SBayesR(19), MegaPRS(20), Table 1 ). Some of these methods (PC+T, LDpred2, MegaPRS, Lassosum and PRS-CS) require a ‘tuning sample’, a GWAS cohort with known trait status that is independent of both discovery and target samples, used to select parameters needed to generate the PGSs in the target sample. Whereas only GWAS summary statistics are needed for discovery samples, individual level genotype data are needed for tuning and target samples. Information about the LD structure is supplied by a reference data set of genome-wide genotypes which can be independently collected from the GWAS data, but from samples of matched ancestry.

Table 1.

Summary of methods used to generate PGS

Method	Distribution of SNP effects (β)	Tuning sample	Pre-defined parameters	Parameters estimated in tuning sample
PC+T	None	Yes	-	P value threshold
SBLUP	$\beta ~N(0,\frac{h_g^2}{m})$ $h_g^2$: SNP-based heritability, m: number of SNPs; $\lambda =m\left(1-h_g^2\right)/h_g^2$	No	λ LD radius in kb	-
Ldpred2-Inf	Same as SBLUP	No	$h_g^2$, LD radius in cM or kb	-
LDpred-funct	${\beta }_j~N\left(0,c{\sigma }_j^2\right)$ ${\sum }_{j=1}^M{1}_{{\sigma }_j^2>0}c{\sigma }_j^2=h_g^2,c$ is a normalizing constant ${\sigma }_j^2$ is the expected per SNP-heritability under the baseline-LD annotation model estimated by stratified LDSC from the discovery GWAS within LDpred-funct software	No	$h_g^2$, LD radius in number of SNPs	-
LDpred2	${\beta }_j~\{\begin{array}{c}N\left(0,\frac{h_g^2}{\pi m}\right),\text{with}\text{probability}\text{of}\pi \\ 0,\text{with}\text{probability}\text{of}1-\pi \end{array}$ When sparsity is “true” the βj for the SNPs is the (1-π) partition are all set to zero.	Yes	$h_g^2$, π software default values, LD radius in cM or kb	π, sparsity
Lassosum	$f(\mathbf{\beta })={\mathbf{y}}^{\text{T}}\mathbf{y}+(1-s){\mathbf{\beta }}^{\text{T}}{\mathbf{X}}_{\text{r}}^{\text{T}}{\mathbf{X}}_{\mathbf{r}}\mathbf{\beta }-2{\mathbf{\beta }}^{\text{T}}{\mathbf{X}}^{\text{T}}\mathbf{y}+\mathbf{s}{\mathbf{\beta }}^{\text{T}}\mathbf{\beta }+2\lambda \Vert \beta {\Vert }_1^1$ Xr: genotype of LD reference	Yes	LD Blocks	λ, s
PRS-CS	${\beta }_j~N\left(0,\frac{{\sigma }^2}{n}{\psi }_j\right)$ ψj~G(a, δj) δj~G (b,ϕ), ϕ is a global scaling parameter. n is sample size	Yes	a=1, b=0.5 Sample size LD Blocks	ϕ
PRS-CS-auto	Same as PRS-CS, but estimates ϕ from the discovery GWAS.	No	a=1, b=0.5 Sample size LD Blocks	-
SBayesR	${\beta }_j\mid \pi ,{\sigma }_{\beta }^2~\{\begin{array}{cc}\hfill 0,& \text{with}\text{probability}\text{of}{\pi }_1\hfill \\ \hfill N\left(0,{\gamma }_2{\sigma }_{\beta }^2\right),& \text{with}\text{probability}\text{of}{\pi }_2\hfill \\ & ⋮\\ \hfill N\left(0,{\gamma }_c{\sigma }_{\beta }^2\right),& \text{with}\text{probability}\text{of}1-{\sum }_{c=1}^{C-1}{\pi }_c\hfill \end{array}$ ${\sigma }_{\beta }^2~Inv-{\chi }^2(d.f.=4)$ πi ~ Dir(1), estimated from discovery GWAS in SBayesR software γi are scaling parameters	No	LD radius in cM or kb, C = 4, γ software default values	-
MegaPRS	Lasso: βj~DE (λ/σj) Ridge regression: ${\beta }_j~N\left(0,v{\sigma }_j^2\right)$ $\text{BOLT-LMM:}{\beta }_j~\{\begin{array}{c}N\left(0,\left(1-f_2\right)/\pi {\sigma }_j^2\right),\text{with}\text{probability}\text{of}\pi \\ N\left(0,\left(f_2\right)/(1-\pi ){\sigma }_j^2\right),\text{with}\text{probability}\text{of}1-\pi \end{array}$ f2 is the proportion of the total mixture variance in the second normal distribution. BayesR: similar to SBayesR with C=4, and πi and γi estimated in the tuning sample ${\sigma }_j^2$ is the expected per SNP-heritability under BLD-LDAK model using SumHer	Yes	LD radius in cM or kb, Parameters used in BLD-LDAK, Grid search parameter values for each method	The tuning cohort is used to estimate the parameters that maximize prediction for each model, and from these the model that maximizes prediction is selected.

Distributions: N: normal distribution; G: gamma distribution; Inv − χ²: inverse chi-squared distribution, Dir: Dirichlet distribution; DE: Double exponential distribution; $\Vert \mathbf{\beta }{\Vert }_1^1={\sum }_i\left|{\beta }_i\right|$. When $h_g^2$ (SNP-based heritability) is a pre-defined parameter it is estimated from the discovery GWAS, where “discovery GWAS” is the genome-wide set of association statistics (SNP ID, reference allele, frequency of reference allele, association effect size for reference allele, standard error of effect size, association p-value, sample size). We use bold for matrix notation and italics for scalar notation. cM: centimorgan; kb: kilobase pair

Briefly, PC+T (P-value based clumping and thresholding, also known as the P+T or C+T method) uses the GWAS effect size estimates as SNP weights and includes independent SNPs (defined by an LD r² filter for a given chromosomal window distance) with association P-values lower than a threshold (chosen after application in a tuning sample). PC+T is the most commonly used and basic method, and so is the benchmark method here. The other methods assume either that all SNPs have an effect size drawn from a normal distribution (SBLUP and LDpred2-Inf) or that SNP effects are drawn from mixtures of distributions with the key parameters defining these architectures estimated through Bayesian frameworks (LDpred2, PRS-CS, SBayesR). LDpred-funct and MegaPRS include functional annotation to SNPs to up/down weight their contributions to the PGSs, which could improve prediction accuracy if this functional information helps to better separate true and false positive associations(21). The MegaPRS software implements a suite of methods (Table 1) and selects the method, together with its parameter estimates, that maximises prediction in the tuning cohort. MegaPRS utilises the BLD-LDAK model(22) where the variance explained by each SNP depends on its allele frequency, LD and functional annotations. Notably, some methods (SBayesR, PRS-CS-auto and LDpred2-auto) do not require a tuning cohort, so that the SNPs selected and their weights reflect only the properties of the discovery sample. Since LDpred2-auto is shown to perform similarly to LDpred2, we do not include it in comparisons made here. We apply these methods to data from the Psychiatric Genomics Consortium (PGC) working groups for schizophrenia (SCZ)(23, 24) and major depressive disorder (MDD)(12, 25, 26) (Tables S1 and S2). We select SCZ and MDD to study as they have the largest GWAS samples for psychiatric disorders to date but are diverse in lifetime risk, and are representative of psychiatric disorders which have all been shown to be highly polygenic (27). The PGC provides a useful resource for undertaking this study because it brings together many independently collected cohorts for GWAS meta-analysis. This allows the application of repeated leave-one-cohort-out GWAS analyses generating robust conclusions from evaluation of PGS applied across multiple left-out target cohorts.

Materials and Methods

Data

All samples were of European ancestry with full details in the Supplementary Note, Table S1 and S2. Briefly, GWAS summary statistics were available from PGC SCZ for 37 European ancestry cohorts (24) (31K SCZ cases and 41K controls) of which 34 had individual level data available. PGS were calculated in each of the 30 cohorts (target samples) using the GWAS discovery sample based on a meta-analysis of 37–2 = 35 cohorts (24) i.e., the target sample was excluded from the discovery sample as well as a sample selected to be a tuning sample. Analyses were repeated using four different tuning samples, two of which were large (swe6:2313; gras: 2318) and two were small (lie2:406; msaf:466). Similarly, GWAS MDD summary statistics were available from 248K cases and 563K controls(25), which included data from the 26 cohorts from PGC MDD with individual level data (15K cases and 24K controls). We left one cohort out of those 26 cohorts in turn as the target sample, and then used a meta-analysis of remaining data as discovery samples. A cohort(25), not included in the discovery GWAS was used as the tuning sample (N=1,679).

Baseline SNP selection

For baseline analyses, only SNPs with minor allele frequency (MAF) > 0.1 and imputation INFO score > 0.9 (converted to best-guess genotype values of 0, 1 or 2) were selected. Sensitivity analyses relaxed the MAF threshold to MAF > 0.05 or 0.01 and INFO score threshold to 0.3. All methods were conducted using HapMap3 SNPs, except the method PC+T, which was conducted based on all imputed SNPs (8M in SCZ, and 13M in MDD).

Prediction methods

We define a PGS of an individual, j, as a weighted sum of SNP allele counts: ${\sum }_{i=1}^m{\widehat{b}}_i{x}_{ij}$, where m is the number of SNPs included in the predictor, ${\widehat{b}}_i$ is the per allele weight for the SNP, x_ij is a count of the number (0, 1, or 2) of trait-associated alleles of SNP i in individual j. We compared ten risk prediction methods, described in the Supplemental Note and summarized in Table 1. The methods differ in terms of the SNPs selected for inclusion in the predictor and the ${\widehat{b}}_i$ values assigned to the SNPs. All methods use the GWAS summary statistics as the starting point, but each makes choices differently for which SNPs to include and for the ${\widehat{b}}_i$ values to assign. Some methods use a tuning cohort; parameter estimates that maximize prediction in that tuning cohort are selected for application in the target sample. Several methods employ an LD reference sample to infer the expected correlation structure between SNP association statistics, those recommended by each software implementation are used.

Evaluation of out-of-sample prediction

The accuracy of prediction in each target cohort was quantified by 1) Area under the receiver operator characteristic curve (AUC; R library pROC(35)). AUC can be interpreted as a probability that a case ranks higher than a control. 2) The proportion of variance on the liability scale explained by PGS(36). We used the population lifetime risk of SCZ and MDD as 1% and 15% respectively to convert the variance explained in a linear regression to the liability scale(25, 28, 37). 3) Odds ratio (OR) of tenth PGS decile relative to the first decile. 4) Odds ratio of tenth PGS decile relative to those ranked in the middle of the PGS distribution, which is calculated as the average of OR of tenth decile relative to fifth and sixth decile. 5) Standard deviation unit increase in cases. The PGS in each target cohort were scaled by standardising the PGS of controls and applying the standardisation to cases:$\frac{PG{S}_{case}-mean\left(PG{S}_{control}\right)}{SD\left(PG{S}_{control}\right)}$, where SD is standard deviation. This does not impact PGS evaluation statistics but simply means that PGS are in SD units for all cohorts. The regression analyses for evaluation statistics 2–4 include 6 ancestry principal components as covariates. These covariates are not included in the AUC model and the standard deviation unit increase in cases model (see Supplementary Note).

Results

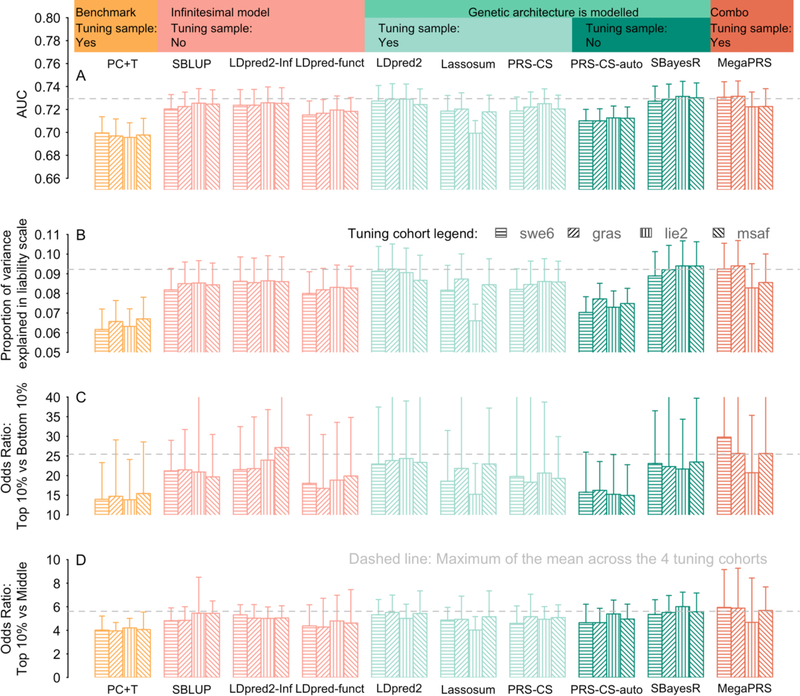
Prediction evaluation statistics based on all ten PGS methods and applied to SCZ across 30 study cohorts (Figure 1, Figure S1, Table S3 and S4), and to MDD across 26 cohorts (Figure S2, Table S5 and S6) are presented. There is variability in prediction statistics across target cohorts (as observed before(12, 28)) which is not a reflection of sample size (Figure S3 and Table S4 for SCZ, Figure S4 and Table S6 for MDD). Some significant associations were found from regression of prediction statistics on principal components (PCs) estimated from genome-wide SNPs (for SCZ Figure S3, but not MDD Figure S4), where the PCs capture both within-European ancestry and array differences between cohorts. The correlations of PGS between different methods are high (Table S7), but are lowest between PC+T and other methods (minimum 0.68). In contrast, the correlations between the other nine methods are always > 0.82. In theory, LDpred2-Inf and SBLUP are the same method. In practice, there are differences in implementation (e.g., different input parameters associated with definition of LD window) and although the correlation between their PGS is 0.974 the prediction accuracy is consistently higher for LDpred2-Inf. For SCZ, the AUC for all nine methods that directly model genetic architecture, other than PRS-CS-auto, are significantly higher than the PC+T method at the nominal level (Figure 1A). PGS from LDpred2, SBayesR and MegaPRS are significantly higher than the PC+T method after Bonferroni correction (p-value < 0.0011=0.05/45 (45 pairwise comparisons between 10 methods), one-tailed Student’s t-test). For MDD none of the differences between methods were significant (Figure S2A). For both SCZ and MDD across all statistics, regardless of tuning cohorts, LDpred2, SBayesR and MegaPRS, show relatively better performance (median across target cohorts) than other methods, although there is no significant difference between the nine methods that directly model genetic architecture. For variance explained on the liability scale, the PC+T PGS explained 6.4% for SCZ, averaged over the median values across the four tuning cohorts (Figure 1B), while it was 8.9%, 9.0%, and 9.2% for MegaPRS, LDpred2, and SBayesR, corresponding to an increase of 39%, 41% and 44%, respectively. For MDD although the variance explained is lower in absolute terms, 2.2% for PC+T vs 3.4% for MegaPRS, 3.5% for LDpred2 and 3.5% for SBayesR; the latter represents a 59% increase (Figure S2B).

Figure 1. Prediction results for SCZ case/control status using different PGS methods.

The PGS were constructed from SCZ GWAS summary statistics excluding the target cohort and a tuning cohort (shading legend). Each bar reflects the median across 30 target cohorts, the whiskers show the 95% confidence interval for comparing medians. The area under curve (AUC) statistic (A) can be interpreted as the probability that a case ranks higher than a control. Panel (B) is the proportion of variance explained by PGS on the scale of liability, assuming a population lifetime risk of 1%. The third panel (C) is the odds ratio when considering the odds of being a case comparing the top 10% vs bottom 10% of PGS. The bottom panel (D) is the odds of being a case in the top 10% of PGS vs odds of being a case in the middle of the PGS distribution. The middle was calculated as the averaged odds ratio of the top 10% ranked on PGS relative to the 5th decile and 6th decile. PC+T (also known as P+T) is the benchmark method which is shown in orange. Pink shows the methods that use an infinitesimal model assumption. The green shows the methods that model the genetic architecture, with light green for the methods using a tuning cohort to determine the genetic architecture of a trait; dark green shows the methods learning the genetic architecture from discovery sample, without using a tuning cohort. Dark orange is for MegaPRS using the BLD-LDAK model that assume the distribution of SNP effect depends on its allele frequency, LD and function annotation. MegaPRS assign four priors to each of SNP: LASSO, Bridge, BOLT-LMM, BayesR. Each prior has different hyperparameters that identified using the tuning cohort. The dashed grey lines are the maximum of the average across the four tuning cohorts. The sample sizes of the tuning cohorts are swe6: 1094 cases,1219 controls; lie2: 137 cases, 269 controls; msaf: 327 cases, 139 controls; gras: 1086 cases, 1232 controls.

We provide several evaluation statistics that focus on those in the top 10% of PGS, because clinical utility of PGS for psychiatric disorders is likely to focus on individuals that are in the top tail of the distribution of predicted genetic risk. The odds ratio for top vs bottom decile are large, ranging from 14 for PC+T to 30 for MegaPRS for SCZ and 3 for PC+T to 3.7 for SBayesR for MDD. While these top vs bottom decile odds ratios (Figure 1C and S2C) are much larger than the odds ratio obtained by using PGS to screen a general population (Figure 1D and 2D) or patients in a healthcare system to identify people at high risk(38, 39), these comparisons are useful for research purposes, which could, for example, make cost-effective experimental designs focussing on individuals with high vs low PGS(40). The odds ratio of top 10% vs middle 10% are much less impressive, up to median of 6 for SCZ and 2 for MDD, but more fairly represents the value of PGS in population settings. These values can be benchmarked against risk in 1^st degree relatives of those affected, which are of the order of 8 for SCZ and 2 for MDD; low values are always expected for MDD because it is more common (lifetime risk ~15% compared to ~1% for SCZ). The odds ratio values are particularly high for some cohorts (Table S4), because in some SCZ cohorts the bottom 10% include very few or no cases, especially in cohorts with relatively small sample sizes.

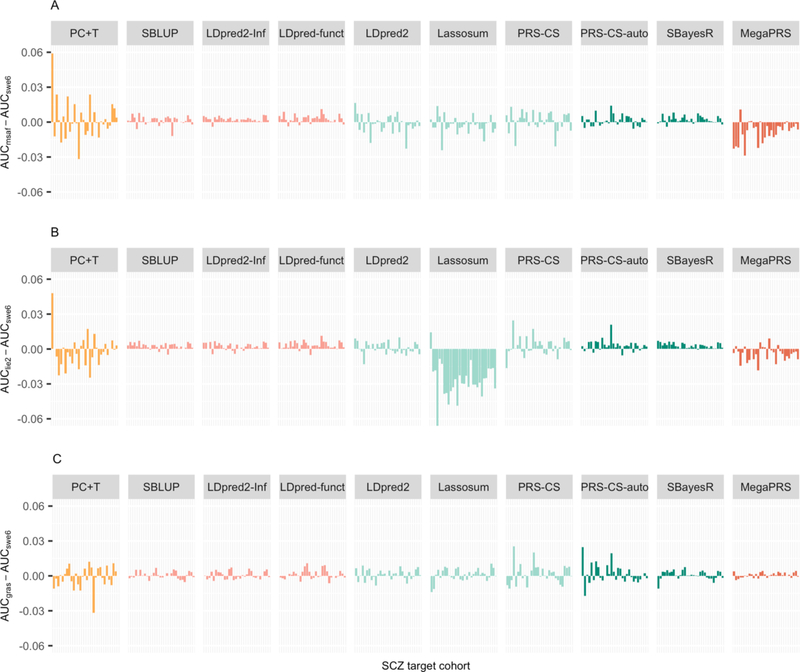
Figure 2. Sensitivity analyses using different tuning cohorts comparing different PGS methods.

Differences in the AUC of SCZ of a PGS method when using different tuning cohorts. The different bars in each method (x-axis) refer to different validation cohorts ordered by sample size. The y-axis is the AUC difference when using alternative tuning cohort (i.e. lie2 (137 cases, 269 controls), msaf (327 cases, 139 controls), or gras (1086 cases, 1232 controls)), compared to ‘swe6’ (1094 cases, 1219 controls). The MAF QC threshold is 0.1. Note: SBLUP, LDpred2-Inf and LDpred-funct, PRS-CS-auto and SBayesR do not need a tuning cohort, but serve as a benchmark to the other methods which need a tuning cohort. These methods differ when a different tuning cohort is left out because the discovery GWAS also changes.

The impact of tuning cohort.

Five methods (i.e., PC+T, LDpred2, Lassosum, PRC-CS, and MegaPRS) use tuning cohorts to determine key parameters for application of the method into the target cohorts. Tuning parameters impact results in two ways. First, the parameters may be dependent on the choice of tuning cohort. Second, the discovery GWAS sample may be reduced in size (and hence power) if a tuning cohort needs to be excluded from the discovery GWAS. In all our analyses the tuning cohort is excluded from all GWAS discovery samples so that GWAS discovery sample is not variable across methods for each target cohort. Our results show that the tuning cohort can have considerable impact (Figures 1, 2). In our results, the tuning cohort that generates higher PGS is method dependent and differs between cohorts. For the methods that use tuning samples, the larger tuning samples (swe6 and gras) mostly generate higher prediction statistics compared to the two smaller tuning samples (lie and msaf), but the differences are not statistically significant. Although methods SBLUP, LDpred2-Inf, LDpred-funct, PRS-CS-auto and SBayesR require no tuning cohort, they serve as a benchmark, since the differences in their results reflect differences in the changed discovery samples (e.g., msaf is in the discovery sample, when swe6 is the tuning cohort, and vice versa), as well as the stochasticity inherent in the Gibbs sampling of Bayesian methods.

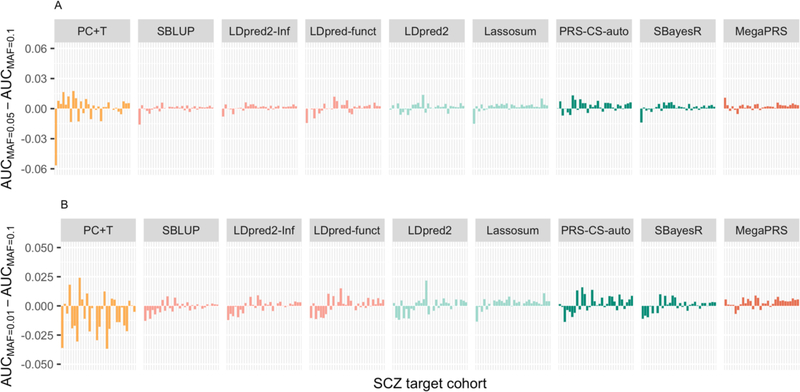
The impact of MAF/INFO threshold.

A MAF threshold of 0.1 and a INFO threshold of 0.9 are used to be consistent with applications in the PGC SCZ(28) and PGC MDD(25) studies, which had been imposed recognising that these thresholds generated more robust PGS results than using lower threshold values. In the second sensitivity analysis applied to the SCZ data, the MAF threshold was relaxed to 0.05 or 0.01 (Figure 3). The prediction evaluation statistics increase for some cohorts and decrease for others (trends with sample size were not significant). PC+T is more impacted that the other nine methods. Across target cohorts, different evaluation statistics were almost identical when including less common SNPs (Table S3). Relaxing the INFO score to 0.3 has a negligible effect (Figure S5).

Figure 3. Sensitivity analyses using different MAF quality control thresholds.

Differences in AUC of SCZ of a PGS method when using different MAF QC thresholds. The different bars in each method (x-axis) refer to different validation cohorts ordered by sample size. The y-axis is the AUC difference between analyses using A) MAF<0.05 and MAF <0.1 B) MAF<0.01 and MAF <0.1 as a QC threshold. The tuning cohort is ‘swe6’.

Discussion

Comparison of PGS risk prediction methods showed that all nine methods that directly model genetic architecture had higher prediction evaluation statistics over the benchmark PC+T method for SCZ and MDD. While the differences between these nine methods were small, we found that MegaPRS, LDpred2, and SBayesR consistently ranked highest. Given that the PGS is a sum of many small effects, a normal distribution of PGS in a population is expected (and observed Figures S6–9). In idealised data, such as the relatively simple simulation scenarios usually considered in method development, all evaluation statistics should rank the same, but with real data sets this is not guaranteed. This is the motivation for considering a range of evaluation statistics. Our focus on statistics for those in the top 10% of PGS is relevant to potential clinical utility. In the context of psychiatry, it is likely that this will focus on people presenting in a prodromal state with clinical symptoms that have not yet specific to a diagnosis(11, 41). High PGS in those presenting to clinics could help contribute to clinical decision-making identifying individuals for closer monitoring or earlier intervention. Since a genetic-based predictor only predicts part of the risk of disease, and since a PGS only predicts part of the genetic contribution to disease it is acknowledged that PGS cannot be fully accurate predictors. Hence, the discriminative ability of PGS is low in the general population and the use of PGS in clinical settings requires evaluation including related ethical issues (42). Nonetheless, PGS, in combination with clinical risk factors, could make a useful contribution to risk prediction(41, 43, 44).

In sensitivity analyses that used different quality criteria for SNPs, e.g. MAF of 0.01 vs 0.05, INFO of 0.3 vs 0.9, we concluded that, currently, there is little to be gained in PGS from including SNPs with MAF < 0.10 and INFO < 0.9 for the diseases/dataset studied (Table S8 and S9). This result may seem counter-intuitive since variants with low MAF are expected to play an important role in common disease, and some may be expected to have larger effect sizes than more common variants(45, 46). However, sampling variance is a function of allele frequency (≈ var (y)/ (2*MAF (1-MAF)*n)), where y is the phenotype and n is sample size), such that a variant of MAF =0.01 has sampling variance 9 times greater than a variant of MAF=0.1. Moreover, in real data sets small sample size of contributing cohorts mean that technical artefacts can accumulate to increase error in effect size estimates particularly of low frequency variants. Our conclusion that little is gained from including variants of MAF < 0.1 and reducing INFO threshold needs to be revisited as larger individual cohorts in discovery samples and larger target cohorts accumulate. Moreover, our comparison of methods uses only study samples of European ancestry. More research and data are needed to understand the properties of prediction methods within other ancestries and across ancestries, given potential differences in genetic architectures (in terms of number, frequencies and effect sizes of causal variants) and LD between measured variants and causal variants(47, 48).

For both SCZ and MDD, while the methods other than PC+T had similar performance, LDpred2, MegaPRS, and SBayesR saw the highest prediction accuracy in most of the comparisons. We note that we did not consider a version of PC+T that has been shown to have higher out of sample prediction compared to the standard implementation(13). This method conducts a grid search in a tuning cohort to determine LD r² and INFO score thresholds for SNPs as well as the P-value threshold. Since the optimum LD threshold is likely to vary across genomic regions, the grid search approach is less appealing than the methods which implicitly allow this to vary. A sensitivity analysis in which we varied the r² threshold in the PC+T showed only a small gain from optimising this (Table S10). LDpred2 has a version that does not require a tuning sample, LDpred2-auto, but the authors showed the two methods give similar results. SBayesR assumes that the SNP effects are drawn from a mixture of four distributions, which allows more flexibility in distributions of SNP effects by varying the proportion of SNPs in each distribution. Hence, SBayesR can fit essentially any underlying architecture in term of variance explained by each SNP so that the SBLUP, LDpred2-Inf and LDpred2 models are, in principle, special cases of the mixture model used in the SBayesR (although method implementations are different). In addition to traits with a highly polygenic genetic architecture, we have recently shown that SBayesR outperforms other methods for two less polygenic diseases, Alzheimer’s disease (49) (which includes the APOE locus which has a very large effect size) and amyotrophic lateral sclerosis (50) (for which there is evidence of greater importance of low MAF variants compared to SCZ(51)). The original SBayesR publication showed that in both simulations and applications to real data, the method performed well across a range of traits with different underlying genetic architectures. MegaPRS uses four different priors for the distribution of SNP effect, i.e. Lasso, Ridge, BOLT-LMM, and BayesR (Table 1). It rescales SNP effects based on each of those priors and for each method selects the combination of parameters that maximises prediction in the tuning sample and then selects the best method amongst these. Hence, MegaPRS is a collection of the other methods and the SNP distribution selected varies depending on both tuning and target (Table S11). It selects BayesR 87% of the time when the tuning samples were large (otherwise BOLT-LMM) and selects Lasso 78% of the time when tuning samples were small. We implemented MegaPRS using the BLD-LDAK model recommended by the authors which assumes that the distribution of SNP effects depend on its allele frequency and functional annotation. While adding functional annotation to up or down weight SNPs is appealing, in practice there seemed to be no advantage in MegaPRS compared to LDpred2 and SBayesR that did not use functional annotations. Surprisingly, LDpred-funct method performed consistently less well than LDpred2-Inf, but this should be revisited as currently LDpred-funct is only available as a preprint (16).

Another study has compared 8 PGS methods for 8 disease/disorder traits (including MDD) and 3 continuous phenotypes comparing methods in two large community samples, the UK Biobank and the Twins Early Development Study (52). Consistent with our results, SBayesR attained a high prediction accuracy for MDD although they reported performance of SBayesR varied across traits. Since SBayesR expects effect size estimates and their standard errors to have properties consistent with the sample size and with the LD patterns imposed from an external reference panel, if GWAS summary statistics have non-ideal properties (perhaps resulting from meta-analysis errors or approximations) then SBayesR may not achieve converged solutions. SBayesR, in general, is more sensitive to any inconsistent properties between GWAS and LD reference samples than those methods that select hyperparameters based on cross-validation in a tuning sample, such as LDpred2 (15). We note that the LDpred-funct preprint reported SBayesR to perform well across a range of quantitative and binary traits. A key advantage of SBayesR is that there is no need for the user to tune or select model or software parameters. Moreover, it does not need a tuning cohort to derive SNP effect weights but learns the genetic architecture from the properties of the GWAS results. Computationally it is also very efficient, using one CPU, it takes approximately 2 hours to generate SNP weights based on each discovery sample and predict into the left-out-cohort using a MCMC chain of 10,000 iterations (the computing time can be reduced by running a shorter chain since a negligible change in prediction accuracy was found after 4,000 iterations), which compares to PRS-CS: 40 hours using 5 CPUs, LDpred2: 5 hours using 15 CPUs, MegaPRS: 1 hours using 5 CPUs. Last, given that SBayesR uses only HapMap3 SNPs that are mostly well-imputed it should be possible to provide these SBayesR SNP weights as part of a GWAS pipeline to apply in external target samples.

All methods are compared using their default parameters settings. An optimum setting of each method could potentially increase the prediction accuracy. Most likely the optimum parameter settings are trait (genetic architecture) dependent(13). Here, we find that all methods that more formally model the genetic architecture than PC+T perform better than the PC+T, but there is little to choose between those methods. For application in psychiatric disorders, which are all highly polygenic traits, we particularly recommend LDpred2, MegaPRS and SBayesR which consistently rank high in all comparisons.