Abstract
Respiratory illness is the primary cause of mortality and impairment in the life span of an individual in the current COVID–19 pandemic scenario. The inability to inhale and exhale is one of the difficult conditions for a person suffering from respiratory disorders. Unfortunately, the diagnosis of respiratory disorders with the presently available imaging and auditory screening modalities are sub-optimal and the accuracy of diagnosis varies with different medical experts. At present, deep neural nets demand a massive amount of data suitable for precise models. In reality, the respiratory data set is quite limited, and therefore, data augmentation (DA) is employed to enlarge the data set. In this study, conditional generative adversarial networks (cGAN) based DA is utilized for synthetic generation of signals. The publicly available repository such as ICBHI 2017 challenge, RALE and Think Labs Lung Sounds Library are considered for classifying the respiratory signals. To assess the efficacy of the artificially created signals by the DA approach, similarity measures are calculated between original and augmented signals. After that, to quantify the performance of augmentation in classification, scalogram representation of generated signals are fed as input to different pre-trained deep learning architectures viz Alexnet, GoogLeNet and ResNet-50. The experimental results are computed and performance results are compared with existing classical approaches of augmentation. The research findings conclude that the proposed cGAN method of augmentation provides better accuracy of 92.50% and 92.68%, respectively for both the two data sets using ResNet 50 model.
Keywords: Respiratory signals, Data augmentation, Conditional generative adversarial networks, Correlation metrics, Deep convolutional neural networks
1. Introduction
Respiratory-allied infections, such as Chronic Obstructive pulmonary diseases (COPD), acute bronchitis, emphysema and bronchopneumonia are the major causes of mortality in the world [1]. Several pulmonary function tests such as auscultation, spirometry and arterial blood gas test exist in practice. Auscultation is predominantly followed for all patients and the process is economical and provides a non-intrusive method of screening. Additionally, depending on the patient's needs, spirometry is used and it involves Forced Oscillation Technique (FOT). FOT measures the air pressure and flow and helps in estimating the respiratory impedance. Several studies in literature [[2], [3], [4]] proved better results using the respiratory impedance measurement for asthma and COPD patients. However, the auscultation method is simple, patient friendly and easier to obtain data than spirometry or radiation imaging [5]. Lung sound signals are typically classified as normal and abnormal. Normal breath sounds are heard over the chest wall or trachea. Abnormal sound signals are additional lung sounds superimposed on normal breath sounds. Both normal and abnormal sound signals vary in frequency. For instance, the frequency range of the normal breathing sounds extends up to 1000 Hz, wherein the majority of the power in this range is found between 60 Hz and 600 Hz. Abnormal sounds, such as wheezing or crackles appears at frequencies beyond 700 Hz to 2000 Hz.
Even though the investigation procedure using stethoscope is effortless, abrupt pandemic outbreak such as COVID-19 intensify the infections and the abnormal sounds observed has reliable distributive features [6]. Multiple scientific studies show that patients with chronic respiratory disorders have around 5.97–fold higher risk of getting infected with COVID-19 [7]. World health organization [WHO] report recommends that the doctor-patient proportion need to be 1:1000. In India, with the estimated 1.38 billion population, there is one physician for every 1457 citizens which is comparatively lesser than WHO's standards [8]. For this reason, it is essential to devise a machine-driven model to assist and lessen the burden of medical experts in making accurate diagnosis of lung disorders.
In recent times, the European Union has recognized various directions of research in the field of pathogenic respiratory disorders [9]. Identification of lung disorders from lung sounds with the development of digital stethoscopes and based on algorithms plays a vital role in the active field of investigation [10,11]. Earlier research works concentrated on creation of features manually for classifying vesicular and abnormal lung sounds using conventional machine intelligence [12,13]. Lately, frameworks based on deep structured learning has drawn the attention in categorizing the disorders using various morphological features, 2D data and one dimensional vectors [14,15]. Generally, DNNs are highly data-intensive and often demand vast amount of data to produce positive outcomes. However, creating a qualitative data directory with annotation needs time. To meet the needs and enlarge the training samples, one possible approach is data augmentation (DA) [16] wherein different methods are involved to build a modern data set according to the existing dataset. Conventional DA techniques include, geometrical changes such as time and pitch shifting, time stretching and addition of noise to the actual data.
In literature, several efforts have been carried out for augmenting image database. Le Cun et al. [17] demonstrated the classification of handwritten characters using gradient based algorithms with Convolutional neural network (CNN) classifier. Krizhevsky et al. [18], exploited few options of DA approach such as plane, patch and intensity level flipping in true color images on the ImageNet database. H.Inoue in 2018, introduced a novel method of DA, titled sample pairing [19], wherein new images are generated by superimposing two different images in random manner. Chawla et al. [20] suggested an over-sampling methodology on the mammography dataset which comprises of vast number of normal sample images and limited number of abnormal images.
Besides medical imaging, in the past few years, DA approaches have been the target in signal processing fields and obtained global attention in achieving significant improvement in performance especially for physiological signals. Several authors experimented DA techniques using noise in different data sets such as EEG, EMG and sEMG and evaluated the models using CNN [[21], [22], [23], [24]]. To expand the atrial fibrillation database, Ping Cao et al. [25] proposed a modern DA approach wherein electrocardiogram (ECG) episodes are augmented on the base of replication, chaining and resampling. Furthermore, to produce stable predictions, DA techniques have been experimented in many other fields such as acoustic environments, speech recognition and body worn sensor data. The authors [[26], [27], [28], [29]] explored DA techniques in the speech repository, auditory signals and sensor based models and classified enhanced data set using CNN with good accuracy.
Besides the conventional methods, presently, GANs are envisioned to be promising for DA when dealt with image and time sequence data. In Ref. [30], the authors utilized recurrent GANs for creating naturalistic actual–valued health care data. In Ref. [31], the authors experimented GANs using LSTM and Bi-LSTM on MIT-BIH Arrhythmia Database for generating sinusoidal waves and ECG signals and proved promising outcomes. Pedro Narvaez et al. employed GAN to produce normal heart signals and evaluated the framework using machine learning models [32]. Yi Ma et al. [33] proposed LungRN + NL ResNet network for classifying lung sounds and utilized mix up augmentation method for enhancing only the abnormal data set. Yang et al. [34] Introduced special attention mechanisms for categorizing lung sounds using residual networks and achieved 54.14% average score. Koki Minami et al. [35] utilized wavelet and STFT for representing 1D signals as images to classify respiratory data set using CNN with mix up augmentation method. In Ref. [36], the authors augmented COVID-19 data set and experimented with Data De-noising auto encoder and achieved 4% improvement in accuracy compared to conventional MFCC features. Lorris Nanni et al. [37] employed standard image and signal augmentation for training CNNs to classify animal audio data set.
As per research studies, though extensive studies have been carried out to generate artificial physiological signals such as ECG and EEG, only brief work has been realized for respiratory datasets. The motivation of the present study is to develop a competent Artificial intelligence model that can assist the physician and serve as an efficient decision-making tool to ascertain the respiratory disorder identified and strengthen the diagnosis and subsequent treatment of the patients. As the respiratory signal dataset required for training the deep learning algorithms is available only in limited numbers in publicly available datasets, the accuracy of prediction of the lung disorders through deep learning algorithms is poor. Hence in this work, the existing respiratory signal data set is expanded using Conditional GAN and deep learning algorithms are trained with original and mimicked data for respiratory signal classification. The rest of the paper is organized as follows: Section 2 focuses on materials and methods used for synthetic generation of respiratory signals. Section 3 discusses about the different evaluation metrics and experimental results based on correlation and classifier performance. Finally, Section 4 concludes the outcomes of data augmentation method studied in predictive modeling of lung sound signals.
2. Materials and methods
ICBHI challenge dataset [38], a well–known lung sound dataset is employed in this study of research. Two groups of research teams collected these audio files from the General Hospital, Greece and Hospital Infante D. Pedro, Portugal. This freely accessible repository for respiratory sounds is acquired from 126 patients and it contains 6898 respiratory cycle patterns which were marked up as normal, crackles and wheezes. Crackles are disrupted and atonal sounds which lies in the frequency range between 100 Hz and 2 KHz and stretch out to less than 25 ms. In addition to frequency, one of the sound characteristics that can be used to distinguish two analogous sound is pitch with two variants viz. high pitched and low pitched. Wheezes are continuous high-pitched harmonious sounds resulting from circulation of air through confined air ducts and varies with the frequency of >400 Hz. The other sound with similar pathological characteristics as wheeze is rhonchi which is low pitched musical tones having the frequency of <200 Hz. The collected files ranges from 10 s to 90 s and recorded using different stethoscope such as LittC2SE, Litt3200 and Meditron from various chest locations. On the whole, the original data base consists of 509 lung sound signals in which 73 signals corresponds to normal class, 281 audio signals are crackles, 122 files are wheezes and the 33 are low pitched wheezes namely rhonchi.
To provide a more generalized high-performance model, in addition to ICBHI 2017 challenge data set, the experimentation is carried out with other respiratory publicly available data sets such as RALE (Respiration acoustics Laboratory Environment) [39] and Think labs Lung sound library [40]. This comprises of 137 audio files, of which, 32 belongs to normal class, 32 files are crackles, 30 corresponds to low pitched wheezes namely rhonchi and 43 belongs to wheezes. These data sets are considered to be relatively small for training DNN. Therefore, the core concentration of this work is to build an augmented data base using conditional Generative adversarial networks (cGAN). A comparative study is also carried out to find the best augmentation approach relevant to the lung sound data base.
2.1. Conditional GAN based augmentation for generating synthetic biomedical signals
In this section, conditional GAN (cGAN) method of DA is used to create augmented data set that mimics actual input data. In cGAN, two networks viz. generator (G) and discriminator (D) are involved in the training process. Both these networks mutually act as challengers in synthetic generation of signals. In other words, the networks play the min-max game and the mathematical equation [41] for the discriminator loss (L) function is given b0y,
| (1) |
| (2) |
where in the above equation signifies the probability that the original data is predicted by the network, denotes the input of random variables from the network. As the role of discriminator is to precisely categorize real and fake samples, the final loss function of discriminator is given by combining and maximizing the above equations.
| (3) |
In contrary to the discriminator, the generator loss function is minimized and given by,
| (4) |
Taking into account the entire database, the value function is given by,
| (5) |
Where.
denotes the original data distribution,
represents the distribution of data from the generator,
represents the expected value over all real (original) data instances and
represents the expected value over all random inputs i.e. fake data to the generator
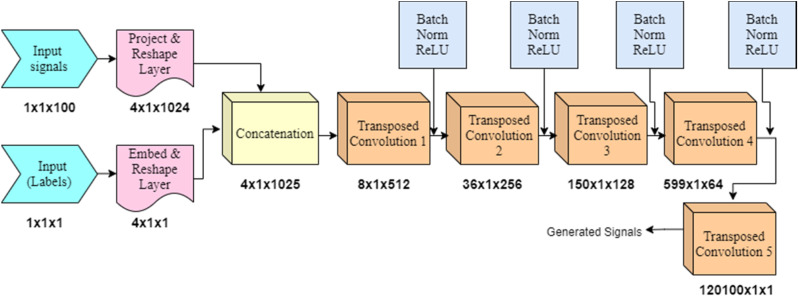
The generator network is fed with input containing arbitrary noise. In the generator network, the series of transposed convolutional layers up-samples the input feature vectors. A series of transposed convolutional layers are used with different number of channels such as 512, 256, 128 and 64. The architecture of generator network is shown in Fig. 1 . The dimensions of the signal feature vector are represented under the blocks at each stage. This model produces samples in the similar form as the input data analogous to the same tag.
Fig. 1.
Generator network architecture.
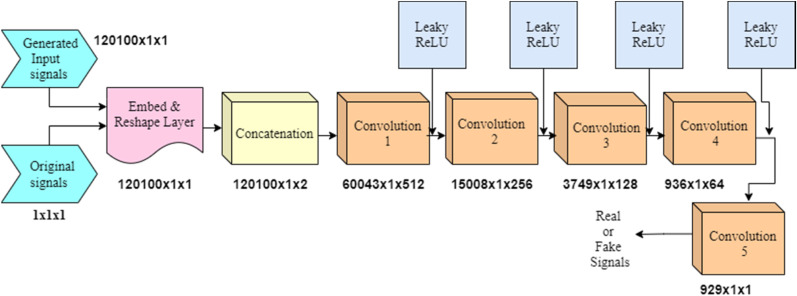
Subsequently, the array of labeled audio set comprising of both original samples and generated ones are fed to the discriminator network which is shown in Fig. 2 . This network uses series of convolution layers and tries to sort the samples as “actual” or “created” from the given batch of input samples. The values given below the blocks represent the dimensions of signal feature vectors reduced at each stage of the convolutional layers with 512, 256, 128 and 64 length filters.
Fig. 2.
Discriminator network architecture.
Similar to traditional augmentation techniques, the respiratory signals are generated synthetically using conditional GANs. The cGAN model is trained with MATLAB 2020a using custom training. Followed by every loop, the parameters of the network are updated for each iteration. For our study, the cGAN is trained for different epochs namely, 25, 50, 75, 100, 200 and 300.
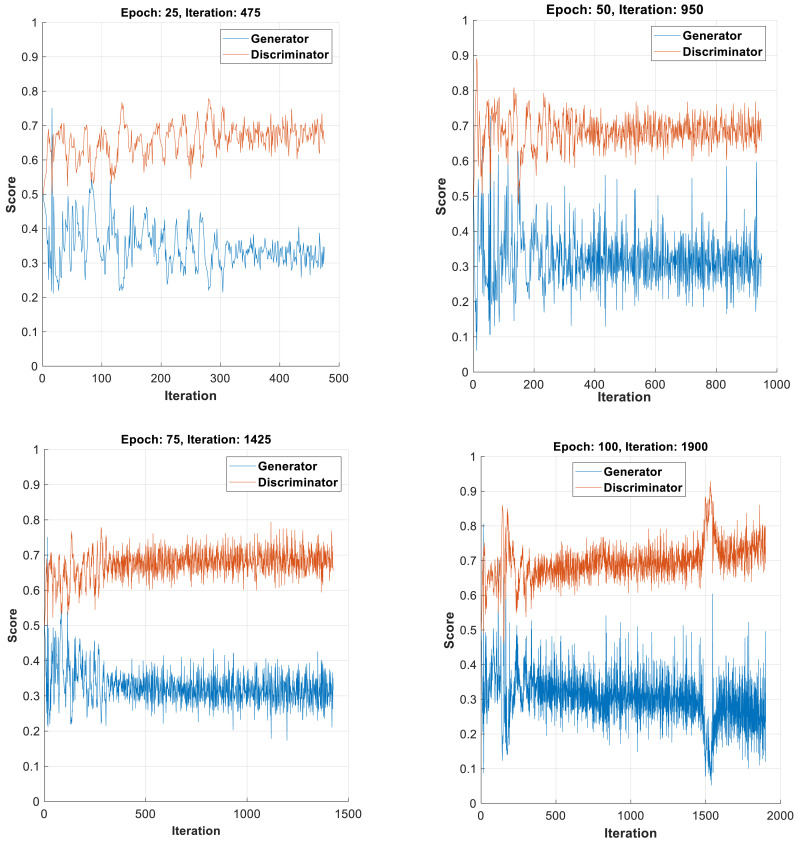
During the training phase, both the generator and discriminator networks challenge mutually to attain their targets and this can be visualized in the form of score plot with y-scale ranging from 0 to 1. The training plot of both networks for all classes of respiratory signals for different epochs are shown in Fig. 3 (a–d). For training, the network uses Adam optimizer with learning rate of 0.0002, gradient decay factor of 0.5 and mini batch size of 27. In all Fig. 3(a–d), the plot of the generator model oscillates over time which indicates that the generator produces same type of images leading to the concept of mode collapse. Hence, the iterations are increased to improve the potency of the generator network. On increasing the iterations from 25 in steps of 25, it is observed that at 100 epochs, the discriminator network overpowers the generator network and thereby categorizes majority of signals precisely. Therefore the process of training is paused with 100 epochs. On further increasing the epochs to 200 and 300, non-convergence between generator and discriminator curves was observed and the experimentation resulted in mode collapse and divergence. In addition, at epochs beyond 100, the augmented signals showed dissimilarity with the original signals. This lead to reduced classification performance with the CNN-LTSM classifier. As a result, the training was stopped at 100 epochs and this model was considered for testing.
Fig. 3.
(a–d): Training plots of Generator and Discriminator for different epochs.
3. Results and discussion
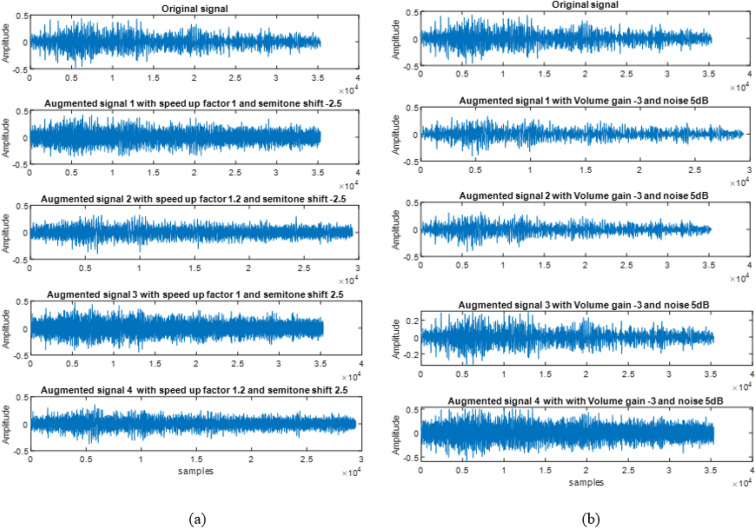
In this work, 1D GANs are implemented to enhance the lung signal data set. In addition, the scope for strengthening the performance of deep learning models in classifying the respiratory disorders with and without data augmentation are analyzed with various pre-trained models. Some of the samples of original and augmented signals for sequential and independent based categorical augmentation [16,37] are shown in Fig. 4 a and b. The augmented signals shown in Fig. 4a depends on the chosen parameter such as time stretching (1, 1.2) and pitch shift with semitone values (−2.5, 2.5).
Fig. 4.
Augmented signals of (a) Sequential [16] and (b) Independent Categorical Augmentation [37].
Similarly Fig. 4b illustrates the augmented signals for independent mode of augmentation. In this mode, the augmented signals does not depend on the value of chosen parameters such as volume gain control and noise. The subplot in Fig. 4b shows four different augmented signals with volume gain control value of −3 and noise of 5 dB.
3.1. Assessment of similarity using time and frequency domain metrics
In order to acquire greater understanding regarding the effect of augmentation on the performance of the model, it is extremely important to estimate the similarity and coherency in the energy distribution of both the original and augmented signals. To measure this, in this work, two phases of evaluation metrics are analyzed. The first phase includes metrics such as wavelet coherence and dynamic time warping. In the second phase, correlation values between the features of original and augmented signals are also observed. This includes Mel Frequency Cepstral coefficients (MFCC) and few spectral descriptors such as spectral entropy, skewness, kurtosis and spectral spread.
-
•
Wavelet Coherence (WC) is a metric used to observe the time frequency relationship between two time sequence signals namely original and augmented. This metric relies on continuous wavelet transform and illustrates alternating cross-correlations between two temporal signals. Wavelet coherence measure locates the portions of the signals represented in time frequency plane [42] with two conditions.
-
(i)
Two signals varying with same time period.
-
(ii)
Both signals not necessarily having high energy.
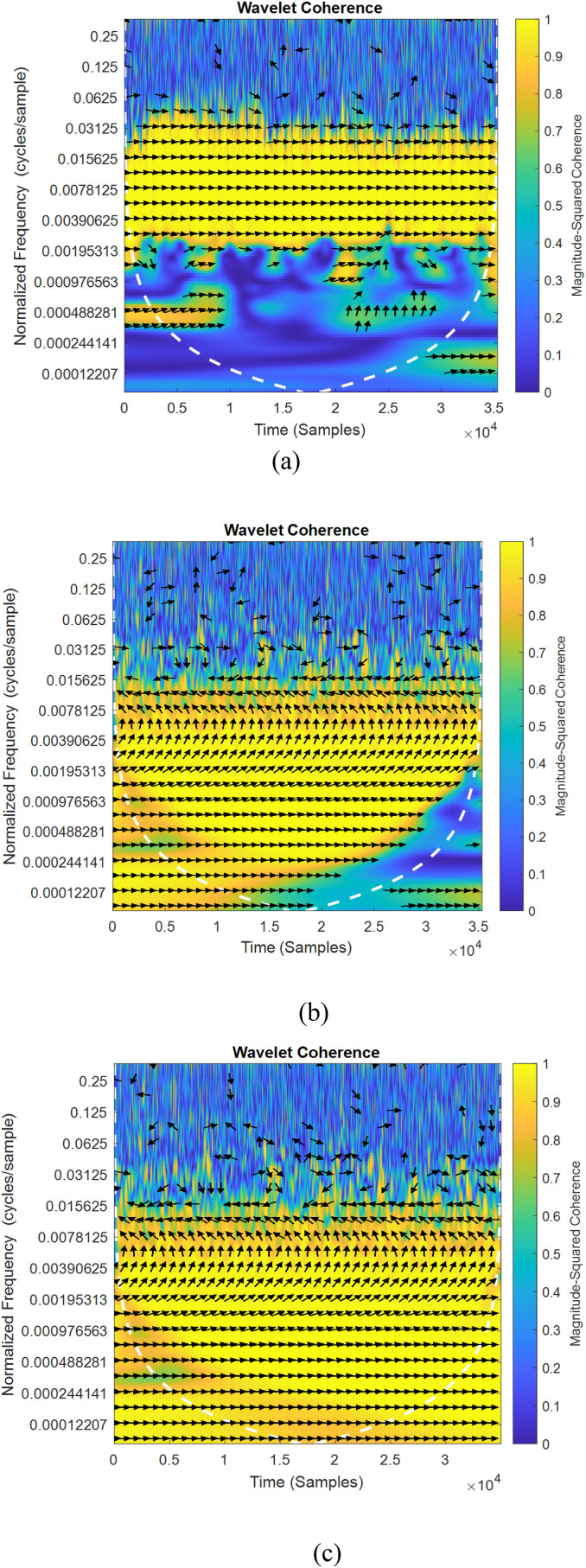
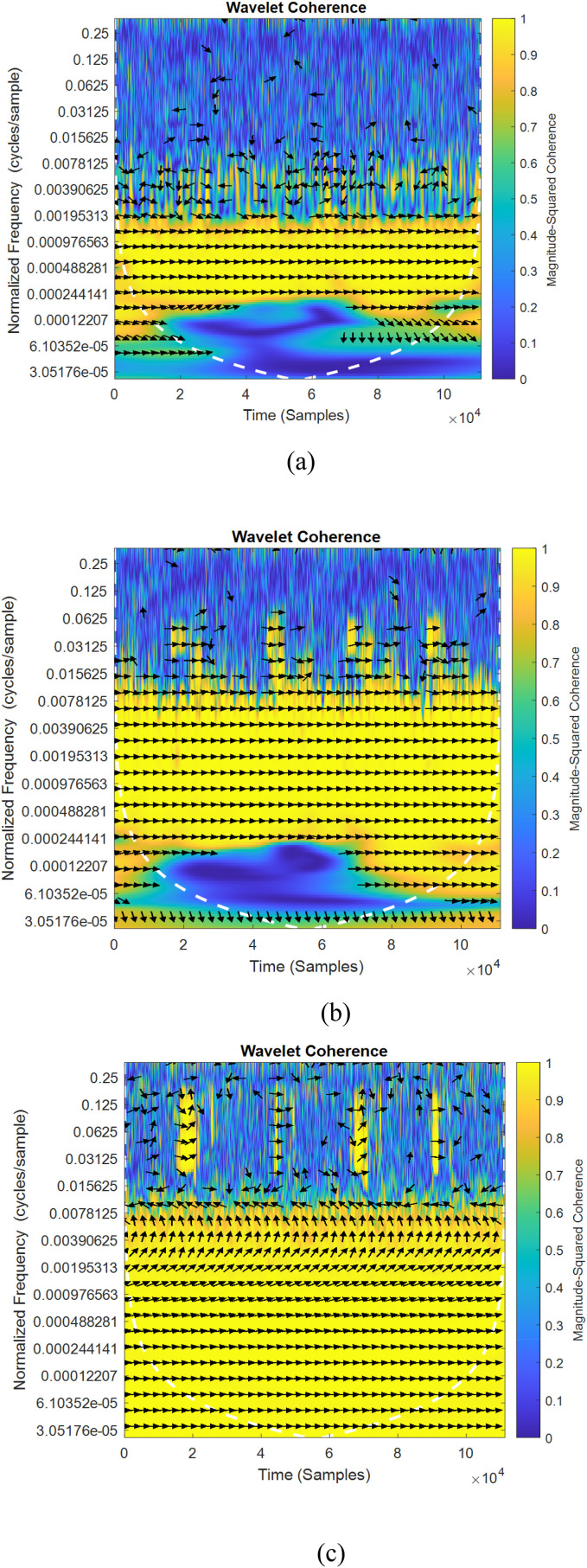
Fig. 5, Fig. 6 shows the sample of wavelet coherence similarity between original and augmented signals considering the existing two classical methods [16,37] and proposed method of data augmentation algorithms for normal and abnormal signals. The sampling frequency considered for the plot is 8000 Hz for normal signal and 11025 Hz for abnormal signal. In the figures, wavelet coherence is plotted in normalized frequency (cycles/samples) in y axis.
Fig. 5.
(a–c) and 6(a–c) Wavelet coherence similarity plots for normal and abnormal lung sounds (a) Sequential [16] (b) Independent [37] (c) cGan.
Fig. 6.
(a-c) Wavelet coherence similarity plots for normal and abnormal lung sounds (a) Sequential [16] (b) Independent [37] (c) cGan.
To specify the quantity of co-movements between signals, the value of coherency varies from yellow color (indicating greater value of coherency) to blue (lower value of coherency) color. The white traces drawn in dashed lines specifies the cone of influence. The portions represented in yellow indicates the meaningful correlation between two time series signal frequency components and their starting and trailing times. The in-phase behavior of both signals (i.e. arrow pointing to the right) in Fig. 5, Fig. 6 indicates that there is zero phase difference between the original and augmented signals. In all the depicted figures, it is observed that the yellow portion is varied for different methods of augmentation. It is also observed that, the maximum coherency is observed in Fig. 5, Fig. 6c which proves that conditional GAN augmented data resembles original signals much better and therefore can best be utilized for classification.
-
•
Dynamic Time Warping (DTW) estimates the deviation and also provides the aligned signals value viz. Euclidean distance between two signals through non-linearity warping. To measure the difference, this metric matches the amplitude of original signal at time ‘T’ with amplitudes of augmented signals at time T+1,T-1 and T+2, T-2.
In our study, the mean Euclidean distance is calculated for both normal and abnormal signals for all augmented sets. Table 1 shows the Euclidean distance metric for classical methods [16,37] and proposed method of augmentation. The values for both cases indicate that the mean Euclidean distance value between original and augmented signal are lesser and very closer in the proposed method of augmentation compared to the classical approaches. This in turn reveals that the similarity between original and augmented signal is greater and thereby indicates similarity.
-
•
Mel Frequency Cepstral Coefficients (MFCC) is one of the feature extraction methods which mainly involves windowing the audio signal, implementing discrete Fourier transform of the windowed signal and subsequently taking the logarithm of the magnitude portion. Followed by this, the signals are warped on Mel scale and applied with inverse discrete cosine transform.
-
•
Spectral Descriptors:
-
(i)
Spectral Centroid is computed using weighted arithmetic average of the periodic components present in the signal with magnitudes of Fourier transform being considered as weights.
-
(ii)
Spectral skewness indicates the dissimilarity of the probability density of an arbitrary quantity. Spectral spread (SS) is the second central moment of the spectrum which characterizes the average difference of the spectrum close to the centroid.
-
(iii)
Spectral kurtosis is a measure which signifies the existence of sequence of transients in the signal and their positions in the spectral domain.
-
(iv)
Spectral Entropy estimates the stochasticity and deformity present in the power spectrum during specific interval of time.
Table 1.
Mean Euclidean distance metric for normal and abnormal (Wheeze) signal.
In this work, the results are evaluated for all the above spectral features for the three types of data augmentation technique considered in this work and tabulated in Table 2 . The existing studies which used the Sequential-categorical and independent DA method [16,37] were tested on ICBHI lung sound data set and tabulated for comparison. The obtained results indicates that the cGAN method performs better compared to the existing methods.
Table 2.
Correlation coefficient between spectral features for different data augmentation methods.
| DA Methodology | Data set | MFCC | Spectral centroid | Spectral skewness | Spectral spread | Spectral kurtosis | Spectral entropy |
|---|---|---|---|---|---|---|---|
| Original Data set (Without Augmentation) | ICBHI (Lung sound Data set) | 0.9965 | 0.1765 | 0.1340 | 0.10 | 0.34 | 0.13 |
| Sequential–Categorical [16] | 0.9974 | 0.31 | 0.34 | 0.24 | 0.33 | 0.29 | |
| Sequential–Categorical [37] | 0.9990 | 0.40 | 0.42 | 0.30 | 0.42 | 0.45 | |
| cGAN | 0.9993 | 0.88 | 0.73 | 0.56 | 0.69 | 0.87 | |
| cGAN | RALE(Lung Sound Data set) | 0.9991 | 0.82 | 0.75 | 0.63 | 0.76 | 0.77 |
3.2. Assessment of similarity using non-linear metrics
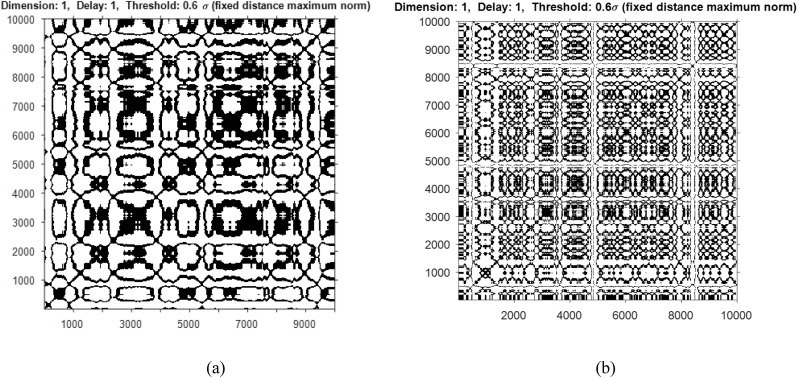
In addition to time domain and frequency domain metrics, the results are also evaluated using non-linear metrics such as Cross Recurrence Quantification Analysis (CRQA) and Mutual Information. CRQA analyzes the non-stationary data and detects the phase transition between the time series signals. A symmetric matrix wherein the matrix elements can reoccur during certain duration of time can be visualized using recurrence plot. Fig. 7 a and b shows the cross recurrence plot of a sample of normal and abnormal signal (wheeze) considered for the study. The behavior of the signal indicates periodic structure with drift representing recurrences. For plotting the cross recurrence, the embedding dimension was taken as 1, time delay ‘τ’ as 1 and Threshold as 0.6.
Fig. 7.
Recurrence plot of a sample of (a) normal lung signal and (b) abnormal signal (wheeze).
Table 3 shows the different measures of the recurrence quantification analysis. It is inferred from the values that in terms of Recurrence Rate and Laminarity, cGAn produces comparable results to classical augmentation techniques while it produces better entropy values indicating higher correlation, for both normal and abnormal cases. Further, the lower frequency (normal) has higher Recurrence Rate indicating more clusters of recurrence points compared to higher frequency (abnormal) case.
Table 3.
Recurrence quantification analysis.
| Cross Recurrence Quantification Metrics | Normal |
Abnormal |
||||
|---|---|---|---|---|---|---|
| Sequential [16] | Independent [37] | cGAN | Sequential [16] | Independent [37] | cGAN | |
| Recurrence Rate (RR) | 0.3321 | 0.3722 | 0.3722 | 0.3451 | 0.3501 | 0.3578 |
| Determinism | 0.9918 | 0.9932 | 0.9932 | 0.739 | 0.8188 | 0.9997 |
| Lmax (Diagonal Max Line) | 43.1112 | 42.332 | 48.1112 | 35.01 | 36.03 | 38.8864 |
| Entropy | 3.18 | 2.67 | 3.9227 | 2.36 | 4.6042 | 4.7778 |
| Laminarity | 0.991 | 0.99 | 0.9967 | 0.997 | 0.997 | 0.998 |
Mutual information (MI) metric measures the mutual dependence between two time series signals and it is calculated using the expression,
| (6) |
where represents the original and augmented signals. The average value of MI obtained is tabulated in Table 4 . It is observed from Table 4, that higher value of MI is obtained for proposed cGAN method of augmentation which indicates that the generated signals resembles more closely with original signals in both data sets.
Table 4.
Mutual Information between original and augmented signals.
3.3. Impact of augmentation in classifier performance
To quantify the effect of augmentation and its performance, we assess our model with three pre-trained CNN architectures namely Alexnet, GoogLeNet and ResNet50. Each lung sound signal from all classes are augmented with all three techniques of augmentation to provide 2036 signals for each approach. In order to perform classification, the original and augmented sound signals are transformed to scalograms of time frequency distribution. All the transformed images are fed to the pre-trained models as input for classification.
The experimentation is carried out in MATLAB 2020a for all categories of lung sounds without and with expansion in the data set. The entire scalogram image data base is sub divided into 70% for training and 30% for testing. For the classification with original data base, 357 of 509 images are used for training and 153 scalogram images are utilized for testing. In the same way, for classifying the augmented data base, 1425 images are considered for testing and 611 are used for testing in every method of augmentation. The network is modeled for 20 epochs with initial learning rate of 0.0001 and batch size of 27 with Adam optimizer. The results of classification accuracy is tabulated for three classifiers considering both respiratory data sets in Table 5 .
Table 5.
Classification accuracy performance of model without and with augmentation approaches using different deep learning architectures.
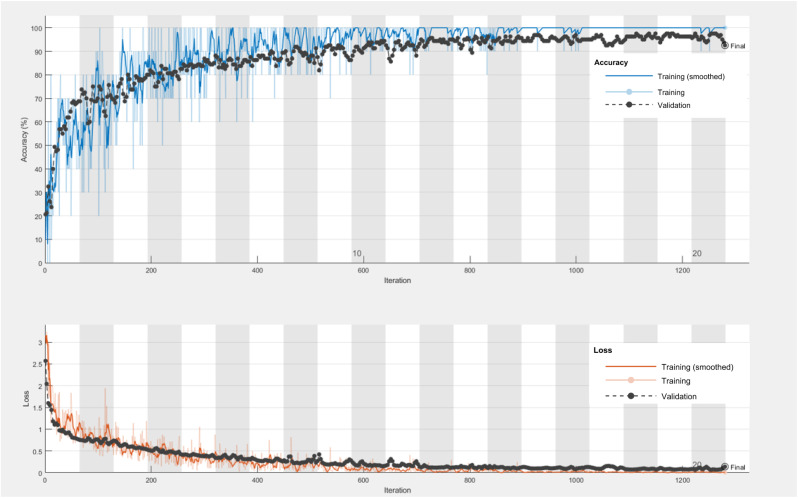
The experimental results in Table 5 demonstrate that Resnet50 outperforms the other two CNN models in both instances viz. original data set and augmented data set. It also proves that compared to the existing approaches, sequential and independent mode of augmentation, generation of artificial respiratory signals using cGAN yields better accuracy of 92.50% using the ResNet- 50 classifier. This is due to the fact that, the generated signals using cGAN resembles very closely the original respiratory signals and hence better classification is observed. The training progress of cGAN with accuracy and loss plot for 20 epochs of Resnet-50 model producing 92.50% as accuracy is shown in Fig. 8 . The confusion matrix of Resnet-50 classifier for both cases of with and without augmentation is presented in Table 6 .
Fig. 8.
Accuracy and loss plot of Resnet-50 classifier using cGAN based augmentation with 20 epochs.
Table 6.
a& 6b. Confusion matrices of ResNet 50 network without/with Augmentation.
| Normal | Crackle | Wheeze | Rhonchi | |
|---|---|---|---|---|
| Normal | 18 | 3 | 0 | 1 |
| Crackle | 9 | 71 | 1 | 3 |
| Wheeze | 3 | 4 | 25 | 5 |
| Rhonchi | 0 | 0 | 0 | 10 |
| Normal | Crackle | Wheeze | Rhonchi | |
|---|---|---|---|---|
| Normal | 79 | 4 | 2 | 3 |
| Crackle | 7 | 317 | 4 | 9 |
| Wheeze | 6 | 3 | 133 | 4 |
| Rhonchi | 1 | 1 | 2 | 36 |
The rows and columns of confusion matrix tabulated in Table 6, corresponds to predicted class and actual class. In concise, in Table 6a i.e. for the data set without augmentation, out of the 30 samples in normal, 77 in crackle, 26 in wheeze and 19 in rhonchi belonging to the actual class, only 18 in normal, 71 in crackle, 25 in wheeze and 10 in rhonchi belongs to the predicted class. In addition, the false positives and false negatives for all classes are found to be 4, 13, 12, and 0 and 12, 7, 1, and 9 respectively.
Similarly, in Tables 6b and i.e. with augmentation, the number of cases correctly predicted are 79 in normal, 317 in crackle,133 in wheeze and 36 in rhonchi out of the number of actual 93 samples in normal, 325 in crackle, 141 in wheeze and 52 in rhonchi. The false positives and negatives for all classes are 9, 20, 13, and 4 and 14, 8, 8, and 16 respectively. The other metrics such as class wise accuracy, Precision, Recall, F1 score and class prediction error are also calculated using TP, FP and FN for both cases of without and with augmentation and are tabulated in Tables 7 a and 7b.
Table 7.
Precision and Recall for ResNet 50 model without/with Augmentation.
| Class | Data set | Accuracy | Precision | Recall | F1 Score | Class Prediction Error |
|---|---|---|---|---|---|---|
| Normal | Original Data base | 89.54% | 0.82 | 0.60 | 0.69 | 0.1046 |
| Crackle | 86.93% | 0.85 | 0.91 | 0.88 | 0.1307 | |
| Wheeze | 91.5% | 0.68 | 0.96 | 0.79 | 0.085 | |
| Rhonchi | 94.12% | 1 | 0.53 | 0.69 | 0.0588 | |
| Normal | Augmented Data Base | 96.24% | 0.90 | 0.85 | 0.87 | 0.0376 |
| Crackle | 95.42% | 0.94 | 0.98 | 0.96 | 0.0548 | |
| Wheeze | 96.56% | 0.91 | 0.94 | 0.93 | 0.0354 | |
| Rhonchi | 96.73% | 0.90 | 0.69 | 0.78 | 0.0327 |
From Table 7, it is observed that the class wise accuracy is found to be high for all classes, roughly more than 95% for the case of classification with augmentation compared to the case of without augmentation. In addition, the F1 score is high for all classes in augmented data base which shows that the validation accuracy is better for augmented data in all cases. The class prediction error is also found to be less than 0.05 for all classes of respiratory sounds.
Furthermore, the results investigated for respiratory data set with different augmentation methods in previous studies are tabulated in Table 8 . From the table, it is evident that the conditional GAN method of augmentation with scalogram as time frequency representation produces good accuracy of 92.50% (ICBHI) and 92.68% (RALE & Think Labs Lung sounds Library) compared to other methods of augmentation experimented with spectrograms.
Table 8.
Performance Comparison of existing studies and proposed work.
| Methodology | Input | Data set | Trained Network | Accuracy |
|---|---|---|---|---|
| Mix up Augmentation [33] | Spectrogram | ICBHI | ResNet | 52.26% |
| Spatial Attention Block [34] | Spectrogram | ICBHI | ResNet-18 | 54.99% |
| Mix up Augmentation [35] | Spectrograms & Scalograms | ICBHI | CNN-RNN | 0.81 (harmonic score) |
| Mix up Augmentation [36] | Spectrogram | COVID-19 Sound Data set | 1D-CNN | 86.89% |
| Proposed Method Augmentation of lung sound dataset with cGAN | Spectrogram | ICBHI | ResNet-50 | 89.2% |
| Proposed Method (Augmentation of lung sound dataset with cGAN) | Scalogram | RALE & Think Labs Lung Sounds Library | ResNet-50 | 92.68% |
| Proposed Method (Augmentation of lung sound dataset with cGAN) | Scalogram | ICBHI | ResNet-50 | 92.50% |
4. Conclusion
The current study investigates cGAN based augmentation approach for respiratory signal classification using different deep learning architectures. Synthetic generation of signals using cGAN utilizes random array as input. To quantify the performance of generated augmented signals in clinical diagnosis, the correlation between original and generated signals is assessed through wavelet coherence, dynamic time warping and distinct spectral correlation metrics. The results of the correlation analysis demonstrate that the augmented signals seems to be almost similar as that of the original signals when experimented with conditional GAN method of augmentation. Lastly, the effect of augmentation is analyzed on network classification accuracy with scalograms as input to the pre-trained models Alexnet, GoogleNet and Resnet-50. The overall inference is that there is considerable improvement in the accuracy of all networks with augmentation compared to study with original data base. Additionally, the validation accuracy of ResNet-50 classifier yields better accuracy of 92.50% (ICBHI) and 92.68% (RALE and Think Labs Lung sounds Library) for cGAN method of augmentation compared to the classical methods. In the future, the work can be extended with other types of GAN using custom training loop with layer normalization to produce better results.
Declaration of competing interest
NONE DECLARED.
References
- 1.Cukic V., Lovre V., Dragisic D., Ustamujic A. Asthma and chronic obstructive pulmonary disease (COPD)–differences and similarities. Mater. Soc. Med. 2012;24(2):100. doi: 10.5455/msm.2012.24.100-105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Copot D., De Keyser R., Derom E., Ionescu C. Structural changes in the COPD lung and related heterogeneity. PLoS One. 2017;12(5) doi: 10.1371/journal.pone.0177969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Assadi I., Charef A., Copot D., De Keyser R., Bensouici T., Ionescu C. Evaluation of respiratory properties by means of fractional order models. Biomed. Signal Process Control. 2017;34:206–213. [Google Scholar]
- 4.Ionescu C.M., Copot D. Monitoring respiratory impedance by wearable sensor device: protocol and methodology. Biomed. Signal Process Control. 2017;36:57–62. [Google Scholar]
- 5.Bohadana A., Izbicki G., Kraman S.S. Fundamentals of lung auscultation. N. Engl. J. Med. 2014;370(8):744–751. doi: 10.1056/NEJMra1302901. [DOI] [PubMed] [Google Scholar]
- 6.Wang B., Liu Y., Wang Y., Yin W., Liu T., Liu D., Luo F. Characteristics of Pulmonary auscultation in patients with 2019 novel coronavirus in China. Respiration. 2020;99(9):755–763. doi: 10.1159/000509610. [DOI] [PubMed] [Google Scholar]
- 7.Wang B., Li R., Lu Z., Huang Y. Does comorbidity increase the risk of patients with COVID-19: evidence from meta-analysis. Aging (Albany NY) 2020;12(7):6049. doi: 10.18632/aging.103000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.https://timesofindia.indiatimes.com/india/india-has-one-doctor-for-every-1457-citizens-govt/articleshow/70077266.cms
- 9.https://www.erswhitebook.org/chapters/respiratory-research/
- 10.Polat H., Güler İ. A simple computer-based measurement and analysis system of pulmonary auscultation sounds. J. Med. Syst. 2004;28(6):665–672. doi: 10.1023/b:joms.0000044968.45013.ce. [DOI] [PubMed] [Google Scholar]
- 11.Reichert S., Gass R., Brandt C., Andrès E. Analysis of respiratory sounds: state of the art. Clin. Med. Circ. Respir. Pulm Med. 2008;2 doi: 10.4137/ccrpm.s530. CCRPM-S530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chambres G., Hanna P., Desainte-Catherine M. IEEE; 2018, September. Automatic Detection of Patient with Respiratory Diseases Using Lung Sound Analysis; pp. 1–6. (2018 International Conference on Content-Based Multimedia Indexing (CBMI)). [Google Scholar]
- 13.Jakovljević N., Lončar-Turukalo T. International Conference on Biomedical and Health Informatics. Springer; Singapore: 2017. November). Hidden markov model based respiratory sound classification; pp. 39–43. [Google Scholar]
- 14.Acharya J., Basu A. Deep neural network for respiratory sound classification in wearable devices enabled by patient specific model tuning. IEEE transactions on biomedical circuits and systems. 2020;14(3):535–544. doi: 10.1109/TBCAS.2020.2981172. [DOI] [PubMed] [Google Scholar]
- 15.Bardou D., Zhang K., Ahmad S.M. Lung sounds classification using convolutional neural networks. Artif. Intell. Med. 2018;88:58–69. doi: 10.1016/j.artmed.2018.04.008. [DOI] [PubMed] [Google Scholar]
- 16.Salamon J., Bello J.P. Deep convolutional neural networks and data augmentation for environmental sound classification. IEEE Signal Process. Lett. 2017;24(3):279–283. [Google Scholar]
- 17.LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-based learning applied to document recognition. Proc. IEEE. 1998;86(11):2278–2324. [Google Scholar]
- 18.Krizhevsky A., Sutskever I., Hinton G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012;25:1097–1105. [Google Scholar]
- 19.Inoue H. Data augmentation by pairing samples for images classification. arXiv preprint arXiv:1801.02929. 2018 [Google Scholar]
- 20.Chawla N.V., Bowyer K.W., Hall L.O., Kegelmeyer W.P. SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002;16:321–357. [Google Scholar]
- 21.Bashivan P., Rish I., Yeasin M., Codella N. Learning representations from EEG with deep recurrent-convolutional neural networks. arXiv preprint arXiv:1511.06448. 2015 [Google Scholar]
- 22.Yin Z., Zhang J. Cross-session classification of mental workload levels using EEG and an adaptive deep learning model. Biomed. Signal Process Control. 2017;33:30–47. [Google Scholar]
- 23.Atzori M., Cognolato M., Müller H. Deep learning with convolutional neural networks applied to electromyography data: a resource for the classification of movements for prosthetic hands. Front. Neurorob. 2016;10:9. doi: 10.3389/fnbot.2016.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Côté-Allard U., Fall C.L., Drouin A., Campeau-Lecours A., Gosselin C., Glette K., Gosselin B. Deep learning for electromyographic hand gesture signal classification using transfer learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2019;27(4):760–771. doi: 10.1109/TNSRE.2019.2896269. [DOI] [PubMed] [Google Scholar]
- 25.Cao P., Li X., Mao K., Lu F., Ning G., Fang L., Pan Q. A novel data augmentation method to enhance deep neural networks for detection of atrial fibrillation. Biomed. Signal Process Control. 2020;56 [Google Scholar]
- 26.Abeßer J., Mimilakis S.I., Gräfe R., Lukashevich H., Fraunhofer I.D.M.T. Proc. Of the Detection and Classification of Acoustic Scenes and Events 2017 Workshop (DCASE2017) 2017. November). Acoustic scene classification by combining autoencoder-based dimensionality reduction and convolutional neural networks; pp. 7–11. [Google Scholar]
- 27.Rebai I., BenAyed Y., Mahdi W., Lorré J.P. Improving speech recognition using data augmentation and acoustic model fusion. Procedia Computer Science. 2017;112:316–322. [Google Scholar]
- 28.Janssen L.A.L., Arteaga I.L. Data processing and augmentation of acoustic array signals for fault detection with machine learning. J. Sound Vib. 2020;483 [Google Scholar]
- 29.Um T.T., Pfister F.M., Pichler D., Endo S., Lang M., Hirche S., Kulić D. Proceedings of the 19th ACM International Conference on Multimodal Interaction. 2017, November. Data augmentation of wearable sensor data for Parkinson's disease monitoring using convolutional neural networks; pp. 216–220. [Google Scholar]
- 30.Esteban C., Hyland S.L., Rätsch G. Real-valued (medical) time series generation with recurrent conditional gans. arXiv preprint arXiv:1706.02633. 2017 [Google Scholar]
- 31.Delaney A.M., Brophy E., Ward T.E. Synthesis of realistic ecg using generative adversarial networks. arXiv preprint arXiv:1909. 2019 [Google Scholar]
- 32.Narváez P., Percybrooks W.S. Synthesis of normal heart sounds using generative adversarial networks and empirical wavelet transform. Appl. Sci. 2020;10(19):7003. [Google Scholar]
- 33.Ma Y., Xu X., Li Y. 25–29 October 2020. Lung RN+ NL: an Improved Adventitious Lung Sound Classification Using Non-local Block ResNet Neural Network with Mixup Data Augmentation; pp. 2902–2906. (Proceedings of the Interspeech 2020). Shanghai, China. [Google Scholar]
- 34.Yang Z., Liu S., Song M., Parada-Cabaleiro E., Schuller12 B.W. 25–29 October 2020. Adventitious Respiratory Classification Using Attentive Residual Neural Networks; pp. 2912–2916. (Proceedings of the Interspeech 2020). Shanghai, China. [Google Scholar]
- 35.Minami K., Lu H., Kim H., Mabu S., Hirano Y., Kido S. Automatic classification of large-scale respiratory sound dataset based on convolutional neural network. in Proc. ICCAS. 2019:804–807. [Google Scholar]
- 36.Lella K.K., Alphonse P.J.A. Automatic COVID-19 disease diagnosis using 1D convolutional neural network and augmentation with human respiratory sound based on parameters: cough, breath, and voice. AIMS Public Health. 2021;8(2):240–264. doi: 10.3934/publichealth.2021019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nanni L., Maguolo G., Paci M. Data augmentation approaches for improving animal audio classification. Ecol. Inf. 2020;57 [Google Scholar]
- 38.Rocha B.M., Filos D., Mendes L., Vogiatzis I., Perantoni E., Kaimakamis E., Maglaveras N. Springer; Singapore: 2017, November. Α Respiratory Sound Database for the Development of Automated Classification; pp. 33–37. (International Conference on Biomedical and Health Informatics). [Google Scholar]
- 39.The R.A.L.E. Repository. Rale.ca.N.P.,2017.Web.28 Feb.2017.
- 40.https://www.thinklabs.com/lung-sounds
- 41.Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Bengio Y. Generative adversarial networks. Commun. ACM. 2020;63(11):139–144. [Google Scholar]
- 42.Lakshmi Priya B., Jayalakshmy S., Pragatheeswaran J.K., Saraswathi D., Poonguzhali N. Scattering convolutional network based predictive model for cognitive activity of brain using empirical wavelet decomposition. Biomed. Signal Process Control. 2021;66 [Google Scholar]