Topological spin/structure couplings in layered chiral magnet Cr_1/3TaS₂: The discovery of spiral magnetic superstructure

Significance

Magnets in which chirality of crystal lattice gives rise to noncollinear spin orders are ideal playgrounds for studies of novel physical phenomena originating from the nontrivial topology of magnetic textures. Most studies have been focused on homochiral materials, while topological magnetic states of heterochiral magnets have rarely been explored. Here, we report a layered chiral helimagnet with highly tunable topological heterochiral states. Tuning the chiral domain density, we have observed a topological magnetic texture that has the form of a spiral unfolding in the radial direction. In weak in-plane fields, this spiral magnetic superstructure transforms into a nonspiral array of concentric rings. Our results open a horizon for studies of tunable topological magnetic textures.

Abstract

Chiral magnets have recently emerged as hosts for topological spin textures and related transport phenomena, which can find use in next-generation spintronic devices. The coupling between structural chirality and noncollinear magnetism is crucial for the stabilization of complex spin structures such as magnetic skyrmions. Most studies have been focused on the physical properties in homochiral states favored by crystal growth and the absence of long-ranged interactions between domains of opposite chirality. Therefore, effects of the high density of chiral domains and domain boundaries on magnetic states have been rarely explored so far. Herein, we report layered heterochiral Cr_1/3TaS₂, exhibiting numerous chiral domains forming topological defects and a nanometer-scale helimagnetic order interlocked with the structural chirality. Tuning the chiral domain density, we discovered a macroscopic topological magnetic texture inside each chiral domain that has an appearance of a spiral magnetic superstructure composed of quasiperiodic Néel domain walls. The spirality of this object can have either sign and is decoupled from the structural chirality. In weak, in-plane magnetic fields, it transforms into a nonspiral array of concentric ring domains. Numerical simulations suggest that this magnetic superstructure is stabilized by strains in the heterochiral state favoring noncollinear spins. Our results unveil topological structure/spin couplings in a wide range of different length scales and highly tunable spin textures in heterochiral magnets.

Chirality resulting from broken-mirror symmetry emerges in all parts of nature, living or not, microscopic or macroscopic. Time-reversal symmetry is spontaneously broken at a microscopic level by ordered spins in magnetic materials. Chiral magnets, in which these two phenomena occur simultaneously, are a promising playground for studies of novel states of matter and phenomena, such as skyrmion lattices (1–6), arrays of chiral magnetic solitons (7, 8), and colossal magnetoelectricity (9). Intriguingly, nature often prefers homochiral arrangements (10), as exemplified by DNA molecules and quartz crystals. In fact, most of the recent studies on chiral magnets were focused on physical properties in homochiral states (1–9). On the other hand, chiral domain boundaries that are structurally distinct from the domains they separate may have a profound effect on magnetic textures, especially in heterochiral magnets with strong spin-lattice coupling. This suggests the potential existence of novel spin textures in heterochiral magnets, beyond domain walls and skyrmions, which have not been explored so far. In this work, we demonstrate that structural chirality of a layered chiral helimagnet Cr_1/3TaS₂, resulting from displacements of sulfur ions caused by intercalated Cr ions, can be systematically tuned to obtain heterochiral states with millions of chiral domains in one single crystal. The magnetic helicity interlocked with the structural chirality gives rise to topological structural and magnetic “vortex” domains. In addition, a spiral magnetic superstructure composed of microscopic cycloidal magnetic solitons (CyMS) is found by tuning the structural chiral domain (SCD) density and concomitant internal strains. An applied magnetic field triggers a topological transition between the spiral magnetic superstructure and an array of concentric rings. We propose a mechanism for the formation of these unusual patterns and study them by numerical simulations.

Interlocked Structural Chirality and Magnetic Helicity

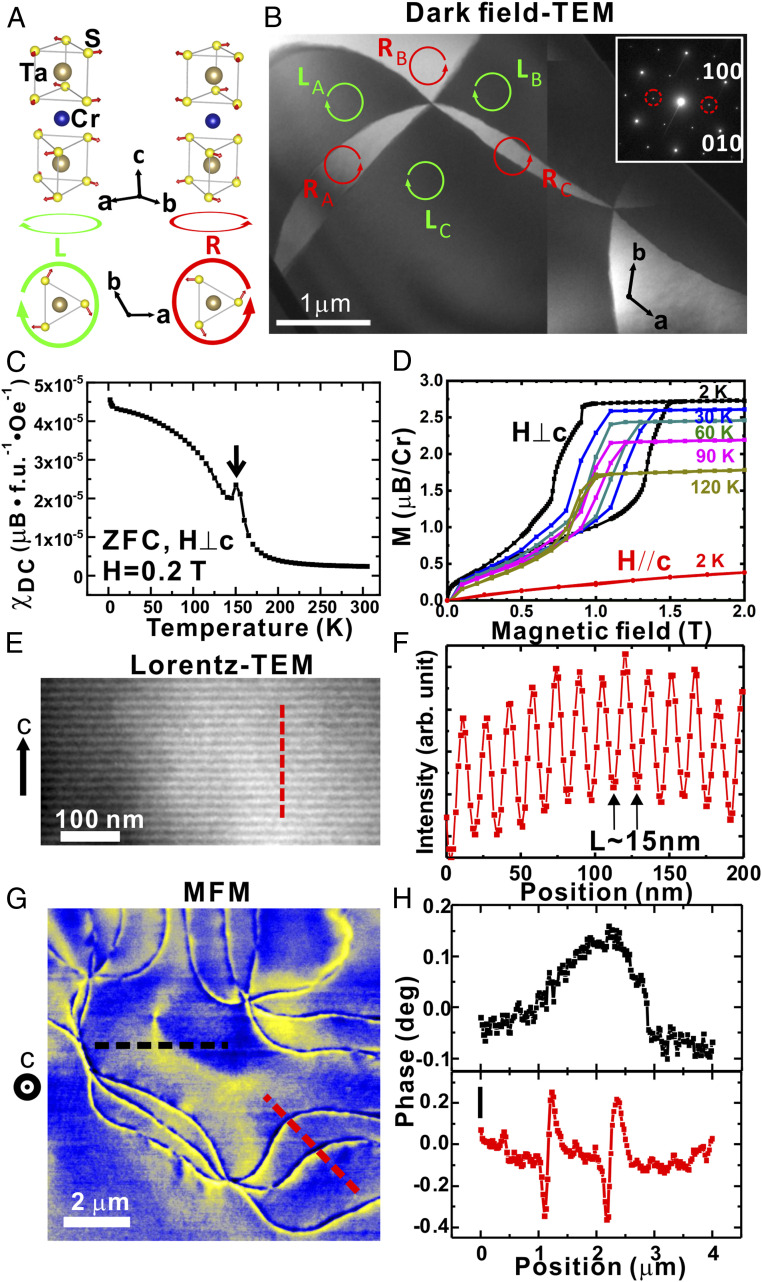
Cr_1/3TaS₂ (chiral hexagonal space group P6₃22) (11) is a highly cleavable intercalated transition metal dichalcogenide (TMD) exhibiting a rare topological heterochiral state with submicron-sized SCDs. At the atomic scale, Cr³⁺ ions intercalated between 2H-type TaS₂ layers form a triangular lattice that induces additional structural twists in TaS₂ layers, leading to an overall nanoscale chiral structure (chiral pitch ∼1.2 nm along the c-axis) (11). Fig. 1A shows two possible chiral structures: left-handed and right-handed enantiomers. We have observed an additional set of spots in the electron diffraction pattern due to the √3a × √3a-type superlattice deformation of the P6₃/mmc parent structure of Cr_1/3TaS₂ (Fig. 1 B, Inset), which is a signature of the lattice chirality. The dark-field transmission electron microscopy (TEM) image of quenched Cr_1/3TaS₂ crystals (Materials and Methods) in Fig. 1B manifests clear micrometer-scale bright and dark regions, corresponding to left-handed and right-handed SCDs. Six different SCDs merge at a center point forming a cloverleaf pattern with alternating chirality similar to ferroelectric domains in hexagonal rear-earth manganites (12) and antiferromagnetic domains in hematite films (13). Utilizing different imaging conditions, one can obtain a clear contrast inversion of SCDs (SI Appendix, Fig. S1). Note that such a SCD pattern has only been observed in a related material, Fe_1/3TaS₂, in which it was confirmed to be a topological vortex configuration (14). A schematic crystal structure near a vortex core is shown in SI Appendix, Fig. S1E. Two types of SCDs (left-handed and right-handed) and three types of antiphase domains (A-, B-, and C-type) lead to a “Z₂×Z₃ domains with Z₆ vortex” configuration (15). The direction of structural distortion, described by the angle θ in SI Appendix, Fig. S1E, rotates through the angle 2π/3 across the domain wall separating two adjacent chiral domains. The total angle change around the merging point is +4π (−4π), corresponding to topological charge (winding number) of +2/−2 of a structural vortex/antivortex in Cr_1/3TaS₂. We believe that the vortex SCDs found in Fe_1/3TaS₂ and Cr_1/3TaS₂ are present in many related intercalated TMDs that have not been carefully characterized so far.

Fig. 1.

The coupling of structural chirality and magnetic helicity in Cr_1/3TaS₂. (A) Left-handed (L) and right-handed (R) chiral structures of Cr_1/3TaS₂. Blue balls indicate Cr atoms, while brown and yellow balls stand for Ta and S atoms, respectively. Red arrows show the displacement directions of S atoms. The lower parts are top views of the TaS₂ layer beneath an intercalated Cr atom. (B) Dark-field TEM image of a quenched specimen using √3a × √3a superlattice spots (labeled with red dashed circles) at room temperature and the relevant electron diffraction pattern (Inset). The image shows vortex–antivortex pair formed by alternating chiral domains. (C) Magnetic susceptibility as a function of temperature in 2 kOe with H⊥c and the zero-field-cooled (ZFC) condition. The anomaly of the helical spin order is marked by the black arrow. (D) Out-of-plane (H//c) and in-plane (H⊥c) magnetization curves as a function of magnetic field. (E) Side-view L-TEM images at 22 K, demonstrating the emergence of helical magnetic order. (F) The line profile of the red dashed line in E, indicating a helical pitch L≈15 nm along the c-axis. (G) MFM image of the ab-plane surface of a quenched specimen at 80 K, demonstrating the interlocking between MHDs and structural vortex domains in Cr_1/3TaS₂. The line profiles of (H) black and (I) red dashed lines in G, showing a broad magnetic antiphase domain wall and sharp helical domain walls, respectively.

In addition, Cr_1/3TaS₂ undergoes a transition into a helical spin order with the wave vector along the c-axis and a helical pitch about 10 times larger than the structural chiral pitch. Cr_1/3TaS₂ was previously reported to show a ferromagnetic state below a Curie temperature of ∼110 K with spins of Cr³⁺ ions parallel to the ab-plane (16, 17). However, the temperature dependence of our direct current (DC) magnetic susceptibility (Fig. 1C) shows a clear kink-like behavior right below the magnetic ordering temperature of ∼150 K. This anomaly is a telltale sign of the onset of a helical magnetic order commonly observed in monoaxial helimagnets (8, 18), such as Cr_1/3NbS₂. The same anomaly shows up in the alternating current (AC) magnetic susceptibility measurements (SI Appendix, Fig. S1G). The magnetization as a function of the in-plane magnetic field (Fig. 1D) also shows a clear metamagnetic transition at ∼0.5 to 1.5 T, similar to that observed in Cr_1/3NbS₂ at the transition from a chiral soliton lattice to the field-induced ferromagnetic state. The helical nature of the magnetic structure of Cr_1/3TaS₂ is unambiguously confirmed by our Lorenz TEM (L-TEM) studies. Typical periodic black and white contrasts produced by spins in the helical order are evident in the L-TEM image at 22 K (Fig. 1E). A line profile in Fig. 1F, taken from Fig. 1E, indicates that the helical pitch length L of Cr_1/3TaS₂ is ∼15 nm, which is significantly shorter than that (∼48 nm) in Cr_1/3NbS₂ (SI Appendix, Note 1). The magnetic helicity, defined by the spin rotating direction along the c-axis, can be either left-handed or right-handed (SI Appendix, Fig. S1F).

To investigate potential interplays between SCDs and magnetic helical domains (MHDs) in Cr_1/3TaS₂, we performed systematic magnetic force microscopy (MFM) measurements on crystals that were quenched to induce high-density SCDs. Sharp magnetic domain wall contrasts with micrometer-scale cloverleaf patterns are observed at 80 K (Fig. 1G), similar to the SCD patterns observed in our TEM experiments. Since the easy-plane anisotropy of Cr_1/3TaS₂ confines spins to hexagonal ab-plane, all magnetic domain walls should be of Néel type. This conclusion is in agreement with the antisymmetric line profile in Fig. 1I, characteristic of Néel walls in MFM (19). We also observe other antiphase-type magnetic domains within each SCD domain, which are the source of broad magnetic contrasts in Fig. 1H (SI Appendix, Note 2). Thus, MFM can sense the stray field from the helical spin order with a rather long pitch at MHD walls that are strongly coupled to SCD walls (SI Appendix, Note 3). In other words, MHDs are interlocked by preexisting topological structural domains. This topological coupling between XY-type helical spins and structural chirality in Cr_1/3TaS₂ is in sharp contrast to the previously studied Fe_1/3TaS₂ showing no coupling between SCDs and ferromagnetic domains formed by Ising spins (14).

Tunable Heterochiral State and Spiral Magnetic Superstructures

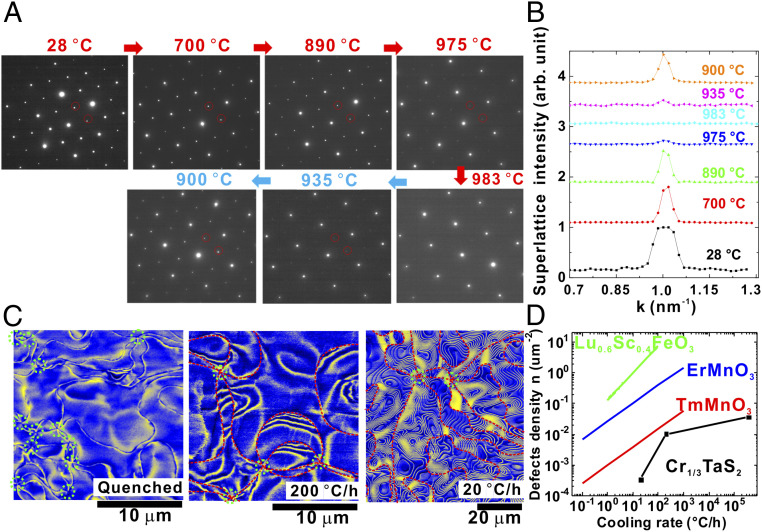
These results show that Cr_1/3TaS₂ is an ideal platform for studying physical phenomena emerging from the strong coupling between the heterochiral crystal lattice and helical magnetism. Encouragingly, we found that Cr_1/3TaS₂ undergoes an achiral-to-chiral structural transition at ∼980 °C, identified by our high-temperature electron diffraction experiments (Fig. 2 A and B). The size of SCDs/MHDs in Cr_1/3TaS₂ can be systematically tuned from a micrometer to a macroscopic scale using different cooling rates during this structural transition. This domain-size tunability (Fig. 2 C and D) is a consequence of the Kibble–Zurek mechanism, which is also at play in hexagonal rare-earth manganites (20) and ferrites (21). To our best knowledge, Cr_1/3TaS₂ is the only chiral material that exhibits a systematically tunable heterochiral state so far. In slowly cooled (20 °C/h) crystals, the SCDs/MHDs are predominantly loop shaped and more than ∼50 μm in size (SI Appendix, Fig. S2A). Vortices and antivortices form pairs and their density is very low (Fig. 2C). The interlocking of SCDs and MHDs at a micrometer scale also persists at macroscopic scales.

Fig. 2.

Chiral structural transition and tunable topological heterochiral states. (A) Sequential high-temperature electron diffraction patterns of Cr_1/3TaS₂ indicating an achiral-to-chiral structural transition at ∼980 °C. Superlattice spots related to the chiral structure (red dashed circles) disappear and reappear upon warming and cooling across the transition. (B) Line profiles of the superlattice peak intensity as a function of temperature (shifted vertically for clarity). (C) MFM image at 80 K of specimens with different cooling rates across this chiral structural transition. Domain walls between structural chiral/MHDs in 200 °C/h and 20 °C/h cooled specimens are shown with red dashed lines. Vortices/antivortices are marked by green dashed circles. (D) The topological defect density in Cr_1/3TaS₂ as a function of the cooling rate compared to those of ferroelectric compounds following the Kibble–Zurek mechanism (20, 21).

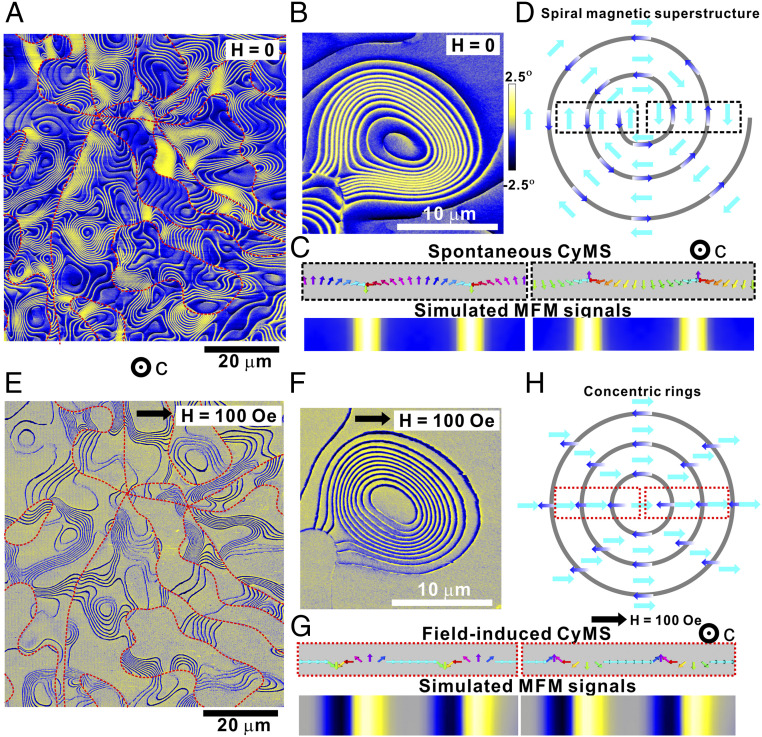
Strikingly, the density of topological SCDs strongly affects magnetic domain patterns. The magnetic antiphase domain walls inside a large SCD/MHD tend to form a well-ordered macroscopic spiral magnetic superstructure (Fig. 3 A and B). Based on MFM simulations (Fig. 3C), this state can be best described by an effective magnetic moment configuration never observed before (Fig. 3D) that consists of periodic CyMS separating domains with the same spin orientation. In other words, this spiral magnetic superstructure composed of CyMS is a special ordered arrangement of magnetic antiphase domain walls in the hexagonal plane, which does not form in dense SCD/MHD networks. Magnetic spiral patterns are rare, and the only two other examples are the nanometer-scale spiral pattern of Heisenberg spins resulting from the rotating helical axis in FeGe crystals (22) and the out-of-plane dynamic spiral pattern of Ising spins observed in iron garnet films under AC magnetic fields (23). Those spin textures are very different from the spontaneously formed spiral magnetic superstructure and CyMS in Cr_1/3TaS₂ with XY spins, which has a fixed helical axis and the strong easy-plane anisotropy. Interestingly, the separation between two adjacent CyMS varies significantly from ≤220 nm to ≥10 μm (SI Appendix, Fig. S2), making this magnetic texture a promising candidate for high-density and highly tunable information storages. One can also define the spirality of an in-plane spiral magnetic superstructure by their clockwise (CW) or counter-clockwise (CCW) path going from the center to the rim of the spiral pattern along the domain wall. Although the helicity of MHD is locked to the chirality of SCD, spiral magnetic superstructures with both spiralities (CW or CCW) may coexist within each SCD/MHD (Fig. 3A and SI Appendix, Fig. S2A), implying that the mechanism for spiral magnetic superstructure and CyMS formation is independent of magnetic helicity.

Fig. 3.

Spiral magnetic superstructure and CyMS. MFM images of a slowly cooled (20 °C/h) specimen at 80 K in (A, B) 0-Oe and (E, F) 100-Oe in-plane magnetic fields, showing large chiral structural domains interlocked with helical magnetic domains, which contain CyMS. The walls separating structural chiral/MHDs (red dashed lines in A and E) are lines at which CyMS (yellow/blue lines) terminate abruptly. Their positions do not change under magnetic fields and different magnetic thermal cycles (heating up to 300 K). Structural vortices/antivortices are located at intersections of six red lines. The c-axis is pointing out of the plane. Schematic effective magnetic moment configurations (cyan and blue arrows) of (D) spiral magnetic superstructure (H = 0 Oe) and (H) concentric rings (H = 100 Oe), respectively. The 100-Oe magnetic field is pointing from the left to the right of the image. Proposed magnetic spin structures and the corresponding simulated MFM contrasts of (C) spontaneous CyMS (black dotted box) and (G) field-induced CyMS (red dotted box) in magnetic field. All spins lie in the ab-plane.

Topological Transition in Magnetic Fields

Interestingly, the spiral magnetic superstructure can be turned into a nonspiral state consisting of concentric rings after cooling in an in-plane magnetic field as small as 100 Oe (Fig. 3 E and F). This state is composed of field-induced CyMS (Fig. 3G) arranged in the concentric ring configuration. The large-scale MFM image in Fig. 3E further confirms that all spiral magnetic superstructures observed previously are either erased or converted into concentric rings (Fig. 3H) by the applied magnetic field without any exception. As spiral and nonspiral magnetic textures cannot be obtained from one to another by a continuous deformation, this transformation is a topological transition triggered by field-cooling. A higher in-plane field of 1,000 Oe completely removes all magnetic antiphase domains in both quenched and slowly cooled samples, and only the SCD/MHD wall contrasts are still visible (SI Appendix, Fig. S3).

Mechanism for Spiral Magnetic Superstructure Formation and Numerical Simulations

Next, we discuss a possible mechanism for the spiral magnetic superstructure formation in Cr_1/3TaS₂. The emergence of noncollinear spin textures in noncentrosymmetric magnets is phenomenologically described by Lifshitz invariants—free-energy terms linear in magnetization gradients, which are enabled by the lack of inversion symmetry. P6₃22 crystal symmetry allows for two Lifshitz invariants: $M_x\hspace{0.17em}{\overleftrightarrow{\partial }}_z{M}_y$ and $M_z\hspace{0.17em}{\overleftrightarrow{\partial }}_y{M}_x-M_z\hspace{0.17em}{\overleftrightarrow{\partial }}_x{M}_y$, where $\mathit{M}$ is the magnetization and $M_a\hspace{0.17em}{\overleftrightarrow{\partial }}_b{M}_c=M_a\hspace{0.17em}{\partial }_b{M}_c-M_c\hspace{0.17em}{\partial }_b{M}_a.$ The first invariant results from the interlayer Dzyaloshinskii–Moriya interaction (DMI) that induces the helical spins with the wave vector along the c-axis. The second invariant favors a helical spin with a wave vector in the ab-plane, which in Cr_1/3TaS₂ is apparently suppressed by the easy-plane magnetic anisotropy. The in-plane spin rotation and CyMS can originate from the magnetoelastic coupling of noncollinear spins to local strains described by the strain tensor, $u_{ab}$,

$$E_{me}=-g{\displaystyle \int }\hspace{0.17em}dV\left(u_{zx}{M}_x\hspace{0.17em}{\overleftrightarrow{\partial }}_x{M}_y+u_{zy}{M}_x\hspace{0.17em}{\overleftrightarrow{\partial }}_y{M}_y\right).$$ [1]

Since Cr_1/3TaS₂ is a soft and stretchable layered material, it is not surprising that the crystal can sustain large strains that affect spin interactions. The magnetoelastic coupling to shear strain Eq. 1 can originate from the Heisenberg exchange striction (Materials and Methods). In addition, a nonuniform normal strain, described by $u_{zz}$ or $u_{xx}+u_{yy}$ dependent on in-plane coordinates, locally modifies the interlayer DMI and hence the helical spin wavelength, resulting in nonuniform spin textures in the ab layers.

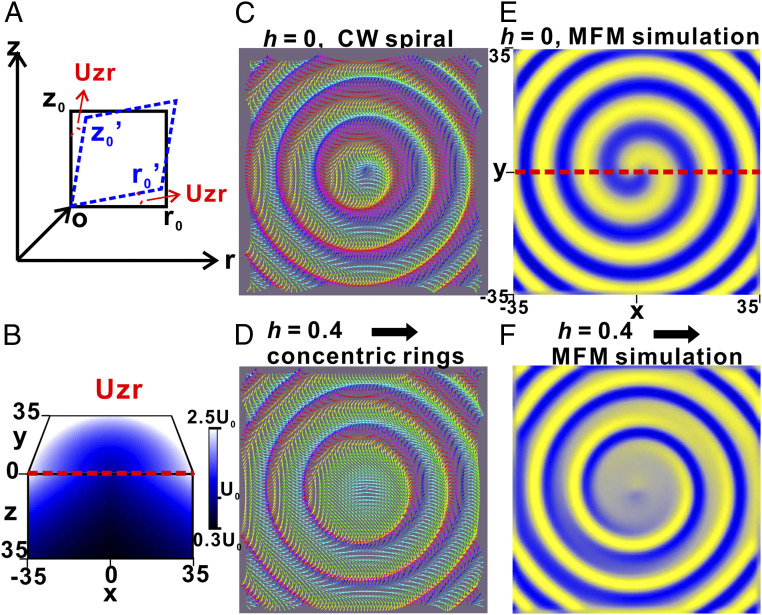
We performed numerical simulations of spin configurations on the 71 × 71 × 81 spin lattice with the magnetoelastic coupling to shear strains and a nonuniform interlayer DMI (the model is described in Materials and Methods). In cylindrical coordinates, the shear strain component, $u_{zr}$ (Fig. 4A), gives rise to the energy term, $-\hspace{0.17em}{D}_r{\partial }_r\mathrm{\Phi }$, $\mathrm{\Phi }$ being the angle describing the in-plane spin orientation, which induces spin rotations along the radial direction. To describe the experimentally observed decrease of the distance between the domain walls near the edges of the structural domains, we assumed that the strain-induced effective DMI, $D_r\propto u_{zr}$, increases from the center to periphery and varies from the surface to the bulk (Fig. 4B). We have also considered the interlayer DMI, $-\hspace{0.17em}{D}_z{\partial }_z\mathrm{\Phi }$, with $D_z$ dependent on r and z, which results in a similar spin rotation. Fig. 4C shows the minimal-energy spin configuration in the upper layer, which has the spiral domain structure. In an applied in-plane magnetic field, the spin configuration transforms into an array of concentric ring domains (Fig. 4D). Simulations of the MFM signal based on these numerically obtained spin configurations produce images (Fig. 4 E and F) consistent with our experimental observations. Our model also explains the coexistence of CW and CCW spiral magnetic superstructure within each SCD/MHD, since spirality is determined by the sign of the shear strain, $u_{zr}$, which can be either positive or negative (SI Appendix, Fig. S4). The observed large-density difference of CyMS could be attributed to a nonuniform distribution of local strains in real crystals. We expect the magnitudes of these intrinsic strains to be small (e.g., less than 0.1%), given that no associated features are observed in the AFM topography. Further quantitative studies by other sensitive strain-mapping techniques in the future may be needed to obtain the absolute strain value. Intriguingly, our simulation results resemble a recently predicted “ripple state” in centrosymmetric, honeycomb-lattice antiferromagnet with frustrated exchange interactions (24), although the underlying microscopic mechanisms are completely different. All in all, our simulations demonstrate that strains can have a strong effect on DMI (25) through the magnetoelastic coupling and are thus likely responsible for the observed magnetic textures in Cr_1/3TaS₂.

Fig. 4.

Numerical simulations of spiral magnetic superstructures in Cr_1/3TaS₂ with strains. (A) A sideview schematics of the shear strain $u_{zr}=\frac{1}{2}\left(\frac{\partial u_z}{\partial r}+\frac{\partial u_r}{\partial z}\right)$ in cylindrical coordinates. The z-direction is parallel to the crystalgraphic c-axis. (B) The strain distribution $u_{zr}=U_0\text{exp}\left(\frac{r}{40}-\frac{z}{30}\right)$ used for the simulation, which increases from the center to periphery and decreases from the surface into the bulk (Materials and Methods). Spin configurations in the top layer, for the in-plane horizontal magnetic field (C) h = 0 and (D) h = 0.4, where h is the dimensionless magnetic field pointing from the left to the right of the image. The sign of the strain $u_{zr}$ and induced DMI $D_r$ are negative, which gives rise to the CW spiral magnetic superstructure. (E, F) Corresponding simulated MFM images for C and D, respectively, showing spontaneous spiral magnetic superstructure and concentric rings under magnetic fields.

Discussion

Interestingly, the spiral magnetic superstructures show only slight variations in different magnetic thermal cycles, which suggests that the local strains might be intrinsically embedded in the lattice (SI Appendix, Fig. S5). Given that the strains and the concomitant magnetic patterns can be altered significantly by changing the chiral domain density (Fig. 2), these intrinsic strains are likely associated with SCD walls formed at the achiral-to-chiral transition at ∼980 °C. Thus, the high tuneability of heterochiral domains provides a natural way of strain engineering in Cr_1/3TaS₂, which leads to the formation of exotic magnetic textures. Another interesting possibility is that the strains and magnetic textures appear together spontaneously, as a result of strong magnetoelastic coupling in Cr_1/3TaS₂. On the other hand, the fact that CyMS terminate sharply at SCD walls (Figs. 2C and 3) implies that the coupled structural chirality and magnetic helicity also play a role in the formation of the spiral magnetic superstructure. Therefore, we believe that the topological coupling between structural chirality and magnetic helicity and the strains tunable by structural chiral boundaries are two essential ingredients for the emergence of the spiral magnetic superstructure and CyMS. These magnetic textures, first discovered in Cr_1/3TaS₂, should be generic for chiral helimagnets in which both conditions are met. In particular, it would be interesting to explore the closely related compound, Cr_1/3NbS₂, which could be another host for nanoscale CyMS and macroscopic spiral magnetic superstructures.

Our results show that chiral structures and related topological defects in Cr_1/3TaS₂ occur at a remarkably wide variety of length scales: from the nanometer-sized structural chiral pitch (1.2 nm), magnetic helical pitch (15 nm), and CyMS pitch (∼200 nm or larger) to the macroscopic scale (1 to 100 μm) of topological vortex domains (SI Appendix, Fig. S6), demonstrating rich physics of multiscale topological textures.

In addition to these discoveries in bulk crystals, the layered two-dimensional (2D) nature of Cr_1/3TaS₂ and other magnetic-ion-intercalated TMD compounds (26) offer many exciting research opportunities, such as studies of effects of strain, strain gradients, and lattice dimensionality, and can be used to make functional artificial heterostructures controlled by intrinsic and extrinsic strains.

In summary, we have shown that Cr_1/3TaS₂ is a layered monoaxial chiral helimagnet with a tunable heterochiral state. The size of the chiral domains can be widely tuned by varying the cooling rate at the phase transition, at which the ordering of intercalated Cr ions results in chiral displacements of S ions. The coupled chiral and MHDs form topological vortex patterns in Cr_1/3TaS₂. The sufficiently large domains contain unusual spiral magnetic superstructures, which loose their spirality and transform into arrays of concentric rings under an applied magnetic field. We suggest that the spiral magnetic textures result from intrinsic strains present in the heterochiral state, which favor noncollinear spins. These results open a realm of emergent topological magnetic textures in layered heterochiral materials, which may find applications in strain-tunable magnetic devices, possibly even down to the 2D limit.

Materials and Methods

Crystal Growth.

High-quality plate-like single crystals of Cr_1/3TaS₂ with shiny surfaces and a regular hexagonal shape (SI Appendix, Fig. S1I) were prepared by a chemical vapor transport technique. High-purity raw Cr, Ta, and S powders were mixed and sealed in an evacuated quartz tube and then annealed in a two-zone furnace for 200 h with the hot and cold ends at 1,060 °C and 950 °C, respectively. Afterward, the quartz tube containing crystals was either quenched into iced water or slowly cooled to room temperature at a cooling rate of 20 °C/h or 200 °C/h. X-ray diffraction of the single crystal shows clean (0, 0, L) peaks without any impurity phases (SI Appendix, Fig. S1H).

TEM and L-TEM.

For dark-field TEM, thin specimens with large hexagonal ab-plane surfaces were prepared by mechanical exfoliation followed by Ar-ion milling and studied using a JEOL-2010F field-emission TEM. SCDs were taken using ± ($1/3$, $1/3$, $0)$ superlattice spots along [001] or [102] zone axes under the Friedel’s pair breaking conditions. In situ high-temperature electron diffraction experiments were carried out using a JEOL-2000FX TEM with a high-temperature specimen holder at National Taiwan University in Taiwan. Using a focused ion beam lift-out technique, L-TEM samples were prepared for the observation with the electron beam perpendicular to the c-axis. JEOL ARM 200CF at Brookhaven Lab was used for Lorentz phase imaging with a slightly under-focus (−50 μm). A customized liquid-helium cooling holder (HCHDT3010, Gatan Inc.) was used to cool down specimens to low temperatures.

Magnetic Measurements, MFM, and Micromagnetic Simulations.

Magnetic properties of large shiny Cr_1/3TaS₂ crystals of a regular hexagonal shape were measured in a Magnetic Property Measurement System (Quantum Design). Clean hexagonal ab-plane surfaces of Cr_1/3TaS₂ crystals were scanned using a temperature-variable AFM system (Attocube) with a dual-pass mode (lift height ∼35 nm) and commercial magnetic tips with Co/Cr coating layers. MFM is sensitive to the out-of-plane component of the local magnetization. As all the moments in Cr_1/3TaS₂ lie in the ab-plane, MFM mainly detects stray fields at the domain walls of the helical domains or magnetic antiphase domains. To generate in-plane magnetic fields for the MFM specimen, a large in-plane magnetized permanent magnet was placed beneath the specimen before the cooling process. The magnetic field strength was tuned by varying the thickness of the magnet and measured using a gauss meter before each MFM cooling experiment. Simulations of the MFM image were performed using the built-in MFM function of the software suite Mumax3. The MFM domain pattern was first manually introduced into a drawn image where possible spin configurations can be assigned to all of the domains. Using these possible spin configurations as inputs in Mumax3, simulated MFM images can be obtained to compare with experimental results.

Theoretical Model and Numerical Simulations.

The energy density of the model in cylindrical coordinates $\left(r,\phi ,z\right)$ for the in-plane magnetization vector, $\left(M_x,M_y\right)=M\left(\cos \mathrm{\Phi },\sin \mathrm{\Phi }\right),$ is given by

$$\epsilon =\frac{1}{2}{J}_z{\left({\partial }_z\mathrm{\Phi }\right)}^2+\frac{1}{2}{J}_{\perp }\left[{\left({\partial }_r\mathrm{\Phi }\right)}^2+\frac{1}{r^2}{\left({\partial }_{\phi }\mathrm{\Phi }\right)}^2\right]-D_z{\partial }_z\mathrm{\Phi }-D_r{\partial }_r\mathrm{\Phi }-\frac{D_{\phi }}{r}{\partial }_{\phi }\mathrm{\Phi },$$ [2]

where the first two terms originate from the Heisenberg exchange interactions in the directions parallel and perpendicular to the c-axis, respectively. The third term describes interlayer DMIs, which give rise to the helical spins with the wave vector, $Q_z=\frac{D_z}{J_z}$, along the c-axis. The last two terms result from the strain-induced Lifshitz invariant (Eq. 1) that in cylindrical coordinates has the form, ${\epsilon }_{\text{me}}=-g{M}^2\left(u_{zr}{\partial }_r\mathrm{\Phi }+u_{z\phi }\frac{1}{r}{\partial }_{\phi }\mathrm{\Phi }\right),$ so that $D_r\propto u_{zr}$ and $D_{\phi }\propto u_{z\phi }$. Despite the anisotropic form of this magnetoelastic interaction, it can originate from the Heisenberg exchange striction,

$$-g\text{'}\left(u_{zx}{\partial }_z\mathit{M}\cdot {\partial }_x\mathit{M}+u_{zy}{\partial }_z\mathit{M}\cdot {\partial }_y\mathit{M}\right)=-g\mathit{\text{'}}\left({\partial }_z\mathit{M}\cdot \left(u_{zr}{\partial }_r\mathit{M}+u_{z\phi }\frac{1}{r}{\partial }_{\phi }\mathit{M}\right)\right).$$ [3]

For the helical spins with ${\partial }_z\left(M_x,M_y\right)=Q_{z}M\left(-\sin \mathrm{\Phi },\cos \mathrm{\Phi }\right)$, we then obtain ${\epsilon }_{\text{me}}$ with $g=g\text{'}{Q}_z$.

We minimized the energy of the $71\times 71\times 81$ spin lattice with periodic boundary conditions in the x- and y-directions and open boundary conditions along the z-axis using the Landau–Lifshitz–Gilbert equation with an artificially large damping parameter. Rather than considering planar spins (Eq. 2), we actually simulated Heisenberg spins with strong, easy-plane magnetic anisotropy. The spatially nonuniform strain was modeled by $D_{\phi }=0$ and $D_r=D_{r0}{e}^{\frac{r}{40}-\frac{z}{30}}$, where distances are measured in units of the lattice constant and $z=0$ for the upper layer (Fig. 4B). We have also allowed for spatial variations of the helical spin wave vector, $Q_z$, by considering the r-dependent DMI, $D_z=D_{z0}{e}^{-\frac{r}{40}}$. Fig. 4C showing the spin in the upper layer has been obtained for $\frac{D_{z0}}{J_z}=0.7$ and $\frac{D_{r0}}{J_z}=-0.2$. For $D_{r0}<0$, the spiral unfolds CW from the center to the periphery, whereas for $D_{r0}>0$, it unfolds CCW. The sign change of $D_{z0}$ affects the density of the spiral coils. The spin configuration in the in-plane magnetic field applied along the x-direction was simulated by adding the term $-h\cos \mathrm{\Phi }$ to Eq. 2, where $h\propto H_x.$ $h$ = 0.4 was used to obtain Fig. 4D. Strong z-dependence of $D_r$ gives rise to dislocations in the spatial distribution of the angle $\mathrm{\Phi }$ inside the sample, which may account for sharp magnetic domain walls. Numerical simulation of the dislocations requires, however, much-bigger spin lattices.

Data Availability

All study data are included in the article and/or SI Appendix.