The cost of correcting for error during sensorimotor adaptation

Significance

Improving the process of learning from error can play a critical role in applied settings such as rehabilitation. Previous work has generally focused on reward as a variable that may modulate learning. However, in response to an erroneous movement, the nervous system often engages a reflex that corrects for that error, thus expending time and energy. Here, we modulated this cost of error and found that increasing the cost increased how much the brain learned from error. Thus, the landscape of the loss associated with the act of correcting for error regulates the rates of sensorimotor learning.

Abstract

Learning from error is often a slow process. In machine learning, the learning rate depends on a loss function that specifies a cost for error. Here, we hypothesized that during motor learning, error carries an implicit cost for the brain because the act of correcting for error consumes time and energy. Thus, if this implicit cost could be increased, it may robustly alter how the brain learns from error. To vary the implicit cost of error, we designed a task that combined saccade adaptation with motion discrimination: movement errors resulted in corrective saccades, but those corrections took time away from acquiring information in the discrimination task. We then modulated error cost using coherence of the discrimination task and found that when error cost was large, pupil diameter increased and the brain learned more from error. However, when error cost was small, the pupil constricted and the brain learned less from the same error. Thus, during sensorimotor adaptation, the act of correcting for error carries an implicit cost for the brain. Modulating this cost affects how much the brain learns from error.

In machine learning, the error in the output of an artificial neural network is evaluated by a loss function that depends on the difference between the output and the desired one. This loss function is a mathematical description of the cost of error, which in turn is the principal driver of how much the network learns from error. In analogy to machine learning, during sensorimotor tasks human learning also depends on a loss function (1) that tends to grow with error magnitude (2). This implies that in principle, altering the landscape of the sensorimotor loss function should affect the rate of learning. However, it has been difficult to find ways to modulate the sensorimotor loss function.

Previous approaches have considered inducements such as money (for humans) and food (for animals), thus associating an explicit cost to the movement error. For humans, associating error magnitude with monetary gains or losses can be effective in some cases (3–5) but not others (6, 7). More recent results suggest that when there is an effect of reward on the rate of learning, it acts primarily through recruitment of the explicit, cognitive component of adaptation not the implicit, unconscious component (8). On the other hand, in monkeys the presence of reward for one direction of saccade but not another (9), or one target of visual pursuit but not another (10), tends to increase the rate of learning for the rewarded direction or target.

Here, we began with the idea that if an error occurs during a movement, that error often engages a reflexive response that attempts to correct for the error, which in turn consumes time and energy. Thus, an implicit cost of the erroneous act is the penalty of time and energy paid during correction. For example, if a saccadic eye movement misses the target, the resulting error is followed by a corrective saccade. However, corrective movements carry a cost because they delay the acquisition of reward (11). Thus, a natural loss function for movement error is the time that is expended in the act of producing the correction. If this time could be linked with a utility, then the landscape of the loss function may be altered, resulting in modulation of learning rates.

Here, we designed a paradigm that combined saccade adaptation with decision-making in a random dot motion discrimination task. Like traditional saccade adaptation tasks, subjects made a saccade toward a visual target and experienced an error that encouraged a corrective movement. However, unlike traditional tasks, the corrective saccade carried a cost: it consumed time needed to acquire information for the decision-making task. We varied this cost via coherence of the moving dots and found that increasing the error cost robustly increased how much the brain learned from error.

Results

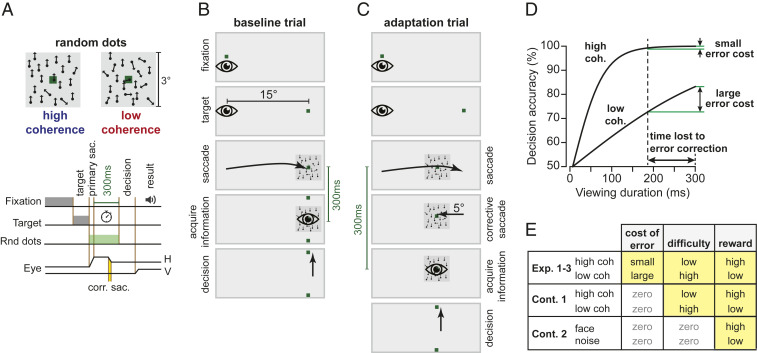
Subjects made center-out horizontal saccades to a visual target (a green dot, 0.5° × 0.5°) at ±15°. At the conclusion of their primary saccade, they viewed an image that contained random dot motion (Fig. 1A). Their objective was to detect the direction of motion of the dots, which was either upward or downward and was reported by making a vertical saccade. After this vertical saccade, feedback was provided regarding decision accuracy.

Fig. 1.

Experiment design. (A) Trials began with a random fixation interval (250 to 750 ms) after which a primary target was placed at ±15° along the horizontal axis. After conclusion of the primary saccade, subjects were presented with a random dot motion image with high or low coherence. The objective was to detect the direction of motion, which was either upward or downward and was reported by making a vertical saccade, after which we provided feedback regarding decision accuracy. Subjects were limited to only 300 ms from the end of their primary saccade to view the image. Thus, the time consumed by the corrective saccade (reaction time and saccade duration) reduced the time available to place the image on the fovea. (B) During the baseline block of trials, the random dot image was presented at the primary target location. (C) During adaptation trials, the image was placed at a location 5° away from the primary target, producing a movement error that was followed by a corrective saccade (gain down). (D) Hypothetical landscape of the error cost. The period spent correcting for error carried a cost that depended on stimulus coherence. (E) We sought to explore the effects of three factors on learning: cost of error, task difficulty, and reward.

In the baseline block, the random dot image was centered at the target (Fig. 1B). However, during the adaptation block the image was centered 5° away from the target, resulting in a gain-down form of adaptation (Fig. 1C). Thus, during adaptation the subjects made a saccade to the target and then followed that with a corrective saccade to a location near the center of the image (SI Appendix, Fig. S1). Importantly, the movement error and the resulting corrective saccade carried a cost because the subject had only 300 ms from the end of their primary saccade to view the image. Thus, if the subject learned from movement error and adapted their primary saccade, the corrective saccade would consume less time, allowing them to view the random dots for a longer period and therefore arrive at a more accurate decision.

In order to modulate the landscape of the loss function, we varied the coherence of the random dots. As the subjects viewed the random dots, their brain accumulated evidence for each possibility (upward or downward motion). Evidence accumulation (Fig. 1D) is roughly the temporal integral of the instantaneous difference between the number of dots that move upward versus downward. This means that evidence grows faster when the motion is more coherent (more of the dots move in a single direction). Because time is lost for correcting for error (reaction time plus movement duration of the corrective saccades), for the low-coherence image this loss will impose a large cost and produce a significant reduction in decision accuracy. In contrast, for the high-coherence image, the same loss will have little or no effect on decision accuracy (12). Thus, by varying motion coherence, we varied the cost of error, which we hypothesized would change learning rates.

In summary, when the target was presented to one side of the screen, coherence of the image was low, making the corrective saccade costly because it took precious time away from viewing the image. However, when the target was presented to the other side of the screen, coherence was high, making the corrective saccade less costly. Critically, the probability of success (reward) was greater for the stimulus that had high coherence, and task difficulty (attention) was greater for the stimulus that had low coherence. Thus, we performed a series of experiments (Fig. 1E) to disentangle the effects of cost of error, task difficulty, and reward.

Cost of Error Increased Both the Rate and the Asymptote of Adaptation.

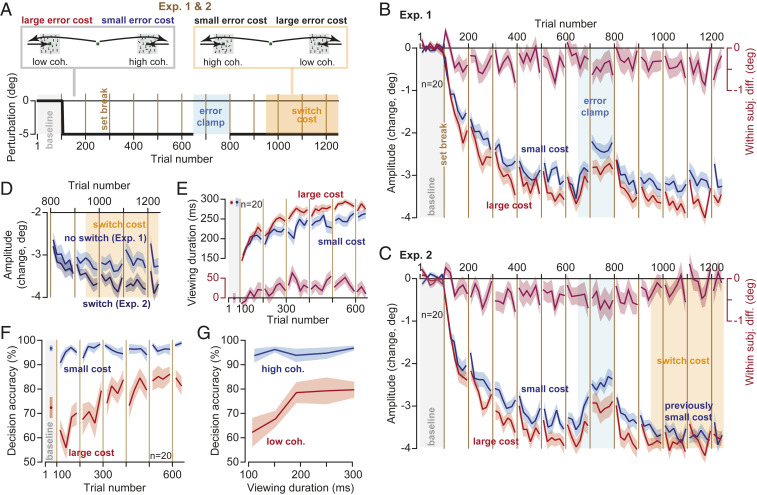
In Experiment 1 (Exp. 1, n = 20 subjects, Fig. 2A), during adaptation trials one target was always associated with large error cost (low image coherence) and the other target was always associated with small error cost (high image coherence). During baseline trials, as well as during adaptation, the probability of a correct decision was much higher for the small-cost target (Fig. 2F, Linear Mixed Models, trials 401 to 650, within-subject effect of cost, F(1,72.375) = 6.144, P = 0.016). Yet, the subjects learned more from errors that carried a large cost (Fig. 2B), as indicated by the fact that adaptation rate was faster for the low-coherence image (Linear Mixed Models on amplitude change, trials 51 to 400, within-subject effect of trial F(1,279.258) = 840.866, P < 0.0005, and trial by cost interaction F(1,114.807) = 4.867, P = 0.029).

Fig. 2.

Cost of error modulated the rate and the asymptote of learning. (A) Subjects experienced 550 adaptation trials followed by 150 error-clamp trials. In Experiment 1 (Exp. 1), this was followed by another 450 adaptation trials (trials 801 to 1,250), which established the asymptote of performance. In Exp. 2, after an initial 150 adaptation trials (trials 801 to 950), at trial 951 without warning the side that previously displayed large-cost stimuli (low coherence) switched to displaying small-cost stimuli (high coherence). (B and C) Amplitude of primary saccades with respect to baseline. Large error cost increased both the rate and the asymptote of adaptation. (D) Increasing the error cost rescued adaptation levels. In Exp. 1, the side that had small cost retained that cost. In Exp. 2, the side that had small cost was switched to a large cost. (E) The time spent viewing the random dot image increased for both the small- and the large-cost stimuli, but the increase was greater for the large-cost stimulus. Faster adaptation provided more viewing time to perform motion discrimination. Data from Exp. 1. (F) Decision accuracy for small- and large-cost stimuli over the course of the experiment. Reward rate was higher for the high-coherence (small error cost) image. Data from Exp. 1. (G) A change in viewing period produced large changes in decision accuracy for the low-coherence image but it had little or no consequence for the high-coherence stimulus. Compare this error landscape to the hypothetical one in Fig. 1D. Data from Exp. 1. Bin size in B–E is 8 trials, in F is 12 trials, and in G is 50 ms. Error bars are SEM.

Following a block of adaptation, we imposed a block of error-clamp trials that eliminated movement error. As expected, without errors to sustain adaptation, saccade amplitude returned toward baseline (Fig. 2B, Linear Mixed Models, trials 651 to 800, within-subject effect of trial, F(1,169.059) = 22.689, P < 0.0005, no trial by cost interaction, F(1,78.921) = 0.022, P = 0.882). Following the error-clamp block, further training brought performance toward a plateau (Fig. 2B, trials 951 to 1,250). However, adaptation remained higher for the side with the larger error cost (Linear Mixed Models, trials 951 to 1,250, within-subject effect of cost F(1,130.828) = 5.466, P = 0.021).

Thus, the rate of adaptation, as well as the asymptote of adaptation, was greater toward the target that carried a large cost of error, not the target that carried a greater probability of success.

Increasing the Cost of Error Rescued Low Adaptation.

If error cost is a causal mechanism that modulates learning from error, then a change in error cost should produce a change in adaptation. Because Exp. 1 had established that the asymptote of adaptation was greater for the large error cost stimulus, we checked whether we could rescue adaptation by increasing its cost.

In Exp. 2, subjects (n = 20) began with stimuli that were identical to Exp. 1: large error cost to one side, small error cost to the other. However, at trial 951 (Fig. 2A, switch cost), without warning the side that previously displayed large-cost images (low coherence) switched to displaying small-cost images (high coherence). Similarly, the side that previously displayed small-cost images switched to displaying large-cost images.

During the initial phase of the experiment (trials 101 to 650), adaptation rate was faster toward the side that carried a large error cost (Fig. 2C, Linear Mixed Models, trial by cost interaction, F(1,105.689) = 8.000, P = 0.006), thus confirming the findings of Exp. 1. However, the switch from small to large cost produced convergence of saccade amplitudes for the two sides (Fig. 2C, Linear Mixed Models, trials 801 to 1,250, trial by cost interaction F(1,234.931) = 9.050, P = 0.003). We compared saccade amplitude in Exp. 1 when there was no switch in cost (during trials 801 to 1,250), with the condition in which the cost switched (Exp. 2). The switch in cost rescued a zero slope learning curve to one that exhibited further learning (Fig. 2D, Linear Mixed Models, trial (within-subject) by switch (between-subject) interaction, F(1,147.996) = 7.138, P = 0.008).

It is noteworthy that adaptation rate was greater for the large-cost stimulus, despite the fact that the stimulus on the opposite side was more rewarding (Fig. 2F, Linear Mixed Models on probability of success, trials 101 to 650, Exp. 1, within-subject effect of cost F(1,196.654) = 165.725, P < 0.0005, as well as a trial by cost interaction F(1,195.069) = 27.166, P < 0.0005). The consequences of greater reward for the small-cost stimulus was readily present in the reaction time of the primary saccades: as in many previous experiments (13–19), saccades toward the more rewarding stimulus exhibited a shorter reaction time (SI Appendix, Fig. S2, Linear Mixed Models, trials 101 to 650, Exp. 1, within-subject effect of trial by cost interaction, F(1,339.649) = 5.320, P = 0.022). That is, greater reward was associated with greater vigor (earlier reaction time), but not better adaptation. Rather, adaptation rate was higher for the stimulus that carried a greater cost.

We assumed that the time spent correcting for error carried a cost that depended on stimulus coherence (Fig. 1D). To check the validity of our assumption, we quantified the relationship between decision accuracy (Fig. 2F) and viewing time (Fig. 2E) for each stimulus. For the high-coherence stimulus, a change in the viewing period produced little or no change in decision accuracy (Fig. 2G). On the other hand, for the low-coherence stimulus a change in viewing period produced large changes in decision accuracy (Fig. 2G, interaction of viewing period by decision accuracy, F(1,69.680) = 5.872, P = 0.018). This confirmed that the time spent correcting for the movement error carried little or no cost for the high-coherence stimulus (small cost), whereas the same expenditure was quite costly for the low-coherence stimulus (large cost).

In summary, adaptation rate was greater toward the stimulus that carried a greater error cost, not the stimulus that was more rewarding. When the error cost increased (switch cost), so did the asymptote of performance, suggesting a causal relationship between the cost of error and adaptation.

Cost of Error Increased Learning from Error and Not Retention.

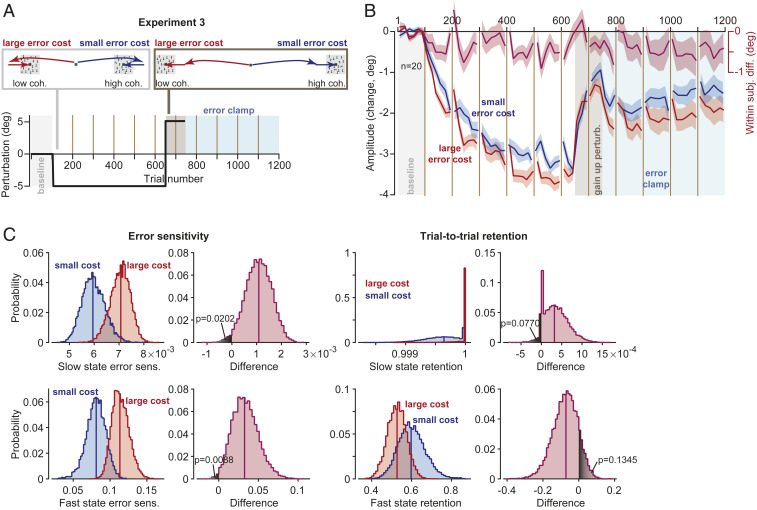
The fact that cost of error modulated the rate of adaptation as well as the asymptote of performance raised the question of whether this cost affected sensitivity to error, trial-to-trial retention, or both. To consider these possibilities, in Experiment 3 we implemented a spontaneous recovery paradigm and then analyzed the results using a state-space model of adaptation (20).

In Exp. 3 (Fig. 3A), subjects (n = 20) began with stimuli that were identical to Exps. 1 and 2: large error cost to one side, small error cost to the other. We again observed that adaptation was faster toward the stimulus with large error cost (Fig. 3B, Linear Mixed Models, trials 51 to 400, trial by cost interaction, F(1, 105.334) = 4.635, P = 0.034). After the initial adaptation period, we reversed the direction of movement errors (trials 651 to 750) to induce “extinction,” resulting in a sharp change in saccade amplitude toward baseline. Following error reversal, subjects experienced a long period of error-clamp trials (trials 751 to 1,200). As expected (21), during the error-clamp period saccade amplitude exhibited spontaneous recovery toward the adapted state (Fig. 3B, trials 751 to 850, Linear Mixed Models, within-subject effect of trial, F(1,151.553) = 6.019, P = 0.015).

Fig. 3.

Cost of error affected sensitivity to error but not retention. (A) Experiment design for the spontaneous recovery paradigm. (B) Amplitude of primary saccades with respect to baseline. (C) A two-state model was fit to the data, and error sensitivity and retention were estimated for the fast and slow states using a permutation procedure (Methods). The plots show the resulting distribution of parameter values and the within-population differences in parameter values due to change in cost. Bin size in B is eight trials. Error bars are SEM.

We next applied a state-space model and estimated error sensitivity and trial-to-trial retention. When the cost of error was large, error sensitivity was elevated for both the slow (Fig. 3C, permutation n = 10,000, P = 0.0202, one-tailed) and the fast state (Fig. 3C, P = 0.0088, one-tailed). In contrast, cost of error did not appear to affect trial-to-trial retention (Fig. 3C, slow state, permutation n = 10,000, P = 0.0770, one-tailed; fast state, P = 0.1345, one-tailed).

To check the robustness of this result, we reconsidered the data during the adaptation period in Exp. 1, 2, and 3 (SI Appendix, Fig. S3A), with the caveat being that because this data set did not contain a spontaneous recovery period, we did not have sufficient power to consider a two-state model and thus fitted a single-state set of equations. We again found that error sensitivity was larger for the large-cost target (SI Appendix, Fig. S3D, permutation n = 10,000, P = 0.0167, one-tailed), with no significant effect on the trial-to-trial retention (SI Appendix, Fig. S3D, permutation n = 10,000, P = 0.4671, one-tailed).

In summary, cost of error increased sensitivity to error, not retention.

Faster Adaptation Provided More Time for Decision-Making.

We had assumed that adaptation would afford subjects more time to view the image and thus help them make more accurate decisions. To check for this, we combined the data for the three experiments (n = 60 subjects). As expected, large error cost coincided with a faster rate and a greater extent of adaptation (SI Appendix, Fig. S3A, Linear Mixed Models, trials 51 to 400, within-subject effect of trial, F(1,805.341) = 2,375.814, P < 0.0005, trial by cost interaction, F(1,325.928) = 11.707, P = 0.001, and trials 401 to 650, within-subject effect of cost, F(1,314.388) = 7.305, P = 0.007). This increased rate of adaptation for the large-cost stimulus provided more time to view the moving dots (SI Appendix, Fig. S3B, Linear Mixed Models, trials 101 to 400, within-subject effect of trial, F(1,777.619) = 474.593, P < 0.0005, trial by cost interaction, F(1,315.380) = 8.398, P = 0.008, and trials 401 to 650, within-subject effect of cost, F(1,286.550) = 5.409, P = 0.021). Finally, as saccades adapted and the viewing period increased, so did decision accuracy (SI Appendix, Fig. S3C). The impact of increased viewing period on decision accuracy was much greater when time was more valuable (i.e., low-coherence stimulus, SI Appendix, Fig. S3C, trials 101 to 400, trial by cost interaction, F(1,218.776) = 15.681, P < 0.0005).

Control Experiments: Eliminating the Error Cost Equalized Rates of Adaptation.

There are potential confounds in our interpretation. First, the task was harder for the low-coherence stimulus, making it possible that learning rate was not driven by the cost of error but rather the greater attention or cognitive load required for the more difficult task. Second, the probability of reward (success) was lower for the low-coherence stimulus. It is conceivable that the increased reward impaired adaptation rates. Thus, we performed a series of additional experiments (Fig. 1E).

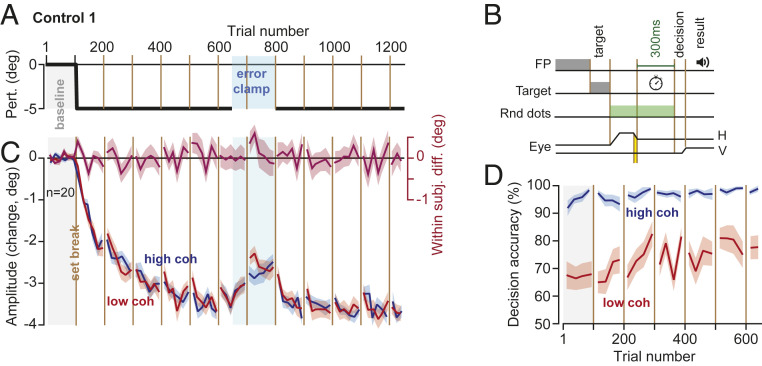
To test for the effect of task difficulty, we performed an experiment (Control 1) in which the cost of error was equal for the two stimuli, but task difficulty was greater for one of them. Subjects (n = 20) made a primary saccade to targets at ±15° and again were presented with an image that was centered 5° away (Fig. 4A). However, unlike the main experiments, here the subjects were provided with 300 ms to view the random dot image regardless of their primary saccade amplitude. That is, the time allowed to view the image did not start until eye position was within 2° of the center of the image (Fig. 4B). With this subtle change, we removed the cost associated with movement error: now the time expended during error correction did not affect the period available to view the image.

Fig. 4.

Control experiment: eliminating the error cost equalized rates of adaptation. (A and B) Design was similar to Exp. 1 to 3, with one crucial difference; the time available for viewing the random dot image did not start until the eye landed around the image. Thus, the subjects had 300 ms to view the random dots regardless of their primary saccade amplitude. (C) Primary saccade amplitude with respect to baseline. There were no significant within-subject differences in the rate or asymptote of adaptation. (D) Decision accuracy (and thus success rate) remained high for the high-coherence image. Bin size in C is 8 trials, in D is 12 trials. Error bars are SEM.

As before, decision accuracy was greater for the side that contained the high-coherence image, confirming that on one side the task remained more difficult than the other (Fig. 4D, Linear Mixed Models, trials 401 to 650, within-subject effect of coherence, F(1,81.687) = 30.455, P < 0.0005). Indeed, decision accuracy at both start and end of adaptation was similar among Control 1 and the main experiment groups (Linear Mixed Models, no between-subject effect of experiment type, F(2,294.000) = 2.258, P = 0.106, or trial by experiment type interaction, F(2,294.000) = 2.035, P = 0.133). However, while saccade amplitude exhibited adaptation (Fig. 4C, Linear Mixed Models, trials 51 to 400, within-subject effect of trial, F(1,280.370) = 808.509, P < 0.0005), we found no significant within-subject difference between the low- and high-coherence stimuli (Fig. 4C, Linear Mixed Models, trials 401 to 650, no within-subject effect of coherence, F(1,94.522) = 0.650, P = 0.422, trials 51 to 400, no trial by coherence interaction, F(1,116.255) = 2.548, P = 0.113). Furthermore, we found no significant within-subject difference in the asymptotic learning between the two types of stimuli (Fig. 4C, Linear Mixed Models, trials 951 to 1,250, no within-subject effect of coherence, F(1,108.028) = 0.189, P = 0.665).

To check for the influence of reward independent of both the cost of error and task difficulty, we performed a second control experiment. In Control 2 (SI Appendix, Fig. S4), the primary target was always a noisy image. However, when this image appeared to one side, there was a 50% probability that following the onset of the primary saccade it would be replaced with the image of a face, thus producing a positive reward prediction error (15). When it appeared on the other side, it remained the same noisy image. We found that both the primary saccade (SI Appendix, Fig. S4 B, Lower plot, Linear Mixed Models, trials 1 to 650, within-subject effect of reward prediction error, F(1,308.942) = 4.362, P = 0.038) and the corrective saccade (SI Appendix, Fig. S4C, Linear Mixed Models, trials 101 to 650, within-subject effect of reward prediction error, F(1,266.928) = 18.103, P < 0.0005) had shorter reaction times for the stimulus that was paired with positive reward prediction errors. However, the increased reward had no significant effect on adaptation rates (SI Appendix, Fig. S4 B, Upper plot, Linear Mixed Models, trials 51 to 400, no within-subject effect of trial by reward prediction error interaction, F(1,85.624) = 1.130, P = 0.291, trials 401 to 650, no effect of reward prediction error, F(1,106.906) = 0.866, P = 0.354).

Another limitation of our main experiments was that while one direction of movement experienced a high error cost, another direction experienced a low cost. Can error cost be used to increase learning for all directions? To answer this question, we performed a multiday experiment (Exp. 4, n = 16 subjects, SI Appendix, Fig. S5A). During one session, all targets were paired with a high error cost, but on a different session (a week apart) this cost was removed. We found that the increased cost of error enhanced the learning rate (SI Appendix, Fig. S5C, main group, Linear Mixed Models, trials 41 to 320, within-subject effect of trial by cost interaction, F(1,117.319) = 5.895, P = 0.017, trials 241 to 320, within-subject effect of cost, F(1,44.825) = 4.859, P = 0.033). In addition, during a control experiment (SI Appendix, Fig. S5C, control group, n = 14 subjects, Linear Mixed Models, trials 41 to 320, within-subject effect of trial by cost interaction, F(1,137.468) = 5.752, P = 0.018, trials 241 to 320, within-subject effect of cost, F(1,52.387) = 5.237, P = 0.026) in which one direction of movement was paired with cost of error while the other direction was not, we again confirmed the findings of our main experiments.

In summary, eliminating the cost of error while maintaining task difficulty eliminated the effects on the learning rates. Increasing the reward rate while keeping task difficulty and cost of error constant produced no changes in learning rates. Thus, among the three variables that we considered (cost of error, task difficulty, and reward rate), cost of error alone was a robust factor in modulating the learning rates.

Pupil Dilation Coincided with Increased Cost of Error.

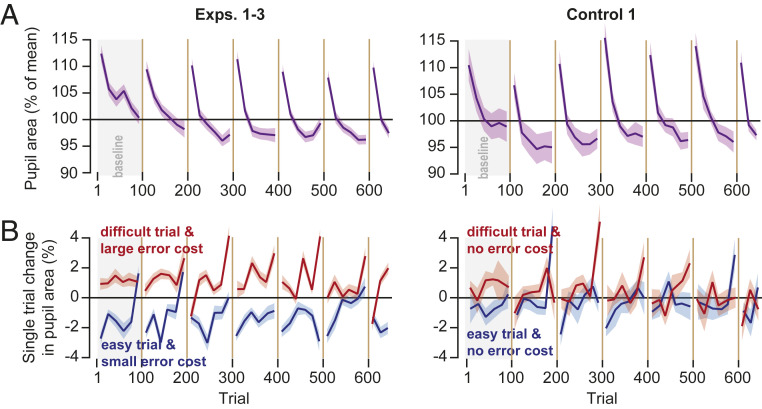
What might be the neural mechanism that links cost of error with adaptation? To approach this question, we considered pupil dilation as a proxy for activation of the brainstem neuromodulatory system (22). We measured pupil diameter as subjects fixated the center target and found that at the onset of each block the pupil was dilated but then progressively constricted as the trials continued (Fig. 5A). Following a set break, the pupil once again dilated. These patterns were present in the main experiments, as well as in Control 1 (Fig. 5A, Linear Mixed Models, trials 101 to 600, within-subject effect of trial, main experiments: F(1,1728.945) = 476.108, P < 0.0005; Control 1: F(1,568.797) = 244.765, P < 0.0005). If we view pupil diameter as a proxy for arousal, then it appears that there was a general decline in arousal within each block of trials, followed by sharp recovery due to set breaks.

Fig. 5.

Pupil diameter changed in response to trial conditions. (A) Pupil area at the beginning of each trial, normalized to the overall mean. Pupil was most dilated when the block of trials started. It gradually constricted as the trials continued within the block, then recovered following a set break. (B) Within-trial change in pupil diameter as a function of trial conditions. The plots show the change in pupil diameter from fixation at the start of each trial to onset of fixation at the start of the subsequent trial. Pupil area increased in the trial that had increased difficulty but error cost of that trial modulated this increase. Bin size is eight trials. Error bars are SEM.

Next, we asked how the conditions of each trial affected pupil diameter. For each subject and each trial, we compared pupil size at center fixation (trial onset) to the fixation at the onset of the next trial before the target was displayed. This within-trial response served as our proxy for how the neuromodulatory system reacted to the events that had transpired during that trial.

We found that in the baseline block, the trials that were more difficult (low coherence) produced pupil dilation, whereas trials that were easy (high coherence) produced pupil constriction (Fig. 5B). The difference in the pupil response to the stimulus content of each trial was present in the baseline block of both the main group and the control group (Fig. 5B, Linear Mixed Models, trials 1 to 100, within-subject effect of coherence, main experiments: F(1,330.466) = 55.835, P < 0.0005; control experiment: F(1,106.150) = 5.191, P = 0.025). Thus, as has been noted before (23), when the trial included a more difficult decision-making process, requiring a greater cognitive load, it produced greater pupil dilation.

In the main experiments, as the adaptation blocks began the pupil continued to dilate in trials that were difficult and had large cost (Fig. 5B, Linear Mixed Models, trials 101 to 650, within-subject effect of cost, F(1,1256.571) = 111.057, P < 0.0005). In the Control 1, the trials were still more difficult for the low-coherence stimulus, but the error cost was equalized between the two stimuli. Interestingly, in the control experiment the pupil response to trial difficulty appeared to dissipate (Fig. 5B, Control 1, Linear Mixed Models, trials 101 to 650, no within-subject effect of coherence, F(1,507.790) = 1.224, P = 0.269). We were concerned that this difference in the two groups may have been because of the larger group size in the main experiments. However, the statistical pattern was also present in each of the main experiments (Linear Mixed Models, trials 101 to 650, within-subject effect of cost, Exp. 1: F(1,424.491) = 91.192, P < 0.0005; Exp. 2: F(1,404.040) = 19.123, P < 0.0005; Exp. 3: F(1,435.689) = 21.073, P < 0.0005). In addition, comparing the within-subject difference in within-trial pupil dilation between Exp. 1 and Control 1 showed an effect of experiment type (Linear Mixed Models, trials 101 to 650, between-subject effect of experiment type, F(1,1316) = 20.427, P < 0.0005).

In summary, the pupil progressively constricted during each block of trials, suggesting a waning of attention but then dilated following each set break, suggesting partial recovery. The pupil also responded to the conditions of each trial: in more difficult trials (low coherence), the pupil dilated. However, cost of error modulated this response; the within-trial change in pupil diameter was greater when the trial was both difficult and incurred a large error cost.

Discussion

When movements produce an unexpected outcome, the nervous system often produces a reflexive response that corrects for error. This corrective movement consumes time and energy, providing an implicit loss that may affect learning. Here, we used saccade adaptation as a model of sensorimotor learning and explored whether imposing a cost on the time spent correcting for error could modulate learning from error.

To impose a cost on error, we combined decision-making with adaptation. In the resulting paradigm, it was costly to make a movement that ended with a large error because both visual acuity and the ability to detect differential motion drops rapidly with distance from the fovea (24). Thus, the erroneous saccade was followed by a corrective movement that placed the image on the fovea but took time away from the limited period available to acquire information and make an accurate decision. By modulating the value of time, we modulated the cost of error and found that an increased error cost robustly increased the rates of sensorimotor adaptation.

However, imposing a cost of error also changed other aspects of the task: its difficulty, and its reward rate. For example, errors that were more costly occurred in trials in which decision-making was more difficult and thus the reward rate was lower. To find the effects of error cost independently of task difficulty and reward rate, we performed two control experiments. In Control 1, we maintained the disparity in difficulty and the rate of reward but removed the error cost. This eliminated the effects on the learning rates. In Control 2, we maintained the disparity in the rate of reward but removed task difficulty and error cost. This also eliminated the effects on the learning rates. Thus, error cost stood out as the critical factor that modulated learning rates.

Earlier studies have considered the effects of explicit inducements on retention of motor memories (3, 25, 26). For example, Abe et al. (25) showed that monetary reward was effective in improving retention of motor memories during a force-tracking task. Galea et al. (3) also found that during a visuomotor rotation task presence of reward was associated with greater retention. In contrast, Steel et al. (27) reported that during serial-reaction-time and force-tracking tasks, neither reward nor punishment benefitted retention. We implemented a spontaneous recovery paradigm and assessed the effects of error cost on both error sensitivity and trial-to-trial retention. We found that while error cost increased error sensitivity, it did not have a significant effect on retention.

Meermeier et al. (28) examined effects of implicit reward on saccade adaptation by using neutral (noise) or highly engaging images. They found that adaptation rates were not affected when the time allowed to view the images was unrestricted. Our Control 2 experiment confirmed this finding. However, Meermeier et al. (28) observed that when they limited the time that the subjects had to view the highly engaging images, the result was an increase in the learning rates. If we view their results in the framework of cost of error, we see that while increasing reward had no effect on adaptation rates, imposing a cost on the corrective saccade (limiting the time available to view the valuable image) increased the rate of adaptation.

There are of course other factors that influence how much the brain learns from error (2, 29–31). For example, Marko et al. (2) and Hanajima et al. (32) noted that error sensitivity was relatively high for small errors and low for large errors. Herzfeld et al. (33) and Leow et al. (34) showed that in environments where errors were likely to be consistent, subjects increased their error sensitivity. Albert et al. (35) observed that large variability in the trial-by-trial sequence of errors tended to suppress learning from error. Conscious of these potential pitfalls, we kept the perturbation size consistent over the course of the experiment and also controlled the statistics of the error that the subjects experienced as they made saccades. Despite this, the rate of learning was greater toward the stimulus that carried a greater error cost.

We found that increasing the cost of error rescued low adaptation, suggesting a potentially causal relationship between the cost of error and adaptation rates. Previous studies (35, 36) have also found that modulating error sensitivity affected the asymptote of performance during motor learning.

In our saccade task, the pupil progressively constricted as the trials wore on within a block of trials, suggesting a decline in arousal (37), but then dilated following the set break at the start of the next block, suggesting a partial recovery. The resulting saw-tooth pattern in pupil diameter was reminiscent of behavioral changes during adaptation in many other experiments: rapid adaptation that follows set breaks, and gradual adaptation that ensues with progression of trials (21, 38–40).

Within each trial, during the baseline block the pupil dilated in response to stimuli that required greater mental effort (low-coherence stimuli) and constricted in response to stimuli that required smaller effort (high-coherence stimuli). During the adaptation block, when the stimuli carried an error cost the pupil continued to dilate in response to the high-cost, greater mental effort stimuli. However, when the error cost was equalized in the control experiment, the dilation in response to stimuli that required greater mental effort waned. These results raise the possibility that pupil dilation is not only a correlate of attention and mental effort invested in the task but also a correlate of learning from error.

The potential link between pupil diameter and learning from error is noteworthy because it may highlight one pathway with which the brain modulates learning. Changes in pupil size are due to a band of muscles that surround the pupil, which in turn are controlled by motoneurons that reside in the Edinger–Westphal nucleus in the brainstem. Neurons in the intermediate layers of the superior colliculus project to this nucleus (41). As a result, weak microstimulation of the intermediate layers of the superior colliculus can produce a transient increase in pupil diameter that reaches its peak at around 300 to 500 ms (42, 43). Notably, some superior colliculus neurons project to the contralateral inferior olive (44), which provide climbing fibers that carry error information to Purkinje cells of the cerebellum. For example, the climbing fiber carries information regarding the visual error following conclusion of a saccadic eye movement (45–48), which in turn guides plasticity in Purkinje cells and affects trial-to-trial learning (49). Notably, the amount that the cerebellum learns from error may be related to the state of the superior colliculus: in trials in which collicular neurons respond more strongly to the visual error, there is greater trial-to-trial learning (50, 51). Thus, on the one hand the superior colliculus contains the neural machinery to control pupil size and on the other hand, it provides information to the cerebellum regarding saccade-related visual errors.

Improving how we learn from our erroneous movements is a critical factor in applied settings such as rehabilitation (6). Previous work has generally focused on reward as a variable that may modulate learning. Here, we took advantage of the fact that movements that contain an error are often followed by corrective actions. By imposing a cost on this corrective action, we found a way to help the brain learn faster.

Methods

Subjects.

A total of n = 128 healthy subjects (18 to 54 y of age, mean ± SD = 23 ± 7, 66 females) participated in our study. The procedures were approved by the Johns Hopkins School of Medicine Institutional Review Board. All subjects signed a written consent form.

Data Collection Procedure.

We considered three factors that could influence motor learning: cost of error, task difficulty, and reward. Our experiment design is summarized in Fig. 1E and SI Appendix, Fig. S5B.

In main experiments (1 to 3), control 1, and control 2, participants sat in front of an LED (light-emitting diode) monitor (27-inch, 2,560 × 1,440 pixels, light gray background, refresh rate 144 Hz) placed at a distance of 35 cm while we measured their eye position at 1,000 Hz (Eyelink 1000+). Each trial began with presentation of a fixation point (a green dot, 0.5° × 0.5°) that was drawn near the center of the screen; the fixation point was placed randomly in a virtual box at −1° to +1° along the horizontal axis and −1° to +1° along the vertical axis, where (0, 0) refers to center of the screen. After a random fixation interval of 250 to 750 ms (uniform distribution), the fixation point was erased, and a primary target was placed at 15° to the right or left along the horizontal axis.

In the main experiments (1 to 3), removal of the central fixation and presentation of the primary target (a green dot, 0.5° × 0.5°) served as the go signal for the primary saccade. After detecting primary saccade onset, the primary target was erased and a random dot image was displayed. The image was a 3° × 3° box with invisible borders containing a 0.5° × 0.5° green dot at the center and 100 0.1° × 0.1° white dots moving at 5°/s either upwards or downward with a predefined coherence.

The coherence was implemented via the portion of the dots that were moving either upwards or downward (the rest of the dots were moving in a random direction). For example, if the coherence was 75% in upward direction, 75 points moved at 90° at 5 °/s speed and 25 points moved at 25 randomly assigned directions with 5 °/s speed. The locations of the 100 dots were assigned randomly at the beginning. When a dot hit one of the invisible borders, its position got reset to the opposite border while maintaining its angle and speed. The source code for generating the random dot image is available for download from the project’s OSF (Open Science Framework) repository (https://doi.org/10.17605/osf.io/H24J8, ESN_Moving_Dots.c). In addition, a Matlab version of the code was included along with the c-code (ESN_Moving_Dots.m).

The location of random dot image was defined based on the trial type: during baseline trials the image was centered at primary target location. During perturbation trials, the image was centered at 5° from the primary target toward the center of the screen. During error-clamp trials, the image was centered at the location of the primary saccade offset.

During adaptation trials, following completion of the primary saccade subjects produced a corrective saccade to place the random dot image on their fovea. This corrective movement carried a cost because it reduced the time available for the subject to view the image. This is because following detection of primary saccade offset, the image was available for only a limited time. The limited availability of the information and the fact that corrective saccade’s reaction time and execution time took away time from viewing this image were key factors in our experiment design.

In the main experiments (1 to 3), the image was present for only 300 ms after primary saccade offset. This was the only time available to view the image and decide on the direction of motion of the random dots. Following this 300-ms period, the image was erased, and two targets were displayed at 5° above and below the image. Subjects reported their perceived direction of motion by making an upward or downward saccade. Following this decision, they received feedback regarding their decision accuracy via an auditory tone: a 1,000 Hz (beep) 30-ms long sound for a correct decision and a 500 Hz (boop) 30-ms long sound for an incorrect decision. At the end of this period, the decision targets were removed, and the center fixation point appeared at a random location near the center of the screen, in the bounding box defined above.

Modulating Cost of Error.

During the adaptation phase of the main experiments, the viewing period was set to be up to 300 ms from primary saccade offset, but in practice, at the beginning of learning it was around 150 ms due to reaction time and duration of the corrective saccade. Thus, by adapting the primary saccade (reducing the size of the corrective saccade), subjects would have more time to view the image, increasing the accuracy of perceiving the direction of motion. To vary the cost of error, trials consisted of two types of stimuli. For targets on one side of the screen, coherence of the random dots was low (65 to 75%), imposing a large cost on the error; the corrective saccade took precious time away from viewing the moving dots. For targets on the other side of the screen, coherence of the random dots was high (95 to 100%). Here, the error cost was small: the time consumed by the corrective saccade was relatively inconsequential for the ability to perceive motion of the dots.

In a control experiment (Control 1, described below), subjects received 300 ms to view the random dot image irrespective of the level of the adaptation. This served to remove the cost of error for the low- and high-coherence stimuli.

Experiments 1 to 3.

The logic of these experiments is illustrated in Fig. 1E. n = 60 subjects participated in Exp. 1 to 3 (20 subjects in each). Each experiment started with 50 familiarization trials (no perturbations). During these trials, the images appeared at the primary target location at various coherence levels to familiarize the participants with the saccadic task and motion discrimination paradigm. The collected data during the familiarization period was excluded from analysis.

After the familiarization block, the baseline block commenced. The baseline consisted of 100 trials and ended with a 30-s set break. In this block, subjects experienced 50 low-coherence trials on one side of the screen and 50 high-coherence trials on the other side. The coherence side was counterbalanced between subjects. Since each subject experienced both type of stimuli (low versus high coherence), we used a within-subject comparison for all statistical analysis.

Next, subjects experience 550 gain-down perturbation trials (trials 101 to 650), during which the random dots image was displayed 5° away from the primary target toward the center of the screen. The consistent experience of this perturbation gradually resulted in adaptation of the primary saccades. We asked how does cost of error modulated the rate of adaptation.

All experiments included an error-clamp period. In these trials, the perturbation was removed, and the image was centered at the end position of the primary saccade.

Control 1.

This experiment (n = 20 subjects) removed cost of error but maintained task difficulty and reward as factors that could influence the rate of learning. In contrast to Exp. 1 to 3 in which the time to view the image was reduced because of the corrective saccade, in this control experiment (Fig. 4B) the timer did not start until the eye landed around (4° × 4°) the random dot image (3° × 3°). This made it so that the time spent correcting for error did not compete with the time needed to view the random dot motion, thus equalizing the cost of error for the low- and high-coherence images.

Control 2.

This experiment (SI Appendix, Fig. S4, n = 18 subjects) removed cost of error as well as task difficulty but maintained implicit reward as a factor that could influence the rate of learning. The primary target was always the image of a noise patch (3° × 3°), presented at ±15° with respect to central fixation. A green dot always appeared at the center of every image. Upon initiation of the primary saccade, the primary target was erased and replaced by another image at 5° closer to central fixation. When the primary target was to one side, the replacement image had 50% probability of being a face, thus resulting in a positive reward prediction error (15). For the other side, the replacement image was always a noise patch, thus resulting in a zero reward prediction error. The facial images were gathered from the Internet (500 total images) and were modified in a way that the center of the two eyes was located at the center of the image. The noise images were constructed by shuffling the pixels of each face image (500 × 500 pixels). This ensured that the luminance and color content of the two categories were identical.

Experiment 4 and Control 3.

Our main experiments (Exp. 1 to 3) introduced a high error cost for one direction of movement and a low error cost for another direction. In a more general setting, one would wish to enhance learning rates in all directions. To test whether this could be achieved, in Exp. 4 (n = 16 subjects, SI Appendix, Fig. S5A) we tested the same subjects on two sessions, separated by one week.

We simplified the decision-making task: rather than judging the direction of motion of random dots, subjects had a limited amount of time (250 ms from primary saccade offset) to view a cue image. In some trials, this cue image provided them with information necessary for decision-making. In other trials, the cue image was irrelevant for decision-making.

In Exp. 4 and Control 3, participants sat in front of an LED monitor (32-inch, 1,920 × 1,080 pixels, light gray background, refresh rate 60 Hz) placed at a distance of 40 cm while we measured their eye position at 1,000 Hz (Eyelink 1000+). Each trial began with presentation of a crosshair-shaped fixation stimulus (1.5° × 1.5°) around the center of the screen. During the fixation, a target (the image that represented the number “0,” 1.5° × 1.5°) appeared at ±15° for 200 ms, but the subjects were not allowed to saccade to it. Rather, they waited for the removal of the fixation stimulus (an additional 200 to 500 ms) and then made a saccade to the remembered location. At the onset of this primary saccade, the cue target (1.5° × 1.5°) was placed 5° away from the previewed target. The cue target contained either a stimulus that carried a large cost or no cost. For example, if the cue image contained three black dots, then the correct decision was a saccade to the target labeled “3” (1.5° × 1.5°). If the cue image contained random noise, then the image was irrelevant for decision-making—the correct decision was a saccade to any target.

In the main group (SI Appendix, Fig. S5B), during one session 90% of the cues on both sides were images that were important for decision-making and thus carried a large error cost. During another session, 90% of the cues on both sides were irrelevant for decision-making and thus had zero error cost. The sessions were counterbalanced across the participants.

In the control group (n = 14 subjects), we sought to reproduce the results of the main experiments in this simplified decision-making paradigm. Thus, we tested the subjects during a single session, with movements to one side encountering images that had a high error cost and movements to the other side encountering zero cost (SI Appendix, Fig. S5B, control group).

Data Analysis.

Eye position data were acquired using an EyeLink 1000+ system (SR Research) at 1,000 Hz. During the online data acquisition, we used a second-order Savitzky–Golay filter with seven datapoints to estimate the eye velocity. The onset of the primary saccades was detected when the eye velocity increased above 20°/s or the eye position left the area (4° × 4°) around the start target (whichever happened first). The source code for online estimation of eye velocity is available for download from the project’s OSF repository (https://doi.org/10.17605/osf.io/H24J8, ESN_Eye_Filt.c). Primary saccade offset was detected when the eye velocity fell below 75 °/s and the eye position was inside a rectangle (9° × 4°), which contained the area around the primary and secondary target locations and the region in between.

Eye position data in offline analysis were filtered with a second-order Butterworth low-pass filter with cutoff frequency of 100 Hz. Eye velocity data were calculated as the derivative of the filtered position data. Saccades were identified with a speed magnitude threshold of 20°/s and minimum hold time of 10 ms at saccade end (i.e., velocity magnitude could not exceed the cutoff for a minimum 10 ms after endpoint). Corrective saccade onset and offset were detected identically to the primary saccades, using 20°/s threshold on velocity magnitude. We measured change in primary saccade amplitude with respect to the average saccade amplitude in the first block in each condition.

Viewing period of the random dot image was measured based on the amount of time that the eye position was inside of an imaginary box of size 4° × 4° centered on the image. In the case of the Control 1 experiment, the moment when the eye position entered this region started the 300-ms timer.

Decision accuracy was measured based on the number of correct decision responses divided by the total number of trials for each condition (high versus low coherence).

Pupil area was measured by EyeLink 1000+ system (SR Reseach) and was reported in the system’s arbitrary pixel coordinate system. We blanked this data during eyeblink events to account for divergence in eye tracking. To combine and compare the pupil data across participants and experiments, we measured the percentage change for each participant by dividing the pupil data by the average pupil area over the entire recording for that subject. To control for differences in visual stimulus properties, we computed the average normalized pupil area during 200-ms window of time when participants were fixating on the start target (0.5° × 0.5° green dot). Next, we measured the change in normalized pupil area from one trial to the next to quantify how the conditions of each trial affect pupil dilation (Fig. 5B).

Statistical analyses were performed using SPSS and Linear Mixed Models. We used stimulus type (two levels, categorical) and bins of trials (multiple levels, hierarchical) and tested within-subject effect of those independent variables. To test between-subject effect of experiment type, we used Linear Mixed Models with bins of trials (multiple levels, hierarchical, within-subject variable) and experiment type (two levels, categorical, between-subject variable) without repeated measurements as independent variables. Statistical analyses were performed under the assumption of first-order autoregressive to model the covariance matrix. We used intercept, stimulus/experiment type, bins of trials, and trial by stimulus/experiment type interaction as fixed effects and the intercept as a random effect.

State-Space Model of Learning.

After the experience of a movement error, humans and other animals change their behavior on future trials. In the absence of error, adapted behavior decays over time. Here, we used a state-space model (20) to capture this process of error-based learning. Here, the internal state of an individual x, changes from trials n to n+1 due to learning and forgetting:

$$x^{(n+1)}=a{x}^{\left(n\right)}+b^{\left(n\right)}{e}^{\left(n\right)}+{\epsilon }_x^{\left(n\right)}.$$ [1]

Forgetting is controlled by the trial-to-trial retention a. The rate of learning is controlled by the error sensitivity b. Learning and forgetting are stochastic processes affected by internal state noise ${\epsilon }_x$: a normal random variable with zero-mean and SD of ${\sigma }_x$.

While we cannot directly measure the internal state of an individual, we can measure their movements. The internal state x leads to a movement y according to the following:

$$y^{\left(n\right)}=x^{\left(n\right)}+{\epsilon }_y^{\left(n\right)}.$$ [2]

The desired movement is affected by execution noise, represented by ${\epsilon }_y$: a normal random variable with zero-mean and SD of ${\sigma }_y$. To complete the state-space model described by Eqs. 1 and 2, we must operationalize the value of an error, e. In sensorimotor adaptation, movement errors are determined both by motor output of the participant (y) and the size of the external perturbation (r):

$$e^{\left(n\right)}=r^{\left(n\right)}-y^{\left(n\right)}.$$ [3]

We used Eqs. 1–3 to estimate the trial-to-trial retention a and error sensitivity b during each experiment design.

We used permutation (10,000 iterations) of the population data to estimate the parameters of the single-state and two-states models. We formed population data by randomly sampling (with replacement) the subjects and then computed the average adaptation curve for the population. In each iteration for each subject, we stacked all the data for a given stimulus type together and as a result formed two time series for each subject, one for each stimulus type. Then, since the number of trials were balanced over subjects and stimuli, we combined the data for a given stimulus and computed the average population data for that stimulus. We fitted single-state and two-states models of the learning to the population data using Least Mean Square optimization method.

After computing the distribution of each model parameter, we next computed the distribution of within-population difference between the large- and small-cost conditions. To test whether there was a significant effect of cost, we used the within-population difference and integrated the region from zero (no difference) to minus infinity, resulting in a P value (Fig. 3C and SI Appendix, Fig. S3D). It should be mentioned that the P value computed here was a one-tailed P value and should be compared to 0.025 for the two-tailed assumption.

Data Availability

Anonymized data and codes have been deposited in OSF (Open Science Foundation) repository https://doi.org/10.17605/OSF.IO/H24J8 (52).