Electrochemical removal of amphoteric ions

Significance

Water treatment is required for a sustainable potable water supply and can be leveraged to harvest valuable elements. Crucial to these processes is the removal of charge pH-dependent species from polluted water, such as boron, ammonia, and phosphate. These species can be challenging for conventional technologies. Currently, boron removal requires several reverse-osmosis stages, combined with dosing a caustic agent. Capacitive deionization (CDI) promises to enable effective removal of such species without chemical additives but requires a deep understanding of the coupled interplay of pH dynamics, ion electrosorption, and transport phenomena. Here, we provide a detailed theory tackling this topic and show both theoretically and experimentally highly counterintuitive design rules governing pH-dependent ion removal by CDI.

Abstract

Several harmful or valuable ionic species present in seawater, brackish water, and wastewater are amphoteric, weak acids or weak bases, and, thus, their properties depend on local water pH. Effective removal of these species can be challenging for conventional membrane technologies, necessitating chemical dosing of the feedwater to adjust pH. A prominent example is boron, which is considered toxic in high concentrations and often requires additional membrane passes to remove during seawater desalination. Capacitive deionization (CDI) is an emerging membraneless technique for water treatment and desalination, based on electrosorption of salt ions into charging microporous electrodes. CDI cells show strong internally generated pH variations during operation, and, thus, CDI can potentially remove pH-dependent species without chemical dosing. However, development of this technique is inhibited by the complexities inherent to the coupling of pH dynamics and ion properties in a charging CDI cell. Here, we present a theoretical framework predicting the electrosorption of pH-dependent species in flow-through electrode CDI cells. We demonstrate that such a model enables insight into factors affecting species electrosorption and conclude that important design rules for such systems are highly counterintuitive. For example, we show both theoretically and experimentally that for boron removal, the anode should be placed upstream and the cathode downstream, an electrode order that runs counter to the accepted wisdom in the CDI field. Overall, we show that to achieve target separations relying on coupled, complex phenomena, such as in the removal of amphoteric species, a theoretical CDI model is essential.

Global freshwater scarcity is increasing due to population growth, increased water consumption per capita, and shrinking freshwater bodies due to climate change and overextraction (1–3). About 4 billion people are subject to severe water scarcity for at least 1 mo per year (4), and increasing parts of the global population are predicted to face chronic water scarcity (5). Consequently, there has been increasing demand for efficient water treatment and desalination technologies over the past few decades (6, 7). Water treatment also provides an opportunity for recovery of valuable elements from feedwater (8, 9).

Commonly used technologies for water treatment and desalination are pressure-driven, membrane-based separation technologies, such as reverse osmosis (RO) (7, 10, 11), nanofiltration, and ultrafiltration (12, 13). In these membrane processes, water is pressed through the membrane, while the membrane retains ions and other compounds to a certain degree. Two important mechanisms for the rejection of ions and molecules by membranes are size exclusion (14, 15) and charge repulsion (14–16). An ion’s volume includes its hydration shell, which often plays an important role in the rejection.

The charge of several common pollutants and valuable solutes depends on solution pH, and such species are characterized as amphoteric, weak acids or weak bases. Arsenic acid, As(V), and especially arsenous acid, As(III), are toxic ions and, therefore, should be removed during drinking water treatment (17–19). Boron is considered toxic when at high concentrations in water (20, 21) and can be detrimental to plant growth (22–24). Phosphate and ammonia should be removed from wastewater, as these ions can negatively affect the surface-water quality when present at high concentrations (1, 25–27). They are also desirable to recover during water treatment (8, 9, 27–29), as they are important nutrients (30). Acetate is a small amphoteric organic acid and is often removed and recovered during sugar production (31, 32). As the hydrated radius of the previously mentioned species varies with charge, rejection of such species by membranes is generally pH-dependent and may be highly challenging under certain conditions (33).

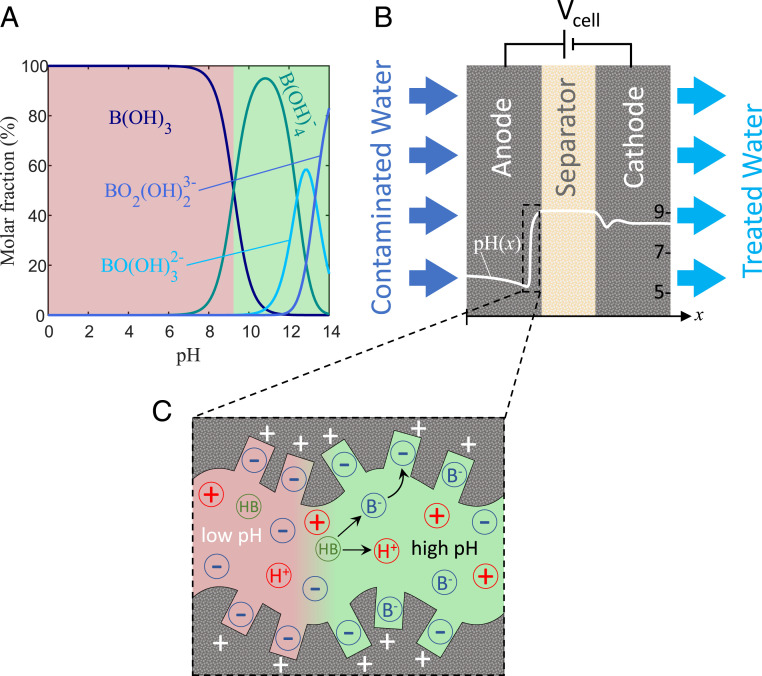
Boron is an example of an amphoteric ion that can be poorly rejected in membrane-based systems. Boron is present in a protonated form, B(OH)₃, under standard pH conditions (pH of surface water is generally between 7 and 8) and can dissociate into ${{\mathrm{B}\left(\mathrm{O}\mathrm{H}\right)}_4}^{-}$ and ${{\mathrm{B}\mathrm{O}\left(\mathrm{O}\mathrm{H}\right)}_3}^{2-}$ at higher pH (Fig. 1A). Since B(OH)₃ is not charged, the hydration of the molecule is weak, and B(OH)₃ passes through an RO membrane more easily, resulting in a low removal rate. Boron removal is generally only around 50 to 60% for feedwater with a pH below 8, but values as low as 10 to 30% have also been reported (34–38). To increase boron removal with RO, it is a common practice to pass desalinated water multiple times through an RO membrane (39–41). Another practice is to dose, after the first RO pass and before the second RO pass, a caustic solution to adjust pH to higher values (41–43). This adjustment results in boron primarily appearing as ${{\mathrm{B}\left(\mathrm{O}\mathrm{H}\right)}_4}^{-}$ and ${{\mathrm{B}\mathrm{O}\left(\mathrm{O}\mathrm{H}\right)}_3}^{2-}$ species, which are blocked by the RO membrane due to their larger hydrated size and their negative charge.

Fig. 1.

Schematic demonstrating boron removal by a CDI cell. (A) Boron is pH-dependent in water and plotted is the molar fraction of the various boron-containing species as a function of water pH. (B) A CDI cell with an anode placed upstream and a snapshot of the developed pH profile within the electrodes. (C) A snapshot of ion and charge distributions near the anode/separator interface, showing boric acid dissociation and electrosorption.

Capacitive deionization (CDI) is an emerging membraneless electrochemical separation technology used for water treatment and desalination. CDI cells employ a cyclic process of alternatingly charging and discharging a pair of porous electrodes, for instance, made of microporous carbon particles. During the charging step, ions are removed from the feedwater by electrosorption into the electrodes, and during discharge, the electrodes are regenerated, and ions are released into a brine stream. Several cell designs for CDI have been proposed, including flow-by electrode CDI, membrane CDI, and flow-through electrode (FTE) CDI (44), the latter schematically shown in Fig. 1B. In FTE CDI, the solution flows through the electrodes (44, 45), which allows the use of a thinner separator compared to other cell designs, enabling reduced cell resistance (46) and faster desalination, but can lead to enhanced electrode degradation (47, 48). Recent breakthroughs in CDI focus on its ability to remove ions selectively from polluted feedwaters (49–56) and new electrode materials based on intercalation compounds or Faradaic reactions (57–61).

During charging of a CDI cell with microporous electrodes, large pH differences naturally develop in the cell, with pH values as high as $\sim$10 reported in the cathode and as low as $\sim$3 in the anode (62, 63). Several mechanisms have been proposed to explain these pH differences, including side reactions such as oxygen reduction (62–66), the difference in diffusion coefficients between ionic species present in solution, and electrosorption of H⁺ and ${\mathrm{O}\mathrm{H}}^{-}$ (48, 62, 66). Thus far, one theoretical model was developed including pH effects in membrane CDI (66), with significant deviations between model and experiment, and no models have been developed for membraneless CDI, to our knowledge. Thus, pH effects and dynamics in CDI remain poorly understood, and the in situ-generated pH gradients in a CDI cell remain largely unexploited.

In the present work, we utilize these strong differences in local pH of charging CDI cells to ensure that amphoteric species, weak acids and weak bases are charged and consequently can be electrosorbed into the electrodes (Fig. 1 B and C). Though there are several experimental studies (67–76), no theory has yet been developed to predict and guide the removal of such species by CDI. However, given the complexities involving pH dynamics in CDI, a validated model is essential to unlock the enormous potential of CDI to remove amphoteric ions without the need for chemical additives to adjust feed pH. We here provide such a theory, a model coupling electrosorption into micropores to local pH dynamics and acid–base equilibria with a transient description of multicomponent ion transport in porous electrodes and for the case with pH-dependent ions present in the feed. Our model predicts highly counterintuitive design rules for the removal of such species by CDI, which we validate experimentally using boron as a case study. In future work, the theoretical framework presented here can be adapted to any mixture of amphoteric species and can more generally be used to improve the understanding of pH dynamics in electrochemical systems.

Results and Discussion

In this section, we employ the theoretical framework presented in Materials and Methods. This model captures local pH variations in the CDI cell and the simultaneous electrosorption of pH-dependent species present in the feedwater. We consider an FTE CDI cell (see Fig. 1B) with feedwater containing both salt and a pH-dependent species. To electrosorb the latter species effectively, they must be present in an ionic form while flowing through the CDI cell. For example, ammonia is largely protonated and positively charged at neutral and low pH values ($\mathrm{p}{K}_{\mathrm{a}}$ 9.25), while boron is largely deprotonated and negatively charged at high pH conditions ($\mathrm{p}{K}_{\mathrm{a}}$ 9.24) (Fig. 1A). Thus, to remove boron, high pH is required in the anode, and for ammonia removal, neutral or low pH is required in the cathode.

Here, we illustrate the theory by analyzing the electrosorption of boron as a case study and compare the theoretical predictions to experimental data. We consider the case where pH does not exceed the value of 10, as model results will show that boron acts as a buffer to maintain pH below 10 at conditions studied here. Therefore, we neglect the presence of ${\text{BO(OH)}}_3^{\hspace{0.17em}2-}$ and BO₂${\text{(OH)}}_2^{\hspace{0.17em}3-}$ in the solution (Fig. 1A), and we only account for B(OH)₃, which hence will be referred to as HB, and ${{\mathrm{B}\left(\mathrm{O}\mathrm{H}\right)}_4}^{-}$, which will be denoted ${\mathrm{B}}^{-}$. The feedwater we consider has a composition resembling the effluent from an RO system, so with relatively low salt (NaCl) concentration on the order of $\sim 1\hspace{0.17em}\mathrm{m}\mathrm{M}$, a boron concentration of 0.37 mM (4 mg/L), and a near-neutral pH $\left(6\le {\mathrm{p}\mathrm{H}}_{\mathrm{F}}\le 7\right)$ (77).

Electrode Order Affects Local pH and Boron Removal.

The order of the electrodes refers to which electrode is placed upstream and which downstream in the FTE CDI cell. This order directly affects local pH values and, ultimately, will be a central consideration for successful boron removal. Conventional wisdom is that during CDI cell charging, the solution in the cathode macropores becomes basic and in the anode acidic (62, 64). Naively, we may expect that at feed velocities characterized by Péclet number of order unity and above ($\mathrm{P}\mathrm{e}\equiv v_{\mathrm{w}}{l}_{\mathrm{e}}/D_{\mathrm{s}}$, with $v_{\mathrm{w}}$ the superficial flow velocity, $l_{\mathrm{e}}$ the electrode thickness, and $D_{\mathrm{s}}$ the effective salt diffusion coefficient; Table 1), the cathode should be placed upstream so that the high pH solution can be advected into the anode, allowing for boron electrosorption. As we will show, model and experimental results both prove that this expectation is not correct.

Table 1.

Parameters used in all the simulations performed for this research

Property	Value	Description
$l_{\mathrm{a}\mathrm{n}}=l_{\mathrm{c}\mathrm{a}\mathrm{t}}=l_{\mathrm{e}}$	0.6 mm	Electrode thickness*
$m_{\mathrm{a}\mathrm{n}}=m_{\mathrm{c}\mathrm{a}\mathrm{t}}=m_{\mathrm{e}}$	0.109 g	Electrode mass*
$l_{\mathrm{s}\mathrm{e}\mathrm{p}}$	$65\hspace{0.17em}\mathrm{\mu }\mathrm{m}$	Separator thickness*
$p_{\mathrm{s}\mathrm{e}\mathrm{p}}$	0.8	Separator porosity*
${\tau }_{\mathrm{s}\mathrm{e}\mathrm{p}}$	$p_{\mathrm{s}\mathrm{e}\mathrm{p}}^{-0.5}$=1.12	Separator tortuosity*
$l_{\mathrm{r}\mathrm{e}\mathrm{s}}$	40$l_{\mathrm{e}}$=24 mm	Reservoir thickness†
$p_{\mathrm{r}\mathrm{e}\mathrm{s}}$	1	Reservoir porosity†
${\tau }_{\mathrm{r}\mathrm{e}\mathrm{s}}$	$p_{\mathrm{r}\mathrm{e}\mathrm{s}}^{-0.5}$=1	Reservoir tortuosity†
$D_{\mathrm{s}}$	$\frac{1}{2}{\left(D_{\mathrm{N}\mathrm{a}}^{-1}+D_{\mathrm{C}\mathrm{l}}^{-1}\right)}^{-1}$=	Salt equivalent diffusion
	1.576 ${\mathrm{m}}^2/\mathrm{s}$	coefficient
$t_{\mathrm{c}\mathrm{o}\mathrm{l}}$	10 min	Effluent collection time*
$V_{\mathrm{m}\mathrm{i}\mathrm{x}}$	1.86 mL	Downstream mixing volume*
$A_{\mathrm{c}}$	6.25 ${\mathrm{c}\mathrm{m}}^2$	Electrode cross-section area*

^*Parameters obtained from the experimental setup.

^† Parameters used to describe long reservoirs.

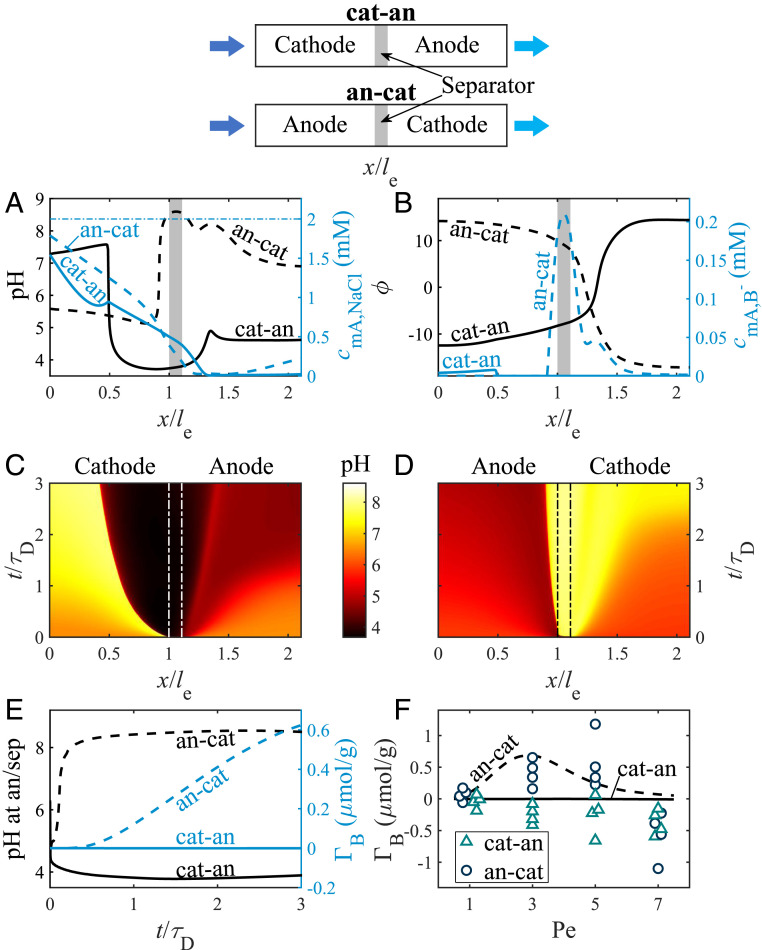
In Fig. 2 A–E, we compare the predicted salt, boron, potential, and pH profiles of two cell configurations operated with Pe = 3 and a charging voltage of $V_{\mathrm{c}\mathrm{h}}=$1.0 V (Tables 1 and 2). In the first configuration, the cathode is placed upstream (cat-an; solid lines), and for the second, the cathode is placed downstream (an-cat; dashed lines). Fig. 2A shows predicted pH profiles (left y axis, black lines) and macropore salt concentration (right y axis, blue lines), defined by $c_{\mathrm{m}\mathrm{A},\mathrm{N}\mathrm{a}\mathrm{C}\mathrm{l}}\equiv \frac{1}{2}\left(c_{{\mathrm{m}\mathrm{A},\mathrm{N}\mathrm{a}}^{+}}+c_{{\mathrm{m}\mathrm{A},\mathrm{C}\mathrm{l}}^{-}}\right)$, both as a function of the location scaled by $l_{\mathrm{e}}$ and at $t/{\tau }_{\mathrm{D}}=2$, where ${\tau }_{\mathrm{D}}$ is the electrode diffusion time, defined as $l_{\mathrm{e}}^2/D_{\mathrm{s}}$. In Fig. 2A, we see that for both configurations, the salt concentration decreases through the upstream electrode in the flow direction and is close to zero throughout most of the downstream electrode. For the cat-an configuration, the pH profile includes three distinct regions. First, in the upstream electrode (cathode) near the inlet, there is a relatively high pH of $\sim$7.5. In the downstream half of the cathode, a sharp pH decrease to $\sim$3.7 is observed. The latter feature runs contrary to conventional wisdom that the solution in the charging cathode is alkaline (62, 78). Then, toward the downstream region of the anode, pH rises again to values of $\sim$4.6. For the an-cat configuration, the pH profile is changed significantly, with pH $\sim$5.8 in the upstream part of the anode, followed by a sharp increase in pH close to the separator to $\sim$8.6. The latter feature is contrary to conventional wisdom, that solution in the charging anode is acidic (62, 78). Decreasing pH values are predicted along the flow direction in the cathode, reaching a value of $\sim$6.9 at the effluent.

Fig. 2.

Predictions and experimental results for an FTE CDI cell with cathode placed upstream (cat-an; solid lines) or downstream (an-cat; dashed lines) for feed salt concentration, $c_{\mathrm{F}}$, of 2 mM; feed boron concentration, $c_{\mathrm{F},\mathrm{B}}$, of 0.37 mM; and charging voltage, $V_{\mathrm{c}\mathrm{h}}$, of 1.0 V, where in A–E, Pe = 3. (A) Predicted pH (left y axis, black lines) and macropore salt concentration (right y axis, blue lines) profiles in the FTE CDI cell. (B) Predicted dimensionless potential (left y axis, black lines) and ${\mathrm{B}}^{-}$ macropore concentration (right y axis, blue lines) profiles. The profiles in A and B are snapshots at $t/{\tau }_D=2$, the gray-shaded rectangles represent the separator, and the horizontal dash-dotted blue line in A represents the feed salt concentration. (C and D) pH in the macropores as a function of dimensionless location and time for cat-an configuration (C) and an-cat (D) configuration. The vertical dash-dotted lines in C and D represent the electrode/separator interfaces. (E) Predicted pH at the anode/separator interface (left y axis, black lines) and electrosorbed boron (right y axis, blue lines), both as a function of dimensionless time. (F) Predicted (lines) and measured (markers) boron electrosorption for an effluent collection time of 10 min as a function of Pe for cat-an (solid line, triangles) and an-cat (dashed line, circles) configurations. Schematics of the two configurations are presented at the top of the figure.

Table 2.

System parameters for simulations compared to experiments (Figs. 2 and 3) or used only for theoretical analysis (Fig. 4)

Property	Value (Figs. 2 and 3)	Value (Fig. 4)	Description
${\mathrm{p}\mathrm{H}}_{\mathrm{F}}$	6.$\mathrm{3}$*	7.0†	Feed pH
$c_{\mathrm{F},\mathrm{B}}$	0.37 m$\mathrm{M}$*	0, 0.37 m$\mathrm{M}$*	Feed boron concentration
EER	2.$\mathrm{57}\hspace{0.17em}\mathrm{\Omega }$‡	$\mathrm{0}\hspace{0.17em}\mathrm{\Omega }$ †	Electronic resistance
$p_{\mathrm{m}\mathrm{A}}$	$\mathrm{0.70}$ *	0.70*	Macropores porosity
${\tau }_{\mathrm{m}\mathrm{A}}$	$p_{\mathrm{m}\mathrm{A}}^{-0.5}$=$\mathrm{1.20}$*	$p_{\mathrm{m}\mathrm{A}}^{-0.5}$=$\mathrm{1.20}$*	Macropores tortuosity
$p_{\mathrm{m}\mathrm{i}}$	0.$\mathrm{154}$*	0.172†	Micropores porosity
$C_{\mathrm{S},\mathrm{X}}=C_{\mathrm{S},\mathrm{Y}}$	200 F/mL‡	150 F/m L†	Stern capacitance
${\alpha }_{\mathrm{m}\mathrm{i},\mathrm{X}}$	0.5	0.5	Acidic groups volume fraction
$c_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{X},\mathrm{t}}$	0.80 M‡	0.25 M†	Concentration of acidic groups
$\mathrm{p}{K}_{\mathrm{X}\mathrm{H}}$	4.9‡	5.0†	Reaction’s pK in the acidic region
${\alpha }_{\mathrm{m}\mathrm{i},\mathrm{Y}}$	1-${\alpha }_{\mathrm{m}\mathrm{i},\mathrm{X}}$=0.5	1-${\alpha }_{\mathrm{m}\mathrm{i},\mathrm{X}}$=0.5	Basic groups volume fraction
$c_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{Y},\mathrm{t}}$	0.60 M‡	0.25 M†	Concentration of basic groups
$\mathrm{p}{K}_{{\mathrm{Y}\mathrm{H}}^{+}}$	8.5‡	9.0†	Reaction’s pK in the basic region

^*The values obtained from the experimental setup.

^† The values assumed for hypothetical pristine electrodes.

^‡ The values obtained from characterization experiments (SI Appendix, Section S3).

Thus, the results of Fig. 2A indicate that the anode should be placed upstream for effective boron removal, counter to our naive expectation. To gain more insight into this unexpected behavior, Fig. 2B shows predicted profiles for dimensionless potential, $\varphi$ (left y axis, black lines), and macropore ${\mathrm{B}}^{-}$ concentration, $c_{\mathrm{m}\mathrm{A},{\mathrm{B}}^{-}}$ (right y axis, blue lines), at $t/{\tau }_{\mathrm{D}}=2$. The potential profiles in Fig. 2B for both configurations are not symmetric about the cell midline, and we see that for both configurations, by far, the strongest electric field (potential gradient) occurs just downstream of the separator. As expected based on the results of Fig. 2A, $c_{\mathrm{m}\mathrm{A},{\mathrm{B}}^{-}}$ for the cat-an configuration is approximately zero across the cell, as the pH is too low for significant boric acid deprotonation. However, for the an-cat configuration, we observe low values in most of the upstream electrode (anode), followed by a strong increase near the anode/separator interface, reaching a maximum value of 0.21 mM at the separator as boric acid is deprotonated in that region, followed by a decrease and lower values of $\sim$0.04 mM in the cathode. Thus, due to strong boric acid deprotonation within the anode, the an-cat configuration is highly promising for effective boron electrosorption.

We argue that this unexpected finding is due to the complicated interplay between salt depletion, H⁺ and ${\mathrm{O}\mathrm{H}}^{-}$ electrosorption and electromigration, and water splitting (Eq. 14). For example, for the an-cat configuration, the low salt concentration $\left(c_{\mathrm{m}\mathrm{A},\mathrm{N}\mathrm{a}\mathrm{C}\mathrm{l}}<0.2\hspace{0.17em}\mathrm{m}\mathrm{M}\right)$ in the cathode leads to enhanced H⁺ electrosorption into the micropores and can cause increases in local ${\mathrm{O}\mathrm{H}}^{-}$ production due to water splitting. The strong electric field in the upstream end of the cathode can increase ${\mathrm{O}\mathrm{H}}^{-}$ electromigration into the anode, increasing pH in the anode, as seen in Fig. 2A.

To expand our understanding of the pH dynamics, we plot in Fig. 2 C and D the spatiotemporal pH (pH as a function of dimensionless location and time) in the macropores for cat-an configuration (Fig. 2C) and an-cat configuration (Fig. 2D). In accordance with the pH profiles presented in Fig. 2A, the solution in the downstream electrode is acidic for the cat-an configuration and basic for the an-cat configuration. Moreover, we observe very sharp pH gradients propagating through the cell for both configurations, resembling a shockwave. For example, in Fig. 2C, we see a sharp front between basic and acidic solution propagating from the separator into the cathode, with decreasing front velocity in time. Macropore salt-concentration profiles with similar features have been observed for CDI (79–81), where their formation was explained by diffusion limitations; i.e., the strong salt adsorption into the micropores results in very low salt concentrations, termed ion starvation, which restrains the downstream ionic fluxes (81). Similarly, here, we hypothesize that the appearance of pH shock-like fronts is a consequence of the strong electrosorption of either H⁺ or ${\mathrm{O}\mathrm{H}}^{-}$ ions by the downstream electrode. Simultaneously, the downstream fluxes of H⁺ and ${\mathrm{O}\mathrm{H}}^{-}$ do not balance the enhanced electrosorption, resulting in a depleted region that develops and propagates upstream. In other electrokinetic systems, such as nanochannel–microchannel systems, ion-concentration shockwaves have been observed, propagating with a constant velocity (82). Here, we observe the shock-like fronts propagate with time-dependent velocity, which may be related to the multitude of additional phenomena affecting this system, including advection, electrosorption, and acid–base equilibria. We find that the pH shock-like front propagates faster for the cat-an configuration compared to the an-cat configuration, perhaps due to the differing diffusion coefficients between the cations (H⁺ and Na⁺) and anions (${\mathrm{O}\mathrm{H}}^{-}$, ${\mathrm{C}\mathrm{l}}^{-}$ and ${\mathrm{B}}^{-}$).

To explore the boron dynamics of our CDI cell model, Fig. 2E shows the predicted pH at the anode/separator interface (left y axis, black lines) and the cumulative electrosorbed boron by the cell, ${\mathrm{\Gamma }}_{\mathrm{B}}$ (Eq. 18) (right y axis, blue lines), as a function of time for the cat-an (solid lines) and an-cat (dashed lines) configurations. The pH at the anode/separator interface is a crucial metric. The majority of the anode pore space is generally acidified relative to the feed, so it is only near the anode/separator interface, adjacent to the alkaline solution in the cathode, where boric acid deprotonation and subsequent boron ion electrosorption can occur (Fig. 2 A and D). For both configurations, we observe rapid development of the pH values at the anode/separator interface, before $t/{\tau }_{\mathrm{D}}\sim$ 0.4, to near steady values of $\sim$3.8 for the cat-an configuration and $\sim$8.5 for the an-cat configuration. Thus, for essentially the entire charging process, the an-cat configuration can electrosorb boron, as the solution at the anode/separator interface is alkaline. Predicted boron electrosorption monotonically increases for $t/{\tau }_{\mathrm{D}}\ge$ 0.5, reaching a value of $0.62\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ at $t/{\tau }_{\mathrm{D}}$ = 3. The selectivity of the CDI cell to electrosorb boron over chloride can be quantified by the selectivity factor, ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}$ (Eq. 21), and we find for the an-cat configuration at $t/{\tau }_{\mathrm{D}}$ = 3 a value of ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}$ = 0.42. The latter value shows that ${\mathrm{C}\mathrm{l}}^{-}$ is preferred over boron by the CDI cell. However, we consider this a highly promising result, as 99.89% of all boron in the feedwater is in the neutrally-charged boric acid form.

To validate the model predictions, we compare our theoretical findings with experimental data (see Materials and Methods for details). In Fig. 2F, we plot theoretical (lines) and experimental (markers) values of ${\mathrm{\Gamma }}_{\mathrm{B}}$, as a function of Pe. We include predictions and measurements for boron removal in both cat-an (solid line, triangles) and an-cat (dashed line, circles) configurations. The theoretical predictions in Fig. 2F show an effective boron removal by the cell for the an-cat configuration, where no removal is expected for the cat-an configuration. While comparing theory and experimental results in Fig. 2F, we observe some qualitative agreement for the an-cat configuration for low and moderate flow velocities $\left(1\le \mathrm{P}\mathrm{e}\le 5\right)$. For Pe = 3, we measured a mean boron removal of $0.41\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$, compared to a predicted value of $0.65\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$, where for Pe = 5, we measured a mean boron removal of $0.56\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$, compared to a predicted value of $0.24\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$. However, for high flow velocity $\left(\mathrm{P}\mathrm{e}=7\right)$, we obtain a mean negative value of $-0.57\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$, indicating boron desorption during cell charging. As predicted by the model, for all conditions tested, no significant boron removal was measured in the cat-an configuration. Rather, boron desorption was measured for all analyzed flow velocities. For example, at Pe = 7, a mean boron removal of $-0.38\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ was measured. The desorbed boron likely entered the micropores during the preceding discharging half-cycle, but the model does not predict this desorption phenomenon. Future work can further explore these phenomena, which may result from parasitic Faradaic side reactions, which are not included in the model for this work. Overall, the counterintuitive model prediction that an-cat is the preferred electrode order was also confirmed experimentally.

Optimum Charging Voltage for Boron Removal.

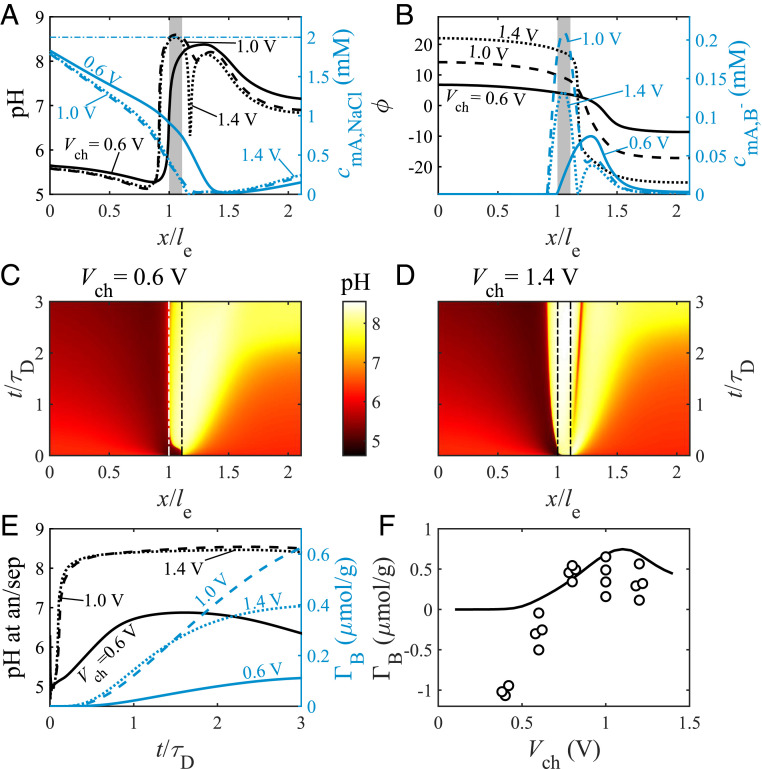
We further investigate the effects of charging voltage on pH dynamics and boron removal, now focusing on a cell with an-cat electrode order. Naively, we would expect to observe a monotonic increase of boron removal with the charging voltage, as previous experimental observations show that pH perturbations in the anode and cathode become more extreme with increased cell voltage (62, 63). In Fig. 3 A–E, we show the predicted salt and charge dynamics of a cell operated with $c_{\mathrm{F}}$ = 2 mM, Pe = 3, and charging voltages of 0.6 V (solid lines), 1.0 V (dashed lines), and 1.4 V (dotted lines); see Tables 1 and 2 for other model parameters used. Fig. 3A shows the profiles of pH (left y axis, black lines) and macropore salt concentration (right y axis, blue lines) at $t/{\tau }_{\mathrm{D}}=2$. The pH profiles for all investigated charging voltages bear significant similarities: acidic values in most of the anode, followed by a strong rise near the anode/separator interface to alkaline values, and maintaining high pH across the separator and much of the cathode. For relatively high $V_{\mathrm{c}\mathrm{h}}$, we observe a distinct pH local minimum in the cathode near to the separator, with a minimum of 8.0 for $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V, and a much lower value of 6.3 for $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V. The salt-concentration profiles for all the analyzed charging voltages bear similarities to the profile presented in Fig. 2A for the an-cat configuration. The salt-concentration profile for $V_{\mathrm{c}\mathrm{h}}$ = 0.6 V decreases more gradually throughout the anode than for higher charging voltages, reaching the minimum concentration farther downstream into the cathode.

Fig. 3.

Predictions and experimental results for an FTE CDI cell with feed salt concentration, $c_{\mathrm{F}}$, of 2 mM; feed boron concentration, $c_{\mathrm{F},\mathrm{B}}$, of 0.37 mM; and Pe = 3. Predictions in A–C are for charging voltage, $V_{\mathrm{c}\mathrm{h}}$, of 0.6 V (solid lines), 1.0 V (dashed lines), and 1.4 V (dotted lines). (A) Predicted pH (left y axis, black lines) and macropore salt concentration (right y axis, blue lines) profiles. (B) Predicted dimensionless potential (left y axis, black lines) and ${\mathrm{B}}^{-}$ macropore concentration (right y axis, blue lines) profiles. The profiles in A and B are for $t/{\tau }_D=2$, gray rectangles represent the separator, and the horizontal dash-dotted blue line in A represents feed salt concentration. (C and D) pH in the macropores as a function of dimensionless location and time for $V_{\mathrm{c}\mathrm{h}}$ of 0.6 V (C) and 1.4 V (D). The vertical dash-dotted lines in C and D represent the electrode/separator interfaces. (E) Predicted pH at the anode/separator (an/sep) interface (left y axis, black lines) and electrosorbed boron (right y axis, blue lines), both as a function of dimensionless time. (F) Predicted (line) and measured (markers) boron electrosorption for an effluent collection time of 10 min versus $V_{\mathrm{c}\mathrm{h}}$.

Fig. 3B presents profiles of $\varphi$ (left y axis, black lines) and macropore ${\mathrm{B}}^{-}$ concentration (right y axis, blue lines) at $t/{\tau }_{\mathrm{D}}=2$. As with Fig. 2B, the potential profiles are asymmetric about the cell midline, and the electric field is highest in the cathode near the separator. The location of the strongest electric field coincides with a sharp local minimum in pH, as seen in Fig. 3A for the case of $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V. For all cell voltages analyzed, the macropore ${\mathrm{B}}^{-}$ concentration is near zero in most of the anode, followed by a sharp increase near the anode/separator interface. For $V_{\mathrm{c}\mathrm{h}}$ = 0.6 V, the maximum of 0.075 mM occurs in the cathode, coinciding with the location of minimum salt concentration seen in Fig. 3A. However, the maximum values of 0.21 mM for $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V and 0.13 mM for $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V occur in the separator. Unexpectedly, these results suggest that boron electrosorption will be less effective at $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V than $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V, which can be explained by the slightly higher pH values developed for $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V presented in Fig. 3A. We explain the lower pH values at $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V by the lower local pH minimum in the cathode for this case. This pH minimum coincides with a local minimum in Na⁺ concentration (SI Appendix, Fig. S1A). Thus, for extremely low Na⁺ concentrations, the local pH decreases instead of increases.

Next, we plot in Fig. 3 C and D the spatiotemporal pH in the macropores for $V_{\mathrm{c}\mathrm{h}}=$0.6 V (Fig. 3C) and 1.4 V (Fig. 3D), where the results for $V_{\mathrm{c}\mathrm{h}}=$1.0 V are presented in Fig. 2D. Similar to Fig. 2 C and D, we observe sharp propagating pH gradients, where for $V_{\mathrm{c}\mathrm{h}}=$1.4 V, we also observe the development of a local pH minimum in the cathode, propagating downstream. The front propagating upstream through the anode for $V_{\mathrm{c}\mathrm{h}}=$1.4 V propagates with time-dependent velocity, similarly to the front for $V_{\mathrm{c}\mathrm{h}}=$1.0 V (Fig. 2D). However, the front near the anode/separator interface for $V_{\mathrm{c}\mathrm{h}}=$0.6 V seems to be static for $0.3\le t/{\tau }_{\mathrm{D}}\le 2.8$ and slowly propagates downstream for $t/{\tau }_{\mathrm{D}}\ge 2.8$, which we explain by the balance between the H⁺ flux downstream and the lower H⁺ electrosorption by the cathode compared to higher $V_{\mathrm{c}\mathrm{h}}$ values. The sharp pH minimum zone in Fig. 3D propagates downstream through the cathode with approximately constant velocity, in accordance with our hypothesis that it is related to the location of near-zero Na⁺ concentration, which also propagates in a similar manner (SI Appendix, Fig. S1B).

To probe the effect of $V_{\mathrm{c}\mathrm{h}}$ on the boron electrosorption dynamics, in Fig. 3E, we plot predicted pH at the anode/separator interface (left y axis, black lines) and ${\mathrm{\Gamma }}_{\mathrm{B}}$ (right y axis, blue lines), both as a function of dimensionless time for charging voltages of 0.6 V (solid lines), 1.0 V (dashed lines), and 1.4 V (dotted lines). For $V_{\mathrm{c}\mathrm{h}}$ = 0.6 V, we observe relatively low pH values at this interface for the entire charging step, never surpassing 7. However, for $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V and 1.4 V, we can see a fast increase in pH at early times, $t/{\tau }_D<0.4$, followed by approximately steady pH at this interface of $\sim$8.5 for $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V and a slightly higher value of 8.6 for 1.0 V. The cumulative boron electrosorption for all the cases is monotonically increasing, but at $V_{\mathrm{c}\mathrm{h}}$ = 0.6 V, the amount of electrosorbed boron is the lowest, ${\mathrm{\Gamma }}_{\mathrm{B}}$ = $0.11\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ at $t/{\tau }_{\mathrm{D}}$ = 3, followed by $0.37\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ for $V_{\mathrm{c}\mathrm{h}}$ = 1.4 V, and $0.60\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ at $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V. Moreover, for $V_{\mathrm{c}\mathrm{h}}$ = 0.6 V, ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}=0.072$ at $t/{\tau }_{\mathrm{D}}$ = 3, 0.42 for 1.0 V, and 0.27 for 1.4 V, so that $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V shows the highest boron selectivity and boron electrosorption.

Next, we compare these theoretical predictions to experimental measurements; see Materials and Methods for more details about the experimental setup. In Fig. 3F, we compare theoretical (line) and experimental (circles) values of ${\mathrm{\Gamma }}_{\mathrm{B}}$ as a function of $V_{\mathrm{c}\mathrm{h}}$. The theoretical predictions in Fig. 3F show an optimum charging voltage for boron removal of $\sim$1.1 V. We explain the existence of an optimum charging voltage by the competing effects of beneficial pH rise due to increased H⁺ electrosorption in the cathode as the voltage is increased and a deleterious development of a local pH minimum in the cathode occurring only at high voltages (Fig. 3 A and D). For the parameters used here, the optimal balance between these two mechanisms occurs for $V_{\mathrm{c}\mathrm{h}}\sim$ 1.1 V. Good quantitative agreements between theory and experiments are obtained for high charging voltages ($V_{\mathrm{c}\mathrm{h}}\ge$ 0.8 V); however, at lower voltages, the model predicts no boron storage, and the experiments show significant boron desorption, as discussed for Fig. 2F. Overall, experiments and theory agree that increasing cell voltage does not necessarily lead to improved boron removal and that an optimum cell voltage is achieved at around 1 V.

Effects of Feed Salt Concentration and Velocity on Local pH.

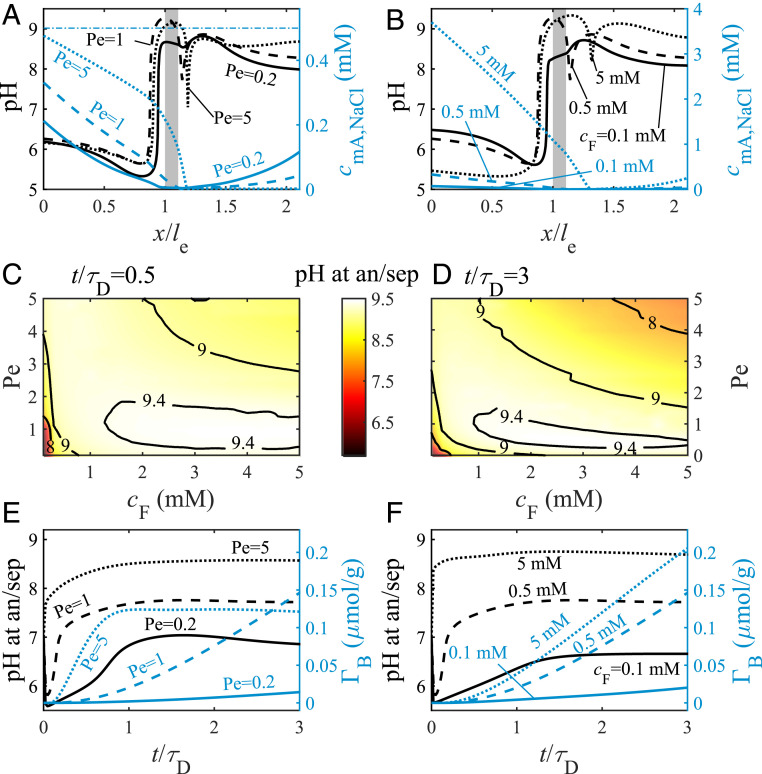
Having established that our theory captures key trends in boron electrosorption, we now investigate theoretically the effects of the flow velocity and feed salt concentration on pH dynamics and boron electrosorption. In Fig. 4 A–D, we present the theoretical analysis of a cell operated with solely salt in the feedwater and no pH-dependent species, whereas in Fig. 4 E and F, we include boric acid in the feed. Model parameters used are tabulated in Tables 1 and 2. Fig. 4A presents the effect of the flow velocity, quantified by Pe, on the pH in the cell, plotting the pH (left y axis, black lines) and macropore salt concentration (right y axis, blue lines) profiles at $t/{\tau }_D=3$, for Pe = 0.2 (solid lines), 1 (dashed lines), and 5 (dotted lines), all with $c_{\mathrm{F}}$ = 0.5 mM and $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V. For the case of low flow velocity, $\mathrm{P}\mathrm{e}=0.2$, in Fig. 4A, we observe very low salt concentrations across the whole cell, with near-zero concentration in the separator. For moderate and high flow velocities, Pe = 1 and 5, we observe a decreasing salt concentration across the anode, followed by very low concentration throughout the cathode. For all Pe tested, the pH profiles of the three analyzed cases show low pH values across most of the anode of $\sim$6.0 and high pH values of $\sim$8.5 across the separator and cathode.

Fig. 4.

Predictions for an FTE CDI cell with NaCl-containing feedwater (A–D) or NaCl and boron-containing feedwater (E and F) with charging voltage, $V_{\mathrm{c}\mathrm{h}}$, of 1.0 V. (A and B) Predicted pH (left y axes, black lines) and macropore salt concentration (right y axes, blue lines) profiles at $t/{\tau }_D=3$, where the gray rectangles represent the separator, and the horizontal dash-dotted blue line in A represents the feed salt concentration. (A and E) Results for $\mathrm{P}\mathrm{e}=0.2$ (solid lines), 1 (dashed lines), and 5 (dotted lines), all with feed salt concentration, $c_{\mathrm{F}}$, of 0.5 mM. (B and F) Results for $c_{\mathrm{F}}$ = 0.1 mM (solid lines), 0.5 mM (dashed lines), and 5 mM (dotted lines), all with Pe = 1. (C and D) Predicted pH at the anode/separator (an/sep) interface as a function of $c_{\mathrm{F}}$ and Pe at $t/{\tau }_{\mathrm{D}}=0.5$ (C) and $t/{\tau }_{\mathrm{D}}=3$ (D). (E and F) Predicted pH at the anode/separator interface (left y axes, black lines) and electrosorbed boron (right y axes, blue lines), both as a function of dimensionless time.

Fig. 4B plots the pH (left y axis, black lines) and macropore salt concentration (right y axis, blue lines) profiles at $t/{\tau }_D=3$, for $c_{\mathrm{F}}=0.1\hspace{0.17em}\mathrm{m}\mathrm{M}$ (solid lines), 0.5 mM (dashed lines), and 5 mM (dotted lines), all with $\mathrm{P}\mathrm{e}=1$ and $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V. For all salt concentrations, the pH profiles in Fig. 4B are similar: low pH values in the anode, followed by an increase near the anode/separator interface, and high pH values across the separator and the cathode. The pH at the anode/separator interface for $c_{\mathrm{F}}=0.1\hspace{0.17em}\mathrm{m}\mathrm{M}$ is 8.3, 9.1 for $5\hspace{0.17em}\mathrm{m}\mathrm{M}$, and 9.3 for $c_{\mathrm{F}}=2\hspace{0.17em}\mathrm{m}\mathrm{M}$. To conveniently visualize the effect of flow velocity and feed salt concentration on the important metric of pH at the anode/separator interface, in Fig. 4 C and D, we present colormaps and contour plots at $t/{\tau }_{\mathrm{D}}=0.5$ (Fig. 4C) and $t/{\tau }_{\mathrm{D}}=3$ (Fig. 4D). For early times, the pH at the anode/separator interface is above 9 for most of the investigated parameter range, while for later times, the pH decreases somewhat at high values of $c_{\mathrm{F}}$ and Pe. However, over almost the entire parameter set investigated here, pH at the anode/separator interface is high enough to be suitable for significant boric acid dissociation and boron electrosorption in the anode.

In Fig. 4 E and F, we extend the analysis for feedwater with both NaCl and boron. Fig. 4 E and F plot the pH at the anode/separator interface (left y axis, black lines) and ${\mathrm{\Gamma }}_{\mathrm{B}}$ (right y axis, blue lines), both as a function of dimensionless time. Fig. 4E shows results for Pe = 0.2 (solid lines), 1 (dashed lines), and 5 (dotted lines), all with $c_{\mathrm{F}}$ = 0.5 mM, while Fig. 4F shows results for $c_{\mathrm{F}}=0.1$ mM (solid lines), 0.5 mM (dashed lines), and 5 mM (dotted lines), all with Pe = 1.

The pH values for Pe = 0.2 in Fig. 4E are relatively low during the whole process, followed by the values for Pe = 1, whereas for Pe = 5, a strong pH increase is observed at early times reaching values above 8.5, followed by a steady and moderate increase. For Pe = 0.2 and 1, we observe a monotonic increase of ${\mathrm{\Gamma }}_{\mathrm{B}}$ in the investigated time range, while for Pe = 5, we observe strong boron removal at $t/{\tau }_{\mathrm{D}}\le$ 0.9, followed by a steady value. Also, ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}=0.51$ at $t/{\tau }_{\mathrm{D}}=3$ for Pe = 0.2, 0.84 for Pe = 1, and 0.097 for Pe = 5. The pH values in the anode in Fig. 4E follow the trends presented in Fig. 4A, where the presence of boron in the system restrains the pH rise. The boron-removal values presented in Fig. 4E are logical, as boron adsorption increases with pH. However, the lack of boron removal for Pe = 5 at $t/{\tau }_{\mathrm{D}}$ > 0.9 may be due to the relatively high ${\mathrm{C}\mathrm{l}}^{-}$ concentration near the anode/separator interface, which competes with boron to be stored in anode micropores.

The pH values for $c_{\mathrm{F}}$ = 0.1 mM presented in Fig. 4F are low at all times during charging, while significantly higher pH values are seen for $c_{\mathrm{F}}$ = 0.5 mM. For $c_{\mathrm{F}}$ = 5 mM, the pH reaches $\sim$8.7 for $t/{\tau }_{\mathrm{D}}\ge$ 0.2. Thus, boron removal is very low for $c_{\mathrm{F}}$ = 0.1 mM, while for $c_{\mathrm{F}}$ of 0.5 mM and 5 mM, higher values are predicted, reaching $0.204\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ at $t/{\tau }_{\mathrm{D}}$ = 3 for the latter case. Moreover, ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}=0.15$ at $t/{\tau }_{\mathrm{D}}=3$ for $c_{\mathrm{F}}$ = 0.1 mM, 0.84 for 0.5 mM, and 0.90 for 5 mM.

In addition to analyzing the effects electrode order, $V_{\mathrm{c}\mathrm{h}}$, Pe, and $c_{\mathrm{F}}$ have on pH dynamics and boron electrosorption, we performed a sensitivity analysis to probe the effect the cell-geometric parameters such as separator and electrode thickness on the pH and boron dynamics, all with Pe = 1, $c_{\mathrm{F}}$ = 0.5 mM, and $V_{\mathrm{c}\mathrm{h}}$ = 1.0 V (SI Appendix, Figs. S2–S4). For the separator, we studied the range $20\hspace{0.17em}\mathrm{\mu }\mathrm{m}\le l_{\mathrm{s}\mathrm{e}\mathrm{p}}\le 200\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, which is the range implemented in typical FTE CDI cells (83, 84). We found a small effect of separator thickness on the boron removal, where a thinner separator with $l_{\mathrm{s}\mathrm{e}\mathrm{p}}=20\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ is predicted to show a slightly higher boron removal of $0.16\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ at $t/{\tau }_{\mathrm{D}}=3$, compared to $0.15\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ for $l_{\mathrm{s}\mathrm{e}\mathrm{p}}=65\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ and $0.13\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ for $l_{\mathrm{s}\mathrm{e}\mathrm{p}}=200\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. For the electrodes, we studied doubled and halved thicknesses of each electrode, and we found that a cathode with l_cat = 0.3 mm results in increased boron removal from $0.15\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$ to $0.26\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}/\mathrm{g}$, where a thicker cathode or either a thinner or thicker anode should be avoided.

Conclusions

The removal of pH-dependent species from water is important, both for water purification and resource recovery, but is often challenging to accomplish with conventional membrane-based technologies. We establish a theory for the removal of such species by membraneless CDI cells, leveraging the large internal pH gradients generated in the cell during cell charging. Our proposed theoretical framework extends traditional CDI theory by including in the feedwater both pH dynamics and species which can be protonated or deprotonated depending on local pH.

Both our model and validating experiments showed important and counterintuitive design rules for the removal of boron, our example pH-dependent species. Despite conventional wisdom in CDI, we found that the anode should be placed upstream to achieve effective boron removal and that increasing cell voltage does not necessarily lead to improved boron removal. We also report on phenomena such as pH shock-like fronts propagating upstream, predicted by our model.

In the future, the model presented here can be refined to further improve predictions, for example, by including Faradaic side reactions. Novel cell configurations can be explored with this framework toward amphoteric ion removal, such as a stack of electrode pairs connected in series. Overall, our findings indicate that CDI cells, when their design is guided by the proposed theoretical model, have a high potential toward the removal of polluting amphoteric species from feedwaters.

Materials and Methods

Experimental Apparatus.

Activated carbon cloth (ACC-5092-15, Kynol GmbH) with $600\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ thickness, $0.53\mathrm{m}\mathrm{L}/\mathrm{g}$ specific micropore volume, and $\sim \mathrm{1,400}{\mathrm{m}}^2/\mathrm{g}$ surface area (56) was used as the electrode material. This material was characterized in several previous CDI studies (47, 53, 56, 78, 85–89). The carbon was cut into electrode squares with a cross-sectional area of $6.25\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$. Electrodes were rinsed with deionized water, dried for 3 h at $80\hspace{0.17em}°$C, then weighed immediately.

The FTE CDI cell was described and illustrated in ref. 56. Briefly, the cell consists of two electrodes electronically isolated by a separator (Omnipore JHWP polytetrafluoroethylene [PTFE] membrane; Merck; $65\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ thickness). Graphite current collectors contacted the backside of each electrode, and holes were milled into each collector to allow water passage. The upstream reservoir is located just upstream of the first current collector, and, likewise, the downstream reservoir was located just downstream of the second collector. The cell was enclosed on both sides by milled polyvinylidene fluoride (PVDF) blocks, which contain ports for fluid flow and air evacuation. Compressible expanded PTFE gaskets sealed the cell.

Feedwater composed of 0.37 mM ($4\hspace{0.17em}\mathrm{m}\mathrm{g}/\mathrm{L}$) boric acid (>99.5%; Bio-Lab) and 2 mM NaCl (>99.5%; SDFCL) was prepared with 18.2 M$\mathrm{\Omega }$cm deionized water (Synergy; Merck KGaA). Prior to each CDI experiment, the feedwater was purged of dissolved oxygen by nitrogen gas bubbling for 20 min in a 0.5-L glass feed tank under stirring. A peristaltic pump (Masterflex 07551-30, Cole-Parmer) transported the feedwater through the cell and conductivity sensor (Tracedec 390-50, Innovative Sensor Technologies GmbH) to measure effluent ionic conductivity. A pH electrode (iAquatrode Plus Pt1000, Metrohm AG) measured feed pH, which is reported in SI Appendix, Table S1 for all experiments.

The electrodes were initially discharged at 0 V with a voltage source (2400 Source Meter, Keithley Instruments), while feedwater flowed through the cell until the current was negligible. The cell was then charged for 12 min at a given voltage and flow rate and discharged for 30 min at 0 V for three consecutive charge–discharge cycles. The long discharge step allowed the cell to reequilibrate with the incoming feedwater before the subsequent charge step. Effluent conductivity was measured for the duration of the experiment, and during the charge step of the third (limit) cycle, the effluent solution was collected continuously for 10 min beginning from the moment when effluent conductivity decreased below the feed conductivity value. Feedwater samples were also collected for analysis.

Boron concentrations in the collected samples were measured with the Azomethine-H method of López et al. (90), with reagents obtained from Merck. Absorbance was measured at 414 nm against a blank reference solution with an Evolution 300 spectrophotometer (Thermo Fisher Scientific). Boron concentration was interpolated from a calibration curve constructed from the absorbances of 1 to 5 $\mathrm{m}\mathrm{g}/\mathrm{L}$ standard solutions.

Theory.

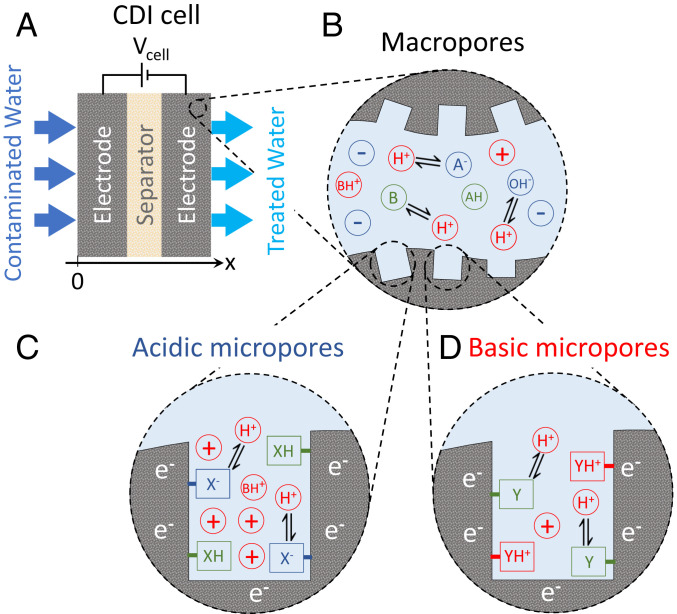
To describe the transport and removal of amphoteric species in an electrochemical cell employing porous electrodes, we present a theoretical framework that describes the coupled processes of: 1) ion transport due to advection, diffusion, and migration; 2) ongoing association and dissociation reactions of water and pH-dependent ions; and 3) ion adsorption in electrical double layers (EDLs), including pH-dependent chemical surface groups. In the porous electrodes, we distinguish two different types of pores: macropores, which serve as transport pathways (Fig. 5B), and micropores, in which ions are electrosorbed into overlapping EDLs (Fig. 5 C and D).

Fig. 5.

Schematic overview of a CDI cell for the removal of pH-dependent ions. (A) The FTE CDI cell consists of two porous electrodes with a porous layer (“separator”) in between. Feedwater, which contains inert and pH-dependent ions, flows through the separator and ions are electrosorbed by the electrodes. (B) In the macropores, which serve as transport pathways, the local pH is evaluated at each position, as well as the pH-dependent chemical equilibria between ions and H⁺ and ${\mathrm{O}\mathrm{H}}^{-}$. (C and D) Ions are electrosorbed in the micropores which have chemical surface groups with pH-dependent charge. Acidic (C) and basic (D) regions.

To describe ion electrosorption in the electrodes, we use the multiequilibria amphoteric modified Donnan [(ME-)amph-mD] model (91). This model is an extended version of the amphoteric modified Donnan (amph-mD) model, which has been extensively validated and shown to describe experimental data well (54, 66). The amph-mD model considers the presence of a fixed number of chemical groups in the micropores, but omits the pH dependency of these groups. In contrast, the (ME-)amph-mD model includes this pH dependency (92–94).

In the (ME-)amph-mD model, there are acidic and basic regions, with different pH-dependent chemical groups. In the present work, we only consider monovalent chemical groups, reacting only with H⁺ or ${\mathrm{O}\mathrm{H}}^{-}$ ions (Fig. 5 C and D). We consider local chemical equilibrium between the protonated and deprotonated surface groups, depending on an equilibrium constant, $K_{\mathrm{a}}$, and local pH (92, 93, 95). In the acidic regions, the chemical groups are neutral (protonated) or negatively charged (deprotonated), marked as ${\mathrm{X}}^{-}$ in Fig. 5C, while in the basic regions, they are neutral (deprotonated) or positively charged (protonated), marked as ${\mathrm{Y}\mathrm{H}}^{+}$ in Fig. 5D.

The chemical charge in acidic and basic region is, respectively, given by

$${\sigma }_{{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{X}}_i}=-\left(1-{\delta }_{\mathrm{m}\mathrm{i},{\text{H}}^{+}{,\mathrm{X}}_i}\right)\cdot c_{{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{X}}_i,\mathrm{t}},$$ [1]

$${\sigma }_{{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{Y}}_j}={\delta }_{\mathrm{m}\mathrm{i},{\text{H}}^{+}{,\mathrm{Y}}_j}\cdot c_{{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},\mathrm{Y}}_j,\mathrm{t}},$$ [2]

where $c_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},R,\mathrm{t}}$ is the concentration of chemical groups in the $R$-th region. The fraction of protonated chemical group in each region, ${\delta }_{\mathrm{m}\mathrm{i},{\text{H}}^{+},R}$, is given by

$${\delta }_{\mathrm{m}\mathrm{i},{\text{H}}^{+},R}=\frac{1}{1+K_R/c_{\mathrm{m}\mathrm{i},{\mathrm{H}}^{+},R}},$$ [3]

where $K_R$ is the reaction constant of the chemical group in region $R$. The concentration of H⁺ in each of the micropores regions R is given by the Boltzmann equation, which also applies to all ions,

$$c_{\mathrm{m}\mathrm{i},i,R}=c_{\mathrm{m}\mathrm{A},i}\cdot \exp \left(-z_i\mathrm{\Delta }{\varphi }_{\mathrm{D},R}\right),$$ [4]

where $c_{\mathrm{m}\mathrm{i},i,R}$ is the concentration in region $R$, $c_{\mathrm{m}\mathrm{A},i}$ is the concentration in the adjacent macropore, $z_i$ is the ion valence, and $\mathrm{\Delta }{\varphi }_{\mathrm{D},R}$ is the Donnan potential in region $R$. The Donnan potential, as all other potentials, can be multiplied by the thermal voltage, $V_{\mathrm{T}}\equiv k_{\mathrm{B}}T/e$, to arrive at a dimensional voltage, where $k_{\mathrm{B}}$ is the Boltzmann constant, $T$ is the absolute temperature, and $e$ is the elementary charge.

In each micropore region, the ionic charge is

$${\sigma }_{\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{c},R}=\sum _i{z}_i\cdot c_{\mathrm{m}\mathrm{i},i,R},$$ [5]

which can be combined with a charge balance, which states that the sum of electronic charge, ionic charge, and chemical charge is equal to zero,

$${\sigma }_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c},R}+{\sigma }_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},R}+{\sigma }_{\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{c},R}=0,$$ [6]

where ${\sigma }_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c},R}$ is the electronic charge in region $R$, which relates to the Stern capacitance and the Stern potential by

$${\sigma }_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c},R}\cdot F=V_{\mathrm{T}}\cdot C_{\mathrm{S},R}\mathrm{\Delta }{\varphi }_{\mathrm{S},R},$$ [7]

where $F$ is the Faraday constant, $C_{\mathrm{S},R}$ is the Stern capacitance, and $\mathrm{\Delta }{\varphi }_{\mathrm{S},R}$ is the Stern potential, both in region $R$.

All of these relations are evaluated in all the regions (types of micropores) across the entire set of two electrodes in the CDI cell. For each two types of adjacent micropore regions, the summation of $\mathrm{\Delta }{\varphi }_{\mathrm{D},R}$ and $\mathrm{\Delta }{\varphi }_{\mathrm{S},R}$ is equal to the difference between the electrical potential in the electrode and in the macropores (at that position). Thus, at each position $x$, in each electrode, we evaluate the following equation:

$${\varphi }_{\mathrm{E},k}-{\varphi }_{\mathrm{m}\mathrm{A}}=\mathrm{\Delta }{\varphi }_{\mathrm{D},R}+\mathrm{\Delta }{\varphi }_{\mathrm{S},R},$$ [8]

where ${\varphi }_{\mathrm{m}\mathrm{A}}$ is the dimensionless potential in the macropores, the subscript “E” refers to the electrode region, and the subscript “k” refers to the electrode type, which is either the anode (an) or the cathode (cat). Though the macropore potential is position-dependent, the electrode potential ${\varphi }_{\mathrm{E},k}$ is assumed to be invariant within a given electrode. These potentials ${\varphi }_{\mathrm{E},k}$ are related to the charging voltage by the expression

$$V_{\mathrm{T}}\left({\varphi }_{\mathrm{E},\mathrm{a}\mathrm{n}}-{\varphi }_{\mathrm{E},\mathrm{c}\mathrm{a}\mathrm{t}}\right)=V_{\mathrm{c}\mathrm{h}}-I\cdot \mathrm{E}\mathrm{E}\mathrm{R},$$ [9]

where $I$ is the electric current through the cell and EER refers to external electronic resistance (46).

To describe transport of ions in the macropores, we use the Nernst–Planck equation,

$$J_i=v_{\mathrm{w}}{c}_{\mathrm{m}\mathrm{A},i}-D_{\mathrm{m}\mathrm{A},i}\left(\frac{\partial c_{\mathrm{m}\mathrm{A},i}}{\partial x}+z_i{c}_{\mathrm{m}\mathrm{A},i}\frac{\partial {\varphi }_{\mathrm{m}\mathrm{A}}}{\partial x}\right),$$ [10]

where $J_i$ is the molar superficial flux of ion $i$ across the electrode, $v_{\mathrm{w}}$ is the superficial velocity of the water, $x$ is the position, and $D_{\mathrm{m}\mathrm{A},i}$ is the effective ion-diffusion coefficient in the macropores, given by $D_{\mathrm{m}\mathrm{A},i}\equiv D_{\infty ,i}\cdot p_{\mathrm{m}\mathrm{A}}/{\tau }_{\mathrm{m}\mathrm{A}}$, where $D_{\infty ,i}$ is the diffusion coefficient in free solution, $p_{\mathrm{m}\mathrm{A}}$ is the macropore porosity, and ${\tau }_{\mathrm{m}\mathrm{A}}$ is the macropore tortuosity.

Mass conservation holds at each position in the electrodes. Therefore, we evaluate for each ion the mass balance equation

$$\begin{array}{cc}\hfill p_{\mathrm{m}\mathrm{A}}& \frac{\partial c_{\mathrm{m}\mathrm{A},i}}{\partial t}+p_{\mathrm{m}\mathrm{i}}\frac{\partial }{\partial t}\hspace{0.17em}\sum _R{\alpha }_{\mathrm{m}\mathrm{i},R}\left(c_{\mathrm{m}\mathrm{i},i,R}+{\delta }_{\mathrm{m}\mathrm{i},i,R}\cdot c_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},R,\mathrm{t}}\right)=\hfill \\ \hfill & -\frac{\partial J_i}{\partial x}+{\dot{\gamma }}_i,\hfill \end{array}$$ [11]

where $p_{\mathrm{m}\mathrm{i}}$ is the micropore porosity, and ${\alpha }_{\mathrm{m}\mathrm{i},R}$ is the fraction of the total micropore volume that is in region R. For all ions that do not adsorb to (react with) the chemical groups in the micropores (here, all ions but H⁺), ${\delta }_{\mathrm{m}\mathrm{i},i,R}=0$. The final term, ${\dot{\gamma }}_i$, is the production rate of the $i$-th ion due to acid–base reactions at that x position, either in macropores or in any of the micropore regions. For inert ions, which do not participate in acid–base reactions, such as Na⁺ and ${\mathrm{C}\mathrm{l}}^{-}$, ${\dot{\gamma }}_i=0$. For amphoteric ions, the value of ${\dot{\gamma }}_i$ is generally nonzero and unknown. But even then, an explicit evaluation of ${\dot{\gamma }}_i$ is not required, as discussed next.

Indeed, it is possible to derive mass balances in which ${\dot{\gamma }}_i$ has disappeared, following the approach described in the literature (96–99). We derive a total mass balance equation for a group of species, marked by $G$, which includes all species that are in chemical equilibrium with each other. Examples of a group, $G$, are all species that include the boron atom, or all species in the group of carbonate ions (carbonic acid, bicarbonate, and carbonate). At each position in the system, the summation of the production rates, ${\dot{\gamma }}_i$, of all species in a group, $G$, is equal to zero, i.e., ${\sum }_{i\in G}{\dot{\gamma }}_i=0$. Consequently, summing Eq. 11 over the individual species within group $G$, all ${\dot{\gamma }}_i$ terms cancel, resulting in the mass balance equation

$$\sum _{i\in G}\left(p_{\mathrm{m}\mathrm{A}}\frac{\partial c_{\mathrm{m}\mathrm{A},i}}{\partial t}+p_{\mathrm{m}\mathrm{i}}\frac{\partial }{\partial t}\sum _R{\alpha }_{\mathrm{m}\mathrm{i},R}{c}_{\mathrm{m}\mathrm{i},i,R}\right)=-\sum _{i\in G}\frac{\partial J_i}{\partial x}.$$ [12]

The approach presented by Eq. 12 eliminates the ${\dot{\gamma }}_i$ terms from the system of equations that is solved. To solve the resulting set of equations, we assume that the acid–base reactions between the ions within a group are infinitely fast, i.e., these species are in chemical equilibrium. Thus, we evaluate at each position in the system and at each moment the following chemical equilibrium conditions for the group:

$$K_i\cdot \left[{\mathrm{R}}_i\right]=\left[{\mathrm{P}}_i\right]\cdot \left[{\text{H}}^{+}\right],$$ [13]

where $K_i$ is the equilibrium constant, ${\mathrm{P}}_i$ is the product, and ${\mathrm{R}}_i$ is the reactant,* all of the $i$-th acid–base reaction. Similarly, we consider the water-dissociation equilibrium, ${\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{O}\mathrm{H}}^{-}$, described by

$$K_{\mathrm{w}}=\left[{\mathrm{H}}^{+}\right]\cdot \left[{\mathrm{O}\mathrm{H}}^{-}\right].$$ [14]

Next, we consider electroneutrality at each position in the macropores and in the separator

$$\sum _i{z}_i\cdot c_{\mathrm{m}\mathrm{A},i}=0,$$ [15]

and derive a local charge balance by multiplying Eq. 11 by $z_i$ and summing the resulting equations over all ions, including H⁺ and ${\mathrm{O}\mathrm{H}}^{-}$, resulting in

$$p_{\mathrm{m}\mathrm{i}}\frac{\partial }{\partial t}\sum _R\left(\frac{\partial {\sigma }_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m},R}}{\partial t}+\frac{\partial {\sigma }_{\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{c},R}}{\partial t}\right)=-\frac{\partial }{\partial x}\sum _i{z}_i{J}_i.$$ [16]

Only the micropores contribute to the left-hand side of Eq. 16, because charge does not accumulate in the macropores (Eq. 15). Furthermore, charge conservation in the acid–base reactions, ${\sum }_{i\in G}{z}_i\cdot {\gamma }_i=0$, eliminates the term associated with the reaction rates, ${\dot{\gamma }}_i$. We can make the replacement ${\sum }_i{z}_i\cdot J_i\equiv J_{\mathrm{c}\mathrm{h}}$, where $J_{\mathrm{c}\mathrm{h}}$ is the current density. This current density varies across each electrode (from zero at each outside) to arrive at a value at the electrode–separator interface that is then unvarying across the separator, and this value, $J_{\mathrm{c}\mathrm{h},\mathrm{s}\mathrm{e}\mathrm{p}}$, is related to the macroscopically observable current $I$ by the expression $I=F\cdot A_{\mathrm{c}}\cdot J_{\mathrm{c}\mathrm{h},\mathrm{s}\mathrm{e}\mathrm{p}}$, where $A_{\mathrm{c}}$ is the electrode cross-section area.

Next, we describe ion transport across the separator, a thin layer of porous material allowing the transport of water and ions, but not electrons. To do so, we use a mass balance equation for all the inert ions, Eq. 11; a mass balance for all amphoteric groups of the form of Eq. 12; the charge balance, Eq. 16; the electroneutrality condition, Eq. 15; and the chemical equilibria, Eqs. 13 and 14. In these equations, the subscript “mA” is replaced by “sep,” referring to the separator, and we set $p_{\mathrm{m}\mathrm{i}}=0$ and $p_{\mathrm{m}\mathrm{A}}=p_{\mathrm{s}\mathrm{e}\mathrm{p}}=0.8$. On both separator/electrode interfaces, we consider continuity of the flux of all ions and continuity of concentration and potential. Similar boundary conditions apply on the two outsides of the two electrodes, where they interface to long upstream and downstream reservoirs, in which we set $p_{\mathrm{m}\mathrm{i}}=0$ and $p_{\mathrm{m}\mathrm{A}}=p_{\mathrm{r}\mathrm{e}\mathrm{s}}=1$. At the entrance of the upstream reservoir, $c_i=c_{\mathrm{F},i}$ and $J_{\mathrm{c}\mathrm{h}}=0$ are applied, where $c_{\mathrm{F},i}$ is the feed concentration of the $i$-th ion. At the exit of the downstream reservoir, $J_i=v_{\mathrm{w}}{c}_i$ and $J_{\mathrm{c}\mathrm{h}}=0$ are applied. A key initial condition is the total amount of electronic charge in the system of the two electrodes together, which we set to zero. When initially the cell is at equilibrium and short-circuited, this implies that at each position in each electrode, the electronic charge in the acidic micropores is equal in magnitude, and opposite in sign, to that in the basic micropores (when ${\alpha }_{\text{acidic}}={\alpha }_{\text{basic}}=0.5$ and the two electrodes are chemically identical, as in the current case).

Theoretical Description of the Experiment

We add several extensions to the theoretical framework presented in the previous subsection for precise description of the experimental apparatus used in this work. First, we follow the method described by Guyes et al. (83) and account for the mixing of the solution before reaching the conductivity sensor placed downstream of the cell

$$V_{\mathrm{m}\mathrm{i}\mathrm{x}}\frac{\partial c_{\mathrm{c}\mathrm{s},i}}{\partial t}=A_{\mathrm{c}}{v}_{\mathrm{w}}\left(c_{\mathrm{m}\mathrm{A},i,\mathrm{e}\mathrm{ff}}-c_{\mathrm{c}\mathrm{s},i}\right),$$ [17]

where $V_{\mathrm{m}\mathrm{i}\mathrm{x}}$ is the mixing volume, $c_{\mathrm{c}\mathrm{s},i}$ is the concentration at the conductivity sensor, and $c_{\mathrm{m}\mathrm{A},i,\mathrm{e}\mathrm{ff}}$ is the effluent concentration, both of the $i$-th species. Moreover, collection of treated solution begins only when the conductivity value at the sensor reaches values below the feed conductivity, imitating the experimental approach. Next, we quantify the electrosorption of the $i$-th ion, ${\mathrm{\Gamma }}_i$, using the following definition

$${\mathrm{\Gamma }}_i=\frac{\mathrm{\Delta }{N}_i}{m_{\mathrm{a}\mathrm{n}}+m_{\mathrm{c}\mathrm{a}\mathrm{t}}},$$ [18]

where $\mathrm{\Delta }{N}_i$ is the amount of stored ion, in moles; $m_{\mathrm{a}\mathrm{n}}$ is the anode mass; and $m_{\mathrm{c}\mathrm{a}\mathrm{t}}$ is the cathode mass. To calculate (for the model) or measure (for the experiment) the value of $\mathrm{\Delta }{N}_i$ for a real system, we follow the definition proposed by Hawks et al. (100)

$$\mathrm{\Delta }{N}_i\equiv {\int }_{t_{\mathrm{c}\mathrm{o}\mathrm{l}}}{A}_{\mathrm{c}}{v}_{\mathrm{w}}\left(c_{\mathrm{F},i}-c_{\mathrm{c}\mathrm{s},i}\right)dt,$$ [19]

where $t_{\mathrm{c}\mathrm{o}\mathrm{l}}$ is the collection time of effluent. Similarly, to calculate $\mathrm{\Delta }{N}_i$ for an ideal system, where no mixing is taking place downstream of the cell, the following expression is used

$$\mathrm{\Delta }{N}_i\equiv {\int }_{t_{\mathrm{c}\mathrm{o}\mathrm{l}}}{A}_{\mathrm{c}}{v}_{\mathrm{w}}\left(c_{\mathrm{F},i}-c_{\mathrm{e}\mathrm{ff},i}\right)dt.$$ [20]

Last, we define the selectivity factor to quantify the selective adsorption of B over ${\mathrm{C}\mathrm{l}}^{-}$, ${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}$. To that end, we use the definition proposed in literature (51, 56, 94)

$${\beta }_{\mathrm{C}\mathrm{l}}^{\mathrm{B}}\equiv \frac{{\mathrm{\Gamma }}_{\mathrm{B}}}{{\mathrm{\Gamma }}_{{\text{Cl}}^{-}}}\cdot \frac{c_{{\mathrm{F},\mathrm{C}\mathrm{l}}^{-}}}{c_{\mathrm{F},\mathrm{B}}},$$ [21]

where subscript B refers to a summation over all boric acid species, B(OH)₃, ${\text{B(OH)}}_4^{-}$, ${\text{B(OH)}}_3^{\hspace{0.17em}2-}$, and ${\text{B(OH)}}_2^{\hspace{0.17em}3-}$.

Tables 1 and 2 present the values used in this work. Table 1 presents the parameters used for all the simulations. Table 2 presents values of the parameters that differ between the simulations, including the simulations that were compared to experiments (Figs. 2 and 3) and the simulations for theoretical analysis alone (Fig. 4). The parameters used to describe the electrodes are based on previous works (53, 56, 78, 87, 89); characterization experiments which are described in detail in SI Appendix, Section S3; and, in the case of the theoretical analysis (Fig. 4 and the third column of Table 2), the values assumed for hypothetical pristine (as given) electrodes with equal amount of acidic and basic chemical surface groups. In addition, the experimental boron adsorption is reported in SI Appendix, Table S1 for all experiments.

Data Availability

All study data are included in the article and/or supporting information.