Nonlinear rotational spectroscopy reveals many-body interactions in water molecules

Significance

Since water vapor exists everywhere around us and is crucial to life, the stable complexes that water molecules form with each other and with various environmental constituents have been studied extensively. Transient, metastable complexes are more elusive. A recently developed method, two-dimensional rotational spectroscopy, directly measures correlations between the rotational transitions in a conventional spectrum. Measurements of water vapor showed that rotations of one water molecule can change the rotational frequencies of another. Distinct spectral peaks provide direct experimental signatures of previously unseen complexes between the water molecules involved. The sensitivity of the method to intermolecular interactions has directly identified metastable cooperative behavior in one of the most extensively studied molecular species and promises new insights about many others.

Abstract

Because of their central importance in chemistry and biology, water molecules have been the subject of decades of intense spectroscopic investigations. Rotational spectroscopy of water vapor has yielded detailed information about the structure and dynamics of isolated water molecules, as well as water dimers and clusters. Nonlinear rotational spectroscopy in the terahertz regime has been developed recently to investigate the rotational dynamics of linear and symmetric-top molecules whose rotational energy levels are regularly spaced. However, it has not been applied to water or other lower-symmetry molecules with irregularly spaced levels. We report the use of recently developed two-dimensional (2D) terahertz rotational spectroscopy to observe high-order rotational coherences and correlations between rotational transitions that were previously unobservable. The results include two-quantum (2Q) peaks at frequencies that are shifted slightly from the sums of distinct rotational transitions on two different molecules. These results directly reveal the presence of previously unseen metastable water complexes with lifetimes of 100 ps or longer. Several such peaks observed at distinct 2Q frequencies indicate that the complexes have multiple preferred bimolecular geometries. Our results demonstrate the sensitivity of rotational correlations measured in 2D terahertz spectroscopy to molecular interactions and complexation in the gas phase.

Water has attracted extensive spectroscopic interest because of its critical implications for theoretical and applied sciences (1, 2). Water shows anomalous properties because of complicated fluxional hydrogen-bonded networks and has been investigated by Raman and infrared spectroscopy (3, 4), sum frequency spectroscopy (5), optical Kerr effect spectroscopy (6), vibration-rotation-tunneling spectroscopy (7), and recently by two-dimensional (2D) infrared spectroscopy (8, 9) and 2D Raman-terahertz (THz) spectroscopy (10). In the gas phase, water is of utmost importance for atmospheric science, astrophysics, combustion research, and fundamental chemistry and physics (1, 11, 12). Although the pure rotation spectrum of water vapor has been well known for decades (13, 14), nonlinear THz spectroscopy of water rotational dynamics has not been previously reported. Nonlinear rotational spectroscopy in the microwave spectral range is well established (15), but because of the small moments of inertia of water, most of its rotational transition frequencies lie in the THz frequency range (Fig. 1). Nonlinear THz rotational spectroscopy was reported only recently (16, 17), and 2D THz rotational spectroscopy (10, 18, 19) more recently still. As in 2D spectroscopy of vibrational, electronic, and other degrees of freedom (9, 20–25), 2D rotational spectroscopy can reveal correlations between rotational states, many-body effects, and distinct multiple-field interactions that cannot be observed by linear spectroscopy (26). The large dipole moment of water, manifest in strong atmospheric absorption in the THz window (27–31), and the existence of water dimers and larger clusters with complex structures and dynamics (7, 32, 33), suggest that 2D spectroscopy of water could generate previously elusive insights (34–37).

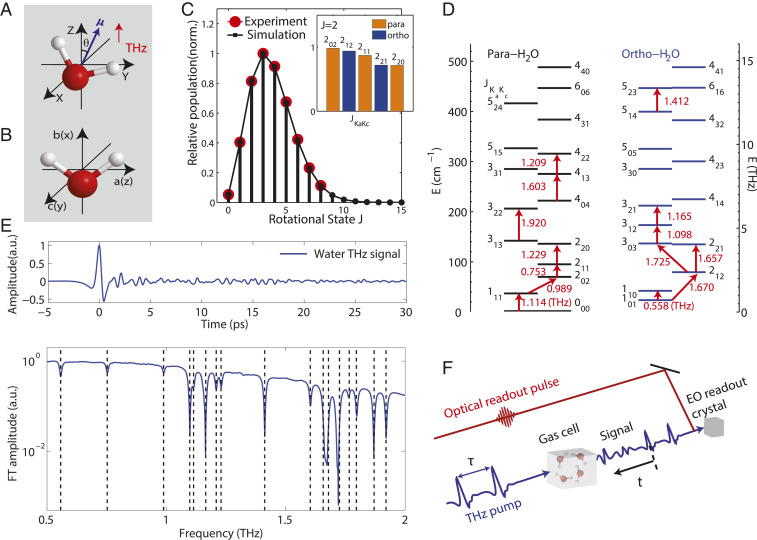
Fig. 1.

Overview of the experiment. (A) Water molecule in the laboratory frame, showing the dipole moment μ at an angle θ from the Z axis (THz polarization direction). (B) Water molecule in the molecule-fixed frame with the three moments of inertia I_a, I_b, and I_c along the corresponding axes. (C) Relative population distribution as a function of the J rotational quantum number. All relevant K_a and K_c components are included in the population distribution. (Inset) The relative population distribution within the state J = 2. (D) Rotational energy levels of para-H₂O and ortho-H₂O molecules. Red arrows illustrate rotational transitions and transition frequencies involved in this work. (E) Measured THz FID (Top) and Fourier transform (Bottom) showing rotational transitions (marked by dashed vertical lines) of water vapor in ambient air. (F) Schematic illustration of the 2D THz experimental setup. Linear THz spectra (example in E) are measured with only one THz pump pulse.

Two-dimensional THz rotational spectroscopy has not been extended previously to water or any asymmetric-top molecules, although such molecules, whose rotational spectra are complicated because all three of their moments of inertia are unequal, are the majority of naturally occurring molecular species. Unlike a linear or symmetric-top molecule, in which the spectroscopic transitions between successive total rotational angular momentum levels denoted by the quantum number J are spaced by even-integer multiples of a common factor, the rotational constant B, the asymmetric-top nature of water molecules leads to irregularly spaced rotational energy levels. These levels are described approximately by quantum numbers J, K_a, and K_c that indicate the total angular momentum and its symmetry-axis projections (1, 2). The spectrum of water vapor consists of many transitions, with $\mathrm{\Delta }J=-1,0,+1$ (P, Q, and R branches) all allowed and, for each, changes $\mathrm{\Delta }{K}_a=\pm 1,\mathrm{\Delta }{K}_c=\pm 1$ (1, 2). The large centrifugal distortion of water and the distinct sets of rotational states occupied by its nuclear spin isomers (even symmetry for para, odd symmetry for ortho) further complicate its rotational spectrum (1, 2, 38). A typical THz time-domain free-induction decay (FID) signal from water vapor at ambient conditions, induced by a weak single-cycle THz pulse, is shown in Fig. 1E. The irregular oscillations arise from more than 15 transitions (Fig. 1D) that contribute significantly to the water vapor absorption spectrum in the 0.1- to 2-THz region.

Results

The 2D THz experimental setup is illustrated schematically in Fig. 1F and described further below (Materials and Methods). Briefly, a pair of THz pulses with variable time delays were focused on the water vapor sample in a gas cell at about 60 °C and 150 Torr pressure. The induced THz signal was detected in an electro-optic crystal by a variably delayed optical readout pulse, the time-dependent polarization rotation of which reveals the temporal profile of the signal field. The signal was collected at a 1-kHz repetition rate, with a total data acquisition time of 2 to 3 d as both time delays are swept. Fourier transformation (FT) of the signal as a function of both time delays yields the 2D spectra (Figs. 2–4). In order to resolve closely spaced peaks near 1.0 THz, separate measurements with long FID detection times (up to 300 ps) were recorded (Fig. 3 A–C).

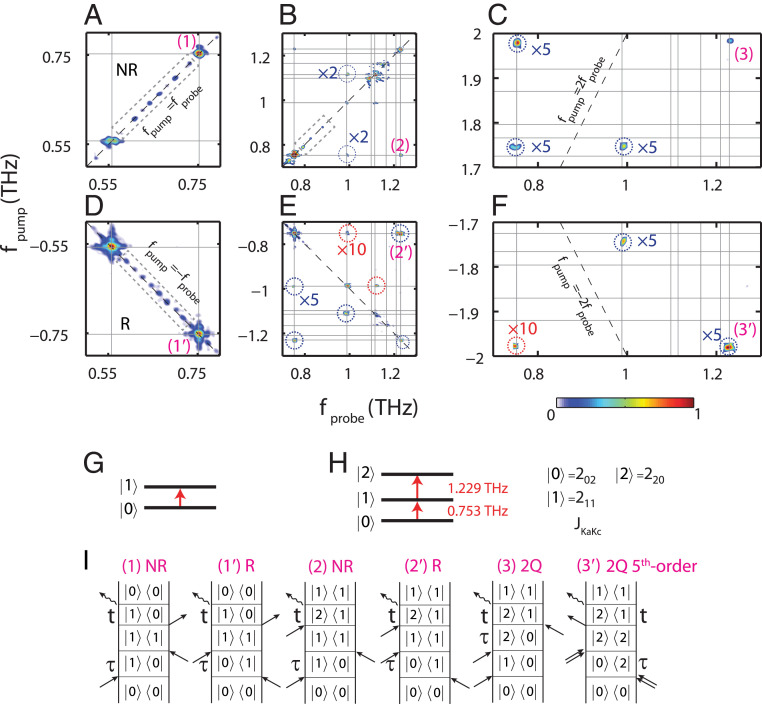
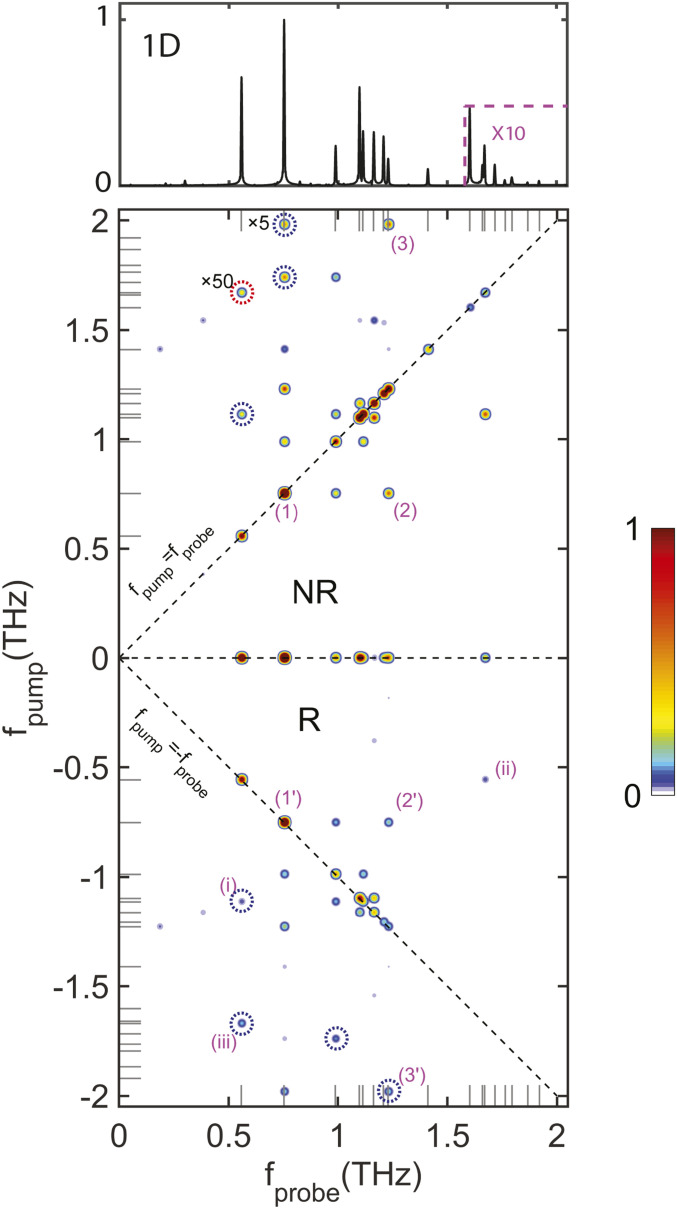
Fig. 2.

Two-dimensional rotational spectra of water vapor at 60 °C. (A–C) NR 2D rotational spectrum. (D–F) R 2D rotational spectrum. (G) Two-level system diagram. (H) Three-level system diagram. All 2D spectra are based on the same color bar. Relatively weak, evenly spaced features in gray dashed boxes (in A, B, and D) arise from acetonitrile residue in the gas cell, and they do not significantly affect the nonlinear signals of water vapor. Representative peaks are labeled (1) to (3) and (1′) to (3′), and their Feynman diagrams are shown in I. The interpulse delay, τ, and the detection time, t, are also shown. All other 2D signals shown here can be interpreted in a similar manner.

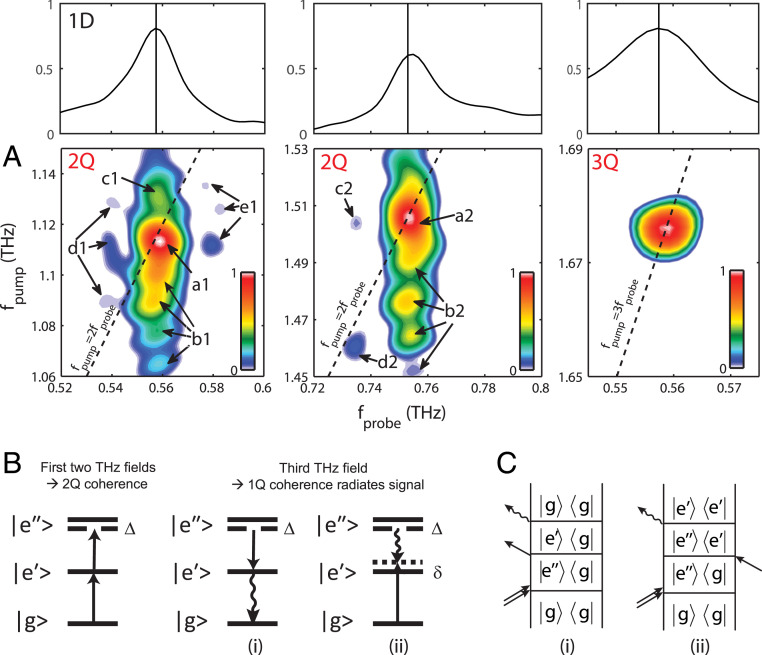
Fig. 4.

Many-body interactions in water vapor. (A) 2Q spectra near $f_{probe}=0.558\hspace{0.17em}\text{THz},f_{pump}=1.115\hspace{0.17em}\text{THz}$ (Bottom Left) and $f_{probe}=0.753\hspace{0.17em}\text{THz},f_{pump}=1.506\hspace{0.17em}\text{THz}$ (Bottom Middle) and 3Q spectrum at $f_{probe}=0.558\hspace{0.17em}\text{THz},f_{pump}=1.673\hspace{0.17em}\text{THz}$ (Bottom Right) from water vapor at 60 °C. a1 and a2 are 2Q diagonal peaks. b1, c1, and b2 are 2Q off-diagonal features. d1, e1, c2, and d2 are side peaks that arise from distinct coherence pathways. Correspondences between peaks in the 1D spectrum and the 2Q peaks (indicated by vertical lines) are shown (Top). (B) Energy ladder diagram of water complexes with many-body interactions. The ground state $|g\rangle$, the singly excited state $|e\text{'}\rangle$, and the doubly excited states $|e\text{'}\text{'}\rangle$ are illustrated. Energy level shifts (denoted as Δ and δ; see also SI Appendix, Fig. S18) occur due to many-body interactions. Solid lines show the excited levels without interaction-induced shifts. The first two THz fields generate the 2Q coherence, which does not radiate. The third THz field may project |e″> downward (i) to the singly excited level |e′>, resulting in a coherence between |e′> and |g> that radiates at the usual 1Q transition frequency. Alternatively, the third THz field may promote from |g> to |e′>, resulting in a coherence between |e′> and |e″> whose frequency depends on the intermolecular geometry and whose shift from the usual 1Q transition frequency may be different from the 2Q frequency shift Δ. (C) Coherence pathways corresponding to the field interactions (i) and (ii) in B and to 2Q peaks which may show various spectral shifts along the pump (2Q) and probe (1Q) axes.

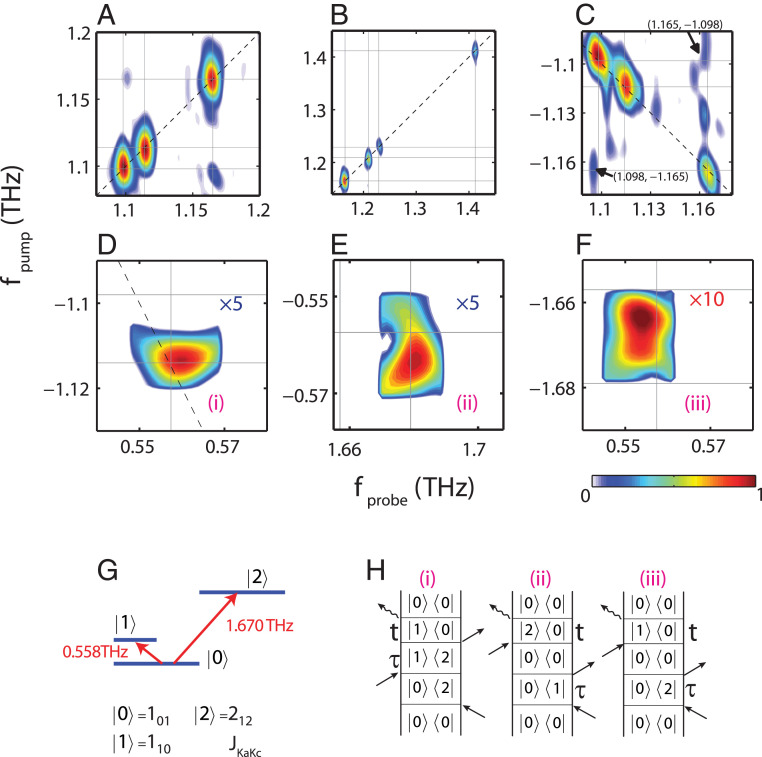
Fig. 3.

Close-up view of 2D rotational spectra of water vapor at 60 °C. (A–C) Spectra recorded with extended detection time (up to 300 ps) in order to resolve closely spaced peaks. The two cross-peaks at $f_{probe}=1.098\hspace{0.17em}\text{THz},f_{pump}=-1.165\hspace{0.17em}\text{THz}$ and $f_{probe}=1.165\hspace{0.17em}\text{THz},f_{pump}=-1.098\hspace{0.17em}\text{THz}$ labeled in C arise from rotational coherences among levels $|3_{03}⟩,\hspace{0.17em}|3_{12}⟩,\hspace{0.17em}and\hspace{0.17em}|3_{21}⟩$. (D–F) Close-up views of three peaks. (G) V-type system diagram. All 2D spectra are based on the same color bar. Representative peaks (i) to (iii) and their Feynman diagrams are shown in H. Features that appear in A and C but are not mentioned in the paper arise from noise.

Fig. 2 shows the experimental 2D THz rotational spectra. The spectra mainly consist of nonrephasing (NR) (Fig. 2 A–C) and photon-echo or rephasing (R) (Fig. 2 D–F) parts. Many nonlinear spectroscopic peaks appear along the $f_{pump}=\pm f_{probe}$ diagonals. These peaks can be understood in terms of a two-level system model (Fig. 2G) and the Feynman diagram in Fig. 2I (1). The field interaction from the first pulse induces a coherence between the rotational states $|0\rangle$ and$\hspace{1em}|1\rangle$, described by the density matrix element $\left|1\rangle \langle 0\right|$; the successive two interactions from the second pulse can convert the coherence first into a population state, $\left|1\rangle \langle 1\right|$, and then into the coherence, $\left|1\rangle \langle 0\right|$, which radiates at the same frequency as the first. For example, the rotational states $|2_{02}\rangle$ and $|2_{11}⟩$denoted as $|0\rangle$ and $|1\rangle$, respectively, give rise to the NR diagonal peak at $\left(f_{probe}=0.753\text{THz},f_{pump}=0.753\text{THz}\right)$, indicated as peak (1) in Fig. 2A. The third field interaction may alternatively convert the population $\left|1\rangle \langle 1\right|\hspace{1em}$into a new coherent superposition, $\left|2\rangle \langle 1\right|,$ which radiates at a new frequency. This leads to off-diagonal or cross-peaks, such as the one at $\left(f_{probe}=1.23\text{THz},f_{pump}=0.753\text{THz}\right)$ (Fig. 2B, Feynman diagram (2) in Fig. 2I) that results from the three levels, $|2_{02}⟩,|2_{11}⟩,\text{and}\hspace{0.17em}|2_{20}⟩$. Similar sequences, in which the first field interaction produces the coherence $\left|0\rangle \langle 1\right|$, yield R signals observed as $(f_{probe}=0.753\text{THz},f_{pump}=-0.753\hspace{1em}\text{THz})$ [peak (1′) in Fig. 2D] or $(f_{probe}=1.23\text{THz},f_{pump}=-0.753\text{THz})$ [peak (2′) in Fig. 2E], respectively. An example of the time-dependent nonlinear signal field E_NL(t), recorded with a specified time delay τ between the incident THz pulses, is shown in SI Appendix, Fig. S4. FT of signals with respect to temporal variables t and τ yields the 2D spectrum as functions of $f_{probe}$ and $f_{pump}$, respectively.

Some diagonal peaks between 0.5 and 0.8 THz, which arise from coherences of an extremely small quantity of adventitious gaseous acetonitrile residue from previous experiments (Figs. 2 A, B, and D), appear but do not significantly affect the 2D spectra of the water molecules, with the exception of the resonance associated with the $|J=30\rangle \to |J\text{'}=29\rangle$ transition at 0.552 THz in acetonitrile, which interferes with that of the $|1_{01}\rangle \to |1_{10}\rangle$ transition in water, leading to slightly split double-peaks at $(f_{probe}=0.558\text{THz},f_{pump}=0.558\text{THz})$ (Fig. 2A). The 2D THz spectra show no cross-peaks at mixed frequencies that belong to both water and acetonitrile molecules or between para- and ortho- water molecules, indicating that distinct constituent species and different nuclear spin isomers of the same molecular source generate independent spectra, similar to the behavior of alkali-metal atoms in 2D electronic spectra (39–41). We note that far weaker peaks than those from acetonitrile, due to water dimers, also appear. Their analysis requires careful subtraction of the acetonitrile peaks and consideration of signal levels far weaker than those of interest in this paper and will be presented in a separate publication.

Sum-frequency signals (SFs) and difference-frequency signals (DFs) appear, which arise from ladder-type (Fig. 2H) and V-type (Fig. 3G) transitions, respectively. The SFs (Fig. 2 C and F) are two-quantum (2Q) signals in which two successive field interactions from the first THz pulse generate a coherent superposition of three rotational states $|0⟩,|1⟩$, and $|2⟩$, which includes a 2Q coherence $\left|2\rangle \langle 0\right|$. The 2Q coherence does not radiate, but its phase-dependent interaction with the THz field in the second pulse produces a radiating one-quantum (1Q) coherence $\left|2\rangle \langle 1\right|$ or $\left|1\rangle \langle 0\right|$ whose amplitude and/or phase oscillate at the $\left|2\rangle \langle 0\right|$ coherence frequency as the interpulse time delay τ is varied. The 2Q frequency is thereby revealed in the FT with respect to the interpulse delay τ along with the radiating signal coherence frequency in the FT with respect to the detection time t. An example of this type of coherence is the peak at $(f_{probe}=1.23\text{THz},f_{pump}=1.98\text{THz})$ in Fig. 2C [labeled as peak (3)]. DF signals can be observed in a so-called V-type system consisting of the three ortho water states, $|0\rangle =|1_{01}\rangle$, $|1\rangle =|1_{10}\rangle$, and $|2\rangle =|2_{12}\rangle$ (Figs. 1D and 3G). The excited rotational states $|1\rangle$ and $|2\rangle$ share the same ground state $|0\rangle$, and the transition between the two excited states is forbidden by the selection rule (ΔK_a = ±1, ΔK_c = ±1). The DF signals come from the coherence $\left|1\rangle \langle 2\right|$ induced by two interactions from the first THz pulse, applied in succession, starting from the initial population state, $\left|0\rangle \langle 0\right|$ (diagram (i) in Fig. 3H). This is also a 2Q coherence, and although (just like the SF 2Q coherence $\left|2\rangle \langle 0\right|$) it is not radiative and therefore cannot be observed in a conventional linear spectrum, the $|1⟩\leftrightarrow |2⟩$ coherence becomes observable in 2D spectroscopy through the third field interaction, from the second THz pulse, which projects onto either of the coherences $\left|1\rangle \langle 0\right|$ or $\left|0\rangle \langle 2\right|$ that radiate at frequencies of $f_{probe}=$ 0.558 THz and 1.670 THz, respectively.

Based on the energy levels of individual water molecules, no 2Q resonant peak is anticipated near $(f_{probe}=0.753\text{THz},f_{pump}=1.506\text{THz})$ along the line $f_{pump}=2f_{probe}$, since the $|2_{02}⟩\to |2_{11}⟩$ transition at 0.753 THz is not followed by a second transition at the same frequency. Surprisingly, a strong 2Q signal appears at $f_{probe}=0.753\text{THz}$, as shown in Fig. 4A. In addition, 2Q off-diagonal features, that consist of discrete peaks, extend downward from both of the 2Q diagonal peaks at $f_{probe}=0.558\hspace{1em}\text{THz}$ and $f_{probe}=0.753\text{THz}$. These features can be explained by the collective resonances induced by many-body interactions in water molecules, similar to effects observed in 2D electronic spectra of atomic vapors (40, 41) and quantum wells (24). For example, two molecules with identical two-level systems can create a system with a ground state, a degenerate pair of singly excited states, and a doubly excited state (Fig. 4B). Dipole–dipole interactions between the water molecules could split and shift the singly excited-state energies and create correlations between the successive transitions, yielding 2Q diagonal and off-diagonal peaks, as shown in Fig. 4A. The three-quantum (3Q) signal can be understood similarly but does not play a major role in this work because only a diagonal 3Q peak was observed (Fig. 4A; see also SI Appendix, Figs. S13 and S22).

Discussion

Owing to the small shifts (∼20 GHz) measured in our 2Q off-diagonal frequencies, in contrast to the completely different rotational spectrum of the known hydrogen-bonded water dimer (33, 42, 43), we attribute the 2Q off-diagonal features to the transient formation of weakly bound metastable water complexes (32, 43, 44). We assume that these are predominantly molecule pairs, which we refer to below as “complexes” to avoid confusion with the H-bonded dimer. The presence of metastable water complexes and their previously reported properties were inferred from indirect experimental evidence and theoretical considerations including constituent analysis of atmospheric continuum absorption (29), pressure-dependent infrared absorption spectral intensity variation of the stretching OH band (44), and the expected contributions of metastable complexes with sufficiently long lifetimes to the partition function (43, 44). In contrast, we report here spectral features that arise directly from the metastable complexes. A lower limit of ∼100 ps for the lifetime of the complexes can be estimated from the linewidths of the 2Q off-diagonal peaks along the pump axis. This value is equal to our maximum time delay between the two THz pump pulses and is therefore instrumentally limited. Note that at the experimental pressure of 150 Torr the mean free time between molecular collisions is about 1.1 ns, so weakly interacting complexes can survive for longer than 100 ps without being destroyed by collisions with other molecules. Two-dimensional spectroscopy permits direct access to the metastable complexes, which may represent precursor or intermediate states on paths toward formation of H-bonded dimers.

None of the 1Q signals in our 2D spectra (e.g., peaks in Fig. 2 A, B, D, and E) show any off-diagonal peaks or continua arising from many-body interactions. The doubly excited states revealed in the off-diagonal 2Q peaks are different from the rotational states of individual water molecules. In a molecule-pair complex, the rotational excitation of one molecule influences the rotation of the other in a way that modifies the 2Q energy. The many-body interactions that form the complex are not sufficiently strong to prevent independent rotations of the individual molecules (in contrast to the H-bonded dimer, which rotates as a single unit), but are strong enough to cause measurable shifts in the energy when both molecules are rotationally excited. In addition, the off-diagonal 2Q signals in Fig. 4A (and also in SI Appendix, Fig. S16) show multiple closely spaced peaks. We believe that these multiple peaks must be associated with multiple preferred intermolecular complex geometries. The fine structure in these spectral features highlights the sensitivity of rotational correlations to intermolecular interactions and the metastable complexes that arise from them.

Another possible source for 2Q and 3Q signals is the radiative interaction (17) in which the emitted THz field that results from the interaction of the incident THz field with one molecule can subsequently serve as the excitation field for another molecule. However, this type of radiative interaction does not generate molecular excited states different from those that exist in individual water molecules and thus can make no contribution to the 2Q off-diagonal peaks. A simulation of the 2D spectra based on the rotational Hamiltonian for noninteracting symmetric-top molecules and including the known water transition dipoles and centrifugal distortion (described in detail in SI Appendix) reproduces the main features well, as shown in Fig. 5. To confirm the distinct sources of the 2Q off-diagonal and diagonal peaks, we analyzed the observed ratio between their heights at two sample temperatures (SI Appendix, Fig. S21). The ratio of the 2Q off-diagonal peak heights to the 2Q diagonal peaks increases by a factor of about 4.9 when the temperature is increased from room temperature (21 °C) to 60 °C, which increases the water vapor pressure from 18 Torr to 150 Torr, i.e., by a factor of 8.3. We show further in SI Appendix, Figs. S15 and S16 that the ratios of 2Q off-diagonal peaks to a strong 1Q peak $\left(f_{probe}=0.558\text{THz},f_{pump}=0.558\text{THz}\right)$ that clearly arises from individual water molecules change by comparable amounts with temperature, while the ratios of the 2Q diagonal peaks to 1Q peaks do not change significantly (SI Appendix, Fig. S21). These results demonstrate that the 2Q off-diagonal peaks arise uniquely from molecule-pair complexes, the concentrations of which depend on the square of the water vapor pressure. The 2Q diagonal peaks as well as the 3Q peak apparently arise substantially from individual molecules, likely due to their radiative interactions and nonlinear responses (see SI Appendix, Fig. S19). We note that the intensity increase with temperature in 2Q off-diagonal peaks relative to that of the others is less than a factor of 8.3, that is, the concentration of the complex increases by somewhat less than the square of the water vapor pressure, because the higher temperature shifts the chemical equilibrium toward separated water molecules. A calculation, which includes the appropriate Boltzmann factors (presented in SI Appendix), indicates molecule-pair complex binding energies of roughly 10 kJ/mol, with a considerable range of values (8.4 to 17 kJ/mol) deduced from the different 2Q off-diagonal peaks. The average value is smaller than the binding energy of the H-bonded dimer (33, 42).

Fig. 5.

Simulated 2D spectrum of water vapor at 60 °C. Positive and negative f_pump frequencies correspond respectively to NR and R or echo signals. No intermolecular interactions are included in the simulation. Several weaker peaks shown inside dotted circles are magnified by factors indicated (blue circle: ×5; red circle: ×50). Peaks with labels (1) to (3), (1′) to (3′), and (i) to (iii) correspond to those in the experimental spectra of Figs. 2 and 3. The short gray lines at the lower, upper, and left edges indicate conventionally measured rotational transition frequencies. For guidance, the simulated one-dimensional rotational spectrum of water molecules is shown (Top). Simulations including phenomenologically introduced interactions are presented in SI Appendix, Fig. S15, where weak higher-order nonlinear spectral peaks are also discussed.

Conclusions

Nonlinear 2D rotational spectra of water vapor have shown R (photon echo), NR, and multiple-quantum signals that arise from different field-induced pathways between rotational states. The sensitivity of 2D spectra to correlations between transitions has enabled observations of such correlations between rotations of distinct molecules. Intermolecular rotational correlations have not been observed previously. In the case of water, energy shifts of 2Q rotational coherences and the nonlinear dependence of 2Q off-diagonal spectral peak heights on water vapor pressure clearly reveal the presence of previously unseen metastable molecule-pair complexes with multiple preferred geometries and allow an estimate of the binding energies of these complexes. Our work paves the way for systematic study of intricate intermolecular interactions and energy transfer mechanisms that give rise to correlations between ordinarily unrelated rotational transitions. Many experimental refinements are possible, including the introduction of a third THz pulse (45, 46), which would enable measurements at variable population times and could yield the lifetimes of transient complexes. Such measured lifetimes would be distinct from the dephasing times derived from spectral linewidths. Considerable reduction in data acquisition time may be enabled by incorporating single-shot spectroscopy methods to eliminate the need for one of the variable delays (47–49) or through high-resolution multidimensional spectroscopy with frequency combs (39), which have been generated and used for linear spectroscopy of water vapor at THz frequencies (50). Multidimensional THz rotational spectroscopy holds promise for many applications including measurement of enantiomeric excess (15), molecular cluster identification and characterization, and coherent manipulation of molecular orientation.

Materials and Methods

Sample Preparation.

A capped storage vessel (25 mL; Chemglass Life Sciences) with a sidearm served as a liquid water container. About 5 mL liquid water was pipetted into the storage vessel at room temperature. The sidearm of the vessel was connected to a stainless-steel transfer line (∼50 cm long), the other end of which was linked to a gas cell with a 1.25-cm path length. Three valves were equipped to adjust the gas flow. Liquid water in the storage vessel was frozen into ice using liquid nitrogen, following a vacuum pumping process to eliminate air in the storage vessel, the transfer line, and the gas cell before ice melted.

The storage vessel was then sealed by the cap and immersed in a warm water bath heated by a hotplate. The temperature was stabilized at approximately 60 °C to avoid water condensation. A temperature-controllable silicone heating tape (Cole-Parmer) was wrapped around the system in order to maintain a stable temperature (copper wires were also used at local turning points for the same purpose). By slightly unscrewing the cap of the storage vessel, water vapor was allowed to slowly diffuse into the gas cell via the transfer line. A few minutes was allowed for the gas pressure to equilibrate (∼150 Torr at 60 °C). The gas cell was then sealed and moved into the experimental setup while the heating tape was still attached and turned on until the experiment was completed.

THz Time-Domain Spectroscopy (THz-TDS).

A typical THz-TDS system (51) was used to record the temporal profile of water vapor from ambient air at room temperature (SI Appendix, Fig. S1). A mode-locked Ti:sapphire oscillator (78-MHz repetition rate, 150-mW average power, 800-nm central wavelength, <100-fs pulse duration) was used to pump a direct current biased photoconductive antenna (PCA) made of low-temperature-grown gallium arsenide (LT-GaAs). The generated single-cycle THz field (∼1 ps, 0.1- to 5-THz spectrum) was collected by four 90° off-axis parabolic mirrors and detected by another PCA. A small portion of the femtosecond laser beam was split and sent into an optical delay line, attenuated, and used to read out the THz field profile. The THz field amplitude was proportional to the time-averaged photocurrent and detected by a lock-in amplifier. The coherent nature of the detection ensures a high signal–noise ratio on the order of $1.0\times {10}^4$.

Two-Dimensional THz Spectroscopy.

Two Ti:sapphire amplifier systems (Coherent; 1-kHz repetition rate, 800-nm central wavelength) were used in our experiments. One delivered 35-fs pulses and had an output power of 7 W; the other delivered 100-fs pulses and had 3.5 W output power. Using either system, 95% of the output power was divided into two equal parts with time delays between them controlled by a mechanical delay stage. Both parts were directed into the same lithium niobate (LN) crystal to generate two time-delayed, collinearly propagating THz pulses by the tilted-pulse-front technique. The generated THz pulses (SI Appendix, Fig. S2) were collected by four 90° off-axis parabolic mirrors and focused on the gas sample in the gas cell. The remaining 5% of the laser output was attenuated, routed into a third path to read out the THz signals by electro-optic sampling in a 2-mm ZnTe crystal. Dry air was used to purge the experimental setup to avoid THz absorption by water vapor from ambient air. The two THz electric field amplitudes were 440 kV/cm and 290 kV/cm using the 35-fs laser system and 300 kV/cm and 350 kV/cm using the 100-fs laser system. Two-dimensional spectra in the close-up view (Fig. 3) were measured using the 100-fs laser system, and all other signals were obtained using the 35-fs laser system.

Differential Chopping Technique.

Differential chopping was employed to separate nonlinear THz signals from strong linear signals (SI Appendix, Figs. S3 and S4). Two optical choppers were placed in the two optical paths to modulate the optical pulses used for THz generation. One chopper was operating at 500-Hz frequency, the other at 250 Hz. Each chopper was put in one optical path. Within four sequential laser shots, THz pulses from both paths 1 and 2 denoted as $E_{12}$, only from path 1 denoted as $E_1$, only from path 2 denoted as $E_2$, and none denoted as $E_{BG}$ were produced, respectively. The two choppers and the laser were synced to a data acquisition card (National Instruments) that was used to measure the signal output from EO sampling. Each data point was averaged over 100 laser shots in order to achieve a signal–noise ratio of around 5,000. The total acquisition time period for a complete 2D scan was roughly 2.5 d.

Data Availability

All study data are included in the article and/or SI Appendix.