Cavitation controls droplet sizes in elastic media

Significance

Biological cells use liquid-like droplets to partition their proteins spatially. These droplets are typically surrounded by an elastic matrix, like the cytoskeleton or chromatin, but how the matrix affects droplets is unclear. To elucidate this, we introduce a theoretical model describing experiments in a synthetic system. We show that regular arrangements of large droplets with controlled sizes coexist with droplets on the mesh size when the elastic matrix can break under stress. We thus demonstrate how elastic matrices can control droplets. Similar effects could play a role in biological cells, and our theory forms the basis for further investigations.

Abstract

Biological cells use droplets to separate components and spatially control their interior. Experiments demonstrate that the complex, crowded cellular environment affects the droplet arrangement and their sizes. To understand this behavior, we here construct a theoretical description of droplets growing in an elastic matrix, which is motivated by experiments in synthetic systems where monodisperse emulsions form during a temperature decrease. We show that large droplets only form when they break the surrounding matrix in a cavitation event. The energy barrier associated with cavitation stabilizes small droplets on the order of the mesh size and diminishes the stochastic effects of nucleation. Consequently, the cavitated droplets have similar sizes and highly correlated positions. In particular, we predict the density of cavitated droplets, which increases with faster cooling, as in the experiments. Our model also suggests how adjusting the cooling protocol and the density of nucleation sites affects the droplet size distribution. In summary, our theory explains how elastic matrices affect droplets in the synthetic system, and it provides a framework for understanding the biological case.

Phase separation has emerged as a powerful concept to explain how biological cells structure their interiors (1, 2). It explains how membraneless compartments with distinct chemical composition, called biomolecular condensates, form spontaneously. In contrast to classical liquid−liquid phase separation, these condensates exist in complex, crowded environments, for example, provided by the cytoskeleton in the cytosol or the chromatin in the nucleus. This fundamentally affects the behavior of condensates: Their coarsening is slowed down by subdiffusive motion (3), they are supported against gravity by the F-actin network in the nuclei of large cells (4), and their assembly depends on the stiffness of their surrounding (5, 6). Another example is artificially induced condensates, which typically appear in soft regions of the chromatin (7). Taken together, these experiments and recent numerical simulations (8) demonstrate that condensates react to the elastic properties of their surroundings (9), but the detailed dynamics are still unclear.

The interaction of droplets with soft elastic matrices can be studied in detail in a synthetic system, where oil droplets are induced in a PDMS (Polydimethylsiloxane) matrix by lowering the temperature (10). Similar to the biological case, droplets are biased toward softer regions in this system (11, 12). This elastic ripening is absent when the elastic properties of the system are homogeneous. Instead, all observable droplets attain similar sizes, and their positions are correlated (10). Interestingly, one observes smaller droplets in stiffer systems and at higher cooling rates (10). This implies that the final state is governed by nonequilibrium processes, which is also demonstrated by the bidisperse emulsions that form after increasing the cooling rate during the experiment (11).

Theoretical models of droplets growing in an elastic matrix have to describe how the matrix affects the droplets’ dynamics. In the simplest case, the matrix exerts a pressure on the droplets proportional to the local stiffness, which is sufficient to explain elastic ripening (13). Moreover, assuming a strain-stiffening surrounding can explain why droplets attain the same size, which decreases with stiffness (14–16). However, these equilibrium models cannot describe the dependence on the cooling rate.

In this paper, we present a dynamic theory of droplet formation in elastic matrices, which is based on the assumption that droplets can break the surrounding matrix. We show that, in this case, some droplets cavitate and grow macroscopically, while a large fraction are restricted to mesh size. The cavitated droplets have a similar size, which decreases with a higher cooling rate. We motivate our theory by first considering how the elastic matrix affects a single droplet. We then couple the dynamics of multiple droplets via the diffusion of monomers in the dilute phase. Using numerical simulations and analytical approximations, we demonstrate that this model can explain the relevant experimental observations of the synthetic system.

External Pressure Governs Dynamics of Droplets

To understand how droplets interact with an elastic matrix, we first consider a single spherical droplet of radius $R$. Motivated by experimental observations (10, 17), we assume that the droplet excludes the matrix completely. Droplet growth is driven by the differences in chemical potential and osmotic pressure between the droplet and its surroundings. We show, in SI Appendix, that this can be captured by a driving strength $g$, which quantifies the energy gain when the droplet volume $V=\left(4\pi /3\right)R^3$ increases. However, when the droplet grows, its surface area $A=4\pi R^2$ also increases, which comes at a cost proportional to the surface energy $\gamma$. Moreover, the matrix surrounding the droplet must be displaced, which we capture by an elastic energy $F_E\left(V\right)$. Taken together, the free energy $F$ of the entire system reads

$$F=-g\hspace{0.17em}V+\gamma A+F_E\left(V\right),$$ [1]

where we, for simplicity, first consider constant driving strength $g$ and surface energy $\gamma$.

A droplet will grow spontaneously when the free energy decreases ($\partial F/\partial V<0$), that is, if

$$g>P\left(R\right)\hspace{1em}\hspace{1em}\text{with}\hspace{1em}\hspace{1em}P\left(R\right)=P_{\gamma }\left(R\right)+P_E\left(R\right),$$ [2]

where $P_{\gamma }=2\gamma /R$ is the Laplace pressure due to the surface tension $\gamma$ (18, 19), and $P_E=\partial F_E/\partial V$ is the pressure exerted by the elastic matrix; see SI Appendix. A droplet thus grows when the driving strength $g$ exceeds the pressure $P$ exerted on the droplet. A stationary state with droplet radius $R^{*}$ is reached when $g=P\left(R^{*}\right)$, which is stable if ${\partial }^{2}F/\partial V^2>0$, or

$$P^{\prime }\left(R_{*}\right)>0.$$ [3]

A droplet is thus stable when the exerted pressure increases with its size.

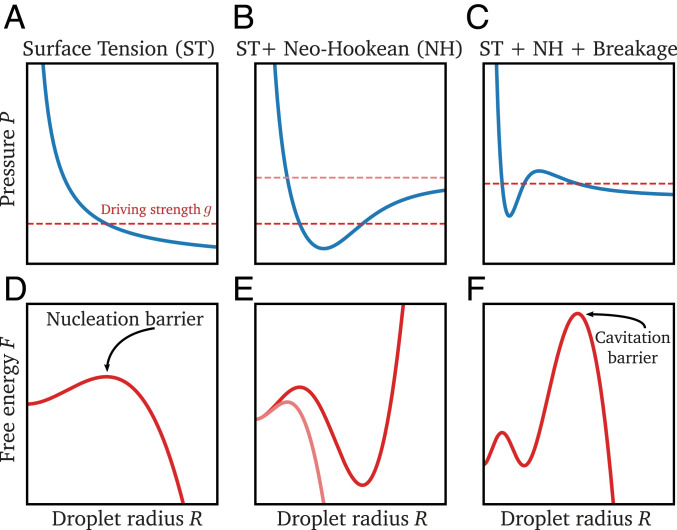
Without an elastic matrix, the droplet is only affected by the Laplace pressure $P_{\gamma }$; see Fig. 1A. The corresponding free energy shown in Fig. 1D demonstrates that surface tension dominates for small droplets. In particular, droplets can only grow spontaneously ($\partial F/\partial V<0$) after overcoming a nucleation barrier, for example, by thermal fluctuations (homogeneous nucleation) (20) or thanks to nucleation sites that lower the barrier (heterogeneous nucleation); see SI Appendix. Once the droplet is big enough, the energy decreases with increasing radius, and the droplet is always unstable ($P_{\gamma }^{\prime }\left(R\right)<0$). Droplet growth is then only restricted by the available amount of material.

Fig. 1.

Breakage of the mesh implies a cavitation barrier. Example of pressure $P=P_E+P_{\gamma }$ exerted on a droplet during growth (A−C) and corresponding free energy $F$ (D−F) as a function of the droplet radius $R$. $F$ is obtained from Eq. 1 for fixed driving strength $g$ (red dashed lines in A−C). Without an elastic mesh ($P_E=0$), the pressure curve is monotonously decreasing (A). After crossing a nucleation barrier, droplets grow until all material is absorbed (D). An elastic matrix increases the pressure once the droplet grows beyond mesh size (B). This can lead to an energy minimum where droplets are stable (E). If the mesh can break, the pressure curve exhibits a local maximum (C), which leads to a cavitation barrier (F).

An Elastic Matrix Restricts Droplet Growth

An elastic matrix surrounding the droplet exerts an additional pressure and thus potentially opposes growth; see Eq. 2. The pressure exerted by the matrix depends on its elastic response. For small deformations, the response can be characterized by the Young’s modulus $E$. However, droplets can grow much larger than the mesh size $\ell$, implying large deformations of the matrix. The simplest model describing such hyperelastic material is the neo-Hookean model, where the pressure on a spherical cavity of radius $R$ is monotonically increasing ($P_E^{\prime }\left(R\right)>0$) and converges at large radii to $P_E=5E/6$ (21). If the driving strength $g$ is lower than the maximal pressure, the system opposes further droplet growth and leads to a stable radius $R_{*}$ when $g=P\left(R_{*}\right)$; see Fig. 1B. This steady state corresponds to a minimum in the free energy; see Fig. 1E. Therefore, an elastic mesh providing resistance to droplet growth can stabilize droplets.

Breakage Provides a Cavitation Barrier for Droplets.

The neo-Hookean model is often too simple to describe realistic materials, in part because it does not account for breaking bonds in the elastic mesh. To capture breakage, we next consider a stress−strain curve that has a maximal pressure $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$ at a finite radius $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$; see Fig. 1C. Similar to the neo-Hookean model, we consider an increasing pressure when droplets grow beyond the mesh size $\ell$. However, at the critical radius $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$, the mesh cannot sustain the stress anymore and breaks, resulting in a pressure decrease (22). The stability criterion given in Eq. 3 indicates that droplets with $R=R_{\mathrm{c}\mathrm{a}\mathrm{v}}$ are unstable and will thus expand rapidly in a cavitation event (23, 24).

The nonmonotonous stress−strain relation shown in Fig. 1C results in a free energy that has two energy barriers; see Fig. 1F. The first barrier is the familiar nucleation barrier, while the second one is the cavitation barrier. The local minimum between the two barriers corresponds to the stable state described in the case of the neo-Hookean model. However, with breakage, droplets can overcome the second barrier and cavitate if the driving strength $g$ exceeds $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$. The growth of such droplets would then only be limited by the available amount of material, similar to the case without any elastic matrix.

Multiple Droplets Grow When Temperature Is Decreased

In the experiments of Style et al. (10), multiple oil droplets appeared simultaneously when the temperature was lowered. Since lowering the temperature corresponds to increasing the driving strength $g$, cavitated droplets appear when $g$ reaches the maximal pressure exerted by the surrounding matrix. If this maximal pressure increases with the overall stiffness, we predict that lower temperatures are necessary to create droplets in stiffer systems, which was indeed observed (11). However, this qualitative analysis does not distinguish between the neo-Hookean and the breakage model, since both allow simultaneous growth of droplets.

To distinguish the neo-Hookean from the breakage model, we need to analyze the droplet dynamics in detail. Since the droplets are spherical in the experiments (10), we expect that direct elastic interactions mediated by the mesh are negligible. This assumption is consistent with the observation that a droplet growing in PDMS remains spherical and only affects the mesh in a thin layer surrounding the droplet when its radius is smaller than the elasto-adhesive length scale (17, 22). In our case, the elasto-adhesive length scale, given by the ratio of the fracture energy to the Young’s modulus $E$, is about 100 $\mathrm{\mu }\text{m}$ (17) and thus larger than all droplets. Taken together, this suggests that droplets do not strongly interact via elastic deformations of the mesh. Instead, the dynamics of growing droplets are coupled because they compete for the material dissolved in the dilute phase. We analyze this situation using a theory, where we describe a collection of immobile droplets by their positions ${\overrightarrow{x}}_i$ and their radii $R_i$ together with the concentration field $c\left(\overrightarrow{x}\right)$ of droplet material in the dilute phase (13). For simplicity, we assume that the concentration $c_{\mathrm{i}\mathrm{n}}$ inside each droplet is constant, droplets are in equilibrium with their immediate surrounding, and the dilute phase can be approximated as an ideal solution. In this case, the concentration right outside the interface of a droplet is given by (13)

$$c_{\mathrm{e}\mathrm{q}}\left(P,T\right)=c_{\mathrm{s}\mathrm{a}\mathrm{t}}\left(T\right)\exp \left(\frac{P}{c_{\mathrm{i}\mathrm{n}}{k}_{\mathrm{B}}T}\right),$$ [4]

where $P\left(R\right)$ is the pressure exerted by the surrounding, $c_{\mathrm{s}\mathrm{a}\mathrm{t}}$ is the equilibrium concentration in the absence of an elastic mesh in the thermodynamic limit, $k_B$ is Boltzmann’s constant, and $T$ is the system’s temperature.

Droplets grow when their surrounding is supersaturated ($c>c_{\mathrm{e}\mathrm{q}}$). The droplet growth rate reads (13)

$$\frac{\mathrm{d}{R}_i}{\mathrm{d}t}=\frac{D}{R_i{c}_{\mathrm{i}\mathrm{n}}}\left[c\left({\overrightarrow{x}}_i\right)-c_{\mathrm{e}\mathrm{q}}\left(P\left(R_i\right),T\right)\right],$$ [5]

where $D$ is the diffusivity of the droplet material in the dilute phase. The concentration in the dilute phase obeys

$${\partial }_{t}c=D{\nabla }^{2}c-c_{\mathrm{i}\mathrm{n}}\sum _i\frac{\mathrm{d}{V}_i}{\mathrm{d}t}\delta \left({\overrightarrow{x}}_i-\overrightarrow{x}\right),$$ [6]

where the last term accounts for material exchange with the droplets, which is proportional to the rate of change of the droplet volumes $V_i$ (13). Combined with no-flux conditions at the system’s boundary, Eqs. 5 and 6 conserve the total amount of droplet material.

We simulate the system by mimicking the experimental protocol of Style et al. (10). In particular, we consider a linear relation between the saturation concentration $c_{\mathrm{s}\mathrm{a}\mathrm{t}}$ and temperature $T$ together with a constant cooling rate. Consequently, $c_{\mathrm{s}\mathrm{a}\mathrm{t}}$ decreases linearly from the initial value $c_0$ until it reaches the minimal value $c_0-\mathrm{\Delta }c$ at the final temperature,

$$c_{\mathrm{s}\mathrm{a}\mathrm{t}}\left(t\right)=\left\{\begin{array}{cc}{c}_0-\alpha t\hspace{1em}\hfill & t<\frac{\mathrm{\Delta }c}{\alpha }\hfill \\ c_0-\mathrm{\Delta }c\hspace{1em}\hfill & \text{otherwise},\hfill \end{array}\right.$$ [7]

where $\alpha$ is the rate of the decrease. As $c_{\mathrm{s}\mathrm{a}\mathrm{t}}$ is lowered, the equilibrium concentration $c_{\mathrm{e}\mathrm{q}}$ also decreases (Eq. 4), implying a larger supersaturation $c-c_{\mathrm{e}\mathrm{q}}$, which corresponds to a higher driving strength $g$. Starting with a homogeneous system at high temperature (high $c_{\mathrm{s}\mathrm{a}\mathrm{t}}$), droplets will nucleate once $g$ is large enough to cross the nucleation barrier; see Fig. 1. We show, in SI Appendix, that homogeneous nucleation is basically impossible in the parameter range of the experimental system. Consequently, droplets must nucleate heterogeneously at nucleation sites. This suggests that surface tension effects are negligible for small droplets. In fact, surface tension is also negligible for large droplets, since Ostwald ripening is slow (see SI Appendix), suggesting that the total pressure $P$ is always dominated by the elastic pressure $P_E$. We thus neglect surface tension for simplicity and rather assume that droplets form quickly at nucleation sites. In particular, we initialize our simulations with many small droplets with radii on the order of the mesh size and focus on the subsequent dynamics. The radius at which droplets are initialized is unimportant, since they are restricted by the elastic matrix to have a small radius $R$ that is governed by the condition $g=P\left(R\right)$. Consequently, many microscopic droplets coexist early in the simulation.

Droplets can grow macroscopically ($R\gg \ell$) when the driving strength $g$ exceeds the pressure exerted by the mesh. Since realistic meshes are heterogeneous (25), the exerted pressure will vary slightly from droplet to droplet. To capture such heterogeneity for the neo-Hookean model (NH), we consider variable mesh sizes ${\ell }_i$, and give the pressure as (26)

$$P_i^{\mathrm{N}\mathrm{H}}\left(R\right)=E\left(\frac{5}{6}-\frac{2{\ell }_i}{3R}-\frac{{\ell }_i^4}{6R^4}\right)\hspace{1em}\hspace{1em}\text{for}\hspace{1em}R\ge {\ell }_i,$$ [8]

where $E$ is the macroscopic Young’s modulus of the material. Conversely, in the breakage model (BR), we choose random cavitation pressures $P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\left(i\right)}$, since this parameter dominates the cavitation barrier. We thus consider the simple form

$$P_i^{\mathrm{B}\mathrm{R}}\left(R\right)=\left\{\begin{array}{cc}0\hspace{1em}\hfill & R<\ell \hfill \\ P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\left(i\right)}\frac{R-\ell }{R_{\mathrm{c}\mathrm{a}\mathrm{v}}-\ell }\hspace{1em}\hfill & \ell \le R\le R_{\mathrm{c}\mathrm{a}\mathrm{v}}\hfill \\ P_{\infty }\hspace{1em}\hfill & R>R_{\mathrm{c}\mathrm{a}\mathrm{v}},\hfill \end{array}\right.$$ [9]

where we keep both $\ell$ and $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$ fixed for all droplets, since varying these parameters does not affect the results significantly; see SI Appendix. Eq. 9 implies that the external pressure increases linearly when the droplet grows beyond the mesh size $\ell$ until it reaches the cavitation radius $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$. Beyond this threshold, the mesh breaks and provides a constant resistance quantified by a pressure $P_{\infty }<P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\left(i\right)}$, which we keep the same for all droplets to suppress elastic ripening (13).

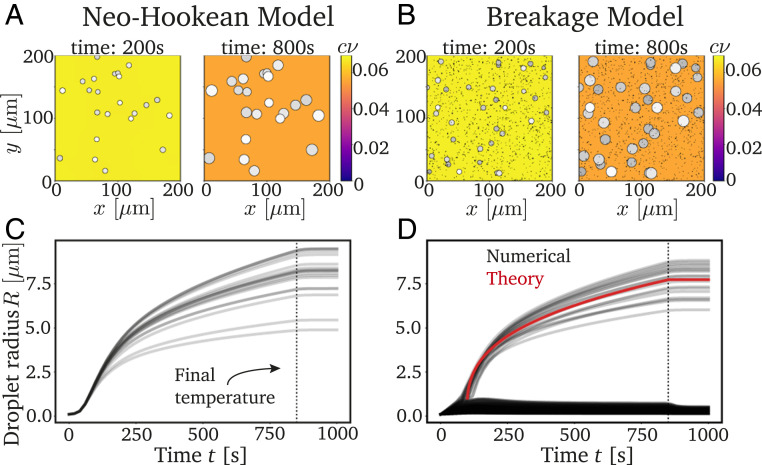
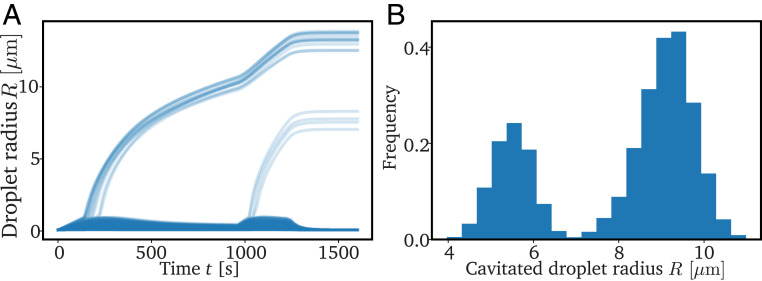
Fig. 2 shows typical simulations of Eqs. 4–7 for both the neo-Hookean model (Eq. 8) and the breakage model (Eq. 9). In both cases, macroscopic droplets appear, and they grow with very similar rates. However, the breakage model additionally exhibits a large number of microscopic droplets, which do not grow. Since these microscopic droplets are likely not visible in the experiment, both models appear to yield monodisperse emulsions, although this requires an extremely homogeneous mesh in the neo-Hookean model. In contrast, the models behave differently when we nucleate new droplets during the simulation: While all newly nucleated droplets grow in the neo-Hookean model, in the breakage model, most new droplets are restricted to microscopic sizes; see SI Appendix. Consequently, we expect that the breakage model leads to a more uniform size distribution of large droplets in realistic situations.

Fig. 2.

Decreasing temperatures cause monodisperse emulsions in the neo-Hookean model (A and C) and breakage model (B and D). (A and B) The 2D projections of typical simulations at two time points. The color indicates the concentration $c$ in the dilute phase, and droplets are marked with disks where brightness indicates depth. (C and D) Droplet radii $R$ as a function of time $t$ showing that large droplets are monodisperse after reaching the final temperature at $t=\mathrm{\Delta }c/\alpha$ (dotted black line). The red line in D shows the theoretical prediction given by Eq. 10. The model parameters are $\alpha$ = 1.864 $\cdot$ 10⁻⁵ s⁻¹$\cdot$$\nu$⁻¹, $E$ = 186 kPa, $\mathrm{\Delta }c$ = 0.0159 ${\nu }^{-1}$, $D$ = 50 $\mathrm{\mu }$m²$\cdot$s⁻¹, $c_{\mathrm{i}\mathrm{n}}={\nu }^{-1}$, and $c_{\mathrm{i}\mathrm{n}}{k}_{\mathrm{B}}T$ = 11 MPa, where $\nu =0.37{\text{nm}}^3$ is the molecular volume. For the neo-Hookean model, we sample $\ell$ uniformly between 0.1 and 0.102 $\mathrm{\mu }$m (25) and use $m$ = 7 $\cdot$ 10⁻⁶ $\mathrm{\mu }$m⁻³. For the breakage model, we have $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$ = 1 $\mathrm{\mu }$m, $m$ = 1.875 $\cdot$ 10⁻⁴ $\mathrm{\mu }$m⁻³, $\eta /m$ = 10⁵$E$ $\mathrm{\mu }$m³, $P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{min}=\hspace{0.17em}E$, and $P_{\infty }$ = 5/6$E$.

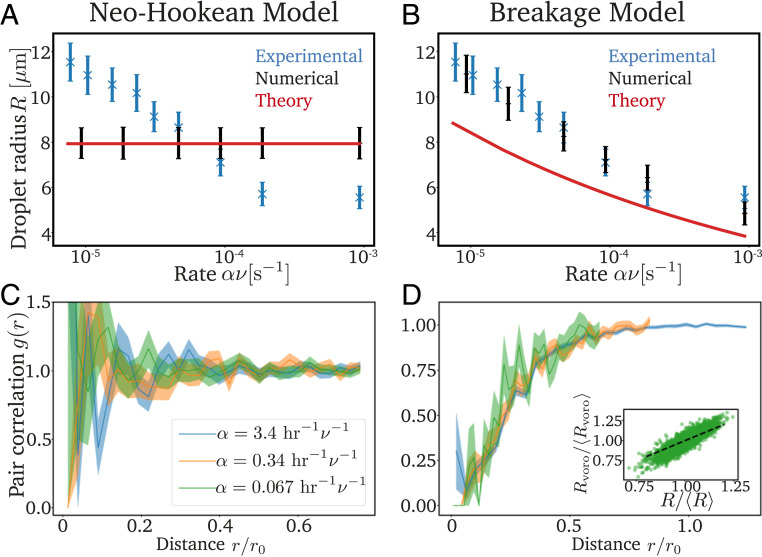
To see which of the two models provides a better explanation of the experiments, we next test their predictions quantitatively. Here, we use the experimentally measured values of $D$, $\mathrm{\Delta }c$, $\alpha$, $P_{\infty }$, $E$, and $c_{\mathrm{i}\mathrm{n}}$, while the values of the mesh size $\ell$ and the cavitation radius $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$ are arbitrary and do not affect the predictions of the model; see SI Appendix. The only relevant parameter, which we adjust to match the experimental data, quantifies the ratio of the mesh heterogeneity $\eta$ to the density $m$ of nucleated droplets. We first focus on the intriguing nonequilibrium effect that higher cooling rates lead to more and smaller droplets. In the neo-Hookean model, the average droplet size $⟨R⟩$ is independent of the cooling rate $\alpha$ (Fig. 3A), while $⟨R⟩$ and the associated standard deviation match the experimental data in the breakage model (Fig. 3B and SI Appendix, Fig. S4). The two models also differ in the spatial distribution of large droplets, which we quantify by the pair correlation function, similar to the experiments (10). Fig. 3C shows that droplets are uniformly distributed in the neo-Hookean model, since their positions are solely controlled by their nucleation. In contrast, droplet cavitation is correlated in the breakage model (Fig. 3D), leading to a low probability of finding two large droplets close to each other, similar to the experiments (10). The shown data collapse suggests that the size of the depletion region scales with the mean droplet separation. Moreover, the volume surrounding a droplet, measured from a Voronoi tessellation, is strongly correlated with its size; see Fig. 3D, Inset. The fact that our simulations match the experimental data quantitatively suggests that breakage is a crucial aspect.

Fig. 3.

The breakage model explains the experimental data. (A and B) Comparison of the experimental data [blue crosses (10)], numerical simulations (black symbols), and analytical predictions (red lines) for the radius $R$ of the cavitated droplets as a function of the rate $\alpha$ with which the saturation concentration decreases for the neo-Hookean model and the breakage model. (C and D) Pairwise correlation function $g\left(r\right)$ of the cavitated droplets scaled to the mean droplet separation $r_0=1.24\hspace{0.17em}{n}^{-1/3}$ (see SI Appendix) for three rates $\alpha$. Inset in D shows the correlation between the radius $R$ of droplets and the size $R_{\mathrm{v}\mathrm{o}\mathrm{r}\mathrm{o}}$ of their surrounding, which is obtained from a Voronoi tesselation. Model parameters in A−D are as in Fig. 2, except for $\eta /m=3\cdot 10^{5}E\hspace{0.17em}\mathrm{\mu }{\text{m}}^3$.

Large Droplets Suppress Further Cavitation by Depleting Their Vicinity

To understand how breakage affects the droplets’ dynamics, we next investigate why some droplets cavitate while others remain small; see Fig. 2D. Initially, all droplets are small and grow due to the decreasing saturation concentration by absorbing the excess material from the dilute phase. Note that droplets in a softer environment, that is, with a lower $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$, exhibit a lower equilibrium concentration $c_{\mathrm{e}\mathrm{q}}$ (Eq. 4), and thus grow faster. This initial growth phase continues until the droplet with the lowest $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$ reaches its cavitation radius $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$. At this point, the elastic matrix no longer provides enough resistance ($\partial P/\partial R<0$), and the droplet radius becomes unstable; see Eq. 3. The droplet thus cavitates by recruiting material from the dilute phase as fast as possible in a diffusion-limited process. Such a quickly growing droplet depletes its surroundings, effectively fixing the local driving strength to $g=P_{\infty }$. Consequently, other droplets in the vicinity cannot cavitate and will remain small forever. Taken together, the growth of a cavitated droplet prevents the cavitation of other droplets in its surroundings, while droplets farther away might still grow, which qualitatively explains the observed pair correlation function; see Fig. 3D.

The numerical data shown in Fig. 2D suggest that all droplets that become large cavitated at very similar times, $t=t_{\mathrm{c}\mathrm{a}\mathrm{v}}$, and grow with similar rates. To understand the growth dynamics, we first consider cavitated droplets that are homogeneously distributed with a number density $n$. Assuming that the cavitated droplets absorb all excess material from the dilute phase, we predict their volume to increase as

$$V\left(t\right)=V_{\mathrm{c}\mathrm{a}\mathrm{v}}+\frac{\alpha }{n{c}_{\mathrm{i}\mathrm{n}}}\left(t-t_{\mathrm{c}\mathrm{a}\mathrm{v}}\right),$$ [10]

where $V_{\mathrm{c}\mathrm{a}\mathrm{v}}=\left(4\pi /3\right)R_{\mathrm{c}\mathrm{a}\mathrm{v}}^3$. The red line in Fig. 2D shows that the equivalent prediction for the droplet radius explains the mean growth dynamics of cavitated droplets. In fact, this analysis is also valid for the neo-Hookean model shown in Fig. 2C, since droplets also start growing around the same time and absorb all excess material in this case. Taken together, this analysis indicates that the large droplets are monodisperse, because they start growing at the same time and grow with the same rate. However, while these conditions are met artificially by our setup of the neo-Hookean model, they are self-organized in the breakage model by controlling which droplets cavitate.

The final droplet size can be estimated by evaluating Eq. 10 at the time $t_{\mathrm{fi}\mathrm{n}\mathrm{a}\mathrm{l}}=\mathrm{\Delta }c/\alpha$, when the final temperature is reached. For simplicity, we consider the case where droplets are large compared to the cavitation threshold $R_{\mathrm{c}\mathrm{a}\mathrm{v}}$, which also implies $t_{\mathrm{c}\mathrm{a}\mathrm{v}}\ll t_{\mathrm{fi}\mathrm{n}\mathrm{a}\mathrm{l}}$ and leads to $V_{\mathrm{fi}\mathrm{n}\mathrm{a}\mathrm{l}}\approx \mathrm{\Delta }c/\left(n{c}_{\mathrm{i}\mathrm{n}}\right)$. This approximation correctly predicts that the final droplet volume is independent of the quench rate $\alpha$ in the neo-Hookean model where the droplet density $n$ is set by the initial condition; see Fig. 3A. Conversely, in the breakage model, the density of cavitated droplets might depend on the quench rate $\alpha$, which could explain the observed size dependence shown in Fig. 3B.

Number and Size of Cavitated Droplets Depend on Quench Rate and Cavitation Thresholds

To understand why faster cooling leads to more and smaller droplets, we next focus on the cavitation process in the breakage model. Since cavitated droplets suppress further cavitation in their vicinity, we hypothesize that this suppression is less efficient when the system is cooled faster, implying that more droplets can cavitate overall.

To estimate the final density $n$ of cavitated droplets, we analyze a simplified theoretical model. The main idea is to study a fixed density $n$ of cavitated droplets and test whether additional droplets could cavitate in this situation. The best estimate is then the lowest value of $n$ where no more droplets cavitate. For simplicity, we consider a homogeneous distribution of cavitated droplets, allowing us to focus on a single droplet of radius $R=R_{\mathrm{c}\mathrm{a}\mathrm{v}}$ in a spherically symmetric domain of volume $n^{-1}$. We then obtain the concentration field $c\left(r\right)$ around the droplet by solving the diffusion equation with the boundary condition $c\left(R_{\mathrm{c}\mathrm{a}\mathrm{v}}\right)=c_{\mathrm{e}\mathrm{q}}\left(P_{\infty },T\right)$; see SI Appendix. Additional cavitation takes place in the dilute phase if there is a droplet whose critical concentration $c_{\mathrm{c}\mathrm{a}\mathrm{v}}=c_{\mathrm{e}\mathrm{q}}\left(P_{\mathrm{c}\mathrm{a}\mathrm{v}},T\right)$ is lower than the actual concentration $c$ at its position. Note that the cavitation pressures $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$ are randomly distributed, since the elastic matrix is heterogeneous. However, since cavitation only happens for low $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$, it is sufficient to specify the associated cumulative distribution function $\mathcal{F}\left(P_{\mathrm{c}\mathrm{a}\mathrm{v}}\right)$ to linear order around the lower bound $P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$,

$$\mathcal{F}\left(P_{\mathrm{c}\mathrm{a}\mathrm{v}}\right)=\left\{\begin{array}{cc}0\hspace{1em}\hfill & P_{\mathrm{c}\mathrm{a}\mathrm{v}}<P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\hfill \\ {\eta }^{-1}\left(P_{\mathrm{c}\mathrm{a}\mathrm{v}}-P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\right)\hspace{1em}\hfill & \text{otherwise},\hfill \end{array}\right.$$ [11]

where $P_{\mathrm{c}\mathrm{a}\mathrm{v}}-P_{\mathrm{c}\mathrm{a}\mathrm{v}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\ll \eta$. Here, $\eta$ describes how widely the small cavitation pressures are distributed, thus quantifying the heterogeneity of the mesh. Considering a homogeneous density $m$ of nucleated droplets, we can then calculate the expected value of droplets that cavitate in the volume $n^{-1}$. This theory is self-consistent if exactly one droplet cavitates in this volume, which provides an implicit condition for the sought density $n$ of cavitated droplets; see SI Appendix.

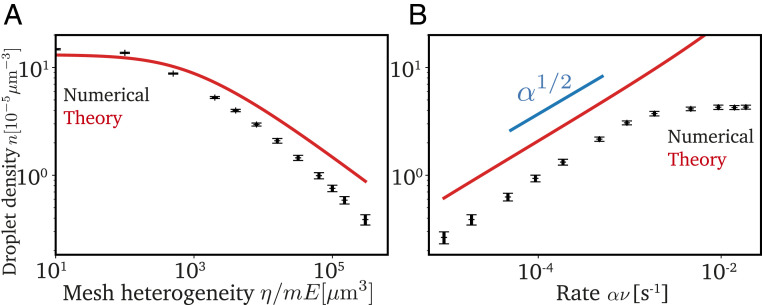
The theory does not have any adjustable parameters, and we thus compare it directly to our numerical simulations. Fig. 4A shows that the density $n$ of cavitated droplets decreases when fewer droplets nucleate (smaller $m$) or cavitation thresholds $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$ are more widely distributed (more heterogeneous network, higher $\eta$). This is because these two parameters define how many nucleated droplets possess a very low threshold, cavitate first, and then suppress cavitation of additional droplets. Conversely, Fig. 4B shows that more droplets cavitate when the system is cooled faster. Since the total amount of material taken up by droplets is conserved, this implies smaller droplets for faster cooling, consistent with Fig. 3B. While our theory shows the same trends as the numerical simulations, it consistently overestimates $n$ by roughly a factor of 2 in most cases. This is likely because we assumed a homogeneous distribution of the droplets with the lowest cavitation threshold, while, in reality, two droplets with low threshold might outcompete each other, effectively leading to a higher cavitation threshold than we anticipate. However, our theory indicates that the cavitated droplets deplete the dilute phase, thus suppressing further cavitation. Since this depletion is diffusion limited, decreasing temperature slowly implies stronger suppression, leading to fewer and larger droplets.

Fig. 4.

Suppression of cavitation by large droplets explains numerical data. (A) Density $n$ of cavitated droplets from numerical simulations (black symbols) compared to the analytical prediction (red line) as a function of the mesh heterogeneity $\eta$. (B) Density $n$ as a function of the rate $\alpha$ with which the saturation concentration decreases. Model parameters in A and B are given in Fig. 2, except $\eta /m$ = 3$\cdot$10⁵$E$ $\mathrm{\mu }$m³ in B.

Increasing Cooling Rates Cause Bidisperse Emulsions

We showed that the number and size of the cavitated droplets depends on the depletion of the dilute phase and thus the cooling rate. This implies that additional droplets could cavitate when the cooling rate is increased, while lowering the cooling rate should merely slow down droplet growth. Indeed, experiments by Rosowski et al. (11) showed a bimodal droplet size distribution when the cooling rate was rapidly increased in the middle of the experiment. To explain this observation, we perform a numerical simulation where we rapidly increase the cooling rate well after the first generation of droplets has cavitated. This results in a second generation of cavitated droplets, which then grow together with the previously cavitated ones; see Fig. 5. We show, in SI Appendix, that other size distributions are possible when the rate is changed multiple times. Taken together, this demonstrates that different droplet size distributions can be engineered by adjusting the cooling protocol.

Fig. 5.

Increasing cooling rate yields bidisperse emulsion. Shown are the droplet radii as a function of time (A) and the droplet size distribution (B) from a numerical simulation with $\eta /m$ = 3$\cdot$10⁵$E$ $\mathrm{\mu }$m ³, $E$ = 80 kPa, and $\alpha$ = 7.77$\cdot$10⁻⁶ s⁻¹$\cdot \nu$⁻¹ for $t<960\text{s}$, then $\alpha$ = 3.11$\cdot$10⁻⁵ s⁻¹$\nu$⁻¹. Other parameters are as in Fig. 2.

Heterogeneous Nucleation Might Explain More Cavitated Droplets in Stiffer Systems

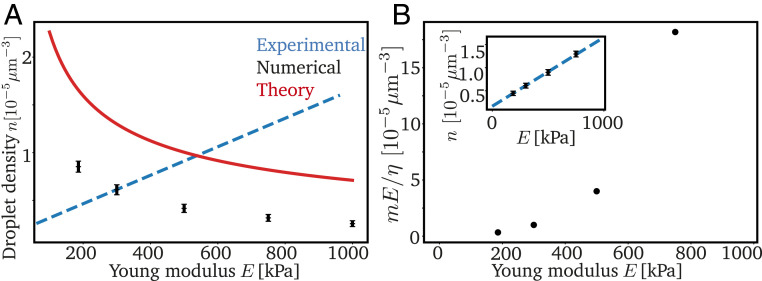
So far, we have investigated how the density and sizes of the observed droplets depend on the cooling rate $\alpha$. Another important observation of Style et al. (10) is that the droplet density $n$ increases linearly with the Young’s modulus $E$ of the elastic matrix. This implies that stiffer matrices lead to smaller droplets. Unfortunately, it is difficult to connect $E$, which measures the macroscopic response of the matrix to small strains, to the microscopic details required by our model. We thus next consider several possibilities to elucidate which microscopic picture could explain the experimental data.

In the simplest case, the bulk modulus $E$ is connected to the pressure curve $P\left(R\right)$. For example, the neo-Hookean model implies $P^{\mathrm{N}\mathrm{H}}\left(R\to \infty \right)=5/6E$; see Eq. 8. The relation is more complicated for the breakage model, but recent experiments (22) indicate that the cavitation pressure $P_{\mathrm{c}\mathrm{a}\mathrm{v}}$ and the pressure $P_{\infty }$ exhibited by large droplets scale with $E$. Using this scaling in our model, we obtain slightly smaller droplet densities for stiffer matrices, opposite to what we expect from the experiments; see Fig. 6A. Consequently, the scaling of the pressure with $E$ cannot explain the observed data.

Fig. 6.

Increasing nucleation density could explain stiffness dependence. (A) Droplet density $n$ as a function of Young’s modulus $E$. Our numerical (black symbols) and analytical (red line) theory, based on a linear scaling of pressures with $E$, cannot explain the experimental data [blue dashed line (10)]. (B) Predicted nucleation site density $m$ as a function of $E$ to match the measured $n\left(E\right)$ shown in Inset. (Inset) The $n\left(E\right)$ from experiments [blue dashed line (10)] and numerical simulations (black symbols). Model parameters in A and B are $\alpha$ = 2.33$\cdot$10⁻⁵ s⁻¹$\cdot \nu$⁻¹, and are given in Fig. 2.

Our model yields more (and smaller) cavitated droplets when the density $m$ of nucleated droplets is increased. Indeed, we can explain the observed linear increase of the density $n$ of cavitated droplets with $E$ by postulating that $m$ strongly increases with $E$; see Fig. 6B. So far, it is not clear how droplets actually nucleate in the elastic network, but it is likely that heterogeneous nucleation plays a role; see SI Appendix. Note that the mesh monomers are unlikely to act as heterogeneous nucleation sites, since they seem to be repelled from droplets. However, cross-linking molecules or catalysts that are used to create the PDMS matrix (10) could act as nucleation sites. In this case, stiffer gels would have more nucleated droplets simply because they contain more of these molecules (10, 11, 22). Moreover, stiffer networks might be more homogeneous (25), which would be captured by a smaller mesh heterogeneity $\eta$. Taken together, these two effects might explain our prediction that the parameter $m/\eta$ increases strongly with $E$.

Conclusions

We identified a mechanism to create monodisperse emulsions, where some growing droplets break the surrounding elastic matrix in a cavitation event. While these droplets become macroscopic, most droplets stay constrained by the matrix and do not grow significantly beyond mesh size. The cavitation barrier imposed by the elastic matrix thus separates the stochastic nucleation phase from a deterministic growth phase. The resulting cavitated droplets have correlated positions and similar sizes, which can be controlled by the cooling rate. Our model agrees quantitatively with experiments (10, 11), and it suggests how this mechanism can be used to create microscopic patterns in technological applications.

Monodisperse emulsions also emerge in other situations of driven phase separation. For instance, supplying more droplet material externally (27), internally using solubility gradients (28), or by chemical reactions (29) all lead to narrower droplet size distributions than expected from the standard Lifshitz−Slyozov argument (30). In all these cases, the diffusive flux between droplets that normally drives Ostwald ripening is dominated by the flux of the supplied droplet material. In our system, all droplets additionally start growing at similar times, because they cross the cavitation barrier at similar saturation concentrations. Taken together, this ensures that droplets reach similar sizes, despite multiple opposing processes: Besides the heterogeneities in the elastic properties that cause the dispersion in our model, thermal fluctuations might also contribute. Moreover, both Ostwald ripening, driven by surface tension, and Elastic ripening, driven by stiffness gradients over long length scales (11, 13), will affect the droplet size distribution in realistic systems. Finally, the heterogeneous nucleation that is required to form droplets in the experimental system might also affect the dynamics. In fact, we speculate that it can explain the observed increase in droplet density in stiffer meshes. It will be interesting to study all these interactions in the future.

We expect similar behaviors for biomolecular condensates, which often form as a response to changes in temperature, pH, salt concentration, or protein concentration in cells (31–34). Moreover, chemical modifications, like posttranslational modifications, allow cells to actively regulate condensates (35, 36). All these changes could, in principle, drive droplet formation, similar to the cooling in our example. Biomolecular condensates are also typically constrained by elastic matrices (3, 8, 9), which can limit their growth. Moreover, biopolymer gels often rearrange dynamically, implying that the mechanical stress exerted by droplets can relax and they can grow further, akin to the cavitation event in our model. Beyond our current description, the rearrangement implies viscoelastic behavior (37–39), and biopolymer gels also often display strain stiffening (40). There is also the possibility of droplets wetting the mesh instead of excluding it completely (16). Taken together with the fact that the size of typical condensates is comparable to the gel’s mesh size, we thus expect a rich phenomenology. Our theory provides a robust starting point for such future investigations.

Materials and Methods

The numerical simulations were performed using the py-pde python package (41) using an explicit Euler stepping with a second-order discretization of the spatial derivative in Eq. 6. Here, droplets are considered point-like, and the dilute concentration $c\left({\overrightarrow{x}}_i\right)$ in their vicinity is obtained using bilinear interpolation.

Data Availability

Source code data have been deposited in Zenodo (https://doi.org/10.5281/zenodo.4923528) (42).