Abstract
Individual behaviors play an essential role in the dynamics of transmission of infectious diseases, including COVID-19. This paper studies a dynamic game model that describes the social distancing behaviors during an epidemic, assuming a continuum of players and individual infection dynamics. The evolution of the players’ infection states follows a variant of the well-known SIR dynamics. We assume that the players are not sure about their infection state, and thus, they choose their actions based on their individually perceived probabilities of being susceptible, infected, or removed. The cost of each player depends both on her infection state and on the contact with others. We prove the existence of a Nash equilibrium and characterize Nash equilibria using nonlinear complementarity problems. We then exploit some monotonicity properties of the optimal policies to obtain a reduced-order characterization for Nash equilibrium and reduce its computation to the solution of a low-dimensional optimization problem. It turns out that, even in the symmetric case, where all the players have the same parameters, players may have very different behaviors. We finally present some numerical studies that illustrate this interesting phenomenon and investigate the effects of several parameters, including the players’ vulnerability, the time horizon, and the maximum allowed actions, on the optimal policies and the players’ costs.
Keywords: COVID-19 pandemic, Games of social distancing, Epidemics modeling and control, Nash games, Nonlinear complementarity problems
Introduction
COVID-19 pandemic is one of the most important events of this era. Until early April 2021, it has caused more than 2.8 million deaths, an unprecedented economic depression, and affected most aspects of people’s lives in the larger part of the world. During the first phases of the pandemic, non-pharmaceutical interventions (primarily social distancing) have been one of the most efficient tools to control its spread [13]. Due to the slow roll-out of the vaccines, their uneven distribution, the emergence of SARS-CoV-2 variants, age limitations, and people’s resistance to vaccination, social distancing is likely to remain significant in large part of the globe for the near future.
Mathematical modeling of epidemics dates back to early twentieth century with the seminal works of Ross [33] and Kermack and McKendrick [24]. A widely used modeling approach separates people in several compartments according to their infection state (e.g., susceptible, exposed, infected, recovered, etc.) and derives differential equations describing the evolution of the population of each compartment (for a review, see [1]).
However, the description of individual behaviors (practice of social distancing, use of face masks, vaccination, etc.) is essential for the understanding of the spread of epidemics. Game theory is thus a particularly relevant tool. A dynamic game model describing voluntary implementation of non-pharmaceutical interventions (NPIs) was presented in [32]. Several extensions were published, including the case where infection severity depends on the epidemic burden [6], and different formulations of the cost functions (linear vs. nonlinear, and finite horizon vs. discounted infinite horizon or stochastic horizon) [11, 15, 37]. Aurell et al. [4] study the design of incentives to achieve optimal social distancing, in a Stackelberg game framework. The works [2, 10, 12, 17, 22, 30, 31, 39] study different aspects of the coupled dynamics between individual behaviors and the spread of an epidemic, in the context of evolutionary game theory. Network game models appear in [3, 18, 27, 29], and the effects of altruism on the spread of epidemics are studied in [8, 14, 23, 26]. Another closely related stream of research is the study of the adoption of decentralized protection strategies in engineered and social networks [19, 21, 36, 38]. A review of game theoretic models for epidemics (including also topics other than social distancing, e.g., vaccination) is presented in [9, 20].
This paper presents a dynamic game model to describe the social distancing choices of individuals during an epidemic, assuming that the players are not certain about their infection state (susceptible (S), infected (I), or removed (R)). The probability that a player is at each health state evolves dynamically depending on the player’s distancing behavior, the others’ behavior, and the prevalence of the epidemic. We assume that the players care both about their health state and about maintaining their social contacts. The players may have different characteristics, e.g., vulnerable versus less vulnerable, or care differently about maintaining their social contacts.
We assume that the players are not sure about their infection state, and thus, they choose their actions based on their individually perceived probabilities of being susceptible, infected, or removed. In contrast with most of the literature, in the current work, players—even players with the same characteristics—are allowed to behave differently. We first characterize the optimal action of a player, given the others’ behavior, and show some monotonicity properties of optimal actions. We then prove the existence of a Nash equilibrium and characterize it in terms of a nonlinear complementarity problem.
Using the monotonicity of the optimal solution, we provide a simple reduced-order characterization of the Nash equilibrium in terms of a nonlinear programming problem. This formulation simplifies the computation of the equilibria drastically. Based on that result, we performed numerical studies, which verify that players with the same parameters may follow different strategies. This phenomenon seems realistic since people facing the same risks or belonging to the same age group often have different social distancing behaviors.
The model presented in this paper differs from most of the dynamic game models presented in the literature in the following ways:
The players act without knowing their infection state. However, they know the probability of being susceptible, infected, or recovered, which depends on their previous actions and the prevalence of the epidemic.
The current model allows for asymmetric solutions, i.e., players with the same characteristics may behave differently.
The rest of the paper is organized as follows. Section 2 presents the game theoretic model. In Sect. 3, we analyze the optimization problem of each player and prove some monotonicity properties. In Sect. 4, we prove the existence of the equilibrium and provide Nash equilibrium characterizations. Section 5 presents some numerical results. Finally, ‘Appendix’ contains the proof of the results of the main text.
The Model
This section presents the dynamic model for the epidemic spread and the social distancing game among the members of the society.
We assume that the infection state of each agent could be susceptible (S), infected (I), recovered (R), or dead (D). A susceptible person gets infected at a rate proportional to the number of infected people she meets with. An infected person either recovers or dies at constant rates, which depend on her vulnerability. An individual who has recovered from the infection is immune, i.e., she could not get infected again. The evolution of the infection state of an individual is shown in Fig. 1.
Fig. 1.

The evolution of the infection state of each individual
We assume that there is a continuum of agents. This approximation is frequently used in game theoretic models dealing with a very large number of agents. The set of players is described by the measure space , where is the Borel -algebra and the Lebesgue measure. That is, each player is indexed by an .
Denote by the probability that player is susceptible, infected, removed, or dead at time t. The dynamics is given by:
| 1 |
where are positive constants, and is the action of player i at time t. The quantity describes player i’s socialization, which is proportional to the time she spends in public places. The quantity , which denotes the density of infected people in public places, is given by:
| 2 |
For the actions of the players, we assume that there are positive constants , , such that . The constant describes the minimum social contacts needed for an agent to survive, and is an upper bound posed by the government.
The cost function for player i is given by:
| 3 |
where T is the time horizon. The parameter depends on the vulnerability of the player and indicates the disutility a player experiences if she gets infected. The quantity corresponds to the probability that player i gets infected before the end of the time horizon. (Note that in that case the infection state of the player at the end of the time horizon is I, R, or D.) The second term corresponds to the utility a player derives from the interaction with the other players, whose mean action is denoted by :
| 4 |
The third term indicates the interest of a person to visit public places. The relative magnitude of this desire is modeled by a positive constant . Finally, constant indicates the importance player i gives on the last two terms that correspond to going out and interacting with other people.
Considering the auxiliary variable :
| 5 |
and computing S(T) by solving (1), the cost can be written equivalently as:
| 6 |
Without loss of generality, assume that for all .
Assumption 1
(Finite number of types) There are M types of players. Particularly, there are values such that the functions are constant for , , . Denote by the mass of the players of type j. Of course
Remark 1
The finite number of types assumption is very common in many applications dealing with a large number of agents. For example, in the current COVID-19 pandemic, people are grouped based on their age and/or underlying diseases to be prioritized for vaccination. Assumption 1, combined with some results of the following section, is convenient to describe the evolution of the states of a continuum of players using a finite number of differential equations.
Assumption 2
(Piecewise constant actions) The interval [0, T) can be divided in subintervals , with , such that the actions of the players are constant in these intervals.
Remark 2
Assumption 2 indicates that people decide only a finite number of times () and follow their decisions for a time interval . A reasonable length for that time interval could be 1 week.
The action of player i in the interval is denoted by .
Assumption 3
(Measurability of the actions) The function is measurable.
Under Assumptions 1–3, there is a unique solution to differential equations (1), with initial conditions , and the integrals in (2), (4) are well defined (see Appendix A.1). We use the following notation:
For each player, we define an auxiliary cost, by dropping the fixed terms of (6) and dividing by :
| 7 |
where , and . Denote by the set of possible actions for each player. Observe that minimizes over the feasible set U if and only if it minimizes the auxiliary cost . Thus, the optimization problem for player i is equivalent to:
| 8 |
Note that the cost of player i depends on the actions of the other players through the terms and . Furthermore, the current actions of all the players affect the future values of and through the SIR dynamics.
Assumption 4
For a player i of type j, denote . Assume that the different types of players have different ’s. Without loss of generality, assume that
Assumption 5
Each player i has access only to the probabilities and and the aggregate quantities and , but not the actual infection states.
Remark 3
This assumption is reasonable in cases where the test availability is very sparse, so the agents are not able to have a reliable feedback for their estimated health states.
In the rest of the paper, we suppose that Assumptions 1–5 are satisfied.
Analysis of the Optimization Problem of Each Player
In this section, we analyze the optimization problem for a representative player i, given and , for .
Let us first define the following composite optimization problem:
| 9 |
where:
| 10 |
The following proposition proves that (8) and (9) are equivalent and express their solution in a simple threshold form.
Proposition 1
-
(i)
If is optimal for (8), then .
-
(ii)
Problems (8) and (9) are equivalent, in the sense that they have the same optimal values, and minimizes (8) if and only if there is an optimal A for (9) such that attains the minimum in (10).
-
(iii)
Let and . For , the function f is continuous, non-increasing, convex, and piecewise affine. Furthermore, it has at most N affine pieces and , for .
-
(iv)
There are at most vectors that minimize (8).
-
(v)
If is optimal for (8), then there is a such that implies , and implies .
Proof
The idea of the proof of Proposition 1 is to reduce the problem of minimizing (8) into the minimization of the sum of the concave function with a piecewise affine function f(A). Then, the candidates for the minimum are only the corner points and of f(A) and the endpoints of the interval, where f is defined. The form of the optimal action comes from a Lagrange multiplier analysis of (10). For a detailed proof, see Appendix 2.
Remark 4
Part (v) of the proposition shows that if the density of infected people in public places is high, or the average socialization is low, then it is optimal for a player to choose a small degree of socialization. The optimal action for each player depends on the ratio . Particularly, there is a threshold such that the action of player i is for values of the ratio below the threshold and for ratios above the threshold. Note that the threshold is different for each player.
Remark 5
The fact that the optimal value of a linear program is a convex function of the constraints constants is known in the literature (e.g., see [35] chapter 2). Thus, the convexity of the function f is already known from the literature.
Corollary 1
There is a simple way to solve the optimization problem (8) using the following steps:
Compute .
- For all compute with:
and . Compare the values of , for all , and choose the minimum.
We then prove some monotonicity properties for the optimal control.
Proposition 2
Assume that for two players and , with parameters and , the minimizers of (9) are and , respectively, and and are the corresponding optimal actions. Then:
-
(i)
If , then .
-
(ii)
If , then , for .
-
(iii)
If , then either for all k, or for all k.
Proof
See Appendix 3.
Remark 6
Recall that . Thus, Proposition 2(ii) expresses of the fact that if (a) a person is more vulnerable, i.e., she has large , or (b) she derives less utility from the interaction with the others, i.e., she has smaller , or (c) it is more likely that she is not yet infected, i.e., she has larger , then she interacts less with the others.
Remark 7
The optimal control law can be expressed in feedback form (see Appendix A.4.1).
Nash Equilibrium Existence and Characterization
Existence and NCP Characterization
In this section, we prove the existence of a Nash equilibrium and characterize it in terms of a nonlinear complementarity problem (NCP).
We consider the set , defined in Proposition 1. Let be the members of the set and be the mass of players of type j following action . Let also be the distribution of actions of the players of type j and be the distribution of the actions of all the players.
Denote by:
| 11 |
the set of possible distributions of actions of the players of type j and by the set of all possible distributions.
Finally, let be the vector function of auxiliary costs; that is, the component is the auxiliary cost of the players of type j playing a strategy , as introduced in (7), when the distribution of actions is . We denote the vector of the auxiliary costs of the players of type j playing , .
Let us recall the notion of a Nash equilibrium for games with a continuum of players (e.g., [28]).
Definition 1
A distribution of actions is a Nash equilibrium if for all and :
| 12 |
Let be the value of problem (8), i.e., the minimum value of the auxiliary cost of an agent of type j. This value depends on , through the terms and . Define and . We then characterize a Nash equilibrium in terms of a nonlinear complementarity problem (NCP):
| 13 |
where means that .
Proposition 3
-
(i)
A distribution corresponds to a Nash equilibrium if and only if it satisfies the NCP (13).
-
(ii)A distribution corresponds to a Nash equilibrium if and only if it satisfies the variational inequality:
14 -
(iii)
There exists a Nash equilibrium.
Proof
See Appendix A.5.
Remark 8
In principle, we can use algorithms for NCPs to find Nash equilibria. The problem is that the number of decision variables grows exponentially with the number of decision steps. Thus, we expect that such methods would be applicable only for small values of N.
Structure and Reduced-Order Characterization
In this section, we use the monotonicity of the optimal strategies, shown in Proposition 2, to derive a reduced-order characterization of the Nash equilibrium.
The actions on a Nash equilibrium have an interesting structure. Assume that is a Nash equilibrium and:
| 15 |
is the set of actions used by a set of players with a positive mass. Let us define a partial ordering on . For , we write if for all . Proposition 2(iii) implies that is a totally ordered subset of (chain).
Lemma 1
There are at most N! maximal chains in , each of which has length . Thus, at a Nash equilibrium, there are at most different actions in .
Proof
See Appendix A.6.
For each time step k, denote by the fraction of players who play , that is, . Given any vector , we will show that there is a unique , such that the corresponding actions satisfy the conclusion of Proposition 2(iii) and induce the fractions . An example of the relationship between and is given in Fig. 2.
Fig. 2.
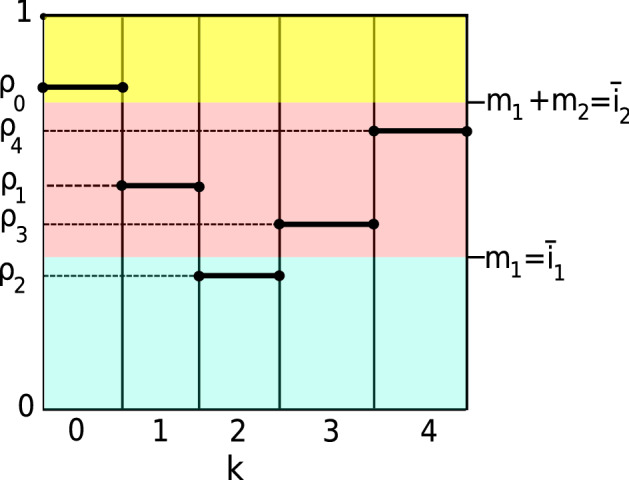
In this example, and there are types of players, depicted with different colors. The mass of players below each solid line play , and the mass of players above the line play . Example 1 computes from
Let us define the following sets:
Let be a reordering of such that . Consider also the set of actions with:
| 16 |
and , for all k. Observe that . The following proposition shows that the set , defined in (15) is subset of the set .
Before stating the proposition, let us give an example.
Example 1
Consider the fractions described in Fig. 2. There are three types of players with total mass , and with corresponding colors blue, pink, and yellow. In this example, we assume that the actions of each player are given by:
| 17 |
The sets are given by:
The sets are given by:
The actions are given by:
| 18 |
The mass of the players of each type following each action is described in the following table:
| Type | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 |
|---|---|---|---|---|---|---|---|---|
| Mass | ||||||||
| Action |
The following proposition and its corollary present a method to compute from in the general case (i.e., without assuming a set of actions in a form similar to (17)).
Proposition 4
Assume that , with , be a set of actions satisfying the conclusions of Proposition 2. Then:
-
(i)
For , either or .
-
(ii)
If for some , it holds , then -almost surely all the players have the same action on , i.e., .
-
(iii)Up to subsets of measure zero, the following inclusions hold:
where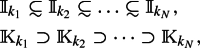
 indicates that . Furthermore, .
indicates that . Furthermore, . -
(iv)
For -almost all , the action is given by , for -almost all , , and for -almost all , .
Proof
See Appendix A.7.
Corollary 2
The mass of players of type j with action is given by:
| 19 |
where we use the convention that , and . Thus:
| 20 |
Proof
Remark 9
There are at most combinations of j, l such that
Let us denote by the value of vector computed by (20).
Example 2
The situation is the same as in Example 1, but without assuming that the actions are given by (17). Then, Corollary 2 shows that is given by the table in Example 1.
Proposition 5
The fractions correspond to a Nash equilibrium if and only if:
| 21 |
where is the cost of action , for a player of type j. Furthermore, is continuous and nonnegative.
Proof
See Appendix A.8.
Remark 10
The computation of an equilibrium has been reduced to the calculation of the minimum of an dimensional function. We exploit this fact in the following section to proceed with the numerical studies.
Numerical Examples
In this section, we give some numerical examples of Nash equilibria computation. Section 5.1 presents an example with a single type of players and Sect. 5.2 an example with many types of players. Section 5.3 studies the effect of the maximum allowed action on the strategies and the costs of the players.1
Single Type of Players
In this subsection, we study the symmetric case, i.e., all the players have the same parameter . The parameters for the dynamics are and which correspond to an epidemic with basic reproduction number , where an infected person remains infectious for an average of 6 days. (These parameters are similar to [22] which analyzes COVID-19 epidemic.) We assume that and that there is a maximum action set by the government. The discretization time intervals are 1 week, and the time horizon T is approximately 3 months (13 weeks). The initially infected players are . We chose this time horizon to model a wave of the epidemic, starting at a time point where of the population is infected. We assume that .
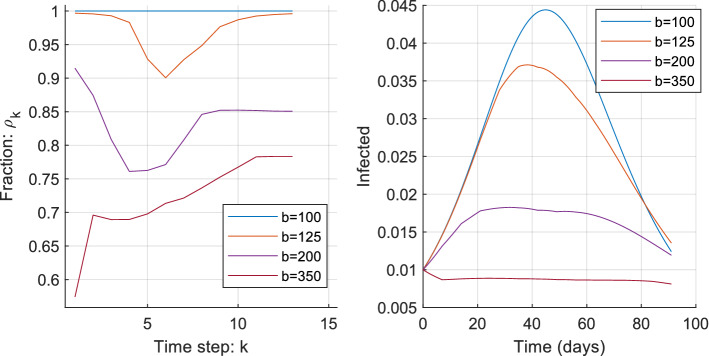
We then compute the Nash equilibrium using a multi-start local search method for (21). Figure 3 shows the fraction of players having action at each time step and the evolution of the total mass of infected players for the several values of b. We observe that, for small values of b, which correspond to less vulnerable or very sociable agents, the players do not engage in voluntary social distancing. For intermediate values of b, the players engage voluntary social distancing, especially when there is a large epidemic prevalence. For large values of b, there is an initial reaction of the players which reduces the number of infected people. Then, the actions of the players return to intermediate levels and keep the number of infected people moderate. In all the cases, voluntary social distancing ‘flattens the curve’ of infected people mass, in the sense that it reduces the pick number of infected people and leaves more susceptible persons in the end on the time horizon.
Fig. 3.
a The fractions , for , for different values of b. b The evolution of the number of infected people under the computed Nash equilibrium
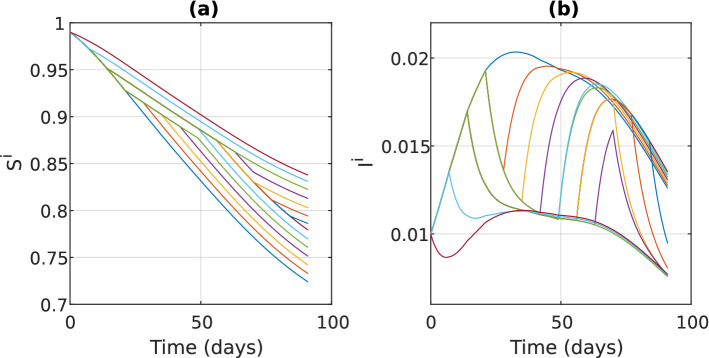
We then present some results for the case where . Figure 4 illustrates the evolution of and , for the players having different strategies. We observe that the trajectories of ’s do not intersect. What is probably interesting is that the trajectories of may intersect. This indicates that, toward the end of the time horizon, it is probable for a person who was less cautious, i.e., she used higher values of , to have a lower probability of being infectious.
Fig. 4.
The evolution of the probabilities and , for players following different strategies, for . Different colors are used to illustrate the evolution of the probabilities for players using different strategies
Many Types of Players
We then compute the Nash equilibrium for the case of multiple types of players. We assume that there are six types of players with vulnerability parameters . The sociability parameter is equal to 1, for all the players. The masses of these types are and . The initial condition is for all the players , and the time horizon is 52 weeks (approximately a year). Here, we assume that the maximum action is . The rest of the parameters are as in the previous subsection.
Figure 5 presents the fractions and the evolution of the probability of each category of players to be susceptible and infected. Let us note that the analysis of Sect. 4.2 simplifies a lot the analysis. Particularly, the set has dimensions, while Problem (21) only 52.
Fig. 5.
a The fractions of players having an action . Note that the fractions correspond to players of all types. Since , for all the types, it holds , and thus, the more vulnerable players cannot have an action higher than the less vulnerable ones. b The probability of a class of people to be susceptible and infected. The colored lines correspond to the probabilities of being susceptible and infected , for the several strategies of the players. The bold black line represents the mass of susceptible and infected persons (Color figure online)
Effect of
We then analyze the case where the types of the players are as in Sect. 5.2, and the initial condition is for all the players, for various values of . The time horizon is 13 weeks.
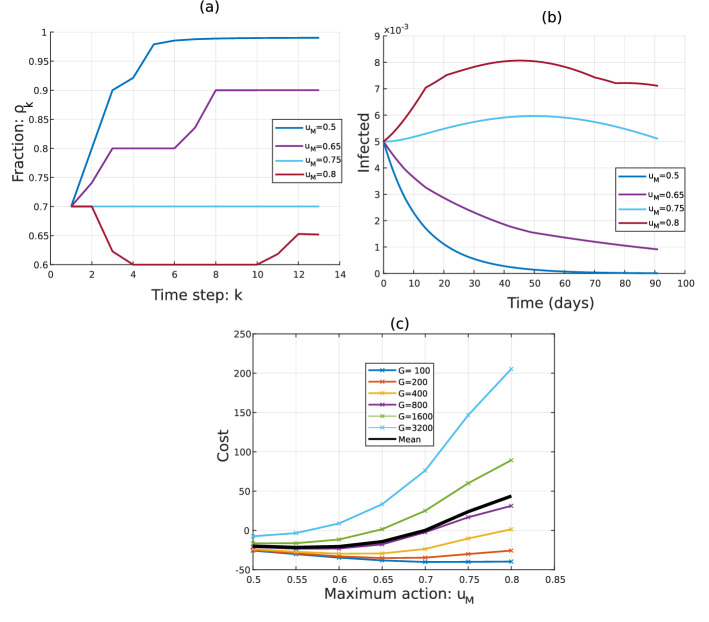
Figure 6a illustrates the equilibrium fractions , for the various values of . We observe that as increases, the fractions decrease. Figure 6b shows the evolution of the mass of infected players, for the different values of the maximum action . We observe that as increases, the mass of infected players decreases. Figure 6c presents the cost of the several types of players, for the different value of the maximum action . We observe that players with low vulnerability () prefer always a larger value of , which corresponds to less stringent restrictions. For vulnerable players (e.g., ), the cost is an increasing function of ; that is, they prefer more stringent restrictions. For intermediate values of G, the players prefer intermediate values of . The mean cost in this example is minimized for .
Fig. 6.
a The fractions , for the several values of the maximum action . b The mass of infected people as a function of time, for the different values of the maximum action . c The cost for the several classes of players, for the different values of the maximum action . The bold black line represents the mean cost of all the players
Conclusion
This paper studied a dynamic game of social distancing during an epidemic, giving an emphasis on the analysis of asymmetric solutions. We proved the existence of a Nash equilibrium and derived some monotonicity properties of the agents’ strategies. The monotonicity result was then used to derive a reduced-order characterization of the Nash equilibrium, simplifying its computation significantly. Through numerical experiments, we show that both the agents’ strategies and the evolution of the epidemic depend strongly on the agents’ parameters (vulnerability, sociality) and the epidemic’s initial spread. Furthermore, we observed that agents with the same parameters could have different behaviors, leading to rich, high-dimensional dynamics. We also observe that more stringent constraints on the maximum action (set by the government) benefit the more vulnerable players at the expense of the less vulnerable. Furthermore, there is a certain value for the maximum action constant that minimizes the average cost of the players.
There are several directions for future work. First, we can study more general epidemics models than the SIR. Second, we can investigate different information patterns, including the cases where the agents receive regular or random information about their health state. Finally, we can compare the behaviors computed analytically with real-world data.
A Appendix: Proof of the Results of the Main Text
A.1 Existence of Solution to (1)
Note that the first two equations in (1) do not depend on and . Thus, it suffices to show that the first two equations of (1) have a unique solution.
For any , if solve the differential equations (1), with initial condition , then remain in . Thus, we consider the solution of the differential equations:
| 22 |
where , and .
Consider the Banach space , and let . Then, under Assumptions 1,3, it holds . For each interval , the differential equations (22) with the corresponding initial conditions can be written as:
| 23 |
where for , the value of is given by:
where is a linear bounded operator with . For the initial condition, it holds , and is computed from the solution of (23) on the interval , for . For all k, is Lipschitz and thus there is a unique solution to (23) (e.g., Theorem 7.3 of [7]). Furthermore, both and are measurable and bounded. Thus, the integrals in (4), (2) are well defined.
Note that from Assumption 1, we only used the fact that are measurable and not the piecewise constant property.
Proof of Proposition 1
-
(i)
Since and , the cost (7) is strictly concave, with respect to . Thus, the minimum with respect to is either or .
-
(ii)Since U is compact and is continuous, there is an optimal solution for (8). Denote by this solution. Further, denote by and the values of problems (8) and (9), respectively. Then, for , we have
where the first inequality is due to the definition of and the second inequality is due to the definition of . To contradict, assume that . Then, there is some A and an such that:
Thus, there is a such that and . Combining with (24), we get , which contradicts the definition of . For minimizing (8), the problem (9) is minimized for and attains the minimum in (10). To see this, observe that otherwise we would have . On the other hand, assume that A minimizes (9) and attains the minimum in (10). Then, . Furthermore, since , it holds , and thus, minimizes .24 -
(iii)
The set is non-empty if and only if . Thus, the f(A) is finite if and only if .
For , there exists an optimal solution that attains the minimum in (10). Since (10) is a feasible linear programming problem, there is a Lagrange multiplier (e.g., Proposition 5.2.1 of [5]), and minimizes the Lagrangian:
Thus, , if and , if . To compute f(A), we reorder k, using a new index , such that is non-increasing. Let:25
Then:
where . Thus:
for . It holds:
Therefore, f is continuous and piecewise affine. Furthermore, since is non-increasing with respect to , the slope of f is non-decreasing, i.e., it is convex. Thus, f is differentiable in all except of the points with . The linear parts of f are at most N. -
(iv)Since is strictly concave in A, there are at most possible minima of , which correspond to the points of non-differentiability of f in and the points and . Observe that for or , there is a unique minimizing (10). We then show that for all the non-differentiability points A of f, there is a unique minimizing (10). If A is a non-differentiability point, there is a such that and . We then show that the unique minimizer in (10) is given by for and for . Indeed, is feasible and if is another feasible point, it holds:
Multiplying by , we get:
Then, using that , , and that for , it holds and for , it holds , we have:
and the inequality is strict if for some , . Therefore, is optimal and if is also optimal, then it should satisfy for all . Combining this with the fact that and , we get . -
(v)We have shown that if is optimal, then there is a such that for and for . Then, using the original index k, the optimal control can be expressed as:
where .
A.3 Proof of Proposition 2
-
(i)Since is optimal for and is optimal for , it holds:
Adding these equations and reordering, we get:
And since , we get -
(ii)Using (v) of Proposition 1, and , we get:
where is the Heaviside function, i.e., if and otherwise. Therefore, . -
(iii)Assume that for , and . Then, using (v) of Proposition 1 we have:
which is a contradiction.
A.4 Optimal Control and Equilibria in Feedback Form
A.4.1 Optimal Control in Feedback Form
In this section, we express the optimal control law in feedback form using dynamic programming. Let be the optimal cost-to-go from time k of a player with parameters :
| 26 |
where . The optimal cost-to-go can be expressed as:
We call the ‘auxiliary cost-to-go.’
Proposition 6
-
(i)
The auxiliary cost-to-go is non-increasing and concave in .
-
(ii)
The optimal cost-to-go is non-decreasing in , non-increasing in , and non-increasing and concave in .
-
(iii)
The optimal control law can be expressed in threshold form. That is, there are constants such that the optimal control law for each player satisfies: if and if . For , both and are optimal.
Proof
-
(i)The auxiliary cost-to-go can be written as:
Then, applying the principle of optimality we get:27
We use induction. For , the auxiliary cost-to-go is given by . That is, is non-increasing and concave in . Assume that it holds for . Then, for each fixed , the quantity:28
is non-increasing and concave in . Using (28), i.e., minimizing with respect to , we conclude to the desired result. -
(ii)
The monotonicity properties of are a direct consequence of its definition (26). The concavity of the optimal value follows easily from (i).
-
(iii)
From Proposition 1(i), we know that the optimal is in the set, . Using Proposition 2 to the subproblem starting at time step k, and applying the principle of optimality, we get the desired result. The fact that if , then both and are optimal, is a consequence of the continuity of .
Remark 11
Propositions 6(iii) and 1(v) both express the optimal actions for a player i. The primary difference is that Proposition 1(v) uses dynamic programming, and thus, the policies obtained can better handle uncertainties in the individual dynamics of player i.
Equilibrium in Feedback Strategies
Consider a Nash equilibrium that induces the fractions , the mean actions , and the mass of infected people in public places , for . Consider also the auxiliary cost-to-go function defined in (27), and the corresponding thresholds . Then, based on the strategies in Proposition 28(iii) we will describe a Nash equilibrium in feedback strategies. Consider the set of strategies:
| 29 |
.
Proposition 7
The set of strategies (29) is a Nash equilibrium.
Proof
Observe that the set of strategies (29) generates the same actions with the Nash equilibrium .
A.5 Proof of Proposition 3
-
(i)
Assume that a satisfies (13) and fix a . For any l such that , it holds , that is . Thus, is a Nash equilibrium.
Conversely, assume that is a Nash equilibrium and fix a . There is an l such that . Since is a Nash equilibrium, it holds and for all other , it holds , which implies (13).
-
(ii)Assume that is a Nash equilibrium and . Then, . Since is a Nash equilibrium, it holds:
Thus, (14) holds.Conversely, assume that (14) holds, for some . If is not a Nash equilibrium, then there is a j, l such that and . Then, if is such that , taking , we get , which is a contradiction.
-
(iii)
With a slight abuse of notation, we write to describe the quantities when the distribution of actions is and to describe the auxiliary cost of a player of type j who plays action when the distribution of the actions is .
Lemma 2
The quantities , are continuous on .
Proof
The state of the system evolves according to the set of differential equations:
where , , , and:
The initial conditions are , , (Assumption 1) and .
The right-hand side of the differential equations depends continuously on through the term . Furthermore, remain in [0, 1] for all . Thus, the state space of the system remains in and the right-hand side of the differential equation is Lipschitz. Thus, Theorem 3.4 of [25] applies and , and z(t) depend continuously on . Thus, depends continuously on . Furthermore, is continuous (linear) on . Finally, the auxiliary cost , due to its form (7), depends continuously .
To complete the proof, observe that is continuous and is compact and convex. Thus, the existence is a consequence of Corollary 2.2.5 of [16].
Remark 12
An alternative would be to use Theorem 1 of [34] or Theorem 1 of [28], combined with Lemma 2 to prove the existence of a mixed Nash equilibrium and then use Assumption 1, to construct a pure strategy equilibrium. However, the reduction to an NCP is useful computationally.
A.6 Proof of Lemma 1
Every maximal chain begins with the least element and ends at the greatest element . Every two consecutive elements of a maximal chain , differ at exactly one point; otherwise, there exists a vector : and thus the chain is not maximal.
Thus, beginning from and changing at each step one point from to , we get a sequence of -ordered vectors. So, every maximal chain has length .
Then, we prove that the number of such chains is N! using induction.
For , it is easy to verify that we have two chains of 3 elements.
For , we have n! maximal chains of elements. Then, for we consider one of the previous chains and at each of its elements, we add an extra bit: . We observe that if , then for all it should hold , in order for the new vectors to remain ordered under .
Denote by the point that change from to . For each choice of , we take two ordered vectors and in the new chain, so we have two . Thus, we have possible choices for the . This way we observe that from each chain in , we can construct chains in .
Remark 13
The fact that has at most elements is also a consequence of Corollary 1.
A.7 Proof of Proposition 4
-
(i)
To contradict, assume that and . Then, there is a pair of players such that and , which contradicts Proposition 2(iii).
-
(ii)Without loss of generality, assume that . Then:
Thus, . Combining with and the definition of , we get . -
(iii)
The equality is immediate from the definition of . Consider a pair . There are two cases, and . In the first case, we cannot have . Thus, from (i) we have . If , then
 from part (ii).
from part (ii).The inclusion is immediate from the definition.
-
(iv)
Let . Then, since for . On the other hand, -almost all satisfy , for . Thus, for -almost all , the action is given by (16). The proof is similar for , and .
A.8 Proof of Proposition 5
If corresponds to a Nash equilibrium, then combining (13) and (20) we conclude that . Conversely, since all the terms of (21) are nonnegative, implies that if , then . Combining this with (20), we conclude that if for some j, l, , then , where . That is, is a Nash equilibrium.
From (20), we observe that is continuous with respect to , since is the Lebesgue measure. Moreover, (21) can be expressed as:
The fact that is nonnegative is a result of (13). Furthermore, from Lemma 2, is continuous with respect to . Additionally, , which is the minimum of for all , is continuous with respect to as the minimum of continuous functions. So, is continuous with respect to and is continuous with respect to as composition of continuous functions.
Footnotes
Data availability: The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.
This article is part of the topical collection “Modeling and Control of Epidemics” edited by Quanyan Zhu, Elena Gubar and Eitan Altman.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ioannis Kordonis, Email: jkordonis1920@yahoo.com.
Athanasios-Rafail Lagos, Email: lagosth@mail.ntua.gr.
George P. Papavassilopoulos, Email: yorgos@netmode.ntua.gr
References
- 1.Allen LJ, Brauer F, Van den Driessche P, Wu J (2008) Mathematical epidemiology, vol 1945, Springer
- 2.Amaral MA, de Oliveira MM, Javarone MA (2020) An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. arXiv preprint arXiv:2008.05979 [DOI] [PMC free article] [PubMed]
- 3.Amini H, Minca A (2020) Epidemic spreading and equilibrium social distancing in heterogeneous networks [DOI] [PMC free article] [PubMed]
- 4.Aurell A, Carmona R, Dayanikli G, Lauriere M (2020) Optimal incentives to mitigate epidemics: a Stackelberg mean field game approach. arXiv preprint arXiv:2011.03105
- 5.Bertsekas DP (1997) Nonlinear programming. J Oper Res Soc 48(3):334–334
- 6.Bhattacharyya S, Reluga T. Game dynamic model of social distancing while cost of infection varies with epidemic burden. IMA J Appl Math. 2019;84(1):23–43. doi: 10.1093/imamat/hxy047. [DOI] [Google Scholar]
- 7.Brezis H (2010) Functional analysis. In: Sobolev spaces and partial differential equations, Springer
- 8.Brown PNN, Collins B, Hill C, Barboza G, Hines L (2020) Individual altruism cannot overcome congestion effects in a global pandemic game. arXiv preprint arXiv:2103.14538
- 9.Chang SL, Piraveenan M, Pattison P, Prokopenko M (2020) Game theoretic modelling of infectious disease dynamics and intervention methods: a review,” Journal of biological dynamics, vol. 14, no. 1, pp. 57–89 [DOI] [PubMed]
- 10.Chen FH (2009) “Modeling the effect of information quality on risk behavior change and the transmission of infectious diseases,” Mathematical biosciences, vol. 217, no. 2, pp. 125–133 [DOI] [PubMed]
- 11.Cho S (2020) Mean-field game analysis of SIR model with social distancing. arXiv preprint arXiv:2005.06758
- 12.d’Onofrio A, Manfredi P (2009) Information-related changes in contact patterns may trigger oscillations in the endemic prevalence of infectious diseases. J Theor Biol 256(3), 473–478 [DOI] [PubMed]
- 13.ECDC (2020) Guidelines for the implementation of non-pharmaceutical interventions against COVID-19
- 14.Eksin C, Shamma JS, Weitz JS. Disease dynamics in a stochastic network game: a little empathy goes a long way in averting outbreaks. Sci Rep. 2017;7(1):1–13. doi: 10.1038/srep44122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Elie R, Hubert E, Turinici G. Contact rate epidemic control of COVID-19: an equilibrium view. Math Model Nat Phenomena. 2020;15:35. doi: 10.1051/mmnp/2020022. [DOI] [Google Scholar]
- 16.Facchinei F, Pang J-S (2007) Finite-dimensional variational inequalities and complementarity problems, Springer
- 17.Funk S, Salathé M, Jansen VA (2010) “Modelling the influence of human behaviour on the spread of infectious diseases: a review,” Journal of the Royal Society Interface, vol. 7, no. 50, pp. 1247–1256 [DOI] [PMC free article] [PubMed]
- 18.Hota AR, Sneh T, Gupta K (2020) Impacts of game-theoretic activation on epidemic spread over dynamical networks. arXiv preprint arXiv:2011.00445
- 19.Hota AR, Sundaram S. Game-theoretic vaccination against networked SIS epidemics and impacts of human decision-making. IEEE Trans Control Netw Syst. 2019;6(4):1461–1472. doi: 10.1109/TCNS.2019.2897904. [DOI] [Google Scholar]
- 20.Huang Y, Zhu Q (2021) Game-theoretic frameworks for epidemic spreading and human decision making: a review. arXiv preprint arXiv:2106.00214 [DOI] [PMC free article] [PubMed]
- 21.Huang Y, Zhu Q. A differential game approach to decentralized virus-resistant weight adaptation policy over complex networks. IEEE Trans Control Netw Syst. 2019;7(2):944–955. doi: 10.1109/TCNS.2019.2931862. [DOI] [Google Scholar]
- 22.Kabir KA, Tanimoto J. Evolutionary game theory modelling to represent the behavioural dynamics of economic shutdowns and shield immunity in the COVID-19 pandemic. R Soc Open Sci. 2021;7(9):201095. doi: 10.1098/rsos.201095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Karlsson C-J, Rowlett J. Decisions and disease: a mechanism for the evolution of cooperation. Sci Rep. 2020;10(1):1–9. doi: 10.1038/s41598-020-69546-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kermack WO, McKendrick AG (1927) A contribution to the mathematical theory of epidemics. In: Proceedings of the royal society of London, series A, containing papers of a mathematical and physical character, vol 115, no 772, pp 700–721
- 25.Khalil HK, Grizzle JW (2002) Nonlinear systems, vol 3, Prentice Hall, Upper Saddle River
- 26.Kordonis I, Lagos A-R, Papavassilopoulos GP (2020) Nash social distancing games with equity constraints: how inequality aversion affects the spread of epidemics. arXiv preprint arXiv:2009.00146
- 27.Lagos A-R, Kordonis I, Papavassilopoulos G (2020) Games of social distancing during an epidemic: local vs statistical information. arXiv preprint arXiv:2007.05185 [DOI] [PMC free article] [PubMed]
- 28.Mas-Colell A. On a theorem of Schmeidler. J Math Econ. 1984;13(3):201–206. doi: 10.1016/0304-4068(84)90029-6. [DOI] [Google Scholar]
- 29.Paarporn K, Eksin C, Weitz JS, Shamma JS. Networked SIS epidemics with awareness. IEEE Trans Comput Soc Syst. 2017;4(3):93–103. doi: 10.1109/TCSS.2017.2719585. [DOI] [Google Scholar]
- 30.Poletti P, Ajelli M, Merler S (2012) “Risk perception and effectiveness of uncoordinated behavioral responses in an emerging epidemic,” Mathematical Biosciences, vol. 238, no. 2, pp. 80–89 [DOI] [PubMed]
- 31.Poletti P, Caprile B, Ajelli M, Pugliese A, Merler S (2009) “Spontaneous behavioural changes in response to epidemics,” Journal of theoretical biology, vol. 260, no. 1, pp. 31–40 [DOI] [PubMed]
- 32.Reluga TC. Game theory of social distancing in response to an epidemic. PLoS Comput Biol. 2010;6(5):e1000793. doi: 10.1371/journal.pcbi.1000793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ross R (1916) An application of the theory of probabilities to the study of a priori pathometry. In: Proceedings of the royal society of London, series A, containing papers of a mathematical and physical character, vol 92, no 638, pp 204–230
- 34.Schmeidler D (1973) “Equilibrium points of nonatomic games,” Journal of statistical Physics, vol. 7, no. 4, pp. 295–300
- 35.Shapiro A, Dentcheva D, Ruszczyński A. Lectures on stochastic programming: modeling and theory. Philipedia: SIAM; 2014. [Google Scholar]
- 36.Theodorakopoulos G, Le Boudec J-Y, Baras JS (2012) “Selfish response to epidemic propagation,” IEEE Transactions on Automatic Control, vol. 58, no. 2, pp. 363–376
- 37.Toxvaerd F (2020) Equilibrium social distancing, Cambridge working papers in economics
- 38.Trajanovski S, Hayel Y, Altman E, Wang H, Van Mieghem P. Decentralized protection strategies against SIS epidemics in networks. IEEE Trans Control Netw Syst. 2015;2(4):406–419. doi: 10.1109/TCNS.2015.2426755. [DOI] [Google Scholar]
- 39.Ye M, Zino L, Rizzo A, Cao M (2020) Modelling epidemic dynamics under collective decision making. arXiv preprint arXiv:2008.01971