Nearside-Farside Analysis of the Angular Scattering for the State-to-State H + HD → H₂ + D Reaction: Nonzero Helicities

Abstract

We theoretically analyze the differential cross sections (DCSs) for the state-to-state reaction, H + HD(v_i = 0, j_i = 0, m_i = 0) → H₂(v_f = 0, j_f = 1,2,3, m_f = 1,..,j_f) + D, over the whole range of scattering angles, where v, j, and m are the vibrational, rotational, and helicity quantum numbers for the initial and final states. The analysis extends and complements previous calculations for the same state-to-state reaction, which had j_f = 0,1,2,3 and m_f = 0, as reported by Xiahou C.; Connor J. N. L.. Phys. Chem. Chem. Phys. 2021, 23, 13349–13369. Motivation comes from the state-of-the-art experiments and simulations of Yuan et al.. Nature Chem. 2018, 10, 653–65829686377 who have measured, for the first time, fast oscillations in the small-angle region of the degeneracy-averaged DCSs for j_f = 1 and 3 as well as slow oscillations in the large-angle region. We start with the partial wave series (PWS) for the scattering amplitude expanded in a basis set of reduced rotation matrix elements. Then our main theoretical tools are two variants of Nearside-Farside (NF) theory applied to six transitions: (1) We apply unrestricted, restricted, and restrictedΔ NF decompositions to the PWS including resummations. The restricted and restrictedΔ NF DCSs correctly go to zero in the forward and backward directions when m_f > 0, unlike the unrestricted NF DCSs, which incorrectly go to infinity. We also exploit the Local Angular Momentum theory to provide additional insights into the reaction dynamics. Properties of reduced rotation matrix elements of the second kind play an important role in the NF analysis, together with their caustics. (2) We apply an approximate N theory at intermediate and large angles, namely, the Semiclassical Optical Model of Herschbach. We show there are two different reaction mechanisms. The fast oscillations at small angles (sometimes called Fraunhofer diffraction/oscillations) are an NF interference effect. In contrast, the slow oscillations at intermediate and large angles are an N effect, which arise from a direct scattering, and are a “distorted mirror image” mechanism. We also compare these results with the experimental data.

1. Introduction

The H + H₂ → H₂ + H reaction and its isotopic variants are important benchmarks in the theory of chemical reaction dynamics. In particular, measurements and calculations of state-to-state differential cross sections (DCSs) can provide detailed information on the dynamics and mechanism of this class of reactions.

Recently, an important experimental advance has been reported by Yuan et al.¹ for the H + HD → H₂ + D reaction. They have measured, for the first time, fast oscillations in the small-angle region of the degeneracy-averaged DCSs (abbreviated as daDCSs). They reported daDCSs for the following two transitions.

R1

In reaction (R1), v_i, j_i and v_f, j_f are the initial and final vibrational and rotational quantum numbers of the diatomic molecules, respectively. The experiment of Yuan et al.¹ used a high-resolution molecular-beam apparatus, crossed at 150°, with a velocity map imaging product detection at a translational energy of 1.35 eV. These daDCS measurements are the current state-of-the-art. Related experimental work can be found in refs (2−5).

The purpose of the present paper is to analyze and quantitatively understand the daDCSs of Yuan et al.¹ To do this, we start with the helicity (or body-fixed) representation for the scattering amplitude. We then have to consider the following 16 state-to-state DCSs

R2

where m_i and m_f are the helicity quantum numbers for the initial and final states, respectively.

In our earlier paper⁶ (denoted XC1), which is a companion to this one, we studied theoretically the DCSs for the four state-to-state transitions in reaction (R2) with m_f = 0, namely

R3

In particular, we analyzed the dynamics of the angular scattering for reaction (R3) in order to understand the physical content of the structure in the four helicity-resolved DCSs.⁶ We discovered: glory scattering at small angles, broad or “hidden” nearside rainbows, Nearside-Farside (NF) interference effects (sometimes called Fraunhofer diffraction/oscillations), a “CoroGlo” test to distinguish corona and forward glory scattering, and a “distorted mirror image” mechanism present at intermediate and large angles.⁶

In this paper, we focus on the DCSs for state-to-state transitions with nonzero helicities. This reduces the number of DCSs in reaction (R2) to 12. A further reduction is possible because the DCSs for m_f = −1, −2, −3 are equal to those for m_f = +1, +2, +3, respectively. This leaves the following six DCSs to be analyzed.

R4

We will often write 000 → 011, 000 → 021, 000 → 031, 000 → 022, 000 → 032, and 000 → 033 for the six transitions or, more simply, 011, 021, 031, 022, 032, and 033.

There is a fundamental difference between DCSs with m_f = 0 and those with m_f > 0 for reactions of the type (R3) and (R4). All DCSs with m_f > 0 are identically equal to zero in the forward (θ_R = 0°) and backward (θ_R = 180°) directions in the center-of-mass reference frame, which is a consequence of the conservation of angular momentum. Furthermore, the partial wave series (PWS) for the scattering amplitude for m_f = 0 uses a basis set of Legendre polynomials, whereas for m_f > 0 the basis set consists of reduced rotation matrix elements (also called Wigner or little d functions), which simplify to associated Legendre functions when m_i = 0. This means the theoretical analysis is more complicated and difficult for the m_f > 0 case compared to m_f = 0.

Now there has been one previous NF analysis of DCSs for chemical reactions with m_f > 0, which was made more than 20 years ago.⁷ In this work, Dobbyn et al.⁷ made the following important observation (on page 1117):

“...although the PWS becomes more complicated for more general types of collisions, this has little impact on the physical insight provided by a NF analysis”.

Thus, in this paper, (two variants of) NF theory will be used to provide physical insight into the reaction dynamics. Note that the NF theory was used extensively in XC1.⁶ In particular, an NF analysis has the advantage that the semiclassical (asymptotic) picture is still evident, even though semiclassical techniques, such as the stationary phase or saddle point methods, are not applied. Note that Yuan et al.¹ have conjectured on the role an NF analysis plays in explaining oscillatory structures in their DCSs. The two NF theories we use are

• (1)For a PWS with a basis set of Wigner functions, we use three NF decompositions: unrestricted (^unresNF),⁸restricted (^resNF),^9,10 and restrictedΔ (^resΔNF).⁷ The ^unresNF decomposition is a straightforward generalization⁸ of the NF decomposition for a Legendre PWS.^8,11 The ^unresNF DCSs incorrectly diverge as θ_R → 0°, 180°. In contrast, the ^resNF and ^resΔNF DCSs correctly go to zero as θ_R → 0°, 180°.^7,9,10

  The properties of the caustics of Wigner functions as well as those for reduced rotation matrix elements of the second kind play an important role in the definitions of ^resNF and ^resΔNF.^7,9,10 We also perform a resummation for a PWS of Wigner functions,¹² since it is well-known that a resummation can improve the physical effectiveness of an NF decomposition.¹³⁻¹⁹ In fact, the present paper is the first time that resummation theory has been combined with the ^resNF and ^resΔNF decompositions.

  The above remarks apply, in particular, to NF analyses of the full DCSs for the six transitions. We also report the results (including resummations) of the ^unresNF decomposition for the Local Angular Momentum (LAM), since this provides important additional insights into the reaction dynamics.¹³⁻¹⁶

• (2)A simple approximate N model, the Semiclassical Optical Model (SOM), which was originally introduced by Herschbach.^20,21 It is particularly useful for understanding structures in a DCS at intermediate and large angles for direct reactions.^6,7

This paper is organized as follows: Section 2 summarizes the partial wave theory and explains our conventions and definitions for the DCSs and LAMs. This section also includes a discussion of the caustic properties that we need and summarizes the ^unresNF, ^resNF, and ^resΔNF decompositions. Section 3 outlines the resummation for a PWS of Wigner functions. The properties of the input scattering matrices for the six transitions are presented in Section 4; we use the same accurate scattering matrix elements employed by Yuan et al.¹ in a simulation of their experiments. In Section 5, we discuss in detail the behavior of the ^unresNF, ^resNF, and ^resΔNF DCSs at small and large angles, as this has not been done before. Our results for the full and NF DCSs and LAMs, including resummations, are presented and discussed in Sections 6 and 7, respectively. The SOM DCSs at intermediate and large angles are presented and discussed in Section 8. We report daDCSs in Section 9, where we make comparisons with the experimental data. Our conclusions are in Section 10. Most of our results are presented graphically.

Appendix A proves that the state-to-state m_i = 0 DCSs for m_f = −1, −2, −3 and m_f = +1, +2, +3 are equal, respectively. In applications of the NF theory, it is essential to use unambiguous and consistent definitions for the special functions (of the first and second kinds) employed in the various NF decompositions. In Appendix B, we gather together the precise mathematical definitions that we use, since there is often more than one definition in the literature.

We also emphasize the following: This paper complements and extends XC1,⁶ where additional discussions and references can be found. These two papers illustrate the potency of the NF theory for divers applications.

2. Partial Wave Theory

2.1. Partial Wave Series

We start with the helicity (or body-fixed) PWS representation of the scattering amplitude for reaction (R4) at a fixed translational (or total) energy^22,23

1

where k_0,0 is the translational wavenumber for relative motion in the initial channel, J is the total angular momentum quantum number, S̃_000→0jfmf^J is a modified scattering matrix element, and d_mf,0(θ_R) is a reduced rotation matrix element (also called a Wigner function or “little d” function) as defined by Edmonds.²⁴ The reactive scattering angle θ_R is the angle between the incoming H atom and the outgoing H₂ molecule in the center-of-mass reference frame. Thus, θ_R = 0° and θ_R = 180° define the forward and backward directions, respectively. In practice, the upper limit of J = ∞ in the PWS is replaced by a finite value, J = J_max. This assumes that all partial waves with J > J_max can be neglected. In our applications, there are ∼40 numerically significant coherent partial waves, which makes the direct physical interpretation of the PWS very difficult or impossible. In addition, a constant phase has been omitted from eq 1.

The corresponding state-to-state DCS is given by

2

The PWS representation (1) is also valid for m_f = 0, as further analyzed in detail for the H + HD reaction in XC1;⁶ however, DCSs with m_f = 0 will only be needed in Section 9, when we discuss daDCSs. In passing, we note that the PWS (1) remains valid for m_f < 0, provided the starting value of the summation is replaced by J = |m_f|. This is only needed in Appendix A. In the remainder of this paper, we will often drop the channel labels from f, k, S̃, σ, etc. to keep the notation simple. We will also write S̃_J ≡ S̃^J.

To provide additional insight into the reaction dynamics, we also perform a Local Angular Momentum analysis.¹³⁻¹⁶ The LAM analysis provides information on the total angular momentum variable that contributes to the scattering at an angle θ_R under semiclassical conditions. It is defined by

3

Note that the arg in eq 3 is not necessarily the principal value in order that the derivative be well-defined.

Next we describe the unrestricted NF decomposition for the full PWS (1), which is the simplest NF decomposition, and we point out a limitation when m_f > 0.

2.2. Unrestricted Nearside-Farside Decomposition (^unresNF)

We exactly decompose f(θ_R) by writing it as the sum of two subamplitudes N and F, namely⁸

4

This is accomplished by exactly decomposing the d_mf,0^J(θ_R) in eq 1 into traveling angular functions of degree J and order m_f

5

where, for θ_R ≠ 0,π

6

In eq 6, the e_mf,0^J(θ_R) are reduced rotation matrix elements of the second kind (also known as “little e” functions) and defined in Appendix B. We see in eq 6 that the d_mf,0(θ_R) are linear combinations of reduced rotation matrix elements of the first and second kinds or, equivalently, from Appendix B, a linear combination of Jacobi functions of the first and second kinds.

Using eqs 4–(6), the N and F subamplitudes are given by (θ_R ≠ 0,π)

7

which is called the unrestricted NF decomposition. The adjective “unrestricted” is added because eq 7 can be used for all θ_R ∈ (0,π) with no restriction on the sum over J. We also sometimes write ^unresNF. The corresponding N and F DCSs are given by

8

With the help of eqs 2 and (8), we obtain

9

Equation 9 is the Fundamental Identity for Full and NF DCSs and is exact.²⁵

Similarly, we can define (unrestricted) N and F LAMs

10

There is an exact Fundamental Identity for Full and NF LAMs analogous to eq 9, although more complicated in form.²⁵ As before, the args in eq 10 are not necessarily principal values in order that the derivatives be well-defined.

However, there is a problem with the unrestricted decomposition for m_f > 0. Although the ^unresNF decomposition (5)–(7) is mathematically exact, its physical usefulness requires that the d_mf,0^J(θ_R) and e_mf,0(θ_R) oscillate as θ_R varies in the range of (0°,180°). Figures 1 and 2 examine this point by showing plots of the little d and little e functions, respectively, versus θ_R/ deg for J = 10, m_i = 0, and (a) m_f = 0 (the Legendre case), (b) m_f = 1, (c) m_f = 2, (d) m_f = 3. Note that the little d function has J – m_f zeros and the little e function has J – m_f + 1 zeros. We make the following observations about Figures 1 and 2:

• We see that the little e function diverges as θ_R → 0°, 180°, which means that the N,F components of eq 6 also diverge. Then we have the unfortunate situation in the interesting forward and backward regions that σ^(N,F)(θ_R)→∞, whereas σ(θ_R) → 0; i.e., although the NF decomposition (5)–(7) is mathematically exact, it is not physically meaningful at small and large angles.

• We see there are angular regions where the little d and little e functions are oscillatory (which can be called classically allowed regions) separated from two nonoscillatory regions (classically forbidden regions) when θ_R is close to 0°, 180°. We can distinguish between these regions using the notion of caustics, which are discussed next.

Figure 1.

Plots of d_mf, mi^J (θ_R) vs θ_R/deg for J = 10, m_i = 0 (a) m_f = 0, (b) m_f = 1, (c) m_f = 2, (d) m_f = 3. The vertical pink lines indicate the caustic angles at (a) 0°, 180°, (b) 5.7°, 174.3°, (c) 11.5°, 168.5°, (d) 17.5°, 162.5°.

Figure 2.

Plots of e_mf, mi^J (θ_R) vs θ_R/deg for J = 10, m_i = 0 (a) m_f = 0, (b) m_f = 1, (c) m_f = 2, (d) m_f = 3. The vertical pink lines indicate the caustic angles at (a) 0°, 180°, (b) 5.7°, 174.3°, (c) 11.5°, 168.5°, (d) 17.5°, 162.5°.

2.3. Caustic Properties of d_mf,0^J(θ_R) and e_mf,0(θ_R)

The boundaries between the two classically forbidden regions and the classically allowed region in Figures 1 and 2 can be conveniently characterized by two caustic angles,^9,10 denoted θ_R min^(J,m_f) and θ_R max, for given values of J and m_f. They are defined by the divergence of the primitive Wentzel-Kramers-Brillouin (WKB) approximation for two linearly independent solutions of the second-order differential equation satisfied by the little d and little e functions, which become the associated Legendre differential equation because m_i = 0.

The caustic angles can be found from eq (5.13) of ref (26), and they are determined by sin θ_R = m_f/J, which results in

11

For J = 10, the caustics occur at: θ_R min^(10,m_f) = 0° (m_f = 0), 5.7° (m_f = 1), 11.5° (m_f = 2), 17.5° (m_f = 3). The corresponding values for θ_R max are 180° (m_f = 0), 174.3° (m_f = 1), 168.5° (m_f = 2), 162.5° (m_f = 3). These caustic angles are marked on Figures 1 and 2 as vertical pink lines. Note that the caustics for the Legendre case (m_f = 0) are always at 0° and 180° for all values of J ≥ 1. The caustic angles are shown in a different way in Figure 3 on a (θ_R/deg, J) plot^9,10 for m_f = 1,2,3 and J = 1(1)30. This figure shows clearly that θ _R min^(J,m_f) → 0 and θ _R max → π as J increases for a fixed value of m_f.

Figure 3.

Values of θ_R min^(J, m_f)/deg and θ_R max/deg (black solid circles) on a (θ_R/deg, J) plot for m_i = 0 and m_f = 1,2,3. Passing through the black solid circles are the curves, J = m_f/sin θ_R, colored red for m_f = 1, orange for m_f = 2, and green for m_f = 3.

The above discussion implies that the d_mf,0^J(N,F)(θ_R) values only exhibit an oscillatory behavior (for a given J and m_f) in the angular range

12

This in turn implies that the NF decomposition (7) should work best when θ_R satisfies the inequality (12).

An inspection of Figure 3 shows, for given values of θ_R, J, and m_f, that there is a minimum value of J, denoted J_min^(m_f)(θ_R), such that θ_R satisfies the inequality (12). For m_f > 0, we have

13

where int(x) ≡ integer part of x. Sometimes, +1 is added to the right-hand-side of eq 13 to exclude the case where J = m_f. In practice, it makes little difference whether +1 is added or not.^9,10 We confirmed this is the case in our calculations for all six transitions. The physical reason is that the PWS (1) receives its main numerical contribution from partial waves with J ≫ m_f, helped by the (2J + 1) factor.

The comments just given lead us to introduce the restricted nearside-farside decomposition, denoted ^resNF, which we discuss next.

2.4. Restricted Nearside-Farside Decomposition (^resNF)

The decomposition in which partial waves with J < J_min^(m_f)(θ_R) are omitted from eqs 1 and (7) defines ^resNF.^9,10 The restricted N,F subamplitudes are given by

14

And the corresponding ^resNF DCSs are

15

Note that ^resNF is an approximate decomposition because it omits partial waves from classically forbidden regions of θ_R; that is, it neglects the following terms in the PWS (1)

16

The contribution of each partial wave in eq 16 is nonoscillatory and small in magnitude. Notice that eqs 13 and (14) are, in general, discontinuous functions of θ_R. As a result, the corresponding DCSs also exhibit discontinuities, although, as we shall see in Section 5, they are usually small and confined to small and large angles. In addition, there is no global LAM for ^resNF because of the discontinuities. Having identified the Δf(θ_R) term of eq 16, we can include it in the ^resNF decomposition—this gives rise to the restrictedΔ nearside-farside decomposition, denoted ^resΔNF, which we discuss next.

2.5. RestrictedΔ Nearside-Farside Decomposition (^resΔNF)

The ^resΔNF decomposition is obtained when we combine eq 16 with eq 14 to obtain an improved version of ^resNF. We have for the subamplitudes⁷

17

And the corresponding ^resΔNF DCSs are

18

Notice that ^resΔNF is an exact NF decomposition, unlike eq 14, which is approximate. Similar to ^resNF, eq 17 is also a discontinuous function of θ_R, although the discontinuities are usually small in the corresponding DCSs and confined to small and large angles—examples are provided in Section 5. In addition, there is again no global LAM for ^resΔNF because of these discontinuities.

Note: If, for a given θ_R, we have that J_min^(m_f)(θ_R) is equal to m_f, then ^unresNF, ^resNF, and ^resΔNF become equivalent.

Practical Remark

It can often happen that J_min^(m_f)(θ_R), for particular values of θ_R and m_f, can exceed J_max, that is, J_min(θ_R) > J_max. For example, J_min^(m_f = 3)(θ_R = 0.1°) = 1718, but J_max = 40. Then many computer programs applied directly to eqs 14–(18) will crash as they attempt to use values of S̃_J that are undefined for J > J_max, when the upper limit of J = ∞ has been replaced by J = J_max. This problem can be avoided by adding sufficient S̃_J ≡ 0 to the PWS for J > J_max.

3. Resummation of the Partial Wave Series

It is well-established that a resummation of a Legendre PWS can significantly improve the physical effectiveness of an NF decomposition.¹³⁻¹⁹ Totenhofer et al.¹⁹ have provided an extensive discussion of the Legendre case. This same improvement in NF physical effectiveness occurs for a basis set of little d functions, although this has only been studied for a single example, namely, Ar + HF rotationally inelastic scattering.¹²

It has been found previously that the biggest effect for cleaning the N,F DCSs and N,F LAMs of unphysical oscillations occurs on going from resummation order, r = 0 (no resummation, i.e., eq 1) to resummation order, r = 1. There is usually a smaller cleaning effect for further resummations, r = 1 to r = 2 and r = 2 to r = 3.

Whiteley et al.¹² have resummed the PWS (1), which we now write as f_r=0(θ_R), from r = 0 to r = 1. We do not repeat the derivation here, which exploits the recurrence relation obeyed by the little d functions; rather, we simply write down the final result for the resummed representation for f_r=1(θ_R). From eq (3.9) of ref (12) with m_i = 0, we have

19

where β ≡ β₁ ≡ β₁^(r=1) is the resummation parameter, and

20

with

21

and

22

23

Equation 19 also assumes that (1 + β cos θ_R) ≠ 0. Notice that eq 20 is valid for J = m_f, as proven in the Appendix of ref (12). For this case, we see from eq 22 that g_mf^m_f = 0.

An NF decomposition of eq 19 can now be made

24

with the corresponding N,F subamplitudes given by (θ_R ≠ 0,π)

25

and the corresponding N,F r = 1 DCSs are

26

Similar equations apply to the ^resNF and ^resΔNF decompositions. For the unrestricted NF decomposition, the NF r = 1 LAMs are given by

Notice that the full amplitudes, f_r=0(θ_R) and f_r=1(θ_R), are independent of β and numerically the same for a given value of θ_R. This is also true for the full LAMs, LAM_r=0(θ_R) and LAM_r=1(θ_R).

In our applications, we need to choose a value for the resummation parameter β. We extend the prescription used by Anni et al.¹³ and solve the linear equation

27

This results in

These values are used in the resummation calculations of Sections 5–7. The general result is

4. Properties of the Input Scattering Matrix Elements

We use the same S matrix elements that were computed by Yuan et al.¹ and used for the m_f = 0 analyses in XC1.⁶ The Boothroyd-Keogh-Martin-Peterson potential energy surface number two (BKMP2) was employed.²⁷ Converged S matrix elements were obtained for translational energies E_trans up to 3.5 eV. All our results are for E_trans = 1.35 eV, which is the same translational energy as that employed in the molecular-beam experiments. The masses used are m_H = 1.0078 u and m_D = 2.0141 u, with the initial translational wavenumber being k = 11.692 a₀^–1. For each transition, J_max is ∼40.

Figure 4 shows graphs of |S̃_J| versus J for the three transitions 000 → 011, 000 → 021, 000 → 031, while Figure 5 shows plots for the remaining three transitions 000 → 022, 000 → 032, 000 → 033. Figures 6 and 7 display the corresponding plots for arg S̃_J/rad versus J. Note that all the curves start at J = m_f. A perusal of Figures 4–7 reveals the following:

• For five of the transitions, the global maximum in an |S̃_J| plot is at the first peak as J increases from J = m_f. The exception is the 031 case, where the maximum occurs at the second peak. The peaks are then followed by subsidiary local maxima; these play an important role in the interpretation of the intermediate- and large-angle scattering using the SOM in Section 8. The overall shapes of the m_f = 1,2,3 curves in Figures 4 and 5 are similar to those for the four m_f = 0 transitions, with the exception that the global maxima of the |S̃_J| curves are always at J = 0 when m_f = 0 (see Figure 1 of XC1 (i.e., ref (6))).

• Figures 6 and 7 show that the plots of arg S̃_J/rad versus J are roughly quadratic in shape. The kinks in some of the curves are seen to correspond to near-zeros in |S̃_J|, where the phase of S̃_J varies more rapidly with J. The curves in Figures 6 and 7 have similar properties to the arg S̃_J/rad plots for m_f = 0 (see Figure 2 of XC1 (i.e., ref (6))).

• Note that, in the NF analysis, only the values of S̃_J at J = 0,1,2,... are used. To help guide the eye, the points (black solid circles) in Figures 4–7 have been joined by straight lines. This was also done in Figures 1 and 2 of XC1.⁶ When we want a smooth continuation of the {S̃_J} to real values of J, for example, for use in an asymptotic (semiclassical) analysis, we would typically use a cubic B-spline interpolation.⁶ Notice also that the kinks do not affect the NF analysis nor the asymptotic analysis, as explained in XC1.⁶

Figure 4.

Plots of | S̃_J | vs J at E_trans = 1.35 eV. The black solid circles are the numerical S matrix data, {| S̃_J |}, at integer values of J, which have been joined by straight lines. The transitions are (a) 000 → 011, (b) 000 → 021, and (c) 000 → 031.

Figure 5.

Plots of | S̃_J | vs J at E_trans = 1.35 eV. The black solid circles are the numerical S matrix data, {| S̃_J |}, at integer values of J, which have been joined by straight lines. The transitions are (a) 000 → 022, (b) 000 → 032, and (c) 000 → 033.

Figure 6.

Plots of arg S̃_J/rad vs J at E_trans = 1.35 eV. The black solid circles are the numerical S matrix data, {arg S̃_J/rad}, at integer values of J, which have been joined by straight lines. The transitions are (a) 000 → 011, (b) 000 → 021, and (c) 000 → 031.

Figure 7.

Plots of arg S̃_J/rad vs J at E_trans = 1.35 eV. The black solid circles are the numerical S matrix data, {arg S̃_J/rad}, at integer values of J, which have been joined by straight lines. The transitions are (a) 000 → 022, (b) 000 → 032, and (c) 000 → 033.

We next consider in more detail the properties of the ^unresNF, ^resNF, and ^resΔNF decompositions.

5. Properties of the Unrestricted, Restricted and RestrictedΔ Nearside-Farside Decompositions Including Resummations

In Sections 2.2, 2.4, and 2.5, we developed the theory for the ^unresNF, ^resNF, and ^resΔNF decompositions, respectively, for r = 0; the extension of the theory to r = 1 was given in Section 3. In the present section, we investigate in detail how these three decompositions (including resummations) influence the corresponding N,F DCSs at small and large angles, as this has not been investigated before. In Figure 8, we plot four N DCSs for the 000 → 011 transition at large angles, namely, for θ_R = 140^◦–180^◦. The upper panel shows DCSs for r = 0, and the lower panel shows DCSs for r = 1.

Figure 8.

Plots of four PWS N DCSs in the large-angle region from θ_R = 140° to θ_R = 180° for the transition 000 → 011 at E_trans = 1.35 eV for (a) r = 0 and (b) r = 1. Purple long-dashed curve: PWS/N/unres. Lilac dashed curve: PWS/N/res. Red solid curve: PWS/N/resΔ. Red dashed curve: Least-squares-fit to PWS/N/resΔ.

We begin our discussion with the ^resN DCS (lilac dashed curve) and the ^resΔN DCS (red solid curve) in Figure 8. We note the following:

• By construction, the ^resN and ^resΔN DCSs tend to zero as θ_R →180^◦. Their discontinuities are clearly visible on the scale of the drawings. The density of jumps increases as θ_R →180^◦; this is expected from Figure 3.

• The ^resΔN DCS is usually smaller than the ^resN DCS for both r = 0 and r = 1. Now both the ^resN subamplitude and the Δf(θ_R)/2 term in eq 17 are complex-valued quantities, which means that destructive interference can occur, resulting in the ^resΔN DCS being smaller than the ^resN DCS.

• The first discontinuity for increasing θ_R occurs at θ_R ≈ 150° for r = 0 but at θ_R ≈ 161^◦ for r = 1. This behavior can be understood because J_min^(m_f=1)(θ_R), which is equal to int(m_f/sin θ_R) by eq 13, jumps from J = 1 at θ_R ≈ 149.9° to J = 2 at θ_R ≈ 150.0°, causing a discontinuity in the PWS (14) and in the resulting ^resΔN and ^resN DCSs.

  In contrast, for r = 1, the J = m_f = 1 term is put equal to zero by the choice of β in eq 27, resulting in the PWS (25) starting at J = m_f + 1 = 2. Then the first jump occurs for J = 2 at θ_R ≈ 160.5° to J = 3 at θ_R ≈ 160.6°.

• Because of congestion in the graphs, it is difficult for the eye to follow the jumps in the ^resΔN and ^resN DCSs in Figure 8, especially as θ_R → 180°. However, it is the general trend in these DCSs that is of interest. We therefore made least-squares-fits to the ^resΔN DCSs. These are shown as red dashed curves for r = 0 and r = 1 in Figure 8a,b, respectively.

We also plotted the ^unresN DCSs (purple long-dashed curves) for r = 0 and r = 1 in Figure 8. As expected, they tend to infinity as θ_R → 180°. The beneficial effect of cleaning can be seen because the ^unresN r = 0 DCS starts to diverge at θ_R ≈ 150°, whereas for r = 1, the ^unresN DCS diverges at a larger angle, namely, θ_R ≈ 170°.

The results discussed above for the 000 → 011 transition have all been for N DCSs at large angles. We also did a similar analysis for the N DCSs at small angles and obtained analogous results (not shown). In addition, we also calculated ^unresF, ^resF, and ^resΔF DCSs at large and small angles and obtained comparable results (also not shown). Finally, we performed ^unresNF, ^resNF, and ^resΔNF analyses for the remaining five transitions at large and small angles, again finding similar results (not shown) to the 011 case.

The least-squares-fits to the ^resΔNF DCSs are used in the next section, where we report NF analyses of the full DCSs for all the transitions.

6. Full and Nearside-Farside DCSs Including Resummations

Figure 9 shows logarithmic plots of the full and ^resΔN, ^resΔF r = 1 DCSs versus θ_R for the 000 → 011, 000 → 021, and 000 → 031 transitions. The corresponding DCSs for the 000 → 022, 000 → 032, and 000 → 033 transitions are displayed in Figure 10. For clarity of viewing, notice that, at large and small angles, least-squares-fits to the ^resΔN and ^resΔF DCSs are plotted, as explained in Section 5. We use the following color conventions for the DCSs in Figures 9 and 10 as well as in some other figures.

• Full PWS: black solid, with the label, “PWS”.

• ^resΔN r = 1 PWS: red solid, with the label, “PWS/N/resΔ”.

• Fit to ^resΔN r = 1 PWS: red dashed, with the label, “Fit to PWS/N/resΔ”.

• ^resΔF r = 1 PWS: blue solid, with the label, “PWS/F/resΔ”.

• Fit to ^resΔF r = 1 PWS: blue dashed, with the label, “Fit to PWS/F/resΔ”.

Figure 9.

Plots of log σ(θ_R) vs θ_R/deg at E_trans = 1.35 eV for r = 1. Black curve: PWS. Red solid curve: PWS/N/resΔ. Blue solid curve: PWS/F/resΔ. Red dashed curves: least-squares-fits to PWS/N/resΔ in the small- and large-angle regions. Blue dashed curves: Least-squares-fits to PWS/F/resΔ in the small- and large-angle regions. The transitions are (a) 000 → 011, (b) 000 → 021, and (c) 000 → 031.

Figure 10.

Plots of log σ(θ_R) vs θ_R/deg at E_trans = 1.35 eV for r = 1. Black curve: PWS. Red solid curve: PWS/N/resΔ. Blue solid curve: PWS/F/resΔ. Red dashed curves: least-squares-fits to PWS/N/resΔ in the small- and large-angle regions. Blue dashed curves: least-squares-fits to PWS/F/resΔ in the small- and large-angle regions. The transitions are (a) 000 → 022, (b) 000 → 032, and (c) 000 → 033.

We first examine the full DCS for the 000 → 011 transition in Figure 9a. As θ_R increases from 0° to 180°, we observe the following.

• The DCS = 0 a₀² sr^–1 at θ_R = 0° followed by the next observation listed here.

• Fast oscillations in an angular range extending up to θ_R ≈ 50°, accompanied by a decreasing DCS. This behavior merges into the next observation listed here.

• An increasing DCS with slow oscillations, which extend into the large-angle region.

• The DCS = 0 a₀² sr^–1 at θ_R = 180°.

The full DCSs for the remaining five transitions exhibit similar properties to the 011 case and are not discussed separately. We can also compare with the four full DCSs for the m_f = 0 case shown in Figure 3 of XC1.⁶ We see that the m_f = 0 and m_f > 0 DCSs are alike, the main difference being (a) the m_f = 0 DCSs are nonzero at θ_R = 0°,180° unlike the m_f > 0 DCSs, (b) the angular regions separating the fast and slow oscillations are slowly varying for m_f = 0, whereas there are pronounced minima when m_f > 0.

Next, we examine the ^resΔN, ^resΔF r = 1 DCSs in Figures 9 and 10, making use of the exact Fundamental Identity for Full and N,F DCSs given by eq 9, which is also valid for the r = 1 case.²⁵ In angular regions where there are fast oscillations, we see that the ^resΔN and ^resΔF r = 1 DCSs are varying relatively slowly with θ_R, which tells us that the fast oscillations in the full DCSs arise from NF interference. Another name for the fast oscillations is Fraunhofer diffraction/oscillations. In contrast, the slow oscillations are seen to be ^resΔN-dominated. Thus, we have the important result from the NF analysis that the fast and slow oscillations arise from different physical mechanisms. This is also the case for the m_f = 0 DCSs.⁶

We can extract useful information from the periods Δθ_R of the fast oscillations. A simple NF model shows that these oscillations are analogous to the interference pattern from the well-known “Young’s double-slit experiment”, as explained in a molecular scattering context in Appendix A of ref (28). This analogy was also used in XC1,⁶ and it yields the simple relation

28

where J_eff is an effective total angular momentum variable characteristic of the NF oscillations. For example, for the m_f = 0 DCSs, we have J_eff = J_g + 1/2, where J_g is the glory angular momentum variable, defined as the position of a local maximum in a plot of arg S̃(J)/rad versus J (see Figure 2 of XC1⁶). Figures 9 and 10 show that Δθ_R usually lies in the range of Δθ_R = 6°–7°, which is similar to the m_f = 0 DCSs. Then eq 28 gives J_eff = 30.0–25.7. An inspection of Figures 6 and 7 shows that these values for J_eff are also close to a local maximum in the arg S̃(J)/rad plots.

7. Full and Nearside-Farside LAMs Including Resummations

A full and N,F LAM analysis provides information on the value of the total angular momentum variable that contributes to the scattering at an angle θ_R, under semiclassical conditions. An important tool^16,25 for interpreting a LAM plot is the exact Fundamental Identity for Full and N,F LAMs, which is also valid for r = 1 and is analogous to the identity for DCSs given by eq 9.

Figure 11 shows a full and N,F LAM plot for the 000 → 011 transition using the ^unresNF decomposition for r = 0 and r = 1. We first make the following observations on the full LAM.

• The full LAM shows oscillations at small angles. At intermediate and larger angles it becomes monotonic and increases except for θ_R around 140°.

• The full LAM changes from F dominance to N dominance as θ_R increases in the small-angle region. This is the same behavior shown by the F and N r = 1 DCSs in Figure 9a.

• The spike at θ_R ≈ 46.2° corresponds to the minimum in the full DCS—see Figure 9a. Thus, the full LAM plot provides a clear indication of a change in the mechanism for the reaction as θ_R increases.

Figure 11.

Plots of LAM (θ_R) vs θ_R/deg at E_trans = 1.35 eV for the 000 → 011 transition, showing results for both r = 0 and r = 1. Black curve: PWS. Red solid curve: PWS/N/r = 1. Red dashed curve: PWS/N/r = 0. Blue solid curve: PWS/F/r = 1. Blue dashed curve: PWS/F/r = 0. The fainter blue solid and dashed curves show where the F LAM(θ_R) is not physically significant.

Next, we examine the N and F r = 0,1 LAMs in Figure 11 and note the following.

• The effect of cleaning the N,F r = 0 LAMs is very striking, with nonphysical oscillations for θ_R ≲ 50° being replaced by slower variations in the N,F r = 1 LAMs.

• It is known that N and F LAMs that are nearly zero, or oscillate about zero, are nonphysical.^13,15,16 It can be seen in Figure 11 that this occurs for both the r = 0 and r = 1 F LAMs when θ_R ≳ 50°. The corresponding curves are drawn in a fainter blue compared to the F LAMs for θ_R ≲ 50°.

• An averaging of the N and F r = 1 LAMs for 10° ≤ θ_R ≤ 45° gives −28.1 and 28.2, respectively. The value J ≈ 28 is consistent with the information obtained from the periodicity of the fast oscillations in Section 6. An inspection of Figure 6a shows that J ≈ 28 is close to a local maximum in the arg S̃(J)/rad plot.

• The N r = 1 LAM for θ_R ≳ 50° is close to the full N LAM. And both of them monotonically increase (except for θ_R ≈ 140°) and are similar to the LAM for a hard-sphere collision.¹³ This implies that the SOM model, which is an approximate N theory incorporating hard-sphere dynamics, should be approximately valid at intermediate and large scattering angles. This point is confirmed in Section 8.

The properties of the full and N,F r = 0,1 LAMs for the other transitions are similar to those for the 011 case and are not shown separately. Overall, we can say that the information given by the LAM analysis is consistent and complementary to that in the DCS plots of Figures 9 and 10.

8. Semiclassical Optical Model (SOM) DCSs at Intermediate and Large Angles

The SOM is a simple procedure, introduced by Herschbach,^20,21 for calculating the DCSs of state-to-state reactions. In XC1,⁶ we applied the SOM to the four m_f = 0 transitions and showed that the SOM provided valuable insights into structures in the DCSs at intermediate and large angles. In particular, we found that the SOM and PWS DCSs are distorted mirror images of the corresponding P_J ≡ |S̃_J|² versus J plots, with J = 0,1,2,.... The theory for the SOM has been given in XC1,⁶ and below we just state the working equations when m_f > 0.

The SOM DCS is given by

29

with P_J ≡ P(J) and

30

where J = m_f, m_f + 1,.... In eqs 29 and (30), d is the sum of the radii of two hard spheres representing the reactants and is the only adjustable parameter in the theory. The above equations assume that J ≤ kd; otherwise, σ_SOM (θ_R) ≡ 0. Notice that the SOM only depends on the value of the modulus |S̃_J| and is independent of arg S̃_J. In NF terminology, the SOM is an approximate N theory, which should work best for direct rebound reactions, in particular, at intermediate and backward angles in the DCS.

The SOM and PWS DCSs are compared in Figures 12 and 13 for the six transitions in the range of θ_R = 50°–180°. Now, for the m_f = 0 case, we obtained values of d by fitting the SOM DCS to the PWS DCS at, or close to, θ_R = 180°. This does not work for m_f > 0 because the PWS DCSs are equal to 0 a₀² sr^–1 at θ_R = 180°. Instead, we obtained d by fitting the SOM DCS at, or close to, the PWS peak nearest to θ_R = 180°. An exception is the 000 → 031 transition in Figure 12c, for which the second nearest peak was used (note, this DCS exhibits the most detailed structure out of the six transitions). The values we used for d are given in the figures.

Figure 12.

Plots of σ (θ_R) vs θ_R/deg at E_trans = 1.35 eV for the angular range from θ_R = 50° to θ_R = 180°. Black curve: PWS. Red curve: SOM. The transitions are (a) 000 → 011, (b) 000 → 021, and (c) 000 → 031.

Figure 13.

Plots of σ (θ_R) vs θ_R/deg at E_trans = 1.35 eV for the angular range from θ_R = 50° to θ_R = 180°. Black curve: PWS. Red curve: SOM. The transitions are (a) 000 → 022, (b) 000 → 032, and (c) 000 → 033.

It can be seen in Figures 12 and 13 that the SOM reproduces the main features in the PWS DCSs, with larger deviations as the PWS DCSs become more structured. This is encouraging, considering the simplicity of the SOM, and, like the m_f = 0 case, it tells us that the SOM and PWS DCSs are distorted mirror images of the corresponding P_J versus J plots. As expected, the SOM does not reproduce the NF interference (or Fraunhofer) oscillations in the PWS DCSs for θ_R ≲ 50° (not shown). Finally, we note that the values for d lie in the range of 1.44–1.97a₀, which are much less than the sum of the radii at the saddle point for the BKMP2 potential energy surface, which is d^‡ = r_HH^‡ + r_HD^‡ = 3.514 a₀. This tells us, as was also found for m_f = 0, that the scattering at intermediate and large angles arises mainly from small values of J or, equivalently, from small-impact parameters.

9. Degeneracy Averaged Differential Cross Sections (daDCSs)

In this section, we calculate degeneracy averaged DCSs (daDCSs) and compare with the experimental daDCSs for the two transitions v_i = 0, j_i = 0 → v_f = 0, j_f = 1 and v_i = 0, j_i = 0 → v_f = 0, j_f = 3. The usual definition of a daDCS is

31

In our applications, we have a single initial state, namely, v_i = 0, j_i = 0, m_i = 0, so eq 31 simplifies to

32

A further simplification is possible when m_i = 0 because, as shown in Appendix A, DCSs for m_f = −1,–2,–3 are equal to those for m_f = +1,+2,+3, respectively. We can write eq 32 in the form

33

where the sum is zero if j_f = 0. Equation 33 can also be written in a more compact way, namely

34

where the prime on the Σ sign means “multiply the first term in the sum by 1/2”.

We can also substitute eqs 1 and (2) into eq 34, obtaining

35

Equation 35 is a more explicit version of eq 1 of Yuan et al.¹

Figure 14a compares the calculated daDCS using eq 35 for the transition 00 → 01 with the experimental data. The corresponding results for the 00 → 03 transition are in Figure 14b. A single scaling factor has been applied to the experimental data to compare with the calculations.¹ The results in Figure 14a,b are an extension of the corresponding figures of Yuan et al.¹ because we included estimated experimental uncertainties. These are a 10% error in the measurements and an angular uncertainty of 1.5°.¹ It can be seen that the agreement between the calculated and experimental daDCSs is very good, in particular, for the NF interference (Fraunhofer) oscillations at θ_R ≲ 40°; these are shown in more detail in the insets. In the experiments, also note that ∼97% of the HD molecules in the molecular beam are in their ground state, and the translational energy uncertainty is ∼1.2%.¹

Figure 14.

Plots of degeneracy averaged σ(θ_R) (daDCS) vs θ_R/deg at E_trans = 1.35 eV. (a) The transition 00 → 01 (red), together with experimental results and their estimated errors (blue). (b) The transition 00 → 03 (purple), together with experimental results and their estimated errors (blue). (c) Black curve: Degeneracy averaged, σ(θ_R), for the 00 → 0 transition, which is summed over j_f = 0,1,2,3. The four colored curves show the degeneracy averaged σ(θ_R) for the transitions 00 → 00 (orange), 00 → 01 (red), 00 → 02 (green), and 00 → 03 (purple).

If an experiment cannot resolve individual j_f states, then it is necessary to sum over these states. We have

36

Figure 14c shows a plot of σ_00→0(θ_R) versus θ_R over the whole angular range. It can be seen that the structure in σ_00→0(θ_R) (black curve) is largely washed out, even though the individual σ_00→0jf(θ_R) in eq 36 (colored curves) possess distinct fast and slow oscillations, although less pronounced than the helicity-resolved DCSs in Figures 9 and 10. We can also relate our results and notations to the figures in the Supporting Information (SI) and main text of ref (1), with the following clarifications noted.

• (a)Figure 6(c) (SI) is a dimensionless plot, as is Figure 5c (main text).¹
• (b)The three curves for K^′ = 1,2,3 in Figure 5b (main text) show 2 × σ_000→03K′(θ_R).¹
• (c)The units for the labels on the ordinates of Figures 6(a), 6(b), and 7 (SI) are a₀² sr^–1.¹
• (d)The red curve for K^′ = 1 in Figure 6(b) (SI) shows 2 × σ_000→011(θ_R).¹
• (e)The red curve for K^′ = 1 in Figure 7(c) (SI) shows 2 × 10³× [σ_000→011(J_max,θ_R) – σ_000→011(J_max −1,θ_R)] versus J_max at θ_R = 4°.¹ Here J_max makes explicit the finite upper value for the PWS when used in eqs 1 and (2).
• (f)The blue curve for K^′ = 0 in Figure 7(c) (SI) shows 10³× [σ_000→010(J_max,θ_R) – σ_000→010(J_max −1,θ_R)] versus J_max at θ_R = 0.4°, not 4°.¹
• (g)The three curves for K^′ = 1,2,3 in Figure 7(d) (SI) show 2 × 10³× [σ_000→03K′(J_max,θ_R) – σ_000→03K′(J_max – 1,θ_R)] versus J_max at θ_R = 6°.¹
• (h)The blue curve for K^′ = 0 in Figure 7(d) (SI) shows 10³ × [σ_000→030(J_max,θ_R) – σ_000→030(J_max – 1,θ_R)] versus J_max at θ_R = 6°.¹

10. Conclusions

We have theoretically analyzed structures in the DCSs of the ground-state reaction H + HD → H₂ + D for the product states 011, 021, 031, 022, 032, and 033. The calculations extend and complement our previous analyses in XC1⁶ for the cases 000, 010, 020, and 030, making 10 DCSs in all. The motivation comes from the experiments and simulations of Yuan et al.,¹ who have measured for the first time fast oscillations in the small-angle region of the daDCSs for j_f = 1 and 3 as well as slow oscillations in the large-angle region.

Our main theoretical tools were two variants of Nearside-Farside theory: (1) We applied unrestricted, restricted, and restrictedΔ NF decompositions, including resummations, to the helicity PWS, which is expanded in a basis set of little d functions. We analyzed in detail the properties of restricted and restrictedΔ NF DCSs and showed that they correctly go to zero in the forward and backward directions when m_f > 0, unlike the unrestricted NF DCSs, which incorrectly go to infinity. We also calculated LAMs to obtain further insights into the reaction dynamics. Properties of little e functions played an important role in the NF analysis, as do the caustics associated with the little d and little e functions. (2) We applied an approximate N theory at intermediate and large angles, namely, the Semiclassical Optical Model.

We showed that the fast oscillations at small angles (sometimes called Fraunhofer diffraction or oscillations) arise from an NF interference effect. In contrast, the slow oscillations at large angles are an N effect and arise in the DCS as a distorted mirror image of the corresponding P_J versus J plot. We also compared with the experimental daDCSs, obtaining very good agreement.

Our analyses confirm the earlier insight of Dobbyn et al.⁷ that as the PWS increases in complexity, this has little impact on the physical insight provided by an NF analysis.

Appendix A

This Appendix proves the following identity for PWS DCSs when m_f = 1,2,3,...,j_f (the identity is trivially true for m_f = 0).

A1

That is, the DCSs for m_f and −m_f are equal when m_i = 0. Now the vibrational quantum numbers v_i and v_f do not change in the following, so they will be omitted from now on to simplify the notation. Note that all quantum numbers are integers.

We begin by writing the helicity or body-fixed S matrix element S̃_{jimi → jfmf}^J as a linear combination of space-fixed S matrix elements, which are labeled by J, j_i, j_f and by l_i, l_f, the initial and final orbital angular momentum quantum numbers, respectively. We have^9,22,23

A2

where ⟨j₁m₁, j₂m₂| jm⟩ is a Clebsch-Gordan coefficient with m = m₁ + m₂.

For m_i = 0, eq (A2) simplifies to

A3

We next replace m_f > 0 by −m_f < 0 in eq (A3) to obtain

A4

Now we have the relation [ref (24), page 42, eq (3.5.17)]

so eq A4 becomes

A5

Next we note, from ref (24), page 46, eq (3.7.3), and page 49, eq (3.7.14), that ⟨j_i 0, J 0 | l_i0 ⟩ is zero unless j_i + J + l_i = an even number, which means we can introduce a factor of +1 = (−1)^j_i+J+l_i into eq (A5). In addition, there is the conservation of parity relation, (−1)^j_i+l_i = (−1)^j_f+l_f, so for the phase factor we find (−1)^j_f+J+l_f = (−1)^j_i+J+l_i = +1 and obtain

A6

Comparing the right-hand sides of eq A3 and (A6) we see they are the same, so

A7

Now the PWS (1) for the scattering amplitude remains valid for negative helicities, provided the starting value of the summation is replaced by J = |m_f|. When m_f > 0 is replaced with −m_f < 0, in eq 1 we get

Finally with the help of the relation [ref (24), page 60, eq (4.2.5)]

together with the result, eq (A7), we find that the moduli of the scattering amplitudes for m_f and −m_f are equal, which then gives us the identity, eq (A1).

Appendix B

In the development and application of NF theory (NFology), it essential to use unambiguous and consistent definitions for the special functions (of the first and second kinds) used in the various NF decompositions. Here we give the precise mathematical definitions of the functions that we use, since there is often more than one convention in the literature.

For the little d function, which is also known as a reduced rotation matrix element (of the first kind) or Wigner function, we use the definition from ref (24), page 58, eq (4.1.23).

B1

The definition of P_J–mf^(m_f,m_f)(cos θ_R), a Jacobi polynomial, has become standardized (ref (24), page 57). Note that the Jacobi polynomial in eq (B1) is a special case of a Jacobi function of the first kind.(29) Important special values are

where δ_mf 0 is a Kronecker delta function.

For the little e function, which is also called a reduced rotation matrix element of the second kind, we use¹⁰

B2

where Q_J–mf^(m_f, m_f)(cos θ_R) is a Jacobi function of the second kind, which is a second independent solution of the Jacobi differential equation. We use Szegö’s definition as given in ref (29), page 78, eq (4.62.9). Note that Q_J–mf(cos θ_R) is defined “on the cut”, −1 < cos θ_R < + 1.

Since m_i = 0 in our applications, we also have the following important simplifications. From ref (24), page 59, eq (4.1.24), we get

B3

and from section 2 in the Appendix of ref (10), we have

B4

In eqs B3 and (B4), P_J^m_f(cos θ_R) and Q_J(cos θ_R) are Ferrers’ associated Legendre functions of the first and second kinds, respectively.³⁰ They are defined by (ref (24), page 22, eq (2.5.10)).

B5

The P_J(cos θ_R) in eq (B5) is a Legendre polynomial of degree J, which is a special case of a Legendre function of the first kind of degree J. The Q_J(cos θ_R) in eq (B5) is a Legendre function of the second kind of degree J. Note: the other definition in common use, but not used in this paper, is that of Hobson, in which the right-hand-side of eq (B5) is multiplied by (−1)^m_f.

We also have the following simple results

and

The following asymptotic approximations are frequently useful.^7,10 They are valid for a fixed value of m_f, J → ∞, and 0 < θ_R< π.

and

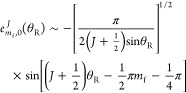The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “125 Years of The Journal of Physical Chemistry”.