Machine learning for outcome predictions of patients with trauma during emergency department care

Abstract

Objectives

To develop and evaluate a machine learning model for predicting patient with trauma mortality within the US emergency departments.

Methods

This was a retrospective prognostic study using deidentified patient visit data from years 2007 to 2014 of the National Trauma Data Bank. The predictive model intelligence building process is designed based on patient demographics, vital signs, comorbid conditions, arrival mode and hospital transfer status. The mortality prediction model was evaluated on its sensitivity, specificity, area under receiver operating curve (AUC), positive and negative predictive value, and Matthews correlation coefficient.

Results

Our final dataset consisted of 2 007 485 patient visits (36.45% female, mean age of 45), 8198 (0.4%) of which resulted in mortality. Our model achieved AUC and sensitivity-specificity gap of 0.86 (95% CI 0.85 to 0.87), 0.44 for children and 0.85 (95% CI 0.85 to 0.85), 0.44 for adults. The all ages model characteristics indicate it generalised, with an AUC and gap of 0.85 (95% CI 0.85 to 0.85), 0.45. Excluding fall injuries weakened the child model (AUC 0.85, 95% CI 0.84 to 0.86) but strengthened adult (AUC 0.87, 95% CI 0.87 to 0.87) and all ages (AUC 0.86, 95% CI 0.86 to 0.86) models.

Conclusions

Our machine learning model demonstrates similar performance to contemporary machine learning models without requiring restrictive criteria or extensive medical expertise. These results suggest that machine learning models for trauma outcome prediction can generalise to patients with trauma across the USA and may be able to provide decision support to medical providers in any healthcare setting.

Summary.

What is already known?

• Machine learning methods such as XGBoost and Deep Neural Networks are capable of accurately predicting patient outcomes in complex clinical settings.

• Previous works have demonstrated good performance for predicting hospitalisation or critical outcomes (which includes either intensive care unit admission or patient death).

What does this paper add?

• This study presents a new predictive Deep Neural Network which can generate effective and high-fidelity outcome prediction models for patients with trauma across a broader population than previously demonstrated.

• With the size of the dataset used, we were able to limit the predicted outcome to patient mortality, which is a relatively rare but highly relevant event in the emergency department.

Introduction

Trauma is a leading cause of death in the USA, and each year, thousands of trauma physicians and other front-line healthcare personnel face a critical triage decision: which patients should be prioritised to prevent major complications or death?¹ In 2018 alone, traumatic injuries caused over 240 000 mortalities in the USA.^{2 3} Evidence-based tools such as Injury Severity Score (ISS) can mislead medical professionals into undertriaging patients or incorrectly classifying a patient’s condition as unsurvivable, and regression models are often limited by restrictive model criteria.^4–7 A regression line cannot capture the highly non-linear decision boundary required for accurate patient triage, and with the annual increase of emergency department (ED) visits outpacing the growth of the US population most years,⁸ a more useful prognostic tool will be necessary to achieve better patient outcomes and resource utilisation.⁹

Many researchers over the past 30 years have sought to improve the clinical decision-making process for patient care. McGonigal et al demonstrated the groundbreaking capabilities of neural networks using only Revised Trauma Score, ISS and patient age to provide more accurate predictions than contemporary logistic regression models.¹⁰ Marble and Healy produced a more sophisticated model which could identify sepsis with almost 100% accuracy.¹¹ These studies were only valid for a small subset of patients, though—they narrowed their focus to specific patient conditions. Significant advancements in machine learning (ML) techniques have been made since these papers’ publication, and more effort than ever is pushing towards modelling techniques that generalise across all patients, regardless of age or injury mechanism.

Several recent papers have demonstrated the power of ML in predicting patient outcomes in the hospital and ED, but these were formulated without an abundance of nationally representative data sets, with models restricted to certain age groups, or without the verification of model performance across different injury mechanisms.^12–14 These issues created a gap in clinical understanding about the models’ generalisability across patient demographics and conditions. There is, therefore, a need to study the capabilities of ML on a sufficiently large and diverse national dataset with a focus on generalisability across clinical scenarios. To the best of our knowledge, no study we searched has used ML solely to predict ED death, despite the clinical relevance of such a risk assessment tool in prioritising and triaging critical patients.

With a large dataset that captures patient visit information from across the United States, we hypothesised that an all ages, injury-invariant, generalisable ML model could predict patient mortality in the ED better than current practices. The model’s generalisability across different age groups was validated by examining contemporary mortality prediction models, comparing key performance metrics and analysing performance characteristics across injury types to ensure model invariance.

Methods

Study setting

This retrospective study used 2007–2014 National Trauma Data Bank (NTDB) data. The American College of Surgeons (ACS) collects trauma registry data from hospitals across the USA every year and compiles it into the NTDB. The ACS has created the National Trauma Data Standard (NTDS) Data Dictionary, which ensures the quality and validity of data used by researchers.¹²

Study samples

From 5.8 million patient visits captured in the data, we selected patient with trauma visits with complete ED vitals, a known mode of arrival and transfer status, and a valid outcome (ie, excluding dispositions that were ‘not applicable’, ‘not known/recorded’ or ‘left against medical advice’). Patients not meeting these criteria were removed from the dataset.

Predictor variables

We considered the 77 predictors for mortality shown in table 1, all of which are typically available at the time of patient admission and triage in the ED. Predictors came from the following categories: demographics, ED vitals, comorbidities, injury intent, injury type, injury mechanism, arrival mode and transfer status.^{4 13 14} Over the years, the NTDS has added and removed certain comorbidities. Chronic conditions not represented across all years were removed from the dataset. NTDS External Injury Codes were transformed into injury type, mechanism and intent based on the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) code recorded for the patient.

Table 1.

Predictor and trauma outcome variables

Variable	n=300 847 children		n=1 706 638 adults		% missing
Demographics
Age (year), mean (SD)	10.42	5.91	51.67	20.93
Female sex	99 523	33.92	632 346	37.95
White	196 736	67.06	1 258 913	75.54
Black or African American	51 994	17.72	229 302	13.76
Other race	34 196	11.66	123 493	7.41
Asian	5 079	1.73	27 888	1.67
American Indian	3 348	1.14	14 902	0.89
Race N/A	1 170	0.4	8 551	0.51
Native Hawaiian or Other Pacific Islander	853	0.29	3 411	0.2
ED vitals
Oxygen saturation, mean (SD)	98.26	6.93	96.85	7.44	25.85
Systolic blood pressure, mean (SD)	122.48	19.53	139.89	26.35	3.26
Pulse, mean (SD)	102.42	26.18	87.49	19.13	2.26
Respiratory rate, mean (SD)	21.32	6.82	18.40	4.63	3.24
Temperature, mean (SD)	36.67	1.26	36.52	1.45	11.55
GCS eye, mean (SD)	3.85	0.62	3.84	0.64	6.49
GCS verbal, mean (SD)	4.75	0.87	4.69	0.91	6.54
GCS motor, mean (SD)	5.79	0.91	5.77	0.96	6.54
Injury Severity Score, mean (SD)	7.36	7.21	9.08	7.82	3.37
Comorbidities
Alcoholism	2 420	0.82	152 602	9.16
Angina	8	0	3 873	0.23
Ascites within 30 days	55	0.02	1 265	0.08
Bleeding disorder	668	0.23	96 168	5.77
Chemotherapy	58	0.02	4 358	0.26
Congenital anomalies	2 248	0.77	4 598	0.28
Congestive heart failure	92	0.03	57 005	3.42
Current smoker	10 098	3.44	315 492	18.93
CVA/residual neurological deficit	233	0.08	38 609	2.32
Diabetes mellitus	1 074	0.37	209 902	12.6
Disseminated cancer	34	0.01	11 608	0.7
Oesophageal varices	48	0.02	3 924	0.24
Functionally dependent health status	651	0.22	32 606	1.96
Hypertension requiring medication	1 054	0.36	527 251	31.64
Myocardial infarction	19	0.01	23 487	1.41
No comorbidities	199 555	68.02	442 939	26.58
Obesity	3 684	1.26	110 593	6.64
Prematurity	1 666	0.57	412	0.02
PVD	14	0	7 831	0.47
Respiratory disease	16 312	5.56	137 284	8.24
Steroid use	109	0.04	8 746	0.52
Injury intent
Assault	21 319	7.27	177 543	10.65
Other	228	0.08	3 098	0.19
Self-inflicted	2 449	0.83	25 798	1.55
Undetermined	1 820	0.62	6 135	0.37
Unintentional	265 434	90.48	1 447 143	86.84
Injury type
Blunt	241 153	82.2	1 427 232	85.64
Burn	9 740	3.32	25 843	1.55
Other/unspecified	21 498	7.33	65 390	3.92
Penetrating	18 859	6.43	141 252	8.48
Injury mechanism
Adverse effects, drugs	34	0.01	307	0.02
Adverse effects, medical care	22	0.01	406	0.02
Cut/pierce	8 855	3.02	77 958	4.68
Drowning/submersion	269	0.09	650	0.04
Fall	95 199	32.45	690 746	41.45
Fire/flame	2 874	0.98	15 864	0.95
Firearm	9 982	3.4	63 173	3.79
Hot object/substance	6 866	2.34	9 979	0.6
MVT motorcyclist	3 968	1.35	91 688	5.5
MVT occupant	51 335	17.5	334 239	20.06
MVT other	932	0.32	3 423	0.21
MVT pedal cyclist	4 436	1.51	13 306	0.8
MVT pedestrian	12 745	4.34	47 643	2.86
MVT unspecified	457	0.16	4 193	0.25
Machinery	1 101	0.38	20 115	1.21
Natural/environmental, bites/stings	4 949	1.69	7 497	0.45
Natural/environmental, other	1 543	0.53	5 371	0.32
Other specified and classifiable	8 773	2.99	21 390	1.28
Other specified, not classifiable	1 379	0.47	7 560	0.45
Overexertion	1 490	0.51	4 715	0.28
Pedal cyclist, other	11 880	4.05	25 423	1.53
Pedestrian, other	1 568	0.53	4 819	0.29
Poisoning	330	0.11	647	0.04
Struck by, against	32 068	10.93	111 135	6.67
Suffocation	281	0.1	1 396	0.08
Transport, other	25 462	8.68	80 501	4.83
Unspecified	2 452	0.84	15 573	0.93
Arrived by ambulance	223 432	76.16	1 409 459	84.58
Transferred from other hospital	108 720	37.06	387 609	23.26	0.1
Mortality	1 053	0.36	7 145	0.43

Unless otherwise noted, data are presented as count (percentage) of positive cases.

CVA, cerebrovascular accident; ED, emergency department; GCS, Glasgow Coma Score; MVT, motor vehicle traffic accident; N/A, not available; PVD, Peripheral Vascular Disease.

Outcome variables

The outcome variable being predicted was patient mortality. Patients with a disposition of ‘deceased/expired,’ ‘expired’ or ‘discharged/transferred to hospice care’ were treated as positive cases for patient mortality, as each is explicitly mortality or an expectation of such shortly after discharge.^{15 16} All other valid outcomes were treated as negative for patient mortality. These included general admission to the hospital, admission to a specialised unit within the hospital (intensive care unit (ICU), step-down, etc), transfer to another hospital or discharge from the ED.

Model generation

Data were preprocessed before being passed to the model for training or prediction. Two separate, non-overlapping datasets were constructed; one contained hospital outcomes and the other contained ED outcomes. For each, a training set was created using 70% of the data available, and the remaining 30% was retained as a test set. As there are relatively few mortalities, we used stratification to sample from the pool of mortality and non-mortality cases individually, ensuring each class is represented proportionally. Categorical data were given binary encodings for each variable in a category (one-hot encoding) and numerical data were standardised.¹⁷

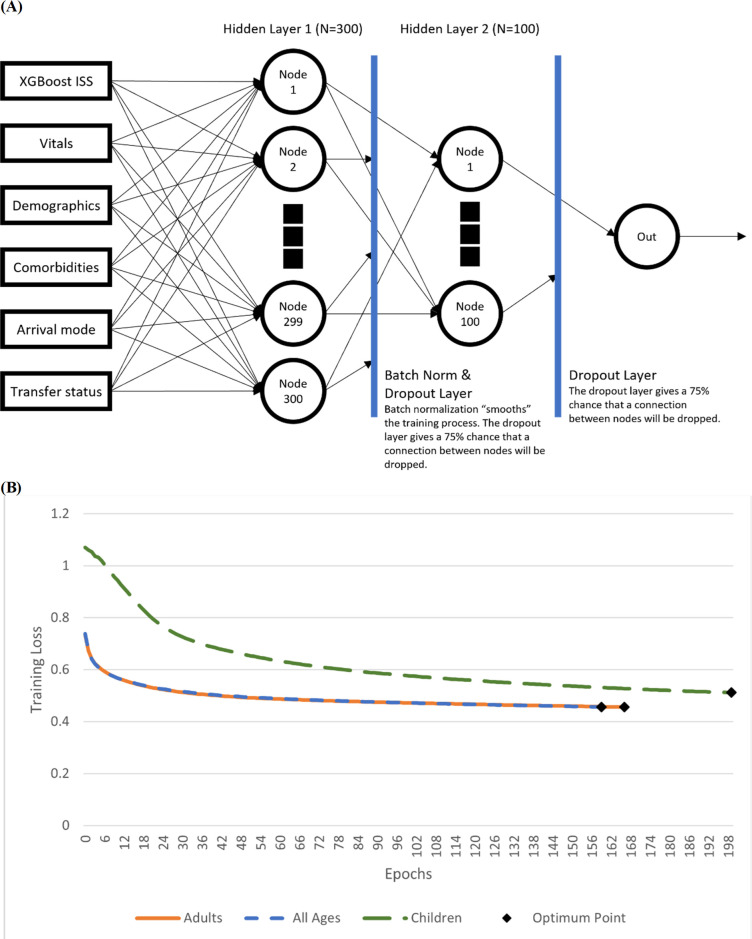
We trained an XGBoost model to predict ISS and add it as a feature in the data, as ISS can be very useful in determining the immediacy of a patient’s condition but is not typically available on patient check-in. Our custom PyTorch model architecture shown in figure 1 was composed of four distinct layers: a single input layer, two hidden layers with 300 and 100 neurons, respectively, and a final output layer which predicted patient mortality.¹⁸ Batch normalisation and drop-out layers were used to prevent overfitting. The final architecture was made specifically for this study and applied to three different age groupings: children, adults and all ages.

Figure 1.

Model architecture and sample training loss. The model consisted of three layers and used both batch normalisation and dropout to smooth training loss and prevent overfitting of the model to the training set. Figure by JDC. ISS, Injury Severity Score.

Because of the scarcity of ED mortality data points, we tried pretraining each model with a coarse learning rate on hospital outcomes to boost its discriminatory capabilities.¹⁹ Then, using a finer learning rate, the model was trained again on the dataset containing ED outcomes. The pretrained model’s performance was compared with one with no pretraining, and the better of the two was selected.

Models were evaluated on sensitivity, specificity, sensitivity-specificity gap, area under receiver operating characteristic curve (AUC), positive predictive value (PPV), negative predictive value (NPV) and Matthews correlation coefficient (MCC). The sensitivity-specificity gap is the linear distance between these two values and explains how far the model is from having perfect predictive capabilities. It is calculated as shown in equation 1.

$${\displaystyle \mathrm{G}\mathrm{a}\mathrm{p}=\left(1-\mathrm{S}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y}\right)+\left(1-\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}\right)}$$

Equation 1: sensitivity-specificity gap

MCC is a balanced measure between true positives (TP), false positives (FP), true negatives (TN) and false negatives (FN) whereby the only means of improving the metric is reducing the total number of misclassifications. It is mathematically identical to Pearson correlation coefficient and is calculated as shown in equation 2.

$${\displaystyle \mathrm{M}\mathrm{C}\mathrm{C}=\frac{\left(\mathrm{T}\mathrm{P}\ast \mathrm{T}\mathrm{N}\right)-\left(\mathrm{F}\mathrm{P}\ast \mathrm{F}\mathrm{N}\right)}{\sqrt{\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}\right)\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}\right)\left(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}\right)\left(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N}\right)}}}$$

Equation 2: MCC

Model verification

To validate model performance, we collected results from other modern ML-based outcome prediction tools and compared our performance metrics. Goto et al and Raita et al’s models predict either patient mortality or admission to the ICU with ED check-in data,^{20 21} while Hong et al used triage data to predict patient hospitalisation.²² These papers did not report a value for MCC. Because no contemporary ML study has tried to generalise to all ages before, we segmented the models into different age groupings. To evaluate model competence in predicting outcomes irrespective of the nature of a patient’s injury, injury mechanisms determined by the reported external injury code were systematically filtered out of the data before training and testing the model.

To verify the model architecture’s effectiveness in learning to predict mortality, we created a second set of models which predicted the overall outcome of a patient, whether in the hospital or in the ED. This was an important step in verifying the model due to the scarcity of ED mortality data points and relative abundance of hospital deaths.

Statistical analysis of excluded patients

Because of the reduction of the dataset from 5.8 million patient visits to two million, we examined whether patients meeting our inclusion criteria had the same distribution as those we excluded, with the goal of comparing their baseline characteristics. We applied Student’s t-test to the patient age, Glasgow Coma Score (GCS) total and ISS and the χ² test to patient gender and presence of comorbidities. For each variable, we calculated a p value with an alpha level of 0.05 to determine whether included and excluded patients were statistically similar. All tests returned a p value of zero, indicating included and excluded patients occupy different distributions. This might imply that excluded patients had a reason some data were missing.

Results

From 2007 to 2014, 5.8 million unique patient with trauma visits were recorded in the NTDB with two million unique visits meeting our inclusion criteria. The data which met these criteria were composed of 300 847 children and 1 706 638 adults. Table 1 shows characteristics of the child and adult populations with respect to the selected predictors and outcomes. From these data, the hospital outcome dataset contained 1 765 545 unique visits, and the ED outcome dataset retained the remaining 245 940.

Model benchmarking

For children, our model achieved similar performance to Goto’s Deep Neural Network (DNN),²⁰ with an improvement in PPV (0.09; 95% CI 0.08 to 0.10), as shown in table 2. Across all other metrics, our model’s performance characteristics fell within the CIs given by the Goto DNN. Additionally, the size of our dataset allows for our 95% CI to be much narrower than the comparison models for children.

Table 2.

Predictor and trauma outcome variables

Model	AUC (95% CI)	Sensitivity (95% CI)	Specificity (95% CI)	Gap*	PPV (95% CI)	NPV (95% CI)	MCC (95% CI)
Child models
Goto LR20	0.78 (0.71 to 0.85)	0.54 (0.39 to 0.69)	0.91 (0.75 to 0.93)	0.55	0.01 (0.01 to 0.02)	0.990 (0.990 to 0.990)	–
Goto DNN20	0.85 (0.78 to 0.92)	0.78 (0.63 to 0.90)	0.77 (0.62 to 0.92)	0.45	0.01 (0.01 to 0.02)	0.990 (0.990 to 0.990)	–
Ours	0.86 (0.85 to 0.87)	0.78 (0.77 to 0.79)	0.78 (0.77 to 0.79)	0.44	0.09 (0.08 to 0.10)	0.992 (0.990 to 0.994)	0.626 (0.613 to 0.639)
Adult models
Raita LR21	0.74 (0.72 to 0.75)	0.50 (0.47 to 0.53)	0.86 (0.82 to 0.87)	0.64	0.07 (0.05 to 0.08)	0.988 (0.988 to 0.988)	–
Raita DNN21	0.86 (0.85 to 0.87)	0.80 (0.77 to 0.83)	0.76 (0.73 to 0.78)	0.44	0.06 (0.06 to 0.07)	0.995 (0.994 to 0.995)	–
Hong Triage DNN22	0.87 (0.87 to 0.88)	0.70	0.85	0.45	0.66	0.870	–
Ours	0.85 (0.85 to 0.85)	0.76 (0.76 to 0.76)	0.80 (0.80 to 0.80)	0.44	0.11 (0.11 to 0.11)	0.990 (0.989 to 0.991)	0.619 (0.614 to 0.624)
All ages models
Ours	0.85 (0.85 to 0.85)	0.74 (0.74 to 0.74)	0.81 (0.81 to 0.81)	0.45	0.12 (0.12 to 0.12)	0.989 (0.988 to 0.990)	0.602 (0.597 to 0.607)

*The gap between sensitivity and specificity. Calculated as follows: Gap=(1−Sensitivity)+(1−Specificity).

AUC, area under curve; DNN, Deep Neural Network; LR, logistic regression; MCC, Matthews Correlation Coefficient; NPV, negative predictive value; PPV, positive predictive value.

The adults-only model showed similar performance to the comparison models. The sensitivity (0.76; 95% CI 0.76 to 0.76) was higher than the Hong Triage DNN²² (0.70) and fell just below the Raita DNN²¹ (0.80; 95% CI 0.77 to 0.83) while still achieving high specificity (0.80; 95% CI 0.80 to 0.80). The sensitivity-specificity gap (0.44) demonstrated that the model was balanced similarly to the comparison models. The all ages model’s performance metrics were generally in line with those from our child and adult only models.

Performance across injury mechanisms

The models for all ages and adults-only both saw an increase in predictive performance across all metrics when excluding fall injuries from the test set. Table 3 shows the adult model without fell exhibited better AUC (0.87; 95% CI 0.87 to 0.87), specificity (0.84; 95% CI 0.83 to 0.85), sensitivity-specificity gap (0.39), PPV (0.16; 95% CI 0.15 to 0.17) and MCC (0.659; 95% CI 0.652 to 0.666) while maintaining similar sensitivity (0.77; 95% CI 0.76 to 0.78) and NPV (0.989; 95% CI 0.988 to 0.990). The model for children was weaker when falling injuries were excluded, with a lower sensitivity (0.71; 95% CI 0.70 to 0.72) and MCC (0.569; 95% CI 0.553 to 0.585). These results revealed that the model was invariant to all injury mechanisms in the NTDS except for falling injuries, which might require additional predictors.

Table 3.

Comparison of performance with and without fall injuries

Model	AUC (95% CI)	Sensitivity (95% CI)	Specificity (95% CI)	Gap*	PPV (95% CI)	NPV (95% CI)	MCC (95% CI)
Child models
With falls	0.86 (0.85 to 0.87)	0.78 (0.77 to 0.79)	0.78 (0.77 to 0.79)	0.44	0.09 (0.08 to 0.10)	0.992 (0.990 to 0.994)	0.626 (0.613 to 0.639)
No falls	0.85 (0.84 to 0.86)	0.71 (0.70 to 0.72)	0.81 (0.80 to 0.82)	0.48	0.12 (0.11 to 0.13)	0.987 (0.983 to 0.991)	0.569 (0.553 to 0.585)
Adult models
With falls	0.85 (0.85 to 0.85)	0.76 (0.76 to 0.76)	0.80 (0.80 to 0.80)	0.44	0.11 (0.11 to 0.11)	0.990 (0.989 to 0.991)	0.619 (0.614 to 0.624)
No falls	0.87 (0.87 to 0.87)	0.77 (0.76 to 0.78)	0.84 (0.83 to 0.85)	0.39	0.16 (0.15 to 0.17)	0.989 (0.988 to 0.990)	0.659 (0.652 to 0.666)
All ages models
With falls	0.85 (0.85 to 0.85)	0.74 (0.74 to 0.74)	0.81 (0.81 to 0.81)	0.45	0.12 (0.12 to 0.12)	0.989 (0.988 to 0.990)	0.602 (0.597 to 0.607)
No falls	0.86 (0.86 to 0.86)	0.77 (0.76 to 0.78)	0.79 (0.78 to 0.80)	0.44	0.13 (0.13 to 0.13)	0.988 (0.987 to 0.989)	0.623 (0.617 to 0.629)

*The gap between sensitivity and specificity. Calculated as follows: Gap = (1−Sensitivity) + (1−Specificity).

AUC, area under curve; MCC, Matthews correlation coefficient; NPV, negative predictive value; PPV, positive predictive value.

Architecture verification

The second set of models, which predicted patients’ overall outcome, outperformed the ED only models in most respects. For children, it achieved superior AUC (0.91; 95% CI 0.91 to 0.91), sensitivity (0.80 95% CI 0.80 to 0.80), specificity (0.92; 95% CI 0.92 to 0.92), sensitivity-specificity gap (0.28), NPV (0.998; 95% CI 0.998 to 0.998), and MCC (0.746; 95% CI 0.742 to 0.750), as could be seen in table 4.

Table 4.

Model performance for varying outcome predictions

Model	AUC (95% CI)	Sensitivity (95% CI)	Specificity (95% CI)	Gap*	PPV (95% CI)	NPV (95% CI)	MCC (95% CI)
Child models
ED only	0.86 (0.85 to 0.87)	0.78 (0.77 to 0.79)	0.78 (0.77 to 0.79)	0.44	0.09 (0.08 to 0.10)	0.992 (0.990 to 0.994)	0.626 (0.613 to 0.639)
Hospital and ED	0.91 (0.91 to 0.91)	0.80 (0.80 to 0.80)	0.92 (0.92 to 0.92)	0.28	0.09 (0.09 to 0.09)	0.998 (0.998 to 0.998)	0.746 (0.742 to 0.750)
Adult models
ED only	0.85 (0.85 to 0.85)	0.76 (0.76 to 0.76)	0.80 (0.80 to 0.80)	0.44	0.11 (0.11 to 0.11)	0.990 (0.989 to 0.991)	0.619 (0.614 to 0.624)
Hospital & ED	0.89 (0.89 to 0.89)	0.79 (0.79 to 0.79)	0.84 (0.84 to 0.84)	0.37	0.12 (0.12 to 0.12)	0.993 (0.993 to 0.993)	0.689 (0.687 to 0.691)
All ages models
ED only	0.85 (0.85 to 0.85)	0.74 (0.74 to 0.74)	0.81 (0.81 to 0.81)	0.45	0.12 (0.12 to 0.12)	0.989 (0.988 to 0.990)	0.602 (0.597 to 0.607)
Hospital & ED	0.90 (0.90 to 0.90)	0.84 (0.84 to 0.84)	0.80 (0.80 to 0.80)	0.36	0.10 (0.10 to 0.10)	0.995 (0.995 to 0.995)	0.711 (0.709 to 0.713)

*The gap between sensitivity and specificity. Calculated as follows: Gap = (1−Sensitivity) + (1−Specificity).

AUC, area under curve; ED, emergency department; MCC, Matthews correlation coefficient; NPV, negative predictive value; PPV, positive predictive value.

Similarly, for adults, the hospital and ED model achieved stronger AUC (0.89; 95% CI 0.89 to 0.89), sensitivity (0.79; 95% CI 0.79 to 0.79), specificity (0.84; 95% CI 0.84 to 0.84), sensitivity-specificity gap (0.37), PPV (0.12; 95% CI 0.12 to 0.12), NPV (0.993; 95% CI 0.993 to 0.993) and MCC (0.689; 95% CI 0.687 to 0.691).

The hospital and ED all-ages model achieved AUC (0.90; 95% CI 0.90 to 0.90), sensitivity-specificity gap (0.36), and MCC (0.711; 95% CI 0.709 to 0.713). These general performance characteristics were between the corresponding metrics for child and adult models, indicating it had generalised for both children and adults.

Discussion

Implementation of our ML architecture on the NTDB provided innovative predictive capabilities that generalise to all trauma age groups and most types of injuries. With our dataset of approximately two million unique visits, we created a single neural network architecture and trained unique models for children, adults and all ages. Our models for children and adults achieved similar performance to the comparison models across most metrics, reinforcing the notion that such performance is possible across a more diverse set of patients than previously tested. These results suggest that our models could generalise well across all ages. However, fall injuries have the potential to confound the model, suggesting that the outcome of fall injuries might require more information than the included predictors provide.

It is important to note that one study not referenced in table 2, the Trauma Quality Improvement Programme (TQIP),^{23 24} has built a logistic regression model for child patient mortality that achieved an AUC of 0.996—almost perfect predictive power—but featured much narrower inclusion criteria than this study. Whereas the TQIP report limited their observations to victims of blunt, penetrating, or abuse-related injuries with at least one Abbreviated Injury Score (AIS) of two or greater, we imposed none of these criteria.²⁵

Our study has advantages over prior publications we’ve found in ML trauma outcome prediction, featuring over two million unique patient encounters from across the USA. While previous studies showed the capabilities of ML as a prognostic tool, none captured the diverse healthcare settings across the USA, demonstrated invariance across injury mechanisms, or focused solely on patient mortality, and only one confirmed that additional data would not improve its model further.^20–22 ML is a data-driven technique, requiring a multitude of unique data points to maximise the model’s predictive power. With our large, diverse set of trauma data, we are confident that our model is optimised for its current architecture, and the narrow CIs indicate it might generalise to patients with trauma across the USA.

While testing model invariance across injury mechanisms, we discovered that excluding fall injuries noticeably affected the model’s predictive capabilities. It is well known that adult fall injuries, especially in the elderly population, can result in hip fractures, leading to complications and death. Current triage guidelines acknowledge the complex nature of ground-level falls on the elderly,²⁶ and at least one study has demonstrated that AIS and GCS are unreliable measures for assessing these patients’ mortality risk levels.²⁷ Although removing these injuries improved the performance of the adult model, the child model achieved slightly worse performance, indicating the model could discern the seriousness of a child’s fall-related injury well. Further investigation will be necessary to find the predictors and ML architecture to overcome this confounding factor.

Our model architecture verification process indicates that the architecture of figure 1 can make predictions highly correlated with a patient’s true outcome. The challenge in achieving reliable results for ED only cases lies in the scarcity of ED mortality data points, not the modelling approach. Widening the inclusion criteria may allow for more training examples to be retained, but it will come at the cost of data richness.

The main limitation of this study is the need for a complete set of patient vitals. Our dataset had approximately 5.8 million unique patient visits, but only two million met our inclusion criteria. While this is sufficient for training, it signifies that there are many clinical scenarios our model cannot handle. However, our study is broader than similar works, as medical research often limits its inclusion criteria to a small subset of patient characteristics. This specialisation improves model performance but makes it irrelevant to many patients in actual clinical settings. Our methods only filter out patients missing important information, such as vitals or demographics; we do not filter by age, injury mechanism or any other categorical value, and we demonstrate the viability of this approach in predicting patient outcomes. The NTDB provides a variety of pertinent facility-related information, but our study excluded it to ensure a fair comparison to contemporary works, as they did not have access to facility variables. Some facilities, like level 1 trauma centres, will be better equipped than others to handle certain types of patients, and that reality is not captured in this study.^28–30 Instead, we based our ML on patient demographics and injury characteristics so prehospital emergency medical services could use the prediction to guide patient with trauma field triage. Finally, the deidentified nature of the data used means our model can only analyse the outcomes of individual visits rather than the patients themselves. A longitudinal study would likely benefit the model, as it could learn the patterns which contribute to patient deterioration over the long-term rather than during a single visit.

Future work

Further research into the defining patient characteristics, model architecture or preprocessing pipeline, which allows the model to differentiate between fatal and survivable fall injuries, is a necessary next step. This will address the performance loss observed when patients who have suffered a fall injury are included in the test set. Additionally, data related to healthcare facilities should be integrated into the predictive model, as this will help discern whether the patient should receive the care necessary to prevent mortality. Finally, the predictor variables selected for this study should be pruned to only include those which aid the model’s performance. This will result in fewer excluded patients and, therefore, more examples of patient mortality for the model to learn from.

Conclusion

A predictive model for patient with trauma mortality from approximately two million unique visits to the US ED was developed, and it achieved similar performance characteristics to contemporary models. However, predictors used in this study did not allow the model to fully differentiate between fatal and survivable fall injuries, as the model saw a significant performance boost when fall injuries were removed from the dataset. Future work will need to determine the predictors or processing methods needed to overcome this confounding factor. Ultimately, this study demonstrates that ML models can make predictions highly correlated with a trauma patient’s true outcome. As a result, healthcare workers in the ED may use them as a risk assessment aid when determining the urgency of a patient’s condition. This approach has the potential to reduce the burden on healthcare personnel, prevent overutilisation of resources due to overtriage and improve the quality of care available to those who truly need it to reduce mortality risk.

Data availability statement

Data may be obtained from a third party and are not publicly available. The National Trauma Data Bank dataset consists of deidentified patient data. It is made available by the American College of Surgeons for researchers meeting their eligibility criteria.

Ethics statements

Patient consent for publication

Not applicable.