Abstract
Recent advancements in multiphoton imaging and vascular reconstruction algorithms have increased the amount of data on cerebrovascular circulation for statistical analysis and hemodynamic simulations. Experimental observations offer fundamental insights into capillary network topology but mainly within a narrow field-of-view typically spanning a small fraction of the cortical surface (less than 2%). In contrast, larger-resolution imaging modalities, like computed tomography (CT) or magnetic resonance imaging (MRI), have whole-brain coverage but capture only larger blood vessels, overlooking the microscopic capillary bed. To integrate data acquired at multiple length scales with different neuroimaging modalities and to reconcile brain-wide macroscale information with microscale multiphoton data, we developed a method for synthesizing hemodynamically equivalent vascular networks for the entire cerebral circulation. This computational approach is intended to aide in the quantification of patterns of cerebral blood flow and metabolism for the entire brain.
In part I, we described the mathematical framework for image-guided generation of synthetic vascular networks covering the large cerebral arteries from the Circle of Willis through the pial surface network leading back to the venous sinuses. Here in part II, we introduce novel procedures for creating microcirculatory closure that mimics a realistic capillary bed. We demonstrate our capability to synthesize synthetic vascular networks whose morphometrics match empirical network graphs from three independent state-of-the art imaging labs using different image acquisition and reconstruction protocols. We also successfully synthesized twelve vascular networks of a complete mouse brain hemisphere suitable for performing whole brain blood flow simulations. Synthetic arterial and venous networks with microvascular closure allow whole brain hemodynamic predictions. Simulations across all length scales will potentially illuminate organ-wide supply and metabolic functions that are inaccessible to models reconstructed from image data with limited spatial coverage.
Keywords: multiphoton imaging, cerebral circulation, vascular synthesis, microcirculation, biphasic blood flow, mouse brain
1. Introduction
Mathematical models of cerebral circulation for hemodynamic simulations combine biophysical principles with vascular anatomical data from medical images. Increasingly, models are becoming an indispensable research tool to integrate and reconcile direct imaging observations1–6, predict cerebral blood flow patterns7–16, oxygen exchange from blood vessels to tissue11–12, elucidate mechanisms of blood flow control, and quantify disruption in pathological states17–20. Previously, we identified shortcomings when reconstructing vascular anatomical networks from raw image data21. As a compliment or alternative to purely image-based network models (=empirical VAN or simply denoted as VAN), network synthesis can systematically integrate imaging data from diverse modalities (μCT, MRI, multiphoton, SEM, etc.) acquired at different length scales to create synthetic vascular networks (sVAN) that match structural, hemodynamic and metabolic properties of empirical VAN. In this combination of papers, we present a large-scale algorithm entitled image-based Cerebral Network Synthesis (iCNS) for synthesizing physiologically sound, anatomically complete cerebrovascular networks. The iCNS algorithm allows us to not only create synthetic counterparts to experimental templates, but also to generate network models of the entire cerebral circulation by extending connectivity and topological information obtained from multimodal neuroimage data to the whole brain. In part I of this series21, we redesigned and significantly expanded constrained constructive optimization (CCO) principles. The iCNS algorithm expands traditional CCO algorithms by methods for integrating image data such as surface reconstructions (=STL files) and reconstructed vascular networks (=backbones). iCNS allows emulation of essential anatomical features (=ring structures without tree-like connectivity) such as the Circle of Willis and the unique spatial arrangement of the large lateral segments that adhere tightly to the cortical surface (=pial networks of the ACA, MCA, PCA territories). Although we believe that minimization of vascular lumen is an elemental building principle for blood supply networks, additional physiological constraints need to be imposed in order to meet the metabolic demands of specific organs. For example, the cerebral arterial blood vessels follow the leptomeningeal surface of the gyrated human cortex. Such additional building principles, when suitably input into our method, enable the generation of artificial networks that reproduce functional blood supply. We will demonstrate our approach to integrate organ specific anatomical constraints for synthesizing consistent cerebrocirculatory networks. Specifically, during step-wise growth of iCNS we enforce leptomeningeal passage of the main pial arteries and veins tracking the cortical surface (pia), the alignment of arterioles and veins penetrating the brain tissue perpendicular to the cortical surface or the branching patterns of long and short penetrating arterioles and veins. Anatomical constraints can be implemented through novel methods such as SampleGenerators that limit the geometric location where artificial segment addition is permitted to occur; and Constraint Functors to enforce desired metric specifications (=position, orientation, size, etc.) that must be followed during each growth stage.
Here in part II, we will investigate the critical innovation of microvascular closure for the generation of mesh-like network structures that connect the arterial and venous circulation through an artificial capillary bed that is both hemodynamically (=shares equivalent blood flow properties) and physiologically consistent (=structural similarity) with image-derived counterparts. Robustness and reproducibility of the iCNS algorithm will be demonstrated by synthesizing hundreds of microvascular networks matching vascular structures from three cohorts (total of N=15 unique image-derived networks) from the murine cerebral vasculature acquired by independent groups using state-of-the-art in-vivo and ex-vivo multiphoton imaging techniques. We will show an approach to map key structural properties affecting hemodynamics computations such as length, diameter, tortuosity spectra, and vessel count from empirical VANs onto synthetic clones (sVANs) with a high degree of statistical agreement. We will also quantify the key structural properties related to hemodynamics for sVAN and assess their statistical similarity to the empirical VANs. We further incorporate macro-, meso- and microanatomical information from various imaging modalities to synthesize twelve cerebrovascular networks (=arteries+capillaries+veins, N=12) spanning the entire hemisphere in mouse.
2. Methods and Materials
2.1. Microcirculatory data acquisition from three different sources
Microcirculatory image data.
We first characterized the cerebral microcirculation of the vibrissa primary sensory cortex using data acquired independently in three state-of-the-art imaging labs3,22,23. These data from three cohorts of mice were acquired with different multiphoton imaging techniques as described in Appendix A and in more detail elsewhere3,22,23. The datasets (VANs) constitute a representative cross section of state-of-the-art imaging data available for the murine microcirculation. The Kleinfeld (KF) cohort (n=4) used ex vivo imaging. The Boas (n=5) and Dunn (n=6) cohorts applied in vivo imaging with open cranial windows. Based on imaging data, vascular network graphs (VANs) were reconstructed as described previously3,24,25.
Segmentation-independent morphometric statistics were computed using cubic Bezier spline segments for all murine image-derived vascular networks as described in Appendix B. We calculated probability density functions (PDFs) and normalized cumulative density functions (CDFs) for length, diameter, surface area, volume, and tortuosity spectra. We also generated global network statistics of segment density, total intravascular volume, volume fraction. For visual inspection of microstructural geometric properties (such as vertical bias of vessels or simulation results), Walk-in-Brain26, a custom in-house 3D immersive visualization platform was used. An overview of dimension and aspects of empirical data sets is given in Figure 1.
Figure 1.
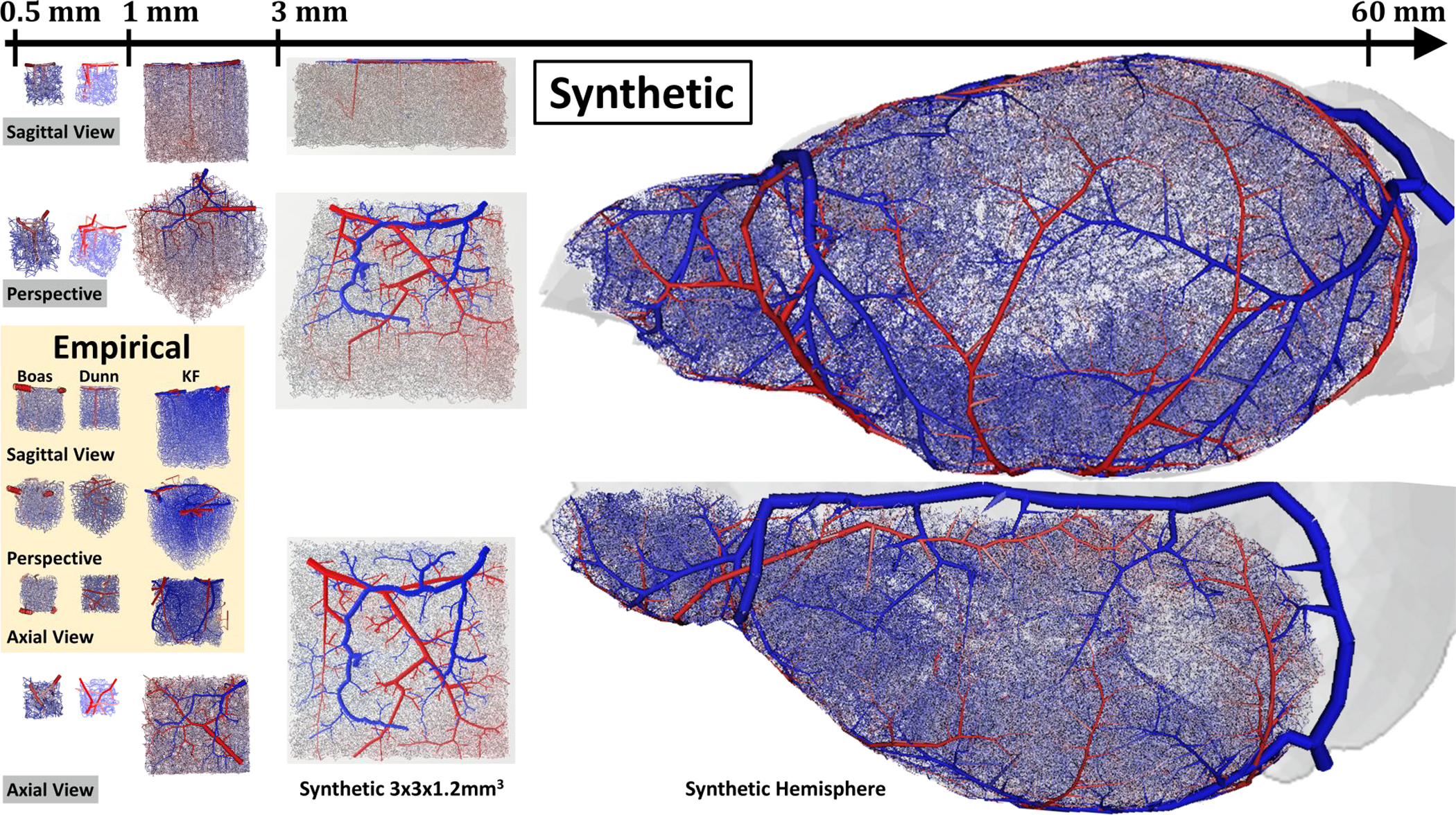
Comparison of length scales of image-derived and synthetic network models of the cerebral circulation in mouse. Empirical data -inlayed box in orange) Three cohorts of empirical networks (Dunn, ED1.1, Boas, EB1.1, Kleinfeld, E1.1) provide excellent topological information about the microcirculation in small sections of the cortex, but are limited by a narrow imaging window. Synthetic data – all VANs outside the orange box) The iCNS algorithm is used to synthesize digital clones of the empirical data (sVAN). In addition, it enables drastic size expansions to construct anatomically sound cerebral networks for a large 3×3×1.2mm3 portion of the cortex (Synthetic 3×3×1.2mm3) or even an entire hemisphere of the mouse (Synthetic Hemisphere). The Synthetic Hemisphere spanning the circulation of one half of the murine brain encompasses pial arteries, penetrating arterioles, precapillaries, capillaries, post-capillaries, ascending venules before finally draining through the venous sinuses. Color represents blood pressure from high (red=120mmHg) to low (blue=5mmHg).
2.2. Large vessel morphometrics and construction of main vascular trees
Morphometric reconstructions of the cortical circulation as well as positions and orientations of the main cerebral arteries (carotid, Circle of Willis that served as backbones for hemisphere growth) were acquired with μCT imaging27 and confirmed with mouse atlases28. More information on the data acquisition and reconstruction can be found in part I of this sequence21. For the synthesis of large cerebrovascular trees extending from the main arterial trunks down to the precapillaries, we use the iCNS algorithm21,29 which significantly extends constrained constructive optimization principles29–32 as described in part I. We derive the mathematical framework of iCNS for generating vascular trees by segment addition that minimized the tree volume, while satisfying hemodynamic blood flow constraints as summarized conceptually in system (1):
| (1) |
where, V is the total vascular tree volume, X is the vector of unknowns which includes the optimal bifurcation coordinates (ξ,η), A is the diagonal resistance matrix, C1 is the graph incidence matrix, q is bulk blood flow, p is blood pressure, is the desired perfusion pressure, and D a diagonal decision matrix to enforce boundary pressures,. The solution of the optimization problem during each segment addition step gives the optimal bifurcation point position (ξ and η) within the bifurcation plane. We refer to part I for a detailed discussion of the essential recursive formulae21 for computing optimal bifurcation point coordinates and segment calibers without the need for inverting the entire flow matrix system. The relationships between diameters and diameter ratios are briefly summarized in Appendix C for completeness.
2.3. Microvascular closures
Microvascular closure aims at synthesizing microvascular structures that connect the arterial and venous sides of the vascular networks in a physiologically consistent fashion. We emphasized achieving hemodynamic equivalence between the empirical and the synthetic VANs. Since blood flow and perfusion are primarily functions of blood vessel lengths, diameters and connectivity, two networks are hemodynamically equivalent if they have similar graph connectivity as well as equal segment length and diameter spectra. Accordingly, we synthesized the arterial and venous branches from the large pial vessels down through the vertical penetrators to the smallest capillaries with number of splined segments, nsgm, of each vessel type matching our image data bases of VANs. This generates trees (an arterial tree and a venous tree), each with a large number of open distal terminal nodes (nTerminals=nsgm/2). Microvascular closure then entails the synthesis of new microvessel segments so that blood can flow from the arterial to the venous side through the capillary bed without any gaps, holes, or dead ends (terminals). In other words, a microvascular closure embodies a network of microvessels which connects open terminal nodes of the arterial tree to segments of the venous tree and conversely, all open terminals of the venous tree will be connected to the arterial side.
Unfortunately, microvascular beds cannot be generated by constrained constructive optimization directly, because its logic only applies to a single binary tree. However, when trying to connect the arterial to the venous graph through new capillary segments, the respective trees would merge thus losing the binary connectivity. Moreover, segment count, diameters, and orientation, as well as connectivity and branching patterns of synthetic networks should match the in vivo microcirculatory angioarchitecture as close as possible. In addition, space filling properties such as tortuosity, mean distance between bifurcations, and closest distance from tissue to nearest capillary are significant metrics for solute exchange across the blood brain barrier and should also be carefully considered. To address these requirements, we developed three microvascular closure algorithms.
Matching terminal closure.
The first method (illustrated conceptually in the top row of Figure 2-top) entails the creation of microcirculatory segments by pairing free arterial terminals with free terminals of the venous tree. While this approach is the most obvious way to connect two sets of terminals, it has several drawbacks. First, finding unique pairings between arterial and venous terminals is a combinatorial problem (specifically, a non-polynomial hard problem), whose computational effort scales exponentially with tree size, making this method intractable for large structures such as the mouse brain.
Figure 2.
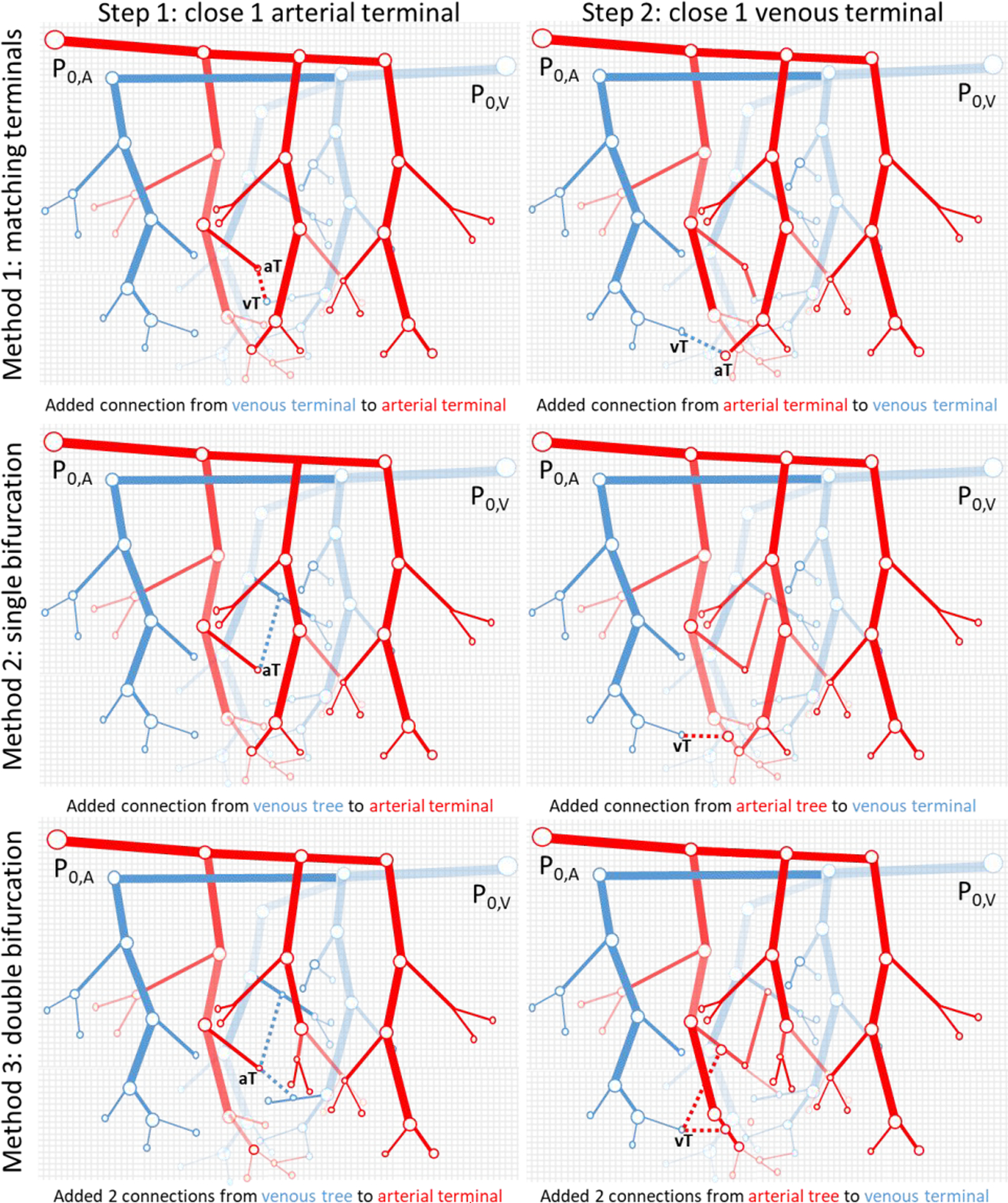
Illustration of the different closure methods between arterial and venous trees. Left Column) In Step 1, a single arterial terminal is joined to the venous tree while in the Right Colum corresponding to Step-2, a venous terminal is closed. The Top Row shows the terminal matching (Method 1) where each terminal from the arterial tree must be paired to a terminal in the venous tree. The Second Row (Method 2) attaches each terminal to a nearby segment of the opposite tree through a new bifurcation in the opposing tree. In the Third Row (Method 3), each terminal attaches to two nearby segments of the opposite tree through two new bifurcations. The closure algorithm repeatedly adds connections in reciprocal manner (arterial closure-step-1, venous closure-step-2) until all terminals are closed on both trees.
The combinatorial explosion can be circumvented by using suitable SampleGenerators (see details in part I) that furnish the coordinates of free arterial segments to the final segment growth stage of the complimentary venous tree, and vice versa. This implementation automatically guarantees that terminal arterial and venous branches fuse into each other without leaving gaps by directing terminal segments into a unique terminal node that is perfused from both sides. However, this method produces microcirculatory segments with further problems. First, because all terminals must be connected to a corresponding terminal on the opposing tree, the segment length cannot be controlled in all connections, meaning the resulting capillary bed will have undesirable length and diameter spectra. For the same reason, the orientation and angles between segments also cannot be controlled, leading to connections that are not physiologically sound. We do not recommend this method and only mention it for conceptual purposes.
Single bifurcation closure.
The second method connects each terminal of the first tree (e.g. arterial) to the other tree (i.e. venous) by generating a new segment between the open terminal and attaching it to an existing segment belonging to the complimentary tree. The node at which this new segment intersects the complimentary tree forms a new bifurcation as shown in Figure 2-middle. This method benefits from simplicity enabling efficient implementation. Unfortunately, this technique also introduces many new connective microsegments with “kinks”, which refers to the often quite acute angle between the segment upstream of the terminal node and the new closure segment resembling a kinked garden hose. Kinked segments introduce a high degree of tortuosity, τ, in the synthetic capillary bed often exceeding the physiological range. Specifically, the tortuosity range of the image-derived VANs has an upper limit of three, τ = [1..3], whereas kinked segments can reach τ~8. The unwanted induction of excessive tortuosity caused by kinked segments can be corrected by replacing the two fused terminal segments (=upstream and closure segment) with a single straight or nearly moderately tortuous segment. This remedy overwrites and, in fact, alters the original position of the terminal node which was initially supplied by the carefully characterized SampleGenerator to precisely meets anatomical constraints (e.g. mean distance to other segments). In other words, rectifying tortuosity can injure, or partially undue anatomical construction constraints carefully enforced in the prior synthesis stage. Furthermore, we note that single bifurcation closure can easily meet a desired total segment count (nsgm, as defined in terms of splined segments which includes all vessel subsections between adjacent bifurcations as described in Appendix B), because closure segment addition does not alter overall segment count or density. We may recommend this closure for simplified hemodynamic simulations, where tortuosity is of minor importance and only preservation of segment lengths and graph connectivity is necessary. On the other hand, this method is not ideal for simulations in three dimensions of oxygen exchange and solute transfer to brain tissue across the blood brain barrier11,12,44.
Double bifurcation closure.
The third algorithm is harder to implement but offers the highest degree of control over vessels length/orientation and sample generation at every level of the capillary bed creation. This method creates two new microsegments that connect one terminal to two existing microsegments of the complimentary tree as illustrated in Figure 2-bottom. Each of the two connections from the open terminal to the complimentary tree is similar to a single bifurcation addition presented above, but with the unique advantage that the terminal becomes a new bifurcation point. The point where each new segment attaches to the complimentary tree can be decided using rigorous optimization or by relaxed (no optimization) segment addition using a geometric heuristic. In both cases, anatomical constraints can be enforced with constraint functors as introduced in part I. Because of the ability to control angles and segment lengths with construction constraints, double bifurcation closure offers the highest level of control over critical morphological parameters such as segment length, angles and segment density, which is necessary for synthesizing a microvascular bed with desired morphometrics. The double bifurcation closure does not suffer from the computational intractability of the matching terminal closure. It also avoids the introduction of excessive tortuosity of the single bifurcation closure. This method proved to be the most effective method for synthesizing sVANs that closely match hemodynamic and morphological statistics of the three cohorts of empirical VANs. We used this method to generate synthetic digital twins for all cohorts of cortical mouse data (N=100 for Cohort 1, N=5 for Cohort 2, and N=5 for Cohort 3). Implementation details for double bifurcation closure are given in Appendix H.
3. Results
3.1. Characterization of morphometrics of cortical circulation with three different sources
Three cohorts of empirical microcirculatory data sets covering the secondary cortex in mouse were analyzed as described in the methods section (KF: N=4; Boas: N=5; Dunn: N=6). This set serves as representative collection of imaging data available for the murine microcirculation. Structural properties and dimensions of the Dunn, Boas and Kleinfeld (KF) cohort of empirical VANs can be inspected in Figure 1. Splined segments (cubic Bezier splines) were used for analysis (as described in Appendix B) to remove any artifacts in raw segment counts caused by image resolution or segmentation choices. CDFs of diameter, length, volume, surface area were calculated for each spline in the network as visualized in Figure 3. We also calculated the cumulative network statistics of segment density, total intravascular volume, volume fraction. These properties are also listed in Table 1.
Figure 3.
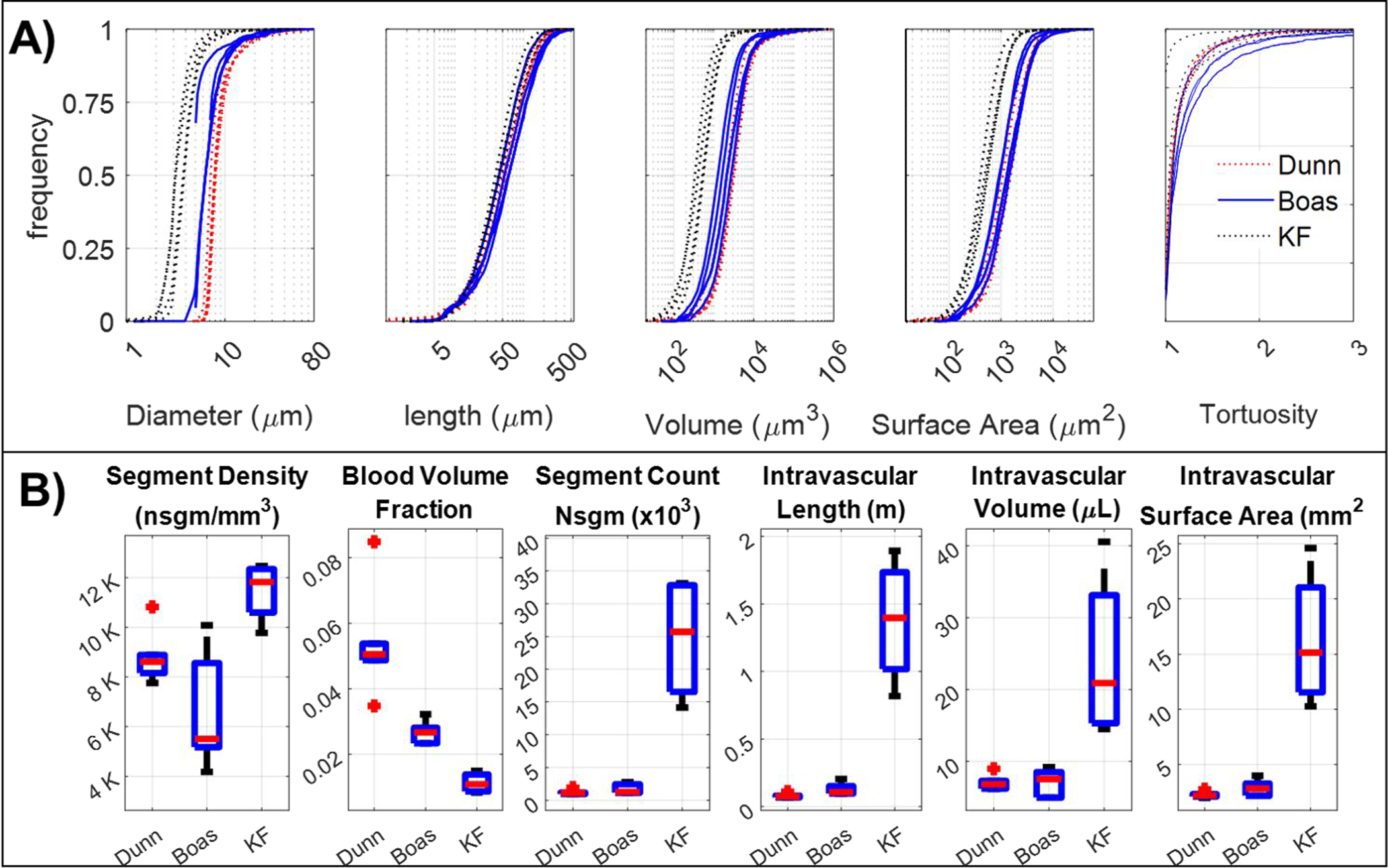
Morphological properties of networks derived from three cohorts of experimental neuroimaging data from the microvasculature in the murine somatosensory cortex. Shown here are representatives from the Dunn (n=6), Boas (n=5), and Kleinfeld (KF, n=4) cohorts. A) Large variability is observed in topology profiles between the different groups, as can be seen for diameter, length, volume and surface area spectra. B) The accumulated statistics of intravascular volume, intravascular length, intravascular surface area, blood volume fraction, segment density and total number of segments (nsgm) also display substantial variability between cohorts.
Table 1.
Listing of network topological properties for different neuroimaging data cohorts of the mouse somatosensory cortex.
| Property | Value |
||
|---|---|---|---|
| Label used for dataset in this paper | Dunn ED1.1 | Boas EB1.1 - EB5.1 | Kleinfeld E1.1 - E4.1 |
|
| |||
| Approximate main dimensions of network (mm) | 0.5×0.5×0.6 | 0.63×0.7×0.61 | 1.2×1.3×1.5 |
| Segment diameter (μm) | 9.15 ± 4.83 | 7.35 ± 4.16 | 3.87 ± 2.2 |
| Segment tortuosity | 1.15 ± 0.29 | 1.24 ± 0.54 | 1.11 ± 0.32 |
| Segment length (μm) | 67.1 ± 53.5 | 76.0 ± 66.6 | 57.0 ± 46.0 |
| Tissue volume (μL) | 0.14 ± 0.02 | 0.26 ± 0.06 | 2.16 ± 0.79 |
| Number of segments/splines (nsgm)* | 1,211 ± 364 | 1,756 ± 759 | 24,669 ± 9,594 |
| Segment density (nsgm/mm3)* | 8,573 ± 1,440 | 6,665 ± 2,371 | 11,473 ± 1,215 |
| Vascular volume fraction (%) | 5.11 ± 1.0 | 2.65 ± 0.3 | 1.13 ± 0.3 |
| Vascular length density (m/mm3) | 0.57 ± 0.05 | 0.49 ± 0.10 | 0.65 ± 0.08 |
| Endothelial surface area density (mm2/mm3) | 16.22 ± 0.5 | 10.86 ± 1.4 | 7.2 ± 1.56 |
| Bifurcation density (nbif/mm3) | 4,403 ± 640 | 4,415 ± 1,554 | 7,453 ± 779 |
| Incidence of multifurcations (% of all nodes)** | 8.3 ± 1.1 | 1.1 ± 1.4 | 6.9 ± 0.9 |
| Long penetrating artery density (nsgm/mm2) | NA | NA | 6.7 ± 1.6 |
| Short penetrating artery density (nsgm/mm2) | NA | NA | 9.4 ± 5.3 |
| Long ascending venule density (nsgm/mm2) | NA | NA | 7.6 ± 3.1 |
| Short ascending venules density (nsgm/mm2) | NA | NA | 16.2 ± 5.2 |
| Long ascending venule/penetrating arteriole ratio | NA | NA | 1.29:1 |
| Short ascending venule/penetrating arteriole ratio | NA | NA | 2.12:1 |
| Overall ascending venule/penetrating arteriole ratio | NA | NA | 1.85:1 |
nsgm – number of segments, NA properties were not assessed
multifurcations are network nodes branching into more than three segments
Assessment of network variability.
The high degree of similarity between the statistics of VANs within each cohort reflects the excellent reproducibility and accuracy of the imaging and reconstruction protocols. However, due to inherent differences between the methodology used to acquire each cohort, domain sizes (imaging window size and cortical depth penetration) vary considerably between VANs from different cohorts. For example, the KF sets reach down to a depth of more than 1500 μm thus capturing the full length of penetrating arteries down to the grey/white matter interface. In contrast, the Boas and the Dunn VANs penetrate about 600 μm into the cortical depth. As a consequence, absolute quantities (cortical tissue volume specific quantities) such as spline segment count, total intravascular tree length, as well as intravascular volume, length, surface area, and surface area vary significantly from cohort to cohort as would be expected from the large variability between tissue volume sizes between cohorts.
Additionally, even relative properties (cortical tissue volume independent quantities) such as blood volume fraction and segment density exhibit a high degree of variance between cohorts as can be seen from the boxplots in Figure 3 despite the fact that the images represent similar regions of the cortex. For example, the blood volume fraction is less than 2% in all KF sets but exceeds 5% in the Dunn cohort with the Boas cohort in between. Moreover, segment density is lowest in Boas at an average of 6,665 nsgm/mm3 compared to 8,573 and 11,473 nsgm/mm3 in Dunn and KF cohorts, respectively. These deviations can be attributed to differences in image acquisition protocols and underscores the unavoidable presence of experimental variability in image reconstructions of the cerebral microcirculation.
We noticed high variability in the diameter, length, and tortuosity information between cohorts. These spectra strongly depend on choices of animal preparation, imaging protocol, and reconstruction methods. For instance, the diameters were generally larger from cohorts using in-vivo imaging (9.15 ± 4.8 μm in the Dunn group and 7.37 ± 4.16 μm in the Boas group) when compared to the ex-vivo counterparts (3.87 ± 2.21 μm in the KF group). For length, segments in the Boas group (76.0 ± 66.6 μm) were longer than those in the Dunn and KF group (67.1 ± 53.5 μm, and 57.0 ± 46.0 μm respectively).
Long/short penetrating vessels.
We studied the connectivity patterns of observable penetrating arterioles and ascending venules in more detail. Upon close inspection, we detected the existence of two distinct types of penetrating vessels emanating from the pial surface and launching into the depth of the cortex. These previously scarcely characterized groups included long penetrators (LPA) and short penetrators (SPA). Long and short penetrators can be differentiated by segment thickness and maximum depth as highlighted in Figure 4. Specifically, long penetrating arteries with an occurrence frequency of 6.7 ± 1.6 nsgm/mm2 of the cortical surface are thicker (which range d > 10 μm at the pial surface) and dive down all the way to neuronal layers V/VI. Short penetrating arteries (9.4 ± 5.3 nsgm/mm2 of the cortical surface) have capillary-like diameters (d<10 μm at the pial surface) and reach only to Layer IV. Additionally, short penetrators have a bush-like appearance with only a few branches distributed uniformly along its length. Long penetrators have sparser trunks but branch numerously in deep Layers IV-VI, thus resembling inverted tree trunks. The distinction of penetrators was most clearly visible in the KF set because of its deeper reach into the cortex. For veins, there are 7.6 ± 3.1 nsgm/mm2 long (LAV) and 16.2 ± 5.2 nsgm/mm2 short ascending veins as measured per mm2 of cortical surface are, whith all statistics also listed in Table 1. We also found that the prevalence of long penetrating arteries (LPAs) was nearly equal to the number long ascending venules (LAVs) in each VAN, specifically the frequency of LAVs to LPAs is 1.29:1. In short penetrators (SAVs and SPAs), we observed a 2.12:1 ratio.
Figure 4.
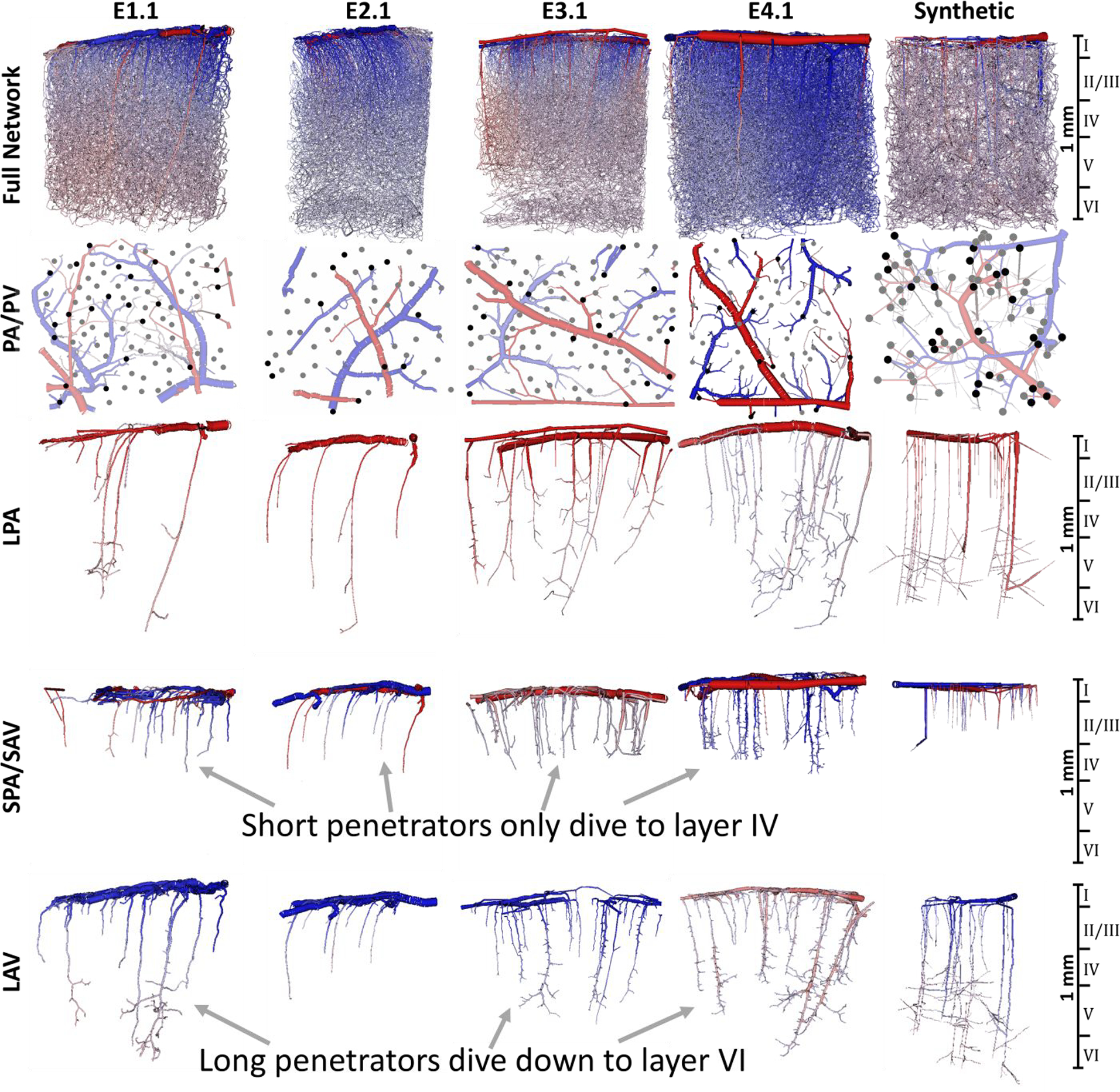
Visualization of the microcirculatory hierarchy of blood vessels in the murine cortex for the four empirical networks from the Kleinfeld group (E1.1, E2.1, E3.1, and E4.1) and a synthetic network (S1.226)22. Top row) The full network shows all blood vessels in the full network. Second row) The extracted pial surface network (pial arteries, PA, and pial veins, PV) with penetrating arterioles (6.7 ± 1.6 long and 9.4 ± 5.3 short nsgm/mm2) and ascending venules (7.6 ± 3.1 long and 16.2 ± 5.2 short nsgm/mm2) labeled with black (long penetrators) and grey dots (short penetrators). Third row) Long penetrating arterioles (LPA) dive down to cortical layers V-VI depth (>825mm). Fourth row) More dense network of short penetrating arteries, SPA and short ascending veins, SAV, which only extend to layer IV. Fifth row) Long ascending venules (LAV) also collect blood from deeper layers than their short counterparts (layer VI). The color reflects blood pressure from high (red = 120mmHg) to low (blue = 5mmHg).
Diameter variability with depth.
We investigated the variability of the diameter spectra as a function of depth, we discovered trend by grouping the segment depths within defined cortical layers22,33,34 with data gathered from the KF cohort, because it is the only cohort to span all neuronal layers (Layers I-VI). We detected layer-dependency depicted in Figure 5, which revealed that the diameter spectra near the surface of the cortex (Layer I) was markedly different than lower layers (Layer II-VI). The mean and variability decrease along the depth of the subcortical region. As an example, we show the spectra of network E2.1 in Figure 5 which displays a stark contrast between the full width at half maximum (FWHM) in Layer I when compared to the lower layers (Layers II-VI). FWHM = the width of the PDF at half the peak frequency. Specifically, the diameter variance is 6.24 um in Layer I, gradually dropping to merely 0.93 um in layer VI. Moreover, the deepest layers have a more prominent peak diameter, meaning there is a high frequency of vessels with similar diameters, indicating higher uniformity. The boxplots of diameter within each layer also reveal that the median is smaller at deeper layers and the spread narrows (=lower variance in lower layers). In general, this trend seems to reflect a higher degree of order in deeper layers of the cortex compared to the surface.
Figure 5.
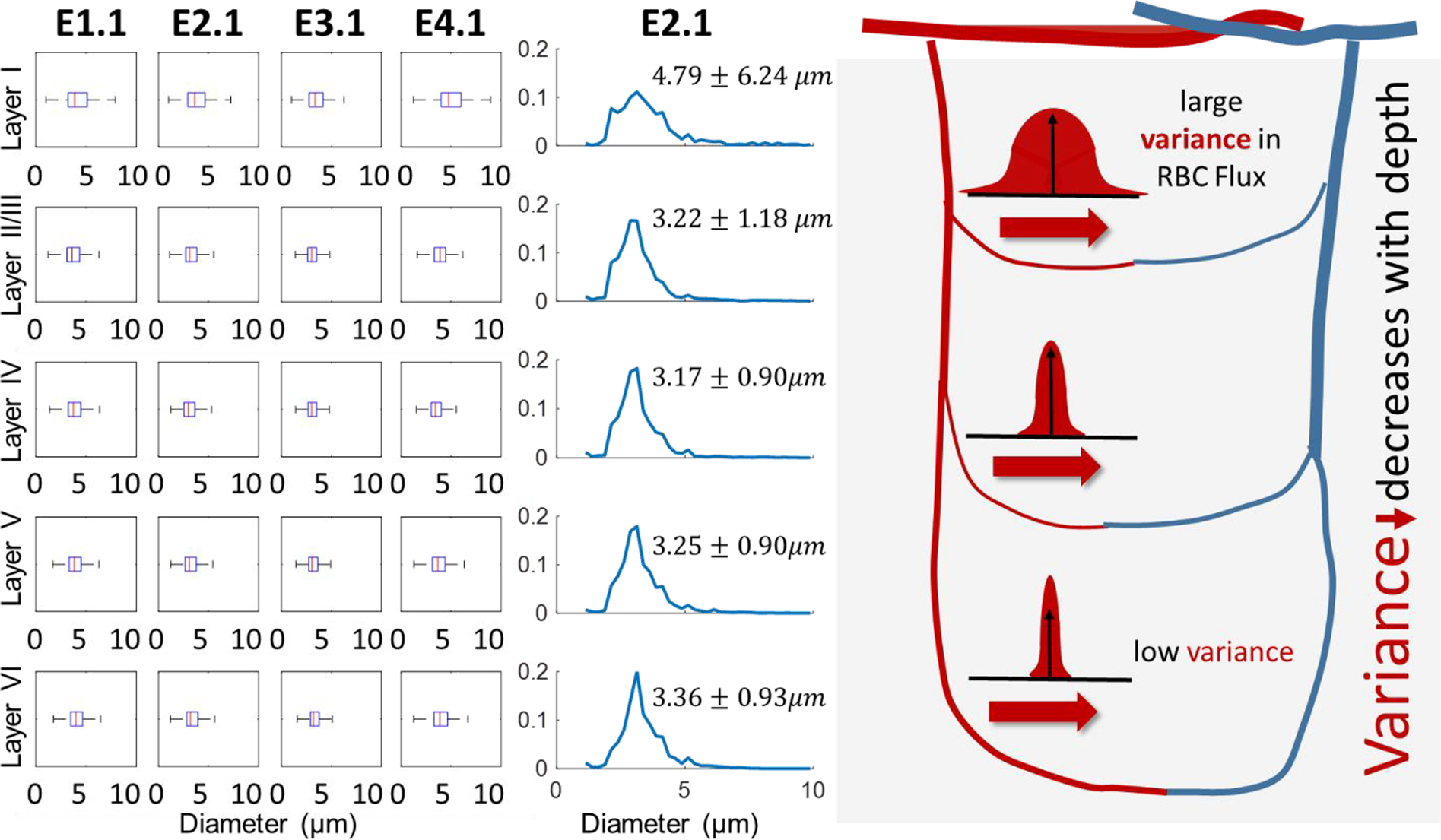
The diameter spectra in the empirical microcirculatory networks as a function of cortical depth of the Kleinfeld cohort (E1.1-E4.1). Variability in diameters decreases in deeper tissues as indicated by the boxplots showing the layer-dependent diameter distributions in four empirical networks (E1.1, E2.1, E3.1, E4.1). The spectra (shown for E2.1, in middle column) exhibit much higher diameter variability in upper cortical layers (standard deviation of 6.24 and 1.18 μm in layers I-II) than deeper regions (standard deviation of ~0.9 μm in layers IV-VI). The more uniform diameter spectra in lower layers may be a factor leading to increased homogeneity in hemodynamic properties in the same layers, such as RBC flux and hematocrit. This phenomenon is illustrated conceptually in the right panel showing RBC flux variability as a function of cortical depth and is discussed in detail elsewhere17. In general, there seems to be more order in deeper layers of the cortex compared to the surface.
3.2. Synthesis of cortical microcirculatory networks (=digital twin network)
In order to emulate the angioarchitecture of the cortical circulation, we used a staged growth paradigm employing the SampleGenerators methodology of the iCNS algorithm as described in part I of this series21. The domain dimensions (given in mm x mm x mm) and the segment density for each vessel type served as input to the synthetic growth. Sample generators helped to enforce anatomically consistent growth rules at each length scale to render statistically matching vessel dimensions, orientations and connectivity. Each stage operated with different sample generators, vessel densities, and sets of constraints. More details on this implementation and pseudocodes are given in Appendix E.
Figure 7 illustrates five main stages required for the synthesis of cortical sVANs. The first step begins with a backbone onto which segments are added using three stages of tree growth, each generating vessels of the three distinct types (pials, penetrators, and capillaries). These stages mirror the complex anatomy of the microvascular bed with highly structured connectivity following three distinct types of vessels: large, lateral pial vessels that convey blood across the surface of the pia matter, penetrating vessels that transmit the blood from the pials deep into the tissue (which further break into long and short penetrators), and an interconnected capillary bed comprised of small vessels that join the penetrating arteries to the ascending venules. More details on the capillary growth stage can be found in appendix E. The final stage (closure) is used to fuse the arterial tree to the venous tree with no gaps as described next.
Figure 7.

Visualization of five stages of synthesizing a complete cortical microcirculatory network in mouse. Top row) shows the gradual evolution of small cortical subsection of similar size to E1.1. Second row) shows color coding of anatomical group labels used during the generation of the sVAN. Bottom row) illustrates stages of growing the LACA territory during the construction of the mouse hemisphere. During each stage of growth, new segments are only allowed to connected to specified anatomical groups as outlined in Table 2. The stages show (from left to right): the backbone forms the initial structure onto which the pial network is grown. The penetrating vessel terminals are then generated perpendicular to the pial surface and attached to the exposed pial terminals. Next, the capillaries (precapillary arterioles, pre-capillaries, capillaries, post-capillaries, and post-capillary venules) fill the space until the desired number of vessels is reached. In the capillary stage, it is possible to relax the volume optimization principle to place the optimal bifurcation point without rigorous optimization. In the final stage, closure between the arteries and veins connects all open terminals from the arterial tree to the venous tree and all the venous terminals to the arterial tree as described in Section 2.3.
The network synthesis method offers control over the formation of highly structured or hierarchical connectivity patterns. Specifically, new segments for a new category (or stage), their attachment can be restricted to certain groups of prior branches; for example new penetrating vessels can only connect to pial vessels. Penetrating arteries cannot connect to the ascending venules or pial veins, it must connect to pial arteries. To control and track the hierarchical order of new attachments, new segments are labeled during with unique identifiers for each synthesis stage. This can be programmatically achieved with an anatomical labeling array spanning all arcs in the VAN with each vessel assigned an anatomical group label. For convenience, we list the anatomical groups onto which new samples can be attached at each stage of growth in Table 2. These groups are also visualized in the middle row of in Figure 7.
Table 2.
Anatomical grouping used in each synthesis stage
| Stage | Groups available for attachment |
|---|---|
|
| |
| Pial Arteries | Pial Arteries |
| Long Penetrating Arteries/Arterioles | Pial Arteries |
| Short Penetrating Arteries/Arterioles | Pial Arteries |
| Pre-Capillary Arterioles | Long and Short Penetrating Arteries/Arterioles |
| Pre-Capillaries | Pre-Capillary Arterioles, Pre-Capillaries |
| Capillaries | Pre-Capillaries, Post-Capillaries |
| Post-Capillaries | Post-Capillary Venules, Post-Capillaries |
| Post-Capillary Venules | Long and Short Penetrating Veins/Venules |
| Long Ascending Veins/Venules | Pial Veins |
| Short Ascending Veins/Venules | Pial Veins |
| Pial Veins | Pial Veins |
Tissue domain size, segment, and morphological constraints were used to synthesize artificial networks with same dimensions, vascular density and hemodynamic properties of the Kleinfeld (KF) cohort (N=100, digital twins). We also fed spectra and domain sizes of the networks in the Boas and Dunn cohort as listed in Table 1. The network naming convention is listed in Appendix A. One sample VAN and its digital twin sVAN are shown alongside statistical comparison of all VANs and sVANs for each cohort in Figure 6. The statistical charts in Figure 6 and Table 3 show excellent agreement between the empirical and synthetic datasets.
Figure 6.
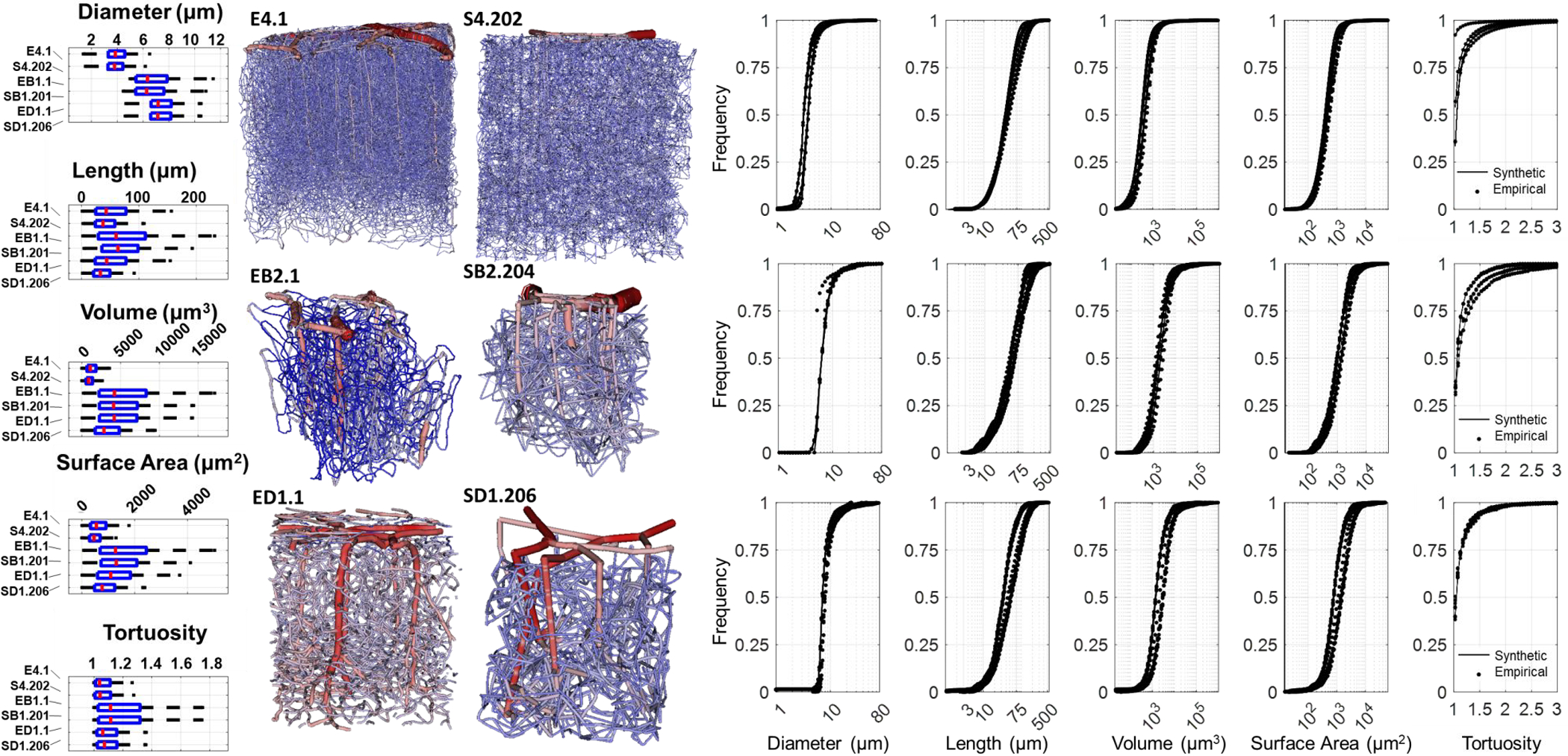
Comparison of morphometric properties of empirical and synthetic networks in mouse. Top) The Kleinfeld (KF), Middle) Boas, and Bottom) Dunn cohorts show excellent match between the empirical (stars) and synthetic counterparts (black lines) as reflected by the tortuosity, diameter, length, volume and surface area distributions. (In all pdf spectra, dots-empirical and lines-synthetic are almost indistinguisable). For a more detailed comparison, two representative networks from each cohort are compared with boxplots, which indicate closer similarity between the networks and their digital clones than between networks of different cohorts. The 3D visualization of the networks also reveal a high degree of structural similarity between the empirical and synthetic networks. We note that the intraspecimen variability among sample networks belonging to the same cohort is larger than the variability between an empirical network and its synthetic counterpart. Of further note, many boundary segments in the empirical imaging datasets are severed, creating unrealistic dead end connections in hemodynmic simulations. In contrast, all segments in digital sVAN are connected in the entire domain with no dangling segments at the boundary or the interior.
Table 3:
Comparative variability between sVANs and VANS of the Kleinfeld cohort.
| Specific Deviation at CDF Frequency 0.5 |
||||
|---|---|---|---|---|
| Diameter (%) | Length (%) | Volume (%) | Surface Area (%) | |
|
| ||||
| Synthetic-Empirical | 1.25 ± 0.57 | 8.91 ± 4.1 | 16.2 ± 4.0 | 13.36 ± 3.6 |
| Empirical-Empirical | 11.08 ± 11.5 | 10.74 ± 8.9 | 34.87 ± 29.9 | 21.86 ± 16.0 |
Comparison and analysis.
We compared the distribution of diameter, length, surface area, volume, and tortuosity of the empirical networks to their synthetic counterparts. We considered the sVANs in agreement with their empirical counterparts because the difference between VANs and its synthetic clone was smaller than the intra-variability amongst the empirical data sets within each cohort as enumerated in Table 3 for the Kleinfeld cohort. The variability between the empirical networks and their respective synthetic clones (the synthetic-empirical deviation) is significantly smaller than the deviation between different networks of the Kleinfeld cohort (empirical-empirical deviation).
We found the segment-by-segment measurements of structural properties relevant to hemodynamic simulations (length, diameter) show excellent agreement between the empirical and synthetic networks in the KF (Kleinfeld) group (E1.1 – E4.1), Boas group (EB1.1 – EB5.1) and Dunn group (ED1.1 – ED4.2) as seen in Figure 6. The surface area (SA) and volume (V) spectra reflect the joint agreement in length and diameter for each segment. In other words, SA and V spectra reflect simultaneous match in both length and diameter. We note that to achieve this high degree of congruency in morphological parameters for these cortical subsections, we tuned properties of the network after the growth stages are complete, to add curvature to the capillaries (to reflect the naturally tortuous nature of the imaged vessels) and the diameter (to match diameter peaks surrounding the imaging threshold) as listed in Appendix D. The final length, tortuosity, and diameter spectra are reasonably close as seen in Figure 6 and listed in Table 3. The networks were compared by measuring the value of the CDF at a frequency of 0.5. This deviation is normalized by the empirical value at the same frequency to give the specific deviation.
This specific frequency shows excellent alignment between the synthetic networks and their empirical clones (with detailed statistics between CDF of synthetic-empirical listed in row 1 of Table 3) when compared to the larger error between the different empirical clones (empirical-empirical row 2 of Table 3). A preliminary analysis of hemodynamic simulations shows that synthetic networks are equivalent in blood flow and total flow resistance across the entire range of perfusion pressures as detailed in Appendix G. A detailed analysis of hemodynamics states in the microcirculation is beyond the scope of this paper, more details on quality of hemodynamic simulations using synthetic networks can be found elsewhere17.
3.3. Network synthesis of the MCA territory and the whole mouse brain.
In Figure 7 bottom row, we also illustrate the growth of the vascular network fed by the anterior cerebral artery (ACA) as one of the stages to synthesize the murine hemisphere. We define the murine cerebral hemisphere as the brain regions supplied by the anterior cerebral artery (ACA), middle cerebral artery (MCA), posterior cerebral artery (PCA) where each territory is synthesized using the same process as the ACA territory but covering different regions of the cortex. All arterial territories are finally drained through the veins of the superior sagittal sinus (SSS).
The morphometric data of the cortex and main arterial branches (=backbones) for hemisphere growth were reconstructed from images collected through μCT27 and a mouse atlas28. More information on the data acquisition and backbone reconstruction can be found in part I of this sequence21. First, we reconstructed the pial surfaces of two murine cortices from neuroimages27,28 generating STL files. The arterial territories (ACA, MCA, and PCA) were labelled manually using ANSYS ICEM (Canonsburg, PA) and an open-source brain atlas28. We set the vessel density equal to the microcirculation data in the KF datasets. The synthesis of the murine ACA territory also serves as a demonstration how diverse physiological data from several imaging sources across different relevant length scales (here, μCT imaging for the large vessels and multiphoton imaging for microvessels) can be seamlessly integrated with the iCNS algorithm to create a more complete structure that approximates murine cerebral circulation at the organ-wide scale. The synthesis took less than 14 CPU hours and the runtime could be drastically reduced by using hashing techniques to accelerate near-neighborhood segment finding. This was not necessary for the synthesis of the mouse hemisphere.
Anatomical variations in hemisphere.
The hemisphere has unique anatomical characteristics that are not observed in the smaller cuboid cortical subsections created in Section 3.2. For example, the hemisphere has three main arterial territories (=three arterial trees) draining through a single venous tree (=one venous tree). Additionally, the arterial territories (ACA, MCA, PCA) are supplied with blood from the Circle of Willis (which is not a tree, but a ring-shaped loop). Finally, the cortical subsections were generated in vertically aligned structured Cartesian meshes.
To account for these geometrical features, the iCNS algorithm synthesized each tree independently. Pial vessels were synthesized while adhering to the triangulated surface mesh representing the cortical surface (as described in part I of this series) but each sample must only be drawn from triangles corresponding to the anatomically correct vascular territory (ACA, PCA, or MCA). Hemisphere closure was achieved with the single bifurcation closure. Although this is not a limitation of the proposed methodology, morphometric differences for different cortical regions were not considered in this first demonstration. We executed the synthesis algorithm multiple times for each of the two mouse brains27,28 to create a total of twelve (12) artificial specimen as visualized in Figure 8. An inventory of networks and the naming convention is given in Figure 8 with visualizations performed using specialized in-house Walk-In Brain software 26,35. Sample whole-mouse circulation networks can also be downloaded from a network repository (instructions and links can be found our public repository36).
Figure 8.
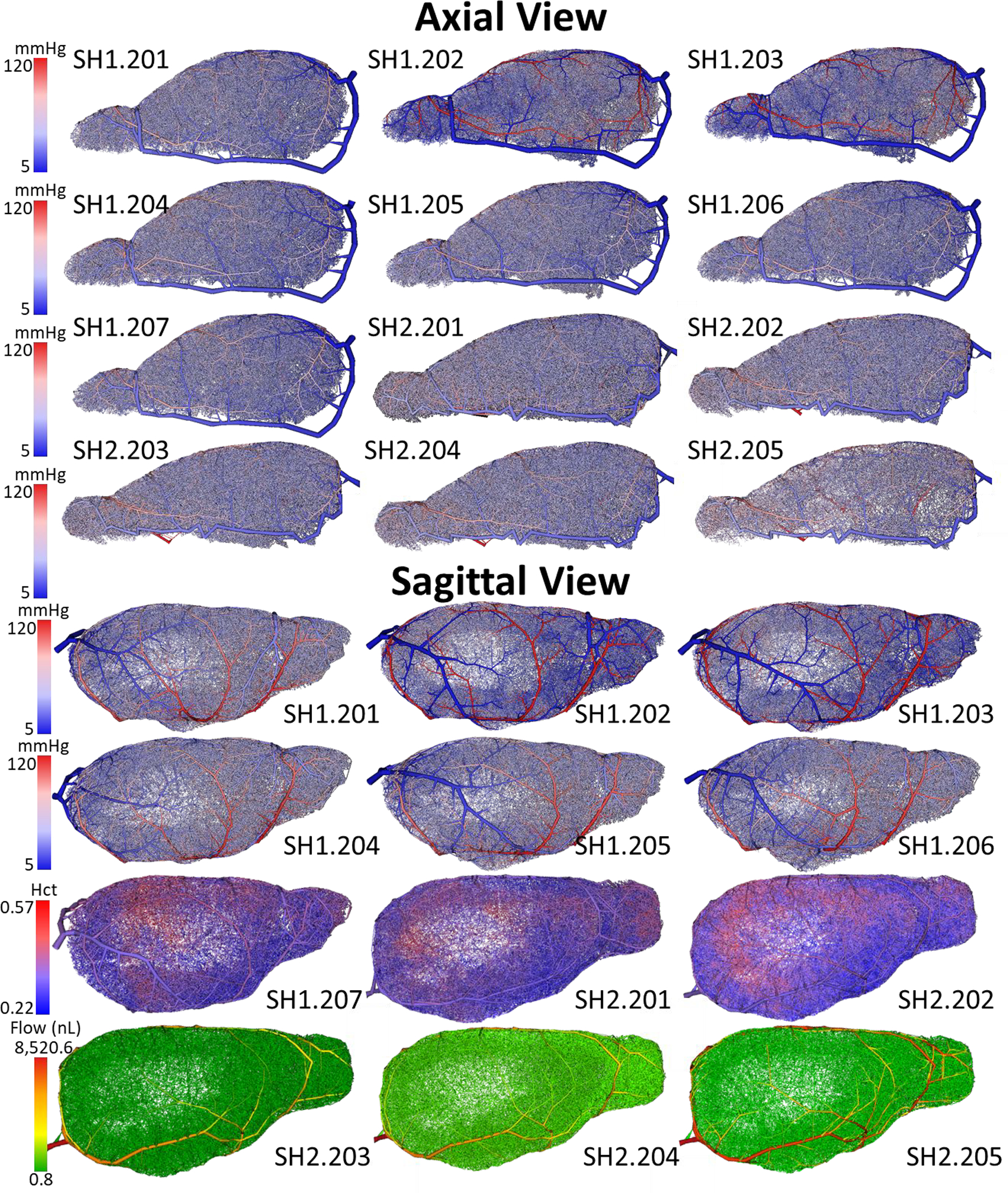
Visualization of the twelve (n=12) synthetic mouse brains (right hemisphere) generated with the iCNS algorithm. Seven networks were synthesized using the cortical reconstruction for mouse-1 (SH1.201-SH1.207). Five networks were generated for a different second specimen, mouse-2 (SH2.201-SH2.205). The color reflects pressure from high at the inlets (red = 120mmHg) through a full capillary bed to a venous drainage (blue = 5mmHg). Blood flow simulations were performed for all twelve samples with pressure reported in all networks (axial view) and SH1.201-SH1.206 in sagittal view. Hematocrit distribution is depicted in SH1.207 and SH2.201 - SH2.202 (sagittal view). Bulk blood flow is also shown for samples SH2.203-SH2.205 in the sagittal view.
3.4. Preliminary simulation of blood distribution patterns for the entire brain
These massive synthetic networks that encompass an entire murine cerebral hemisphere may serve for numerical investigation of the entire cerebral circulation in mouse. We have previously shown10,12,17 that simulations at the whole-organ scale may reveal trends that are harder to identify in smaller cortical sub-sections. The circulatory networks spanning the entire hemisphere are ideally suited for exploring global trends across whole brain regions. Simulation methods described elsewhere17 enabled prediction of blood pressure, blood flow, and red blood cell content (i.e. hematocrit) of every vessel in the hemisphere network in less than 30 CPU minutes and 13.5 GB of memory, with outcomes of blood flow, blood pressure and hematocrit distribution shown in Figure 8. The successful simulation runs demonstrate that our approach makes massive whole brain simulations tangible for a standard desktop workstation.
We observed global trends, in brief: (i) the main pressure drop occurs in the capillary bed, (ii) the pial vessels convey blood along the surface so that vessels closer to the Circle of Willis carry more blood than more distal pials in addition to supplying blood vertically down into the cortex to their penetrating arteries, (iii) the red blood cell density varies as a function of depth (denser RBCs at deeper cortical layers), and (iv) the cortical blood supply is highly heterogeneous (depth dependent) and cannot be represented well by a unique averaged value. These findings are in agreement with our previous work simulating the cortical subsections and validated with a model of the MCA territory in mouse17.
Boundary condition assignment.
Additionally, one of the most impactful assumptions in hemodynamic simulations is the assignment of boundary conditions at terminal nodes of the vascular network. In traditionally reconstructed vascular network models (open arterial trees with no closure or severed capillaries), one must assign numerous (hundreds to thousands) unknown pressure or flow values at the distal terminals, which are generally not directly measurable and exhibit a high degree of variability. In contrast, due in our fully-connected synthetic vascular networks, hemodynamic simulations for the entire circulation in a mouse brain hemisphere require only four boundary assignments at the basilar artery, the two Carotid arteries, and at the superior sagittal sinus vein. Blood flow or even blood pressure in the basilar and carotid arteries have been measured extensively across many species4,37,38, thus making our boundary conditions at these macroscopically observable inlets more reliable than previously needed assumptions for the distal tree nodes that cannot be reliably measured.
4. Discussion
In this series of papers (part I,21 and part II, this manuscript), we emphasized the need for microvascular closure which forms a physiologically functional connection between the arterial and venous blood flow. A key innovation of this manuscript is our proposed closure algorithms to create artifical microvascular beds that match hemodynamic properties of in vivo specimen. Our double bifurcation closure was found to provide the most realistic sVANs as a result of its ability to control segment length, orienation, and tortuosity. In the capillary growth stage, it is possible to relax the volume optimization principle to place the optimal bifurcation point without the need for rigorous optimization which can become time consuming. Closure fuses the arterial tree to the venous tree with no gaps. The microcirculation thus comprises segments created and in capillary growth stage together will all closure segments. It is worth noting that closures were previosuly achieved using Voronoy tesselation10,20, homogenization without discrete capillaries39, or shortcircuiting segments18. To the best of our knowledge, our algorithm is the first closure that connects arterial and venous tree to a microcircuit which simultanously matches several morphometric properties essential for hemodyanics simulations (specifically diameters, tortuosity and vessel density) of real capillary beds.
Multiphoton data was collected from three separate neuroimaging labs and served as three cohorts (named after the labs they were collected from: Kleinfeld (KF): N=4, Boas: N=5, and Dunn: N=6; that represent a cross-section of available microanatomical data about the murine cortical blood supply derived from state-of-the-art neuroimaging and reconstruction protocols. The statistical properties of these cohorts were analyzed in detail to obtain the relevant anatomical parameters necessary to synthesize hemodynamically equivalent networks (sVANs). Hemodynamically relevant properties (listed in Table 1) including branching order, connectivity, vessel caliber, and tortuosity guided our iCNS algorithm for creating sVANs with similar blood perfusion to their experimentally-derived VAN counterparts.
We then applied the iCNS algorithm, complete with a novel capillary closure to generate sVANs with matching critical topological aspects for all three cohorts of VANs from the murine vibrissa primary sensory cortex. We demonstrated that a digital twin of an experimental VAN can be constructed by using its topological profile described by a small number of input statistics (cortical tissue volume, segment density at each hierarchical level, tortuosity, and diameter spectra). We also showed here, for the first time, how the cumulative density functions of key hemodynamic parameters, such as length, diameter, tortuosity, vessel count can be matched to a desired degree of accuracy.
The versatility and robustness of the iCNS algorithm was exemplified by synthesizing a large number (N=110) of sVANs that matched relevant morphometrics of their experimental counterparts in three different cohorts of multiphoton image data. The deviation between the sVANs and their respective original VAN template was, in fact, found to be smaller than the deviation between any two experimental samples from the same cohort. With respect to the targeted hemodynamically-relevant properties (diameter, length, surface area, volume, and tortuosity), sVANs and experimental VANs were found to be structurally similar. Since simplified continuity and momentum equations typically used for large scale hemodynamics simulations10–12,17,18,21,41 are only sensitive to network connectivity, segment diameter, and length, blood flow predictions based on these simplified models will give similar results, at least in a statistical sense as we showed previously17. We also conducted hemodynamic simulation studies (see Appendix G) that demonstrated similar values of blood perfusion in synthetic and empirical networks over the entire range of physiological pressure drops across the microcirculation. A more detailed discussion and results of hemodynamic equivalence studies can be found in Appendix G. This suggests that digital twins (sVANs) can serve as surrogates for experimentally acquired VANs in blood flow simulations for the cortical microcirculation.
Moreover, these anatomically sound circulatory networks can serve as a ground thruth or a phantom model for validating homogenization techniques7,20 or reconstruction techniques3,24,25,42. Homogenization can be a useful tool for simplifying massive microvascular computations, but its validation can benefit from comparison with a more complete model presented here to ensure that critical trends are not lost by diverse homogenization assumptions. Synthetic networks may also serve as imaging phantoms for developing reconstruction techniques and can be an excellent method for creating a large database of phantoms for training neural network algorithms for centerline and diameter reconstruction.
Inter-cohort variability.
Detailed statistical analysis of the data indicated that the intra-cohort variability between VAN samples within the same cohort was relatively small, attesting to the high quality and reproducibility of state-of-the-art neuroimaging and vascular reconstruction technologies used by each lab. The significant differences in size and cortical depth penetration observed between different cohorts affected global network properties (such as number of segments, total surface area of the endothelial cell layer forming the blood brain barrier, and others). Moreover, we also observed significant variability in sample size-independent properties such as segments density, blood volume fraction, and the diameter spectra. These variances between morphometric data from different cohorts in different labs can be explained by fundamental differences in the experimental protocol. For example, ex-vivo imaging is known to have smaller vessels than in-vivo counterparts because the pressure maintained by the living brain is disrupted and vessels begin to collapse. In addition to the differences in imaging protocols, more variability is introduced by the unique choices made by each team during image reconstruction steps for generating segment connectivity, centerline and diameter information. For example, the diameter information is interpreted by the reconstruction algorithms due to thresholding settings that delineate the vascular and extravascular spaces in the images. In effect, vessel diameters were found to be the most uncertain of the morphometric parameters.
Penetrators.
Detailed visual and statistical inspection of the cortical angioarchitecture revealed the scarcely characterized presence of two types of penetrating vessels emanating from the cortical surface and diving perpendicularly down into deeper tissues. We have termed these two groups: long penetrators with a branching pattern resembling inverted trees reaching into the deepest cortical layers (Layers V and VI) and short penetrators with a bush-like structure feeding capillaries in the top layers (Layers I-III). These patterns of long and short penetrators were visible in the penetrating arteries/arterioles and were also seen in ascending veins/venules.
Depth Dependence.
We also discovered an increase in vessel diameter homogeneity in lower layers. This trend was evident through an observed smaller standard deviation of diameters in the lower layers than in layers closer to the cortical surface as seen in Figure 5. Figure 5 also shows a smaller mean diameter and tighter variance in lower layers compared to the vessels closer to the cortical surface. We have previously reported the simulation-based observation of more homogeneous microflow (=less variability of hematocrit) in deeper layers compared to flow patterns closer to the surface17. We also inferred that hematocrit increases in blood vessels reaching deeper cortical tissues. The implication of a higher state of order in deeper cortical layers was later experimentally verified43. The trend of more uniform diameter distributions in the deeper cortical Layers reported here supports the theory of layer dependence for hemodynamic states in the cortical circulation.
Expansion to larger structures.
The ability to emulate macro-, meso- and microvascular networks (guided directly by image data or indirectly by morphometic statistics) enabled us to generate massive circulatory networks that substantially extended the limited field-of-view observed in neuroimaging windows. For example, Figure 1 shows a massive artificial cortical slab with complete pial and subcortical circulation spanning 3×3×1.2 mm3. Blood and oxygen exchange simulations44 conducted on such large structures can be helpful in quanitying hemodynamic and metabolic functions without the need to impose uncertain boundary assumptions. Ample distance to domain limits is essential for exploring inherent flow patterns as a function of vascular topography without the risk of secondary effects attributable to choices of boundary conditions or simplifying assumptions.
We successfully integrated data from multiple sources (multiphoton, μCT, and mouse atlases) to inform the iCNS algorithm for generating twelve cerebrovascular networks spanning the entire murine cortical hemisphere. With these massive organ-wide networks, we can begin to investigate the vascular reserve, collateral reperfusion after a stroke, and drug residence time. These investigations are difficult in the smaller VANs or sVANs because the majority of the vascular structure (the VANs span ~1–2% of the cortical circulation in mouse) is missing; leading to skewedness of simulation results or invisible trends due to nearby artificial boundaries.
4.1. Outlook on the human circulation.
A main thrust of neurovascular research aims at elucidating fundamental perfusion and control principles in normal and pathological states of the human brain. Unfortunately, it is not feasible to perform invasive imaging or to conduct exhaustive experimentation on humans as can be performed in mice. It is also known that the human brain has substantial structurally differences from the mouse brain, making the intuitive extrapolation of findings in mouse to humans unreliable. To overcome this impasse, data acquired from animal models in combination with synthetic networks trained and validated with mouse neuroimaging data could serve as a digital bridge for addressing questions about human brain function. In fact, one of the major differences between the mouse and human brains is a substantial size difference which is compounded by additional geometric complexity (deep and numerous gyrations). In comparison, the cortical volume (grey matter) in mouse is estimated at ~150 mm3 from our reconstructions 27,28 compared to ~458,000 mm3, 45 in the healthy adult human brain roughly a 3,000-fold increase in size by volume. Additionally, the vascular density of the murine cerebrovasculature17,22 is ~11,474 nsgm/mm3 compared to 8,800 nsgm/mm3 in humans46. Assuming these volumes and vascular densities as a rough basis would give 1.72M segments in the whole mouse brain and an approximate target number of 4.03B segments for the human brain. The size differences between mouse and human brain can be appreciated in
Figure 9, which shows a synthetic mouse calculation in comparison to a prototype of the cortical blood supply in a human brain synthesized with the iCNS algorithm and methods described here for mouse.
Figure 9.
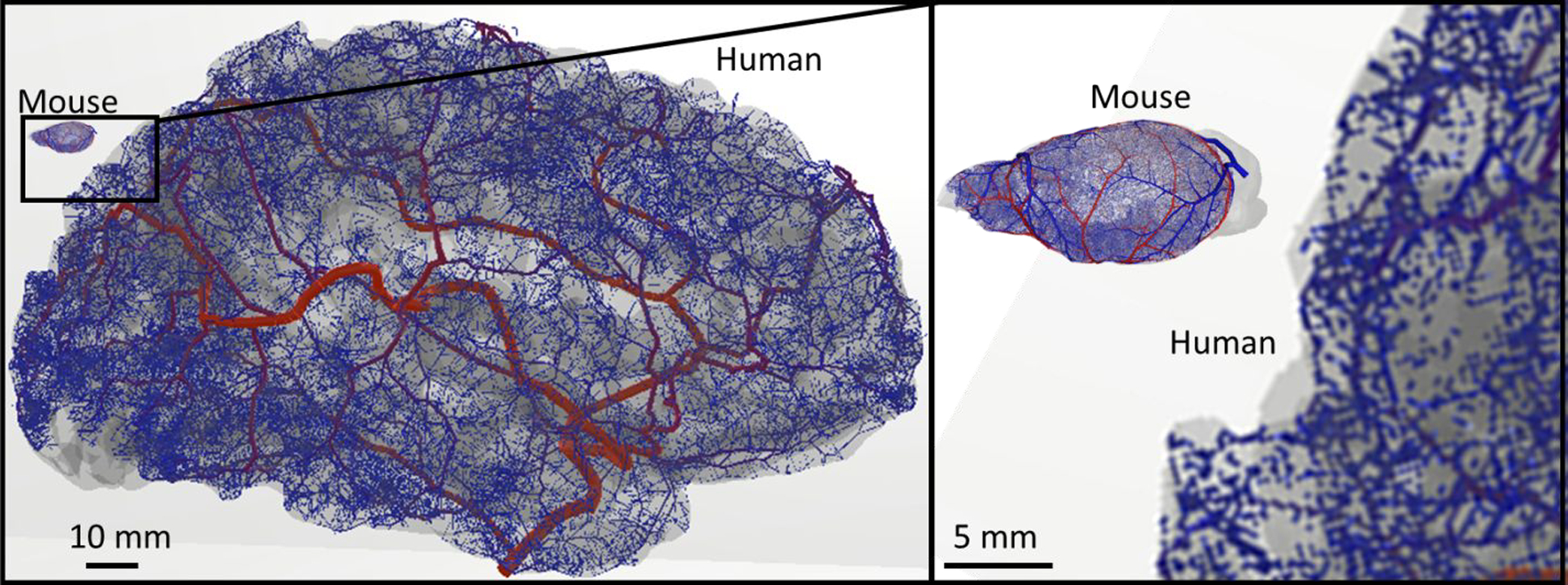
Extension of vascular synthesis methodology from the mouse to the human brain. The iCNS algorithm was applied to a human cortical surface reconstruction for growing a network of the main cerebral arteries including the Circle of Willis, the MCA, PCA, and ACA reaching down to the level of the distal pial vessels. This result shows that the same principles of synthesis and staged growth used in the mouse hemisphere was successful in producing fully-closed vascular structures for the human brain.
We have input morphometric data from humans10,46,47 into the network synthesis of the iCNS framework. As a first step, we used anatomical reconstructions for cortical surface and main arterial trees in human subjects5,48,49 to generate a prototype of the cerebral circulation of the complete arterial tree in humans. The resulting synthetic human arterial network depicted in
Figure 9 shows the CoW, the ACA, MCA, and PCA of the left hemisphere in a normal human subject giving rise to pial surface arteries and penetrating arteries/arterioles. Surface growth21 was successfully applied to generate pial vessels along the highly tortuous gyrations of the human cortex. Penetrating arteries/arterioles on the cortex were created with SampleGenerators reproducing patterns seen in human46,47. Such an artificial human circulation network could then be useful for comparing hemodynamic states and oxygen delivery in healthy and diseased human brains.
While several other groups have made valuable contributions to the synthesis of vascular structures for the human20,39,40, an anatomically consistent, realistic capillary bed has never been built at the human brain scale. The results reported in the current manuscript mark the largest circulatory networks ever created that delineate every blood vessel at the macro, meso and microscale including the full capillary bed with closure, thus suggesting the readiness of the proposed synthesis methods for the building of a full human brain.
4.2. Limitations
Space filling.
While we believe that our artificial VANs approach hemodynamically equivalence of their empirical counterparts, we realize that some differences in space filling properties of the capillary bed still exist. For example, traditional CCO optimization generates planar bifurcations with straight segments. In experimental VANs, many bifurcations are not planar and vascular segments especially small microvessels twist and turn. We have overcome this shortcoming in part by imposing statistically equivalent tortuosity, yet identical tortuosity does not guarantee equivalence in the curvature and orientation of segment paths relative to each other.
Alignment bias.
We also observed that the angles between the main segment axes and the cortical surface (data shown in Appendix F), although seeming random to the naked eye, have an orientational bias. While our synthesis partially captures some of this preferred alignment (vertical predominance in the orientation of penetrating arteries by staged growth of vertical penetrating arteries/veins), synthetic branches have a higher degree of randomness than the empirical structures at the microlevel. The preferred vertical-horizontal alignment in empirical VANs compared to the more random orientation of the synthetic segment would affect solute exchange simulations such as oxygen extraction. Since our aims here were hemodynamic simulations, not mass exchange, we did not tackle this issue in this paper yet. Limitations concerning space filing and alignment biases require further research.
Adaptations to other brain regions and other organs.
The synthesis of circulatory networks for an entire mouse hemispheres requires statistical information about the spatial variabilty of morphometric quantities across different functional cortical regions. Since our reconstructed imaging data concerned the vibrissa primary sensory cortex, we used its metrics and parameters for the synthesis of the hemisphere network. This is admittedly a simplification which leads to a uniform topological profile across the entire cortical surface, lacking spatial heterogeneities that is known to occur in different brain regions. This spatial variablity can, however, be easily incorported into the iCNS algorithm as stage input for a speciifc region. Thus, it is not a limitation of the methodology; rather a limitation of the availability of reconstructed neuroimaging data across the entire cortex. As more extensive reconstructions from brain-wide neuroimaging become available 28,50,51, the metrics accounting for topological differences between diverse functional brain regions can be used as input to the iCNS algorithm and enforced during synthesis.
We believe that in principle volume minimization is sufficient to build physiological vascular structures also for different organs such as the retina, the heart, and the blood supply of lung or muscle tissue. Our algorithm has methods for considering additional physiological constraints in order to satisfy the functional need for the blood supply needed in the specific organ. Our experience teaches that functional similarities give rise to similar network morphometry, which does not necessarily encompass an entire organs. For example, there is similarity in the coronal arteries and the pial arterial surface, both delivering blood along a surface. However, the microanatomical differences between the heart (muscle) and the neuronal architecture (layered neurons and glia in the cortical columns) leads us to speculate that the microcapillary properties are not identical.
5. Conclusions.
The demonstrated ability to synthesize artificial circulation models of the whole mouse brain enabled hemodynamic simulations of cerebral blood perfusion and metabolism as a function of network topology over all relevant length scales (arteries, capillaries, and veins). Our anatomically accurate microvascular closure matches hemodynamically relevant morphometric spectra and parameters which, as far as we know, has never been accomplished before with classical constrained constructive optimization or other synthesis methods. This algorithm enabled the synthesis of large portions of the cortical circulation matching desired morphometric input data from different imaging sources thus creating a more comprehensive, connected and quantitative picture of brain function.
Pathological alterations may impose additional constraints on network construction. Synthetic structures that mimic normal hemodynamic states is an important intermediate goal we believe has been achieved to a large extent in this set of two papers. For the study of neurological and cerebrovascular disease (CVD), two question arise. How do pathologies alter structural network properties? Second, which functional biological deviations does a specific CVD induce? We envision that structural and functional deviations from the normative case can be systematically and conveniently studied with synthetic networks. For example, reduction in vascularization can be controlled by lowering the segment count in the respective growth stage. Alternatively, network models for normal specimen can be thinned to match CVD characteristics. The highly structured anatomical segment addition logic and ability to track hierarchical segment labels during the growth stage offer a systematic handle on segment hierarchy in synthetic networks that empirical data sets do not possess. Moreover, other subtle parameters changes, such as angular orientation or tortuosity can be manipulated (e.g. tortuosity parameter, α, increases segment arc length without altering nodal positions). Functionally, hemodynamics simulations that mimic microinfarcts or temporal occlusions cause by leukocytes can easily be specified by manipulating segment resistance directly or via the changing diameter relations. The critical benefit in the deployment of synthetic networks stems from the ability to artificially create and simulate network effects due to subtle highly controllable changes. This constitutes a viable compliment to deriving insights by statistical analysis of large number of empirical VAN from different animal or human specimen. Comparative studies in synthetic networks with controllable changes provides a new instrument to the scientific and systematic investigation of cerebrovascular disease.
Mechanistic brain-wide computations are becoming an exploratory tool for testing and validating hypotheses for underlying functional mechanisms behind cerebral autoregulation, collateral reperfusion after stroke, or pathologies such as hypoxia-induced neurodegeneration associated with old age. Our approach overcomes the need to make uncertain assumptions about hemodynamic states at the microscale. Hemodynamic and metabolic simulations for the brain are expected to better elucidate control mechanisms and metabolic regulation for the entire organ across all length scales. Our whole-brain scale vascular model presented here is a significant step towards whole-brain hemodynamic simulations.
Acknowledgements
This work was supported in part by the National Institute of Neurological Disorders and Stroke Grant 1R21NS099896, National Institute of Aging, Grant/Award Number: 1R56AG066634-01 and the National Science Foundation (NSF) Division of Chemical, Bioengineering, Environmental, and Transport Systems (CBET) Grant CBET-1301198.
Appendix A: Imaging data acquisition
Kleinfeld cohort (KF).
Four murine subjects had undergone post-mortem perfusion by a peristaltic pump at a rate of 1 ml/min to fix the vascular structure post-mortem. Once curation was completed, the brain was removed and imaged in a significant section (~1×1×1 mm) of the vibrissa primary sensory cortex by two-photon laser scanning microscopy (2PLSM) [22,52,53]. The vessels were subsequently reconstructed into a vascular network graph with corresponding diameter information. Each vessel fell under one of the following labels: pial arteries, penetrating arterioles, capillaries, ascending venules, or pial veins. The automated labeling was informed by vessel size, depth, and Strahler order [24]. In the case of capillaries, a diameter threshold of 6 μm was employed. All protocols were approved by the Institutional Animal Care and Use Committee at University of California, San Diego. More details on segmentation can be found elsewhere [22,24].
Boas cohort (Boas).
Five C57BL/6 mice (male, 25–30 g, n=5) were anesthetized by isoflurane (1–2% in a mixture of O2 and air) under constant temperature (37 °C). A cranial window in the dura was removed and sealed with a 150-μm-thick microscope coverslip. During the experiments, a catheter was used in the femoral artery to monitor systemic blood pressure and blood gases. The catheter also administered the two-photon dyes. During the measurement period, mice breathed a mixture of O2, and air under the 0.7–1.2% isoflurane anesthesia. The cortical vasculature was imaged using 600 × 600 × 662 μm stacks with 1.2 × 1.2 × 2.0 μm voxel sizes under a 20X Olympus objective (NA=0.95). The vasculature was highlighted by labeling the plasma with 500nM of dextran-conjugated fluorescein (FITC). All experimental procedures were approved by the Massachusetts General Hospital Subcommittee on Research Animal Care. More details on segmentation can be found in [4].
Dunn cohort (Dunn).
In the two-photon laser system, a titanium:sapphire (Ti:S) oscillator (Mira 900, Coherent) beam is steered to a pair of galvanometer scanners (6125HB, Cambridge Technology) driven by servo driver amplifier boards (671215H-1HP, Cambridge Technology). A Keplerian telescope beam expander consisting of a B-coated scan lens (f = 80.0 mm, AC254–080-B, Thorlabs) and tube lens (f = 200.0 mm, LA1979-B-N-BK7, Thorlabs) is used to fill the back aperture of the microscope objective (XLUMPLFLN20XW 0.95 NA or XLPLN25XSVMP2 25X 1.0 NA, Olympus). Excitation and emission paths are separated with a 775 nm cutoff dichroic mirror (FF775-Di01–52×58, Semrock). Fluorescence is epi-collected, transmitted through either a 510/84 bandpass filter (FF01–510/84–25, Semrock) or a 609/181 bandpass filter (FF01–609/181–25, Semrock), and detected by a photomultiplier tube (H10770PB-40, Hamamatsu Photonics). Image acquisition was controlled using custom software (LabVIEW, National Instruments) and image frames were collected at a 512 × 512 pixel size. Image stacks were collected at a z-resolution of 5 μm and three frames were averaged from 0–200 μm cortical depths, five frames from 200–500μm, eight frames from 500–700 μm, and twelve frames beyond 700 μm. All mice specimens imaged by Ti:S were excited at λex=800 nm. More details on segmentation can be found elsewhere [25].
Table A1.
Naming convention of synthetic murine circulations matching empirical VANs.
| Empirical data set name | Synthetic data set name | Volume (mm3) | Cohort |
|---|---|---|---|
|
| |||
| E1.1, E2.1, E3.1, E4.1 | S1.201-S1.225, S2.201-S2.225, 53.201-S3.225, S4.201-S4.225 | 2.156 ± 0.789 | Kleinfeld |
| EB1.1, EB2.1, EB3.1, EB4.1, EB5.1 | SB1.201-SB1.205 | 0.081 ± 0.003 | Boas |
| ED1.1, ED2.1, ED3.1, ED3.2, ED4.1, ED4.2 | SD1.201-SD1.206 | 0.136 ± 0.024 | Dunn |
| -- | S3×3.201 | 9.0 ± 0.0 | 3×3×1.2 mm3 |
| EH1.1, EH2.1, EH3.1, EH4.1, EH5.1* | SH1.201-SH1.207, SH2.201-SH2.205 | 83.5 ± 9.1 | Hemisphere |
the empirical hemisphere networks are reconstructed from images as described in part 1 [1]
Appendix B: Statistical analysis of cerebrovascular angioarchitecture
Image invariant segmentation by splines.
Image segmentation of multiphoton image data produces cylindrical segments of arbitrary length depending on image thresholds and algorithms used, see [4,24,25,48,49]. Unfortunately, this means that segment count and spatial partitioning in reconstructed networks are not standardized, meaning the raw segment count is not a suitable basis for morphometric analysis. Furthermore, the incidents of properties as a function of segment count will be sensitive to the number of segments; making this an unsuitable method for comparison. Instead, we encoded a unique and modality invariant segmentation by grouping all raw segments between any two bifurcation points into a single spline segment (termed a spline). We propose using splined segments, each of which encompasses the string of cylinders that connects two adjacent bifurcations. Thus, splines reflect all cylindrical segments that are in-series (they act as in-series resistors in the blood flow equations). Since the number of bifurcation points and their connectivity are unique regardless of reconstruction method, after conversion to splines, two networks are reconstruction method-independent and can be compared to one another.
Representation of spline data information.
Once the vascular network has been converted to splines, topological characteristics (diameter, position, length, etc.) for each spline were calculated and recorded. We calculated the normalized PDF and CDF of each property including length, diameter, surface area, volume, and tortuosity. We average the small variations between cylinders of the same spline to get a single diameter value for the spline. We also calculated cumulative network statistics of segment density, total intravascular volume, volume fraction.
Appendix C: Recursion relation for the segment addition
The iCNS growth principles (segment addition through CCO) generates realistic tree-like structures but with the drawback that all synthetic segments are represented as straight cylinders. In contrast, in-vivo microvascular VANs have mostly curved segments with tortuosity larger than unity, τ > 1. Furthermore, the smooth diameter spectra generated by balancing the tree during iCNS may not reflect the high occurrence of capillaries with diameters near the imaging threshold. When making our synthetic clones, characteristics of the VANs should be preserved. To match the naturally tortuous segments, we chose to modify the aVAN splines by adding tortuosity (for details see [11]) until the desired length and tortuosity spectra matched. In the aVANs, we also chose matched the uneven diameter spectra by directly adjusting some segment diameters. To identify how much to change each spline, we used an unsupervised spectrum matching method as detailed in Appendix D with accompanying details regarding when to use this matching technique.
We derive the mathematical framework of iCNS for generating vascular trees by segment addition that minimized the tree volume, while satisfying hemodynamic blood flow constraints as summarized by System (1):
| (1) |
where, V is the vascular tree volume, X is the vector of unknown bifurcation coordinates, A(ξ, η) is the diagonal resistance matrix, C1 is the connectivity matrix, C2 is the network incidence matrix, q is bulk blood flow, and p is blood pressure. In the blood flow problem, , are desire perfusion pressures, and , are known inlet or outlet flows. The decision matrix D can be used to create a single compact formulation for Dirichlet (pressure,) or Neumann (flux,) boundary conditions. For more details on the matrix formulations [37,38]. The solution of the optimization problem gives the optimal position ξ and η for the bifurcation point within the bifurcation plane.
Under the assumption that all terminal nodes discharge equal amounts of flow at identical terminal pressure potentials, a tree with given segment geometry (=positions are set for all bifurcation, inlet, and outlet nodes), will have all diameters recursively computed as described here. The root segment caliper, d0, can be uniquely determined by the desired perfusion flow rate, q, and perfusion pressure drop between inlet arterial pressure and distal terminal pressure, described by the Δp term as in eq. (2). All other segment calibers in the entire network can then be expressed as a function of the root diameter as in eq. (3). At each bifurcation, segment diameters follow from Murray’s law, eq. (4), and diameter ratios βi and βj, eq. (5). The diameter ratios depend only on reduced resistances, ρk, which are functions of segment lengths and the discharge capacity, Nk, the subtree supplied by a given segment as in eq. (6). By using these equations, matrix inversion for the computation of hemodynamic constraints implying blood flow and pressure fields is avoided. Solving the flow problem constraints using matrix inversion repeatedly for every segment addition during the synthesis would certainly render this approach computationally intractable.
| (2) |
| (3) |
| (4) |
where
| (5) |
| (6) |
| (7) |
Appendix D. Matching Characterizing the topology of a network
In the main manuscript, we describe synthetic networks that match the hemodynamic profile of image-derived counterparts. We used a post-processing step executed after synthesis completion to fine tune segment tortuosity and diameter spectra to match the VANs. The process to characterize a vascular network follows:
Create splines by agglomerating straight segments between bifurcations.
Calculate and record the diameter, length, and tortuosity CDFs from the empirical aVAN and corresponding VAN (note, a direct CDF can be inserted in lieu of a VAN CDF if one is available)
Cycle through the segments in the aVAN, modifying each segment in the synthetic network to match the corresponding segment in the empirical network. If desired, the CDFs can be binned to match the synthetic network to any spectrum regardless of divisions.
D1. Unsupervised matching of topological spectra
To begin, we assume the two normalized CDFs of the VAN and aVAN do not match, such as the tortuosity differences between the aVAN (full of straight segments) and the experimental VAN (with naturally curved segments). Here, we use the example of length but the theory works for any segment property. An example of two spectra that do not match can be seen in Figure D1.
Figure D1.
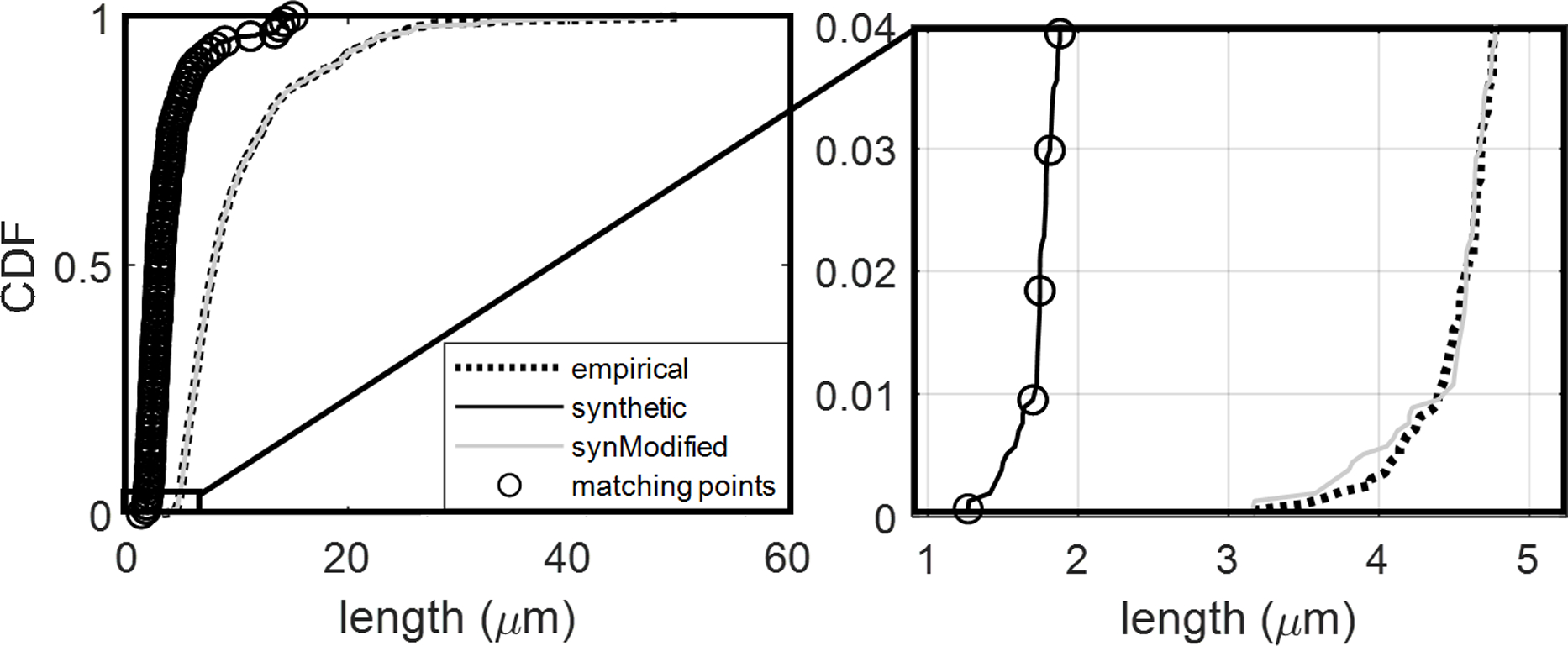
Illustration of unsupervised spectrum matching method for CDFs of two datasets. The original synthetic length spectra (black solid line) shows a known degree of mismatch when compared to the target (dotted black line). When the length is matched at points designated by the black circles (N=101 points), the adjusted aVAN (gray solid line) has a much closer match to the experimental VAN CDF. The magnified first few matching points have been visualized for the example used below.
The goal of this algorithm is to modify the aVAN segments so that the new aVAN CDF matches the corresponding VAN CDF. A natural first approach of how to modify the segments in the aVAN is to adjust all vessels by the same amount; for example, making all segments 20% longer. While this is a reasonable approach, the difference between the two CDFs is not a fixed rate, but rather it varies throughout the range of length. For example, the value (x-position) of the first representative point (black circle) in the CDF is 1.3 μm for the aVAN and 3.1 μm in the VAN, which requires the aVAN value of 1.3 to be multiplied by a factor of α=2.385. The second point needs to modify the aVAN value of 1.8 μm by α=3.20 to achieve the VAN value of 4.5 μm. Because the two values of α don’t match (α=2.385 vs α=3.2), a constant value of α is insufficient. For the best match between the aVAN and the VAN counterpart, we propose selecting a series of representative points along the CDF, calculating the value of α to match all representative points, and linearly interpolating the value of α for all other points in the CDF (=points that lie between the representative points).
We also observe that the experimental VANs reveal highly tortuous (curved) segments, whereas the iCNS algorithm generates only straight segments (no tortuosity). Thus, we opted to add tortuosity to existing vessels in the network as previously described [11] until the aVANs resembled experimental VANs. This was programmatically accomplished by first calculating the necessary adjustments to match the length CDFs between the aVAN and the VAN counterpart. Then, the tortuosity CDF was matched between the aVAN and the VAN. By sorting the length adjustments, the tortuosity can be applied to the appropriate segments with the smallest tortuosity applied to segments that are already the correct length and the highest tortuosity is added to vessels having the largest length disparity.
Appendix E. Implementation iCNS for synthesis of the cerebral circulation
In this section we will describe implementation details for the synthesis of the entire cerebral circulation. The iCNS algorithm can either grow two simultaneous trees (arteries and veins) into each other or it can grow all trees independently and only join the arteries with the veins prior to the closure stage. We will describe the synthesis for the hemisphere, as the cortical subsections (aVANs) are merely simplified cases of the hemisphere.
The synthesis of the murine hemisphere involves independently synthesizing three arterial trees and one venous tree prior to the closure stage. Each tree is synthesized following:
Load the Circle of Willis
Create/load a backbone of main blood vessels
Set the depth of cortex
Calculate the surface area and volume of the territory
Calculate the number of segments to grow at each stage
Synthesize pial segments
Synthesize long penetrators
Synthesize pre-capillary arterioles (or post-capillary venules when growing veins)
Synthesize a portion of the capillary bed
Synthesize short penetrators
Synthesize the remaining capillaries
After steps (i)-(xi) have been completed for all trees, step (xii) commences which synthesizes the closure while adhering to the condition that arterial terminals can only attach to venous segments (and likewise venous terminals can only attach to arterial segments).
Each synthesis stage is controlled by choosing proper constraints, sample generators, and the number of vessels. In Table E1, we show how the same procedure (growNSegments) can be called to synthesize the vessels in each stage. Each stage is defined by a sample generator, constraints, and the number of segments to grow and the backbone for the tree can be grown using the list of point coordinates (ptCoordMx) and the connectivity which can be defined from a reconstruction or a simple hard-coded segment. With this design, the same procedure can be called with different inputs at each stage during growth. The choice of sample generators dictates where the new terminal points will be generated, thus controlling the new segments in the domain. We note that the prismSampleGenerator may be replaced with analytic samplers such as a hexahedronSampleGenerator or a sphericalSampleGenerator when appropriate.
The synthesis of pial vessels was covered extensively in part I of this series but in short, it uses classic CCO principles and a planarTriangleSampleGenerator to generate samples adhering to the STL mesh of the cortical surface. This can be replaced with the analytic hexahedralSampleGenerator with a very shallow depth when growing in a hexahedral domain (such as replicating a cortical VANs). We enforce the desired number of penetrating vessels by expanding the pial network until the number of terminals matches the specified number of penetrators (long + short penetrators). We calculated a density of 6.7±1.6 nsgm/mm2 long and 9.4±5.3 nsgm/mm2 short arterial penetrators from the Kleinfeld datasets (see Section 3.1 for more information on this choice).
After the pial vessel density is reached, the perpendicularPrismSampleGenerator is set and the penetrating vessels are formed by connecting a perpendicular sample point directly to a pial terminal. The capillaries are then formed using a volumeSampleGenerator which samples evenly throughout the space. Once the trees are completed, the closure stage creates two instances of a sampleGeneratorFromPointCoordinateList that are populated from the open terminals of the arterial and venous networks. Typical constraints used in each stage of synthesis to recreate Kleinfeld-like networks are listed in Table E2.
Table E1.
Code progression of the iCNS algorithm during staged growth.
| growNSegments(SG, nSgm, constraints) | SG = sampleGeneratorFromPtCoordList(PtCoordMx, connectivity) | Backbone |
| nSgm = length(connectivity) | ||
| Constraints = newList() | ||
| growNSegments(SG, nSgm, constraints) | SG = surfaceSampleGenerator(surfaceMesh, meshGroupID) | Pials |
| nSgm = (surfaceArea*penetratorDensity)*2 | ||
| constraints = newList([maxL, minL, minAngle, maxAngle]) | ||
| growNSegments(SG, nSgm, constraints) | pialTerminals = terminals | Long Penetrators |
| SG = perpendicularPrismSampleGenerator(surfaceMesh, meshGroupID, corticalDepth, terminals) | ||
| nSgm = longPenetratorDensity*corticalSurfaceArea | ||
| constraints = newList([maxL, minL, minAngle, maxAngle]) | ||
| growNSegments(SG, nSgm, constraints) | SG = prismSampleGenerator(surfaceMesh, meshGroupID, corticalDepth) | Capillaries |
| nShortPenetrators = shortPenetratorDensity*corticalSurfaceArea | ||
| nRemainingVessels = vesselDensity*corticalVolume − currentVesselCount − nShortPenetrators | ||
| nSgm = (nRemainingVessels/3) //2 new vessels for each terminal + 1 new vessel for closure | ||
| constraints = newList([maxLength, minLength, minNSL]) | ||
| growNSegments(SG, nSgm, constraints) | nSgm = shortPenetratorDensity*corticalSurfaceArea | Short Penetrators |
| SG = perpendicularPrismSampleGenerator (surfaceMesh, meshGroupID, corticalDepth, terminals | ||
| constraints = newList([maxL, minL, minAngle, maxAngle]) | ||
| growNSegments(SG, nSgm, constraints) | SG = prismSampleGenerator(surfaceMesh, meshGroupID, corticalDepth) | Capillaries |
| nRemainingVessels = vesselDensity*corticalVolume − currentVesselCount | ||
| nSgm = (nRemainingVessels/3) //2 new vessels for each terminal + 1 new vessel for closure | ||
| constraints = newList([maxL, minL, minNSL]) | ||
| growNSegments(SG, nSgm, constraints) | terminalPtCoords = getPtCoords(nwk.Terminals) | Closure |
| SG = sampleGeneratorFromPtCoordList(terminalPtCoords, null) | ||
| nClosures = nTerminals | ||
| constraints = newList([maxAngle, maxL, minL, minNSL]) | ||
Table E2.
Typical constraints used in synthesizing cortical microvascular structures
| Stage | maxL (μm) | minL (μm) | minAngle (°) | maxAngle (°) | minNSL (μm) | maxNSL (μm) |
|---|---|---|---|---|---|---|
|
| ||||||
| Backbone | NA | NA | NA | NA | NA | NA |
| Pials | NA | 10 | NA | 90 | 30 | NA |
| Long penetrators | NA | NA | 80 | 100 | 0.45 · CD | 0.9 · CD |
| Capillaries | 100–200 | 50–100 | NA | NA | 245–520 | NA |
| Short penetrators | NA | NA | 85 | 95 | 0.1 · CD | 0.35 · CD |
| Capillaries | 7–100 | 5–50 | NA | NA | 123–245 | NA |
| Closure | 80 | 5 | 15 | 180 | 5 | NA |
- CD: cortical depth, NSL: new segment length, L: length (new segment or existing segment), NA: not used
During capillary synthesis, the most restrictive constraints are set while growing the first capillaries. In the capillary growth stage, it is possible to relax the volume optimization principle to place the optimal bifurcation point without the need for rigorous optimization which can become time consuming. On the other hand, we believe that the requirement to balance the tree to maintain equal blood flow in terminals is important to achieve realistic perfusion patterns. Accordingly, we employ CCO logic in the capillary growth stage, but optionally relax the volume optimization objective by placing the bifurcation point at preset coordinates using heuristic rules (for example, at the midpoint of the shortest segment). The diameter computation for the entire tree is still calculated recursively with Murray’s law (or if desired by constant shear stress assumptions) as described in Appendix C.
As the trees expand, the constraints are relaxed because the space becomes more densely populated with vessels and appropriate connections become harder to find. We also note that the closure stage must be allowed to relax the constraints. This is because the sampleGeneratorFromPointCoordinateList must use all the predefined points and cannot disregard any sample due to constraints. The workflow diagram for simultaneous and independent tree growth is given in Figure E1. The inventory of synthetic structures is listed in Table A1.
Figure E1.
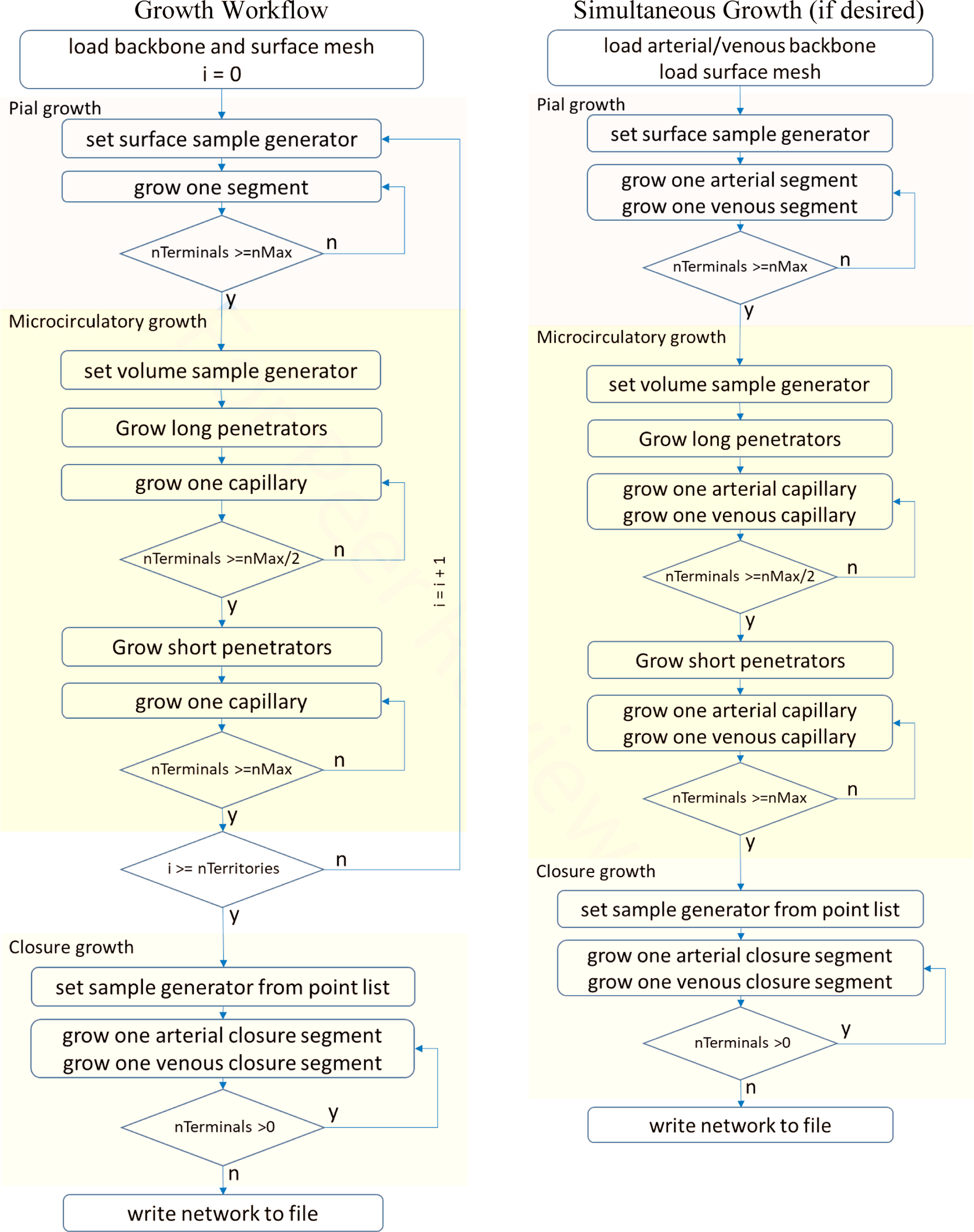
Workflow diagram of staged growth. Left) The growth algorithm reflects two stages for penetrator growth to ensure a structural match to the empirical networks. Right) The simultaneous growth (arteries and veins simultaneously) can be used to enforce a non-intersection constraint if desired.
Appendix F: Characterization of the capillary bed
Figure F1.
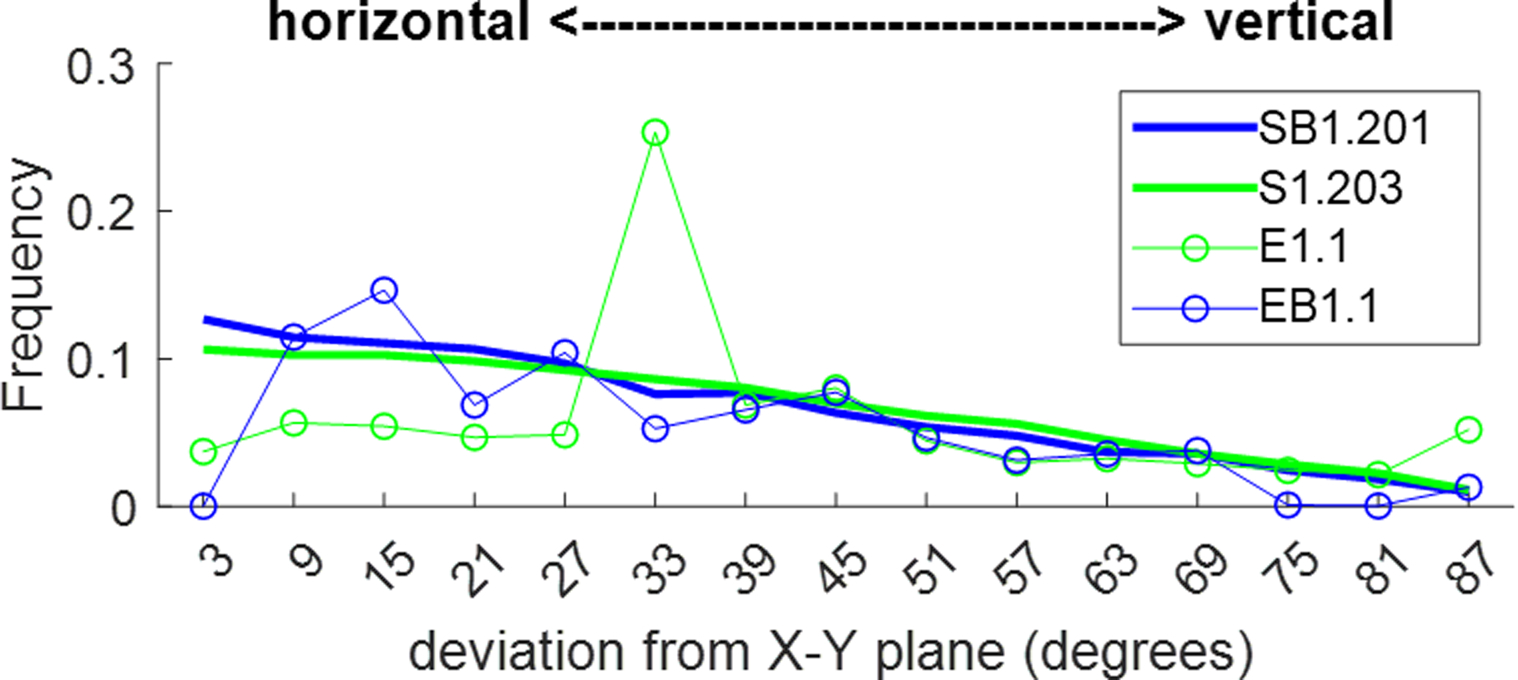
Preliminary investigation of vertical aligment bias in empirical and synthetic networks. The empirical network E1.1 shows a significant peak around 33° while EB1.1 shows a valley (no occurrence) at <5°. The current space-filling algorithm for assigning the capillaries follows a slight tendancy towards horizontal with very little bias towards vertical connectivity. This is a point to investigate in depth in future work.
Appendix G: Synthetic network hemodynamic performance
We conducted hemodynamics simulations to assess the total blood flow resistance in the empirical and synthetic data sets. For this purpose, the pressure drop between pial arterial input and pial venous outflow was varied over a wide range from 55–155 mmHg. The total flow was computed using techniques discussed elsewhere [18]. The resulting perfusion was plotted as a function of pressure drop across the network. Figure G1 shows that the flow-pressure relationship is almost linear despite the complex cortical network configuration in the empirical networks. The slope in the flow/pressure trends is indicative of the total resistance of the entire VAN. It can be seen that the total resistances in the three VANs reported are similar. The fourth empirical sample also reflects this similarity but was not reported here, because it exhibited a 30% lower resistance than the other samples of its cohort, with several other properties lying outside the rest of the cohort as reported previously [13].
Moreover, the variability between the synthetic and its empirical twin, with an average of 9.93% deviation at 0.5 frequency of the CDF (as described in Section 3.2), is less than the variance between the empirical data sets to the same cohort, with an average of 19.9% deviation.
Finally, the plots the normalize flow pressure relationships demonstrating that the flow and pressure relationship between different sets empirical and synthetic are in excellent agreement. These preliminary simulations confirm the hemodynamics equivalence of the empirical data sets and their synthetic clones.
Figure G1.
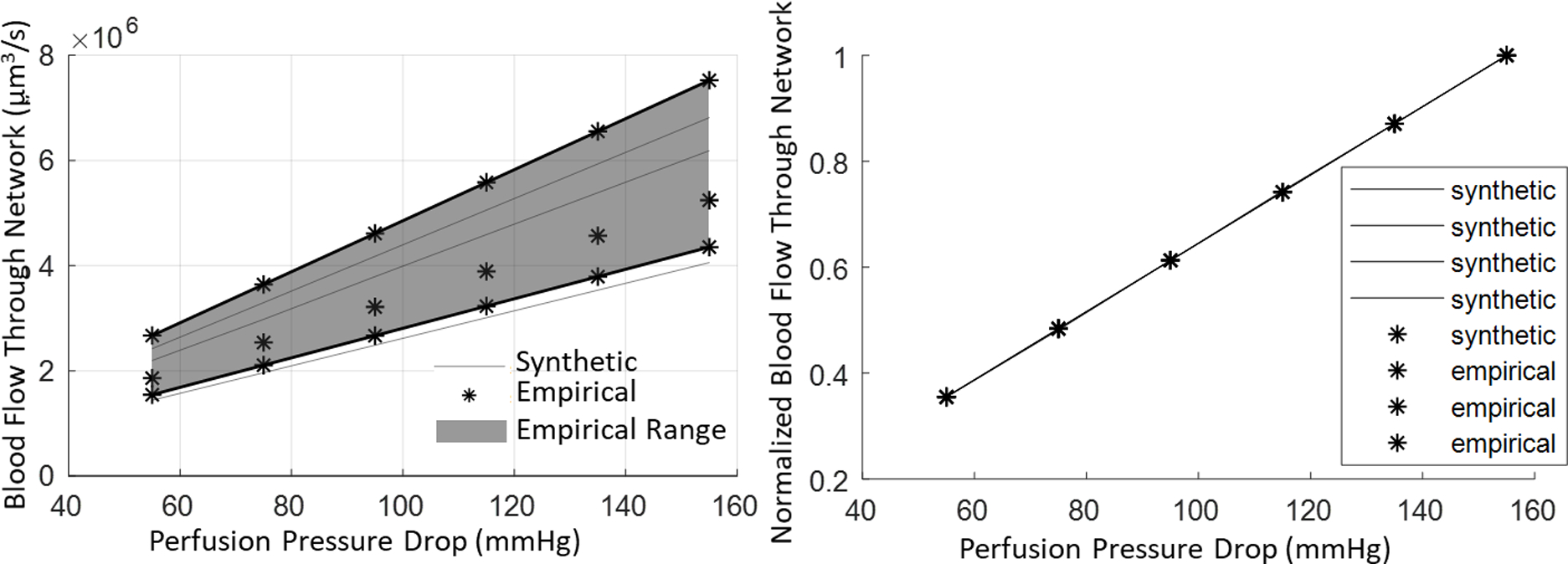
Perfusion flow rates of synthetic networks and their empirical counterparts across parametrically varied perfusion pressures. (Left) By varying the pressure, we are able to see similar performance between the empirical and synthetic VANs, where the synthetic networks receive reasonable flows when compared to their empirical counterparts. (Right) The normalized perfusion flow reflects excellent similarity between the VAN performance during pressure variability. (Normalized flow is computed as the total predicted perfusion divided by the hypothetical perfusion at 155 mmHg pressure drop as reference).
Appendix H: Implementation of double bifurcation closure.
The steps of the double bifurcation closure include: (I) selecting an open terminal, (II) identifying a list of near-neighborhood segments from the opposing tree, (III) choosing the two (2) closest segments from the list that fit all constraints (minimum length, maximum length, bifurcation angle, etc.), (IV) adding a segment between the terminal and the first of the two chosen segments on the other tree, (V) calculating the new bifurcation position using optimization or a geometric heuristic as described in Section 2.2, and finally (VI) repeating steps (IV) and (V) to attach the terminal to the second of the two chosen segments on the opposing tree. Steps (I) - (VI) are executed for each terminal on both trees (arteries and veins).
A pseudocode for these steps is given in Table 1. Specifically, in line 2, we use the sample generator described in part I of this manuscript that generates a sample point from the list of terminals from the opposing tree. In line 3 the two segments of the opposing tree are chosen as described in steps (II)-(III). Then, in lines 4 and 5, each of these two segments are attached using the add_fork routine which executes steps (IV)-(V). This routine entails adding a new segment between the current segment and a point (in this case the terminal point of the arterial tree). This process can attach to the segment either with or without optimization but must always adhere to the list of constraints. Once the terminal has been attached to both close segments of the opposing tree, the terminal is removed from the sample generator list and the vessel calipers are recalculated. This process is repeated for all terminals in both trees. After all terminals of both trees are closed, the resulting vascular network reflects a fully connected aVAN complete with arteries, veins, and a physiologically consistent capillary bed.
Table H 1.
Pseudocode for microvascular closure algorithm
| 1. | FOR i = 1 TO nTerminals DO |
| 2. | terminal aT = venTerminalSampleGeneratorList.getSample //arterial terminal |
| 3. | segments vS = choose closest two ∈ close_segment_list(venous_tree, constraintList) |
| 4. | add_fork (venous_tree, aT, vS[0]) // with or without optimizing |
| 5. | add_fork (venous_tree, aT, vS[1]) // with or without optimizing |
| 6. | remove(venTerminalSampleGeneratorList, aT) |
| 7. | balanceTree(venous_tree, d0) // update venous_tree diameter ratios |
| 8. | terminal vT = artTerminalSampleGeneratorList.getSample //venous terminal |
| 9. | segment aS = choose closest two ∈ close_segment_list(arterial_tree, constraintList) |
| 10. | add_fork (arterial_tree, vT, aS[0]) // with or without optimizing |
| 11. | add_fork (arterial_tree, vT, aS[1]) // with or without optimizing |
| 12. | remove(artTerminalSampleGeneratorList, vT) |
| 13. | balanceTree(artery_tree, d0) // update arterial_tree diameter ratios |
| 14. | ENDFOR |
Footnotes
Data and Code Availability Statement
The experimental source data for this study were provided by collaborating labs (co-authors). Experimental sources data can be accessed through the references provided in the methods section and open source public repositories (e.g. https://github.com/BUNPC/VAN_DataSets, https://github.com/LPPDAdmin). Samples of synthetic network data are available at https://github.com/LPPDAdmin
6 Bibliography
- 1.Gagnon L, Smith AF, Boas DA, Devor A, Secomb TW, Sakadžić S. Modeling of Cerebral Oxygen Transport Based on In vivo Microscopic Imaging of Microvascular Network Structure, Blood Flow, and Oxygenation. Front Comput Neurosci. 2016. August;10:00082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gagnon L, Sakadžić S, Lesage F, Musacchia JJ, Lefebvre J, Fang Q, et al. Quantifying the Microvascular Origin of BOLD-fMRI from First Principles with Two-Photon Microscopy and an Oxygen-Sensitive Nanoprobe. J Neurosci. 2015. February 25;35(8):3663–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fang Q, Sakadžić S, Ruvinskaya L, Devor A, Dale AM, Boas DA. Oxygen Advection and Diffusion in a Three Dimensional Vascular Anatomical Network. Opt Express. 2008. October 27;16(22):17530–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ghaffari M, Tangen K, Alaraj A, Du X, Charbel FT, Linninger AA. Large-scale subject-specific cerebral arterial tree modeling using automated parametric mesh generation for blood flow simulation. Comput Biol Med. 2017. December 1;91:353–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ghaffari M, Hsu C-Y, Linninger AA. Automatic reconstruction and generation of structured hexahedral mesh for non-planar bifurcations in vascular networks. In: Computer Aided Chemical Engineering. Elsevier; 2015. p. 635–40. [Google Scholar]
- 6.Ii S, Kitade H, Ishida S, Imai Y, Watanabe Y, Wada S. Multiscale modeling of human cerebrovasculature: A hybrid approach using image-based geometry and a mathematical algorithm. PLoS Comput Biol. 2020;16(6):e1007943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.El-Bouri WK, Payne SJ. Multi-scale homogenization of blood flow in 3-dimensional human cerebral microvascular networks. J Theor Biol. 2015. September 7;380:40–7. [DOI] [PubMed] [Google Scholar]
- 8.Payne SJ, El-Bouri WK. Modelling dynamic changes in blood flow and volume in the cerebral vasculature. NeuroImage. 2018. August 1;176:124–37. [DOI] [PubMed] [Google Scholar]
- 9.Park CS, Payne SJ. A generalized mathematical framework for estimating the residue function for arbitrary vascular networks. Interface Focus. 2013;3(2):20120078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Linninger AA, Gould IG, Marinnan T, Hsu C-Y, Chojecki M, Alaraj A. Cerebral Microcirculation and Oxygen Tension in the Human Secondary Cortex. Ann Biomed Eng. 2013. November 1;41(11):2264–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gould IG, Linninger AA. Hematocrit Distribution and Tissue Oxygenation in Large Microcirculatory Networks. Microcirculation. 2015. January 1;22(1):1–18. [DOI] [PubMed] [Google Scholar]
- 12.Gould IG, Tsai P, Kleinfeld D, Linninger A. The capillary bed offers the largest hemodynamic resistance to the cortical blood supply. J Cereb Blood Flow Metab. 2017. January 1;37(1):52–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schmid F, Tsai PS, Kleinfeld D, Jenny P, Weber B. Depth-dependent flow and pressure characteristics in cortical microvascular networks. PLOS Comput Biol. 2017. February 14;13(2):e1005392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.D’Angelo C. Finite element approximation of elliptic problems with Dirac measure terms in weighted spaces: applications to one-and three-dimensional coupled problems. SIAM J Numer Anal. 2012;50(1):194–215. [Google Scholar]
- 15.D’Angelo C, Quarteroni A. On the coupling of 1d and 3d diffusion-reaction equations: application to tissue perfusion problems. Math Models Methods Appl Sci. 2008. August;18(08):1481–504. [Google Scholar]
- 16.Park CS, Payne SJ. Modelling the effects of cerebral microvasculature morphology on oxygen transport. Med Eng Phys. 2016. January 1;38(1):41–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hartung G, Vesel C, Morley R, Alaraj A, Sled J, Kleinfeld D, et al. Simulations of blood as a suspension predicts a depth dependent hematocrit in the circulation throughout the cerebral cortex. PLOS Comput Biol. 2018. November 19;14(11):e1006549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lorthois S, Cassot F, Lauwers F. Simulation study of brain blood flow regulation by intra-cortical arterioles in an anatomically accurate large human vascular network. Part II: Flow variations induced by global or localized modifications of arteriolar diameters. NeuroImage. 2011. February 14;54(4):2840–53. [DOI] [PubMed] [Google Scholar]
- 19.Payne SJ, Oakes CNJ, Park CS. Vasomotion does inhibit mass exchange between axisymmetric blood vessels and tissue. J Theor Biol. 2012. June 7;302:1–5. [DOI] [PubMed] [Google Scholar]
- 20.Peyrounette M, Davit Y, Quintard M, Lorthois S. Multiscale modelling of blood flow in cerebral microcirculation: Details at capillary scale control accuracy at the level of the cortex. PLOS ONE. 2018. January 11;13(1):e0189474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Linninger A, Hartung G, Badr S, Morley R. Mathematical synthesis of the cortical circulation for the whole mouse brain-part I: theory and image integration. Comput Biol Med. 110, 265–275, 2019. [DOI] [PubMed] [Google Scholar]
- 22.Blinder P, Tsai PS, Kaufhold JP, Knutsen PM, Suhl H, Kleinfeld D. The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow. Nat Neurosci. 2013. July;16(7):889–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Perillo EP, Jarrett JW, Liu Y-L, Hassan A, Fernée DC, Goldak JR, et al. Two-color multiphoton in vivo imaging with a femtosecond diamond Raman laser. Light Sci Appl. 2017;6(11):e17095–e17095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kaufhold JP, Tsai PS, Blinder P, Kleinfeld D. Vectorization of optically sectioned brain microvasculature: Learning aids completion of vascular graphs by connecting gaps and deleting open-ended segments. Med Image Anal. 2012. August;16(6):1241–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mihelic S, Sikora W, Hassan A, Williamson M, Jones T, Dunn A. Segmentation-less, automated vascular vectorization robustly extracts neurovascular network statistics from in vivo two-photon images. bioRxiv. 2020; [Google Scholar]
- 26.Hartung G, Alaraj A, Linninger A. Chapter 21 - Walk-In Brain: Virtual Reality Environment for Immersive Exploration and Simulation of Brain Metabolism and Function. In: Martín M, Eden MR, Chemmangattuvalappil NG, editors. Computer Aided Chemical Engineering [Internet]. Elsevier; 2016. [cited 2018 Mar 19]. p. 649–58. (Tools For Chemical Product Design; vol. 39). Available from: http://www.sciencedirect.com/science/article/pii/B9780444636836000216 [Google Scholar]
- 27.Ghanavati S, Yu LX, Lerch JP, Sled JG. A perfusion procedure for imaging of the mouse cerebral vasculature by X-ray micro-CT. J Neurosci Methods. 2014. January 15;221(Supplement C):70–7. [DOI] [PubMed] [Google Scholar]
- 28.Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature. 2006. December 6;445:168. [DOI] [PubMed] [Google Scholar]
- 29.Karch R, Neumann F, Neumann M, Schreiner W. A three-dimensional model for arterial tree representation, generated by constrained constructive optimization. Comput Biol Med. 1999. January;29(1):19–38. [DOI] [PubMed] [Google Scholar]
- 30.Schreiner W. Computer generation of complex arterial tree models. J Biomed Eng. 1993. March 1;15(2):148–50. [DOI] [PubMed] [Google Scholar]
- 31.Schreiner W, Neumann F, Neumann M, Karch R, End A, Roedler SM. Limited Bifurcation Asymmetry in Coronary Arterial Tree Models Generated by Constrained Constructive Optimization. J Gen Physiol. 1997. February 1;109(2):129–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Karch R, Neumann F, Neumann M, Schreiner W. Staged Growth of Optimized Arterial Model Trees. Ann Biomed Eng. 2000. May 1;28(5):495–511. [DOI] [PubMed] [Google Scholar]
- 33.DeFelipe J, Alonso-Nanclares L, I. Arellano J. Microstructure of the neocortex: comparative aspects. J Neurocytol. 2002;31(3–5):299–316. [DOI] [PubMed] [Google Scholar]
- 34.Lefort S, Tomm C, Floyd Sarria J-C, Petersen CCH. The Excitatory Neuronal Network of the C2 Barrel Column in Mouse Primary Somatosensory Cortex. Neuron. 2009. January 29;61(2):301–16. [DOI] [PubMed] [Google Scholar]
- 35.Desai B, Hobbs J, Hartung G, Xu G, Gokaslan ZL, Linninger A, et al. Image-guidance technology and the surgical resection of spinal column tumors. J Neurooncol. 2017. February 1;131(3):425–35. [DOI] [PubMed] [Google Scholar]
- 36.Hartung G, Linninger A. LPPD Vascular Anatomical Network Repository. https://github.com/LPPDAdmin. Chicago, USA; 2020. [Google Scholar]
- 37.Park CS, Hartung G, Alaraj A, Du X, Charbel FT, Linninger AA. Quantification of blood flow patterns in the cerebral arterial circulation of individual (human) subjects. Int J Numer Methods Biomed Eng. 2020;36(1):e3288. [DOI] [PubMed] [Google Scholar]
- 38.Park CS, Alaraj A, Du X, Charbel FT, Linninger AA. An efficient full space-time discretization method for subject-specific hemodynamic simulations of cerebral arterial blood flow with distensible wall mechanics. J Biomech. 2019;87:37–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.El-Bouri WK, Payne SJ. Multi-scale homogenization of blood flow in 3-dimensional human cerebral microvascular networks. J Theor Biol. 2015. September 7;380:40–7. [DOI] [PubMed] [Google Scholar]
- 40.Ii S, Kitade H, Ishida S, Imai Y, Watanabe Y, Wada S. Multiscale modeling of human cerebrovasculature: A hybrid approach using image-based geometry and a mathematical algorithm. PLoS Comput Biol. 2020;16(6):e1007943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Payne SJ. Cerebral Blood Flow and Metabolism: A Quantitative Approach. World Scientific; 2017. [Google Scholar]
- 42.Damseh R, Cheriet F, Lesage F. Modeling the Topology of Cerebral Microvessels Via Geometric Graph Contraction. In: 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI). IEEE; 2020. p. 1004–8. [Google Scholar]
- 43.Li B, Esipova TV, Sencan I, Kılıç K, Fu B, Desjardins M, et al. More homogeneous capillary flow and oxygenation in deeper cortical layers correlate with increased oxygen extraction. Elife. 2019;8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hartung G, Badr S, Moeini M, Lesage F,Kleinfeld D, Alaraj A, et al. (2021) Voxelized simulation of cerebral oxygen perfusion elucidates hypoxia in aged mouse cortex. PLoS Comput Biol 17(1): e1008584. 10.1371/journal.pcbi.1008584, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lemaitre H, Goldman AL, Sambataro F, Verchinski BA, Meyer-Lindenberg A, Weinberger DR, et al. Normal age-related brain morphometric changes: nonuniformity across cortical thickness, surface area and gray matter volume? Neurobiol Aging. 2012;33(3):617–e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cassot F, Lauwers F, Fouard C, Prohaska S, Lauwers-Cances V. A Novel Three-Dimensional Computer-Assisted Method for a Quantitative Study of Microvascular Networks of the Human Cerebral Cortex. Microcirculation. 2006;13(1):1–18. [DOI] [PubMed] [Google Scholar]
- 47.Duvernoy HM, Delon S, Vannson J. Cortical blood vessels of the human brain. Brain Res Bull. 1981;7(5):519–79. [DOI] [PubMed] [Google Scholar]
- 48.Hsu C-Y, Ghaffari M, Alaraj A, Flannery M, Zhou XJ, Linninger A. Gap-free segmentation of vascular networks with automatic image processing pipeline. Comput Biol Med. 2017. March 1;82:29–39. [DOI] [PubMed] [Google Scholar]
- 49.Hsu C-Y, Schneller B, Alaraj A, Flannery M, Zhou XJ, Linninger A. Automatic recognition of subject-specific cerebrovascular trees. Magn Reson Med. 2016. December 27;1(77):398–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Xiong B, Li A, Lou Y, Chen S, Long B, Peng J, et al. Precise Cerebral Vascular Atlas in Stereotaxic Coordinates of Whole Mouse Brain. Front Neuroanat [Internet]. 2017. December 19 [cited 2018 Mar 28];11. Available from: 10.3389/fnana.2017.00128/full [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Miyawaki T, Morikawa S, Susaki EA, Nakashima A, Takeuchi H, Yamaguchi S, et al. Visualization and molecular characterization of whole-brain vascular networks with capillary resolution. Nat Commun. 2020;11(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]


