NUCLEAR ENHANCEMENT OF THE PHOTON YIELD IN COSMIC RAY INTERACTIONS

Abstract

The concept of the nuclear enhancement factor has been used since the beginning of γ-ray astronomy. It provides a simple and convenient way to account for the contribution of nuclei (A > 1) in cosmic rays (CRs) and in the interstellar medium (ISM) to the diffuse γ-ray emission. An accurate treatment of the dominant emission process, such as hadronic interactions of CRs with the ISM, enables one to study CR acceleration processes and CR propagation in the ISM, and provides a reliable background model for searches of new phenomena. The Fermi Large Area Telescope launched in 2008 provides excellent quality data in a wide energy range 30 MeV–1 TeV where the diffuse emission accounts for the majority of photons. Exploiting its data to the fullest requires a new study of the processes of γ-ray production in hadronic interactions. In this paper we point out that several commonly used studies of the nuclear enhancement factor fail to account for the spectrally averaged energy loss fraction which ensures that the energy fraction transferred to photons is averaged properly with the spectra of CR species. We present a new calculation of the spectrally averaged energy loss fraction and the nuclear enhancement factor using the QGSJET-II-04 and EPOS–LHC interaction models.

1. INTRODUCTION

Launched in 2008, the γ-ray telescope Fermi Large Area Telescope provides excellent statistics together with superior angular and energy resolution in a wide energy range from 30 MeV–1 TeV (Atwood et al. 2009). This energy range is dominated by the diffuse Galactic emission, which is the brightest source on the γ-ray sky. Studies of the diffuse γ-ray emission and extended sources provide invaluable information about cosmic ray (CR) intensities and spectra in distant locations. Understanding the diffuse emission enables us to study particle acceleration processes and CR propagation in the interstellar medium (ISM), and disentangle new phenomena and/or exotic signals (Strong et al. 2007; Su et al. 2010; Ackermann et al. 2012).

The continuous γ-ray emission is generated mainly through the decay of neutral pions and kaons produced in hadronic CR interactions with the ISM, inverse Compton scattering of CR electrons off interstellar photons, and bremsstrahlung. The nuclear component of CRs is dominated by protons, but heavier nuclei also provide an essential contribution to the γ-ray yield. The latter depends on the energy range and on the spectra of the CR species. However, CR spectra and abundances could vary in different locations making an accurate evaluation of their contribution to the γ-ray yield rather difficult.

In all studies of the diffuse γ-ray emission, the effects of heavier nuclei (A > 1) in CRs and in the target material are usually taken into account by simply rescaling the γ-ray yield from pp-interactions to the CR-ISM γ-ray yield with a so-called nuclear enhancement factor ε_M. While such a rescaling is a convenient approximation, application of a single enhancement factor in many cases could result in significant errors. In fact, there is no a universal enhancement factor as the rescaling factor depends on the abundances of CRs and the ISM, on the individual spectral shapes of CR species, and on the kinematics of the processes involved, e.g., pA versus Ap yields.

γ-ray production in pp-interactions has been studied in the past using model fits to the data (Stecker 1973, 1989; Stephens & Badhwar 1981; Dermer 1986a, 1986b), and Monte Carlo simulations (Mori 1997, 2009; Kamae et al. 2006; Kachelrieß & Ostapchenko 2012). The values of the nuclear enhancement factor derived by different authors vary from 1.45–2.0, due to the differences in the description of pp-interactions, nuclei abundances, and the scaling formalism. The dependence of ε_M on the spectral shapes of CR species was always neglected, except for a trivial dependence on the relative abundances of CR nuclei. Since the γ-ray data become rather accurate, a new study of the nuclear enhancement factor is warranted.

In this work we study how the spectral shape of the CR species and the kinematics of the processes affect ε_M. We use the QGSJET-II-04 event generator, which accurately reproduces accelerator data (Ostapchenko 2011), to simulate pp-, pA-, and AA-interactions, and compare the results with the most recent calculation by Mori (2009) and with another event generator EPOS-LHC (Pierog et al. 2013) tuned to the data of the Large Hadron Collider (LHC).

2. NUCLEAR ENHANCEMENT FACTOR

The photon yield $q_{\gamma }^{ij}\left(E_{\gamma }\right)$. from scattering of CR species of type i with differential intensity⁴I_i(E) on a target of type j of density n_j is given by

$$q_{\gamma }^{ij}\left(E_{\gamma }\right)=n_j{\int }_{E_{\gamma }}^{\infty }dE\frac{d{\sigma }^{ij\to \gamma }\left(E,E_{\gamma }\right)}{d{E}_{\gamma }}{I}_i(E),$$ (1)

where dσ^ij→γ (E, E_γ)/dE_γ is the differential inclusive cross section for photon production. For a power-law spectrum, $I_i(E)=K_i{E}^{-{\alpha }_i}$, introducing the energy fraction taken by γ-rays, z = E_γ/E, and the spectrally averaged moment

$$Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)={\int }_0^{1}dz{z}^{\alpha -1}\frac{d{\sigma }^{ij\to \gamma }\left(E_{\gamma }/z,z\right)}{dz},$$ (2)

we can rewrite the photon yield from channel ij as

$$q_{\gamma }^{ij}\left(E_{\gamma }\right)=n_j{I}_i\left(E_{\gamma }\right)Z_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right).$$ (3)

Note that in Equation (3) we evaluate the CR intensity I_i(E) at the photon energy E_γ.

To compare with the most recent approach of Mori (2009), we can factorize out the inelastic cross section ${\sigma }_{\text{inel}}^{ij}(E)$ and the photon multiplicity $N_{\gamma }^{ij}(E)$ from the definition of the moment, i.e., we define⁵

$${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)=\frac{Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)}{{\sigma }_{\text{inel}}^{ij}\left(E_{\gamma }\right)N_{\gamma }^{ij}\left(E_{\gamma }\right)},$$ (4)

with

$$N_{\gamma }^{ij}(E)={\int }_0^{1}dz{f}_{ij\to \gamma }(E,z).$$ (5)

Here we introduced also the normalized (per inelastic event) photon energy distribution

$$f_{ij\to \gamma }(E,z)=\frac{1}{{\sigma }_{\text{inel}}^{ij}(E)}\frac{d{\sigma }^{ij\to \gamma }(E,z)}{dz}.$$ (6)

If the inclusive photon cross section satisfied Feynman scaling,

$$\frac{d{\sigma }^{ij\to \gamma }(E,z)}{dz}=F(z),$$ (7)

${\tilde{Z}}^{ij}=1$ would hold for the particular case α = 1; on the other hand, for α = 2, ${\tilde{Z}}^{ij}$ would correspond to the average energy fraction taken by a produced photon (cf. Equations (2) and (4)–(7)).

We can now rewrite the photon yield from a channel ij as

$$q_{\gamma }^{ij}\left(E_{\gamma }\right)=n_j{I}_i\left(E_{\gamma }\right){\sigma }_{\text{inel}}^{ij}\left(E_{\gamma }\right)N_{\gamma }^{ij}\left(E_{\gamma }\right){\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right).$$ (8)

It is easy to see from Equation (8) that the photon yield is not just proportional to the inelastic cross section ${\sigma }_{\text{inel}}^{ij}\left(E\right)$ and the number $N_{\gamma }^{ij}\left(E\right)$ of photons produced per interaction, but depends rather on the spectrally averaged energy fraction transferred to photons—via the “Z-factors” defined in Equations (2) and (4). Thus, the yield generally depends on both the production spectrum of photons from a channel ij and the spectrum of CR species $I_i(E)\propto E^{-{\alpha }_i}$—the steeper the spectrum and the smaller the average energy fraction 〈z〉 transferred to photons, the smaller ${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right)$ is and thus the photon yield.

The nuclear enhancement factor ε_M due to the admixture of nuclei in CRs and in the ISM is determined by

$$\begin{gathered} {\epsilon }_{\text{M}}=1+\sum _{i+j>2}{\epsilon }_{ij}=1+\sum _{i+j>2}\frac{n_j{I}_i\left(E_{\gamma }\right)Z_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right)}{n_p{I}_p\left(E_{\gamma }\right)Z_{\gamma }^{pp}\left(E_{\gamma },{\alpha }_p\right)} \\ =1+\sum _{i+j>2}\frac{n_j{I}_i\left(E_{\gamma }\right)}{n_p{I}_p\left(E_{\gamma }\right)}\frac{{\sigma }_{\text{inel}}^{ij}}{{\sigma }_{\text{inel}}^{pp}}\frac{N_{\gamma }^{ij}}{N_{\gamma }^{pp}}\frac{{\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right)}{{\tilde{Z}}_{\gamma }^{pp}\left(E_{\gamma },{\alpha }_p\right)} \\ =1+\sum _{i+j>2}\frac{n_j{I}_i\left(E_{\gamma }\right)}{n_p{I}_p\left(E_{\gamma }\right)}{m}_{ij}^{\gamma }\left(E_{\gamma }\right)C_{ij}\left(E_{\gamma },{\alpha }_i,{\alpha }_p\right), \end{gathered}$$ (9)

where we introduced also the individual contributions ${\epsilon }_{ij}\left(E_{\gamma }\right)=q_{\gamma }^{ij}\left(E_{\gamma }\right)/q_{\gamma }^{pp}\left(E_{\gamma }\right)$ of each channel to ε_M, the ratio of inelastic cross sections and multiplicities

$$m_{ij}^{\gamma }(E)=\frac{{\sigma }_{\text{inel}}^{ij}(E)}{{\sigma }_{\text{inel}}^{pp}(E)}\frac{N_{\gamma }^{ij}(E)}{N_{\gamma }^{pp}(E)},$$ (10)

and the ratio of the Z-factors $C_{ij}\left(E_{\gamma },{\alpha }_i,{\alpha }_p\right)={\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },{\alpha }_i\right)/{\tilde{Z}}_{\gamma }^{pp}\left(E_{\gamma },{\alpha }_p\right)$. Note that the correction factors C_ij, which depend both on the energy distribution of the produced photons and on the slopes of the primary CR spectra, were missing in the definition of ε_M used by Mori (2009). As a consequence, the contributions of CR nuclei with A > 1 to the nuclear enhancement factor should deviate from the results obtained in that study. Indeed, as noted above, the correction factors C_ij disappear from Equation (9) only for the (unrealistic) assumption of the validity of Feynman scaling and for the (impractical) case of α = 1. On the other hand, for steeply falling spectra, such as in the case of Galactic CRs, α ≫ 1, the region of large z gives the dominant contribution to the integral defining $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$, i.e., it is the photon spectral shape in the very forward direction, rather than the photon multiplicity $N_{\gamma }^{ij}$, which dominates $Z_{\gamma }^{ij}$.

To illustrate the latter point, let us compare the factors $m_{ij}^{\gamma }(E)$ (Equation (10)) and the ratios $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)/Z_{\gamma }^{pp}\left(E_{\gamma },\alpha \right)$ for α ≫ 1, for the cases of nucleus–proton (j = p) and proton–nucleus (i = p) interactions. While $m_{pj}^{\gamma }=m_{jp}^{\gamma }$ by virtue of the Lorentz invariance, the behavior of $Z_{\gamma }^{ip}$ can be understood from the well-known relation (see Białas et al. 1976) for the mean number of interacting (“wounded”) projectile nucleons $\langle n_{{\mathrm{w}}_{\text{p}}}^{ij}\rangle$ in nucleus–nucleus collisions:

$$\langle n_{{\mathrm{w}}_{\text{p}}}^{ij}(E)\rangle =\frac{i{\sigma }_{\text{inel}}^{pj}(E)}{{\sigma }_{\text{inel}}^{ij}(E)},$$ (11)

which holds both in the Glauber approach and in the Reggeon field theory, if one neglects the contribution of target diffraction, as demonstrated by Kalmykov & Ostapchenko (1993). This leads, in turn, to an approximate superposition picture for the forward (z → 1) spectra of secondary photons:

$$\begin{gathered} \frac{d{\sigma }^{ij\to \gamma }(E,z)}{dz}={\sigma }_{\text{inel}}^{ij}(E)f_{ij\to \gamma }(E,z) \\ \underset{z\to 1}{\to }{\sigma }_{\text{inel}}^{ij}(E)\left[\langle n_{{\mathrm{w}}_{\text{p}}}^{ij}(E)\rangle f_{pj\to \gamma }(E,z)\right] \\ =i\frac{d{\sigma }^{pj\to \gamma }(E,z)}{dz}, \end{gathered}$$ (12)

which thus gives $Z_{\gamma }^{jp}/Z_{\gamma }^{pp}\simeq j>m_{pi}^{\gamma }$ for α_j = α_p = α ≫ 1 (cf. Equation (2)). On the other hand, assuming that in proton–nucleus and proton–proton interactions the shapes of the photon production spectra are similar in the forward direction, i.e., f_pj→γ (E, z) ≃ f_pp→γ (E, z) at large z, one obtains⁶

$$\frac{Z_{\gamma }^{pj}}{Z_{\gamma }^{pp}}\simeq \frac{{\sigma }_{\text{inel}}^{pj}}{{\sigma }_{\text{inel}}^{pp}}<m_{pj}^{\gamma }.$$ (13)

Thus, CR nuclei generally provide a larger contribution to the nuclear enhancement factor ε_M, compared to previous calculations based on $m_{ij}^{\gamma }$, while the opposite is true for the contribution of nuclear species from the ISM.

3. NUMERICAL RESULTS

The normalized Z-factors ${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$ were calculated using the QGSJET-II-04 model by Ostapchenko (2011). Table 1 compares the dependence of ${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$ on the CR spectral index α for different production channels ij → γ for two photon energies E_γ = 10 and 100 GeV. Note that ${\tilde{Z}}_{\gamma }^{ij}$ (cf. Equation (4)) specifies the difference between the factor $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$, which defines the partial photon yield from the channel ij →γ, and the product ${\sigma }_{\text{inel}}^{ij}\left(E_{\gamma }\right)N_{\gamma }^{ij}\left(E_{\gamma }\right)$.

Table 1.

Normalized Z-factors ${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$ Calculated with QGSJET-II-04

Reaction	α = 1.5	α = 2	α = 2.5	α = 3	α = 3.5	α = 4
Eγ = 10 GeV
p p → γ	6.3 × 10−1	8.6 × 10−2	2.3 × 10−2	8.3 × 10−3	3.6 × 10−3	1.8 × 10−3
p He → γ	6.3 × 10−1	8.3 × 10−2	2.1 × 10−2	7.5 × 10−3	3.2 × 10−3	1.6 × 10−3
He p → γ	6.7 × 10−1	9.4 × 10−2	2.5 × 10−2	9.3 × 10−3	4.1 × 10−3	2.1 × 10−3
He He → γ	6.8 × 10−1	9.0 × 10−2	2.3 × 10−2	8.4 × 10−3	3.6 × 10−3	1.8 × 10−3
Eγ = 100 GeV
p p → γ	2.9 × 10−1	3.5 × 10−2	8.4 × 10−3	2.8 × 10−3	1.2 × 10−3	5.7 × 10−4
p He → γ	2.8 × 10−1	3.2 × 10−2	7.4 × 10−3	2.4 × 10−3	1.0 × 10−3	4.8 × 10−4
He p → γ	3.0 × 10−1	3.7 × 10−2	9.0 × 10−3	3.0 × 10−3	1.3 × 10−3	6.2 × 10−4
He He → γ	2.9 × 10−1	3.4 × 10−2	7.9 × 10−3	2.6 × 10−3	1.1 × 10−3	5.1 × 10−4

It is clear that ${\tilde{Z}}_{\gamma }^{ij}$ decreases strongly for steeper spectral slopes. This is not surprising since the ratio $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)/{\sigma }_{\text{inel}}^{ij}\left(E_{\gamma }\right)$ corresponds to a spectrally averaged fraction of the primary energy, z = E_γ/E, taken by the produced photons, rather than to the photon multiplicity—the steeper the spectral slope, the smaller the part of the very forward production spectrum of photons f_ij→γ (z) that contributes to the integral in Equation (2). This explains also why ${\tilde{Z}}_{\gamma }^{ij}$ decreases with energy, especially for large α. For relatively small α, the integral in Equation (2) receives a noticeable contribution from the region of small z, which corresponds to the central rapidity plateau in the center-of-mass frame for the given process and which is responsible for the rise of the photon multiplicity $N_{\gamma }^{ij}(E)$ with energy due to the violation of Feynman scaling for f_ij→γ (E, z) at small z. However, for large α the ratio $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)/{\sigma }_{\text{inel}}^{ij}\left(E_{\gamma }\right)$ is governed by the energy dependence of the production spectrum f_ij→γ (E, z) at z → 1, which satisfies approximately Feynman scaling. For α ≫ 1 this leads to⁷

$$\frac{{\tilde{Z}}_{\gamma }^{ij}\left(E_2,\alpha \right)}{{\tilde{Z}}_{\gamma }^{ij}\left(E_1,\alpha \right)}\propto \frac{N_{\gamma }^{ij}\left(E_1\right)}{N_{\gamma }^{ij}\left(E_2\right)},$$ (14)

i.e., ${\tilde{Z}}_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$ decreases with energy inversely proportional to the photon multiplicity in the process.

For practical applications, more important are the ratios $Z_{\gamma }^{ij}/Z_{\gamma }^{pp}$ that enter the expressions for the partial contributions ε_ij to the nuclear enhancement factor in Equation (9). The respective results for different production channels and for different spectral indices calculated with QGSJET-II-04 are compiled in Table 2 for E_γ = 10 and 100 GeV; the corresponding ratios $m_{ij}^{\gamma }$ of inelastic cross sections and multiplicities (Equation (10)) are also shown for comparison. These results confirm our qualitative expectations from the previous section—the actual enhancement factor for He+p collisions, compared to the pp case, is noticeably higher than estimated from $m_{\text{He}p}^{\gamma }$, while for p+He interactions the opposite is true. Obviously, the discussed trends are stronger for steeper CR spectra (larger α) due to the increasing dominance of the very forward part of the photon production spectrum. The same qualitative behavior is observed when comparing the ratios $Z_{\gamma }^{ij}/Z_{\gamma }^{pp}$ and the factors $m_{ij}^{\gamma }$, as calculated using the SIBYLL 2.1 (Ahn et al. 2009) and EPOS-LHC (Pierog et al. 2013) models (Table 2), though the numerical results prove to be quite model-dependent.⁸

Table 2.

Ratios $Z_{\gamma }^{ij}/Z_{\gamma }^{pp}$ and $m_{ij}^{\gamma }$ Factors for Different Production Channels ij → γ

	$Z_{\gamma }^{ij}/Z_{\gamma }^{pp}$
Reaction	α = 1.5	α = 2	α = 2.5	α = 3	α = 3.5	α = 4	$m_{ij}^{\gamma }$
	QGSJET-II-04: Eγ = 10 GeV
p He → γ	3.77	3.61	3.47	3.40	3.36	3.34	3.74
He p → γ	4.01	4.11	4.15	4.18	4.22	4.27	3.74
He He → γ	14.0	13.5	13.2	13.0	12.8	12.6	12.9
	QGSJET-II-04: Eγ = 100 GeV
p He → γ	3.72	3.49	3.38	3.31	3.26	3.24	3.85
He p → γ	4.04	4.10	4.13	4.14	4.15	4.16	3.85
He He → γ	13.8	13.2	12.8	12.5	12.3	12.2	13.7
	SIBYLL 2.1: Eγ = 100 GeV
p He → γ	3.54	3.21	3.03	2.91	2.83	2.78	3.71
He p → γ	3.71	3.76	3.77	3.77	3.78	3.79	3.71
He He → γ	11.7	10.7	10.2	9.63	9.35	9.13	12.4
	EPOS-LHC: Eγ = 100 GeV
p He → γ	3.60	3.57	3.45	3.33	3.24	3.18	4.10
He p → γ	3.94	4.20	4.45	4.72	4.89	5.12	4.10
He He → γ	13.5	13.7	13.5	13.3	13.2	13.1	14.6

Table 3 shows Z-factors $Z_{\gamma }^{ij}$ for various channels of photon production in CR interactions. For these calculations we use two up-to-date hadronic interaction models, QGSJET-II-04 and EPOS-LHC. These results can be used for calculations of the nuclear enhancement factor when the combined spectrum of a group of CR nuclei can be approximated by a power law, $I_i(E)=K_i{E}^{-{\alpha }_i}$.

Table 3.

Z-factors $Z_{\gamma }^{ij}\left(E_{\gamma },\alpha \right)$ (mbarn) for Different Production Channels ij → γ

Projectile Nucleus	Target Nucleus	α = 2	α = 2.2	α = 2.4	α = 2. 6	α = 2.8	α = 3
	QGSJET-II-04: Eγ = 10 GeV
p (A = 1)	p	5.45	3.06	1.84	1.17	0.771	0.529
He (A = 4)	p	22.4	12.6	7.62	4.85	3.22	2.21
CNO (A = 14)	p	76.8	43.8	26.6	17.1	11.4	7.89
Mg-Si (A = 25)	p	138	78.9	48.2	31.0	20.7	14.4
Fe (A = 56)	p	298	171	105	67.2	45.0	31.2
p (A = 1)	He	19.7	10.9	6.48	4.07	2.68	1.83
He (A = 4)	He	73.7	41.0	24.4	15.3	10.1	6.86
CNO (A = 14)	He	271	152	91.2	57.7	38.1	26.1
Mg-Si (A = 25)	He	473	266	160	101	66.8	45.7
Fe (A = 56)	He	1010	569	342	216	143	97.5
	QGSJET-II-04: Eγ = 100 GeV
p (A = 1)	p	5.93	3.20	1.86	1.14	0.736	0.492
He (A = 4)	p	24.3	13.1	7.65	4.72	3.04	2.04
CNO (A = 14)	p	83.3	45.4	26.6	16.5	10.7	7.21
Mg-Si (A = 25)	p	149	81.7	48.0	29.8	19.4	13.1
Fe (A = 56)	p	330	181	107	66.7	43.4	29.3
p (A = 1)	He	20.7	11.0	6.33	3.85	2.45	1.63
He (A = 4)	He	78.1	41.7	23.9	14.6	9.29	6.16
CNO (A = 14)	He	285	153	88.6	54.3	34.9	23.3
Mg-Si (A = 25)	He	506	273	159	97.7	63.0	42.2
Fe (A = 56)	He	1100	596	346	213	137	92.1
	QGSJET-II-04: Eγ = 1 TeV
p (A = 1)	p	6.85	3.61	2.05	1.24	0.786	0.519
He (A = 4)	p	28.4	15.0	8.51	5.14	3.26	2.14
CNO (A = 14)	p	95.6	50.6	28.9	17.6	11.2	7.39
Mg-Si (A = 25)	p	174	92.4	53.0	32.3	20.6	13.6
Fe (A = 56)	p	378	202	117	71.3	45.7	30.5
p (A = 1)	He	23.7	12.2	6.83	4.07	2.56	1.67
He (A = 4)	He	89.2	46.1	25.8	15.4	9.66	6.31
CNO (A = 14)	He	321	167	93.5	55.8	35.0	22.9
Mg-Si (A = 25)	He	567	296	167	100	63.3	41.6
Fe (A = 56)	He	1260	660	375	226	143	94.6
	EPOS-LHC: Eγ = 10 GeV
p (A = 1)	p	5.83	3.31	2.00	1.27	0.844	0.578
He (A = 4)	p	26.0	15.0	9.27	6.00	4.04	2.82
CNO (A = 14)	p	89.6	52.3	32.4	21.1	14.3	9.99
Mg-Si (A = 25)	p	156	91.5	57.1	37.4	25.5	18.0
Fe (A = 56)	p	342	203	128	84.6	58.2	41.4
p (A = 1)	He	20.7	11.4	6.68	4.12	2.64	1.75
He (A = 4)	He	82.5	46.3	27.7	17.5	11.5	7.79
CNO (A = 14)	He	309	175	106	67.7	44.9	30.8
Mg-Si (A = 25)	He	562	322	196	126	83.7	57.6
Fe (A = 56)	He	1200	692	424	273	183	128
	EPOS-LHC: Eγ = 100 GeV
p (A = 1)	p	6.34	3.49	2.06	1.29	0.837	0.564
He (A = 4)	p	26.6	14.9	9.01	5.75	3.84	2.66
CNO (A = 14)	p	95.4	54.9	33.8	22.0	15.0	10.6
Mg-Si (A = 25)	p	167	96.2	59.1	38.3	25.9	18.1
Fe (A = 56)	p	373	216	134	87.9	60.0	42.4
p (A = 1)	He	22.6	12.3	7.18	4.44	2.88	1.94
He (A = 4)	He	86.5	47.2	27.7	17.2	11.2	7.60
CNO (A = 14)	He	321	177	105	66.3	43.7	29.9
Mg-Si (A = 25)	He	582	324	193	122	80.2	54.7
Fe (A = 56)	He	1320	744	449	286	190	130
	EPOS-LHC: Eγ = 1 TeV
p (A = 1)	p	7.61	4.15	2.45	1.54	1.01	0.693
He (A = 4)	p	31.1	17.3	10.3	6.51	4.31	2.96
CNO (A = 14)	p	106	60.2	36.7	23.7	16.0	11.3
Mg-Si (A = 25)	p	192	110	68.2	44.7	30.6	21.8
Fe (A = 56)	p	433	253	159	105	73.6	53.1
p (A = 1)	He	25.3	13.4	7.73	4.71	3.01	2.00
He (A = 4)	He	98.3	53.1	31.0	19.2	12.5	8.44
CNO (A = 14)	He	360	197	116	72.7	47.5	32.3
Mg-Si (A = 25)	He	654	361	214	135	88.7	60.6
Fe (A = 56)	He	1480	829	498	317	210	145

As an illustration, we perform a calculation of ε_M in the energy range E_γ = 10–1000 GeV, based on Equation (9), using the high-energy limit of the parameterization of the spectra of groups of CR nuclei by Honda et al. (2004); the respective parameters K_i and α_i are given in Table 4 for convenience. The values of ε_M are given in Table 5 for the two interaction models. As we already emphasized above, our results for partial contributions to the nuclear enhancement factor from proton–nucleus (ε_pj) and nucleus–proton (ε_ip) collisions demonstrate important differences from the approach by Mori (2009) and manifest a significant model dependence (cf. Table 2). However, the respective corrections work in the opposite directions and partly compensate each other. As a consequence, our results for ε_M in this particular case, for both interaction models considered, agree within 5% with those of Mori (2009), who used a different event generator, DPMJET-III.

Table 4.

Spectral Parameterizations for Groups of CR Nuclei (Honda et al. 2004)

	Groups of Nuclei
Parameters	H (A = 1)	He (A = 4)	CNO (A = 14)	Mg-Si (A = 25)	Fe (A = 56)
K	14900	600	33.2	34.2	4.45
α	2.74	2.64	2.60	2.79	2.68

Table 5.

Nuclear Enhancement Factors ε_M Calculated for CR Composition Given in Table 4

	Photon Energy (GeV)
Models	10	100	1000
QGSJET-II-04	1.85	1.95	2.09
EPOS-LHC	1.88	2.02	2.09

Figure 1 shows the energy dependence of the partial contributions ε_ij for p+He, He+p, and He+He channels. It is noteworthy that the smaller index α_He of the He component compared to protons has a twofold impact on ε_{He p} and ε_{He He}: first, the relative abundance of He increases with energy, and, second, the respective Z-factors become larger for smaller α.

Figure 1.

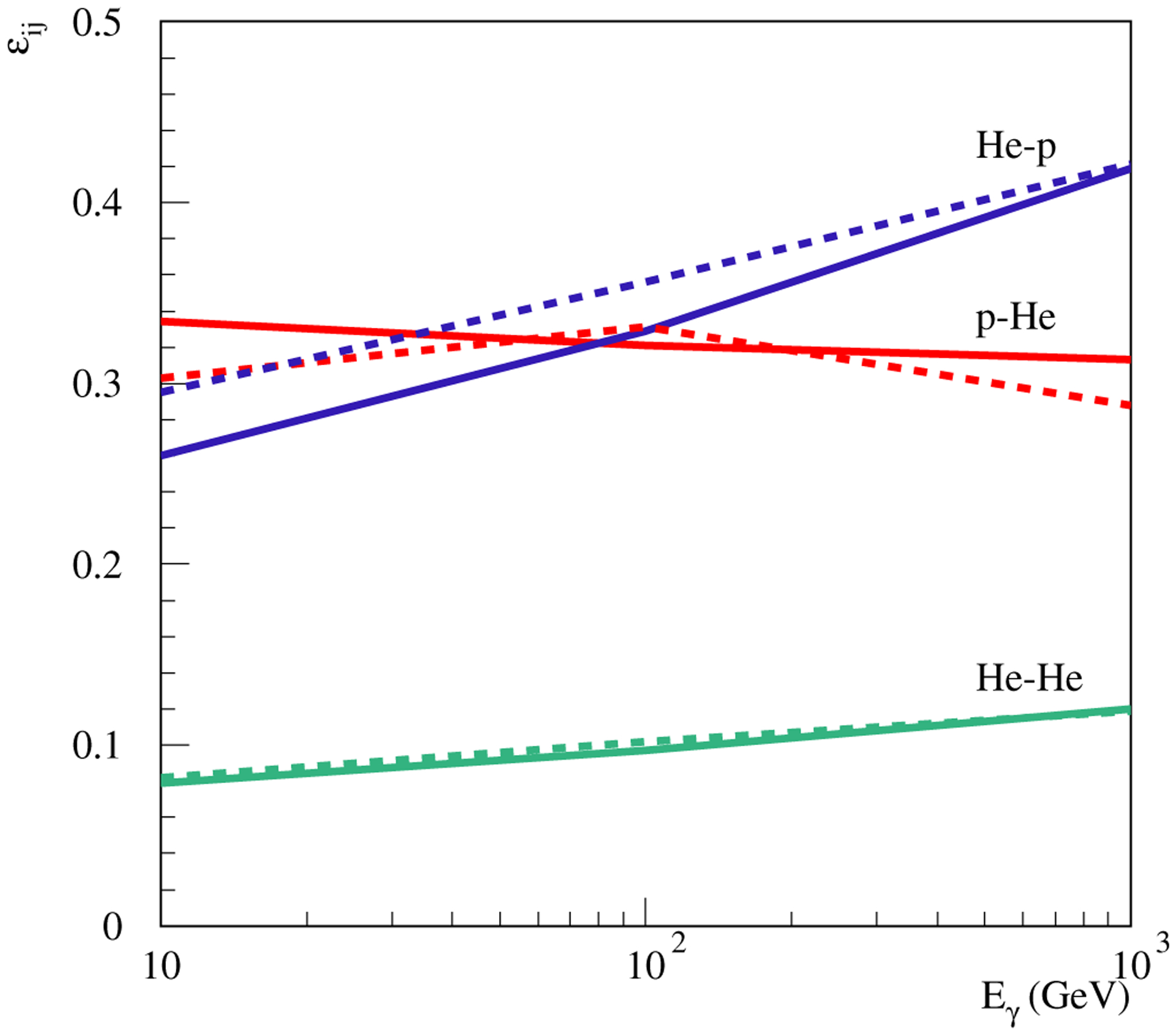
Partial contributions ε_ij to ε_M for several reaction channels, as indicated in the plot, calculated with QGSJET-II-04 (solid lines) and EPOS-LHC (dashed lines) models.

Finally, it is worth stressing that the concept of the nuclear enhancement factor does not work in the case of a sharp change in the CR spectral index, as, e.g., around a spectral break at 230 GV found⁹ in the p and He combined data by ATIC-2 (Panov et al. 2009), CREAM (Yoon et al. 2011), and PAMELA (Adriani et al. 2011). In such a case, a direct convolution of the spectra for different groups of CR nuclei with the respective photon production distributions, as in Equation (1), is more appropriate. Additionally, if such spectral breaks are observed at different energies per nucleon for different groups of nuclei (e.g., Adriani et al. 2011), which is natural to expect from rigidity-dependent processes of CRs acceleration and propagation, one may expect a strong energy dependence of the resulting enhancement factor.

4. CONCLUSION

The concept of the nuclear enhancement factor ε_M provides a simple and convenient way to account for the contribution of heavier nuclei in CRs and in the ISM to the diffuse γ-ray emission. The latter is comparable to the contribution of protons, the most abundant species in CRs and the ISM. We have shown that the value of the enhancement depends strongly on the spectral shapes of CR species: not only via the respective energy dependence of the partial abundances of primary nuclei, but also via the spectrally averaged photon energy fraction. It is the latter point which was missed in previous calculations. The provided tables allow a calculation of ε_M for an arbitrary composition of CRs and the ISM for a reasonably wide range of power-law indices. The results for ε_M agree approximately with calculations by Mori (2009) for the same spectra of CR species (Honda et al. 2004), although we found somewhat larger values of ε_M at energies E_γ > 100 GeV.