Cosmic-Ray Propagation in Light of the Recent Observation of Geminga

Abstract

The High Altitude Water Cherenkov (HAWC) telescope recently observed extended emission around the Geminga and PSR B0656+14 pulsar wind nebulae (PWNe). These observations have been used to estimate cosmic-ray (CR) diffusion coefficients near the PWNe that appear to be more than two orders of magnitude smaller than the diffusion coefficients typically derived for the interstellar medium from measured abundances of secondary species in CRs. Two-zone diffusion models have been proposed as a solution to this discrepancy, where the slower diffusion zone (SDZ) is confined to a small region around the PWN. Such models are shown to successfully reproduce the HAWC observations of the Geminga PWN while retaining consistency with other CR data. It is found that the size of the SDZ influences the predicted positron flux and the spectral shape of the extended γ-ray emission at lower energies that can be observed with the Fermi Large Area Telescope. If the two observed PWNe are not unique, then it is likely that there are similar pockets of slow diffusion around many CR sources elsewhere in the Milky Way. The consequences of such a picture for Galactic CR propagation is explored.

1. Introduction

The sources of majority of cosmic rays (CRs) are believed to be supernovae (SNe) and supernova remnants (SNRs), which are capable of accelerating particles to multi-PeV energies. As CRs propagate through the interstellar medium (ISM), they scatter off the magnetic turbulences in a process that on large scales can be described with a diffusive transport equation (Ginzburg & Syrovatskii 1964; Berezinskii et al. 1990). The spectrum of turbulence controls the value of the diffusion coefficient and its energy dependence because the CR particles most efficiently scatter on turbulence that is comparable in size to their gyroradii. The turbulence is assumed to initially form at large scales and then cascade down to smaller scales, thus affecting particles at all rigidities. The power-law shape of the energy spectrum of turbulence (Kolmogorov 1941; Iroshnikov 1964; Kraichnan 1965) translates into a power-law rigidity dependence of the diffusion coefficient, with the index taking a value between 0.3 and 0.6. Observations of the ratios of stable secondary-to-primary species in CRs and the abundances of radioactive secondaries are usually employed to determine both the power-law index and normalization of the diffusion coefficient averaged over a significant volume of the interstellar space surrounding the solar system (e.g., Strong & Moskalenko 1998; Strong et al. 2007; Jóhannesson et al. 2016), typically several kiloparsec in radius. Recent estimates of the power-law index and normalization vary somewhat depending on the details of the propagation models. Values of the index between ~0.2 and ~0.6 are found with a normalization of a few times 10²⁸ cm² s⁻¹ at a rigidity of 4 GV (e.g., Génolini et al. 2017; Yuan et al. 2017; Boschini et al. 2018a; Wu & Chen 2019).

Pulsars are rapidly spinning and strongly magnetized neutron stars that are at the final stage of the stellar evolution. They are formed in SN explosions and can often be found inside their associated SNR. Pulsars represent a class of CR sources that have not been considered as extensively as the more usual scenario of acceleration in SNR shocks, but the fact that they may produce CRs is well known (Arons 1981; Harding & Ramaty 1987; Boulares 1989). However, recent measurements of positrons in CRs (Adriani et al. 2009; Ackermann et al. 2012a; Aguilar et al. 2014) in excess of predictions of propagation models (Protheroe 1982; Moskalenko & Strong 1998), made under the assumption of their entirely secondary production in the ISM, elevated pulsars to be one of the primary candidate sources responsible for this excess (e.g., Harding & Ramaty 1987; Boulares 1989; Atoyan et al. 1995; Hooper et al. 2009; Malyshev et al. 2009; Yüksel et al. 2009). The magnetospheres of rapidly rotating neutron stars are capable of producing electrons and positrons in significant numbers and accelerating them to very high energies, resulting in a pulsar wind nebula (PWN) that is observable from radio to high-energy γ-rays (Gaensler & Slane 2006); an archetypical example of such a source is the Crab pulsar and its PWN. The accelerated particles eventually escape from the PWN into the ISM, and some of them can reach the solar system. Therefore, PWNe can be natural candidates responsible for the puzzling excess of CR positrons observed by several experiments.

Recent observations of the extended TeV emission around the Geminga and PSR B0656+14 PWNe by the High Altitude Water Cherenkov (HAWC) telescope constrain the diffusion coefficient in their vicinities to be about two orders of magnitude smaller than the average value derived from observations of CRs (Abeysekara et al. 2017). The application of such slow diffusion to the local Milky Way results in a contradiction with other CR observations, in particular observations of high-energy CR electrons and positrons. Fast energy losses of TeV particles through inverse Compton (IC) scattering and synchrotron emission limits their lifetime to ~100 ky (Strong & Moskalenko 1998). If such slow diffusion is representative for the ISM within about a few hundred parsecs of the solar system, the sources of the TeV particles detected at Earth also need to be within a few tens of parsecs. Profumo et al. (2018) highlighted that such nearby sources have not been identified and proposed a two-zone diffusion model with the slow diffusion confined to a small region around the PWN. Other authors have considered similar scenarios with varying details (Evoli et al. 2018; Fang et al. 2018; Tang & Piran 2019). Interestingly, a similar suppression of the CR diffusion was observed in the Large Magellanic Cloud around the 30 Doradus star-forming region, where an analysis of combined γ-ray and radio observations yielded a diffusion coefficient, averaged over a region with radius 200–300 pc, an order of magnitude smaller than the typical value in the Milky Way (Murphy et al. 2012). Meanwhile, the strong suppression of the diffusion coefficient around an SNR due to the excitation of magnetic turbulence by escaping CRs was predicted some time before the HAWC observations were reported (e.g., Ptuskin et al. 2008; Malkov et al. 2013; D’Angelo et al. 2016, see also references therein). A similar mechanism may also be at work in PWNe.

In this paper, the two-zone diffusion model is explored using the latest version of the GALPROP⁴ propagation code (Porter et al. 2017; Jóhannesson et al. 2018). The results indicate that such a model is a viable interpretation for the HAWC observations and confirm similar conclusions made by other authors. Predictions for lower energy γ-ray emission that can be observed with the Fermi Large Area Telescope (Fermi-LAT) are made, and the contribution of energetic positrons coming from Geminga to the observed CR positron flux in different scenarios is studied. Effects of the size of the slower diffusion zone (SDZ) and the properties of the accelerated electrons/positrons are taken into account, as is the effect of the proper motion of Geminga. Unless both Geminga and PSR B0656+14 are special cases, it is expected that there are more regions of slower diffusion around other PWNe in the Milky Way. The implications that such inhomogeneity of the diffusion in the ISM can have on the CR distribution throughout the Milky Way is also explored.

2. A Model for Geminga

2.1. Physical Setup

It is assumed that the Geminga pulsar is injecting accelerated electrons and positrons into the ISM in equal numbers with a fraction η of its spin-down power converted to pairs. After injection, the particles propagate via a diffusive process. The pulsar parameters used for this paper are identical to those from Abeysekara et al. (2017), and the energy distribution of the injected electrons/positrons is described with a smoothly joined broken power law:

$$\frac{dn}{dp}\propto E_k^{-{\text{γ}}_{\text{0}}}{\left[1+{\left(\frac{E_k}{E_b}\right)}^{\frac{{\gamma }_1-{\gamma }_0}{s}}\right]}^{-s}.$$ (1)

Here, n is the number density of electrons/positrons, p is the particle momentum, E_k is the particle kinetic energy, and γ₁ is a power-law index at high energies. The smoothness parameter s = 0.5 is assumed constant and so is the low-energy index γ₀ = −1 and the break energy E_b = 10 GeV. This low-energy break effectively truncates the injected particle spectrum that is not expected to extend unbroken to lower energies (e.g., Amato 2014). The break is required to keep the value of η below 1 for the largest values of γ₀ considered. The truncation occurs at energies below that explored in this paper and has no effect on the results. The injection spectrum is normalized so that the total power injected is given by the expression

$$L(t)=\eta {\dot{E}}_0{\left(1+\frac{t}{{\tau }_0}\right)}^{-2},$$ (2)

where ${\dot{E}}_0$ is the initial spin-down power of the pulsar and τ₀ = 13 kyr (Abeysekara et al. 2017). The initial spin-down power is calculated using the current spin-down power of Ė = 3.26 × 10³⁴ erg s⁻¹ assuming that the pulsar age is T_p = 340 kyr. The distance to Geminga has been determined to be 250 pc (Faherty et al. 2007). The spatial grid for the propagation calculations with GALPROP is right-handed with the Galactic center (GC) at the origin, the Sun at (x, y, z) = (8.5, 0, 0) kpc, and the z axis oriented toward the Galactic north pole. This coordinate system places Geminga at (8.7407, 0.0651, 0.0186) kpc at the current epoch.

Previous interpretations of the HAWC observations have assumed that the Geminga pulsar is a stationary object (Evoli et al. 2018; Fang et al. 2018; Profumo et al. 2018; Tang & Piran 2019). Only Tang & Piran (2019) discussed the effect of the proper motion of Geminga, but concluded that it has little effect on electrons generating the observed TeV γ-ray emission because of their short cooling timescale. Faherty et al. (2007) measured the proper motion of Geminga to be 107.5 mas yr⁻¹ in R.A. and 142.1 mas yr⁻¹ in decl. Transforming this into Galactic coordinates leads to −80.0 mas yr⁻¹ in longitude and 156.0 mas yr⁻¹ in latitude. Assuming a constant proper velocity that is currently perpendicular to the line of sight, the corresponding velocity in the spatial grid coordinate system is (v_x, v_y, v_z) = (24.3, −89.9, 182.6) km s⁻¹, with Geminga originally located at (8.7320, 0.0963, −0.0449) kpc. In this case, Geminga was bom in an SN explosion of a star that has traveled from the direction of the Orion OB1a association (Smith et al. 1994). While the TeV γ-ray emission is not significantly affected by the proper motion, the large traveled distance and proximity of Geminga to the Sun should produce a “trailing” tail of CRs whose γ-ray emissions may be observable at lower energies with Fermi-LAT.

For the two-zone diffusion model, the diffusion coefficient in a confined region around the pulsar is assumed to be lower than that in the ISM, due to the increased turbulence of the magnetic field. This region will hereafter be called a “slower diffusion zone” (SDZ). It is also assumed that the stronger turbulence does not change the power spectrum and hence the rigidity dependence of the diffusion coefficient is the same for the SDZ and the ISM. Let r be the distance from the center of the SDZ, then the spatial dependence of the diffusion coefficient is given by

$$D=\beta {\left(\frac{R}{R_0}\right)}^{\delta }\{\begin{array}{ll}{D}_z,& r<r_z,\\ D_z{\left[\frac{D_0}{D_z}\right]}^{\frac{r-r_z}{r_t-r_z}},& r_z⩽r⩽r_t,\\ D_0,& r>r_t.\end{array}$$ (3)

Here, β is the particle velocity in units of the speed of light, D₀ is the normalization of the diffusion coefficient in the general ISM, D_z is the normalization of the diffusion coefficient within the SDZ with radius r_z, R is the particle rigidity, and R₀ = 4 GV is the normalization (reference) rigidity. In the transitional layer between r_z and r_t, the normalization of the diffusion coefficient increases exponentially with r from D_z to the interstellar value D₀. Depending on the exact origin of the SDZ, its radius can be time dependent, as can its location. To be consistent with the HAWC observations, both r_z and r_t have to be of the order of a few tens of parsec at the current time.

The effect of the SDZ around the PWN on the spectra and distribution of injected electrons/positrons and their emission may depend on its origin. Two general categories distinguished by the origin of the SDZ are considered. For the first category, the SDZ is due to events external to the PWN itself (external SDZ) that may be related to the progenitor SNR, or the surrounding environment. It is assumed that the particle propagation time in the zone is much longer than the time necessary to generate such a zone itself (“instant” generation), and its location is fixed. For the second category, the SDZ is assumed to be associated with and generated by the PWN itself (PWN SDZ). Therefore, the SDZ is moving with the Geminga pulsar and its size increases proportionally to the square root of time. This is in qualitative agreement with the evolution of a PWN as determined from simulations (e.g., van der Swaluw 2003) and observations (Abdalla et al. 2018).

For the PWN SDZ, the expectation is that there may be a link between the pulsar that is generating the magnetic turbulence and the surrounding interstellar plasma. In this case, the pulsar would transfer a momentum to the medium within the SDZ. To estimate the evolution of the velocity of Geminga, a simple model is put forward. It is assumed that the radius of the SDZ region r_z around Geminga is increasing in a diffusive manner so that $r_z(t)=\mu \sqrt{t}$, where μ is a constant. It is further assumed that a fraction f of the ISM within r_z is swept by the PWN and sped up to the velocity v of the pulsar. Using conservation of momentum dp = −vdM gives v = v₀(M₀/M)², where v₀ and M₀ ≈ M_☉ are the initial velocity and mass of the system, respectively. Substitution of r_z(t) and v(M) into the mass conservation formula $dM=f\pi \rho r_z^{2}vdt$ yields the time evolution of the velocity of Geminga:

$$v=\frac{v_0}{{\left(3A_d{v}_0{t}^2/2+1\right)}^{2/3}}.$$ (4)

Here, $A_d=f\pi \rho {\mu }^2/M_0$ is the drag coefficient and ρ ≈ 0.03 M_☉ pc⁻³ is the mass density of the ISM. Equation (4) can be integrated to get the full traveled distance:

$$\lambda (t)=v_{0}t{ }_2{F}_1\left(\frac{1}{2},\frac{2}{3};\frac{3}{2};-\frac{3A_d{v}_0{t}^2}{2}\right),$$ (5)

where ₂F₁ is the hypergeometric function. Further assuming that r_z(T_p) ≈ 30 pc and that f ≈ 10⁻³, the distance traveled by Geminga is λ(T_p) ≈ 330 pc and its initial velocity is v₀ ≈ 4300 km s⁻¹. This places the birth of Geminga at the location of Orion OB1a, which is at a distance of 330 pc from its current location. This is a very intriguing possibility, but in this case, v₀ is much higher than the observed velocities of any other neutron stars that reach only up to 1000 km s⁻¹ (e.g., Hobbs et al. 2005). Assuming f ≈ 10⁻⁴ results in a more reasonable speed of v₀ ≈ 400 km s⁻¹ and a total distance traveled of λ(T_p) ≈ 100 pc. A moderate slowdown agrees with observations of older pulsars having, on average, smaller velocities than young pulsars (Hobbs et al. 2005).

2.2. Calculation Setup

The calculations are made using the latest release of the GALPROP code (see footnote 4; Porter et al. 2017; Jóhannesson et al. 2018). The GALPROP code solves the diffusion–advection equation in three spatial dimensions, allowing for diffusive reacceleration in the ISM—see the website and GALPROP team papers for full details. Of major relevance for this paper, the code fully accounts for energy losses due to synchrotron radiation and IC scattering. The resulting synchrotron and IC emission is calculated for an observer located at the position of the solar system. The IC calculations (Moskalenko & Strong 2000) take into account the anisotropy of the interstellar radiation field (ISRF). The current calculations employ the magnetic field model of Sun et al. (2008) described by their Equation (7) and the R12 model for the ISRF developed by Porter et al. (2017). While the turbulent magnetic field is expected to be larger in the SDZ, the magnetic field model is not updated to account for this. The expected increase in the synchrotron cooling rate and corresponding electromagnetic emissions will not significantly affect the results presented below.

The code has also been enhanced to use non-equidistant grids to allow for increased resolution in particular areas of the Milky Way, in this case around Geminga. This improvement to GALPROP is inspired by the the Pencil Code⁵ (Brandenburg & Dobler 2002), where the use of analytic functions can have advantages in terms of speed and memory usage compared to purely numerical implementations for non-uniform grid spacing. The current run uses the grid function

$$z(\zeta )=\frac{ϵ}{a}\tan \left[a\left(\zeta -{\zeta }_0\right)\right]+z_0$$ (6)

for all spatial coordinates ζ = x, y, z, where ϵ, a, ζ₀, z₀ are parameters. This function maps from the linear grid ζ to the nonlinear grid in each of the spatial coordinates x, y, z. The equations are solved on the ζ grid after the differential equations have been updated to account for the change in the first and second derivatives.

The parameters of the grid function are chosen such that the resolution is 2 pc at a central location that is defined below for each calculation, but goes up to 0.1 kpc at a distance of 700 pc from the grid center. This setup provides about a 0°.2 resolution on the sky for objects located at a distance of 250 pc along the line of sight toward the center of the grid. To minimize the artificial asymmetry, the grid has the current location of Geminga close to the center of a pixel and close enough to the center of the non-equidistant grid so that there is little distortion due to the variable pixel size. For the chosen parameters, the grid size is approximately uniform within a box having a width of ~60 pc, which is not enough to enclose the entire evolution of the Geminga PWN. The resolution and size of the grid is bounded by computation costs; the selected parameters are a result of a compromise among accuracy, memory requirements, and computation speed. This necessarily means that the start and (or) end of the evolution of Geminga are (is) not fully resolved. Because the diffusion process smooths the distribution of particles as time evolves, the grid is chosen such that the current location of Geminga, and hence the TeV γ-ray emission, is always well resolved, but sometimes this may come with a small decrease of spatial resolution at its birthplace.

The calculations are performed in a square box with a width of 8 kpc. This is wide enough so that the CR propagation calculations in the solar neighborhood are not affected by the boundary conditions. The non-equidistant grid allows the boundaries to be extended this far without imposing large computational costs. A fixed time step of 50 yr is used for the calculations. This is small enough to capture the propagation and energy losses near the upper boundary of the energy grid, which is 1 PeV. The upper energy boundary is chosen to be well above that for the particles producing the HAWC data. The lower energy boundary is set at 100 MeV, much lower than the cutoff in the injection spectrum. The energy grid is logarithmic with 16 bins per decade.

The values of D₀ = 4.5 × 10²⁸ cm² s⁻¹ and δ = 0.35 are chosen to match the latest AMS-02 data on secondary CR species (see Section 3). The SDZ diffusion coefficient of D_z = 1.3 × 10²⁶ cm² s⁻¹ at R₀ = 4 GV corresponds to the value derived from the HAWC observations at higher energies (Abeysekara et al. 2017). No attempt is made to independently fit the latter to the HAWC observations because each propagation calculation is computationally expensive, taking ~24 hr to complete on a modern 40 core CPU. The calculations also include diffusive reacceleration with an Alfvén speed v_A = 17 km s⁻¹, as determined from the fit to the secondary-to-primary data. To save CPU time, the calculations are made using electrons only, because the energy losses and propagation of positrons and electrons are identical. When comparing to the measured positron flux at Earth, the calculated particle flux is simply divided by two. The IC emission is calculated on a HEALPix (Górski et al. 2005) grid having an order of 9, giving a resolution of about 0°.1. The IC emission is evaluated on a logarithmic grid in energy from 10 GeV to 40 TeV with 32 energy planes.

2.3. Results

2.3.1. Stationary Model

For a comparison with results of previous studies, the first set of calculations is performed assuming that there is no proper motion of Geminga. The index of the injection spectrum is fixed to γ₁ = 2.0, and the efficiency parameter is η = 0.26. The SDZ is centered at the current location of Geminga, l_G, b_G) = (195°.14, 4°.26), and is static in size. The spatial grid is also centered at the same location. Several combinations of (r_z, r_t) are used, covering a range from 30 to 50 pc for r_z and from 50 to 70 pc for r_t. Calculations are also made using a model with (r_z, r_t) = (∞, ∞) for a comparison with the results from Abeysekara et al. (2017). Figure 1 (top panel) shows the angular profile of the surface brightness of the modeled IC emission evaluated over the energy range from 8 to 40 TeV and compared with the data from HAWC. The resulting profile is clearly independent of the size of the SDZ, because the cooling time limits the diffusion length at the corresponding CR electron energies (≳100 TeV) to be ≲10 pc. The same cannot be said for the IC emission evaluated for the energy range from 10 to 30 GeV, which is also shown in Figure 1 (bottom panel). Because of the longer cooling timescales, the emission profile is highly sensitive to the size of the SDZ, via both r_z and r_t. A smaller SDZ size leads to a correspondingly lower number density of CR electrons/positrons within the zone, which produces a flatter profile and fainter emission in the GeV energy range.

Figure 1.

Surface brightness of the modeled IC emission shown as a function of angular distance from the current location of Geminga. The models shown here assume Geminga is stationary, γ₁ = 2.0, and the SDZ is stationary and centered at Geminga. The top panel shows the energy range 8–40 TeV compared to the observations of HAWC (Abeysekara et al. 2017). The bottom panel shows the model predictions for the energy range 10–30 GeV. The different curves represent different assumptions about the size of the SDZ, encoded as SDZ(r_z, r_t) in the legend.

Calculations with different values of γ₁ = 1.8 and 2.2 are made using (r_z, r_t) = (30, 50) pc. The conversion efficiency, η, is correspondingly updated for these models to provide consistency with the HAWC data. The values are η = 0.18 and η = 0.75 for γ₁ = 1.8 and γ₁ = 2.2, respectively. The average spectrum of the IC emission over a circular region of 10° in radius around the current location of Geminga is shown in Figure 2. The models are all tuned to agree with the HAWC data and, therefore, the predicted profiles differ significantly at lower energies. Also shown is the prediction made using the isotropic assumption for the IC cross section (dotted curve in the upper panel), which is a commonly used approximation that ignores the angular dependence of the ISRF. Using the isotropic approximation underpredicts the emission by ~10%, at 10 TeV and ~25% at 10 GeV. The discrepancy between the IC emission calculated with the realistic angular distribution of the ISRF and with the isotropic distribution depends on the adopted electron injection spectrum and the size of the SDZ, with softer injection spectra and larger SDZs producing larger differences.

Figure 2.

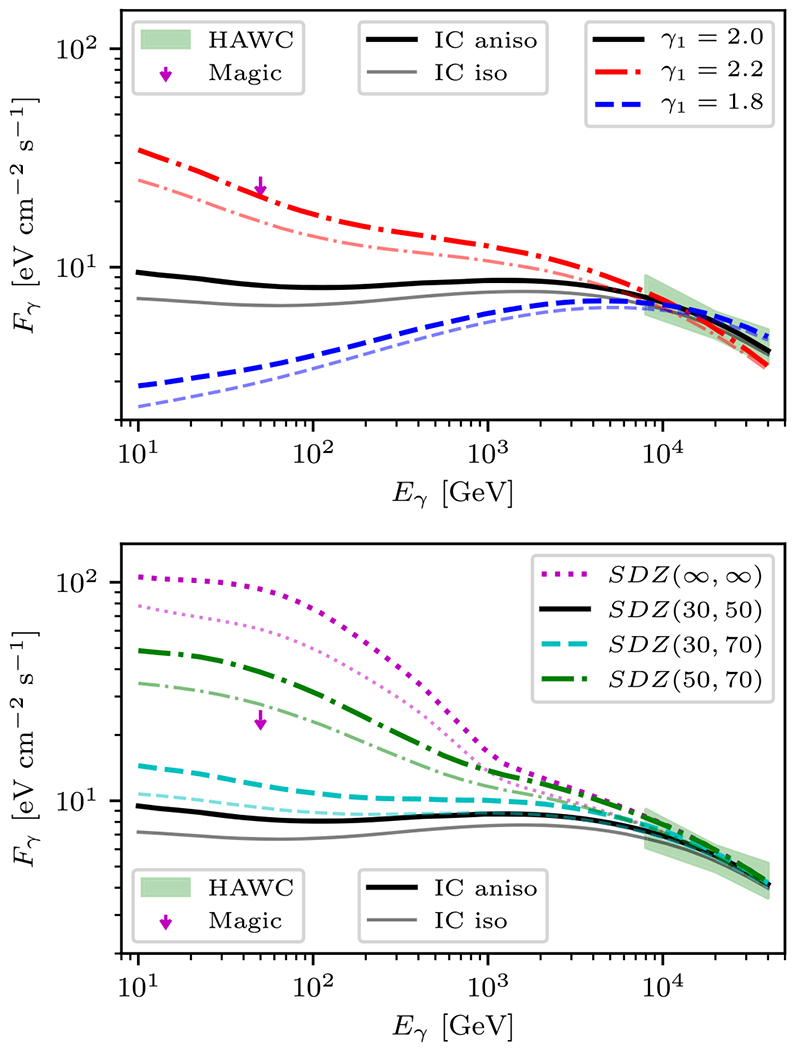
Spectrum of IC emission averaged over a 10° wide region around the current location of Geminga. The models shown here assume Geminga is stationary and that the SDZ is stationary and centered at Geminga. The top panel shows the spectrum for different values of γ₁ as indicated in the legend, but using fixed values of (r_z, r_t) = (30, 50) pc. The bottom panel shows the spectrum for models with different pairs of (r_z, r_t), but fixed value of γ₁ = 2.0. The green shaded region corresponds to HAWC observations, assuming a diffusion profile for the spatial distribution (Abeysekara et al. 2017), and the magenta arrow is the upper limit from observations with the MAGIC telescope corrected for the diffusion profile (Tang & Piran 2019).

Kinematically, the energy dependence of the discrepancy can be understood as follows: the very highest energy γ-rays are produced in head-on collisions from backscattered soft photons, where the ultrarelativistic electrons “see” the angular distribution of soft photons concentrated in a narrow (head-on) beam. Meanwhile, for lower electron energies, the angular distribution of the background photons is considerably more important and more significantly affects the energy of the upscattered γ-rays. The softer injection spectra have more low-energy electrons, and there is more confinement for low-energy electrons for larger sizes of the SDZ. The surface brightness profile is also slightly affected by the isotropic assumption of the IC emission as shown in Figure 1 (bottom panel). The profile is more peaked under the isotropic assumption; the underprediction in the wings of the profile is ~10% deeper than that near the center. Consequently, using the averaging made for the isotropic approximation has some effect that can produce an incorrect determination of the diffusion coefficient from the shape of the profile. Accurate calculation of the anisotropic IC emission depends on the knowledge of the electron and ISRF intensity distributions in the vicinity of the PWN. Evaluation of the induced uncertainty due to the use of the isotropic approximation on determination of the diffusion coefficient properties for other PWN observations requires calculating the IC emissions at their locations in the Galaxy.

Also shown in Figure 2 is the effect of the size of the SDZ on the average spectrum. A larger SDZ size results in a larger electron number density that, in turn, leads to increased emission in the GeV energy range. The observations made with the MAGIC telescope (Ahnen et al. 2016; updated to match the diffusion profile by Tang & Piran 2019) constrain both the particle injection spectrum and the size of the SDZ. A smaller SDZ and/or harder particle injection spectrum is required by the observations. The perceived degeneracy between the size of the SDZ and the injected spectrum of the particles from this figure is broken when the angular profile of the low-energy emission is taken into account. Changing the injection spectrum will not affect the shape of the angular profile while changing the SDZ size does. The angular extent of the emission should therefore be a good indicator of the size of the SDZ.

One of the main conclusions of the study by Abeysekara et al. (2017) is that the unexpected rise in the positron fraction as measured by PAMELA (Adriani et al. 2009), Fermi-LAT (Ackermann et al. 2012a), and AMS-02 (Aguilar et al. 2013, 2014; Accardo et al. 2014) cannot be due to the positrons accelerated by the Geminga PWN. This conclusion is based on a one-zone diffusion model constructed to agree with the HAWC data. For a two-zone diffusion model, the conclusion can be quite different. Profumo et al. (2018) and Fang et al. (2018) found that the positron excess could easily be reproduced with such a model using a power-law injection spectrum for positrons (and electrons) with index of 2.34 and 2.2, respectively. Tang & Piran (2019) also used data from the MAGIC telescope to constrain the model and found that a harder particle injection spectrum below a break energy of 30 TeV was necessary, which resulted in a calculated positron flux at Earth that did not fully explain the rise in the positron fraction.

Figure 3 shows the positron flux at Earth as predicted by the models considered in this paper, where the top and bottom panels illustrate models with different SDZ sizes and the effect of changing γ₁, respectively. The results clearly show a strong variation in the expected positron flux at Earth. A smaller SDZ leads to a larger flux of positrons at Earth because of the larger effective diffusion coefficient. Only if the SDZ extends all the way to the solar system are the results of Abeysekara et al. (2017) reproduced. Larger values of γ₁ also result in a larger positron flux at Earth in the observed energy range; meanwhile, values larger than γ₁ ≈ 2.2 are excluded as the predicted positron flux would exceed the data for an SDZ of size (r_z, r_t) = (30, 50) pc.

Figure 3.

Predicted flux of positrons at Earth. The models shown here assume Geminga is stationary and that the SDZ is stationary and centered at the current location of Geminga. The top panel shows the spectrum for different values of γ₁ as indicated in the legend, but using a fixed SDZ size (r_z, r_t) = (30, 50) pc. The bottom panel shows the spectrum for models with different pairs of (r_z, r_t), but fixed value of γ₁ = 2.0. The points are AMS-02 data (Aguilar et al. 2014).

2.3.2. Accounting for Proper Motion

So far, the calculations have been made considering a stationary source located at the current position of Geminga (l_G, b_G). However, such an approximation is not supported by its observed large proper motion. In the following analysis, the proper motion is taken into account, but different assumptions are made on the origin of the SDZ and the value of the drag coefficient A_d introduced in Equation (4). The different assumptions are referred to as scenarios A to D and detailed below. For scenarios A and B, the SDZ is assumed to be stationary and is unrelated to Geminga. In both scenarios, A_d = 0 and the pulsar velocity is constant. Scenario A assumes that the SDZ is centered on the current position of Geminga by chance, and that the parameters of the zone are (r_z, r_t) = (30, 50) pc. Scenario B assumes that the SDZ is centered at the birthplace of Geminga. In this scenario, the SDZ has to be much larger to extend from the birthplace of Geminga to its current location, (r_z, r_t) = (90, 110) pc. The center of the spatial grid is placed at (8.7358, 0.0962, −0.0124) kpc for both of these scenarios. This is about halfway between the birthplace and the current location of Geminga for the x and y axes, but only a quarter of the way for the z axis. As described earlier, the location of the center of the grid is set to give the current location of Geminga preference over its birth location.

For scenarios C and D, the center of the SDZ follows the location of Geminga and its size increases proportionally to the square root of time, normalized such that the final size of the SDZ is (r_z, r_t) = (30, 50) pc. The difference between these two scenarios is the value of the drag coefficient, A_d. In scenario C, A_d = 0 and the velocity is constant over time, while in scenario D, A_d = 2.636 × 10⁻⁸ pc⁻¹ yr⁻¹, giving Geminga an initial velocity of 410 km s⁻¹ at a position of (8.72775, 0.113017, −0.0787255) kpc. For numerical stability, the gradient of the diffusion coefficient is limited to be less than one order of magnitude per grid pixel. Because the ratio D₀/D_z ~ 300, it is necessary to increase D_z initially for scenarios C and D to fulfill this condition until the difference between r_t and r_z corresponds to the size of 2 pixels in all directions of the grid. Correspondingly, D_z is increased by up to an order of magnitude for the first few thousand years only, but this stability requirement does not significantly affect the results. The center of the spatial grid in scenario C is the same as that in scenarios A and B, while in scenario D the center of the grid is at (8.7300, 0.1075, −0.0213) kpc to better resolve the entire evolution of Geminga. Again, the center is about halfway between the origin and current location of Geminga for the x and y axes, but only a quarter of the way for the z axis. For scenarios A through D, the variables (r_t, r_z) are fixed to the values provided above and γ₁ = 2.0. The influence of these parameters in the scenarios is similar to those already shown in the calculations for a stationary source. In particular, a softer (harder) injection spectrum for the particles leads to a softer (harder) spectrum for the resulting positron flux and low-energy γ-ray flux.

Figure 4 shows the angular profile of the surface brightness in the energy range 8–40 TeV compared to the HAWC observations (Abeysekara et al. 2017). For comparison, the results of the model with stationary Geminga, (r_z, r_t) = (30, 50) pc and γ₁ = 2.0, are also shown. As expected, all models agree well with the data and significantly overlap. Though it is not seen in the figure, the emission is still reasonably symmetric around the current location of Geminga. To quantify the symmetry, the standard deviation of the distribution of intensities of pixels in the calculated HEALPix maps within each angular bin is calculated. The standard deviation in each angular bin is of the order of 5%–10% only. Meanwhile, some differences between models are also noticeable: the largest standard deviation of the emission core is seen in scenario D because of the larger proper velocity of the PWN, while the largest deviation in the tail is seen in scenario B with the largest SDZ size.

Figure 4.

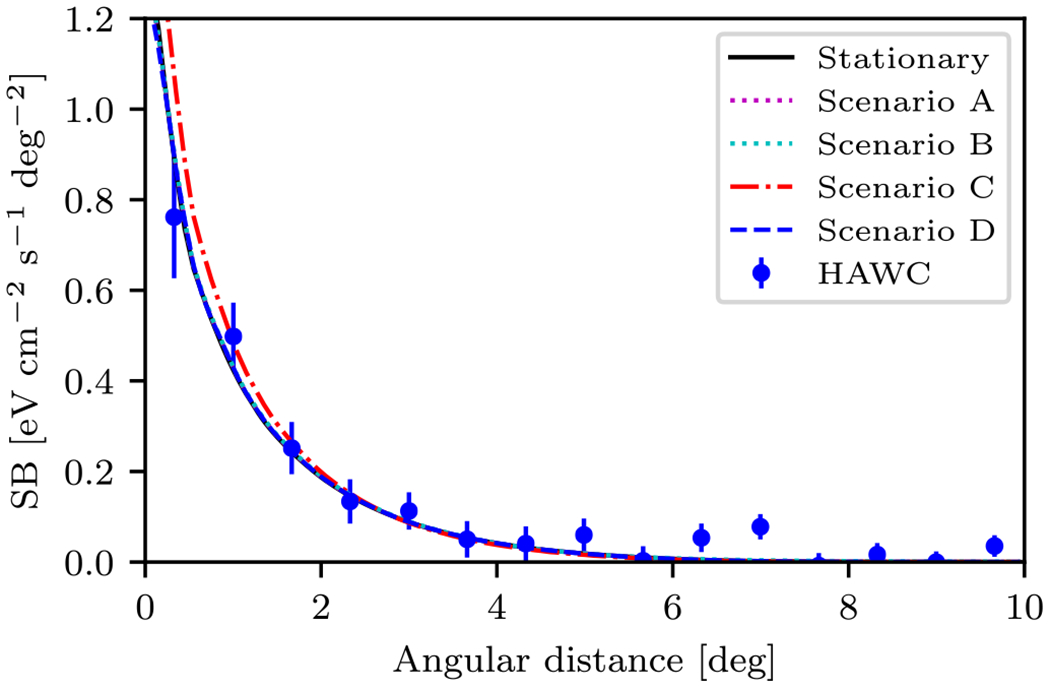
Surface brightness of the modeled IC emission for scenarios A through D shown as a function of the angular distance from the current location of Geminga. Also shown is the profile for the model with a stationary Geminga PWN with (r_z, r_t) = (30, 50) pc and γ₁ = 2.0. The data points show the profile observed by HAWC (Abeysekara et al. 2017).

In contrast, at lower energies, all models produce quite different distributions of the surface brightness. In particular, considerable asymmetry in the intensity maps around 10 GeV is seen in Figure 5, especially for scenario B with the largest SDZ. All scenarios where Geminga is moving show a distinctive tail in the low-energy range. In the extreme case of scenario B, the tail is exceptionally broad and the emission of the tail is, in fact, much brighter than that at the current location of Geminga. The differences between other scenarios are small and hard to distinguish in these maps. The tail in scenario C is slightly more extended than in scenarios A and D. Observations of the Geminga PWN at 10 GeV will thus hardly be able to distinguish between these scenarios, but may be able to verify the presence of the tail in scenario B.

Figure 5.

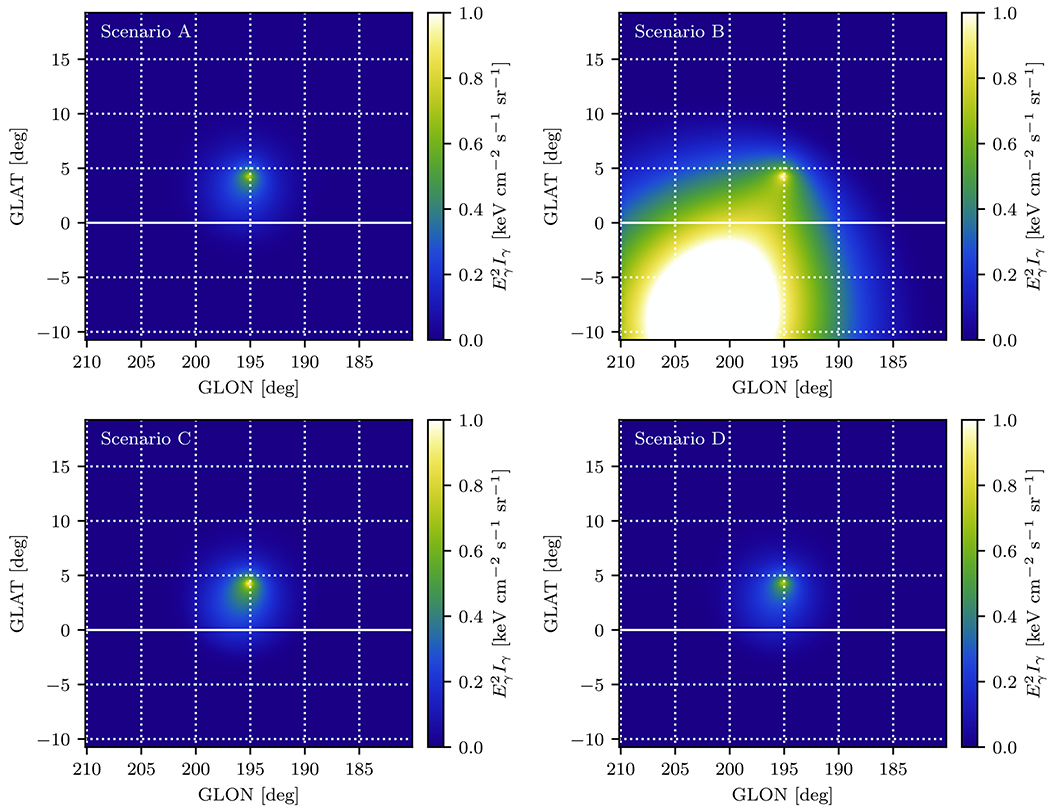
IC intensity maps evaluated at 10 GeV around the current location of Geminga. Shown are maps for scenarios A (top left), B (top right), C (bottom left), and D (bottom right). The maps are displayed using the colormap bgyw from the colorcet package (Kovesi 2015).

Despite their similar γ-ray emission maps (with exception of scenario B), all scenarios predict different positron fluxes at Earth (Figure 6). For energies below 1 TeV, the positron flux in scenario A is about a factor of 5 larger than that predicted for scenarios C and D. The difference between scenarios C and D is much smaller and mostly at the highest energies where scenario D produces a higher flux. This is due to the faster movement of the diffusion zone in scenario D that allows the CR particles to escape quickly once the diffusion zone has left them behind. This is somewhat idealized, and it is more likely that the SDZ will have a shape elongated along the direction of motion. For such a case, the results would become closer to scenario B, with a longer IC emission tail at low energies and smaller flux of positrons at low and high energies, but with a larger peak at around 300 GeV.

Figure 6.

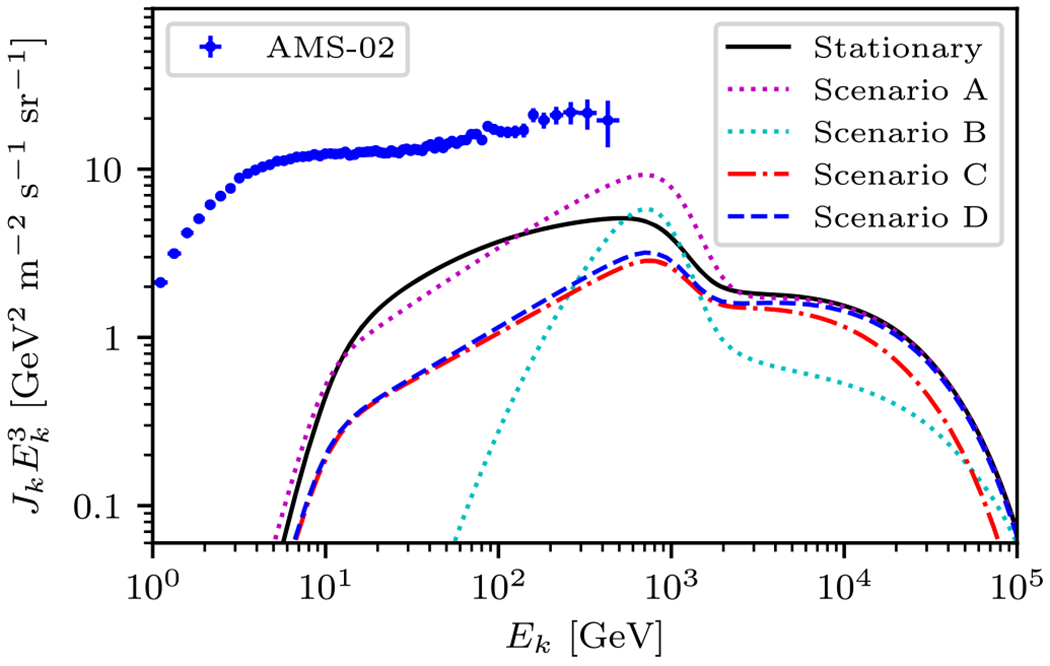
Predicted positron fluxes at Earth for scenarios A through D. Also shown are the results for a model where Geminga is stationary with (r_z, r_t) = (30, 50) pc and γ₁ = 2.0. The points are AMS-02 data (Aguilar et al. 2014).

In addition to IC emission, GAFPROP can calculate the predicted synchrotron emission from the models. In a magnetic field with a strength of several micro-Gauss, as is expected in the vicinity of Geminga, the particles responsible for the TeV γ-ray emission will also emit synchrotron photons with energies of ~keV. Because of the shape of the electron/positron spectrum of the injected particles from Geminga, the emission in radio and millimeter wavelengths is significantly dimmer than that from CR electrons from the Milky Way at large. At keV energies, the synchrotron emission follows a profile similar to that of the TeV IC emission, being peaked at the current location of Geminga with a half width of about a degree. Figure 7 shows the spectrum of the average intensity of the synchrotron emission within a degree of the current location of Geminga. All of the models considered predict a similar intensity level of the emission that approximately follows a power law I ∝ E^−1.8. The calculations are cut off at few tens of keV because the electron spectrum can only be reliably determined up to the energies corresponding to the HAWC observations; anything beyond that is an extrapolation. This energy is reached already at a few keV in the synchrotron spectrum. The synchrotron emission is close to the level of the diffuse X-ray emission observed in the Milky Way ridge (Valinia et al. 2000), but significantly less intense than that observed from the Geminga pulsar and the apparent nearby tails (Pavlov et al. 2010).

Figure 7.

Synchrotron intensity averaged over a region around the current location of Geminga with a radius of 1° for scenarios A through D. Also shown are the results for a model where Geminga is stationary with (r_z, r_t) = (30, 50) pc and γ₁ 2.0.

3. Implications for Propagation throughout the Milky Way

If the results for the two PWNe reported in Abeysekara et al. (2017) are not special cases, then it is likely that there are similar pockets of slow diffusion around many CR sources elsewhere in the Milky Way. The effective diffusion coefficient would thus be smaller in regions where the number density of CR sources is higher. Secondary CR species with different inelastic production cross sections (e.g., $\stackrel{\_}{p}$ versus B) probe different propagation distances. Interpretations of their data would yield different average diffusion coefficients, as was indeed found by Jóhannesson et al. (2016). Starburst galaxies with a large star formation rate are expected to have very slow diffusion and should exhibit an energy-loss-dominated spectrum of γ-ray emission that is much flatter than that observed from galaxies where the leakage of CRs dominates the energy losses. Interestingly, exactly such an evolution of the spectral shape is observed when galaxies with different star formation rates, such as the Magellanic Clouds, Milky Way, and M31 versus NGC 253, NGC 4945, M82, and NGC 1068, are compared (Ackermann et al. 2012b, and references therein).

Here it is assumed that the distribution of SDZs follows that of the CR sources, while the exact origin of these SDZs is not essential. With current CR propagation codes and reasonable resources, resolving the entire Milky Way with a few parsec grid size on short timescales is intractable. A simpler approach must, therefore, be taken to explore the effects such SDZs have on the propagation of CRs throughout the Milky Way. Assuming that the properties of CR propagation and the distribution of CR sources vary on average very little over the residence time of CRs in the Milky Way, a steady-state model can be used. Also assuming that the residence time of CRs in the Milky Way is larger than the active injection time of the CR sources, the CR source distribution can be assumed to be smooth with injected power that is approximately constant with time. These two approximations have been extensively used in the past and are the starting point of almost all studies on CR propagation across the Milky Way.

As was shown in the previous section, the effect of an SDZ is a local increase of the density of CRs for a certain period of time, leading to an increase of CR reaction rates with the ISM contained within the SDZ. CRs thus spend more time in the vicinity of their sources compared to a model with a homogeneous diffusion. This is equivalent to an effective decrease of the diffusion coefficient averaged over a larger volume. Even though such an approximation does not account for the detailed spatial distribution of the individual SDZs, it does account for the increased interaction rate with the ISM, such as energy losses and generation of secondary CR particles. Therefore, this approximation should still provide for the correct spectra and abundances of CR species.

Assuming that CRs first propagate through an SDZ with diffusion coefficient D_z and radius x_z that is embedded in a region with diffusion coefficient D₀ and radius x₀ ≫ x_z, their residence time in the total volume can be estimated as

$$\tau \sim \frac{x_0^2}{D_0}+\frac{x_z^2}{D_z}.$$ (7)

Assuming a single average diffusion coefficient D, the residence time can also be expressed as

$$\tau \sim \frac{x_0^2}{D}.$$ (8)

Combining the two equations results in

$$D\approx D_0{\left[1+{\left(\frac{x_z}{x_0}\right)}^2\frac{D_0}{D_z}\right]}^{-1}.$$ (9)

Assuming that there is an SDZ around each CR source, the density of SDZs is the same as the CR source number density, q(x), where x is the spatial coordinate. Let V_z be the volume of each SDZ and ΔV be the volume of an element in the spatial grid used in the calculation. Then, for each volume element,

$$\frac{x_z}{x_0}\approx {\left[\frac{V_z}{\text{Δ}V}\underset{\text{Δ}V}{{\displaystyle \int }}q(\mathit{x})dV\right]}^{1/3}\approx {\left[q_x{V}_z\right]}^{1/3},$$ (10)

where q_x is the CR source number density at the center of the volume element. The value Q = ∫_V q(x)dV is the total number of active CR sources in the Galaxy at any given time, and QV_z is then the combined volume of all SDZs in the Galaxy. Assuming that the SN rate is 0.01 yr⁻¹, and each source continuously accelerates particles for ~10⁵ yr, there are ~10³ active CR sources at any given time. Assuming a radius of x_z ~ 30 pc for each source, the combined volume of all SDZs is QV_z ≈ 0.1 kpc³. This value is in good agreement with estimates from Hooper et al. (2017) and Profumo et al. (2018). The ratio x_z/x₀ in Equation (10) depends on the product of the number of SDZs and their sizes. Because of this, equivalent results can be obtained also for, e.g., fewer SDZs of larger sizes, provided that the total occupied volume is the same and their distribution follows q(x). Equation (9) also depends on the value of D₀/D_z, which is set to 300 in the following calculations and is similar to the value used in the Geminga calculations. The results described below, therefore, are valid across different model assumptions, provided they are consistent with Equation (9).

The modified diffusion described above has been implemented in the GALPROP code to test its effect on the propagation of CR species in the Milky Way. With a switch in the configuration file, it is now possible to change to a diffusion configuration such that

$$D(\mathit{x})=D_0{\left\{1+{\left[q(\mathit{x})V_z\right]}^{2/3}\frac{D_0}{D_z}\right\}}^{-1}$$ (11)

Therefore, even with D₀ and D_z fixed, the effective diffusion coefficient is still spatially varying, where the total volume of SDZs in the Milky Way is a normalization parameter QV_z ≈ 0.1 kpc³, as explained above. In principle, the number distribution of CR sources can be different from the distribution of their injected power into CRs in the Milky Way, but here they are assumed identical. Two models, SA0 and SA50, are used for the CR source density distribution (Porter et al. 2017). The SA0 model is a 2D axisymmetric pulsar-like distribution (Yusifov & Küçük 2004) for the CR source density in the disk. The SA50 model has half of the injected CR luminosity distributed as the SA0 density and the other half distributed as the spiral arms for the R12 ISRF model. Each CR source model is paired with both a constant homogeneous diffusion and the modified diffusion described above, resulting in a total of four models. The model calculations are performed on a 3D spatial grid that now includes the whole Milky Way using the grid function defined in Equation (6). The parameters of the grid function are chosen such that the resolution in the x and y coordinates is 200 pc at the GC, increasing to 1 kpc at a distance of 20 kpc, which is also the boundary of the grid. At the distance of the solar system, the resolution is about 350 pc in the x direction and the Sun is located at the center of a volume element. In the z direction, the resolution is 50 pc in the plane, increasing to 200 pc at the boundary of the grid at |z| = 6 kpc. The energy grid is logarithmic, ranging from 3 MeV to 30 TeV with 112 energy planes.

The distribution of the effective diffusion coefficient D(x) in the Galactic plane is shown in Figure 8, where the numbers correspond to its value at the normalization rigidity R₀ = 4 GV. The spiral arm structure of the SA50 model is clearly visible. The maximum change in the effective diffusion coefficient is about a factor of 3, which corresponds to a peak value of x_z/x₀ ~ 10⁻³. All models employ the R12 ISRF from Porter et al. (2017) and the 3D gas distributions from Jóhannesson et al. (2018). The same standard procedure for parameter adjustment to match the recent observations of CR species listed in Table 1 is followed for all source density models. Solar modulation is treated using the force-field approximation (Gleeson & Axford 1968), one modulation potential value for each observational period. The use of the latter is justified by the available resources and the main objective of this paper, i.e., to study the effect of the modified CR diffusion in a self-consistent manner, rather than to update the local interstellar spectra of CR species or to accurately determine the propagation parameters.⁶ The procedure for parameter tuning is the same as that used by Porter et al. (2017) and Jóhannesson et al. (2018). The propagation parameters are first determined by fitting the models to the observed spectra of CR species. Be, B, C, O, Mg, Ne, and Si. These are then kept fixed and the injection spectra for electrons, protons, and He fitted separately. To reduce the number of parameters, only the most relevant primary abundances are fitted simultaneously with the propagation parameters while the rest are kept fixed. Because the injection spectra of all CR species are normalized relative to the proton spectrum at normalization energy 100 GeV/nucleon, the procedure is repeated to ensure consistency. One iteration provides a satisfactory accuracy in all cases. The only difference from the procedure described in Porter et al. (2017) and Jóhannesson et al. (2018) is the inclusion of elemental spectra of Be, C, and O from AMS-02 and the elemental spectra from, ACE/CRIS, while the data from HEAO-C3 and PAMELA has been removed.

Figure 8.

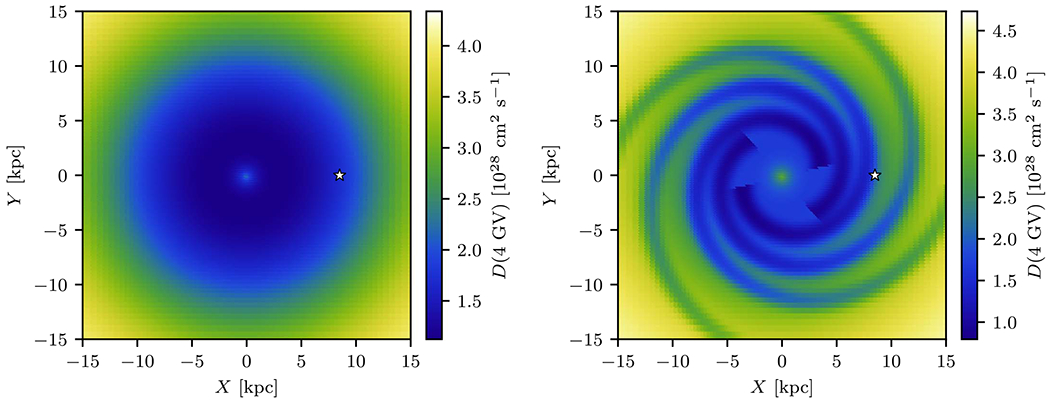
Diffusion coefficient evaluated in the Galactic plane at the normalization rigidity R₀ = 4 GV for a model where the effective diffusion coefficient is given by Equation (11). The left panel shows the distribution of the diffusion coefficient for the SA0 model while the right panel shows that for the SA50 model. The location of the Sun is marked as a white star, and the GC is at (0, 0). The maps are displayed using the colormap bgyw from the colorcet package (Kovesi 2015).

Table 1.

Data Sets Used to Derive Propagation Parameters

Instrument	Data Sets	References
AMS-02 (2011–2016)	Be, B, Be/B, Be/C, B/C, Be/O, B/O	I
AMS-02 (2011–2016)	C, O, C/O	II
AMS-02 (2011–2013)	e−	III
AMS-02 (2011–2013)	H	IV
AMS-02 (2011–2013)	He	V
ACE/CRIS (1997–1998)	B, C, O, Ne, Mg, Si	VI
Voyager 1 (2012–2015)	H, He, Be, B, C, O, Ne, Mg, Si	VII

References. (I) Aguilar et al. (2018), (II) Aguilar et al. (2017), (III) Aguilar et al. (2014), (IV) Aguilar et al. (2015a), (V) Aguilar et al. (2015b), (VI) George et al. (2009), (VII) Cummings et al. (2016).

Table 2 lists the best-fit parameters for the four models considered. The parameters are similar for all models, and the modified diffusion and different source distributions only slightly affect the best-fit values. Most interestingly, despite the fact that the value of the effective diffusion coefficient exhibits strong spatial variations in the Galactic plane including at the solar system location, where it is about a factor of 2 smaller compared to that in the model with homogeneous diffusion (Figure 8), the value of D₀ is not significantly different from that obtained for the homogeneous model. This is connected with the relatively small volume affected by the modified diffusion regions because they are associated with the CR sources, which have a relatively narrow distribution about the Galactic plane with exponential z scale height 200 pc. The modified diffusion slightly affects the low-energy part of the spectrum, resulting in smaller modulation potentials and Alfvén speeds. Overall, the addition of the SDZs does not significantly alter the global diffusive properties of the ISM.

Table 2.

Final Propagation Model Parameters

Parameter	Homogeneous Diffusion		Modified Diffusion
	SA0	SA50	SA0	SA50
iD0,xx [1028 cm2 s−1]	4.36	4.55	4.41	4.78
i δ	0.354	0.344	0.358	0.360
vA [km s−1]	17.8	18.1	15.7	17.6
ii γ 0	1.33	1.43	1.40	1.47
ii γ 1	2.377	2.399	2.403	2.381
iiR1 [GV]	3.16	3.44	3.80	3.82
ii γ 0,p	1.96	1.99	1.92	1.93
ii γ 1,p	2.450	2.466	2.469	2.453
ii γ 2,p	2.391	2.355	2.359	2.321
iiR1,p [GV]	12.0	12.2	11.3	11.3
iiR2,p [GV]	202	266	213	371
ΔHe	0.033	0.035	0.039	0.032
ii γ0,e	1.62	1.49	1.46	1.46
ii γ1,e	2.843	2.766	2.787	2.762
ii γ2,e	2.494	2.470	2.506	2.480
ii R1,e [GV]	6.72	5.14	5.03	5.13
ii R2,e [GV]	52	69	69	69
iii Jp	4.096	4.113	4.102	4.099
iii Je	2.386	2.362	2.288	2.345
ivq0,4He [10−6]	92495	91918	92094	93452
ivq0,12C [10−6]	2978	2915	2912	2986
ivq0,16O [10−6]	3951	3852	3842	3956
ivq0,20Ne [10−6]	358	327	322	359
ivq0,24Mg [10−6]	690	704	681	744
ivq0,28Si [10−6]	801	786	762	833
vΦAMS,I [MV]	729	741	709	729
vΦAMS,II [MV]	709	729	696	729
vΦACE/CRIS [MV]	359	370	345	354

Notes.

ⁱD(R) ∝ βR^δ, D₀ is the normalization at R₀ = 4 GV.

ⁱⁱThe injection spectrum is parameterized as q(R) ∝ R^−γ₀ for R ⩽ R₁, q(R) ∝ R^−γ₁ for R₁ < R ⩽ R₂, and q(r) ∝ R^−γ₂ for R > R₂. The spectral shape of the injection spectrum is the same for all species except CR p and He. R₁ and R₂ are the same for p and He and γ_i,He = γ_i,p − Δ_He.

ⁱⁱⁱThe CR p and e⁻ fluxes are normalized at the solar location at a kinetic energy of 100 GeV. J_p is in units of 10⁻⁹ cm⁻² s⁻¹ sr⁻¹ MeV⁻¹, and J_e is in units of 10⁻¹¹ cm⁻² s⁻¹ sr⁻¹ MeV⁻¹.

^ivThe injection spectra for isotopes are normalized relative to the proton injection spectrum at 100 GeV/nuc. The normalization constants for isotopes not listed here are the same as those given in Jóhannesson et a2016).

^vThe force-field approximation is used for calculations of the solar modulation and is determined independently for each model and each observing period. Φ_AMS,I and Φ_AMS,II correspond to the 2011–2016 and 2011–2013 observing periods for the AMS-02 instrument, respectively.

A comparison between the calculated spectra of CR species and data is shown in Figure 9. The models agree reasonably well with the data and deviate less than 10% from the measurements for most elements. The largest systematic deviations shown are around 10 GeV for B and C, where the relative residuals are as large as ~20%. The residuals for Be and O are similar (not shown). These are likely caused by the lack of freedom in the injection spectra for the primaries, because the deviations are hardly visible in the secondary-to-primary ratios of which B/C is shown in the figure for illustration. If the deviations were caused by propagation effects, they would be stronger in the secondary component and be correspondingly more prominent in the secondary-to-primary ratios. Deviations from the H and He data are smaller, and the feature at 10 GeV is not visible. Figure 9 also shows that the models agree with each other to within 5% for all elements, and this further illustrates that the addition of the SDZ pockets does not strongly affect predictions for the local spectra of CR species.

Figure 9.

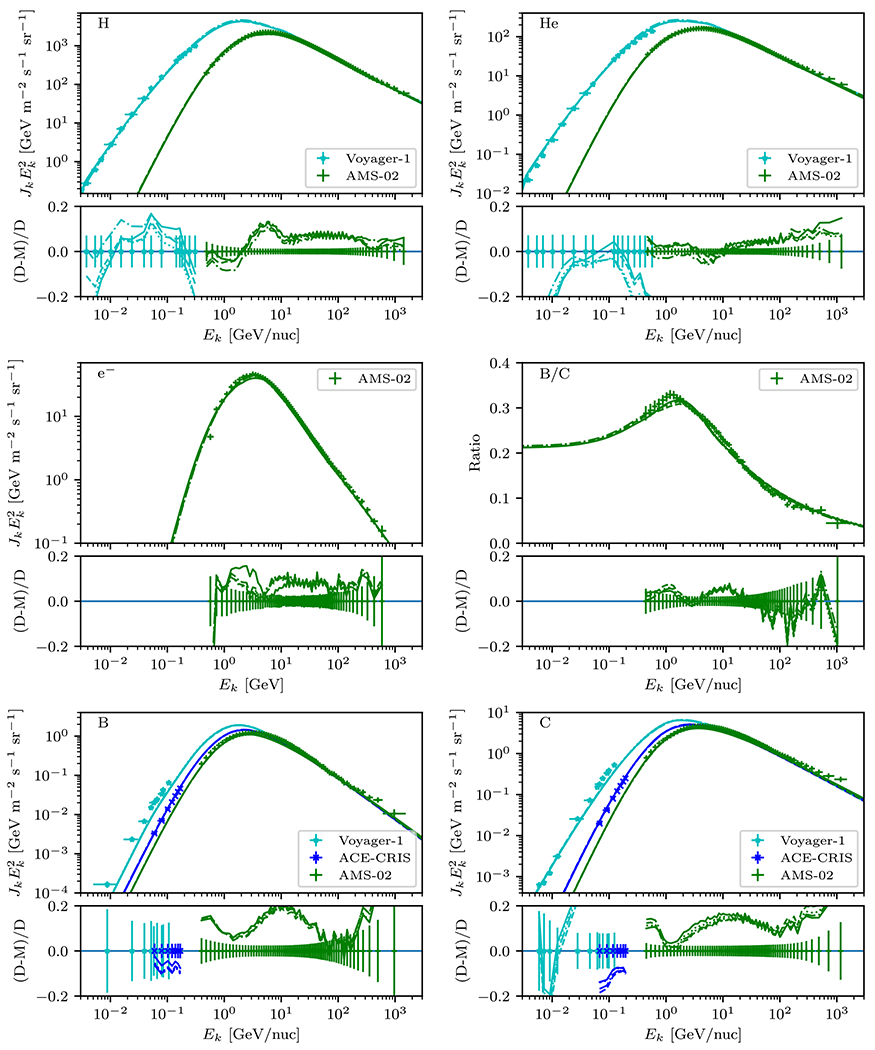
A comparison between the best-fit model predictions and observation of CR species near the solar system. The bottom panel of each subfigure shows the data subtracted from the model in units of data flux. References to the data are provided in Table 1. For uniformity of the presentation, AMS-02 data have been converted from rigidity to kinetic energy per nucleon units using the isotopic composition of each element as measured by ACE/CRIS, but the likelihood in the fitting procedure is calculated using rigidity. Different curves represent the four different models considered. The SA0 and SA50 cases with homogeneous diffusion are shown as solid and dotted lines, respectively, while the SA0 and SA50 cases with the modified diffusion are shown as dashed and dashed–dotted lines, respectively. Note that there is significant overlap between the lines for the different models for the top panels of the subfigures.

4. Discussion

Observations of the γ-ray emission from two PWNe made by HAWC (Abeysekara et al. 2017) provide direct insight into the diffusive properties of the ISM on small scales. Combined with direct measurements of the spectra of CR species in the solar neighborhood, the HAWC observations point to quite different diffusion coefficients in the space surrounding the Geminga and PSR B0656+14 PWNe compared to the ISM at large, with those associated with the former (SDZs) about two orders of magnitude smaller than the latter. The size of the SDZs is constrained by the upper limits of γ-ray emission at lower energies obtained by the MAGIC telescope to be ≲100 pc (Ahnen et al. 2016; Tang & Piran 2019). Observations by the Fermi-LAT may be used to further constrain the properties of the SDZs, although it may be difficult to break a degeneracy between the size of the diffusion zone and the shape of the injection spectra of CR electrons and positrons. This is particularly true for PWNe with a large proper motion, like the case of Geminga, which significantly affects the shape of the IC emission in the energy range of Fermi-LAT.

One of the main claims of Abeysekara et al. (2017) is that positrons produced by Geminga provide a negligible fraction of the positrons observed by the AMS-02 instrument (Aguilar et al. 2014). This statement is correct only if the diffusion coefficient is small in the entire region between Geminga and the solar system. Using a two-zone model consistent with both HAWC and MAGIC observations of Geminga, the predicted positron flux can vary over a wide range from a small fraction to almost the entire observed positron flux, dependent on the assumed properties of the SDZ and the injection spectrum. Even if the γ-ray emission can be constrained with the Fermi-LAT observations, changing the SDZ properties can result in a variation of the predicted flux by a factor of a few. This is illustrated by Scenarios A and C shown in Figures 5 and 6: while the predicted γ-ray emission differs only marginally, the predicted positron flux differs by about a factor of 5.

If the results for the two PWNe reported in Abeysekara et al. (2017) are not special cases, then it is likely that there are similar pockets of slow diffusion around many CR sources elsewhere in the Milky Way. In the likely case that the distribution of the SDZs follows the distribution of CR sources, CRs spend more time in the inner Milky Way and generally in the plane than in the outer Milky Way or its halo. Despite this, the predicted fluxes of secondary CR species near the solar system are not strongly affected (see Figure 9), and the propagation model parameters obtained with SDZs included are very close to those determined for models using homogeneous diffusion (see Table 2). This is a nontrivial result because the production rate of secondary CR species may also increase in the same regions of slow diffusion provided there is enough interstellar gas there. Compared to a model with homogeneous diffusion, the density of CRs should increase toward the inner Milky Way where the distribution of CR sources peaks. Correspondingly, the interstellar high-energy γ-ray emission should also be brighter in the direction of the inner Milky Way. At the same time, this differs from the results of the analysis of the Fermi-LAT data, which indicate that the gradient is even smaller than predicted by models with two-dimensional axisymmetric geometry and homogeneous diffusion (e.g., Abdo et al. 2010; Ackermann et al. 2011). An updated analysis that uses three-dimensional spatial models and includes localized propagation effects may lead to a new interpretation of the distribution of the diffuse emission and of the Fermi-LAT data.

In this study, the GALPROP framework, which is fully capable of calculating the spectrum and distribution of the expected interstellar diffuse γ-ray emission, was used, but because of the assumptions incorporated into the modified diffusion model, the predictions of the diffuse emission would be impractical. The sources of CRs are transient in nature and spatially localized and so are the potential SDZs associated with them. Depending on the exact nature of the SDZs, CR particles may be confined within these regions for a significant fraction of their residence time in the Milky Way, contrary to the assumption made in Equations (9) and (10). This may lead to the incorrect brightness distribution of the predicted γ-ray emission, which is sensitive to the details of the CR distribution throughout the Milky Way. Properly accounting for the transient nature of CR sources in the entire Milky Way is beyond the scope of this work, but will be addressed by a forthcoming paper.

One plausible explanation for the generation of SDZs near CR sources is the self-excitation of Alfvén waves by the CRs themselves as they stream out into the ISM. Such streaming instabilities have been discussed since the early 1970s (Skilling 1971) and are reviewed by Amato & Blasi (2018). The instabilities have also been used as a possible explanation for the slow diffusion around the Geminga pulsar (Evoli et al. 2018; Fang et al. 2019). The size and magnitude of the effect of streaming depends on the gradient of the CR distribution and the properties of the ISM, in particular the number density of neutrals and the Alfvén speed. Numerical studies of CR diffusion near SNRs reveal that lower number densities lead to smaller sizes for the SDZ, but also smaller changes in the diffusion constant (Nava et al. 2016, 2019). It is also expected that the injection spectrum is time dependent and may lead to an energy dependence of the diffusion coefficient in SDZs that is quite different from that in the ISM. Such models for the SDZ around Geminga would be in agreement with the HAWC observation that only constrains the diffusion at the highest energies, but produce a wide range of predictions for the expected flux of CR positrons near the solar system as well as for the expected spectrum of IC emission at low energies. In turn, this would result in an increased CR flux in the inner Galaxy that is dominated by the high-energy particles, leading to a hardening of the spectrum that has been indeed observed by the Fermi-LAT (Selig et al. 2015; Acero et al. 2016; Ajello et al. 2016; Yang et al. 2016). Furthermore, the production of secondary CR particles could be affected by the grammage accumulated by CR particles near the SNRs (D’Angelo et al. 2016) that should result in the modification of the behavior of the B/C ratio at high energies. Such modification has not been observed so far, at least up to rigidities ~10 TV (AMS-02 Aguilar et al. 2018). Exploration of these effects is deferred to future work.

To summarize, observations of the SDZs made by HAWC provide an interesting opportunity to get insight into the fairly complex details of the CR propagation phenomenon. The extension of these observations onto the whole Milky Way in specialibus generalia quaerimus is, however, a nontrivial task, and further understanding of the origin and properties of the SDZs is necessary to get a correct picture.