High-energy Gamma Rays from the Milky Way: Three-dimensional Spatial Models for the Cosmic-Ray and Radiation Field Densities in the Interstellar Medium

Abstract

High-energy γ-rays of interstellar origin are produced by the interaction of cosmic-ray (CR) particles with the diffuse gas and radiation fields in the Galaxy. The main features of this emission are well understood and are reproduced by existing CR propagation models employing 2D galactocentric cylindrically symmetrical geometry. However, the high-quality data from instruments like the Fermi Large Area Telescope reveal significant deviations from the model predictions on few to tens of degrees scales, indicating the need to include the details of the Galactic spiral structure and thus requiring 3D spatial modeling. In this paper, the high-energy interstellar emissions from the Galaxy are calculated using the new release of the GALPROP code employing 3D spatial models for the CR source and interstellar radiation field (ISRF) densities. Three models for the spatial distribution of CR sources are used that are differentiated by their relative proportion of input luminosity attributed to the smooth disk or spiral arms. Two ISRF models are developed based on stellar and dust spatial density distributions taken from the literature that reproduce local near- to far-infrared observations. The interstellar emission models that include arms and bulges for the CR source and ISRF densities provide plausible physical interpretations for features found in the residual maps from high-energy γ-ray data analysis. The 3D models for CR and ISRF densities provide a more realistic basis that can be used for the interpretation of the nonthermal interstellar emissions from the Galaxy.

1. Introduction

The high-energy γ-ray sky is dominated by the emissions produced by cosmic-ray (CR) particles interacting with matter and radiation fields in the interstellar medium (ISM) of the Milky Way. Observations of these interstellar emissions began with the OSO-III satellite in the late 1960s (Kraushaar et al. 1972) and were followed by the spaceborne experiments SAS-2 and COS-B in the early- and mid-1970s, COMPTEL and EGRET on the Compton Gamma-Ray Observatory (CGRO) in the 1990s, and the present-day Fermi Large Area Telescope (LAT; Atwood et al. 2009). Each of these instruments has represented a significant advance over its predecessor, with the Fermi-LAT providing the highest-sensitivity data to date for ≳30 MeV energies.

Because γ-rays are not deflected by magnetic fields, and their absorption in the ISM is negligible over Galactic distances up to energies of ~30 TeV (Moskalenko et al. 2006), they directly probe CR intensities and spectra in distant locations, far beyond the comparatively small region accessible by direct CR measurements. Describing the interstellar emissions using models for the CR propagation and interactions in the ISM has been very successful in explaining many features of the multiwavelength diffuse spectrum of the Galaxy (for a review, see Strong et al. 2007).

Physical modeling codes such as GALPROP (Moskalenko & Strong 1998, 2000a; Strong & Moskalenko 1998; Strong et al. 2000; Vladimirov et al. 2011) can reproduce the general features of the interstellar γ-ray emission over the whole sky, showing that the CR physics and interactions producing it are well understood. However, it is the residuals from when interstellar emission models (IEMs) are subtracted from the data that provide the potential for identifying new phenomena in high-energy γ-rays. Their understanding requires a careful assessment of the modeling inputs, in particular those related to the CR source and ISM densities.

To date, the most extensive study of high-energy IEMs has been made by the Fermi-LAT team (Ackermann et al. 2012) using a grid of 128 a priori GALPROP models normalized to reproduce local CR data. The grid entries are categorized by four CR source spatial density models from the literature (supernova remnants, two pulsars, and OB stars), multiple CR propagation halo sizes, and other parameters related to the interstellar gas. These IEMs employ a 2D⁴ galactocentric cylindrical symmetry, which has been the norm since the CGROera due to the limited quality of the γ-ray data, information on ISM distributions, and computing resources available. Examination of the residual maps developed in that work shows ~few to tens of degrees scale features that are asymmetric about the meridian defined by Galactic longitude l = 0° and the Galactic plane. Some of them are likely related to large-scale structures in the CR and ISM distributions that are not properly accounted for by the 2D-based IEMs. Another notable analysis is the Fermi-LAT team investigation of the γ-ray emission toward the inner Galaxy (Ajello et al. 2016, hereafter IG16), which uses a subset of the 128 model grid as baseline IEMs to develop estimates for the foreground/background from the Galaxy and enable extraction of the γ-ray emission from within ~1 kpc about the Galactic center (GC). An attempt to compensate for the modeling limitations of the 2D IEMs is made in that work by introducing new degrees of freedom for the inverse Compton (IC) component and fitting the γ-ray emission outside of a 15° × 15° region about the GC to estimate the foreground/background. An interesting result of the application of the procedure developed by IG16 is that for galactocentric radii R ~ 3–8 kpc, the baseline IEM predictions need to be scaled upward by ~20%–30% to account for the positive residuals for Galactic longitudes 15° ≲ ∣l∣ ≲ 80°. In addition, they found that the IC emission within R ~ 1–2 kpc of the GC is strongly dominant compared to that produced by CRs interacting with the gas there. These somewhat puzzling results are difficult to further interpret using the 2D-based IEMs. The larger parameter space afforded by 3D models is a logical next step in the evolution of physics-based modeling of the high-energy interstellar emissions from the Galaxy.

The GALPROP code has been capable of 3D CR propagation calculations since the beginning (Strong & Moskalenko 1998, 2001a, 2001b), but this mode has had limited usage because of the available data quality and computing resources necessary. Even the current data and theory do not provide for a complete 3D model of the ISM to be built. Thus, studying the effects of 3D structures on various observables is still at its early stages.

It was recognized early on that the 3D spatial density distribution of the CR sources within ~1 kpc of the solar system is particularly important for modeling the CR electron/positron data (Shen 1970; Shen & Mao 1971), which has been subsequently expanded with time-dependent calculations (e.g., Atoyan et al. 1995; Swordy 2003; Kobayashi et al. 2004). At larger scales, spiral arm models for the CR source density have been considered using analytic methods (e.g., Shaviv 2003) and with 3D numerical calculations employing toy-model setups (e.g., Shaviv et al. 2009; Gaggero et al. 2013; Benyamin et al. 2014; Kissmann et al. 2015), but their focus has been on the CR particle spatial distributions in the ISM, while consequences of the associated diffuse emissions were omitted.

Only relatively recently has 3D numerical modeling of the high-energy interstellar emissions from the Galaxy been done: Johannesson et al. (2013, 2016) using GALPROP, Kissmann et al. (2017) and Niederwanger et al. (2017) using the PICARD code, and Nava et al. (2017) using a Monte Carlo code. The GALPROP calculations use both 3D CR source and gas density models, while the PICARD-based and Nava et al. (2017) works employ a spiral arm model for the CR source densities but 2D models for the ISM densities. So far, 3D interstellar radiation field (ISRF) models have not been used, though they are necessary for comprehensive treatment of the CR electrons and positrons and their high-energy emissions.

In this paper, a study is made of the high-energy interstellar emissions calculated using 3D models for the CR source and ISRF densities in the Galaxy. The new release of the GALPROP code is employed for the CR propagation and high-energy interstellar emission calculations.⁵ Three CR source density models are considered that have the injected CR power distributed as an axisymmetric smooth disk, 50%/50% smooth disk/spiral arms, or 100% spiral arms. This work also uses the Fast Radiation Numerical Kalculation of Interstellar Emission (FRaNKIE) code (Porter et al. 2008, 2016) to calculate two ISRF Galaxy-wide spectral intensity distributions based on self-consistently derived stellar and dust density models taken from the literature that reproduce local near- to far-infrared observations. It will be shown that the combination of 3D CR source and ISRF density models produces an interstellar emission intensity at Earth that is more structured than the 2D case. Features related to the nonaxisymmetric structures included in the CR source and ISRF density models can be identified in the interstellar emission residual maps, which can provide useful information on the CR and ISRF densities far beyond where local CR data are able to probe. It will also be shown that, with the addition of a population of CR sources distributed according to the stellar bulge/bar spatial densities from either of the ISRF models, the models with spiral arms provide a plausible physical explanation for the puzzling results from the analysis of high-energy γ-rays toward the inner Galaxy obtained by the Fermi-LAT team (IG16).

2. Models

2.1. Cosmic-Ray Propagation (GALPROP Code)

Theoretical understanding of CR propagation in the ISM is the framework that the GALPROP code is built around. The key idea is that all CR-related data, including direct measurements, γ-rays, synchrotron radiation, etc., are subject to the same physics and must therefore be modeled simultaneously. The GALPROP project now has nearly 20 yr of development behind it. The original FORTRAN90 code has been public since 1998, and a rewritten C++ version was produced in 2001. The last major public source code release was version 54 (Vladimirov et al. 2011). A new version of the GALPROP code is made available with this paper following improvements made over a number of years (Jóhannesson et al. 2016; Moskalenko et al. 2016); the new features are summarized in the Appendix. The latest releases are always available at the dedicated website, which also provides the facility to run GALPROP via a web browser interface.⁶ The website also contains links to all GALPROP team publications, together with detailed information on CR propagation and the different versions of the code and supporting data sets. Below, a brief review of the CR production and propagation relevant to the present paper is made. Further details are given by Trotta et al. (2011), and more information can be found in the review by Strong et al. (2007).

GALPROP numerically solves the system of partial differential equations describing the particle transport with a given source distribution and boundary conditions for all species of CRs. Propagation is described using the diffusion-reacceleration equation, which has proven to be remarkably successful at modeling transport processes in the ISM. The processes involved include diffusive reacceleration and, for nuclei, nuclear spallation, secondary particle production, radioactive decay, electron capture and stripping, electron knock-on, and electron K-capture, in addition to energy loss from ionization and Coulomb interactions. For CR electrons and positrons, important processes are the energy losses due to ionization, Coulomb scattering, bremsstrahlung (with the neutral and ionized gas), IC scattering, and synchrotron emission.

Galactic properties on large scales, including the diffusion coefficient, halo size, Alfvén velocity, and/or advection velocity, as well as the mechanisms and sites of CR acceleration, can be probed by measuring stable and radioactive secondary CR nuclei. The ratio of the halo size to the diffusion coefficient can be constrained by measuring the abundance of stable secondaries such as B. Radioactive isotopes (¹⁰Be, ²⁶Al, ³⁶Cl, ⁵⁴Mn) then allow the resulting degeneracy to be lifted (e.g., Ptuskin & Soutoul 1998; Strong & Moskalenko 1998; Webber & Soutoul 1998; Moskalenko et al. 2001). However, the interpretation of the peaks observed in the secondary-to-primary ratios (e.g., B/C, [Sc+Ti+V]/Fe) around energies of a few GeV/nucleon, remains model-dependent.

CR propagation in the heliosphere is described by the Parker (1965) equation. The modulated fluxes significantly differ from the interstellar spectra below energies of ~20–50 GeV/nucleon but correspond to the ones actually measured by balloon-borne and spacecraft instruments. Spatial diffusion, convection with the solar wind, drifts, and adiabatic cooling are the main mechanisms that determine the transport of CRs to the inner heliosphere. These effects have been incorporated into realistic (time-dependent, 3D) models (e.g., Florinski et al. 2003; Potgieter & Langner 2004; Langner et al. 2006; Boschini et al. 2017). The “force-field” approximation that is ordinarily used (Gleeson & Axford 1968) instead characterizes the modulation effect as it varies over the solar cycle using a single parameter: the “modulation potential.” Despite having no predictive power, the force-field approximation is a useful low-energy parameterization of the modulated spectrum for a given interstellar spectrum.

The focus in this work is on the CR-induced γ-ray emission from different realizations of the CR source and ISRF distributions. The propagation model is therefore limited to diffusive reacceleration with an isotropic and homogeneous diffusion coefficient that has a power-law dependence with rigidity. The CR injection spectra are modeled as rigidity-dependent broken power laws with parameters derived as in a recent study (Jóhannesson et al. 2016). Electrons, protons, and He each have two breaks, while elements with Z > 2 are modeled with a single break. The extra break for the low-mass elements is to model the spectral change observed at rigidities above 100 GV (Adriani et al. 2011; Aguilar et al. 2014, 2015a). The CR source density distribution is a mixture of a disk and four spiral arms that have the same exponential scale height (200 pc) perpendicular to the Galactic plane. The smooth disk spatial density follows the radial distribution of pulsars as given by Yusifov & Küçük (2004). The spiral arm spatial density is that of the four major arms in the R12 model (Section 2.2.3) and assumes an identical injection of CR power by each arm. Three such models are considered with a 100% (2D) disk, 50% disk/50% arm, and 100% spiral arm contribution. These are termed SA0, SA50, and SA100 following the proportion of injected CR luminosity by the spiral arms. The normalization for the injected CR power of each source density model is obtained by requiring the propagated CR intensities to agree with the local CR observations, where all calculations made in this paper use the IAU-recommended Sun-GC distance of R_S = 8.5 kpc (Kerr & Lynden-Bell 1986).

2.2. Interstellar Radiation Field

The ISRF is the result of emission by stars and the scattering, absorption, and reemission of absorbed starlight by dust in the ISM. Early models for the ISRF were motivated to enable predictions of the Galactic IC emission at MeV γ-ray energies (Cowsik & Voges 1974; Piccinotti & Bignami 1976; Shukla & Paul 1976; Bignami & Piccinotti 1977). Mathis et al. (1983; hereafter MMP83) presented calculations of the ISRF from UV to far-infrared wavelengths at a few locations with a model that has been widely used. Bloemen (1985) extended the MMP83 work to study the IC emission in the context of COS-B data but noted the model shortcomings toward the inner Galaxy because of the artificial cutoff for R ≲ 3 kpc in the stellar spatial distribution. Chi & Wolfendale (1991) augmented the MMP83 stellar model with the dust emission results described by Cox et al. (1986) and recalculated the spatial distribution of the ISRF energy density. This work was used by the EGRET team as input for their modeling of the high-energy interstellar γ-ray emission (Bertsch et al. 1993; Hunter et al. 1997). Strong et al. (2000) employed stellar population models (Wainscoat et al. 1992) and dust emissivities derived from COBE/DIRBE data (Sodroski et al. 1997) to reevaluate the ISRF energy density distribution.

Despite the increasing sophistication of the inputs, these early calculations were not self-consistent because they did not couple the starlight absorption by dust with reemission. Porter & Strong (2005) described the first work to combine the stellar emission with a self-consistent dust scattering/absorption/reemission radiation transfer calculation using the FRaNKIE code. Porter et al. (2008) extended the calculations to produce the spatially varying anisotropic intensity of the ISRF using a 2D stellar and dust density distribution. The Fermi-LAT team (Ackermann et al. 2012) used a revision of the Porter et al. (2008) work for the study of high-energy γ-ray IEMs calculated using the GALPROP CR propagation code. The spectral intensity distribution used for the Ackermann et al. (2012) study represents the latest publicly available model for the ISRF that is distributed from the GALPROP website.⁷

The Galactic structure is spatially complex with spiral arms (e.g., Vallée 2014, 2016, and references therein), a central region that is dominated by a bulge/bar complex (e.g., Hammersley et al. 2000; Benjamin et al. 2005; Cabrera-Lavers et al. 2007), and warped stellar/dust disks (e.g., Freudenreich 1998, hereafter F98). Sophisticated 3D models have been developed for the spatial densities of stellar populations (e.g., Robin & Creze 1986; Wainscoat et al. 1992). But their emphasis is on calculating counts of stars as observed from Earth. Three-dimensional spatial models that include asymmetric elements, such as a central bulge/bar, spiral arms, and warped stellar/dust disks, have been fit to infrared data (e.g., F98; Drimmel & Spergel 2001), but they obtain only emissivities and do not make radiation transfer calculations. The most comprehensive 3D modeling to date (Robitaille et al. 2012, hereafter R12) uses the SKY model (Wainscoat et al. 1992; Cohen 1993, 1994) as input for the HYPERION code (Robitaille 2011) to self-consistently calculate predictions for local observed intensities from near- to far-infrared wavelengths. R12 produced an optimized version of the SKY model that is consistent with Spitzer and IRAS data in a narrow band of latitude about the Galactic plane for longitudes −60° ⩽ l ⩽ 60°. However, the spectral intensity was only evaluated locally for comparison with the data.

There is no unique description of the Galactic structure, even with the diversity of models so far employed to fit for the different spatial distributions of stars and dust in the Galaxy. A hybrid combining different spatial elements and their parameters from the collection studied in the literature without a full fitting procedure can lead to inconsistent models. This is because of convariance between the presence of individual elements and their derived parameters, particularly for the major components such as the stellar disk, arms, and bulge. Because the purpose of this paper is to make the first steps toward incorporating 3D spatial structure into the description of the ISRF employed by CR propagation and interstellar emissions codes like GALPROP, such an optimization is not made. Instead, two models of the stellar and dust distributions are chosen from the literature: the R12 and F98 models, whose references are given above. They employ different spatial densities for both the stars and the dust but produce intensities very similar to those of the data for near- to far-infrared wavelengths at the solar system location (see below). The spatial differences can be summarized: the former model has an axisymmetric bulge and smooth disk and major spiral arms and local arm segments near the solar system, while the latter has a nonaxisymmetric bulge and smooth disk; the details are given in Sections 2.2.3 and 2.2.4.

The FRaNKIE code is used to calculate the Galaxy-wide spectral intensity distribution for the R12 and F98 models, which is necessary for the lepton IC energy losses and γ-ray production. Its solution method for the radiation transport has evolved from the ray-tracing method initially employed by Porter & Strong (2005) to using simulation techniques similar to other Monte Carlo radiation transfer codes (e.g., Gordon et al. 2001; Bianchi 2008; Robitaille et al. 2012; Camps & Baes 2015), where luminosity packets are injected according to user-specified spatial and spectral distributions, and the propagation history of each packet is traced to produce observables that are recorded at observer locations. The propagation includes self-consistent scattering, absorption, and reemission by dust, the optical properties and spatial distributions of which are also user-specified. A description of the code is provided by Porter et al. (2016), and recent developments will be covered elsewhere (T. A. Porter et al. 2017, in preparation). The essential components for a model “run” (stellar and dust distributions) are described below, and the simulation geometry and other details are given in Section 3.2.

2.2.1. Stellar Luminosity Density

The input spectral luminosity density follows the SKY model approach of representing the stellar content of the Galaxy using a table of spectral types (also similar to earlier work; e.g., Garwood & Jones 1987). The table includes early-type stars, main-sequence stars, asymptotic branch giants and other giants/supergiants, and exotics. There are 87 types (see Table 2 of Wainscoat et al. 1992) characterized by a local disk number density, fractional contribution across the spatial components of the SKY model (bulge, disk, ring, arms, halo), scale height perpendicular to the Galactic plane, and spectral information for photometric filters from UV to mid-infrared wavelengths. Number densities of individual types were determined by Wainscoat et al. (1992) by adjusting them to obtain a luminosity function agreeing with data at visual and infrared wavelengths. The relative contribution of the stellar types across the spatial components was assigned by Wainscoat et al. (1992) based on physical considerations (see their Section 2.2.4 for details): the arms and star-forming ring contain predominantly young stars (mainly spectral types O through A), with the smooth disk containing all types and the bulge absenting the young and hot stars and star-forming regions.

R12 noted that the spectral characteristics of the early-type stars in the SKY model did not adequately represent the UV portion of the spectrum, which is important for the heating of the smallest dust particles. They improved the spectral representation at these wavelengths by using photospheric models from Castelli & Kurucz (2004) that were rescaled to the Wainscoat et al. (1992) absolute magnitudes. In addition, R12 modified the early-type stellar content of the spiral arms to further optimize the model, in particular depleting arms 1 and 1′ of stellar types other than O and B and increasing the number densities of O and B types for arms 2 and 2′ (see Section 2.2.3 for the meaning of the arm designations). Both of these modifications are employed in this paper.

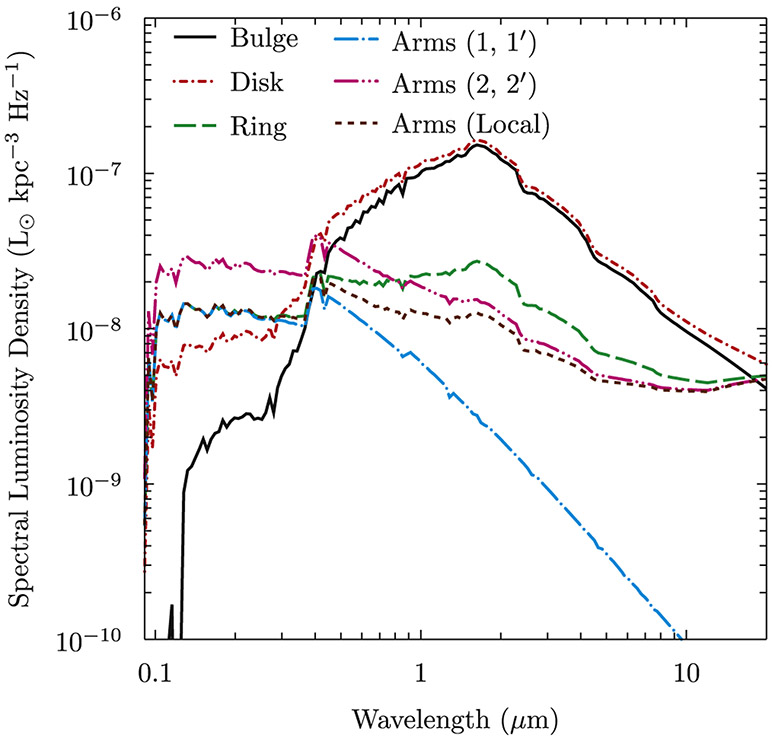
Figure 1 shows the spectral luminosity density for the major components of the R12 model at their normalization position in the plane (GC for the bulge, R_S for the disk and arms, R_R = 0.45 R_S for the ring; see Section 2.2.3). Each curve is obtained by summing over the 87 type spectra weighted by their spatial densities for the respective geometrical component. For the F98 model, the bulge, disk, and local arm luminosity densities shown in Figure 1 are used for the bar, old disk, and “average” arm components (see Section 2.2.4).

Figure 1.

Spectral luminosity density for the major R12 model components. Line styles: solid, bulge; short–dashed–dotted, disk; long–dashed, ring; long–dashed–dotted, arms 1 and 1′; long–dashed–double–dotted, arms 2 and 2′; short–dashed, local arms, local arms. See Section 2.2.3 for the meaning of the arm designations.

2.2.2. Dust Properties

The dust composition model of Draine & Li (2007) is used in this paper. The model describes a mixture of neutral and ionized polycyclic aromatic hydrocarbon (PAH) molecules and carbonaceous and amorphous silicate dust grains based on earlier work (Li & Draine 2001) with adjustments (Draine 2003) and optimizations to obtain better agreement with Spitzer data. Each species is characterized by a size distribution function (Weingartner & Draine 2001). The dust grains in the model are assumed to be spherical, with the absorption and scattering cross sections computed for PAH and carbonaceous grains (Li & Draine 2001) and “smoothed” astronomical silicate (Draine & Lee 1984; Laor & Draine 1993; Weingartner & Draine 2001) using a Mie code with data taken from B. T. Draine’s website.⁸

2.2.3. R12 Spatial Model

The R12 spatial model has the same five stellar spatial components as the SKY model: axisymmetric bulge, exponential disk, star-forming ring, spiral arms (four major and two minor local “spurs”), and halo. Each stellar spatial component is characterized by a normalizing factor, spatial density distribution, and spectral luminosity density (Section 2.2.1). R12 retained the same global normalizing factors for the bulge, ring, arms, and halo (ρ_B, ρ_R, ρ_A, and ρ_H) as determined by Wainscoat et al. (1992). The R12 optimizations made compared to the SKY model are for the geometric parameters and stellar content of the spiral arms and dust density distribution to better describe Spitzer and IRAS data.

The bulge stellar density has the form

$${\rho }_{\text{bulge}}(R,Z)={\rho }_B\sum _i{\rho }_{\text{bulge},\mathrm{i}}{S}^{-1.8}{e}^{-S^3},$$ (1)

where ρ_B = 3.6 and

$$S=\frac{\sqrt{R^2+K_1^2{Z}^2}}{R_1},$$ (2)

where the bulge axis ratio and scale radius are K₁ = 1.6 and R₁ = 2 kpc, respectively. The sum is over the individual space densities for the i = 1, … ,87 stellar types used for the spectral luminosity model (Section 2.2.1).

The stellar disk has the functional form

$${\rho }_{\text{disk}}(R,Z)=\sum _i{\rho }_{\text{disk},i}{e}^{-(R-R_S)∕D_R}{e}^{-\mid Z\mid ∕H_{Z,i}},$$ (3)

where the radial scale length is D_R = 3.5 kpc and ρ_disk,i and H_Z,i are the space density and scale height perpendicular to the Galactic plane, respectively, of the ith stellar type.

The star-forming ring stellar density is Gaussian in R centered on R_R = 0.45 R_S, with half-width σ_R = 0.064 R_S.

$${\rho }_{\text{ring}}(R,Z)={\rho }_R\sum _i{\rho }_{\text{ring},i}{e}^{-(R-R_R{)}^2∕2{\sigma }_R^2}{e}^{-\mid Z\mid ∕H_{Z,i}},$$ (4)

where ρ_R = 25 and the sum is again over stellar types with the scale heights H_Z,i as for Equation (3).

The spiral arm component has four main arms and two local (to the solar system) “spurs.” In the original SKY model, the four main logarithmic arms have equal weight with a single local arm segment. Cohen (1994) split the local segment into two smaller spurs. The R12 arms are optimized by adjusting their start positions and changing the density profile perpendicular to the arm axis from a step function for the SKY model to a Gaussian. Also, the densities of the O and B spectral types for arms 2 and 2’ (Table 2) are increased by a factor of 2, while all but the O and B spectral types are eliminated from arms 1 and 1’. R12 identified arms 1 and 1′ as the Norma and Sagittarius arms and arms 2 and 2′ as the Scutum–Centaurus and Perseus arms, respectively.

Table 2.

Data Used for Determining the Propagation Parameters

Instrument	Isotopes	References
AMS-02 (2011–2016)	B/C	I
AMS-02 (2011–2013)	e −	II
AMS-02 (2011–2013)	H	III
AMS-02 (2011–2013)	He	IV
HEA03-C2 (1979–1980)	B, C, O, Ne, Mg, Si	V
Voyager-1 (2012–2015)	H, He, B, C, O, Ne, Mg, Si	VI
PAMELA (2006–2008)	B, C	VII

References. I: Aguilar et al. (2016); II: Aguilar et al. (2014); III: Aguilar et al. (2015a); IV: Aguilar et al. (2015b); V: Engelmann et al. (1990); VI: Cummings et al. (2016); VII: Adriani et al. (2014).

The functional form for the arm shape is

$${\varphi }_j(R)={\alpha }_j\log \left(\frac{R}{R_{\text{min},j}}\right)+{\varphi }_{\text{min},j},$$ (5)

where α_j, R_min,j, and ϕ_min,j are parameters that are given in Table 1. The major arms have an angular extent of 6 rad starting from their minimum radii, while the local spurs are considerably shorter (0.55 rad). The arms have the same radial and vertical and profile function as the stellar disk (Equation (3)) with the sum over stellar types including the fractional densities as the other components, and the global normalization pre-factor ρ_A = 5. For the main arms (j = 1, 1′, 2, 2′), the Gaussian profile perpendicular to the arm axis has σ_j = 0.55 kpc. The local spurs are modeled as a step function following the original SKY model with density given by Equation (3) inside and zero elsewhere.

Table 1.

R12 Spiral Arm Parameters

Arm	α	Rmin (kpc)	ϕmin (rad)	Extent (rad)	σ (kpc)	Width (kpc)
1	4.18	3.800	0.234	6.00	0.55	…
1′	4.18	3.800	3.376	6.00	0.55	…
2	4.19	4.500	5.425	6.00	0.55	…
2′	4.19	4.500	2.283	6.00	0.55	…
L	4.57	8.100	5.847	0.55	…	0.30
L′	4.57	7.591	5.847	0.55	…	0.30

The fifth component is the ellipsoidal stellar halo, but its contribution is minor and thus is omitted from the calculations.

The dust spatial density for the R12 model is an exponential disk with a central hole

$${\rho }_{\text{dust}}(R,Z)={\rho }_{\text{dust},0}{e}^{-\frac{\mid Z\mid }{H_{\text{dust}}}}\times \{\begin{array}{cc}{f}_0{e}^{-\frac{(R-{\mu }_0{)}^2}{2{\sigma }_0^2}},\hfill & R<R_{\text{smooth}}\hfill \\ e^{-\frac{R}{D_R}},\hfill & R⩾R_{\text{smooth}}\hfill \end{array}\phantom{\}},$$ (6)

where ρ_dust,0 = 10⁻²⁵ g cm⁻³, H_dust = 100 pc, and R_smooth, f₀ ensure a smooth transition between the exponential radial profile and the inner hole,

$$R_{\text{smooth}}={\sigma }_0^2∕D_R+{\mu }_0,$$ (7)

$$f_0=\frac{e^{-R_{\text{smooth}}∕D_R}}{e^{-(R_{\text{smooth}}-{\mu }_0{)}^2∕2{\sigma }_0^2}}.$$ (8)

R12 tried various values of μ₀ and σ₀, Ending that μ₀ = 4.5 kpc and σ₀ = 1 kpc provided adequate agreement for the far-infrared data. These values are used in this paper.

2.2.4. F98 Spatial Model

The F98 model has a nonaxisymmetric stellar bulge and exponential disks for the stellar and dust distributions. F98 determined the parameters of the spatial components by fitting to COBE/DIRBE near-infrared (1.25–4.9 μm) data. A separate emissivity normalization was obtained from the fits for the bar and disk stellar and dust distributions for each of the four DIRBE wavebands used in the study, but the spatial parameters (e.g., stellar or dust disk radial scale length) remain the same across all wavebands. F98 evaluated different models based on the bar radial spatial profile: Model S (sech²), Model E (exponential-to-power), and Model P (power-law-with-core). The best-fit Model S for R_S = 8.5 kpc is used in this paper.

The central region of the Galaxy in this model is dominated by an ellipsoidal bar. Its spatial distribution is given by

$$\begin{gathered} {\rho }_{\text{bar}}(R,\varphi ,Z)={\rho }_{\text{bar},0}{\text{sech}}^2(R_{\mathrm{b}}) \\ \times \{\begin{array}{cc}1,\hfill & R⩽R_{\text{end}}\hfill \\ e^{-[(R_{\mathrm{b}}-R_{\text{end}})∕H_{\text{end}}{]}^2},\hfill & R>R_{\text{end}}\hfill \end{array}\phantom{\}}, \end{gathered}$$ (9)

where ρ_bar,0 is the normalization and R_b is the bar radial coordinate,

$$R_{\mathrm{b}}^{C_{\parallel }}=R_{\perp }^{C_{\parallel }}+(\mid Z^{\prime }\mid ∕A_Z{)}^{C_{\parallel }}$$ (10)

$$R_{\perp }^{C_{\perp }}=(\mid X^{\prime }\mid ∕A_X{)}^{C_{\perp }}+(\mid Y^{\prime }\mid ∕A_Y{)}^{C_{\perp }},$$ (11)

with X′, Y′, and Z′ evaluated in the bar frame. This is described by body-centered axes with a rotation⁹ with respect to the Sun-GC line of ϕ_bar and a pitch angle β_bar, where the latter is the angle between the bar major axis and the Galactic plane, and A_X, A_Y, and A_Z are the bar axis scale lengths.

The stellar and dust disks are exponential in R with an inner and outer truncation, with a sech² distribution in Z and R-dependent warping. Their spatial distribution is given by the expression

$${\rho }_{\text{disk}}(R,Z)={\rho }_{\text{disk},0}H(R,\varphi )e^{-R∕H_R}{\text{sech}}^2\left(\frac{Z-\overline{Z}}{H_Z}\right),$$ (12)

where ρ_disk,0 is the disk normalization; H(R, ϕ) is the hole function describing the inner radial truncation,

$$H(R,\varphi )=1-e^{-(R_H∕D_H{)}^{{\alpha }_H}},$$ (13)

X} with D_H the hole scale radius, $R_H^2=X^{\prime 2}+(ϵY^{\prime }{)}^2$ evaluated in bar-centered coordinates with X′ the bar major axis and ϵ the hole eccentricity; H_R is the disk radial scale length; H_Z is the disk scale height; and $\overline{Z}\equiv \overline{Z}(R,\varphi )$ models the warp so that $\overline{Z}=0$ for u = R − R_W ⩽ 0, while for u > 0,

$$\overline{Z}(R,\varphi )=A(c_{1}u+c_2{u}^2+c_3{u}^3)\sin (\varphi -{\varphi }_w)$$ (14)

with a straight line of nodes at azimuth ϕ_w. For the “old” stellar disk, A = 1 while it is a fit parameter for the dust disk. The stellar and dust disks are smoothly truncated for R > R_max by setting H_R = 0.5 kpc in Equation (12).

Table 4 (column 3) from F98 and Figure 12 from the same work (for the disk warp polynomial coefficients) give the values for the various spatial parameters described above, and they are used in this paper. The emissivities for the old stellar disk and bar from F98 are given only for the four DIRBE wavebands used in that analysis. For the FRaNKIE calculations, the spectral luminosity density from UV to longer wavelengths is needed. To set these for the old stellar disk and bar, the disk and bulge spectral luminosity densities from Figure 1 are folded with the DIRBE spectral responses¹⁰ and scaled to the F98 emissivities to provide the correct normalization. By contrast, the emissivities for the dust disk over the DIRBE wavebands determined by F98 represent a mixture of contributions by stars, scattering, and stochastic heating of very small dust grains by early-type stars. However, the emissivity of the latter is not linearly related to the input luminosity of the young stars that are acting as heating sources, and so it is not possible to obtain a simple rescaling to determine the normalization for the spectral luminosity density, as done for the old stellar disk and bar. To account for the contributions by young stars, the spatial distribution given by F98 for the heating sources for the dust disk is used: it is a warped exponential disk with the same radial scale length as the old disk but with a scale height/warp that follows the dust disk. The original SKY model spiral arm spectral luminosity density (“local” arm in Figure 1) is taken for its input luminosity spectrum, because this represents an average spectrum that does not have any of the major arm specific optimizations introduced by R12. The young star input luminosity for the F98 model is then obtained using the FRaNKIE calculations (Section 3.2) by adjusting its normalization so that the predicted 3.5/4.9 μm profiles, which also include the old disk and bar contributions, agree with the data. The dust spatial distribution employs the F98 dust disk, assuming the fitted parameters for the scale lengths/heights, hole, and warp from that paper. Its normalization is taken to be the same as the R12 dust density at R_S = 8.5 kpc, corresponding to a central normalization of ρ_dust,0 = 1.5 × 10⁻²⁵ g cm⁻³ using the dust properties model described in Section 2.2.2.¹¹

Figure 12.

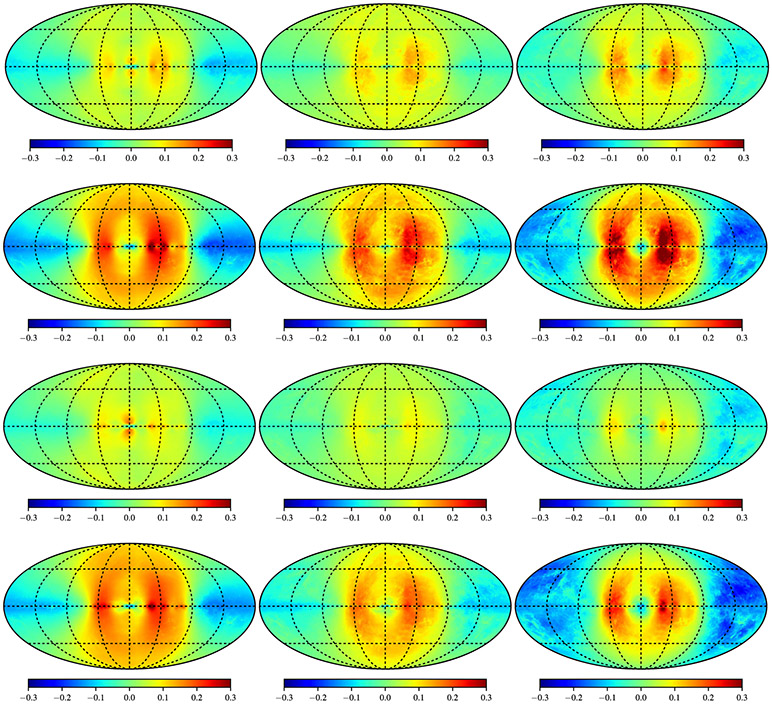
Fractional residual maps for the SA50–R12 (first row), SA100–R12 (second row), SA50–F98 (third row), and SA100–F98 (fourth row) model combinations with the SA0–Std reference case. Left to right are the fractional residuals for a given model combination with increasing energy at 10.6 MeV, 1.2 GeV, and 79 GeV. The maps are in Galactic coordinates with l, b = 0°, 0° at the center. The longitude meridians and latitude parallels have 45° spacing.

3. Calculations

3.1. Cosmic Rays

The generation of secondary CRs depends on the amount of matter traversed as their primary counterparts propagate through the ISM from their sources. Thus, the secondary intensities and spectra in the Galaxy depend on the details of the assumed propagation model, as well as the spatial distributions of the CR source and interstellar gas densities. The parameters of the CR propagation therefore need to be tuned dependently on the CR source spatial density and gas density¹² models for a self-consistent description when reproducing observations of CR secondary species, such as B.

For each of the SA0, SA50, and SA100 CR source densities, the propagation model parameter tuning is made using a maximum-likelihood fit employing the data listed in Table 2. To reduce the number of parameters in each fit, the procedure is split into two stages, similar to the analysis described by Cummings et al. (2016). The propagation model parameters that are fit for are listed in Table 3. There is a strong degeneracy between the halo height and the normalization of the diffusion coefficient. Even though using radio nuclei (¹⁰Be, ²⁶Al, ³⁶Cl, ⁵⁴Mn) constrains the halo size significantly, the range of possible values remains quite wide. Instead of fitting for both simultaneously, the halo height is set to 6 kpc, in good agreement with previous analyses (e.g., Moskalenko et al. 2005; Orlando & Strong 2013; Jóhannesson et al. 2016). The first stage of the procedure fits for the other propagation model parameters together with the injection spectra and abundances of Z > 2 elements. With the propagation parameters and the injection spectra for Z > 2 determined, they are held constant. The injection spectra for electrons, protons, and He are then obtained in the second stage of the procedure. To reduce the number of parameters, the injection spectrum of He is coupled with that of the protons, such that the locations of the breaks are the same and all the indices are smaller by a value Δ_He that is a parameter in the fit procedure. This is similar to the linking of the proton and He spectra for the analysis described by Jóhannesson et al. (2016). Fourteen parameters are determined by the first stage of the procedure, while the second stage fits for 15 parameter values.

Table 3.

Final Model Parameters

Parameter	SA0	SA50	SA100
D0,xx [1028 cm2 s−1]a	4.37	4.47	4.71
δ a	0.494	0.508	0.483
νA[km s−1]	7.64	9.19	7.34
γ 0 b	1.47	1.61	1.66
γ 1 b	2.366	2.350	2.381
R1 [GV]b	3.64	3.92	4.12
γ 0,H	1.74	1.78	1.74
γ 1,H b	2.350	2.342	2.351
γ 2,H b	2.178	2.206	2.207
R1,H [GV]b	5.78	6.18	5.62
R2,H [GV]b	304	226	332
ΔHe	0.026	0.018	0.017
γ 0,e b	1.63	1.66	1.61
γ 1,e b	2.765	2.756	2.756
γ 2,e b	2.378	2.332	2.329
R1,e [GV]b	5.95	6.18	6.06
R2,e[GV]b	103	120	100
Jp [10−9 cm−2 s−1 sr−1 MeV−1]c	4.598	4.562	4.599
Je [10−11 cm−2 s−1 sr−1 MeV−1]c	1.221	1.209	1.250
q0,4He/q0,p × 10−6d	93892	94157	93416
q0,12C/q0,p × 10−6d	2882	2867	2746
q0,16O/q0,p × 10−6d	3780	3873	3645
q0,20Ne/q0,p × 10−6d	356	358	333
q0,24Mg/q0,p × 10−6d	644	654	609
q0,28Si/q0,p × 10−6d	742	762	718
ΦHEAO3–C2 [MV]e	857	849	827
ΦPAMELA [MV]e	578	578	572
ΦAMS [MV]e	610	640	594

Notes.

^aD(R) ∝ βR^δ; D(R) is normalized to D₀ at 4 GV.

^bThe injection spectrum is parameterized as $q(R)\propto R_0^{\gamma }$ for R < R₁ q(R) ∝ R^γ1 for R₁ < R < R₂, and q(r) ∝ R^γ2 for R > R₂. The spectral shape of the injection spectrum is the same for all species except H.

^cThe proton and e⁻ flux is normalized at the solar location at a kinetic energy of 100 GeV.

^dThe injection spectra for isotopes are adjusted as a ratio of the proton injection spectrum at 100 GeV. The isotopes not listed here have the same value as that found in Jóhannesson et al. (2016).

^eThe force-field approximation is used for the solar modulation of CRs. The modulation potential is assumed to be dependent only on the time and location of the observations.

The results of the fitting procedure are given for the SA0, SA50, and SA100 CR source density models in Table 3. The calculations are made for a Cartesian spatial grid with dimensions ±20 kpc for the X and Y coordinates, with ΔX, Y, Z = 0.125 kpc and a CR kinetic energy grid covering 10 MeV/nucleon to 1 TeV/nucleon with logarithmic spacing at 10 bins/decade. The span and sampling of the spatial and energy grids are chosen to enable realistic and efficient computations given the available resources.¹³ The spatial grid subdivision size allows adequate sampling of the CR and ISM density distributions. The X, Y size of the grid is sufficient to ensure that CR leakage from the Galaxy is determined by the size of the confinement region perpendicular to the Galactic plane at the solar system location where the propagation model parameters are fitted; it has been shown that there is only a weak effect on parameters determined for 2D models using 20 and 30 kpc maximum radial boundaries (Ackermann et al. 2012).

The change in parameters between the models is small but statistically significant. However, there is no obvious trend for most of the parameters. That is, the values for SA50 are not always between the values for SA0 and SA100. Note that the propagation parameters ν_A and δ determined here differ from those obtained by Jóhannesson et al. (2016) and Cummings et al. (2016) because of the data sets employed. The larger value of the δ parameter comes from the reduced Alfvén speed obtained by the fits: higher Alfvén speeds create a larger bump around ~1 GeV for the B/C than exhibited by the AMS-02 data that are used for this paper.

The CR model spectra and data are shown in Figure 2. The calculated spectra agree well with the data and are generally well within the data uncertainties, where the experiment systematic and statistical are added in quadrature. The model predictions are very similar, being within ~5% of each other. But some deviations from the data occur; in particular, the He spectrum is overpredicted between 1 and 10 GeV, while the proton spectrum is underpredicted for the same energy range. This is an indication that more freedom is needed for the injection spectrum of He than is allowed by the fitting procedure. However, the discrepancies are within ~20%, which is a sufficient level of agreement for the calculations in this paper.

Figure 2.

CR data with CR source density models SA0 (solid curves), SA50 (dotted curves), and SA100 (dashed curves) overlaid. Protons (top left), He (top right), e⁻ (middle left), B/C (middle right), B (bottom left), and C (bottom right).

For the Z > 2 elements, the last data point in the spectrum from HEAO3-C2 seems to be overpredicted. Without further observations at higher energies, it is difficult to say if this is due to unknown systematic uncertainties in the data or incorrect model predictions. The PAMELA C spectrum indicates that the modeled spectrum may be slightly too hard, but this small discrepancy for the high-energy CR spectra will not affect the interstellar emission calculations (Section 3.3). The modeled spectra agree well with the B/C observations from AMS-02, even though there is some underprediction at the highest energies while overpredicting at the lower energies. The low-energy AMS-02 data is in tension with the B and C spectra of HEAO3-C2 and PAMELA for the same energy ranges. This may be due to the force-field approximation that is used for treating the solar modulation here, which is likely providing an inadequate description during the high solar activity period of the AMS-02 data-taking. There are also hints of this disagreement in the proton and He spectra, where the Voyager data is not well matched by the models.

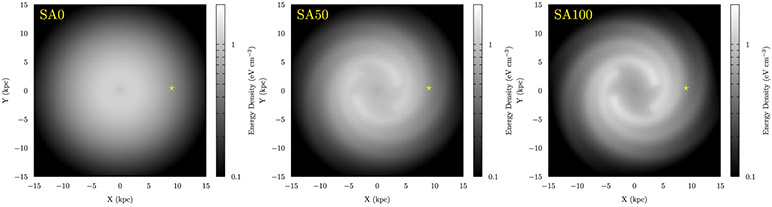
Figure 3 shows the spatial distribution for the integrated CR energy densities at the plane for each of the source density models used in this paper. The bulk of the CR energy density (and hence CR pressure) comes from protons with momenta ~1–few GeV/c. The long residence times at these energies produce a smoothing of the CRs in the ISM compared to the initial source density distributions. This is particularly evident for the SA100 model (right panel), where the bulk of the injection along each of the arms is narrowly concentrated; but inside the solar circle, the subsequent propagation smooths the CRs into a quasi-ring of high energy density for R ~ 3–7 kpc. Outside the plane, the decrease of the total CR energy density is approximately logarithmic with increasing ∣Z∣ near the GC and drops to zero at the halo edge according to the boundary condition there.

Figure 3.

Total CR energy densities at the plane for the SA0 (left), SA50 (middle), and SA100 (right) source density models used in this paper. The yellow star marks the location of the solar system in each panel. The maximum of the energy density is ~1.2–1.5 eV cm⁻³, depending on the density model.

The corresponding total injected CR powers for the SA0, SA50, and SA100 models are 5.32 × 10⁴⁰, 5.14 × 10⁴⁰, and 4.93 × 10⁴⁰ erg s⁻¹, respectively. For the SA0 model, the injected CR proton power is 5.00 × 10⁴⁰, primary electrons 1.77 × 10³⁹, and He and heavier nuclei 1.41 × 10³⁹ erg s⁻¹. Likewise, the injected CR powers for the SA50 model are 4.83 × 10⁴⁰, 1.77 × 10³⁹, and 1.33 × 10³⁹ erg s⁻¹, and for the SA100 model they are 4.62 × 10⁴⁰, 1.77 × 10³⁹, and 1.31 × 10³⁹ erg s⁻¹ for protons, primary electrons, and He and heavier nuclei, respectively. These injected powers are within ~20% of those found by Strong et al. (2010) using 2D GALPROP models and within a factor of ~2 of the canonical estimate for the total CR injected power of 10⁴¹ erg s⁻¹ (e.g., Drury & Strong 2017 and references therein).

The major difference in injected powers by the different CR source density distributions is for the nuclei. Because the normalization for the CR spectra is to the data, which are collected at the solar system location, more power is required for the SA0 model because the region of highest source density is further away than that for the other density distributions. Strong et al. (2010) noted that the required injected CR power changes with varying halo height, but this is not a consideration in this paper because the size of the CR confinement region is constant.

3.2. Interstellar Radiation Field

The simulation volume for the radiation transfer calculations is a box with dimensions ±15 kpc for the X, Y coordinates and ±3 kpc for the Z coordinate because this effectively encapsulates all of the input stellar luminosity and dust for the R12 and F98 models and hence ensures that computation resources are not wasted for regions that contribute negligibly to the spectral intensity distribution. A Cartesian grid is used to segment the simulation volume. The X, Y coordinates have regular spacing ΔX, Y = 0.125 kpc, while the Z coordinate uses a logarithmic spacing with 25 bins covering 0.001–3 kpc plus an additional linear bin for that closest to the Galactic midplane (52 in total). The wavelength grid spans 0.0912–10,000 μm with 256¹⁴ logarithmically spaced bins.

To record the spectral intensity distribution, a cylindrical grid is used because of the radial and angular dependence of the spatial densities for the R12 and F98 models. Any choice of grid spacing is a compromise balancing computational resources and overall accuracy. The following grid is found to provide adequate sampling for the typical sizes of the simulation volumes used for GALPROP CR propagation and interstellar emission calculations (halo sizes ~4–10 kpc perpendicular to the Galactic plane and maximum X, Y boundaries ~20 kpc). The spacing is variable in galactocentric radius with ΔR = 0.1 kpc near the GC, ΔR = 0.25 kpc to the solar circle, ΔR = 1 kpc beyond to 15 kpc, and ΔR = 5 kpc beyond that to R = 30 kpc. Azimuthally, the spacing is at Δϕ = 10°. The Z coordinates for the camera locations are ±20, ±10, ±5, ±2, ±1, ±0.5, ±0.25, ±0.1, and 0 kpc. Note that the ISRF sampling grid entirely encloses the spatial grid for the GALPROP calculations made in this paper.

Each ISRF model calculation (R12, F98) uses 5 × 10⁸ luminosity packets with HEALPix Nside = 8 maps¹⁵ to determine the Galaxy-wide spectral intensity distributions that are employed for the calculations with GALPROP. These statistics are sufficient because integrating over the ISRF spectral intensity when determining the e^± energy losses and IC emissivities smooths any artifacts due to Monte Carlo noise. However, for the data/model comparison for the line profiles, higher statistic runs are made using 5 × 10¹⁰ luminosity packets with HEALPix Nside = 1024 maps. Even with the higher statistics runs, there is unavoidable Monte Carlo noise, typically where the intensities are lowest.

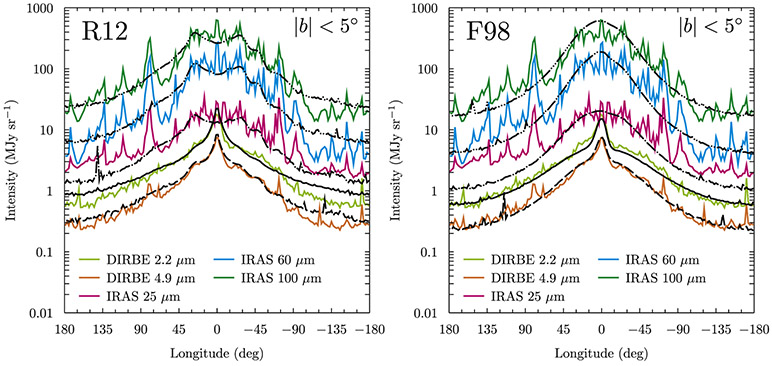
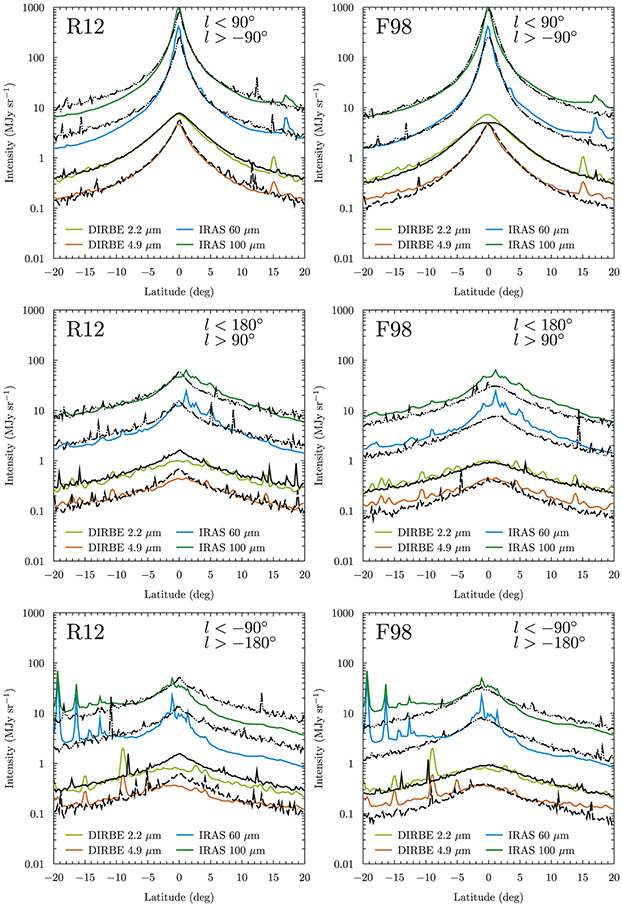
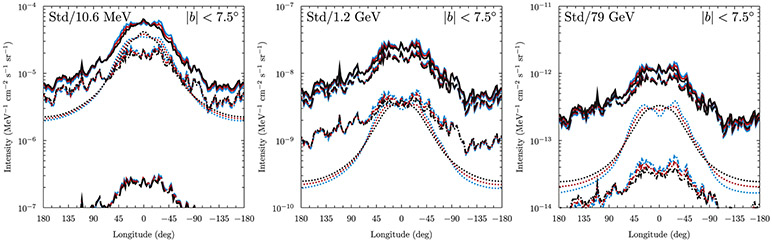
Figure 4 shows the predicted longitude profiles for latitudes −5° < b < 5° for the R12 (left) and F98 (right) models overlaid with the data from COBE/DIRBE¹⁶ and the reprocessed IRAS data.¹⁷ The all-sky model intensity maps are convolved with the instrumental bandpasses and point-spread functions, then averaged over the latitude band to construct the profiles. The models use density distributions for the stars and dust that do not distinguish individual sources. Therefore, the comparison with the data is made without point-source subtraction.

Figure 4.

Longitude profile averaged over −5° < 5 < b° for the modified SKY (left, R12) and COBE/DIRBE bar/disk (right, F98) models. Colored curves show the data for COBE/DIRBE and reprocessed IRAS, while black lines show the model predictions convolved with the instrumental bandpass overlaid on the data for the COBE/DIRBE 2.2 μm (solid) and 4.9 μm (long-dashed) and the IRAS 25 μm (long-dashed–dotted), 60 μm (long-dashed–double-dotted), and 100 μm (long-dashed–triple-dotted) bands.

The bulk features of the intensity profiles are generally successfully reproduced by each model. The R12 model traces the structure of the data more closely for −60° ⩽ l ⩽ 60° because this is the region that it has been optimized over. Outside of this longitude range, the R12 intensities tend to be higher than the data at near-infrared wavelengths. This is due to the scale length of the stellar disk, which produces a shallower profile than the data indicate toward the outer Galaxy, and the presence of the local arms that also contribute in this region. The F98 model agrees well with the near-infrared data over all longitudes due to the smaller radial scale length for the stellar disks. However, the structure in the data for −60° ⩽ l ⩽ 60° is not reproduced because the spiral arms are treated as an averaged disk component for this model. For the mid- and far-infrared wavebands, the better correspondence of the profile structure by the R12 model is again no surprise because it was optimized to reproduce the features in the data tracing the spiral arm tangents. The F98 model adequately traces the intensity profile given its comparative simplicity to the R12 model. Both models underpredict the mid-infrared in the outer Galaxy. For the R12 model, this is most likely due to mismodeling of the stellar luminosity content of the local arms. For the F98 model, it is their absence that causes the lower intensity in these regions.

Figure 5 shows the predicted latitude profiles and data for the Galactic quadrants 1 and 4 (top), 2 (middle), and 3 (bottom). For the inner quadrants, both R12 and F98 perform fairly well at reproducing the profiles. The major difference is the lower intensity by the F98 model within a couple of degrees either side of the Galactic plane for the 2.2 μm band. It comes from the larger dust column due to the shorter radial scale length and smaller inner “hole” region for the dust disk in the F98 model. For the outer Galactic quadrants (2 and 3), the R12 model intensities are too high and display insufficient asymmetry about the plane compared to the data. These mismatches are a result of the stellar disk radial scale length and local arm populations discussed earlier and the lack of warping for both the stellar and dust disks. The F98 intensities match the asymmetries in the data for the outer quadrants much better and mostly reproduce the intensities over all wavebands well. There are underpredictions for the second quadrant and out of the plane that are most likely from the absence of the local arms, which contribute over all wavebands via the direct stellar emission along with the associated dust heating.

Figure 5.

Latitude profiles for the R12 (left) and F98 (right) models. Line colors and styles are the same as in Figure 4, except the IRAS 25 μm band is not shown to allow for straightforward separation of the profiles.

The discrepancies between the R12 and F98 model predictions and local observations are generally minor.¹⁸ Integrating the intensities over the sky produces all-sky averaged values for the R12 and F98 models that are close to the data and well within the experimental uncertainties for all wavebands, thus showing the general consistency for both R12 and F98 calculations with the observations.

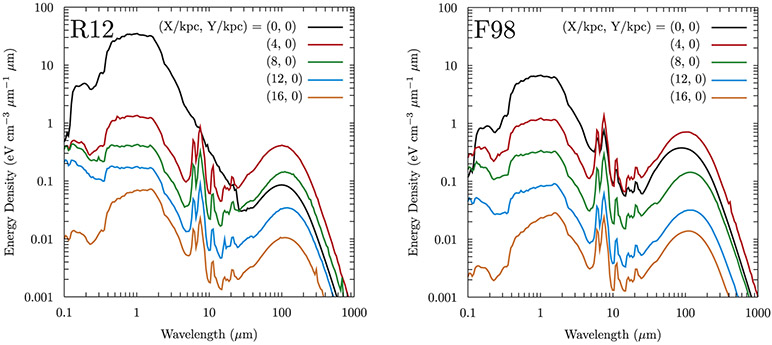
While the predicted intensities locally are very similar, those elsewhere in the Galaxy can vary considerably between the R12 and F98 models. Figure 6 shows the spectral energy density (SED) variation with the X coordinate in the Galactic plane. Near the GC, the R12 model is considerably more intense at UV/optical to near-infrared wavelengths compared to F98. This comes from several differences: the R12 model has a stellar disk that continues toward the GC, while the F98 model has a holed stellar disk; the R12 bulge luminosity is higher than that for the F98 model; and the hole in the R12 dust disk has a larger radius than that of the F98 model. Consequently, the absorption near the GC for the R12 model is lower. However, the general trend of a shift in the peak of the far-infrared emission to shorter wavelengths from the intense radiation field over the inner Galaxy is present for both the R12 and F98 models independent of the dust density there. The other major difference is the spatial variation of the SED from far-UV to ~0.5 μm wavelengths that reflects how the early-type stars are modeled. The variation of the UV and optical spectral intensity for the R12 model with X outside the region about the GC is driven predominantly by the crossing of the various arms as X increases out to ~12 kpc. In particular, for the R12 model, the locations shown in the figure sample the interarm (X = 4 kpc) and in-arm (X = 8 and 12 kpc) regions. For the F98 model, such variations are absent because the young stars in the arms are treated using spatial averaging.

Figure 6.

ISRF spectral energy density for the R12 (left) and F98 (right) models, showing the variation with a positive X coordinate in the Galactic plane.

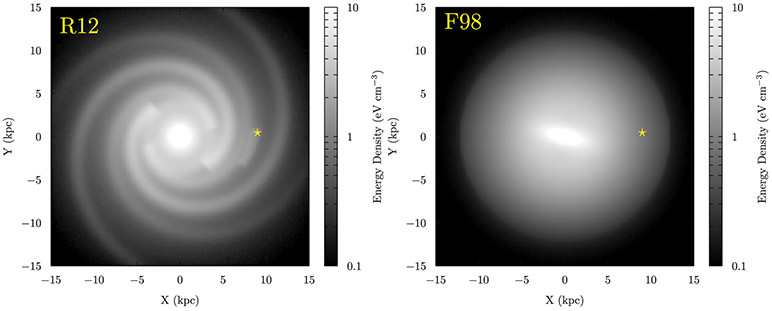
The variation of the wavelength-integrated SED predicted for the R12 and F98 models across the Galaxy at the midplane is shown in Figure 7. The R12 model produces a more structured spatial distribution for the energy density, with features related to the stellar luminosity model clearly evident. The variation of the SED shown in Figure 6 (left) from the crossing of interarm/arm regions with the X coordinate is also readily understood where the maxima of emission are clearly visible near X ~8 and ~12 kpc, respectively. For the F98 model, the asymmetric bulge produces a clearly elongated region of high energy density dominating the inner Galaxy region. On either side of the minor axis of the bulge are shallow minima in the energy density distribution, and, outside of ~4 kpc about the GC, the stellar disk is the only significant contributor.

Figure 7.

Integrated ISRF energy densities in the Galactic plane for the R12 (left) and F98 (right) models. The yellow star marks the location of the solar system in each panel. Note that the energy density saturates the scale in and about the GC for both models.

The spatial variation of the SED outside of the Galactic plane (not shown) is most sensitive to the details of the stellar luminosity and dust model for ∣Z∣ ≲ 1–5 kpc, with the effect dependent on position relative to the GC. Close to the GC, the intensities of the respective models differ the most but become comparable for ∣Z∣ ≃ 5 kpc, while toward the outer Galaxy, they are similar for somewhat lower height ∣Z∣ ≃ 1 kpc. The falloff of the intensity with the Z coordinate is approximately logarithmic for both models. At a distance ~10 kpc above the plane near the GC, the energy density for either model is similar to that of the CMB, and at a distance of ~20 kpc it becomes comparable that of the extragalactic background light (e.g., Hauser & Dwek 2001; Mazin & Raue 2007).

3.3. γ-Rays

High-energy interstellar emissions are calculated using GALPROP for the SA0, SA50, and SA100 source density models (Section 3.1) and the standard 2D (Std; Ackermann et al. 2012) and 3D ISRF models (Section 3.2). The SA0 CR source density and Std ISRF (SA0–Std) are used as the reference case. This combination corresponds to the 2D CR source and ISRF density scenario that has been the standard approach for interstellar emission modeling in the past.

The spatial and CR kinetic energy grid used for the CR propagation model parameter tuning (Section 3.1) is also employed here, with γ-rays calculated from 1 MeV to 100 GeV energies using a logarithmic energy grid with 10 bins decade⁻¹ spacing. Higher γ-ray energies correspond to CRs with energies ≳1 TeV, where the steady-state source injection paradigm employed in this paper is less valid (Strong & Moskalenko 2001b; Bernard et al. 2013). The ISRF model sampling grid differs from that used for the CR calculations, and bilinear/trilinear (2D/3D) interpolation is used to determine the ISRF spectral intensity over the grid used for the GALPROP calculations. Inelastic collisions by primary CR nuclei with the interstellar gas yield γ-rays and other particles. The secondary CR e^± from these interactions are included, together with the primary electrons in the interstellar emission calculations, because they produce a nonnegligible contribution for γ-ray energies ≲10 MeV (Porter et al. 2008; Bouchet et al. 2011). All calculations of the IC contribution use the anisotropic scattering cross section (Moskalenko & Strong 2000b) that accounts for the full directional intensity distribution for each of the Std, R12, and F98 models.

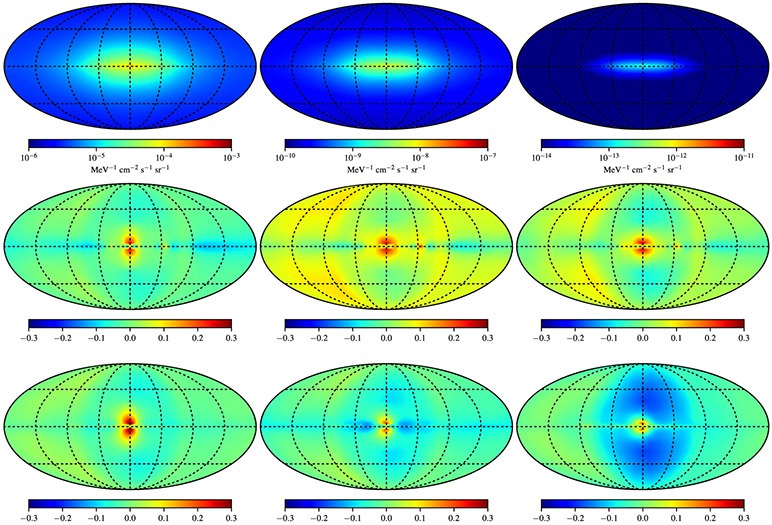
How the different CR source densities affect the γ-ray intensities observed at Earth is examined first using calculations made with the Std ISRF and the SA0, SA50, and SA100 models. Changing the CR source density affects both nuclei and leptons and hence the summed interstellar emissions from π⁰-decay, bremsstrahlung, and IC processes. Figure 8 (top row) shows the total γ-ray intensity for the reference model combination (SA0–Std) for 10.6 MeV, 1.2 GeV, and 79 GeV energies. The middle and bottom rows show the fractional residuals, (SA50-SA0)/SA0 and (SA100-SA0)/SA0, for the same energies. Figure 9 shows the corresponding longitude profiles separated according to γ-ray production processes (π⁰-decay, bremsstrahlung, and IC) for each of the CR density models averaged over $\mid b\mid ⩽7_{{}^{.}}^{{}_{°}}5$ for the same energies.

Figure 8.

Top row: total intensity (π⁰-decay, bremsstrahlung, and IC) at 10.6 MeV (left), 1.2 GeV (middle), and 79 GeV (right) for the SA0–Std reference case. Middle and bottom rows: fractional difference maps for the SA50–Std and SA100–Std model combinations, respectively. The maps are in Galactic coordinates with l, b = 0°, 0° at the center. The longitude meridians and latitude parallels have 45° spacing. While the fractional residual color scale is shown for a maximum ±30% difference, there are features for the SA100 CR source density model for the low- and high-energy maps that are outside the scale bounds. These are near the direction of the GC and toward l ~ ±30°–45°, where the spiral arm tangents contribute most along the line of sight.

Figure 9.

Longitude profiles averaged over $-7_{\cdot }^{\circ }5⩽b⩽7_{\cdot }^{\circ }5$ for the Std ISRF and SA0, SA50, and SA100 CR source density models. Line styles: solid, total; dashed, π⁰-decay; dashed-dotted, bremsstrahlung; dotted, IC. Line colors: black, SA0; red, SA50, cyan, SA100.

For the low-energy (10.6 MeV) bin, the γ-ray intensity has a negligible π⁰-decay contribution and hence reflects the CR e^± densities in the ISM. For the outer Galactic quadrants, the major contribution is by bremsstrahlung, with bremsstrahlung and IC approximately 50% each for 45° ⩽ ∣l∣ ⩽ 90° and IC dominant for −45° ⩽ l ⩽ 45°. The low-energy fractional residuals can be interpreted using this information. For quadrants 2 and 3, the depletion of CRs from the smooth disk as the spiral arm injection power fraction is increased produces progressively less bremsstrahlung because of the correspondingly lower CR e^± densities in the outer Galaxy. Toward the inner Galaxy, a doughnut-like feature with excess emission concentrated near l ~ ±45° and extending to high latitudes is evident. This is caused by the pileup along the line of sight of the IC emissions by CR e^± propagating from their spiral arm injection regions, with the more intense emissions from the inner arms coming from the higher injected luminosities there due to the arm radial profile. The overall angular width of the excess feature increases with the spiral arm injected power fraction and reflects that the lower-energy CR e^± effectively diffuse about the arms and out of the plane. In and about the GC, the deficit is related to the paucity of CR e^± in this region. The lack of CR sources (e.g., for the SA100 density model, there are no CR sources within ~3 kpc of the GC, producing a low CR energy density; see the right panel of Figure 3) and quick energy losses mean that there are much lower emissions from this region.

For the 1.2 GeV maps, the γ-ray intensity is dominated by interactions of the CRs with the interstellar gas (only ~10% of the γ-rays are produced by the IC process around these energies). The fractional residuals are more highly structured because of the different CR densities in the ISM produced by the SA50 and SA100 density models. They are higher in and about the spiral arms and illuminate the gas that is near these regions differently from the CR densities produced for the SA0 model. The doughnut-like excess emission, particularly for the SA100 density model, is also present at these energies. It is more concentrated toward the plane than for the lower energies because the gas scale height is much smaller than that of the ISRF. Even though the CR nuclei producing γ-rays with energies ~1 GeV effectively fill the Galactic volume, only relatively nearby ones (~100–500 pc) injected in the arms contribute to producing the excess features around these γ-ray energies. (The lower-energy maps have contributions by CR e^± that have propagated far above the plane, which is the reason for their broader latitude coverage.) By contrast, the deficit seen at lower energies about the GC is not as deep. Because the CR nuclei lose energy much slower than the electrons/positrons, they diffuse effectively to fill the inner region, even for the SA100 density model.

The 79 GeV maps generally exhibit the same residual features as the lower energies, but the concentration of excess emission is more pronounced about the spiral arm regions. Because the IC is a greater proportion of the γ-ray emission at these energies (~25%–30%), the enhancements about the arms are mainly due to the primary CR electrons. The energy losses are quick, and the primary CR electron densities are high close to their injection regions. Hence, the excess emission is much higher for lower latitudes about l ~ ±45° than for the lower energies.

At all energies, the negative residuals in the outer Galaxy for the SA100 model are deeper than those for the SA50 case. This comes from the lack of the smooth CR “disk” component there, the difference between the smooth disk and arm radial scale lengths, and the effective cutoff in the arm density distributions because of their finite angular extent (Table 1).

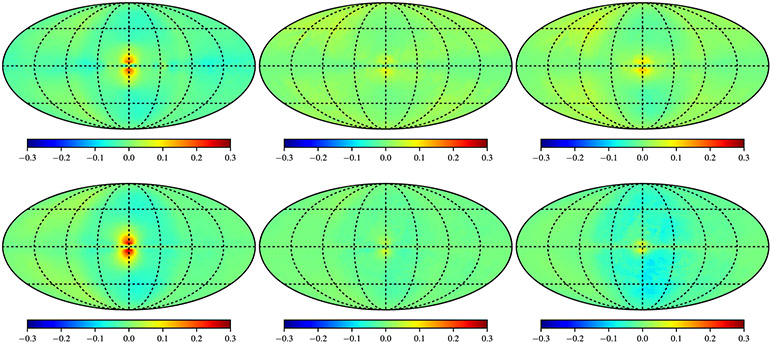
The effect on the IC component of changing from the Std to R12/F98 ISRF models is illustrated in Figure 10, where the IC intensity (top row) for the SA0–Std model combination is shown at 10.6 MeV, 1.2 GeV, and 79 GeV energies (left to right), together with the fractional residuals for the SA0–R12 (middle row) and SA0–F98 (bottom row) combinations. The residuals at all energies exhibit a feature around the GC that is associated with the Galactic bulge/bar. The ISRF spectral intensity over the spatial region dominated by this component is higher for both the R12 and F98 models compared to the Std. In addition, the R12 and F98 model bulge/bars have larger scale heights than that of the Std model. These major differences produce the fractional residuals that show a spatial morphology with strongly positive “lobes” above and below the GC that are model- and energy-dependent. The energy dependence reflects the effect of the energy losses on the CR e^± toward the inner Galaxy for the R12 and F98 models.

Figure 10.

Top row: IC intensity at 10.6 MeV, 1.2 GeV, and 79 GeV energies (left to right) for the SA0–Std reference case. Middle and bottom rows: fractional residuals for the SA0–R12 and SA0–F98 model combinations, respectively. The maps are in Galactic coordinates with l, b = 0°, 0° at the center. The longitude meridians and latitude parallels have 45° spacing, as in Figure 8.

Elsewhere, the R12 model shows numerous residual features across the sky that are directly related to the presence of the spiral arms. Close to the plane, these are due to the four main spiral arms (Table 1), where hot/cold regions in the residuals come from the localized enhanced/decreased spectral intensities (Figure 7, left panel). At intermediate and high Galactic latitudes, the excesses have contributions by both the main and local arms. For γ-ray energies of ~1 GeV, the CR e^± producing the IC emission¹⁹ have energies of ~few–10 GeV and are distributed throughout the disk and into the halo. The broadly distributed features for ~1 GeV come from both nearby and relatively far away in the Galaxy. Meanwhile, for higher-energy γ-rays, the residual maps display features out of the plane that are due to localized features because the CR e^± producing these emissions are relatively close to their injection sites.

The residuals for the F98 model are less structured than those for R12. The major differences are related to the asymmetric bar, which produces strong enhancements around the GC and smaller enhancements outside of the plane. Those close to the GC are related to the higher spectral intensity and spatial distribution of the bar compared to the Std ISRF model. Outside the plane, the enhancements come from the anisotropic scattering of the outward-moving photons from the inner Galaxy, where the effect is higher for quadrant 2 compared to that for quadrant 3 because the directional intensity of the bar is stronger there. About the Galactic plane, the F98 model is comparable or has a small deficit to the Std ISRF because the former has a smaller radial scale length for the disk populations (the Std ISRF disk radial scale length is similar to that of the R12 model). Even though the normalization of the F98 disk is higher compared to the Std ISRF, the smaller radial scale length gives a comparatively reduced spectral intensity away from the inner Galaxy.

For the SA0 CR source density model, the effect of changing the target density model for the ISRF on the total γ-ray intensity is, however, not as stark as the changes in the IC component maps. This is illustrated in Figure 11, where the fractional residuals with the reference case for the SA0–R12 and SA0–F98 model combinations are shown. For the lowest energy (10.6 MeV) maps, the residuals due to the higher spectral intensities for the R12/F98 bulge/bar are most strongly seen. This comes from the primacy of the IC component at the lower energies toward the inner Galaxy, as discussed earlier.

Figure 11.

Fractional residuals for the total intensity (π⁰-decay, bremsstrahlung, and IC) at 10.6 MeV (left), 1.2 GeV (middle), and 79 GeV (right) for SA0–Std and the SA0–R12 (top) and SA0–F98 (bottom) model combinations. The maps are in Galactic coordinates with l, b = 0°, 0° at the center. The longitude meridians and latitude parallels have 45° spacing, as in Figure 8.

Combining the SA50 and SA100 CR density models with the 3D ISRF models yields the fractional residuals with respect to the SA0–Std reference that are shown in Figure 12. From left to right, the columns are increasing with energy, as in Figures 8 and 10. From top to bottom, the rows correspond to the SA50–R12, SA100–R12, SA50–F98, and SA100–F98 model combinations and show a rich structure that depends on both the CR source densities and propagation and the ISRF target density model.

For the R12 ISRF model, there is a multiplier effect of the CR densities with the ISRF densities in and about the arm regions. The emissions are more intense and broadly distributed on the sky than simply altering the CR source or ISRF to include spiral structure for either spatial distribution model. This is the case even around ~1 GeV, where the CRs effectively fill the Galactic volume—the features from the double arm “enhancement” from the CR source and ISRF density models are evident. For the low-energy maps (10.6 MeV), the effect of the more luminous bulge in the R12 model is also visible. The higher spectral intensity of the ISRF in and about the GC region compensates for the reduced CR density to produce an excess, or reduced deficit, compared to the SA0–Std combination.

In contrast, for the F98 ISRF model and SA50/SA100 combinations, there is no multiplier effect because distinct spatial components for the spiral arms are only present for the CR source densities. But the residual maps are more than a simple reflection of the changing CR source densities because the F98 ISRF model also produces structural differences due to its different stellar luminosities and spatial structures compared to the Std model (Figure 10). Toward the inner Galaxy, the low-energy maps show more of an enhancement/reduced deficit compared to the SA50/SA100–R12 cases because of the bulge luminosity and shape. Meanwhile, the excesses identified previously as associated with CRs injected into the ISM in and about the arm regions are not as intense at higher latitudes because of the reduced IC emissions out of the plane.

4. Discussion

The residuals shown in Figures 8 and 12 display many interesting features. The question is then what resemblance, if any, do they have to large-scale residuals from analysis of real γ-ray data? A comparison can be made with the results of IG16 because the SA0–Std reference model of this paper is very close to the “Pulsars” IEM from that paper.²⁰ The residuals of IG16 from the top panels of Figure 2 are obtained by subtracting the baseline “Pulsars” IEM and a fitted low-intensity isotropic intensity from the Fermi-LAT data, which enables direct comparison with the residuals calculated in this paper.

The focus of the discussion will be toward the inner Galactic quadrants, because it is in this region where the major differences related to the 3D CR source and ISRF densities are important.²¹ Generally, the IG16 fractional residuals show excesses ≳30% that extend out of the plane for −45° < l < 45°. These are somewhat higher but similar in spatial distribution to the SA50/SA100 residuals shown in Figure 12, where there are peaks near l ~ 45° and l ~ −30° corresponding to the spiral arm enhancements together with a general infill up to ∣b∣ ~ 45° latitudes. Because the IEMs calculated in this paper have not been optimized using γ-ray data, perfect agreement is not expected. But it is interesting that for longitudes outside of the inner ±45°, the IG16 positive residuals are mainly clustered near the plane, while for longitudes inside they have extensions to high latitudes.²² The delineation is distinct and aligned with where the spiral arms provide major contributions for the SA50/SA100 IEMs, as shown in Figure 12.

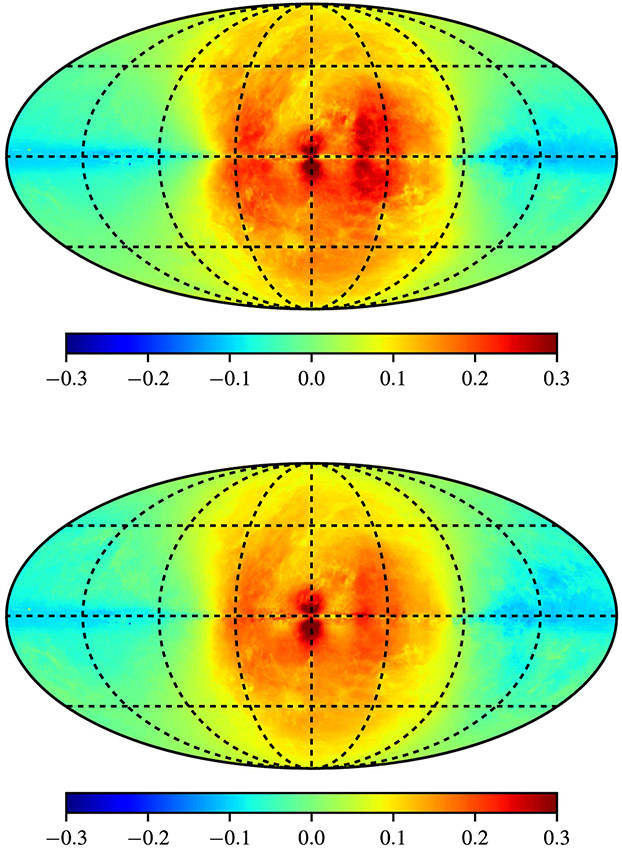
However, the SA50/SA100 model combinations have the central “hole” about the GC caused by the lower CR energy density in that region. The residuals shown in Figure 2 of IG16 have the region about ∣l∣ ≲ 20° and ∣b∣ ≲ 50° obscured,²³ but the level of the residuals under these masks is similar to, if not higher than, those over the rest of the −45° ⩽ l ⩽ 45° region. A resolution to obtain comparable residual excesses that infill the region about the GC for the SA50/SA100 models is to introduce an extra source density model that provides additional CR power there. An explanation for such an additional component is that it could be a bulge-related population of CR accelerators that injects a combination of nuclei and leptons.²⁴ To examine this possibility, the SA100–R12 and SA100–F98 model combinations are recalculated using the bulge/bar for each ISRF model as the hypothetical additional CR central source density distribution (Equation (1) for the SA100–R12 combination, termed “SA100/R12B,” and Equation (9) for the SA100–F98 combination, termed “SA100/F98B”), assuming the same nuclei-to-lepton ratio for the CR bulge/bar as for the spiral arms. Because this is testing a simple “what-if?” scenario, no likelihood fitting of γ-ray data is made. Instead, the normalization of the total injected CR power for the additional source density component is obtained for each model combination by adjusting its value by eye so that the residuals around the GC seen in the second/fourth row (middle) of Figure 12 are sufficiently filled and at least comparable to the residuals elsewhere for the SA100 models toward the inner Galaxy.

Figure 13 shows the fractional residuals for energies ~1 GeV for the SA100/R12B–R12 (top) and SA100/F98B–F98 (bottom) model combinations. For both modified CR source density models, the central “hole” in the residuals is filled to give excesses ~30%–40%. The adjustment could be made to give a higher fraction and still be consistent with what is seen in the IG16 residuals, but as described above, these calculations are made to serve an illustrative purpose, and no additional fine-tuning is made. Also, note that no refitting of the propagation parameters is performed, or indeed necessary, because the CRs from the bulge/bar addition produce negligible contributions at the solar system (see Figure 14, right panels).

Figure 13.

Fractional residual map at 1.2 GeV for the SA100/R12B–R12 (top) and SA100/F98B–F98 (bottom) CR source and ISRF density model combinations. The map is in Galactic coordinates with l, b = 0°, 0° at the center. The longitude meridians and latitude parallels have 45° spacing.

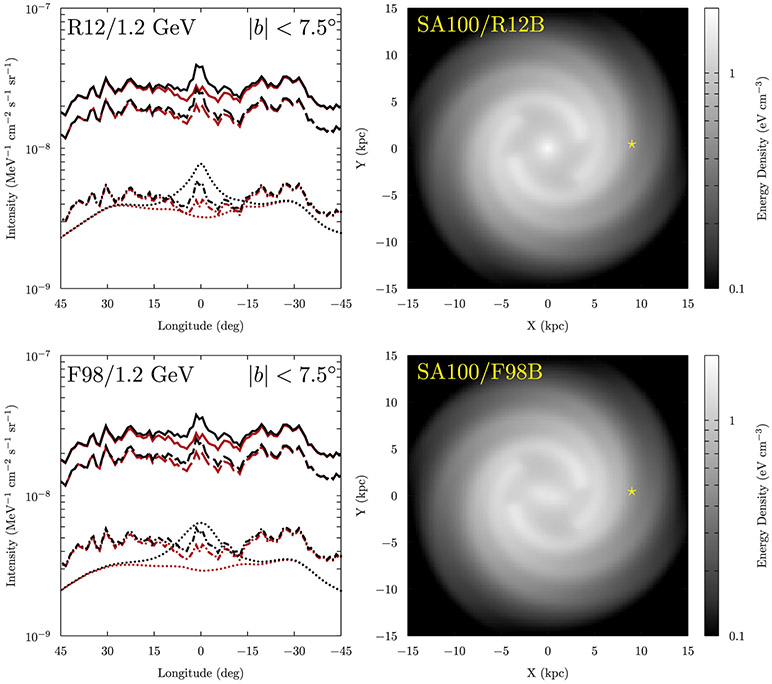
Figure 14.

Left panels: longitude profile for the intensity at 1.2 GeV averaged over $-7_{\cdot }^{\circ }5⩽b⩽7_{\cdot }^{\circ }5$. The top panel shows the SA100–R12 combination (red lines) and SA100/R12B–R12 combination (black lines). The bottom panel shows the SA100–F98 combination (red lines) and SA100/F98B–F98 combination (black lines). Line styles: solid, total; long-dashed, π⁰-decay; dashed-dotted, bremsstrahlung; dotted, IC. Right panels: spatial distribution of integrated CR energy density at the Galactic plane for the SA100/R12B (top) and SA100/F98B (bottom) CR source density models. The yellow star shows the location of the solar system.

The addition of the bulge/bar CR source density model produces residuals that show a large excess close to the GC with lobe-like structures above/below the GC similar to those seen at lower energies (Figures 11 and 12). The interactions of both the nuclei and leptons, however, contribute at ~1 GeV energies (as can be seen in the left panels of Figure 14) that show the longitude profiles of the intensity at 1.2 GeV averaged over $-7_{\cdot }^{\circ }5⩽b⩽7_{\cdot }^{\circ }5$ for the SA100/R12B–R12 (top) and SA100/F98B–F98 (bottom) combinations. The increased injection of the nuclei and leptons creates more π⁰-decay and bremsstrahlung with the gas in the inner Galaxy. But the strong enhancement of the IC emission is due to the combined effect of the higher CR and ISRF intensities in this region, similar to the density effect enhancing the IC emissions from the arms for the SA50/SA100–R12 model combinations. There is also asymmetry of the IC emission profile from the SA100/F98B–F98 combination about the GC because of the angular offsets with respect to the Sun-GC line of the bar spatial distributions for the CR and ISRF densities (Figures 7 and 14).

The results for SA100/R12B and SA100/F98B provide a framework for understanding the results obtained by IG16 related to rescaling of the 2D baseline IEMs to produce their final foreground/background IEMs and the strong contribution by IC emission in and about the GC region. Figure 15 of IG16 compares the variation with galactocentric radius of the GALPROP-predicted fluxes >1 GeV for the adjusted components (π⁰-decay and IC) of the baseline IEMs and the fitted results over the 15° × 15° region about the GC. The fit results for the “Pulsars” IEM, which uses the SA0 CR source density model of this paper, for the range 3.5 kpc ≲ R ≲ 8 kpc give an upscaling that is approximately the same (~20%–30%) for the π⁰-decay and IC emission, while for R ≲ 1.5 kpc the IC emission is upscaled by larger factors.

Comparing the energy density distributions for the SA0 and SA50/100 models (Figure 3), those with spiral arms have higher CR intensities for 3 kpc ≲ R ≲ 7 kpc by ~20%. Because the propagation smooths the CRs injected by the arms into a quasi-axisymmetric ring, it is perhaps no accident that the fits using the 2D models by IG16 find that a broader (in R) distribution of CR intensities is needed to reproduce the data. The interpretation then is that at least some nonnegligible fraction of CR sources can be located in the spiral arms.

The SA100 and additional CR bulge/bar source density is one piece of the puzzle that can be used to understand the origin of the IC emission in and about the GC found by IG16. The SA0 CR source density with its normalization condition at the solar circle is insufficiently peaked toward the GC to provide the injected CR power that would approximate that by the additional R12B/F98B bulge/bar components introduced in this paper. The other piece of the puzzle is the intensity of the ISRF in and about the GC from the bulge/bar for the R12/F98 models. The Std ISRF has a lower intensity over the inner Galaxy compared to either of the ISRF models used in this paper. The dual effect of the higher CR and ISRF intensities associated with these centrally peaked distributions is the critical combination required to understand how the dominant IC γ-ray emissions from the central few kpc about the GC can be produced. Comparing the SA0–Std IC emission averaged over $-7_{\cdot }^{\circ }5⩽l⩽7_{\cdot }^{\circ }5$ in Figure 9 (middle) to that obtained by averaging over the same longitude range for the SA100/R12B–R12 and SA100/F98B–F98 combinations (Figure 14, left panels), the increase for the additional bulge/bar models is a factor of ~2–3 higher. IG16 found that fitting the IC for the same region >1 GeV requires an increase by a factor of ~4 compared to their baseline “Pulsars” model (the same as the SA0–Std combination). This is fairly close to the enhancements that are calculated with the additional CR bulge/bar model combinations considered in this paper.

Extracting the physical properties of a putative CR bulge/bar and ISRF density across the inner Galaxy will require further work. Because the additional CR bulge/bar population is a negligible contribution at the solar system, local CR data cannot provide useful information on its characteristics, and the viable techniques will rely on electromagnetic signatures. For the current illustrative calculations, the corresponding injected CR powers are 1.84 × 10³⁹ erg s⁻¹ (SA100/R12B) and 1.94 × 10³⁹ erg s⁻¹ (SA100/F98B), which are a factor of ~25 smaller than the injected power for the SA100 source density model (the injection spectrum parameters are taken to be the same as the spiral arm components, as given in Table 3 for the SA100 density model). Increasing the input CR power for either the R12B or F98B additional component produces correspondingly higher residuals; e.g., a 50% increase for the R12B component gives positive residuals that are instead ~40%–50% about the GC, which is comparable to the IG16 residuals there. But these numbers assume the spatial parameters for the R12/F98 bulge/bar distributions used in this paper and that the CR bulge/bar injects nuclei and leptons with the same ratio as the spiral arms.

Optimizations to the models for the CR source and ISRF density distributions can be made. Determining a more realistic mixture of CR sources attributed to spiral arms and a smoothly distributed disk component than that used in this paper (50% or 100%) is one such improvement. This paper assumes that the CR spiral arm density and disk components have the same averaged spectral characteristics and that the spiral arms all inject the same CR power. However, most likely the arms are not as equally balanced: the R12 ISRF model has higher (stellar) luminosities for arms 2 and 2′ (Figure 1) coming from the hot young stars that are the progenitors for typical CR sources such as pulsars and supernova remnants. The spatial distributions of the arms also may not be as symmetric as assumed. The fractional residuals in Figure 2 of IG16 are higher near l ~ 45° than l ~ −30°, somewhat opposite of the trend, particularly for the combinations using the R12 ISRF model shown in Figures 12 and 13. To remedy this may require modifications of the spatial parameters and weighting the injected CR powers for individual arms differently than done here. While these aspects of the CRs injected in the spiral arms have not been investigated in this paper because of the already considerable number of models and parameters, they are an additional element that should be addressed by future work. Possible distributions that could also be used are the NE2001 model of Cordes & Lazio (2002) and Cordes (2004) or that of Drimmel & Spergel (2001). The NE2001 model has been used to investigate 3D CR distributions in the ISM by Werner et al. (2015) but not, so far, to calculate IEMs with 3D ISM target density distributions. Studies of other nearby spiral galaxies can also guide the construction of suitable source density distributions for the bulge/bar and arms (e.g., Aramyan et al. 2016; Hakobyan et al. 2016). In addition, the production of an optimized ISRF model is a key ingredient that will require further work. Better determination of arm model parameters, including distributing dust in them as well as stars and whether stellar/dust arms are coaligned (e.g., Vallée 2014), the description of the nonaxisymmetric structures across the inner Galaxy (e.g., Babusiaux & Gilmore 2005; López-Corredoira et al. 2005; Green et al. 2011; Zoccali & Valenti 2016), warps and flaring in the stellar disk (e.g., López-Corredoira & Molgó 2014), and possibly other details are essential.

Lower-energy γ-ray data (≲50 MeV) can be used to test the predictions made for the CR lepton source and ISRF density models developed in this paper because of the minimal emissions by π⁰-decay production in this energy regime. Bouchet et al. (2008, 2011) analyzed INTEGRAL/SPI data using 2D GALPROP-generated models and found that the interstellar emission from the Galactic ridge toward the inner Galaxy likely has an IC origin but needs some combination of higher electron and/or ISRF intensities to be consistent with the data. Bearing in mind the sensitivity of the data, reanalysis with models as developed in this paper can enable better determination of the CR and ISRF densities necessary. For the ~1–30 MeV energy range, COMPTEL on the CGRO has provided the best data to date, but the resolution and sensitivity are limited. Major changes to the background rejection algorithms for the Fermi-LAT have significantly enhanced its sensitivity below 100 MeV energies for the so-called Pass-8 data²⁵, opening the way to using these data down to the COMPTEL energy range with the possibility of even some small overlap in coverage. Also, proposed medium-energy γ-ray instruments such as e-ASTROGAM (De Angelis et al. 2016; Tatischeff et al. 2016) and AMEGO²⁶ will significantly improve the data quality in this energy range.

The emissions from CRs losing energy near their sources at higher energies also offers opportunities to test the predictions made by models such as have been considered in this paper. For leptons, the rapid energy losses ≳100 GeV energies in and about the enhanced ISRF energy densities of the spiral arms produce signatures that can be related to the average injected CR power for different arms. This is also true toward the inner Galaxy, where the hypothetical CR bulge/bar population can be similarly tested because of its localization. Analysis of Fermi-LAT data can accomplish this up to energies ~100 s of GeV energies, which is sufficient for modeling and testing the CR injection in the steady-state picture that is assumed in this work. Higher energies probe the regime where the CR injection by individual sources becomes important, but these are beyond the scope of the calculations made in this paper.

Finally, it should be noted that the lobe-like excesses and “pinching” toward the GC shown in Figure 13 have similarities to the so-called “EEE” residual component of the IEM developed to support the generation of the Third Fermi Point-source Catalog (see Figures 10 and 11 of Acero et al. 2016). It was suggested by Acero et al. (2016) that these are the endpoints toward the GC of the so-called “Fermi Bubbles” (e.g., Su et al. 2010), whose origin has been widely speculated. Acero et al. (2016) employed a 2D axisymmetric GALPROP-calculated IEM using a slightly different CR source density distribution and the Std ISRF as its basis and the long-established method of dividing the interstellar emission components into galactocentric annuli and fitting to the γ-ray data for their respective emissivities (e.g., Strong et al. 1988; Strong & Mattox 1996). However, Acero et al. (2016) did this only for the gas-related emission components (π⁰-decay and bremsstrahlung) and used an all-sky GALPROP-predicted IC intensity map with refitting only for its spectral characteristics. This does not have the flexibility of the method of IG16 for accounting for mismodeling of the IC emission. (Note that IG16 found no evidence for a residual like the “EEE” component.) The residuals shown in Figure 13 (for 1.2 GeV) are very similar to those at 3.4 and 22 GeV, which are the energies that the “EEE” residual is shown for in the bottom middle and right panels of Figure 10 of Acero et al. (2016). Their shape about the GC is somewhat similar to that of the “EEE” component there, and the difference between the averaged IC intensities for either the SA100/R12B–R12 or SA100/F98B–F98 combination and reference model within the 5° × 5° region about the GC are ~5 × 10⁻¹⁰ and ~7 × 10⁻¹² MeV⁻¹ cm⁻² s⁻¹ at those energies, respectively. These are within ~30% of those for the “EEE” component for the same region, suggesting that a plausible explanation for its origin is that there is a mismodeling of the CR source and ISRF densities by the 2D IEMs combined with the inflexibility of the fits by Acero et al. (2016) for treating the IC emission spatial distribution on the sky. Fitting for the IC intensity in galactocentric annuli, as done by IG16, would allow the 2D approach to better account for mismodeling of this component, which can enable these simplified IEMs to maintain some utility for supporting the generation of point-source catalogs and analyses of γ-ray data in localized regions where the physical interpretation of the large-scale interstellar emission is not the major objective.

5. Summary

New calculations of the high-energy interstellar emissions produced by CRs interacting with the ISM of the Galaxy have been made with the latest release of the GALPROP code. These have used 3D spatial models for the CR source and ISRF densities. The 3D ISRF models are also new calculations with the FRaNKIE code that include spatial distributions to account for the nonaxisymmetric features of the stellar distribution in the Milky Way, such as the spiral arms and bar. Compared with 2D galactocentric axisymmetric models, those including 3D structure show features in all-sky γ-ray maps that can be attributed to specific spatial elements, such as the spiral arms. These features depend on the CR source and ISRF density models, with the models that have localized increases in both CR and ISRF intensities producing enhanced IC emissions. This is evident for all model combinations involving the SA50/SA100 CR source density models, the R12 ISRF model, and the additional “CR bulge/bar” SA100/R12B and SA100/F98B combinations.

The calculations presented in this paper can be used to better interpret analyses of γ-ray data. They have been used here to provide a plausible physical interpretation for results obtained by the Fermi-LAT team in their analysis of γ-ray data toward the inner Galaxy. In particular, the upscaling outside of the inner Galaxy needed for the interstellar emission predicted by the 2D-based IEMs that they employed can be understood as mismodeling of the CR source density there: the spiral arm source density model produces a higher CR energy density in the ISM compared to a smooth disk when the propagated CR intensities for each are similarly normalized to the CR data. The spatial distribution of CR energy density in the ISM for the spiral arms can be fit somewhat successfully even with an axisymmetric model because the propagation smooths the CR source density from these localized injection regions into a quasi-axisymmetric distribution for galactocentric R ~ 3–7 kpc. The strong IC emission found by the Fermi-LAT team toward the GC comes from the combined effect of a population of CR accelerators localized in and about the inner Galaxy injecting CRs that interact with the intense ISRF in this region. The spatial characteristics of this additional CR “bulge/bar” source density are modeled using the same distributions employed for the respective calculations of the 3D ISRF models in this paper.

This work has demonstrated the need for detailed modeling of the distribution of CR sources and the ISRF that takes into account the 3D structure of the ISM. The residual structure in the calculated maps resembles features that have been previously interpreted as possible signs of new physics. However, further work is needed to optimize the models and more carefully tune them to the available data.

Appendix

GALPROP Version 56 Features

The improvements made to GALPROP include significant modifications to its architecture, as well as numerous technical improvements and inclusion of additional physics code. An overview of the major changes is given here, while specific examples of command line configuration/build/installation/execution are provided at the GALPROP website (http://galprop.stanford.edu). Forums and a bugzilla are also available at the website.

Architecturally, previous versions of GALPROP are monolithic, with the code and configuration required to detect external libraries and build the GALPROP library and executable contained in the source distribution. With the new release, this changes to a single external dependency on the GALTOOLSLIB library. Because of reuse considerations—the FRaNKIE, GALGAS (Johannesson et al. 2016), and GaRDiAn (Ackermann et al. 2012) packages also developed by members of the GALPROP team use many common elements and similar configuration and build procedures—core functionality across all code bases is abstracted into this library. GALTOOLSLIB includes utility code for parameter parsing (e.g., reading the galdef configuration file of a GALPROP run), specifying spatial distributions (e.g., for CR source densities), libraries for the representation of results (e.g., sky maps with HEALPix), core physics routines for the nuclear reaction network and energy losses, and other commonly reused code. Its required external library dependencies are CFitsIO²⁷ and CCfits,²⁸ CLHep,²⁹ the Gnu Scientific Library,³⁰ HEALPix,³¹ and Xerces-C.³² Optional external library dependences are libastro from XEphem,³³ WCSLIB,³⁴ OpenCL,³⁵ and CppUnit.³⁶ WCSLIB and libastro are used for both reading and writing data in different map projections. OpenCL can be used to distribute calculations across CPUs and compute accelerators for FRaNKIE and GALGAS but is not needed for GALPROP runs. CppUnit is a framework that is used by the various packages developed by the GALPROP team for unit testing.

The configuration and build process previously employed the Gnu autoconf³⁷ and automake³⁸ tools. These are deprecated with the new release, and now the configuration/build/installation uses CMake.³⁹ The minimum requirement for building GALTOOLSLIB and GALPROP is CMake 3.0. The base language support requires a C/C++ compiler that implements the C++11 standard and a Fortran 77/90 compiler. Minimum requirement compiler versions tested for this release include gcc/g++ 4.9 and recent Intel compilers. Almost any recent Fortran compiler is sufficient.

Supported build targets are Linux and OSX, with other Unix-like variants possible. It is likely that if the target system has the minimum language support noted above and allows for the installation of necessary external libraries, then GALTOOLSLIB can be installed. Following successful installation of GALTOOLSLIB, the straightforward build and installation of the separate GALPROP library and executable is enabled by pointing the command line configuration invocation to the GALTOOLSLIB location. This configures the paths using scripts generated by the GALTOOLSLIB installation. The standard “make && make install” following the configuration will build and install the libraries and executable in the specified directories. To ensure end-user sanity, it is highly recommended to employ consistency with the configuration/build/installation process for GALTOOLSLIB and GALPROP. That is, use the same compilers and configuration for all steps.

Technical and physics improvements have focused on better memory layout and computational speed and making GALPROP more flexible as a general code for calculating CR propagation and interstellar emissions from galaxies, instead of just for the Milky Way. Many of the internal structures and loops have been reorganized to take advantage of data and code caches on modern CPUs. Parallelization has been mainly at the loop level with OpenMP for earlier versions,⁴⁰ but now more advanced constructs are taken advantage of, including vectorization facilities of the OpenMP 4 specification where implemented by compiler vendors. New solvers for the diffusive transport equations, in particular, take advantage of the vectorization to dramatically increase the speed of the 3D mode so that the solutions take only a small fraction of time compared to earlier versions.

More options are now available for the distributions of the interstellar gas and CR sources. This is done via the galstruct library included in GALTOOLSLIB, which reads XML files describing the distributions of the gas and CR sources. The galstruct library is easily extended with new modules and functionality, and it includes many predefined distributions. With this new mechanism, it is possible to include many different source classes in a single GALPROP run. The current release includes two source classes, one for backward compatibility so prior run configuration files still work without modification and a new class using the galstruct library for the spatial properties and injection spectra. The new framework allows easy incorporation of multiple spectral models. It currently includes a multiple broken power law and a smoothly joined multiple broken power law. The power laws can in both cases be a function of rigidity, kinetic energy, momentum, or total energy through a user-selected parameter. Each isotope can also have a separate injection spectrum. Relative normalization of the isotopes has also been improved and can now be specified in terms of either a single point in energy or an integrated band in energy. Using the integrated bands has helped stability when modifying GALPROP parameters in maximum-likelihood fits because it reduces the degeneracy of the spectral parameters of different isotopes.

The system of the propagation equations has been generalized to allow for spatial variations in the diffusion coefficient. Scaling of the diffusion coefficient and the Alfvén speed with the strength of the Galactic magnetic field is used for modeling of the interstellar emissions by Ackermann et al. (2015; their model C).

The sky map integrator has been rewritten using a variable step size integrator that is both faster and more accurate. The location of the observer can also now be arbitrary in (X, Y, Z). The integrator also allows for the absorption of γ-rays on the ISRF, which is implemented following Moskalenko et al. (2006). It is a user-selectable option to include this. If selected, the e^± pairs resulting from the absorption are included as an additional source of secondary leptons. The individual lepton production cross section is taken from Boettcher & Schlickeiser (1997). The position-dependent pair source function assumes an isotropic γ-ray and ISRF photon distribution, which is not formally correct but significantly reduces the computational cost and does not introduce significant error.

The output IC maps are generalized to allow for an arbitrary spatial splitting; in particular, their splitting can be set to match the splitting of the gas-related emission. This allows for more flexible template fitting as used, e.g., in the analysis of the emission from the inner Galaxy by IG16.

The 3D treatment of the magnetic field now includes regular and random components that can be specified differently in the disk and plane. Temperature and polarization of radio and microwave synchrotron emission can be calculated. Synchrotron I, Q, and U Stokes parameters are calculated and output as HEALPix maps. Radio absorption and free–free emission are included; more details can be found in Strong et al. (2011), Orlando & Strong (2013), and Orlando et al. (2016).

CR secondary e^±, γ-rays, and $\overline{p}$ are produced by CR nuclei interactions with the interstellar gas. Kachelriess et al. (2015) analyzed $\overline{p}$ production in pp, pA, and AA interactions using EPOS-LHC and QGSJET-II-04. The $\overline{p}$ yields of the two MC generators agree reasonably well with each other and the available experimental data. Therefore, the results of these generators can be used to reliably predict the $\overline{p}$ yield outside the energy range covered by fixed target accelerator data, $E_{\overline{p}}\approx 10-100$ GeV. The $\overline{p}$ yields differ by a factor of a few from the yields of parameterizations based on the fixed target data commonly used in astrophysics and that are also the basis of the $\overline{p}$ calculations made with earlier GALPROP versions. The new $\overline{p}$ yield calculations are a user-selected option with this release of GALPROP.