AAfrag: Interpolation routines for Monte Carlo results on secondary production in proton–proton, proton–nucleus and nucleus–nucleus interactions

Abstract

We provide a compilation of predictions of the QGSJET-II-04m model for the production of secondary species (photons, neutrinos, electrons, positrons, and antinucleons) that are covering a wide range of energies of the beam particles in proton–proton, proton–nucleus, nucleus–proton, and nucleus–nucleus reactions. The current version of QGSJET-II-04m has an improved treatment of the production of secondary particles at low energies: the parameters of the hadronization procedure have been fine-tuned, based on a number of recent benchmark experimental data, notably, from the LHCf, LHCb, and NA61 experiments. Our results for the production spectra are made publicly accessible through the interpolation routines AAfrag which are described below. Besides, we comment on the impact of Feynman scaling violation and isospin symmetry effects on antinucleon production.

1. Introduction

A large variety of applications in astrophysics and astroparticle physics relies on a precise knowledge of the cross sections for production of secondary species in hadronic interactions. Prominent examples are indirect dark matter searches using cosmic rays (CRs), where a putative signal represents an excess over the regular background produced in astrophysical processes [1], and the spectrum of CRs deciphered from observations of the electromagnetic emission produced in their interactions in the interstellar gas [2]. Such applications typically employ empirical parameterizations of secondary production cross sections tuned to available accelerator data [3,4]. Despite the evident convenience of such parameterizations, this approach has a number of caveats. In particular, it usually relies on empirical scaling laws when extrapolating outside the measured kinematic range. Meanwhile, high-energy extrapolations of such empirical parameterizations are generally unreliable. Besides, this approach does not work well when there is a variety of nuclei species in CRs (beam) and in the interstellar gas (target). The latter is usually cured by an application of the so-called empirical “nuclear enhancement” factor, which varies substantially between different publications [5]. Meanwhile, as it has been demonstrated in Ref. [6], properly defined nuclear enhancement factors depend both on the nature of interacting particles and on the spectral slopes of the CR spectra of individual nuclei.

A number of serious issues associated with the traditional approach prompted us to reevaluate the production of secondaries using Monte Carlo generators for hadronic interactions, that describe the production of secondary photons, neutrinos, positrons, antiproton and antineutrons in proton–proton, proton–nucleus, and nucleus–nucleus collisions consistently within the same framework [6,9–11]. To this end, a special effort has been made to improve the low-energy behavior of the QGSJET-II-04 Monte Carlo generator [12], which is widely used in CR astrophysics to treat high-energy interactions. In particular, we aimed at the accurate description of antiproton production [11] that is of special interest for indirect dark matter searches.

In this work, we provide a compilation of predictions of the QGSJET-II-04m model [11] for the production of secondary species (photons, neutrinos, electrons, positrons, antiprotons and antineutrons) that are covering a wide range of energies of the beam particles in proton–proton, proton–nucleus, nucleus–proton, and nucleus–nucleus reactions. Compared to Ref. [11], the current version of QGSJET-II-04m has an improved treatment of the production of secondary particles at low energies: the parameters of the hadronization procedure have been fine-tuned, based on a number of recent benchmark experimental data, notably, from the LHCf, LHCb, and NA61 experiments. Our results for the production spectra are made publicly available through the interpolation routines AAfrag which are described below.

2. Selected results

The quality of the description of secondary particle production by the QGSJET-II-04m model is illustrated in Figs. 1–4. In Fig. 1, the results of this model for the spectra of photons as function of the Feynman scaling variable $x_{\text{F}}=2p_{\parallel }/\sqrt{s}$ in the center-of-mass (c.m.) frame are compared to the corresponding experimental data for pp-collisions at rather low incident proton momenta, 8.8 and 12.4 GeV/c [7,8]. In turn, in Fig. 2, we plot the calculated spectrum of neutral pions in the c.m. frame together with the data of the LHCf experiment [13] for proton–proton collisions at 7 TeV c.m. energy. Both the low- and high-energy data sets are well described by the results of the QGSJET-II-04m model.

Fig. 1.

Calculated Feynman x spectra $d{\sigma }_{pp}^{\gamma }/d{x}_{\text{F}}$ of photons (red line) in the c.m. frame for pp-collisions at 8.8 GeV/c (left) and 12.4 GeV/c (right), compared to experimental data (black errorbars) from Refs. [7,8].

Fig. 4.

Calculated laboratory momentum spectra of antiprotons, $d{\sigma }_{p\text{He}}^{\overline{p}}/dpd{p}_t$, for pHe-collisions at 6.5 TeV/c for different p_t intervals [from top to bottom: 0.4–0.6, 0.7–0.8, 0.9–1.1, 1.2–1.5 GeV (left) and 0.6–0.7, 0.8–0.9, 1.1—1.2, 1.5–2.0 GeV (right)], compared to data of the LHCb experiment [15].

Fig. 2.

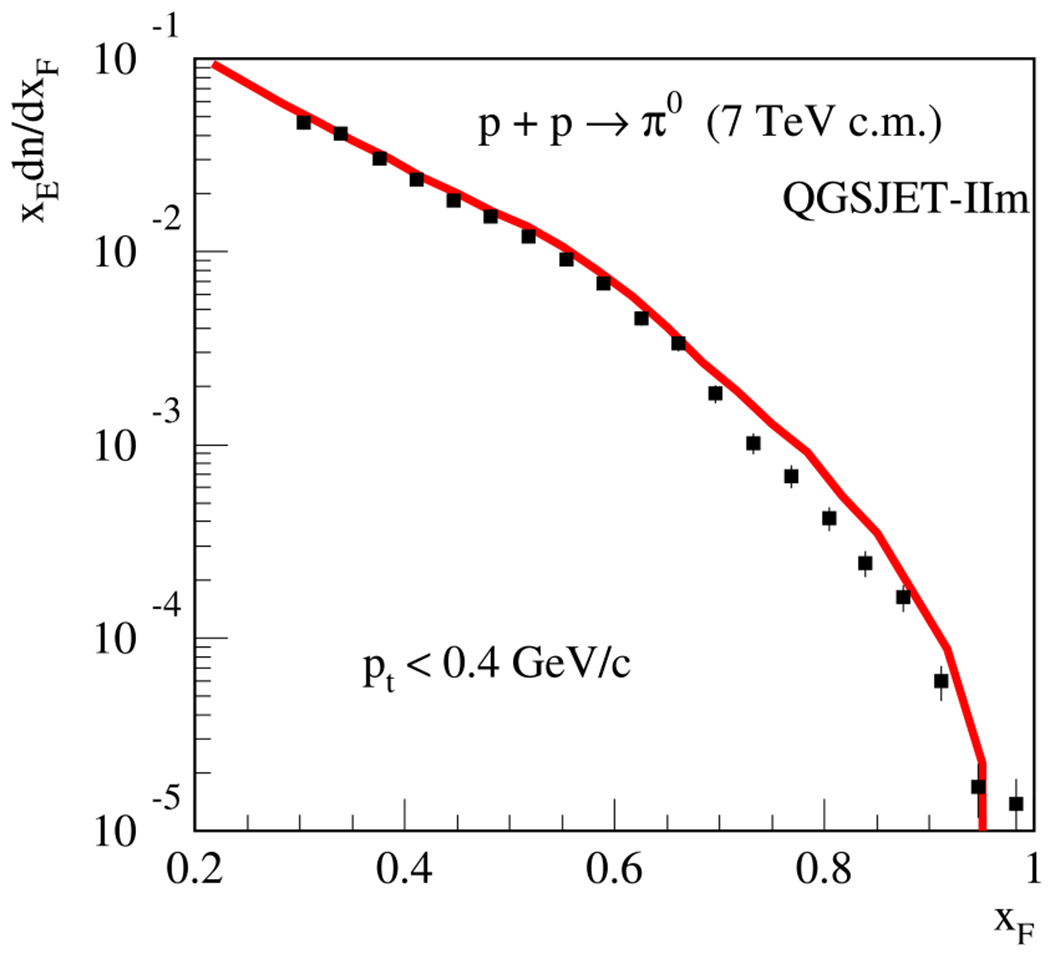
Calculated invariant energy spectrum $x_{E}d{n}_{pp}^{{\pi }^0}/d{x}_{\text{F}}$, with $x_{\text{E}}=2E/\sqrt{s}$, of neutral pions (red line) in the c.m. frame for pp-collisions at $\sqrt{s}=7$ TeV, compared to the data (black errorbars) of the LHCf experiment [13].

Concerning low energy antiproton ($\overline{p}$) production, important constraints on hadronic interaction models are provided by the recent results of the NA61 experiment [14]. The calculated rapidity distributions of the produced antiprotons in the c.m. frame (solid red lines) are compared in Fig. 3 to the experimental data (black errorbars) for pp-collisions at different incident proton momenta: 31, 40, 80, and 158 GeV/c. Additionally the results for the parameterization [3] are shown as dotted black lines. As discussed previously in Ref. [11], a significant uncertainty for the predicted flux of cosmic ray antiprotons at low ($E_{\overline{p}}^{\text{kin}}$ < 10GeV) energies is caused by the rather weak experimental constraints on the $\stackrel{\_}{p}$ yield from proton–proton collisions close to the production threshold. In particular, the substantially larger $\stackrel{\_}{p}$ yield predicted by the QGSJET-II-04m model in that energy range gave rise to an almost factor two higher antiproton flux at $E_{\overline{p}}^{\text{kin}}$ = 1 GeV [11], compared to the calculations based on the parameterization of Ref. [3]. This uncertainty is now greatly reduced by the NA61 data, e.g., as one can see in the leftmost panel of Fig. 3: The strong suppression of the $\overline{p}$ yield near the threshold, which is predicted by the parameterization of Ref. [3], is not supported by the experimental data.

Fig. 3.

Calculated rapidity distributions dn/dy of antiprotons (solid red lines) and antineutrons (dashed blue lines) for pp-collisions at different incident momenta (from left to right: 31, 40, 80, and 158 GeV/c), compared to NA61 data on $\stackrel{\_}{p}$-production [14] (black errorbars). Additionally the results for the parameterization [3] are shown as dotted black lines.

A very important high energy benchmark are studies of proton–helium collisions by the LHCb experiment, performed in the fixed target mode [15]. A comparison of our calculations with the corresponding experimental data for the momentum distribution of secondary antiprotons in the laboratory frame for proton–helium collisions at 6.5 TeV/c is plotted in Fig. 4. There is a generally satisfactory agreement with the data, particularly at relatively large antiproton momenta which is of main importance for astrophysical applications. While previously available experimental data on very high energy $\stackrel{\_}{p}$ production were restricted to central rapidity range, the LHCb results provide an important baseline for high energy extrapolations of forward production spectra of antiprotons.

3. Feynman scaling violation and isospin symmetry

As discussed in Refs. [6,11], the differences between various interaction models or parameterizations of production spectra in the predicted secondary CR fluxes can be conveniently analyzed using the so-called Z-factors. These are defined as the spectrally averaged energy fraction transferred to the produced particles of a given type in proton–proton, proton–nucleus, or nucleus–nucleus interactions. Z-factors may be introduced when the spectra of ambient CRs in the relevant energy range can be approximated by a power law. For the production of secondary CRs of the type X (X = γ, e^±, ν, $\overline{p}$, $\overline{n}$) in collisions of a primary particle i with the gas component j of the interstellar medium, the Z-factor is defined as [16]

$$Z_{ij}^X\left(E_X,{\alpha }_i\right)={\int }_0^{1}dz{z}^{{\alpha }_i-1}\frac{d{\sigma }_{ij}^X\left(E_X/z,z\right)}{dz},$$ (1)

where ${\alpha }_i$ is the slope of the primary CR spectrum, z denotes the energy fraction transferred to the particles X, and $d{\sigma }_{ij}^X\left(E_0,z\right)/dz$ the corresponding production spectrum. For the assumed case of a power-law primary flux, the partial contribution to the secondary flux of the particles X factorizes into a product of the primary flux I_i and the Z-factor,

$$q_{ij}^X\left(E_X\right)\propto I_i\left(E_X\right)Z_{ij}^X\left(E_X,{\alpha }_i\right).$$ (2)

Thus all the dependence on the interaction model in use is contained in the Z-factor $Z_{ij}^X$.

For illustration, in Fig. 5 we compare our results for the energy dependence of $Z_{pp}^{\overline{p}+\overline{n}}$ for α = 2.7, shown by the red solid line, with the one obtained from the parameterization of $\overline{p}$ production from Ref. [3], shown as a black dotted line. In the latter case, equal production yields of $\overline{p}$ and $\overline{n}$ are assumed, i.e. the dotted line corresponds to $2Z_{pp}^{\overline{p}}$. As one can see on the left panel of Fig. 5, the main difference between the two results originates from the violation of the Feynman scaling in the high energy limit, which is properly accounted for by the QGSJET-II-04m model. In contrast, the parameterization of Ref. [3] gives rise to perfect Feynman scaling at high energies. It is worth stressing that the origin of these scaling violations is rather nontrivial, resulting from both the energy-rise of the inelastic cross section and a modification of the shape of the momentum spectra. Some recent parameterizations of secondary particle production assume that the momentum spectra scale at sufficiently high energies (see, e.g., Ref. [17]), i.e. that the factorization

$$\frac{x_{E}d{\sigma }_{pp}^X\left(s,x_{\text{F}}\right)}{d{x}_{\text{F}}}\simeq {\xi }_X\left(s\right)f\left(x_{\text{F}}\right)$$ (3)

holds. Moreover, they parameterize the resulting s-dependence of ${\xi }_X\left(s\right)$ using experimental data on the height of the rapidity plateau in the c.m. frame, setting

$${\xi }_X\left(s\right)\propto {\frac{d{\sigma }_{pp}^X}{dy}|}_{y=0}{=x_E\frac{d{\sigma }_{pp}^X}{d{x}_{\text{F}}}|}_{x_{\text{F}}=0}.$$ (4)

Such an assumption leads to a violation of energy conservation in the high energy limit and gives rise to a considerable overestimation of secondary CR spectra. This holds especially for photons, positrons, and neutrinos, because an important contribution to their production spectra comes from the hadronization of valence quarks of the incident proton. Because of the increase of multiple scattering [18], the height of the central rapidity plateau rises asymptotically as a power of energy, $d{\sigma }_{pp}^X/{dy|}_{y=0}\propto s^{{\Delta }_{\text{eff}}}$, and thus the factor ${\xi }_X$ in Eq. (3) rises with the same slope. This would imply, in turn, that the average energy fraction transferred to secondary particles of any given type X, $\langle Z_E^X\left(s\right)\rangle \propto {\xi }_X\left(s\right)/{\sigma }_{pp}^{\text{inel}}\left(s\right)$, has an unlimited rise—which is clearly nonphysical. In reality, the steep energy rise of the central rapidity plateau is accompanied by a moderate “softening” of the very forward part of the production spectra, because multiple scattering processes have to share the energy [19], as illustrated in Fig. 6 for the particular case of neutral pion production.

Fig. 5.

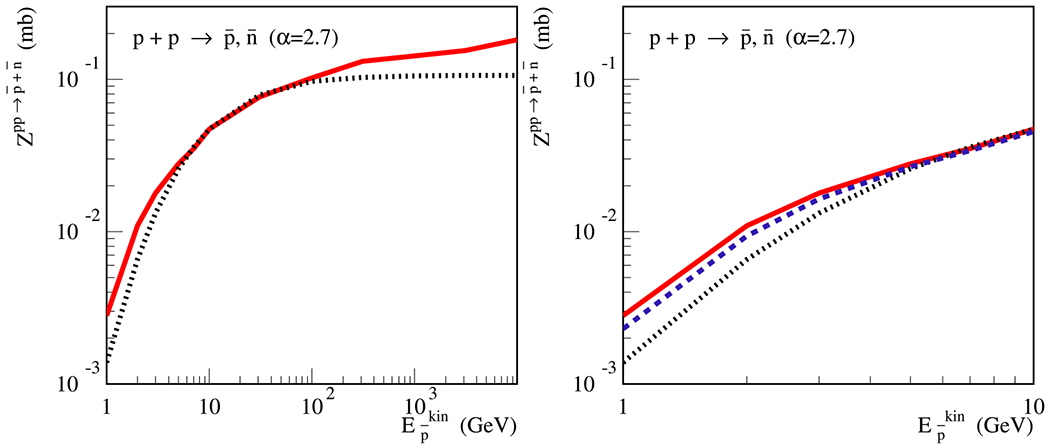
Left: $Z_{pp}^{\overline{p}+\overline{n}}$ calculated using the QGSJET-II-04m model (red solid line) and $2Z_{pp}^{\overline{p}}$ calculated using the parameterization of Ref. [3] (black dotted line) – both for the primary proton spectral slope α = 2.7. The right panel zooms into the low-energy part and contains also $2Z_{pp}^{\overline{p}}$ calculated using QGSJET-II-04m (blue dashed line).

Fig. 6.

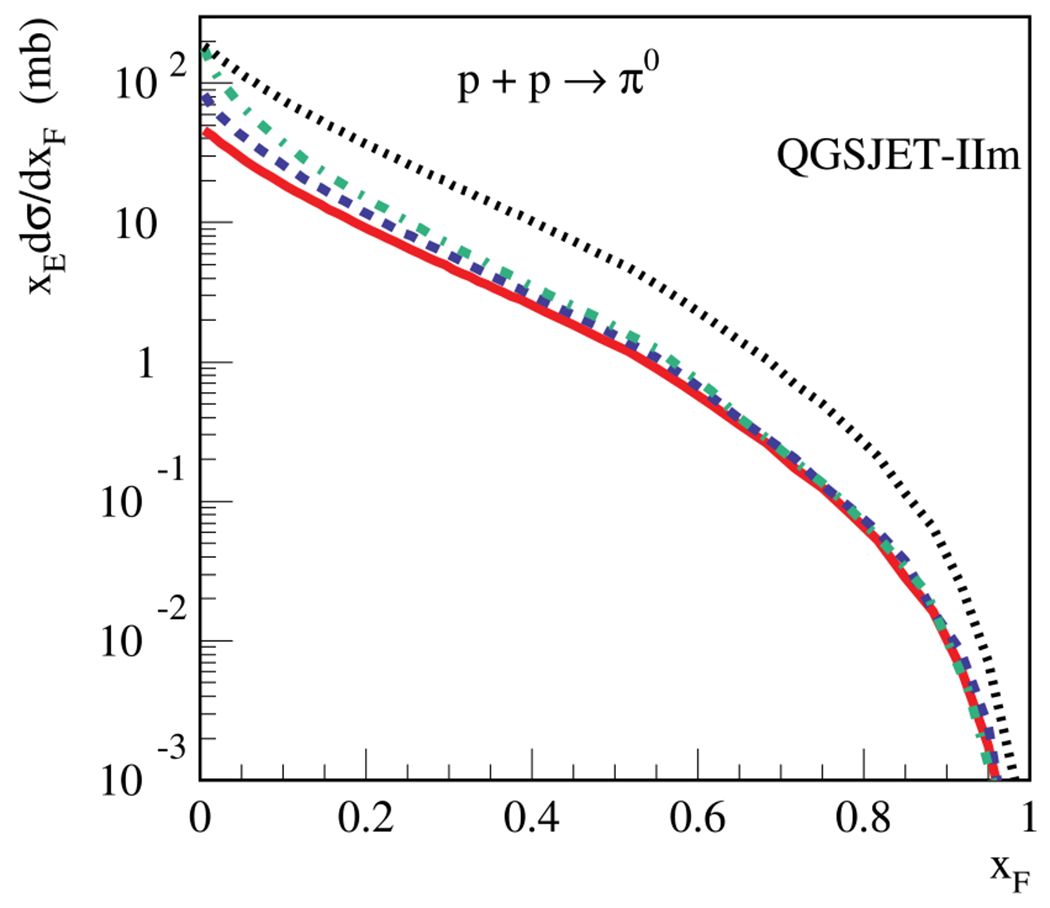
Invariant energy spectrum of neutral pions, $x_{E}d{\sigma }_{pp}^{{\pi }^0}/d{x}_{\text{F}}$, in c.m. frame for pp-collisions at $\sqrt{s}={10}^2$, 10³, and 10⁴ GeV – solid, dashed, and dashed–dotted lines respectively. Dotted line corresponds to a rescaling of the spectrum from $\sqrt{s}={10}^2$ GeV to $\sqrt{s}={10}^4$ GeV, according to the rise of the height of the central rapidity plateau.

Let us now discuss the difference between the solid and dotted lines at low-energies $E_{\overline{p}}^{\text{kin}}$ < 10 GeV which can be seen in the right panel of Fig. 5. These differences are partly explained by the larger $\stackrel{\_}{n}$ (compared to $\stackrel{\_}{p}$) yield close to the production threshold. This is illustrated by the blue dashed line in the same panel, which corresponds to $2Z_{pp}^{\overline{p}}$ from the QGSJET-II-04m model. At the first sight, such a $\overline{n}/\overline{p}$ enhancement seems surprising: while isospin symmetry is not an exact one for strong interactions, it holds with a very good accuracy, thanks to the small mass difference between the u and d quarks. Taking into account that both $\overline{p}$ and $\overline{n}$ originate from a central production mechanism, without involving valence quarks of the colliding protons, one expects equal average yields of antiprotons and antineutrons.

The origin of the unexpected neutron enhancement is related to the valence quark content of the proton (uud) and the suppression of heavy baryon production close to the production threshold. To explain this in more detail, let us remark that in the low-energy regime particle production in pp-collisions is dominated by the so-called “undeveloped cylinder” diagrams, as exemplified in Fig. 7. In such a case, a valence quark from one of the colliding protons (projectile u-quark in Fig. 7) combines with a diquark from the other proton (target uu-diquark in Fig. 7) to form a final baryon. At the same time, a string of color field is being formed between the remaining valence diquark and quark (ud – d string in Fig. 7). With those diquark and quark sitting on the string ends and flying apart, the string breaks and gives rise to additional secondary hadron production via a creation of quark–antiquark and diquark–antidiquark pairs from the vacuum.

Fig. 7.

Example diagram of the undeveloped cylinder type, which contributes to antiproton production in pp-collisions.

Returning back to our case of interest, near-threshold production of antiprotons and antineutrons, we can neglect final states containing heavy baryon resonances and consider only the $ud\stackrel{\_}{u}\stackrel{\_}{d}$-diquark contribution to this hadronization process. Using simple quark counting rules, we are left with only four possible final states with the following relative weights: (1) $ppp\stackrel{\_}{p}$ – 2/9; (2) $ppn\stackrel{\_}{n}$ – 7/18; (3) $pn\stackrel{\_}{p}{\Delta }^{++}$ – 5/18; (4) $nn\stackrel{\_}{n}{\Delta }^{++}$ – 1/9. Accounting for the decay of the Δ⁺⁺, this seems to yield equal multiplicities for $\stackrel{\_}{p}$ and $\stackrel{\_}{n}$. However, according to our reasoning, close to the threshold we have to neglect the 3rd and 4th configurations of final states since they are suppressed because of the high mass of the Δ⁺⁺ resonance. This immediately gives rise to an almost factor of 2 enhancement of the $\stackrel{\_}{n}/\stackrel{\_}{p}$ yield.

It is worth stressing that this effect quickly fades away as the collision energy increases. This can be seen in Fig. 3, where we plot the rapidity distributions of produced antineutrons with dashed blue lines: the relative $\stackrel{\_}{n}/\stackrel{\_}{p}$ excess changes from ≃ 20% to ≃ 5% when the incident proton momentum increases from 31 GeV/c to 158 GeV/c. The same effect is also clearly seen in the right panel of Fig. 5: the solid and dashed lines coincide at sufficiently high energies. In contrast, in some recent parameterizations one assumes a substantial violation of the isospin symmetry by postulating a large energy-independent excess of antineutrons (see, e.g., Ref. [20]).

4. Program structure and example output

4.1. Program structure

The program consists of two files AAfrag101.f90 and user101.f90. The file AAfrag101.f90 contains the module spectra, the main program, the initialization and the interpolation subroutines. For standard applications no changes in this file are necessary. The file user101.f90 contains as an example the calculation of secondary spectra for incident proton energy E_p = 100 GeV.

More precisely, the file AAfrag101.f90 starts with the module spectra containing the definition of internal variables and the values of some constants. The following main program calls first the initialization subroutine init and then the subroutine user_main contained in the file user101.f90. The latter subroutine has to be adopted by the users for their specific needs.

The initialization is performed by two subroutines, init_low and init_high. The latter initializes a grid logarithmic in primary energy at primary energies E_p ≥ 10 GeV, while the former defines an additional grid linear in primary energy for the reaction k = {1, 2, 3, 4} at lower energies. The two subroutines read the data files for the secondary production cross sections calculated in various QGSJET-II-04m runs which are collected in the folder Tables.

The functions spec_gam(E_p,E_s,k), spec_nu_tot(E_p,E_s,q,k), spec_elpos(E_p,E_s,q,k), spec_pap(E_p,E_s,q,k), and spec_nan(E_p,E_s,q,k) interpolate the production spectra $E_s^{2}d{\sigma }^k\left(E_p,E_s\right)/d{E}_s$ of the secondaries {γ, ν, e⁻, e⁺, ν_i, p, $\stackrel{\_}{p}$, n, $\stackrel{\_}{n}$} in proton–proton (k = 1), proton–helium (k = 2), helium–proton (k = 3), helium–helium (k = 4), carbon–proton (k = 5), aluminium–proton (k = 5), and iron–proton (k = 6) reactions. The connection between the variable q and the particle type is specified in Table 1, while the mass numbers of target and projectile nuclei are given for the various reactions in Table 2. Alternatively to the function spec_nu_tot(E_p,E_s,q,k) which provides the spectrum for an individual neutrino type, the function spec_nu_tot(E_p,E_s,k,spec) returns the sum of the ν_e, ν_e, ${\stackrel{\_}{\nu }}_e$ and ${\stackrel{\_}{\nu }}_{\mu }$ spectra. Note that we keep (anti-) neutrons stable. Thus antinucleons can be used for studies of antideuteron production. Moreover, neutron escape from magnetized sources can be employed in CR studies.

Table 1.

Dependence of the particle type on the variable q.

Function	q = 1	q = 2	q = 3	q = 4
spec_nu(E_p,E_s,q,k)	νe	${\stackrel{\_}{\nu }}_e$	νμ	${\stackrel{\_}{\nu }}_{\mu }$
spec_elpos(E_p,E_s,q,k)	e −	e +
spec_pap(E_p,E_s,q,k)	p	$\stackrel{\_}{p}$
spec_nan(E_p,E_s,q,k)	n	$\stackrel{\_}{n}$

Table 2.

Beam and target particles implemented in AAfrag.

Reaction	1	2	3	4	5	6	7
Beam-target	p–p	p–He	He–p	He–He	C–p	Al–p	Fe–p
Mass number	1–1	1–4	4–1	4–4	12–1	26–1	56–1

The primary energy E_p denotes the total energy of the primary nucleus in GeV, E_s the energy in GeV of the produced secondary, and the differential production cross sections are measured in mbarn. The minimal interpolated primary energy varies from E_p = 5 GeV for protons to 100 GeV for iron, while the maximal energy is E_p = 10²⁰ eV.

4.2. Example output

The files spec_gam, spec_nu,spec_nu_tot, spec_elpos, spec_aprot, and spec_aneut contain the production spectra $E_s^{2}d{\sigma }^k\left(E_p,E_s\right)/d{E}_s$ of photons, the four neutrinos ν_e, ν_e, ${\stackrel{\_}{\nu }}_e$ and ${\stackrel{\_}{\nu }}_{\mu }$, their sum, electrons and positrons, antiprotons, and antineutrons for the case of proton–proton collisions at E_p = 100 GeV.

5. Summary

We compared the results of an updated version of QGSJET-II-04m to a wide range of experimental results covering both low- and high-energy data, finding a satisfying agreement between the measured and the calculated energy spectra. We discussed the reason for the apparent enhancement of the $\stackrel{\_}{n}/\stackrel{\_}{p}$ yield at low energies and demonstrated that it is explained by a threshold effect. Our results for the production spectra of photons, neutrinos, electrons, positrons, and antiprotons in proton–proton, proton–nucleus, nucleus–proton, and nucleus–nucleus collisions are made publicly available through the described interpolation routines AAfrag.

Program summary.

Program Title: AAfrag 1.01

Program Files doi: http://dx.doi.org/10.17632/6f73jz6jx8.1

Licensing provisions: CC by NC 3.0.

Programming language: Fortran 90

Supplementary material: see http://aafrag.sourceforge.io

Nature of problem: Calculation of secondaries (photons, neutrinos, electrons, positrons, protons, and antiprotons) produced in hadronic interactions

Solution method: Results from the Monte Carlo simulation QGSJET-II-04m are interpolated.