Abstract
It is widely accepted that cosmic rays (CRs) up to at least PeV energies are Galactic in origin. Accelerated particles are injected into the interstellar medium where they propagate to the farthest reaches of the Milky Way, including a surrounding halo. The composition of CRs coming to the solar system can be measured directly and has been used to infer the details of CR propagation that are extrapolated to the whole Galaxy. In contrast, indirect methods, such as observations of γ-ray emission from CR interactions with interstellar gas, have been employed to directly probe the CR densities in distant locations throughout the Galactic plane. In this article we use 73 months of data from the Fermi Large Area Telescope in the energy range between 300 MeV and 10 GeV to search for γ-ray emission produced by CR interactions in several high- and intermediate-velocity clouds (IVCs) located at up to ~7 kpc above the Galactic plane. We achieve the first detection of IVCs in γ rays and set upper limits on the emission from the remaining targets, thereby tracing the distribution of CR nuclei in the halo for the first time. We find that the γ-ray emissivity per H atom decreases with increasing distance from the plane at 97.5% confidence level. This corroborates the notion that CRs at the relevant energies originate in the Galactic disk. The emissivity of the upper intermediate-velocity Arch hints at a 50% decline of CR densities within 2 kpc from the plane. We compare our results to predictions of CR propagation models.
Keywords: cosmic rays, Galaxy: halo, gamma rays: ISM, ISM: clouds
1. INTRODUCTION
Cosmic rays (CRs) are a wide-spread phenomenon, pervading galaxies and intergalactic space. They are directly detected within the solar system with spacecraft, balloon-borne instruments, and ground-based instruments. Other methods to study CRs include observations of radio synchrotron emission and γ rays produced in interactions of CRs with interstellar gas, radiation, and magnetic fields. CRs consist of all known stable and long-lived isotopes ranging from the most abundant hydrogen and helium nuclei through the traces of very rare Actinides, and particles such as electrons, positrons, and antiprotons. The energy density of CRs in the interstellar medium (ISM) is comparable to those of the Galactic interstellar radiation field, magnetic field, and turbulent motions of the interstellar gas. CRs are one of the essential components of the Galactic ecosystem (e.g., Ferrière 2001), affecting the thermal, chemical, and magnetohydrodynamical state of the ISM (e.g., Ptuskin et al. 2006; Indriolo et al. 2009). Emission from CRs interacting within the Milky Way is also a source of foregrounds/backgrounds for many observations spanning from radio to γ rays.
Observations of X-ray and γ-ray emission from Galactic objects such as supernova remnants, pulsars, and massive star clusters reveal the presence of energetic particles, suggesting that efficient acceleration processes occur in their vicinities (for recent reviews see, e.g., Reynolds 2008; Bykov 2014). The Galactic origin of CRs is also supported by γ-ray observations of external galaxies, which indicate that the CR densities are not universal (e.g., Sreekumar et al. 1993) and are correlated with the star formation properties of the galaxies (e.g., Ackermann et al. 2012b). Also, the radial sizes of radio halos measured in external, edge-on spiral galaxies appear to be correlated with active star formation in their disks (Dahlem et al. 1995).
CR particles accelerated in sources in the Galactic disk are injected into the ISM where they propagate through a surrounding halo before escaping into the intergalactic space (e.g., Strong et al. 2010). This paradigm is substantiated in models that can reproduce reasonably well all the related observables (for a recent review see, e.g., Strong et al. 2007). The propagation of particles in the ISM leads to the destruction of primary nuclei via spallation and gives rise to secondary nuclei and isotopes that are rare in nature and to other particles. The observed abundances of stable secondary CR nuclei (e.g., boron) and radioactive isotopes (10Be, 26Al, 36Cl, 54Mn) allow the separate determination of the confinement halo size and diffusion coefficient (e.g., Strong & Moskalenko 1998) which is somewhat model dependent. Typical constraints on the halo height arising from such a method are 4–6 kpc (e.g., Moskalenko et al. 2001; Trotta et al. 2011).
Observations of edge-on external galaxies show directly the existence of radio halos extending to kiloparsec distances perpendicularly to their disks (e.g., Dahlem et al. 1994) and sometimes up to ~15 kpc (Irwin et al. 1999). Radio observations of large-scale synchrotron emission from the Milky Way were also interpreted in the context of diffusion models as indicating a vertical extent of the halo of 4–10 kpc (e.g., Strong et al. 2000), with values of ~10 kpc favored based on a recent analysis including WMAP and 408 MHz observations (Orlando & Strong 2013). The discrepancies between halo sizes determined with different methods are not necessarily surprising. The method based on the direct detection of CR nuclei provides the size of the effective volume filled with CRs that are still confined to the Milky Way. In contrast, observations of synchrotron emission show larger halos because part of the emission may be generated by particles that are leaking into the intergalactic space, i.e., that are already beyond the “point of no return.”
The Large Area Telescope (LAT) on the Fermi Gamma-ray Space Telescope mission (Atwood et al. 2009) has been surveying the sky since 2008 in a wide energy range of 20 MeV to >300 GeV. These observations provide information about CR particles (mostly protons and electrons) in distant locations that can be used to study CR propagation (e.g., Ackermann et al. 2012a). Measurements with the LAT confirmed earlier observations (e.g., Strong et al. 1988) that the radial gradient of the γ-ray emissivity (γ-ray emission rate per hydrogen atom) in the ISM outside the solar circle is much smaller than that in the density of putative CR sources (Abdo et al. 2010; Ackermann et al. 2011). This can be interpreted as another hint of a ~10 kpc CR confinement halo because it facilitates radial diffusion of CRs and compensates for the paucity of CR sources in the outer Galaxy.
In this work we propose a more direct method to constrain the propagation of CRs in the halo of the Milky Way with LAT data. Although the interstellar gas in the Milky Way is largely confined to the Galactic plane with a scale height for atomic hydrogen of ≲300 pc across much of the disk (Kalberla & Kerp 2009), certain populations of interstellar clouds are known to exist at much greater distances from the plane. So-called high-velocity clouds (HVCs) and intermediate-velocity clouds (IVCs) are interstellar clouds of atomic hydrogen, H i, with line of sight velocities inconsistent with Galactic rotation (see, e.g., van Woerden et al. 2005). The demarcation between HVCs and IVCs is conventionally taken to be a Doppler-shifted velocity with an absolute value between 80 and 100 km s−1 with respect to the local standard of rest.
The distances and metallicities of HVCs/IVCs can be inferred from spectroscopic observations of foreground and background stars. HVCs typically have metallicities less than solar and are generally considered to be remnants of the formation of the Milky Way, having existed in the halo of the Galaxy since the disk formed, or old tidal streams extracted from nearby dwarf galaxies (Wakker 2002). Some IVCs have metallicities much closer to solar and these may be gas ejected from the plane, e.g., by Galactic fountains (Wakker 2002). No molecular gas, e.g., CO emission, has been detected in HVCs (Wakker et al. 1997), and IVCs are also typically free of CO emission as well.
These clouds have low column densities, N (H i) ~ 1019−1020 cm−2, but can subtend hundreds of square degrees. The exposure of the LAT sky survey is deep enough for HVCs/IVCs to conceivably be detected in diffuse γ-ray emission and used to estimate the CR densities in the Galactic halo. These clouds are not actively forming stars and are believed to be free of internal sources of CRs and hence any γ-ray emission from them samples the large-scale distribution of Galactic CRs.
The article is structured as follows. In Section 2 we describe our criteria for selecting a sample of HVCs/IVCs for study. In Section 3 we discuss the γ-ray and multiwavelength survey data we use. Section 4 provides the details of how we derive the H i maps, in particular how we fit spectral components with different line of sight velocities to achieve kinematic separation of interstellar gas by distance along the line of sight, and other maps of ISM tracers to accurately account for foreground gas in the local neighborhood. In Section 5 we introduce the γ-ray analysis procedure to measure or constrain the CR densities in the targets, and the procedure we implemented to estimate systematic uncertainties. In Section 6 we discuss the results for the individual regions that we studied and the implications for the propagation of CRs in the halo of the Milky Way. The conclusions are in Section 7. Appendix A provides more technical information about the derivation of the maps of the ISM, including an iterative approach to unbiasing the maps of the column density in the dark neutral medium (DNM). Appendix B describes how we computed uncertainties and upper limits with the jackknife method for evaluating the systematic uncertainties.
2. TARGETS
Wakker (2001) reports the most complete census to date of IVCs and HVCs, including lower and upper limits on their distances (which we refer to as distance brackets), from spectrophotometric distances of foreground and background stars. In order to be able to constrain the CR densities in well-defined regions of the Milky Way halo, we select as targets for our analysis clouds in Wakker (2001) for which distance (altitude) brackets have been determined. We summarize the selected targets in Table 1, grouped in three regions of interest (ROIs) as used for the analysis later. In each case the ROIs enclose the parts of the clouds associated with the foreground and background stars used for determining the distance brackets.
Table 1.
Target Regions and Complexes
| Region | ROI | Complex |
d (kpc) |
z (kpc) |
Metallicity (relative to solar) |
vLSR (km s−1) |
|
|---|---|---|---|---|---|---|---|
| Center (l, b) | Pixels | ||||||
| A | (155°, 37°) | 161, 18 | Low-Latitude IV Arch | 0.9–1.8 | 0.6–1.2 | 1.0 ± 0.5 | −90 < vLSR < −40 |
| Complex A | 4.0–9.9 | 2.6–6.8 | 0.02–0.4 | vLSR < −90 | |||
| B | (182°, 57°) | 125, 141 | Lower IV Arch | 0.4–1.9 | 0.4–1.7 | ~1 | −60 < vLSR < −15 |
| Upper IV Arch | 0.8–1.8 | 0.7–1.7 | ~1 | vLSR < −60 | |||
| C | (251°, 69°) | 85, 117 | IV Spur | 0.3–2.1 | 0.3–2.1 | … | −90 < vLSR < −20 |
Note. The ROIs are defined as rectangular regions in a plate carrée projection in Galactic coordinates, centered at each ROI center position and with the number of pixels of width given above. See text for details.
The brackets in d and z, and the metallicities are taken from Wakker (2001). The metallicity of the IV Spur is unknown.
The ranges in velocities with respect to the local standard of rest, vLSR, are the preliminary boundaries that we use in Section 4.1 to construct the N (H i) maps.
Region A encompasses an IVC known as the low-latitude intermediate velocity (IV) Arch, and an HVC known as Complex A. The low-latitude IV Arch has a mass of 1.5–6 × 105 M☉ at a distance of 0.9–1.8 kpc from the Sun, corresponding to a distance above the plane of z = 0.6–1.2 kpc. According to Wakker (2001) the distance (comparable to that of the Perseus arm of the Galaxy), the metallicity (close to solar), and negative velocities in the range of −20 to −30 km s−1 (higher than the Perseus arm itself in this direction) are all compatible with the characteristics of a high interarm cloud that is part of the return flow of gas injected from the disk into the halo by a fountain process. Complex A is a distant HVC with the narrowest distance bracket7 of 4.0–9.9 kpc (z = 2.6–6.8 kpc), which implies a mass of (0.3–2) × 106 M☉. Its low metallicity suggests that this HVC is a relic of the ancient universe, a clump of gas that never underwent star formation and is now falling into the Milky Way.
Region B encompasses two IVCs that are together known as the IV Arch. The gas in the IV Arch is seen in two distinct velocity ranges: > −60 km s−1 (the lower IV Arch) and < −60 km s−1 (the upper IV Arch).8 We consider in this analysis only the portion of the IV Arch seen at Galactic longitudes l > 150°, for which there is a distance bracket for the lower part of the Arch of 0.4–1.9 kpc (z = 0.4–1.7 kpc). At lower longitudes the distance is less reliably determined, and part of the lower IV Arch may be associated with a CO core with distance <0.3 kpc from the solar system (Wakker 2001). On the other hand, the upper IV Arch has a distance bracket of 0.8–1.8 kpc (z = 0.7–1.7 kpc). Therefore, whether the two velocity components of the IV Arch are also physically separated entities is uncertain. The total mass of the IV Arch is of the order of several 105 M☉, and its metallicity is not well determined, but possibly close to solar (Wakker 2001).
Region C encompasses the IV Spur, which is an extension of the IV Arch at lower velocities and higher Galactic latitudes. The distance bracket is 0.3–2.1 kpc (z = 0.3–2.1 kpc), which implies a mass of 0.2–2.8 × 105 M☉. The metallicity is unknown.
All the target objects discussed reside in a relatively small sector of the Milky Way with 130° ≲ 1 ≲ 280° and b > 25°. This is in fact one of the regions richest in IVCs and HVCs and for which Wakker (2001) could get access to stellar probe observations.
Furthermore, in recent years distance brackets have been determined for additional, lower-mass IVCs and HVCs (e.g., Wakker et al. 2008). Such clouds have ratios of mass over distance square of the order of ≲102 M☉ kpc−2. Therefore, for normal γ-ray emission rates per H atom, as measured in the Galactic disk, we expect total fluxes of ≲10−10 cm−2 s−1 at energies >100 MeV. These fluxes are one order of magnitude or more below the LAT sensitivity level (Ackermann et al. 2012c). Therefore, we do not expect to be able to use LAT observations of these clouds to constrain their CR densities, and we do not include them among our targets. Conversely, the clouds selected for the analysis all have mass over distance square ratios of the order of ≳103 M☉ kpc−2, and hence expected γ-ray fluxes ≳10−9 cm−2 s−1, in the range detectable by the LAT.
We have not included among our targets Complex GCP, also known as the Smith Cloud, because this HVC is seen at Galactic latitudes ∣b∣ < 20° toward the inner Galaxy, where the diffuse γ-ray foregrounds from the Galactic disk are brighter and more challenging to model. We leave Complex GCP for future studies. We note that Drlica-Wagner et al. (2014) and Nichols et al. (2014) searched for γ-ray emission associated with Complex GCP due to exotic processes related to hypothetical dark matter particles, and did not report on any significant detections.
3. DATA
3.1. γ-ray Data
The LAT is a pair-conversion γ-ray telescope for the energy range 20 MeV to >300 GeV. The instrument is described in Atwood et al. (2009), and its on-orbit performance discussed in Ackermann et al. (2012c). We use LAT observations accumulated from the beginning of the Science phase of the mission, MET9 239500801 (2008 August 4), up to MET 431481603 (2014 September 4), for a total of 73 months. We use the P7REP data set (Bregeon et al. 2013) and select “Clean” class events in order to limit the contamination from backgrounds due to residual CRs misclassified as γ rays in the study of large-scale diffuse features.
We apply further restrictions to the data set used:
We select only time intervals when the LAT was operated in normal Science mode (e.g., excluding calibration data) and when the data quality was considered good (e.g., excluding solar flares which caused pile-up phenomena in the detector).
We retain only candidate γ rays detected at inclinations from the Earth zenith <95°, in order to limit the contamination from the bright γ-ray emission produced by CR interactions in the Earth’s atmosphere that forms extended features in the sky.
We consider only candidate γ rays with measured energies between 300 MeV and 10 GeV. Below 300 MeV the LAT angular resolution rapidly deteriorates (Ackermann et al. 2012c), which makes separating different components of diffuse γ-ray emission based on their morphologies more difficult. Additionally, below ~300 MeV one would need to model the residual emission from CR interactions in the upper atmosphere. This can introduce a faint diffuse glow at moderately high declinations, which would need to be modeled, and would further complicate the study of faint extended features especially near the North Celestial pole (NCP) where our targets are located. Above 10 GeV the photon counts are sparse and the data are not very useful to constrain CR interactions in clouds owing to their spectrum being softer than inverse-Compton (IC) emission from Galactic CR electrons and isotropic backgrounds (e.g., Ackermann et al. 2012a). Limiting the energy range also helps to attenuate the systematic uncertainties due to the spectral models assumed for the various components of the γ-ray sky.
For the γ-ray analysis described in this section and elsewhere in the article we used the official LAT Science Tools, version v09r34p01.10
3.2. Interstellar Medium Tracer Data
If the CR densities are uniform within a cloud, the γ-ray intensities are simply proportional to the target gas column densities. Thus, in order to model γ-ray emission from IVCs and HVCs and foreground emission from local gas we rely on a set of ISM tracers described here.
We employ as tracer of atomic gas the Leiden-Argentine-Bonn (LAB) all-sky survey of the 21 cm H i emission line by Kalberla et al. (2005). The survey provides the H i line brightness temperatures over a grid of (with an effective angular resolution of ), and covers velocities with respect to the local standard of rest from −450 to +400 km s−1, at a resolution of 1.3 km s−1. Data were corrected for stray radiation reaching a residual noise contamination <0.09 K for most directions in the sky. We use data from Kalberla et al. (2005) to derive N (H i) column-density maps as described in Section 4.1.
Molecular hydrogen cannot be traced directly in its most common cold state. The most widely used surrogate tracer is the 2.6 mm line of 12CO. For this work we use a map of CO brightness temperature integrated over Doppler velocities, WCO, derived from the Center for Astrophysics composite CO survey (Dame et al. 2001) supplemented with higher-latitude observations of the Ursa Major region (de Vries et al. 1987). The CO data, denoised using the moment-masking technique (Dame 2011), were used to construct the WCO map on a grid. The WCO intensities are assumed to be proportional to the molecular hydrogen column densities N (H2).
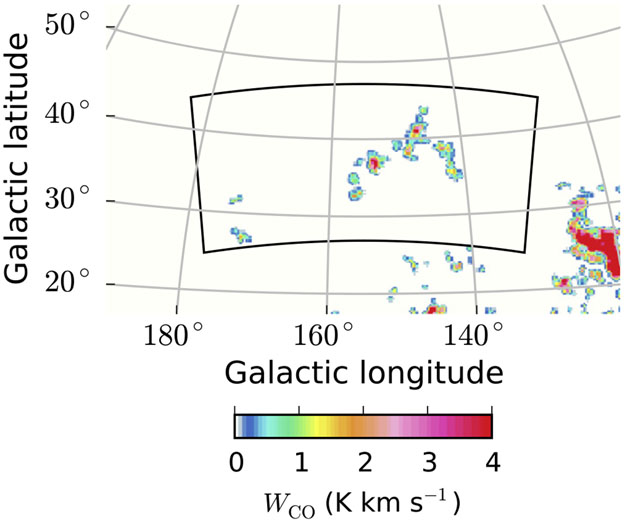
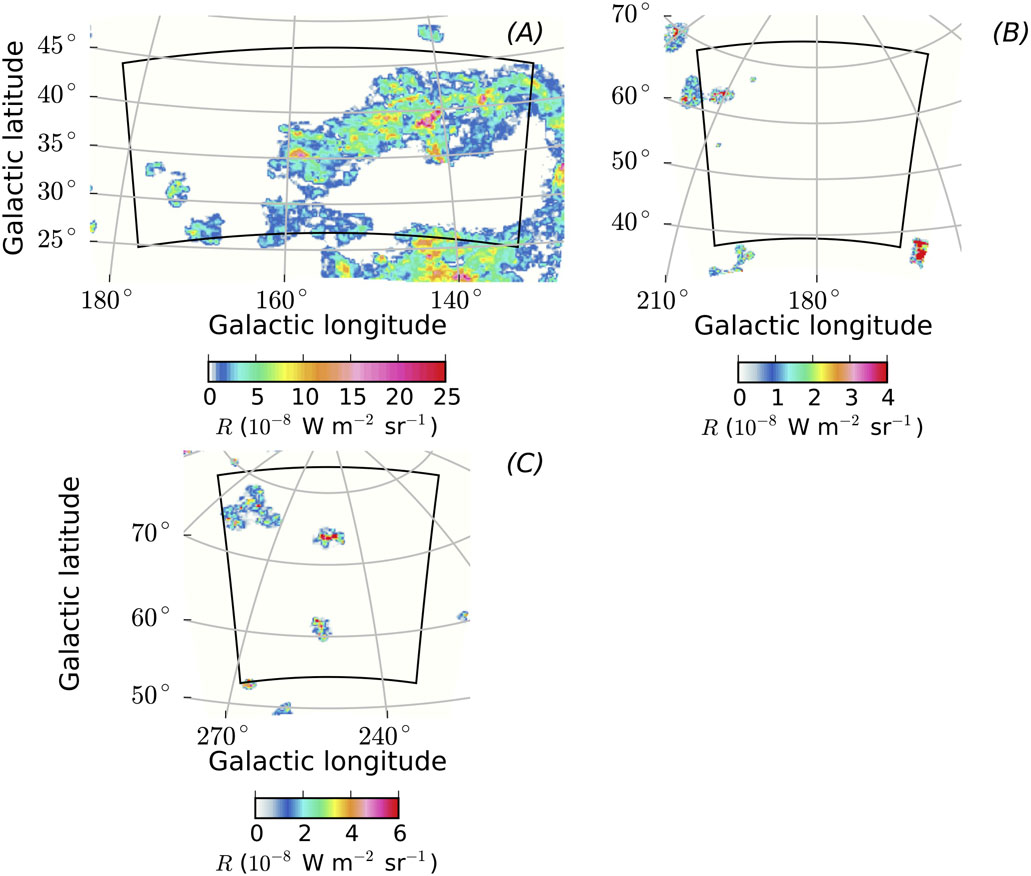
Only ROI A contains significant CO emission (Figure 1). The CO emission detected is associated with the Ursa Major molecular clouds, located at a few 100 pc from the solar system (e.g., de Vries et al. 1987). Note that, according to the results from the component separation of the all-sky survey performed using the Planck-HFI instrument (Planck Collaboration XIII 2014), there is no significant CO emission in our ROIs besides what is included in this CO map.
Figure 1.
WCO intensities in the direction of ROI A. The map is shown in zenithal equidistant projection. Blank pixels are set to zero. The black line shows the border of the ROI.
Various observations indicate that a linear combination of N (H i) and WCO maps does not properly account for the totality of the ISM neutral gas, but large fractions of the gas can be in a DNM phase, also known as dark gas (e.g., Magnani et al. 2003; Grenier et al. 2005; Abdo et al. 2010; Langer et al. 2010; Planck and Fermi Collaborations 2014). The DNM may be composed of molecular gas not associated with CO, revealed, e.g., by alternative tracers like CH (e.g., Magnani et al. 2003), that is likely to exist because the CO molecule is more prone to photodissociation than H2 in the external layers of molecular clouds (e.g., Wolfire et al. 2010; Smith et al. 2014). There can also be a contribution from atomic gas overlooked because of the approximations applied in deriving column densities from the H i line intensities (Fukui et al. 2015). On large scales the DNM in the Milky Way is best traced by dust thermal emission or extinction and γ rays, which reveal correlated excesses on top of the components traced by H i and CO that can be interpreted as a contribution from undetected, but otherwise normal, neutral interstellar matter (e.g., Grenier et al. 2005; Abdo et al. 2010; Planck and Fermi Collaborations 2014).
In order to trace the DNM in this work we rely on the all-sky model of thermal dust emission by the Planck Collaboration XI (2014) based on Planck and IRAS data (Planck public data release R1.20). We test both the map of optical depth at 353 GHz, τ353, and the map of total dust radiance, R. The angular resolution of these maps is 5′. They are used to construct maps of the DNM as described in 4.2.
4. CONSTRUCTION OF THE INTERSTELLAR MEDIUM TRACER MAPS
For each ROI we construct maps of the N (H i) column densities for different complexes along the line of sight, and maps of the DNM column densities. The maps are constructed over regions that include at least 5° boundaries around the ROI in order to properly take into account the point-spread function (PSF) of the LAT in fits of the models to the γ-ray data.
4.1. Construction of the H i Maps
The column densities of atomic gas, N (H i), in IVCs and HVCs and those in the local foreground gas can be separated based on Doppler velocities in order to separate contributions from CR interactions with gas in different locations in the Galaxy. To do so we adapt the procedure described in Abdo et al. (2010). The procedure used in this work has three steps.
For each ROI we define some preliminary velocity boundaries that separate different components along the line of sight, namely low-velocity (local) gas and gas in HVCs/IVCs (Table 1).
For each line of sight on the grid of the LAB survey we adjust the velocity boundaries so that they fall at the closest minimum (or inflection point) in the brightness temperature profile. The column density N (H i) associated with each component is proportional to the integral of the brightness temperature over velocity within the adjusted velocity boundaries.
For each line of sight on the H i grid we fit to the brightness temperature profile a combination of Gaussian functions centered at the profile maxima (or inflection points if a maximum is not found for a velocity component) and use the results of the fit to correct the column densities of each component for the spillover from/into the adjacent components.
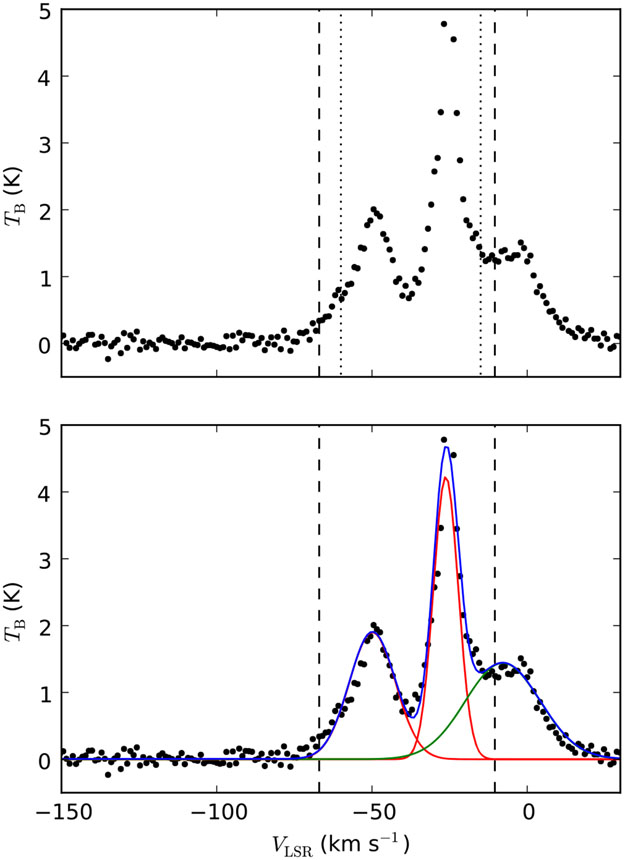
The procedure is illustrated for an example line of sight in Figure 2. Technical details of the procedure are illustrated by (Tibaldo 2011, 2.1.2, Appendix B).
Figure 2.
H i brightness temperature, TB, as a function of Doppler velocity with respect to the local standard of rest, VLSR, for the line of sight at , . The upper panel illustrates how the preliminary velocity boundaries (dotted vertical lines) are adjusted to fall at the nearest minima or inflection points of the TB profile (dashed vertical lines). The bottom panel illustrates the fitting procedure to correct the N (H i) column densities for spillover from one region to the next: in red Gaussian functions associated with peaks of the IV component, in green the Gaussian function associated with the peak of the low-velocity (local) component, in blue the total (no peaks were detected in this direction for the high-velocity component).
In region A we set the preliminary velocity boundaries at −40 km s−1 to separate local gas from the low-latitude IV Arch, and at −90 km s−1 to separate the low-latitude IV Arch from Complex A. At latitudes b < 24° there is a significant contribution at higher velocities from gas in the disk of the Galaxy belonging to the Perseus and outer arms. Because Abdo et al. (2010) found that the γ-ray emissivity of the gas in these arms is compatible with the local emissivity, we assign all of this gas to the local component. We note that in any case this low-latitude region is not included in the ROI, but only used as part of the border to ensure a proper convolution of the model with the LAT PSF.
In region B we set the preliminary velocity boundaries at −15 km s−1 to separate local gas from the lower IV Arch, and at −60 km s−1 to separate the lower from upper IV Arch. In the case of region C we set the preliminary velocity boundaries at −20 km s−1 to separate local gas from the IV Spur, and at −90 km s−1 to separate the IV Spur from high-velocity gas; no significant emission is present at high velocities and the corresponding map is not used in the construction of the γ-ray model.
The Gaussian fits reproduce the measured brightness temperature profiles within ~5% on average (for the ratio of the integral of the absolute values of the differences between measured and fitted temperature along the line of sight to the integral of measured temperatures). The fit is significantly worse along a few lines11 of sight with differences up to ~25%. The magnitude of the correction for the spillover is on average 3% of the uncorrected column densities. (The average is the largest for ROI B, where it is ~6%.) Even though the correction is only approximate, owing to the imperfect modeling of the temperature profiles by the Gaussian functions, the average magnitudes of the errors are <0.5% of the total column densities. In a small subset of the lines of sight (~0.5%) the fits do not converge properly, mostly due to the faintness of H i emission in these high-latitude regions. In such cases we do not apply any correction for spillover.
We have calculated the N (H i) column densities under the approximation of small optical depth. An approximate correction for H i optical depth based on the assumption of a uniform spin temperature has often been used in the literature (e.g., Abdo et al. 2010; Planck and Fermi Collaborations 2014), but the low column densities in the regions studied make the effect of the correction small. Assuming a uniform spin temperature of 80 K (as in Planck Collaboration XXIV 2011) would increase the column densities on average at most by 5% for the local component in region A, and less for other components and regions. We also note that, by using dust maps to trace gas missed by the N (H i) and WCO maps as described in 4.2, we are effectively accounting also for H i densities underestimated due to the approximation of small optical depth.
We replace the N (H i) column density seen in ROI A at , b = 37° with the average of neighboring lines of sight owing to an anomalous temperature profile indicative of an artifact in the LAB data.
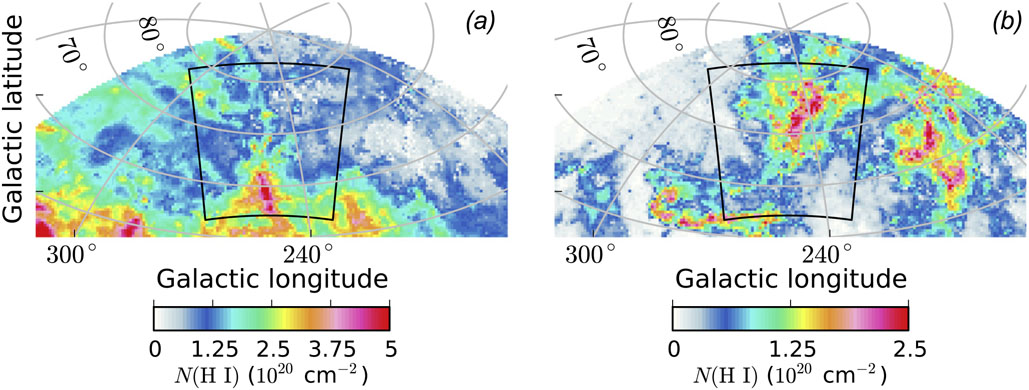
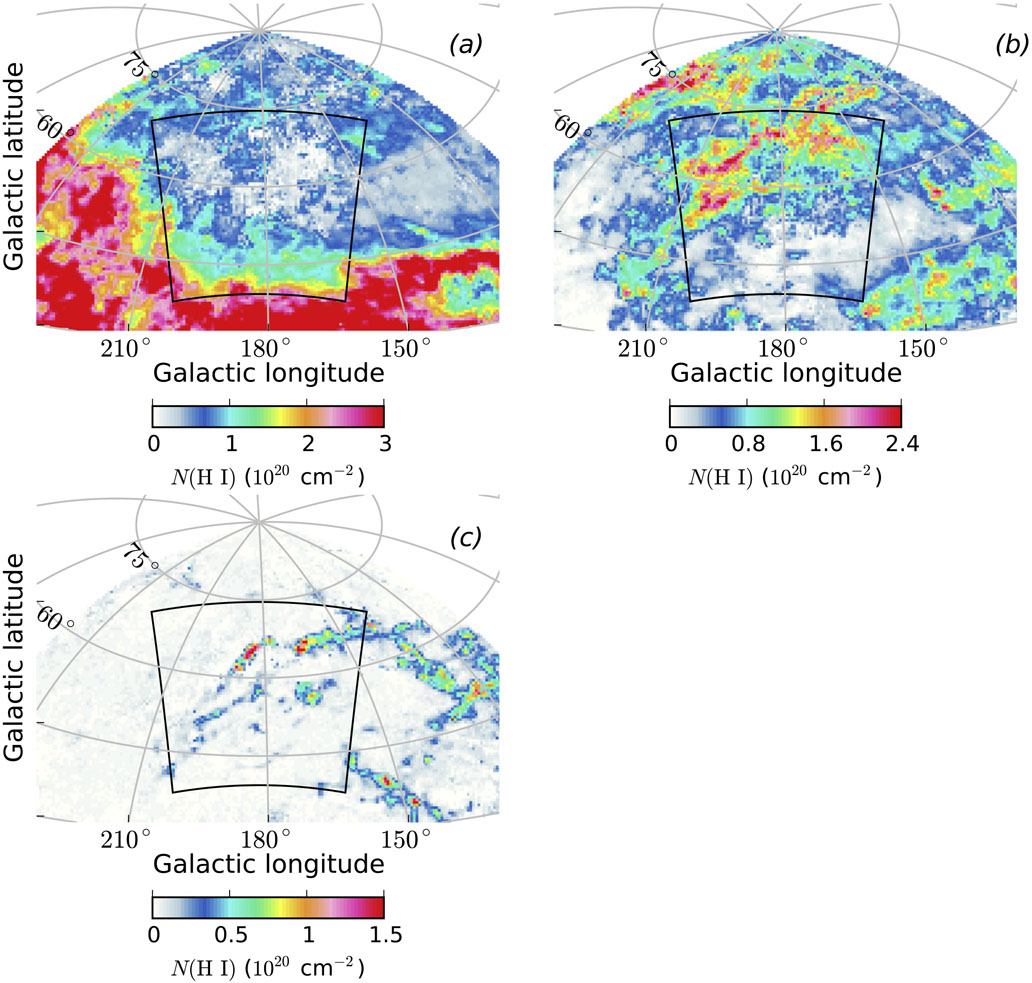
The resulting N (H i) maps are shown in Figures 3-5. Figures 4(a) and (b) show some level of anticorrelation between higher/lower N (H i) intensity regions. This is due to some genuine anticorrelation between the intensities of H i emission in velocity space. At the same time, the lower IV Arch shows a bright feature at ~ −30 km s−1 that blends into the local H i components, which makes the separation particularly challenging. This is addressed by the spillover correction.
Figure 3.
N (H i) column density maps for ROI A: (a) low-velocity (local) component, (b) the low-latitude IV Arch, (c) Complex A. The black lines show the border of ROI A, as used in the analysis. The maps are shown in zenithal equidistant projection.
Figure 5.
N (H i) column density maps for ROI C: (a) the low-velocity (local) component and (b) the IV Spur. There is no significant H i emission at high velocities in the ROI. The black lines show the border of ROI C, as used in the analysis. The maps are shown in zenithal equidistant projection.
Figure 4.
N (H i) column density maps for ROI B: (a) low-velocity (local) component, (b) the lower IV Arch, (c) the upper IV Arch. The black lines show the border of ROI B, as used in the analysis. The maps are shown in zenithal equidistant projection.
4.2. Construction of the DNM Maps
Since the work of Grenier et al. (2005) on the construction of models of interstellar γ-ray emission, dust residuals, i.e., total dust opacity or extinction minus the best-fit linear combination of H i and WCO maps, have been used to trace the DNM, neutral interstellar matter not properly traced by the linear combination of N (H i) and WCO. However, the original implementation of this method has two limitations: (1) the fit of the dust map is biased by the missing DNM component; (2) the effect of the assumptions on the stated errors in the fit of the dust maps is overlooked.
Recently, the Planck and Fermi Collaborations (2014) performed an analysis of Planck and LAT data of the Chameleon interstellar complex where they refined the original method by: (1) developing a “circular” fitting method, where dust residuals are used to model the DNM in the γ-ray analysis, and γ-ray residuals to model the DNM in the dust analysis iteratively until a stable solution is found and (2) exploring several assumptions on the errors used in the fits and folding the differences into the errors on the final results.
The method developed by the Planck and Fermi Collaborations (2014) derives a map of the DNM column densities from γ rays to use in fitting the dust maps. Owing to the low gas column densities (on average one order of magnitude lower than in the Chameleon complex) and the limited statistics of the γ-ray data set, it was not applicable to our ROIs. We therefore developed an alternative method to acknowledge and address the issue of the missing DNM component in the dust fit that does not rely on γ-ray data and is described in the rest of the section.
Owing to the limited angular resolution of γ-ray data and the other ISM tracers, and to the input projections accepted by the LAT Science Tools, we reproject the maps from the Planck Collaboration XI (2014) onto the grid chosen for the γ-ray analysis in each ROI.
Under the assumptions that dust grains are well mixed with gas in the cold and warm phases of the ISM (e.g., Bohlin et al. 1978), and that the properties of dust grains and photon fields are uniform within each phase and complex, we build a model for the dust map D (i.e., the map of optical depth at 353 GHz, τ353, or radiance, R) by assuming that either quantity is proportional to the atomic and molecular column densities as traced by N (H i) and WCO, respectively, plus an isotropic term representing any zero-level shift, for example, due to residual contamination from the cosmic infrared background.
| (1) |
Here and in the following equations we indicate with yH i,ı the dust specific power (opacity) per hydrogen atom, and with yCO the specific power (opacity) per WCO unit in the molecular phase. We use indices ı = 1, 2, 3 to label the complexes separated kinematically along the line of sight as described in Section 4.1. The model M0 is fit to the dust map D using the minimum χ2 method. The χ2 is defined, for a generic model M, as
| (2) |
Following the work of the Planck and Fermi Collaborations (2014), we consider different possible assumptions on the uncertainties σ(l, b). Our baseline assumption is that the uncertainties are mainly due to imperfections of the model because of the assumption of proportionality between radiance/opacity and gas column densities. In the absence of a reliable estimate of the uncertainties on M, we assume the uncertainties to be σ(l, b) ∝ M(l, b). We empirically consider two alternative hypotheses to assess the impact of this choice:
σ(l, b) ∝ D(l, b), which tests how the agreement between M and D affects the results of the fits and
σ(l, b) ∝ στ(l, b), where στ(l, b) is the map of statistical uncertainties on τ353 provided by the Planck Collaboration XI (2014) (for fits of τ353 only).
We initially assume that the proportionality coefficients are 30% for the model or the dust map itself, and 1 when using στ(l, b). These are adjusted later as a part of the iterative procedure to obtain a reduced χ2 = 1. The χ2 is minimized to determine the best-fit coefficients, and .
From the results we derive a dust residual map
| (3) |
The map is then filtered to extract the significant positive residuals associated with the DNM. The residual map is convolved with a Gaussian kernel with standard deviation of 1° in order to suppress statistical fluctuations while retaining large-scale real features. Then we build a histogram of the residuals and we fit a Gaussian curve to the core of the distribution, within ±2 standard deviations of the distribution itself. We set a threshold at 2 standard deviations of the fitted Gaussian curve, and produce the filtered residual map by retaining pixels of the original residual map when the values in the convolved residual map are above the threshold and setting other pixels to 0.
Then we proceed iteratively to refine the model. At each iteration α = 1, 2, …:
- The model is defined:
(4) We fit the model Mα to the dust map D minimizing the χ2 as defined in Equation (2);
- The dust residual map is built:
where and are the best-fit coefficients.(5) We filter to extract the significant positive residuals following the procedure described for iteration 0.
The iterative procedure is stopped when the two following conditions are simultaneously satisfied: (1) the differences between all the best-fit coefficients in iteration α and iteration α − 1 are compatible with 0 within 1σ statistical uncertainties from the fit and (2) the difference between minimum χ2 in iteration α and iteration α − 1 is < 1.
After the first pass just described, the scaling coefficients for the uncertainties σ(l, b) are re-defined, so that the reduced χ2 = 1 in the latest iteration. Requiring the reduced χ2 to equal 1 ensures that the statistical uncertainties from the fit are truly representative of the differences between dust maps and models. This, in turn, also makes the criteria to stop the iteration of the fitting procedure more meaningful, even if only in a data-driven fashion. Using the new scaling coefficients we perform a second pass, after which the final reduced χ2 values are found to be 1 within 1% in all ROIs and variants of the maps. The distribution of the residuals in the final iteration does not show any significant negative values, which demonstrates how the procedure is appropriately addressing the initial bias due to the missing template for the DNM (see Appendix A for further details). The scaling coefficients for the errors on τ353 provided by the Planck Collaboration XI (2014) are found to be systematically greater than 1. The error map represents only statistical uncertainties from a fit where the dust thermal emission spectral energy distribution was fitted using a modified blackbody spectrum. Hence, a scaling coefficient greater than 1 may capture the presence of systematic errors, or discrepancies between the distribution in the sky of dust optical depth and our simple model based on the assumption that the optical depth scales with gas column densities.
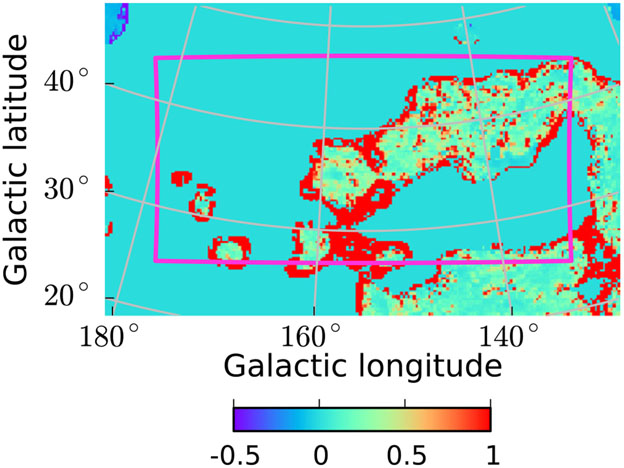
Because the Planck Collaboration XI (2014) recommends the use of R as the best dust column-density tracer at high latitudes, we take as our baseline DNM templates those obtained from R assuming that the error is proportional to the model. These maps are shown in Figure 6. We note that the DNM component is particularly abundant in ROI A, where it follows a known interstellar structure dubbed the NCP Loop (Meyerdierks et al. 1991), possibly related to the Ursa Major molecular complex (e.g., Pound & Goodman 1997). Further results from the analysis described in this section are discussed in Appendix A.
Figure 6.
DNM templates built from radiance R, as determined from the iterative fitting procedure for the three ROIs A, B, and C. The black lines show the borders of the ROIs. The errors to define the χ2 for the fit were assumed to be proportional to the model in Equation (4), with the proportionality constant defined so that the reduced χ2 in the final fit is 1. The maps are shown in zenithal equidistant projection.
5. γ-RAY ANALYSIS
5.1. Model Building
The γ-ray emission measured using the LAT can be modeled as the sum of diffuse components and discrete sources. Diffuse emission is produced in the interstellar space of the Milky Way by energetic interactions of CRs with gas, via nuclear collisions leading to γ-ray production mainly through neutral pion decay and by electron Bremsstrahlung, and with low-energy radiation fields, due to IC scattering by electrons.
Multiple studies of interstellar γ-ray emission have shown that CR fluxes can be approximated as uniform on the scales of interstellar complexes located away from potential CR sources (e.g., Abdo et al. 2010; Planck and Fermi Collaborations 2014). Under this hypothesis, the γ-ray intensities from interactions with gas are proportional to the target gas column densities. We can therefore model the diffuse intensity as a combination of the gas tracer maps described in Section 4. We assume the spectral shape to be that measured using LAT data for the local interstellar space (Casandjian 2015) in order to perform the fit over a broad energy range. This assumption will be critically evaluated against the data in the assessment of systematic uncertainties (Section 5.4). For each tracer map we allow a free scaling coefficient in the model, to define the overall CR flux in that component.12
The IC component is modeled based on the work by de Palma et al. (2013). They considered eight models of IC emission calculated using the GALPROP13 code (Moskalenko & Strong 2000; Strong et al. 2000; Porter et al. 2008) for different values of some model parameters, and tuned them to the LAT data over the whole sky. The work by de Palma et al. (2013), originally based on the LAT P7 data, was recently updated for a P7REP data selection consistent with our data set. For the IC component we allow in the fit a free scaling coefficient, as well as a log-parabolic spectral correction to mitigate the effect of uncertainties in the local electron spectra. Among the models in de Palma et al. (2013), we arbitrarily select that with the CR source distribution based on the work by Lorimer (2004), a maximum height of the CR confinement halo of 10 kpc and a H i spin temperature of 150 K. The other models presented in de Palma et al. (2013) will be used later in Section 5.4 to assess the impact of this choice on the results.
Finally, there is a diffuse component with almost isotropic distribution over the sky interpreted as the superposition of extragalactic diffuse γ-ray emission and residual backgrounds from CR interactions in the LAT misclassified as γ rays. This is modeled using a spectral shape derived from the LAT data (see de Palma et al. 2013 for the details of the procedure) consistently with our IC models, separately for γ rays converting in the front and back sections of the LAT tracker, which are characterized by different residual background rates relative to their acceptances. Owing to limitations in the assumption that the residual CR background can be treated as an isotropic γ-ray term, we allow a free scaling coefficient in the fit also for this term. Note that, due to the limited size of the ROIs and the quasi-isotropic distribution of IC γ-ray emission in the models, both IC and isotropic components have to be considered as effective background templates in our fits and the respective scaling factors are not the object of any interpretation in this work.
We incorporate point sources from the 3FGL list (Fermi-LAT Collaboration 2015). For each ROI we include in the model all the sources within 10° from the ROI border. The source positions are fixed at their catalog values. We assume for each source the spectral shape given in the catalog as well. For sources outside the ROI but within 10° from the ROI border all the spectral parameters are fixed at their catalog values. For sources inside the ROI we leave all the spectral parameters free if the average significance S of the source in 3FGL is >θ1, just the global normalization free if θ2 < S < θ1, and all the parameters fixed otherwise. The thresholds θ1 and θ2 are chosen for each ROI so that the number of free parameters associated with sources is <35 to prevent convergence problems in the fitting procedure. The pairs of thresholds (θ1, θ2) chosen are (15σ, 9σ), (30σ, 13σ), and (10σ, 5σ), for regions A, B, and C, respectively. We verified that none of the 3FGL sources are positionally coincident with structures in the N (H i) maps in Figures 3-5. Following a visual inspection of the residual maps after a preliminary analysis we left free in addition to those sources also 3FGL J0809.5+5342 in ROI A and 3FGL J 1159.2+2914 in ROI C. We will show later in Figures 7-9 that additional two years of data in our analysis with respect to 3FGL do not introduce any additional sources that significantly affect the results of the analysis.
Figure 7.
Counts (left) and residuals after subtraction of the best-fit baseline model (right) for ROI A. Counts and residuals are summed over the entire energy range from 300 MeV to 10 GeV. Residuals are expressed in units of approximate standard deviations, calculated as counts minus model-predicted counts divided by the square root of counts. The maps are shown in the plate carrée projection centered at the ROI center used for the γ-ray analysis, and are smoothed for display using a Gaussian kernel of .
Figure 9.
Counts (left) and residuals after subtraction of the best-fit baseline model (right) for ROI C. See the caption of Figure 7 for details.
To summarize, for each ROI the model for the γ-ray intensities is described by Equation (6).
| (6) |
There, qLIS(E) stands for the tabulated emissivity spectrum of H i in the local interstellar space from Casandjian (2015). N (H i)ı are the H i column density maps that we constructed in Section 4.1, so that, for each complex xH i is the scaling factor with respect to the local emissivity. Kinematically separated complexes along the line of sight are numbered as (1) low-velocity, i.e., local gas, (2) and (3) IVCs and HVCs. WCO is the CO intensity map described in Section 3.2 (used only for ROI A); hence xCO can be interpreted as the scaling factor that transforms the local H i emissivity into γ-ray emissivity per WCO intensity unit in the region studied. Similarly, is one of the templates of the DNM constructed in Section 4.2, and xDNM is the scaling factor that transforms the local H i emissivity into γ-ray emissivity per dust radiance (or optical depth) unit. IC represents the IC emission model: xIC is an overall global scaling factor, αIC and βIC are the parameters of the log-parabolic spectral correction, while E0 is a reference energy which was set to 700 MeV (the choice is arbitrary because the parameter is degenerate with the others). Finally, Iiso is the tabulated isotropic background spectrum (different for front- and back-converting events), with xIso as the common scaling factor, and SRC represents the model for individual sources described above.
5.2. Analysis Procedure and Baseline Results
Using the data set described in Section 3.1, for each ROI in Table 1 we build binned count cubes with spacing in angle and 15 logarithmically spaced energy bins from 300 MeV to 10 GeV for front- and back-converting events. The model in Equation (6) is fit to the data by using the binned likelihood analysis procedure implemented in the Science Tools that takes into account the LAT exposure and PSF. We employ a joint likelihood technique to independently treat the front- and back-converting events in the fit in order to exploit the better angular resolution of the former. We use the P7REP_V15_CLEAN LAT instrument response functions.
The maximum likelihood values of the coefficients of the interstellar emission models for the baseline analysis are reported in Table 2. In Figures 7-9 we show the count maps and residual maps summed over the entire energy range. The residual maps do not show any large-scale structures correlated with the templates used to model the γ-ray emission. Some localized residuals may hint at missing point sources not included in 3FGL, which was developed using the first 48 months of LAT observations, as opposed to the 73 months used in our analysis.
Table 2.
Interstellar Best-fit Coefficients from the Baseline Analysis
| Parameter | ROI A | ROI B | ROI C |
|---|---|---|---|
| x H i,1 | 0.999 ± 0.017 | 0.94 ± 0.07 | 1.08 ± 0.04 |
| x H i,2 | 0.94 ± 0.16 | 1.08 ± 0.04 | 0.68 ± 0.06 |
| x H i,3 | … | ||
| x CO a | 2.3 ± 0.2 | … | … |
| x DNM b | 0.24 ± 0.03 | 0.34 ± 0.09 | |
| x IC | 1.19 ± 0.05 | 1.31 ± 0.05 | 1.82 ± 0.09 |
| α IC | −0.158 ± 0.014 | −0.06 ± 0.02 | 0.02 ± 0.05 |
| β IC | 0.045 ± 0.008 | 0.02 ± 0.01 | −0.026 ± 0.014 |
| x Iso | 0.978 ± 0.017 | 1.03 ± 0.02 | 0.96 ± 0.04 |
Notes. See Equation (6) for a definition of the model parameters. The numbering scheme for the xH i,ı coefficients is: (1) low-velocity, i.e., local gas, (2) and (3) IVCs and HVCs.
Asymmetric error bands are computed using Minos when the best-fit value is at the boundary imposed during the likelihood optimization process.
1020 cm−2 (K km s−1)−1.
1032 sr W−1.
For each target (HVC or IVC) in Table 1 we calculate the test statistic TS, defined as
| (7) |
where is the maximum likelihood for the model that includes the source of interest, while is the maximum likelihood of the minimal model where the contribution from the source is set to null. TS is expected to be distributed as a χ2 with a number of degrees of freedom given by the difference of the number of free parameters in the two models (e.g., Mattox et al. 1996). We consider a target cloud as detected if TS > 25, which formally corresponds to a 5σ confidence level that the likelihood improvement is not due to statistical fluctuations. As detailed in Protassov et al. (2002), the distribution of TS may deviate from a χ2 if the minimal model corresponds to a point on the topological border of the phase space of the parameters of the model including the source, which applies to our situation. However, the TS values for our detected targets all greatly exceed the threshold.
The TS values are reported in Table 3. For target HVCs and IVCs that are not detected we calculate a 95% confidence level (c.l.) upper limit on xH i based on a Bayesian integration of the likelihood profile as applied for measurements in the 2FGL catalog (Nolan et al. 2012, 3.5).
Table 3.
Target Detections and Upper Limits
| Region | Complex | TS | 95% c.l. upper limit |
|---|---|---|---|
| A | Low-Latitude IV Arch | 127 | … |
| Complex A | 0 | 0.21 | |
| B | Lower IV Arch | 750 | … |
| Upper IV Arch | 0 | 0.23 | |
| C | IV Spur | 154 | … |
Note. See Equation (7) for the definition of TS.
The upper limits are expressed as a fraction of the emissivity of local H i.
In Figure 10 we show the γ-ray emission components associated with detected IVCs, evaluated by subtracting from the total γ-ray counts the components attributed to individual sources and foreground/background interstellar emission by the likelihood fit. Contours from the N (H i) maps inferred from the 21 cm observations in Figures 3-5 are overlaid. The morphologies of the γ-ray detected signals follow closely the known H i structures in the low-latitude IV Arch and lower IV Arch. In the case of the IV Spur a cluster of γ-rays is associated with the densest part of the cloud, but the visual comparison is hampered by limited statistics in the γ-ray data set.
Figure 10.
γ-ray emission associated with the detected targets: total counts minus the contributions attributed by the fit to all emission components in Equation (6) but (A) the low-latitude IV Arch, (B) the lower IV Arch, (C) the IV Spur. The maps were smoothed using a 2° Gaussian kernel to suppress statistical fluctuations and enhance extended features. The overlaid contours of H i column density have levels (A) 0.6 × 1020 and 1.2 × 1020 atoms cm−2, (B) 0.8 × 1020 and 1.6 × 1020 atoms cm−2, (C) 0.9 × 1020 and 1.8 × 1020 atoms cm−2.
5.3. Spectra of the Detected Clouds
A key assumption of our model is that the emission of the gaseous components has a spectrum described by the emissivity spectrum of local gas qLIS from Casandjian (2015), modified only by a global scaling factor over the whole energy range from 300 MeV to 10 GeV. While this assumption is expected to hold for the local (low-velocity) gas, there may be spectral variations for clouds at great distance from the disk.
For clouds detected in our analysis we can use the data to verify how well the qLIS spectrum reproduces the observed one. To do so we perform the γ-ray analysis independently in six broad energy bins logarithmically spaced from 300 MeV to 10 GeV. In these fits the spectral parameters are frozen to their determination over the entire energy range except for the normalizations. Figure 11 shows as a reference the scaling factors of local H i emissivity in the three regions studied. Figure 12 shows the scaling factors for the emissivity of all the detected IVCs with respect to local.
Figure 11.
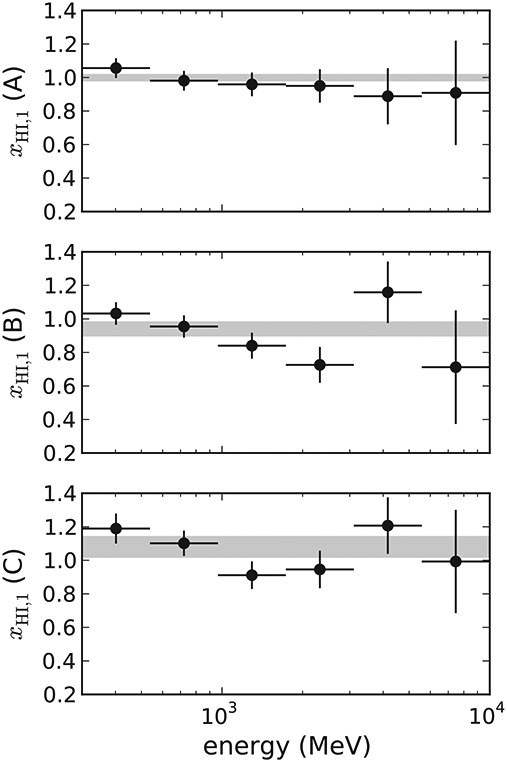
Scaling factor of local H i emissivity, xH i,1, as a function of energy for the three regions A, B, and C. The shaded bands indicate the values obtained from the analysis over the entire energy range with their 1σ statistical uncertainties.
Figure 12.
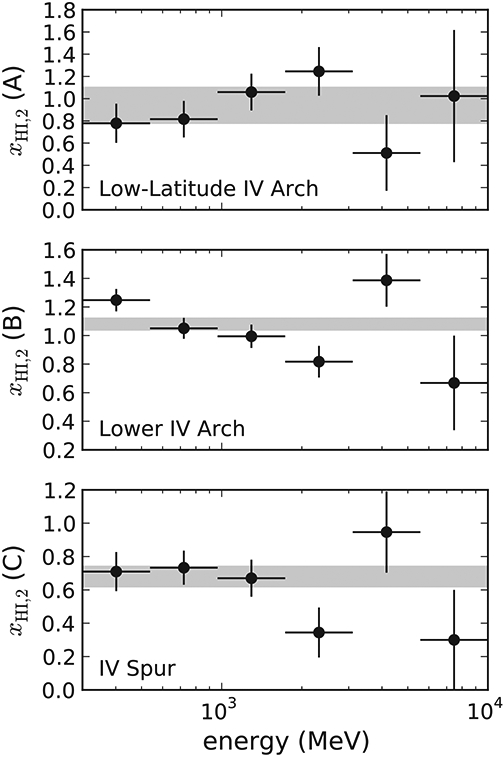
Scaling factors of H i emissivity in three IVCs, xH i,2, as a function of energy in regions A, B, and C. The shaded bands indicate the values obtained from the analysis over the entire energy range with their 1σ statistical uncertainties.
The scaling factors are all consistent within statistical uncertainties with the value determined from the fit over the entire energy range. In region A the residuals show a negative trend that indicates a spectrum softer than the average in the local ISM. Similar trends may be present for both the local ISM and IV gas in region B. It is not clear if this is real or due to any small imperfections in the modeling, but further investigation on this aspect is beyond the scope of this work and left for future studies. For the scope of our analysis it is justified to use the global scaling factors over the whole energy range because they are compatible within 1σ with the weighted average of the values for the separate energy bins.
5.4. Assessment of Systematic Uncertainties
5.4.1. Uncertainties of Inputs to the γ-ray Interstellar Emission Model
Some inputs to the model in Equation (6) are subject to important uncertainties, most notably the DNM column densities, IC emission, and the spectrum of undetected clouds. We explored the associated systematic uncertainties by changing the modeling assumptions and evaluating the impact on the best-fit parameters for the γ-ray analysis.
For each region we modified the baseline DNM template by using the alternative templates from Section 4.2 based on different assumptions for the errors in the determination of the DNM template, and replacing dust radiance with optical depth.
We also changed the IC model by using alternative models as described in de Palma et al. (2013), which included assuming maximum heights of the CR confinement halo of 4 and 10 kpc, and replacing the CR source distribution inferred from pulsar observations (Lorimer 2004) with that by Case & Bhattacharya (1998) based on supernova remnant observations.14 These are two of the most important input parameters to GALPROP to determine the morphology and spectrum of IC emission (Ackermann et al. 2012a).
Finally, we have shown in Section 5.3 that for detected targets the assumption that the emission spectrum follows the emissivity in the local ISM is appropriate, but we cannot do the same for targets that are not significantly detected, i.e., Complex A and the Upper IV Arch. We explored possible variations with respect to the local emissivity spectrum based on the set of propagation models in Ackermann et al. (2012a). We calculated the ratios of the emissivity spectra in those models at all locations in the outer Galaxy (where our clouds are located) over the emissivity spectrum at the solar circle. We parametrized the extrema of these ratios with two functions of energy
| (8) |
and
| (9) |
Equation (8) captures the softening due to energy-dependent escape that is expected near the boundaries of the confinement region in the outer Galaxy for sources located mostly in the inner Galaxy. In addition, Equation (9) captures a low-energy hardening predicted by high-reacceleration models in Ackermann et al. (2012a) at larger Galactocentric radii.15 Note that both functions indicate a softer spectrum. In order to be conservative we explore the extreme assumptions that the emissivity spectrum may actually be harder at the locations of the undetected targets by inverting the signs of the exponents
| (10) |
and
| (11) |
We use these functions to modify the emissivity spectra of the undetected clouds, by multiplying the local emissivity spectrum qLIS in Equation (6) by the correction function and scaling it so that the emissivity integrated in the 300 MeV to 10 GeV range is the same as for qLIS. In this way, we can still interpret the upper limits on xH i for the undetected components as scaling factors with respect to the local emissivity, and, at the same time, explore the impacts on the other fit parameters.
We repeat the baseline analysis described in Section 5.2 for all the combinations of the model variations described above, and, for each parameter, we take the extreme variations with respect to the baseline fit as our estimate of the systematic uncertainty related to the model. In the cases of upper limits for undetected targets we use the worst, i.e., largest upper limits in the discussion that follows.
We summarize the scaling factors for H i emissivity in the different regions and complexes in Table 4, including the spread due to inputs to the γ-ray interstellar emission model as determined through the methodology described in this subsection. In general, the emissivity spread for the detected complexes is driven by the choice of the DNM template, and, to a lesser extent, the choice of IC model for local gas (which is less structured, hence more degenerate with IC emission). For non-detected complexes the systematic uncertainties are dominated by the choice of the emissivity spectrum. The results in ROI B show a stronger dependence on the assumed IC model, which affects also the determination of the lower IV Arch emissivity and the upper limit on the emissivity of the upper IV Arch at 2 statistical σ level.
Table 4.
H i Emissivity Scaling Factors
| Region | Complex | Scaling Factor |
Stata | Sys (Model)b |
Sys (Jackknife)c |
|---|---|---|---|---|---|
| A | Local | 0.99 | 0.02 |
+0.04 −0.14 |
0.08 |
| Low-Latitude IV Arch | 0.94 | 0.15 |
+0.26 −0.01 |
0.08 | |
| Complex A | <0.21 | <0.22 | <0.001 | ||
| B | Local | 0.94 | 0.07 |
+0.13 −0.22 |
0.08 |
| Lower IV Arch | 1.08 | 0.04 |
+0.10 −0.08 |
0.09 | |
| Upper IV Arch | <0.23 | <0.45 | <0.01 | ||
| C | Local | 1.08 | 0.04 |
+0.05 −0.09 |
0.09 |
| IV Spur | 0.68 | 0.06 |
+0.09 −0.03 |
0.06 | |
Notes. Upper limits are provided at 95% confidence level.
1σ statistical uncertainty from the likelihood analysis.
Systematic spread from varying some inputs to the γ-ray interstellar emission model (see Section 5.4.1).
1σ uncertainty or 95% c.l. upper limit from the distributions obtained with the jackknife test (see Section 5.4.2).
5.4.2. Jackknife Tests
So far we have characterized the statistical uncertainties in the fit parameters in Section 5.2 and systematic uncertainties related to some inputs to the model in Section 5.4.1. However, other potential sources of systematic uncertainties are related to the assumption that the emissivity scaling coefficients for each component are constant across a given ROI, and to the presence of regions with large deviations or mismodeled individual sources driving the fits.
To characterize the magnitude of these uncertainties we perform jackknife tests where we repeat the analysis described in Section 5.2 150 times for each ROI, each time masking a circular region with random center within the ROI and covering 20% of the ROI area. The mask size was chosen to be much larger than the 68% event containment radius of the LAT for front-converting photons at the lowest end of the energy range at 300 MeV and large enough to probe possible mild variations of the CR densities across the complexes studied.
Figures 13-15 show the distributions of the H i emissivity scaling coefficients for the three ROIs. The distributions all peak within 1σ from the best-fit values obtained from the baseline analysis and have standard deviations smaller than or comparable to the 1σ statistical uncertainties from the γ-ray fits. This shows that from a statistical point of view the obtained parameter values are representative of the entire ROIs.
Figure 13.

Distribution of the xH i scaling coefficients in ROI A from the jackknife tests. In each panel the solid vertical line marks the best-fit value from the baseline analysis, and the dashed lines delimit its ±1σ statistical uncertainty interval.
Figure 15.

Distribution of the xH i scaling coefficients in ROI C from the jackknife tests. See the caption of Figure 13 for details.
In ROI A, Figure 13, the distribution of the scaling coefficients for Complex A, xH i,3, narrowly peaks at zero, showing that this parameter is always at the boundary of the allowed values. In the rest of the work, we will make use only of the upper limit on the Complex A emissivity that, on the contrary, is a robustly determined quantity. Similar considerations hold for the upper IV Arch in ROI B. In all ROIs, most notably in ROI A, the distribution of the scaling coefficients xH i,2 for the IVCs show tails at low or high values, which suggests that emissivities lower or higher than average are possible within the gas encompassed by the respective templates.
To take into account these uncertainties in our estimates of the emissivities we compute, based on the distributions of the fit parameters in Figures 13-15, the 1σ confidence intervals for detected complexes and 95% c.l. upper limits for complexes that are not significantly detected, as reported in Table 4 (details of the derivation are given in Appendix B). For the detected complexes the confidence intervals are of the same magnitude as the statistical errors. Hence we will combine them with the other uncertainties for the discussion that follows. In the case of the complexes that are not significantly detected the sources of uncertainty probed through the jackknife tests (such as possible variations of the CR densities across the complexes studied) have an impact on the emissivity upper limits much smaller than those due to uncertainties in the analysis model inputs and those encoded by the statistical error from likelihood fit, so they will be neglected.
6. RESULTS AND DISCUSSION
6.1. The γ-ray Emissivities of HVCs and IVCs
The H i emissivity scaling coefficients in Table 4 can be converted into emissivity values. To do so we multiply them by the integrated emissivity between 300 MeV and 10 GeV from Casandjian (2015), i.e., 7.1 × 10−27 s−1 sr−1 H−1. Note that this rests on the measurement described in Section 5.3 that the shape of the emissivity spectrum is the same as in the local ISM for detected complexes, and is valid within the extreme variations parametrized in Equations (8)-(11) for those that are not significantly detected.
The conversion into emissivities requires taking into account one additional source of systematic uncertainty, i.e., the characterization of the LAT instrument response, and in particular its effective area. Based on the estimate of the systematic uncertainties of the LAT effective area in Ackermann et al. (2012c), the systematic error on the local emissivity by Casandjian (2015) integrated between 300 MeV and 10 GeV is 0.6 × 10−27 s−1 sr−1 H−1.
Note also that in many HVCs and IVCs the ratio of the ionized gas mass to the neutral atomic gas mass is much larger than in the local ISM and close to unity (e.g., Wakker et al. 2008). If the column densities of ionized gas are correlated with those of neutral gas the scaling factors in the γ-ray fits will be overestimated to encompass the emission from ionized gas. In this respect our estimates of scaling factors and emissivities should be regarded as an upper limit to the real values. The same consideration applies to the potential presence of CO-dark molecular gas in HVCs/IVCs. Aside from the emissivity scaling coefficient slightly larger than 1 for the lower IV Arch there is no clear indication of such effect from our analysis.
The final results for the emissivities of the targets are summarized in Table 5. For the purpose of interpretation we will rely on those findings and on the emissivity scaling factors in Table 4, which to a good approximation are not subject to uncertainties due to the LAT instrument effective area.
Table 5.
Emissivities of HVCs and IVCs
| Region | Complex |
z (kpc) |
γ-ray emissivity | Stata | Sys (LAT)b (10−27 s−1 sr−1 H−1) |
Sys (model)c | Sys (Jackknife)d |
|---|---|---|---|---|---|---|---|
| A | Low-latitude IV Arch | 0.6–1.2 | 6.7 | 1.1 | 0.6 |
+1.8 −0.1 |
0.6 |
| Complex A | 2.6–6.8 | <1.7 | |||||
| B | Lower IV Arch | 0.4–1.7 | 7.7 | 0.3 | 0.7 |
+0.7 −0.6 |
0.6 |
| Upper IV Arch | 0.7–1.7 | <3.5 | |||||
| C | IV Spur | 0.3–2.1 | 4.8 | 0.4 | 0.4 |
+0.6 −0.2 |
0.4 |
Notes. z brackets are replicated from Table 1 for the reader’s convenience. Data sources are listed there.
γ-ray emissivities are integrated between 300 MeV and 10 GeV.
We provide 95% confidence level upper limits for the worst-case scenario from the model variations considered and taking into account uncertainties due to the LAT effective area.
1σ statistical uncertainty from the likelihood analysis.
Error from uncertainties in the LAT effective area.
Systematic spread from varying some inputs to the γ-ray interstellar emission model (see Section 5.4).
1σ uncertainty or 95% c.l. upper limit from the distributions obtained with the jackknife test (see Section 5.4.2).
The γ-ray emissivities are a proxy for the CR densities in the complexes studied. Owing to the cross sections for γ-ray production in nucleon–nucleon inelastic collisions (e.g., Kamae et al. 2006), the γ-ray energies studied between 300 MeV and 10 GeV constrain the CR densities from energies of ~3 GeV/nucleon up to ~200 GeV/nucleon. Note that while we do not expect significant changes in the He/H ratio because both elements are primordial, the abundances of metals, i.e., elements heavier than He, are known to vary in HVCs and IVCs and depending on the metallicity of target gas the emissivity per H atom can vary up to <5% of the total (e.g., Mori 2009). Furthermore, the total emissivity depends also on the CR composition and spectra of the different elements at a level up to 20%–30% of the total emissivity per H atom (Kachelriess et al. 2014). Part of the emissivity variations (Table 5) or, equivalently, differences in the emissivity scaling factors (Table 4) therefore can be attributed to variations in the CR elemental composition and of their spectra, as well as to the uncertain metallicity of the targets (Wakker 2001).
Our measurement of the local gas emissivity in each ROI agrees well with unity, indicating the robustness of the analysis procedure and assumptions. The emissivity of the IV Arch indicates a ~50% decrease of the CR densities with respect to the local value within 2 kpc from the Galactic plane, while the HVC Complex A provides the strongest limit on the CR densities at a few kpc above the disk. The implications of these results are discussed in the following sections.
6.2. Testing the Origin of CRs in the Galactic Disk
If CRs originate in the disk of the Milky Way and diffusively propagate in the surrounding halo we expect the CR densities, and hence the γ-ray emissivities, to decrease with distance z from the disk itself.16 We test this hypothesis against our data in Table 4 by computing the Kendall τ rank correlation coefficient. Using the emissivity scaling coefficients in Table 4, and adopting for z the mean within the bracket for targets in Table 1, and z = 0 kpc for the local gas in each ROI, we obtain τ = −0.54. The negative value indicates, indeed, a negative correlation of emissivity with ∣z∣.
We calculate the significance of this trend by comparing the τ of the actual data with a distribution of the τ coefficients obtained from the null hypothesis of no correlation between emissivity and z. We generate null hypothesis data sets starting from the real data set using the following procedure.
We draw a set of emissivity scaling coefficients with normal distribution centered at the measured values and with σ equal to the sum in quadrature of statistical uncertainties and systematic uncertainties from the jackknife tests in Table 4 for significantly detected targets and local foreground gas in each ROI.
We add upper limits at the values measured in Table 4 for targets which are not significantly detected.
We randomly shift both scaling factors and upper limits with uniform probability distribution within the systematic uncertainty brackets from the model input variations in Table 4 (assuming the bracket to be symmetric for upper limits).
We draw a set of z values with uniform probability distribution within the brackets in Table 1, and add three elements with z = 0 to represent the local foreground gas in each ROI.
We randomly shuffle in an independent fashion the emissivity scaling factors and z sets so obtained to be consistent with the null hypothesis of no correlation between the two quantities.
The distribution of 30,000 null hypothesis data sets shows that there is a 2.5% chance probability to obtain a τ coefficient < −0.54.
Therefore, our measurements provide evidence at 97.5% confidence level that the γ-ray emissivity per H atom decreases with distance from the disk of the Galaxy. This corroborates the notion that CRs at the relevant energies from GeV to TeV originate in the Galactic disk by directly tracing the distribution of CRs in the halo for the first time. Our result goes far beyond the test of the Galactic origin of CRs proposed by Ginzburg (1973), i.e., measurement of the γ-ray emissivity of Magellanic Clouds, that was performed by Sreekumar et al. (1993).
We note that we also expect a decrease in gas metallicity, hence emissivity per H atom, with distance from the disk if the most distant targets like Complex A are primeval gas falling into the Milky Way (Wakker 2001). However, the expected effect of at most ~5% on the γ-ray emissivities (Mori 2009) is not sufficient to explain the magnitude of the variations observed between the scaling coefficients in Table 4. Changes in the spectra of the different CR elements could also cause emissivity variations. However, the magnitude of this effect is estimated to be at most 20%–30% of the total emissivity per H atom (taking into account He in both CRs and the ISM), lower than the decrease of emissivity of >50% for the Upper IV Arch and of >75% for Complex A that we measured.
Additionally, in the region of the outer Galaxy where our targets are located the distance to the center of the Milky Way increases with increasing distance from the disk as well. While some propagation models advocate a sizable decrease of CR densities with increasing Galactocentric radius, observations (Abdo et al. 2010; Ackermann et al. 2011) indicate that the gradient of CR densities is marginal up to 15 kpc from the Galactic center. We conclude that the observed emissivity decrease as a function of z is more likely due to diffusion in the halo. A quantitative comparison with propagation models follows in the next section.
6.3. Comparison with CR Propagation Models
We compare our results with predictions from GALPROP. We will rely on the set of GALPROP models in Ackermann et al. (2012a) that have been compared extensively to direct CR measurements and LAT data, and which include a number of variations of the most relevant and uncertain parameters of the calculations. In Ackermann et al. (2012a) the CR transport equations were solved for the case of cylindrical symmetry, based on the assumption that CRs are injected in the disk of the Milky Way and propagate in a cylindrical volume with boundaries at maximum radius from the center of the Galaxy Rmax and maximum height from the disk zmax where the CR particle number densities are required to go to zero.
Figure 16 shows the emissivity scaling factors from Table 4 against predictions from the models in Ackermann et al. (2012a). The model predictions are calculated for distances along the line of sight approximately corresponding to the peak gas column densities for each ROI.17 We normalized the model emissivities to the value in the disk at the solar circle. The model emissivities at the solar circle integrated from 300 MeV to 10 GeV in γ-ray energy were found to be within ~7% from the measurement in Casandjian (2015). Note that the calculation of the emissivities in Ackermann et al. (2012a) only accounts for interactions between CR and interstellar gas nuclei with atomic number ⩽2. Rescaling to the locally measured emissivity takes into account the contribution from metals in the targets and heavier CR species. Variations of the target gas metallicities are not taken into account in these models, and could produce a further decrease of emissivity up to at most 5% with increasing z (Mori 2009).
Figure 16.
For ROIs A, B, and C we compare the emissivity scaling factors in Table 4 (gray rectangles) with predictions from the models in Ackermann et al. (2012a) (curves). The horizontal widths of the rectangles indicate the z brackets of target IVCs and HVCs, i.e., the range between lower and upper limits on their altitudes (Table 1). The dark gray rectangles have vertical size corresponding to the statistical uncertainties, while for the light gray rectangles the vertical size encompasses the sum in quadrature of statistical uncertainties and systematic uncertainties from the jackknife tests, augmented by the systematic spread from variations to the analysis model inputs from Table 4. The emissivity of local gas is assigned to the range from z = 0 kpc to z = 0.3 kpc (disk). The model curves from Ackermann et al. (2012a) were calculated for the line of sight indicated in the legend of each panel, approximately corresponding to the column density peaks of the target complexes. The curves are color-coded based on the maximum heights zmax of the CR confinement halo in the models.
The model parameter with the largest impact on the vertical gradient of CR densities, or, equivalently, γ-ray emissivities, is the maximum height of the confinement halo zmax. Models in Ackermann et al. (2012a) assume values of zmax between 4 and 10 kpc. While there is a broad agreement between models and measurements, the rapid decrease of the emissivities within 2 kpc from the disk inferred from the upper limit for the upper IV Arch seems to favor smaller values of zmax. The lower and upper IV Arch have similar altitude brackets, 0.4–1.7 and 0.7–1.7 kpc, respectively, but their emissivities are consistent with local for the first and < 50% of local for the latter. This is not necessarily contradictory because the distance brackets are pairs of upper and lower limits on the distances; hence the two clouds may be separated by a physical distance up to ~1 kpc.
To obtain a crude estimate of zmax from our results we fit to the emissivity scaling factors of IVCs and HVCs from Table 4 a function
| (12) |
where ϵ is the emissivity expressed as a fraction of the emissivity at z = 0, zmax is the maximum height of the confinement halo and β is an index which modifies the steepness of the vertical gradient. Equation (12) with β = 1 is an accurate z-dependent part of the solution of the diffusion equation in the plane-parallel geometry (infinitely thin Galactic plane) with a uniform source distribution when only ionization losses are assumed (e.g., Jones et al. 2001). The GALPROP models in Ackermann et al. (2012a) have vertical emissivity gradients at given Galactocentric radius characterized by 1 < β < 1.5. Values of β greater than 1 result from energy dependent escape at the radial boundary of the propagation model and, to a lesser extent, from energy losses of nuclei. In any case, we stress that the functional form in Equation (12) holds only in diffusion-dominated scenarios where it is required that the CR densities go to zero at z = zmax.
We perform the fit by using a maximum likelihood method where we neglect the different Galactocentric distances of the targets. We assume for the emissivity scaling factors a Gaussian probability distribution with σ given by the quadratic sum of statistical uncertainties, jackknife uncertainties, and the largest brackets from model input variations from Table 4. Upper limits including systematic uncertainties from Table 4 are assumed to be the 95% containment value of a Gaussian probability distribution. Finally, we assume that the probability distribution of target distances is uniform within the brackets in Table 1. Owing to the paucity of the data points, rather than fitting the index β to the data we assume the extreme values β = 1 and β = 1.5 as found from the fits to GALPROP predictions. The best fit to the data is obtained for zmax = (2.2 ± 1.9) kpc, and zmax = (1.8 ± 2.1) kpc for the two values of β. Note that the profile would be steeper, hence zmax smaller, if the emissivities were biased by the presence of unaccounted ionized gas in HVCs/IVCs.
This method provides an estimate of zmax < 6 kpc (2σ upper containment value from the fits above). Most of the constraining power on the zmax parameter, however, at present comes from the upper limit on the emissivity of the upper IV Arch. The latter hints at a possible tension with indications from the modeling of other observables related to CRs. Differences with respect to studies of synchrotron emission (Orlando & Strong 2013) can be understood if the densities of CR electrons beyond the boundaries of the confinement halo are sufficient to produce the emission observed in the domain from radio to microwaves. However, the interpretation of the flat radial profile of γ-ray emission produced by interactions of CR nuclei in the outer disk of the Milky Way in terms of a large zmax of the order of ~10 kpc in the context of GALPROP models similar to those considered here (Abdo et al. 2010; Ackermann et al. 2011) seems to be disfavored.
The observed emissivities of the HVC and IVCs were compared to predictions from the limited set of diffusive reacceleration models for a simplified axisymmetric model of the Galaxy in Ackermann et al. (2012a). Other models proposed in the literature include CR-driven Galactic winds and anisotropic diffusion (e.g., Breitschwerdt et al. 2002), and a non-uniform diffusion coefficient that increases with the Galactocentric radius and the distance from the Galactic plane (e.g., Shibata et al. 2007), as well as more sophisticated ways of modeling the Milky Way structure (e.g., Werner et al. 2015), but further comparison to theoretical models is beyond the scope of this article.
Finally, we note that the CR propagation equations are often solved assuming that the CR particle number densities go to zero at the boundaries of the propagation volume. This assumption has little effect on the predicted CR fluxes for the Galaxy as a whole and at a considerable distance from the boundaries. However, close to the halo boundaries one may expect significant deviations from the model predictions and tracing the CR distribution in the halo can provide unique model-independent information about its structure and extent. Studies of the CR outflow from the Milky Way into the intergalactic space that are still in their infancy (e.g., Everett et al. 2012) could also benefit from the method illustrated in this work.
7. CONCLUSIONS
We have searched for high-energy γ-ray emission from a sample of HVCs and IVCs in the halo of the Milky Way at different distances from the Galactic disk using 73 months of data from the LAT in the energy range between 300 MeV and 10 GeV.
We have achieved the first detections of IVCs in γ rays, the low-latitude IV Arch, the lower IV Arch, and the IV Spur, and set constraints on the emission from the remaining targets, the upper IV Arch and the HVC Complex A (Table 4). The spectra of the detected complexes were all consistent within statistical uncertainties with that of gas in the local interstellar space.
We find evidence at 97.5% confidence level that the γ-ray emissivity per H atom of the clouds decreases as a function of distance from the disk. This corroborates the notion that CRs are accelerated in the Galactic disk and then propagate in a surrounding halo, for the first time in a direct way.
The γ-ray emissivity per H atom of the upper IV Arch hints at a 50% decline of the CR densities within 2 kpc from the disk. The upper limit on the emissivity of Complex A at 22% of the local value gives the most stringent constraint to date on the fluxes of CRs at few kpc from the Milky Way disk.
Our results can be compared to CR propagation models and inform further development to more realistically take into account the escape of CRs from the halo of the Milky Way and the outflow of particles merging into the local intergalactic medium.
At the same time, the observational constraints can be improved if distance brackets for more HVCs and IVCs in the mass-distance range detectable by the LAT are measured or existing brackets are made more constraining, e.g., by the ongoing Gaia survey (e.g., de Bruijne 2012).
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This work was partially funded by NASA grant NNX13O87G. I. V. M., E. O., and T. A. P. acknowledge NASA’s support of GALPROP development through grant NNX13AC47G. The authors acknowledge the use of HEALPix (http://healpix.jpl.nasa.gov/, Górski et al. 2005) in some parts of the analysis. We made use of data products based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. L.T. thanks B.P. Wakker for an insightful discussion on the determination of distance brackets for IVCs and HVCs, as well as E. Charles and P. Mertsch for stimulating conversations.
Facilities: Fermi, Planck.
Figure 8.
Counts (left) and residuals after subtraction of the best-fit baseline model (right) for ROI B. See the caption of Figure 7 for details.
Figure 14.

Distribution of the xH i scaling coefficients in ROI B from the jackknife tests. See the caption of Figure 13 for details.
Table 8.
Results from R Fit in ROI B
| σ ∝ R | σ ∝ M | |
|---|---|---|
| σ Scaling factor | 14% | 17% |
| Number of iterations | 6 | 5 |
| χ2/n.d.f. | 0.996 | 1.008 |
| y H i,1 a | 2.187 ± 0.010 | 2.246 ± 0.013 |
| y H i,2 a | 1.982 ± 0.011 | 2.168 ± 0.014 |
| y H i,3 a | 0.46 ± 0.03 | 1.07 ± 0.04 |
| y res | 0.986 ± 0.015 | 0.98 ± 0.06 |
| R iso b | 0.935 ± 0.012 | 1.039 ± 0.016 |
Note.
10−32 W sr−1 H−1.
10−10 W m−2 sr−1.
Table 9.
Results from τ353 Fit in ROI B
| σ ∝ στ | σ ∝ τ353 | σ ∝ M | |
|---|---|---|---|
| σ Scaling factor | 7.0 | 36% | 32% |
| Number of iterations | 5 | 6 | 8 |
| χ2/n.d.f. | 0.994 | 1.003 | 0.994 |
| y H i,1 a | 0.729 ± 0.005 | 0.680 ± 0.003 | 0.708 ± 0.006 |
| y H i,2 a | 0.390 ± 0.005 | 0.351 ± 0.003 | 0.401 ± 0.007 |
| y H i,3 a | 0.146 ± 0.012 | 0.152 ± 0.012 | 0.221 ± 0.018 |
| y res | 1.03 ± 0.02 | 0.98 ± 0.02 | 1.07 ± 0.06 |
| τ iso b | 0.50 ± 0.06 | 0.00 ± 0.01 | 2.60 ± 0.08 |
Note.
10−26 cm2 H−1.
10−9 mag.
Table 10.
Results from R Fit in ROI C
| σ ∝ R | σ ∝ M | |
|---|---|---|
| σ Scaling factor | 11% | 13% |
| Number of iterations | 6 | 7 |
| χ2/n.d.f. | 1.058 | 1.027 |
| y H i,1 a | 2.045 ± 0.011 | 2.259 ± 0.013 |
| y H i,2 a | 2.124 ± 0.019 | 2.32 ± 0.02 |
| y res | 1.000 ± 0.014 | 1.00 ± 0.04 |
| R iso b | 1.38 ± 0.02 | 1.25 ± 0.02 |
Note.
10−32 W sr−1 H−1.
10−10 W m−2 sr−1.
APPENDIX A
ADDITIONAL RESULTS ON THE ISM
The analysis described in this paper is aimed at determining the CR content of IVCs and HVCs. Nevertheless, we obtained results relevant to the properties of interstellar gas and dust in such clouds, as well as in the local complexes seen in their foregrounds. This appendix summarizes these results, including some methodological aspects.
A.1. Example of Results from the Iterative Dust Fitting Procedure
In this section we take as an example ROI A to illustrate some details of the iterative fitting procedure applied to the dust maps in Section 4.2. We follow the fit of the radiance map, R, for the assumption that the errors are proportional to the model M from Equation (4) in calculating the χ2. The results from all iterations are shown in Figures 17-19.
Figure 17.

Best-fit parameters of the model described in Equation (4) for ROI A in each iteration of the dust analysis. We show as an example the case for which the radiance map R is considered and the errors in the χ2 definition are assumed to be proportional to M.
Figure 19.
Normalization of the residual dust component, yres, (left), and χ2 value (right) for ROI A in each iteration of the dust analysis. We show as an example the case for which the radiance map R is considered and the errors in the χ2 definition are assumed to be proportional to M.
Figures 17 and 18 show how the scaling coefficients of the H i and CO maps change significantly during the iterative procedure and how they stabilize at a final value at the end. This can be interpreted as removing the bias due to the missing DNM component in the initial iteration, which is alleviated as the missing component is recovered based on the data themselves.
Figure 18.

Variation of the best-fit parameters of the model described in Equation (4) for ROI A in each iteration of the dust analysis with respect to the previous one (expressed as the number of 1σ statistical uncertainties from the fits). We show as an example the case for which the radiance map R is considered and the errors in the χ2 definition are assumed to be proportional to M.
Figure 20 shows the difference between the filtered dust residual maps from the last iteration and the initial one. It is evident that borders exist between the H i-dominated and DNM-dominated, and between the DNM-dominated and CO-dominated regions, where the missing component is not recovered from the residuals in the initial iteration. This can be understood because the H i and CO components in the initial fit compensating for the missing DNM component.
Figure 20.
Difference of the filtered dust residual map from the last iteration minus the map from iteration zero, divided by the former. We show as an example in ROI A the case for which the radiance map R is considered and the errors in the definition of the χ2 are assumed to be proportional to M as defined in Equation (4). The map is shown in the plate carrée projection used in the dust and γ-ray fits for ROI A, and the magenta line shows the border of the region considered in the fit.
Finally, we note that while in the initial iterations of the fits there are often both positive and negative significant residuals, only positive ones are found at the end of the iterative procedure. This is consistent with our working hypothesis that the missing DNM component traced by the dust maps is recovered by the template determined from the iterative procedure.
A.2. Fitting Coefficients for the Dust Maps
The final fit coefficients, reduced χ2 values, and error scaling factors for all the fits performed are given in Tables 6-11. In ROI B there are no significant positive residuals when fitting τ353, so the iterative procedure was not performed. The number of iterations varies depending on the region and the number of free parameters considered, ranging from at least five in ROI B up to at most 30 in ROI A.
Table 6.
Results from R Fit in ROI A
| σ ∝ R | σ ∝ M | |
|---|---|---|
| σ Scaling factor | 15% | 12% |
| Number of iterations | 12 | 11 |
| χ2/n.d.f. | 1.006 | 1.000 |
| y H i,1 a | 2.160 ± 0.008 | 2.025 ± 0.007 |
| y H i,2 a | 3.19 ± 0.04 | 2.41 ± 0.03 |
| y H i,3 a | 0.00 ± 0.01 | 0.000 ± 0.006 |
| y CO b | 3.84 ± 0.18 | 4.48 ± 0.10 |
| y res | 1.001 ± 0.002 | 1.000 ± 0.007 |
| R iso c | 0.731 ± 0.019 | 0.811 ± 0.016 |
Note.
10−32 W sr−1 H−1.
10−12 W cm−2 sr−1 (K km s−1)−1.
10−10 W m−2 sr−1.
Table 11.
Results from τ353 Fit in ROI C
| σ ∝ στ | σ ∝ τ353 | σ ∝ M | |
|---|---|---|---|
| σ Scaling factor | 5.4 | 23% | 26% |
| Number of iterations | 8 | 7 | 6 |
| χ2/n.d.f. | 1.018 | 1.018 | 0.994 |
| y H i,1 a | 0.745 ± 0.003 | 0.682 ± 0.003 | 0.865 ± 0.004 |
| y H i,2 a | 0.320 ± 0.006 | 0.300 ± 0.005 | 0.377 ± 0.007 |
| y res | 1.001 ± 0.004 | 0.992 ± 0.011 | 1.033 ± 0.039 |
| τ iso b | 0.000 ± 0.005 | 0.000 ± 0.003 | 0.000 ± 0.006 |
Note.
10−26 cm2 H−1.
10−9 mag.
The scaling factors for the errors on τ353 given by the Planck Collaboration XI (2014) are ~5. Possible reasons for this are discussed in Section 4.2. The scaling factors obtained when assuming σ ∝ R are 10%–15%; when assuming σ ∝ τ353 they are ~25%. It can be expected that the dispersion on R is smaller because this is an integrated quantity rather than referring to a specific frequency.
We note that the yH i,ı coefficients can have a physical interpretation in terms of average specific power, i.e., power radiated by dust per H atom, per unit solid angle, , and average specific opacity, i.e., optical depth of the dust per H atom, . Non-zero coefficients for IVCs are consistent with previous measurements of dust thermal emission from this class of objects (e.g., van Woerden et al. 2005, Chapter 9, and references therein), and, for ROIs A and B, with the measurements of metallicities close to solar (Table 1). On the other hand, the yH i,3 coefficient for Complex A being compatible with 0 in Tables 6 and 7 is consistent with the low metallicity measured in this cloud (Wakker 2001).
Table 7.
Results from τ353 Fit in ROI A
| σ ∝ στ | σ ∝ τ353 | σ ∝ M | |
|---|---|---|---|
| σ Scaling factor | 4.9 | 23% | 24% |
| Number of iterations | 11 | 9 | 5 |
| χ2/n.d.f. | 0.993 | 1.003 | 1.000 |
| y H i,1 a | 0.738 ± 0.002 | 0.728 ± 0.002 | 0.806 ± 0.003 |
| y H i,2 a | 0.879 ± 0.013 | 0.859 ± 0.016 | 0.899 ± 0.021 |
| y H i,3 a | 0.01 ± 0.03 | 0.00 ± 0.01 | 0.000 ± 0.006 |
| y CO b | 2.30 ± 0.08 | 2.31 ± 0.09 | 3.2 ± 0.2 |
| y res | 0.995 ± 0.014 | 0.997 ± 0.013 | 1.001 ± 0.001 |
| τ iso c | 0.00 ± 0.01 | 0.000 ± 0.012 | 0.000 ± 0.005 |
Note.
10−26 cm2 H−1.
10−6 (K km s−1)−1.
10−9 mag.
A.3. Differences between Alternative Determinations of the DNM Column Density Templates
In Figure 21 we show the relative difference between different determinations of the DNM column density templates for ROI A, namely the difference between the baseline determination of the DNM column densities based on R assuming σ ∝ M (see Equation (4) for a definition of the quantities), and from two alternative determinations based on R assuming σ ∝ R (left), and based on τ353 assuming σ ∝ M (right). For the second case we calculated the average R/τ353 ratio in non-empty pixels of the two maps and used it to convert τ353 in equivalent R.
Figure 21.
Differences between alternative determinations of the DNM column density templates for ROI A. Left: difference between the DNM template derived from R assuming σ ∝ M minus the DNM template derived from R assuming σ ∝ R, divided by the former. Right: difference between the DNM template derived from R assuming σ ∝ M minus the DNM template derived from τ353 assuming σ ∝ M converted into R by multiplying by 1.88 × 10−2 W m−2 sr−1 mag−1, the average of the ratios between non-zero pixels in the two maps), divided by the former. The magenta line shows the border of ROI A where the dust fit was performed. The maps are shown in the plate carrée projection used for the dust and γ-ray fits in ROI A.
The figure illustrates how the different assumptions influence the final DNM template, for example how some regions have DNM only for one of the cases and not the other, and how the contrast within the map can change. For these reasons we considered the different determinations of the DNM template in the assessment of the systematic uncertainties for the γ-ray analysis in Section 5.4.
A.4. WCO, Dust Specific Opacity and Power in the Local DNM from the γ-ray Analysis
The results in Section 5 can constrain some properties of the local ISM seen in the foreground of the HVCs and IVCs, in particular the XCO = N (H2)/WCO ratio in the Ursa Major molecular clouds, and the average specific power radiated by dust per H atom and unit solid angle, , and the average specific opacity per H atom, in the DNM for the other regions.
These quantities can be extracted from the parameters in Equation (6) under the assumption that the same CR fluxes illuminate the atomic gas traced by H i and the molecular gas traced by CO or the gas in the DNM. Then, XCO = xCO/2xH i, and (when the DNM is traced using R), or (when the DNM is traced using τ353). In ROI B we do not detect any significant γ-ray emission associated with the sparsely populated DNM templates, therefore we exclude it from the following discussion.
First, we check the assumption that the spectrum of CRs illuminating the different phases in the local gas complexes is the same in each ROI. Figure 22 shows the xCO and xDNM coefficients as a function of energy from the analysis in energy bins in Section 5.3. Within the large statistical uncertainties the spectra of the emissivities in each ROI are consistent with those of H i in Figure 11, all of them being consistent with the spectrum of gas in the local interstellar medium from Casandjian (2015). There is no clear analog of the softening in Figure 11 for ROI A for either CO-traced gas or the DNM. However, the softening may be present and hidden by the large statistical uncertainties.
Figure 22.

Best-fit values for xCO and xDNM (Equation (6)) from the analysis in multiple energy bins (see Section 5.3) in ROI A and C. In each panel the points show the values as a function of energy with their statistical uncertainties. The shaded bands show the ±1σ interval from the analysis over the entire energy range (see Section 5.2).
Given the fact that the spectra are consistent within the statistical uncertainties, we extract from the fit coefficients the properties of the local ISM discussed above. We take into account the systematic uncertainties related to inputs to the interstellar emission model using the results of the analysis in Section 5.4.1 and from the jackknife tests presented in Section 5.4.2. The ISM properties are reported in Table 12. They are similar to those inferred from LAT data for other nearby interstellar complexes (e.g., Planck and Fermi Collaborations 2014), demonstrating that the modeling of the foregrounds in our analysis is robust. The XCO ratio in the Ursa Major molecular clouds that we obtain is consistent with other estimates from alternative methods in the literature (e.g., de Vries et al. 1987).
Table 12.
Local ISM Properties from the γ-ray Analysis
Note. No CO emission is detected in ROI C. The γ-ray scaling coefficients for the DNM maps derived from τ353 in ROI C were always consistent with 0. The statistical uncertainties take into account the covariances of the fit parameters.
1020 cm−2 (K km s−1)−1.
10−32 W sr−1 H−1.
10−26 cm2 H−1.
APPENDIX B
EVALUATION OF ERRORS AND UPPER LIMITS WITH THE JACKKNIFE METHOD
In this appendix we summarize the method used to evaluate uncertainties and upper limits from the jackknife tests in Section 5.4.2. Following Dudewicz & Mishra (1988), given the jackknife estimates θı with ı = 1, …, N let
| (13) |
be their arithmetic mean. A quantity known as Jı is defined as
| (14) |
If we define
| (15) |
the 1σ uncertainty of θ is
| (16) |
The (1 − α) c.l. upper limit on θ is
| (17) |
where tα,N−1 is the upper αth quantile of the Student’s t distribution with N − 1 degrees of freedom.
Footnotes
HVC Complex C has a broader distance bracket of 3.7–11.2 kpc (Wakker et al. 2007). We leave it for future studies.
The nomenclature refers to the absolute value of the velocity.
Fermi Mission Elapsed Time, measured in seconds since 2000 January 1.
The Science Tools are available along with LAT data from the Fermi Science Support Center, http://fermi.gsfc.nasa.gov/ssc.
Out of 11,421, 34,001, and 32,421 analyzed in region A, B, and C, respectively.
HVCs and IVCs span volumes much larger than those of interstellar complexes studied so far using LAT data. Were there any variations of CR densities within the clouds, the scaling coefficient would represent an average CR flux over it.
We note that the derivation of the Galactic supernova remnant distribution in Case & Bhattacharya (1998) is subject to uncertainties and discordant with some later works (e.g., Green 2014). In our study, though, we use it only as a way to probe the uncertainties due to the modeling of CR propagation relying on the previous work by Ackermann et al. (2012a) and de Palma et al. (2013).
Our choice to include this effect in the evaluation of systematic uncertainties is conservative, because the low-energy hardening is a feature that appears only in models with high reacceleration, while models with convection or pure diffusion models are also viable (Ackermann et al. 2012a).
Owing to the distances to other massive star-forming galaxies, any contributions from CRs escaping from even the closest systems would be too small to affect this conclusion and also smaller that the uncertainty of our emissivity measurements.
This accounts for the different ranges of Galactocentric radius in each line of sight. The effect is clearly visible for ROI A in Figure 16 where the profiles are concave, and the curves for zmax = 10 kpc bifurcate into two families for Rmax = 20 kpc and Rmax = 30 kpc due to particle escape at the radial boundary.
REFERENCES
- Abdo AA, Ackermann M, Ajello M, et al. 2010, ApJ, 710, 133 [Google Scholar]
- Ackermann M, Ajello M, Albert A, et al. 2012c, ApJS, 203, 4 [Google Scholar]
- Ackermann M, Ajello M, Allafort A, et al. 2012b, ApJ, 755, 164 [Google Scholar]
- Ackermann M, Ajello M, Atwood WB, et al. 2012a, ApJ, 750, 3 [Google Scholar]
- Ackermann M, Ajello M, Baldini L, et al. 2011, ApJ, 726, 81 [Google Scholar]
- Atwood WB, Abdo AA, Ackermann M, et al. 2009, ApJ, 697, 1071 [Google Scholar]
- Bykov AM 2014, A&ARv, 22, 77 [Google Scholar]
- Bohlin RC, Savage BD, & Drake JF 1978, ApJ, 224, 132 [Google Scholar]
- Bregeon J, Charles E, & Wood M Fermi LAT Collaboration 2013. in Proc. Fourth International Fermi Symp., ed. Omodei N, Brandt TJ, & Wilson-Hodge C, eConf C121028, arXiv:1304.5456 [Google Scholar]
- Breitschwerdt D, Dogiel VA, & Völk HJ 2002, A&A, 385, 216 [Google Scholar]
- Casandjian J-M 2015, ApJ, 806, 240 [Google Scholar]
- Case GL, & Bhattacharya D 1998, ApJ, 504, 761 [Google Scholar]
- Dahlem M, Dettmar R-J, & Hummel E 1994, A&A, 290!, 384 [Google Scholar]
- Dahlem M, Lisenfeld U, & Golla G 1995, ApJ, 444, 119 [Google Scholar]
- Dame TM 2011, arXiv:1101.1499 [Google Scholar]
- Dame TM, Hartmann D, & Thaddeus P 2001, ApJ, 547, 792 [Google Scholar]
- de Bruijne JHJ 2012, Ap&SS, 341, 31 [Google Scholar]
- de Palma F, Brandt TJ, Johannesson G, & Tibaldo L Fermi LAT Collaboration 2013. in Proc. 2012 Fourth International Fermi Symp., ed. Omodei N, Brandt TJ, & Wilson-Hodge C, eConf C121028, arXiv:1304.1395 [Google Scholar]
- de Vries HW, Heithausen A, & Thaddeus P 1987, ApJ, 319, 723 [Google Scholar]
- Drlica-Wagner A, Gómez-Vargas GA, Hewitt JW, Linden T, & Tibaldo L 2014, ApJ, 790, 24 [Google Scholar]
- Dudewicz EJ, & Mishra S 1988, Modern Mathematical Statistics (New York: Wiley; ) [Google Scholar]
- Everett J, Zweibel E, Benjamin B, et al. 2012, in EAS Publications Ser. 56. The Role of the Disk–Halo Interaction in Galaxy Evolution: Outflow vs. Inflow, ed. de Avillez MA, 73 [Google Scholar]
- Fermi-LAT Collaboration 2015, ApJS, in press (arXiv:1501.02003) [Google Scholar]
- Ferrière KM 2001, RvMP, 73, 1031 [Google Scholar]
- Fukui Y, Torii K, Onishi T, et al. 2015, ApJ, 798, 6 [Google Scholar]
- Ginzburg VL 1973, SvPhU, 15, 626 [Google Scholar]
- Górski KM, Hivon E, Banday AJ, et al. 2005, ApJ, 622, 759 [Google Scholar]
- Green DA 2014, in IAU Symp. 296. Supernova Environmental Impacts, ed. Ray A & McCray RA, 188 [Google Scholar]
- Grenier IA, Casandjian J-M, & Terrier R 2005, Sci, 307, 1292. [DOI] [PubMed] [Google Scholar]
- Indriolo N, Fields BD, & McCall BJ 2009, ApJ, 694, 257 [Google Scholar]
- Irwin JA, English J, & Sorathia B 1999, AJ, 117, 2102 [Google Scholar]
- Jones FC, Lukasiak A, Ptuskin V, & Webber W 2001, ApJ, 547, 264 [Google Scholar]
- Kachelriess M, Moskalenko IV, & Ostapchenko SS 2014, ApJ, 789, 136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalberla PMW, Burton WB, Hartmann D, et al. 2005, A&A, 440, 775 [Google Scholar]
- Kalberla PMW, & Kerp J 2009, ARA&A, 47, 27 [Google Scholar]
- Kamae T, Karlsson N, Mizuno T, Abe T, & Koi T 2006, ApJ, 647, 692 [Google Scholar]
- Langer WD, Velusamy T, Pineda JL, et al. 2010, A&A, 521, L17 [Google Scholar]
- Lorimer DR 2004, in IAU Symp. 218, Young Neutron Stars and Their Environments, ed. Camilo F & Gaensler BM (San Francisco, CA: ASP; ), 105 [Google Scholar]
- Magnani L, Chastain RJ, Kim HC, et al. 2003, ApJ, 586, 1111 [Google Scholar]
- Mattox JR, Bertsch DL, Chiang J, et al. 1996, ApJ, 461, 396 [Google Scholar]
- Meyerdierks H, Heithausen A, & Reif K 1991, A&A, 245, 247 [Google Scholar]
- Mori M 2009, APh, 31, 341 [Google Scholar]
- Moskalenko IV, Mashnik SG, & Strong AW 2001, ICRC, 5, 1836 [Google Scholar]
- Moskalenko IV, & Strong AW 2000, ApJ, 528, 357 [Google Scholar]
- Nichols M, Mirabal N, Agertz O, Lockman FJ, & Bland-Hawthorn J 2014, MNRAS, 442, 2883 [Google Scholar]
- Nolan PL, Abdo AA, Ackermann M, et al. 2012, ApJS, 199, 31 [Google Scholar]
- Orlando E, & Strong A 2013, MNRAS, 436, 2127 [Google Scholar]
- Planck Collaboration XXIV 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration XI 2014, A&A, 571, A11 [Google Scholar]
- Planck Collaboration XIII 2014, A&A, 571, A13 [Google Scholar]
- Planck and Fermi Collaborations 2014, A&A, in press (arXiv:1409.3268) [Google Scholar]
- Porter TA, Moskalenko IV, Strong AW, Orlando E, & Bouchet L 2008, ApJ, 682, 400 [Google Scholar]
- Pound MW, & Goodman AA 1997, ApJ, 482, 334 [Google Scholar]
- Protassov R, van Dyk DA, Connors A, Kashyap VL, & Siemiginowska A 2002, ApJ, 571, 545 [Google Scholar]
- Ptuskin VS, Moskalenko IV, Jones FC, Strong AW, & Zirakashvili VN 2006, ApJ, 642, 902 [Google Scholar]
- Reynolds SP 2008, ARA&A, 46, 89 [Google Scholar]
- Shibata T, Honda N, & Watanabe J 2007, APh, 27, 411 [Google Scholar]
- Smith RJ, Glover SCO, Clark PC, Klessen RS, & Springel V 2014, MNRAS, 441, 1628 [Google Scholar]
- Sreekumar P, Bertsch DL, Dingus BL, et al. 1993, PhRvL, 70, 127. [DOI] [PubMed] [Google Scholar]
- Strong AW, Bloemen JBGM, Dame TM, et al. 1988, A&A, 207, 1 [Google Scholar]
- Strong AW, & Moskalenko IV 1998, ApJ, 509, 212 [Google Scholar]
- Strong AW, Moskalenko IV, & Ptuskin VS 2007, ARNPS, 57, 285 [Google Scholar]
- Strong AW, Moskalenko IV, & Reimer O 2000, ApJ, 537, 763 [Google Scholar]
- Strong AW, Porter TA, Digel SW, et al. 2010, ApJL, 722, L58 [Google Scholar]
- Tibaldo L 2011, PhD thesis, Università di Padova & Université Paris Diderot http://www.infn.it/thesis/thesis_dettaglio.php?tid=5908
- Trotta R, Jóhannesson G, Moskalenko IV, et al. 2011, ApJ, 729, 106 [Google Scholar]
- van Woerden H, Wakker B, Schwarz U, & de Boer K (ed.) 2005, High-Velocity Clouds, Vol. 312 (Netherlands: Springer; ) [Google Scholar]
- Wakker BP 2001, ApJS, 136, 463 [Google Scholar]
- Wakker BP 2002, in Proc. 17th IAP Coll., Matter in Galaxies and Intergalactic Space: Observational and Theoretical Results, with Special Emphasis on New Data from FUSE, HST, and VLT, ed. Ferlet R, et al. (Paris: Frontier Group; ), arXiv:astro-ph/0109210 [Google Scholar]
- Wakker BP, Murphy EM, van Woerden H, & Dame TM 1997, ApJ, 488, 216 [Google Scholar]
- Wakker BP, York DG, Howk JC, et al. 2007, ApJL, 670, L113 [Google Scholar]
- Wakker BP, York DG, Wilhelm R, et al. 2008, ApJ, 672, 298 [Google Scholar]
- Werner M, Kissmann R, Strong AW, & Reimer O 2015, APh, 64, 18 [Google Scholar]
- Wolfire MG, Hollenbach D, & McKee CF 2010, ApJ, 716, 1191 [Google Scholar]