Lpp positions peptidoglycan at the AcrA-TolC interface in the AcrAB-TolC multidrug efflux pump

Abstract

The multidrug efflux pumps of Gram-negative bacteria are a class of complexes that span the periplasm, coupling both the inner and outer membranes to expel toxic molecules. The best-characterized example of these tripartite pumps is the AcrAB-TolC complex of Escherichia coli. However, how the complex interacts with the peptidoglycan (PG) cell wall, which is anchored to the outer membrane (OM) by Braun’s lipoprotein (Lpp), is still largely unknown. In this work, we present molecular dynamics simulations of a complete, atomistic model of the AcrAB-TolC complex with the inner membrane, OM, and PG layers all present. We find that the PG localizes to the junction of AcrA and TolC, in agreement with recent cryo-tomography data. Free-energy calculations reveal that the positioning of PG is determined by the length and conformation of multiple Lpp copies anchoring it to the OM. The distance between the PG and OM measured in cryo-electron microscopy images of wild-type E. coli also agrees with the simulation-derived spacing. Sequence analysis of AcrA suggests a conserved role for interactions with PG in the assembly and stabilization of efflux pumps, one that may extend to other trans-envelope complexes as well.

Significance

The cell envelope in Gram-negative bacteria is unique in that it possesses two membranes, both inner and outer. A number of complexes span the entire periplasm, although how they contend with the peptidoglycan (PG) cell wall, a thin, mesh-like network anchored to the outer membrane, is often unknown. Here, we model one of these complexes, the multidrug efflux pump AcrAB-TolC, in an accurate model of the cell envelope. Molecular dynamics simulations, as well as cryo-electron microscopy, are used to resolve distances between the PG layer and the two membranes. In particular, the simulations reveal detailed interactions between PG and AcrAB-TolC, which may influence the assembly and stabilization of the fully formed efflux pump.

Introduction

In addition to their cytoplasmic inner membrane (IM), Gram-negative bacteria are distinguished by the possession of a second, outer membrane (OM). The two membranes are separated by an ∼20- to 30-nm space known as the periplasm, in which numerous proteins are present with various functions such as nutrient import and waste export, assembly of the OM and intervening cell wall, and exhibiting virulence. This region of the bacterial cell, i.e., membranes, cell wall, and periplasm, is collectively known as the cell envelope (1).

In addition to proteins localized to one of the two membranes or to the periplasm (2), there are trans-envelope complexes that span all three. Because of the lack of chemical energy in the periplasm, active processes must couple to an energy-generating complex in the IM. For example, nutrient import by TonB-dependent transporters in the OM depends on a proton-motive-force-driven ExbB-ExbD-TonB complex in the IM (3,4). Multidrug efflux pumps represent another class of active trans-envelope complexes and are one of the intrinsic antibiotic resistance mechanisms present in a number of pathogenic Gram-negative bacterial species (5, 6, 7).

Structural data on complete efflux pumps have come exclusively from cryo-electron microscopy, primarily of AcrAB-TolC of Escherichia coli (8, 9, 10, 11, 12). This tripartite pump is composed of a proton-motive-force-driven AcrB residing in the IM, a membrane fusion protein AcrA in the periplasm, and a porin TolC in the OM. All structural studies support a 3:6:3 stoichiometry for AcrB, AcrA, and TolC, respectively.

In Gram-negative bacteria, the peptidoglycan cell wall (PG) forms a single thin (∼4-nm) porous layer between the IM and OM (13,14). All trans-envelope complexes and processes must cross this layer, yet until recently, structures of efflux pumps did not resolve where the pump intersects the PG layer. Many schematic depictions placed it at the equatorial domain of TolC, which is roughly in the middle of the periplasmic-exposed portion of the protein (15, 16, 17, 18, 19). In E. coli, the position of PG is constrained by its covalent linkage to Braun’s lipoprotein (Lpp), the most abundant protein in E. coli (1), which is also anchored to the OM by a triacylated N-terminus (20, 21, 22, 23). Lpp is ∼9 nm long, which, in contrast to the above depictions, would place the PG beyond TolC’s equatorial domain, assuming Lpp is oriented perpendicular to the OM and PG. Recent cryo-tomography studies of AcrAB-TolC in vivo have revealed this to be the case, with the PG layer localizing to the interface between TolC and AcrA (24,25).

Accurately modeling trans-envelope complexes of Gram-negative bacteria is challenging for a number of reasons, including, e.g., the large size of the system; the distinct compositions of the two membranes; and the periodic, covalently connected, and disordered nature of PG (26). In López et al., extensive atomistic (up to 1 μs for the 1.26-million-atom system) and coarse-grained simulations of the Pseudomonas aeruginosa efflux pump MexAB-OprM have been reported (27). The pump was simulated including both the IM and OM, although PG was not present. The simulations led to a proposal for how MexA and OprM (homologous to AcrA and TolC, respectively) can work together to open a channel (27). Two other studies come from Khalid and co-workers. In the first, AcrAB-TolC was simulated in a coarse-grained representation of the cell envelope, although the system also lacked PG (28). In the second, atomistic simulations of the PG-interacting proteins OmpA and TolR were found to contribute to stabilizing the PG in the cell envelope even without Lpp (29).

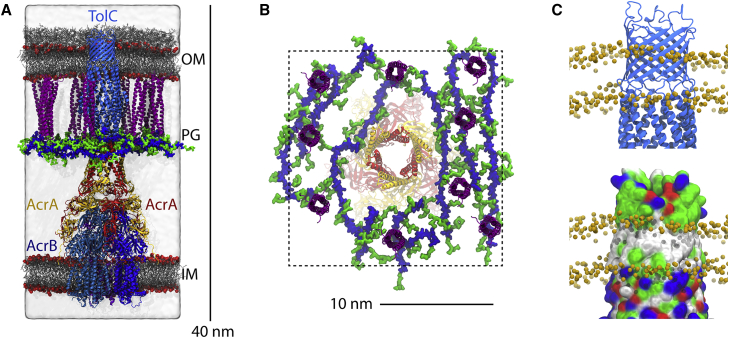
In this study, we present an atomistic model of the AcrAB-TolC efflux pump embedded in the E. coli cell envelope, including accurate, detailed representations of the IM, OM, and PG layers (Fig. 1 A). The sizes and positions of the components from the modeling, equilibrium simulations, and free-energy calculations are mostly found to be in good agreement with previously determined experimental data as well as new analysis of cryo-electron microscopy (cryo-EM) images presented here. Thus, our model of the cell envelope can serve as a prototype for future modeling and simulation efforts of this critically important subcellular region.

Figure 1.

Complete atomic model of the efflux pump embedded in the E. coli cell envelope. The AcrB trimer in the IM is in shades of blue, and TolC in the OM is in light blue. AcrA copies in site 1 (binding between two copies of AcrB) are in red, and those in site 2 (binding exclusively to one copy of AcrB) are in yellow. The Lpp trimers (nine in total) are in purple and are covalently linked to the PG in blue (glycan strands) and green (peptide chains). (A) Profile view. Both membranes are shown as gray sticks, and the red spheres represent phosphorus atoms in lipids and lipid A. Water is shown in a white, transparent surface representation. The system is 40 nm from top (extracellular region) to bottom (cytoplasm). (B) Top view from the extracellular side illustrating the placement of Lpp trimers and PG around AcrA. The dotted line is the periodic boundary. (C) Hydrophobic belt of TolC does not align with its β-barrel (30). The top panel shows TolC in light blue, with the extent of the hydrophobic core of the OM indicated by the positions of C2 atoms in the lipid/LPS aliphatic tails (orange spheres). The bottom panel is the same as the top except that TolC is shown in a surface representation colored by residue type (white hydrophobic, green polar, blue basic, and red acidic). To see this figure in color, go online.

Materials and methods

System construction

Proteins

The initial model of the AcrAB-TolC complex was taken from the cryo-EM-fitted apo structure from Wang et al. (Protein Data Bank (PDB): 5V5S) (12), which includes six copies of AcrA, the trimeric AcrB, and the trimeric TolC. Residues 273 of AcrA and 258 of AcrB, which had been mutated to cysteine to form stabilizing disulfide bonds (12), were reverted to their native serine. AcrZ, a small transmembrane protein that modulates the behavior of AcrB (31), was not included in the experimental construct used for imaging and therefore was also not included here.

Because the membrane-proximal domain of AcrA was not resolved in previous crystal structures, we attempted to improve our model. We used coordinates from 5V5S as the template and also included inter-residue contact restraints obtained from coevolution analysis. The GREMLIN web server with default settings was used to perform the coevolution analysis, predict inter-residue contacts, and generate the required restraint files. Fragment files were obtained from the Robetta web server (32,33). RosettaCM (34) and the RosettaScripts interface (35) were used to generate 10,000 models each of chains D and E from the cryo-EM structure. The top model of each chain (based on the sum of the Rosetta energy and the restraint score) was then selected for use in molecular dynamics (MD) simulations. A comparison between the new membrane-proximal domains and their counterparts in PDB: 5V5S revealed a similar overall structure, although with improved secondary structure content (Fig. S1).

Missing AcrA N-terminal residues Cys25 to Met37 were modeled as unstructured and added. Residues 1–24 are a signal sequence and are cleaved during maturation (36,37). As AcrA is known to be lipidated, the N-terminal cysteine of each copy was triacylated, with one acyl tail attached to the N-terminal nitrogen atom and two acyl tails attached to the sulfur atom (38). This lipid anchor was inserted into the periplasmic leaflet of the IM.

Nine copies of the triple helix of Lpp (20) (PDB: 1EQ7 (21)) were added, giving a density of 1 Lpp trimer/40 nm². We arrived at this number by assuming that E. coli is a cylinder of radius 0.5 μm and a length of 1 μm and capped by hemispheres of radius 0.5 μm, giving a surface area of 6.3 μm² = 6.3 × 10⁶ nm². There are ∼500,000 copies of Lpp per cell (166,667 trimers) (1), meaning that if evenly distributed, there is one Lpp trimer roughly every 38 nm². Each Lpp was lipidated at its N-terminus with the three tails inserted into the periplasmic leaflet of the OM. One Lpp of each trimer was also covalently bonded to a meso-diaminopimelate (mesoDAP) residue of a PG peptide chain at its C-terminus, with the two following Ala residues of the peptide chain removed (39).

Membranes

The IM and OM were constructed using CHARMM-GUI (40) and equilibrated separately. The IM was built around AcrB to match the Top6 distribution for the E. coli IM given in Pandit and Klauda (41,42). Specifically, 202 PMPE, 55 POPE, 55 QMPE, 41 PMPG, 41 PYPG, 37 YOPE, and 27 PVCL2 (cardiolipin) were placed in each leaflet (see Table S1 for full lipid names). Although cardiolipin was not in the original Top6 membrane model, it was added because of its previously reported interactions with AcrB (28,31). The lipidated N-termini of AcrA were also included in the upper leaflet; the difference in lipid areas between the two leaflets is accounted for by AcrB.

TolC was embedded in a model OM. The outer leaflet is composed exclusively of 186 lipopolysaccharide (LPS) molecules of the rough RaLPS chemotype, which contains lipid A and 10 inner- and outer-core sugars (3). The inner leaflet was constructed to match a ratio of 75:20:5 PPPE/PVPG/PVCL2 distribution based on Wu et al. (43). Specifically, 352 PPPE, 94 PVPG, and 23 PVCL2 were used. In addition to water, divalent Mg²⁺ and Ca²⁺ ions were added at a 4:1 ratio to neutralize the large negative charge on LPS (44). To match the areas of the two leaflets, a symmetric bilayer of the duplicated inner leaflet was first built and equilibrated under constant pressure for 27 ns until it reached a stable area equivalent to the expected area of the outer leaflet based on an area/LPS of 1.8 nm² (3,45). Surprisingly, the hydrophobic band of TolC does not align with its β-barrel, explaining its placement in the membrane (Fig. 1 C), as also seen previously (30).

The IM was equilibrated for 35 ns at constant pressure until it stabilized at dimensions of 18.9 nm × 18.9 nm, after which it was run an additional 30 ns at constant area. The OM was run for 54 ns at constant pressure until it stabilized at dimensions of 19.0 nm × 19.0 nm, after which it was run an additional 14 ns at constant area with dimensions set to match those of the IM precisely.

Cell wall

The model of the cell wall was constructed by reverse coarse graining a patch of PG under tension from previously published simulations of a coarse-grained sacculus (46). The patch was chosen to have a sufficiently large hole to accommodate the efflux pump. Each bead in the CG model represents two disaccharides (each composed of an N-acetylglucosamine and an N-acetylmuramic acid) and one stem pentapeptide (46). To reverse coarse grain the model, we first centered an atomistic model of two disaccharides and two pentapeptide stems (Fig. S2 A) on each bead, aligned with its bond to the next one. The second pentapeptide had been excluded from the CG model as it projects out of the plane of the PG layer and was presumed to not form significant interactions (46). Bonds for the glycans and peptides to neighboring ones were added where dictated by the CG model (Fig. S2 B); the final atomistic model was then minimized to eliminate distortions introduced in the reverse coarse-graining process (Fig. S2 C). There are 11 glycan strands with lengths ranging from 4 to 18 disaccharides (average 10.5; standard deviation (SD) 4.8). Out of 116 five-amino-acid peptide chains branching off each disaccharide, 60 were cross-linked to one another, giving a cross-linking fraction of 52%, as is typical for E. coli (14,47). In an 8.5-ns simulation of the cell wall in water under constant pressure, the dimensions relaxed to 17.0 nm × 15.9 nm, indicating that in the production runs, the PG-network strain is 0.19 in the glycan direction and 0.11 in the peptide direction.

Assembling the system

After equilibration of the IM, OM, and PG, these components were combined with the completed structure of the AcrAB-TolC complex. This system was then solvated with water. Trial simulations of 1 ns each were run to determine the amount of water in the periplasm necessary to reach a density of 1 g/cm³ and avoid compression or expansion. An additional 150 mM of NaCl was added to neutralize the system and bring it to a physiological salt concentration. The final system size is 1.45 million atoms. Before equilibration, it had dimensions of 18.9 nm × 18.9 nm × 39.0 nm.

Simulation methods

All simulations were carried out with NAMD 2.13 (48) or NAMD3 (49). The CHARMM36 force field for lipids (50) and the CHARMM36m force field for proteins (51,52) were used along with TIP3P water (53). Previously developed force field parameters for PG (14) were also used. For equilibration and subsequent free-energy calculations, a multiple-time-stepping procedure was employed, with bonded and short-range nonbonded interactions calculated every 2 fs; long-range electrostatics were calculated every 4 fs using the particle mesh Ewald method (54). For the extended equilibrium simulations, a uniform 4-fs time step was used along with hydrogen mass repartitioning (55,56). In all simulations, the van der Waals cutoff was set to 1.2 nm, with a force-based switching function applied from 1.0 to 1.2 nm. A constant temperature of 310 K was maintained using Langevin dynamics. Unless stated otherwise, a constant pressure of 1 atm was maintained independently in the z and xy dimensions using the Langevin piston method (57). Visualization and analysis were done using VMD (58).

To refine the starting model, we used MD flexible fitting with symmetry restraints applied to the three copies of AcrB, three copies of TolC, and three pairs of AcrA (59,60). The model was fitted to the cryo-EM map of the apo state of the efflux pump (EMD-8636) (12) over the course of a 7-ns simulation with gscale (coupling to the map) of 0.3, followed by minimization for 2000 steps at gscale of 5.0. The root mean-square deviation (RMSD) between the initial and final conformations is 0.2 nm.

Free-energy calculations

The potential of mean force (PMF) for the full system containing the efflux pump in Fig. 2 A was calculated using replica-exchange umbrella sampling (REUS) (61, 62, 63) and the weighted histogram analysis method, as implemented in WHAM (64,65). Initial states were generated from the pre-MD flexible fitting model of the efflux pump using steered MD on a collective variable defining the separation between the OM and the PG (66). Starting from the equilibrium position, the OM-PG distance was either increased or decreased at a rate of 0.1 nm/ns using steered MD for 22 ns in each direction. Restraints were added to keep the PG layer planar during these simulations. A total of 55 windows were used, spaced every 0.05–0.1 nm over a range of 9.4–12.6 nm with force constants ranging from 150 to 500 kcal/mol ⋅ nm². The REUS calculation was run for 25 ns/window; the convergence of the PMF is shown in Fig. S3 A.

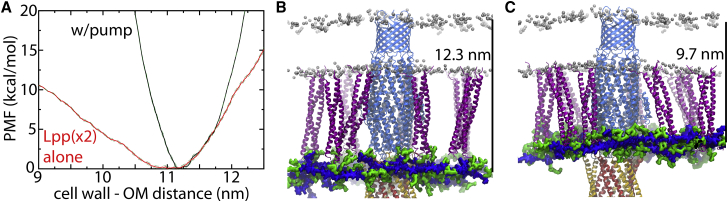
Figure 2.

Free-energy calculation of PG position. (A) PMF of PG’s position with respect to the OM for the system with the full efflux pump (black) and for two Lpp trimers alone (red; see also Fig. S3). Green dotted lines represent ±1 SD. (B and C) Snapshots from the end of REUS simulations at the extreme distances explored (labeled in each panel). TolC, Lpp, and AcrA are in light blue, purple, and orange/yellow, respectively. Glycan strands of the PG are in blue and peptide chains are in green. Phosphorus atoms of the membrane are shown as silver spheres. Core sugars of the OM are not shown. To see this figure in color, go online.

The system containing two Lpp trimers bridging the PG and the OM was taken from a previous study (67); it contains ∼150,000 atoms and has lateral dimensions of 7.9 nm × 7.9 nm. Initial states for the REUS were generated by reducing or expanding the distance between the PG and the OM at a rate of 0.01 nm/ns. In total, 36 windows spaced every 0.1 nm were used, covered a range of 9.0–12.5 nm. The calculation was run for 30 ns/window, and convergence is illustrated in Fig. S3 B.

For both PMFs, additional 2-ns simulations for each window with restraints on the collective variable (k = 1000 kcal/mol ⋅ nm²) were run; from these, the correlation time at each point was estimated using ACFCalculator (68), as done previously (69). The correlation times were included as input for bootstrapping error analysis in WHAM (65).

Strains and growth

E. coli strain K12 was grown aerobically in Luria-Bertani medium at 37°C until an OD₆₀₀ of 0.6 was reached. Cells were pelleted at 6000 × g for 5 min at 4°C and resuspended to an OD₆₀₀ of 12 in Luria-Bertani medium.

Cryo-EM

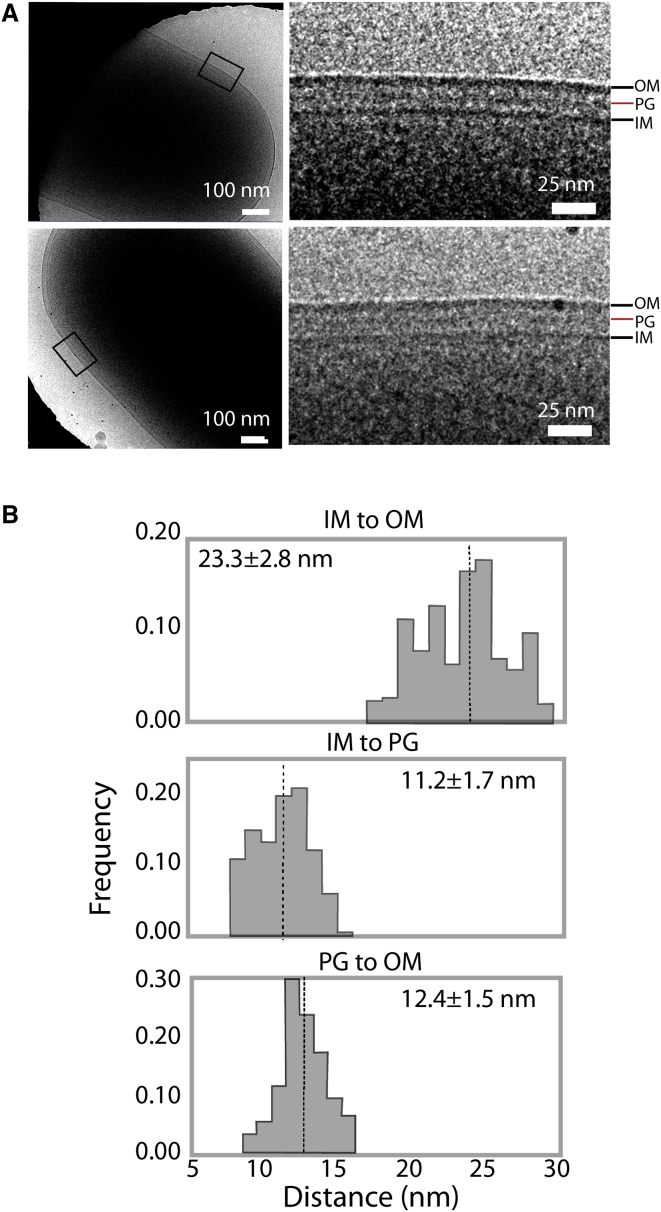
Cryo-EM experiments were performed as in (22,70), but with minor changes. Briefly, UltraAuFoil R2/2 grids (200 mesh; Quantifoil Micro Tools, Großlöbichau, Germany) were glow discharged for 60 s at 10 mA. 2.5 μL of cell premixed with 10-nm colloidal gold (Sigma-Aldrich, St. Louis, MO) was applied to a glow-discharged grid and plunge frozen into an ethane/propane mixture using a Vitrobot MkIV (FEI Company, Hillsboro, OR) (wait time 60 s, blot time 5 s, blot force 3, drain time 1 s, humidity 100%). Stored grids were loaded into a 200 keV FEI Tecnai TF20 FEG transmission electron microscope (FEI Company) equipped with a Falcon II direct electron detector (FEI Company) using a Gatan 626 cryogenic holder (Gatan, Pleasanton, CA). Projection images of ∼100 cells were collected using Leginon automated data-collection software 3.0 (71) with a defocus of −4 to 5 μm, and a pixel size of 0.828 nm (nominal magnification 25,000×). Images were manually curated for cells in which a clear density could be seen between the IM and OM, which we interpreted as the PG layer. From these images, small areas of 15 cells, in which we were confident that a density for PG could be seen, were manually segmented down the center of the IM, OM, and the PG density using 3dmod from the IMOD package (72). Custom scripts were then used to break the contours into 0.5-nm intervals and measure the distances between pairs of contours at each interval.

Sequence analysis

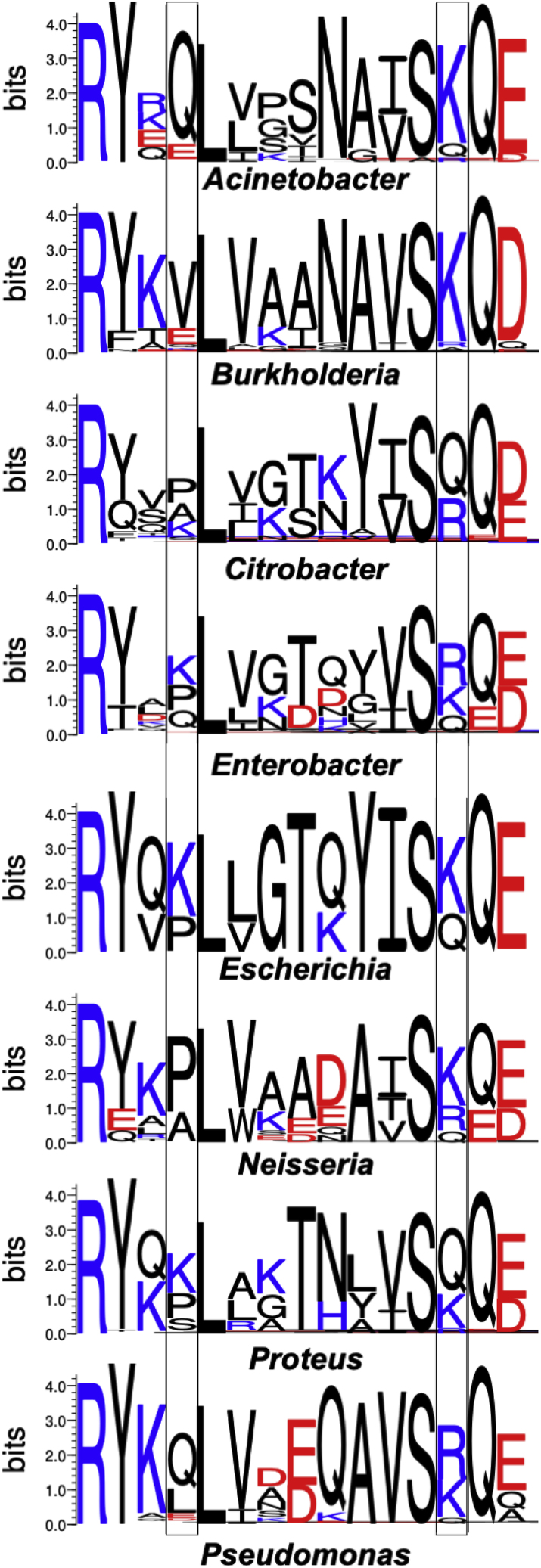
We performed separate protein BLAST searches of the non-redundant (nr) database for homologs of AcrA from E. coli str. K-12 substr. MG1655 (AYG20409.1) against the following eight genera: Acinetobacter (taxid: 469), Burkholderia (taxid: 32008), Citrobacter (taxid: 544), Enterobacter (taxid: 547), Escherichia (taxid: 561), Neisseria (taxid: 482), Proteus (taxid: 583), and Pseudomonas (taxid: 286). For each search, the maximal target sequences were set to 1000. For each set of sequence matches, duplicates were removed, as were sequences with long insertions or deletions. The remaining sequences were then used to generate a multiple sequence alignment with Clustal Omega (73). We then generated WebLogo (74) representations of sequence conservation in the region corresponding to residues 128–142 in E. coli AcrA.

Results

Construction and equilibration of the complete model

A recent high-resolution cryo-EM structure of the AcrAB-TolC efflux pump was used to initiate building of the model (PDB: 5V5S) (12); MD flexible fitting was used to optimize the fit of the model to the cryo-EM map. The complex was embedded in models of both the IM for AcrB and an LPS-containing OM for TolC. The PG model was extracted from a previous coarse-grained simulation of an entire sacculus (46) and then converted to an atomistic model (14,46). Nine Lpp coiled-coil trimers were evenly distributed based on the expected density of 1 Lpp trimer/38 nm² (1). Each Lpp’s N-terminal cysteine was triacylated and embedded in the OM inner leaflet (38), and the C-terminus (Lys58) from one monomer of each trimer was covalently linked to a mesoDAP amino acid in the PG (39). The final system size is 1.45 million atoms (Fig. 1). See Materials and methods for more details of the system construction and Table S2 for a list of all production simulations.

The full system was equilibrated in stages. First, all pump proteins were restrained to their original positions for 10 ns, followed by 10 ns with just their backbones restrained. Starting from the end state of the latter stage, four replicas were run for 20 ns with symmetry restraints (60) applied to the pump followed by 280 ns of unrestrained equilibration. The RMSD for the entire efflux pump was 0.4–0.6 nm by the end of the simulations (Fig. S4). The AcrB and TolC trimers were individually significantly more stable than the pump overall, whereas the AcrA hexamer was less stable. Although we previously found that a single copy of AcrA bound in site 1 is less flexible than a single copy bound in site 2 when TolC is not present (75), in the assembled pump, AcrA copies in site 1 have a higher RMSD than those in site 2 (Fig. S4). Looking at individual AcrA copies, the θ angle, which defines the position of the α-helical domain relative to the AcrB-bound domains (Fig. S5 A), typically remains near its starting value (Fig. S5, B–E). The φ angle fluctuates much more than the other two measured angles, which also matches its behavior observed in its free and AcrB-only-bound states (75).

Whereas LPS diffuses extremely slowly, inner-leaflet OM lipids diffuse at rates comparable to symmetric bilayers (3). We measured the rate of diffusion for these lipids as well as the lipid anchors of Lpp embedded in the OM’s inner leaflet (Table S3). The Lpp anchors diffused at a rate of (4.9 ± 0.4) × 10⁻⁸ cm²/s, which was only slightly less than other OM lipids and sufficient to allow them to move 1–2 nm from their starting positions during equilibrium simulations.

The initial placement of the PG was chosen to align roughly with the length of Lpp, which is ∼9 nm, giving a center-center distance between the PG and the OM, including all core sugars on the LPS, of initially 11.4 nm. Over the four simulations, this distance was reduced to 11.0 ± 0.1 nm. The center-center distance between the OM and IM was similarly stable at 28.0 ± 0.1 nm.

Finally, for comparison to a recent cryo-tomography study in which the components of the AcrAB-TolC pump were overexpressed (24), we also measured the length of the pump. We generated 1.5-nm-resolution density maps every 20 ns from the last 200 ns of each simulation and then averaged them using Chimera (76). The size of the pump in the resulting map is 33.9 nm, in rough agreement with the value of 33 nm given in Shi et al. (24) (Fig. S6).

Energetics of PG distance from the OM

To determine whether the equilibrium position of the PG relative to the membranes and to the pump was biased by its construction, we performed REUS simulations and calculated the one-dimensional PMF as a function of the cell wall’s position along the trans-envelope axis relative to the position of the OM. The minimum of the PMF is at 11.2 nm separation (Fig. 2 A). This distance is similar to the average separation observed in the equilibrium simulation (11.0 nm). The PMF sharply rises on either side of this minimum, reaching 10 kcal/mol within 1 nm, which agrees with the negligible fluctuations observed in the equilibrium simulations (SD of 0.1 nm).

To expand the distance between the PG and the OM, the peptide chains of the PG connected to Lpp trimers extend out of plane (Fig. 2 B). Conversely, to reduce the distance between the PG and the OM, the Lpp trimers tilt (Fig. 2 C), reaching angles relative to the membrane plane of 60° (90° would be perfectly perpendicular). Tilting of Lpp has been observed previously in equilibrium MD simulations with OmpA present (77). We also calculated the kink angle along the Lpp helices using the VMD Bendix plugin (78). Shown in Fig. S7 for three different end states of the REUS simulations, kinking was almost always less than 30°, except near the center at Ser33. This kink appears to be similar to that observed in previous simulations (77).

To determine the intrinsic resistance of Lpp to compression or extension, we also built a system containing just two Lpp trimers bridging the PG and the OM and calculated the PMF for the distance between them (Figs. 2 A and S8). The minimum of the PMF is at 11.0 nm, although the basin is broad, with the PMF being less than 1 kcal/mol over the range 10.6–11.4 nm. At a compressed distance of 9 nm, the two Lpp trimers are tilted in the same direction, with tilt angles of 50–60° relative to the membrane (Fig. S8). We also calculated the kink angle along Lpp as before, finding again some tendency to bend near Ser33 (Fig. S9). We also saw an occasional kink near the C-terminus, as observed previously (77).

Comparison of the simulations to cryo-EM data on WT E. coli

For comparison to the simulated PG-OM and OM-IM distances, we obtained and analyzed cryo-EM images of wild-type (WT) E. coli cells, i.e., ones without discernible efflux pumps. We discerned a region of darker density in the periplasm consistent with PG demonstrated experimentally in previous studies, ∼10 nm beneath the OM (79). This PG was not uniformly visible in the images, so areas from 15 cells in which it could clearly be seen were segmented out for analysis (Fig. 3 A). The center-center IM-OM distance was 23.3 ± 2.8 nm, which is only slightly less than the 24.6 nm measured for 38 cells previously by Asmar et al. (22) (Fig. 3 B). Both measurements are notably lower than what we observed in our simulations (28.0 nm) and what was estimated by Shi et al., in which the efflux pump was overexpressed (30–31 nm) (24). However, we note there was significant variability between the WT cells with the smallest average IM-OM distance for the segmented regions being 19.0 ± 1.0 nm and the largest being 28.0 ± 2.0 nm (Fig. 3 B).

Figure 3.

Cryo-EM of the E. coli cell envelope. (A) Cryo-EM projection images show density between the IM and OM interpreted as the PG layer. (B) From the projection images in (A), small areas of 15 cells where PG was clearly visible were segmented and the distances between the IM, OM, and PG were measured. The dotted line is the mean distance. To see this figure in color, go online.

We also quantified the PG-OM distance in the cryo-EM images. We found the center-center PG-OM was 12.4 ± 1.5 nm over all cells (Fig. 3 B). Our simulated equilibrium (11.0 nm) and energetically optimal (11.2 nm based on the PMF) distances are within 1 SD. Yet again, we observed a wide variability between individual cells, with the smallest being 9.7 ± 0.6 nm and the largest being 15.0 ± 0.2 nm. The smallest distance matches the most compressed state simulated with the efflux pump (Fig. 2 C), suggesting that the Lpp trimers are unlikely to tilt further than observed. In contrast, the largest distance is more than can be accommodated by the Lpp trimer even in its most extended state. This large distance suggests either that Lpp has become mostly decoupled from the PG or the OM in some cells or that it unfolds partially.

Interactions between the PG and the pump

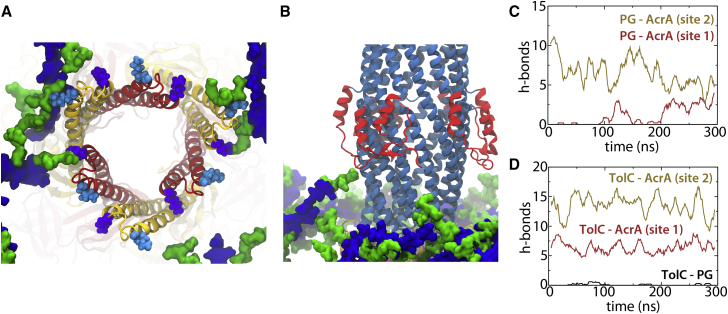
As noted above, the PG is positioned near the tips of the α-hairpin of AcrA (Fig. 1). PG contains a few negatively charged carboxyl groups on each peptide chain, including D-glutamate, mesoDAP, and the C-terminus. Over the course of the 300-ns equilibrium simulations, a number of hydrogen bonds between the PG and AcrA were observed (7.9 ± 3.8). Most prevalent are those with Lys131 and Lys140, both of which form at least one and as many as eight hydrogen bonds with PG during most of the simulation (Fig. 4 A); these interactions persisted during the REUS simulations as well, because the free PG peptide chains are ∼2 nm long. Other residues forming hydrogen bonds with PG included Lys109, Lys114, Asn120, Gln123, Asn127, Arg128, and Lys130. Although PG forms more hydrogen bonds with AcrA copies in site 2 than those in site 1 (Figs. 4 C and S10), alternative arrangements of PG than the one modeled here may produce different distributions.

Figure 4.

Interactions between PG, AcrA, and TolC. (A) Example frame from one simulation replica showing interactions between PG and Lys131 (cyan, space-filling representation) or Lys140 (purple) from AcrA. (B) Example of a rare interaction between PG and the equatorial domain (red) of TolC. (C) Hydrogen bonds between AcrA and PG over time. The colors represent three copies of AcrA in site 1 (red) and three in site 2 (gold) as in (A) and in Fig. 1. (D) Hydrogen bonds between AcrA and TolC as well as PG and TolC over time. Plots for other replicas are included in Figs. S10 and S11. To see this figure in color, go online.

Interactions between PG and TolC were rarely observed in our simulations (Figs. 4 D and S11). Residues on TolC that formed hydrogen bonds with PG included Gln142, Asn145, Lys345, and Lys383. We also occasionally observed a close approach of a peptide branch of PG to the equatorial domain of TolC, which formed interactions with Lys202 (Fig. 4 B). Cross-linking using a DTSSP (3,3′-Dithiobis(sulfosuccinimidylpropionate)) linker (length 1.2 nm) found PG interaction sites on both AcrA and TolC, including the equatorial domain (24). Additionally, hydrogen bonds between the PG and the TolC equatorial domain were occasionally observed during REUS simulations, but only when the distance was less than 10.5 nm.

We observed 20.3 ± 3.7 hydrogen bonds on average between AcrA and TolC across all four replicas (Fig. 4 D), with roughly 2/3 of them coming from the same three copies of AcrA in site 2 that were observed to interact with PG, likely explaining why AcrA copies in site 2 are more stable than those in site 1 (Fig. S4). Predominant interactions included Arg128 on AcrA (site 1) with Ser363 on TolC, Tyr137 (AcrA, site 1) with Asp356 on TolC, Tyr137 (AcrA, site 2) with Asp138 (TolC), and Glu142 (AcrA, site 2) with Arg143 (TolC). Arg128 on AcrA was previously recognized to form a critical interaction with TolC (80), and it is also observed to occasionally form hydrogen bonds with PG (at least one formed 25% of the simulation time).

We examined the conservation of the residues of AcrA observed to interact with PG. We carried out BLASTP searches on homologs of AcrA across eight genera (Fig. 5). Residues Arg128, Leu132, and Ser139 are universally conserved, and all three have been implicated in function (80). Focusing on PG-interacting residues Lys131 and Lys140 (Fig. 4 A), neither are well conserved. However, residue 140 is either a lysine, an arginine, or a glutamine, all of which can potentially form hydrogen bonds with negatively charged PG residues. Residue 131 is more mixed, although if 130 is also included, a lysine, arginine, or glutamine is found in over half of the sequences. These results suggest that one to two residues, one on either side of the tip of the AcrA α-helical hairpin (or that of its homologs), may contribute to interacting with PG in most species.

Figure 5.

Sequence conservation in homologs of AcrA for the region corresponding to residues 128–142 in AcrA from E. coli. Residues corresponding to Lys131 and Lys140 in E. coli AcrA are highlighted in boxes. See Materials and methods for details. Figure generated with WebLogo (74). To see this figure in color, go online.

Discussion

Here, we have constructed and simulated one of the most detailed models to date of the E. coli multidrug efflux pump AcrAB-TolC in its native cell envelope at atomistic resolution. This model, which includes the IM, PG, and OM layers, illuminates the spacing between each and how they engage with the pump. Simulations further confirm that the PG layer localizes to the junction between AcrA and TolC, in contrast to many earlier schematic depictions of the assembled pump but in agreement with recent cryo-tomography data (24).

PG is anchored to the OM by multiple copies of the trimeric coiled-coil protein Lpp (Fig. 1). Lpp dictates the spacing between the OM and PG as well as the overall size of the periplasm (22). Our simulations and free-energy calculations determined the center-center distance between PG and OM to be 11.0–11.2 nm (Fig. 2 A), slightly less than that observed in our own cryo-EM images with no efflux pump present (12.4 nm; Fig. 3). Our experimentally measured PG-OM distances varied between cells, ranging from 9.7 to 15.0 nm. Our simulated compression illustrates how the lower bound can be accommodated (with modest tilting of Lpp trimers), but the longer distance is beyond the apparent range of Lpp, at least without some unfolding. It is known that the number of PG-OM connections varies during the cell cycle; Lpp binding to PG increases by 70% as cells enter stationary phase (23,47). This variability likely affects the observed PG-OM distance as well, although it will require further study to identify a clear relationship, if any exists. We expect that a lower density of Lpp trimers would allow for more variability in the PG-OM distance, possibly explaining the large range observed experimentally.

We also compared the OM-IM distances in simulations and cryo-EM images. In simulations with the pump, we measured the OM-IM distance to be 28.0 nm, which is in rough agreement with previously published tomograms in which the pump is overexpressed (30–31 nm) (24). However, in the cryo-EM images presented here, in which likely no pumps were present, the OM-IM distance was measured to be 23.3 nm, similar to that observed in previous studies (22,70), although variability was again large across cells (19.0–28.0 nm). A shorter distance between the OM and IM could accommodate an alternative mode of interaction in which AcrA ensconces a larger portion of TolC, as suggested by some mutagenesis studies (81,82). We also note that the osmolarity of the medium will affect this distance (83,84).

The position of the PG layer at AcrA-TolC interface may play a role in assembly of the efflux pump. From previous simulations and free-energy calculations, it was found that binding of AcrA to AcrB limits the former’s flexibility (75), which would bring the tip of the α-helical hairpin domain of AcrA near the PG. This tip is stabilized by hydrogen bonds with PG in our simulations, primarily through AcrA residues Lys131 and Lys140. Such stabilization would preserve the AcrAB subcomplex in an assembly-competent state before binding to TolC (24). These two residues are not well conserved, although a lysine, arginine, or glutamine is always found for residue 140 and frequently found for residues 130 and 131 (Fig. 5). Although the spacing between IM, PG, and OM may vary between bacterial species, it is regulated through multiple mechanisms (22), including in species that lack a Lpp homolog (67). Thus, efflux pumps may also take advantage of the regulated spacing to optimize their own assembly. Furthermore, other trans-envelope complexes and processes may also use PG for assembly, stabilization, and recruitment. For example, TonB, a protein that binds to and energizes OM transporters, can also bind to PG, possibly in a surveillance mode of action (85).

Editor: Philip Biggin.