Spatial control over near-critical-point operation ensures fidelity of ParABS-mediated DNA partition

Abstract

In bacteria, most low-copy-number plasmid and chromosomally encoded partition systems belong to the tripartite ParABS partition machinery. Despite the importance in genetic inheritance, the mechanisms of ParABS-mediated genome partition are not well understood. Combining theory and experiment, we provided evidence that the ParABS system—DNA partitioning in vivo via the ParA-gradient-based Brownian ratcheting—operates near a transition point in parameter space (i.e., a critical point), across which the system displays qualitatively different motile behaviors. This near-critical-point operation adapts the segregation distance of replicated plasmids to the half length of the elongating nucleoid, ensuring both cell halves to inherit one copy of the plasmids. Further, we demonstrated that the plasmid localizes the cytoplasmic ParA to buffer the partition fidelity against the large cell-to-cell fluctuations in ParA level. The spatial control over the near-critical-point operation not only ensures both sensitive adaptation and robust execution of partitioning but also sheds light on the fundamental question in cell biology: how do cells faithfully measure cellular-scale distance by only using molecular-scale interactions?

Significance

Sensitive response and robust execution of functions against uncertainties define a central theme of biological processes. Exploiting the widespread ParA-mediated bacterial partition as the model system, we present a general strategy to address this dichotomy. We show the low-copy-number plasmid “self-drives” by both localizing cytoplasmic ParA nearby and “creating” and “following” the ParA gradient on the nucleoid. The plasmid-localized activities combine to buffer against cellular fluctuations and operate near a critical point in the parameter space, which adapts the plasmid segregation distance to the cell length. This ensures the replicated plasmids always partition into the two different cell halves, maximizing partition fidelity. Spatial control over near-critical-point operation provides a mechanism that faithfully measure cellular-scale distance by using only molecular-scale interactions.

Introduction

Cellular processes must establish the right operating point in a very large parameter space that allows robust execution of biological function and simultaneously sensitive adaptation to environmental cues. What is the character of this right operating point? How do cells find and maintain it? It is postulated that all living systems operate near the edge of phase transition (1), i.e., near a critical point at which the system is halfway between two phases in its parameter space. This way, the system has the equal probability to operate in either of the two phases with the maximal susceptibility and displays large fluctuations with a diverging correlation length. Thus, operating near such a critical point could allow the system to sensitively and rapidly respond to changes in the environment. Indeed, there are increasing data—ranging from developmental biology to neuroscience—supporting this notion (2, 3, 4, 5). For instance, patterns of gap gene expression in the early Drosophila embryo were reported to exhibit signatures of criticality, wherein the divergence of correlation length between gene expressions was proposed to adapt the spatial patterning to the embryo growth (3). Likewise, evidence suggested that neural systems operate at criticality teetering between stability and chaos that maximizes their information processing capacity (2). However, this evidence is largely statistical inference from experimental data and lack the physical mechanisms that give rise to the near-critical-point behavior. Crucially, it is unclear how cellular processes maintain the robustness of operating near the critical point in the presence of ever-lasting noises (e.g., the fluctuations in gene expression at a single-cell level (6, 7, 8)). From this perspective, we set out to examine the physical mechanism of bacterial DNA segregation with the emphasis on how the operating point of DNA partition machinery is controlled to maximize the partition fidelity. We exploited low-copy-number plasmid partition in the bacteria as the model system by combining theoretical modeling with experimental testing.

Segregating replicated genomes before cell division is essential to ensure faithful genetic inheritance. Despite its simple form, partitioning of low-copy-number plasmids in bacteria is robust with an extremely low error rate (less than 0.1% per generation) (9) and provides a tractable paradigm to understand fundamental principles of genome segregation (10). Most low-copy-number plasmids are actively partitioned—by a conserved tripartite ParABS system—along the nucleoid, a rod-like structure consisting primarily of condensed chromosomal DNA. Although cargo trafficking in vivo typically utilizes cytoskeletal filament or motor-protein-based mechanisms, the ParABS machinery utilizes none of the conventional mechanisms for partitioning (11, 12, 13, 14). How the ParABS system drives genome partitioning has puzzled the field since its first postulation in the replicon theory (15).

The key elements of ParABS system are as follows (10): ParA is an ATPase that binds nonspecifically to DNA in the nucleoid in an ATP-bound dimeric state. ParB is the adaptor protein. It binds specifically at a centromere-like site parS on the plasmid and sequence nonspecifically around parS to form large clusters called partition complexes (PCs). ParB regulates ParA DNA binding by 1) direct interaction that provokes its release from the nucleoid (13), and by 2) stimulating the ATPase activity that convert ParA in the ADP-bound form that do not bind nucleoid DNA (16,17). It is not understood how the chemical energy provided by ATP hydrolysis is harnessed to ensure the PC partition fidelity beside its important implication in separating newly duplicated parS sites (18).

Spatial-temporal features of the ParABS system expose some clues of its inner workings. PCs move around and frequently switch directions over the cell length (11,19, 20, 21, 22, 23). Because the timing of PC replication and segregation is not directly coupled to cell cycle and the nucleoid itself keeps elongating before cell division (24, 25, 26), the replicated PCs can be anywhere along the nucleoid length when they start to split apart (22). Intriguingly, the replicated PCs always first move apart persistently and then position themselves with the separation being approximately half of the cell length (11,19,20,22,27). Although segregating by half of the cell length ensures the partition fidelity by always positioning the replicated PCs in the different cell halves, it precipitates the following questions. First, given that the PCs locally interact with the nucleoid, which elongates in proportion to the cell length (28), the question becomes: how do the PCs have the global “view” of and adapt their separation to the length of the elongating nucleoid and, ultimately, the half of the cell length? Second, what ensures the partition robustness in the presence of ever-lasting noises, e.g., the fluctuations in protein levels? Addressing these questions lay at the heart of one of the fundamental questions in cell biology: how do cells faithfully measure cellular-scale distance by only using molecular-scale interactions?

We previously established the ParA protein gradient-based Brownian ratchet model—a new mechanism of processive cargo transport without resorting to filament or conventional stepping motor proteins (e.g., myosins, kinesins, or dynein) (29,30). With multiple ParA-ParB bonds tethering a parS-coated cargo to a DNA carpet, ParB-stimulated bond dissociation triggers the release of the ParA from the DNA carpet, the randomness of which results in a force imbalance that drags the cargo forward. Critically, the time delay in resetting ParA DNA-binding affinity generates a ParA-depletion zone behind the forward-moving cargo (14,29,31), perpetuating the asymmetry and persistent movement. As such, the ParABS system can work as a Brownian ratchet: the ParB-bound cargo “self-drives” by both creating and following a ParA gradient over the DNA. This protein gradient-based Brownian ratchet model provides a conceptual framework that allowed us to explain—for the first time, to our knowledge, in a coherent manner—the diverse motility patterns of PCs evidenced in vivo (32) and starts to gain support from in vivo experiments (33, 34, 35, 36). However, our effort so far focused on a highly simplified picture, it is unclear 1) whether and how this Brownian ratchet mechanism can adapt the plasmid segregation distance to the length of an elongating nucleoid, and 2) how the PC partition ensures its fidelity against cellular noises.

Here, we show that 1) this ParA-gradient-based Brownian ratcheting of bacterial low-copy-number plasmid partitioning operates near a critical point in vivo, and 2) the spatial controls over the near-critical-point operation allow both sensitive adaptation of partition to the nucleoid length and robust execution of partition to buffer against noises.

Materials and methods

Bacterial strains and plasmids

Escherichia coli K-12 strains are derivatives of DLT1215 (37) and transformed with the plasmids pJYB240 (38), pJYB243 (39), or pJYB249 (38). Cultures were grown at 37°C with aeration in Luria-Bertany (LB) broth (40) containing thymine (10 μg.mL⁻¹) and antibiotics as appropriate: chloramphenicol (10 μg.mL⁻¹) and kanamycin (50 μg.mL⁻¹). For microscopy and plasmid stability assays, cultures were grown at 30°C with aeration in M9 minimal medium supplemented with 0.4% glycerol, 1 mM magnesium sulfate (MgSO₄), 0.1 mM calcium chloride (CaCl₂), 1 μg.mL⁻¹ thiamine, 20 μg.mL⁻¹ leucine, and 40 μg.mL⁻¹ thymine supplemented or not with 0.2% casamino acids. The generation times in M9 Glycerol (M9Gly) with or without 0.2% casamino acids are 45 or 242 min, respectively.

Plasmid stability assays for plasmid-copy-number determination

Experiments were started from colonies of E. coli cells carrying the plasmids under test. Overnight cultures in M9Gly, with or without casamino acids, containing chloramphenicol were diluted 250-fold into the same medium and grown to A₆₀₀ = 0.25. Samples were then diluted serially into fresh medium without chloramphenicol and were processed as described previously (41). To determine the fraction of cells that retained the plasmid, samples were taken at the beginning and after 5, 10, 20, and 30 generations or after 25 generations for growth in the absence or presence of casamino acids, respectively. The loss frequency (f) per generation is calculated using the following formula: f = 1 − (cell carrying the F-plasmid/total cell)^1/g, where g is the generation number, as previously described (39).

The plasmid copy number at cell division (n) is calculated from the probability of having one plasmid-free cell at cell division as a function of the copy number, P₀ = 2^{(1 − n)}, from which we obtained the theoretical frequency of random loss per generation. The copy number per cell is ln2 (naperian logarithm) time n (19).

Epifluorescence microscopy and analysis

Overnight cultures were inoculated into fresh media at a concentration permitting at least 10 generations of exponential growth and incubated at 30°C to an optical density (OD_{600 nm}) of ∼0.25. Samples (0.7 μL) were deposited to the surface of a layer of 1% agarose buffered in M9 solution, as described (42). The cells were imaged at 30°C using an Eclipse Ti-E/B wide field epifluorescence microscope (Nikon, Tokyo, Japan) with a phase contrast objective (CFI Plan Apochromat LBDA 100× oil NA1.45; Nikon) and a Semrock filter YFP (Excitation: 500BP24; Dichroic mirror: 520; Emission: 542BP27; IDEX Health & Science, Rochester, NY) or fluorescein isothiocyanate (Ex: 482BP35; DM: 506; Em: 536BP40). Images were taken using an Andor Neo SCC-02124 camera (Oxford Instruments, Abingdon, UK) with illumination at 80% from a SpectraX source Led (Lumencor, Beaverton, OR) and exposure times of 0.2–1 s. Nis Elements AR software (Nikon) was used for image capture and editing. Image analyses were performed using ImageJ plugins. The average foci number per cell was measured using the “Cell Counter” plugins. Tracking the PC and nucleoid length was done in the MicrobeJ plugin (43,44). It involves finding the cells of interest and tuning the parameters in MicrobeJ to get the data. Specifically, for each identified cell, we recorded the length of the cell, integrated fluorescence of ParA, and the peak positions of ParB fluorescence intensity, which were then used to represent the positions of the PCs. We also recorded the fluorescence profile of the nucleoid along the long axis of the cell, from which the nucleoid length of the cell was derived using the full-width-half-height approach. For ParA-PC colocalization analysis, we used a self-developed (Centre de Biologie Intégrative) Python-based tool (Distance2MaxProfile: https://imaprocess.pythonanywhere.com/Analymage/detail_projet/20/).

Results

Model development

Going beyond our previous modeling efforts (29,30,32), we built the in vivo model—to specifically capture how ParA-mediated PC partition responds to the dynamical changes—associated with nucleoid elongation during cell growth. The qualitative model features are described below (Fig. 1), followed by the quantitative mathematical formulation.

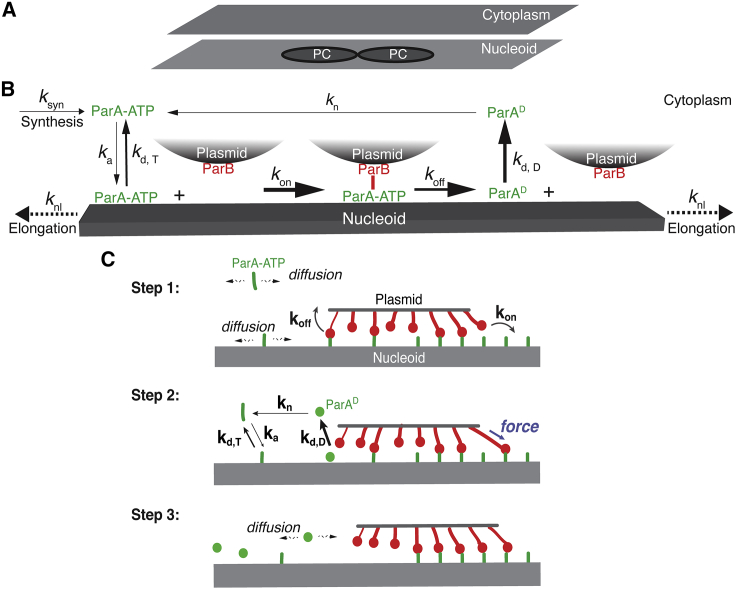
Figure 1.

Model description. (A) Model setup. The model describes each PC as a circular disk and the nucleoid and the cytoplasm as the rectangular domains that share the same dimensions. (B) Biochemical scheme of ParABS system. Briefly, ParB molecules are fixed on the PCs, whereas the ParA·ATP molecules exchange between the cytoplasm and nucleoid surface with the kinetic rates of k_a and k_{d, T}, respectively. The PC-bound ParB will rapidly bind to the local nucleoid-bound ParA·ATP at the rate of k_on, followed by a fast dissociation at the rate of k_off. The dissociation of ParA-ParB bond drives the nucleoid-bound ParA into a distinctive state, ParA^D, which rapidly turns over into the cytoplasm at the rate of k_{d, D}. At a very slow rate (k_n), the cytoplasmic ParA^D will revert into the ParA·ATP that can rebind to the nucleoid. Last, to capture the essential effects of cell growth on the ParABS system, the nucleoid keeps elongating at the rate of k_nl, and ParA·ATP molecules are synthesized at the rate of k_syn. (C) Mechanochemical coupling of ParA-ParB bond dynamics underlies ParA gradient-based Brownian ratcheting. The Brownian ratcheting consists of three stochastic steps. Step 1: although some of the ParA-ParB bonds are dissociating, others are forming. The free ParA molecules diffuse along the nucleoid and in the cytoplasm, whereas all the ParB molecules are fixed the PC. Step 2: thermal fluctuation prestretches the forming ParA-ParB bond that pulls the PC forward. At the back of the PC, the ParA-ParB bond dissociation converts the ParA·ATP into a distinctive state (ParA^D) with a rapid turnover into the cytoplasm. Because of the slow ParA^D-to-ParA·ATP conversion, there is a time delay to replenish the local ParA·ATP on the nucleoid. This results in a ParA depletion trailing behind the PC. Step 3: the initial movement of PC creates an asymmetric local ParA concentration gradient (higher at the front, lower at the back). This breaks symmetry and drives the directed and persistent PC movement.

Our model begins with two PCs arranged side-by-side to mimic the replicated PCs and examines the subsequent partition dynamics. As a starting point of the modeling, we depict each PC as a circular disk of ∼100 nm in radius (34,39), the nucleoid as a flat rectangle, and the cytoplasm as a two-dimensional (2D) domain of the same dimension as the nucleoid (Fig. 1 A). This is an approximation based on the following considerations. In bacteria such as E. coli, the cytoplasm mainly occupies the space of 100–200 nm wide between the nucleoid and cell membrane. Because the free ParAs diffuse rapidly in cytoplasm (∼3 μm²/s) (45), it only takes ParA ∼1–10 ms to diffuse across this short distance. Therefore, on the timescale considered (approximate seconds to minutes), the concentration profile of cytosolic ParA is uniform in the direction vertical to the nucleoid surface, which allows us to simplify the cytoplasm as a flat 2D domain, which serves as a reservoir of free ParAs. Thus, the 2D domain of cytoplasm in the model represents the effective interface of exchanging free ParAs between the cytoplasm and the nucleoid, whose dimensions was set to be the same.

To capture the dynamic changes associated with nucleoid elongation and cell growth, the model describes two effects. First, with their widths fixed at 1.0 μm, the nucleoid and cytosolic domains elongate at a constant rate (∼6–18 nm/min) measured by our experiments (Fig. 1 B), in which we imaged HU-mCherry-tagged nucleoid over time in E. coli growing in minimal growth medium. The initial nucleoid length is set to be 2 μm, if not otherwise mentioned. Second, the model depicts that concurrent with nucleoid elongation, new ParA molecules are generated to keep ParA concentration constant. This captures the essence of observed autoregulation of ParA expression (46,47) and Western blot measurements showing the constant ParA concentration on population level (39).

Accordingly, the model depicts the moving boundary lengthwise and imposes hard-wall boundary condition for ParA and ParB at all edges of the simulation domain. Although ParB only localizes to the PCs (39), ParA can exchange between the nucleoid and the cytoplasm in accordance with the reaction-diffusion scheme (Fig. 1, B and C). Specifically, ParA·ATP binds to vacant, unoccupied locations of the nucleoid at a basal rate (13,48) and can transiently unbind and rebind to adjacent vacant sites via lateral diffusion (45). Upon binding to plasmid-bound ParB, the ParA·ATP no longer diffuses but forms a ParA·ATP-ParB bond, tethering the PC to the nucleoid through the nucleoid-ParA·ATP-ParB-plasmid linkage. For simplicity, we refer to the entire linkage as the ParA-ParB bond (Fig. 1 C).

The ParA-ParB bond formation and the subsequent deformation, similar to deforming a spring, generates a restoring force on the PC (Fig. 1 C). The vector sum of many individual ParA-ParB bonds across the PC collectively generates a net force that displaces the PC. The movement of PC in turn changes the bond configurations. When random events (e.g., PC diffusion and stochastic ParA-ParB bond dynamics) break symmetry, the PC moves forward with the ParA-ParB bonds broken at its back (Step 1 in Fig. 1 C).

We define the resulting disengaged ParA to be in a distinctive state, ParA^D (Fig. 1 B). Although the model does not specify whether ParA^D corresponds to an ATP-bound or ADP-bound state, it recapitulates two key aspects of disengaged ParA. First, ParA^D dissociates from the nucleoid faster than the basal turnover rate of ParA·ATP, which reflects the known effect of ParB-mediated stimulation on ParA release from the nucleoid (13,48). Second, once ParA^D dissociates into the cytoplasm, it slowly reverts to the ATP-bound state competent for DNA binding (13,48). This time delay results in a ParA-depletion zone trailing behind the moving PC, which subsequently can be refilled by cytosolic and nucleoid-associated ParA·ATP.

As the PC moves forward, the ParBs on the leading edge of the PC continue to establish new bonds with ParA·ATP on unexplored regions of the nucleoid, where the ParA·ATP concentration is higher (Step 2 in Fig. 1 C). PC movement therefore maintains the asymmetric ParA concentration gradient that in turn supports further forward movement (Step 3 in Fig. 1 C), resulting in a directed and persistent movement. Conceptually, our model is a 2D burnt-bridge Brownian ratchet model (49,50) in which mechanical actions of the multiple bonds not only facilitate the forward cargo movement but collectively provide tethering that quenches the cargo lateral diffusion. This drives the directed and persistent movement.

To quantitatively elucidate the proposed mechanism, we numerically computed our model with the parameters capturing in vivo conditions (Table S1). While increasing over time, the bulk-part number of ParA molecules in the nominal case was set to be approximately several thousands in the model, in accordance with the measurements (51,52). The nucleoid-bound ParA·ATPs were initially in chemical equilibrium with their cytosolic counterparts and were randomly distributed on the nucleoid, which is modeled as a rectangle domain with 5 × 5 nm square lattices of ParA·ATP-binding sites. ParBs were permanently distributed with a uniform density of ∼0.013 ParB dimers/nm² over the PC, quantitatively reflecting the measured high propensity of ParB to spreading around the parS site on the plasmid (39,53, 54, 55). We modeled each ParA-ParB bond as an elastic spring. The vertical distance between the nucleoid and the PC was fixed at the equilibrium length of ParA-ParB bond (L_e). The stochastic reactions involving PC-bound ParB and nucleoid-bound and cytosolic ParAs are simulated with the kinetic Monte Carlo scheme according to the reaction scheme (Fig. 1 B).

The simulation workflow is as follows. At each simulation time step, each ParB can interact with available ParA·ATP within a distance L_a, and bind only one ParA at a time with a rate of k_on (Step 1 in Fig. 1 C). The probability of binding is proportional to $e^{-\left(1/2\right)\left(K_{\text{S}}{\left(L-L_{\text{e}}\right)}^2/k_{B}T\right)}$ for L_a > L > L_e; otherwise, it is 0. K_S is the spring constant of the bond, L denotes the separation between ParB and ParA·ATP. If this bond forms, L is the instantaneous bond length, and$\left(1/2\right)K_{\text{S}}{\left(L-L_{\text{e}}\right)}^2$ represents the associated elastic energy penalty. Importantly, given the model parameters, this energy penalty is less than the thermal energy, k_BT. Consequently, thermal energy is sufficient to prestretch the newly formed bond, which in turn provides an elastic force $\overrightarrow{f}=K_S\left(L–L_{\text{e}}\right)\overrightarrow{n}$ (Step 2 in Fig. 1 C), where $\overrightarrow{n}$ is the unit vector of the ParA-ParB bond orientation along the tangent direction of nucleoid surface. In the simulation, we calculate the vector sum of the elastic forces from all the ParA-ParB bonds over the PC. This net force together with the PC diffusion drives PC motion for one simulation step (Step 3 in Fig. 1 C), following the Langevin-like dynamics: $\left(k_{B}T/D_p\right)\left(d{\overrightarrow{X}}_p/dt\right)=\sum _i{\overrightarrow{f}}_i+\overrightarrow{\zeta }\left(t\right)$. Here, ${\overrightarrow{X}}_p$ is the centroid position of the PC, D_p is the diffusion constant of the PC, ${\overrightarrow{f}}_i$ is the elastic force from the ith ParA-ParB bond on the PC, and $\overrightarrow{\zeta }\left(t\right)$ represents random force resulting from thermal motion of the solvent molecules with $\overrightarrow{\zeta }\left(t_1\right)\overrightarrow{\zeta }\left(t_2\right)$ = $\left(2k_{B}T/D_p\right)\delta \left(t_1–t_2\right)$, and δ(t₁ − t₂) is the Dirac δ-function.

In the next time step, the lengths and orientations of the ParA-ParB bonds are updated by the PC motion, from which the dissociation rates of the existing ParA-ParB bonds are calculated: when the bond extension exceeds the maximum, L_m (i.e., (L − L_e) > L_m)), the bond breaks instantaneously; otherwise, the dissociation rate is k_off. This dissociation reaction is next implemented in the stochastic simulation. The resulting ParA^D will be released into cytoplasm and convert at a slow rate of k_n $\left(k_{\mathrm{n}}\ll k_{\mathrm{off}}\right)$ to ParA·ATP. Additionally, new ParA·ATPs are generated in cytosol concurrently with the elongation of nucleoid and cytoplasmic domains at the rate of k_nl. These ParA·ATPs can bind to the nucleoid with a rate of k_a.

Meanwhile, PC movement from the previous time step permits PC-bound ParBs to explore new territory and form bonds with available ParA·ATPs, and vacancies on the nucleoid can be refilled by ParA·ATP rebinding from the cytosol or diffusing from adjacent sites on the nucleoid. These ParA·ATPs can establish new bonds with ParB if the PC is nearby. We then update the net force from all the ParA-ParB bonds, including changes in existing bonds and newly formed bonds. The movement of the cargo is then calculated as in the previous time step. We repeat these steps throughout the simulation over time. The simulation time step was chosen to be fixed at 10⁻⁴ s, which conforms to the limitation of Langevin dynamics and kinetic Monte Carlo simulations, yields consistent simulation results, and is cost effective. The model testing on the choice of time step was conducted in our previous work (29).

ParABS-mediated PC partition operates near a critical point

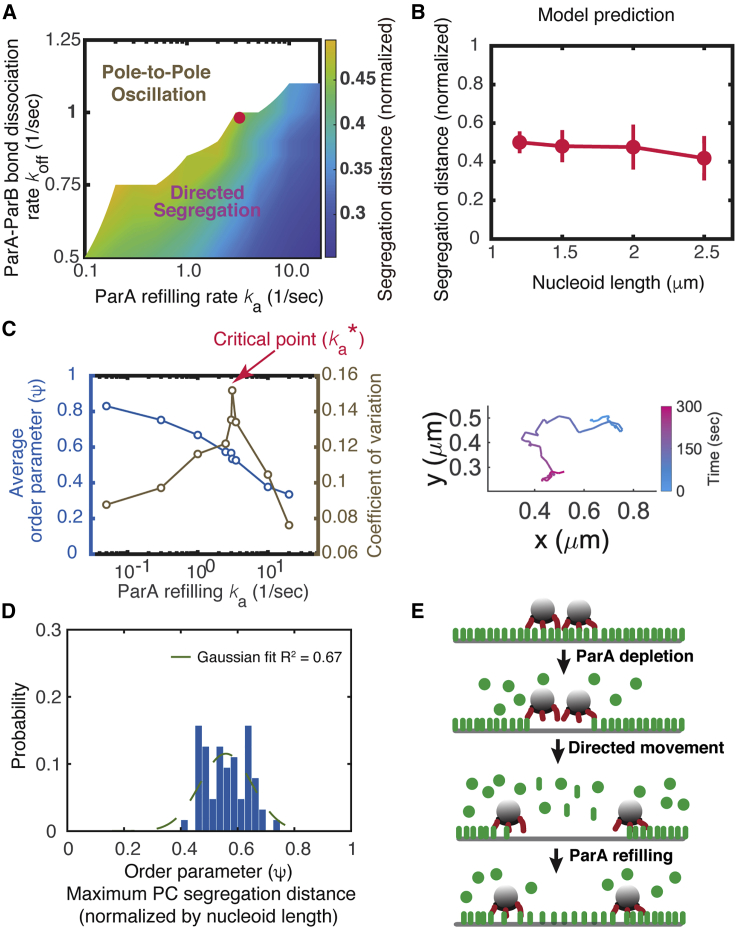
Exploiting agent-based stochastic simulations of our model allows us to calculate the phase diagram of PC segregation motility with an elongating nucleoid (Fig. 2 A). It is characterized by two key control parameters, i.e., the ParA-ParB bond dissociation rate, k_off, and the ParA-nucleoid binding rate, k_a. In line with our previous work (32), Fig. 2 A shows that the replicated PCs display different motility patterns in different parameter regimes: 1) directed segregation, in which the PCs persistently move apart for a while, followed by positioning with local excursions, and 2) pole-to-pole oscillation, in which the PCs move back and forth along the nucleoid length between the two poles (Fig. S1). We note that for each point in the phase diagram, we ran stochastic simulations for ≥36 trajectories of 10-min dynamical evolution of the system, starting from the same initial condition and parameter set. The 10-min simulation time was chosen because 1) it is the same duration by which we extracted the PC segregation data in our experiment (see below), and 2) the simulated segregation distance at the end of the simulation has already reached the steady state so that our analysis is expected to hold up for a longer simulation time (Fig. S2). Unless otherwise mentioned, the segregation distance refers to the instantaneous distance between the two PCs at 10 min after they started to segregate. We used this PC segregation distance as a proxy to infer the partition fidelity; as suggested by our previous work (32), the more the PC segregation deviates from the half length of nucleoid, the more likely will the two PCs end up in the same half of the dividing cell, compromising the partition fidelity.

Figure 2.

Predicted feature of near-critical-point operation of ParA-mediated PC partition. (A) Predicted phase diagram of PC motility controlled by (k_a and k_off). Here, the ParA concentration is kept constant as ~3500 molecules per micron of nucleoid length, and other parameters are kept fixed (see Table S1 for details). In our phase diagram calculation, k_off and k_a were varied by changing their absolute values, i.e., k_off = 0.5/s, 0.75/s, 0.85/s, 0.9/s, 1.0/s, etc., and k_a = 0.1/s, 0.2/s, 0.5/s, 1.0/s, 2.0/s, 2.5/s, 3.0/s, 4.0/s, etc. The log scale of k_a reflects the fact that the dependence of model result on k_a is, in general, less sensitive than k_off. The relative smooth phase boundary in the phase diagram reflects a balance between the quality of the figure and computational load. The red dot marks the critical point, which is further defined in (B). (B) Segregation distance adapts to 1/2 of the nucleoid length at the critical point in the parameter space. (C) Predicted characteristics of near-critical-point operation. Left: average order parameter ψ (i.e., averaged maximal segregation distance between PCs normalized by the nucleoid length over ≥36 trajectories of 10-min evolution) increases continuously as the ParA refilling rate decreases, whereas the variance of the order parameter peaks around the critical point $\left(k_{\mathrm{a}}^{\ast }\right)$. Note that the order parameter evolves similarly as a function of the ParA-ParB dissociation rate, k_off. Right: corresponding representative simulation trajectory of PC excursion with the parameter set at this critical point. (D) Predicted statistical distribution of order parameter ψ at the critical point (n = 64). (E) Schematic illustration of the physical nature of near-critical-point partitioning. For (A) and (B), the segregation distance refers to the instantaneous distance between the two PCs at 10 min after they started to segregate.

Our calculation suggested that the ParA-gradient-based Brownian ratcheting could allow the replicated PCs to undergo directed segregation and adapt their segregation distance at ∼0.5 of the increasing nucleoid length (Fig. 2 B). This ensures the two PCs to always end up in the different cell halves, maximizing the partition fidelity. Importantly, this partition fidelity requires the ParABS system to operate in a very special parameter regime (e.g., the red dot denoted in Fig. 2 A), which represents the transition of PC motility from directed segregation to pole-to-pole oscillation.

Next, we more rigorously formulated the PC partition problem in the framework of dynamical phase transition. We defined the order parameter (ψ)—which distinguishes different states of PC segregation motility—as the maximal segregation distance between the two PCs normalized by the nucleoid length within the 10-min duration. Accordingly, the average order parameter in Fig. 2 C is 0.56 at the transition point between directed segregation and pole-to-pole oscillation. Deviating away from this transition regime, the PCs either undergoes reduced segregation with limited excursion (e.g., the average order parameter ∼0.35 in Fig. S1 A) or oscillate from pole to pole (e.g., the average order parameter ∼0.85 in Fig. S1 B). Either way, the variations of their order parameter distribution are very narrow (Fig. S1, A and B). In contrast, at this particular parameter set, the PCs are predicted to undergo directed segregation but with extensive excursions (the right panel in Fig. 2 C). More importantly, the corresponding statistical distribution of ψ is very broad and non-Gaussian (Fig. 2 D), and the correlation length between the PC movements peaks (∼420 nm) (Fig. S3 A). Together, these general features are akin to the signatures of critical dynamics (56). We note that, technically, the concept of critical point in statistical physics only applies to infinite-large systems. With our finite-size system here, we used the term of critical point in a broader sense. With this perspective, the PC partition is predicted to operate at a critical point.

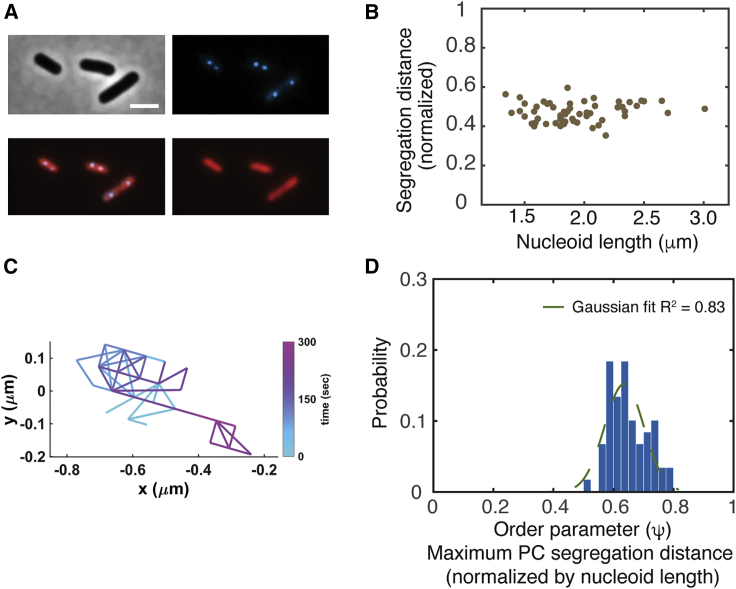
To test the prediction, we conducted time-lapse epifluorescence microscopy experiments using the well-established F-plasmid partition system in E. coli (10,38). The F plasmid is present at approximately two copies per chromosome per cell (57). We used functional fluorescent fusion proteins ParB_F-mTq2 (38) and HU-mCherry to label the mini-F plasmid and the nucleoid, respectively (Fig. 3 A). E. coli cells were grown in two different conditions, giving rise to two generation times of 45 and 242 min with an average mini-F copy number per cell of 3.6 and 2.8, respectively (see Table 1). In these two conditions, we found that cells displayed 3.1 and 2.2 fluorescent foci per cell, respectively, indicating that during most of the cell cycle, plasmids are not clustered.

Figure 3.

Near-critical-point operation of ParA-mediated PC partition. (A) Experimental setup of two-color live-cell imaging of F plasmids in wild-type E. coli. Cells are observed in phase contrast (top left) and in the blue (top right) and red (bottom right) channels for fluorescence microcopy to observe ParB_F-mTq2 or ParA_F-mVenus, respectively. Shown is the overlay of blue and red channel (bottom left). Scale bars, 2 μm. (B) Experimental data demonstrate that PC segregation distance adapts to 1/2 of the nucleoid lengths (n = 58). Data from cells grown at 30°C in MGly with or without casamino acids were represented on the same graph because they display the same trend. The segregation distance refers to the instantaneous distance between the two PCs at 10 min after they started to segregate. (C) A representative saltatory trajectory of PC excursion. (D) Non-Gaussian distribution of order parameter ψ (i.e., the maximal PC segregation distance of PC normalized by the nucleoid length within 10-min duration) (n = 60).

Table 1.

High fidelity of F-plasmid partition in E. coli

	Loss ratea		Copy numberb
Generation timec T (min)	pJYB249	pDAG115	At cell division (n)	Per cell (cn)	Average foci number per celld (fn)	Clusterization ratioe
45	<0.001	0.058 ± 0.1	5.16	3.57	3.13	0.12
242	0.001	0.128 ± 0.002	4.06	2.81	2.18	0.22

The level of plasmid F clusterization is low in fast and slow E. coli growing conditions. The clusterization level is estimated by the difference between the average number of foci and the average number of plasmids per cell.

^aThe loss rate of the plasmids used in the microscopy assay (pJYB249) and in the determination of the plasmid copy number (pDAG115) were obtained from at least three independent measurements, except for pJYB249 grown in the presence of CSA performed in duplicate. pDAG115 is a partition defective mini-F plasmid (41) that allows for estimating the copy number at cell division (see Materials and methods).

^bThe plasmid copy number per cell is ln2 times the copy number at cell division n (19).

^cThe generation time (T) was estimated from measurements of culture optical densities at 600 nm.

^dThe number of foci per cell was determined by epifluorescence microscopy.

^eThe clusterization ratio is determined by the following formula: (cn − fn)/cn.

Then, we measured the nucleoid size along the long cell axis and the distance between two PCs in two-foci cells, in which we imaged the PC partitioning process for 10 min after the two PCs started to segregate. Our data showed that the PC segregation distance (at the 10-min time point) adapts to half of the nucleoid length independently of the growth condition as the nucleoid increased from 1.2 to 3.0 microns (Fig. 3 B). Critically, the PCs indeed undergo extensive excursion (Fig. 3 C). The order parameter (ψ)—defined as the maximal segregation distance normalized by the nucleoid length during the 10 min—displays a broad distribution with the average of 0.65 (Fig. 3 D). This is akin to the predicted case at the critical point (Fig. 2, C and D). Additionally, the correlation length of the PC movements is measured to be ∼500 nm (Fig. S3 B), similar to the predicted value (∼420 nm) (Fig. S3 A). In contrast, our data are distinct from the predicted cases that deviate away from the critical point (Fig. S1), in which not only the distribution of order parameter ψ is much narrower, but their averages are either too small (∼0.35) or too large (∼0.85). To more rigorously gauge whether and how our results differ from a Gaussian distribution, we resorted to two statistical measures. First, we calculated the excess kurtosis value, which is 0 for the perfect Gaussian and −1.2 for the uniform distributions. The excess kurtosis value is −0.75 for our experimental data and −1.0 for the model result (Figs. 2 D and 3 D, respectively). Second, we calculated the χ²-value between the cumulative distribution functions of our data and Gaussian distribution. The χ²-value is 0 for the perfect Gaussian: the larger it is, the more the result deviates from Gaussian distributions. With this measure, the χ²-value is 8.9 for our experimental data and 6.6 for our model result (Figs. 2 D and 3 D, respectively). Together, the order parameter of our PC segregation data has the average of 0.65 with a broad distribution that saliently deviates from a Gaussian distribution, supporting the prediction that the PC partition operates at a critical point (Fig. 2 D).

We interpret the physical nature of this near-critical-point PC partition as follows (Fig. 2 E): replicated PCs undergoes directed segregation because of their initial side-by-side arrangement. As they deplete the ParA underneath from the nucleoid, the local nucleoid-bound ParA concentration field becomes asymmetric for each PC, which sets the directed movement. As the PCs move apart, each PC associates with a ParA-depletion zone, like “a sphere of influence.” It takes some time for the depleted ParAs to rebind the nucleoid, which eventually re-establish the symmetric ParA distribution surrounding each of the PCs, thus positioning the PCs. As such, the ParA-ParB bond dissociation confers the PC directed segregation, whereas ParA refilling event hinders it. The balance between these two activities defines the critical point. At this critical point, the PC’s ParA-depletion zones (or spheres of influence) overlap with a linear dimension comparable with the nucleoid length, the essence of which is qualitatively captured by the long correlation length between PC movements (Fig. S3). This allows the PCs to feel not only the presence of each other but the boundary of the elongating nucleoid.

Together, our results suggest that although the ParA-ParB interaction is local, operation of ParA gradient-based Brownian ratchet mechanism—near a critical point—can provide the PCs a global view, allowing sensitive adaptation of their segregation distance to the increasing nucleoid length. That is, the near-critical-point operation allows ParA-mediated partition machinery to measure the cellular distance by molecular interactions.

ParABS-mediated PC partition is robust against cell-to-cell ParA level variations

Given the sensitive nature of partitioning near a critical point, the next question is as follows: how does the ParABS-mediated partition manage to buffer against fluctuations inside cells, a central topic of control for any biological systems? We are attracted to the view that the control parameters of a cell are hard-wired genetically—shaped by the long evolutionary process—to a critical point that is biologically most advantageous for survival and proliferation (58). In light of this, genome partition is a subprocess enslaved to the entire cell dynamics; the robustness of genome partition specifically refers to how well it copes with the uncertainties originated from outside of the cell or from other parts of the intracellular dynamics.

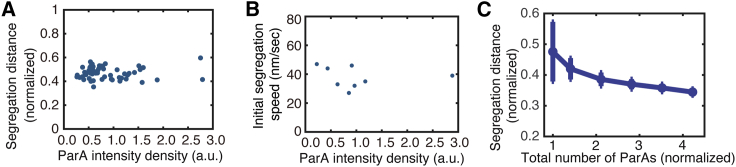
To begin to characterize the cellular fluctuations relevant to ParABS-mediated partition, we measured the intracellular ParA concentration by coupling ParA to mVenus fluorescent peptide (ParA_F-mVenus) in cells, allowing the detection of the nucleoid length and PC positioning (as above). The data showed that [ParA] varies from cell to cell over 10-fold in wild-type E. coli (Fig. 4 A). Despite the large variations of [ParA], the PC partition still adapts the separation distance to ∼0.5 of various nucleoid lengths (Fig. 4 A), ensuring the high partition fidelity observed with a plasmid loss rate ≤0.1% (see Table 1).

Figure 4.

Robustness of PC partition against variations of ParA level. (A) Experimental data showing the PC segregation distance normalized by the nucleoid length is insensitive to the large cell-to-cell ParA level fluctuations (n = 58). (B) Initial segregation speed is insensitive to the ParA level. (C) This model cannot buffer the near-critical-point partition against ParA level fluctuations. For (A) and (C), the segregation distance refers to the instantaneous distance between the two PCs at 10 min after they started to segregate.

To understand the robustness measure adopted by the PC partition system, we reasoned that both the ParA-ParB dissociation rate, k_off, and the ParA-nucleoid binding rate, k_a, might change with the [ParA]. This way, the partition could still operate near the critical point when [ParA] varies, i.e., rather than at a fixed point in the parameter space in Fig. 2 A, the partition operates along the transition line between the states of pole-to-pole oscillation and directed segregation. To explore this possibility, we tried to measure the ParA_F-ParB_F dissociation rate k_off by monitoring the PC foci segregation rates. According to our model, the PC segregation speed is proportional to the ParA_F-ParB_F bond dissociation rate (32). Our data show that the PC segregation speed, although varying somewhat, is insensitive to the [ParA] (Fig. 4 B).

As demonstrated by our previous modeling result (32), the speed of directed segregation equals to the ParA-ParB bond dissociation rate (k_off) times a constant characteristic of individual ParA-ParB bond length. Given the experimental data in Fig. 4 B showing that the segregation speed is insensitive to the variation in ParA intensity, this suggests that the ParA-ParB bond dissociation rate (k_off) is insensitive to the variation in ParA intensity. We reasoned that because the partition machinery operates at a critical point in the parameter space (k_a^∗ and k_off^∗), as demonstrated in Figs. 2 and 3, the fixed k_off^∗ means that the k_a^∗ is insensitive to the [ParA] variation in our system. We are therefore attracted to the idea that both k_a^∗ and k_off^∗ remain insensitive to the [ParA] variation. Following this line of argument, our simulation showed that with the fixed k_a^∗ and k_off^∗, the segregation distance in the model decreases sharply as [ParA] increases (Fig. 4 C), inconsistent with the observations (Fig. 4 B). This discrepancy suggests the partition robustness entails additional factor(s) and thus precipitates the question of what buffers the robustness of PC segregation against [ParA] variations.

PC-mediated ParA localization underlies partition robustness against bulk [ParA] variations

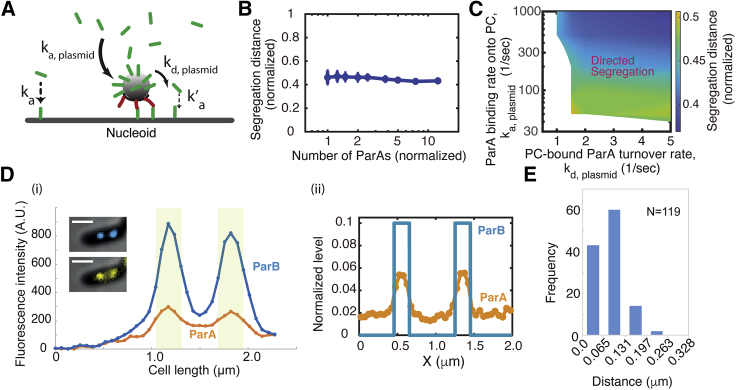
Based on in vitro and in vivo data suggesting that ParA could bind to the plasmid through its interaction with ParB and nonspecific DNA (11,13,16), our leading hypothesis is that the intracellular ParA could localize around the PC and create a local environment that buffers the partitioning against the bulk [ParA] variation (Fig. 5 A). To test the hypothesis, we first extended the in vivo model to incorporate this PC-mediated ParA localization effect. We assumed the cytosolic ParA to have a high binding affinity to PC but with a transient lifetime before turning over into cytoplasm (Fig. 5 A), characterized by the k_{a, plasmid} and k_{d, plasmid} rates. Because of the finite size of the PC, the model imposed an upper limit in the number of ParA molecules, approximately hundreds that simultaneously localize to the PC. This saturation level is based on the in vitro measurements (13,31). We further assumed that right after releasing from the PC, the ParA has a reduced propensity to bind to the nucleoid. This last assumption is based on the observation that the interaction with ParB not only speeds up the dissociation of ParA from nucleoid but inhibits the ParA-nucleoid binding (13). Below, we will present the typical model result. Additional model investigations on how the PC-mediated ParA localization effects influence the fidelity of PC partition are presented in Fig. S4, which shows that the essential features in Fig. 5 persists in a broad range of parameter space.

Figure 5.

PC localization of ParA explains the partition robustness. (A) Model scheme of PC-mediated ParA localization. The red rod represents the PC-bound ParB, and green rod the ParA. The arrows denote the conversion reaction, wherein the thicker the arrow is, the faster is the reaction. The dotted arrow represents the relatively slow reaction that a cytosolic ParA bind to nucleoid. (B) The amended model can ensure the fidelity of near-critical-point partition against the ParA level fluctuations. Note, the same parameter set here also simultaneously ensures the sensitive adaptation of segregation distance to nucleoid lengths (see Fig. S5C). (C) Predicted phase diagram of the dependence of PC partition fidelity on the ParA localization effects. For each point in the phase diagram, we ran stochastic simulations for ≥36 trajectories of the 10-min dynamical evolution of the system, starting from the same initial condition and parameter set. The segregation distance reports the average value of ≥36 trajectories at the end of the simulation. (D) Representative spatial profiles of ParA and PC along the cell length. (i) Live-cell experimental result. Line scan analysis of the fluorescence intensities in arbitrary units along cell length. Blue and orange lines correspond to the blue (ParB_F-mTq2) and yellow (ParA_F-mVenus) channels, respectively. The corresponding cell images is displayed in the graph. Scale bars, 1 μm. The gray area corresponds to four pixels (262 nm) around the PC peak. (ii) Model result. (E) Histogram of PC-ParA colocalization. For (B) and (C), the segregation distance refers to the instantaneous distance between the two PCs at 10 min after they started to segregate.

Equipped with this ParA localization effect, simulating this integrated mathematical model shows that it preserves the key features of near-critical-point operation (Fig. S5, A and B) and especially the sensitive adaptation of PC segregation distance to the nucleoid lengths (Fig. S5 C). More importantly, these PC-localization effects of ParA could simultaneously explain the robustness of partitioning evidenced in E. coli. (Fig. 4 A). That is, the segregation of the replicated PCs by the half of the nucleoid length remains largely insensitive to the [ParA] variations (Figs. 5 B and S5 C). Such a buffering effect entails an appropriate ParA accumulation around the PC (Fig. 5 C). When the on rate (k_{a, plasmid}) is too slow, the PC not only depletes the ParA from underneath but cannot supply enough ParA to refill the depletion zone underneath so that the PC becomes diffusive (the lower portion of Fig. 5 C). When the on rate is too fast and the off rate is too slow, the PC will accumulate too many ParAs so that the nucleoid-bound ParA will become very sparse, likewise favoring diffusive movement (the upper left corner of Fig. 5 C). However, as the off rate increases while keeping the on rate very fast, the PC will funnel the cytoplasmic ParA to the local nucleoid at very high concentration. This significantly increases the overall ParA binding to nucleoid, immobilizing the PCs (the upper right corner of Fig. 5 C). In these extreme limits, the partition system loses its robustness of adapting the PC segregation distance to the half of an elongating nucleoid (Fig. 5 C). To ensure the PC partition fidelity, the ParA thus is expected to localize around the PCs with only severalfold accumulation at its peak concentration.

To begin to test this prediction, we resorted to live-cell imaging to discern whether and how ParA accumulates around the PC. To better resolve the subcellular pattern, we sought the experimental conditions that have a low amount of ParA without perturbing other key factors of the system. We took the advantage of our observation that in wild-type cells, ParA distributes asymmetrically between the two daughter cells at cell division (Fig. S6 A), which not only underlies the large cell-to-cell variation of [ParA] (Fig. 4 A) but presents a natural testing ground of our model. We thus focused our analyses on the newborn cells that have inherited a low amount of ParA_F-mVenus (Fig. S6 A), which allows for a better detection of localized signals. In these cells with low intracellular amount of ParA, we also imaged the PC locations with ParB_F-mTq2 that form intense foci. We measured the peak intensity along the cell length for both ParA and ParB by applying a line scan analysis. Although ParA-mVenus displays faint foci, they appeared very close to PCs; importantly, they did not result from cross-fluorescence imaging (Fig. S6 B). Fig. 5 Di presents a representative measurement, and Fig. S6 C provides more detailed analysis. Briefly, in the 58 cells analyzed, we observed that the vast majority of them (41 cells) display the same number of ParA and ParB foci, 14 cells display one more ParA focus than ParB, and three cells have one more ParB focus than ParA. However, we could not accurately measure the ParA intensity accumulation around PC because of 1) the cell-to-cell variation in [ParA], and 2) the depletion of ParA provoked by ParB. Nevertheless, the observation of discrete ParA patches indicates that ParA accumulates several-fold compared with the intracellular level in the close vicinity of PCs, consistent with our predictions (Fig. 5 Dii). To further quantify the degree of colocalization of the ParA and ParB foci, we measured the distance between the peak intensities for each pair of ParA and ParB foci (n = 119; Fig. 5 E). We found that for 98% of the pairs, the ParA and ParB peak intensities are within two pixels (131 nm). Given the 200–250-nm resolution of epifluorescence microscopy due to the light diffraction limit, our data show that ParA and ParB foci are highly colocalized, providing strong support to the predicted PC-ParA colocalization. Importantly, regardless of the ParA levels (Figs. 4 and S6), the corresponding PC segregation distance always adapts to approximately half of the nucleoid length (Fig. 3 A) with a very low error rate of the partitioning (<0.1%) (see Table 1). Combining our model and experimental data, we suggest that PC-mediated ParA localization underlies the fidelity of PC partitioning against [ParA] variations.

Discussion

In this study, we provided direct evidence—with a mechanistic underpinning—that the partitioning of low-copy-number plasmids operates near a critical point. The near-critical-point operation allows the partition machinery to gauge the size of the entire nucleoid and, accordingly, adapt the plasmid segregation distance to the half length of the elongating nucleoid (Fig. 3). Segregating by half of the nucleoid length renders that each cell half always inherits at least one PC, ensuring the partition fidelity, which is also observed in other ParABS systems (e.g., (59)). We further provided the data suggesting that the PC localizes cytoplasmic ParA to its neighborhood. This spatial control creates a local environment that buffers the near-critical-point partition against the fluctuations in bulk [ParA] (Fig. 5), which allows the cell to manage the dichotomy of sensitive adaptation and robust execution of low-copy-number plasmid partitioning. This way, each PC defines its own sphere of power that allows the PC to “self-drive” by generating the path ahead and erasing the trail behind.

This model predicts ParA-PC-localization effects by only focusing on the simplest biochemical scheme. Nonetheless, we indeed observed the ParA-PC localization when the ParA level is low in wild-type cells (Fig. 5, D and E). Given that 1) PC is much smaller in size than the nucleoid, and 2) it competes with the nucleoid to bind the same pool of cytoplasmic ParA, this observation indicates that ParA-PC binding affinity must be much higher than its nucleoid-counterpart. Because ParA binds to nonspecific DNA, without preference for plasmid over chromosome DNA, its colocalization with PC is expected to arise from its interactions with the PC-bound ParB. This notion is consistent with the extensive experimental evidence that the PC-bound ParB interacts with the cytoplasmic ParA (60, 61, 62). We thus expect ParA to localize around the PC when its level increases in wild-type cells, although it would be difficult to experimentally discern its localization pattern with a high background. Importantly, according to our model (Fig. 5, B and C), this PC localization of ParA ensures the fidelity of PC partition regardless of the ParA level variations that naturally occur in wild-type cells (Fig. 4 A; Table 1).

The direct testing of how the PC-localized ParA drives the partition fidelity of the parS-carrying DNA is not simple. Point mutations that disrupt ParA-ParB interactions and compromise ParA ATPase activity were identified, e.g., ParA_F-K120Q and ParA_F-K120R (63). These mutations that drastically changed the spatial profile of ParA_F from foci (Fig. 5 D) to uniform distribution along the nucleoid (64) were reported to increase the loss rate of the F plasmids by 400–800-fold (63). These observations would be consistent with the model proposal that decreasing the PC localization of ParA compromises the partition fidelity (i.e., the lower left corner of Fig. 5 C). We caution, however, that the point mutations render the PC to lose contact with the nucleoid and, hence, the active partition after all (34). It is possible that localizing to PC is integral of ParA’s normal activities. Thus, identifying a ParA variant that is specifically perturbed in its PC localization but not in other activities essential to partition is not easily accessible. Such a study is also be complicated with the transient interactions between ParA and ParB that both exist in different biochemical states (13,48,65). The recent findings that ParB binds CTP (62,66,67) and that parS-mediated CTP hydrolysis stimulates ParA interaction (62,67) could open interesting molecular clues to control this interaction.

Moreover, our model describes the PC partitioning along the nucleoid surface as a 2D problem. Recent experiments, however, suggest that the PC may move inside the nucleoid (34). Let us consider the simplest three-dimensional (3D) case first, followed by more complex scenarios. The simplest 3D scenario is that the interactions between the PC-bound ParB and nucleoid-bound ParA are still along the surface of the PC and the nucleoid should have the void space that allows the PC to move through. In this scenario, the PC moving through the nucleoid is like a sphere moving through a hollow cylinder. Now, unfolding the hollow cylinder will render a flat substrate, akin to our 2D model. Within this simplest 3D case, the 3D effects could alter several key parameters of this model. First, trapping inside the nucleoid likely slows down the diffusion of the PC. Second, the number of ParA-ParB bonds in 3D might be different from its 2D counterpart because some ParB buried within the PC may not be available for bond formation with the nucleoid-bound ParA. Third, the nucleoid DNA density, instead of being uniform, is reported to have high- and low-density regions (34). In this regard, our phase diagram studies show that the essence of our conclusion—i.e., the nature of critical-point-operation of PC partition and the effect of PC localization of ParA on the robustness against [ParA] variations—is largely preserved against variations of these relevant model parameters (Fig. S7).

We note that a more realistic 3D model may contain many factors that are currently not well characterized. For instance, we do not know the interior landscape of the nucleoid or whether and how the nucleoid DNA changes its conformation to accommodate the PC movement. Additionally, instead of acting as impenetrable structures, the PC and nucleoid could be amorphous so that ParA and ParB are able to freely enter and exit, offering a more complex interaction network that remains to be explored. Given these uncertainties, we will leave the 3D model to our future study.

Likewise, the self-drive of our Brownian ratcheting consists of a persistent “driving” followed by the positioning during directed segregation. Conceptually, this is akin to a positive feedback followed by a delayed negative feedback in stochastic biochemical network, the temporal dynamics of which can give rise to bi-stability and checkpoint (68). However, our system plays out not only in time but in space; it is an open question of whether and how this self-drive of our system involves the ingredients of bi-stability and checkpoint. Our future study will explore how the PC-mediated ParA localization influences the mathematical structure of spatial-temporal feedbacks in our system.

Furthermore, this PC-mediated ParA localization effect has its own limitation in ensuring the partition fidelity (Fig. S8 A). When the nucleoid becomes too long, this model would predict the partition machinery to lose its ability of adapting the segregation distance to half of the nucleoid length. Interestingly, as the nucleoid gets longer, the low-copy-number plasmids are reported to replicate accordingly to keep the plasmid/chromosome ratio constant. The latter events increase the number of PC foci. This way, each PC focus “commands” a unitary length of nucleoid as its power of sphere, resulting in the following equidistant pattern (22,69): the two PCs on the same nucleoid segregate by 1/2 of the nucleoid length, whereas the three PCs will segregate by ∼1/3 of that nucleoid length and so on. A size scaling emerges between the PC interdistance and the nucleoid length as a function of PC foci numbers. Although the notations of size scaling and size control have been indicated in biological systems (70, 71, 72, 73, 74), our work here provides a functional perspective in a way similar to spindle-cell size scaling (75).

Conversely, the spatial control over near-critical-point operation defines an optimal PC size that maximizes the upper limit of nucleoid length that the PC partitioning can adapt its segregation distance (Fig. S8 B). This is because PC size directly determines how many ParA-ParB bonds can be formed: if the PC is too small, then there will be too few ParA-ParB bonds to quench the diffusive motions and drive the directed PC movement. On the other hand, if the PC is too large, then it will yield too many ParA-ParB bonds so that the PC will get anchored for a long time, preventing movement. Consistent with this view, the optimal PC size can be modulated by the biochemical kinetics of ParA-ParB interactions (e.g., the off rate of ParA-ParB bond), which operates near the critical point. For instance, the faster the off rate, the larger the optimal PC size becomes (Fig. S8 C). For the given parameter set in Fig. S8 C, the optimal PC size is predicted to range between ∼62 and 130 nm. Because the PC is modeled as a 2D circular disk here, the predicted PC size should correspond to a 3D sphere with half its size, if we assume that they share the same surface area and, hence, the same number of ParA-ParB bonds. In this sense, the predicted optimal PC size in 3D would be ∼31–65 nm. Strikingly, this is consistent with the PC size of 43 ± 7 nm measured in vivo by super-resolution microscopy (38). In the light of partition fidelity, our results here provide a functional viewpoint of PC size regulation: 1) PC size may be optimized for the maximal ability of adapting PC partition to the nucleoid length, and 2) this optimal PC size can vary from system to system, depending on the kinetics of ParA partition machinery. In a bigger picture, although PC localizes the ParA, as demonstrated in this study, the ParA may reciprocally regulate the PC size (38), both of which contribute to the fidelity of PC partition. These findings bring up an interesting question of exactly how this feedback between ParA-mediated PC size regulation and PC-mediated ParA localization shapes the PC formation and the subsequent partitioning processes, which we will study in the near future.

Lastly, because low-copy-number plasmids provide selective advantages for bacterial survival, connecting the physical mechanism with the fidelity of DNA partition could allow us to understand how evolution might shape the near-critical-point behavior of a biological process to maximize its function. Interestingly, although widely conserved in both genome segregation (i.e., plasmids and chromosomes) and subcellular organelle trafficking in bacteria (76,77), the ParABS-mediated partitioning displays distinct spatial-temporal features in these different systems (12,78, 79, 80). With these diverse spatial-temporal dynamics, our work provides a starting point to shed light on how the near-critical-point operation of the same machinery adapts to different systems with different sizes and geometries. In a broader context, reaction-diffusion processes of molecular systems were proposed to function as a ruler to measure the cellular distances in bacteria (e.g., the dynamics of the Min-CDE system facilitates the determination of cell division site (81, 82, 83) or the intracellular machinery controls the flagellum length (84,85)). In general, the reaction and diffusion parameters need to be fine-tuned to achieve this length control and sensing. It remains unknown whether these systems operate near a critical point and how they ensure the robust measurement of cellular distance against noises. We suggest that the principles of spatial controls over the near-critical-point operation provide a possible solution to this fundamental question of cell biology: how do cells faithfully measure cellular-scale distances by only using molecular-scale interactions? We will investigate along this direction in the future.

Author contributions

J.-Y.B. and J.L. designed the research project. L.H. and J.R. performed the model computation and experimental testing, respectively. L.H., J.R., J.-Y.B., and J.L. analyzed the data and wrote the manuscript.

Editor: Anatoly Kolomeisky.