Multiscale computational study of ligand binding pathways: Case of p38 MAP kinase and its inhibitors

Abstract

Protein kinases are one of the most important drug targets in the past 10 years. Understanding the inhibitor association processes will profoundly impact new binder designs with preferred binding kinetics. However, after more than a decade of effort, a complete atomistic-level study of kinase inhibitor binding pathways is still lacking. As all kinases share a similar scaffold, we used p38 kinase as a model system to investigate the conformational dynamics and free energy transition of inhibitor binding toward kinases. Two major kinase conformations, Asp-Phe-Gly (DFG)-in and DFG-out, and three types of inhibitors, type I, II, and III, were thoroughly investigated in this work. We performed Brownian dynamics simulations and up to 340 μs Gaussian-accelerated molecular dynamics simulations to capture the inhibitor binding paths and a series of conformational transitions of the p38 kinase from its apo to inhibitor-bound form. Eighteen successful binding trajectories, including all types of inhibitors, are reported herein. Our simulations suggest a mechanism of inhibitor recruitment, a faster ligand association step to a pre-existing DFG-in/DFG-out p38 protein, followed by a slower molecular rearrangement step to adjust the protein-ligand conformation followed by a shift in the energy landscape to reach the final bound state. The ligand association processes also reflect the energetic favor of type I and type II/III inhibitor binding through ATP and allosteric channels, respectively. These different binding routes are directly responsible for the fast (type I binders) and slow (type II/III binders) kinetics of different types of p38 inhibitors. Our findings also echo the recent study of p38 inhibitor dissociation, implying that ligand unbinding could undergo a reverse path of binding, and both processes share similar metastates. This study deepens the understanding of molecular and energetic features of kinase inhibitor-binding processes and will inspire future drug development from a kinetic point of view.

Significance

Designing a “kinetically favorable” inhibitor has been reported as a potential direction toward new drug development. Understanding protein-ligand association processes is a crucial step to approach the design. However, after a decade of effort, it is still a lack of knowledge of ligand binding processes. This is because the binding processes are not approachable by traditional experimental measurements, and the simulation timescale to capture the entire binding paths limited the study by the current computational power. In this work, we aim to propose a mechanism of kinase inhibitor association processes by using the p38 kinase as a model system.

Introduction

Protein kinases function as phosphotransferases that catalyze the transfer of phosphate groups from high-energy donor molecules to specific substrates (1). This process is critical in metabolism, signal transduction, protein regulation, gene expression, proliferation processes, and many cellular pathways (2). Because of their significant roles in human physiology, protein kinases have become a group of major drug targets, and a growing interest in developing kinase inhibitors has recently culminated in diverse clinical usages (3). The traditional strategy of drug discovery is to characterize a set of ligands that show the best binding affinity with a favorable thermodynamic equilibrium constant (K_d) of its protein target. However, recently, ligand binding and unbinding kinetics (measured by the reaction on-rate constant k_on and off-rate constant k_off) have been broadly considered critical predictors of drug efficacy and selectivity (4,5). For example, slower k_off would make drug more efficacious. Therefore, in this study, we attempted to understand the mechanism of inhibitor association processes regarding different protein kinase conformations and different types of inhibitors.

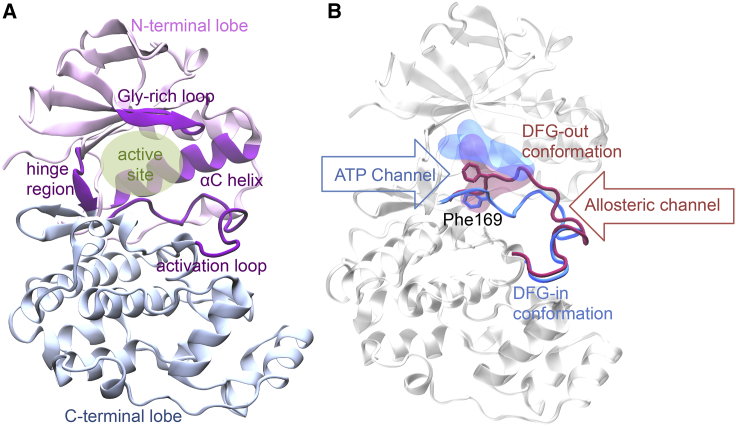
p38 mitogen-activated protein kinase is one of the most investigated kinases of interest as a drug target. All protein kinases are structurally conserved. Similar to other kinases, p38 is structurally formed by two subdomains, the N-terminal lobe and the C-terminal lobe (6). The two lobes are connected by a flexible linker region, also called the hinge region. The hinge region and parts of the activation and glycine-rich loop form a binding pocket accessed by ATP and kinase inhibitors (Fig. 1 A). The activation loop has a conserved Asp-Phe-Gly (DFG) motif that regulates kinase activation by controlling a Phe residue. Two major side-chain orientations of Phe have been identified: the activated and inactivated conformations of p38 correspond to the Phe side chain buried into the αC helix (called the DFG-in conformation) and exposed to solvent molecules (called the DFG-out conformation), respectively (Fig. 1 B; (7)). By flipping the DFG from the in-to-out conformation, it opens up a hydrophobic pocket between the N-terminal and C-terminal lobes. Although previous studies have tended to illustrate the free energy landscape of the DFG transition (8, 9, 10), the movement and population between the DFG-in and DFG-out states are still poorly understood (11).

Figure 1.

Sketch of the p38 protein kinase. (A) The overall p38 structure. Pink and blue show the N- and C-terminal lobes, respectively. Purple indicates the protein hinge region, αC helix, Gly-rich loop, and activation loop. (B) Two major conformations of the p38 protein: DFG-in (blue) and DFG-out (magenta). The ligand active sites regarding the different DFG conformations are highlighted in blue and red. The Phe169 residues in the DFG motif are shown in bond representations. To see the figure in color, go online.

In the past two decades, thousands of inhibits targeting kinases have been identified. The structures of the kinase-ligand-bound conformations are used to classify the inhibitors (12). Type I inhibitors, including most small molecules, facilitate the ATP binding pocket by binding to the active protein kinase conformation, DFG-in. In contrast, type II inhibitors occupy both the ATP binding site and a nearby allosteric hydrophobic pocket with an inactive conformation, DFG-out. Additionally, type III and IV inhibitors bind to two different regions within the allosteric pocket. When type I inhibitors bind to an active kinase, the activation loop adopts a DFG-in conformation, making the ATP binding pocket fully exposed to the solvent; thus, a passageway forms between the ATP binding site and the solvent that is accessible to the inhibitors, called the ATP channel. However, when type II inhibitors bind to an inactive kinase, the activation loop switches to a DFG-out conformation, which narrows the ATP channel and opens up the allosteric pocket; thus, a possible pathway between the allosteric pocket and the solvent to facilitate the inhibitors is called the allosteric channel (Fig. 1 B; (13)).

Through past efforts, rich structural data on kinase inhibitor complexes are available to elucidate the inhibitor binding modes with different protein conformations. Numerous investigations in drug screening assays (14), protein dynamics (15,16), and free energy calculations (17,18) have also been executed to develop kinase inhibitors against different diseases in the pharmaceutical industry. To understand the kinetic property of ligand unbinding, steered molecular dynamics (MD) simulations, adaptive biasing force simulations, and umbrella sampling methods (13,19, 20, 21) have been applied to exploit the favorable dissociation pathways of type I, II, and III inhibitors, along with different kinase systems. Furthermore, the MD simulation timescale is typically within tens of microseconds, so artificial biasing forces must be added in the association or dissociation simulations to obtain the trajectory of ligand entry or exist. Although a previous study tended to perform unbiased MD to simulate ligand association pathways of Src kinases (22), the intermediate states and energy transitions underlying the binding processes still remain unclear.

In this work, we employed Brownian dynamics (BD) simulations and Gaussian-accelerated MD (GaMD) simulations to map the inhibitor binding paths, protein conformational changes, and free energy profiles of type I, II, and III inhibitors in association with both active and inactive p38 kinase. The BD technique facilitates large timescale sampling and has been broadly applied in ligand association and channeling kinetics studies (23,24). Although BD serves as a good tool to provide a general picture of ligand association pathways, it is unable to represent the intermediate states and protein conformational rearrangements because proteins are typically rigid during the entire simulation. To address this issue, all-atom GaMD simulations were developed to achieve unconstrained enhanced sampling, overcoming the issue of reaction coordinate-based methods that are highly dependent on the users’ choices. By adding a Gaussian-based boost potential to smooth the potential energy surface, GaMD is now a rigorous tool for characterizing ligand binding, capturing large conformational changes, and allowing new applications on allosteric regulation, enzyme dynamics, carbohydrate dynamics, nucleic acids (25). GaMD accelerates conformational transitions by orders of magnitude and allowed users to accurately recover the original free energy profile (26). This approach has successfully characterized ligand binding events in the G-protein-coupled receptor and HIV protease (27,28). On the other hand, GaMD could access millisecond-timescale simulations by running a few hundreds of nanoseconds, similarly to the results obtained using the specialized Anton 2 supercomputer (29,30).

Four p38 inhibitors, SB203580, SK86002, diaryl urea, and pyrazolourea analogs (abbreviated SB2, SK8, DU, and PUA, respectively), were used in the study (Table 1). The SK8, DU, and PUA compounds are type I, II, and III inhibitors, respectively, excluding binding to either DFG-in or DFG-out conformation, whereas SB2 is a special type I inhibitor that can regulate both active (DFG-in) and inactive (DFG-out) p38. Also, note that SB2 and SK8 exhibit faster association rate constants 2–∼3 orders of magnitude higher than DU and PUA (Table 1). By sampling the preferred ligand association pathways, together with the simulations of ligand-free and ligand-bound p38 at the two endpoints, we were able to describe the role of intermediate states, protein-ligand interactions, and allosteric motions in their binding kinetics. We present ligand motions using BD and GaMD first and then discuss protein motions during ligand entry.

Table 1.

List of p38 inhibitors, including chemical structures, equilibrium constant (K_d), association rate constant (k_on), dissociation rate constant (k_off), and DFG conformations in p38-inhibitor complexes

Name and Chemical Structure	Kd (nM)	kon (M−1 s−1)	koff (s−1)	ΔGexp (kcal/mol)	PDB Code	DFG
SB2 (type I)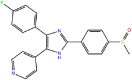	11.5	1.5 × 107	1.8 × 10−1	−10.9	1A9U (DFG-in)	in and out
					3GCP (DFG-out)
SK8 (type I)	86.5–180	4.3 × 107	7.7	−9.7	N/A in p38	in
					4LL5 in Pim-1 kinase
DU (type II)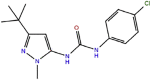	1160	1.2 × 105	1.4 × 10−1	−8.2	1KV1	out
PUA analog (type III)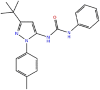	21	7.3 × 104	1.6 × 10−3	−10.5	3HV7 analog	out

The experimental data was reported from (28).

Materials and methods

Molecular systems

The apo p38 proteins with DFG-in and DFG-out conformations were built based on Protein Data Bank (PDB): 1A9U and 1W82, respectively. The SB2, SK8, and DU inhibitors were extracted from PDB: 1A9U, 4LL5, and 1KV1, and the PUA was constructed according to the ligand template in PDB: 3HV7 (Table 1).

GaMD

GaMD is an enhanced conformational sampling method of biomolecules that functions by adding a harmonic boost potential to reduce the system energy barriers. The boost potential was applied to the entire system, including proteins, inhibitors, and solvent molecules. Users do not need to preselect the reaction coordinate to apply the biased potential. When the system potential $V\left(r\right)$is lower than a reference energy E, the modified potential $V^{\ast }\left(\stackrel{\rightharpoonup }{r}\right)$ of the system can be calculated as follows:

$$V^{\ast }\left(\stackrel{\rightharpoonup }{r}\right)=V\left(\stackrel{\rightharpoonup }{r}\right)+\Delta V\left(\stackrel{\rightharpoonup }{r}\right)$$

$$\Delta V\left(\stackrel{\rightharpoonup }{r}\right)=\{\begin{array}{l}\frac{1}{2}k{\left(E-V\left(\stackrel{\rightharpoonup }{r}\right)\right)}^2,\text{if}V\left(\stackrel{\rightharpoonup }{r}\right)<E\hfill \\ 0,\text{if}V\left(\stackrel{\rightharpoonup }{r}\right)\ge E\hfill \end{array},$$ (1)

where k is the harmonic force constant. To ensure that the boost potential does not alter the overall shape of the original potential surface, the following criteria need to be satisfied:

$$V_{max}\le E\le V_{min}+\frac{1}{k},$$ (2)

where V_max and V_min are the system maximal and minimal potential energies, respectively. We then define $k\equiv k_0\frac{1}{V_{max}-V_{min}}$. By plugging into Eq. 1, the following equation is obtained:

$$\Delta V\left(\stackrel{\rightharpoonup }{r}\right)=\frac{1}{2}{k}_0\frac{1}{V_{max}-V_{min}}{\left(E-V\left(\stackrel{\rightharpoonup }{r}\right)\right)}^2,\text{when}V\left(\stackrel{\rightharpoonup }{r}\right)<E$$ (3)

Thus, the boost potential can be modified by either changing the threshold energy E or the effective force constant k₀. E can be simply controlled by setting to its lower bound, $E=V_{max}$, or upper bound, $E=V_{min}+\frac{1}{k}$, according to Eq. 3. To ensure accurate reweighing of free energy using cumulant expansion, the user-specified upper limit of ${\sigma }_0$, needs to be small enough to satisfy ${\sigma }_{\Delta V\left(\stackrel{\rightharpoonup }{r}\right)}\le {\sigma }_0$, where ${\sigma }_{\Delta V\left(\stackrel{\rightharpoonup }{r}\right)}$ is the standard deviation of the system’s boost potential. When E is set to the lower bound, k₀ can be calculated as follows:

$$k_0=\min \left(1.0,k_0^{\prime }\right)=\text{min}\left(1.0,\frac{{\sigma }_0}{{\sigma }_V}\frac{V_{max}-V_{min}}{V_{max}-V_{avg}}\right),$$ (4)

where V_avg and ${\sigma }_V$ are the average and standard deviation of the system potential energies. When E is set to the upper bound, k₀ is set to the following equation:

$$k_0=k_0^{"}\equiv \left(1-\frac{{\sigma }_0}{{\sigma }_V}\right)\frac{V_{max}-V_{min}}{V_{max}-V_{avg}},$$ (5)

if $k_0^{"}$ is calculated between 0 and 1. Otherwise, k₀ is calculated through Eq. 4. More details can be found in previous studies (26,31).

In the energetic reweighting process of GaMD simulations, the probability distribution of a selected reaction coordinate $A\left(\stackrel{\rightharpoonup }{r}\right)$ can be written as p∗(A), where $\stackrel{\rightharpoonup }{r}$ is a collection of atomic positions $\left\{\stackrel{\rightharpoonup }{r_1},\dots ,\stackrel{\rightharpoonup }{r_N}\right\}$. Given the boost potential of each frame, p∗(A) can be reweighted to recover the canonical ensemble distribution, p(A), as follows:

$$p\left(A_j\right)=p^{\ast }\left(A_j\right)\frac{{\langle e^{\beta \text{Δ}V\left(\stackrel{\rightharpoonup }{r}\right)}\rangle }_j}{{\sum }_{j=1}^M{\langle e^{\beta \text{Δ}V\left(\stackrel{\rightharpoonup }{r}\right)}\rangle }_j},j=1,\dots ,M,$$ (6)

where M is the number of bins, $\beta =k_{B}T$, and $\langle e^{\beta \text{Δ}V\left(\stackrel{\rightharpoonup }{r}\right)}\rangle$ is the ensemble-averaged Boltzmann factor of $\text{Δ}V\left(\stackrel{\rightharpoonup }{r}\right)$ for simulation frames found in the j^th bin. To reduce the energetic noise, the ensemble-averaged reweighting factor can be approximated using cumulant expansion (32,33):

$$\langle e^{\beta \Delta V}\rangle =\exp \left\{\sum _{k=1}^{\infty }\frac{{\beta }^k}{k!}{c}_k\right\},$$ (7)

where the first three cumulants are given by the following equation:

$$\begin{array}{l}{c}_1=\langle \Delta V\rangle ,\\ c_2=\langle \Delta V^2\rangle -{\langle \Delta V\rangle }^2={\sigma }_{\Delta V}^2\text{, and}\\ C_3=\langle \Delta V^3\rangle -3\langle \Delta V^2\rangle \langle \Delta V\rangle +2{\langle \Delta V\rangle }^3.\\ \end{array}$$ (8)

When the boost potential follows a near-Gaussian distribution, cumulant expansion to the second provides an approximation for free energy calculations (34). The reweighted free energy is calculated by $F\left(A\right)=-k_{B}T\ln p\left(A\right)$.

GaMD simulation setup

To obtain inhibitor association pathways of p38 kinase, the inhibitors were initially placed ∼80 Å away from the active site of the kinase. A single protein might be diffused with one, four or eight inhibitors simultaneously (Table 1). The Amber FF14SB and General Amber Force Field were applied to the protein and inhibitors, respectively (35,36). Before solvation, energy minimization on the hydrogen atoms, protein side chains, and the entire protein was performed for 500, 5000, and 5000 steps, respectively. Then, the system was solvated in TIP3P water molecules ∼12 Å between the box edge and the solutes to create a rectangular box (37). Na⁺ ions were added to neutralize the system using the ion parameters developed by Joung and Cheatham (38). Further energy minimization of the protein and the complex system (protein and water molecules) was performed for 1000 and 5000 steps, respectively. Periodic boundary conditions were applied during the simulation, and long-range electrostatics were accounted for using the particle mesh Ewald summation method (39).

GaMD simulation protocol

GaMD simulations of p38 systems were performed on the Amber 14 package with an efficient GPU implementation (26,40,41). The simulation started from water equilibration and then gradually heated the complex system to 50, 100, 150, 200, 250, and 300 K for 10 ps at each temperature. Before executing GaMD simulations, a 20 ns conventional MD simulation was further performed at 300 K with the isothermal–isobaric ensemble (NPT) to ensure that the system reached equilibrium. Bonds containing hydrogen atoms were restrained using the SHAKE algorithm (42), and the Langevin thermostat with a damping constant of 2 ps⁻¹ was turned on to maintain a temperature of 300 K. Electrostatic interactions were calculated using the particle mesh Ewald summation (39) with a cutoff of 12.0 Å. The time step of simulation was set to 2 fs.

Next, for each system, we proceeded a 10-ns conventional MD simulation to collect the potential statistics such as V_max, V_min, and V_avg for calculating GaMD acceleration parameters; a short GaMD simulation (2 ns) with applied boost potential but without updating V_max-, V_min-, and V_avg-values; and a long GaMD simulation (100 ns) with the updated boost potential. From this point, we continued performing 269 independent GaMD simulations from 400 to 13,700 ns. Dual-boost level acceleration of both the dihedral energetic and the total potential energetic terms was applied. The simulations were set to either the lower or upper bound (details in Table S1). The average and standard deviation of the system potential energies were calculated every 500 ps. The upper limit of the boost potential standard deviation, ${\sigma }_0$, was set to 6.0 kcal/mol for both the dihedral and total potential energetic terms. The resulting trajectories were collected every 0.1 ps for analysis.

GaMD analysis

We clustered the apo p38 conformations obtained from GaMD simulations using the g_cluster program in the Gromacs 4.5.5 package (43), following the algorithm described by Daura et al. (44). The program counted the number of neighbors using a 0.3 Å cutoff and then selected the structure with the largest number of neighbors as a cluster. These clustered p38 conformations were applied in subsequent BD simulations. Volumes of the p38 inhibitor active site were predicted using the POVME program, version 2.0, with snapshots extracted every 50 ps from the GaMD simulations (45). The CPPTRAJ script in the Amber package (46) was utilized to calculate (RMSD), RMSF, atom-atom distance, and principal component. The GaMD trajectories and snapshots were examined using both VMD and PyMol packages (47,48).

The PyReweighting (34) toolkit was used to reweight the GaMD simulations to compute one-dimensional and two-dimensional potential of mean force (PMF) profiles. All reweighting simulations were based on cumulant expansion to the second order. A bin size of 0.25 Å was applied to construct the PMF profiles of root-mean-square deviation (RMSD) and distance.

BD simulation

We performed BD simulations using the BrownDye package (49). The software allows the users to compute the second-order reaction rate constant of the encounter of two rigid bodies moving according to BD. The BD method is powerful to compute the ligand association rate constant in a diffusion-control reaction through a statistical manner, whereas the protein-ligand conformational arrangements are typically neglected because both protein and ligand are rigid. In the simulations, the p38 proteins were built in an all-atom model, whereas the inhibitor was modeled as a single sphere of 2.0 Å radius without charges. Because the inhibitors are not distinguishable, the association rate constant reported from BD is according to the protein structure and electrostatic properties. Before running the simulations, the PROPKA program version 3.0 (50) was used to assign the static protonation states of the proteins at physiological pH 7.0. Then, the software PDB2PQR version 1.8 (51) was applied to generate the charges and radius of each atom with the Amber force field (52). Dummy atoms, without charge or radius, were placed at the center of the inhibitor active site to help define the location where the substrate binds. The electrostatic grids of the protein systems were constructed through the Adaptive Poisson-Boltzmann Solver program version 1.4 (53,54) at 0.20 M ionic strength. The BD simulations were initialized by randomly diffusing the substrate bead around the receptor, and then the substrate started to travel under the influence of the hydrodynamic and electrostatic forces between the molecules. BD simulations were terminated when either the reaction occurred or the substrate escaped. If the inhibitor molecules reached a spherical region within 1 Å away from the dummy atom, we considered the reaction to have occurred (the inhibitor bound). Substrate escape was defined by the travel of the inhibitor to a spherical boundary around the protein large enough that the forces between the substrate and receptor were spherically symmetrical (49). The maximal number of steps in the BD simulations was set to 100,000,000. BD trajectories were output every 100 steps. Moreover, 50,000 copies of the BD trajectories were performed at each protein conformation. To characterize the protein surface area at which the substrate beads tended to stay, for every step at each BD trajectory, we computed the distance between the substrate bead center and residue Cα-atom. Thus, the probability of the substrate beads reaching within 7 Å of each residue was calculated. Residues identified as having a high probability were further mapped to the p38 structures.

Results

Inhibitor association pathways modeled by BD simulations

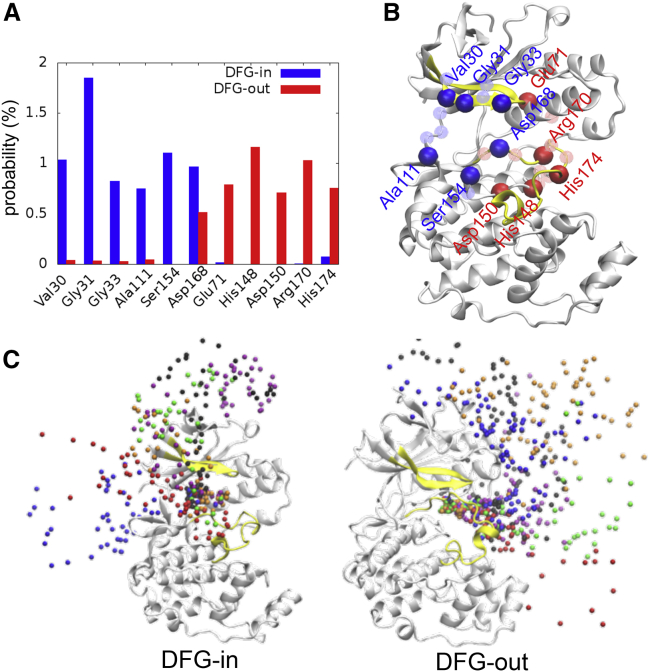
The apo p38 crystal structures, including both DFG-in and DFG-out conformations (Fig. 1 B), were considered receptors to model the inhibitor association using BD. To avoid the bias of a restricted receptor conformation during the simulations, additional eight apo p38 structures (four DFG-in and four DFG-out) sampled and clustered by GaMD simulations, were also computed in the BD to obtain better statistical data. Each p38 inhibitor was modeled as a single bead diffused 60–70 Å away from the protein at different positions initially. We performed 15,000 BD simulations on each DFG conformation; 200 and 188 BD trajectories revealed that the inhibitors successfully reached the active site of the DFG-in and DFG-out proteins, respectively, whereas the inhibitors escaped in the rest of the simulations.

To deepen the understanding of the association processes, we particularly focused on BD trajectories showing a successful binding event. The distance between an inhibitor and the Cα-atom of each residue was calculated for every step/position during the diffusion, which allows us to describe the surface region on the p38 protein on which the inhibitors tended to remain during the binding processes. Fig. 2 A shows the amino acids that present a high probability of a substrate-residue distance shorter than 7 Å, indicating that the inhibitors were inclined to interact with different residues in association with different DFG conformations. These residues are distributed along with ATP and allosteric channels when the inhibitors diffuse to DFG-in and DFG-out conformations, respectively (Fig. 2 B). The selected BD trajectories, shown in Fig. 2 C, further illustrate that the inhibitors displayed different binding pathways with respect to different p38 conformations. The inhibitors gathered near the ATP channel in DFG-in p38, whereas the inhibitors approached the active site through the allosteric channel in DFG-out p38.

Figure 2.

BD simulations of inhibitor association pathways. (A) The distances between each inhibitor position and residue Cα-atom were calculated. The bar graph demonstrates the probability that the distance is shorter than 7 Å. Only amino acids with probability >0.7% are shown in the graph. Blue and red indicate results from the simulations of DFG-in and DFG-out p38, respectively. (B) Residues showing favorable interactions with inhibitors are highlighted on the p38 structure. Bright and light beads indicate the residues with probabilities >0.7 and >0.5%, respectively. Blue and red show the results calculated from DFG-in and DFG-out p38, respectively. Yellow color shows the activation and Gly-rich loop. (C) Some BD trajectories were selected to show the binding paths. Each bead color represents an independent BD simulation. To see the figure in color, go online.

The BD simulations also enabled us to estimate the inhibitor association rate constant, k_on. The computed k_on-value of a DFG-in protein is 6.6 ± 1.6 × 10⁷ M⁻¹ s⁻¹, which is in good agreement with the experimental measurements (Table 1). This suggests that, in the case of DFG-in p38, the diffusion dominates the ligand binding process. After the ligand reaches the binding site, the step of protein-ligand conformational rearrangements is fast. However, our computed k_on of DFG-out p38, 1.6 ± 0.8 × 10⁷ M⁻¹ s⁻¹, overestimated the binding kinetics, being three orders faster than the reported data (Table 1). The results imply that protein-ligand conformational rearrangements cannot be ignored in the DFG-out p38, and the rearrangement is time-consuming and dominates the ligand association rate. The computed k_on values from BD conclude that the diffusion process and conformational rearrangement is a critical step that determines the ligand association to DFG-in and DFG-out p38, respectively. The difference could be attributed to structural variation between the two DFG conformations. To achieve binding, inhibitors need to pass through either an ATP or allosteric channel. Although the volumes of the two channels are similar (∼598 Å³ in ATP (DFG-in) and 622 Å³ in allosteric (DFG-out)), the channel shapes are quite different. In a DFG-in p38 system, the active site is open and exposed to the solvent. Once the inhibitors approached a nearby binding area, the complexes were quickly formed. However, in a DFG-out p38, the inhibitors need to pass through a long and narrow channel before reaching the active site (Fig. S1). Large-scale conformational adjustments of the protein were expected to accommodate inhibitor entry. The rigid protein structures in the BD simulations limited our ability to accurately evaluate these conformational changes during inhibitor association, resulting in a miscomputed k_on-value for DFG-out p38. Therefore, we next performed an all-atom dynamic study to draw a complete picture of the inhibitor association processes considering protein flexibility.

Overview of inhibitor association pathways modeled by GaMD simulations

We performed 269 GaMD simulations, including two p38 conformations (DFG-in and DFG-out) and four inhibitors (SB2, SK8, DU, and PUA), to model inhibitor binding paths. The simulation time of each sampling ranged from 500 ns to ∼14 μs. Two types of RMSD calculations were applied to evaluate whether the inhibitors successfully reached the active site. First, we computed the RMSD of all heavy atoms of the inhibitors using a crystal structure as a reference coordinate, namely, ha-RMSD, to approximate the conformational similarity between the sampled inhibitors and the crystal form. The other RMSD calculations were performed according to the center of mass of the inhibitors, called com-RMSD, which can describe the overall inhibitor positions during the binding processes.

As type I inhibitors SB2 and Sk8 bind fast to the protein, we successfully obtained multiple binding paths (four paths for DFG-in:SB2, seven paths for DFG-in:SB2, and five paths for DFG-in:SB2). All simulations showed that com-RMSD and ha-RMSD were less than 0.4 and 1.7 Å, respectively, suggesting that the inhibitors were in the active site and formed all key interactions with the protein. However, type II and III inhibitors, DU and PUA, bind slowly to the protein, and only one complete binding path for DU and PUA was achieved. Some simulations (four paths of DFG-in:SB2 and four paths of DFG-in:SB2) showed low com-RMSD but high ha-RMSD, suggesting that although the inhibitors could move to the binding site, they were still experiencing conformational arrangements, and a part of the major interactions with the protein was missing. For the rest of the simulations, the inhibitors either stayed on the protein surface or moved in the solution; thus, both com-RMSD and ha-RMSD were larger than 10 Å. All results are summarized in Table S1.

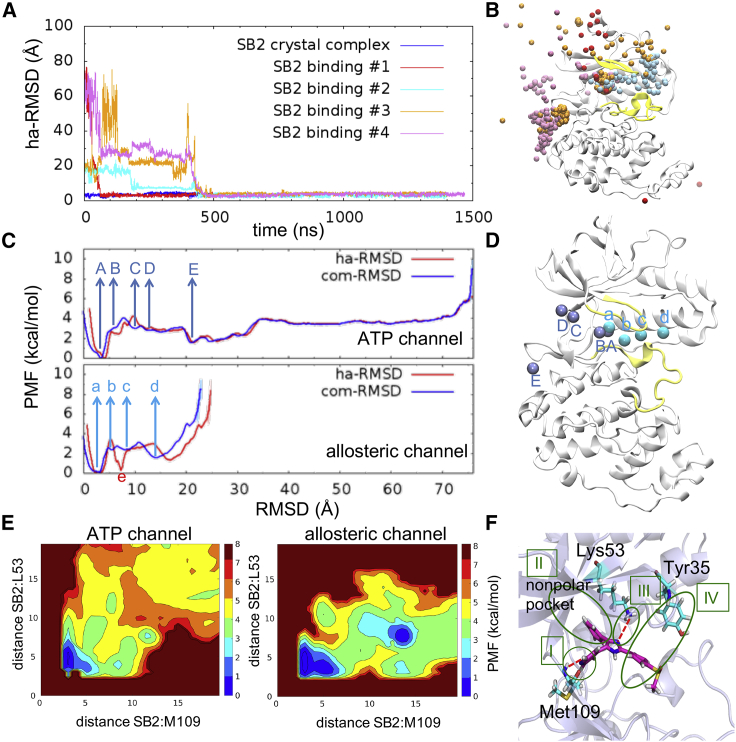
Association pathways of SB2 inhibitor with DFG-in p38 and DFG-out

The SB2 inhibitors diffused to DFG-in and DFG-out p38 because crystal studies have shown that they can bind to both conformations (55). In the analysis of the four successful binding paths of DFG-in:SB2, three SB2 inhibitors were bound to the protein along the ATP channel, whereas a single trajectory showed binding through the allosteric channel (Fig. 3 B). PMF calculations of both association pathways are shown in Fig. 3 C, and each low-energy intermediate state of the ligand is presented in Fig. 3 D. Although both channels allowed SB2 to bind to the active site and approach the lowest energy state (state A and state a), the free energy transitions along each path were different. Before reaching the ATP channel, the SB2 inhibitor might be tracked in a small pocket at the protein surface (state E). After SB2 was close to the channel entrance (state C), crossing the 0.47 kcal/mol barrier, the inhibitor reached state B and then quickly assumed the final bound state A. However, when SB2 encountered the allosteric channel, it required 1.55 kcal/mol to move into the channel, although the PMF of SB2 was low at the channel entrance (state d). This free energy landscape indicated that SB2 association through the allosteric channel requires higher energy than the ATP channel. Moreover, we identified a low PMF state e along the allosteric channel when ha-RMSD was near 7.25 Å. This state indicates that the inhibitor was at the active site, but a part of the key protein-ligand interactions was missing. The conformational arrangement of the system toward the final bound state required 3.12 kcal/mol, suggesting that SB2 experienced a higher energy barrier when passing through the allosteric channel.

Figure 3.

Association of SB2 with DFG-in p38. (A) ha-RMSD plot of four binding trajectories. (B) Association of four successful binding paths is labeled by four different colored beads. Yellow indicates the p38 Gly-rich and activation loop. (C) One-dimensional PMF plot according to the paths of ATP and allosteric channels. Red and blue beads show ligand ha-RMSD and com-RMSD, respectively. Uppercase and lowercase letters represent the energy minimum of the ATP and allosteric channel, respectively. (D) Blue and cyan beads indicate SB2 positions at the low-energy states along the ATP and allosteric channels, respectively. (E) Two-dimensional potential mean force profile evaluated by the distance between SB2 and residue Met109 and Lys53. (F) The four major interactions formed between SB2 and p38 DFG-in. To see the figure in color, go online.

In the DFG-in:SB2 crystal-bound structure, we noticed four major ligand-protein interactions: 1) pyridine N of SB2 forms a charge attraction with backbone N of Met109, 2) the fluorophenyl ring stays in a nonpolar pocket formed by N-terminal domain β-sheets, 3) the N3 atom of the imidazole SB2 ring interacts with the Lys53 side chain, and 4) the phenyl ring of the 4-methylsulfinylphenyl group forms a stacking interaction with Tyr35 (Fig. 3 F). In simulations of the binding paths, the above interactions were gradually formed in the order of I, II, III, and IV. Interaction I serves as a primary component. Once this attraction forms, the inhibitors are able to stay in the active site, allowing the remaining rearrangements of the ligand rings. Interactions II and III formed at a similar time, which stabilized the overall ligand-bound structure. However, interaction IV was less stable. Simulations of the ligand-bound complex also indicated that this interaction was on and off because of the flexibility of the Gly-rich loop. Fig. 3 E evaluated the free energy transition to form interactions I and III, which shows that the PMF of SB2 was low at the entrance of the allosteric channel: ∼3 kcal/mol to pass through the channel and to form interactions I and III. However, less than 2 kcal/mol PMF was needed to cross the ATP channel and form key attractions, suggesting that the ATP channel is a favorable association pathway of DFG-in:SB2 binding.

In the binding of DFG-out:SB2, all binding paths revealed that SB2 inhibitors reached the active site through the ATP channel (Fig. S2 B). According to the PMF plot (Fig. S2 C), 1.03 kcal/mol was needed for SB2 to reach the entrance of the binding site (from state D to C), and the inhibitor took 1.47 kcal/mol (barrier in state B) to rearrange the interactions with the protein to approach the final bound conformation. Compared with the paths of DFG-in:SB2 binding, the inhibitor experienced fewer conformational changes and lower energy barriers in association with DFG-out.

Association pathways of SK8 inhibitor with DFG-in p38

In five successful binding paths of DFG-in:SK8, four showed that the inhibitors were along the ATP channel to reach the binding, whereas only one SK8 binds to p38 through the allosteric channel (Fig. S3 B). In the DFG-in:SK8 pathways, the inhibitors first bound to the protein surface, state D, as shown in Fig. S3, C and D. The energy required to remove the inhibitor from the surface pocket toward the ATP channel was ∼1.93 kcal/mol. Once SK8 reached the channel entrance (state C), the interactions were rapidly formed while passing a small energy barrier of 0.55 kcal/mol. Additionally, SK8 experienced conformational rearrangements after approaching the active site, such as states E and F. The energy barrier in these states is ∼1 kcal/mol. However, when SK8 experienced the allosteric channel, 1.70 kcal/mol was required for the inhibitor to pass the channel entrance, moving from state d to c. The inhibitor then further moved from state b to the final bound form (state a) by crossing another energy barrier, 0.93 kcal/mol. These results indicate that the ATP channel is a preferred path once the inhibitors achieve the channel entrance.

Note that in DFG-in:SK8 crystal complex, SK8 forms interactions I, II, and III with the protein, the same as the DFG-in:SB2 complex (Fig. 3 F). The association paths of SK8 revealed that interaction I is a principal attraction, forming first, and then interactions II and III could either gradually or simultaneously form. The overall binding paths of SK8 are very similar to the DFG-in:SB2 binding.

Association pathways of DU and PUA analog inhibitor with DFG-out p38

Compared with SB2 and SK8, which reached the final bound state within 1 μs, DU and PUA required significantly longer time to complete binding, requiring more than 3 and 13 μs to obtain a complete binding path for DU and PUA, respectively. Although it is not fair to directly compare the binding timescale from GaMD with experimental binding kinetics, the trend of the simulation time, t_PUA > t_DU > t_SB2 ≅ t_SK8, agrees well with the experimental k_on listed in Table 1.

In all simulations, both DU and PUA reached the active site along the allosteric channel. In the DFG-out:DU binding paths, after DU approached the channel entrance (state B in Fig. S4), an additional 2.22 kcal/mol was needed for DU to further move it into the active site. In cases of DFG-out:PUA binding, PUA needed to cross multiple energy barriers (∼1 kcal/mol of each barrier) to form the final complex (Fig. S4). Two amino acids, Leu73 and Ile143, play key roles in the DU and PUA association. The residues control the opening of the allosteric channel. The inhibitors contacted the residues before moving into the channel. Once the hydrophobic interactions between the inhibitors and the residues formed, significant time was needed for the system to break the interactions and let the inhibitors move forward. This explains why inhibitors usually take longer to reach the active site if they encounter the allosteric channel for binding. Moreover, the structure of PUA has an additional methyl benzene ring compared with DU; thus, PUA needs more time than DU for conformational arrangements to finalize binding.

Protein conformational transitions during inhibitor association

Proteins are anticipated to undergo conformational transitions in response to ligands. We first examined the major motions of apo p38 before binding and then explored the protein dynamics during ligand association processes. p38 proteins display a packing structure with two lobes linked by a hinge region. Principal component analysis showed that the two lobes exhibit a breathing motion. The lobes move toward and away using a flexible hinge linker (Fig. S5), resulting in elasticity of the active site that could either expand or compress to sandwich inhibitors. Our RMSF calculations (Fig. S6) agreed with the recent NMR study (56) stating that the Gly-rich loop, the hinge region, and the activation loop are three flexible areas in apo p38, suggesting that fluctuations of these regions may play a key role in protein dynamics. Therefore, we further examined the role of protein hinge motions during inhibitor binding.

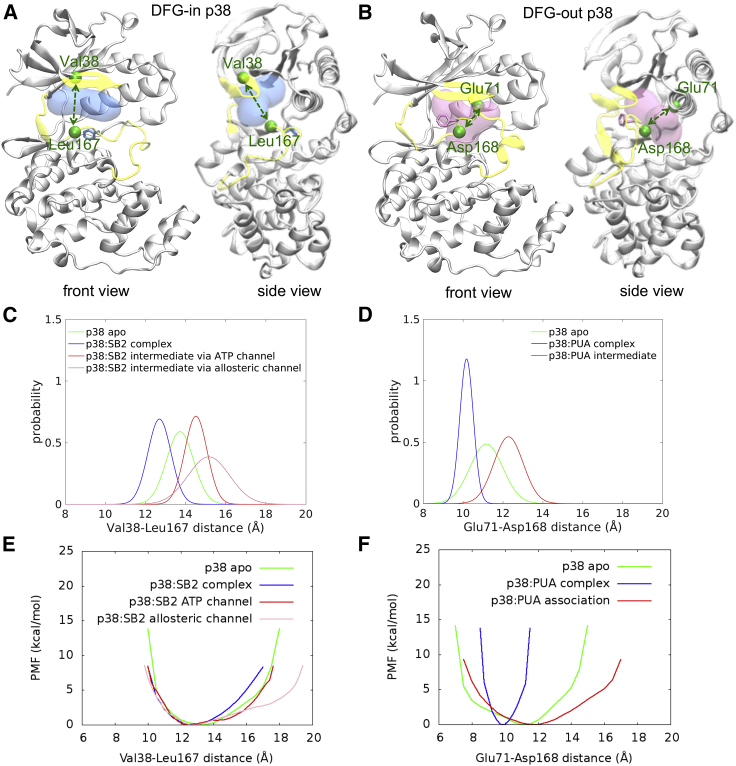
Type I inhibitors bind to the ATP pocket. The binding includes relocation of the Gly-rich and activation loop; thus, we characterized the protein motions by evaluating the changes in the hinge distance between Val38 and Leu167 (Fig. 4 A). Fig. 4 C shows that the Val38-Leu167 distances of the apo and bound DFG-in p38 were 13.73 and 12.70 Å, respectively, indicating that the binding shortened the distance between the two loops. However, the distance was increased to 14.52 Å for inhibitor recruitment through the ATP channel, and a further opening to 15.38 Å was found when the inhibitors accessed binding through the allosteric channel. The distance distribution of the allosteric channel is wider than the ATP channel, suggesting that the protein experienced sizable transitions in binding via the allosteric channel. In addition, the PMF calculations of both channels revealed the same global energy minimum near 12.70 Å and a shallow local energy minimum with an equilibrium position at 14.20 Å of the ATP channel and 16.80 Å of the allosteric channel (Fig. 4 E). Although the protein eventually reached the final bound state through either path, the active site remarkably opened when the inhibitors bound by the allosteric channel. Our findings suggest that hinge motions contribute significantly to inhibitor association, and type I inhibitors prefer to adopt the ATP channel in binding because of the favorable energy in metastates.

Figure 4.

Protein conformational changes studied by the Val38-Leu167 and Glu71-Asp168 distances. Val38-Leu167 and Glu71-Asp168 distances were calculated to study the protein hinge motion of DFG-in (A) and DFG-out (B) conformations. Blue and red represent the ligand-bound positions of the DFG-in and DFG-out inhibitors, respectively. Phe169 in the DFG motif is shown in the bond form. The Gly-rich loop, hinge region, and activation loop are highlighted in yellow. The distance distribution and PMF profile of DFG-in (C and E) and DFG-out (D and F) p38 were also evaluated. Note that the distance distribution was fitted the probability histograms through the Gaussian method. Only intermediate states were considered (red and pink) when the inhibitor is in the channel. To see the figure in color, go online.

The association of type II/III inhibitors, which bind through the allosteric channel, correlates the motion of the activation loop and αC helix; therefore, the distance between Glu71 and Asp168 was computed to elucidate protein conformational changes (Fig. 4 B). Similar to the type I inhibitors, ligand binding shortened the hinge distance from 11.17 Å (apo state) to 10.18 Å (bound state) (Fig. 4 D). To recruit the inhibitors, the distance extended to 12.28 Å during the binding processes. Although both type II and III inhibitors reached the crystal-bound form in our simulations, the protein conformation still encountered insufficient sampling and did not fully converge. Thus, the global energy minima in the PMF profile (Fig. 4 F) calculated from the association trajectories showed an equilibrium position at ∼11.8 Å, which was not consistent with the crystal-bound position, ∼9.75 Å. Therefore, more aggressive sampling is expected to further decrease the energy barrier for the observation of protein conformational arrangements.

Discussion

In this study, by exploiting extensive GaMD simulations with cumulative sampling times greater than 340 μs, we probed step-by-step conformational dynamics and free energy profiles of inhibitor binding pathways for p38 kinase, which could not be obtained experimentally. The routes of SB2 association with DFG-in/DFG-out p38 and SK8 association with DFG-in p38 were successfully clarified, and the energy-minimal conformations from GaMD simulations are the same as those captured from crystal structures. In addition, the simulations unraveled multiple low-energy (intermediate) states along different binding routes. However, this GaMD simulations still suffer from insufficient sampling to fully capture the protein conformational changes of the DU and PUA inhibitor binding to DFG-out p38. Because substrate binding to p38 may result in backbone dynamics at a catalytic region on the μs-ms timescale (56), but it remains challenging for the current simulation tools to map an entire course and calculate a converged free energy profile. Thus, the continuing development of enhanced sampling techniques is necessary to study large complex systems or an event over hundreds of milliseconds.

Through the computational framework of combining BD and MD studies, we showed that substrate binding at the ATP pocket, such as type I inhibitors, is more favorable through the ATP channel with a lower PMF, whereas the association of type II/III inhibitors occurs predominantly along the allosteric channel. All of the above inhibitor associations to p38 are accompanied by the changes in protein allosteric networks, especially the protein hinge region. The apo p38 protein has natural fluctuations in the Gly-rich loop, hinge region, and activation loop. The association of type I inhibitors basically occurs along with this breathing motion; hence, protein dynamics lead to a shift in the energy landscape and ultimately drive ligand binding. In contrast to type I inhibitor binding at the protein surface cleft, type II/III inhibitors are located inside the deeper pocket, so that both the nearby loops and helices need to experience large conformational changes to open the binding pocket for ligand access, resulting in energetically unfavorable motions. Therefore, if binding only requires the protein’s natural fluctuations, such as for type I inhibitors, then it occurs quickly and easily; however, if the protein has to move somewhere else, which is not its internal dynamics, it makes binding slow and difficult. The different binding paths and protein dynamics explain the fast (type I) and slow (type II/III) binding kinetics of p38 kinase.

With increased attention given to ligand dissociation kinetics, the unbinding pathways of p38 inhibitors have been investigated in recent years (13,21). Studies reported the intermediate states of the inhibitors escaping from the active site, and the dissociation processes echoed our findings of the association. For example, the SB2 association with DFG-in p38 involved a step-by-step course of bond formation in order of interaction I to IV (Fig. 3 F), whereas SB2 dissociation showed a reverse process in breaking the interactions gradually from IV to I. The binding and unbinding of SK8 presented the same behavior. This confirms that interaction I is a lead factor, quick to form and slow to break. Moreover, the PMF calculations revealed the favorable dissociation pathways of type I and type II/III inhibitors via the ATP and allosteric channels, respectively, and the unbinding of type II/III inhibitors required a sizable protein rearrangement compared with type I binders (21), implying that the system underwent similar metastates and local energy minima while shifting the energy landscape during ligand association and dissociation processes. This finding explains the kinetic fact that faster binders escape quickly and slower binders escape slowly.

Nearly every eukaryotic kinase has a conserved DFG motif, and the flipping of Phe in the motif between the in and out conformations directly contributes to the ligand binding specificity; thus, the equilibrium of these two alternative states has been extensively studied. Because the structure of apo DFG-out p38 is still not available by crystallography, one outstanding question is whether the presence of the DFG-out conformation is induced by ligand binding. Early accelerated MD simulations (57) proposed an induced-fit hypothesis, whereas both NMR (55) and free energy studies (18) suggested a dynamic equilibrium model in which the two DFG positions have an equal population in the apo state. In our ∼270 simulations of ligand association, the ligands did not show any tendency to change the DFG position in either the diffusion or binding steps (Fig. S7), illustrating that the DFG conformation remained the same during all simulations. This indicates a pre-existing DFG motif in the ligand binding process and leads to a conformational selection mechanism of binding specificity.

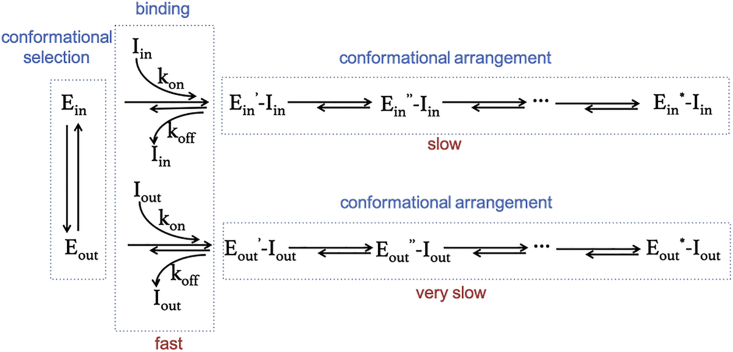
Our BD and GaMD results allowed us to envision a complete ligand association process and concluded that the inhibitor binding to p38 involves at least two steps: a fast step of ligand diffusion to a preorganized DFG-in/out p38 followed by a slow step of protein-ligand conformational rearrangements where the second step of the arrangements involves a repeat process in which the ligand forms transient interactions with the protein, breaks these attractions, moves slightly away from the active site, and rebinds (Fig. 5). This mechanism of fast physical binding selection with slow induced conformational change agrees well with the kinetic model claimed from experimental studies of Abl and Src kinase (10,58) and computational studies of HIV protease (28,59). Because conformational rearrangements appear to be a rate-limiting step during the association, ligand size and the number of rotatable bonds in it directly influence binding kinetics. In general, DFG-in inhibitors are usually smaller than DFG-out inhibitors, so they are able to pass along both the ATP and allosteric channels, although binding via the allosteric channel is energetically unfavorable due to necessitating a large-scale protein conformational transition. However, the components of DFG-out inhibitors are somewhat more complicated, with a combination of multiple rings and functional groups, which may result in stereoscopic hindrance; thus, this supports the general understanding that only an ample space, the allosteric channel, is able to regulate accessibility of the ligands. After the inhibitors reach the active site, the increased number of rotatable bonds in the DFG-out inhibitors causes more intermediate states to form. In addition, the conformational transition during the binding encountered multiple high-energy barriers, so that the intermediate structures became trapped in the local energy basin. Accordingly, this intricate rearrangement process of DFG-out versus DFG-in inhibitors discloses a difficult and slow course of shifting the energy landscape toward the global energy minimum.

Figure 5.

Process of ligand association with p38 protein. E_in and E_out represent the apo p38 protein with the DFG loop in the “in” and “out” positions, respectively. I_in and I_out are the ligands specifically binding to the DFG-in and DFG-out protein conformations, respectively. E_in′ -I, E_in^′′-I, E_out′ -I, and E_out^′′-I correspond to ligand-bound p38 in a different conformational state (intermediate state). E_in^∗-I and E_out^∗-I specify the conformation in global energy minima, also shown in the crystal structure. To see the figure in color, go online.

Author contributions

Y.-m.M.H. designed the work, performed the simulations, analyzed the data, and wrote the manuscript.

Editor: Alan Grossfield.