Abstract
The process of genome packaging in most of viruses is poorly understood, notably the role of the genome itself in the nucleocapsid structure. For simple icosahedral single-stranded RNA viruses, the branched topology due to the RNA secondary structure is thought to lower the free energy required to complete a virion. We investigate the structure of nucleocapsids packaging RNA segments with various degrees of compactness by small-angle x-ray scattering and cryotransmission electron microscopy. The structural differences are mild even though compact RNA segments lead on average to better-ordered and more uniform particles across the sample. Numerical calculations confirm that the free energy is lowered for the RNA segments displaying the larger number of branch points. The effect is, however, opposite with synthetic polyelectrolytes, in which a star topology gives rise to more disorder in the capsids than a linear topology. If RNA compactness and size account in part for the proper assembly of the nucleocapsid and the genome selectivity, other factors most likely related to the host cell environment during viral assembly must come into play as well.
Significance
Many single-stranded RNA viruses package their genome through a self-assembly process occurring within the host cell. Their survival depends upon the capability of capsid proteins to selectively capture the segments of viral RNA among a sea of host cell molecules and, concomitantly, to build up a defectless capsid. By using a model icosahedral virus, we observed that nucleocapsids packaging compact RNA segments were slightly better assembled than with loosely folded segments, whereas the trend was opposite for capsids packaging synthetic polyelectrolytes with compact and extended topologies. As a consequence, the genome selectivity cannot rely solely on the RNA topology, and environmental factors at the viral assembly site must ensure the production of viable virions.
Introduction
Positive-sense, single-stranded (ss)RNA viruses are ubiquitous in the environment, with members infecting all kingdoms of life apart from Archaea (1). Some of them cause important public health issues because of a lack of vaccines (e.g., hepatitis C virus), curative treatments (e.g., coronaviruses), or most often both (e.g., dengue virus). Part of the difficulty of fighting the associated diseases comes from their life cycle, which alternates between well-protected virions and unprotected but intracellular, biologically active viral RNAs and proteins that hijack the biological systems of the host cell. Every ssRNA virus possesses a genome, either in the form of one RNA molecule or split into several molecules in the case of segmented genomes. The genome is protected by a protein shell called capsid, the composition and structure of which vary but is generally remarkably simple. In the simplest cases, the building blocks of these capsids, called capsid proteins (CPs), have identical sequences and can self-assemble to form objects with spherical or diverse geometries (2, 3, 4). One of the most remarkable shared characteristics of these viruses is their ability to spontaneously self-assemble within the host cell. Contrary to double-stranded DNA and RNA viruses, which generally package their genome inside preformed capsids using nonspontaneous, ATP-consuming mechanisms, ssRNA viruses package their genome during the capsid assembly (5,6). This co-assembly process has been the center of many studies, and a general understanding of the process has been achieved (7, 8, 9, 10). Being spontaneous, the nucleocapsid self-assembly relies only on RNA-protein and protein-protein interactions. Yet, the presence of RNAs is not mandatory for the capsid formation because many in vitro studies have shown the formation of empty capsids (11, 12, 13). These studies, as well as simulation studies, determined the local forces ruling protein-protein interactions, especially the existence of hydrophobic interaction between subunits (14, 15, 16, 17). However, the biological relevance of these experiments is somewhat questionable because RNAs (either viral or nonviral) are always present in the infected cell, and the physicochemical conditions, in particular pH and ionic strength, used to trigger the self-assembly of empty capsids are often nonphysiological. Moreover, RNA can lower the energy barrier to assembled capsids and thus favors the formation of virions (18). The resulting nucleocapsids generally possess a highly regular structure with very few defects. The main driving force arises from the electrostatic attractive interactions between the negatively charged nucleotides and the positively charged, RNA-binding domain of the CPs protruding toward the interior of the capsid (19,20).
However, many details of the co-assembly mechanisms are still elusive. In particular, how viruses selectively package their own genome and not the host RNAs is still a matter of debate (6). Genome replication and transcription, as well as nucleocapsid self-assembly, generally occur in the cytoplasm (21). In this crowded environment, viral RNAs are outnumbered by the large number of host RNAs present. A common strategy adopted by ssRNA viruses is to compartmentalize their genome and possibly proteins into organelle-like structures, generally in the form of membrane invaginations or vesicles (21). The spatial proximity is likely to reduce the packaging competition between host and viral RNAs. Nevertheless, significant amounts of nonviral RNAs were found to be packaged during the nucleocapsid assembly (22), indicating that despite compartmentalization, viral RNAs have to compete with nonviral ones.
To package their own genome, ssRNA viruses developed several strategies of packaging selectivity (6). One of the most important strategies is the presence of sequences and/or structures embedded in viral RNAs that can specifically interact with CPs of the cognate virus. These specific elements—coined “packaging signals”—have been shown to be necessary, but not always sufficient, to explain the packaging selectivity observed during an infection. Many RNA sequences have been identified as packaging signals, and sometimes several of them can be found on a given RNA molecule (6,23). As Twarock et al. stated (24), this illustrates “the crucial roles of multiple dispersed, specific interactions between viral genomes and coat proteins in capsid assembly.”
Packaging signals are often recognized by viral proteins from the secondary structures they can form (e.g., hairpin-like structures). However, nonspecific RNA structures can also play a large role for packaging selectivity. For instance, RNA length can contribute greatly to the packaging selectivity. Several competition studies determined that longer RNAs were preferentially packaged (25,26). However, there seems to be an optimal length—which is usually close to the length of the viral RNAs—because longer RNAs are shared between multiple, nonclosed capsids (27,28). The length factor is relevant in vivo because viral genomic RNAs tend to be larger than RNAs of the host cell (29). Besides, the natural tendency of RNA for basepairing leads to the constitution of structures akin to branched polyelectrolytes. The level of branching depends upon RNA sequence, and viruses have evolved to have highly branched and compact RNAs (30,31). Compactness has been shown to increase the packaging efficiency both in in vitro experiments (26) and in simulation studies (32,33). Moreover, increased compactness seems to allow longer RNA molecules to be packaged by viral CPs (33, 34, 35). However, the relationship between compactness and selectivity is not straightforward because it was shown in some conditions that linear RNAs could be packaged more efficiently than branched RNAs of the same length (28). An explanation could be that a high level of branching can lead to an increased stiffness that may be detrimental for packaging selectivity (36). The connection between RNA structure and packaging selectivity is then far from being thoroughly understood.
Despite the discovery of various strategies of packaging selectivity, their relative importance during an infection is unknown and is likely to be virus specific. Here, we focus our work on the cowpea chlorotic mottle virus (CCMV), a model virus of the Bromoviridae family. This multipartite virus has a segmented genome of four RNA molecules split into three nucleocapsids, each of them hosting around 3000 nucleotides (37). The capsids are homomultimers of CPs that follow the Caspar-Klug quasiequivalence principle of icosahedral symmetry (38,39). They are natively under the shape of T = 3 capsids, i.e., comprising 180 CPs (40). CCMV packaging selectivity strategy is not clearly established because no specific packaging signal has been found so far (6), although there is evidence that RNA length is an important factor (26). On the contrary, studies done on the closely related brome mosaic virus (BMV) showed the existence of packaging signals (41). Besides, competition experiments showed that BMV RNAs were packaged preferentially over CCMV RNAs into CCMV capsids (26). This improved selectivity for noncognate RNAs tends to confirm the lack of packaging signals for CCMV RNAs. However, because of the high similarities between BMV and CCMV genomes, shared packaging selectivity strategies may still be present.
In our study, we compare the structure of CCMV nucleocapsids packaging RNA segments belonging to CCMV and BMV, as well as a nonrelated segment derived from rotavirus. All segments are similar in length, but numerical calculations reveal that they display different numbers of branch points. Secondly, we investigate the structure of capsids packaging synthetic polyelectrolytes with linear and star topologies. By investigating the structures and thermodynamics of nucleocapsid assemblies as a function of the cargo topology in physiological conditions, we advance our understanding of the nonspecific packaging selectivity of icosahedral ssRNA viruses.
Materials and methods
CCMV protein purification
CCMV virions were purified from infected cowpea leaves (Vigna unguiculata) by following the purification method previously developed (9,42). CCMV CPs were then isolated from their viral RNAs by an ultracentrifugation-based method. Briefly, virions were dialyzed against 500 mM CaCl2, 1 mM EDTA, 1 mM dithiothreitol (DTT), 0.5 mM phenylmethylsulfonyl fluoride, and 50 mM Tris-HCl (pH 7.5). The dialyzed solution (∼10 mL) was centrifuged at 150,000 × g for 18 h using an Optima XPN-80 ultracentrifuge (Beckman Coulter Life Sciences, Indianapolis, IN). 0.5 mL aliquots were collected, and their protein purity was measured by spectrophotometry using a NanoDrop 2000 spectrophotometer (Thermo Fisher Scientific, Waltham, MA). Aliquots with A260/A280 < 0.66 were deemed pure and were pooled then concentrated using an Amicon Ultra-4 (10 kDa) centrifugal filter unit. CP concentrations were estimated by ultraviolet absorbance at 280 nm. Virions were stored at −80°C and CPs kept at 4°C until use.
RNA production
RNAs were produced by in vitro transcription from recombinant plasmids. Plasmids coding for each RNA were transformed in 10-β competent E. coli cells (New England Biolabs, Ipswich, MA), produced and purified by a NucleoBond Xtra plasmid DNA purification kit (Macherey-Nagel, Düren, Germany), and linearized using the appropriate restriction enzyme. The linearized plasmid containing a T7 promoter was then transcribed using a MEGAscript T7 Transcription Kit (Thermo Fisher Scientific). Newly produced RNAs were finally purified using a MEGAclear Transcription Clean-Up Kit (Thermo Fisher Scientific) and placed in a moderate ionic strength buffer (50 mM NaCl, 1 mM EDTA, and 50 mM Tris-HCl (pH 7.5)). RNA concentration was measured using the RNA mode of a NanoDrop 2000 spectrophotometer (Thermo Fisher Scientific). RNA length and purity were checked by running an agarose gel electrophoresis (Fig. S1). UltraPure DNase/RNase-Free Distilled Water (Invitrogen, Carlsbad, CA) was used for every experiment involving RNA. Three RNA segments were used in this study: RNA 1 of BMV (B1), RNA 2 of CCMV (C2), and RNA 2 of the bovine rotavirus strain RF (RF2). Nucleoprotein complexes were produced by dialyzing a mixture of CPs initially in high ionic strength buffer (500 mM NaCl, 0.5 mM DTT, 1 mM EDTA, 50 mM Tris-HCl (pH 7.5)) and RNA against a moderate ionic strength buffer. Final concentrations were estimated by spectrophotometric measurements following the method proposed by Porterfield and Zlotnick (43).
Deuterated poly(styrene sulfonic acid)
Deuterated linear and star polystyrene (Polymer Source, Dorval, Canada) were used. Sulfonation was performed by adapting a method previously developed (44). 1.1 g of phosphorus pentoxide was dissolved in 5 mL of concentrated sulfuric acid. 100 mg of deuterated polystyrene dissolved in 15 mL of cyclohexane was then added before agitation for 2 h at 50°C. The reaction setup was placed in argon to prevent any presence of water. The mixture was cooled down, and 10 g of ice was added. The aqueous phase was collected, placed in a dialysis tube, and thoroughly dialyzed against pure sterile water for 2 weeks. Pure deuterated poly(styrene sulfonic acid) dPSS was finally freeze-dried before storage. Our previous investigations revealed that the method yields a degree of sulfonation around 95% (9).
SAXS
Small-angle x-ray scattering (SAXS) measurements were performed at the SWING beamline of the SOLEIL synchrotron facility (Saint-Aubin, France). The wavelength of the monochromatic beam was set to λ = 1.03 Å, and two-dimensional (2D) scattering images were recorded using an Eiger X 4M detector (Dectris, Philadelphia, PA) with a sample-to-detector distance of 2 m, which provided scattering wavenumbers Q (Q = 4π/λsin(θ/2), where θ is the scattering angle) ranging from 3.2 × 10−3 to 0.57 Å−1. The temperature was maintained at 20°C using a thermostated circulating water bath. For each sample, 40 measurements were taken with a beam exposure time of 1 s. The scattering intensities were converted into absolute units after subtracting the contribution of the buffer solution. Experimental uncertainties were calculated after circular averaging using the Foxtrot software package.
The forward scattering intensity (I0) of a mixture of subunits (dimeric CPs) and RNA is given by
| (1) |
with ΔbRNA and ΔbS the excess scattering lengths of RNA and subunits, respectively; XN the molar concentration of nucleoprotein complexes comprising N subunits (X0 XRNA the molar concentration of bare RNA); and XS the molar concentration of free subunits. The mean number of subunits cannot be calculated without the knowledge of the standard deviation (SD) of N. However, an upper limit can be inferred from I0 regardless of the probability distribution of N (9) and reads
| (2) |
with Γ and the forward scattering intensity produced by a mixture of noninteracting subunits and RNA. cRNA and cS are the total molar concentrations of RNA and subunits, respectively. ΔbRNA and ΔbS were estimated experimentally from solutions of purified virions and subunits by using Eq. 1.
Cryotransmission electron microscopy
4 μL of solution was deposited onto a holey carbon grid (Quantifoil R2/2; Großlöbichau, Germany) ionized by glow discharge. The grid was blotted with a filter paper for 1.5 s and directly plunged into liquid ethane cooled down by liquid nitrogen using an FEI Vitrobot (FEI, Hillsboro, Oregon) operated at room temperature and 100% relative humidity. The grids were stored in liquid nitrogen until use. Frozen samples were transferred into a Gatan 626 cryo-holder (Gatan, Pleasanton, CA) and observed at −180°C via a JEOL 2010F microscope (Tokyo, Japan) equipped with a 200 kV field emission gun. The samples were imaged with a magnification of ×50,000 using a minimal dose system, and the images were collected with a Gatan Ultrascan 4K charge coupled device (CCD) camera at 2.5 μm of nominal defocus.
Image analysis was performed with cryoSPARC (45). After contrast transfer function (CTF) correction, a first round of automated particle picking (cryoSPARC “blob picking”) was performed. This initial picking was manually curated to confirm real particles and remove clear nonprotein artifacts (tubular structures were retained). Particles were extracted in a 256-pixel box (nominal pixel size: 2.36 Å), and two rounds of 2D classification were performed (see the numbers of particles used in Table 1. For the sake of clarity, only the five most populated classes of particles were displayed.
Table 1.
Number of particles used in the cryoSPARC analysis
| Sample | Number of micrographs | Number of manual picks | Number of particles after 2D cleanup |
|---|---|---|---|
| CP-B1 | 34 | 2890 | 1911 |
| CP-C2 | 14 | 1226 | 1076 |
| CP-RF2 | 44 | 3680 | 3472 |
ITC
Isothermal titration calorimetry (ITC) measurements were carried out using a MicroCal PEAK-ITC (Malvern Panalytical, Malvern, UK). The reaction cell (250 μL) was loaded with an RNA solution (cRNA = 0.2 μM, 50 mM NaCl, 1 mM EDTA, 50 mM Tris-HCl (pH 7.5)) containing B1, C2, or RF2, and the syringe was filled with a CP solution (cS = 100 μM, 500 mM NaCl,1 mM EDTA, 50 mM Tris-HCl (pH 7.5)). The experiments were done in triplicate at 25°C by injecting 34 μL of CP solution (split into 17 injections) into the cell with an equilibration interval of 200 s. To take into account the salt dilution as well as the protein-protein interactions, control experiments without RNA were performed and subtracted to the titration curves before curve fitting. Variation enthalpy (ΔH), stoichiometry of the reaction (N), and dissociation constant (KD) were obtained by nonlinear least-squares fitting of the experimental data using the single set of independent binding sites model of the Origin software provided with the instrument.
SANS
Small-angle neutron scattering (SANS) measurements were performed on the D22 spectrometer at the Institut Laue Langevin (Grenoble, France). The samples were contained in 1-mm-thick quartz cells, and all measurements were done at room temperature. Data were normalized by using the direct beam, and the buffer contribution was subtracted from these corrected data. The scattering wavenumbers Q covered the range between 4 × 10−3 and 0.45 Å−1 by setting two sample-to-detector distances of 11.2 and 2 m, respectively, with a wavelength of 6 Å. Exposure time was ∼1 h at large sample-to-detector distance and 10 min at short distance.
Porod volumes were estimated by using GNOM and DATPOROD from the ATSAS suite (46). The mean number of subunits within capsids was then inferred from the Porod volume of a sample of interest and from that of a solution of native virions in 68% D2O (to contrast match the RNA genome), given that the capsids of native virions possess 90 subunits.
The scattering data were fitted with the SASfit package (47) by a model of vesicles of core radius R with a gaussian polydispersity characterized by an SD ΔR on the core radius. In the particular case of capsids packaging linear dPSS, a structure factor of sticky hard spheres was implemented to reproduce the increase of intensity at very small Q-values. The model was supplemented with a Guinier law and a constant background to account for free subunits in solution.
Numerical calculations
After the experimental observations, we introduce a model to study the spontaneous packaging of both C2 and RF2 by CPs in a T = 3 icosahedral structure. We present the capsid as a hollow sphere with 180 positively charged N-terminal tails (modeled as solid cylinders) extended toward its interior. As for the genome, we model it as a flexible negatively charged polyelectrolyte, interacting attractively with the positive charges on the N-terminal domains of capsid proteins.
To consider the impact of the secondary structure of RNA, we used field-theoretical techniques developed for branched polymers. Because the strength of RNA basepairing is relatively weak, we consider the annealed case in which the genome branchiness can easily be changed as a result of its interaction with the positive charges on the CPs (48). Using the ground-state dominance approximation (49,50), in which case only the dominant contribution to the genome partition function is considered, the free energy of the genome-capsid complex in a salt solution at the mean-field level can be written as (33,35,51, 52, 53)
| (3) |
where β is the inverse of temperature in the units of energy, a is the Kuhn length of the polymer, e is the elementary charge, μ is the density of monovalent salt ions, and τ is the linear charge density of polyelectrolyte. The Bjerrum length λB = e2β/4πε is ∼0.7 nm for water at room temperature. A very detailed derivation of Eq. 3 can be found in (35,54).
The field Ψ(r) in Eq. 3 represents the monomer density field and Φ(r) the electrostatic potential. The quantity ρ(r) denotes the density of positive charges on the N-terminal tails of capsid proteins. The first term in Eq. 3 corresponds to the entropic cost of deviation from a uniform polymer density. The last two terms of Eq. 3 are associated with the electrostatic interactions between the polymer segments, the N-terminal capsid proteins, and the salt ions at the level of the Poisson-Boltzmann theory (51,55, 56, 57). The term W[Ψ]is associated with the free energy density of an annealed branched polymer with the excluded volume interaction (58, 59, 60),
| (4) |
where fe and fb are the fugacities of the end and branched points of the annealed chain, respectively (54), and υ is the effective excluded volume of each monomer. It is worth mentioning that in this model, the stem-loop or hairpin configurations of RNA are considered as end points. The parameters Ce(r) = feΨ are associated with the density of end points and Cb(r) = fbΨ3 with the density of branch points.
Using the fugacities fe and fb, the expectation number of end and branched points, Ne and Nb, can be written as
| (5) |
It is important to note that the number of end and branched points are related as follows,
| (6) |
because there is only one chain in each capsid and no closed loops within the secondary structure of the genome. The chain is linear if fb = 0, and the number of branched points increases as fb increases. Using Eqs. 5 and 6, we vary fb and find fe. To this end, fe is not a free parameter.
By minimizing the free energy with respect to the fields Ψ(r) and Φ(r) subject to the constrain that the total number of monomers inside the capsid is constant, we obtain three self-consistent nonlinear coupled equations for the interior and exterior of the capsid,
| (7a) |
| (7b) |
and
| (7c) |
where λD = 1/ is the (dimensionless) Debye screening length and E is Lagrange multiplier enforcing the fixed monomer number inside the shell. The polymer concentration in the exterior of the capsid is zero, Ψ = 0. The details of the derivations of all equations given above can be found in (35,54).
Solving the three coupled above equations, we obtain the genome density profiles for C2 and RF2 that minimize the free energy inside the capsid. For the numerical calculation, we set the radius of the T = 3 capsid to R = 12 nm and the number of negative charges on the capsid to 1800. Similar to the experimental condition, the salt concentration is 100 mM.
Results
RNA compactness
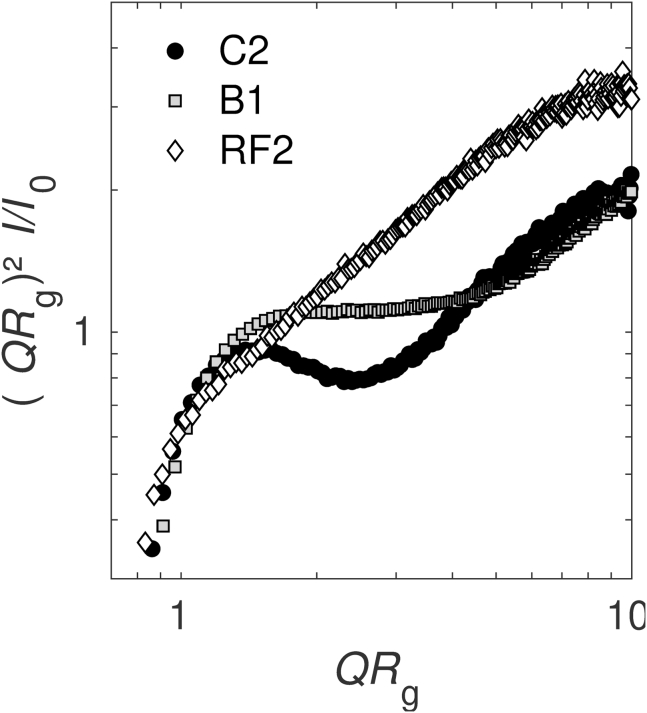
Three RNA segments were used for this study: RNA1 of BMV (denoted B1), RNA2 of CCMV (C2), and RNA2 of the bovine rotavirus strain RF (RF2) (61). These RNAs were chosen for their similar length (3234, 2767, and 2687 nucleotides, respectively) and RF2 also because it is not packaged as such by the rotavirus capsid, in contrast to B1 by the BMV CP and C2 by the CCMV CP. Thus, the secondary structure of RF2 has no reason for being optimized by evolutionary processes for packaging purpose. Moreover, because each of them codes for a different protein, their sequence identities are very low, with very few regions of sequence similarity. Structural characterization of these RNA segments was performed by SAXS. This ensemble-averaging technique gives information about the size, shape, and dispersity of suspended objects. RNAs are rather disordered objects, and their form factors differ from those of well-organized structures. To obtain information about RNA conformations, the SAXS data were converted into a dimensionless Kratky plot (Fig. 1). This representation emphasizes the differences between the pattern of compact objects and that of random chains (62). The three RNA segments had neatly distinct patterns. C2 RNA displayed a bell-shaped curve in the low to intermediate QRg that was related to the overall compactness of the molecule (63). B1 RNA had a pattern similar to C2 but showed a plateau instead of a decrease of intensity in the intermediate QRg region (Rg denotes the radius of gyration). A bell-shaped curve, as seen with C2, is attributed to a partially folded conformation, whereas the presence of a plateau, as seen with B1, is characteristic of a less compact structure (63). The Kratky plot of RF2 displayed a continuous increase of intensity, which is reminiscent of a rigid, elongated object. Therefore, RF2 is likely hybridized over longer segments on average than C2 and B1.
Figure 1.
SAXS curves of RNA segments. RNA samples were dialyzed in a moderate ionic strength buffer (50 mM NaCl, 1 mM EDTA, 50 mM Tris-HCl (pH 7.5)), and their final concentration was cRNA = 0.5 g ⋅ L−1. The dimensionless Kratky plot representation was chosen to compare the degrees of compactness. Rg is the radius of gyration, I the scattering intensity, and I0 the value of I extrapolated at Q = 0. Rg of B1 was estimated to be 12 nm, whereas that of C2 and RF2 was ~10 nm.
Ensemble-averaged structures of nucleocapsids packaging various RNA segments
Each CCMV CP is a 190-amino-acid-long polypeptide (20.3 kDa) (40). In the absence of RNA, CCMV CPs can form a wide variety of polymorphs (e.g., dimers, hollow capsids, tubes), depending on the pH and ionic strength of the solution (12). The building block of all these polymorphs is the dimer of CP, which will be hereafter referred to as the subunit. Recently, a strong attention was directed toward the formation of nucleocapsids (8,9,64). A reason for that is the fact that the physicochemical conditions used to form nucleocapsids in vitro are not always biologically relevant (e.g., acidic pH). In this study, we chose to be close to physiological conditions (pH 7.5, ionic strength of 100 mM), and we probed the structural differences of nucleocapsids packaging different RNA segments.
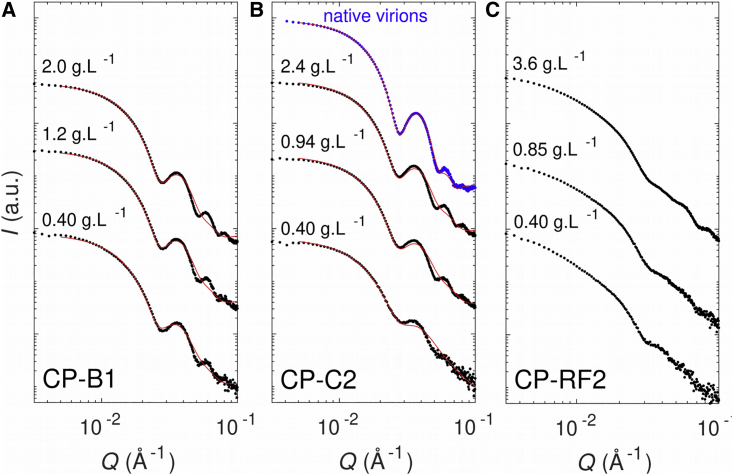
First, we studied the structure of particles formed by mixing CCMV CPs and RNA segments at different concentrations using SAXS. A scattering curve of native virions is given for reference (Fig. 2 B, blue curve) and showed pronounced oscillations, characteristic of monodisperse sphere-like nucleocapsids. In comparison, the SAXS curves of CP-C2 mixtures (Fig. 2 B) showed oscillations that became more pronounced when the CP concentration increased but were always less marked than the reference curve. Differences in form factor could be quantified by fitting the experimental curves with a polydisperse vesicle model and by estimating polydispersity values (Table S1). From the lowest to the highest concentration, there was a clear decrease in polydispersity (ΔR/R going from 32 to 26%, R being the inner radius of the vesicle), but even the most concentrated sample was still more polydisperse than native virions measured in the same physicochemical condition (ΔR/R = 20%). The decrease in polydispersity means that the objects became more ordered upon increased concentration. The disorder-order transition of CCMV nucleocapsids was established by Monte Carlo simulations (65), which highlighted the crucial role of elastic energy during assembly. CP-B1 curves (Fig. 2 A) show form factors that are highly similar to CP-C2 curves, indicating the presence of sphere-like objects. However, the increase of concentration only slightly reduced polydispersity (ΔR/R going from 28 to 26% in the concentration range studied). This is due to the fact that at low concentration, oscillations were already highly pronounced, indicating the presence of well-formed nucleocapsids. Thus, under identical physicochemical condition and similar concentration, the noncognate B1 RNA appeared to be better at forming nucleocapsids. However, it is worth mentioning that at even lower concentration and higher ionic strength, CP-B1 mixtures formed amorphous particles instead of closed nucleocapsids (66). Finally, CP-RF2 curves showed totally distinct scattering patterns (Fig. 2 C). In the low Q region (Q ≤ 0.01 Å−1), the intensity did not reach a plateau, indicating the existence of long-range intermolecular interactions (structure factor). In the intermediate Q region (0.01 ≤ Q ≤ 0.1 Å−1), oscillations were absent, which indicated that the objects were nonhomogeneous, partially assembled nucleocapsids. For these reasons, we did not apply any model to fit CP-RF2 curves.
Figure 2.
SAXS curves of nucleocapsids. CCMV CPs were mixed with RNAs and dialyzed in a moderate ionic strength buffer (50 mM NaCl, 50 mM Tris-HCl (pH 7.5)): B1 (A), C2 (B), and RF2 (C). For each system, three concentrations were measured with the CP/RNA mass ratio kept constant. Exact CP and RNA concentrations can be found in Table S1. Curves were fitted by a polydisperse vesicle model (solid red lines). Native virions dialyzed in the same buffer were used as a reference (blue curve). To see this figure in color, go online.
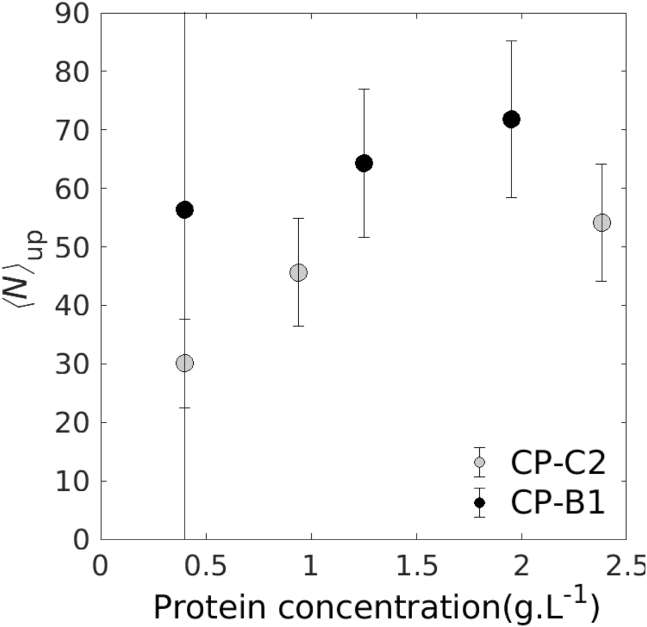
The presence of a plateau in the scattering curves of B1 and C2 mixtures gave us access to the forward scattering intensities I0 that are directly related to the mass of the particles. Using an analytical method previously developed (9), an approximation of the number of bound subunits per RNA could be deduced (Fig. 3). Native virions placed under the same physicochemical condition were used as a reference for determination. Their scattering curve was typical of swollen nucleocapsids (Fig. 2 B), and a -value of 90 subunits was imposed, as expected for T = 3 icosahedral capsids. By comparison, C2 and B1 mixtures had on average fewer bound subunits per RNA segment (Fig. 3, gray and black disks, respectively), indicating that under this condition, most of the objects were partially assembled nucleocapsids. In both cases, there was a clear increase of upon increase of both CP and RNA concentrations, which confirmed the existence of nonspecific interactions. However, at similar concentrations, -values of CP-B1 mixtures were always higher than those of CP-C2 mixtures. This could be explained by the slightly larger length of B1 compared to C2, which resulted in more binding sites.
Figure 3.
Mean number of bound subunits per RNA segment calculated from the scattering curves in Fig. 2. CP-C2 mixtures (gray disks) and CP-B1 mixtures (black disks) of varying protein concentrations are indicated. The protein/RNA mass ratio was around 3.5 and 4.0 for CP-C2 and CP-B1, respectively. Error bars are standard errors of the mean.
Morphology at the single-particle level
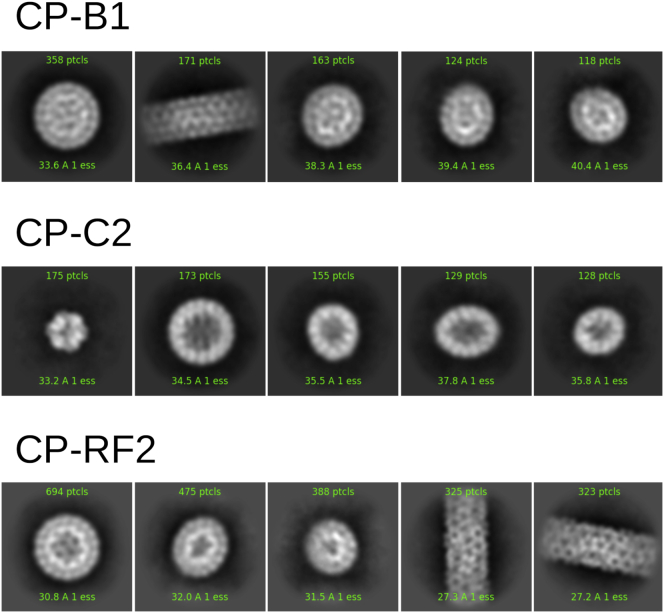
We investigated the morphology of the nucleocapsids made with each of the three RNA segments by cryotransmission electron microscopy (cryoTEM). To do so, we carried out 2D classification over more than a thousand particles for each kind of nucleocapsid (Fig. 4). It turned out that in all cases, some sphere-like particles were formed, and their size was consistent with T = 3 icosahedral nucleocapsids (see Table S2). The rest of the identified particles looked like the pieces of nucleocapsids seen under various orientations. In the case of CP-B1 and CP-RF2 mixtures, nanotubes comprising some defects were identified as well. It must be noted here that, unlike SAXS measurements, this 2D classification did not reflect the actual composition of the samples. Only those particles that were structurally similar enough were grouped into homogeneous classes by the cryoSPARC software, whereas amorphous and loosely ordered particles were assigned to junk classes and not retained for further analysis (see Fig. S2 for typical cryoTEM views of the samples). Nonetheless, Fig. 4 indicates that even though RF2 induced a lower degree of order and/or more variability than B1 and C2 across a large set of particles as evidenced by SAXS data (Fig. 2) at the single-particle level, a significant number of spherical nucleocapsids were completed or partially assembled.
Figure 4.
CryoTEM 2D classification for nucleocapsids with B1, C2, and RF2. CP concentrations were 4, 4, and 3.6 g ⋅ L−1, and CP/RNA mass ratios were 6, 6, and 5.5, respectively. The size of each box is 604 Å. To see this figure in color, go online.
The presence of nanotubes coexisting with the CP-B1 and CP-RF2 particles, but not with the CP-C2 ones, was unexpected. Because in this cryoTEM study, we used a CP/RNA mass ratio around 6 and the stoichiometry in a native virion is of 3.6, CPs were in excess in the solution. CPs alone are known to form nanotubes under these pH and ionic strength conditions (12), so we could indeed expect the CPs in excess to make nanotubes. The fact that they were not seen in the presence of C2 might simply be an artifact caused by the preparation of the microscopy grid; it happens from time to time that large anisotropic objects are sorted out and gathered in a particular location on the grid during the sample blotting and freezing.
RNA binding affinity
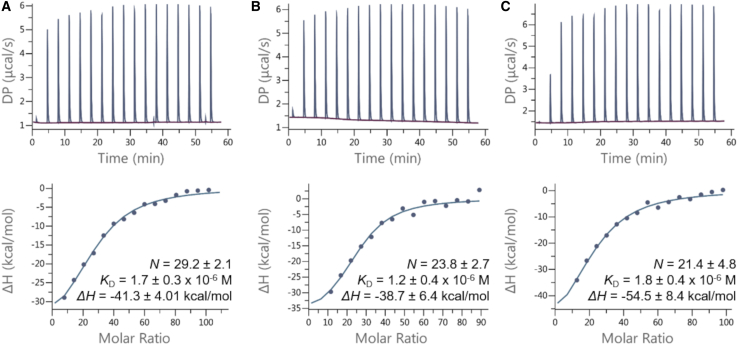
To assess differently the binding affinity of CPs for the various RNA segments, we carried out ITC experiments (Fig. 5). This technique measured the heat exchange of an RNA solution during the addition of a CP solution. The large positive peaks seen after each injection (upper panels) were mainly due to the dilution of the salts present in the CP solution. Once the control subtracted, peaks became negative (exothermic) and were directly linked to interactions between CPs and RNAs. Fitting the titration curves gave us information about the stoichiometry N (number of subunits per RNA molecule), the dissociation constant KD (inversely correlated to the affinity) and the variation of enthalpy ΔH.
Figure 5.
ITC experiments of CCMV CPs mixed with RNA segments: B1 (A), C2 (B), and RF2 (C). Upper panels: raw data of the heat exchange. Each spike corresponds to one injection of a CP solution (100 μM) in an RNA solution (0.2 μM). Lower panels: integrated heat of each injection after subtraction of the dilution signal and titration curve fitted according to a model of independent binding sites. Stoichiometry (N), dissociation constant (KD), and variation of enthalpy (ΔH) are shown. Each value was the average of three replicas. To see this figure in color, go online. Uncertainties are standard errors of the mean.
First, the three systems studied had a negative ΔH, confirming the electrostatic nature of the interactions at play (67). Secondly, the N-values obtained by ITC could in principle be compared to as measured by SAXS. The N-values were sensibly lower than for each CP-RNA mixture. For instance, B1 and C2 N-values were 29.2 and 23.8, whereas the lowest were 56.3 and 30.1, respectively. Because ITC and SAXS experiments were done using commensurate CP and RNA concentrations (with different CP/RNA molar ratios), concentration effects could not be the cause of this discrepancy. However, an explanation can come from the fact that ITC cannot probe athermic reactions or reactions whose heat variations cancel out. In our case, conformational changes of CPs, which are expected to happen during nucleocapsid assembly, may interfere with the accurate titration of CP-RNA interactions. This can lead to underestimations of the actual stoichiometry of the reaction. Such a bias was observed for proteins interacting on hydroxyapatite (68) and silica surfaces (69). However, despite this discrepancy, a relative comparison could be done and similar trends between N and could be observed. Both values were neatly lower than the stoichiometry of a complete nucleocapsid, i.e., 90, which indicates that a large fraction of the particles were partially assembled. B1 interacted with more subunits than C2 and RF2. Again, this can partially be explained by the slightly longer length of the B1 RNA compared to the others. Furthermore, although we could not calculate -values for CP-RF2 mixtures using SAXS data, N-values could be obtained and indicated that C2 and RF2 interacted with the same number of subunits.
Finally, KD measured for each system were highly similar from one another, around 1.5 μM. This is in agreement with KD-values for CCMV CPs interacting with small RNAs measured by fluorescent correlation spectroscopy (KD = 2–3 μM) (64). This is also consistent with NMR measurements (Fig. S3), which revealed an intermediate to fast exchange rate (from 2 s−1 up to 1000 s−1 and >1000 s−1, respectively) between the bound and free states of CPs. Then, despite forming different assemblies, the three RNAs did not exhibit any difference in terms of binding affinity with CCMV CPs. As a consequence, the topological differences between the studied RNA segments do not seem to influence the binding affinity.
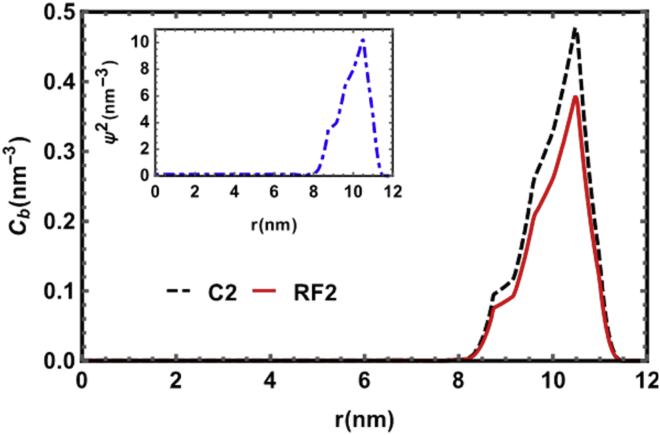
Calculated density profiles of branch points
The results of numerical calculations are given in Fig. 6 as a plot of the density profile of branch points and nucleotide density (inset graph) as a function of r, the distance from the center of the capsid; see the section Numerical calculations for the details. The black dashed line is the density profile of branch points for C2, and the red solid line is for RF2. The number of branch points was obtained through RNASubopt, a program in the Vienna RNA package (70). Generating an ensemble of secondary structures for sequences of C2 and RF2, we calculated the thermally averaged number of branch points from the secondary structures of each RNA. We found that whereas the number of monomers for C2 and RF2 were close, i.e., 2767 and 2687, respectively, the difference between the number of branch points was more significant: 60 for C2 and 48 for RF2. The number of branch points for B1 was calculated previously (53) and was estimated to be 65.
Figure 6.
Branch density profile versus r, the distance from the center of the capsid. The dashed black line and red solid line correspond to the branch density profiles for C2 and RF2, respectively. The dot-dashed blue line (inset graph) is the nucleotide density profile for C2 and RF2, which is almost the same for both. The capsid radius is R = 12 nm, N-terminal tail length is 4 nm, and the salt concentration 100 mM. The total number of positive charges on the capsid interior is 1800. To see this figure in color, go online.
Fig. 6 clearly shows that the branch point density for C2 was larger than that for RF2, whereas their nucleotide densities (inset) were almost the same. Using the profiles for RF2 and C2, we calculated the encapsulation free energy and found that it was lower for C2 (−3367 kBT, with kB the Boltzmann constant and T the temperature) than for RF2 (−3358 kBT). Because C2 and RF2 had almost the same nucleotide density profile inside the capsid, the difference of their encapsulated free energy was mainly due to the difference in their number of branch points. This slight difference in free energy explains why, experimentally, the nucleocapsids packaging C2 were statistically more uniform and better ordered across the sample than those packaging RF2.
Packaging linear versus star polyelectrolyte
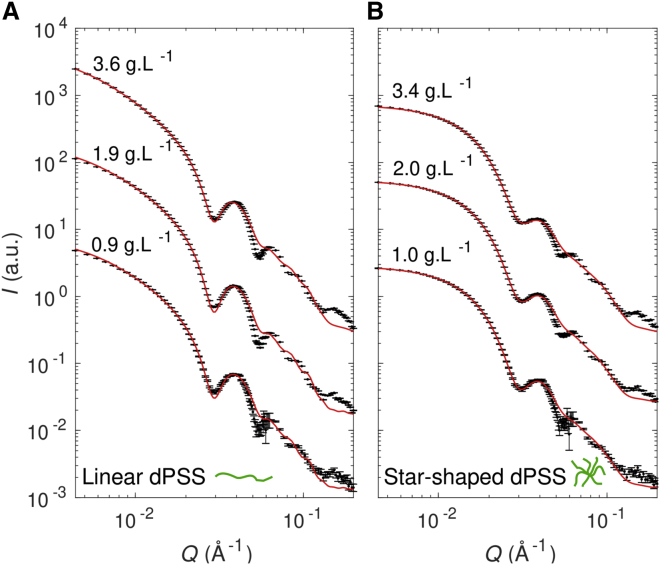
To get further insight into the physical role of the branched topology in the packaging mechanism of RNA, we assembled virus-like particles containing linear and star synthetic polyelectrolytes. PSS is a negatively charged, flexible homopolymer with a linear charge density close to that of ssRNA (∼-0.33 e⋅ Å−1). It is an excellent model to test the selective capabilities of CPs without the specific molecular recognition arising from RNA sequence. Our linear PSS had a molecular mass of 162 kDa (758 repeat units), and star PSS had a molecular mass of 160 kDa (749 repeat units) and comprised 17 arms. Thus, both PSSs possessed a similar number of charges—one negative charge per repeat unit—but a different topology. Virus-like particles were formed with various concentrations of CCMV CPs, but the CP/PSS mass ratio was kept around 6 in all cases. The structure of the capsids was investigated by using SANS with the contrast variation method. Data were collected on the D22 spectrometer at the Institut Laue Langevin, a neutron source delivering one the highest fluxes worldwide. Virus-like particles packaging dPSS were dialyzed against a buffer solution containing 100% D2O in such a way that the contrast of dPSS with solvent vanished and solely the scattering signal arising from the capsids was detected. This methodology enabled us in the past to measure accurately the mass of capsids (71). In principle, the scattering intensity arising from RNA could be contrast matched with 68% D2O. However, the contrast between CP and the solvent containing 68% D2O was so weak that we could not probe the capsid structure by SANS in the presence of RNA.
Fig. 7 depicts SANS patterns of virus-like particles packaging linear and star dPSS. As mentioned previously, in 100% D2O, the scattering curves reflect the morphology of the capsids only. The CP concentrations for each dPSS topology were sufficiently close to allow a direct comparison of the capsid morphologies. Oscillations of the SANS patterns were slightly more pronounced with the linear dPSS (Fig. 7 A) than with the star one (Fig. 7 B). Such oscillations are characteristic of spherically symmetric objects, and the fact that their amplitudes are damped indicated a morphological variability across the population and/or the presence of defects within the capsids.
Figure 7.
Effect of polyelectrolyte topology on capsid structure. SANS patterns of capsids packaging linear (A) and star (B) dPSS in 100% D2O in moderate ionic strength buffer (50 mM NaCl, 50 mM Tris-HCl (pD 7.5)). The CP concentrations are indicated next to each curve, and the CP/PSS mass ratio was set to 6. The scattering data were fitted with a polydisperse vesicle model (red solid line; see Materials and methods for details). To see this figure in color, go online.
Table 2 gives the mean number of subunits per capsid inferred from the Porod volume. The values were all around 60, which would suggest the formation of T = 2 icosahedral capsids, comprising, however, a few defects. Notice that the capsids packaging star dPSS contained slightly more subunits than those with linear dPSS. To obtain a measure of this morphological variability, at least in an approximate fashion, the experimental scattering curves were fitted with a model of polydisperse vesicles (red curves in Fig. 7). The relative SD on the core radius, ΔR/R, turned out to be two or threefold higher for capsids with star dPSS than those with linear dPSS, which means that the latter were more uniform across the population and/or with fewer defects than the former. Nevertheless, the SANS patterns on Fig. 7 A exhibited an increase of intensity at very small Q-values, which is characteristic of an attractive interaction between the capsids, fairly reproduced by introducing a sticky hard sphere interaction potential in the structure factor of the model of polydisperse vesicles (red curves in Fig. 7 A). An explanation might be that the long chains of linear dPSS (contour length >150 nm) partly exited out of the capsid and linked the neighboring capsids, which was much less likely with star dPSS (end-to-end distance ∼20 nm).
Table 2.
Characteristics of capsids packaging dPSS inferred from SANS patterns
| Sample | CP concentration (g ⋅ L−1) | ΔR/R (%) | |
|---|---|---|---|
| Linear dPSS | 0.9 | 58 | 8.5 |
| 1.9 | 59 | 9.5 | |
| 3.6 | 59 | 16 | |
| Star dPSS | 1.0 | 68 | 30 |
| 2.0 | 64 | 34 | |
| 3.4 | 66 | 41 |
is the mean number of subunits in the capsids estimated from the Porod volume, and ΔR/R is the polydispersity on the core radius of a vesicle model.
Conclusions
This study compared the structure of CCMV nucleocapsids packaging various RNA segments with similar lengths but decreasing levels of compactness; C2 belongs to CCMV genome, B1 comes from a close relative, namely BMV, and RF2 is an unrelated segment derived from rotavirus genome. ITC measurements showed that the binding affinity of CCMV CPs for each RNA was of the same magnitude, which indicated that there was no specific mechanism of recognition in the form of packaging signals. Yet, SAXS patterns showed that the nucleocapsids packaging C2 and B1 exhibited a higher degree of order than those packaging RF2. A closer look at the single-particle level by cryoTEM revealed that even in the latter case, some spherical nucleocapsids resembling native virions were formed, whereas the majority of the other particles seemed partially assembled or amorphous. Because RF2 had a lower number of branch points than C2, theoretical calculations revealed that the free energy for packaging RF2 was slightly higher than for packaging C2. The difference was, however, mild and could explain the presence of a significant fraction of spherical nucleocapsids in both cases.
The last set of experiments carried out with synthetic polyelectrolytes demonstrated that a branched topology does not always guarantee a good packaging in terms of morphological structure of capsids. Indeed, capsids packaging linear polyelectrolytes were more ordered and/or less variable than those enclosing star polyelectrolytes carrying the same number of charges. This finding is in good agreement with competition experiments demonstrating that linear, structureless polyU were packaged preferentially in comparison with viral RNA of the same length (28). In a previous work, we reported that an average number of eight linear chains of this molecular weight was packaged within each capsid (71). Therefore, one can imagine that it may be energetically less favorable to coat the interior of a capsid with a few star polyelectrolytes, whereas linear chains can readily cover the surface because each monomer can sit next to the wall. There may be a tradeoff between the compactness offered by a branched topology and the easiness of coating the capsid interior to neutralize the RNA-binding domain of CPs. Additionally, the electrostatic repulsion between star polyelectrolytes should be stronger because of their compactness.
In a biological context, CCMV virions self-assemble inside the host cell near the endoplasmic reticulum (6,21), that is, in a dense and crowded milieu. Because the viral genome lacks packaging signals ensuring its specific recognition by CPs, the virus must have developed a strategy to prevent the uptake of cellular RNA, which would jeopardize its survival. Our work confirms that the compactness of viral RNA can favor its packaging, but it does not imply an all-or-nothing process in which less compact exogenous RNA will be simply rejected. Instead, nucleocapsids packaging nonviral RNA have a larger variability and are mostly partially assembled. Because CPs can rapidly unbind RNA segments as long as capsids are not closed up, it gives a competitive advantage to more compact viral RNA that will capture CPs by completing more virions. Nonetheless, the most powerful driving force for the selectivity of viral genome might be the spatial proximity between the RNA replication site and that of CP translation. The segments of viral RNA might be packaged near the exit of ribosomes by a highly concentrated flow of CPs, thus ensuring the purity of the RNA content and facilitating the proper assembly of icosahedral capsids through the chemical potential (65).
Author contributions
L.M., L.G., R.L.R., C.S., and G.T. performed the experiments. L.M., K.K., C.S., S.B., and G.T. analyzed the data. Y.D., S.P., and R.Z. carried out the simulations. L.M. and G.T. wrote the article.
Acknowledgments
Plasmid coding for CCMV RNA 2 was kindly provided by Christian Beren at University of California Los Angeles. Plasmid coding for BMV RNA 1 was provided by Rees Garmann at Harvard University. We are grateful to Didier Poncet for the supply of plasmid coding for rotavirus RF RNA 2 and for his help in RNA production. We thank Jéril Degrouard, Aurélien Thureau and Anne Martel for their technical assistance with cryoTEM, SAXS and SANS, respectively.
L.M., R.L.R., S.B., and G.T. acknowledge financial support from the Agence Nationale de la Recherche (contract ANR-16-CE30-0017-01). K.K. is supported by Agence Nationale de Recherches sur le Sida et les hépatites virales (ANRS) | Maladies infectieuses émergentes. Y.D., S.P., and R.Z. are supported by the National Science Foundation through award DMR-1719550. The electron microscopy imaging is supported by “Investissements d’Avenir” LabEx PALM (contract ANR-10-LABX-0039-PALM). We also acknowledge the SOLEIL synchrotron and the Institut Laue Langevin for allocation of beam time on the SWING and D22 beamlines, respectively. Financial support from the IR-RMN-THC FR 3050 CNRS for conducting the research is gratefully acknowledged.
Editor: Wilma Olson.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.08.021.
Supporting material
References
- 1.Zhang Y.-Z., Chen Y.-M., Holmes E.C. Expanding the RNA virosphere by unbiased metagenomics. Annu. Rev. Virol. 2019;6:119–139. doi: 10.1146/annurev-virology-092818-015851. [DOI] [PubMed] [Google Scholar]
- 2.Roos W.H., Bruinsma R., Wuite G.J.L. Physical virology. Nat. Phys. 2010;6:733–743. [Google Scholar]
- 3.Bruinsma R.F., Klug W.S. Physics of viral shells. Annu. Rev. Condens. Matter Phys. 2015;6:245–268. [Google Scholar]
- 4.Zandi R., Dragnea B., Podgornik R. On virus growth and form. Phys. Rep. 2020;847:1–102. [Google Scholar]
- 5.Speir J.A., Johnson J.E. Nucleic acid packaging in viruses. Curr. Opin. Struct. Biol. 2012;22:65–71. doi: 10.1016/j.sbi.2011.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Comas-Garcia M. Packaging of genomic RNA in positive-sense single-stranded RNA viruses: a complex story. Viruses. 2019;11:253. doi: 10.3390/v11030253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Perlmutter J.D., Hagan M.F. Mechanisms of virus assembly. Annu. Rev. Phys. Chem. 2015;66:217–239. doi: 10.1146/annurev-physchem-040214-121637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Garmann R.F., Comas-Garcia M., Gelbart W.M. Physical principles in the self-assembly of a simple spherical virus. Acc. Chem. Res. 2016;49:48–55. doi: 10.1021/acs.accounts.5b00350. [DOI] [PubMed] [Google Scholar]
- 9.Chevreuil M., Law-Hine D., Tresset G. Nonequilibrium self-assembly dynamics of icosahedral viral capsids packaging genome or polyelectrolyte. Nat. Commun. 2018;9:3071. doi: 10.1038/s41467-018-05426-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bruinsma R.F., Wuite G.J.L., Roos W.H. Physics of viral dynamics. Nat. Rev. Phys. 2021;3:76–91. doi: 10.1038/s42254-020-00267-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Johnson J.M., Tang J., Zlotnick A. Regulating self-assembly of spherical oligomers. Nano Lett. 2005;5:765–770. doi: 10.1021/nl050274q. [DOI] [PubMed] [Google Scholar]
- 12.Lavelle L., Gingery M., Ruiz-Garcia J. Phase diagram of self-assembled viral capsid protein polymorphs. J. Phys. Chem. B. 2009;113:3813–3819. doi: 10.1021/jp8079765. [DOI] [PubMed] [Google Scholar]
- 13.Tresset G., Le Coeur C., Bressanelli S. Norovirus capsid proteins self-assemble through biphasic kinetics via long-lived stave-like intermediates. J. Am. Chem. Soc. 2013;135:15373–15381. doi: 10.1021/ja403550f. [DOI] [PubMed] [Google Scholar]
- 14.Ceres P., Zlotnick A. Weak protein-protein interactions are sufficient to drive assembly of hepatitis B virus capsids. Biochemistry. 2002;41:11525–11531. doi: 10.1021/bi0261645. [DOI] [PubMed] [Google Scholar]
- 15.Kegel W.K., van der Schoot P. Competing hydrophobic and screened-coulomb interactions in hepatitis B virus capsid assembly. Biophys. J. 2004;86:3905–3913. doi: 10.1529/biophysj.104.040055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tresset G., Chen J., Lansac Y. Two-dimensional phase transition of viral capsid gives insights into subunit interactions. Phys. Rev. Appl. 2017;7:014005. [Google Scholar]
- 17.Chen J., Lansac Y., Tresset G. Interactions between the molecular components of the cowpea chlorotic mottle virus investigated by molecular dynamics simulations. J. Phys. Chem. B. 2018;122:9490–9498. doi: 10.1021/acs.jpcb.8b08026. [DOI] [PubMed] [Google Scholar]
- 18.Bruinsma R.F., Comas-Garcia M., Grosberg A.Y. Equilibrium self-assembly of small RNA viruses. Phys. Rev. E. 2016;93:032405. doi: 10.1103/PhysRevE.93.032405. [DOI] [PubMed] [Google Scholar]
- 19.Schneemann A. The structural and functional role of RNA in icosahedral virus assembly. Annu. Rev. Microbiol. 2006;60:51–67. doi: 10.1146/annurev.micro.60.080805.142304. [DOI] [PubMed] [Google Scholar]
- 20.Beren C., Cui Y., Gelbart W.M. Genome organization and interaction with capsid protein in a multipartite RNA virus. Proc. Natl. Acad. Sci. U S A. 2020;117:10673–10680. doi: 10.1073/pnas.1915078117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.den Boon J.A., Diaz A., Ahlquist P. Cytoplasmic viral replication complexes. Cell Host Microbe. 2010;8:77–85. doi: 10.1016/j.chom.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Routh A., Domitrovic T., Johnson J.E. Host RNAs, including transposons, are encapsidated by a eukaryotic single-stranded RNA virus. Proc. Natl. Acad. Sci. USA. 2012;109:1907–1912. doi: 10.1073/pnas.1116168109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Patel N., White S.J., Stockley P.G. HBV RNA pre-genome encodes specific motifs that mediate interactions with the viral core protein that promote nucleocapsid assembly. Nat. Microbiol. 2017;2:17098. doi: 10.1038/nmicrobiol.2017.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Twarock R., Bingham R.J., Stockley P.G. A modelling paradigm for RNA virus assembly. Curr. Opin. Virol. 2018;31:74–81. doi: 10.1016/j.coviro.2018.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Qu F., Morris T.J. Encapsidation of turnip crinkle virus is defined by a specific packaging signal and RNA size. J. Virol. 1997;71:1428–1435. doi: 10.1128/jvi.71.2.1428-1435.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Comas-Garcia M., Cadena-Nava R.D., Gelbart W.M. In vitro quantification of the relative packaging efficiencies of single-stranded RNA molecules by viral capsid protein. J. Virol. 2012;86:12271–12282. doi: 10.1128/JVI.01695-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cadena-Nava R.D., Comas-Garcia M., Gelbart W.M. Self-assembly of viral capsid protein and RNA molecules of different sizes: requirement for a specific high protein/RNA mass ratio. J. Virol. 2012;86:3318–3326. doi: 10.1128/JVI.06566-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beren C., Dreesens L.L., Gelbart W.M. The effect of RNA secondary structure on the self-assembly of viral capsids. Biophys. J. 2017;113:339–347. doi: 10.1016/j.bpj.2017.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yoffe A.M., Prinsen P., Ben-Shaul A. Predicting the sizes of large RNA molecules. Proc. Natl. Acad. Sci. USA. 2008;105:16153–16158. doi: 10.1073/pnas.0808089105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gopal A., Egecioglu D.E., Gelbart W.M. Viral RNAs are unusually compact. PLoS One. 2014;9:e105875. doi: 10.1371/journal.pone.0105875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tubiana L., Božič A.L., Podgornik R. Synonymous mutations reduce genome compactness in icosahedral ssRNA viruses. Biophys. J. 2015;108:194–202. doi: 10.1016/j.bpj.2014.10.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Singaram S.W., Garmann R.F., Ben-Shaul A. Role of RNA branchedness in the competition for viral capsid proteins. J. Phys. Chem. B. 2015;119:13991–14002. doi: 10.1021/acs.jpcb.5b06445. [DOI] [PubMed] [Google Scholar]
- 33.Li S., Erdemci-Tandogan G., Zandi R. Impact of a nonuniform charge distribution on virus assembly. Phys. Rev. E. 2017;96:022401. doi: 10.1103/PhysRevE.96.022401. [DOI] [PubMed] [Google Scholar]
- 34.Perlmutter J.D., Perkett M.R., Hagan M.F. Pathways for virus assembly around nucleic acids. J. Mol. Biol. 2014;426:3148–3165. doi: 10.1016/j.jmb.2014.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Erdemci-Tandogan G., Wagner J., Zandi R. Effects of RNA branching on the electrostatic stabilization of viruses. Phys. Rev. E. 2016;94:022408. doi: 10.1103/PhysRevE.94.022408. [DOI] [PubMed] [Google Scholar]
- 36.Dong Y., Li S., Zandi R. Effect of the charge distribution of virus coat proteins on the length of packaged RNAs. Phys. Rev. E. 2020;102:062423. doi: 10.1103/PhysRevE.102.062423. [DOI] [PubMed] [Google Scholar]
- 37.Sivanandam V., Mathews D., Rao A.L.N. Functional analysis of the N-terminal basic motif of a eukaryotic satellite RNA virus capsid protein in replication and packaging. Sci. Rep. 2016;6:26328. doi: 10.1038/srep26328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Caspar D.L., Klug A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
- 39.Lorman V.L., Rochal S.B. Density-wave theory of the capsid structure of small icosahedral viruses. Phys. Rev. Lett. 2007;98:185502. doi: 10.1103/PhysRevLett.98.185502. [DOI] [PubMed] [Google Scholar]
- 40.Speir J.A., Munshi S., Johnson J.E. Structures of the native and swollen forms of cowpea chlorotic mottle virus determined by X-ray crystallography and cryo-electron microscopy. Structure. 1995;3:63–78. doi: 10.1016/s0969-2126(01)00135-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Choi Y.G., Rao A.L.N. Packaging of brome mosaic virus RNA3 is mediated through a bipartite signal. J. Virol. 2003;77:9750–9757. doi: 10.1128/JVI.77.18.9750-9757.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ali A., Roossinck M.J. Rapid and efficient purification of Cowpea chlorotic mottle virus by sucrose cushion ultracentrifugation. J. Virol. Methods. 2007;141:84–86. doi: 10.1016/j.jviromet.2006.11.038. [DOI] [PubMed] [Google Scholar]
- 43.Porterfield J.Z., Zlotnick A. A simple and general method for determining the protein and nucleic acid content of viruses by UV absorbance. Virology. 2010;407:281–288. doi: 10.1016/j.virol.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vink H. A new convenient method for the synthesis of poly(styrenesulfonic acid) Makromol. Chem. 1981;182:279–281. [Google Scholar]
- 45.Punjani A., Rubinstein J.L., Brubaker M.A. cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nat. Methods. 2017;14:290–296. doi: 10.1038/nmeth.4169. [DOI] [PubMed] [Google Scholar]
- 46.Franke D., Petoukhov M.V., Svergun D.I. ATSAS 2.8: a comprehensive data analysis suite for small-angle scattering from macromolecular solutions. J. Appl. Cryst. 2017;50:1212–1225. doi: 10.1107/S1600576717007786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Breßler I., Kohlbrecher J., Thünemann A.F. SASfit: a tool for small-angle scattering data analysis using a library of analytical expressions. J. Appl. Cryst. 2015;48:1587–1598. doi: 10.1107/S1600576715016544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.van der Schoot P., Zandi R. Impact of the topology of viral RNAs on their encapsulation by virus coat proteins. J. Biol. Phys. 2013;39:289–299. doi: 10.1007/s10867-013-9307-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.de Gennes P.-G. Cornell University Press; Ithaca, NY: 1979. Scaling Concepts in Polymer Physics. [Google Scholar]
- 50.Li S., Orland H., Zandi R. Self consistent field theory of virus assembly. J. Phys. Condens. Matter. 2018;30:144002. doi: 10.1088/1361-648X/aab0c6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Borukhov I., Andelman D., Orland H. Random polyelectrolytes and polyampholytes in solution. Eur. Phys. J. B. 1998;5:869–880. [Google Scholar]
- 52.Siber A., Podgornik R. Nonspecific interactions in spontaneous assembly of empty versus functional single-stranded RNA viruses. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:051915. doi: 10.1103/PhysRevE.78.051915. [DOI] [PubMed] [Google Scholar]
- 53.Erdemci-Tandogan G., Wagner J., Zandi R. RNA topology remolds electrostatic stabilization of viruses. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014;89:032707. doi: 10.1103/PhysRevE.89.032707. [DOI] [PubMed] [Google Scholar]
- 54.Wagner J., Erdemci-Tandogan G., Zandi R. Adsorption of annealed branched polymers on curved surfaces. J. Phys. Condens. Matter. 2015;27:495101. doi: 10.1088/0953-8984/27/49/495101. [DOI] [PubMed] [Google Scholar]
- 55.Borukhov I., Andelman D., Orland H. Polyelectrolyte solutions between charged surfaces. Europhys. Lett. 1995;32:499–504. [Google Scholar]
- 56.Shafir A., Andelman D., Netz R.R. Adsorption and depletion of polyelectrolytes from charged surfaces. J. Chem. Phys. 2003;119:2355–2362. [Google Scholar]
- 57.Siber A., Božič A.L., Podgornik R. Energies and pressures in viruses: contribution of nonspecific electrostatic interactions. Phys. Chem. Chem. Phys. 2012;14:3746–3765. doi: 10.1039/c1cp22756d. [DOI] [PubMed] [Google Scholar]
- 58.Lubensky T.C., Isaacson J. Statistic of lattice animals and dilute branched polymers. Phys. Rev. A. 1979;20:2130–2146. [Google Scholar]
- 59.Lee S.I., Nguyen T.T. Radial distribution of RNA genomes packaged inside spherical viruses. Phys. Rev. Lett. 2008;100:198102. doi: 10.1103/PhysRevLett.100.198102. [DOI] [PubMed] [Google Scholar]
- 60.Elleuch K., Lequeux F., Pfeuty P. Crosslink effects on equilibrium polymers. J. Phys. I France. 1995;5:465–474. [Google Scholar]
- 61.Troupin C., Dehée A., Garbarg-Chenon A. Rearranged genomic RNA segments offer a new approach to the reverse genetics of rotaviruses. J. Virol. 2010;84:6711–6719. doi: 10.1128/JVI.00547-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Durand D., Vivès C., Fieschi F. NADPH oxidase activator p67(phox) behaves in solution as a multidomain protein with semi-flexible linkers. J. Struct. Biol. 2010;169:45–53. doi: 10.1016/j.jsb.2009.08.009. [DOI] [PubMed] [Google Scholar]
- 63.Gopal A., Zhou Z.H., Gelbart W.M. Visualizing large RNA molecules in solution. RNA. 2012;18:284–299. doi: 10.1261/rna.027557.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Comas-Garcia M., Garmann R.F., Gelbart W.M. Characterization of viral capsid protein self-assembly around short single-stranded RNA. J. Phys. Chem. B. 2014;118:7510–7519. doi: 10.1021/jp503050z. [DOI] [PubMed] [Google Scholar]
- 65.Panahandeh S., Li S., Zandi R. How a virus circumvents energy barriers to form symmetric shells. ACS Nano. 2020;14:3170–3180. doi: 10.1021/acsnano.9b08354. [DOI] [PubMed] [Google Scholar]
- 66.Garmann R.F., Comas-Garcia M., Gelbart W.M. Role of electrostatics in the assembly pathway of a single-stranded RNA virus. J. Virol. 2014;88:10472–10479. doi: 10.1128/JVI.01044-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Maassen S.J., Huskens J., Cornelissen J.J.L.M. Elucidating the thermodynamic driving forces of polyanion-templated virus-like particle assembly. J. Phys. Chem. B. 2019;123:9733–9741. doi: 10.1021/acs.jpcb.9b06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Goobes R., Goobes G., Stayton P.S. Thermodynamics of statherin adsorption onto hydroxyapatite. Biochemistry. 2006;45:5576–5586. doi: 10.1021/bi052321z. [DOI] [PubMed] [Google Scholar]
- 69.Marichal L., Degrouard J., Pin S. From protein corona to colloidal self-assembly: the importance of protein size in protein–nanoparticle interactions. Langmuir. 2020;36:8218–8230. doi: 10.1021/acs.langmuir.0c01334. [DOI] [PubMed] [Google Scholar]
- 70.Lorenz R., Bernhart S.H., Hofacker I.L. ViennaRNA package 2.0. Algorithms Mol. Biol. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tresset G., Tatou M., Porcar L. Weighing polyelectrolytes packaged in viruslike particles. Phys. Rev. Lett. 2014;113:128305. doi: 10.1103/PhysRevLett.113.128305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.