Randomization-based confidence intervals for cluster randomized trials

Summary

In a cluster randomized trial (CRT), groups of people are randomly assigned to different interventions. Existing parametric and semiparametric methods for CRTs rely on distributional assumptions or a large number of clusters to maintain nominal confidence interval (CI) coverage. Randomization-based inference is an alternative approach that is distribution-free and does not require a large number of clusters to be valid. Although it is well-known that a CI can be obtained by inverting a randomization test, this requires testing a non-zero null hypothesis, which is challenging with non-continuous and survival outcomes. In this article, we propose a general method for randomization-based CIs using individual-level data from a CRT. This approach accommodates various outcome types, can account for design features such as matching or stratification, and employs a computationally efficient algorithm. We evaluate this method’s performance through simulations and apply it to the Botswana Combination Prevention Project, a large HIV prevention trial with an interval-censored time-to-event outcome.

1. Introduction

In a cluster randomized trial (CRT), groups of people rather than individuals are randomly assigned to receive different interventions. The correlation among individual-level outcomes must be taken into account in the statistical analysis. With continuous, count, or binary outcomes, this is typically done using a generalized linear mixed model (GLMM) fit via likelihood-based methods (Breslow and Clayton, 1993) or a marginal model fit via a generalized estimating equation (GEE) (Liang and Zeger, 1986). Similar mixed and marginal approaches exist for correlated right-censored time-to-event outcomes (Cai and Prentice, 1995; Ripatti and Palmgren, 2000; Therneau and others, 2003; Wei and others, 1989) and interval-censored outcomes (Bellamy and others, 2004; Gao and others, 2019; Goggins and Finkelstein, 2000; Kim and Xue, 2002; Kor and others, 2013; Li and others, 2014). These parametric and semiparametric methods generally require correct specification of distributional assumptions or a large number of clusters to maintain nominal type I error and confidence interval (CI) coverage. Although various small-sample corrections have been proposed, their performance can vary depending on the particular CRT scenario (Scott and others, 2017; Leyrat and others, 2018).

Randomization-based inference is an alternative approach that is distribution-free and exact. That is, it does not require specification of a particular parametric family of probability distributions and does not rely on a large number of clusters to be valid (Edgington, 1995; Ernst, 2004). Recently, there has been a resurgence of interest in randomization-based inference for CRTs, but this body of work has focused on hypothesis testing, not CIs.

It is well-known that, in theory, a randomization-based CI can be obtained by inverting a randomization test, i.e., by searching for and selecting the most extreme treatment effect values not rejected by the test. This approach requires carrying out randomization tests of a non-zero null hypothesis, such as 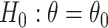, where 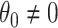. With continuous outcomes and two treatment groups, this can be done by transforming all individual-level outcomes in one group by some fixed value (Edgington, 1995, Section 4.1). Beyond continuous outcomes, however, randomization testing a non-zero null—and consequently calculating a CI—is more difficult. Among the papers that have considered randomization-based CIs for non-continuous outcomes in the CRT setting, most resort to a cluster-level approach (Gail and others, 1996; Hughes and others, 2019; Raab and Butcher, 2005; Thompson and others, 2018). For example, Gail and others (1996) used randomization-based inference in a large smoking cessation CRT with a binary outcome, but used a cluster-level summary statistic to calculate a CI. This allowed them to apply the usual transformation approach to a continuous cluster-level measure. Cluster-level approaches based on unweighted summary statistics can suffer from suboptimal efficiency when cluster sizes vary substantially because they do not incorporate the differing amounts of information contributed by each cluster. Although weighting methods or incorporation of individual-level covariates can improve the efficiency of a cluster-level analysis, the former typically requires accurate estimation of the intracluster correlation coefficient, which is difficult to obtain in practice, and the latter typically requires a two-stage approach (Hayes and Moulton, 2017, Section 11.1).

Individual-level regression approaches, on the other hand, more naturally incorporate proper weights and covariate information in a single model; however, only a handful of papers have considered individual-level approaches for randomization-based CIs. For exponential family outcomes, although the duality of testing and CIs has been pointed out (Braun and Feng, 2001,Ji and others, 2017), no details were given as to how to carry out the necessary non-zero null hypothesis test for non-continuous outcomes. In discussing methods for covariate-adjusted randomization tests and their application to balanced CRTs, Raab and Butcher (2005) mentioned an approach for binary outcomes by introducing an offset term into a logistic model to calculate adjusted residuals, but did not pursue or develop this idea further. For time-to-event outcomes, Wang and De Gruttola (2017) briefly described in the discussion how permutation tests can be inverted to obtain interval estimates when the parameter of interest is one in an accelerated failure time model. This approach required transformation of the unknown time-to-event outcomes and cannot be used to make inference about a treatment effect based on a Cox proportional hazards model. The difficulty in constructing randomization-based CIs for non-continuous and survival outcomes can manifest in an inconsistency between the p-value and CI reported in practice, where the former is calculated via randomization-based inference and the latter is not. For example, in the Botswana Combination Prevention Project, a recently published large HIV prevention trial with an interval-censored outcome, the authors used a randomization test for the primary analysis, but resorted to a semiparametric Cox model to calculate a CI (Makhema and others, 2019).

In this article, we propose a general method to construct randomization-based CIs for the intervention effect using individual-level data from a CRT. This approach accommodates various outcome types (e.g., continuous, binary, count, right- or interval-censored time-to-event), can account for design features in randomization (e.g., matching, stratification), and employs a computationally efficient algorithm. We introduce notation and present our approach in Section 2. Simulations in Section 3 demonstrate the properties of our method and compare it to alternatives. In Section 4, we reanalyze data from the Botswana Combination Prevention Project using the proposed approach to obtain a randomization-based CI for the intervention effect. We conclude with a discussion in Section 5 and give a link to our R package in Section 6.

2. Methods

2.1. Setting and notation

Consider a CRT with two groups: intervention (or treatment) and no intervention (or control). Suppose we have a total of 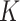clusters, 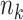individuals in the 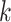th cluster, 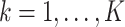, and 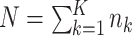total observations in the study. Let 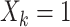indicate assignment to the intervention, 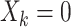for no intervention, and 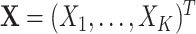denote the entire random treatment vector. Assign 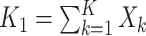clusters to intervention and the remaining 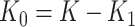to no intervention according to some predefined randomization scheme. Let 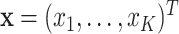denote the resulting observed treatment vector post-randomization. In this article, we consider a wide range of outcomes including continuous, binary, and count data, as well as time-to-event data subject to right- or interval-censoring. For exponential family outcomes, let 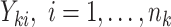, denote the outcome random variable for the 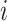th individual in the 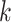th cluster. Collect all cluster-specific outcomes in a vector 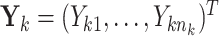and all study outcomes in a vector .

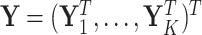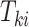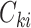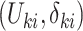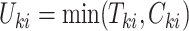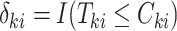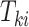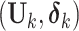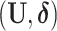When outcomes of interest are times-to-event, we follow the conventional notation. For right-censored data, let and denote the underlying survival time and potential censoring time for an individual measured from study entry. The observation for an individual is , where and is an indicator of whether is observed. We use and to denote cluster-specific and all study outcomes, respectively. We assume that censoring is noninformative: that is, 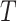and 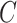are conditionally independent given 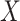. For interval-censored data, we again let 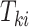denote the time-to-event measured from study entry. We consider 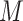distinct monitoring times at which the outcome of interest is assessed. The interval-censored outcome for an individual is 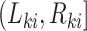, where 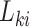is the last observed monitoring time individual 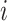in cluster 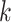is event-free, and 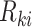is the first observed monitoring time the event of interest for this individual has occurred. Individuals who remain event-free at the last observed monitoring time are right-censored with observed interval 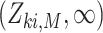. 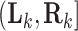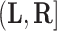We use and to denote cluster-specific and all study outcomes, respectively. We again assume noninformative interval censoring conditional on 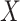, i.e.,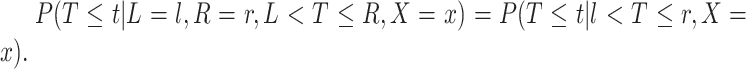

Throughout, our focus is on estimating the randomized intervention effect.

2.2. Randomization-based CIs

We propose a randomization-based approach to construct a CI for the intervention effect that does not rely on parametric distributional assumptions or a large number of clusters to be valid. This method can be used to make inference about a marginal (i.e., cluster-average) or conditional (e.g., covariate-adjusted, cluster-specific) intervention effect, and applies for exponential family outcomes (Section 2.2.1) and right- or interval-censored survival outcomes (Section 2.2.2).

2.2.1. Exponential family outcomes

Let us conceive of the sample of clusters as being representative of some hypothetical reference population of clusters. In our case, consider the population model

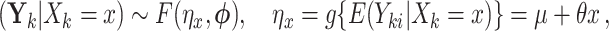(2.1)

for all 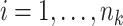and 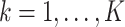. Here, 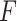is an arbitrary multivariate distribution characterized by 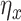and 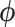, a vector of nuisance parameters not affected by treatment assignment (i.e., 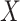only affects 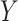through the mean model). For example, if outcomes were generated from the linear mixed model 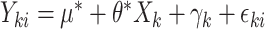with random cluster intercepts 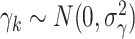and independent residual error terms 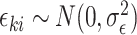, these data would coincide with population model (2.1) where 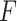is the multivariate normal distribution with each element of the mean vector corresponding to 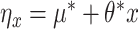and an exchangeable covariance matrix parameterized by 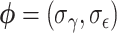. For now, we define the parameter of interest as the marginal treatment effect

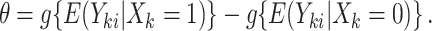(2.2)

With a continuous outcome and the identity link, 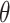corresponds to the difference in means between populations under intervention and no intervention; with a binary outcome and the logit link, 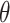corresponds to the log odds ratio between these two populations; with a count outcome and the log link, 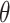is the log incidence rate ratio.

Invariance can be used to justify the validity of a randomization test under a population model like (2.1) (Lehmann and Romano, 2005, Section 15.2). Under population model (2.1) and 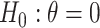, 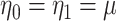. This implies that the distribution of 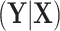is invariant under permutations of 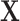that adhere to the cluster-level randomization scheme used in the study. Thus, by Theorem 15.2.1 of Lehmann and Romano (2005), a randomization test using a statistic based on our data 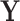and 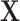will be level 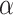, the pre-specified type I error rate, and can be carried out in the following way. First, we fit the marginal model

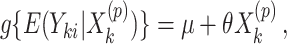(2.3)

using the observed treatment vector 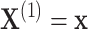to obtain the observed marginal treatment effect estimate, 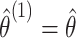. Then for 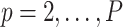, we randomly permute elements of 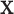in accordance with the randomization scheme, fit model (2.3) using the permuted treatment vector 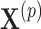, and obtain a new estimate 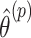. The p-value is calculated as the proportion of 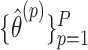as or more extreme than 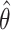. This Monte Carlo approximation to the exact p-value is used in practice because complete enumeration of all possible treatment assignment vectors is often infeasible (Dwass, 1957). We reject the null hypothesis of no treatment effect if this p-value is less than 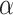. An appropriate number of permutations 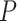for the randomization test can be based on the standard error (SE) of the Monte Carlo approximation, i.e., by ensuring the SE expression 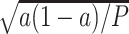is adequately low for a particular p-value = 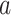, or most conservatively for .

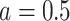A randomization-based confidence set for 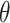can be obtained by inverting this randomization test. This requires testing null hypotheses of the form 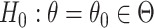and collecting the set of values not rejected by these tests. For simple settings with continuous outcomes (e.g., a two-sample t-test), this can be done by subtracting the hypothesized value 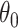from individual-level outcomes in one group, which reformulates the problem back into testing a zero null hypothesis. For linear regression settings, tests can be constructed by removing treatment effects and working with residuals. However, such approaches do not apply to non-continuous outcomes (e.g., binary, time-to-event), which are commonly used in CRTs. Our approach overcomes this challenge by working with model (2.3) directly. Rather than attempting to transform the individual-level outcomes, we carefully obtain values of the test statistic that form the randomization distribution under each non-zero null hypothesis. We can rewrite the marginal model as

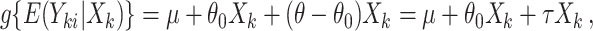(2.4)

and test an equivalent null hypothesis of 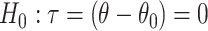. This requires obtaining estimates 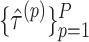under different randomizations, each of which can be calculated by fitting the model

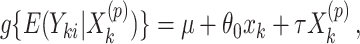(2.5)

using the observed treatment vector 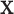for the fixed offset term 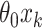and the permuted treatment vector 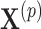for the offset-adjusted treatment effect term 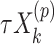. Under population model (2.1) and 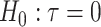, the only functional relationship preventing 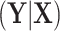from being invariant is a (transformed) mean shift of 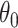between treatment and control clusters. By including the fixed offset term 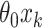in model (2.5) across all 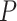permutations, we eliminate this shift, resulting in invariance and, thus, a level 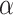randomization test for any 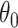. Carrying out this test across all 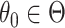and collecting the set of values not rejected by these tests provides a 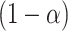randomization-based confidence set for 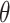, the bounds of which form a 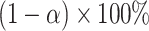CI for 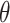. This method uses individual-level data and works for a generic outcome and link function. For a continuous outcome with the identity link, this coincides exactly with the commonly used approach of transforming the outcome directly.

Note that like other randomization-based methods, because the randomization distribution of our test statistic is discrete, an exact arbitrary size 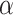test may require a randomized testing procedure, i.e., flipping a biased coin for values on the boundary of the rejection region in order to obtain exact size 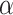; otherwise, the test is level 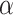and the corresponding confidence level can be conservative. For example, if there were only 50 unique equiprobable values of the test statistic in the randomization distribution, the largest achievable randomization test p-value less than 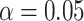is 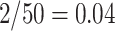; inverting this test would result in a 96% CI. This conservativeness becomes negligible as the number of values in the randomization distribution increases.

Summarizing up to this point, we have the following results. Given population model (2.1), a randomization test of 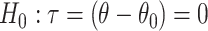using 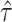from offset-adjusted model (2.5) is level 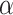. Correspondingly, the set of 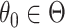not rejected by this randomization test form a 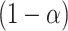confidence set for 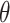, the bounds of which form a 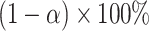CI.

This CI approach is quite flexible: it can be generalized to obtain interval estimates for covariate-adjusted and cluster-specific treatment effects. Let 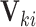denote a vector of cluster- or individual-level covariates. Suppose that we are interested in estimating 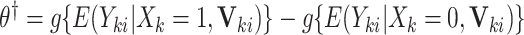, and the population model is given by

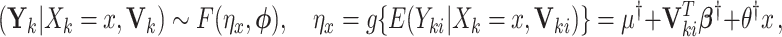(2.6)

where 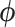is not affected by treatment assignment. A level 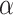randomization test of 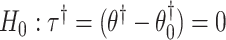can be obtained using the randomization distribution formed by 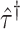from the offset-adjusted model

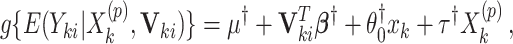(2.7)

because after controlling for 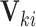and removing the covariate-adjusted treatment effect 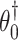via the fixed offset term, the distribution of 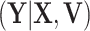is invariant under permutations of 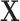. Collecting all 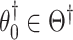not rejected by this test forms a 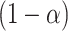confidence set for 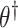, the bounds of which form a 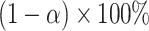CI. Similar results can be obtained for the cluster-specific treatment effect 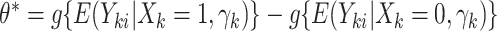using the offset-adjusted GLMM

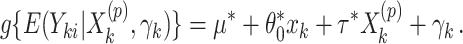(2.8)

These conditional approaches might result in improved efficiency of the randomization-based CI, but in general relate to a different (conditional, not marginal) intervention effect.

2.2.2. Time-to-event outcomes

For right-censored data, suppose that we are interested in estimating 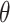, the marginal log hazard ratio (HR) of treatment in the Cox proportional hazards model 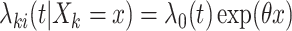. Consider the population model

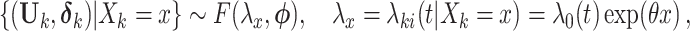(2.9)

where 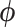is a vector of nuisance parameters not affected by treatment assignment and where censoring is noninformative. Following similar arguments to before, a level 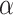randomization test of 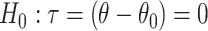can be obtained using the randomization distribution of 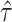from the offset-adjusted proportional hazards model

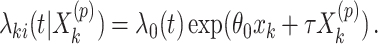(2.10)

A corresponding 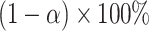CI for 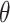can be obtained by inverting this randomization test. Similar results apply to interval-censored data, where instead of (2.9), the population model would now become 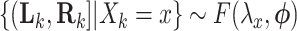, where .

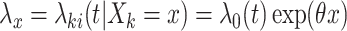2.2.3. Other considerations

More generally, this randomization-based approach to CIs can be used to make inference about the intervention effect in models that accommodate an offset term. Other than proper randomization, validity of this method relies on correct specification of the population model. This assumption is more flexible than its counterpart in mixed models because, although we similarly postulate a common distribution 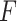across clusters, aside from the mean (or proportional hazards) model, the form of this distribution is left completely unspecified; i.e., correct specification of a particular probability distribution is not required. It can be more restrictive than other semiparametric methods (e.g., GEEs) because the population models considered here limit the effect of intervention to one aspect of the distribution (the mean for exponential family outcomes and hazard function for survival outcomes). Importantly, however, its validity does not rely on the number of clusters being large. Another advantage of randomization-based inference is the ease of accounting for design features, such as matching or stratification, in the analysis. When carrying out the randomization test, we simply consider only those treatment permutations possible under that particular design. For example, if 20 clusters were randomized in pairs, we would sample 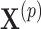from the 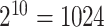possible pair-matched randomizations as opposed to all 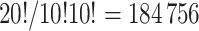unrestricted randomizations. In these scenarios, randomization-based inference could even outperform parametric and semiparametric methods in terms of efficiency, since these alternatives often ignore such aspects of the study design.

2.3. Computational implementation

In addition to the difficulty of testing a non-zero null hypothesis, another stumbling block that limits the use of randomization-based CIs is the computational challenge. A standard grid or binary search requires performing randomization tests at many 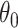to identify the bounds, each test consisting of a large number of permutations to construct the null distribution. For a typical CRT-sized data set, this could take hours or days to calculate a single CI. Instead, we adapted an efficient search procedure (Garthwaite, 1996) to our offset-adjusted approach, which can reduce the computation time down to seconds or minutes. At each step of this sequential search for the lower or upper bound, the estimate is updated based on only a single permutation of the data—thus, a single model fit. As the number of steps increases, estimates converge in probability to the correct CI bounds, i.e., the bounds that would be obtained if we carried out a full randomization test at every possible 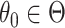(Garthwaite, 1996).

More specifically, suppose we carry out a 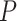-step search for 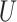, the correct upper confidence limit of 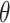defined in (2.2) (note, this 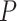could be different from that we used for the randomization test). At the 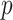th step of the search, we fit model (2.5) with the current value of the upper limit 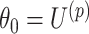and permuted treatment vector 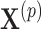to obtain the permuted offset-adjusted estimate 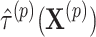. We also directly calculate the observed offset-adjusted estimate 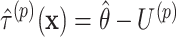based on the initial fit of model (2.3). We update the upper limit based on whether the permuted estimate is larger than the observed estimate

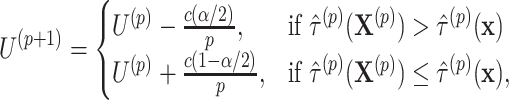(2.11)

where 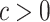is a chosen step length constant. On average, this corresponds to stepping down if the randomization-based p-value of 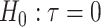versus 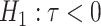is smaller than 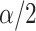and stepping up if it is greater than 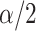. This makes sense, since 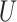would correspond to a p-value of exactly 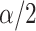for this one-sided randomization test. An independent search is carried out for the correct lower limit 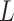in a similar fashion using

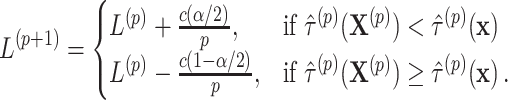(2.12)

To avoid early steps changing dramatically in size, the 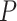-step search should begin w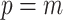ith with 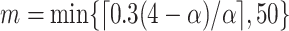(Garthwaite, 1996). Thus, 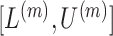correspond to our chosen starting values and the final updated values 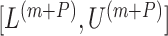are adopted as the CI.

Though this efficient search algorithm substantially reduces the computational burden of randomization-based CIs, its performance could be affected by the starting values, step length, or total number of steps chosen. Detailed guidance on choosing these tuning parameters can be found in Section 3 of Garthwaite (1996). Based on their recommendations, we use 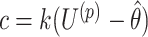and 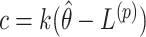for the upper and lower bound search, respectively, where 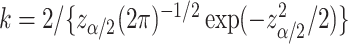and 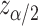is the upper 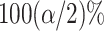point of the standard normal distribution. Starting values are based on 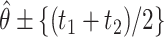, where 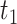and 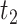are the second smallest and second largest permuted offset-adjusted estimates from a randomization test of 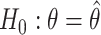using 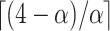permutations. Diagnostic plots (e.g., Figure 3) can be used to guide (or confirm) adequate choice of 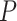. We can also choose 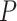based on the asymptotic variance of the coverage of a 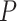-step search

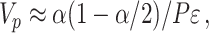(2.13)

where 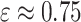for the recommended value of 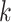above. Using (2.13), we can either choose an acceptable 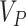and solve for 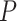, or choose 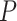and ensure this results in an acceptable 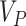. Finally, we echo some practical suggestions made by Garthwaite (1996), such as monitoring convergence of the CI bounds, restarting the procedure if the starting values seem poor, using multiple chains with different starting values, and considering different step length constants—all of which can be implemented using our R package (see Section 6).

Fig. 3.

Efficient search for a randomization-based 95% CI for the intervention effect in the Botswana Combination Prevention Project, using the procedure adapted from Garthwaite (1996). Here, we monitor four separate chains using different starting values. The first 5000 (of 20 000 total) steps of our final CI estimate are indicated by bold black lines; other chains (included to assess adequate convergence) are indicated by thin colored lines. This figure appears in color in the electronic version of this article.

For longer searches (e.g., 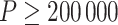), Garthwaite and Jones (2009) proposed an improvement on this algorithm by taking larger steps during later phases of the search and averaging, rather than using only the final values, for CI estimation. Details on this extension can be found in the supplementary material available at Biostatistics online. In addition to the procedure outlined above, we implemented this alternative search for our data example in Section 4.

3. Simulations

We carried out simulations to evaluate the performance of this randomization-based approach and compare it to alternative methods. Simulations were run in R 3.4.1 or higher. Results for each simulation scenario were based on 10 000 independently generated data sets.

3.1. Binary outcome

First, we considered a parallel CRT with a binary outcome. Data were generated from the GLMM

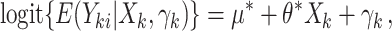(3.14)

where 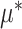was the cluster-conditional log odds of the outcome in the control group, and 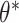was the cluster-conditional log odds ratio associated with treatment. We drew random cluster effects from a normal distribution centered at zero, i.e., 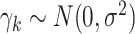. We set the population-level prevalence of the outcome in the control group at 25% (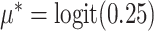). We examined different intracluster correlation coefficients ( 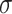= 0.1, 0.2, 0.5, which induced ICC 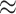0.001, 0.01, 0.05), underlying treatment effects ( 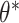= 0, 0.25, 0.5), numbers of clusters ( 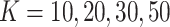with 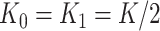), and ranges of cluster sizes ( 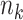drawn uniformly from 10 to 50 and 100 to 200). Each true marginal treatment effect 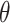induced by data generating model (3.14) was approximated using Gauss–Hermite quadrature.

We analyzed each data set with our proposed randomization-based method. We targeted the marginal treatment effect 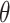defined in (2.2) by using 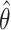from model (2.3) for the randomization test of no treatment effect and 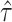from model (2.5) for the randomization-based CI, both with 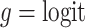. The p-value and each bound of the 95% CI were based on 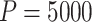, which provided sufficiently accurate p-value estimates (e.g., SE 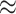0.003 for p-value = 0.05) and acceptable coverage precision of the CI search based on (2.13) (e.g., 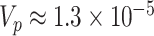for 95% coverage). We also considered three alternative approaches. First, we fit a marginal model via GEE using the standard sandwich variance estimator. We also fit a small-sample adjusted GEE using the 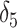adjustment proposed by Fay and Graubard (2001), which has been shown to perform well in CRTs with a small number of clusters (Scott and others, 2017). Both GEEs targeted the marginal treatment effect 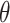as well. Finally, we fit GLMM (3.14) via maximum likelihood, which targeted the cluster-conditional treatment effect 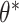instead. We used a Laplace approximation (default in lme4::glmer() in R) to approximate the log likelihood. All three of these alternative models were correctly specified and used two-sided Wald tests and corresponding 95% CIs. CI coverages were calculated with respect to the true value of the target parameter, i.e., 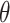for randomization-based inference and GEE, and 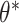for GLMM.

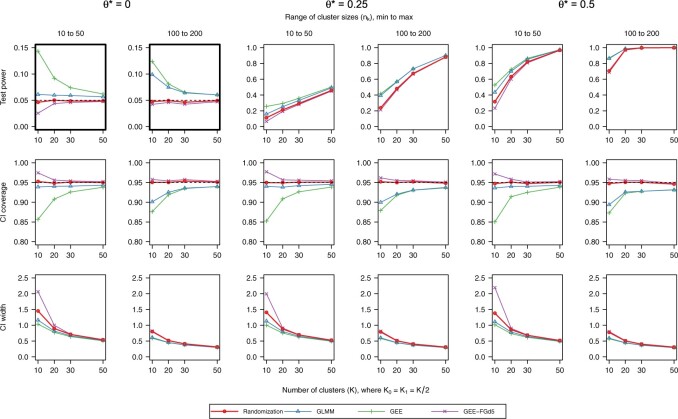
Results for ICC 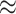0.01 are presented in Figure 1. In general, randomization-based inference resulted in nominal type I error rates (0.046–0.050), nominal CI coverages (0.946–0.954), and CI widths ranging from 0.31 to 1.45. The small-sample adjusted GEE resulted in conservative type I error rates (0.025–0.048), nominal to conservative CI coverages (0.948–0.978), and wider CIs (0.31–2.19), especially when 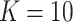and cluster sizes were small. The GLMM and standard GEE both had inflated type I error (e.g., 0.10 and 0.12, respectively, for 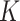= 10 and 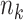from 100 to 200), undercoverage (e.g., 0.90 and 0.88), and the narrowest CIs.

Fig. 1.

Simulation results of a parallel CRT with a binary outcome (ICC 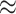0.01). Methods considered include randomization-based inference (Randomization), a logistic GLMM fit via maximum likelihood (GLMM), a marginal model fit via a GEE, and a small-sample adjusted GEE (GEE-FGd5). Two bold upper-left plots have a different y-axis range from others in the first row for clarity. This figure appears in color in the electronic version of this article.

Results for ICC 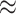0.001 and 0.05 are presented in Figures S1 and S2 of the supplementary material available at Biostatistics online. Both GEE approaches got worse as ICC and cluster sizes decreased: the standard GEE approach became more liberal while the small-sample adjusted GEE became more conservative. GLMM size and coverage became more liberal as ICC and cluster sizes increased. Randomization-based inference performed well for all settings we examined.

In terms of efficiency, our randomization-based approach outperformed the small-sample adjusted GEE, especially with smaller numbers of clusters, cluster sizes, and ICC. Across all scenarios, it provided equivalent or better power and CI widths while maintaining nominal type I error and coverage. While the GLMM and unadjusted GEE methods appeared to yield better efficiency, this result was distorted by their inflated type I error rates and undercoverage. In fact, in scenarios where the asymptotic approaches had close to nominal type I error and coverage (e.g., 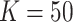or ICC 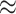0.001 for GLMM), randomization-based inference resulted in very minimal efficiency loss compared to these alternative methods.

Computation times in R varied by simulation scenario, but ranged anywhere from about 20 seconds (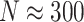) to 4 min (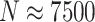) to calculate a single randomization-based CI with 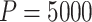permutations, run in parallel across two logical CPUs on a MacBookAir8,1 with a 1.6 GHz Intel Core i5 (see Table S1 in the supplementary material available at Biostatistics online).

3.2. Time-to-event outcome

Next, we considered a pair-matched CRT with an interval-censored time-to-event outcome. This simulation was designed to align closely with our data example in Section 4, the Botswana Combination Prevention Project. Event times were generated from an exponential frailty model

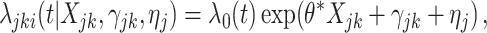(3.15)

where now 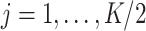and 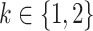jointly index each cluster, 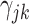is a cluster-specific random effect, and 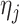is a pair-specific random effect, both drawn independently from a 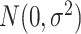. Actual study visit times were drawn uniformly within a 2-month window centered around an annually scheduled visit, resulting in an interval-censored outcome. Loss to follow-up occurred at a constant exponential rate of about 10% each year and individuals were followed for at most 3 years. Each data set had 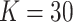clusters with sizes ranging from 250 to 350 individuals.

We examined coverage and efficiency of our randomization-based approach across different underlying treatment effects (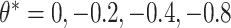) and within-cluster and -pair correlations (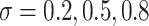). Randomization-based inference was based on 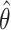, the estimated log HR from an interval-censored Weibull regression model

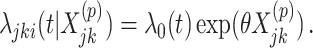(3.16)

We sampled 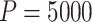permutations from all possible 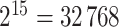pair-matched randomizations. For comparison, we fit two Weibull frailty models: the first corresponded to model (3.15) without (i.e., only accounting for within-cluster correlation), the second without 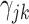(i.e., only accounting for within-pair correlation). This was done because there is currently no reliable software in R to fit an interval-censored survival model with more than one frailty term for data sets with large cluster sizes. Wald tests and CIs were used for these alternative approaches. We note that the treatment effect parameter 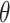in marginal model (3.16) or in either single-frailty conditional model is generally different from 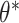in the data generating model (3.15). The true values for these parameters were obtained via simulation. We also point out that data generation model (3.15), a proportional hazards model conditional on both frailties, does not necessarily induce a proportional hazards model marginally or conditional on only a single frailty (Martinussen and Andersen, 2018; Ritz and Spiegelman, 2004). In other words, all three analysis models are misspecified, making the precise interpretation of the target parameter difficult. As such, the results presented here illustrate the robustness of each method to model misspecification.

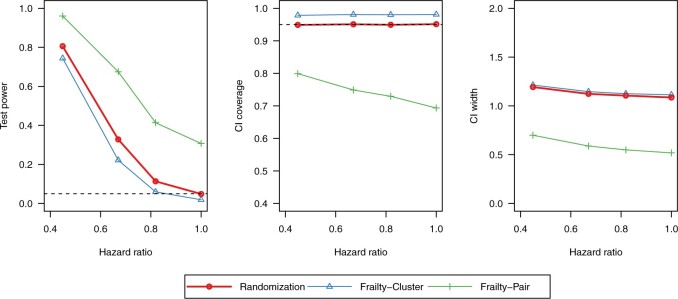
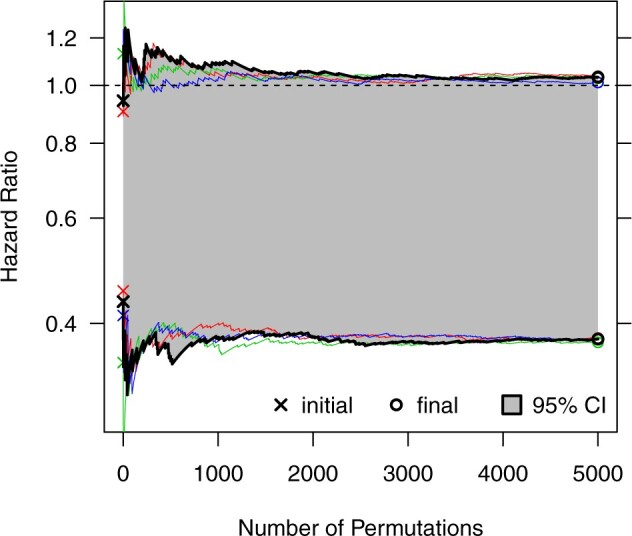
Results for 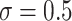are presented in Figure 2. Across all scenarios, randomization-based inference resulted in nominal type I error (0.048–0.053) and coverage (0.935–0.952). The Weibull model with a cluster-specific frailty resulted in conservative type I error (0.012–0.037) and coverage (0.963–0.988), while the model with a pair-specific frailty resulted in drastically inflated type I error (0.082–0.592) and severe undercoverage (0.408–0.957). Type I error, coverage, and convergence of both frailty models generally got worse as the within-cluster and -pair correlations increased (see Figures S3 and S4 and Table S2 in the supplementary material available at Biostatistics online). Of note, even these relatively simple parametric survival models with a single frailty term had trouble converging up to about 15% of the time for these moderately sized CRT data sets, whereas randomization-based CIs targeting the treatment effect parameter in a marginal model could always be calculated. For this larger (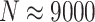) and more complex CRT setting, it took approximately 8 min to compute a single randomization-based CI in R with 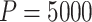permutations (computed in parallel across two logical CPUs on a MacBookAir8,1 with a 1.6 GHz Intel Core i5).

Fig. 2.

Simulation results of a pair-matched CRT with an interval-censored time-to-event outcome (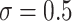). Methods considered included randomization-based inference (Randomization), a Weibull model with a frailty term for community (Frailty-Cluster), and with a frailty term for pair (Frailty-Pair). This figure appears in color in the electronic version of this article.

4. Application to the Botswana Combination Prevention Project

The Botswana Combination Prevention Project (BCPP) was a pair-matched CRT to test whether a combination prevention intervention package could reduce population-level cumulative HIV incidence over 3 years of follow-up (Makhema and others, 2019). A total of 30 communities were randomized: 15 to the intervention arm (combination prevention package) and 15 to the control arm (enhanced standard of care). Randomization was done using a pair-matched design with community matching based on population size and age structure, existing health services, and geographic location. The primary individual-level outcome was time to HIV infection, measured at annual study visits within a cohort of individuals identified as HIV-negative among a 20% random sample of eligible households at baseline. That is, we had an interval-censored time-to-event outcome for each cohort participant. The HIV-incidence cohort was composed of 8551 participants with a median of 308 (minimum 106 and maximum 392) from each of the 30 communities. There were a total of 147 HIV infections, 57 in the intervention group (annualized HIV incidence, 0.59%) and 90 in the control group (annualized HIV incidence, 0.92%). The median follow-up time was 29 months. The prespecified unadjusted primary analysis, which was based on a randomization test, yielded a p-value of 0.09. The estimated HR corresponding to treatment based on a pair-stratified Cox model was 0.65 with a 95% CI of [0.46–0.90].

We targeted the marginal log HR 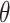from model (3.16) and applied our randomization-based approach to the BCPP data. To confirm an adequate choice of 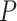, in addition to considering p-value accuracy and coverage precision, we monitored four separate chains of length 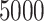, each using different initial values: first using our chosen values, second using initial values based on an asymptotic Wald CI ignoring within-cluster correlation, and third (and fourth) using initial values wider (and narrower) than the final values from the first chain. The four chains for each bound converged towards each other, began to gently oscillate around similar values, and all ended within 0.025 of each other on the HR scale (see Figure 3). Based on these characteristics, we deemed that 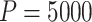resulted in acceptable convergence and demonstrated adequate robustness to different starting values for these data. It was computationally feasible, however, for us to increase to 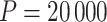to allow for even further refinement of the final CI limits (see Figure S5 in the supplementary material available at Biostatistics online). This resulted in an estimated HR of 0.64 (95% CI [0.37–1.04], p-value = 0.06). Calculation of the CI based on 20 000 permutations for each bound took about 40 min to run in R (computed in parallel across two logical CPUs on a MacBookAir8,1 with a 1.6 GHz Intel Core i5). Similar to our simulations in Section 3.2, we also fit two separate Weibull frailty models to account for the within-community and -pair correlation. Respectively, these approaches resulted in estimated HRs of 0.64 (95% CI [0.43–0.95], p-value = 0.03) and 0.64 (95% CI [0.45–0.90], p-value = 0.01). Finally, to align closely with the CI approach taken in the BCPP, we considered a pair-stratified Weibull model to estimate the treatment effect. Randomization-based inference for this model yielded a 95% CI of [0.37–1.05] (p-value = 0.07), while the likelihood-based analysis produced [0.46–0.91] (p-value = 0.01), both with point estimates of 0.65. All of these results are summarized in Table 1. Comparable CIs were found using the improved search procedure in Garthwaite and Jones (2009) (see Figure S6 and Table S3 in the supplementary material available at Biostatistics online).

Table 1.

Estimated HR of the intervention effect in the Botswana Combination Prevention Project. Methods considered include randomization-based inference (Randomization), both marginal and pair-stratified, a Weibull model with a frailty term for community (Weibull, Frailty-Cluster), with a frailty term for pair (Weibull, Frailty-Pair), and a pair-stratified Weibull model (Weibull, Pair-Stratified).

Methods	HR	95% CI	p-value
Randomization, Marginal	0.640	0.374–1.039	0.064
Randomization, Pair-Stratified	0.646	0.369–1.054	0.068
Weibull, Frailty-Cluster	0.640	0.432–0.947	0.025
Weibull, Frailty-Pair	0.641	0.453–0.905	0.012
Weibull, Pair-Stratified	0.646	0.457–0.913	0.013

Consistent with the results in Makhema and others (2019), the randomization-based p-values and CIs did not reach the pre-specified 0.05 level, while those based on models with stronger parametric assumptions or asymptotic approximations did. This discrepancy could be due to the usual robust-efficiency trade-off between distribution-free and parametric likelihood-based methods. As a threshold of 0.05 is not a magic number, all of these methods do provide evidence supporting an effect of the intervention on reducing HIV incidence. Nevertheless, it would have been desirable to report a p-value and CI using the same randomization-based analysis method. This was not possible at the time of the BCPP analysis, however, due to the unavailability of methods to obtain a randomization-based CI for correlated interval-censored survival outcomes.

5. Discussion

In this article, we proposed a fast and flexible approach to obtain randomization-based CIs using individual-level data from a CRT. We demonstrated that this method has good properties and performs well compared to other methods, even when the modeling assumptions of those alternatives were met. Randomization-based inference is especially attractive for analyzing CRTs, as it does not require specification of a particular distribution and does not rely on a large number of clusters to maintain nominal type I error and CI coverage. Another advantage of randomization-based inference is the ease with which one can account for restricted designs simply by limiting the set of treatment permutations considered in the analysis.

Some have raised concern with randomization-based inference when a different number of clusters are randomized to each arm (Braun and Feng, 2001; Gail and others, 1996). It is important to clarify that a randomization test does guarantee nominal type I error—even with a different number of clusters in each arm—under a null hypothesis corresponding to entire distributions being identical, e.g., 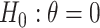under population model (2.1). This may not be the case, however, when testing a weaker null hypothesis corresponding to only some components of the distributions being equal. For example, if treatment does affect the cluster variances (e.g., where some component of 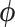in population model (2.1) depends on treatment), then a randomization test of the null hypothesis of equal means and its corresponding CI would be liberal when the arm with fewer clusters has larger variance and conservative when it has smaller variance (Gail and others, 1996; Romano, 1990). This is an important distinction to keep in mind, especially if imbalanced treatment allocations and differences in variances are expected to be substantial.

As the number of clusters or size of the clusters becomes large, randomization-based CIs using individual-level data could become computationally burdensome. With a large number of small clusters (e.g., households), this is luckily where alternative semiparametric approaches like GEE perform reasonably well. With a small number of large clusters (e.g., entire communities), most of the computational burden may be alleviated by using a cluster-level randomization-based analysis, as many have suggested (Gail and others, 1996; Hughes and others, 2019; Raab and Butcher, 2005; Thompson and others, 2018). An unweighted cluster-level analysis may lead to some loss of statistical efficiency if cluster sizes vary substantially, although this impact would be minimal when all clusters have large sizes.

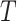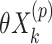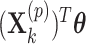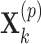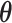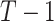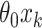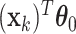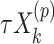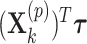More than two (say, ) treatment groups could be accommodated in a randomization test, for example, by replacing in model (2.3) with , where and are vectors of length . Similarly for the CI, we would fit model (2.5) replacing with for the fixed offset term and with for the permuted offset-adjusted treatment effect term. In theory this seems to be a straightforward extension, but in practice this means the CI search procedure must take place over a 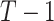dimensional space, which introduces further complexity in computing. Complex CRT designs (e.g., stepped wedge) and other outcome types and regression models could be handled by modifying the model, the permutation procedure, or both.

Finally, we have focused our work on CRTs, but this randomization-based CI approach using offset adjustment can be used with independent outcomes or in other correlated data settings, such as randomized clinical trials with repeated measurements. For survival outcomes, we focused on a proportional hazards model, but the method can be applied to an accelerated failure time model provided the corresponding population model is correctly specified.

6. Software

An R package for our method is available online at https://github.com/djrabideau/permuter.

Supplementary material

Supplementary material is available online at http://biostatistics.oxfordjournals.org.

Funding

Research reported in this publication was in part supported by the National Institute Of Allergy and Infectious Diseases of the National Institutes of Health under Award Number R01 AI136947 and T32 AI007358. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.