Summary
Computer-coded verbal autopsy (CCVA) algorithms predict cause of death from high-dimensional family questionnaire data (verbal autopsy) of a deceased individual, which are then aggregated to generate national and regional estimates of cause-specific mortality fractions. These estimates may be inaccurate if CCVA is trained on non-local training data different from the local population of interest. This problem is a special case of transfer learning, i.e., improving classification within a target domain (e.g., a particular population) with the classifier trained in a source-domain. Most transfer learning approaches concern individual-level (e.g., a person’s) classification. Social and health scientists such as epidemiologists are often more interested with understanding etiological distributions at the population-level. The sample sizes of their data sets are typically orders of magnitude smaller than those used for common transfer learning applications like image classification, document identification, etc. We present a parsimonious hierarchical Bayesian transfer learning framework to directly estimate population-level class probabilities in a target domain, using any baseline classifier trained on source-domain, and a small labeled target-domain dataset. To address small sample sizes, we introduce a novel shrinkage prior for the transfer error rates guaranteeing that, in absence of any labeled target-domain data or when the baseline classifier is perfectly accurate, our transfer learning agrees with direct aggregation of predictions from the baseline classifier, thereby subsuming the default practice as a special case. We then extend our approach to use an ensemble of baseline classifiers producing an unified estimate. Theoretical and empirical results demonstrate how the ensemble model favors the most accurate baseline classifier. We present data analyses demonstrating the utility of our approach.
Keywords: Bayesian, Classification, Epidemiology, Hierarchical modeling, Regularization, Transfer learning, Verbal autopsy
1. Introduction
Verbal autopsy—A survey of the household members of a deceased individual, act as a surrogate for medical autopsy report in many countries. Computer-coded verbal autopsy (CCVA) algorithms are high-dimensional classifiers that predict cause of death (COD) from these high-dimensional family questionnaires which are then aggregated to generate national and regional estimates of cause-specific mortality fractions (CSMF). These estimates may be inaccurate as CCVA are usually trained using non-local information not representative of the local population of interest. This problem is a special case of transfer learning, a burgeoning area in statistics and machine learning.
Classifiers trained on source-domain data tend to predict inaccurately in a target domain different from the source-domain in terms of marginal and conditional distributions of the features (covariates) and labels (responses) (Shimodaira, 2000). Various domain adaptation strategies have been explored for transfer learning of generic classifiers which adjust for this distributional difference between the two domains. We refer the readers to Weiss and others (2016) and Pan and Yang (2010) for a comprehensive review of transfer learning for classification problems. We focus on the setting where there is abundant labeled source-domain data, abundant unlabeled target-domain data, and limited labeled target data. Transfer learning approaches pertaining to this setting include multi-source-domain adaptation (CP-MDA, Chattopadhyay and others, 2012), neural networks (TCNN, Oquab and others, 2014), adaptive boosting (TrAdaBoost, Dai and others, 2007; Yao and Doretto, 2010), feature augmentation method (FAM, Daumé III, 2009), spectral feature alignment (SFA, Pan and others, 2010) among others.
All of the aforementioned transfer learning classification approaches are motivated by applications in image, video or document classification, text sentiment identification, and natural language processing where individual classification is the goal. Hence, they usually focus on the individual’s (e.g., a person’s or an image’s) classification within a target domain (e.g., a particular population) with training performed in data from a different source-domain.
Social and health scientists such as epidemiologists are often more interested with understanding etiological distributions at the population-level rather than classifying individuals. For example, we aim to estimate national and regional estimates of cause-specific fractions of child mortality. Hence, our goal is not individual prediction but rather transfer learning of population-level class probabilities in the target domain. None of the current transfer learning approaches are designed to directly estimate population-level class membership probabilities.
Additionally, the extant transfer learning approaches rely on large source-domain databases of millions of observations for training the richly parameterized algorithms. The sample sizes of datasets in epidemiology are typically orders of magnitude smaller. Most epidemiological applications use field data from surveys, leading to databases with much smaller sample sizes and yet with high-dimensional covariates (survey records). For example, in our application, the covariate space is high-dimensional ( 200–350 covariates), the “abundant” source-domain data have around
200–350 covariates), the “abundant” source-domain data have around 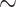 2000 samples, while the local labeled data can have as few as 20–100 samples. Clearly, in such cases, the local labeled data are too small to train a classifier on a high-dimensional set of covariates, as the resulting estimates will be highly variable. A baseline classifier trained on the larger source-domain data will tend to produce more stable estimates, but the high precision will come at the cost of sacrificing accuracy if the source- and target-domains differ substantially.
2000 samples, while the local labeled data can have as few as 20–100 samples. Clearly, in such cases, the local labeled data are too small to train a classifier on a high-dimensional set of covariates, as the resulting estimates will be highly variable. A baseline classifier trained on the larger source-domain data will tend to produce more stable estimates, but the high precision will come at the cost of sacrificing accuracy if the source- and target-domains differ substantially.
Our parsimonious solution to this bias-variance trade-off problem is to use the baseline classifier trained on source-domain information to obtain an initial prediction of target-domain class probabilities, but then refine it with the labeled target-domain data. We proffer a hierarchical Bayesian framework that unifies these two steps. With 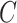 classes and
classes and  -dimensional covariates, the advantage of this new approach is that the small labeled data for the target domain is only used to estimate the
-dimensional covariates, the advantage of this new approach is that the small labeled data for the target domain is only used to estimate the 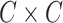 confusion matrix of the transfer error (misclassification) rates instead of trying to estimate
confusion matrix of the transfer error (misclassification) rates instead of trying to estimate  parameters of the classifier directly from the target-domain data. Since
parameters of the classifier directly from the target-domain data. Since  , this approach considerably reduces the dimensionality of the problem. To ensure a stable estimation of the confusion matrix, we additionally use a regularization prior that shrinks the matrix towards identity unless there is substantial transfer error. We show that, in the absence of any target-domain labeled data or in case of zero transfer error, posterior means of class probability estimates from our approach coincide with those from the baseline learner, establishing that the naive estimation that ignores transfer error is a special case of our algorithm. We devise a novel, fast Gibbs sampler with augmented data for our Bayesian hierarchical model.
, this approach considerably reduces the dimensionality of the problem. To ensure a stable estimation of the confusion matrix, we additionally use a regularization prior that shrinks the matrix towards identity unless there is substantial transfer error. We show that, in the absence of any target-domain labeled data or in case of zero transfer error, posterior means of class probability estimates from our approach coincide with those from the baseline learner, establishing that the naive estimation that ignores transfer error is a special case of our algorithm. We devise a novel, fast Gibbs sampler with augmented data for our Bayesian hierarchical model.
We then extend our approach to one that uses an ensemble of input predictions from multiple classifiers. The ensemble model accomplishes method-averaging over different classifiers to reduce the risk of using one method that is inferior to others in a particular study. We establish a theoretical result that the class probability estimates from the ensemble model coincides with that from a classifier with zero transfer error. A Gibbs sampler for the ensemble model is also developed, as well as a computationally lighter version of the model that is much faster and involves fewer parameters. Simulation and data analyses demonstrate how the ensemble sampler consistently produces estimates similar to those produced by using our transfer learning on the single best classifier.
Our approach is also post hoc, i.e., only uses pre-trained baseline classifier(s), instead of attempting to retrain the classifier(s) multiple times with different versions of training data. This enables us to use publicly available implementations of these classifier(s) and circumvents iterative training runs of the baseline classifier(s) which can be time-consuming and inconvenient in epidemiological settings where data collection continues for many years, and the class probabilities needs to be updated continually with the addition of every new survey record. The post hoc approach also ensures we can work with non-statistical classifiers that do not use a training data but some sort of source-domain information (e.g., CCVA algorithms InterVA and EAVA).
The rest of the manuscript is organized as follows. We present the motivating application in Section 1.1. In Sections 2 and 3, we present the methodology and its extension to the ensemble case. Section 4 considers the extension where class probabilities can be modeled as a function of a few covariates like age, sex, seasons, spatial regions, etc. Section 5 presents simulation results. Section 6 returns to the motivating dataset and uses our transfer learning model to estimate national CSMFs for children deaths in India and Tanzania. We end the manuscript in Section 7 with a discussion of limitations and future research opportunities. A glossary of the different abbreviations used throughout the text is. provided in Table 1.
Table 1.
Glossary of acronyms used in the manuscript
| Acronym | Full form | Acronym | Full form |
|---|---|---|---|
| VA | Verbal autopsy | PHMRC | Population Health Metrics Research Consortium |
| CCVA | Computer-coded VA | COMSA | Countrywide Mortality Surveillance for Action |
| COD | Cause of Death | CSMF | Cause-Specific Mortality Fraction |
| CSMFA | CSMF accuracy | GS-COD | Gold-standard Cause of Death |
1.1. Motivating dataset
In low- and middle-income countries, it is infeasible to conduct full autopsies for the majority of deaths due to economic and infrastructural constraints, and/or religious or cultural prohibitions against autopsies (AbouZahr and others, 2015; Allotey and others, 2015). An alternative method to infer the COD (or “etiology”) is to conduct verbal autopsy (VA)—a systematic interview of the relatives of the deceased individual—to obtain information about symptoms observed prior to death (Soleman and others, 2006). Statisticians have developed several specialized classifiers that predict COD using the high-dimensional VA records as input. Examples include Tariff (James and others, 2011; Serina and others, 2015), InterVA (Byass and others, 2012), InSilicoVA (McCormick and others, 2016), the King and Lu method (King and others, 2008), EAVA or expert algorithm (Kalter and others, 2015), etc. Software for many of these algorithms are publicly available, e.g., Tariff (Li and others, 2018c), InSilicoVA (Li and others, 2018a), InterVA (Thomas and others, 2018), and the openVA R-package (Li and others, 2018b) has consolidated most of these individual software into a single package. Generic classifiers like random forests (Breiman, 2001), naive Bayes classifiers (Minsky, 1961), and support vector machines (Cortes and Vapnik, 1995) have also been used (Flaxman and others, 2011; Miasnikof and others, 2015; Koopman and others, 2015) for classifying verbal autopsies. Predicted COD labels for each VA record in a nationally representative VA database is aggregated to obtain national CSMF—the population-level class membership probabilities, that are often the main quantities of interest for epidemiologists, local governments, and global health organizations.
Formally, a CCVA algorithm is simply a classifier using the 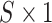 covariate vector (VA report)
covariate vector (VA report) 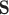 to predict
to predict 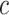 —one of
—one of 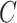 possible COD categories. Owing to the high dimensionality of the covariate space (VA record consists of responses to 200–350 questions), learning this mapping
possible COD categories. Owing to the high dimensionality of the covariate space (VA record consists of responses to 200–350 questions), learning this mapping 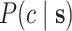 requires substantial amount of gold standard (labeled) training data. Usually in the country of interest, VA records are available for a large representative subset of the entire population, but gold standard cause of death (GS-COD) is ascertained for only a very small fraction of these deaths. In other words, there is abundant unlabeled data but extremely limited labeled data in the target domain. The ongoing project Countrywide Mortality Surveillance for Action (COMSA) Mozambique typify this circumstance, where, in addition to conducting a nationally representative VA survey, researchers will have access to gold standard COD for a small number of deaths from one or two local hospitals using minimally invasive autopsies (MIA) (Byass, 2016). Budgetary constraints and socio-cultural factors unfortunately imply that only a handful of deaths can eventually be autopsied (up to a few hundred).
requires substantial amount of gold standard (labeled) training data. Usually in the country of interest, VA records are available for a large representative subset of the entire population, but gold standard cause of death (GS-COD) is ascertained for only a very small fraction of these deaths. In other words, there is abundant unlabeled data but extremely limited labeled data in the target domain. The ongoing project Countrywide Mortality Surveillance for Action (COMSA) Mozambique typify this circumstance, where, in addition to conducting a nationally representative VA survey, researchers will have access to gold standard COD for a small number of deaths from one or two local hospitals using minimally invasive autopsies (MIA) (Byass, 2016). Budgetary constraints and socio-cultural factors unfortunately imply that only a handful of deaths can eventually be autopsied (up to a few hundred).
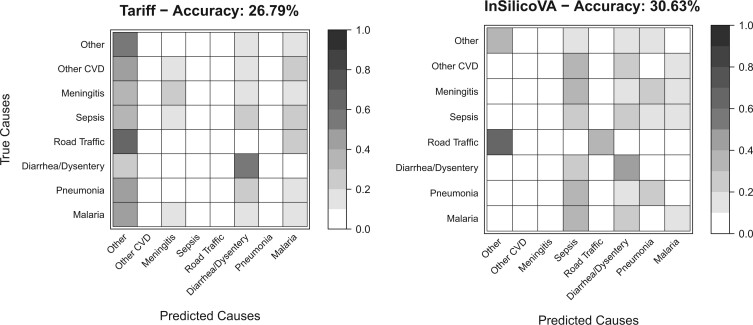
Lack of sufficient labeled target-domain data implies that CCVA classifiers need to be trained on non-local data like the publicly available Population Health Metrics Research Consortium (PHMRC) Gold Standard VA database (Murray and others, 2011a), that has more than 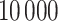 paired physician and VA assessments of cause of death across four countries. However, there exists considerable skepticism about the utility of CCVA trained on non-local data (McCormick and others, 2016; Flaxman and others, 2018). To illustrate the issue, in Figure 1, we plot the confusion matrices between the true COD of the PHMRC child cases in Tanzania against the predicted COD for these cases using two CCVA algorithms, Tariff and InSilicoVA, both trained on all PHMRC child data non-local to Tanzania. Both matrices reveal very large transfer errors, some as high as
paired physician and VA assessments of cause of death across four countries. However, there exists considerable skepticism about the utility of CCVA trained on non-local data (McCormick and others, 2016; Flaxman and others, 2018). To illustrate the issue, in Figure 1, we plot the confusion matrices between the true COD of the PHMRC child cases in Tanzania against the predicted COD for these cases using two CCVA algorithms, Tariff and InSilicoVA, both trained on all PHMRC child data non-local to Tanzania. Both matrices reveal very large transfer errors, some as high as 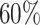 indicating that the naive estimates of population-level class probabilities from CCVA classifiers trained on non-local source data are likely to be inaccurate thereby highlighting the need for transfer learning in this application. Additionally, like for any other application area, there exists considerable disagreement about which CCVA algorithm is the most accurate (Leitao and others, 2014; McCormick and others, 2016; Flaxman and others, 2018). In our experience, no method is universally superior, and a robust ensemble transfer learning approach guarding against use of inaccurate classifiers is desirable.
indicating that the naive estimates of population-level class probabilities from CCVA classifiers trained on non-local source data are likely to be inaccurate thereby highlighting the need for transfer learning in this application. Additionally, like for any other application area, there exists considerable disagreement about which CCVA algorithm is the most accurate (Leitao and others, 2014; McCormick and others, 2016; Flaxman and others, 2018). In our experience, no method is universally superior, and a robust ensemble transfer learning approach guarding against use of inaccurate classifiers is desirable.
Fig. 1.
Confusion matrices for PHMRC child cases in Tanzania using Tariff and InSilicoVA trained on all cases outside of Tanzania. CVD, cardio-vascular diseases.
2. Transfer learning for population-level class probabilities
2.1. Naive approach
Let 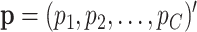 denote the true population-level class probabilities in a target domain where we have abundant unlabeled covariate data, which we denote by
denote the true population-level class probabilities in a target domain where we have abundant unlabeled covariate data, which we denote by  , and a very small labeled data
, and a very small labeled data 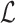 of paired labels
of paired labels 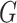 and covariates
and covariates 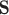 . Our estimand is
. Our estimand is 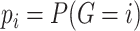 where
where 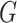 denote the true (gold standard) class-membership. For a case
denote the true (gold standard) class-membership. For a case 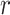 with covariate
with covariate 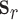 , let
, let 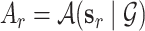 denote the predicted class membership, based on
denote the predicted class membership, based on 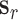 , from the baseline classification algorithm
, from the baseline classification algorithm 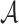 trained on some large “gold-standard” information
trained on some large “gold-standard” information 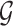 . Our methodology is agnostic to the type of
. Our methodology is agnostic to the type of 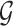 , it can be either a labeled data set from the source-domain or set of context-specific information (e.g., medical guidelines for determining COD) used to construct the classifier. If we do not use any transfer learning, the naive estimate of
, it can be either a labeled data set from the source-domain or set of context-specific information (e.g., medical guidelines for determining COD) used to construct the classifier. If we do not use any transfer learning, the naive estimate of 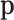 from
from 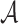 is given by
is given by
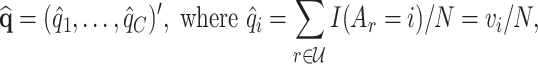 |
(2.1) |
where 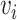 is the number of observations in
is the number of observations in 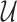 classified by
classified by 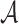 to category
to category 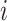 , and
, and 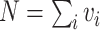 is the sample size of
is the sample size of 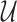 . If
. If 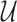 is large enough to be representative of the target population, it is clear that
is large enough to be representative of the target population, it is clear that
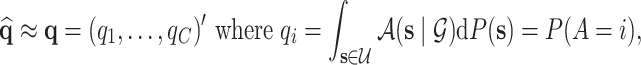 |
i.e., 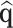 is the method-of-moments estimator of
is the method-of-moments estimator of 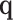 .
.
Unless the algorithm 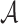 trained on source-domain information perfectly agrees with the true membership assignment mechanism
trained on source-domain information perfectly agrees with the true membership assignment mechanism 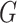 in the target domain, there is no reason to consider
in the target domain, there is no reason to consider 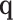 or
or 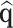 to be a good estimate of
to be a good estimate of 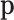 . More realistically, accuracy depends on how similar the algorithm
. More realistically, accuracy depends on how similar the algorithm 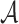 is in the source- and target-domains. Hence, more generally we can think of
is in the source- and target-domains. Hence, more generally we can think of 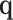 as the expected population class probabilities in the target domain that would be predicted by
as the expected population class probabilities in the target domain that would be predicted by 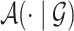 .
.
Marginally, both 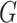 and
and 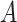 are categorical variables. So, we can write
are categorical variables. So, we can write
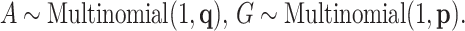 |
(2.2) |
To infer about 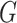 from
from 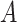 , we need to model their joint distributions. We express
, we need to model their joint distributions. We express  where
where 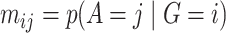 . In matrix notation, we have
. In matrix notation, we have 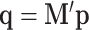 where
where 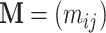 is a transition matrix (i.e.,
is a transition matrix (i.e., 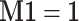 ) which we refer to as the confusion matrix. First note that, if
) which we refer to as the confusion matrix. First note that, if 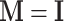 , then
, then  and hence this subsumes the case where class probabilities from the baseline algorithm is trusted as reliable surrogates of the true class probabilities.
and hence this subsumes the case where class probabilities from the baseline algorithm is trusted as reliable surrogates of the true class probabilities.
For transfer learning to improve estimation of 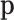 , instead of assuming
, instead of assuming 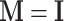 , we can opt to use the more general relationship
, we can opt to use the more general relationship 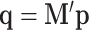 and estimate the transfer error rates
and estimate the transfer error rates 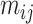 ’s from
’s from 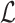 . Let
. Let 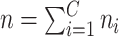 denote the sample size of
denote the sample size of 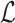 with
with 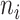 denoting the number of objects belonging to class
denoting the number of objects belonging to class 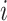 . Also let
. Also let
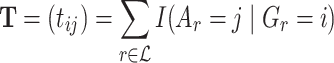 |
denote the transfer error matrix for algorithm 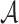 . Like many transfer learning algorithms, exploiting the transfer errors is key to our strategy. It is clear that
. Like many transfer learning algorithms, exploiting the transfer errors is key to our strategy. It is clear that 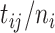 is a method-of-moments estimator of
is a method-of-moments estimator of 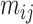 .
.
We can use these estimates of 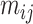 , along with the earlier estimate of
, along with the earlier estimate of 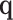 to obtain a substantially improved estimate of
to obtain a substantially improved estimate of 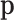 . Formally we can specify this via a hierarchical model as:
. Formally we can specify this via a hierarchical model as:
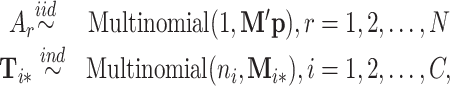 |
(2.3) |
where for 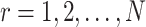 , and for any matrix
, and for any matrix  ,
, 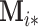 and
and 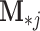 denote its
denote its 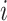 th row and
th row and 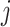 th column respectively. The top-row of (2.3) represents the relationship
th column respectively. The top-row of (2.3) represents the relationship 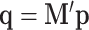 and yields the method-of-moments estimators
and yields the method-of-moments estimators 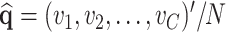 . The bottom-row of (2.3) is consistent with the naive estimates
. The bottom-row of (2.3) is consistent with the naive estimates 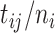 of
of 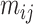 .
.
To estimate 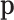 , one can adopt a modular two-step approach where first
, one can adopt a modular two-step approach where first 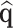 and
and 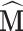 are calculated separately and then obtain
are calculated separately and then obtain
 |
where 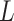 is some loss function like the squared-error or, more appropriately, the Kullback–Liebler divergence between the probability vectors. This approach fails to propagate the uncertainty in the estimation of
is some loss function like the squared-error or, more appropriately, the Kullback–Liebler divergence between the probability vectors. This approach fails to propagate the uncertainty in the estimation of 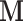 in the final estimates of
in the final estimates of 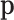 . Benefits of a one-stage approach over a two-stage one has been demonstrated in recent work in transfer learning (Long and others, 2014). Alternatively, one can estimate the joint MLE of
. Benefits of a one-stage approach over a two-stage one has been demonstrated in recent work in transfer learning (Long and others, 2014). Alternatively, one can estimate the joint MLE of 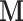 and
and 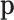 from (2.3).
from (2.3).
The advantage of this simple transfer learning method is that it circumvents the need to improve the individual predictions of 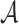 and directly calibrates the population-level class probabilities
and directly calibrates the population-level class probabilities 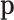 , which are the quantities of interest here. We deliberately model the distribution of
, which are the quantities of interest here. We deliberately model the distribution of 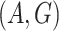 marginalized over the covariates
marginalized over the covariates 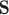 , allowing us to use this in situations where the covariates are discarded after predictions or cannot be provided due to privacy concerns, and only the predictions
, allowing us to use this in situations where the covariates are discarded after predictions or cannot be provided due to privacy concerns, and only the predictions 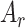 are available. Even if the covariates were available, trying to use the extremely small
are available. Even if the covariates were available, trying to use the extremely small 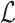 to estimate
to estimate 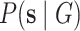 relationship is not advisable. Instead, we efficiently exploit the small local training data
relationship is not advisable. Instead, we efficiently exploit the small local training data  to reduce cross-domain bias learning about the (
to reduce cross-domain bias learning about the (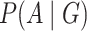 ) confusion matrix. This involves estimation of only
) confusion matrix. This involves estimation of only 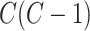 parameters as opposed to the
parameters as opposed to the 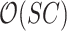 parameters if trying to estimate
parameters if trying to estimate 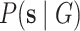 . For verbal autopsy data,
. For verbal autopsy data,  is typically around
is typically around 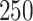 while we can choose
while we can choose 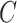 to be small focusing on the top 3–5 causes. Hence, our approach achieves considerable dimension reduction by switching from the original covariate space to the predicted class space.
to be small focusing on the top 3–5 causes. Hence, our approach achieves considerable dimension reduction by switching from the original covariate space to the predicted class space.
In (2.3) above, 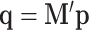 can be directly estimated precisely because
can be directly estimated precisely because  is large. However,
is large. However,  has
has 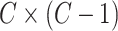 parameters so that if there are many classes, the estimates of
parameters so that if there are many classes, the estimates of 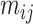 will have large variances owing to the small size of
will have large variances owing to the small size of 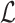 . Furthermore, in epidemiological studies, data collection often spans a few years; in the early stages,
. Furthermore, in epidemiological studies, data collection often spans a few years; in the early stages, 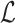 may only have a very small sample size resulting in an extremely imprecise estimate of
may only have a very small sample size resulting in an extremely imprecise estimate of 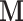 , even if we group the classes to a handful of larger classes. This can lead to an imprecise estimate of
, even if we group the classes to a handful of larger classes. This can lead to an imprecise estimate of 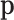 based on estimates of
based on estimates of 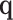 and
and 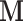 , as the latter will have high variance. Consequently, in the next section we propose a regularized approach that stabilizes the transfer learning.
, as the latter will have high variance. Consequently, in the next section we propose a regularized approach that stabilizes the transfer learning.
2.2. Bayesian regularized approach
We champion the idea that in absence of enough target-domain labeled data, our method should shrink towards the default method familiar to practitioners. If  was not available, i.e., there is no labeled data in the target domain, we only have
was not available, i.e., there is no labeled data in the target domain, we only have  and
and  . Then in many applications (including verbal autopsies) the current practice is to train
. Then in many applications (including verbal autopsies) the current practice is to train  once using
once using 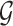 and then predict on
and then predict on 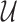 to obtain
to obtain 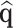 as the estimate for
as the estimate for 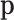 . This is equivalent to setting
. This is equivalent to setting 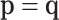 and
and 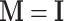 , i.e., assuming that the algorithm
, i.e., assuming that the algorithm 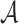 perfectly classifies in the target domain even when trained only using source-domain information
perfectly classifies in the target domain even when trained only using source-domain information 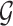 . Extending this argument, when
. Extending this argument, when 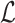 is very small, direct estimates of
is very small, direct estimates of 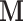 would be unstable and we can rely more on this default practice. Hence, for small
would be unstable and we can rely more on this default practice. Hence, for small 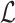 , we will shrink
, we will shrink 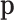 towards
towards 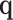 i.e., we shrink towards the default assumption that the baseline learner is accurate. This is equivalent to shrinking the estimate of
i.e., we shrink towards the default assumption that the baseline learner is accurate. This is equivalent to shrinking the estimate of 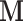 towards
towards 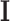 . The simplest way to achieve this is by using the regularized estimate
. The simplest way to achieve this is by using the regularized estimate 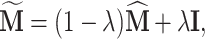 where
where 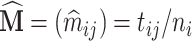 is the unshrunk method-of-moments estimate of
is the unshrunk method-of-moments estimate of 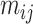 as derived in the previous section. The regularized estimate
as derived in the previous section. The regularized estimate 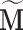 (like
(like 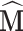 and
and 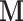 ) remains a transition matrix. The parameter
) remains a transition matrix. The parameter 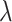 quantifies the degree of shrinkage with
quantifies the degree of shrinkage with 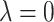 yielding the unbiased method-of-moments estimate and
yielding the unbiased method-of-moments estimate and 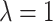 leading to
leading to 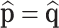 . Hence,
. Hence, 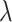 represents the bias variance trade-off for estimation of transition matrices and for small sample sizes some intermediate values of
represents the bias variance trade-off for estimation of transition matrices and for small sample sizes some intermediate values of 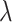 may lead to better estimates of
may lead to better estimates of 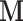 and
and 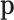 .
.
In epidemiological applications, as data will often come in batches over a period spanning few years, one needs to rerun the transfer learning procedure periodically to update the class probabilities. In the beginning, when 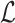 is extremely small, it is expected that more regularization is required. Eventually, when
is extremely small, it is expected that more regularization is required. Eventually, when 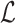 becomes large, we could rely on the direct estimate
becomes large, we could rely on the direct estimate 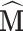 . Hence,
. Hence, 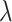 should be a function of the size
should be a function of the size 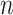 of
of 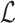 , with
, with 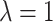 for
for 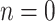 and
and 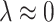 for large
for large 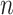 . Furthermore, at intermediate stages, since the distribution of true class memberships in
. Furthermore, at intermediate stages, since the distribution of true class memberships in 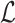 will be non-uniform across the classes, we will have a disparity in sample sizes
will be non-uniform across the classes, we will have a disparity in sample sizes 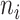 for estimating the different rows of
for estimating the different rows of 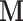 . Consequently, it makes more sense to regularize each row of
. Consequently, it makes more sense to regularize each row of 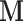 separately instead of using a single
separately instead of using a single 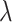 . A more flexible regularized estimate is given by
. A more flexible regularized estimate is given by 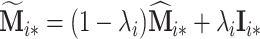 . The row specific weights
. The row specific weights 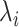 should be chosen such that
should be chosen such that 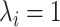 when
when 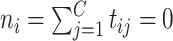 , and
, and 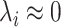 when
when 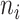 is large. One choice is given by
is large. One choice is given by 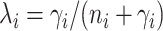 for some fixed positive
for some fixed positive 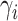 ’s.
’s.
We now propose a hierarchical Bayesian formulation that accomplishes this regularized estimation of any transition matrix 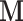 . We consider a Dirichlet prior
. We consider a Dirichlet prior 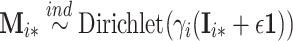 for the rows of
for the rows of 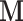 . We first offer some heuristics expounding choice of this prior. We will have
. We first offer some heuristics expounding choice of this prior. We will have 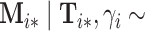 Dirichlet
Dirichlet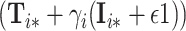 . Hence,
. Hence,
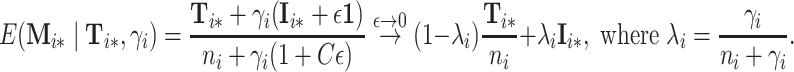 |
Hence, using a small enough 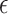 , the Bayes estimator (posterior mean) for
, the Bayes estimator (posterior mean) for 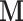 becomes equivalent with the desired shrinkage estimator
becomes equivalent with the desired shrinkage estimator 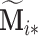 proposed above. When
proposed above. When 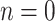 , the Bayes estimate
, the Bayes estimate  , and for large
, and for large 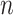 ,
, 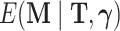 becomes the method-of-moments estimator
becomes the method-of-moments estimator 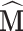 . Hence, the Dirichlet prior ensures that in data-scarce setting,
. Hence, the Dirichlet prior ensures that in data-scarce setting, 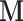 is shrunk towards
is shrunk towards 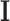 and consequently
and consequently 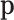 towards
towards 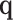 . In Theorem 2.1, we will present a more formal result that looks at the properties of the marginal posterior of
. In Theorem 2.1, we will present a more formal result that looks at the properties of the marginal posterior of 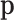 .
.
To complete the hierarchical formulation, we augment (2.3) with the priors:
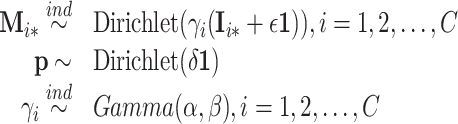 |
(2.4) |
In practice, we need to use a small 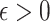 to ensure a proper posterior for
to ensure a proper posterior for 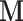 when any off-diagonal entries of
when any off-diagonal entries of 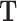 are zero, which is very likely due to the limited size of
are zero, which is very likely due to the limited size of 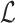 . Note that our model only uses the data from
. Note that our model only uses the data from 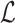 to estimate the conditional probabilities
to estimate the conditional probabilities 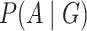 . We do not model the marginal distribution of
. We do not model the marginal distribution of 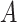 or
or 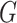 in
in 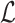 like we do for
like we do for 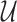 . This is because often data for the labeled set are collected under controlled settings, and marginal distribution of
. This is because often data for the labeled set are collected under controlled settings, and marginal distribution of 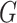 (and hence of
(and hence of 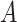 ) for the samples in
) for the samples in  is not representative of their true target-domain marginal distributions. Hence, we only use
is not representative of their true target-domain marginal distributions. Hence, we only use  to estimate the conditional probabilities
to estimate the conditional probabilities 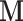 .
.
Our previous heuristic arguments, illustrating the shrinkage estimation of 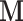 induced by the Dirichlet prior, are limited to the estimation of
induced by the Dirichlet prior, are limited to the estimation of 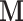 from
from 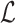 as an independent piece and disregards the data and model for
as an independent piece and disregards the data and model for 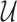 , i.e. the first row of (2.3). In a hierarchical setup, however, the models for
, i.e. the first row of (2.3). In a hierarchical setup, however, the models for 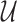 and
and 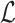 contribute jointly to the estimation of
contribute jointly to the estimation of 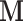 and
and 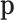 . We will now state a more general result that argues that for our full hierarchical model specified through (2.3) and (2.4), when there is no labeled target-domain data or if the algorithm
. We will now state a more general result that argues that for our full hierarchical model specified through (2.3) and (2.4), when there is no labeled target-domain data or if the algorithm 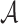 demonstrates perfect accuracy (zero transfer error) on
demonstrates perfect accuracy (zero transfer error) on 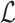 , then the marginal posterior estimates of
, then the marginal posterior estimates of 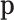 from our model coincides with the baseline estimates
from our model coincides with the baseline estimates 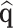 . Before stating the result, first note that the likelihood for
. Before stating the result, first note that the likelihood for 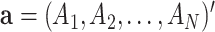 can be represented using the sufficient statistics
can be represented using the sufficient statistics 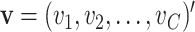 . We can write
. We can write 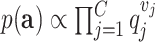 and hence
and hence 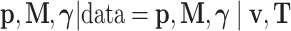 .
.
THEOREM 2.1
If
is a diagonal matrix, i.e., either there is no
, or
classifies perfectly on
, then
. For
,
.
The proofs of the theorems are provided in Section S4 of the Supplementary Materials available at Biostatistics online. Note that Theorem 2.1 is a result about the posterior of our quantity of interest 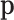 , marginalizing out the other parameters
, marginalizing out the other parameters 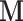 , and the
, and the 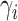 ’s from the hierarchical model specified through (2.3) and (2.4). We also highlight that this is not an asymptotic result and holds true for any sample size as long as we take the limit
’s from the hierarchical model specified through (2.3) and (2.4). We also highlight that this is not an asymptotic result and holds true for any sample size as long as we take the limit 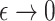 . This is important as our manuscript pertains to epidemiological applications where the sample size of
. This is important as our manuscript pertains to epidemiological applications where the sample size of 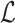 will be extremely small.
will be extremely small.
Theorem 2.1 also does not require any assumption about the underlying data generation scheme and is simply a desirable property of our transfer learning model. If there is no labeled target-domain data, then we give the same estimate from the method currently used by practitioners, i.e., we trust 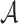 trained on a source-domain and only use the target-domain marginal distributions of
trained on a source-domain and only use the target-domain marginal distributions of 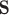 from
from 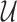 to arrive at the estimates
to arrive at the estimates 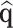 of
of 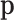 . Similarly, in the best-case scenario, when
. Similarly, in the best-case scenario, when 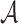 is absolutely accurate for the target domain, Theorem 2.1 guarantees that our model automatically recognizes this accuracy and does not modify the baseline estimates
is absolutely accurate for the target domain, Theorem 2.1 guarantees that our model automatically recognizes this accuracy and does not modify the baseline estimates 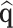 from
from 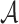 . This shrinkage towards the default method familiar to practitioners, in absence of enough evidence, is a desirable property. The result of Theorem 2.1 is confirmed in simulations in Section 5.
. This shrinkage towards the default method familiar to practitioners, in absence of enough evidence, is a desirable property. The result of Theorem 2.1 is confirmed in simulations in Section 5.
Although Theorem 2.1 is assumption-free, it only concerns with the performance of the model when there is no  or when
or when  is perfect on
is perfect on  . While this is a good sanity check for our model, realistically we will have a small
. While this is a good sanity check for our model, realistically we will have a small  where
where 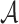 will be inaccurate. In such cases, the performance of our model will of course depend on the data generation process. Hence, we summarize the data generation assumption that drive the model formulation. Since, there is no labeled data in
will be inaccurate. In such cases, the performance of our model will of course depend on the data generation process. Hence, we summarize the data generation assumption that drive the model formulation. Since, there is no labeled data in 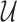 , we need to assume some commonality between
, we need to assume some commonality between 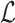 and
and 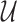 in order for the labeled data in
in order for the labeled data in 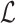 to be useful for estimating the CSMFs in
to be useful for estimating the CSMFs in 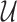 . Hence, the model assumes that the conditional distribution of
. Hence, the model assumes that the conditional distribution of 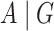 (i.e., the
(i.e., the 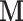 matrix) is same in
matrix) is same in 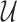 and
and 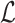 . This is a transportability assumption that the error rates on the validation set
. This is a transportability assumption that the error rates on the validation set 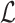 reflects the true error rates in the population
reflects the true error rates in the population 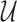 . These rates are then used to correct for bias in the estimates of
. These rates are then used to correct for bias in the estimates of 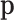 . This process is thus analogous to applying measurement error correction to a study by assuming transportability of the measurement error distribution from some validation samples (Carroll and others, 2006). We would like to emphasize that we do not assume that the marginal distributions of the cause
. This process is thus analogous to applying measurement error correction to a study by assuming transportability of the measurement error distribution from some validation samples (Carroll and others, 2006). We would like to emphasize that we do not assume that the marginal distributions of the cause 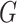 (i.e., the CSMFs) and hence also of the symptoms
(i.e., the CSMFs) and hence also of the symptoms 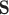 are same in any of
are same in any of 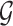 ,
, 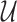 and
and 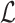 . Of course, the assumption of same confusion matrix
. Of course, the assumption of same confusion matrix 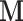 for
for 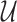 and
and 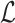 can also be incorrect (all models are wrong). However, the class of models spanned by use of a general
can also be incorrect (all models are wrong). However, the class of models spanned by use of a general 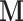 is a superset of the default approach of using the baseline classifier (i.e., assuming
is a superset of the default approach of using the baseline classifier (i.e., assuming 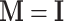 ). Also, we can relax the assumption of constant
). Also, we can relax the assumption of constant 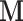 between
between 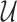 and
and 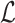 to make entries of
to make entries of 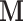 function of some covariates. This model and its implementation is discussed in Section 4. This would lead to substantial increase in parameter dimensionality and is only recommended when
function of some covariates. This model and its implementation is discussed in Section 4. This would lead to substantial increase in parameter dimensionality and is only recommended when 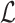 is large.
is large.
2.3. Gibbs sampler using augmented data
We devise an efficient implementation of the hierarchical transfer learning model using a data augmented Gibbs sampler. The joint posterior density can be expressed as
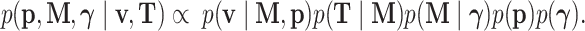 |
Let 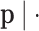 denote the full conditional distribution of
denote the full conditional distribution of  . We use similar notation for other full conditionals. First note that since
. We use similar notation for other full conditionals. First note that since 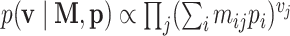 , the full conditional densities
, the full conditional densities 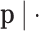 and
and 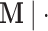 do not belong to any standard family of distributions, thereby prohibiting a direct Gibbs sampler. We here use a data augmentation scheme enabling a Gibbs sampler using conjugate distributions.
do not belong to any standard family of distributions, thereby prohibiting a direct Gibbs sampler. We here use a data augmentation scheme enabling a Gibbs sampler using conjugate distributions.
The term 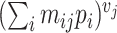 can be expanded using the multinomial theorem, with each term corresponding to one of the partitions of
can be expanded using the multinomial theorem, with each term corresponding to one of the partitions of 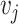 into
into 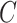 non-negative integers. Equivalently we can write
non-negative integers. Equivalently we can write
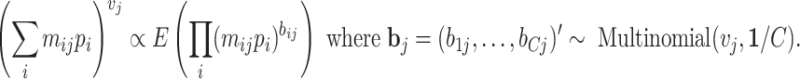 |
Choosing 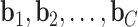 to be independent, we can express
to be independent, we can express 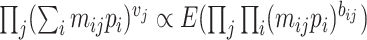 where the proportionality constant only depends on the observed
where the proportionality constant only depends on the observed 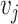 ’s. Using the augmented data matrix
’s. Using the augmented data matrix 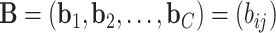 , we can write the complete posterior as
, we can write the complete posterior as
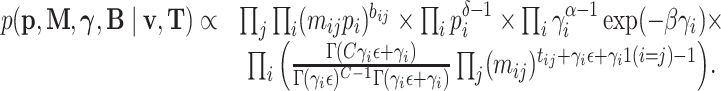 |
(2.5) |
The full conditional distributions can be updated as follows (derivations omitted):
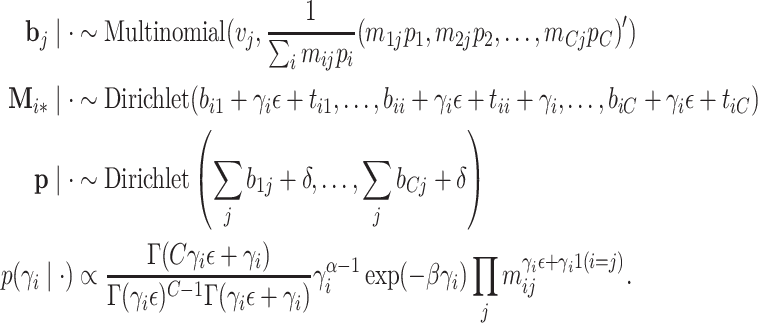 |
The data augmentation ensures that, except the 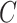
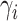 ’s, which are updated using a metropolis random walk with log-normal proposals, all the other
’s, which are updated using a metropolis random walk with log-normal proposals, all the other 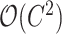 parameters are update by sampling from standard distributions leading to an extremely fast and efficient Gibbs sampler.
parameters are update by sampling from standard distributions leading to an extremely fast and efficient Gibbs sampler.
3. Ensemble transfer learning
Let there be 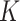 classifiers
classifiers 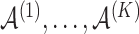 and let
and let 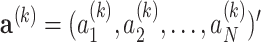 be the predicted class memberships from the
be the predicted class memberships from the 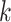 th algorithm for all the
th algorithm for all the 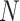 observations in
observations in 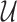 . Let
. Let 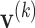 denote the vector of counts of predicted class memberships on
denote the vector of counts of predicted class memberships on 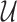 using
using 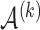 . We expect variation among the predictions from the different classifiers and consequently among the baseline estimates of population-level class probabilities
. We expect variation among the predictions from the different classifiers and consequently among the baseline estimates of population-level class probabilities 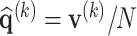 and their population equivalents
and their population equivalents 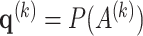 . Since the true population class probability vector
. Since the true population class probability vector 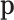 is unique, following Section 2.1 we can write
is unique, following Section 2.1 we can write 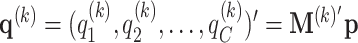 , where
, where 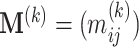 is now the classifier-specific confusion matrix. The predicted class membership for the
is now the classifier-specific confusion matrix. The predicted class membership for the 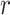 th observation in
th observation in 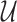 by algorithm
by algorithm 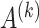 , denoted by
, denoted by 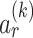 , marginally follows a
, marginally follows a 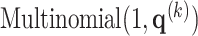 distribution. We have
distribution. We have 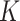 such predictions for the same observation, one for each classifier, and these are expected to be correlated. So, we need to look at the joint distribution of the
such predictions for the same observation, one for each classifier, and these are expected to be correlated. So, we need to look at the joint distribution of the 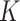
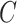 -dimensional multinomial random variables. Since, in its most general form this will involve
-dimensional multinomial random variables. Since, in its most general form this will involve 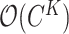 parameters, we use a pragmatic simplifying assumption to derive the joint distribution. We assume that
parameters, we use a pragmatic simplifying assumption to derive the joint distribution. We assume that 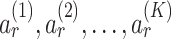 are independent conditional on
are independent conditional on 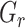 , i.e.,
, i.e.,
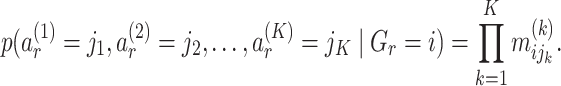 |
(3.6) |
This assumption is unlikely to hold in reality but is a common dimension reducing assumption used in classification problems. For example, the naive Bayes classifier uses this assumption to jointly model the probability of covariates given the true class memberships. Similar assumptions are used by InSilicoVA and InterVA to derive the joint distribution of the vector of symptoms 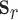 . Here, we are applying the same assumption but not on
. Here, we are applying the same assumption but not on 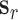 but on the lower-dimensional prediction vector
but on the lower-dimensional prediction vector 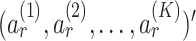 .
.
Under this assumption, the marginal independence of the 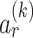 ’s will not generally hold. Instead we will have
’s will not generally hold. Instead we will have
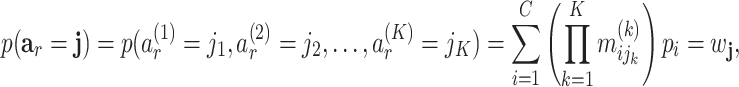 |
(3.7) |
where 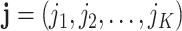 denotes a
denotes a 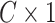 vector index.
vector index.
From the limited labeled data set 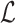 in the target domain, the classifier-specific transfer error matrices
in the target domain, the classifier-specific transfer error matrices 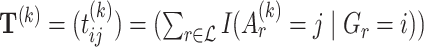 are also known and can be used to estimate the respective confusion matrices
are also known and can be used to estimate the respective confusion matrices 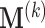 in the same way
in the same way 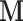 was estimated from
was estimated from 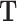 in Section 2.1. To introduce shrinkage in the estimation of
in Section 2.1. To introduce shrinkage in the estimation of 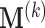 , like in Section 2.2, we assign Dirichlet priors for each
, like in Section 2.2, we assign Dirichlet priors for each 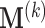 .
.
Let 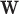 denote a
denote a 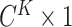 vector formed by stacking up all the
vector formed by stacking up all the 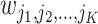 ’s defined in (3.7). The full specifications for the ensemble model that incorporates the predictions from all the algorithms is given by:
’s defined in (3.7). The full specifications for the ensemble model that incorporates the predictions from all the algorithms is given by:
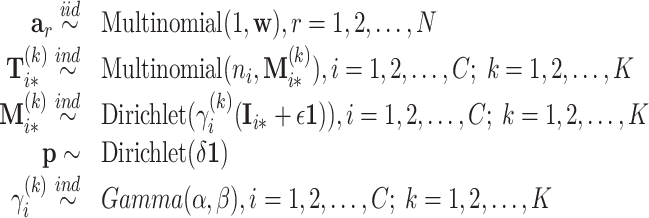 |
(3.8) |
Although 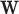 is a
is a 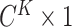 vector, courtesy of the conditional independence assumption (3.6), it is only parameterized using the matrices
vector, courtesy of the conditional independence assumption (3.6), it is only parameterized using the matrices 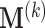 and
and 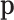 as specified in (3.7), and hence involves
as specified in (3.7), and hence involves 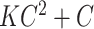 parameters. This ensures that there is adequate data to estimate the enhanced number of parameters for this ensemble method, as for each
parameters. This ensures that there is adequate data to estimate the enhanced number of parameters for this ensemble method, as for each 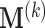 we observe the corresponding transfer error matrix
we observe the corresponding transfer error matrix 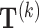 . The Gibbs sampler for (3.8) is provided in Section S3 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org). To understand how the different classifiers are given importance based on their transfer errors on
. The Gibbs sampler for (3.8) is provided in Section S3 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org). To understand how the different classifiers are given importance based on their transfer errors on 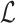 , we present the following result:
, we present the following result:
THEOREM 3.1
If
is diagonal with positive diagonal entries, and all entries of
are
for all
, then
. For
,
.
Theorem 3.1 reveals that if one of the 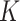 algorithms (which we assume to be the first algorithm without loss of generality) produce perfect prediction on
algorithms (which we assume to be the first algorithm without loss of generality) produce perfect prediction on 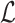 , then posterior mean estimate of
, then posterior mean estimate of 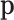 from the ensemble model coincides with that of the baseline estimate from that classifier. The perfect agreement assumed in Theorem 3.1 will not occur in practice. However, simulation and data analyses will confirm that the estimate of
from the ensemble model coincides with that of the baseline estimate from that classifier. The perfect agreement assumed in Theorem 3.1 will not occur in practice. However, simulation and data analyses will confirm that the estimate of 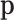 from the ensemble model tend to agree with that from the single-classifier model in Section 2.2 with the more accurate algorithm. This offers a more efficient way to weight the multiple algorithms, yielding a unified estimate of class probabilities that is more robust to inclusion of an inaccurate algorithm in the decision making. In comparison, a simple average of estimated
from the ensemble model tend to agree with that from the single-classifier model in Section 2.2 with the more accurate algorithm. This offers a more efficient way to weight the multiple algorithms, yielding a unified estimate of class probabilities that is more robust to inclusion of an inaccurate algorithm in the decision making. In comparison, a simple average of estimated 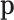 ’s from single-classifier transfer learning models for each of the
’s from single-classifier transfer learning models for each of the  algorithms would be more adversely affected by inaccurate algorithms.
algorithms would be more adversely affected by inaccurate algorithms.
3.1. Independent ensemble model
The likelihood for the top-row of (3.8) is proportional to 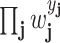 where
where 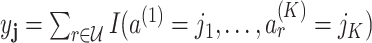 denote the total number of observations in
denote the total number of observations in 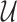 where the predicted class-memberships from the
where the predicted class-memberships from the 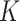 algorithms corresponds to the combination
algorithms corresponds to the combination 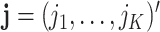 . Even though
. Even though 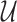 will be moderately large (few thousand observations in most epidemiological applications), unless both
will be moderately large (few thousand observations in most epidemiological applications), unless both 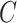 and
and 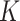 are very small (
are very small (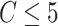 and
and 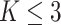 ),
), 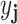 ’s will be zero for most of the
’s will be zero for most of the 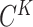 possible combinations
possible combinations 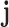 . This will in-turn affect the estimates of
. This will in-turn affect the estimates of 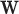 . For applications to verbal autopsy-based estimation of population CSMFs, there are many CCVA algorithms (as introduced in Section 1), and researchers often want to use all of them in an analysis. We also may be interested in more than 3–5 top causes. In such cases, the extremely sparse
. For applications to verbal autopsy-based estimation of population CSMFs, there are many CCVA algorithms (as introduced in Section 1), and researchers often want to use all of them in an analysis. We also may be interested in more than 3–5 top causes. In such cases, the extremely sparse 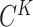 vector formed by stacking up the
vector formed by stacking up the 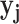 ’s will destabilize the estimation of
’s will destabilize the estimation of 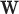 . Also, the Gibbs sampler (see Section S3 of the supplementary material available at Biostatistics online) of the joint-ensemble model introduces an additional
. Also, the Gibbs sampler (see Section S3 of the supplementary material available at Biostatistics online) of the joint-ensemble model introduces an additional 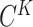 independent multinomial variables of dimension
independent multinomial variables of dimension 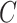 thereby accruing substantial computational overhead and entailing long runs of the high-dimensional Markov chain to achieve convergence.
thereby accruing substantial computational overhead and entailing long runs of the high-dimensional Markov chain to achieve convergence.
In this section, we offer a pragmatic alternative model for ensemble transfer learning that is computationally less demanding. From (3.7), we note that
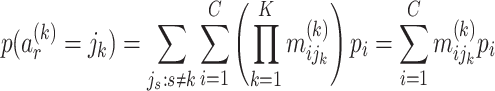 |
(3.9) |
by exchanging the summations. Hence, the marginal distribution of  is
is 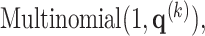 where
where 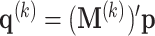 . We model the
. We model the  ’s independently for each
’s independently for each 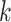 , ignoring the correlation among the predictions in
, ignoring the correlation among the predictions in 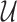 from the
from the 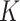 classifiers as follows:
classifiers as follows:
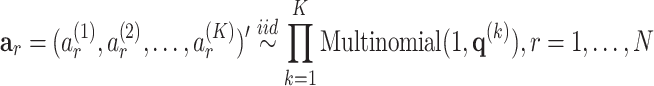 |
(3.10) |
We replace the top-row of (3.8) with (3.10), keeping the other specification same as in (3.8). We call this the independent ensemble model. Note that, while we only use the marginal distributions of the 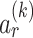 ’s ignoring their joint dependence, the joint distribution is preserved in the model for the transfer errors on
’s ignoring their joint dependence, the joint distribution is preserved in the model for the transfer errors on 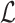 specified in the second-row of (3.8), as all the
specified in the second-row of (3.8), as all the 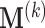 ’s are tied to the common truth
’s are tied to the common truth 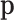 through the equations
through the equations 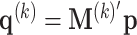 . While the total number of parameters for the joint and independent ensemble models remain the same, eliminating the joint model for each of the
. While the total number of parameters for the joint and independent ensemble models remain the same, eliminating the joint model for each of the  combination of predicted causes from the
combination of predicted causes from the 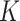 algorithms allows decomposing the likelihood for (3.10) as product of individual likelihoods on
algorithms allows decomposing the likelihood for (3.10) as product of individual likelihoods on 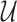 for each of the
for each of the 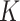 classifiers. Additionally, the Gibbs sampler for the independent ensemble model is much simpler and closely resembles the sampler for the single-classifier model in Section 2.3. We only need to introduce
classifiers. Additionally, the Gibbs sampler for the independent ensemble model is much simpler and closely resembles the sampler for the single-classifier model in Section 2.3. We only need to introduce 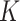
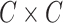 matrices
matrices 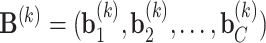 , one corresponding to each CCVA algorithm, akin to the matrix
, one corresponding to each CCVA algorithm, akin to the matrix 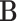 introduced in Section 2.3. The Gibbs sampler steps for the independent ensemble model are:
introduced in Section 2.3. The Gibbs sampler steps for the independent ensemble model are:
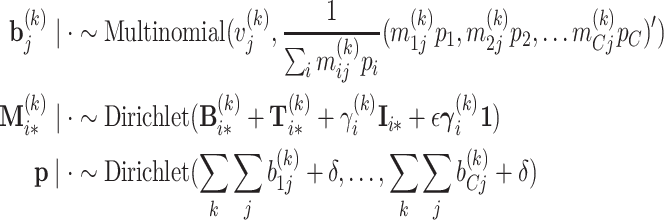 |
Observe that the sampler for the independent model uses 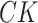 additional parameters as opposed to
additional parameters as opposed to 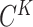 parameters introduced in the joint sampler. This ensures that the Markov Chain dimensionality does not exponentially increase if predictions from more algorithms are included in the ensemble model. The theoretical result in Theorem 3.1 no longer remains true for the independent model. However, our simulation results in Section S5.5 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) show that in practice it continues to put higher weights on the more accurate algorithm and consistently performs similar to or better than the joint model. In Section S1, we present an EM algorithm approach to obtain maximum a posteriori (MAP) estimates for the model as a fast alternative to the fully Bayesian approach adopted here. In Section S2, an algorithm for generating posterior samples of individual-level class predictions is outlined.
parameters introduced in the joint sampler. This ensures that the Markov Chain dimensionality does not exponentially increase if predictions from more algorithms are included in the ensemble model. The theoretical result in Theorem 3.1 no longer remains true for the independent model. However, our simulation results in Section S5.5 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) show that in practice it continues to put higher weights on the more accurate algorithm and consistently performs similar to or better than the joint model. In Section S1, we present an EM algorithm approach to obtain maximum a posteriori (MAP) estimates for the model as a fast alternative to the fully Bayesian approach adopted here. In Section S2, an algorithm for generating posterior samples of individual-level class predictions is outlined.
4. Demographic covariates and spatial information
The transfer-learning model introduced up to this point is focused on generating population-level estimates of the CSMF 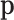 . An important extension for epidemiological applications would be to model
. An important extension for epidemiological applications would be to model 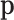 as a function of covariates like geographic region, seasonality, social economic status (SES), sex and age groups. This will enable the estimation of regional and age-sex stratified estimates. In this section, we generalize the model to accommodate covariates. We illustrate for the single-classifier model in Section 2.2; a similar approach extends the ensemble model.
as a function of covariates like geographic region, seasonality, social economic status (SES), sex and age groups. This will enable the estimation of regional and age-sex stratified estimates. In this section, we generalize the model to accommodate covariates. We illustrate for the single-classifier model in Section 2.2; a similar approach extends the ensemble model.
Let 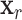 denote a vector of covariates for the
denote a vector of covariates for the 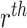 VA record in
VA record in 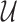 . We propose the following modifications to the model for allowing covariate-specific class distributions
. We propose the following modifications to the model for allowing covariate-specific class distributions 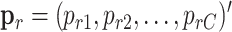 :
:
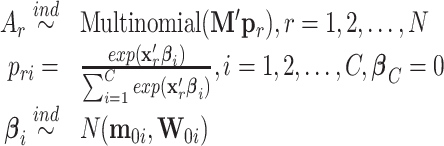 |
(4.11) |
All other components of the original model in (2.3) and (2.4) remain unchanged. The middle row of (4.11) specify a multi-logistic model for the class probabilities using the covariates. The top row uses the covariate specific 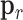 to model the analogous class probabilities
to model the analogous class probabilities 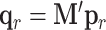 as would be predicted by
as would be predicted by 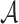 . Finally, the bottom row specifies Normal priors for the regression coefficients. The switch from a Dirichlet prior for
. Finally, the bottom row specifies Normal priors for the regression coefficients. The switch from a Dirichlet prior for 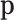 to the multi-logistic model implies we can no longer directly leverage conjugacy in the Gibbs sampler. Polson and others (2013) proposed a Polya-Gamma data augmentation scheme to allow conjugate sampling for generalized linear models. We now show how our own data augmentation scheme introduced in Section 2.3 harmonizes with the Polya-Gamma sampler to create a streamlined Gibbs sampler.
to the multi-logistic model implies we can no longer directly leverage conjugacy in the Gibbs sampler. Polson and others (2013) proposed a Polya-Gamma data augmentation scheme to allow conjugate sampling for generalized linear models. We now show how our own data augmentation scheme introduced in Section 2.3 harmonizes with the Polya-Gamma sampler to create a streamlined Gibbs sampler.
4.1. Gibbs sampler using Polya-Gamma scheme
We will assume there are 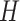 unique combinations of covariate values—for example, if there are four geographic regions and three age groups, then
unique combinations of covariate values—for example, if there are four geographic regions and three age groups, then 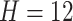 . If we have a continuous covariate, then
. If we have a continuous covariate, then 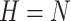 , where
, where 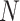 is the number of subjects sampled in
is the number of subjects sampled in 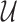 . Then letting
. Then letting 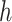 ,
, 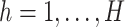 , represent a specific covariate combination
, represent a specific covariate combination 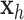 , we can again represent the likelihood for
, we can again represent the likelihood for 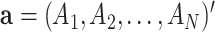 using the
using the 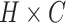 sufficient statistics
sufficient statistics 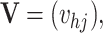 where
where 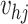 is the total number of subjects with covariate values
is the total number of subjects with covariate values 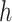 that were predicted to have died of cause
that were predicted to have died of cause 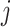 . Let
. Let 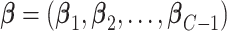 . We now have
. We now have
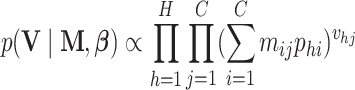 |
and the joint posterior density can now be expressed as
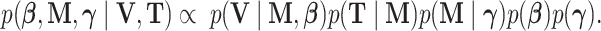 |
The terms that are different from Section 2.3 are 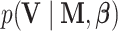 and
and 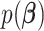 . The sampling step for
. The sampling step for 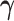 remains exactly the same as previously discussed. We will use a similar data augmentation strategy as in Section 2.3 and combine with a Polya-Gamma data augmentation to sample from this posterior distribution. We expand the term
remains exactly the same as previously discussed. We will use a similar data augmentation strategy as in Section 2.3 and combine with a Polya-Gamma data augmentation to sample from this posterior distribution. We expand the term 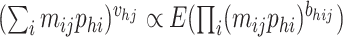 where
where
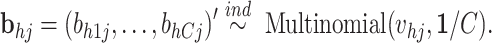 |
Let 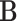 denote the
denote the 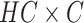 matrix formed by stacking all the
matrix formed by stacking all the 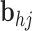 ’s row-wise. We can write
’s row-wise. We can write
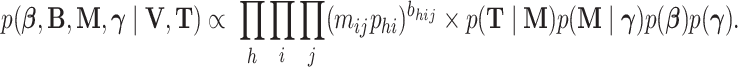 |
The following updates ensue immediately:
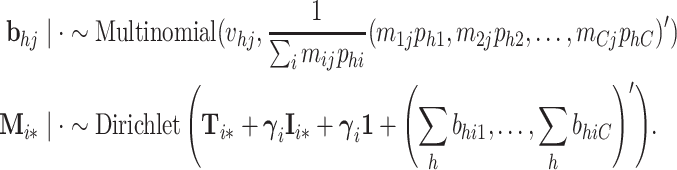 |
For 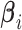 ’s, we introduce the Polya-Gamma variables
’s, we introduce the Polya-Gamma variables 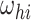 ’s and define
’s and define 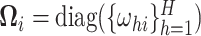 ,
, 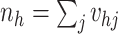 , and
, and 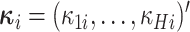 , where
, where 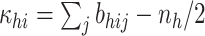 . Defining
. Defining 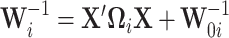 , we then have
, we then have
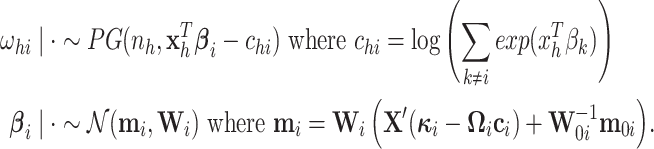 |
Here 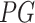 denotes the Polya-Gamma distribution and
denotes the Polya-Gamma distribution and 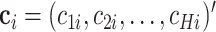 . This completes the steps of a Gibbs sampler where all the parameters except
. This completes the steps of a Gibbs sampler where all the parameters except 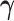 are updated via sampling from conjugate distributions. We can transform the posterior samples of
are updated via sampling from conjugate distributions. We can transform the posterior samples of 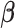 to obtain posterior samples of
to obtain posterior samples of 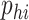 . Estimates of the marginal class distribution for the whole country can also be obtained by using the relationship
. Estimates of the marginal class distribution for the whole country can also be obtained by using the relationship 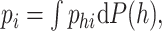 where an empirical estimate of the covariate distribution
where an empirical estimate of the covariate distribution 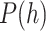 can be obtained from
can be obtained from 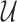 .
.
4.2. Covariate-specific transfer error
Until now, we have assumed that the transition matrix 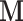 is independent of the covariates. We can also introduce covariates in modeling the conditional probabilities
is independent of the covariates. We can also introduce covariates in modeling the conditional probabilities 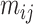 ’s using a similar multi-logistic regression. This model will be particularly useful if there is prior knowledge about covariate-dependent biases in the predictions from a classifier. Letting
’s using a similar multi-logistic regression. This model will be particularly useful if there is prior knowledge about covariate-dependent biases in the predictions from a classifier. Letting 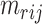 denoting the conditional probabilities
denoting the conditional probabilities 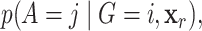 we can model
we can model
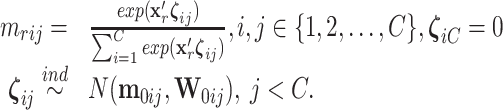 |
(4.12) |
The implementation will involve Polya-Gamma samplers for each row of 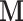 in a manner exactly similar to the sampler outlined above (we omit the details). Since we can only estimate the parameters
in a manner exactly similar to the sampler outlined above (we omit the details). Since we can only estimate the parameters 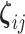 from the limited local data, we can only adopt this approach with a very small set of covariates for modeling the transfer error rates.
from the limited local data, we can only adopt this approach with a very small set of covariates for modeling the transfer error rates.
5. Simulation studies
The PHMRC study, conducted in four countries across six sites, is a benchmark database of paired VA records and GS-COD of children, neonates and adults. PHMRC data are frequently used to assess performance of CCVA algorithms. We conduct a set of simulation studies using the PHMRC data (obtained through the openVA package, version 1.0.5) to generate a wide range of plausible scenarios where the performance of our transfer learning models needs to be assessed with respect to the popular CCVA algorithms. First, we randomly split the PHMRC child data (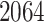 samples) into three parts representing
samples) into three parts representing 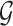 , and initial
, and initial 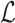 and initial
and initial 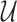 respectively using a 2:1:2 ratio, containing roughly
respectively using a 2:1:2 ratio, containing roughly 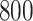 ,
, 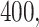 and
and 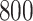 samples, respectively. As accurate estimation of mortality fractions from most prevalent causes are usually the priority, we restrict our attention to four causes: the top three most prevalent causes in the target-domain data (
samples, respectively. As accurate estimation of mortality fractions from most prevalent causes are usually the priority, we restrict our attention to four causes: the top three most prevalent causes in the target-domain data (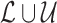 )—Pneumonia, Diarrhea/Dysentery, Sepsis, and an Other cause grouping together all the remaining causes.
)—Pneumonia, Diarrhea/Dysentery, Sepsis, and an Other cause grouping together all the remaining causes.
We wanted to simulate scenarios where both (i) the marginal distributions 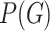 of the classes and (ii) the conditional distributions
of the classes and (ii) the conditional distributions 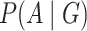 are different between the source- and target-domains. To ensure the latter, given a confusion matrix
are different between the source- and target-domains. To ensure the latter, given a confusion matrix 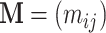 we want
we want 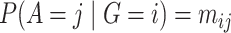 on
on 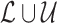 . We will achieve this by discarding the actual labels in
. We will achieve this by discarding the actual labels in 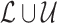 and generating new labels such that an algorithm
and generating new labels such that an algorithm 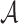 trained on
trained on 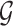 shows transfer error rates quantified by
shows transfer error rates quantified by 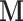 on
on 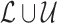 . Additionally, the new labels need to be assigned in a way to ensure that the target-domain class probability vector is
. Additionally, the new labels need to be assigned in a way to ensure that the target-domain class probability vector is 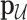 , for any choice of
, for any choice of 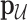 different from the source-domain class probabilities in
different from the source-domain class probabilities in 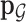 .
.
Note that if the true population class probabilities in the target domain needs to be 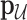 , then
, then 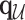 , the population class probabilities as predicted by
, the population class probabilities as predicted by 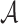 is given by
is given by 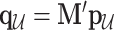 . Hence, we first use
. Hence, we first use 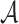 trained on
trained on 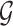 to predict the labels for each case in the initial
to predict the labels for each case in the initial 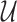 . We then resample cases from the initial
. We then resample cases from the initial 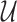 to create a final
to create a final 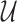 such that the predicted labels of
such that the predicted labels of 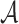 has the marginal distribution
has the marginal distribution 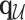 . Next, from Bayes theorem,
. Next, from Bayes theorem,
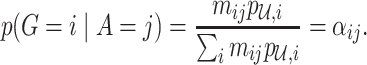 |
For cases in 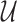 such that
such that 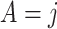 , we generate the new “true” labels from
, we generate the new “true” labels from 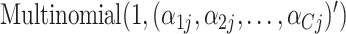 . This data generation process ensures that for any case in
. This data generation process ensures that for any case in 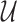 both
both 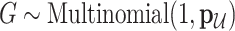 and
and 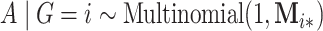 are approximately true. We repeat the procedure for
are approximately true. We repeat the procedure for 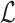 , using the same
, using the same 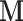 but a different
but a different 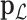 . This reflects the reality for verbal autopsy data where the symptom-given-cause dynamics is same for all deaths
. This reflects the reality for verbal autopsy data where the symptom-given-cause dynamics is same for all deaths 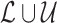 in the new country, but the hospital distribution of causes
in the new country, but the hospital distribution of causes 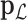 is unlikely to match the population CSMF
is unlikely to match the population CSMF 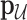 . For resampling to create the final
. For resampling to create the final 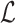 , we also vary
, we also vary 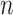 —the size of
—the size of 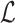 as
as 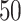 ,
, 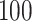 ,
, 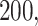 and
and 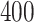 , to represent varying amount of local labeled that will be available at different stages of a project.
, to represent varying amount of local labeled that will be available at different stages of a project.
We consider two choices of 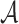 : Tariff (version 1.0.3) and InSilicoVA (version 1.2.2). For
: Tariff (version 1.0.3) and InSilicoVA (version 1.2.2). For 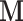 , we use three choices. We have
, we use three choices. We have 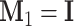 ,
,
 |
and 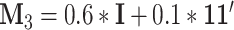 . The first choice represents the case where the algorithm
. The first choice represents the case where the algorithm 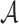 is perfect for predicting in the target domain.
is perfect for predicting in the target domain. 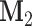 with two large off-diagonal entries and all other off-diagonal ones being zero represents the scenario where there are one or two systematic sources of bias in
with two large off-diagonal entries and all other off-diagonal ones being zero represents the scenario where there are one or two systematic sources of bias in 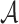 when trained on a source-domain different from the target domain. The specific choice of
when trained on a source-domain different from the target domain. The specific choice of 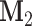 depicts the scenario that
depicts the scenario that 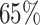 of Diarrhea/Dysentery cases are classified as pneumonia and
of Diarrhea/Dysentery cases are classified as pneumonia and 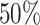 of sepsis deaths are categorized as some other cause. Finally,
of sepsis deaths are categorized as some other cause. Finally,  represents the scenario where there are many small misclassifications.
represents the scenario where there are many small misclassifications.
To ensure that  and
and 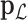 are different, we generate pairs of probability vectors
are different, we generate pairs of probability vectors 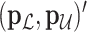 from Dirichlet
from Dirichlet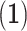 distribution and divide the cases into three scenarios: low: CSMFA
distribution and divide the cases into three scenarios: low: CSMFA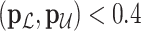 , medium:
, medium: 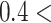 CSMFA
CSMFA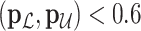 , and high: CSMFA
, and high: CSMFA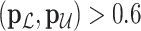 . Here, CSMFA denoting the CSMF accuracy is a metric quantifying the distance of a probability vector (
. Here, CSMFA denoting the CSMF accuracy is a metric quantifying the distance of a probability vector (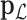 ) from a reference probability vector (
) from a reference probability vector (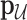 ) and is given by (Murray and others, 2011b):
) and is given by (Murray and others, 2011b):
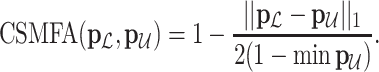 |
For each scenario, we generated 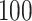 pairs of
pairs of 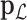 and
and 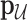 . For each generated dataset, we use all the algorithms listed in Table 2 for predicting
. For each generated dataset, we use all the algorithms listed in Table 2 for predicting 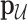 . For an estimate
. For an estimate 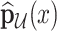 generate by a model
generate by a model 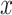 , we assess the performance of
, we assess the performance of 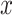 using CSMFA
using CSMFA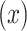 = CSMFA
= CSMFA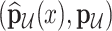 . We present a brief summary of the results here. A much more detailed analysis is provided in Section S5 of the supplementary material (http://www.biostatistics.oxfordjournals.org). Figure 2 presents the CSMFA for all the five models for
. We present a brief summary of the results here. A much more detailed analysis is provided in Section S5 of the supplementary material (http://www.biostatistics.oxfordjournals.org). Figure 2 presents the CSMFA for all the five models for 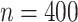 .
.
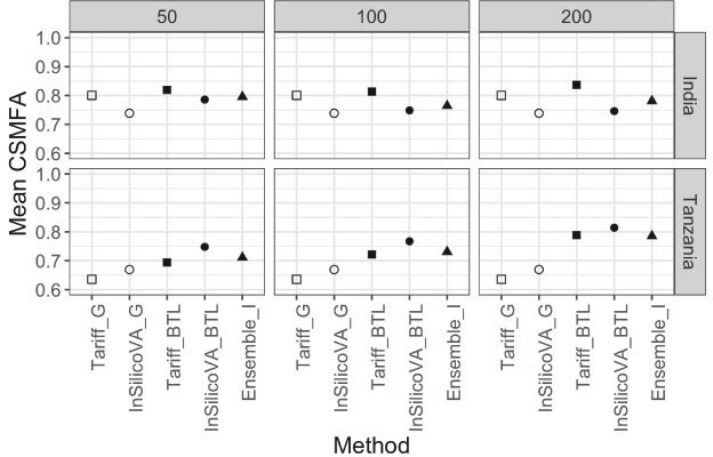
Table 2.
List of models used to estimate population CSMF
| Model name | Description |
|---|---|
Tariff
|
Tariff trained on the source-domain gold standard data 
|
|
Bayesian transfer learner using the output from Tariff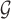
|
InSilico
|
InSilicoVA trained on the source-domain gold standard data 
|
|
Bayesian transfer learner using the output from InSilicoVA
|
Ensemble
|
Ensemble Bayesian transfer learner (independent) using Tariff and Insilico and Insilico
|
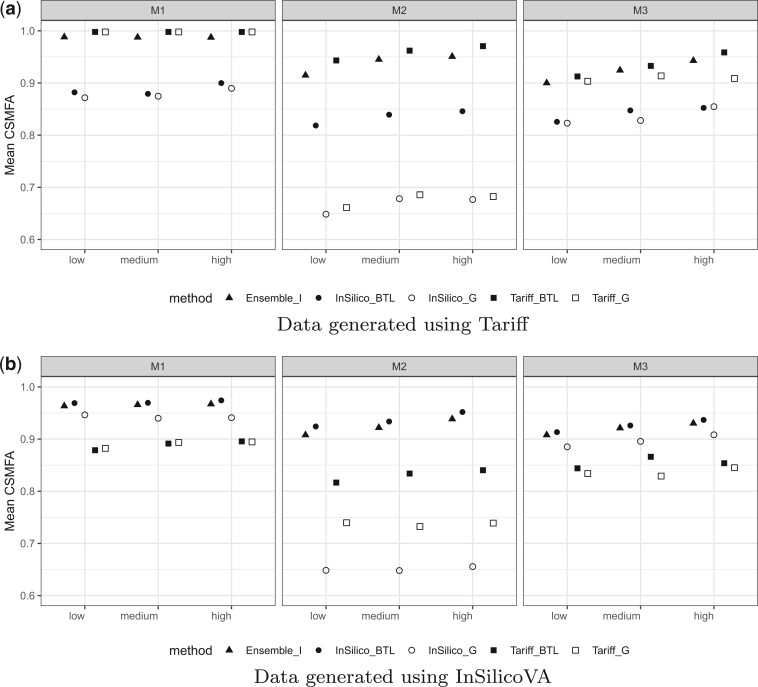
Fig. 2.
CSMF of ensemble and single-classifier transfer learners. (a) Data generated using Tariff. (b) Data generated using InSilicoVA.
The three columns are for the three choices of 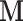 described above, and in each figure the
described above, and in each figure the 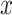 -axis from left to right marks the low, medium, and high settings.
-axis from left to right marks the low, medium, and high settings.
We observe that for almost all settings the Bayesian transfer learning approach was better than its corresponding baseline, i.e., 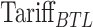 was better than
was better than 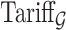 and
and 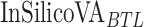 was better than
was better than 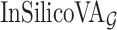 . The improvement in CSMFA was most drastic for
. The improvement in CSMFA was most drastic for 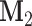 (middle column) where it was as much as
(middle column) where it was as much as 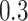 in some cases. Only for
in some cases. Only for 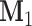 , i.e., when the classifier is assumed to be perfect for predicting in the target domain, we see
, i.e., when the classifier is assumed to be perfect for predicting in the target domain, we see 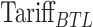 and
and 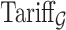 produce similar CSMFA in the (top-left) and
produce similar CSMFA in the (top-left) and 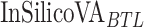 and
and 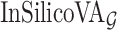 produce similar CSMFA (bottom-left). This just corroborates Theorem 2.1 that the transfer learning keeps things unchanged if the classifier has zero transfer error. We also observe that within each figure, CSMFA’s generally increase as we go from the low to the high setting, indicating that increased representativeness of the class distribution in the small labeled set
produce similar CSMFA (bottom-left). This just corroborates Theorem 2.1 that the transfer learning keeps things unchanged if the classifier has zero transfer error. We also observe that within each figure, CSMFA’s generally increase as we go from the low to the high setting, indicating that increased representativeness of the class distribution in the small labeled set 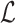 leads to improved performance. Also, across all settings we see that transfer learning based on algorithms used to simulate the data performs better, i.e., for the top-row
leads to improved performance. Also, across all settings we see that transfer learning based on algorithms used to simulate the data performs better, i.e., for the top-row 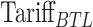 performs better than
performs better than 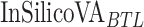 as in this case they respectively correspond to a true and a misspecified model. Similarly, for the bottom-row
as in this case they respectively correspond to a true and a misspecified model. Similarly, for the bottom-row 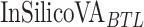 performs better than
performs better than 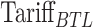 . However, even under model misspecification, the transfer learning models perform better than their baselines, i.e., even when data are generated using Tariff,
. However, even under model misspecification, the transfer learning models perform better than their baselines, i.e., even when data are generated using Tariff, 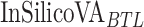 performs better than
performs better than 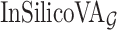 . Finally, across all scenarios, the ensemble learner performs close to the better performing individual learner, highlighting its utility and robustness.
. Finally, across all scenarios, the ensemble learner performs close to the better performing individual learner, highlighting its utility and robustness.
In Section S5 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org), we present more insights into the simulation study. Section S5.1 assesses the impact of the disparity in the class distributions between the source- and target-domains. In Section S5.2, we compare the biases in the estimates of individual class probabilities. Section S5.3 delves into the role of the sample size and quality of the limited labeled set 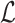 . Section S5.4 demonstrates the value of the Bayesian shrinkage by comparing with the frequentist transfer learning outlined in Section 2.1. In Section S5.5, we compare the joint and independent ensemble models and demonstrate how they favorably weight the more accurate algorithm. Section S5.6 shows how one can use informed shrinkage, if a practitioner has a priori knowledge of which causes are likely to be misclassified by an algorithm. Finally, in Section S5.7, we compare the individual-level prediction performance of the models using the algorithm outlined in Section S5.2.
. Section S5.4 demonstrates the value of the Bayesian shrinkage by comparing with the frequentist transfer learning outlined in Section 2.1. In Section S5.5, we compare the joint and independent ensemble models and demonstrate how they favorably weight the more accurate algorithm. Section S5.6 shows how one can use informed shrinkage, if a practitioner has a priori knowledge of which causes are likely to be misclassified by an algorithm. Finally, in Section S5.7, we compare the individual-level prediction performance of the models using the algorithm outlined in Section S5.2.
6. Predicting CSMF in India and Tanzania
We evaluate the performance of baseline CCVA algorithms and our transfer learning approach when predicting the CSMF for under 5 children in India and Tanzania using the PHMRC data with actual COD labels. We used both India and Tanzania, as they were the only countries with substantial enough sample sizes (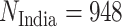 ,
, 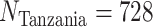 ). For a given country (either India or Tanzania), we first split the PHMRC child data into subjects from within the country (
). For a given country (either India or Tanzania), we first split the PHMRC child data into subjects from within the country (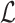 and
and 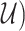 and from outside of the country (
and from outside of the country (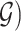 . We then used weighted sampling to select
. We then used weighted sampling to select 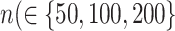 ) subjects from within the country of interest to be in
) subjects from within the country of interest to be in 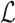 , using weights such that CSMFA
, using weights such that CSMFA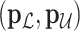 was low. Figure S8 in Section S6 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) shows the difference in the marginal symptom distribution between
was low. Figure S8 in Section S6 of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) shows the difference in the marginal symptom distribution between 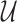 and
and  . All the subjects from the country were put in
. All the subjects from the country were put in  . We trained models
. We trained models 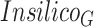 and
and 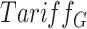 using the non-local data
using the non-local data  , which were then used to predict the top COD for all subjects in
, which were then used to predict the top COD for all subjects in  and
and  . We classified all causes of death into “External,” “Pneumonia,” “Diarrhea/Dysentery,” “Other Infectious,” and “Other.” These predictions were then used to estimate the baseline CSMFs and as an input to our transfer learning models
. We classified all causes of death into “External,” “Pneumonia,” “Diarrhea/Dysentery,” “Other Infectious,” and “Other.” These predictions were then used to estimate the baseline CSMFs and as an input to our transfer learning models 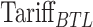 ,
,  , and
, and  . Since the true labels (GS-COD) are available in PHMRC, we calculated the true
. Since the true labels (GS-COD) are available in PHMRC, we calculated the true  for a country as the empirical proportions of deaths from each cause, based on all the records within the country. This
for a country as the empirical proportions of deaths from each cause, based on all the records within the country. This  was used to calculate the CSMF accuracy of each model. This whole process was repeated
was used to calculate the CSMF accuracy of each model. This whole process was repeated 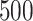 times for each combination of country and value of
times for each combination of country and value of 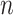 . This made sure that the results presented are average over
. This made sure that the results presented are average over 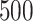 different random samples of
different random samples of 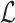 for each country, and are not for an arbitrary sample.
for each country, and are not for an arbitrary sample.
Figure 3 presents the results of this analysis. The top and bottom rows represent the results for India and Tanzania, respectively. The four columns correspond to four different choices of 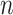 .
.
Fig. 3.
PHMRC analysis: average CSMFA using true GS-COD labels
There are several notable observations. First, regardless of 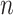 , choice of algorithm
, choice of algorithm  , and country, the calibrated estimates of prevalence from our transfer learning model performed better than or similar to the analogous baseline CSMFs, i.e.,
, and country, the calibrated estimates of prevalence from our transfer learning model performed better than or similar to the analogous baseline CSMFs, i.e., 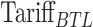 performed better than
performed better than  , and
, and 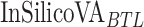 performed better than
performed better than 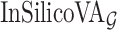 . Second, the magnitude of improvement for the our approach depends on the country and the size of
. Second, the magnitude of improvement for the our approach depends on the country and the size of 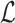 . Within India, the CSMFA of
. Within India, the CSMFA of 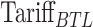 and
and 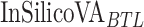 is similar to respectively those from
is similar to respectively those from 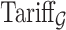 and
and 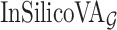 . Tariff does better than InsilicoVA for India with
. Tariff does better than InsilicoVA for India with 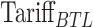 being the best performer. In Tanzania, the baseline InsilicoVA model
being the best performer. In Tanzania, the baseline InsilicoVA model 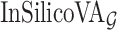 does better than
does better than 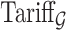 , and similarly
, and similarly 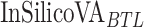 does better than
does better than 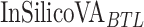 . The improvement of
. The improvement of 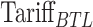 and
and 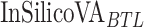 , respectively over
, respectively over 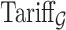 and
and 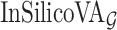 is more prominent than in India, with
is more prominent than in India, with 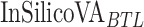 being the most accurate. The magnitude of improvement in the three TL approaches also increased with increase in
being the most accurate. The magnitude of improvement in the three TL approaches also increased with increase in 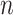 for Tanzania. In Section S7 of the Supplementary material available at Biostatistics online, we investigate the effect of adding more causes of death on the transfer learning CSMFA.
for Tanzania. In Section S7 of the Supplementary material available at Biostatistics online, we investigate the effect of adding more causes of death on the transfer learning CSMFA.
7. Discussion
Epidemiological studies pose unique challenges to transfer learning, stemming from its focus on estimating population-level quantities as opposed to individual predictions, small sample sizes coupled with high-dimensional covariate spaces (survey records), and lack of large training databases available for many other machine learning tasks. Motivated by these settings, we have presented a parsimonious hierarchical model-based approach to transfer learning of population-level class probabilities, using a pre-trained classifier, limited labeled target-domain data, and abundant unlabeled target-domain data.
In order for the transfer learning approach to work, the labeled data 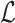 has to be useful for improving CSMF estimation in
has to be useful for improving CSMF estimation in  , i.e., there has to be some commonality between the distributions in
, i.e., there has to be some commonality between the distributions in  and
and  . Usually
. Usually  is not going to be representative of the marginal cause distribution of
is not going to be representative of the marginal cause distribution of  . If additionally, it is also not representative of the conditional distributions of
. If additionally, it is also not representative of the conditional distributions of 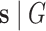 (or, equivalently by marginalizing out
(or, equivalently by marginalizing out 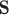 , of
, of 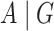 ), then
), then  is of no use to improve CSMF estimation in
is of no use to improve CSMF estimation in  . Hence, our transfer learning is useful when the conditional distributions are same (constant
. Hence, our transfer learning is useful when the conditional distributions are same (constant  ) between
) between  and
and  , or has the same functional form (regression approach of Section 4.2) between
, or has the same functional form (regression approach of Section 4.2) between  and
and  .
.
Shrinkage or regularization is at the core of our approach. In data sets with large numbers of variables (dimensions), regularized methods have become ubiquitous. A vast majority of the literature focuses on shrinking estimates (mostly regression coefficients and covariance or precision matrices) towards some known sub-model. We apply the same principle of regularization in a unique way for estimating the population class probabilities. Instead of shrinking towards any underlying assumptions about the true population distribution, we shrink towards the baseline estimate. In absence of sufficient target-domain data, this is the estimate that is commonly used, and this shrinkage principle is desirable for practitioners familiar with this default method. We show how this shrinkage is achieved by shrinking the confusion matrix towards the identity matrix using appropriate Dirichlet priors. This regularized estimation of a confusion matrix (or any transition matrix) can also be applied in other contexts.
The fully Bayesian implementation is fast, owing to a novel data-augmented Gibbs sampler. The ensemble model ensures robust estimates via data-driven averaging over many classifiers and reduces the risk of selecting a poor one for a particular application. Our simulations demonstrate the value of transfer learning, offering substantially improved accuracy. The PHMRC data analysis makes evident the value of collecting a limited number of labeled data GS-COD in the local population using full or minimally invasive autopsy, alongside the nationwide VA survey. Subsequently using transfer learning improves the CSMF estimates. The results also show how our approach benefits from larger sample sizes of the local labeled set  , and from closer alignment between the marginal class probabilities in
, and from closer alignment between the marginal class probabilities in  and the true target-domain class probabilities.
and the true target-domain class probabilities.
For VA data analyses, we note that while we used a labeled data set in the source-domain as  , in practice it can be any other form of gold standard information sufficient to train a VA classifier. CCVA methods like Tariff and the approach in King and others (2008) represent a traditional supervised learning approach and needs a substantial labeled training dataset
, in practice it can be any other form of gold standard information sufficient to train a VA classifier. CCVA methods like Tariff and the approach in King and others (2008) represent a traditional supervised learning approach and needs a substantial labeled training dataset  . InterVA is a semi-supervised learning approach where
. InterVA is a semi-supervised learning approach where  is a standard matrix of letter grades representing the propensity of each symptom given each cause. InSilicoVA generalizes InterVA and endows the problem with a proper probabilistic framework allowing coherent statistical inference. It adapts to the type of
is a standard matrix of letter grades representing the propensity of each symptom given each cause. InSilicoVA generalizes InterVA and endows the problem with a proper probabilistic framework allowing coherent statistical inference. It adapts to the type of  and can work with either the default symptom-cause matrix used in InterVA or estimate this matrix based on some labeled training data of paired VA and GS-COD records. Our transfer learning is completely agnostic to the choice of this baseline CCVA algorithm and the form of
and can work with either the default symptom-cause matrix used in InterVA or estimate this matrix based on some labeled training data of paired VA and GS-COD records. Our transfer learning is completely agnostic to the choice of this baseline CCVA algorithm and the form of  they require. We only need the predictions from a pre-trained algorithm for all observations in
they require. We only need the predictions from a pre-trained algorithm for all observations in 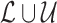 .
.
One important direction forward would be to generalize this approach for more complex COD outcomes. Currently COD outcome is viewed as a discrete variable taking values on a set of causes like pneumonia or sepsis. In practice, death is a complex chronological series of several events starting from some root causes and ending at the immediate or proximal cause. In addition to understanding prevalence of causes in the population, another goal for many of the aforementioned programs is to identify medical events that occurred before death for which an intervention could prevent or delay mortality. Extending the current setup for hierarchical or tree-structured COD outcome would be a useful tool to address this aim. Many CCVA algorithms, in addition to predicting the most likely COD, also predict the (posterior) distribution of likely causes. Our current implementation only uses the most likely COD as an input. An extension enabling the use of the full predictive distribution as an input can improve the method. Finally, the VA records, containing about  questions for thousands of individuals, naturally has several erroneous entries. Preprocessing VA records to eliminate absurd entries and records entails onerous manual efforts. It is challenging to develop quality control models for VA data due to the high dimensionality of the symptoms. Akin to what we did here, one can consider dimension reduction via the predictions of CCVA algorithms for automated statistical quality control.
questions for thousands of individuals, naturally has several erroneous entries. Preprocessing VA records to eliminate absurd entries and records entails onerous manual efforts. It is challenging to develop quality control models for VA data due to the high dimensionality of the symptoms. Akin to what we did here, one can consider dimension reduction via the predictions of CCVA algorithms for automated statistical quality control.
8. Software
R-package “calibratedVA” containing code to obtain estimates of population CSMFs from our transfer learning approach using baseline predictions from any verbal autopsy algorithm is available at https://github.com/jfiksel/CalibratedVA/. The package also contains the code for the ensemble model for using outputs from several VA algorithms. A vignette describing how to navigate the package and demonstrating the use of the methodology is provided in https://github.com/jfiksel/CalibratedVA/blob/master/vignettes/CalibratedVA.Rmd. All results in this article can be recreated using the scripts contained in https://github.com/jfiksel/BayesTLScripts.
Supplementary Material
Acknowledgments
We thank the editors, the associate editor, and the reviewers for their feedback which improved the manuscript.
Conflict of Interest: None declared.
Funding
Bill & Melinda Gates Foundation (OPP1163221 to A.D., A.A., and S.Z.) to Johns Hopkins University for the Countrywide Mortality Surveillance for Action project in Mozambique; and Epi/Biostats of Aging Training Grant, Funded by National Institute of Aging (T32AG000247 to J.F.).
References
- AbouZahr, C., De Savigny, D., Mikkelsen, L., Setel, P. W., Lozano, R., Nichols, E., Notzon, F. and Lopez, A. D. (2015). Civil registration and vital statistics: progress in the data revolution for counting and accountability. The Lancet 386, 1373–1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allotey, P. A., Reidpath, D. D., Evans, N. C., Devarajan, N., Rajagobal, K., Bachok, R., Komahan, K. and SEACO Team. (2015). Let’s talk about death: data collection for verbal autopsies in a demographic and health surveillance site in Malaysia. Global Health Action 8, 28219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman, Leo. (2001). Random forests. Machine Learning 45, 5–32. [Google Scholar]
- Byass, P. (2016). Minimally invasive autopsy: a new paradigm for understanding global health? PLoS Medicine 13, e1002173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byass, P., Chandramohan, D., Clark, S. J., D’ambruoso, L., Fottrell, E., Graham, W. J., Herbst, A. J., Hodgson, A., Hounton, S., Kahn, K.. and others. (2012). Strengthening standardised interpretation of verbal autopsy data: the new interva-4 tool. Global Health Action 5, 19281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll, R. J., Ruppert, D., Stefanski, L. A. and Crainiceanu, C. M. (2006). Measurement Error in Nonlinear Models: A Modern Perspective. 2nd ed.Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- Chattopadhyay, R., Sun, Q., Fan, W., Davidson, I., Panchanathan, S. and Ye, J. (2012). Multisource domain adaptation and its application to early detection of fatigue. ACM Transactions on Knowledge Discovery from Data (TKDD) 6, 18. [Google Scholar]
- Cortes, C. and Vapnik, V. (1995). Support-vector networks. Machine Learning 20, 273–297. [Google Scholar]
- Dai, W., Yang, Q., Xue, G.-R. and Yu, Y. (2007). Boosting for transfer learning 2007. In: International Conference on Machine Learning, Corvallis, OR. [Google Scholar]
- Daumé, H. III (2007). Frustratingly easy domain adaptation. Proceedings of the 45th Annual Meeting of the Association of Computational Linguistics 2007, 256–263. [Google Scholar]
- Flaxman, A. D., Joseph, J. C., Murray, C. J. L., Riley, I. D. and Lopez, A. D. (2018). Performance of insilicova for assigning causes of death to verbal autopsies: multisite validation study using clinical diagnostic gold standards. BMC Medicine 16, 56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman, A. D., Vahdatpour, A., Green, S., James, S. L. and Murray, C. J. L. (2011). Random forests for verbal autopsy analysis: multisite validation study using clinical diagnostic gold standards. Population Health Metrics 9, 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James, S. L., Flaxman, A. D. and Murray, C. J. L. (2011). Performance of the tariff method: validation of a simple additive algorithm for analysis of verbal autopsies. Population Health Metrics 9, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalter, H. D., Roubanatou, A.-M., Koffi, A. and Black, R. E. (2015). Direct estimates of national neonatal and child cause-specific mortality proportions in Niger by expert algorithm and physician-coded analysis of verbal autopsy interviews. Journal of Global Health 5, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King, G., and Lu, Y. (2008). Verbal autopsy methods with multiple causes of death. Statistical Science 23, 78–91. [Google Scholar]
- Koopman, B., Karimi, S., Nguyen, A., McGuire, R., Muscatello, D., Kemp, M., Truran, D., Zhang, M. and Thackway, S. (2015). Automatic classification of diseases from free-text death certificates for real-time surveillance. BMC Medical Informatics and Decision Making 15, 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitao, J., Desai, N., Aleksandrowicz, L., Byass, P., Miasnikof, P., Tollman, S., Alam, D., Lu, Y., Rathi, S. K., Singh, A.. and others. (2014). Comparison of physician-certified verbal autopsy with computer-coded verbal autopsy for cause of death assignment in hospitalized patients in low- and middle-income countries: systematic review. BMC Medicine 12, 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, Z., McCormick, T. and Clark, S. (2018a). InSilicoVA: Probabilistic Verbal Autopsy Coding with ’InSilicoVA’ Algorithm. R package version 1.2.2.https://CRAN.R-project.org/package=InSilicoVA.
- Li, Z., McCormick, T. and Clark, S. (2018b). openVA: Automated Method for Verbal Autopsy. R package version 1.0.6.https://CRAN.R-project.org/package=openVA.
- Li, Z., McCormick, T. and Clark, S. (2018c). Tariff: Replicate Tariff Method for Verbal Autopsy. R package version 1.0.3.https://CRAN.R-project.org/package=Tariff.
- Long, M., Wang, J., Ding, G., Pan, S. J. and Philip, S. Y. (2014). Adaptation regularization: a general framework for transfer learning. IEEE Transactions on Knowledge and Data Engineering 26, 1076–1089. [Google Scholar]
- McCormick, T. H., Li, Z. R., Calvert, C., Crampin, A. C., Kahn, K. and Clark, S. J. (2016). Probabilistic cause-of-death assignment using verbal autopsies. Journal of the American Statistical Association 111, 1036–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miasnikof, P., Giannakeas, V., Gomes, M., Aleksandrowicz, L., Shestopaloff, A. Y., Alam, D., Tollman, S., Samarikhalaj, A. and Jha, P. (2015). Naive Bayes classifiers for verbal autopsies: comparison to physician-based classification for 21,000 child and adult deaths. BMC Medicine 13, 286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minsky, M. (1961). Steps toward artificial intelligence. Proceedings of the IRE 49, 8–30. [Google Scholar]
- Murray, C.J., Lopez, A.D., Black, R., Ahuja, R., Ali, S.M., Baqui, A., Dandona, L., Dantzer, E., Das, V., Dhingra, U. and Dutta, A. (2011a). Population Health Metrics Research Consortium gold standard verbal autopsy validation study: design, implementation, and development of analysis datasets. Population Health Metrics, 9, 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, C. J. L., Lozano, R., Flaxman, A. D., Vahdatpour, A. and Lopez, A. D. (2011b). Robust metrics for assessing the performance of different verbal autopsy cause assignment methods in validation studies. Population Health Metrics 9, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oquab, M., Bottou, L., Laptev, I. and Sivic, J. (2014). Learning and transferring mid-level image representations using convolutional neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2014. pp. 1717–1724. [Google Scholar]
- Pan, S. J., Ni, X., Sun, J.-T., Yang, Q. and Chen, Z. (2010). Cross-domain sentiment classification via spectral feature alignment. In: Proceedings of the 19th International Conference on World Wide Web 2010. ACM, pp. 751–760. [Google Scholar]
- Pan, S. J. and Yang, Q. (2010). A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering 22, 1345–1359. [Google Scholar]
- Polson, N. G., Scott, J. G. and Windle, J. (2013). Bayesian inference for logistic models using pólya–gamma latent variables. Journal of the American Statistical Association 108, 1339–1349. [Google Scholar]
- Serina, P., Riley, I., Stewart, A., James, S. L., Flaxman, A. D., Lozano, R., Hernandez, B., Mooney, M. D., Luning, R., Black, R.. and others. (2015). Improving performance of the tariff method for assigning causes of death to verbal autopsies. BMC Medicine 13, 291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimodaira, H. (2000). Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference 90, 227–244. [Google Scholar]
- Soleman, N., Chandramohan, D. and Shibuya, K. (2006). Verbal autopsy: current practices and challenges. Bulletin of the World Health Organization 84, 239–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, J., Li, Z., McCormick, T., Clark, S. and Byass, P. (2018). InterVA5: Replicate and Analyse ‘InterVA5’. R package version 1.0.2. [Google Scholar]
- Weiss, K., Khoshgoftaar, T. M. and Wang, D. D. (2016). A survey of transfer learning. Journal of Big Data 3, 9. [Google Scholar]
- Yao, Y. and Doretto, G. (2010). Boosting for transfer learning with multiple sources. In: 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE; 2010, pp. 1855–1862. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.