IDEAL: a Vector-Raster Hybrid Model for Efficient Spatial Queries over Complex Polygons

Abstract

Geometric computation can be heavy duty for spatial queries, in particular for complex geometries such as polygons with many edges based on a vector-based representation. While many techniques have been provided for spatial partitioning and indexing, they are mainly built on minimal bounding boxes or other approximation methods, which will not mitigate the high cost of geometric computation. In this paper, we propose a novel vector-raster hybrid approach through rasterization, where pixel-centric rich information is preserved to help not only filtering out more candidates but also reducing geometry computation load. Based on the hybrid model, we develop an efficient rasterization based ray casting method for point-in-polygon queries and a circle buffering method for point-to-polygon distance calculation, which is a common operation for distance based queries. Our experiments demonstrate that the hybrid model can boost the performance of spatial queries on complex polygons by up to one order of magnitude.

I. Introduction

Spatial data is exploding with the wide availability of imaging and sensing instruments [1], [2], GPS enabled devices, Internet of Things [3], and volunteered geographic information. This has driven numerous spatial enabled applications [4]–[7], and spatial data processing and queries have seen unprecedented popularity. The range of spatial objects spans from simple points to polylines and polygons, and the complexity can vary dramatically due to the nature of geospatial objects. For example, while a bus stop can be represented as a point, we may often see complex polygons such as city boundaries and a contamination area [8]. Complex polygons often come with large boundaries, irregular shapes, or both, and they often require a large number of vertices for accurate vector based representation.

Spatial data has two common representations: vector (or entity) based model and raster (or field) based model [9] (Fig. 1). The vector based model treats geographic/spatial objects as real world entities, and a polygon is a region of the plane bounded by a closed polyline represented by vertices. In raster based model, the underlying geographic space is partitioned (or rasterized) into a raster grid of squares (named pixels or cells). The vector based model has been adopted by spatial data management systems (SDBMS) due to its storage efficiency. The raster model based on rasterization has been widely used in computer graphics [10], but has been largely neglected by GIS and SDBMS community [9].

Fig. 1:

2D object representations

Spatial data processing and queries face unique challenges due to the multi-dimensional nature and heavy duty geometric computation, no matter what representation is used. With the vector based model, numerous spatial access methods have been provided [11] for efficient spatial queries, mainly based on a “filter-and-refine” based approach, where indexing based on approximations of spatial objects is used for filtering as many objects as possible, followed by a refinement step for geometric computation to determine the final spatial relationships [12]–[18]. Those approximations, such as Minimum Bounding Rectangles, Maximum Enclosed Rectangles, or Convex Hulls, are used to estimate the interior region of a polygon and help to retrieve candidate objects in the filtering step [18]. However, as each of those approximations uses only a single element (box, circle, ellipse, among others) to approximate the interior region of the polygon when the shape of the polygon is irregular, the filtering performance could be poor.

To achieve better filtering performance, the raster-based model has been adopted as a global grid index in some commercial spatial data management systems such as Microsoft SQL Server [19], [20] and DB2 Spatial Extender [21], and used for GPU based query processing [22], [23]. The grid index approximates the interior region of the polygon from the vector model with multiple tagged pixels from the raster model. As shown in Fig. 1, the pixels of the raster-based model that are fully covered by the vector-based model of the same object are tagged as interior pixels (light blue), while the pixels that are partially covered by the vector-based model are tagged as boundary pixels (blue). Grid indexing significantly improves the efficiency of spatial data processing for certain types of spatial queries. For instance, when checking the relationship between a point and a polygon which is indexed with the grid index, the pixel which contains the point can be retrieved from the grid index, and if the pixel is tagged as interior, then it can be determined that the point is in the interior side of the polygon, and refinement step can be avoided. However, when the pixel is tagged as boundary and the relationship cannot be determined with the grid index alone, or in the case that both the spatial relationship and the exact distance needs to be evaluated, geometric computations have to be conducted over the primitives such as edges of the entire polygon to identify the accurate result. For spatial data management systems, especially for in-memory spatial data processing over complex polygons, those geometric computations dominate the querying process and need to be further reduced [24], [25].

The complexity of geometric computation based on vector-based model is well known to the SDBMS community. For example, point-in-polygon is a common query to check whether a given point lies in the interior of a polygon. A traditional approach will evaluate the number of polygon edges that intersect with a ray emitted to a fixed direction from the point, and the complexity will be O(N), where N is the number of polygon edges. As another example, distance calculation computes the distance between a point and a polygon, which is a common operation for distance-based queries. A brute-force method for distance calculation is to get the minimum distance between the target point to all the polygon edges, and the complexity will also be O(N). One common method to reduce the number of geometric computations is to triangulate polygons into triangles which are then indexed with spatial indexes like R-tree, which is named individual object level indexing [18]. Such a method significantly reduces the number of primitives fed into the refinement process and improves the query performance. However, the time complexity of triangulating a polygon into triangles and building individual object level index are all O(Nlog(N)) [26]. For polygons with a large number of edges, the processing time could be significant. On the other hand, each polygon can be triangulated into N-2 triangles [26], thus more than N-2 nodes are needed to indexing those triangles, each with at least four float or double numbers to define the space region covered by such node. Therefore the memory space used to index a polygon with individual object level index can be several times larger than the memory space used to store the polygon itself.

To tackle the challenge of spatial queries over complex polygons, in this paper, we take a vector-raster hybrid approach through information-preserving rasterization. The rasterization not only converts a polygon to a grid of pixels, but also maintains information between rasterized pixels (raster) and the polygon (vector) on spatial relationship (interior, boundary or exterior), intersected edges, and vertices of the intersected edges at the pixel level. Indeed, the raster model not only works as a grid index but also provides sufficient knowledge for conducting geometric computations over only part of the polygon primitives. By building spatial querying methods with such a hybrid approach, we can significantly boost the query performance and throughput. Our contributions are summarized as follows.

• We propose IDEAL, a Hybrid Vector Raster Model, by rasterizing a polygon and preserving relationship information between the rasterization pixels and the polygon at the pixel level;

• We introduce cost models for evaluating the time and memory cost for rasterization;

• We create effective spatial querying methods for point-in-polygon and point-to-polygon distance queries on top of the hybrid model;

• We evaluate our approach and analyze key performance factors for utilizing the hybrid model with experiments.

The rest of the paper is organized as follows. The IDEAL model is introduced in Section II. Section III shows spatial querying methods based on the IDEAL model. Section IV demonstrates query efficiency with experiments. A further discussion on the generalization of our method is given in Section V. Related works are discussed in Section VI, followed by Conclusion.

II. Relationship Preserving Rasterization of Polygons

Rasterization (vector-raster conversion) decomposes a vector-based object into a pattern of squares (pixels) on a grid and has been a popular technique in computer graphics for rendering and visualization [10]. Traditional rasterization of a polygon determines what pixels are interior to the polygon and therefore are to be filled for coloring, shading, texturing, transparency, etc. In this section, we will discuss how we repurpose rasterization to create a pixel-centric hybrid model IDEAL combining both pixels and data structures representing fine-grained spatial information for spatial query support.

A. Rasterizing Polygons

Traditional polygon rasterization identifies pixels that intersect with the original polygon and labels them as interior pixels [10]. The MBR of the polygon will be initially partitioned into fixed-sized pixels by vertical (e.g., v1 and v2) and horizontal grid lines (e.g., h1 and h2) (Figure 2), followed by two steps. The first step is to go through all the edges of the polygon and record all the intersection points (named nodes) between those edges and the horizontal grid lines. The second step is to identify the interior pixels with those intersection nodes. Thus, each horizontal grid line will have multiple segments separated by the intersection nodes. Let us assume those segments are labeled from left to right with IDs start from 1, then the odd-numbered segments are outside the polygon, named exterior segments (red lines in Figure 2), and the even-numbered segments are inside the polygon, named interior segments (green lines in Figure 2). For the cases that one of those intersection nodes lies in the left border of the MBR, a dummy exterior segment with zero-length is added as the first segment to make the first segment always an exterior segment. All the pixels with borders intersecting interior segments will be labeled as interior pixels. The second step is also called scanline renderings in polygon rasterization. The above techniques create the labeled interior pixels and will suffice the purpose of rendering and visualization in traditional rasterization applications.

Fig. 2:

Polygon rasterization

Algorithm 1:

Labeling boundary pixels

The grid indexing of the polygon has limited information and is not sufficient to support efficient and accurate spatial queries. For example, edges passing a pixel is critical information for spatial queries and not represented in the traditional grid indexing. Our goal is to create a hybrid model IDEAL, based on the raster-model by preserving essential information for spatial query support without relying on building a vector model (Section III). This is achieved through advancing rasterization by building a lightweight index over the polygon edges with additional information collected during the rasterization process. Note that we will maintain an array of points (x, y) - PPointArray corresponding to the vertices of the original polygon in clockwise order, and a point can be retrieved with its index.

During the first step of rasterization (Algorithm 1), all the pixels that are passed through by edges are labeled as boundary pixels (step 9). As will be discussed in Section III, the edges intersected with a boundary pixel need to be retrieved efficiently when needed. Therefore, for each boundary pixel, we record all the continuous edge sequences that pass through the pixel (step 10). The i^th edge of the polygon can be represented by the i^th and i + 1^th points in the PPointArray. For example, for pixel[2][1] in Figure 2, two edge sequences p₁p₂p₃ and p₄p₅p₆ intersect the pixel. Then we record the positions of p₁ and p₂ for retrieving the first edge sequence, and p₄ and p₅ for retrieving the second edge sequence. Whenever the edges that intersect with a specific boundary pixel are requested, all the edges of those edge sequences can be fetched from the PPointArray efficiently with those position numbers. In the rest of this paper, we use “the edges of a boundary pixel” and “pixel.edges” interchangeably to refer to all the edges that intersect the boundary pixel. In addition, the intersection nodes of both the horizontal grid lines (e.g., n₁ an n₂) and of the vertical grid lines (e.g., n₃ and n₄) will be recorded to conduct scanline rendering and facilitate queries (step 14).

In the second step, the non-boundary pixels which intersect with interior segments are labeled as interior pixels (steps 17–24), and the rest non-boundary pixels which intersect with exterior segments are labeled as exterior pixels. Note that the pixels that intersect both interior segments and exterior segments must already be labeled as boundary pixels since at least one edge passes through it.

Figure 2 shows an example of rasterizing the polygon shown in Figure 1. After checking all the edges, 10 pixels are marked as boundary pixels, and 12 nodes are detected as the intersection nodes of those horizontal and vertical grid lines. After going through all the nodes in h₁ and h₂, the state of pixel[1][1] is set to interior and pixel[3][2] is set to exterior. Figure 2 also marks the edge sequences that pass through pixel[2][1]. While traversing the polygon edges clockwise, the edge sequences p₁p₂p₃ and p₄p₅p₆ are recorded for pixel[2][1].

B. Rasterization Granularity

A polygon can be rasterized into one to an infinite number of pixels if precision allows. The more pixels generated for each polygon, the higher the resolution of the raster model. Since the complexities of common queries based on a vector model are proportional to the number of edges (as discussed in Section I), here we define a constant Edges Per Pixel (EPP) and rasterize a polygon into $N_p=\frac{N_e}{EPP}$ pixels, where N_e is the number of edges. For instance, when EPP equals 10, the polygon with 1,000 edges will be rasterized into 100 pixels. We name the value of EPP as the rasterization granularity. With such configuration, the raster model of a polygon with more edges will contain more pixels. Overall, the overhead of maintaining an additional raster model for each polygon remains the same in percentage.

As listed in Algorithm 1, one rasterization process is implemented with three instruction blocks. First, the pixel that covers each point needs to be located to judge whether one edge crosses pixels (step 5). The time spent on locating the pixels for all points can be represented as N_e × t_p where t_p is the latency of locating the pixel for one point and N_e is the number of edges which also equals to the number of points. Second, the cases that edges cross pixels, or intersect grid lines in another word, need be handled separately (steps 9–14). The time spent on handling the intersections equals N_i×t_i where t_i is the time spent on handling one intersection case and N_i represents the total number of intersections. Here we denote the number of grid lines for one polygon as N_g and assume the MBR of the polygon is a square, thus the number of grid lines in one dimension equals √N_p, and N_g equals 2× √N_p with two dimensions of grid lines. For convex polygons, an arbitrary line intersects with a polygon at most twice. For concave polygons, after analyzing the real-world polygons extracted from Open Street Map [27], we observed that the average number of times one arbitrary line intersects with the boundary of one polygon is smaller than 4, thus we set N_i as 4×N_g as an upper bound. Last, scanline renderings are conducted to determine the states of all pixels (steps 17–24). As each pixel is checked exactly once, the total time spent on the second step can be represented as N_p × t_s where t_s is the time used to rendering one pixel and N_p is the number of pixels which equals $\frac{N_e}{EPP}$. In a sum, the total time spent on rasterizing a polygon can be represented as:

$$\begin{gathered} T_r=N_e\times t_p+N_i\times t_i+N_p\times t_s \\ =N_e\times t_p+8\times \sqrt{\frac{N_e}{EPP}}\times t_i+\frac{N_e}{EPP}\times t_s \end{gathered}$$

where t_p, t_i, and t_s are all constants for a given execution environment. It can be summarized that, when the value of EPP is set, the time spent on rasterizing a polygon increases with the increase of the edges number. Furthermore, for a given polygon, the rasterizing latency decreases with the increase of the EPP value.

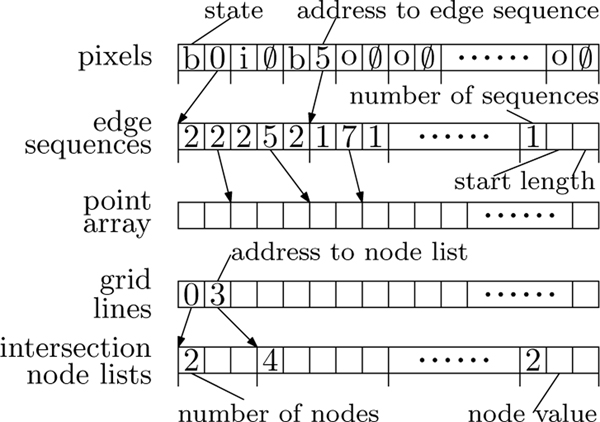
C. Data Structures for IDEAL

Figure 3 shows the in-memory data structure of the IDEAL model. A point array PPointArray stores the points of the original polygon in an array, from which the edges of the polygon can be constructed. Each pixel in the pixels list contains two components: the state of the pixel and a pointer. For a boundary pixel, the pointer points to an edge sequence list that contains the information for retrieving the edge sequences that intersect the specific pixel. For any other pixels, that pointer is nullified. Each edge sequence is represented by a pointer that points to the starting edge and a number that stores the length of the edge sequence. Moreover, each grid line is assigned with a pointer that points to an intersection node list. As all those intersection nodes are aligned with the fixed grids, only one float or double-precision number is needed to record each intersection node along. Besides, one number is needed to store the length of each intersection node list. Some other information like the MBR of the original polygon, the value of EPP, and the total number of edges is also kept in the data structure of IDEAL with a constant space cost.

Fig. 3:

The in-memory data structure of the IDEAL model

In summary, four types of data are used to maintain the in-memory data structure: the state of a pixel (M_s), the pointers (M_p), the length of a list (M_l), and the coordinate value of a point (M_v). As each pixel can be in one of three states, two bits are sufficient to record a state, thus M_s equals 0.25. For the memory efficiency, we use two bytes to store a pointer thus M_p equals 2, and one byte to store the length thus M_l equals 1. Any polygon that contains more than 65,535 edges will be partitioned and any edge sequences longer than 256 will be split to avoid overflow. We use double-precision to store each coordinate value thus M_v equals 8. The memory space M taken by an IDEAL model to store all the components except the point array can be calculated with the formula below:

$$\begin{gathered} M=N_p\times M_s+\left(N_p+N_s+N_g\right)\times M_p \\ +\left(N_b+N_s+N_g\right)\times M_l+N_i\times M_v \end{gathered}$$

where N_p, N_g, and N_i are introduced in the previous section. N_s represents the number of edge sequences. Given the fact that one intersection node is the start of exactly one unique edge sequence, N_s equals N_i. N_b is the number of boundary pixels. In the worst case, all the pixels could be boundary pixels and N_b equals N_p. Therefore, the maximum memory overhead of maintaining the IDEAL model by one polygon can be further reduced to:

$$M=3.25\times \frac{N_e}{EPP}+94\times \sqrt{\frac{N_e}{EPP}}$$

We define the memory overhead as the ratio of the additional memory used over the size of PPointArray which equals N_e× 2 × M_v for two dimensional polygons:

$$\frac{M}{M_p}=\frac{0.203}{EPP}+\frac{5.875}{\sqrt{N_e\times EPP}}$$

It shows that for a given polygon, the finer the rasterization granularity (smaller EPP), the higher the overhead. Meanwhile, when the value of EPP is set, the more edges one polygon contains, the less portion of additional memory overhead is involved by the IDEAL model. For example, the average number of edges for the polygons in our test set is about 1,500. When we set EPP to 10 for a common case, the upper bound of the memory overhead is only about 6.8%.

III. Spatial Queries with Vector-Raster Hybrid Model

Based on the hybrid model enabled by rasterization, we propose querying methods on two typical spatial operations: point-in-polygon test and point-to-polygon distance calculation.

A. Point-in-polygon Test

Algorithm 2:

Point-in-polygon

Point-in-polygon test checks if a point is at the interior or exterior of a given polygon. A classical method for point-in-polygon is ray casting [28]–[30]. For the target point, a horizontal ray is sent to the right side. If the number of polygon edges that intersect with such ray is odd, the point is located at the interior of the polygon. Otherwise, the point is at the exterior of the polygon.

The point-in-polygon test can be significantly accelerated if the polygon is represented with the IDEAL model. As shown in Algorithm 2, for a target point t, we want to check whether it is in a polygon or not. First, the pixels in the raster model are checked. With the MBR of the polygon and the rasterization granularity, gridline positions can be calculated and the pixel where point t is located can be identified (step 1). If the pixel is labeled as interior or exterior, it is guaranteed that t is inside or outside the polygon, and the conclusion can be reported immediately after checking the raster model only (steps 3,5). Otherwise, if the point is in a boundary pixel pix, we will further check the edges of the pixel as discussed next.

Next, we send a ray from t to its right, and the ray intersects with the right border of pixel pix at t′ (step 7). We first evaluate all the edges in pix.edges that intersects with segment tt′ and swap the value of state whenever an intersection inside pix is detected (steps 8–10). We then send another ray from t′ to its bottom and do another ray casting check with all the intersection nodes on the right borders of pix and any other pixels below it (steps 11–14). By doing so we know exactly how many times the polygon border is crossed to get out the MBR of the polygon even only checking a subset of the edges. If the border is crossed an odd number of times, t is inside the polygon (step 15). Otherwise, it is outside the polygon.

Figure 4 shows examples of point-in-polygon tests with IDEAL model. Queries about points a and b can be returned immediately after querying the raster model by checking the states of pixel[1][1] and pixel[3][2]. For point t, the edges of pixel[2][1] need to be further checked. A ray is sent to the right and it intersects with the vertical grid line v₃ at t′. Segment tt′ does not intersect with any edges of pixel[2][1]. After checking all the intersection nodes in pixel[2][1] and pixel[2][0] (n₃ and n₄), one intersection node n₄ is found on the ray sent from t′ to the bottom. Thus a conclusion can be made that t is at the interior side of the polygon.

Fig. 4:

Point-in-polygon test

The performance improvement of conducting a point-in-polygon query with the IDEAL model over the vector model comes from two aspects. First, same as filtering with grid indexing [19], [21], [22], a large portion of queries can be returned immediately after querying the raster model of IDEAL with time complexity of O(1). Second, even when the edges need to be checked, only the edges of a boundary pixel and few intersection nodes need to be checked instead of all the edges of the polygon. As a result, the total amount of geometric computation is significantly reduced.

B. Point-to-polygon Distance Calculation

Point-to-polygon distance calculation returns the minimum distance between a point and the region covered by a polygon. We assume the point is not in the polygon (Otherwise, the distance will be returned as zero). One self-evident fact is that the closest point on the polygon to the target point must lie in the boundary of the polygon. Therefore, a traditional way to compute such distance is to get the minimum distance between the target point to all the edges of the polygon.

Algorithm 3:

Point-to-polygon distance calculation

With the IDEAL model, the edges of different boundary pixels can be checked in a certain order to find the nearest point before checking all the edges. Here we propose an inflating buffer to approach the closest point on the polygon to the target point. As the target geometry is a point, we create a circle buffer centered with the target point and evaluate the boundary pixels intersected by such circle buffer. Algorithm 3 lists the steps of calculating the distance between a point t and a polygon represented with the IDEAL model. The radius of the circle buffer is initially set to the distance between the point to the MBR of the polygon plus half the pixel length (step 3). Note that the distance between t and the MBR will be 0 if t is contained by the MBR. By doing so, the buffer circle will cross the nearest pixels to target t at the beginning. When the circle crosses any boundary pixel pix, the distances of the target point to all the edges of pix are calculated, and the minimum distance value is recorded (steps 8–12).

The distances of the edges of a boundary pixel which is crossed in an earlier round by the circular buffer are unnecessarily closer to the edges of a boundary pixel which is crossed in later rounds. As shown in Figure 5, pixel[1][0] is firstly crossed by the circle buffer centered at a. The closest point b is found after checking the edges it intersects. However, the closest point of a to the polygon is c, which is in pixel[0][1]. Such a case happens only when the current minimum distance is larger than the current radius of the circular buffer. Otherwise, it is guaranteed that all the unchecked edges are farther since the distances from the target point to them must be larger than the radius (steps 13–14). When the current minimum distance is larger than the current radius, we further increase the radius of the circle buffer by one unit of pixel length, which ensures no pixel will be bypassed, and start the next round of checking (step 15).

Fig. 5:

Radius check

Figure 6 shows the processes of getting the distance of a point t and a rasterized polygon in the IDEAL model. In the first round of checking, the edges intersected with pixel[3][0] and pixel[3][1] are checked, and the closest point t′ is determined. The distance between t and t′ is larger than the current radius, thus the radius is increased and the distances between t and the edges intersected with pixel[2][0], pixel[2][1], and pixel[2][2] are calculated. After checking all those edges, the closest point is still t′ and the minimum distance now is smaller than the current radius. We stop there and report the current minimum distance as the distance between t and the polygon.

Fig. 6:

Point-to-polygon distance calculation

The raster model in IDEAL helps to filter the edges that are possibly closer to the target point and find the nearest edge before checking all the edges of the polygon. The total amount of geometric computation involved in point-to-polygon distance calculation is also significantly reduced.

IV. Experimental Evaluation

A. Setup

We run tests with the Open Street Map dataset [27] and geo-tagged Twitter data. We extract the polygons with more than 500 edges, with a total of 221,476 polygons, as complex polygons. The number of edges for complex polygons ranges from 500 to 400,000 and 1,500 on average. The geo-tagged Twitter data contains about 73 million tweets with geolocations.

All the tests are conducted on a workstation with a 24-core CPU (AMD Ryzen Threadripper 3960X at 3.8GHz). It comes with 128GB memory (DDR4 3200) and 2TB SSD (NVMe M.2 PCI-Express 3.0). The OS is Ubuntu 18.04.4 with 5.3.0–40 kernel. The referred IDEAL models and vector models for all systems are loaded into proper in-memory data structures before queries are conducted, thus no disk IO is involved for all tests. Each test is run with multiple threads to ensure that the CPU resource is fully utilized.

B. Comparison Systems

1. Vector model: To compare with querying the vector model, we implement and compare with the multiple step spatial join introduced in [18] and named it VECTOR. In the filtering step, VECTOR performs multiple rounds of filtering with different types of approximations like Minimum Bounding Rectangle (MBR), Convex Hull (CH), and Maximum Enclosed Rectangle (MER) to achieve a higher filtering rate (Fig. 7). In the refinement step, VECTOR triangulates each polygon into triangles and builds an R-tree on those triangles to support efficient containment test and distance calculation at an intra-object level. We also compared our system with the GEOS library [31] (Version 3.7.3) which is the geometry computation engine behind some major spatial data management systems like PostGIS [32] and HadoopGIS [25].

2. Raster model: We also compare our method facilitating a hybrid model with the methods using the raster model as the grid index. We implement the multi-level grid indexing and we name it RASTER. Following the steps introduced in [19], the entire space is partitioned into fixed grids, named cells, for multiple levels. Fig. 8 shows the grid decomposition of space with a single polygon. Similar to the Quad-tree indexing [17], start from level 1, which partitions the entire space into four cells, each cell is checked to see if it covers only the interior or exterior of the polygon with the rasterization process (named spatial tessellation). If a cell covers both the interior and exterior of the polygon, it will be further partitioned into cells in a higher level until the highest level is reached. All cells the polygon intersects are tagged as interior pixels or boundary pixels, and all of those pixels are indexed with a Q-tree for efficient access. For fairness, the number of pixels generated for each polygon in RASTER is set to the number of pixels generated when the IDEAL model is used (EPP=10). Compared with the IDEAL model, which rasterizes the polygon at a single level, when the same number of pixels are used to index a polygon, more boundary pixels can be generated to describe the border of the polygon, therefore the multi-level grid index rasterizes the polygon with lower granularity around the border. We also compare our system with Microsoft SQL Server 2019 with grid indexing enabled (short as MSSQL) [20]. The grid indexing of Microsoft SQL Server can be configured by setting the maximum number of cells per polygon that can be rasterized into. We set it to 8,192 for all tests which is the maximum value it can get. On the other hand, Microsoft SQL Server does not support setting the number of cells individually for each polygon.

Fig. 7:

Approximations and triangulation utilized by multiple step join

Fig. 8:

Multi-level grid index of a space with a single polygon

C. Preprocessing Cost

Firstly, the memory and time cost to preprocess the data for systems IDEAL, RASTER, VECTOR, and MSSQL are evaluated. As shown in Fig. 9, the memory overhead and indexing time of VECTOR are significantly larger than other systems. As shown in Fig. 10, the majority of the memory space and indexing time of VECTOR are used for triangulating polygons and building individual object level indexes. RASTER uses more time for rasterization as it rasterizes the polygon with lower granularity when the same number of pixels are generated. On the other hand, IDEAL uses slightly more memory space than RASTER as it maintains extra information to support refining with only part of the polygon. In a sum, compared with other approaches, the additional memory overhead and preprocessing time taken to maintain the IDEAL model is small.

Fig. 9:

Memory overhead and indexing time for systems

Fig. 10:

The portions of the memory overhead and indexing time taken by getting Maximum Enclosed Rectangle (MER), extracting Convex Hull (CH), triangulating, and building object-level R-tree (R-tree)

Next, we show the efficiency of IDEAL model with real world spatial join queries. For an object o in a given dataset D₁, a spatial join query retrieves a subset of objects S from another dataset D₂, such that all objects in S fulfill certain spatial relationship with o. Such spatial relationship could be intersection, touch, containment, or within a specified distance. We test the containment join and within join with those two basic queries introduced in Section III. An R-tree is created on the complex polygon data set for all the comparing systems.

D. Performance of Containment Spatial Join

The containment spatial join query is implemented with the STContains function in standard SDBMS. Fig. 11a shows the time spent by the point-in-polygon tests. It shows that the point-in-polygon tests on IDEAL model with granularity 10 achieves 6X, 31X, 772X, and 509X performance improvements over the systems RASTER, VECTOR, GEOS, and MSSQL respectively. Note that the preprocessing time is included in the overall querying time for all systems. Fig. 12a shows the percentage of the queries that returned after checking the filtering step only. It shows that VECTOR which indexes with MER and Convex Hull along with MBR achieves worst filtering performance in containment test. In comparison, filtering efficiency of RASTER is slightly better than IDEAL in point-in-polygon test as the granularity of it is smaller. However, as IDEAL further reduces the total amount of geometry computations in the refinement step, containment tests conducted with IDEAL model is 6X faster than simply using grid indexing in the filtering step.

Fig. 11:

Performance comparison of tests using IDEAL model with rasterization granularity 10 versus other methods

Fig. 12:

The filtering rate of different systems over containment and within spatial join tests

E. Performance of Within Spatial Join

To support within spatial join queries, we implement the STWithin function of standard SDBMS systems, which returns true if the distance between two geometries is smaller than a certain value. For each geo-tagged tweet, all the complex polygons within a certain distance from the tweet location and the exact distance between them are returned. The R-tree and the MBR of the complex polygons are used to filter the candidate complex polygons for each tweet before conducting point-to-polygon distance calculations.

Fig. 11b shows the time spent by all the tests for within spatial join query. Querying with IDEAL model improves the query performance by up to 17X, 9X, 123X, and 18X over RASTER, VECTOR, GEOS, and MSSQL respectively. We can also see that grid indexing (IDEAL, RASTER) and object approximations (VECTOR) could help further filter out some candidates along with filtering with the R-tree (Fig. 12b), but the filtering rate is far smaller than the containment test. As a result, the test with RASTER, which conducts geometric computation over the entire polygon at the refinement step, achieves even worse query performance than VECTOR, which triangulates and indexes the polygon to facilitate queries. In contrast, IDEAL achieves the best performance by conducting geometric computation over only a subset of the polygon edges at the refinement step.

F. Impact of the Rasterization Granularity

The granularity, or the value of EPP, is a major factor for the query performance. With a smaller EPP, a polygon can be rasterized into more pixels which approximate the original polygon more precise, thus more candidates can be filtered out in the filtering step. Furthermore, each boundary pixel covers less edges thus less geometric computations are needed to be conducted in the refinement step. As shown in Fig. 13a, the query time of both queries increase almost linearly as the value of EPP increases.

Fig. 13:

Performances of tests on IDEAL models with varies rasterization granularities

Rasterization granularity is also a major factor for both rasterizing performance and run-time memory usage. Fig. 13b shows the changes of the percent of the additional memory overhead and the average time spent on rasterizing all the polygons in the dataset with increasing EPPs. They all show that, for the given dataset, the memory and pre-processing time are almost inversely proportional to the value of EPP, and rasterizing polygons into more pixels (smaller EPP) leads to more memory and computational overhead. Note that polygon rasterization is a one time task and the generated raster model can be reused for all future queries. Thus, the polygon rasterization process can be conducted as a data pre-processing to build indexes for each individual complex polygon. It takes 3.5 seconds to rasterize the entire complex polygon set of 221,476 complex polygons using 48 CPU threads with a rasterization granularities of 10. Compared to the significant performance gain, such one time overhead is negligible.

Choice of EPP value will depend on the application scenario. For instance, when the data are constantly changing and less frequently queried, it is better to choose a larger EPP to avoid high overhead of pre-processing. On the other hand, if the data is static and being heavily queried, a smaller value of EPP should be used to achieve better query performances. Note that the query performance increases linearly with the decrease of EPP, while the overhead increases inversely proportional. When the value of EPP is too small, the increasing rate of the overhead will be significantly larger than the improving rate of the query performance. For instance, when the value of EPP decreases from 20 to 10, the query performance increases only about 10%, but the overhead is almost doubled. Therefore, it is improper to set the value of EPP too small.

V. Discussion

Generalization for Other Query Types.

The IDEAL model can be applied to many other query types. For tests checking whether a certain type of geometry (such as Point, LineString, Polygon, MultiPoint, etc.) is within a polygon, the IDEAL model can always be queried for effective filtering to reduce the number of geometric computations. Spatial operations between polygons can also be accelerated when both of the polygons are represented with the IDEAL model. For instance, for queries to return the area of the intersection of two polygons, the intersected pixel pairs of the two raster models can be retrieved first and the intersected areas of the pixel pairs can be computed independently.

Support of Polygons with Holes.

Polygons with holes are common and can be well supported by the IDEAL model. In the implementation, for each polygon, there will be multiple arrays of points (PPointArrays) maintained to represent the exterior ring and interior rings respectively. The polygon rasterization does not distinguish the edges on the exterior ring or interior ring of the polygon. The points on the exterior ring are stored clockwise, and the points on the interior rings will be stored counter-clockwise. Then the space on the right side (right hand rule) of all edges is at the interior side of the polygon. The point-based query like point-in-polygon and point-to-polygon distance queries work for a polygon with holes, as edges on the interior and exterior rings are treated the same for those queries. However, for polygon-based queries like the polygon-in-polygon test, a special case exists when a polygon s contains a polygon t but a hole of s happens to be contained by t, such as a double-landlocked country [33]. For such case, We can pick a point from each of the interior rings of s, and conduct a point-in-polygon test to see if such point is covered by t. If any point is found inside t, we know the interior ring from which the point is picked from is covered by t, since the edges of the interior ring and t do not intersect with each other. Therefore we can conclude that t is not truly covered by s.

VI. Related Work

Efforts have been made to accelerate the rasterization process. A rasterization algorithm is proposed in [24] to rasterize polygons in parallel. GPU is involved in the rasterizing process in [34]. Hilbert-order rasterization improves the fragment cache performance during the rasterization process [35]. Support of spatial queries with pixels has been discussed in [23], which accelerates the intersection operation among polygons with axis-aligned edges. A new GPU-Friendly geometric data model and algebra is introduced in [36]. [22] converts the spatial aggregation into rendering operations which can be executed with GPU. [37] discusses the other approximates of objects beyond minimum bounding boxes, but does not handle the complexity of individual polygons. There is also work proposed to achieve approximate spatial queries with raster representations [38], [39]. [18] proposes methods to approximate the shape of the polygons like Maximum Enclosed Rectangles (MER), Convex Halls, along with Minimum Bounding Rectangles to achieve a better filtering efficiency before geometry computations need be conducted. However, same as the grid indexing, those methods cannot guide the geometry computations conducted over polygons to reduce the overall geometric computation amount.

Researches have been conducted in supporting efficient spatial queries over hybrid data stored in vector model and raster model. [40] and [41] study how to retrieve top-K areas in the vector model which contains the highest variable values given in the raster model. Raptor makes the spatial query between hybrid model more efficient by avoiding converting one data type to the other [42]. How to query the hybrid dataset in compressed format is studied in [43]. In contrast, IDEAL is a work that facilitate the characteristics of the raster model to guide the spatial queries over vector model, which represents data most commonly in spatial management systems.

VII. Conclusion

In this paper, we introduce a new method to represent a complex polygon with a hybrid raster-vector model IDEAL, where the polygon can be represented with pixels combined with additional knowledge on spatial relationships generated through rasterization. With the pixel-centric model, spatial relationship queries can be effectively determined through pixel-level filtering and fine-grained refinement in boundary pixels using the preserved knowledge. Querying methods based on the IDEAL model are provided for both containment and distance queries, and the experiments demonstrate the superior performance of IDEAL due to the significantly reduced geometric computation. Our approach fills the gap in optimizing spatial queries at the individual geometry level and can be integrated into spatial querying systems to accelerate various types of spatial queries.