Abstract
We propose a deep-learning based annotation-efficient framework for vessel detection in ultra-widefield (UWF) fundus photography (FP) that does not require de novo labeled UWF FP vessel maps. Our approach utilizes concurrently captured UWF fluorescein angiography (FA) images, for which effective deep learning approaches have recently become available, and iterates between a multi-modal registration step and a weakly-supervised learning step. In the registration step, the UWF FA vessel maps detected with a pre-trained deep neural network (DNN) are registered with the UWF FP via parametric chamfer alignment. The warped vessel maps can be used as the tentative training data but inevitably contain incorrect (noisy) labels due to the differences between FA and FP modalities and the errors in the registration. In the learning step, a robust learning method is proposed to train DNNs with noisy labels. The detected FP vessel maps are used for the registration in the following iteration. The registration and the vessel detection benefit from each other and are progressively improved. Once trained, the UWF FP vessel detection DNN from the proposed approach allows FP vessel detection without requiring concurrently captured UWF FA images. We validate the proposed framework on a new UWF FP dataset, PRIME-FP20, and on existing narrow-field FP datasets. Experimental evaluation, using both pixel-wise metrics and the CAL metrics designed to provide better agreement with human assessment, shows that the proposed approach provides accurate vessel detection, without requiring manually labeled UWF FP training data.
Index Terms—: Retinal vessel detection, multi-modal registration, ultra-widefield fundus photography, noisy labels
I. Introduction
Ophthalmologists recognize features of retinal vasculature as important biomarkers associated with multiple diseases. For example, diabetic retinopathy and retinal vein occlusion are characterized by increase in retinal vasculature tortuosity, vessel caliber expansion, and retinal non-perfusion [1]. Therefore, detecting vessels is a fundamental problem in retinal image analysis that has been extensively researched. Existing approaches can be classified into two main categories, supervised and unsupervised, depending on whether they do or do not use labeled training data [2]. Traditionally, the focus was on unsupervised methods that addressed the problem from a variety of perspectives, incuding hand-crafted match filtering [3], [4], morphological processing [5]–[7], multi-scale approaches [8], [9], and matting-based techniques [9]. Recently, supervised learning approaches, specifically deep neural networks (DNNs), have led to significant improvements in retinal vessel segmentation. A variety of DNN architectures have been proposed for retinal vessel segmentation, including per-pixel classifier [10], fully convolutional network [11], [12], U-Net [13]–[16], graph neural network [17], context encoder network [18], and generative adversarial networks [19]. Additionally, several works exploit novel loss functions [20]–[22] and training strategies [23]. These DNN based methods have primarily focused on narrow field (NF) fundus photography (FP), both because NF FP is the predominant format and modality of capture in the clinical setting and because recent efforts have created reasonable sized labeled ground truth datasets for DNN training [4], [24]–[29].
Due to the additional diagnostic information they can offer, vessel detection is also of interest in formats and modalities other than NF FP [30]. Specifically, in this paper, we focus on ultra-wide field (UWF) FP [31] leveraging concurrently captured UWF fluorescein angiography (FA) images. Like NF FP, UWF FP is noninvasive and only involves capture of the retinal images under low-power illumination; even pupil dilation is not required [31]. As shown in Fig. 1(a), UWF FP images provide a wide 200° field-of-view (FOV) in a single high-resolution image, as opposed to the much narrower 30°–50° FOV for NF FP. Manual examination of the UWF images in diagnosis achieves reliable performance comparable to direct clinical examination using an opthalmoscope with pupil dilation. At the same time, UWF FP also reveals additional peripheral retinal vasculature structure that is of diagnostic importance when compared to NF FP [32], [33]. UWF FA, which is shown in Fig. 1(b), represents an alternative modality that also offers a wide FOV and additional diagnostic utility, but has the limitation that it is more invasive, requiring intravenous injection of fluorescein sodium dye.
Fig. 1:
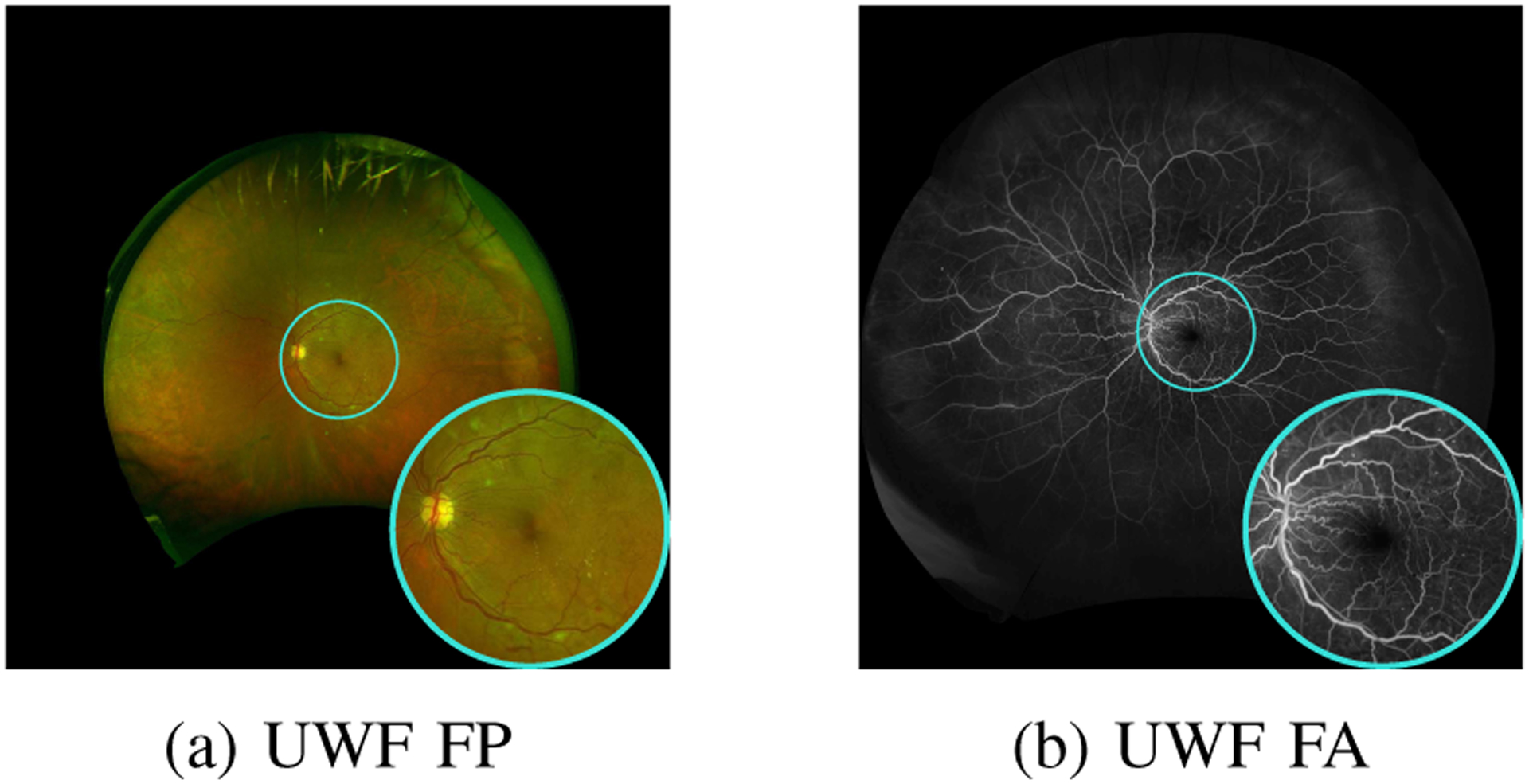
Concurrently captured ultra-widefield (UWF) fundus photography (FP) and UWF fluorescein angiography (FA) image pair. Cyan circles depict the approximate field-of-view for narrow-field FP.
While DNNs trained on NF FP can be applied to UWF FP, the performance is relatively poor in the peripheral region (as demonstrated in Section III-F). The development of DNNs specifically for detecting vessels in UWF FP has been stymied by the paucity of labeled ground truth data. Manually annotating the binary vessel maps for UWF FP is particularly time-consuming and requires clinical-expertise. High-resolution UWF FP exhibits non-uniform illumination and contrast between vessels and background, which makes it challenging and time-intensive to accurately annotate both major and minor vessels across the large FOV; estimates indicate that approximately 18 hours are required for de novo manual annotation for one UWF FP image [34]. Prior work on UWF FP vessel detection [34] therefore proposed the use of pixel-wise hand-crafted features with a shallow, two-layer, multi-layer perceptron that were trained on a limited number of small labeled patches. The approach, however, does not take full advantage of deep learning advances that employ end-to-end training and also learn features in a data-driven fashion.
In this paper, we focus on innovative methodologies that train DNNs for UWF FP vessel detection in an annotation-efficient fashion and eliminate the requirement of manually labeled datasets for supervised learning. To this end, we make the following contributions:
We present a novel iterative framework for vessel detection in UWF FP using DNNs that does not require de novo labeled UWF FP vessel maps. Instead, we rely on datasets that also include concurrently captured UWF FA images, for which effective deep learning approaches for vessel detection have recently become available allowing for accurate vessel detection. The proposed framework then jointly addresses precise registration between the vessel images for the modalities and vessel segmentation in UWF FP, where the two tasks synergistically benefit each other as iterations progress despite the differences in geometry and modality.
We construct a new ground truth labeled dataset, PRIME-FP20, to evaluate retinal vessel detection in UWF FP and to facilitate further work on this problem.
The proposed framework provides a method for accurate vessel detection in UWF FP imagery, a modality that has received limited attention in prior works. The proposed approach significantly outperforms existing methods on the PRIME-FP20 dataset and, on NF FP datasets, achieves performance comparable with state-of-the-art methods designed specifically for NF FP.
We note that an alternative framework for joint vessel segmentation and registration on paired NF FP and NF FA images has also been proposed in [35]. This approach formulates vessel segmentation as a style transfer task (from retinal images to binary vessel maps) and uses one vessel map from the existing dataset as the style target. As we discuss in Section IV and demonstrate in the Supplementary Material, the proposed framework is more effective and achieves better performance than the method in [35].
The rest of the paper is organized as follows. Section II describes the proposed iterative registration and learning framework. In Section III, we perform the detailed analysis of the proposed framework and present the experimental results of vessel detection. A discussion of prior work in [35] that addresses a similar problem and the broader utility of the proposed framework is included in Section IV. Section V concludes the paper.
II. Iterative Registration and Learning approach
As already mentioned, instead of labeled data, training in the proposed approach is accomplished by using a set of concurrently captured UWF FP and UWF FA images, which we denote as , where denotes a simultaneously captured UWF FP and UWF FA image pair (in that order) and M is the number of image pairs. Importantly, we note that while the image pairs for the two modalities are captured during the same clinical visit, they are not aligned and have significant differences in geometry in addition to fundamental differences in the information they contain arising from the differences in the modalities. In the ensuing discussion, we illustrate and describe the processing for one pair , the ith pair, for situations where the same processing flow applies to all pairs.
For each UWF FA image , a corresponding vessel map is obtained using a pre-trained DNN for this modality (shown in green Fig. 2). Our implementation uses [36] though alternative approaches could also be utilized for this purpose. The training of the desired DNN for FP vessel detection is then accomplished as shown in Fig. 2 by iterating between two steps comprising (a) multi-modal registration between the estimated UWF FA vessel map and a current estimate for the UWF FP vessel map and (b) weakly-supervised learning from noisy labels. Specifically, at iteration t, using parametric chamfer alignment, the detected UWF FA vessel map is registered with the current estimate of the UWF FP vessel map. The UWF FA vessel map is warped using the estimated registration transformation to obtain tentative/noisy training labels for pixels in the corresponding UWF FP image . The collective set of such pairs of images for the concurrent UWF FP and FA captured images form the (noisy-labeled) training data . The fundamental differences between FA and FP imaging modalities and invariable errors in the registration contribute to the noise in the labeling. In particular, FA imaging captures fine vessels that are not visible in FP [31]. Consequently, the warped vessel maps contain a large amount of “false positive” labels that are actually background in .
Fig. 2:
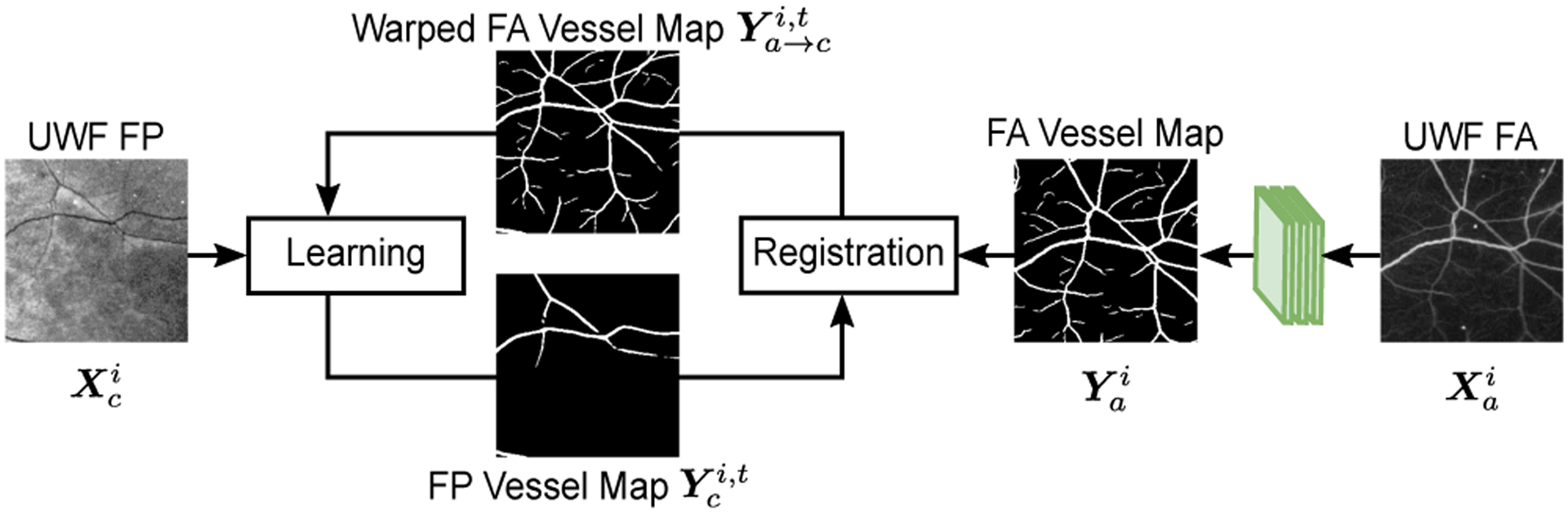
Proposed iterative registration and learning approach for retinal vessel detection in UWF FP without requiring labeled FP vessel data. For clarity, the figure illustrates the processing flow for only the ith pair of UWF FP and UWF FA images, from the complete set of M pairs used for the training.
In the learning step, we propose a robust weakly-supervised learning approach to train DNN that identifies and corrects the noisy labels in the generated dataset. The detected UWF FP vessel map , estimated by the trained DNN, is used for the registration step in the (t + 1)th iteration.
The proposed framework iteratively addresses precise registration and vessel detection, where two tasks synergistically benefit each other as iterations progress. Precise alignment is important to obtain high-quality training labels. Even a small misalignment between the FA and FP images can significantly deteriorate the training data quality by assigning incorrect labels to the image pixels. On the other hand, accurate UWF FP vessel detection, estimated using the weakly-supervised learning approach, helps estimate the registration parameters because chamfer alignment uses detected UWF FP vessel maps for anchoring. Using concurrently captured UWF FP and FA images, the proposed framework accomplishes the training of a DNN for FP vessel detection without requiring labeled UWF FP data. Note that vessel detection in UWF FP images can be performed using the trained DNN without requiring concurrently captured UWF FA images.
Next we provide details for the registration and learning steps that constitute the two major steps in the proposed iterative framework.
A. Vessel Registration via Chamfer Alignment
Binary UWF FA vessel maps are transferred to the corresponding UWF FP images by using a geometric transform that is estimated using the chamfer alignment technique from [36]. To make the presentation self-contained, we include a brief overview here that conveys the key intuition.
We denote the locations of estimated vessel pixels in the UWF FA vessel map by , where are the 2D coordinates of vessel pixel j and Na is the number of vessel pixels in . Similarly, the locations of the Nc vessel pixels in the estimated UWF FP vessel map at iteration t are represented as . Chamfer alignment [37] estimates a parametric geometric transformation to register the points in to those in by minimizing the average squared Euclidean distance between the transformed locations and the closest point in , where β denotes the vector of parameters for the geometric transform. Specifically, define the objective function
| (1) |
with . Then the estimated registration transform is obtained as where β* minimizes L(β). We use a second order polynomial transformation for , which is parameterized by a 12-dimensional parameter vector β and has been shown to be suitable for retinal vessel registration in prior work [36], [38].
In practice, we use a refinement of the basic chamfer alignment approach outlined above that uses a latent-variable based probablistic formulation along with the expectation maximization (EM) algorithm [39] to provide robustness against outlier points that exist in but do not have correspondences in . The robustness against such outliers is particularly crucial in this application setting because, as noted earlier, some fine vessels appear only in because the FA modality detects these much better than FP. We refer readers to [36] for detailed derivations of the parameter estimation with the EM approach. Here we only note that the key intuition can be understood from the fact that, in the EM approach, the arithmetic average in (1) is replaced by a weighted average where the weight for the squared error corresponding to the jth point in corresponds to the estimated posterior probability that it is not an outlier (and has a corresponding point in ). When these posterior probabilities are accurately estimated, the errors for the outlier points effectively drop out from the weighted average, as desired.
For the tth iteration, once the registration transform parameters have been estimated, by applying the corresponding transformation to the UWF FA vessel maps we obtain the warped version as the current estimate of the FA vessel map aligned with the FP imagery, which serves as “noisy labels” for the learning step.
B. Weakly-Supervised Learning with Noisy Labels
While the multi-modal registration provides tentative dataset to train a DNN for detecting vessels in UWF FP, the labels in inevitably contain noise (incorrect labels) due to the fundamental differences in FA and FP modalities. In this sub-section, we analyze the characteristic of the label noise and propose a weakly-supervised learning method to train DNN against label noise.
FA imaging is able to capture the fine retinal vessels better than FP [31]. Consequently, the warped FA vessel maps contain a large number of vessel branches, especially fine vessels, that are not visible in FP modality. Figures 3(a) and Figures 3(b) show a sample UWF FP patch selected from the peripheral region and the corresponding warped UWF FA vessel map, respectively. From these two figures, one can appreciate that the majority of fine vessels are not captured in UWF FP image. In Fig. 3(c), we compare and visualize the differences between the warped vessel map and ground truth labels that are manually annotated from scratch by a human annotator. The red pixels in Fig. 3(c) depict a large proportion of vessel labels in the warped UWF FA vessel map that are actually background in the UWF FP image. On the other hand, the FP vessel pixels that are not in the warped UWF FA vessel map , shown in blue in Fig. 3(c), are a rather small fraction of the FP vessel pixels. Thus, treated as an estimate of the FP vessel map, the warped FA vessel map has low precision but high recall. Therefore, the label noise in is asymmetric: the background labels are largely accurate and the vessel labels potentially have errors.
Fig. 3:

(a) Sample UWF FP patch and (b) the corresponding labels from warped UWF FA vessel map. Red and blue pixels in (c) indicate incorrect vessel labels (“false positive”) and background labels (“false negative”), respectively, in the warped UWF FA vessel map.
We exploit the asymmetry of the label noise and propose a weakly-supervised learning approach to train a DNN using as noisy labels. Formally, we divide pixels in into two sets, and , where pixels in are labeled as vessels (white pixels in Fig. 3(b)) and those in are labeled as background (black pixels in Fig. 3(b)). We further denote and . Our goal is to train a DNN, modeled as a function f with learnable weights W, that outputs a probabilistic vessel map Yc = f(Xc; W) in response to an input FP image Xc. In the tth iteration, weight parameters Wt for the DNN are estimated by minimizing the binary cross-entropy loss, viz.,
| (2) |
where and are the binary cross-entropy loss computed from the predicted vessel probability and in and , respectively, and | · | represents the cardinality. Our motivation is that while DNNs can be over-fitted on noisy labels with sufficient training epochs, in the early training epochs [40], DNNs tend to first learn on the correct labels. Thus the correct and the incorrect labels can be distinguished based on the loss values [41].
In Fig. 4 (left), we plot the training loss values computed after each training epoch for both correct (green) and incorrect (red) labels in . At the early stage of the training, pixels with incorrect labels have larger loss values than the correctly labeled pixels, allowing one to identify the noisy labels from the loss values. In Fig. 4 (right), we show the loss distribution after 20 training epochs for both correctly and incorrectly labeled pixels. We see that the distribution is bimodal and can be modeled as a two-component mixture model.
Fig. 4:
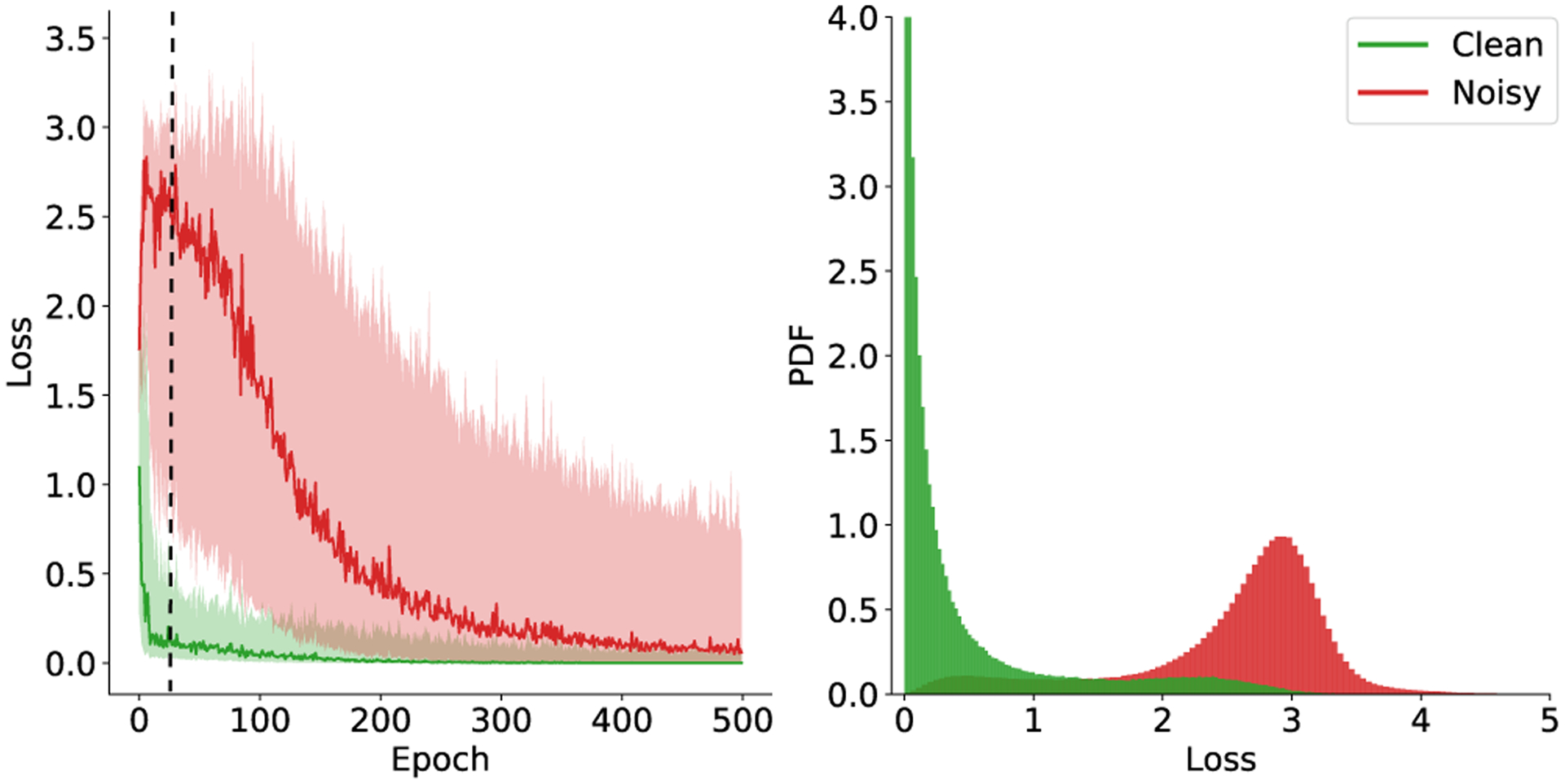
Left: The binary cross-entropy loss for correct (green) and incorrect (red) vessel labels in the course of training. The curve shows the median loss value and the shaded region represents the range between the 15th and the 85th percentile of the loss values. Right: histogram of the training loss after 20 training epochs (indicated by the dash line in the left plot).
To estimate the distribution of , we use the latent variable to indicate if the pixel v in is mislabeled. Given that the label is correct , the conditional probability of is modeled as an exponential distribution with parameter λ. See the green distribution in Fig. 4. And, given , the conditional probability of is modeled as a Gaussian distribution with mean μ and standard deviation σ. See the red distribution in Fig. 4. The distribution of the mixture model for takes the form of
| (3) |
where is the mixing weight that represents the prior probability of latent variable . We adopt the EM algorithm [39] to fit the proposed mixture model. EM algorithm alternates between the E-step and the M-step. In the E-step, we compute the posterior probability , which can be obtained using Bayes’ rule:
| (4) |
In the M-step, we update the parameters of the mixture model. Using the estimated posterior probability, we obtain
| (5) |
The process is repeated until parameters converge. The fitted mixture model provides a tool for analyzing the label noise in the warped vessel maps. The prior probability is an estimate of the amount of correct labels in . More importantly, the posterior probability indicates the probability of pixel being correctly labeled, which allows us to update labels in . Specifically, the label in updated ground truth is computed as
In (6a), the updated label for pixel in is a linear combination of the label in the warped vessel map and the predicted probability vessel map where the coefficients are determined by the posterior probability . Intuitively, if the posterior probability is close to 1, we trust the label in the warped vessel map because the corresponding pixel is correctly labeled. Otherwise, we reduce the weights of label and rely more on the network-predicted probability vessel maps . In (6b), we do not update background labels in because these labels are considered accurate.
The training process is divided into two stages. First, we train the DNN on the tentative noisy dataset for E0 epochs. Then we fit the proposed mixture model on the loss values and obtain the updated labels . In the second stage, we continue to train the DNN on for another E1 epochs. The overall algorithm for the proposed framework is summarized in Algorithm 1.
Note that both the vessel registration and the robust learning steps utilize the EM framework to estimate the posterior probabilities of a pixel being outlier/mislabeled. However, the objectives in these two steps are different and we can not use the posterior probabilities estimated in one step for the other. In the registration step, the EM framework mitigates the effects of outlier vessel points. The outliers are defined as the vessel points in that do not have correspondences in the current estimated vessel map . As we show in Section III-D, some vessels are not properly detected in in the first few iterations. As a result, the outlier pixels in the registration step are not necessarily the same as the mislabeled pixels that need to be identified in the training step.
III. Experiments
In this section, we first introduce a new dataset, PRIME-FP20, that is used for implementing the proposed iterative framework and for evaluating the vessel detection performance. Next, we summarize the evaluation metrics in Section III-B, and describe the implementation details and alternative methods used as baselines in Section III-C. The experimental results are structured as follows. We provide detailed analysis to demonstrate the effectiveness of the proposed iterative framework and the weakly-supervised learning method in Section III-D and Section III-D, respectively. We then compare the proposed framework with alternative methods on the PRIME-FP20 dataset in Section III-F. Finally, we show the boarder utility of the proposed framework for detecting vessels in NF FP in Section III-G.
A. PRIME-FP20 Dataset
We construct a new dataset, PRIME-FP20 [42], for evaluating the performance of vessel detection in UWF FP. The PRIME-FP20 dataset consists of 15 pairs of concurrently captured UWF FP and UWF FA images that are selected from baseline images of patients enrolled in the PRIME study1. The images are captured using Optos California and 200Tx cameras (Optos plc, Dunfermline, United Kingdom) [43]. The system uses a scanning ophthamoscope with a low power laser to capture dual red and green channel UWF FP images and a single channel FA image. All images have the same resolution of 4000 × 4000 pixels and are stored as 8-bit TIFF format with lossless LZW compression. The green channel UWF FP image is used as the input Xc for our vessel detection because it captures information for layers with the retinal vasculature, whereas the red channel captures information from other layers (from the retinal pigment epithileum to the choroid) [43]. For evaluation, ground truth vessel maps for the UWF FP modality are manually labeled by a human annotator using the ImageJ software [44] with the segmentation editor plugins. The available selection tools in ImageJ, such as brush tool and free-hand selection tool were used to mark the vessel pixels in the UWF FP. The annotator repeatedly adjusted image brightness and contrast to precisely label both major and minor vessel branches in different regions. For each UWF FP, we also provide a binary mask for the FOV of the image. To obtain the mask, we simply binarize the green channel of the UWF FP because the pixels intensities out of FOV are close to zero.
 |
B. Evaluation Metrics
For quantitative evaluation, we report the area under the Precision-Recall curve (AUC PR)2, the Dice coefficient (DC), and the CAL metric [45]. The computation of these metrics is summarized in Section S.III of the Supplementary Material.
The AUC PR and the Dice coefficient, although widely used in prior literature, are based on the pixel-wise comparison of the ground truth and the estimated vessel map. However, the pixel-wise comparison does not consider the structure of retinal vasculature and is sensitive to the label ambiguities, particularly for peripheral pixels that only partially belong to vessels. The CAL metric [45] is designed to be less sensitive to label uncertainties and provides better agreement with human assessment of higher level structure. CAL evaluates the consistency between the binary ground truth and the binary predicted vessel map by calculating three individual factors that quantify the consistency with respect to the connectivity (C), the area (A), and the corresponding length of skeletons (L). Each factor ranges between 0 and 1 where 1 indicates perfect consistency to the ground truth. The product of three factors is defined as the overall CAL metrics. The computation of the CAL metrics requires a binary vessel map, to obtain which, we binarize the predicted probabilistic vessel map Yp with a threshold τ = 0.5.
For the experiments on the PRIME-FP20 dataset, we perform the K-fold cross-validation [46] to evaluate the performance of vessel detection, where K is set to 5, and report the statistics of the five evaluation metrics. We only consider pixels within the FOV mask when computing the metrics.
C. Implementation Details and Alternative Methods
To detect UWF FA vessels Xa, we train the U-Net [13] model on the RECOVERY-FA19 dataset [36] that provides eight high-resolution (3900 × 3072 pixels) UWF FA images and the ground truth vessel maps. We use the U-Net model because of its superior performance in medical image segmentation [47]. Detailed training protocol is included in the Supplementary Material (Section S.II-B). We apply the trained model to the UWF FA images and binarize the estimated vessel map with a threshold τ = 0.5.
For the proposed iterative framework, we use the pairs of UWF FP and UWF FA images in the PRIME-FP20 dataset. Note that the proposed framework does not require the ground truth vessel maps for UWF FP in the PRIME-FP20 dataset. These manually labeled ground truth are only used for evaluation in our experiments. We implement the chamfer alignment and the weakly-supervised learning using MATLAB™ and PyTorch [48], respectively. We perform three iterations between registration and learning (T = 3) and provide an empirical evaluation of different number of iterations in Section III-D. In the first iteration, we use a preliminary UWF FP vessel map for chamfer alignment, which is obtained from a DNN pre-trained on existing NF FP dataset. For the weakly-supervised learning step, we use the U-Net [13] model. We set the training epochs E0 = 25 and E1 = 30. Detailed network architectures and training protocol are included in Section S.II of the Supplementary Material.
We consider existing learning-based vessel detection methods for as baselines for comparison. These methods include HED [49], U-Net [13], DRIU [11], CRF [50], NestUNet [14], M2U-Net [51], CE-Net [18], CS-Net [52], RU-Net [15], and IterNet [16]. For each method, we obtained two versions of the network by training on different datasets, and evaluate each version on the PRIME-FP20 dataset. The first dataset for training consisted of UWF FP images and the warped FA labels obtained from the first iteration using the proposed framework, i.e., , where t = 1. The second dataset used for training was the IOSTAR [26] dataset that provides 30 images and binary vessel maps. While the images in the IOSTAR dataset are narrow-field, they are captured with the scanning laser ophthalmoscopy (SLO) technique that is also used in the PRIME-FP20 dataset3.
D. Iterative Registration and Learning Framework
We demonstrate the effectiveness of the proposed iterative framework by showing that both registration and learning benefit from each other and improve progressively.
To quantify registration accuracy, we compute the chamfer distance as the average Euclidean distance between each point in the ground truth binary vessel maps and its closest point in the transformed vessel maps detected in UWF FA. The average chamfer distance under the second-order transformation can be treated as a proxy for the registration error. The blue line with circle markers in Fig. 5(a) shows the average chamfer distance over 4 iterations. In the first iteration, the chamfer distance is on average 1.66 pixels. While the misalignment is slight, it can significantly deteriorate the quality of the training data. The generated tentative ground truth in the first iteration only has a recall of 0.63, which means that 37.0% of true vessels are labeled as background (false negative labels). The third column in Fig. 5(b) shows sample results of the generated ground truth in the first iteration, where the blue pixels highlight the false negative labels. In the third iteration, the chamfer distance drops to 0.77 pixels, yielding accurate training data with a recall increased to 0.83. The fifth column in Fig. 5(b) shows training data obtained from the third iteration.
Fig. 5:
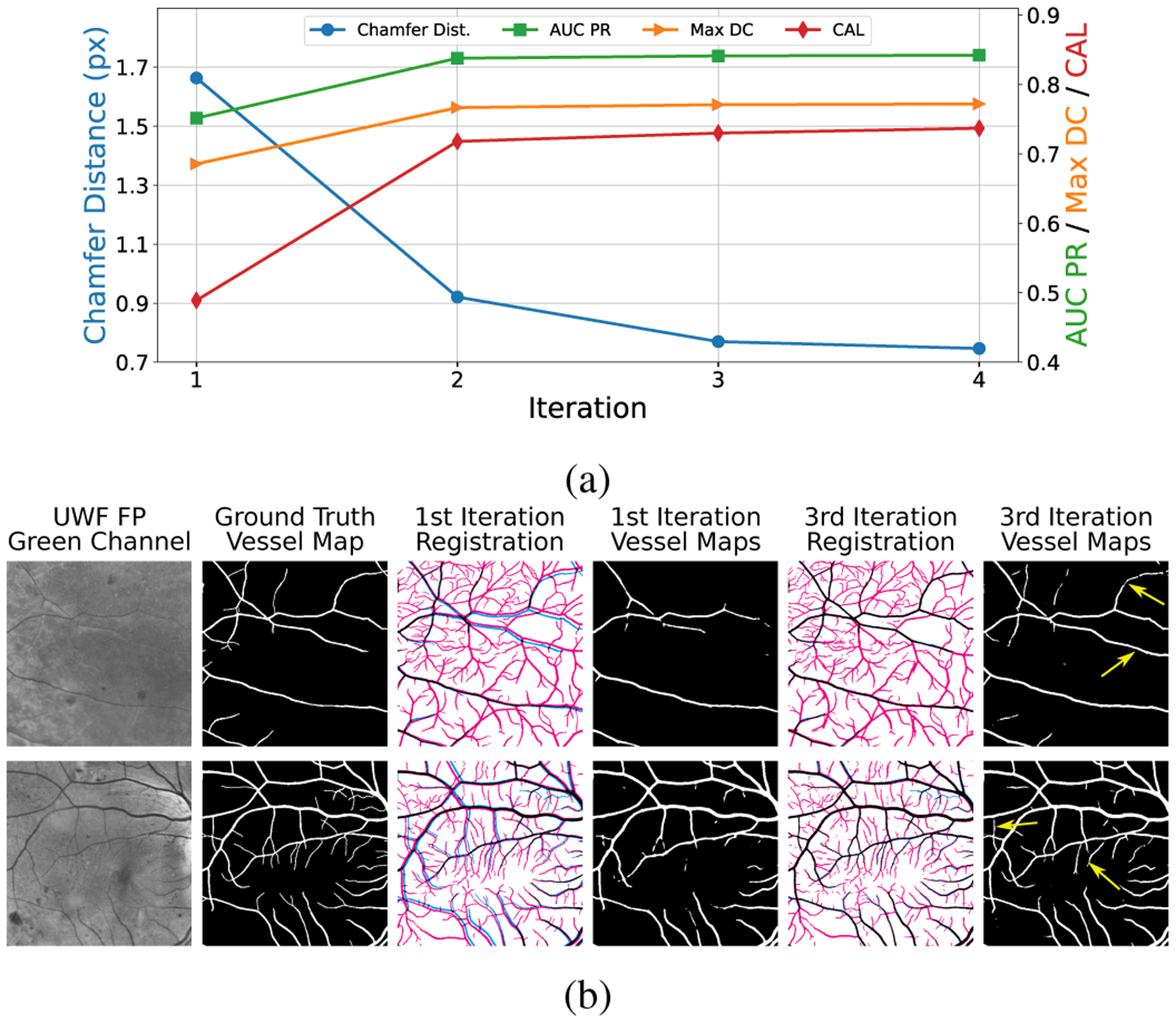
Registration and vessel detection performance as a function of iteration count. (a) the residual chamfer distance, which serves as a good proxy for the registration error, is labeled on the left axis. The axis on the right-hand side, with labels shown in different colors, corresponds to the metrics used for evaluating vessel detection performance. (b) Sample vessel maps obtained in the first and the third iterations. Red and blue pixels indicate incorrect vessel labels (“false positive”) and background labels (“false negative”), respectively, in the warped UWF FA vessel map.
The improved ground truth dataset in turn benefits network training for vessels detection in UWF FP. The fourth and the last columns in Fig. 5(b) show the predicted vessel maps in the first and the third iteration, respectively. The yellow arrows highlight the improved vessel detections that are not correctly identified in the first iteration. We quantify and visualize the performance of vessel detection obtained over 4 iterations in Fig. 5(a). The axes on the right side correspond to the three metrics used for evaluation. It is clear that, as the registration and training proceed, the performance of vessel detection is improved progressively. Additionally, we see that the DNN performance becomes stable after three iterations and going to the fourth iteration offers limited improvement. Thus, we set the total number of iterations T to 3 in our experiments.
E. Robust Learning with Noisy Labels
We conduct detailed analysis for a better understanding of the proposed method for robust learning from noisy labels. Because we focus on the robust learning method, all experimental results reported in this section are performed on the noisy training data that is generated from the last iteration in the proposed framework.
To justify the effectiveness of the proposed robust learning method, we compare the performance of vessel detection with the following alternative training strategies: (1) the standard training approach that directly trains a DNN without any techniques particularly attuned to noisy labels, (2) the re-labeling method that dynamically updates the labels in the training dataset [53], and (3) a re-weighting method that reduces the weight for the noisy labels in the loss function. The re-labeling method seeks to obtain a clean dataset by dynamically updating the training labels using the probabilistic vessel maps predicted from the DNN. The training process is formulated as a joint framework that alternatively optimizes the DNN parameters and the training labels. For the re-weighting method, the idea is to adaptively assign small weights to the potential noisy pixels and to emphasize the clean pixels in the loss function. Specifically, we assign the posterior probability pv as the weighting factor to each pixel in and set the weights to 1 for all pixels in .
The quantitative results obtained from different training methods are listed in Table I. Directly training on the incorrect labels adversely impacts the performance of vessel detection, even though we apply early stopping to prevent the DNN from over-fitting the noisy labels. In addition, it is difficult to determine the stopping criterion because no validation dataset is available in this settings. The re-weighting and the proposed approaches, both of which utilize the posterior probabilities pv to train DNNs, show significant improvement over the direct training and the re-labeling methods. This also demonstrate the effectiveness of the proposed mixture-model-based noisy label identification. Unlike the re-weighting method, which uses pv to reduce the effects of incorrect labels, the proposed robust training approach updates the noisy labels and therefore explicitly forces DNN to learn on the correct prediction.
TABLE I:
Accuracy metrics for vessel detection results obtained with alternative training strategies. All DNNs are trained on the dataset obtained from the third iteration in the proposed framework. The best result is shown in bold.
| Methods | AUC PR | Max DC | CAL (C, A, L) |
|---|---|---|---|
| Direct Training | 0.802 | 0.745 | 0.628 (0.998, 0.777, 0.809) |
| Re-labeling [53] | 0.837 | 0.769 | 0.586 (0.999, 0.729, 0.805) |
| Re-weighting | 0.842 | 0.768 | 0.713 (0.999, 0.833, 0.856) |
| Proposed | 0.842 | 0.772 | 0.730 (0.999, 0.849, 0.860) |
Next, we assess the effects of different mixture models on fitting the loss distribution and estimating the posterior probabilities pv. Specifically, we compare the proposed mixture model with a two-component Gaussian mixture model (GMM) and a two-component beta mixture model (BMM) [41]. A proper mixture model, which provide a good approximation to the loss distribution, should lead to an accurate estimation of the posterior probability pv and an accurate update on the training labels Yu. Thus, we compare the quality of the updated labels with respect to the manually labeled ground truth4. To do so, we fit the mixture models on the same loss distribution and update the labels using (6a) and (6b). Figure 6 plots the AUC PR obtained after each training epoch for different mixture models. We have several observations from this figure. First, the GMM is not a good approximation for the loss distribution and the accuracy of noisy label correction decreases as the training proceeds and is significantly worse than other two mixture models. Second, compared to the BMM, the proposed mixture model provides the more accurate results and the performance is largely stable in the first 70 training epochs. In Fig. 7, we show the sample results of updated labels, the corresponding noisy labels from the warped vessel maps, and the manually labeled ground truth. The “false positive” labels are removed from the warped vessel maps, highlighted by the yellow arrows in Fig. 7, yielding to updated labels that is similar to the ground truth labels. In Section S.IV of the Supplementary Material, we present intermediate results in a visual format, specifically, the predicted vessel maps and the posterior probabilities estimated using the proposed mixture model, that provide additional insight into the working of the EM-based noisy label correction in the proposed approach.
Fig. 6:
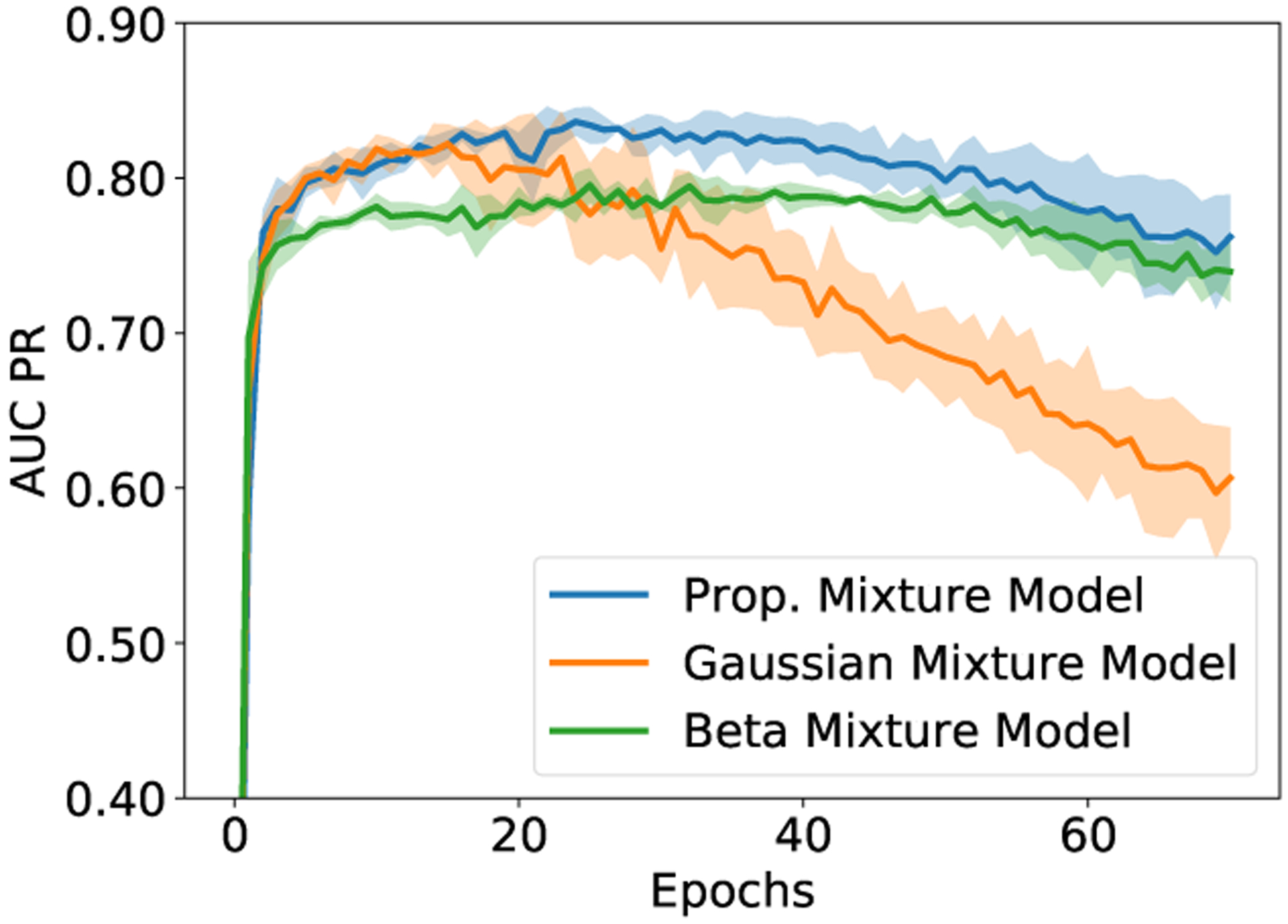
AUC PR obtained with alternative mixture models for modeling the loss distribution as a function of training epochs. The curves show the average AUC PR values over 5-fold cross-validation, and the shaded region represents the one standard deviation from the mean AUC PR values.
Fig. 7:
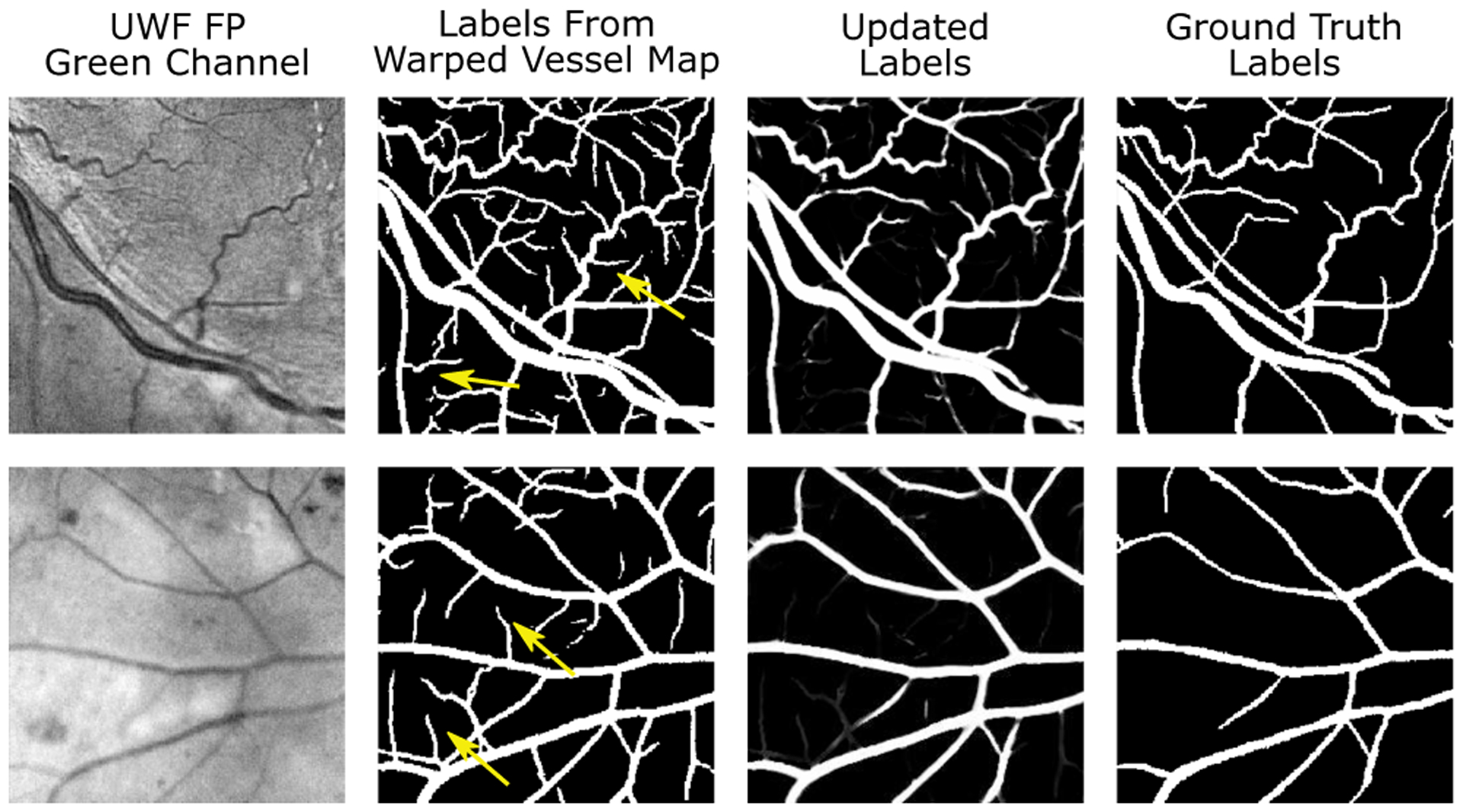
Sample results of noisy label correction in the proposed framework. Additional results, including the predicted vessel maps and the posterior probabilities, are provided in Section S.IV of the Supplementary Material.
F. Evaluation on the PRIME-FP20 Dataset
As mentioned in Section III-B, we perform 5-fold cross-validation to assess the results of vessel detection on the PRIME-FP20 dataset. Table II lists the quantitative results obtained from the proposed iterative framework and the existing methods. The proposed iterative framework performs remarkably well and significantly outperforms other methods with respect to all evaluation metrics, achieving an AUC PR of 0.845, the maximum Dice coefficient of 0.776, and an overall CAL of 0.730. Notably, the performance metrics for the proposed framework are quite close to the annotation-intensive approach, where a U-Net model is trained manually labeled clean dataset with the same 5-fold cross-validation (The row labeled U-Net* in Table II). We show sample results of the detected vessel maps obtained from different methods in Fig. 8 and provide more visual results in the Section S.V of the Supplementary Material. In Fig. 8, we see that the existing DNNs trained on NF fundus images perform poorly in the peripheral region. We attribute this poor performance to the fact that the peripheral region contains artifacts that are not visible in the NF dataset. Such artifacts normally have dark and curvilinear structures that can be misinterpreted as vessels in the image. For example, the yellow arrows in the enlarged view of region III highlight the “false positive” detection region that is not a vessel but an eyelash shadow appearing in the periphery. Compared to the DNNs trained on NF images, the proposed iterative framework accurately detects vessel maps from different regions in UWF FP. See the enlarged view of regions III and IV for the result patches selected from the periphery and the central retina, respectively.
TABLE II:
Quantitative metrics assessing vessel detection accuracy for different methods on the PRIME-FP20 dataset. Existing methods are trained on two different datasets: the registration-transfer-labeled dataset obtained from the first iteration of the proposed framework and the IOSTAR [26] dataset. The row U-Net* lists the results from a U-Net trained on manually labeled PRIME-FP20 dataset that does not contain noisy labels. The baseline CRF method does not converge when trained on transfer-labeled dataset. The best result is shown in bold.
| Method | Year | Trained on noisy PRIME-FP20 | Trained on IOSTAR | ||||
|---|---|---|---|---|---|---|---|
| AUC PR | Max DC | CAL (C, A, L) | AUC PR | Max DC | CAL (C, A, L) | ||
| U-Net* [13] | - | 0.869 | 0.796 | 0.755 (0.999, 0.869, 0.870) | - | - | - |
| HED [49] | 2015 | 0.752 | 0.690 | 0.584 (0.999, 0.765, 0.761) | 0.723 | 0.683 | 0.451 (0.997, 0.640, 0.700) |
| U-Net [13] | 2015 | 0.773 | 0.713 | 0.547 (0.998, 0.723, 0.751) | 0.746 | 0.704 | 0.547 (0.998, 0.727, 0.752) |
| DRIU [11] | 2016 | 0.752 | 0.700 | 0.558 (0.999, 0.747, 0.739) | 0.728 | 0.691 | 0.495 (0.999, 0.698, 0.705) |
| CRF [50] | 2017 | - | - | - | 0.563 | 0.550 | 0.341 (0.994, 0.577, 0.590) |
| NestUNet [14] | 2018 | 0.749 | 0.698 | 0.596 (0.999, 0.776, 0.765) | 0.754 | 0.716 | 0.567 (0.999, 0.747, 0.757) |
| M2U-Net [51] | 2019 | 0.730 | 0.680 | 0.531 (0.998, 0.731, 0.719) | 0.727 | 0.694 | 0.534 (0.998, 0.720, 0.742) |
| CE-Net [18] | 2019 | 0.753 | 0.702 | 0.510 (0.998, 0.689, 0.731) | 0.757 | 0.718 | 0.574 (0.999, 0.752, 0.762) |
| CS-Net [52] | 2019 | 0.771 | 0.712 | 0.559 (0.998, 0.747, 0.742) | 0.772 | 0.721 | 0.565 (0.998, 0.746, 0.755) |
| RU-Net [15] | 2019 | 0.758 | 0.702 | 0.579 (0.999, 0.767, 0.753) | 0.757 | 0.707 | 0.559 (0.999, 0.737, 0.758) |
| IterNet [16] | 2020 | 0.798 | 0.736 | 0.607 (0.999, 0.765, 0.785) | 0.746 | 0.717 | 0.553 (0.999, 0.732, 0.753) |
| Proposed | 2020 | 0.841 | 0.771 | 0.730 (0.999, 0.849, 0.860) | - | - | - |
Fig. 8:
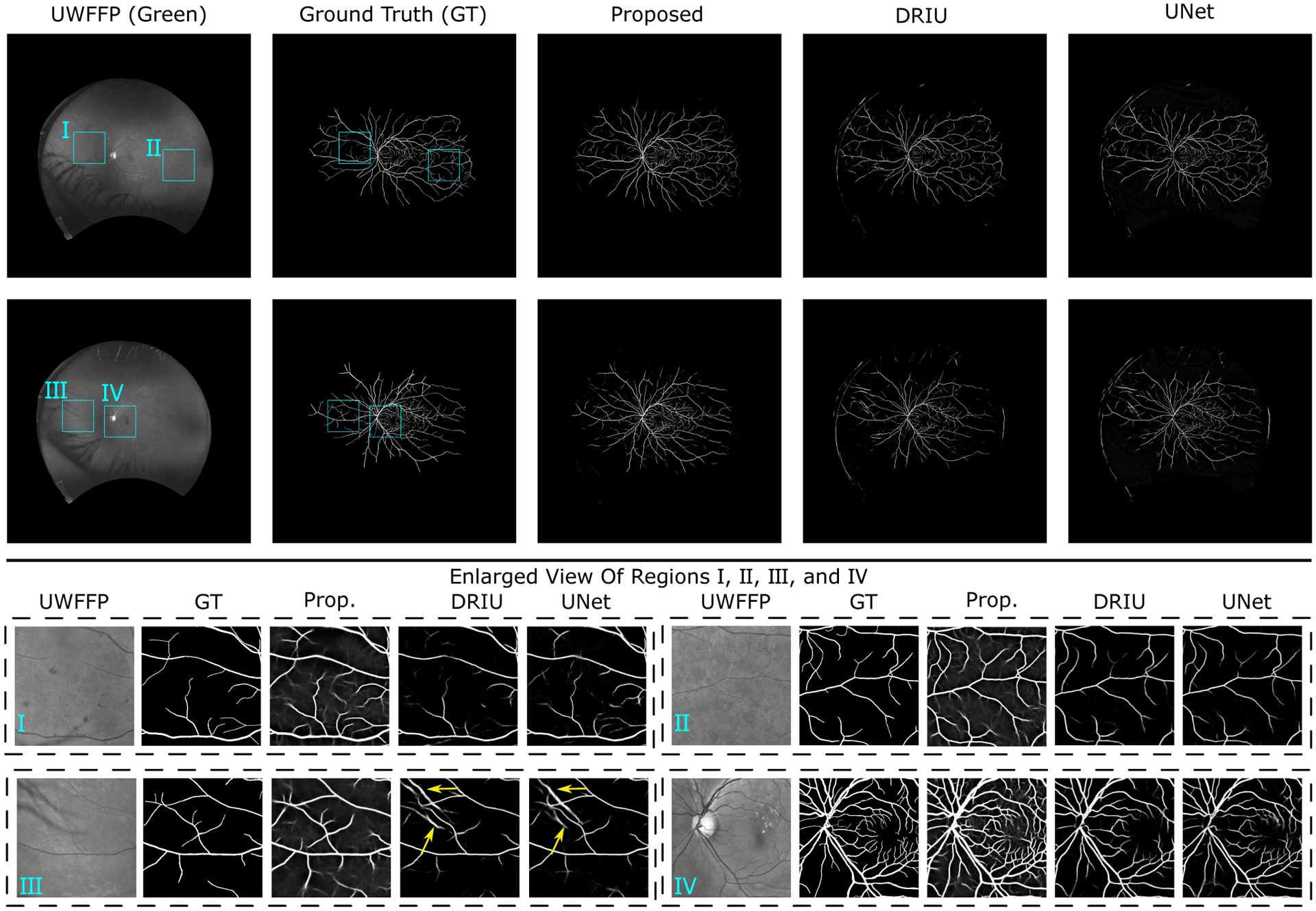
Sample images and detected vessel maps for the proposed approach and alternatives from the PRIME-FP20 dataset. The contrast-enhanced enlarged views I-IV, marked by the cyan rectangles in the full image, are included. Additional visual results are provided in Section S.V of the Supplementary Material.
Comparing the results in Table II across different training datasets for each of the alternative approaches, we observe that most networks perform better when trained on the noisy PRIME-FP20 dataset obtained in the first iteration of the proposed framework compared with training on the IOSTAR dataset, even without using any learning approaches that are attuned to noisy labels. These results further reinforce the benefits of the proposed registration based transfer approach for generating training data for UWF FP modality.
G. Evaluation on Narrow-Field Fundus Photography
Fundus photography shares common characteristic between the ultra-widefield and the narrow-field modalities. In this section, we demonstrate that the DNN trained only on ultra-widefield images using the proposed framework is capable of detecting vessels in NF FP. To this end, we test the performance of the trained DNN on two public datasets, DRIVE [24] and STARE [4], and compare with the existing learning-based methods for vessel detection. Note that we train the DNN on ultra-widefield images using the proposed weakly-supervised learning approach and evaluate the performance on the NF images. We refer to this experiment as the cross-training evaluation [12], [54] where the training and the test data come from two independent sources. For existing learning-based methods, the models are trained on the DRIVE [24] and evaluated on the STARE [4], and vice versa. These two datasets provide two independent ground truth vessel maps manually labeled by two human annotators. We choose the vessel maps from the first annotator as the ground truth also report the human performance by evaluating the vessel maps made by the second annotator, which is commonly accepted approach in the literature.
Complete results are listed in Table S.III in the Supplementary Material. On the DRIVE dataset, the proposed framework achieves the best performance with the AUC PR of 0.886, the maximum DC of 0.803, and the overall CAL metric of 0.827. Note that the CAL metric is significantly better than those obtained from prior alternatives by large margins and is close to human performance (0.839). The second-best performing method, HED [49], achieves an overall CAL of 0.743. The performance on the STARE dataset, while slightly worse than the best performing method, is comparable to other methods. Specifically, the results obtained from the proposed framework has the AUC PR of 0.884, the maximum DC of 0.795, and the overall CAL metric of 0.756. The results on both datasets reinforce the robustness and the accuracy of the proposed iterative framework. We provide visual results of detected vessel maps in Section S.VII of the Supplementary Material.
IV. Discussion
For narrow field FP and FA images, the problem analogous to the one we address for UWF FP and FA images, has been previously addressed in an alternative approach called SegReg [35]. This approach utilizes paired image-pairs from FP and FA modalities and jointly addresses registration and the training of DNNs for vessel segmentation for both modalities. Trained networks can then be used for vessel detection in each modality individually. We evaluated SegReg on the PRIME-FP20 dataset. Implementation details and visual results are included in Section S.VI of the Supplementary. SegReg performs rather poorly on the PRIME-FP20 dataset, achieving an AUC PR of 0.535 and the maximum Dice coefficient of 0.560, which is not competitive with the other prior methods used for the comparisons in Table S.III. The reasons for the poor performance are twofold. First, SegReg assumes that the registered vessel maps in FA and FP modalities are identical. The assumption, however, does not hold for UWF FP and UWF FA pairs. Second, SegReg estimates the displacement field for registration, which only handles small deformation and therefore requires a good initialization. In addition to its poor detection performance, SegReg also consumes more computational resources for training than the proposed framework – approximately 11.5 hours as opposed to about 3.25 hours for the proposed network on an Nvidia V100 GPU.
Although, in this paper, we considered a very specific problem setting in retinal image analysis and presented our work in that context, the proposed methodology could also be adapted and applied in other situations. Alternative imaging modalities that vary in their ability to resolve different anatomical features (or physiology) are quite common and it is also a common situation that for some patients, data is acquired with a subset of the modalities. Techniques motivated by and/or developed using appropriate adaptations of the proposed method could be useful in these alternative settings, for both medical imaging and other image processing applications. Within the domain of image-based retinal diagnosis, an additional potential application of the proposed framework would be for vessel detection in optical coherence tomography angiography (OCT-A), which is also being increasingly used for examining retinal vasculature. Outside of medical imaging, an analogous problem also arises in understanding the evolution of road networks from a progression of satellite/aerial images captured over an extended duration of time. Later times typically contain more roads than earlier ones and additionally are likely to have precise labeled data compared with older imagery. Although beyond the scope of the current paper, techniques motivated by and/or developed using appropriate adaptations of the proposed method can be expected to useful in these alternative settings. Promisingly for such broader applications, our preliminary experiments indicate that the methodology for learning from noisy labels used in the proposed approach is not heavily reliant on the assumption that the supervising (FA) modality has greater detail than the supervised (FP) modality.
V. Conclusion
The iterative registration and deep-learning framework proposed in this paper provides an effective and annotation-efficient approach for detecting retinal blood vessels in UWF FP imagery without requiring manually labeled UWF FP vessel maps. Experimental evaluations demonstrate that the proposed approach significantly outperforms the existing methods on a new UWF FP dataset, PRIME-FP20, and achieves comparable performance with the state-of-the-arts on existing NF FP datasets. The PRIME-FP20 is made publicly available [42] to facilitate further work on retinal image analysis.
Supplementary Material
Acknowledgments
We thank the Center for Integrated Research Computing, University of Rochester, for providing access to computational resources, and Eric Kegley and Cary Stoever for acquisition of PRIME images. The PRIME study is an investigator-initiated trial supported by Regeneron (Tarrytown, New York) who had no role in the funding, design, or conduct of the development of the methodology presented in this paper.
The work was supported in part by a University of Rochester Research Award, by a distinguished researcher award from the New York state funded Rochester Center of Excellence in Data Science (CoE #3B C160189) at the University of Rochester, by an unrestricted grant to the Department of Ophthalmology from Research to Prevent Blindness, and grant P30EY001319-35 from the National Institutes of Health.
Footnotes
The PRIME study (ClinicalTrials.gov Identifier: NCT03531294) evaluates the impact of intravitreal aflibercept in diabetic retinopathy patients with a baseline diabetic retinopathy severity score level of 47A to 71A inclusive.
We do not choose the Receiver Operating Characteristic (ROC) curve as the evaluation metric because the ground truth label is highly skewed. We provide additional discussion in Supplementary Material (Section S.III).
We also trained the alternative methods on DRIVE [24] and STARE [4] datasets. The performance of the resulting networks was, however, significantly worse than the ones trained on the IOSTAR dataset.
We also evaluated the alternative models using goodness-of-fit criteria. The evaluation presented in Section S.IV of the Supplementary Materials further supports the conclusions presented here.
Contributor Information
Li Ding, Department of Electrical and Computer Engineering, University of Rochester, Rochester, NY 14627, USA..
Ajay E. Kuriyan, Retina Service, Wills Eye Hospital, Philadelphia, PA 19107 & the University of Rochester Medical Center, University of Rochester, Rochester, NY 14642, USA.
Rajeev S. Ramchandran, University of Rochester Medical Center, University of Rochester, Rochester, NY 14642, USA.
Charles C. Wykoff, Retina Consultants of Houston and Blanton Eye Institute, Houston Methodist Hospital & Weill Cornell Medical College, Houston, TX 77030, USA.
Gaurav Sharma, Department of Electrical and Computer Engineering, University of Rochester, Rochester, NY 14627, USA..
References
- [1].Rogers S et al. , “The prevalence of retinal vein occlusion: pooled data from population studies from the United States, Europe, Asia, and Australia,” Ophthalmology, vol. 117, no. 2, pp. 313–319, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Srinidhi CL, Aparna P, and Rajan J, “Recent advancements in retinal vessel segmentation,” J. Med. Syst, vol. 41, p. 70, 2017. [DOI] [PubMed] [Google Scholar]
- [3].Chaudhuri S, Chatterjee S, Katz N, Nelson M, and Goldbaum M, “Detection of blood vessels in retinal images using two-dimensional matched filters,” IEEE Trans. Med. Imaging, vol. 8, no. 3, pp. 263–269, September 1989. [DOI] [PubMed] [Google Scholar]
- [4].Hoover A, Kouznetsova V, and Goldbaum M, “Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response,” IEEE Trans. Med. Imaging, vol. 19, no. 3, pp. 203–210, 2000. [DOI] [PubMed] [Google Scholar]
- [5].Zana F and Klein JC, “Segmentation of vessel-like patterns using mathematical morphology and curvature evaluation,” IEEE Trans. Image Proc, vol. 10, no. 7, pp. 1010–1019, July 2001. [DOI] [PubMed] [Google Scholar]
- [6].Ding L, Kuriyan A, Ramchandran R, and Sharma G, “Multi-scale morphological analysis for retinal vessel detection in wide-field fluorescein angiography,” in Proc. IEEE Western NY Image and Signal Proc. Wksp. (WNYISPW), Rochester, NY, November. 2017, pp. 1–5. [Google Scholar]
- [7].Mendonca AM and Campilho A, “Segmentation of retinal blood vessels by combining the detection of centerlines and morphological reconstruction,” IEEE Trans. Med. Imaging, vol. 25, no. 9, pp. 1200–1213, September 2006. [DOI] [PubMed] [Google Scholar]
- [8].Yu H, Barriga S, Agurto C, Zamora G, Bauman W, and Soliz P, “Fast vessel segmentation in retinal images using multi-scale enhancement and second-order local entropy,” in SPIE Medical Imaging, vol. 8315, 2012, p. 83151B. [Google Scholar]
- [9].Fan Z, Lu J, Wei C, Huang H, Cai X, and Chen X, “A hierarchical image matting model for blood vessel segmentation in fundus images,” IEEE Trans. Image Proc, vol. 28, no. 5, pp. 2367–2377, May 2019. [DOI] [PubMed] [Google Scholar]
- [10].Liskowski P and Krawiec K, “Segmenting retinal blood vessels with deep neural networks,” IEEE Trans. Med. Imaging, vol. 35, no. 11, pp. 2369–2380, November 2016. [DOI] [PubMed] [Google Scholar]
- [11].Maninis K-K, Pont-Tuset J, Arbeláez P, and Van Gool L, “Deep retinal image understanding,” in Intl. Conf. Med. Image Comput. Comput.-Assist. Intervent, 2016, pp. 140–148. [Google Scholar]
- [12].Li Q, Feng B, Xie L, Liang P, Zhang H, and Wang T, “A cross-modality learning approach for vessel segmentation in retinal images,” IEEE Trans. Med. Imaging, vol. 35, no. 1, pp. 109–118, 2016. [DOI] [PubMed] [Google Scholar]
- [13].Ronneberger O, Fischer P, and Brox T, “U-Net: Convolutional networks for biomedical image segmentation,” in Intl. Conf. Med. Image Comput. Comput.-Assist. Intervent, 2015, pp. 234–241. [Google Scholar]
- [14].Zhou Z, Siddiquee MMR, Tajbakhsh N, and Liang J, “UNet++: A nested U-Net architecture for medical image segmentation,” in Deep Learning in Med. Image Analysis, 2018, pp. 3–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Alom MZ, Yakopcic C, Hasan M, Taha TM, and Asari VK, “Recurrent residual U-Net for medical image segmentation,” J. Med. Imaging, vol. 6, no. 1, pp. 1–16, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Li L, Verma M, Nakashima Y, Nagahara H, and Kawasaki R, “IterNet: Retinal image segmentation utilizing structural redundancy in vessel networks,” in IEEE Winter Conf. Applications of Comp. Vision, 2020, pp. 3645–3654. [Google Scholar]
- [17].Shin SY, Lee S, Yun ID, and Lee KM, “Deep vessel segmentation by learning graphical connectivity,” Med. Image Analysis, vol. 58, p. 101556, 2019. [DOI] [PubMed] [Google Scholar]
- [18].Gu Z et al. , “CE-Net: Context encoder network for 2D medical image segmentation,” IEEE Trans. Med. Imaging, vol. 38, no. 10, pp. 2281–2292, October 2019. [DOI] [PubMed] [Google Scholar]
- [19].Son J, Park SJ, and Jung K-H, “Towards accurate segmentation of retinal vessels and the optic disc in fundoscopic images with generative adversarial networks,” J. Digital Imaging, vol. 32, no. 3, pp. 499–512, June 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Cherukuri V, Kumar B G V, Bala R, and Monga V, “Deep retinal image segmentation with regularization under geometric priors,” IEEE Trans. Image Proc, vol. 29, pp. 2552–2567, 2020. [DOI] [PubMed] [Google Scholar]
- [21].Mosinska A, Mrquez-Neila P, Koziski M, and Fua P, “Beyond the pixel-wise loss for topology-aware delineation,” in IEEE Intl. Conf. Comp. Vision, and Pattern Recog, June 2018, pp. 3136–3145. [Google Scholar]
- [22].Mou L, Chen L, Cheng J, Gu Z, Zhao Y, and Liu J, “Dense dilated network with probability regularized walk for vessel detection,” IEEE Trans. Med. Imaging, vol. 39, no. 5, pp. 1392–1403, 2020. [DOI] [PubMed] [Google Scholar]
- [23].Yan Z, Yang X, and Cheng K, “Joint segment-level and pixel-wise losses for deep learning based retinal vessel segmentation,” IEEE Trans. Biomed. Eng, vol. 65, no. 9, pp. 1912–1923, 2018. [DOI] [PubMed] [Google Scholar]
- [24].Staal J, Abràmoff M, Niemeijer M, Viergever M, and van Ginneken B, “Ridge based vessel segmentation in color images of the retina,” IEEE Trans. Med. Imaging, vol. 23, no. 4, pp. 501–509, 2004. [DOI] [PubMed] [Google Scholar]
- [25].Fraz MM et al. , “An ensemble classification-based approach applied to retinal blood vessel segmentation,” IEEE Trans. Biomed. Eng, vol. 59, no. 9, pp. 2538–2548, 2012. [DOI] [PubMed] [Google Scholar]
- [26].Zhang J, Dashtbozorg B, Bekkers E, Pluim JPW, Duits R, and ter Haar Romeny BM, “Robust retinal vessel segmentation via locally adaptive derivative frames in orientation scores,” IEEE Trans. Med. Imaging, vol. 35, no. 12, pp. 2631–2644, December 2016. [DOI] [PubMed] [Google Scholar]
- [27].Budai A, Bock R, Maier A, Hornegger J, and Michelson G, “Robust vessel segmentation in fundus images,” Intl. J. of Biomed. imaging, vol. 2013, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Bankhead P, Scholfield CN, McGeown JG, and Curtis TM, “Fast retinal vessel detection and measurement using wavelets and edge location refinement,” PLOS ONE, vol. 7, no. 3, pp. 1–12, 03 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Decencière E et al. , “Feedback on a publicly distributed image database: the Messidor database,” Image Analysis & Stereology, vol. 33, no. 3, pp. 231–234, 2014. [Google Scholar]
- [30].Abràmoff MD, Garvin MK, and Sonka M, “Retinal imaging and image analysis,” IEEE Rev. Biomed. Eng, vol. 3, pp. 169–208, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Nagiel A, Lalane RA, Sadda SR, and Schwartz SD, “Ultra-widefield fundus imaging: A review of clinical applications and future trends,” RETINA, vol. 36, no. 4, pp. 660–678, 2016. [DOI] [PubMed] [Google Scholar]
- [32].Silva PS, Cavallerano JD, Sun JK, Noble J, Aiello LM, and Aiello LP, “Nonmydriatic ultrawide field retinal imaging compared with dilated standard 7-field 35-mm photography and retinal specialist examination for evaluation of diabetic retinopathy,” Amer. J. Ophthalmology, vol. 154, no. 3, pp. 549–559.e2, 2012. [DOI] [PubMed] [Google Scholar]
- [33].Silva PS, Cavallerano JD, Sun JK, Soliman AZ, Aiello LM, and Aiello LP, “Peripheral lesions identified by mydriatic ultrawide field imaging: Distribution and potential impact on diabetic retinopathy severity,” Ophthalmology, vol. 120, no. 12, pp. 2587–2595, 2013. [DOI] [PubMed] [Google Scholar]
- [34].Pellegrini E et al. , “Blood vessel segmentation and width estimation in ultra-wide field scanning laser ophthalmoscopy,” Biomed. Opt. Express, vol. 5, no. 12, pp. 4329–4337, December 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Zhang J et al. , “Joint vessel segmentation and deformable registration on multi-modal retinal images based on style transfer,” in IEEE Intl. Conf. Image Proc, September. 2019, pp. 839–843. [Google Scholar]
- [36].Ding L, Bawany MH, Kuriyan AE, Ramchandran RS, Wykoff CC, and Sharma G, “A novel deep learning pipeline for retinal vessel detection in fluorescein angiography,” IEEE Trans. Image Proc, vol. 29, no. 1, pp. 6561–6573, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Barrow HG, Tenenbaum JM, Bolles RC, and Wolf HC, “Parametric correspondence and chamfer matching: Two new techniques for image matching,” in Proc. Int. Joint Conf. Artificial Intell, 1977, pp. 659–663. [Google Scholar]
- [38].Gavet Y, Fernandes M, and Pinoli J-C, “Quantitative evaluation of image registration techniques in the case of retinal images,” J. Electronic Imaging, vol. 21, no. 2, pp. 1–8, 2012. [Google Scholar]
- [39].Dempster AP, Laird NM, and Rubin DB, “Maximum likelihood from incomplete data via the EM algorithm,” Journal of the Royal Statistical Society, vol. 39, pp. 1–38, 1977. [Google Scholar]
- [40].Zhang C, Bengio S, Hardt M, Recht B, and Vinyals O, “Understanding deep learning requires rethinking generalization,” in Intl. Conf. Learning Representations, 2017. [Google Scholar]
- [41].Arazo E, Ortego D, Albert P, O’Connor N, and McGuinness K, “Unsupervised label noise modeling and loss correction,” in Intl. Conf. on Mach. Learning, vol. 97, 2019, pp. 312–321. [Google Scholar]
- [42].Ding L, Kuriyan AE, Ramchandran RS, Wykoff CC, and Sharma G, “PRIME-FP20: Ultra-widefield fundus photography vessel segmentation dataset,” IEEE Dataport, 2020. [Online]. Available: 10.21227/ctgj-1367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Optos California Tech Sheet, Optos, 2015. [Online]. Available: https://www.optos.com/globalassets/www.optos.com/products/california/california-brochure.pdf [Google Scholar]
- [44].Schindelin J et al. , “Fiji: an open-source platform for biological-image analysis,” Nature methods, vol. 9, no. 7, p. 676, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Gegundez-Arias ME, Aquino A, Bravo JM, and Marin D, “A function for quality evaluation of retinal vessel segmentations,” IEEE Trans. Med. Imaging, vol. 31, no. 2, pp. 231–239, February 2012. [DOI] [PubMed] [Google Scholar]
- [46].Hastie T, Tibshirani R, and Friedman JH, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. New York, NY: Springer-Verlag, 2009. [Google Scholar]
- [47].Litjens G et al. , “A survey on deep learning in medical image analysis,” Med. Image Analysis, vol. 42, pp. 60–88, 2017. [DOI] [PubMed] [Google Scholar]
- [48].Paszke A et al. , “PyTorch: An imperative style, high-performance deep learning library,” in Adv. in Neural Info. Proc. Sys, 2019, pp. 8024–8035. [Google Scholar]
- [49].Xie S and Tu Z, “Holistically-nested edge detection,” in IEEE Intl. Conf. Comp. Vision, December. 2015, pp. 1395–1403. [Google Scholar]
- [50].Orlando JI, Prokofyeva E, and Blaschko MB, “A discriminatively trained fully connected conditional random field model for blood vessel segmentation in fundus images,” IEEE Trans. Biomed. Eng, vol. 64, no. 1, pp. 16–27, 2017. [DOI] [PubMed] [Google Scholar]
- [51].Laibacher T, Weyde T, and Jalali S, “M2U-Net: Effective and efficient retinal vessel segmentation for real-world applications,” in IEEE Intl. Conf. Comp. Vision, and Pattern Recog. Wksp, June 2019, pp. 115–124. [Google Scholar]
- [52].Mou L et al. , “CS-Net: Channel and spatial attention network for curvilinear structure segmentation,” in Intl. Conf. Med. Image Comput. Comput.-Assist. Intervent, 2019, pp. 721–730. [Google Scholar]
- [53].Tanaka D, Ikami D, Yamasaki T, and Aizawa K, “Joint optimization framework for learning with noisy labels,” in IEEE Intl. Conf. Comp. Vision, and Pattern Recog, 2018, pp. 5552–5560. [Google Scholar]
- [54].Fraz MM et al. , “An ensemble classification-based approach applied to retinal blood vessel segmentation,” IEEE Trans. Biomed. Eng, vol. 59, no. 9, pp. 2538–2548, 2012. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


