A Comprehensive Explanation Framework for Biomedical Time Series Classification

Abstract

In this study, we propose a post-hoc explainability framework for deep learning models applied to quasi-periodic biomedical time-series classification. As a case study, we focus on the problem of atrial fibrillation (AF) detection from electrocardiography signals, which has strong clinical relevance. Starting from a state-of-the-art pretrained model, we tackle the problem from two different perspectives: global and local explanation. With global explanation, we analyze the model behavior by looking at entire classes of data, showing which regions of the input repetitive patterns have the most influence for a specific outcome of the model. Our explanation results align with the expectations of clinical experts, showing that features crucial for AF detection contribute heavily to the final decision. These features include R-R interval regularity, absence of the P-wave or presence of electrical activity in the isoelectric period. On the other hand, with local explanation, we analyze specific input signals and model outcomes. We present a comprehensive analysis of the network facing different conditions, whether the model has correctly classified the input signal or not. This enables a deeper understanding of the network’s behavior, showing the most informative regions that trigger the classification decision and highlighting possible causes of misbehavior.

I. Introduction

The application of deep learning (DL) is in constant expansion in the medical field. DL solutions are approaching state-of-the-art diagnostic accuracy, even performing better than clinicians in some specific tasks [1]. For example, DL algorithms obtained sensitivity and specificity similar to that of a certified ophthalmologist in the detection of referable diabetic retinopathy using retinal fundus images from adults with diabetes [2]. To automatically classify malignant versus benign skin lesion images of epidermal or melanocytic origin, DL-based models have been shown to achieve performance on par with board-certified dermatologists [3]. Beside image analysis, an increasing interest is devoted to time-series data, including the use of long short-term memory recurrent neural networks in pediatric intensive unit care [4] and predictive medicine based on patient history [5]. A specific type of time-series is the electrocardiogram (ECG), representing the electrical signal of the heart. Inside the clinic, a 10 second 12-lead clinical ECG (usually sampled at 500 Hz) is commonly used by cardiologists, providing accurate information on the status of the heart for a short time interval. For non-permanent issues like paroxysmal atrial fibrillation (AF), a common non-persistent form of arrhythmia, a 10 second ECG is unlikely to capture intermittent, but meaningful, real-world cardiac events. Instead, a longitudinal view of cardiac electrical activity is needed [6]. While non-invasive wireless devices can provide continuous single-lead ECG recording for up to two weeks, they provide too much information to be analyzed in the limited time that a clinician can dedicate to a patient, thus an automated analysis such as DL is needed [7]. Accuracy of DL in the automatic identification of arrhythmia from single-lead ECG has been highlighted recently in a retrospective study [8], together with a comparison between DL and manual feature engineering methods [9] showing the benefits of representation learning. Nevertheless, these algorithms are data-driven and leverage complex representations of data, thereby making the interpretation of the underlying model difficult. The lack of transparency and accountability can be detrimental in the clinical setting, where additional information besides the model inputs needs to be combined for final risk assessment [10]. This highlights the need for understanding the model, in order to have a more effective clinical adoption of these methods. There are two solutions to understand the model and its behavior. The first one is to build a transparent (interpretable) model from the ground up, such that its output is meaningful through human readable rules established before training. Traditional symbolic machine learning approaches like decision trees, rule lists and rule sets are usually interpretable and can explicitly model our assumptions for rules, examples and sparsity [11]. Alternatively, if the model is too complex (black-box), it is possible to approximate the relationship between input and output in human-understandable terms after training, explaining how high-level features affect the output.

Since for unstructured and noisy data a black-box DL model may provide higher accuracy, as demonstrated for single-lead ECG data in [9], there have been significant attempts to create human understandable explanations for DL-based models. Most of these efforts were devoted to image classification, where explanations are directly interpretable for humans, e.g., natural association to similar looking details in the analyzed images [12]. The domain specific nature of time-series data makes it difficult to directly transfer these ideas for improved human understanding of the model. The use of attention systems embedded in the network architecture has also been investigated for improving interpretability of DL models, even if with some limitations [13]. In this paper, we focus on local and global explanation techniques applied to time-series data. Local explainability techniques deal with individual examples, and use visualization techniques like saliency maps [14] or deconvolutions [15] to identify specific regions of input that have the most influence on the network output. While they can be very effective in understanding regions of the input that were responsible for a particular prediction, it is not clear which characteristics of the highlighted region trigger a specific output. Thus, global explanations are also needed to capture the overall relationship between input and output variables from all examples in the training set. They may provide useful information for clinicians to understand what feature or part of signal is triggering the model decision.

The goal of this study is to present a model-agnostic explanation framework for models that analyze clinical time-series data. The main contributions are summarized as follows.

• We propose a general pre-processing pipeline for quasi-periodic time-series signals, which will be the basis for the analysis of a DL classification algorithm.

• We introduce global explanation methods to enhance transparency of the decision-making process, and to provide global insights into the model’s behavior.

• We discuss local explanation techniques for biomedical time-series, focusing on individual examples, which can be used to identify important segments/features of the input data.

• As a clinical case study, we consider the detection of AF from single-lead ECG signals. We discuss both global and local explanation results for AF detection, revealing interesting model behaviors in accordance with clinical analysis of these signals.

The rest of the paper is organized as follows. We discuss previous work on explaining DL models and time-series signals in Sec. II. In Sec. III we describe the case study under investigation, in Sec. IV we detail the methods for global and local explanations, while in Sec. V and Sec. VI we present the corresponding quantitative results.¹ Finally, in Sec. VII we discuss results and future directions.

II. Related Work

There has been a variety of work on building interpretable models or explaining predictions of black box models for time-series classification [16]. Classical rule-based models, such as decision trees, decision lists, and decision sets, produce easy to understand decision boundaries in terms of the input features. A popular approach to explainable time-series classification is the use of shapelet-based classifiers, introduced in [17]. Shapelets are short time-series which are used to classify inputs based on whether a shapelet is present in most series of one class and absent from others. Authors in [18] and [19] focus on jointly learning a shapelet-based representation of data, and generating explanations from these internally learned shapelets. Recently, more inherently interpretable architectures have been shown to achieve performance similar to deep networks. Authors in [20] and [21] demonstrated the use of multiple symbolic representations and random convolutional kernels respectively, to obtain accurate classification using linear classifiers.

On the other hand, local proxy methods like LIME [22] and SHAP [23], including frameworks built upon these methods [24], have been used for post-hoc explanations. However for applications of convolutional neural networks (CNNs) in the clinical context, most explanations are presented as visualizations, in order to provide an interpretable feedback that highlights the reason for a certain decision taken by the classifier. In [25], authors explore one-dimensional Class Activation Map (CAM) [26] with an application to time-series classification to highlight the parts of the series that contribute most for a given class identification. Authors in [27] also use a similar technique of Gradient-weighted Class Activation Map (Grad-CAM) [28] for visualizing saliency of the CNN model. Similarly, authors in [29] generate representative attribution maps obtained by layer-wise relevance propagation [30]. Recent work in [31] proposes a framework for evaluation, in order to compare the informativeness of occasionally conflicting explanations generated through these methods.

III. Case Study: Atrial Fibrillation

In order to design a framework for the explainability of quasi-periodic time-series models, we consider the detection of AF from single-lead ECG signals as a case study. This is a clinical task that can be successfully automated, but it needs to be explained in order to be fully useful in a clinical environment. In the clinic, cardiologists analyze short ECG traces by visual inspection to spot anomalous events. Among the many features typically related to AF detection, the most prominent ones can be identified as: absence of the P-wave, the electrical activity representing the atrial depolarization²; irregularity of R-R intervals; and absence of the isoelectric baseline, a short interval without electrical activity between the end of T wave and the start of P wave.

The proposed explainability framework aims at identifying the main signal characteristics leveraged by DL approaches during the detection process. This can verify if the learned representation corresponds to the human understanding of the underlying process.

A. Dataset

The dataset used in this study is publicly available as part of the 2017 PhysioNet and Computing in Cardiology Challenge: AF Classification from a short single-lead ECG recording [32]. All ECG recordings were collected using AliveCor devices. The dataset contains 8,528 single-lead ECG recordings lasting from 9 seconds to just over 60 seconds. All ECG recordings are labeled into one of four categories: normal sinus rhythm (5,154 data points in the public data set), AF (771 data points), other types of arrhythmia (2,557 data points) and noisy data (46 data points). For all the results reported henceforth, the class labels used are referred to as S (normal sinus rhythm), A (atrial fibrillation), O (other arrhythmia) and Z (Noisy signal).

B. Baseline Classification Model

The DL architecture used for all experiments in this study is a MobileNet model [33]. MobileNet is a lightweight CNN primarily used for mobile and embedded applications in computer vision due to its smaller model size and computational complexity. We use an architecture optimized for classification of single-lead ECG signals into one of the four classes described in III–A. The network was trained according to the guidelines in [9]. In general, a CNN learns operations to capture local dependencies in the input signal. A convolution operation consists of a kernel that slides over the input signal, performing element-wise matrix multiplications to output a feature map. Considering a convolutional layer with kernel of size d_K, number of input channels m and number of output channels n, a standard convolution with input dimensionality of d_F has a computational cost of d_K · d_K · m·n · d_F · d_F. The MobileNet architecture is based on depthwise separable convolutions, which split the computation of a standard convolution into two steps: a depthwise convolution and a pointwise convolution. Depthwise convolutions apply a single kernel for each input channel. Pointwise convolutions, implemented as 1×1 convolutions, are used to create a linear combination of the output of the depthwise layer. Depthwise separable convolutions have a much lower cost of d_K · d_K · m·d_F · d_F +m·n·d_F · d_F. For d_K = 3, it leads to a reduction in computation costs by 8 to 9 times. This allows the network to deal with a large number of parameters and high computational complexity [33].

Architecture of the MobileNet model used in this study is described in Tab. I. The model was trained for 200 epochs, with batch size 50, a step-based learning rate annealing policy (starting from a learning rate of 0.1 and reducing by a factor of 3 every 25 epochs). Dropout, gradient clipping, momentum and weight decay were used to stabilize training and improve generalization.

TABLE I:

MobileNet architecture used as baseline classification model.

Layer Type	Kernel Shape / Stride	Input Size
Conv.	16 × 32 / 2	1 × 9000
Depthwise Conv.	16 × 64 / 1	32 × 4500
Depthwise Conv.	16 × 128 / 2	64 × 4500
Depthwise Conv.	16 × 128 / 1	128 × 2250
Depthwise Conv.	16 × 256 / 2	128 × 2250
Depthwise Conv.	16 × 256 / 1	256 × 1125
Depthwise Conv.	16 × 512 / 2	256 × 1125
Depthwise Conv.	16 × 512 / 1	512 × 563
Depthwise Conv.	16 × 512 / 2	512 × 563
Depthwise Conv.	16 × 512 / 1	512 × 282
Depthwise Conv.	16 × 512 / 2	512 × 282
Depthwise Conv.	16 × 512 / 1	512 × 141
Depthwise Conv.	16 × 1024 / 2	512 × 141
Depthwise Conv.	16 × 1024 / 1	1024 × 71
Average Pooling	Pool 1 × 71	1024 × 71
Fully Connected	1024 × 4	1024 × 1

We use 5-fold cross validation to report model performance for global explanation. The data set was split randomly into 5 subsets, maintaining the original distribution between classes. Each unique subset was used as a testing set, while the others were used for training. The accuracy so obtained is 84.38 ± 0.96%, with the confusion matrix reported in Tab. II. Results are reported in terms of average ± standard deviation across the 5 folds.

TABLE II:

Confusion matrix C of the baseline classification model. C_i,j denotes the percentage of ECGs with true label i predicted as label j.

		Predicted Label
		S	A	O	Z
True Label	S	93.01±1.00%	0.43±0.05%	6.04±1.23%	0.51±0.31%
	A	3.95±1.17%	80.08±3.07%	14.91±2.55%	1.05±0.52%
	O	22.48±3.89%	4.55±0.97%	71.76±4.51%	1.20±0.08%
	Z	30.94±3.72%	5.40±3.44%	15.44±5.06%	48.21±4.82%

IV. Methods

In this study, we propose two different approaches to analyze network behavior: 1) global explanation methods, which are used to analyze the overall model behavior for a given class of data, and 2) local explanation methods, which explain how the model makes a specific decision on a single input signal.

Although we primarily focus on the specific case study, the proposed framework is model-agnostic, as it is not limited to any specific model. In the same manner as concept-based methods for model interpretation [34], we aim to provide evidence that the high-level representation, automatically extracted and processed by deep networks, are in accordance with the physiological knowledge of the underlying mechanism.

A. Signal processing

To properly highlight and understand the most important characteristics of the input signal considered by the model, some relevant regions of the ECG should be selected and analyzed independently. To this end, we propose a segmentation procedure (Sec. IV–A.1) for dividing periodic patterns. The signal between two consecutive R-peaks is divided into specific sub-regions corresponding to different phases of the cardiac cycle. We also define a periodicity normalization function (Sec. IV–A.2) to properly analyze the effect of R-R variability on the model’s behavior. R-R variability represents a measure of variation in the beat-to-beat interval, and is a very important ECG feature. Here, we detail the specific processing used for the case study analyzed, but analogous approaches can be applied to other signals with similar periodicity, a common characteristic in human data.

1). Segmentation:

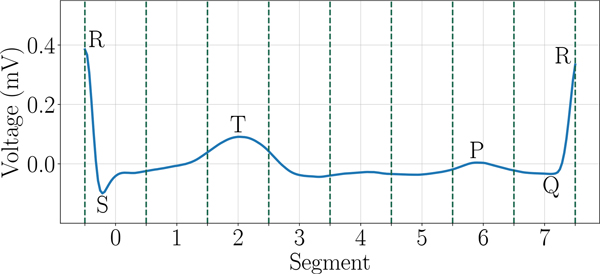
To understand how each sub-region of the cardiac cycle is affecting the classification decision, we define a segmentation function, which can be easily extended to any quasi-periodic signals. For each ECG E in the dataset, we first evaluate the temporal position of all R-peaks. An R-R interval is defined as the segment between two consecutive R-peaks. Each R-R interval is further divided into 8 equally sized segments, which will be used in the analysis³. An example of this segmentation technique is illustrated in Figure 1.

Fig. 1:

Segmentation of one R-R interval into 8 segments of equal length.

2). Periodicity Normalization:

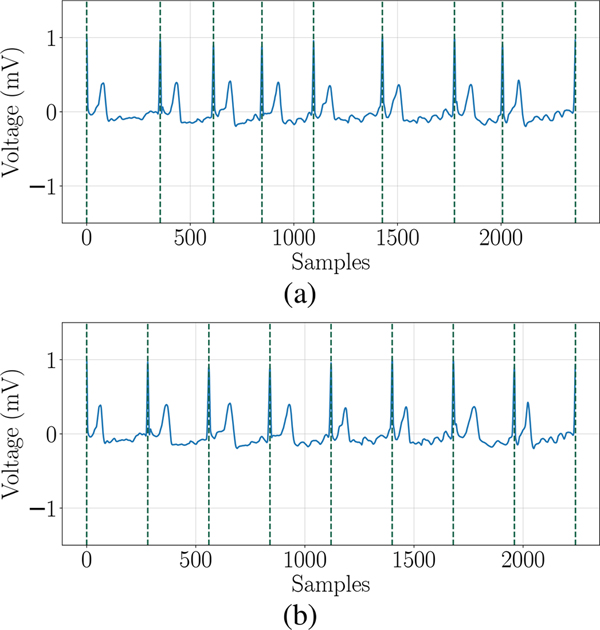
In order to analyze the importance of R-R intervals variability in the detection of AF from ECG signal E, we define a normalized version of the signal $\overline{E}$, by applying a periodicity normalization function. First, we evaluate the median value of all R-R intervals ${\overline{r}}_E$. Then, $\overline{E}$ is obtained by stretching or compressing each R-R interval forcing its duration to be equal to ${\overline{r}}_E$. While the information about R-R variability has been completely removed in the new signal, most of the intra-beat features are unaffected. An example of this normalization technique is illustrated in Figure 2.

Fig. 2:

Illustration of periodicity normalization. (a) Original ECG E. (b) Normalized ECG $\overline{E}$.

B. Global Explanation

The proposed framework includes three different techniques for global explanation: ablation study, permutation study, and LIME method. First, we divide each ECG cycle into 8 segments (numbered 0–7) using the segmentation function defined in Sec. IV–A.1. For most signals the P-wave lies entirely in Segment 6. Segment 4 corresponds to the isoelectric baseline, sometimes extending into segments 3 & 5.

1). Ablation Study:

In general, ablation study refers to a procedure wherein certain parts of the network architecture or input features are removed, and then predictions of the model are analysed to understand the importance of the corresponding ablated section. Specifically to this study, the main goal is to quantify the contribution provided to the network’s decision by each one of the periodic segments defined in Sec. IV–A.1. To emulate the absence of electrical activity in that particular region of the ECG, we effectively removed the information contained in the corresponding segment by replacing it with a straight line through its endpoints. This removal can be achieved through other approaches like replacing the corresponding segment with zero or a scalar mean. But these methods can create discontinuities within the signal which may affect the model outcome during analysis. Similarly, to investigate the importance of R-R interval variability, we leveraged the periodicity normalization function defined in Sec. IV–A.2. The prediction changes of the classification model are then evaluated to estimate how the removed information contributed to the original output. Ablation of specific information in the input signal is one of the most intuitive ways to understand whether and how much the corresponding feature affected the original outcome (feature importance). This procedure highlights the most important regions of the ECG that lead the network to a specific decision. Each of the ECG waves is associated to a specific event of the cardiac cycle, enabling a direct connection from the physiological functioning of the heart to the model’s prediction.

2). Permutation Study:

First introduced in [35], permutation study is a different approach to quantify feature importance. It analyzes how model behavior is affected when the corresponding feature is randomly substituted with values from other samples. This procedure breaks the relationship between feature and target, thus the variation in model output is indicative of how much the model depends on the feature. As opposed to the ablation study, where contribution of the feature is entirely or drastically suppressed, in this case the information content is replaced with a random selection from other data. Also in this case, we focus our study on the effect of each one of the 8 ECG segments, along with R-R interval variability. In order to focus on the specific information, and how it affects predictions, the replacement has to be targeted to the specific feature under analysis. To this end, we propose a permutation based on sample-wise shuffling and periodicity alignment. With sample-wise shuffling, starting from an input ECG sample, we randomly select another ECG having equal or greater number of R-peaks. All occurrences of a specific segment in the original ECG are changed to the corresponding segment of the new sample. To focus even more on the specific characteristic, we consider a permutation with periodicity alignment. In particular, after the replacement, the new segment instance is resampled to have the same length as in the original ECG. This allows to maintain R-R separations in the entire sample, which would otherwise affect the outcome when analyzing a specific segment. The specific analysis for R-R interval variability is then considered separately. In this case, the information between the R-peaks are kept the same, but the signal is resampled to match R-R separations from the permuted ECG. The overall changes in predictions are evaluated before and after permutation for each sample category, thus providing a class-level overview of feature importance.

3). LIME Study:

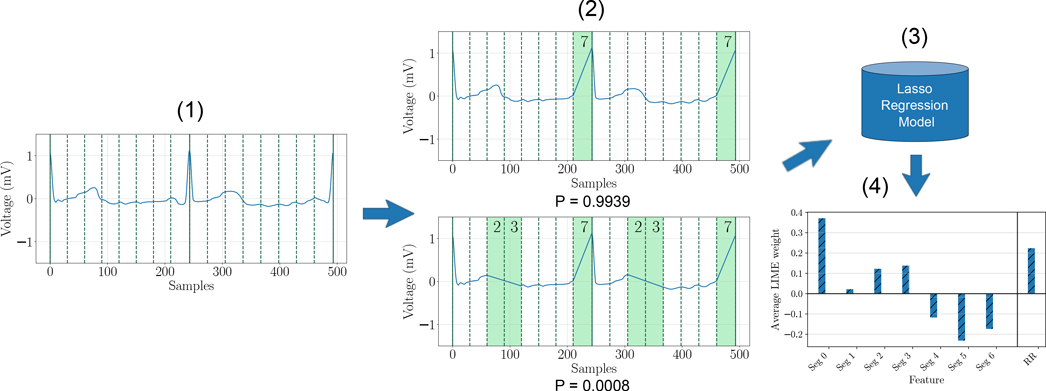
The LIME [22] (Local Interpretable Model-agnostic Explanations) method attempts to explain a system by analyzing how predictions change when a perturbation is applied to input data samples, without additional information about the model. The general idea is to approximate a complex model with a collection of many simpler models, each of which is faithful in the neighborhood of a unique sample. Fig. 3 illustrates how LIME can be used to explain model predictions. Starting from a specific ECG signal, perturbations are generated by removing a random selection of features. These perturbed samples along with their probability scores obtained through the deep network are then used to train an interpretable model (typically Lasso regression or decision tree). The losses for perturbed samples are weighted according to their proximity to the original, which means that the interpretable model incurs a greater cost when it incorrectly labels a sample which is close to the original. This model is an approximation of the deep network only for small regions of the feature space in the neighborhood of the original signal, but can be used to evaluate the contribution of each perturbed feature to the final prediction, as an estimation of overall feature importance.

Fig. 3:

Explaining a prediction using LIME: (1) Original ECG signal (class label S). (2) Perturbed signals with a random subset of segments removed, along with corresponding probability scores for class S obtained through the deep network. (3) Interpretable regression model. (4) Quantitative explanations.

In this study, we apply LIME to each of the 8 ECG segments (defined in Sec. IV–A.1) and to R-R interval variability. The perturbations are achieved in the same way as described for the ablation study (IV–B.1). These perturbed samples are then used to train a Lasso regression model as a local approximation, in order to predict the corresponding class probability scores from the pre-trained deep network. Coefficients of the linear regression model denote the change in class probability score when the corresponding feature is perturbed. These coefficients are used to quantify the corresponding feature importance. Finally, the outcomes for all samples of a specific class are averaged to estimate a class-level feature importance (global explanation).

C. Local Explanation

As opposed to global explanation studies, where the overall performance of the classifier are analyzed, local explanations consider each example in the dataset individually. They try to highlight the sections or features of the input signal that have the most influence on the classifier output. Evaluation of the contribution of each input feature to the output of a model has been largely investigated in the computer vision field [23], [28], [36]. Here, our goal is to extend previous findings to biomedical time-series, which are less intuitive to be interpreted from a visual perspective. To this end, we consider two different approaches: the first is based on saliency maps, to provide a direct evidence of the contribution of individual input samples; the second leverages LIME, which refers to the contributions of the same features presented for global explanation. With local explanations, each example is propagated through the classification network to obtain a probability score for each of the four classes. The class label with the highest probability is said to be the predicted label. In this study we present results for two specific cases:

Case 1) Correct classification with high confidence: we consider examples where the predicted label matches the true label.

Case 2) Incorrect predictions with high confidence: in this case, we consider examples where the predicted label and the true label do not match.

For both cases, 20% of the data was selected as a testing set for local explanations, and has not been used in training.

1). Saliency Map:

We utilize saliency maps with the guided back-propagation technique [37] to highlight the most important regions of input data [14]. Through our analysis we have observed that guided back-propagation, deconvolution and GradCAM all provide similar local explanations, with vanilla back-propagation being noisier. Guided back-propagation method is similar to the vanilla back-propagation approach [14], which provides a model-agnostic approach for computing primary attributions by analyzing the gradient of output with respect to the input, and approximating the network’s behavior with a linear representation. More specifically, the input ECG E is propagated through the classification network to obtain a probability score G_C(E), with C ∈ {S, A,O,Z}. For any class label C, the score G_C(E) is estimated by the first-order Taylor expansion G_C(E) ≈ w^TE + b. Here w is the gradient of G_C with respect to the input, computed using a single pass of the back-propagation algorithm. With guided back-propagation, negative gradients are additionally clamped to zero during the backward pass. The absolute value of the coefficients w are considered an estimation of feature importance.

As any individual ECG signal in the dataset lasts for 9 to 60 seconds, we select an interval of 3 seconds for our study, focusing on the time of highest importance.

2). LIME Study:

With a procedure similar to the one described in Sec. IV–B.3, LIME can also be used for local explanation. In fact, with LIME we can study the contribution of a specific segment (among the 8 segments defined in Sec. IV–A.1) in the classification of a specific ECG signal.

V. Results: Global explanations

A. Ablation and Permutation Studies

The results of ablation and permutation studies for each of the 8 segments and for R-R variability analysis are shown in Tab. III, where the variation of samples predicted as AF by the perturbed model is shown with respect to what was detected by the baseline model. In this case, we focus specifically on the AF class. In the first 8 rows of Tab. III, only one segment is perturbed, while in the following 8 rows we show the impact of a larger perturbation produced by two consecutive segments. We also report the results for R-R variability, as described in Sec. IV–B.

TABLE III:

Results of the ablation (Abl.) and permutation (Perm.) global explanation studies. Change in percentage of samples predicted as AF is reported for each class. Cross-validation variability is reported in terms of standard deviation.

Feature	Total		S		A		O		Z
	Abl.	Perm.	Abl.	Perm.	Abl.	Perm.	Abl.	Perm.	Abl.	Perm.
Seg 0	−0.18±0.68	−1.52±0.81	0.22±0.25	−0.08±0.14	−3.70±2.97	−14.40±6.95	0.37±1.11	−0.46±0.73	−2.51±1.82	−2.16±1.35
Seg 1	0.47±0.26	−0.22±0.50	0.06±0.17	0.20±0.27	2.11±0.87	−7.14±5.26	0.91±0.41	0.95±0.41	−0.35±1.35	0.72±1.43
Seg 2	0.35±0.40	0.22±0.50	0.08±0.07	0.28±0.34	1.45±2.61	−4.89±3.67	0.54±0.77	1.41±0.46	0.72±1.82	2.89±3.73
Seg 3	−0.26±0.30	0.87±0.64	0.02±0.17	0.41±0.33	−1.97±2.88	−0.67±4.92	−0.21±0.57	2.53±1.00	−1.07±0.87	−1.08±4.22
Seg 4	−0.38±0.29	1.84±1.06	−0.14±0.16	0.75±0.85	−2.51±1.64	−2.38±3.47	−0.21±0.71	5.71±1.70	−0.36±1.34	−0.34±2.64
Seg 5	−0.02±0.30	0.63±0.79	0.00±0.11	0.30±0.37	−0.79±2.71	−5.02±3.37	0.08±0.59	3.19±1.73	0.71±1.44	0.01±2.81
Seg 6	1.37±0.46	−1.06±0.78	0.41±0.10	−0.02±0.16	4.88±2.55	−17.56±4.40	2.28±0.71	1.78±1.60	1.45±1.77	0.34±3.50
Seg 7	−0.59±0.47	−3.87±0.55	0.47±0.20	−0.35±0.12	−10.03±3.16	−33.92±5.65	0.25±1.47	−1.86±0.35	−1.44±2.08	−3.59±2.54
Seg 0, 1	−1.34±1.31	0.36±0.46	−0.04±0.24	0.10±0.34	−13.58±8.67	−2.51±3.27	−0.08±1.74	1.53±0.87	−2.51±1.82	2.88±1.84
Seg 1, 2	0.08±0.47	0.21±0.36	0.14±0.25	0.20±0.29	−1.18±3.62	−2.25±3.65	0.41±1.12	1.20±0.61	−0.36±1.78	−1.43±3.28
Seg 2, 3	−1.52±0.37	1.42±0.81	−0.22±0.11	0.83±0.45	−10.95±1.68	0.65±4.44	−1.24±1.63	3.19±1.66	−2.16±2.89	−1.09±4.64
Seg 3, 4	−2.16±0.41	2.20±1.17	−0.22±0.20	1.02±0.54	−17.67±4.32	1.18±3.85	−1.33±1.02	5.34±2.54	−2.52±3.72	−0.72±2.43
Seg 4, 5	−1.95±0.47	1.34±0.70	−0.18±0.13	0.61±0.36	−16.88±2.99	−2.12±2.11	−1.08±1.45	4.27±1.69	−1.08±0.47	−1.44±2.11
Seg 5, 6	1.52±0.48	−0.18±0.38	0.73±0.12	0.26±0.28	3.29±3.08	−10.16±3.87	2.48±0.80	1.95±1.28	2.86±2.44	0.72±1.82
Seg 6, 7	−1.16±1.78	−0.13±0.38	0.51±0.42	0.81±0.43	−17.57±9.78	−14.12±2.52	0.54±2.61	1.99±0.72	−1.79±4.12	2.52±2.92
Seg 7, 0	−6.92±0.60	1.10±0.56	0.12±0.35	1.48±0.48	−66.63±4.16	−8.32±2.92	−3.40±0.91	3.27±0.86	−3.23±2.10	1.08±1.45
R-R variability	−6.88±0.40	5.58±0.94	−0.37±0.07	9.75±0.84	−65.70±2.34	−38.52±3.58	−2.44±1.30	12.67±0.90	−3.97±3.12	−2.90±4.38

The most evident result is related to R-R variability. We observe a major average drop of 65.7% in samples predicted as AF for class A when we remove the variability. This means that out of 100 samples classified as A, when we remove the information about R-R variability only 34 are classified as A. Therefore, the DL model automatically extracts and utilize this information for its final decision. This is also confirmed by the permutation study results, which shows a drop of 38.5% for class A. When the true label is S or O instead, by permuting the information about R-R variability we have an increase in sample incorrectly classified as A, of 9.7% and 12.7%, respectively.

We also observe similar outcomes for all analyses involving segment 7 and 0, which correspond to the QRS complex. Intuitively, this part of the signal is crucial for a correct estimation of R-peaks, and consequently for R-R intervals. This effect is most prominent when both segments are removed (ablation study), with a general drop (considering all samples) of 6.9% of samples classified as AF, and 66.6% specifically for class A.

An interesting outcome is related to segment 6, which corresponds to the P-wave for most samples. When we remove the signal from this area (ablation study), we observe an overall increase in samples detected as AF for all classes with and increase of 0.41%, 4.9%, and 2.3% for class S, A and O, respectively. On the other hand, with the permutation study, which typically entails an increase in P-wave energy, we observe a consistent drop in samples detected as AF, in particular for class A (17.6%). This is in accordance with our intuition: in a cardiac cycle, the P-wave is associated with atrial contraction, but during AF the electrical pulse that cause this contraction is irregular both in location of onset and timing, resulting in complete loss of the P-wave in the ECG tracing. The results show that the model was able to automatically associate the absence of the P-wave to an AF event.

To correctly interpret these results, we should notice that the results for ablation and permutation studies analyze complementary aspects of the same specific feature, as shown in this particular case. For example, ablation removes the effect of the P wave, which leads to a higher percentage of A samples classified as A. On the other hand, permutation introduces P wave into AF signals, which leads to a lower percentage of samples predicted as A. Both the suppression and replacement of information from a sample allow to analyze the importance of the corresponding feature, but interpretation of the induced effects on the model’s behavior lead to a deeper understanding from two different points of view.

Finally, the isoelectric region of the cardiac cycle (segments 3, 4, 5) is another aspect taken into account by the DL model. During an AF event, since the action potential might start from a random area of the atria, and without the usual coordination and synchronous efforts of the sinoatrial (SA) node, there may be some electrical activities also in the hypothetical isolectric section of the cycle. In fact, ablation of segment 4 causes a drop in samples detected as AF by 2.5% for class A, which is increased to 17.7% when both segment 3 and 4 are removed or 16.9% when segments 4 and 5 are removed. Once again, the representation learned by the DL model includes features that are consistent with the clinical interpretation of these signals.

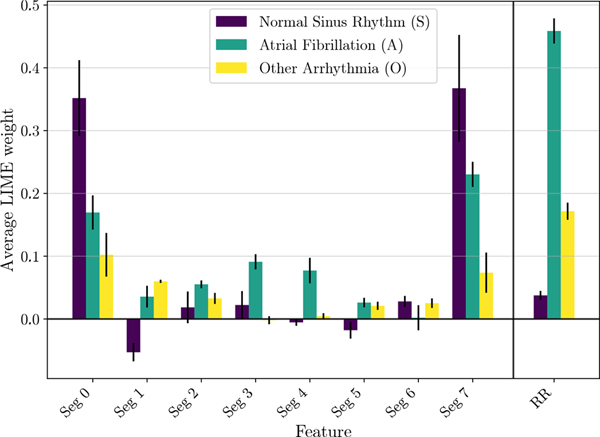
B. LIME Study

Similar results are obtained with LIME and reported in Fig. 4. Results for class Z do not hold practical interpretation, so have been skipped for brevity. For class A, we observe that segments 0 and 7 (corresponding to R-peaks) have the most positive weight from linear regression, on average. This means that if segments corresponding to the peaks are kept, the probability score of correct classification is significantly higher on average as compared to when they are removed. Additionally, an average positive weight for class A can be also noted for segments 3, 4 and 5. This supports the hypothesis that the presence of electrical activity in the isoelectric baseline of the ECG is effectively taken into account by the network for AF detection. As shown in Fig. 4, the highest average LIME weight corresponds to R-R variability. This implies a greater probability score for A on average, which in turn means higher rate of correct classification when the original variability is kept, proving once again the primary importance of this feature during the representation learning process. Also for class S, the most prominent results are related to segments containing the QRS complex (segments 0 and 7). The behavior is similar to what is observed for class A, but the magnitude is even larger. On the other hand, the behavior when R-R variability is removed is vastly different among the two classes. As expected, removing the variability does not significantly affect the probability score of class S.

Fig. 4:

LIME average segment and R-R variability weights for S, A and O classes. Error bars represent the cross-validation variability in terms of standard deviation.

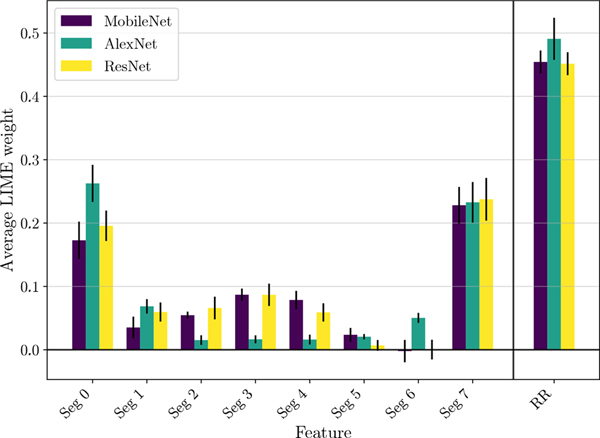
Similar results are shown also for class O, where the R-R normalization leads to a substantial drop in the probability score of O. Segments 0 and 7 (R-peaks) and segment 6 (P-wave) also show significant positive weights. Moreover, segments 3, 4 and 5 have negligible weights, implying that the isoelectric baseline is either present for most samples of class O or considered not important for prediction during the representation learning phase. Nevertheless, it is worth noting that class O is a group containing multiple arrhythmias, thus limiting a direct comparison to human understandable features associated to a specific condition. Global explanations can also be used to compare faithfulness of different architectures to the clinical features (P-Wave, R-R variability, isoelectric baseline). We use LIME quantitative scores to compare the baseline MobileNet architecture with two deep networks: AlexNet and ResNet (further details about the architectures can be found in [9]). These results are reported in Fig. 5. With 5-fold cross validation, AlexNet achieved overall accuracy of 82.06±0.45% and ResNet obtained overall accuracy of 84.93±0.62%. Although performance of all the deep networks is similar in terms of accuracy, we can see significant difference in their use of clinical features. We observe that the baseline MobileNet model and ResNet both have similar LIME weights for all segments and R-R variability. AlexNet presents some differences with respect to the other two, with a noticeable positive weight for Seg. 6. This means that the presence of P-wave would increase the chance of prediction of label A, which is not intuitively explainable from a clinical point of view, and will require additional studies to be properly interpreted.

Fig. 5:

LIME average segment and R-R variability weights for class A. Results for three different architectures are reported: MobileNet, AlexNet and ResNet. Error bars represent the cross-validation variability in terms of standard deviation.

VI. Results: Local Explanations

Since local explanations are unique to each example, we present here representative cases for high confidence correct and incorrect classifications for S, A, and O examples.

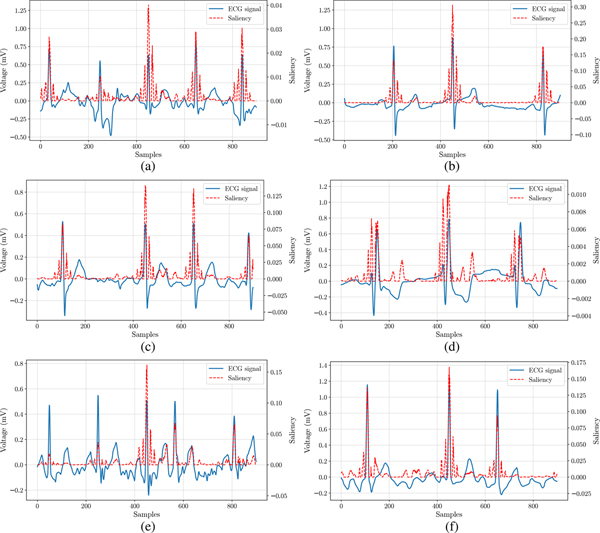
Two examples of class S are reported in Fig. 6a and 6b corresponding to a high confidence correct and incorrect classification, respectively. Saliency maps give an immediate feedback on the parts of the input signal that are considered important for the final DL classification. While the ECG in Fig. 6a was correctly classified as S, Fig. 6b shows an example where the network focuses its attention on a premature atrial contraction event that occurred in a sample labelled as normal sinus rhythm. The high saliency of this region proves that this event is the primary reason for the input being incorrectly classified as O. This is an important outcome, since it shows that the erroneous behavior of the network has been triggered by an anomalous physiological event, and not by some unexplained reason, in a similar way a human may be misled during the analysis. Furthermore, automatic highlighting of these important regions of the signal may be an additional tool for clinicians for a more targeted manual analysis. LIME weights for the same examples are reported in Tab. IV, in order to provide additional insights into the specific information used by the network for high confidence predictions. For class S, we can see that the example classified correctly has a small weight for R-R variability, whereas this feature has a large weight in the example classified incorrectly as O. This confirms that R-R variability is one of the main reason for the classification outcome. Additionally, the LIME weight for Segment 6 is a large positive value, showing that the presence of P wave has been important to classify the erroneous example as O, instead of A.

Fig. 6:

Local explanations using saliency map. (a) S, predicted correctly. (b) S, predicted as O. (c) A, predicted correctly. (d) A, predicted as S. (e) O, predicted correctly. (f) O, predicted as A.

TABLE IV:

Local explanation results using the individual weights from LIME for each segment and for RR variability are reported in the table. Some relevant samples with different class and outcome are considered.

Class	Network Outcome	LIME Weights
		Seg 0	Seg 1	Seg 2	Seg 3	Seg 4	Seg 5	Seg 6	Seg 7	RR
S	predicted correctly	0.27	0.03	−0.04	0.12	−0.06	−0.02	−0.13	0.60	0.03
S	predicted as O	−0.08	0.13	0.01	0.11	0.01	−0.05	0.15	0.12	0.32
A	predicted correctly	0.19	−0.04	−0.07	0.17	0.00	−0.06	0.02	0.20	0.67
A	predicted as S	0.21	−0.07	0.10	0.08	0.02	−0.28	−0.15	0.38	0.05
O	predicted correctly	−0.05	−0.07	0.14	0.03	−1.52	0.00	−0.08	−0.11	0.34
O	predicted as A	0.19	−0.03	−0.08	0.13	0.14	−0.03	−0.03	0.26	0.65

Two examples for class A with high confidence correct and incorrect classification are shown in Fig. 6c and 6d, respectively. The saliency map in Fig. 6c identifies an interval with non uniform separation between R-peaks, as expected for A. The separation between R-peaks seems to be constant in the saliency map from Fig. 6d, which could be a possible reason for the network being incorrectly predicting the corresponding input as S. This hypothesis is also supported by the corresponding LIME weights (Tab. IV). In fact, the example predicted correctly has a very large weight for the R-R variability, as opposed to the small value observed for the example predicted incorrectly as S.

Finally, two examples for class O with correct and incorrect classification are shown in Fig. 6e and 6f, respectively. Fig. 6e shows how the network focuses on specific heartbeats of the input signal, which may be considered the discriminating factors for a general arrhythmia. The LIME weights in Tab. IV reveal that Seg. 4, corresponding to the isoelectric region of the ECG cycles, has a large negative weight, which means that the presence of a signal in Seg. 4 leads to a lower probability score as compared to when it is removed. This confirms that the focus for prediction is not based only on changes in the heart-rate, but a more in-depth analysis is required to discriminate between different arrhythmias. Also for the example shown in Fig. 6f, the network automatically identifies a region with large R-R variability as highly informative. In this case the network wrongly classifies the sample as A, probably due to high noise and the abnormal rhythm.

In all these examples, we observed how the network often focuses on anomalous regions of the ECG, which drove the classification of the signal, in accordance to a manual analysis performed by human experts.

VII. Discussion and Conclusion

Recent improvements in both accuracy and usability of personal medical sensors contributed to a rapid increase in their use and consequently to the collection of large datasets of biomedical data. The availability of such large datasets makes DL methodologies very attractive, with recent outstanding results. Their use in clinical applications, however, is currently a strong source of debate. This is mainly due to their black-box nature, and the challenge to understand which aspects of input data drive the final decisions of the model. To encourage the widespread diffusion of these approaches inside and outside the clinic, it is thus important to be sure that these decisions are driven by a combinations of data features that are appropriate in the specific context.

While classical and interpretable models are typically preferable [10] as they facilitate the work of clinical experts that can confirm the algorithm’s diagnosis or identify a potential artifact triggering the fallacious decision, on the other side it is often difficult to design an interpretable model reaching the performance of a black-box DL model. Also, classical models rely on the selection of a unique set of clinical features, which are usually suggested by clinical studies, and on the subsequent detection of such features in the signal. These approaches typically require a specific domain knowledge to transform unprocessed data into suitable representations that can generalize to unseen data. DL showed its value where other types of classical models have showed poor performance, from forecasts based on electronic medical records [38], to the classification of echocardiograms [39], and other types of medical images [40]. Additionally, DL can be valuable also in the detection of COVID-19 from longitudinal wearable device data [41]. In all these cases, if a native interpretation of the DL output is not possible, a valuable alternative is to rely on post-hoc explanation techniques, highlighting particular features of the input that triggered the DL decisions [42]. Post-hoc explanation techniques can provide both global and local explanations. The former is used to explain the behavior of the DL technique at a high level for any type of input, while the latter focuses on specific input cases and features that triggered the DL decision.

In this work, we focused on explanation of time-series and we chose as a case study the detection of AF from 30 seconds single-lead ECG signals. AF is often undiagnosed [43] and has significant clinical consequences including a 5-fold increase in the risk of stroke. But when diagnosed, there exist therapies proven to be effective in significantly reducing severe consequences. Therefore, there is substantial value in frequent (and potentially automated) screening for individuals at risks [44], [45] and the potential prediction of AF from ECG in normal sinus rhythm [46]. The use of portable devices could facilitate the cost-effective collection of cardiac electrical activity outside of the clinic [47], and a large prospective trial has already been made with commercial smartwatches [48]. Another option involves short at-home measurements of single-lead ECG with other commercial devices, but there is a trade-off between continuous measurements, and intermittent or symptomatic screening [49]. In any case, the interpretation of these signals will be fully useful to cardiologists only if the automatic output can be explained and related to specific features/intervals of the ECG input. In this study, we provide a framework for both global and local interpretation of ECG signals and other quasi-periodic signals alike. Using ablation tests, permutation tests and LIME method, we showed that the network effectively considers physiological features, such as the absence of P-wave, variability of R-R intervals and electrical activity in the isoelectric region of the ECG, as important factors for the classification of AF. We were able to establish that, at least in part, the model leverages features that match with those used by cardiologists in clinical diagnoses. Furthermore, through the use of saliency maps and LIME, we also present local explanations for some relevant examples, which can be used to confer useful information about the model’s behavior for a specific input by highlighting most important regions and features in the input. Moreover, even in the case of erroneous behavior, the network is often misled by actual anomalous conditions in the input signal, that can be easily highlighted and further investigated.

While clinical cardiologists have helped in the definition of clinical features used in the study and interpretation of the explanations, these techniques should be used in a prospective study and their clinical effectiveness should be demonstrated before they can be adopted.

In conclusion, the presented framework enables an in-depth exploration of the DL network and its decision-making process. This exploration will help in understanding the network itself as well as enable new improvements within the architecture, with the ultimate goal of exploiting the immense potential of DL for biomedical data analysis, and help make the use of neural networks more transparent and fully useful for clinicians.