Maximizing efficiency of dipolar recoupling in solid-state NMR using optimal control sequences

Highly efficient optimal control experiments for routine studies of solid proteins by NMR using various MAS frequencies.

Abstract

Dipolar recoupling is a central concept in the nuclear magnetic resonance spectroscopy of powdered solids and is used to establish correlations between different nuclei by magnetization transfer. The efficiency of conventional cross-polarization methods is low because of the inherent radio frequency (rf) field inhomogeneity present in the magic angle spinning (MAS) experiments and the large chemical shift anisotropies at high magnetic fields. Very high transfer efficiencies can be obtained using optimal control–derived experiments. These sequences had to be optimized individually for a particular MAS frequency. We show that by adjusting the length and the rf field amplitude of the shaped pulse synchronously with sample rotation, optimal control sequences can be successfully applied over a range of MAS frequencies without the need of reoptimization. This feature greatly enhances their applicability on spectrometers operating at differing external fields where the MAS frequency needs to be adjusted to avoid detrimental resonance effects.

INTRODUCTION

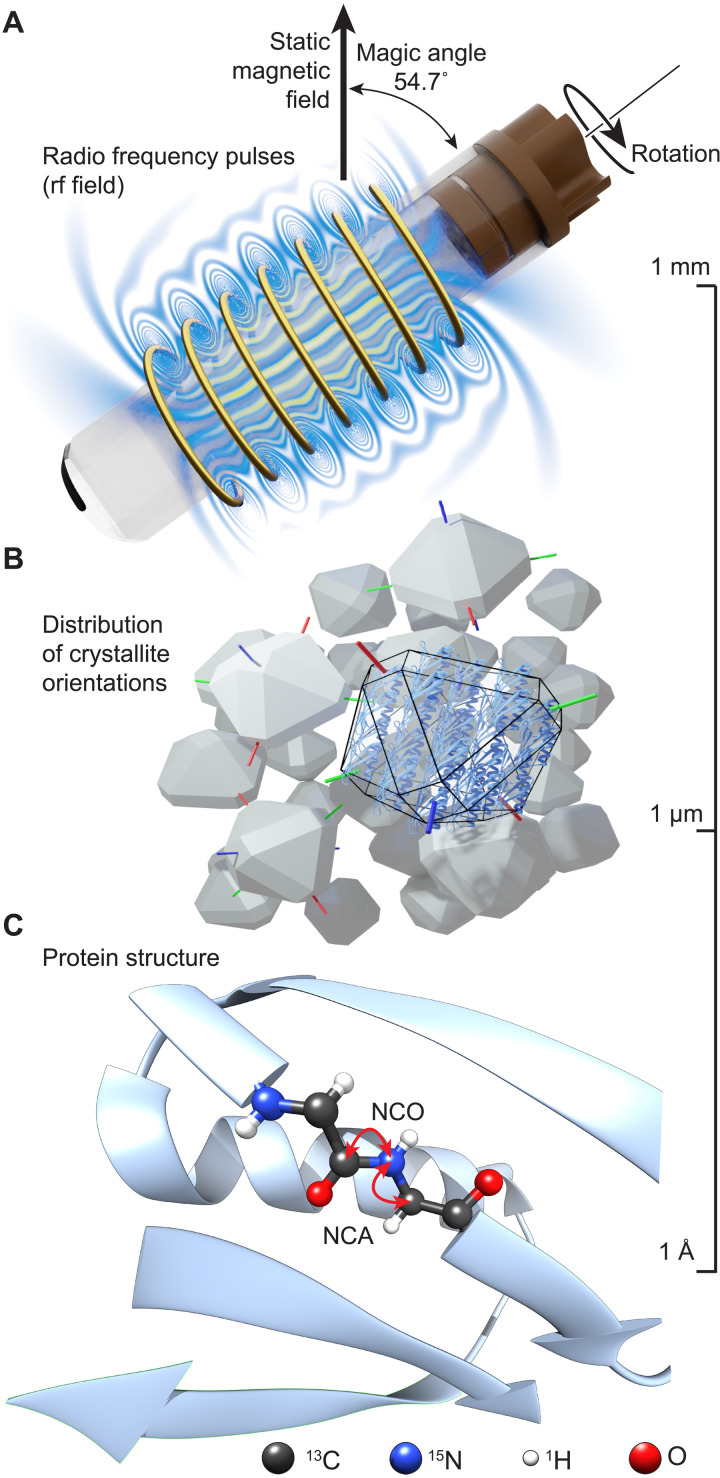
Solid-state nuclear magnetic resonance (NMR) spectroscopy (1) is an atomic-level method to determine the chemical structure, three-dimensional (3D) conformation, and dynamics of solids and semisolids. It is applied to biological macromolecules, organic materials, inorganic solids, and materials chemistry. In contrast to solution-state NMR, where spectra with narrow resonance lines are obtained, solid-state NMR must deal with strong anisotropic interactions and broad lines in spectra of powdered samples. Magic angle spinning (MAS), i.e., the rotation of the sample around an angle of 54.73° (${\text{tan}}^{-1}\sqrt{2}$) with respect to the external magnetic field, averages out anisotropic interactions and yields high-resolution spectra (Fig. 1A). In the experiments, radio frequency (rf) pulses are used that have a characteristic amplitude, phase, and length and allow the manipulation of the magnetization vector associated with a specific nuclear spin. Under specific conditions, application of rf pulses allows the recovery of anisotropic interactions, which is referred to as recoupling. The reintroduction of dipolar couplings during mixing periods, called dipolar recoupling, mediates polarization transfer and allows correlating NMR responses between different nuclei. The efficiency of the polarization transfer depends on the orientation of the principal component of the dipolar coupling tensor of a spin pair in a particular crystallite with respect to the external magnetic field. The total measured signal intensity is then given as the integral over the stochastic distribution of all crystallites in the sample (Fig. 1B).

Fig. 1. Experimental setup of the MAS solid-state NMR experiment of insoluble proteins.

(A) The sample is placed inside a rotor that is oriented at 54.7° with respect to the static magnetic field and rotated within a solenoid coil, which allows the application of rf pulses to manipulate nuclear magnetization. Upon sample rotation, molecules experience periodical modulations of the rf field due to spatial inhomogeneity. Magnetic field lines are drawn schematically. (B) Protein molecules are contained in microcrystals that are randomly oriented in a powder. (C) Atomic level protein structure with arrows illustrating NCA and NCO magnetization transfer pathways between the amide nitrogen and Cα/C′ carbons (NCA/NCO transfers) of the protein backbone. The relative orientation of a bond vector with respect to the external static magnetic field determines the size of the dipolar interaction between the two atoms. The scale on the right indicates typical order of magnitude for object dimensions.

It has been shown recently that MAS solid-state NMR allows the investigation of insoluble proteins (2, 3). Before a structural analysis, the resonance frequencies, the so-called chemical shifts, have to be assigned to the respective nuclei. For proteins, this is accomplished by establishing correlations of chemical shifts between amide nitrogen and carbon atoms of the backbone using NCA and NCO experiments (Fig. 1C) (4). The first experiment that allowed transferring magnetization from ¹⁵N selectively either to ¹³Cα (for NCA) or ¹³C′ (for NCO) is dubbed double cross-polarization (CP) (5) and uses constant-amplitude rf fields on the ¹³C and ¹⁵N channels. The length of the two pulses is referred to as the contact time used in the CP experiment. The rf fields have to satisfy the Hartmann-Hahn matching condition (6, 7), in which the difference of the ¹³C and ¹⁵N rf field amplitudes corresponds to a multiple of the MAS rotation frequency. Experimentally, higher efficiencies are obtained when the constant amplitude is replaced by a sweep of the amplitude through the Hartmann-Hahn condition. Most popular are linear rf ramps (8) or tangential pulse shapes that satisfy an adiabaticity condition (9). These variants were developed in times when only low MAS frequencies (up to 10 kHz) were available and are used without modifications at all other MAS frequencies (up to 110 kHz). The major advantage of these CP experiments with variable amplitude rf field is a partial compensation of rf field inhomogeneities (10, 11).

Solenoid coils are the most common components of rf circuits implemented in current MAS probes to apply rf pulses and to detect the NMR signal. The rf field distribution in these solenoid coils is, however, not ideal. The magnetic fields produced by the coils contain inhomogeneous contributions (12) that are schematically depicted in Fig. 1A. Different parts of the sample experience substantial variations in rf field amplitude and phase. The rf amplitude at the ends of the coil is about 50% smaller than in the center, and the rf phases may vary up to ±30° (12). The inhomogeneity influences the performance of recoupling experiments where rf amplitudes must match resonance conditions related to the MAS frequency (such as the Hartmann-Hahn condition of the CP experiment). If the pulse sequence is not robust enough, then no recoupling will occur in certain parts of the sample. In addition, the spatial rf field inhomogeneities manifest themselves as periodical variations of both the rf amplitude and phase when the sample is rotated, as it is the case for MAS. These variations depend on the position along the coil axis and on the radial distance from the axis. The effect of the temporal rf inhomogeneities was first described in relation to rotary resonance recoupling (13, 14) and was studied in detail recently (12, 15, 16).

Sensitivity is a major issue in biological solid-state NMR applications. In particular, the CP experiment for magnetization transfer between ¹⁵N and ¹³C nuclei is extremely vulnerable to subtle changes in the experimental parameters due to the rather weak dipolar coupling. Its calibration includes many variables and becomes tedious for samples with low sensitivity. Given the difficulty and the delicacy of the experimental setup, the ¹⁵N-¹³C magnetization transfer is a promising target for development of new pulse sequences with improved properties. In addition to analytical approaches such as average Hamiltonian (17) or Floquet theory (18), optimal control provides an efficient alternative to find the best pulse sequence numerically (19–21). In the context of NMR spectroscopy, the optimal control problem is defined as a state-to-state transfer of magnetization, for example, from ¹⁵N to ¹³C for a prototypical spin system accounting for all relevant experimental conditions. A numerical optimization protocol is set up to find the rf amplitudes and phases of all pulse sequence elements to yield the maximal transfer efficiency (19). Optimal control theory provides easy access to the first derivative of the objective function (22) and allows the optimization of tens of thousands of variables at once. Previous applications to MAS solid-state NMR experiments include excitation pulses (23–25), dipolar recoupling methods (26–30), and the synthesis of effective Hamiltonians (31). There are several studies where optimal control was applied specifically to the ¹⁵N-¹³C magnetization transfer problem (26, 32, 33). Although the robustness toward rf amplitude miscalibration was improved by assuming static rf field inhomogeneities, these experiments yielded only small gains in signal-to-noise ratio compared to the tangential shape CP. We have shown recently that substantial experimental improvements are obtained when optimal control–derived pulse sequences additionally account for rotation-induced variations of the rf amplitudes and phases. In particular, the tm-SPICE (temporally modulated spatial rf field inhomogeneity compensation) pulse sequence provides a higher efficiency of the ¹⁵N-¹³C magnetization transfer compared to a conventional linear rf ramp CP experiment (15). Detailed knowledge of the rf field distribution is thus essential. In principle, it is also possible to experimentally map the field distribution like it is done in magnetic resonance imaging (34) and to use these data in the design of optimal control pulses in an NMR imaging experiment of a liquid sample (35). This was, however, not attempted here, as the necessary hardware features (pulsed field gradients) are not available for the MAS solid-state NMR probes, and a numerical model of the rf field was assumed.

So far, optimal control experiments were restricted to a MAS frequency, which was selected for the calculation of the rf shapes. Originally, we had anticipated that different tm-SPICE sequence must be calculated de novo for different MAS frequencies. This would be a major limitation in practical applications since the MAS frequency has to be adapted for different spectrometers to avoid rotational resonance effects between Cα and C′ resonances (36). Here, we demonstrate that optimal control sequences can be successfully applied to a range of MAS frequencies when the rf amplitudes and the length of the shaped pulses are adjusted to keep synchronization with the sample rotation. The application of rf pulses in synchrony with rotation has been the essence of recoupling since the early rotational-echo double-resonance experiment (37), which reintroduces the dipolar coupling averaged out by MAS. This principle has been mastered in recoupling experiments based on rotational symmetry principles introduced by Levitt and colleagues (38, 39), allowing us to distinguish anisotropic interactions based on their rotational properties under rf irradiation. In the case of optimal control, however, synchronization of rf pulses with MAS is not obvious, as they are not periodic.

Optimal control can be used to identify experimental boundary conditions for the maximal achievable transfer (40). In solid-state NMR, however, experimental shortcomings are often only partially accounted for in the optimization. We aim here to identify the best MAS solid-state NMR NCA/NCO pulse sequence that accounts for experimental boundary conditions including a realistic spatial rf field distribution of the solenoidal coil, high magnetic fields, and chemical shift anisotropies of the involved nuclei. We show that optimal control–derived sequences are not sensitive to the experimental condition used but are generally applicable. We demonstrate theoretically, numerically, and experimentally that we achieve similar efficiencies across a wide range of MAS frequencies by rescaling the rf amplitudes and the length of the tm-SPICE pulses. We test the original tm-SPICE sequence (optimized for a spinning frequency of 20 kHz) and a newly calculated sequence optimized for 16.5 kHz in the MAS frequency range of 13 to 20 kHz. tm-SPICE outperforms carefully calibrated ramp-CP experiments in all cases by an average factor of 1.5, both for NCA and NCO transfers. We believe that this general approach that largely decouples the optimal control pulse shapes from the spectrometer used will find widespread application in MAS solid-state NMR.

RESULTS

Maximal achievable magnetization transfer

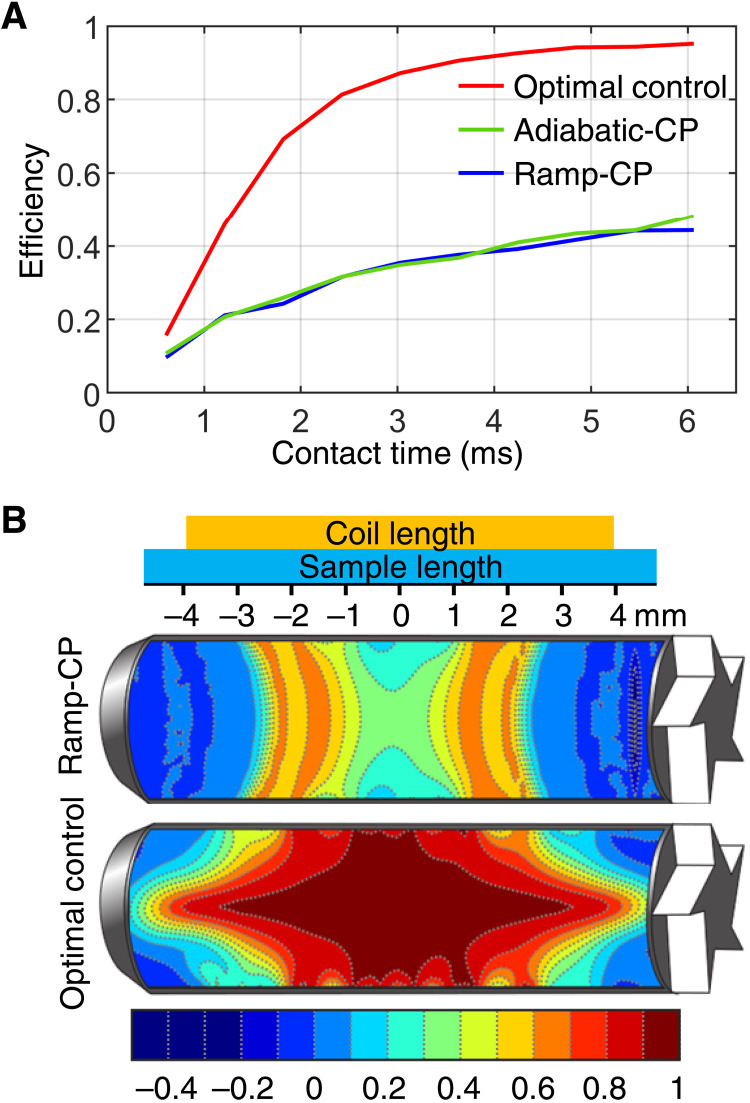
We investigate how the conventional CP techniques cope with the challenges of powder distributions, chemical shift anisotropies, and spatial rf field inhomogeneities generated in the solenoid NMR coil, including temporal modulations. In the rest of the paper, we refer to the linear rf ramp CP as ramp-CP and to the tangential pulse shape CP as adiabatic-CP. We numerically optimize all parameters of these experiments to yield maximal efficiency for the NCA transfer. Figure 2A presents the maximum efficiencies after independent optimizations for each duration of the CP element (contact time). The physical limits of a particular transfer can be estimated by the numerical optimal control protocol (described in Materials and Methods and the Supplementary Materials). From Fig. 2A, it is evident that both conventional CP methods fail to provide efficient recoupling, while optimal control predicts that it should be possible to get almost complete transfer. Ramp-CP and adiabatic-CP provide equal results, and both methods are compared in more detail in the Supplementary Materials, showing their similarities in the rf sweeps through the recoupling condition (the difference of rf amplitudes matching the MAS frequency). The low CP performance follows from the combination of rf inhomogeneity and the rather weak dipolar coupling between ¹⁵N and ¹³C, which is on the order of 1 kHz. Assuming a realistic spatial distribution of rf amplitudes, the recoupling condition cannot be satisfied at once for all parts of the sample. This results in a decreased overall performance. Certain volume elements achieve only a negligible efficiency or even experience a transfer with negative sign, as they meet a distinct recoupling condition (the so-called double-quantum Hartmann-Hahn condition, where the sum of rf amplitudes matches the MAS frequency). Figure 2B illustrates the spatial distributions of the magnetization transfer efficiency for ramp-CP and optimal control sequences optimized for a duration of 60 rotor periods, shown for a cross section of the rotor. The optimal control pulse sequence provides much better efficiency in a large portion of the sample volume compared to the ramp-CP. We note that the situation is different for the ¹H-¹⁵N spin pair, which has a dipolar coupling of about 10 kHz. In this case, the stronger interaction allows larger deviations from the recoupling condition, and the transfer can occur in a larger volume (see the Supplementary Materials). Numerical simulations also show that temporal rf modulations have negligible effects on ramp-CP and adiabatic-CP methods (16), while it is essential to include these in the design of the optimal control sequences (15).

Fig. 2. Highest achievable transfer efficiencies estimated by numerical optimizations.

An efficiency of 1 reflects a quantitative transfer of magnetization from nitrogen to carbon; zero means no transfer, and negative values reflect a change of sign upon magnetization transfer. (A) Transfer efficiency of ramp-CP (blue), adiabatic-CP (green), and optimal control (red) sequences. Pulse sequence parameters were optimized for each contact time independently. In the calculations, the assumed dipolar coupling and chemical shift anisotropy parameters correspond to a ¹⁵N-¹³Cα spin pair, measured in a 700-MHz NMR spectrometer. The sample is rotated with a MAS frequency of 16.5 kHz. Both CP methods suffer strongly from rf inhomogeneity. (B) Illustration of the spatial distribution of the magnetization transfer efficiency for ramp-CP and optimal control sequences optimized for a duration of 60 rotor periods (about 3.6 ms). In case of ramp-CP, magnetization transfer occurs in a restricted volume of the rotor with moderate efficiency, while optimal control yields efficient transfer in almost the full volume.

Adapting optimal control sequences to different MAS frequencies

Motivated by the excellent prediction in favor of optimal control, we replaced CP blocks in the NCA and NCO experiments with tm-SPICE pulse shapes. For the practical implementation at the NMR spectrometer, the tm-SPICE sequences should be easily adaptable to different MAS frequencies. Previously, we limited the application of our optimal control sequences to the MAS frequency ${\mathrm{\omega }}_{\mathrm{R}}^{\text{opt}}$ that was used during the optimization. In MAS solid-state NMR, recoupling of anisotropic interactions is often achieved by applying multiple-pulse schemes synchronized with sample rotation. Using this principle, we show below that tm-SPICE sequences can be adapted for a different MAS frequency ${\mathrm{\omega }}_{\mathrm{R}}^{\text{new}}$ according to the following protocol. Using a scaling factor

$$\mathrm{\xi }={\mathrm{\omega }}_{\mathrm{R}}^{\text{new}}/{\mathrm{\omega }}_{\mathrm{R}}^{\text{opt}}$$ (1)

the new pulse shape is obtained by adjusting the following: (i) length of the new shape, T_new = T/ξ, and (ii) rf amplitudes of the new shape, ${\mathrm{\omega }}_1^{\text{new}}={\mathrm{\omega }}_1^{\text{opt}}·\mathrm{\xi }$.

A rigorous treatment of rescaling is given in the Supplementary Materials, and we outline our arguments here. An optimal control pulse sequence consists of a series of short, constant-amplitude rf pulses. The evolution of the spin system is described by a series of events represented by a propagator. The effect of the pulse sequence is examined at the end by evaluating how much magnetization was transferred. An important aspect of optimal control applied to solid-state NMR is related to the robustness toward crystallite orientation due to the anisotropic nature of involved interactions. The pulse sequence is required to work equally well for all possible crystallite orientations. This is accomplished by repeating the transfer efficiency calculation independently for a representative set of orientations and adding the results together afterward. The total target function is a sum weighted by the relative contributions of each orientation. Last, the target function is optimized using a gradient-based procedure (19, 41). Other specific experimental conditions can be covered as well by simply increasing the sum. For practical reasons, we include robustness toward distributions of chemical shifts of both the ¹⁵N and ¹³C nuclei, reflecting the local differences in a protein molecule. While robustness to spatial and temporal variations of rf amplitude and phase are included in our tm-SPICE calculations (15), it is not required for justifying the rescaling property.

The propagator representing the spin system evolution from time t_k to t_k + Δt is given by

$$\mathit{U}({\mathit{t}}_{\mathit{k}},{\mathit{t}}_{\mathit{k}}+\mathrm{\Delta }\mathit{t})=\text{exp}\{-\mathit{i}[{\mathit{H}}_{\text{int}}({\mathit{t}}_{\mathit{k}})+{\mathit{H}}_{\text{RF}}({\mathit{t}}_{\mathit{k}})]\mathrm{\Delta }\mathit{t}\}$$ (2)

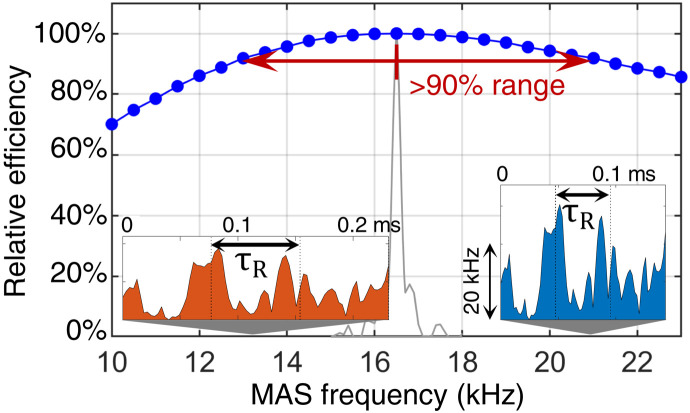
where H_int(t_k) and H_RF(t_k) represent the Hamiltonian of internal spin interactions and the rf pulse Hamiltonian sampled at time t_k, respectively, and they are considered constant over the time Δt. Both Hamiltonians have a form of a product of an interaction strength (dipolar coupling or rf amplitude) and a spin operator. The effect of the pulse sequence will be the same if the propagators remain the same upon a change of MAS frequency and an adjustment of the pulse sequence. The exponent in Eq. 2 contains the terms H_int(t_k)Δt and H_RF(t_k)Δt. Adjusting the pulse length (step 1) is reflected in the substitution Δt → Δt/ξ . In the case of the rf Hamiltonian, this factor is cancelled out by scaling the rf pulse amplitude with ξ (step 2), and the effect of the rf pulse remains unchanged; it maintains its effective flip angle. In the case of the interaction Hamiltonian, the situation is more complex, as the effective coupling d_eff depends on the orientation and time due to MAS. If we assume that only a dipole-dipole interaction contributes, then its amplitudes at different crystallite orientations are scaled down by an amount, which depends on the angle between the internuclear vector and the rotor axis, and d_eff will fall within the interval d_eff ∈ [0, d_max] . On top of this, the effective coupling will be modulated by the sample rotation (see also the Supplementary Materials). By rescaling time, we make sure that the interaction Hamiltonian, H_int(t_k), is sampled at identical relative positions of the rotor during its rotation, both for the original and the rescaled pulse sequence; the sampling of the time dependence remains synchronized upon the change of MAS frequency. At the same time, however, we change the duration of the step propagator, which is now Δt/ξ. The scaling factor 1/ξ can be absorbed into the effective coupling constant, d_eff/ξ, which can be found at different orientation. We note that we designed our pulse sequences to work equally well for all possible crystallite orientations. After rescaling, the step propagator will be thus identical to another original propagator corresponding to a different crystallite orientation. This is true for 1/ξ < 1, i.e., for transformation to higher MAS frequencies. When going to lower MAS frequencies, propagators with d_eff/ξ > d_max will not find their counterparts in the original set, which will lead to a decreased performance of the pulse sequence. For the ¹⁵N-¹³C spin system, the large chemical shift anisotropy interaction dominates over the dipole-dipole interaction. If the principal axis systems of these interactions are not aligned, then H_int evaluated for a particular crystallite orientation is not a simply scaled version of H_int taken at a different orientation. Thus, a decreased performance should be expected. The numerical simulations presented in Fig. 3 show the relative performance of the tm-SPICE NCA sequence optimized at a MAS frequency of 16.5 kHz as a function of the actual MAS frequency. These data confirm that going to lower frequencies has a bigger effect than a transformation to higher MAS frequencies. However, the pulse sequence achieves more than 90% of its nominal transfer efficiency within the range of 13 to 21 kHz. When the sequence is used without rescaling, its efficiency drops to 50% when the MAS frequency deviates by 150 Hz.

Fig. 3. Simulated relative efficiency of the tm-SPICE pulse sequence when applied at different MAS frequencies.

The sequence was optimized for an NCA transfer at 16.5-kHz MAS frequency and readjusted to keep synchronization with sample rotation. The insets show the first three rotor periods (τ_R) of the pulse sequence adapted in duration and rf amplitudes to MAS frequencies of 13 and 21 kHz. The tm-SPICE pulse sequence maintains more than 90% of its performance over a MAS frequency range of 13 to 21 kHz. When the sequence is used without rescaling (shown in gray), its efficiency is lost in a very narrow range.

So far, we ignored the influence of the isotropic (time independent) part of the internal Hamiltonian such as chemical shifts. Propagation under such a Hamiltonian will yield changes when the size of the time increments is altered. However, optimal control sequences are typically optimized to include robustness toward chemical shift changes. As a result, the variation in evolution under time-independent interactions is compensated by design. The readjusting property is common to all optimal control sequences optimized over an ensemble of crystallite orientations and chemical shift distributions. It should, however, be applied with caution and only within a limited range around the nominal MAS frequency. In case of the tm-SPICE-16.5 sequence, the applicable range is about ±20%. Another argument against arbitrary rescaling comes from the length of the sequence that should remain long enough to allow for efficient magnetization transfer mediated by a dipolar coupling of a given size.

NCA and NCO tm-SPICE experiments measured at different MAS frequencies

We demonstrated recently that tm-SPICE sequences work across a range of NMR hardware and protein samples (15). We performed measurements using different generations of Bruker instruments (AVANCE I up to AVANCE NEO), different magnetic fields corresponding to ¹H Larmor frequencies of 400 and 900 MHz, and different NMR coil designs including standard solenoidal coils and Z-coil resonators used in E-free probes (42). tm-SPICE NCA/NCO experiments were demonstrated for model peptides, microcrystalline proteins, amyloid fibrils, and membrane protein samples. In these experiments, the MAS frequency was adjusted to 20 kHz. Here, we test the tm-SPICE sequences for a range of MAS frequencies and adapt rf amplitudes and lengths by rescaling to maintain the synchronization with sample rotation. For comparison, we measure NCA/NCO experiments using a ramp-CP sequence.

First, we calibrated the rf amplitudes to the applied power parameters using a nutation experiment. We note that there is a systematic error in case rf field inhomogeneity is substantial. We have shown previously that the actual rf amplitude in the center of the solenoid coil can be 10% higher than the calibrated value, and the rf amplitude decreases to about half of its maximal value at the ends of the coil (12).

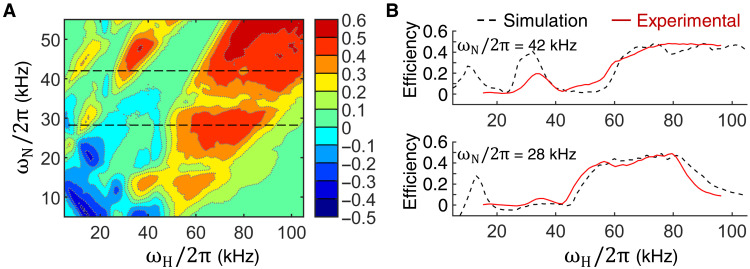
CP conditions for the magnetization transfer from ¹H to ¹⁵N nucleus were established with the help of numerical simulations. Assuming a ¹H, ¹⁵N two-spin system, the expected ramp-CP transfer efficiency was calculated for a broad range of rf amplitudes, mimicking an experimental calibration on the NMR spectrometer with practical limitations of the pulse sequence length to 3.5 ms and using a linear ramp pulse shape going from 70 to 100%. This setup should allow for the compensation of rf field inhomogeneities, and the results reveal areas of good and bad transfer. Figure 4A shows an example of the simulated CP efficiency map assuming a MAS frequency of 16.5 kHz. The results suggest that using the highest possible rf amplitudes on both channels is beneficial. Experimentally, we were limited by the probe capabilities, which allowed a maximum rf field of about 40 kHz for the ¹⁵N channel. Using this value, we approach, however, the rotary resonance recoupling (R3) condition (ω_N ≈ 2ω_R) (13) at MAS frequencies in the range of 16.5 to 19.5 kHz, which compromises efficiency of the magnetization transfer. For 16.5 kHz, it may seem that we are far from the R3 condition, but caution should be taken when rf inhomogeneity comes into play. Therefore, we decided to stay in the regime ω_N/ω_R ∈ (1,2) for ω_R between 16.5 and 19.5 kHz where values ω_N/ω_R = 1.7 seem to provide best efficiency. Figure 4B shows the comparison of the calculated and the experimental efficiencies as a function of the ¹H rf amplitude for two fixed ¹⁵N rf fields. Experiment and simulations agree rather well when a single common scaling factor was applied to the experimental data to fit the values with the simulation.

Fig. 4. Transfer efficiency of the ¹H-¹⁵N ramp-CP experiment.

(A) Transfer efficiency calculated for a contact time of 1 ms and a wide range of rf amplitudes. A 70 to 100% linear ramp was applied on the ¹H channel. Calculations assumed an amide ¹H-¹⁵N spin pair, MAS frequency of 16.5 kHz, and a realistic 3D distribution of rf fields generated by a solenoid coil of a typical 3.2-mm MAS probe. Areas of zero-quantum (positive) and double-quantum (negative) conditions are identified. (B) Traces from the 2D map extracted at fixed ¹⁵N rf amplitudes (black dashed lines) and experimental intensities (red lines) measured as a function of ¹H rf amplitude. The calculated map is used to identify suitable rf parameters for the experiment.

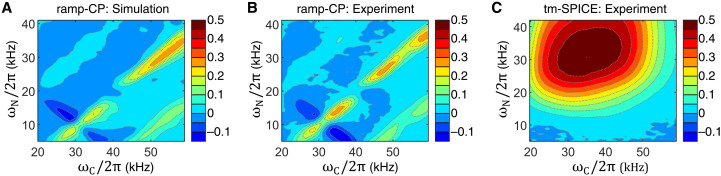
Many parameters should be taken into account in the optimization of the ¹⁵N-¹³C magnetization transfer. For practical reasons, the number of parameters must be restricted. We impose limits on the contact times that are in the range of 3.5 to 5 ms and are thus similar as in the tm-SPICE experiments. A linear ramp going from 90 to 100% was applied on the ¹³C channel. Other parameters are listed in the Materials and Methods. We calculated the transfer efficiencies for the NCA and NCO ramp-CP experiments for a broad range of rf amplitudes similar to that for the ¹H-¹⁵N CP experiment. The resulting 2D efficiency maps are provided in the Supplementary Materials and confirm that higher rf amplitudes on the ¹³C channel allow us to overcome issues related to the large chemical shift anisotropy values and thus yield an improved transfer efficiency in the NCO experiment. In Fig. 5 (A and B), we compare the simulated NCO ramp-CP efficiencies with the experimental values obtained at a MAS frequency of 19.5 kHz. The agreement between experiment and simulation is very good, although many features are not included in the simplified ¹⁵N,¹³C two-spin simulation (effects of remote protons and other ¹³C atoms are ignored). Local optima are identified in the simulation, both zero quantum (positive) and double quantum (negative signal). The simulation demonstrates the sensitivity of the experiment with respect to rf amplitude mismatch. The region of no transfer is only a couple of kilohertz away from the optimum transfer. On the basis of the simulations, we decided to use the optimum at ω_C = 1.7ω_R and ω_N = 0.7ω_R for the NCA experiment. For NCO, we use ω_C = 2.7ω_R and ω_N = 1.7ω_R for all MAS frequencies. For ω_R/2π = 19.5 kHz, this optimum is close to the probe rf power limits. The optimum at ω_C = 1.7ω_R and ω_N = 0.7ω_R provides an alternative with the same experimental efficiency. In strong contrast with the ramp-CP experiment, the tm-SPICE shapes are very robust toward rf amplitude misadjustment. It is demonstrated experimentally in Fig. 5C that the tm-SPICE experiment yields higher signal intensity over a wide range of rf amplitudes.

Fig. 5. NCO transfer efficiencies for ramp-CP and tm-SPICE for a MAS frequency of 19.5 kHz.

Numerical simulations (A) and experimental results (B) for ramp-CP and experimental results for tm-SPICE-20 (C). A linear rf ramp 90 to 100% was applied on the ¹³C channel using a contact time of 3.5 ms. Calculations assumed an ¹⁵N,¹³C′ spin pair, a magnetic field of 16.5 T (corresponding to a ¹H Larmor frequency of 700 MHz), and a realistic 3D distribution of rf fields generated by the solenoid coil. Experimental data were obtained using an f-MLF (N-formyl-MLF) peptide sample. Signal intensities were scaled to match the maximum efficiency in the simulations of ramp-CP, which is 0.31. For ramp-CP, areas of good transfer are clearly identified in the calculation (A), and the map can be used to choose appropriate rf parameters for the experiment (B). The tm-SPICE experiment is very robust toward rf amplitudes and yields high transfers (up to 0.5) over a wide range of rf amplitudes (C).

Last, we set up the NCA and NCO experiments based on tm-SPICE shapes. We calculated these shapes recently for a MAS frequency of 20 kHz, using a 3.5-ms pulse for which the maximal rf amplitudes are restricted to 40 kHz for both the ¹³C and ¹⁵N channels (mean rf amplitudes are below 10 kHz). The contact time corresponding to 70 rotor periods must be maintained when the shapes are readjusted for another MAS frequency. For example, when the rotation frequency is reduced to ${\mathrm{\omega }}_{\mathrm{R}}^{\text{new}}/2\mathrm{\pi }$ = 16.5 kHz, the length of the shapes should be set to 4242.42 μs using a maximal rf amplitude of 40 × (16.5/20) = 33 kHz. We note that the tm-SPICE shapes consist of many element pulses of varying amplitudes and phases and that the mean rf amplitude and the corresponding mean rf power are much smaller than for the continuous wave experiments. To allow for rescaling toward higher MAS frequencies, we created another tm-SPICE shape optimized for ${\mathrm{\omega }}_{\mathrm{R}}^{\text{opt}}/2\mathrm{\pi }$ = 16.5 kHz that has a duration of 60 rotor periods and an rf amplitude limited to 35 kHz (mean rf amplitudes are 10 and 15 kHz for the ¹³C and ¹⁵N channels, respectively). When used at a MAS frequency of 19.5 kHz, this shape should have a length of 3076.92 μs and a maximal rf amplitude of 41.36 kHz. The name of the shape contains the MAS frequency for which it is optimized as an index, e.g., tm-SPICE-16.5 or tm-SPICE-20. These shapes were optimized to cover a chemical shift range of 27, 25, and 15 parts per million (ppm) for the amide nitrogen, Cα, and C′ nuclei, respectively. In principle, the tm-SPICE experiments do not require further experimental optimization. However, we observe systematically that lower rf amplitudes (~10%) on the spectrometer yield higher efficiencies. We explain this by the systematic error of the rf amplitude calibration in the nutation experiment.

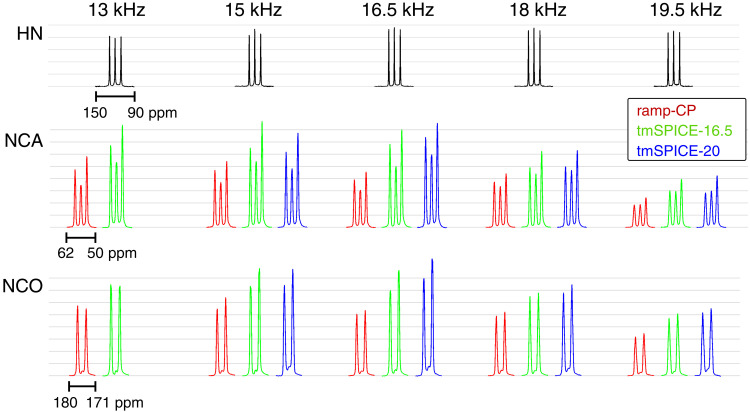
All experimental NCA/NCO spectra measured at MAS frequencies in the range of 13 to 19.5 kHz are summarized in Fig. 6. The spectra are plotted as obtained using identical signal accumulation parameters. Their signal-to-noise ratio can be directly compared. Our tm-SPICE sets outperform ramp-CP experiments at all conditions with an average gain of 1.5. This demonstrates that tm-SPICE sequences can be successfully applied within the range of MAS frequencies between 13 and 19.5 kHz after readjusting the duration and nominal rf amplitudes of the pulse. Together with the higher signal intensity, tm-SPICE shapes have the advantage of robustness toward rf amplitude misadjustment, as demonstrated in Fig. 5C. While ramp-CP shows a strong dependence, with variations of the applied rf fields yielding very narrow recoupling conditions, the tm-SPICE experiment achieves high signal intensity over a wide range of rf amplitudes.

Fig. 6. Overview of f-MLF spectra acquired over a range of MAS frequencies.

(Top) ¹⁵N ramp-CP (linear rf ramp 70 to 100% on ¹H channel) spectra of approximately equal intensity over the whole range of MAS rates. (Middle and Bottom) ¹³C spectra of the Cα and C′ spectral region, respectively, acquired using NCA and NCO experiments with ¹H-¹⁵N and ¹⁵N-¹³C magnetization transfers. While the ¹H-¹⁵N step was carried out using the same pulse sequence element, ramp-CP (linear rf ramp 90 to 100% on ¹³C channel), tm-SPICE-16.5, and tm-SPICE-20 schemes were used for the ¹⁵N-¹³C step, resulting in spectra plotted in red, green, and blue, respectively. The optimal control tm-SPICE set of pulses consistently yields the highest signal intensity, which is about 1.5 times the intensity of the ramp-CP experiments. All NCA and NCO spectra are displayed with a common scale on the y axis, with gray grid lines facilitating visual comparison.

DISCUSSION

Dipolar recoupling is a central concept in the NMR spectroscopy of rotating solids and the key technique for establishing correlations between different nuclei by magnetization transfer. The experimental sensitivity of multidimensional experiments is determined by the quality of the recoupling blocks. In the quest for the best transfer efficiency, many different experimental techniques have been developed, and we expect that many more will follow. We focus here on ¹⁵N-¹³C spin pairs involved in the protein backbone that are characterized by a rather weak dipolar interaction (1 kHz) and strong chemical shift anisotropies (99 ppm for nitrogen, −20 ppm for Cα, and −76 ppm for C′). Magnetization transfer between these nuclei is most frequently accomplished using ramp-CP or adiabatic-CP techniques. Calibration of these experiments is laborious, as it involves many parameters: the duration of the shape; the absolute values of the rf amplitudes used; the slope, curvature, and sign of the rf amplitude sweep; and the choice of the rf channel where the variable rf field is applied (¹³C or ¹⁵N). Different best conditions may apply for NCA and NCO transfers and for different external magnetic fields and, thus, effective chemical shift anisotropies of the involved nuclei. Yet another level of complications arises from the capabilities of the NMR hardware such as amplifier stability, achievable rf amplitudes, and the rf field distribution generated by the solenoidal coil.

Using optimal control, we addressed the following questions: What is the highest achievable transfer efficiency if we assume a high external magnetic field and a realistic spatial distribution of rf fields in the sample? How close to the maximum can we get using the current methods? We show numerically that ramp-CP and adiabatic-CP experiments are not able to provide efficient magnetization transfer simultaneously for molecules located in different parts of the sample. Because of rf inhomogeneity, these methods lead to a constriction of the effective sample volume where recoupling occurs, and their efficiency integrated over the sample volume reaches about 40%. On the other hand, we find pulse sequences designed using our recent tm-SPICE optimization protocol that can mediate almost complete transfer of magnetization in the whole volume of the sample, with a total efficiency of about 95%. It is a remarkable achievement when we realize the conditions at which the pulse sequence is applied: It compensates for a distribution of effective coupling constants in the range [0, d_max], a distribution of rf amplitudes ranging from 50 to 100%, and rf phases from 0° to 30°. At the same time, all these parameters are temporally modulated by the sample rotation, and it is necessary to account for different initial phases of these modulations (see also the Supplementary Materials).

We used our numerical model to predict the magnetization transfer efficiencies for ramp-CP ¹H-¹⁵N and ¹⁵N-¹³C transfers. In these calculations, we map possible recoupling conditions over a wide range of rf amplitudes and search for the highest efficiency. The predictions closely correspond to the experimental results and can be used to guide experimental setup. However, because of their lack of efficiency, we propose that ¹⁵N-¹³C ramp/adiabatic-CP elements should be replaced by optimal control tm-SPICE shapes. These pulses do not require extensive optimization on the spectrometer yet provide higher transfer efficiencies.

We introduced a simple recipe for adjusting the tm-SPICE sequences to the preferred MAS frequency of the experiment. We find that the length and the nominal rf amplitudes of the tm-SPICE shapes have to be rescaled to maintain the rotor synchronization that was obtained by numerical optimization of the shape. This way, the tm-SPICE shapes can be successfully applied over a range of MAS frequencies. Using rf pulses in synchrony with sample rotation is a well-established principle to achieve recoupling in MAS solid-state NMR. The conventional recoupling methods consist of one basic rf element spanning just few rotor periods. It is then repeated many times to gradually build the transferred magnetization. Optimal control sequences are principally different; they are not periodic, and when they are concatenated, no additional magnetization builds up. While the rescaling principle is explained by theory, it also has its limitations. The complicated interplay of orientational dependencies of multiple interactions, together with a spread of isotropic interactions, prohibits arbitrary rescaling. Going very far from the nominal MAS frequency substantially changes the duration of the sequence. It may become too short in a sense that the dipolar interaction does not have enough time to carry out an efficient magnetization transfer. At the other extreme, it may become too long so that the evolution caused by the dipolar interaction is not efficiently manipulated by weak rf pulses. Numerical simulations reveal that our NCA/NCO tm-SPICE shapes retain more than 90% of their efficiency over the MAS frequency range of 13 to 21 kHz, while they were optimized for 16.5 kHz. Adjusting tm-SPICE pulses toward lower MAS frequencies causes larger penalties in transfer efficiency compared to going to higher MAS frequencies. However, for fast (40 to 60 kHz) and ultrafast (80 to 120 kHz) MAS conditions, new tm-SPICE shapes are needed and have to be optimized independently.

An alternative approach to design pulse sequences robust to different MAS frequencies is to include MAS frequencies to the ensemble of conditions over which the pulse sequence is optimized, in the same way as it is done with the distribution of crystallite orientations. These calculations are, however, very demanding, and the resulting pulse sequence fails completely for MAS frequencies outside the optimization ensemble. MAS solid-state NMR experiments are typically performed at one fixed sample rotation frequency, and such robustness is not required. On the basis of our experience, a better strategy is to take advantage of the rescaling property, adjust the pulse sequence, and use it without additional reoptimization. An interesting approach would be to include the rescaling feature directly into the optimal control design, but again, we are limited by computational resources.

We have performed experiments in the MAS frequency range of 13 to 21 kHz and systematically obtained 1.5 times larger signal intensities for the tm-SPICE sequences compared to ramp-CP in both the NCA and NCO experiments. While the gain achieved for the NCA transfer agrees with our previous report on the tm-SPICE-20 shape, we obtained smaller values for the NCO cases in this study. The greatly improved ramp-CP reference experiments in the present work illustrate the caveats when setting up a ¹⁵N-¹³C ramp-CP. Misadjusting the rf amplitudes by a few kilohertz or selecting the wrong regime of rf amplitudes for the Hartmann-Hahn match can result in substantial signal losses. It is easy to imagine that a subtle detuning of the probe during the experiment will have detrimental consequences for the overall performance. A direct advantage of the tm-SPICE experiments is their robustness against variations of rf amplitudes, documented in Fig. 5C. This robustness greatly simplifies the experimental setup for samples that only yield low sensitivity and where an experimental optimization of CP parameters is not feasible.

Our calculations predict that the maximal achievable efficiency for an isolated ¹⁵N-¹³C spin pair is more than twofold higher for an optimal control–derived sequence compared to a ramp/adiabatic-CP experiment in the absence of isotropic chemical shift dispersion (Fig. 2A). These values are not met in our experiments since remote ¹³C nuclei that are coupled to the ¹⁵N-¹³C pair, as well as the surrounding proton bath in a uniformly enriched protein sample, are interfering with the transfer (33). Four spins are considered in the optimization of the tm-SPICE shapes: N, Cα, Cβ, and C′ of a single residue for NCA transfers and N, C′, and the Cα’s of both involved residues for NCO transfers. The calculations assume a distribution of orientations in a powder and a spatial distribution of rf field inhomogeneities in combination with a chemical shift dispersion of the amide nitrogen and carbon atoms (15). Under these conditions, the optimization yields tm-SPICE shapes with a transfer efficiency decreased by 20% compared to the two-spin calculation. In general, an increase of the number of constraints in the optimization leads to slower convergence, and accounting for more surrounding spins turns the calculation very compute time intense and prohibitively inefficient. An additional decrease of the experimental performance compared to numerical calculations might originate from incomplete proton decoupling. We show below, and in the Supplementary Materials in greater detail, that this effect is rather strong and dominates over the effect of adjusting to different MAS frequencies.

We observe a pronounced decrease of the signal intensity with increasing MAS frequencies in both the ramp-CP and tm-SPICE NCA/NCO experiments (see Fig. 6). We note that the ¹H-¹⁵N CP transfer yields nitrogen spectra with almost equal intensity (within 10%) for all MAS frequencies used here. Part of the effect can be attributed to an increased linewidth that is possibly due to non-optimal decoupling. Nevertheless, a large contribution to the signal loss must originate from the ¹⁵N→¹³C transfer itself. We therefore investigated the influence of remote spins using numerical simulations. We have shown previously that insufficient proton decoupling during the transfer decreases the performance of the NCA tm-SPICE-20 experiment. Assuming the leucine spin system in the peptide N-formyl-Met-Leu-Phe (f-MLF; including the heteroatoms N, Cα, Cβ, and C′ and the four directly bonded hydrogen atoms), we find that the numerically predicted NCA transfer efficiency of the tm-SPICE-16.5 sequence drops by 55% when the MAS frequency is increased from 13 to 19.5 kHz and, at the same time, the proton decoupling amplitude is kept constant at 85 kHz during the transfer. To model the NCO transfer, we used a spin system that consists of N, C′, its two neighboring Cα’s, and the four closest protons. In that case, the efficiency decreases by 30%. These values roughly correspond to the experimental observations. Similar simulations performed for ramp-CP suggest that ¹H decoupling at elevated MAS frequencies has a similar detrimental influence. The results are not a direct function of the MAS frequency, as different rf matching conditions are used at different frequencies. In addition, we cannot exclude effects connected to the specific spin system parameters and rf amplitude setup.

To conclude, we have shown that our recent tm-SPICE shapes can be successfully applied at different MAS frequencies when durations and rf amplitudes of the shaped pulses are adjusted accordingly to maintain synchronization with sample rotation. We tested tm-SPICE sets of pulses optimized for NCA and NCO transfers in the MAS frequency range of 13 to 20 kHz. We found tm-SPICE experiments to outperform a carefully calibrated ramp-CP by an average factor of 1.5 in terms of signal intensity. While the ramp-CP is very sensitive to proper calibration, the presented tm-SPICE schemes require virtually no optimization on the spectrometer, as they are very robust toward mis-setting of rf amplitudes. Recently, tm-SPICE was implemented as a magnetization transfer element to yield sequential assignments for various amyloid fibrils (43–45). We anticipate that this method will replace the conventional ramp-CP block, which requires tedious optimization.

MATERIALS AND METHODS

Numerical simulations

All numerical calculations were done using SIMPSON (46, 47). Spin system parameters were derived from the f-MLF crystal structure in Protein Data Bank entry 1Q7O using SIMMOLvmd (48) and are provided in the Supplementary Materials. The static magnetic field was set to 16.45 T, corresponding to a proton Larmor frequency of 700 MHz. For powder averaging, the Zaremba, Conroy and Wolfsberg (ZCW) scheme was used consisting of three-angle set of 144 elements (49). A typical 3.2-mm MAS probe was assumed with a solenoid coil and a 3D distribution of the rf field as described in (12). The calculations were parallelized and run on a high-performance computing facility. Specific parameters of individual calculations can be found in the Supplementary Materials.

The highest achievable efficiency of ramp-CP and adiabatic-CP experiments was estimated using the global search routine implemented in the MATLAB (MathWorks) optimization toolbox, while the actual spin dynamics calculations were conducted in SIMPSON. The rf amplitudes applied on the two channels were optimized together with the slope of the linear ramp or with the sweep range and the shape factor of the tangential shape (see the Supplementary Materials for details). The optimization protocol was repeated 10 times with random initial values to achieve adequate coverage for all possible conditions. Optimal control sequences were generated using the strategy of the tm-SPICE experiment (15), assuming two spins and on-resonance conditions.

To calculate the transfer efficiency of the ¹H→¹⁵N CP, a linear ramp going from 70 to 100% was assumed on the ¹H channel while the amplitude was kept constant on the ¹⁵N channel. The contact time was fixed at 1 ms. The ¹H rf amplitudes were incremented from 5 to 105 kHz in steps of 1 kHz, and the ¹⁵N rf amplitudes were varied from 5 to 55 kHz in steps of 0.5 kHz. For the NCA and NCO CP experiment, a linear ramp going from 90 to 100% was used for the ¹³C channel. ¹³C rf amplitudes were incremented in the range of 5 to 60 kHz with step size of 1 kHz, while the ¹⁵N amplitudes were varied using step sizes of 0.5 kHz in the range of 5 to 55 kHz.

The calculation of the tm-SPICE shapes for the NCA and NCO magnetization transfers at a MAS frequency of 16.5 kHz was done as described in (15) except for adjusting the pulse duration to 60 rotor periods. The rf amplitudes were restricted to 35 kHz for both channels to allow rescaling to higher MAS frequencies. The previously described tm-SPICE shapes optimized for a MAS frequency of 20 kHz have a duration corresponding to 70 rotor periods and use maximal rf amplitudes of 40 kHz on both channels. We refer to these optimal control sets of shapes as tm-SPICE-16.5 and tm-SPICE-20, respectively.

Material

The uniformly ¹³C- and ¹⁵N-labeled tripeptide f-MLF was packed into a Bruker thin-wall 3.2-mm rotor, making use of the complete rotor volume (up to 30 mg of the material).

Instrument

Measurements were performed on a 700-MHz standard bore Bruker AVANCE III HD NMR spectrometer that is equipped with a 3.2-mm HR MAS DVT 700 S3 TL HCND probe. The sample temperature was maintained at 5°C (readout of the probe sensor).

Measurements

The measurements were performed at MAS frequencies of ω_R/2π = 13, 15, 16.5, 18, and 19.5 kHz. For ¹H decoupling during acquisition, an rCW^ApA scheme (50) was used with an rf power corresponding to 85 kHz both for the CW periods and 180° pulses and a timing set to a fraction of 0.98 of the actual rotor period. The ¹³C and ¹⁵N rf powers were calibrated by searching for a null signal corresponding to a 270° pulse applied after CP from protons. The ¹H rf power was calibrated by varying the excitation pulse in the ¹H-¹³C CP experiment where a null signal is obtained with a 180° pulse. Magnetization was transferred from protons to amide nitrogen using a 1-ms-long CP using a 70 to 100% linear ramp applied on the ¹H channel. The rf amplitudes were chosen according to the maps of the best transfer conditions obtained by the numerical simulations described above, avoiding proximity to rotational resonance conditions (ω_N ≈ ω_R or 2ω_R). ¹⁵N rf amplitudes were 42, 42, 28, 30, and 34 kHz for ω_R/2π = 13, 15, 16.5, 18, and 19.5 kHz, respectively. The optimal ¹H rf power was determined experimentally in the range of 78 to 92 kHz to yield maximal signal at each MAS frequency. A similar procedure was used to determine the best conditions for NCO and NCA transfers where a 90 to 100% linear ramp was applied on the ¹³C channel. Contact times were set similarly to the tm-SPICE experiments and were 4.6 and 4 ms for ω_R/2π = 13 and 15 kHz, respectively, and 3.5 ms for the other MAS frequencies. The numerically calculated efficiency maps were used to guide the experimental optimization. For NCA, the ¹³C rf amplitude was set close to 1.7 times the MAS frequency, and the ¹⁵N rf amplitude was optimized near 0.7× ω_R/2π. For NCO, the ¹³C and ¹⁵N rf amplitudes were around 2.7× and 1.7× ω_R/2π, respectively, except for ω_R/2π = 19.5 kHz for which we used 1.7× and 0.7× ω_R/2π, respectively. The parameters for the tm-SPICE pulses were set according to the theoretical values with the length corresponding to 60 and 70 rotor periods for tm-SPICE-16.5 and tm-SPICE-20 sets, respectively. The ¹³C and ¹⁵N rf powers were initially set to correspond to nutation frequencies of 35 × (ω_R/2π/16.5) and 40 × (ω_R/2π/20) for tm-SPICE-16.5 and tm-SPICE-20 sets, respectively, and subsequently optimized within a 2-dB range.

Proton decoupling during the NCA/NCO transfer was not optimized. A CW scheme was used with an 85-kHz rf amplitude, which corresponds to the specified probe limitation.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S10

Table S1

Legends for data S1 to S4

References

Other Supplementary Material for this manuscript includes the following:

Data S1 to S4

View/request a protocol for this paper from Bio-protocol.