Abstract
Protein complexes involved in DNA mismatch repair diffuse along dsDNA as sliding clamps in order to locate a hemimethylated incision site. They have been observed to use a dissociative mechanism, in which two proteins, while continuously remaining attached to the DNA, sometimes associate into a single complex sliding on the DNA and sometimes dissociate into two independently sliding proteins. Here, we study the probability that these complexes locate a given target site via a semi-analytic, Monte Carlo calculation that tracks the association and dissociation of the sliding complexes. We compare such probabilities to those obtained using a nondissociative diffusive scan in the space of physically realistic diffusion constants, hemimethylated site distances, and total search times to determine the regions in which dissociative searching is more or less efficient than nondissociative searching. We conclude that the dissociative search mechanism is advantageous in the majority of the physically realistic parameter space, suggesting that the dissociative search mechanism confers an evolutionary advantage.
I. INTRODUCTION
DNA mismatch repair (MMR) is a molecular process by which errors in a DNA sequence indicated by mismatched base pairs are corrected. Failure of this process is the cause of many cancers [1], but a complete mechanistic description of the process does not yet exist [1-3]. The MMR process is evolutionarily conserved from prokaryotes to eukaryotes [4-6], so Escherichia coli MutS, MutL, and MutH proteins may be productively used to study MMR. In E. coli, MMR consists of the following steps: First, MutS recognizes a mismatched site on a DNA strand and associates with the DNA. This MutS then binds MutL from solution, which in turn can bind MutH. MutH then nicks the newly synthesized, erroneous DNA strand. Excision, followed by polymerization and ligation, complete the repair process [5,6].
Here, we describe a quantitative model of the process by which the MMR proteins determine which strand is newly synthesized. Since E. coli methylates its DNA strands whenever a GATC base sequence appears, a newly synthesized strand differs from existing strands in that it is not yet methylated. A MutL-activated MutH, therefore, nicks the new strand at a hemimethylated site, and the strand containing the nick is excised. To create this nick, however, the hemimethylated site must first be recognized. The hemimethylated sites may be thousands of base pairs away from the mismatch (and therefore the place at which the MutS proteins bind to the DNA), so recognition of hemimethylated sites is not a trivial problem. Through single-molecule probing of the MMR process in vitro, Liu et al. recently found stable toroidal protein clamps (MutS and MutL) diffusing along the DNA strand while transiently associating and dissociating from each other (but, crucially, remaining on the DNA) in order to reach and recognize a hemimethylated site [3]. While these clamps eventually dissociate from the DNA, this occurs on a much longer timescale than the protein-protein association and dissociation on the DNA. It is therefore the protein-protein association-dissociation diffusion mechanism on the DNA that is the subject of our quantitative model presented here.
Several previous studies investigated sliding clamps on DNA. The toroidal, “sliding clamp” protein structure, which we are interested in here, was reported by O’Donnell et al. in the context of an E. coli polymerase, DNA polymerase III holoenzyme, which is stabilized on the DNA by the β-clamp that encircles the DNA [7]. More recently, Daitchmen et al. have used molecular-dynamics simulations to study the diffusion of these protein clamps and report on the way in which the physical properties of the clamps affect the diffusion dynamics [8]. However, all of the previous studies of sliding clamp proteins that we are aware of have focused on individual proteins rather than on interactions between clamps or the search process as a whole.
Protein search processes involving nontoroidal DNA binding proteins have also been studied extensively. Berg et al. [9] derived a complete mathematical model of the search process of a DNA binding protein in terms of association and dissociation rates, as well as geometrical considerations that account for sliding, microscopic jumps, intersegmental transfers, and three-dimensional diffusion. Similarly, Lomholt et al. [10] produced a mathematical model of a search that takes DNA coiling explicitly into account, which allows an extension of the Berg model to include consideration of intersegmental jumps. Furthermore, Benichou et al. [11] found that a combination of three- and one-dimensional diffusion is capable of performing a fast search in the cell nucleus using a fractal description of chromatin. Givaty et al. [12] developed a molecular simulation based on electrostatic forces of DNA binding proteins searching DNA and tracked their motion. They found that the most efficient DNA searches consist of ≈20% sliding and ≈80% three-dimensional diffusion. Reingruber et al. [13,14], derived exact expressions for the duration of transcription-factor searches for DNA promoter sites that involve fast and slow rates of one-dimensional diffusion in addition to three-dimensional diffusion capable of intersegmental transfer. They found that a coiled DNA conformation is necessary for a fast search, and that the addition of the fast one-dimensional diffusion state decreases search time. Works from Mirny et al. [15], Slutsky and Mirny [16], Bauer and Metzler [17], and Zhou [18] also examine the potential role of protein conformational changes in producing a fast search.
The focus of this publication is to quantitatively model the observed protein clamp association-dissociation mechanism present in MMR protein clamp diffusion. While this process is similar to the search mechanisms summarized in the previous paragraph in that it is characterized by transitions between a slow searching state and a fast nonsearching state, the crucial difference lies in the lifetime distribution of the fast state. In particular, the transition from the dissociated fast state into the slow searching state is governed by three-dimensional diffusion in the nontoroidal proteins, whereas the toroidal structure of the proteins that we consider prevents quick release from the DNA and thus restricts their motion to a single dimension. This structure also prevents transfer between nearby DNA segments [7,8,19]. Additionally, although there have been many previous studies that consider searches that switch between fast and slow one-dimensional diffusion states, ours is the first of which we are aware that studies searches in which the switch between fast and slow states is mediated by the separate diffusion of two distinct clamps. As we demonstrate, this results in a qualitatively different lifetime distribution of the fast diffusing state compared with systems in which the fast diffusing states are caused by internal transitions of the diffusing protein. In particular, while the internal transitions generally follow a Poissonian distribution [13,14], in our system the transition out of the fast state follows a Lévy distribution.
After construction of the quantitative model, we investigate whether the one-dimensional association-dissociation mechanism serves to increase the efficiency with which a hemimethylated site is found, as compared with a more straightforward situation in which the proteins are unable to dissociate from one another (or, equivalently, there is only a single protein complex). If this were the case, it could provide an evolutionary pressure favoring the association-dissociation mechanism. We find that, although the association-dissociation mechanism makes little difference at the observed E. coli parameters, there is a much larger section of parameter space in which the association-dissociation mechanism is beneficial as opposed to detrimental when compared with a case in which the proteins do not dissociate.
This paper begins with a summary of the Liu et al. experiments underlying our model, including a tabulation of experimental parameters relevant to the model in Sec. II. In Sec. III, the model itself is described both physically and mathematically. Section IV presents our approach to calculating the probability of finding the hemimethylated site from the model. The main findings concerning the probability of finding the hemimethylated site are then presented in Sec. V, and finally the implications of those results are discussed in Sec. VI, along with potential future directions of research in this area. Several of the detailed derivations and validations are relegated to various Appendixes.
II. EXPERIMENTAL OBSERVATION OF DISSOCIATIVE SEARCH MECHANISM
In this section, we briefly summarize the experimental observations by Liu et al. [3] that underlie the model developed here. Additionally, we compile in Table I experimentally measured quantities used to determine values of model parameters, since we refer to these quantities throughout the paper.
TABLE I.
Summary of relevant quantities measured by Liu et al. [3]. The column labeled “SL value” gives the value of each quantity in the absence of MutH, whereas the column labeled “SLH value” gives the value of each quantity in the presence of MutH. Note that some values were not measured separately in the presence of MutH (indicated by NA), so we will assume that MutH does not change these values. In Liu et al.’s experiment, 17.3 kb of dsDNA was stretched over 4.4 μm, so we use 4.4 μm = 17.3 kb to convert from reported values in μm by Liu et al. to units of bp, which are more convenient for our model.
| Quantity | Symbol | SL value | SLH value |
|---|---|---|---|
| Search complex diffusion constant | D SL,M | (6 ± 3) × 104 bp2/s | (8 ± 5) × 104 bp2/s |
| MutS diffusion constant | DS | (7 ± 2) × 105 bp2/s | NA |
| MutL diffusion constant | DL | (1.4 ± 0.6) × 107 bp2/s | (6 ± 5) × 105 bp2/s |
| MutS-MutL association lifetime | τ A,M | 30 ± 3 s | NA |
| MutS-DNA association lifetime | τS | 185 ± 35 s | NA |
| MutL-DNA association lifetime | τL | 850 ± 150 s | NA |
In the experiment by Liu et al., interactions of E. coli DNA mismatch repair proteins MutS, MutL, and MutH with dsDNA were imaged via total internal reflection fluorescence microscopy. Of particular interest is what will be referred to as the dissociative search mechanism, so-called because of the many cycles in which MutS and MutL associate into a single complex and then dissociate into two separate complexes before reforming a single complex as they diffuse along the DNA in order to locate the hemimethylated site. (We called this mechanism the “association-dissociation mechanism” in the introduction for clarity, but for the remainder of the paper we switch to the less cumbersome “dissociative mechanism.” Note that these “dissociations” refer to the proteins separating from each other while remaining on the DNA, rather than dissociation of the proteins from the DNA itself.)
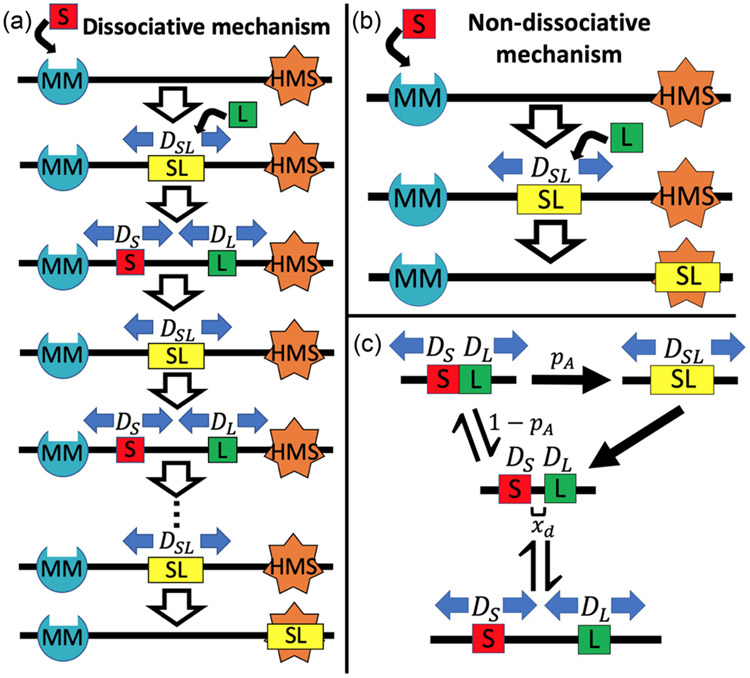
When MutS binds to a mismatch, it forms a stable clamp in the presence of ATP. It then diffuses along the DNA strand. MutL may then bind to MutS, forming a new clamp which diffuses more slowly along the DNA. This slower diffusion implies frequent interaction with the DNA backbone, thus indicating that the MutS-MutL clamp complex is capable of “searching” the DNA for a hemimethylated site [3]. Interestingly, MutL often dissociates from MutS, and the two proteins form two stable and independently diffusing clamps, each of which diffuses along the DNA much more quickly than the MutS-MutL complex and is therefore not interacting with the DNA frequently enough to perform a search [3]. If the dissociated clamps diffuse back into a state in which they are adjacent along the DNA, they are able to re-associate and continue to search the DNA together. This process is represented in cartoon form in Fig. 1(a). Finally, MutH associates with MutL in order to cleave the newly synthesized DNA strand at the hemimethylated site. Measured association lifetimes and diffusion constants for the dissociative search are compiled in Table I. Since some of the values depend on the presence or absence of MutH, the table provides values for both scenarios denoted “SLH” and “SL,” respectively. Note that the diffusion of the MutS protein alone is ≈10 times faster than the diffusion of the MutS-MutL complex, and that the diffusion of the MutL protein in the absence of MutH is a factor of ≈20 faster than that of the MutS protein alone. In the presence of MutH, however, MutS and MutL diffuse at similar rates. Furthermore, the addition of MutH does not seem to have a significant effect on the MutS-MutL diffusion constant [3].
FIG. 1.
(a) Illustration of the dissociative search mechanism. First, MutS forms a sliding clamp at the mismatch site. Then MutS recruits MutL, and they form a MutS-MutL sliding clamp complex capable of recognizing the hemimethylated site. This complex dissociates into independently diffusing MutS and MutL sliding clamps, which in turn re-associate to form the MutS-MutL complex again. This cyclical process continues until either one or both complexes fall off of the DNA or the MutS-MutL complex finds the hemimethylated site. (b) Illustration of the nondissociative search mechanism. First, MutS forms a sliding clamp at the mismatch site. Then MutS recruits MutL, and they form a MutS-MutL sliding clamp complex capable of recognizing the hemimethylated site. In contrast with the dissociative search mechanism, in the nondissociative case MutS and MutL are unable to dissociate from each other. The search therefore continues in the MutS-MutL complex state until one or both of the proteins falls off of the DNA or the hemimethylated site is found. (c) State diagram of the model used to calculate successful hemimethylated site search probabilities in DNA mismatch repair. The DNA is modeled as a one-dimensional track along which the proteins travel. MutS and MutL protein clamps diffuse along the DNA with rates specified by DS and DL, respectively, until they come into contact with each other. They may then either diffuse away from each other without associating or associate into a combined, searching MutS-MutL. These happen with probabilities 1 − pA and pA, respectively. The combined MutS-MutL can in turn diffuse along the DNA with a new rate specified by DSL, and is capable of searching the DNA over which it passes. After an average lifetime τA,μ, this complex dissociates into separate MutS and MutL DNA clamps.
The objective of this work is to quantitatively study the effect of this dissociative mechanism on search efficiency. In particular, there are two competing effects of dissociative diffusion on search efficiency that make its overall effect unclear. Since it makes the overall diffusion faster (compared with a system that always remains in the slow, searching state), it increases the region of the DNA that the protein clamps are able to visit. However, since proteins in the dissociated state are unable to actually search the DNA, the amount of DNA actually searched may decrease if the proteins do not re-associate often enough.
III. MODEL
A. Model structure
To determine the efficiency of the dissociative DNA mismatch repair search mechanism, we propose the microscopic model illustrated in Fig. 1, explicitly in Fig. 1(a) and as a state diagram in Fig. 1(c). Fig. 1(b) shows the nondissociative mechanism to which the dissociative mechanism will be compared.
In the dissociative model, the search begins with an associated MutS-MutL protein complex. The initial associated complex then diffuses in one dimension along the DNA with diffusion constant DSL,μ. The MutS-MutL complex dissociates with some average lifetime τA,μ into independent MutS and MutL clamps initially separated by a distance xd with diffusion constants DS and DL, respectively. The individual MutS and MutL clamps diffuse along the DNA until they come into contact again. Once in contact, the proteins either re-associate with each other with an association probability pA or continue independent diffusion starting from a distance xd with probability 1 − pA. Since pA is not well known, it will be tested over a broad range of values, but we find that the value of pA has only a small effect on the overall search (see Sec. IV C 5). This process continues until the hemimethylated site is either found or the MutS clamp falls off the DNA, thereby setting the total search time tS. The parameters characterizing the search process described by our model are summarized in Table II.
TABLE II.
Summary of stochastic model parameters. The left column describes the physical quantity, and the right column gives the associated symbol.
| Parameter | Symbol |
|---|---|
| MutS-MutL diffusion constant | D SL,μ |
| MutS-MutL association lifetime | τ A,μ |
| MutS diffusion constant | DS |
| MutL diffusion constant | DL |
| Initial separation after dissociation | xd |
| MutS-MutL association probability | pA |
| Total search time | tS |
B. The role of MutH
In the actual MMR scenario, MutH binds to MutL at some point during the search. It then remains complexed with MutL and results in a change of the diffusion constants, as shown in Table I. Since it is unclear at what point in the search MutH enters the process, we consider separately the case in which MutH is present from the beginning of the search (“SLH”) and the case in which MutH enters only after the search is complete (“SL”). These can be seen as limiting cases of the actual process, in which MutH joins MutL at some point during the process. For convenience, we will in our descriptions only refer to MutL and MutS with the understanding that MutL may or may not be bound by MutH and consider the absence or presence of MutH simply by choosing parameter values from the third or fourth column of Table I, respectively.
C. Figure of merit for search efficiency
We quantify the efficiency of the overall search process in terms of the probability that in at least one of ns total individual searches, a MutS-MutL complex reaches the hemimethylated site at x = xmeth within the maximal search time ts. This probability corresponds to the probability that the HMS is located during the MMR process and is given by
| (1) |
A single search starts when the MutS-MutL complex forms on the DNA for the first time. While the MutS and MutL clamps may dissociate many times from one another within a DNA search, the search ends when the HMS is found or when MutS or MutL dissociate from the DNA. The latter sets the total search time ts, which will be varied around the experimental value of the MutS lifetime τs. We use the MutS lifetime to determine the total search time since it is shorter than the MutL DNA lifetime and thus provides the more stringent cutoff [3,6]. Once a search has ended unsuccessfully, the process moves on to the next search, up to ns total searches. If the HMS has still not been found after ns searches, then the overall process is unsuccessful (which occurs with probability ).
While other studies of protein searches on DNA often quantify search efficiency in terms of the time it takes for a protein to locate the target site, we believe that the probabilistic approach described above is more relevant for our system due to the fact that the MutS protein eventually falling off the DNA ends the search attempt irreversibly. Once fallen off, every MutS protein must begin its search again at the mismatch site. Thus, while in other models of search processes, the protein can continue the search indefinitely until it eventually finds its target, in our case the protein must travel the distance from the mismatch to the HMS before it falls off the DNA or the search is in vain. We thus believe the probability to be the most physiologically relevant quantity. In Sec. IV, we describe how we calculate .
D. Simplifying assumptions
To create this model, we have made a number of simplifying assumptions. First, we only consider the case when there are two protein clamps (either MutS and MutL, or MutS and a MutL-MutH complex) on the DNA. This is not the case in the cell but serves as a first approximation. Similarly, there may be other molecules on the DNA aside from the MMR proteins involved in an individual search, which could also lead to complications. We also assume that a HMS is recognized each time a MutS-MutL or MutS-MutL-MutH clamp reaches it. While consideration of these complications is beyond the scope of the current work, we discuss qualitative expectations of the effect of these issues and discuss strategies for the expansion of our work to take these complicating factors into account in Sec. VI.
IV. CALCULATION OF SUCCESSFUL HEMIMETHYLATED SITE SEARCH PROBABILITY
In this section, we describe how we calculate our figure of merit of search efficiency, namely, the successful hemimethylated site search probability defined in Sec. IIIC. As a reminder, a successful search is defined as one in which the MutS-MutL complex visits the hemimethylated site before the cutoff time ts passes at least once among ns independent search attempts.
A. Successful hemimethylated search probability of nondissociative search
The baseline with which we compare is the equivalent probability for searches in which the clamps remain associated with each other for the entire search (pure one-dimensional diffusion), which will be referred to as “nondissociative” or “purely diffusive” searches and denoted . These searches represent the limiting case in which the microscopic association lifetime τA,μ ↔ ∞, and they are illustrated in Fig. 1(b).
The probability of a successful nondissociative search can be derived analytically following Redner [20]. We start with the diffusion equation in the case of a MutS-MutL clamp:
| (2) |
where DSL is the diffusion constant associated with the MutS-MutL clamp and x0 is the position along the DNA at which the nondissociative search begins. p(x, t∣x0)dx is the probability that the clamp will be searching a position within dx around x at time t.
To consider the probability that the search reaches the hemimethylated site xmeth, we first solve this differential equation in the presence of an absorbing boundary condition at xmeth. Mathematically, this condition is expressed as p(xmeth, t) = 0, requiring that the MutS-MutL complex has not arrived at the hemimethylated site. Using the method of images, this solution is given by
| (3) |
which represents the spatial probability density of the search at some time t under the assumption that the search started at x0 and has not yet reached xmeth. Note that this calculation treats the DNA as semi-infinite, since the search ends when the hemimethylated site is reached, and the clamp thus can never reach positions with x > xmeth. The total probability that at time t a clamp has only searched positions x such that x < xmeth (i.e., the probability that the HMS has not been located) is obtained by integrating the probability density over all positions x < xmeth:
| (4) |
The probability that xmeth has been located by a single search is, therefore,
| (5) |
where the superscript (0) indicates that the probability is for a nondissociative search. The overall probability for at least one out of ns searches being successful is given, in analogy to Eq. (1), by
| (6) |
B. Successful hemimethylated search probability of dissociative search
1. Association and dissociation event stepping simulation
To use the model described in Sec. III to calculate successful-search probabilities, we develop a Monte Carlo approach that samples from analytic one-dimensional diffusion probability distributions. This calculation breaks the problem of determining the successful-search probability into the cumulation of the probabilities that each individual microscopic association [the state shown in the top right of Fig. 1(c)] identifies the hemimethylated site.
The probability that an individual microscopic association reaches the HMS can be determined analytically [see Eq. (8) below] if the distance between the position at which the clamps associate x0 and the hemimethylated site xmeth is known. Similarly, the probability distributions of the subsequent microscopic re-association position and time (i.e., the position and time at which MutS and MutL come back together following dissociation from each other) can be determined analytically and are given in Eqs. (11) and (12). In principle, this conceptual framework produces an analytic expression for the successful-search probability involving iterative convolution integrals. In practice, however, this expression is too complex to be used to compute values directly. In particular, we found that the most straightforward way to calculate the many integrals over diffusion position and association lifetime probability distributions was to randomly sample from these distributions many times. Each set of random samples produces a probability of either 1 or 0 that the hemimethylated site was successfully reached, and the average of many of these sets gives the successful-search probability P(xSL = xmeth, t < ts) and therefore the overall successful-search probability .
Another way to think of this iterative random sampling is to imagine that each set of random samples represents a path that the protein clamps can take along the DNA strand which results in either a successful or unsuccessful search. Each path occurs with a frequency proportional to its probability, and therefore setting the successful searches to 1 and the unsuccessful searches to zero and taking the average of many such searches produces the successful-search probability.
The following algorithm is used to carry out this experiment and will be called the association and dissociation event stepping simulation (ADESS):
(1) The clamps start immediately adjacent to each other. We set the starting position of the clamps to x0 = 0, the step counting index to i = 0, and the elapsed time to te = 0. Input a position to search for on a one-dimensional axis (designated the “hemimethylated site” or simply “xmeth”) representing its distance from the initial MutS-MutL association site on the dsDNA. Also choose a cutoff time ts, representing dissociation of the MutS clamp from the dsDNA.
(2) Decide whether the adjacent clamps associate by sampling randomly from a uniform distribution between 0 and 1 and comparing the result to the probability pA that adjacent clamps will associate. If the clamps do not associate, go to step 7.
(3) If the last association position is to the right of the HMS (xi > xmeth), mirror the association position at the HMS by setting xi ≡ xmeth − (xi − xmeth). Due to the symmetry of the system, this operation does not impact the outcome of the search but avoids having to distinguish between cases with xi < xmeth and cases with xi > xmeth in what follows.
(4) Randomly select, using the method of inverse transform, an association lifetime from the probability distribution given by
| (7) |
where τA,μ is the average microscopic association lifetime of the clamps. This represents the time for which the clamps are diffusing together during this association. Denote this time as tassoc. If te + tassoc > ts this is the last association period of the search and thus the last opportunity to find the HMS. In that case, since the search ends at ts, shorten the length of the last association period to the remaining time tassoc ≡ ts − te. In either case, increment te by tassoc.
(5) Decide whether the hemimethylated site xmeth has been reached given the previous association position and lifetime by sampling randomly from a uniform distribution between 0 and 1 and comparing the result r to the probability
| (8) |
that the site has been reached, where xi is the previous association position and DSL,μ is the diffusion rate of the associated clamps. Note that this is simply Eq. (5) evaluated at t = tassoc with start position xi. There are now three possibilities:
(1) If r < Pfind(tassoc), xmeth has been reached, so we proceed to step 9 and set the search value to 1.
(2) If r < Pfind(tassoc) and te ⩾ ts, xmeth has not been reached and the search is over. We therefore proceed to step 9 and set the search value to 0.
(3) If r > Pfind(tassoc) and te < ts, xmeth has not been reached, but the search continues. We therefore proceed to step 6.
(6) Use the previous association position xi and lifetime to randomly select the next dissociation position xi+1 from the probability density function of Eq. (3) at t = tassoc, with an additional normalization factor C that ensures that the probability that xmeth has not been reached is 1 at time t = tassoc. This factor is necessary because we have already determined in the previous step that the hemimethylated site has not been reached:
| (9) |
where
| (10) |
We increase i by one to indicate that the xi+1 determined here is the new position of the two newly dissociated clamps.
(7) Use the dissociation lifetime distribution
| (11) |
to determine how long the clamps remain dissociated (see Appendix A). Here, xd is as before the initial distance of the clamps following dissociation, and Drel is the diffusion constant associated with the fluctuation of the distance between the clamps. Since each clamp is diffusing independently, the distance between them is also diffusing without bias in a particular direction. Denote this chosen lifetime tdissoc and increment the total elapsed time te by tdissoc. If the cutoff time has been reached (te ⩾ ts) mark the search as unsuccessful and go to step 9.
(8) Using the lifetime chosen in the previous step tdissoc, select the next possible association position xi+1 from the distribution of positions at which the relative position of the clamps returns to zero. This distribution is given by the solution to the unbounded diffusion equation with constant DCM associated with the diffusion of the “center of mass” of the dissociated clamps (see Appendix A). In particular,
| (12) |
Increase i by one and return to step 2.
(9) Perform many such searches and assign a value of 1 to all those that are successful and 0 to those in which the cutoff time is reached without success. Take the average value of all of these searches to determine the successful-search probability. Divide the trials into 10 independent blocks of equal number of trials and calculate the search probability for each block to determine standard error.
This procedure gives , and the overall search probability for ns searches is given by
| (13) |
As noted in Sec. IV A, if this calculation is performed in the limit τA,μ → ∞ in step 4, then .
2. Base pair stepping simulation confirms continuum approximation is appropriate
In our derivation above, we have treated the search process as continuous diffusion. This assumption needs to be justified, as Veksler and Kolomeisky argue that improper application of a continuum approximation can lead to misleading results [21]. Physically, the diffusion of the protein clamps is governed by the free-energy landscape of the DNA, which has base pair periodicity. This suggests that the most accurate description of the search process is somewhere between a discrete and continuous description. To verify that the continuum approximation is appropriate, we compare the continuous ADESS to a discrete simulation called the base pair stepping simulation (BPSS) that tracks the diffusion of the MMR proteins at a base pair level using the Gillespie algorithm [22]. This simulation is discussed in more detail in Appendix B, and it demonstrates excellent agreement with the ADESS, as shown in Appendix Fig. 6. This demonstrates that the continuum approximation employed in the ADESS is appropriate and also validates the two numerical codes against each other.
C. Determination of model parameters
The model described above is written in terms of several microscopic parameters. In this section we will determine the values of these parameters. Some of these parameters can be calculated directly from experimentally measured values and are summarized in Table III. For the remainder, summarized in Table IV, we need to make reasonable assumptions about their values.
TABLE III.
Model parameter values calculated from experimental observables. The column labeled “SL value” gives each value in the absence of MutH, whereas the column labeled “SLH value” gives each value in the presence of MutH.
| Parameter | Symbol | SL value | SLH value |
|---|---|---|---|
| Dissociated clamps relative position diffusion constant | D rel | (1.5 ± 0.6) × 107 bp2/s | (1.3 ± 0.5) × 106 bp2/s |
| Dissociated clamps center-of-mass diffusion constant | D CM | (7 ± 3) × 105 bp2/s | (3.2 ± 2.8) × 105 bp2/s |
| MutS-MutL diffusion constant | D SL,μ | (6 ± 3) × 104 bp2/s | (8 ± 5) × 104 bp2/s |
| MutS-MutL association lifetime | τ A,μ | 0.03 s ⩽ τA,μ < 30 s | 0.03 s ⩽ τA,μ < 30 s |
| Distance from hemimethylated site | x meth | 500–3000 bp | 500–3000 bp |
| Total search time | ts | 185 ± 35 s | 185 ± 35 s |
TABLE IV.
Estimated values for model parameters.
| Parameter | Symbol | Value |
|---|---|---|
| Adjacent MutS-MutL association probability | pA | 10−3 ⩽ pA ⩽ 1 |
| MutS-MutL microscopic dissociation distance | xd | 1 bp |
| MutS-MutL macroscopic dissociation distance | xM | 1000 bp |
| Number of searches | ns | 3–10 |
The reason that the values of these parameters must be calculated or estimated rather than be measured directly is that the spatial resolution of the experiment is diffraction limited. Since the wavelength of visible light is on the order of hundreds of nm and the protein footprints are on the order of a few nm, the proteins interact on scales below the spatial sensitivity of the experiment. Importantly, this implies that the clamps can appear to be associated with each other in the experiment, when they are closer than the spatial resolution of the experiment, even though they may or may not be in actual physical contact. In contrast, in our model we define the associated state as the state in which the diffusion of the clamps is coupled, and the clamps have undergone some conformational change that allows them to interact more closely with the backbone and thus changes their diffusion rate. The dissociated state is the state in which the clamps are diffusing independently of each other. To avoid confusion, we will thus for the purposes of describing the calculation of model parameters from experimental observables denote the state in which the clamps are physically associated as “microscopically associated,” the state in which the clamps are physically dissociated but close enough that their positions are indistinguishable within the resolution of the experiment as “proximate,” and the state in which the clamps are physically dissociated and far enough away that their positions are distinguishable as “macroscopically dissociated.” In addition, we use “macroscopically associated” to describe clamps that could be either “microscopically associated” or “proximate” and “microscopically dissociated” for clamps that could be either “proximate” or “macroscopically dissociated.”
1. Diffusion constants of individual clamps
Since diffusion is scale invariant, there is no reason to believe that the microscopic diffusion constants DS and DL of the individual clamps are different from their macroscopically measured values given in Table I. Rewriting the diffusion of two clamps of different diffusion constants in terms of relative and center-of-mass coordinate yields Drel = DS + DL for the diffusion of the relative coordinate and for the diffusion of the center-of-mass coordinate.
2. Association lifetime and complex diffusion constant
The experiment measures the lifetime τA,M and diffusion constant DSL,M of macroscopically associated clamps (see Table I). Since macroscopically associated clamps could be either microscopically associated or proximal, a macroscopic association event consists of a sequence of transitions between the microscopically associated state and the proximal state, where only after multiple excursions into the proximal state do the clamps finally reach a distance that can be resolved in the experiment and thus reach the macroscopically dissociated state. Thus, the macroscopically measured lifetime τA,M is an effective lifetime that integrates over many microscopic dissociation and re-association events, and the macroscopically measured diffusion constant DSL,M is a temporal average of the diffusion constant of microscopically associated clamps DSL,μ and the diffusion constant of the center of mass of individual clamps DCM during their excursions in the proximal state.
In Appendix C A, we explicitly calculate how the macroscopically measured lifetime τA,M that integrates over multiple microscopic dissociation and re-association events depends on the microscopic parameters of the model. Solving this dependence for the microscopic association time yields
| (14) |
where pA is the probability that adjacent MutS and MutL clamps will associate, and ⟨NA⟩ = xM/xd is the number of times the clamps are in a microscopically adjacent state (making microscopic association possible) in a single macroscopic association. xd and xM are the microscopic and macroscopic association distances, respectively, so xd ≪ xM. The approximation in the second line of Eq. (14) holds for our specific values of the parameters as s and τA,M ≈ 30 s. It implies that the time spent in the proximal state has a negligible contribution to the macroscopic association time due to the speed of the dissociated diffusion, even though the fact that a macroscopic association event consists of multiple microscopic association events is relevant, as evinced by the prefactor [(⟨NA⟩ − 1)pA + 1]−1. Accordingly (see Appendix C B), the excursions into the proximal state do not have a significant impact on the diffusion constant either due to their short durations. Thus,
| (15) |
3. Distance from the nearest hemimethylated site
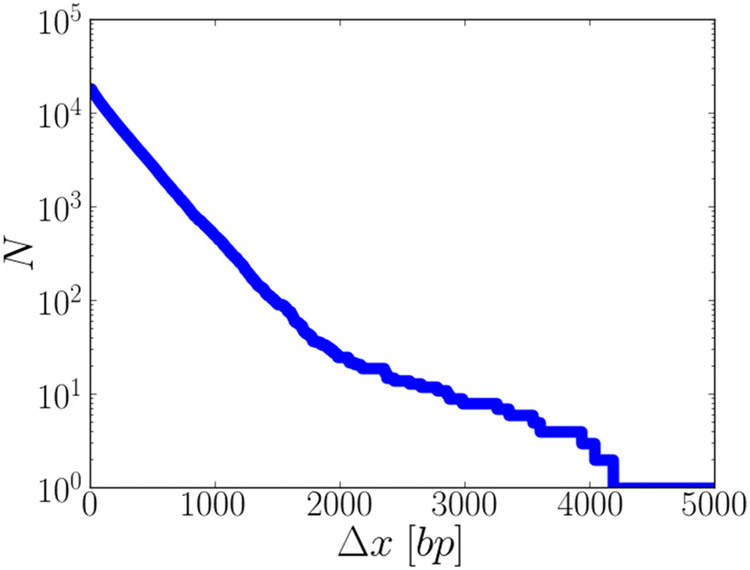
In E. coli, hemimethylation occurs at GATC sites [23-25]. Thus, the distance from a random location in the genome to the nearest hemimethylated site is governed by the distance distribution of adjacent GATC sites, shown in Fig. 2 for the genome of E. coli K-12 MG1655, NCBI RefSeq assembly: GCF_000005845.2. While in 90% of the cases, the distance between neighboring GATC sites is 500 bp or less, the largest distances between adjacent GATC sites reach all the way to 4960 bp. Since the ability to repair mismatches in the genome should depend on being able to identify the closest hemimethylated site even in the worst case scenario of being right in the middle of the two furthest separated GATC sites, we will report search probabilities over a range of xmeth = 500–3000 bp.
FIG. 2.
Cumulative distribution of hemimethylated site distances in the E. coli genome. For each separation (in base pairs) on the horizontal axis, the vertical axis shows the number of adjacent GATC sites in the E. coli K-12 MG1655, NCBI RefSeq assembly GCF_000005845.2 genome with at least that separation. The largest separation between any two GATC sites in the E. coli genome is 4960 bp.
4. Total search time
The search continues until either MutS or MutL dissociates from the DNA. Since the experimentally determined MutS association lifetime τS = 185 ± 35 s is much shorter than the experimentally determined MutL association lifetime τL = 850 ± 150 s, the search time is limited by the MutS association lifetime and thus ts ≈ τS.
5. Dissociation distances, association probability, and number of searches
Unlike the microscopic association lifetime, microscopic diffusion constants, and the distance from hemimethylated sites, the dissociation distances xd and xM, the association probability pA, and the number of searches ns are not determined by experimental observables, and thus cannot be calculated directly. Physical arguments, however, allow the estimation of xd and xM. In particular, the microscopic dissociation distance, i.e., the distance at which the clamps can be considered as independent, is on the order of xd ≈ 1 bp due to the base pair periodicity of the dsDNA free-energy landscape. The macroscopic dissociation distance, i.e., the distance at which two clamps can be resolved in the experiment as being independent, is determined by the diffraction limit and is expected to be about half the wavelength of the fluorescence. For one red and one green fluorophore, this distance is xM ≈ 300 nm ≈ 1000 bp.
Similar physical arguments are unable to provide an estimate for the association probability pA, but arguments can be made to set limits on this parameter. As a probability, the upper limit on pA is evidently 1. Approximation of a lower limit is made possible by the assumption that pA ⩾ Passoc, soln, where Passoc, soln is the probability that a MutL in solution colliding with a DNA-bound MutS will associate. This assumption is plausible since there is only one dimension (namely, rotation around the DNA) in which MutS and MutL clamps already associated with the DNA must align in order to associate with each other, rather than the three dimensions that must align when MutL is not already associated with the DNA. This assumption combined with published experimental results independent of the experiments in Ref. [3] suggests that the association probability should be greater than 0.001 (see Appendix D), i.e.,
| (16) |
In Appendix E we show that the successful-search probability is not very sensitive to the choices of xd, xM, or pA.
Finally, while experiments by Acharya et al. [26], Graham et al. [27], and Hombauer et al. [28] suggest that the DNA mismatch repair process involves multiple MutS-MutL searches for the hemimethylated site, the number of searches in vivo is not well known. We therefore perform this calculation with ns = 3 and ns = 10 to approximate this effect.
V. DISSOCIATIVE SEARCH PERFORMANCE
In this section we systematically compare the success probability of the dissociative search mechanism defined in Eq. (1) with that of a nondissociative search , defined in Eq. (6). The goal is to determine if the dissociative search observed in the experiments by Liu et al. [3] confers an evolutionary advantage of increased success probability over the simpler nondissociative search. The successful-search probability of the dissociative search is calculated numerically using the ADESS approach presented in Sec. IV B 1, while the successful-search probability of the nondissociative search is given analytically by Eq. (5).
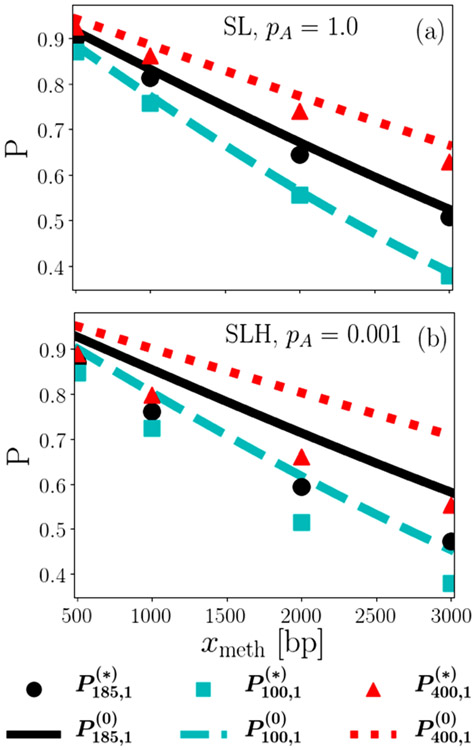
A. Dissociative and nondissociative searches result in similar single-search efficiency for experimental diffusion constants
To obtain an initial intuition about the behavior of the search probabilities, we first look at the single search (ns = 1) probabilities at the experimentally determined values of the diffusion constants. Figure 3 shows the successful-search probability of the dissociative search and of the nondissociative search as a function of distance xmeth from the hemimethylated site. Here, the subscript ts indicates the search cutoff time in seconds, and the subscript 1 indicates that the probability indicated is the success probability for only a single trial. Probabilities are shown for various search times ts within roughly a factor of two from the experimental value of 185 s in both directions. The figure presents results for diffusion constants corresponding to the case where MutH is not associated with MutL and pA = 1 in Fig. 3(a) and for diffusion constants corresponding to the case where MutH is associated with MutL and pA = 0.001 in Fig. 3(b). These are chosen as the two extremes in terms of the differences between dissociative and nondissociative searches, as the results for MutH parameters at pA = 0.001 and for non-MutH parameters at pA = 1 are in between the two cases shown.
FIG. 3.
Preliminary results indicate neither advantage nor disadvantage conferred by dissociative search, but that both are effective in locating the HMS. In this figure, successful-search probabilities of dissociative and nondissociative single searches are plotted as a function of distance xmeth from the hemimethylated site for different search times, indicated by the first subscript. Nondissociative search results are plotted as continuous lines (superscript 0), whereas dissociative search results are plotted using discrete symbols (superscript *). Results in panel (a) use experimental parameters in the case where MutH is not associated with MutL (SL) and the upper limit pA = 1 and (b) when MuH is associated with MutL (SLH) and the lower limit pA = 0.001. The statistical uncertainty is smaller than the size of the symbols.
Surprisingly, the nondissociative search mechanism somewhat, but systematically, outperforms the dissociative mechanism for this choice of parameters, especially for the case of microscopic association probability pA = 0.001. In spite of these differences somewhat favoring the nondissociative search mechanism, both search mechanisms result in sizable successful-search probabilities of at least 0.4 for all parameter values explored here and thus both are likely to support successful DNA mismatch repair, in particular because multiple searches further increase this probability.
B. Dissociative searches confer an advantage across a broad range of diffusion constants under physiological conditions
In the crowded in vivo environment, diffusion is likely significantly slower (10–100 fold) than in vitro [29]. Additionally the diffusion constants, hemimethylated site distances, and association lifetimes of mismatch repair proteins may vary across organisms. In light of these observations, we next characterize the comparative effect of the dissociative search mechanism across a wide range of possible diffusion rates DS and DSL at a number of HMS distances xmeth. Although we only explicitly vary the diffusion rate and hemimethylated site distance, this can be seen as variation of the dimensionless combination on which the probability depends [see Eq. (5)]. Thus, we effectively study variations in association time ts as well as hemimethylated site distance xmeth and diffusion rate.
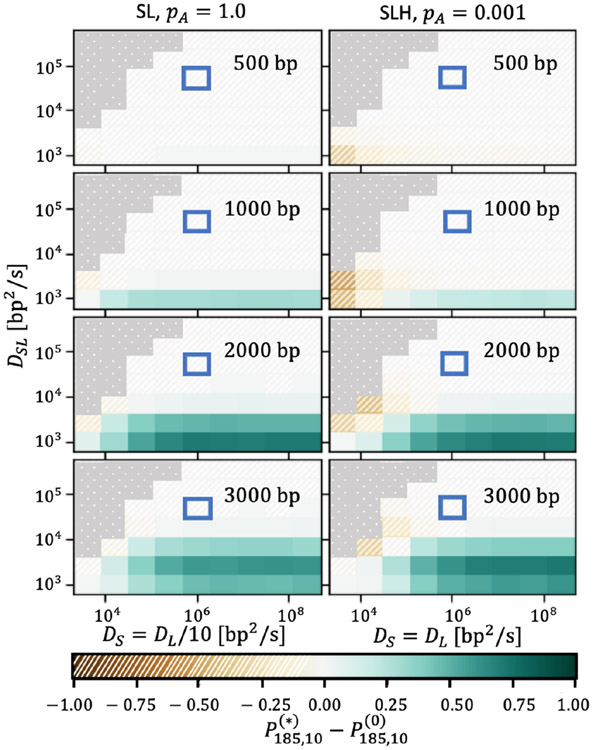
To show the efficacy of the dissociative search mechanism in the scan described above, we calculate and plot the difference between the dissociative overall search probability and the nondissociative overall search probability, given by
| (17) |
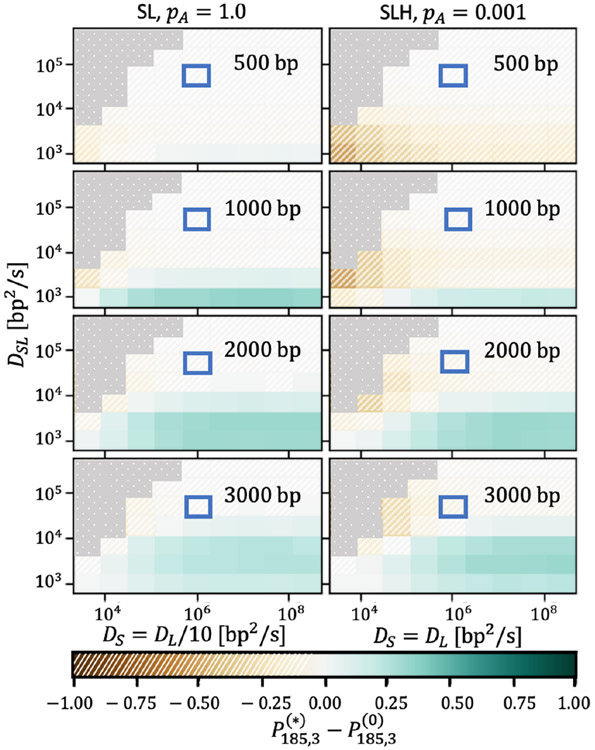
in Figs. 4 (for ns = 3 searches) and 5 (for ns = 10 searches). Positive values of δPts,ns (which correspond to a dissociative mechanism advantage) are shown in solid green, whereas negative values of δPts,ns (which correspond to a dissociative mechanism disadvantage) are shown in hatched brown. Regions in which DSL > DS are blocked out in dotted gray, since these regions are physically unrealistic (the searching state is slower because it must interact more frequently with the DNA).
FIG. 4.
The dissociative search mechanism is advantageous over a broad range of diffusion constants (solid green regions). The MutS-MutL diffusion rate DSL is varied on the vertical axis, and individual MutS diffusion rate DS is varied on the horizontal axis. The color scale indicates the absolute difference between the ADESS dissociative and analytic nondissociative probabilities δP185,3 for ns = 3 searches with a ts = 185 s cutoff time. Regions where δP185,3 < 0 are hatched and brown, while regions with δP185,3 > 0 are solid and green. In the left column, DL = 10DS (appropriate in the absence of MutH) with pA = 1.0, while in the right column, DL = DS (appropriate in the presence of MutH) with pA = 0.001. These columns represent the two extremes in terms of δP185,3, as the results for MutH parameters at pA = 0.001 and for non-MutH parameters at pA = 1 are in between the two cases shown. The square outlined in blue indicates the order of magnitude of experimental diffusion constants, and the regions of the coefficient space such that the diffusion of the “slow” searching state is faster than that of the “fast” state (that is, DSL > DS) are blocked out in dotted gray, since these regions are nonphysical. The hemimethylated site distances xmeth are increased as one moves down the figure vertically, and are indicated in the upper-right corner of each panel.
FIG. 5.
The dissociative search mechanism is advantageous over a broad range of diffusion constants (solid green regions). The MutS-MutL diffusion rate DSL is varied on the vertical axis, and individual MutS diffusion rate DS is varied on the horizontal axis. The color scale indicates the absolute difference between the ADESS dissociative and analytic nondissociative probabilities δP185,10 for ns = 10 searches with a ts = 185 s cutoff time. Regions where δP185,10 < 0 are hatched and brown, while regions with δP185,10 > 0 are solid and green. In the left column DL = 10DS (appropriate in the absence of MutH) with pA = 1.0, while in the right column DL = DS (appropriate in the presence of MutH) with pA = 0.001. These columns represent the two extremes in terms of δP185,10, because the results for MutH parameters at pA = 0.001 and for non-MutH parameters at pA = 1 are in between the two cases shown. The square outlined in blue indicates order of magnitude of experimental diffusion constants, and the regions of the coefficient space such that the diffusion of the “slow” searching state is faster than that of the “fast” state (that is, DSL > DS) are blocked out in dotted gray, since these regions are nonphysical. The hemimethylated site distances xmeth are increased as one moves down the figure vertically and are indicated in the upper-right corner of each panel.
Overall, Figs. 4 and 5 demonstrate that there is a much broader range of diffusion constants, and therefore hemimethylated site distances and association times, for which the dissociative search mechanism is beneficial for mismatch repair hemimethylated site searches as compared with pure diffusion (indicated by the prevalence of solid green regions in these figures). For ten searches, the absolute difference in probability approaches δP185s,10 = 1 (dark green) for the cases in which dissociation is most favorable, whereas for three searches the maximum difference in probability is more modest, with δP185s,3 ≈ 0.5. The case with three searches, however, exhibits a larger regime in which the dissociation mechanism is meaningfully beneficial. Furthermore, there are comparatively small regions of physically realistic parameter space in which the dissociative mechanism is significantly harmful compared with pure diffusion (hatched brown regions). The addition of MutH, the effect of which is shown in the rightmost columns, does not significantly impact these results, although it does slightly decrease the efficacy of the dissociative mechanism.
These results suggest that the dissociative mechanism may be evolutionarily conserved due to its beneficial effect on hemimethylated site searches, as evinced by largely positive values of δPts,ns in these scans. We also note that the dissociative mechanism is particularly favorable at low values of DSL and large xmeth, where the purely diffusive search is less likely to succeed. We therefore speculate that this search mechanism may act as insurance against cases in which the hemimethylated site is difficult to locate.
VI. CONCLUSIONS
Experiments by Liu et al. [3] observed repeated protein-protein association and dissociation between MutS and MutL sliding clamps involved in identification of a hemimethylated site during DNA mismatch repair in E. coli. This naturally raises the question of whether locally searching the DNA in the MutS-MutL associated state and then quickly diffusing along the DNA to a different location when dissociated (i.e., independent MutS and MutL) actually provides an advantage to the search process. Here, we model the dissociative search process, calculate the probability that searching DNA mismatch repair proteins successfully locate the hemimethylated site, and compare the success rate of this dissociative search to the success rate of a simple diffusive search. We find that both search mechanisms are highly efficient for the majority of observed hemimethylated site distances at measured in vitro diffusion rates. Perhaps somewhat surprisingly, there is a slight disadvantage in terms of search probability conferred by the dissociative search mechanism for searches at these in vitro rates. We note, however, that there may be variation in diffusion rate, association lifetime, and hemimethylated site distance among different organisms and that it has been shown that in vivo diffusion can be slower than in vitro diffusion by one or two orders of magnitude [29]. Accordingly, we studied the effect of the dissociative search mechanism across a large range of the parameter space of diffusion rates, association lifetimes, and hemimethylated site distances and found that the dissociative mechanism is either neutral or favorable in most cases. Interestingly, we find the most significant advantages of the dissociative search in the parameter regime where the overall search probabilities in the absence of protein-protein dissociation are small. The dissociative search mechanism may therefore function as an insurance mechanism. This suggests that there is an evolutionary advantage conferred by the dissociative search mechanism.
We note, however, that, in addition to its role in the search for a hemimethylated site, MutL acts as a processivity factor for the DNA helicase UvrD, resulting in the excision that is necessary for the progression MMR process [30]. It therefore could be the case that the observed dissociative mechanism is evolutionarily preferred because the dissociation steps allow MutS to load multiple MutL proteins onto the strand, aiding in excision. This alternative hypothesis would be strengthened if further work determines that in vivo search efficiency is not increased by the dissociative mechanism, although it is also possible that the dissociative mechanism serves a dual purpose: both increasing search efficiency and loading multiple MutL proteins onto the DNA strand.
A. Mismatch repair is mathematically distinct from transcription factor binding site searches
Having described the MMR search process mathematically, it is instructive to compare it to other biological search processes that have been mathematically characterized. The closest such comparison is likely that of a transcription factor (TF) searching for its DNA promoter site. While this search is different from the one we consider in that it has a three-dimensional mode, it also consists of a slow one-dimensional diffusion mode that is capable of searching the DNA as well as a fast one-dimensional diffusion mode that cannot search the DNA [13,14]. One could ask, therefore, whether the MMR search is simply a special case of the TF search. However, we find that the rate of switching between fast and slow diffusion modes is qualitatively different. Reingruber, Holcman, and Cartailler model TF searches, in which the switching dynamics is Poissonian [13,14], while we find that, due to the requirement that MutS and MutL proteins must find each other due to random diffusion to enter the slow state, the transition from fast to slow in MMR follows a Lévy distribution [i.e., p(t) ~ t−2/3 exp (−1/t), see Eq. (11)]. The most important difference between these distributions is that the Lévy distribution is fat-tailed, which means that there are long-lived slow states that never switch back to fast states on the relevant timescales. For instance, Cartailler and Reingruber find that, in the absence of three-dimensional diffusion, the optimal search is one such that the average time spent in fast and slow searching states is the same. Since the mean of the fast-state duration in MMR diverges, it is not even possible in this case to achieve such a state. One could imagine requiring that the modal fast time be the same as the average slow time, but in MMR this would require a “fast” diffusion rate that is slower than the “slow” searching rate and is therefore clearly not optimal.
B. Simplifying assumptions suggest future directions
It is important to emphasize that our treatments of multiple searches and in vivo diffusion here are necessarily approximate. A more detailed treatment that accounts for the interactions between proteins that are initially involved in “separate” searches may be a fruitful avenue for future research: in principle the discrete base pair stepping simulation (discussed in Appendix B A) is capable of tracking more than two proteins, but the current computational cost is too high. Additionally, it is likely possible to expand the association and dissociation event stepping simulation to account for more than two proteins and the presence of other molecules on the DNA strand. In particular, the presence of other molecules on the DNA strand may provide a spatial constraint that prevents the occurrence of the of long-lived dissociation events that decrease the efficiency of the dissociative mechanism. Additionally, the association lifetimes of MutS and MutL suggest that there are likely about five MutL proteins on the DNA for every MutS. Since this search is a one-dimensional process, however, each individual protein only interacts with its nearest neighbors. We therefore do not foresee a significant effect specifically related to the ratio of proteins on the DNA, simply that the presence of (any) additional molecules may decrease the prevalence of long-lived dissociation events and render the search more efficient.
Another assumption that we make is that the first encounter of a MutS-MutL complex with a hemimethylated site results in its recognition followed by an incision. If recognition of the hemimethylated site is stochastic itself, this will also reduce the overall search probability. Incorporating this effect into our approach and quantifying its consequences on the search probabilities of the dissociative and nondissociative searches will be an interesting direction of future research.
A further potential avenue of study is the effect of a more physiological environment on the diffusion constants of the proteins. We note that the in vivo diffusion constants are likely to be smaller than the measured in vitro coefficients, but are not able to quantitatively predict the magnitude of this decrease. A study that determines the actual in vivo diffusion constants of mismatch repair proteins could therefore be very useful. Similarly, determination of diffusion constants in systems other than E. coli would be interesting.
C. Mathematical framework is likely applicable to other biological processes
Beyond describing the specifics of the MutS-MutL search process, our approach here is likely to be applicable to other diffusive processes along DNA in biology. For instance, Zessin et al. observe a fast and slow diffusion rate of proliferating cell nuclear antigen (PCNA), which is a eukaryotic protein similar to a β clamp that also forms a clamp structure during association with DNA [31]. Eukaryotes also exhibit three homologs to both MutS and MutL [6], combinations of which are likely to result in a variety of association, dissociation, and diffusion parameters. In this case, the broad parameter space characterized by our analysis may provide insight into MMR in many organisms.
Despite the work still necessary to fully understand the diffusive search process in DNA mismatch repair, we provide a broad characterization of the observed dissociative search mechanism along with a robust analytical and computational framework with which to study diffusion and interaction of protein clamps in DNA mismatch repair that can provide the basis for generalization to other sliding clamp systems in biology.
ACKNOWLEDGMENTS
This material is based upon work supported by the National Science Foundation under Grant No. DMR-1719316 to R.B. and by the National Institutes of Health under Grants No. GM129764 and No. CA067007 to R.F.
Appendix
APPENDIX A: TIME AND LOCATION OF RE-ASSOCIATION
In this Appendix we derive the probability densities for the time to re-association and the re-association location of two clamps once they have disassociated from each other. These distributions are used in the ADESS approach to update the time and position after a microscopic excursion of the clamps.
A. Independent diffusion of two sliding clamps
While the two clamps are diffusing independently, the state of the system is given by positions xS and xL of the MutS and the MutL clamp along the DNA, respectively. The joint probability distribution for the two clamps follows the diffusion equation
| (A1) |
By analogy to the Schrödinger equation for a two-body quantum-mechanical problem, this equation can be rewritten in terms of relative and center-of-mass coordinates. In particular, substituting
| (A2) |
| (A3) |
| (A4) |
| (A5) |
yields
| (A6) |
which describes independent diffusion of the center of mass coordinate xCM with diffusion constant DCM and the relative coordinate xrel with diffusion constant Drel.
B. Time of re-association
In our model, the microscopic dissociation of the two clamps results in them being separated by the microscopic dissociation distance xd. Since relative and center-of-mass position diffuse independently, the time to reassociation is the time the freely diffusing relative coordinate xrel takes to reach xrel = 0 when starting at xrel = xd. This problem is mathematically equivalent to the problem of the associated clamps reaching the hemimethylated site xmeth after starting at some position x0. We can thus mirror image Eq. (4) [since xrel = 0 provides a left boundary for this problem while xmeth provided a right boundary in the context of Eq. (4)] and replace x0 with xd, xmeth with 0, and DSL with Drel to obtain
| (A7) |
for the probability that, at time t, the two clamps starting at an initial distance of xd have not yet touched. The probability density associated with the return of the distance between the two clamps to 0 from a distance of xd is therefore given by the negative derivative of this probability, i.e.,
| (A8) |
C. Location of re-association
Since at the time of reassociation the two clamps are at the same location, all we have to do to find the location of this event is to follow the motion of the center-of-mass coordinate xCM during the excursion. Since this is a free diffusion, the probability density for the location of the meeting point x of the two clamps after a time t given that they dissociated at some location x0 is
| (A9) |
APPENDIX B: VALIDATION OF ADESS APPROACH AND CONTINUUM APPROXIMATION VIA DISCRETE BASE PAIR STEPPING SIMULATION
In this Appendix, we discuss the base pair stepping simulation (BPSS), which is used to validate the ADESS. In particular, it confirms that discrete and continuous calculations agree. We also show that results are not sensitive to factor-of-two changes in the estimated parameter.
A. Base pair stepping simulation
This simulation keeps track of the states of the system and uses Daniel Gillespie’s “stochastic simulation” algorithm to transition between states [22]. Briefly, each simulation state consists of an either dissociated or associated MutS and MutL, as well as their position(s) along a DNA strand. Transitions between states occur at rates determined by the microscopic parameters, which allow us to track the timing of each state relative to the beginning of the simulation.
The allowed transitions are as follows:
i. For the dissociated state with MutS and MutL adjacent:
(a) MutS moves away from MutL with rate , where xstep = 1 bp is the simulation spatial step size;
(b) MutL moves away from MutS with rate ;
(c) MutS and MutL form an associated complex with rate consistent with pA, in particular . with MutS and MutL spatially separated:
(a) MutS moves away from MutL with rate ;
(b) MutL moves away from MutS with rate ;
(c) MutS moves toward MutL with rate ;
(d) MutL moves toward MutS with rate .
ii. For the associated state:
(a) Move left or right with rate each;
(b) Dissociate with rate kD = 1/τA,μ. After dissociation, the bases are placed 1 bp apart. This is achieved by moving one protein by 1 bp away from the last complex position and leaving the other protein at the last complex position. MutS is moved with probability kS/(kS + kL), and MutL is moved with probability kL/(kS + kL).
To calculate observables with this simulation, we start with the proteins in an associated state at position 0 and track their positions along the strand as a function of time. Assuming that the associated complex searches every position that it passes, the fraction of simulations in which the complex has passed a specific position in the given amount of time is the overall successful-search probability at that position, as in Fig. 6. Additionally, we can use the distance that separates dissociated MutS and MutL clamps at a given time to calculate the macroscopic association time. In particular, the time at which the distance between the clamps first reaches xM is recorded for each simulation and then the distribution of these times is used to calculate a decay constant, as in Fig. 7 below.
B. Agreement with base pair stepping simulation
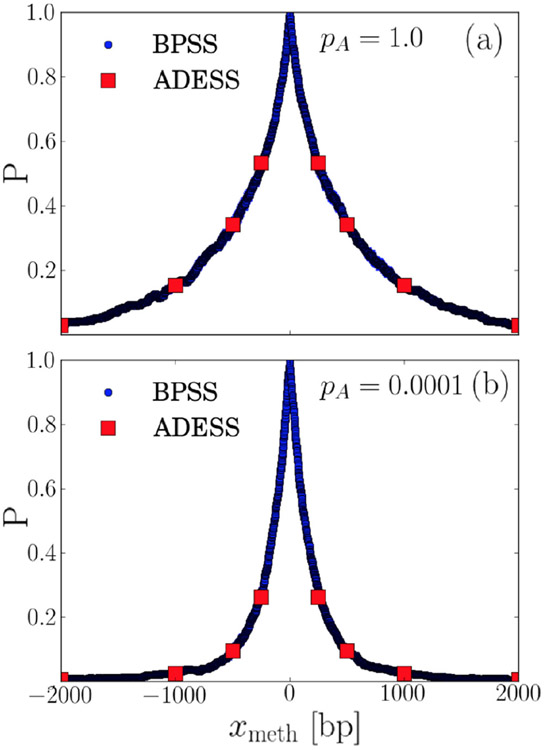
To validate the ADESS approach and the microscopic parameter calculation, we compare ADESS to the more time consuming BPSS. Since the BPSS approach follows every single diffusion step of the clamps, it becomes computationally unfeasible to obtain sufficient statistics for realistic values of the diffusion constants and we thus perform this validation for DS = 104 bp2/s, DSL = 103 bp2/s, and DL = 105 bp2/s, which are each about two orders of magnitude smaller than the actual experimentally determined diffusion constants. Figure 6 compares the search probability calculated using the BPSS approach and the search probability calculated using the ADESS approach and finds them to yield identical results within statistical error for the largest possible value pA = 1 in Fig. 6(a) and the absolutely smallest possible value of pA = 10−4 considered in Appendix D in Fig. 6(b).
FIG. 6.
Comparison between successful-search probabilities for ts = 185 s and ns = 1 calculated using the BPSS (small blue circles) and ADESS (large red squares) validates the ADESS approach. Panel (a) is calculated with pA = 1 and panel (b) with pA = 10−4. The statistical uncertainty is smaller than the size of the symbols.
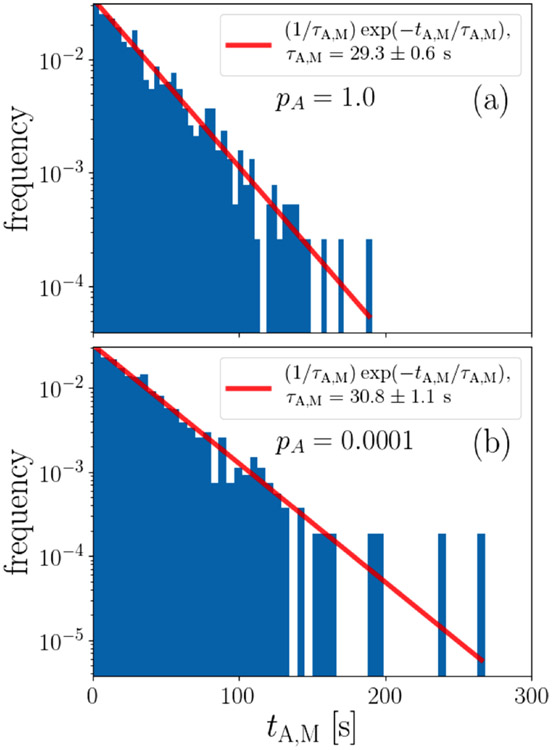
Additionally, the BPSS allows us to validate (Eq. 14) for the microscopic association lifetime τA,μ empirically. In particular, the BPSS approach lets us keep track of the distance between separate clamps and the times at which these distances occur. Using this feature, we calculate the time tA,M for which the clamps remain within the macroscopic association distance xM of each other, i.e., the time until they first reach the macroscopically dissociated state. Figure 7 shows histograms of this time to reach the macroscopically dissociated state calculated from simulations that use the microscopic association lifetime calculated via (Eq. 14). We find that these simulated distributions accurately reproduce the experimentally measured macroscopic association lifetime τA,M ≈ 30 ± 3 s (see Table I), indicating that (Eq. 14) correctly matches the microscopic association lifetime governing the multiple transitions between the microscopically associated and the proximal state to the macroscopic association lifetime observed in experiments.
FIG. 7.
Histogram of simulated macroscopic association times for (a) pA = 1 and (b) pA = 10−4 validates Eq. (14). The line is given by , where τA,M is the average of the simulated macroscopic association times. This line therefore demonstrates that the association time probability decays exponentially with a decay constant consistent with the macroscopic association lifetime of τA,M ≈ 30 ± 3 s measured experimentally in Ref. [3]. The reported standard error of the decay constant is calculated by dividing the simulated data into ten independent blocks and calculating the mean of each of them independently.
APPENDIX C: MICROSCOPIC PARAMETER CALCULATION
The following are the full calculations used to determine the microscopic protein dynamics from experimental observables. In particular, we calculate the microscopic diffusion constant DSL,μ and the microscopic association lifetime τA,μ. The calculations of PM and τ(x) closely follow Ref. [32], a web published early draft of Ref. [33].
A. MutS-MutL association lifetime
First, we calculate the microscopic association lifetime. Consider first the macroscopic association lifetime, which can be written as
| (C1) |
where NA is the number of times the clamps are microscopically adjacent during a single macroscopic association, pA is the probability of microscopic association given that the clamps are adjacent, τR is the average time to return to the adjacent state, and τM is the average time to reach a distance xM without returning to the adjacent state (i.e., the average time to macroscopic dissociation). Note that removing a single adjacent state from the factor multiplied by pA and multiplying it directly by τA,μ ensures that there is at least one microscopic association in every macroscopic association. This must be true physically, since different diffusion rates are observed during macroscopic association.
Consider NA for a complex starting in the aggregate state:
| (C2) |
where PM is the probability for a newly microscopically dissociated complex to go to xM. Thus,
| (C3) |
In order determine PM we first consider PM as a function of the distance between the clamps, which we will denote as x for the remainder of this section to avoid the more cumbersome notation of xrel used in the rest of the paper. Evaluation of this function at x = xd will give PM. [PM(x) will refer to the probability to go to xM from some position x without visiting 0, while PM ≡ PM(xd) refers to the probability to go to xM from xd.] Additionally, since the clamps diffuse with intermittent DNA contact, PM(x) will be calculated under the assumption that the distance between clamps diffuses continuously. This allows us to write
| (C4) |
and therefore
| (C5) |
with the boundary conditions
| (C6) |
The unique solution of this differential equation is
| (C7) |
and thus
| (C8) |
where xd is the separation of the clamps immediately following dissociation. Therefore, we conclude that
| (C9) |
To compute the microscopic association lifetime τA,μ from Eq. (C1), it is also necessary to compute the average return time τR and the average time τM to reach xM. To this end, consider the average time τ(x) for the distance between the clamps to reach either 0 or xM given that the starting distance is x:
| (C10) |
where tp(x) is the time for a path of length x and Pp(x) is the probability of such a path. Consideration of the effect of a single infinitesimal time step δt allows us to write
| (C11) |
Thus, division by the square of some small spatial step δx2 yields
| (C12) |
Therefore,
| (C13) |
where we write the right-hand side in terms of the diffusion constant Drel = DS + DL. The boundary conditions
| (C14) |
allow us to conclude
| (C15) |
We now write this quantity in terms of τR and τM as follows:
| (C16) |
Thus, substitution into Eq. (C1) yields
| (C17) |
Finally, we conclude
| (C18) |
where ⟨NA⟩ = xM/xd.
B. Microscopic diffusion constant
Having computed the microscopic association lifetime, we turn our attention to the microscopic diffusion constant. During microscopic association, the observable quantity, that is, the diffusion of the center of mass of the oscillating dissociative complex, is given by
| (C19) |
where DSL,μ and DCM are the microscopically associated and dissociated complex diffusion rates, respectively, and DM,SL is the measured, macroscopic diffusion rate of the complex. PA and PD are the probabilities that the clamps are associated and dissociated, respectively. As argued in Sec. A 1, . It follows that the quantity needed for the microscopic model, the microscopic diffusion constant, is given by
| (C20) |
Since DM,SL, DS, and DL are measured experimentally, we only need to write PA and PD in terms of observable quantities to obtain a value for DSL,μ. To do this, we observe that the probabilities that the proteins are microscopically associated and dissociated are given by the ratios of average time spent in an associated and dissociated state, respectively, divided by the sum of these times:
| (C21) |
| (C22) |
where τA,μ is the microscopic association time, and τR is the average time to return to the adjacent state. τA,μ is multiplied by the association probability pA because there are 1/pA returns with time τR for every microscopic association. Note that τM does not enter these equations. This is because the final walk from xrel = 0 to xM has only a minor influence on the experimentally measured diffusion rate as τM represents only the last s of the ≈30 s macroscopic association.
Equation (C16) gives an expression for τR in terms of τM, so in order to determine τR we must first compute τM. Fortunately, we can calculate τM in a way that is analogous to the calculation of τ(x) in the previous section. Going back to a discrete picture, during a random walk that results in a separation distance x = xM before reaching x = 0, the first step after dissociation is from x = xd to x = 2xd. Thus,
| (C23) |
where τxd,M(x) is the average time for the distance between the clamps to reach either xd or xM, and Nxd is the number of times the distance reaches xd before going to xM. Modifying the calculation of τ(x) with the appropriate boundary conditions
| (C24) |
we find
| (C25) |
which yields
| (C26) |
Similarly, ⟨Nxd⟩ can be computed in the same way that ⟨NA⟩ was found earlier. In particular,
| (C27) |
where Pxd,M is the probability that the distance goes to xM before xd from distance 2xd.
Using Eqs. (C4) and (C5) with boundary conditions
| (C28) |
we get
| (C29) |
Finally, since we assume that the walk starts at x = 2xd,
| (C30) |
Appropriate substitutions and algebraic manipulations yield
| (C31) |
with
| (C32) |
| (C33) |
where , for the specific values of the parameters and the approximation in the second line holds since Rx ≪ 1 and Rτ ≪ 1. For pA > 0.001 the correction δ(DCM − DSL,M) is ≈3 bp2/s ≈ 0.01% of DSL,M and even for the most extreme worst case value of pA = 10−4 considered in Appendix D we still find δ(DCM − DSL,M) is ≈50 bp2/s ≈ 0.1% of DSL,M.
Thus,
| (C34) |
APPENDIX D: APPROXIMATION OF LOWER LIMIT OF ASSOCIATION PROBABILITY
The lower limit of the association probability can be calculated under the assumption that pA ⩾ Passoc, soln, where Passoc, soln is the probability that a MutL in solution colliding with a DNA-bound MutS will associate. As discussed in the main text, it should be easier for MutL and MutS to bind when they are both already somewhat aligned by their formation of clamp structures on the DNA.
The association probability Passoc, soln is given by the ratio
| (D1) |
where kon, expt is the experimental rate at which MutL associates with MutS on DNA from solution, and kon, max is the rate at which MutS and MutL collide (e.g., the diffusion-limited rate).
We first focus on the diffusion-limited rate. The Smoluchowski equation yields an expression for the diffusion-limited rate constant for two uniform spheres [34]:
| (D2) |
where D is the relative diffusion constant and R is the reaction radius.
Manelyte et al. give the MutS Stokes radius as RS,S ≈ 3 nm [35], and Grilley et al. give the MutL Stoke radius as RS,L ≈ 6 nm [36]. Therefore R ≈ RS,S + RS,L ≈ 10 nm.
To determine the relative diffusion constant D, we use the measured MutS diffusion along the DNA strand, DS = 0.043 ± 0.016 μm2/s, and the Stokes-Einstein diffusion of MutL in water at room temperature, . Thus D ≈ 4 × 10−11 m2/s and the diffusion-limited on rate is
| (D3) |
We can now turn to the experimental on rate. Liu et al. do not measure this rate directly, but they do find the fraction FSL of an ensemble of DNAs on which MutS-MutL complexes associate in equilibrium to be high enough to perform the experiment, i.e., a significant fraction of their constructs shows association of a MutL at their experimental concentration of MutL [3]. We thus choose FSL = 0.1 as a conservative “worst case” estimate with FSL ≈ 1 more likely. This, along with the known MutS dissociation constant with DNA, Kd,S = 0.6 μM [26] and the measured MutL off rate koff,L ~ 1/τon,L ≈ 1/850 s can be used to estimate the desired on rate. The fraction of DNAs with MutS-MutL associated is given by
| (D4) |
and thus
| (D5) |
For the reported [L] ≈ 20 nM and [S] ≈ 10 nM,
| (D6) |
for the worst case estimate FSL = 0.1 and kon,L ≈ 106 M−1 s−1 for FSL = 1. Thus we conclude that
| (D7) |
and therefore
| (D8) |
which gets widened to 10−4 ⩽ pA ⩽ 1 in the worst case of FSL = 0.1.
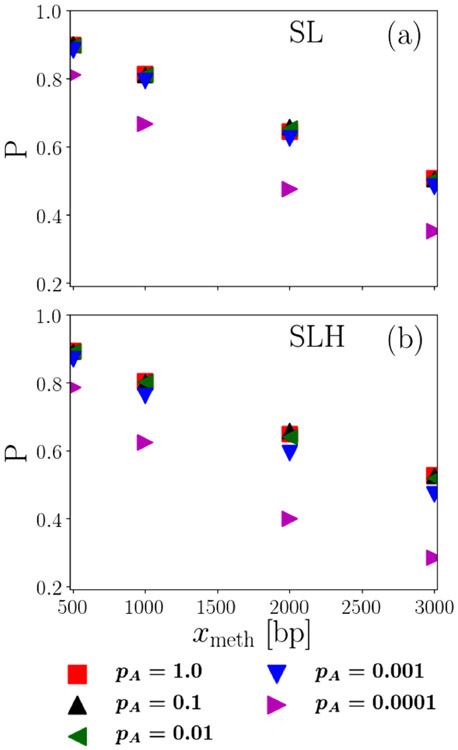
APPENDIX E: ROBUSTNESS OF RESULTS AGAINST VARIATION IN ESTIMATED PARAMETERS
Since several model parameters can only be estimated (see Table IV), we next determine how sensitive our model is to variations in these parameters. The parameter with the largest uncertainty is the microscopic association probability pA. To gauge the sensitivity of the model to this parameter, we hold all other parameters constant at their values given in Tables III and IV (both in the presence of and the absence of MutH) while varying the microscopic association probability over its entire potential range given in Appendix D, all the way down to the “worst case” lower limit of 10−4. Then, we numerically calculate the main observable of our model, namely the probability of a successful search, using the ADESS approach described in Sec. IV B 1.
Figure 8 shows the resulting search probabilities as a function of search distance xmeth for different values of the association probability pA. We note that the successful-search probability is largely independent of the microscopic association probability pA as long as pA ⩾ 0.001 and then drops significantly for pA = 10−4. Since a significantly reduced search probability would be evolutionarily disadvantageous, this provides further evidence that the range 0.001 ⩽ pA ⩽ 1 is more realistic compared with the extreme case of 10−4 ⩽ pA ⩽ 1. In the realistic range, the search probability is largely insensitive to the value of pA.
FIG. 8.
Search probability for ts = 185 s and ns = 1 searches as a function of search distance for different values of the association probability pA indicates that the search probability is not sensitive to variation of pA from 0.001 to 1 but that the search probability drops precipitously below 0.001. Panel (a) was calculated with non-MutH parameters, while panel (b) was calculated with MutH parameters. The statistical uncertainty is smaller than the size of the symbols.
We note that, naïvely, it appears unintuitive for the overall search probability to be so insensitive to three orders of magnitude of variation in the probability that two adjacent clamps successfully form a complex. However, we would like to point out that the microscopic association probability pA appears in Eq. (14) for the microscopic association lifetime. Thus, different values for the microscopic association probability pA yield different values for the microscopic association lifetime τA,μ to keep the macroscopic association lifetime τA,μ consistent with its measured value. The relative insensitivity of the search probability to the value of the microscopic association probability thus indicates that changes to the microscopic association lifetime compensate for the significant variation in microscopic association probabilities over three orders of magnitude. This also explains the change in behavior at pA = 0.001. Since the number of returns of the two clamps before final dissociation is ⟨NA⟩ = 1000 for our parameters, the denominator (⟨NA⟩ − 1)pA + 1 in Eq. (14) is larger than one for pA ⩾ 0.001 and asymptotes to one for pA < 0.001. Thus, for pA ⩾ 0.001 the clamps go through multiple reassociation events before final dissociation, the lifetime of which compensates for the change in the microscopic association probability pA. For pA < 0.001, the probability for even a single reassociation is becoming small and the microscopic association lifetime τA,μ is locked to the macroscopic association lifetime τA,M and is no longer able to compensate for changes in the association probability pA.
FIG. 9.
Comparison of successful-search probability for ns = 1 and ts = 185 s (i.e., ) for factor of two variations in the macroscopic and microscopic dissociation distances. This comparison reveals that these probabilities are not sensitive to the particular value chosen in these estimations. Panel (a) is calculated with pA = 1 and panel (b) with pA = 0.001. All results are shown for experimental parameters in the absence of MutH. The statistical uncertainty is smaller than the size of the symbols.
Similar to our analysis of the sensitivity of the association probability pA, we vary the values of the dissociation distances xd and xM by a factor of two in each direction to determine the sensitivity of the search probability to changes in these parameters at both limits of pA. Figure 9 demonstrates that, for pA = 1 and pA = 10−3, variation of the dissociation distances xd and xM by a factor of two only introduces a relative difference of up to 13%. We thus conclude that the difference between the approximate and exact values of the dissociation distances xd and xM will not significantly affect our results.
References
- [1].Martin-Lopez JV and Fishel R, The mechanism of mismatch repair and the functional analysis of mismatch repair defects in Lynch syndrome. Fam. Cancer 12, 159 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Reyes GX, Schmidt TT, Kolodner RD, and Hombauer H, New insights into the mechanism of DNA mismatch repair, Chromosoma 124, 443 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Liu J, Hanne J, Britton BM, Bennett J, Kim D, Lee Jong-Bong, and Fishel R, Cascading MutS and MutL sliding clamps control DNA diffusion to activate mismatch repair, Nature (London) 539, 583 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wang Jean Y. J. and Edelmann W, Mismatch repair proteins as sensors of alkylation DNA damage, Cancer Cell 9, 417 (2006). [DOI] [PubMed] [Google Scholar]
- [5].Iyer RR, Pluciennik A, Burdett V, and Modrich PL, DNA mismatch repair: Functions and mechanisms, Chem. Rev. (Washington, DC, U. S.) 106, 302 (2006). [DOI] [PubMed] [Google Scholar]
- [6].Fishel R, Mismatch repair, J. Biol. Chem 290, 26395 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].O’Donnell M, Kuriyan J, Kong XP, Stukenberg PT, and Onrust R, The sliding clamp of DNA polymerase III holoenzyme encircles DNA. Mol. Biol. Cell 3, 953 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Daitchman D, Greenblatt HM, and Levy Y, Diffusion of ring-shaped proteins along DNA: case study of sliding clamps, Nucleic Acids Res. 46, 5935 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Berg OG, Winter RB, and Von Hippel PH, Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory, Biochemistry 20, 6929 (1981). [DOI] [PubMed] [Google Scholar]
- [10].Lomholt MA, van den Broek B, Svenja-Marei Kalisch J, Wuite GJ, and Metzler R, Facilitated diffusion with DNA coiling, Proc. Natl. Acad. Sci. USA 106, 8204 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Bénichou O, Chevalier C, Meyer B, and Raphaël Voituriez, Facilitated Diffusion of Proteins on Chromatin, Phys. Rev. Lett 106, 038102 (2011). [DOI] [PubMed] [Google Scholar]
- [12].Givaty O and Levy Y, Protein sliding along DNA: Dynamics and structural characterization, J. Mol. Biol 385, 1087 (2009). [DOI] [PubMed] [Google Scholar]
- [13].Reingruber Jürgen and Holcman D, Transcription factor search for a DNA promoter in a three-state model, Phys. Rev. E 84, 020901(R) (2011). [DOI] [PubMed] [Google Scholar]
- [14].Cartailler J and Reingruber J, Facilitated diffusion framework for transcription factor search with conformational changes, Phys. Biol 12, 046012 (2015). [DOI] [PubMed] [Google Scholar]
- [15].Mirny L, Slutsky M, Wunderlich Z, Tafvizi A, Leith J, and Kosmrlj A, How a protein searches for its site on DNA: The mechanism of facilitated diffusion, J. Phys. A: Math. Theor 42, 434013 (2009). [Google Scholar]
- [16].Slutsky M and Mirny LA, Kinetics of protein-DNA interaction: Facilitated target location in sequence-dependent potential, Biophys. J 87, 4021 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Bauer M and Metzler R, Generalized facilitated diffusion model for dna-binding proteins with search and recognition states, Biophys. J 102, 2321 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhou Huan-Xiang, Rapid search for specific sites on DNA through conformational switch of nonspecifically bound proteins, Proc. Natl. Acad. Sci. U. S. A 108, 8651 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Kong X-P, Onrust R, O’Donnell M, and Kuriyan J, Three-dimensional structure of the β subunit of E. coli DNA polymerase III holoenzyme: A sliding DNA clamp, Cell (Cambridge, MA, U. S.) 69, 425 (1992). [DOI] [PubMed] [Google Scholar]
- [20].Redner S, A Guide to First-Passage Processes (Cambridge University Press, Cambridge, 2001). [Google Scholar]
- [21].Veksler A and Kolomeisky AB, Speed-selectivity paradox in the protein search for targets on DNA: Is it real or not? J. Phys. Chem. B 117, 12695 (2013). [DOI] [PubMed] [Google Scholar]
- [22].Gillespie DT, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem 81, 2340 (1977). [Google Scholar]
- [23].Lacks S and Greenberg B, Complementary specificity of restriction endonucleases of Diplococcus pneumoniae with respect to DNA methylation, J. Mol. Biol 114, 153 (1977). [DOI] [PubMed] [Google Scholar]
- [24].Hattman S, Brooks JE, and Masurekar M, Sequence specificity of the P1 modification methylase (MEco P1) and the DNA methylase (mEco dam) controlled by the Escherichia coli dam gene, J. Mol. Biol 126, 367 (1978). [DOI] [PubMed] [Google Scholar]
- [25].Geier GE and Modrich P, Recognition sequence of the dam methylase of Escherichia coli K12 and mode of cleavage of Dpn I endonuclease. J. Biol. Chem 254, 1408 (1979). [PubMed] [Google Scholar]
- [26].Acharya S, Foster PL, Brooks P, and Fishel R, The coordinated functions of the E. coli MutS and MutL proteins in mismatch repair, Mol. Cell 12, 233 (2003). [DOI] [PubMed] [Google Scholar]
- [27].Graham WJ, Putnam CD, Kolodner RD, et al. , The properties of Msh2–Msh6 ATP binding mutants suggest a signal amplification mechanism in DNA mismatch repair, J. Biol. Chem 293, 18055 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Hombauer H, Campbell CS, Smith CE, Desai A, and Kolodner RD, Visualization of eukaryotic DNA mismatch repair reveals distinct recognition and repair intermediates, Cell (Cambridge, MA, U. S.) 147, 1040 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Konopka MC, Shkel IA, Cayley S, Record MT, and Weisshaar JC, Crowding and confinement effects on protein diffusion in vivo, J. Bacteriol 188, 6115 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Liu J, Lee R, Britton BM, London JA, Yang K, Hanne J, Lee J-B, and Fishel R, MutL sliding clamps coordinate exonuclease-independent Escherichia coli mismatch repair, Nat. Commun 10, 5294 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zessin PJM, Sporbert A, and Heilemann M, PCNA appears in two populations of slow and fast diffusion with a constant ratio throughout S-phase in replicating mammalian cells, Sci. Rep 6, 18779 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Ben-Naim E, Krapivsky PL, and Redner S, “Random walk/diffusion,” http://physics.bu.edu/~redner/542/book/rw.pdf (2008), accessed: 2020-06-22. [Google Scholar]
- [33].Krapivsky P, Redner S, and Ben-Naim E, A Kinetic View of Statistical Physics, edited by Cambridge University Press (Cambridge University Press, Cambridge, 2010). [Google Scholar]
- [34].Smoluchowski MV, Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem 92U, 129 (1917). [Google Scholar]
- [35].Manelyte L, Urbanke C, Giron-Monzon L, and Friedhoff P, Structural and functional analysis of the MutS C-terminal tetramerization domain, Nucleic Acids Res. 34, 5270 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Grilley M, Welsh KM, Su SS, and Modrich P, Isolation and characterization of the Escherichia coli MutL gene product. J. Biol. Chem 264, 1000 (1989). [PubMed] [Google Scholar]