Cohort-Derived Machine Learning Models for Individual Prediction of Chronic Kidney Disease in People Living With Human Immunodeficiency Virus: A Prospective Multicenter Cohort Study

Abstract

Background

It is unclear whether data-driven machine learning models, which are trained on large epidemiological cohorts, may improve prediction of comorbidities in people living with human immunodeficiency virus (HIV).

Methods

In this proof-of-concept study, we included people living with HIV in the prospective Swiss HIV Cohort Study with a first estimated glomerular filtration rate (eGFR) >60 mL/minute/1.73 m² after 1 January 2002. Our primary outcome was chronic kidney disease (CKD)—defined as confirmed decrease in eGFR ≤60 mL/minute/1.73 m² over 3 months apart. We split the cohort data into a training set (80%), validation set (10%), and test set (10%), stratified for CKD status and follow-up length.

Results

Of 12 761 eligible individuals (median baseline eGFR, 103 mL/minute/1.73 m²), 1192 (9%) developed a CKD after a median of 8 years. We used 64 static and 502 time-changing variables: Across prediction horizons and algorithms and in contrast to expert-based standard models, most machine learning models achieved state-of-the-art predictive performances with areas under the receiver operating characteristic curve and precision recall curve ranging from 0.926 to 0.996 and from 0.631 to 0.956, respectively.

Conclusions

In people living with HIV, we observed state-of-the-art performances in forecasting individual CKD onsets with different machine learning algorithms.

In people living with HIV who participate in the Swiss HIV Cohort Study, we observed state-of-the-art performances in forecasting individual onsets of chronic kidney disease with different machine learning algorithms.

With the advent of combined antiretroviral therapy, human immunodeficiency virus (HIV)–related morbidity and mortality have continuously decreased—with people living with HIV (PLWH) having nowadays, under optimal conditions, an almost identical life expectancy to the general population [1–4]. As HIV infection has become a chronic condition, accurate prediction of primarily non-HIV-related comorbidities such as chronic kidney disease (CKD) have gained importance in the individualized care of PLWH [5].

As the occurrence of CKD and of other non-HIV-related chronic conditions may be influenced by hundreds of potentially interacting, static and time-changing factors across the healthcare continuum, data-rich and well-curated HIV cohorts may offer ideal conditions to develop machine learning models and to validate their usefulness to optimize personalized prevention and treatment strategies in PLWH. Cohort-based machine learning is an evolving field in digital epidemiology, which has the potential to improve decision support and underlying prediction models [6, 7]. Previous prediction models of CKD and of other multifactorial conditions may be limited, as it is challenging to account for complex interactions and to analyze high-dimensional datasets (ie, data collections with a multitude of variables) with standard regression models. Conversely, some machine learning prediction models have limited generalizability to other settings with intransparent predictions for single individuals [8].

In the present proof-of-concept study conducted in PLWH, we aimed to evaluate different machine learning algorithms and modeling strategies for individual CKD prediction to exemplify whether machine learning models can be readily trained in a high-dimensional cohort setting. The resulting machine learning prediction models of CKD onsets may become part of an integrated decision support tool for shared decision-making and personalization of prevention and treatment strategies in PLWH. In a wider context, our investigation may be helpful for current large-scale cohorts to assess the feasibility and challenges with cohort-based machine learning prediction.

METHODS

Swiss HIV Cohort Study

The Swiss HIV Cohort Study (SHCS; www.shcs.ch) is a nationwide, prospective multicenter cohort study with semiannual visits and blood collections with an enrollment of > 20 000 HIV-infected adults who live in Switzerland [9]. The SHCS is representative of the HIV epidemic in Switzerland [9]. A standardized protocol is used in the SHCS for data collection: Sociodemographic and clinical data are recorded at study entry, and various laboratory tests are routinely performed at registration. At each follow-up visit, extensive laboratory, clinical, and treatment data are recorded. Additional interim laboratory and clinical evaluations are recorded, if available. The SHCS is registered on the longitudinal study platform of the Swiss National Science Foundation (www.snf.ch/en/funding/programmes/longitudinal-studies).

For the training of pragmatic and individualized machine learning models, most SHCS variables have been used, but potentially identifying variables (including living/working situations), information on sexual behavior, variables recorded only within a short period, genetic/-omics data, and some metadata (eg, name of study nurse) were omitted as defined a priori in the study group and as discussed with a national representative of PLWH. Where applicable, we followed the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) and the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) statements when reporting our study results [10, 11]; furthermore, we used the reporting criteria developed by Luo et al [12].

Study Population and Definitions

After 1 January 2002, when calibrated creatinine measurements were incorporated into the SHCS, we included HIV-infected individuals aged ≥ 18 years with a baseline estimated glomerular filtration rate (eGFR) >60 mL/minute/1.73 m²—independent of antiretroviral treatment regimen/status—and at least 3 calibrated serum creatinine measurements before 10 October 2018. Individuals with a baseline eGFR ≤ 60 mL/minute/ 1.73 m², < 3 creatinine measurements, and/or < 3 months of follow-up were excluded.

We defined the baseline as the first creatinine measurement after 1 January 2002. We followed individuals from baseline until occurrence of CKD or the last recorded creatinine measurement, whichever came first. However, we used horizons of 3–12 months for machine learning prediction of CKD onset.

We defined CKD, our a priori primary outcome, as a confirmed (over 3 months apart) decrease in eGFR ≤ 60 mL/minute/1.73 m², in line with the Kidney Disease–Improving Global Outcomes (KDIGO) algorithm and previous large-scale investigations on CKD in PLWH [5, 13]. As a measure of kidney function, we calculated the eGFR using the well-established Chronic Kidney Disease Epidemiology Collaboration equation, which has been validated extensively in PLWH [14–17].

All participants in the SHCS provided informed consent and the study was approved by the ethical committees of the respective participating centers (Ethikkommission Nordwest und Zentralschweiz project number 2017-02252). We report deviations from the study protocol in the Supplementary Appendix.

Predictive Modeling

We trained a set of data-driven machine learning models (full models) to predict CKD events within prespecified prediction horizons—representing a classification problem, which relied on both static and irregularly sampled time and event series data. We applied the following 5 machine learning algorithms for CKD prediction with single patient visits as unit of observation and parameter tuning (selection) on the validation set:

• 1. Elastic net is a regularized, linear logistic regression method that includes both the lasso (L₁) and the ridge (L₂) penalty via a linear combination [18]. It optimizes the following objective: $\underset{\beta ,\lambda ,\nu }{max}\mathrm{l}\mathrm{o}\mathrm{g}\underset{i=1}{\sum ^N}\log p(y_i|x_i,{\mathrm{\beta }}_i)+\mathrm{\Lambda }{\left|\right|\mathit{\beta }\left|\right|}^2+\mathrm{\nu }{\left|\right|\mathit{\beta }\left|\right|}_1$ where $\{(x_1,y_1),(x_3,y_2),\dots ,(x_N,y_N)\}$ is the training dataset, and β, λ, and ν are the model parameters.

• 2. Random forest models [19] average a collection of de-correlated classification or regression trees, in which a prespecified number of trees are fitted—each on a separate bootstrap sample drawn with replacement from the training data. We describe the details of the algorithm in Supplementary Appendix Table 1.

• 3. Gradient boosting machine [20] is an ensemble approach that iteratively adds simple models to the ensemble such that in each iteration a new model is trained with respect to the updated error of the ensemble learned in the previous iteration. We describe the details of the respective training algorithm in Supplementary Appendix Table 2.

• 4. Multilayer perceptron [21] is a nonlinear machine learning approach—representing a feed-forward neural network with at least 3 fully connected layers. We used the rectified linear unit: $f\left(x\right)=max(0,x)$ as activation function.

• 5. Recurrent neural networks (RNNs) are artificial neural networks that use a directed graph to model the connections between the nodes and are thus directly applicable to temporal sequence data. We used the “long short term memory” architecture [22]. We describe the details of the respective training algorithm in Supplementary Appendix Table 3.

For comparison with data-driven machine learning models, we have manually built logistic regression models (short models) for the different prediction horizons—in analogy to the well-established full risk score model by Mocroft et al for prediction of CKD in PLWH [13]. We used the following predictors: HIV exposure through intravenous drug use (yes, no, or unknown), hepatitis C coinfection (yes or no), birth year, estimated glomerular filtration rate until day of prediction (normalized scale; modeled as described for the data-driven machine learning models), sex (male or female), CD4 cell count until day of prediction (normalized scale; modeled as described for the data-driven machine learning models), hypertension (yes, no, or unknown), prior cardiovascular disease (yes or no), and diabetes mellitus (yes or no). Our manually built logistic regression models use the 2 most recent measurements of the considered variables along with the summary statistics of all their previous measurements.

Dataset Representation

To train our machine learning models, we extracted the anonymized study data from the SHCS main database—comprising a vast collection of static and time-changing (dynamic) variables, which were often irregularly measured as part of the clinical routine. The RNN-based methods process sequences of inputs and can thus use the visit sequence directly. For the remaining machine learning methods, the input information for each individual is a concatenation of the information from the 2 last (most recent) hospital visits and the corresponding summary statistics (mean, median, maximum, standard deviation) from all previous visits. The visit sequence for each patient is derived from the considered observation period determined by the target prediction horizon, and the last (most recent) visits refer to these derived sequences. We describe the detailed data representation and missing value imputation strategy in the Supplementary Appendix.

Model Evaluation

To evaluate the performance of the different machine learning approaches and models, we split all study data into 3 subsets—namely, a training set, a validation set, and a test set. We created the validation and test sets by randomly sampling (without replacement) 10% of the study population. The sampling was stratified with respect to the follow-up length and CKD status—that is, 10% of individuals were at first randomly sampled from the group of individuals that have developed CKD and then 10% were randomly sampled from the group of the individuals that did not develop CKD. The remaining 80% of the individuals comprised the training set.

We applied each of the described machine learning methods to predict CKD events as a set of adjusted hyperparameters to deliver accurate predictions on unseen data. We performed the model selection/hyperparameter tuning process on the validation set. Finally, we evaluated the predictive performance of the best-performing model for each considered approach on the test set (reported in the Results). We considered 4 different evaluation scenarios, each with a different prediction horizon—namely, 90, 180, 270, and 365 days. The prediction horizon specifies how many days in advance we aimed to predict the occurrence of CKD where the time of diagnosis is determined by the second eGFR measurement of the CKD definition used.

Performance Measures

Due to the large CKD imbalance in our dataset (ie, most individuals did not develop CKD), the classification accuracy was not suitable to measure the models’ performance. Therefore, we calculated 5 well-established measures for the class imbalance scenario; namely, the F-score, precision (ie, positive predictive value), recall (ie, sensitivity), area under the receiver operating characteristic curve (ROC-AUC), and area under the precision recall curve (PR-AUC). The precision, recall, and F-score are defined as follows:

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}& {\displaystyle Precision=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}\\ & {\displaystyle Recall=\frac{TP}{TP+FN}}\\ & {\displaystyle F-score=\frac{2\cdot Precision\cdot Recall}{Precision+Recall}}\end{array}}\end{array}}$$

where TP denotes the true positives, FP denotes the false positives, FN denotes the false negatives, and positives refer to the minority class (in our case, individuals with CKD onset).

The precision recall curve is a plot of the recall vs the precision for all possible decision thresholds. As the precision and recall focus only on the correct prediction of the minority class (ie, CKD), the F-score and the PR-AUC reflect the model’s prediction quality for CKD events. The receiver operating characteristic curve is a widely used plot of the false-positive rate (the proportion of false positives out of all negatives) vs the true-positive rate (the proportion of true positives out of all positives) for all possible decision thresholds. The ROC-AUC thus illustrates the ranking ability in binary classification: An ROC-AUC of, for instance, 0.80 indicates that 80% of the predictions are correctly classified (for pairs of individuals with and without the endpoint). For model selection, we used the F-score for the RNN-based approaches and the log loss for the remaining approaches.

Due to the time-consuming model selection process, we performed all experiments and computed all relevant evaluation metrics for 1 training, validation and test split. We believe that our results reflect the predictive quality of the considered machine learning models, as our test set was fairly large.

RESULTS

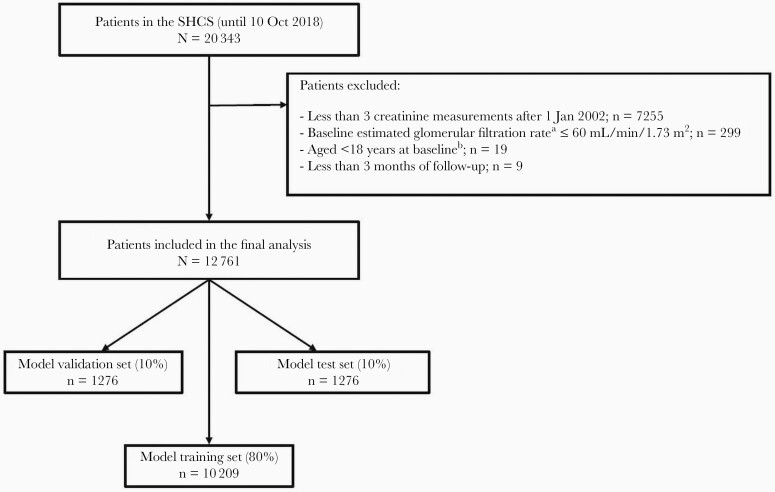
Within the study period, 12 761 individuals were included in the final analysis—with 10 209 (80%), 1276 (10%), and 1276 (10%) of participants’ prospectively collected cohort records contributing to the machine learning model training, validation, and test sets, respectively (Figure 1). We describe the main characteristics of the study population in Table 1: Overall, 1192 of 12 761 (9%) individuals developed CKD within the study period; the median follow-up in individuals with and without CKD was 8 years (interquartile range [IQR], 4–12 years) and 9 years (IQR, 4–15 years), respectively.

Figure 1.

Study population. ^a Calculated using the Chronic Kidney Disease Epidemiology Collaboration equation. ^b Baseline is defined as the first creatinine measurement after 1 January 2002. Abbreviation: SHCS, Swiss HIV Cohort Study.

Table 1.

Main Characteristics of the Study Population

Characteristic	All (N = 12 761)		Individuals Without CKDa (n = 11 569)		Individuals With CKDa (n = 1192)
Age, y, median (IQR)
Baseline	39	(33–46)	48	(33–45)	38	(40–57)
End of follow-up	49	(41–56)	56	(41–55)	49	(50–65)
Sex
Male	9156	(72)	8319	(72)	837	(70)
Female	3605	(28)	3250	(28)	355	(30)
Race/ethnicity
White	9964	(78)	8851	(77)	1113	(93)
Black	1825	(14)	1783	(15)	42	(4)
Hispanic	444	(3)	433	(4)	11	(1)
Asian	482	(4)	458	(4)	24	(2)
Other/unknown	46	(0.4)	44	(0.4)	2	(0.2)
IDU prior to HIV diagnosis
Yes	2287	(18)	2047	(18)	240	(20)
No	10 408	(82)	9465	(82)	943	(79)
Unknown	66	(0.005)	57	(0.005)	9	(0.008)
Ever smoked
Yes	7906	(62)	7158	(62)	748	(63)
No	4815	(38)	4372	(38)	443	(37)
Unknown	40	(0.3)	39	(0.3)	1	(0.1)
Hypertension
Yes	729	(5.7)	575	(5.7)	154	(12.9)
No	11 963	(94)	10 928	(94)	1035	(86.8)
Unknown	69	(0.5)	66	(0.5)	3	(0.3)
eGFRb, mL/min/1.73 m2, median (IQR)
Baseline	103	(90–114)	105	(92–115)	84	(73–96)
End of study	90	(75–104)	93	(80–106)	55	(50–58)
CD4 count, cells/µL, median (IQR)
Baseline	407	(252–597)	410	(255–600)	366	(228–561)
End of study	615	(426–830)	621	(437–839)	536	(362–759)
Viral load, copies/mL, median (IQR)
Baseline	883	(0–35 173)	1040	(0–36 000)	174	(0–23 459)
End of study	0	(0–0)	0	(0–0)	0	(0–0)
Hepatitis B
Positive	510	(4)	464	(4)	46	(4)
Negative	8208	(64)	7563	(65)	645	(54)
Unknown	4043	(32)	3542	(30)	501	(42)
Hepatitis C
Positive	1407	(11)	1272	(11)	135	(11)
Negative	10 022	(79)	9142	(79)	880	(74)
Unknown	1332	(10)	1155	(10)	177	(15)
Ever exposed to TDF
Baseline	2259	(18)	2100	(18)	159	(13)
End of study	9800	(77)	8814	(76)	986	(83)
Ever exposed to ATV/r
Baseline	481	(4)	441	(4)	40	(3)
End of study	3629	(28)	3135	(27)	494	(41)
Ever exposed to LPV/r
Baseline	1783	(14)	1577	(14)	206	(17)
End of study	4043	(32)	3604	(31)	439	(37)

Data are presented as No. (%) unless otherwise indicated. All values are presented at baseline if not stated otherwise. Baseline is defined as the first creatinine measurement after 1 January 2002. Some potential risk factors are not presented, as these variables were not recorded during the entire study period.

Abbreviations: ATV/r, ritonavir-boosted atazanavir; CKD, chronic kidney disease; eGFR, estimated glomerular filtration rate; HIV, human immunodeficiency virus, IDU, intravenous drug use; IQR, interquartile range; LPV/r, ritonavir-boosted lopinavir; TDF, tenofovir disoproxil fumarate.

^a Within the observation period.

^b Calculated using the Chronic Kidney Disease Epidemiology Collaboration equation.

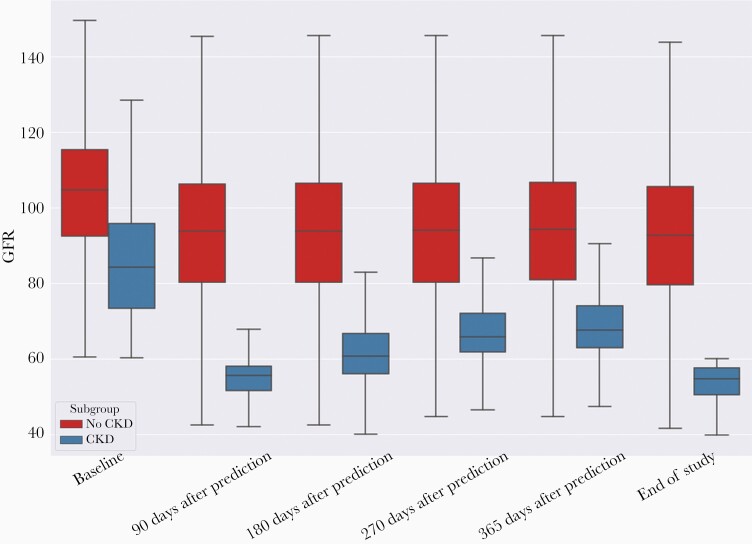
We describe the eGFR distribution of individuals with and without CKD in Figure 2: At baseline, eGFR distributions were partly overlapping between individuals with and without a subsequent CKD—with increased eGFRs of individuals without subsequent CKD onset across prediction horizons. For individuals with and without subsequent CKD, the overlap in eGFR distributions increased over longer prediction horizons. Overall, at day of prediction, the frequency of subsequent eGFR measurements within 365 days was slightly increased for individuals with a decreased eGFR of ≤ 60 mL/minute/1.73 m² compared to individuals with eGFRs > 60 mL/minute/1.73 m² (median, 1.8 [IQR, 1.0–2.5] vs 1.5 [IQR, 0.7–2.3] measurements per month, respectively).

Figure 2.

Overall glomerular filtration rates (GFRs; mL/minute/1.73 m²) in people living with human immunodeficiency virus (N = 12 761). This figure refers to the GFR at the last visit of the visit sequences in the considered observation period that is used to make predictions for 90 days, 180 days, 270 days, and 365 days ahead. The middle line and box indicate the median and interquartile range (IQR), respectively. Whiskers cover the 1.5 IQR. Abbreviations: CKD, chronic kidney disease; GFR, glomerular filtration rate.

We used 64 static and 502 dynamic variables for machine learning model development (full models)—including 28 demographic variables, 159 variables pertaining to treatment information, 93 laboratory variables, and 286 clinical variables. Across prediction horizons and machine learning algorithms, most models achieved similar predictive performances with ROC-AUCs and PR-AUCs ranging from 0.926 to 0.996 (ie, 92.6%–99.6% of predictions are correctly classified for pairs with and without CKD) and from 0.631 to 0.956, respectively (Table 2). In regard to ROC-AUCs and PR-AUCs, the machine learning models’ classification performance can be considered as excellent and moderate to excellent, respectively; the PR-AUCs were lower than the corresponding ROC-AUCs, as CKD events were relatively rare. For comparison with the full machine learning models, we have manually built logistic regression models (short models) based on well-established predictors (Table 2); in most cases, these short models had a worse predictive performance than the full machine learning models for CKD prediction.

Table 2.

Performance of Models to Predict Chronic Kidney Disease Across Different Prediction Horizons (n = 1276 Individuals; Test Set)

Algorithm	Visits Used	Imputation Method	F-score	Precision	Recall	ROC-AUC	PR-AUC
Prediction 90 d in advance
Data-driven machine learning models (full models)
Multilayer perceptron	Last 2 visitsa	Zero imputation	0.782	0.703	0.879	0.979	0.829
		Median forward	0.847	0.858	0.836	0.990	0.890
Gradient boosting	Last 2 visitsa	Zero imputation	0.874	0.852	0.897	0.994	0.933
		Median forward	0.890	0.875	0.905	0.996	0.956
Random forest	Last 2 visitsa	Zero imputation	0.583	0.942	0.422	0.995	0.943
		Median forward	0.836	0.918	0.767	0.994	0.931
Elastic net	Last 2 visitsa	Zero imputation	0.774	0.649	0.957	0.984	0.861
		Median forward	0.846	0.800	0.897	0.992	0.904
Bidirectional recurrent neural network	Full sequence; all previous visits	Zero imputation	0.818	0.786	0.853	0.984	0.874
		Median forward	0.856	0.819	0.897	0.989	0.916
Bidirectional attention recurrent neural network	Full sequence; all previous visits	Zero imputation	0.803	0.797	0.810	0.981	0.867
		Median forward	0.852	0.812	0.897	0.986	0.901
Manually built logistic regression model (short model)	Last 2 visitsa	None	0.807	0.689	0.974	0.990	0.881
Prediction 180 d in advance
Data-driven machine learning models (full models)
Multilayer perceptron	Last 2 visitsa	Zero imputation	0.719	0.716	0.722	0.960	0.777
		Median forward	0.718	0.798	0.652	0.963	0.803
Gradient boosting	Last 2 visitsa	Zero imputation	0.656	0.859	0.530	0.969	0.833
		Median forward	0.789	0.815	0.765	0.970	0.860
Random forest	Last 2 visitsa	Zero imputation	0.115	> 0.999	0.061	0.955	0.803
		Median forward	0.677	0.844	0.565	0.968	0.814
Elastic net	Last 2 visitsa	Zero imputation	0.698	0.629	0.783	0.952	0.768
		Median forward	0.767	0.777	0.757	0.959	0.787
Bidirectional recurrent neural network	Full sequence; all previous visits	Zero imputation	0.722	0.732	0.713	0.965	0.759
		Median forward	0.718	0.706	0.730	0.956	0.730
Bidirectional attention recurrent neural network	Full sequence; all previous visits	Zero imputation	0.694	0.720	0.670	0.963	0.755
		Median forward	0.721	0.712	0.730	0.945	0.792
Manually built logistic regression model (short model)	Last 2 visitsa	None	0.559	0.405	0.904	0.934	0.646
Prediction 270 d in advance
Data-driven machine learning models (full models)
Multilayer perceptron	Last 2 visitsa	Zero imputation	0.678	0.634	0.728	0.948	0.666
		Median forward	0.660	0.753	0.588	0.952	0.735
Gradient boosting	Last 2 visitsa	Zero imputation	0.290	0.833	0.175	0.944	0.702
		Median forward	0.689	0.745	0.640	0.957	0.728
Random forest	Last 2 visitsa	Zero imputation	0.068	> 0.999	0.035	0.928	0.661
		Median forward	0.578	0.788	0.456	0.955	0.739
Elastic net	Last 2 visitsa	Zero imputation	0.647	0.566	0.754	0.942	0.702
		Median forward	0.650	0.756	0.570	0.943	0.716
Bidirectional recurrent neural network	Full sequence; all previous visits	Zero imputation	0.605	0.581	0.632	0.938	0.649
		Median forward	0.661	0.632	0.693	0.940	0.737
Bidirectional attention recurrent neural network	Full sequence; all previous visits	Zero imputation	0.664	0.630	0.702	0.931	0.678
		Median forward	0.664	0.699	0.632	0.934	0.693
Manually built logistic regression model (short model)	Last 2 visitsa	None	0.453	0.310	0.842	0.893	0.504
Prediction 365 d in advance
Data-driven machine learning models (full models)
Multilayer perceptron	Last 2 visitsa	Zero imputation	0.641	0.691	0.598	0.950	0.699
		Median forward	0.628	0.776	0.527	0.950	0.722
Gradient boosting	Last 2 visitsa	Zero imputation	0.220	0.933	0.125	0.945	0.700
		Median forward	0.619	0.663	0.580	0.941	0.710
Random forest	Last 2 visitsa	Zero imputation	0.018	> 0.999	0.009	0.941	0.705
		Median forward	0.527	0.800	0.393	0.952	0.725
Elastic net	Last 2 visitsa	Zero imputation	0.588	0.626	0.554	0.938	0.673
		Median forward	0.512	0.808	0.375	0.935	0.681
Bidirectional recurrent neural network	Full sequence; all previous visits	Zero imputation	0.606	0.656	0.562	0.945	0.631
		Median forward	0.678	0.661	0.696	0.935	0.694
Bidirectional attention recurrent neural network	Full sequence; all previous visits	Zero imputation	0.600	0.643	0.562	0.928	0.632
		Median forward	0.633	0.554	0.738	0.926	0.692
Manually built logistic regression model (short model)	Last 2 visitsa	None	0.423	0.286	0.812	0.883	0.468

Abbreviations: PR-AUC; area under the precision-recall curve; ROC-AUC, area under the receiver operating characteristic curve.

^a And summary statistics from earlier visits during the target observation period, as detailed in the Methods.

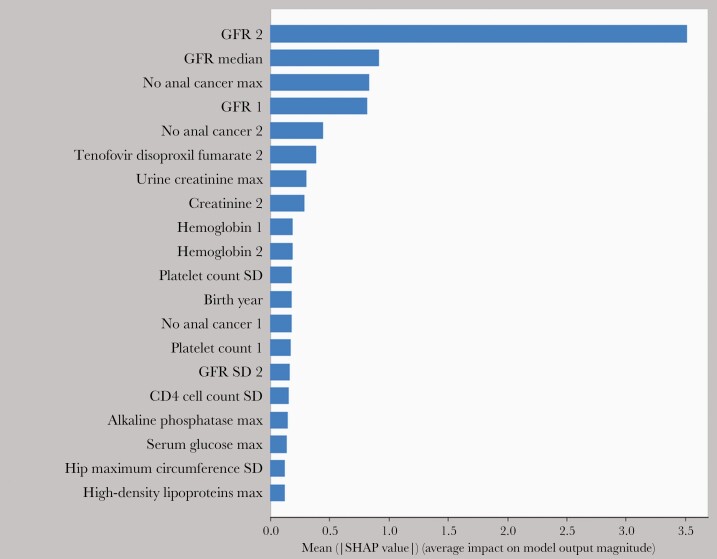
For illustrative purposes, we describe in Figure 3 the variable importance of the highest-scoring predictors for the gradient boosting model (prediction horizon, 180 days). Overall, the eGFR information was the most important marker for CKD prediction within 180 days. Across prediction horizons, we describe the gradient boosting models’ output and individual key predictors for 3 complex cases (Table 3); information on predicted outcome probabilities and the individual variable importance can be obtained for all applied machine learning algorithms to increase the interpretability/transparency of machine learning models and to potentially personalize prevention and treatment decisions.

Figure 3.

Variable importance plot of the gradient-boosting model; 180 days prediction horizon. This hypothesis-generating plot is for illustrative purposes only. Suffix “2” signifies that information from the latest visit was used, whereas suffix “1” signifies that information from the preceding (penultimate) visit was used, both specified with respect to the visit sequence in the considered observation period. The different statistics (median, standard deviation for numerical and maximum for the nominal variables) were computed for all the remaining visits in the target observed hospital visit sequence. The Shapley additive explanation values describe for each variable and individual the change in the expected model prediction when conditioning on that variable. Abbreviations: GFR, glomerular filtration rate; max, maximum; SD, standard deviation; SHAP, Shapley additive explanation.

Table 3.

How Would You Decide? Predicted and Observed Chronic Kidney Disease Outcomes Among 3 Complex Cases Across Prediction Horizons (Gradient-Boosting Model Estimates for Illustrative Purposes)

Individual	Predicted Outcome (CKD Probability)				Observed Outcome				Brief Interpretation and Key Predictor for Single Individuals
	Prediction Horizon, d				Prediction Horizon, d
	90	180	270	365	90	180	270	365
1	No CKD (0.34)	CKD (0.99)	CKD (0.51)	No CKD (0.01)	CKD	CKD	CKD	CKD	Platelet counts and various hematological parameters were strong predictors for CKD in this individual; however, this did not prevent false-negative predictions at 90 d and 365 d. There were dozens of moderate predictors of unclear clinical relevance: These factors have cancelled out at 365 d, as some were preventive and others suggested an incremental CKD risk. This example highlights that a clinician should review every machine learning prediction.
2	No CKD (0.18)	No CKD (0.00)	No CKD (0.00)	No CKD (0.00)	No CKD	No CKD	No CKD	No CKD	Absent cardiovascular risk factors (eg, smoking) were strong predictors against CKD development. However, there were dozens of moderate predictors (potential preventive factors and risk factors) of unclear clinical relevance. The low CKD probability score across prediction horizons, together with a careful review of medical records, may be an indication for clinicians that CKD development is unlikely.
3	No CKD (0.28)	CKD (0.71)	No CKD (0.00)	No CKD (0.02)	No CKD	No CKD	No CKD	No CKD	Cardiovascular risk factors (eg, high systolic blood pressure) and alcohol binge drinking increased the predicted CKD probability substantially—resulting in a false-positive prediction at 180 d; however, high preceding eGFR values were strong predictors against CKD across prediction horizons.

Abbreviations: CKD, chronic kidney disease; eGFR, estimated glomerular filtration rate.

The preparation and structuring of our datasets for machine learning training required 1 month of full-time work. The RNN-based model selection procedure was computing-intensive and required 20–30 hours on a high-performance computing cluster. The corresponding computing time for model selection among the remaining nonlinear approaches was in the order of 1 to 2 hours each. The final model training was fast for all machine learning methods except for the RNN-based methods, which required approximately 30 minutes. Obtaining individual predictions with a trained model was fast (a couple of minutes at most) for all machine learning methods.

DISCUSSION

In this large cohort study, we have developed pragmatic machine learning models to predict CKD onset and derive CKD development probabilities at the point of care in single individuals living with HIV. The respective machine learning models had a rather high predictive performance despite using prediction horizons of 3–12 months, which may decrease the precision (ie, positive predictive value) for CKD predictions. We measured our machine learning models’ predictive power by a set of well-established metrics to improve the comparability across models and studies. In contrast to previous studies, we have included a multitude of static and dynamic factors in our prediction models (data-driven machine learning modeling), which resulted mostly in improved performances for CKD prediction compared to manually built regression models based on a few predictor variables (Table 2) [13, 23]. Our proof-of-concept study provides a reality-check of the feasibility of machine learning prediction studies nested within large epidemiological cohorts.

To the best of our knowledge, this is the first study in which different machine learning models have been developed and internally validated in PLWH for individualized CKD prediction. Previous studies have developed standard regression-based models and scores (eg, by use of Poisson regression) for long-term CKD prediction, which had a good discrimination in external validation [5, 13, 23, 24]. For instance, as part of the Data Collection on Adverse Events of Anti-HIV Drugs study, a full and short risk score were developed to predict CKD over 5 years (but not for shorter prediction horizons)—with the short risk score demonstrating a relatively good predictive performance in external validation (ROC-AUC, 0.85) [13, 24]: These widely used full and short risk scores were developed in PLWH who were not previously exposed to a potentially nephrotoxic antiretroviral agent and included 9 and 6 predictor variables, respectively. In contrast to these 2 CKD risk scores, we used a set of machine learning algorithms and short-term prediction horizons—accounting for individuals with any antiretroviral treatment status and incorporating a variety of static and time-changing variables. These various short-term prediction horizons may be useful to differentiate acute and chronic kidney disease and to evaluate the dynamics and plausibility of machine learning predictions in single individuals over time. For individual CKD predictions, we achieved moderate to excellent discrimination with the given machine learning models. Therefore, our models can be investigated as part of a subsequent implementation study to assess the clinical utility and validity of the present machine learning models, and also for complex cases (Table 3).

Of interest, as illustrated in the variable importance plot of the gradient-boosting model (Figure 3), we observed a number of predictors that are well-established risk factors for CKD (eg, treatment with tenofovir disoproxil fumarate–containing regimens [25]) as well as proxy variables and markers, which may not have a direct effect on CKD development (eg, alkaline phosphatase). This observation highlights that predictive machine learning models may help to build novel causal hypotheses, which can be validated in subsequent causal studies. However, machine learning predictions and corresponding variable importance plots should not be used per se for causal inference, as it requires expert guidance and causal concepts.

While developing machine learning models for CKD prediction, we faced 2 main challenges. First, the preparation and structuring of the datasets for machine learning training was time-consuming, as real-world HIV cohort data include a multitude of static and dynamic data, which are often measured irregularly. Nonetheless, we believe that our data representation can be valuable for future machine learning investigations relying on HIV cohort databases. Second, the machine learning model training and selection was computing-intensive and required a high-performance computing cluster.

Our study has some limitations. First, our machine learning prediction models for CKD may not be generalizable to other healthcare settings and populations: Specifically, the coding practices and parameters may differ between HIV cohorts, which may complicate the application of the same machine learning prediction models across HIV cohorts. Therefore, we did not intend to externally validate our machine learning prediction models as part of this proof-of-concept study. Second, as we used short prediction horizons, target leakage (ie, models include information that is not yet available at the time of prediction) can result in biased and often too optimistic predictive performances. To safeguard against target leakage, we included only variables that were known at the prediction day [26]. However, we cannot exclude the possibility that a few parameters in our machine learning models (eg, laboratory values) would be reported to the treating physician and/or clinical decision support tool some minutes or hours after a potential CKD prediction. Third, follow-up studies should consider including proteinuria in the CKD outcome definition to capture CKD at earlier stages. With the present models, we are unable to predict proteinuria. Fourth, a higher eGFR threshold > 60 mL/minute/1.73 m² could have been chosen for patient selection to prevent immediate switches from the at-risk status to the CKD status; however, this would have excluded a substantial proportion of individuals in the SHCS who are at highest risk of eGFR deterioration. Last, our machine learning model training did not include genetic data (or other -omics data), which might have further improved the machine learning CKD predictions but which are often unavailable for a majority of individuals [27].

In summary, in PLWH, we observed state-of-the-art performances in forecasting individual CKD onsets with different machine learning algorithms. The underlying machine learning methods may help to advance personalized predictions of comorbidities in various populations.

Supplementary Data

Supplementary materials are available at The Journal of Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

Notes

Author contributions. J. A. R., J. B., M. B., C. M., A. R., H. F. G., R. D. K., and C. A. F. developed the study protocol and drafted the manuscript. All authors critically reviewed the study protocol. G. R. and J. B. analyzed the data with input from J. A. R. All authors critically reviewed the manuscript. All authors contributed to the design of the study and approved the final version of the manuscript.

Members of the Swiss HIV Cohort Study (SHCS). Anagnostopoulos A, Battegay M, Bernasconi E, Böni J, Braun DL, Bucher HC, Calmy A, Cavassini M, Ciuffi A, Dollenmaier G, Egger M, Elzi L, Fehr J, Fellay J, Furrer H, Fux CA, Günthard HF (president of the SHCS), Haerry D (deputy of “Positive Council”), Hasse B, Hirsch HH, Hoffmann M, Hösli I, Huber M, Kahlert CR (chairman of the Mother and Child Substudy), Kaiser L, Keiser O, Klimkait T, Kouyos RD, Kovari H, Ledergerber B, Martinetti G, Martinez de Tejada B, Marzolini C, Metzner KJ, Müller N, Nicca D, Paioni P, Pantaleo G, Perreau M, Rauch A (chairman of the scientific board), Rudin C, Scherrer AU (head of data center), Schmid P, Speck R, Stöckle M (chairman of the clinical and laboratory committee), Tarr P, Trkola A, Vernazza P, Wandeler G, Weber R, Yerly S.

Financial support. This study was financed within the framework of the SHCS, supported by the Swiss National Science Foundation (grant number 177499); by SHCS project number 814; and by the SHCS Research Foundation. The data are gathered by the 5 Swiss university hospitals, 2 cantonal hospitals, 15 affiliated hospitals, and 36 private physicians listed at www.shcs.ch/180-health-care-providers.

Potential conflicts of interest. All authors: No reported conflicts of interest.

All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.