Abstract
Time-domain diffuse correlation spectroscopy (TD-DCS) is an emerging optical technique that enables noninvasive measurement of microvascular blood flow with photon path-length resolution. In TD-DCS, a picosecond pulsed laser with a long coherence length, adequate illumination power, and narrow instrument response function (IRF) is required, and satisfying all these features is challenging. To this purpose, in this study we characterized the performance of three different laser sources for TD-DCS. First, the sources were evaluated based on their emission spectrum and IRF. Then, we compared the signal-to-noise ratio and the sensitivity to velocity changes of scattering particles in a series of phantom measurements. We also compared the results for in vivo measurements, performing an arterial occlusion protocol on the forearm of three adult subjects. Overall, each laser has the potential to be successfully used both for laboratory and clinical applications. However, we found that the effects caused by the IRF are more significant than the effect of a limited temporal coherence.
1. Introduction
Diffuse correlation spectroscopy (DCS) is an optical technique that noninvasively measures microvascular blood flow [1–4]. In this technique, traditionally, a continuous wave (CW) laser source is utilized to inject coherent light into the tissue, and the diffusively reflected photons are detected, typically at 2-3 cm from the illumination point. The moving red blood cells within the tissue alter the temporal fluctuations of the detected light intensity. These fluctuations carry information of the probed tissue blood flow and can be quantified based on the intensity autocorrelation function of the detected light [1–3]. CW-DCS has been employed in various in vivo experiments to quantify blood flow index (BFI) ranging from rodents [5,6], human brain [7], muscles [8], and others. The clinical applications of this technique are growing [9–13].
In CW-DCS, discrimination of the detected photons based on their propagation path is not feasible with a single source-detector pair. Conventionally, to increase the contribution of the deep layers to the detected signal, the source-detector separation (SDS) is increased at the cost of a substantial reduction of the detected photons [8]. Recently, the time-domain approach to DCS (TD-DCS) was implemented by employing a pulsed laser, generating coherent picosecond pulses, and a time gating approach. TD-DCS can provide path-length-resolved information, and that was validated by detecting cerebral blood flow of rodents [14]. This technique was extended, using a custom-made Ti:Sapphire laser operated in the active mode-locked regime, to in vivo measurements on adult humans with 1 s temporal resolution, first with a SDS of about 1 cm [15], and then with quasi-null SDS [16]. Besides, portable TD-DCS systems were introduced based on commercial components [17,18], and different theoretical models were developed to quantify depth-resolved BFI by considering the effects of heterogeneous geometries [19,20], finite coherence length, and the instrument response function (IRF) [21,22]. Very recently, TD-DCS operated above the 980 nm water absorption peak was introduced with the potential to increase the signal-to-noise ratio (SNR) and penetration depth [23,24]. Interferometric near-infrared spectroscopy (iNIRS) [25] and time-resolved speckle contrast optical spectroscopy (TR-SCOS) [26] are other techniques that quantify path-length-resolved blood flow information.
The main limitation to the widespread use of TD-DCS in the laboratory and relevant settings (e.g., preclinical and clinical studies) is the availability of an ideal pulsed laser source with proper characteristics in terms of power, pulse width, coherence, stability, and ruggedness. Aiming at understanding the influence of these parameters, in this study, we systematically characterize and compare three pulsed laser sources utilized in the previous studies [15,18,20] and assess their performance as a light source for TD-DCS using phantom and in vivo measurements.
2. Experimental methods
2.1. Optical setup
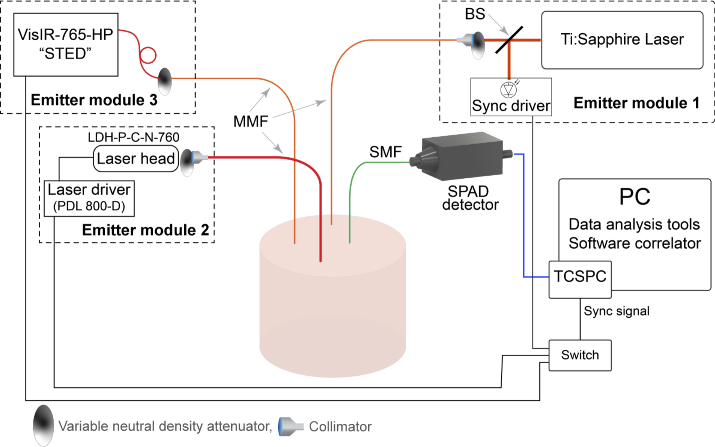
The experimental setup employed in this study was based on three different picosecond pulsed lasers, a single-photon detector, and time-correlated single photon counting (TCSPC) board, as sketched in Fig. 1. The first employed light source was a custom-made Ti:Sapphire laser operated in the active mode-locked regime [15]. The laser generates pulses with a 100 MHz repetition rate and a tunable wavelength () in the range of 700-1030 nm. The laser was operated at 763.3 nm, close to the wavelengths generated by the other emitting modules, with average optical power >100 mW. Light from the laser was coupled to a 62.5 m core diameter graded-index multi-mode fiber (MMF) (GIF625, Thorlabs, Germany) by means of a doublet collimator. A variable neutral density (ND) attenuator (NDC-25C-4, Thorlabs, Germany) was located at the laser output to control the optical power injected into the sample surface (emitter module 1 in Fig. 1). The other two optical sources are commercial picosecond diode lasers (LDH-P-C-N-760 and VisIR-765-HP "STED", PicoQuant GmbH, Germany), electrically driven at an 80 MHz repetition rate. The LDH-P-C-N-760 semiconductor laser head (labeled here with LDH) was connected to an external driver (PDL 800-D, PicoQuant GmbH, Germany) and emitted light pulses with less than 90 ps full-width at half maximum (FWHM) with a nominal average power of 10 mW and an emission wavelength of 760.4 nm. A custom-made optical coupler comprising a variable ND attenuator was connected to the laser head, which allows one to couple the laser light to the emitter fiber at different power levels. Due to the limited power of the laser, we utilized a silica core step-index MMF (M30L01, Thorlabs, Sweden) with a 1 mm core diameter as the emitter fiber to illuminate the sample with average optical power up to 12 mW (emitter module 2 in Fig. 1). The third, commercial, laser VisIR-765-HP "STED" (called VisIR in this study) was a fiber-coupled module generating pulses with 550 ps FWHM at 765.2 nm and delivered a nominal average optical power of 560 mW at the tip of the fiber. Hence, to optically adjust the illumination, we extended the laser fiber by a 62.5 m core diameter graded-index MMF (GIF625, Thorlabs, Germany), and a variable ND attenuator was located at the connection point of two fibers, to adjust the power at the emitter fiber tip up to 50 mW (emitter module 3 in Fig. 1).
Fig. 1.
The sketch of the experimental setup comprising a custom-made Ti:Sapphire laser and two commercial diode lasers. The illumination power of each laser is optically tunable. For each measurement, we used the same sample and separately used each laser into the setup. The detection part was common between all the emitter modules and equipped with a single-mode fiber to collect the diffusely reflected photons and deliver them to the SPAD detector. The TCSPC electronics receive the detected optical signal from the detector to measure the time-of-flight and absolute arrival time of each photon. The recorded data is processed via a software correlator to provide the time-gated intensity autocorrelation functions. MMF = multi-mode fiber, SMF = single-mode fiber, SPAD = single-photon avalanche diode, TCSPC = time-correlated single photon counting, BS = beam splitter
To compare the performance of the lasers, a common detection unit was utilized for all sources. The diffusely reflected photons were collected from the sample surface and delivered to a single-photon avalanche diode (SPAD) detector (PDM, Micro Photon Devices, Italy) via a 4.4 m core diameter, single-mode fiber (SMF) (780HP, Thorlabs, Sweden). Then, the detected photons were time-tagged by a TCSPC board (SPC-130, Becker&Hickl GmbH, Germany). The detection part was common to all emitter modules, and only one emitter module at a time was used. The TCSPC module was synchronized with the laser pulses via a trigger signal generated by each laser module and was switched corresponding to the applied laser.
The instrument response function (IRF) of each emitting module was separately measured before the measurements by positioning the emitter and detection fibers tip in front of each other. A sheet of white paper covered the detection fiber tip to fill up the whole numerical aperture of the fibers [27].
By employing commercial spectrometers, we estimated the coherence length of the lasers. For this aim, we measured the emission spectrum of the Ti:Sapphire laser with a spectral resolution of 0.07 nm (Anritsu MS9710B), and the LDH and VisIR lasers spectrum with 0.02 nm resolution (Yokogawa AQ6370D). To estimate the temporal coherence length, of the laser sources, we used Eq. (1) by assuming a Gaussian profile of the measured power spectral density [28].
| (1) |
where denotes the laser central wavelength, and is the FWHM bandwidth in wavelength.
2.2. Raw data processing
The TCSPC module measures two parameters for each detected photon, namely the absolute arrival time and the time-of-flight (TOF), . The TOF represents the travel time of each detected photon in the medium between source to detection points. By applying a time gate with a width of centered at time , the photon with time-of-flight between can be separated from the other photons. The corresponding absolute arrival time of these selected photons are used to calculate the normalized time-gated intensity autocorrelation function (ACF), defined as: , where is delay time, is the intensity of the selected photons, and represents ensemble averaging, which is equal to temporal averaging for ergodic media.
The normalized intensity ACF can be linked to the normalized electric field ACF, through the Siegert relation [29,30]:
| (2) |
where is the so-called coherence parameter, which accounts for non-ideal correlation, and is modeled by the following equation [15,31].
| (3) |
Here is the normalized distribution of TOF in the medium, is the ACF decay rate, is reduced scattering coefficient of the medium, is the wavenumber of the light in the medium, is the speed of light in vacuum, denotes the medium refractive index, represents the fraction of dynamic to total scattering events, and is Brownian diffusion coefficient of the scatterers. Finally, the product is defined as the blood flow index (BFI) of the sample. As predicted in the diffusing wave spectroscopy (DWS) theory, ACF decay rate linear depends on the TOF [31,32].
By employing a sufficiently narrow time gate, Eq. (3) can be simplified, and the normalized time-gated electric filed ACF is modeled by a single exponential term (Eq. (4)).
| (4) |
Then by substituting Eq. (4) into Eq. (2), the normalized intensity ACF is modeled as follows:
| (5) |
In this study, we employed a narrow time gate with a width of 100 ps to acquire the TOF-resolved autocorrelation function, which is fitted by a theoretical model described in Eq. (5) to estimate the corresponding blood flow index.
2.3. Phantom measurements
We began our evaluation by performing measurements on homogeneous liquid phantoms to characterize the employed emitting modules and assess the noise contribution on the time-gated ACF. The optical properties of the liquid phantoms were measured utilizing a TD-NIRS instrument [33] operated at 750 nm and 2.5 cm SDS, and DTOF moment approach [34]. According to the Van Staveren’s Mie theory [35] and the recipe from [36], the measurement error of caused by differences between the wavelengths of the TD-NIRS (750 nm) and TD-DCS ( 760 nm) emitting modules is about , which can be neglected.
First, we prepared a liquid phantom based on a mixture of Intralipid (B. Braun Melsungen, Germany), distilled water, and black ink, providing optical properties of and at 760 nm. The medium was measured by each of the emitter modules separately, and all the experimental conditions were kept constant across all the measurements. The average optical power delivered to the sample by the Ti:Sapphire and VisIR lasers was 50 mW, and the measurements were carried out at two different SDSs of 10 mm and 15 mm. In the case of the LDH laser, the illumination power was limited to 12 mW, and thus the measurement was performed only at 10 mm. Each measurement had a total duration of 15 min. Then, to evaluate the noise contribution to the signals, we divided the overall experiment into different subsets, each of which comprises a certain number of photons.
To evaluate the influence of the photon counts on the autocorrelation curves, we computed the contrast-to-noise ratio (CNR), i.e., the ratio between the dynamic range of and its average noise level, for the emitting modules at two interoptode distances. In particular, the CNR is defined as [37]:
| (6) |
where, and are the mean values of the ACF and background magnitudes in the presence of noise, respectively, and and are the corresponding standard deviations. Here, the signal is considered as the intercept of the ACF at the earliest lag time and background refers to the averaged value of at large delay times, which is equal to 1 in ergodic systems.
Next, in order to evaluate the capability of each emitter module to quantify the dynamic changes in the probed sample, we carried out a series of measurements on homogeneous liquid phantoms with different diffusion coefficients. The phantoms were made by mixing Intralipid, distilled water, and glycerol to slow down the scattering particles flowing in the phantoms. Since tuning the phantom absorption coefficient does not influence the scattering and dynamic properties [38], no absorber was added to the solutions. We measured four liquid phantoms with glycerol concentrations of 0%, 10%, 30%, and 50%. To tune the reduced scattering coefficient of the media, different concentration of the Intralipid was used in each case [38]. We estimated the optical properties of the media of and . Then to keep the noise contribution to the signal at a constant level along all measurements, the recorded data was divided into new datasets comprising the same number of photons for each trial. All the measurements were carried out at 10 mm SDS, and each repeated five times.
2.4. In vivo measurements
To assess the ability of each laser to measure blood flow changes, we performed a forearm arterial occlusion experiment on the left arm of three healthy male volunteers. The aim of this measurement is to evaluate the performance of the lasers and compare the SNR obtained from the homogeneous human tissue; therefore, to minimize the complexity caused by layered tissue, such as the human head, the measurements were carried out on human skeletal muscles. A 10 mm interoptode separation was applied to obtain an appropriate SNR. The probe, holding emitter and detection fibers, was secured over the subject’s flexor carpi radialis muscle, while a blood pressure cuff was placed on the upper arm of the subject. The superficial layer was measured using a skin caliper. The thickness varied from 2.7 mm to 6.5 mm between the subjects. The measurement protocol consisted of 2 min baseline, 3 min cuff occlusion (200 mmHg), and 5 min recovery after the cuff deflation. The protocol was repeated three times for each subject, in each of which one of the lasers was employed. The measurements were carried out on each subject on the same day, and at least half an hour delay was provided between each repetition. The probe was taken out from the tissue surface during each break, and then it was positioned on the same location marked on the tissue before the measurements. In order to ensure a safe illumination power for human tissue, the optical power of Ti:Sapphire and VisIR lasers was attenuated to deliver an average power of 30 mW to the skin surface. While due to the limited power of the LDH laser, the tissue was illuminated by 12 mW light. For each experiment, we computed the relative BFI (rBFI) for different time gates by normalizing the obtained BFIs to the mean value of the baseline. The protocol was approved by the Ethical Committee of Politecnico di Milano, and it was conducted in agreement with the Declaration of Helsinki. All subjects gave written informed consent prior to the measurement.
3. Results
3.1. Laser sources characterization
To characterize the employed laser modules, the measured emission spectrum and a representative IRF curve of each laser are presented in Fig. 2. The lasers spectrum illustrated in Fig. 2(a-c) indicate the central wavelength, bandwidth, and distribution of emission wavelengths generated by each laser. The spectrum bandwidth provided by Ti:Sapphire and LDH lasers are about 0.9 nm; by using Eq. 1, the coherence lengths of these lasers are 6.1 and 6.3 mm, respectively. In contrast, the VisIR laser spectrum is significantly broader, which causes a shorter coherence length around 1.6 mm.
Fig. 2.
The emission spectrum of LDH (a), Ti:Sapphire (b), and VisIR (c) lasers measured by commercial spectrometers are indicated. The central wavelength of the lasers is located in a narrow range from 760.4 nm to 765.7 nm. The x-axis range in each panel is limited to 1 nm. (d) The synchronized IRFs of the utilized lasers
Figure 2(d) shows the measured IRF acquired by each emitting module. Since the detector and TCSPC electronics used for each source were the same, the difference between the IRF curves mainly corresponds to the pulse shape of the lasers and the emitter fibers. The IRF curves were obtained by averaging 20 repetitions with 1 s recording time. All the curves were normalized to their maximum value and shifted to locate the IRF peak at time zero. The curves width was characterized at different levels and compared in Table 1. The LDH laser provides a sharp IRF peak with a FWHM of 106 ps, however after around 45% of the maximum, the curve width significantly increases. The IRF of the other two modules is broader, with FWHMs of about 185 ps and 535 ps. The measured magnitudes of IRF width and the coherence length of the lasers are listed in Table 1.
Table 1. Comparison of the spectral properties, estimated coherence length (using Eq. (1)), and the IRF curves width, indicated in Fig. 2(d), of the utilized lasers.
| Laser name | Central wavelength [nm] | Spectrum bandwidth [nm] | Temporal coherence length [mm] | FWHM of IRF [ps] | IRF width at 10% of maximum [ps] | IRF width at 1% of maximum [ps] |
|---|---|---|---|---|---|---|
| LDH-P-C-N-760 | 760.4 | 0.095 | 6.1 | 106 | 776 | 1505 |
| Ti:Sapphire | 763.8 | 0.093 | 6.3 | 185 | 575 | 1377 |
| VisIR-765-HP "STED" | 765.7 | 0.359 | 1.6 | 535 | 1173 | 1988 |
3.2. Liquid phantom measurements
To evaluate the trade-off between photon counts, time gate positioning, and the noise contribution to the measured autocorrelation curves, we quantified , CNR, and relative estimation error of ACF decay across different SDSs for all three emitter modules. For this purpose, we divided the datasets acquired from the measurements performed on the liquid phantom (with and ), to series of sub-datasets comprising different photon count levels. In this way, not only we uniformed the noise level across different lasers and tackled the optical power difference between the lasers, but also we assessed the noise contribution to the time-gated autocorrelation curves related to various photon counts.
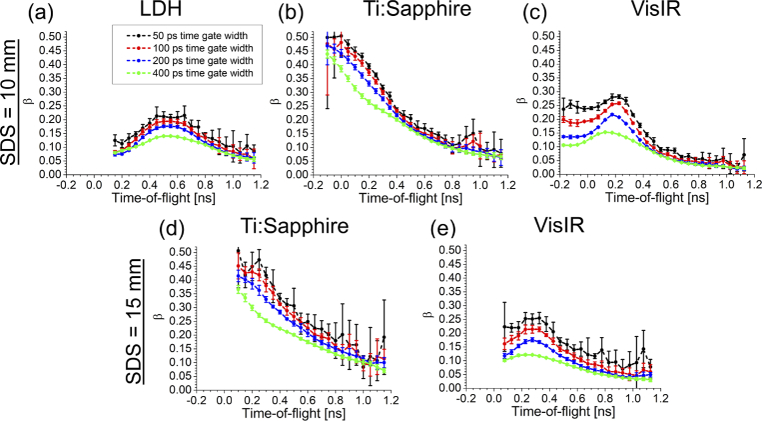
First, to evaluate the coherence between the photons detected at different TOFs, the value was quantified from the early part of the time-gated . For each module, we extracted five trials, each of which comprises around photons. Then, the time-gated autocorrelation curve was obtained for a time gate with variable width from 50 ps to 400 ps, centered at different TOFs. The results presented in Fig. 3 show that the magnitude reduces upon increasing the time gate width. Also, it remains constant for the SDS increasing from 10 mm to 15 mm, although due to the significant reduction of photon counts, the SNR decreased dramatically [39]. In comparison with the laser diodes (LDH and VisIR), Ti:Sapphire laser provides a high value of (around 0.45), which decreases along TOF, while the trend of beta across TOF is different in the case of diode lasers. As seen in Fig. 3(a,c), increases initially, then after reaching a peak, it drops down below 0.1.
Fig. 3.
Coherence parameter measured at different time gates and TOFs for 10 mm (top row) and 15 mm (bottom row) interoptode separations. Each color represents a time gate width varied from 50 ps to 400 ps. The data points represent average values over five repetitions, and the corresponding standard deviations are shown.
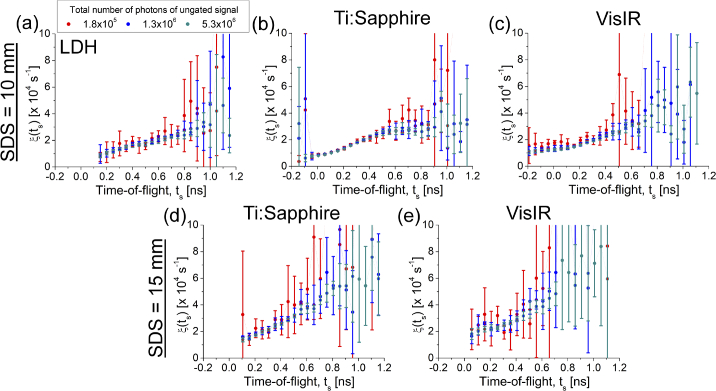
To assess the influence of photon counts on ACF, we quantified the CNR of the time-gated intensity ACF and evaluated the estimation error of ACF decay by fitting the theoretical model introduced by Eq. (5), to the experimentally obtained curves. The CNR calculated for time-gated intensity autocorrelations curves are compared across different photon counts acquired from the ungated signal for each emitter module (Fig. 4). The photon counts considered at each time gate differ based on the time gate location on DTOF. Hence, we used the total number of detected photons as a marker for this evaluation. The results indicate that CNR is not affected by count rate changes. Comparison of the trends indicated in Fig. 3 and Fig. 4 shows that CNR depends on . Consequently, CNR changes depending on properties of the experimental setup, such as detection fiber core diameter and coherence length of the light source.
Fig. 4.
Contrast-to-noise ratio (CNR) of time-gated intensity ACF for the employed emitting modules obtained for different total photon counts acquired from the ungated signal. The top raw indicates the CNR at 10 mm SDS, and the bottom raw corresponds to 15 mm SDS, including only Ti:Sapphire and VisIR lasers.
In contrast, the estimation error of ACF decay mainly depends on the number of detected photons. In order to evaluate the influence of photon counts on the measurement of the ACF decay, we analyzed time-gated ACFs corresponding to a time gate with 100 ps width center at different TOFs for all the emitting modules at 10 mm SDS and also 15 mm for Ti:Sapphire and VisIR modules.
In Fig. 5 the averaged ACF decay obtained from fitting Eq. (5) to the curves and the corresponding standard deviation from five repetitions were presented. The accuracy of estimation of the ACF decay is increased when a larger number of photons is used to build the ACF. According to the diffusion theory, the number of detected photons reduces at late TOFs and large SDSs [40]. Therefore, the SNR of the time-gated ACFs positioned at late TOFs or obtained from 15 mm SDS (Fig. 5(d,e)) are lower [41,42], which causes the broadening of the standard division amplitude.
Fig. 5.
The time-gated autocorrelation decay, obtained from the theoretical model for different TOFs. The average values of ACF decay (data points) over five repetitions and the corresponding standard deviations (vertical whiskers) obtained using each emitting module are illustrated for three photon counts.
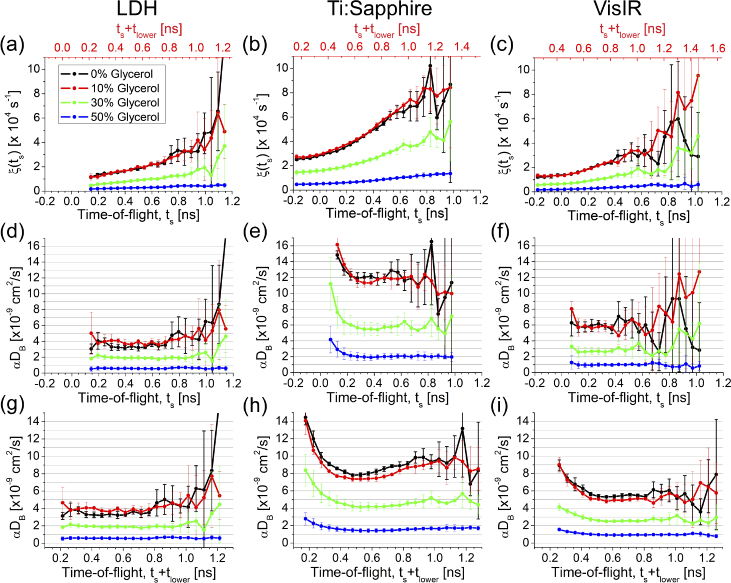
To assess the performance of the different emission modules in the assessment of the particle speed changes in the turbid media, we quantified the of four liquid phantoms with similar optical properties but differing in particle velocity caused by mixing the phantom with glycerol (from zero to 50% glycerol concentration).
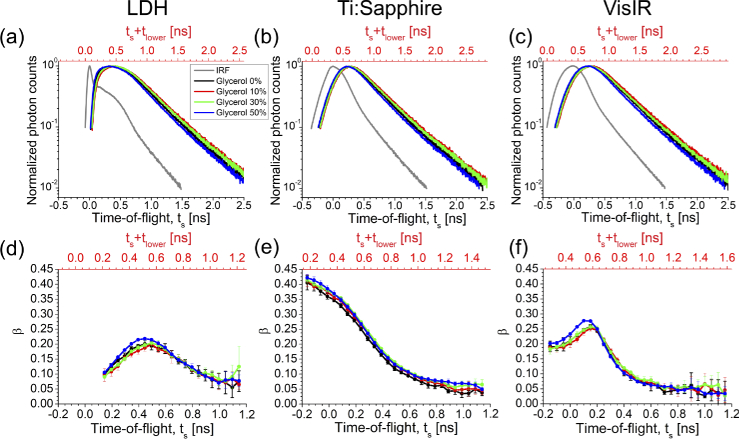
Figure 6(a-c) depicts the IRFs and the DTOFs of the corresponding homogeneous liquid phantoms comprising different glycerol concentrations obtained by each emitting module. The background noise was subtracted from the DTOFs, and the range of the DTOF between 10% of the maximum number of photons on the rising edge and 1% on the falling edge of the DTOF was extracted. Two time-axes are shown in Fig. 6. In the bottom axis, the IRF maximum was considered as time zero. Therefore, the TOF of the photons detected before the IRF peak was quantified by negative values, which for the emitting modules providing broad IRF curve this range includes several hundreds of ps. We also analyzed DTOF by defining the TOFs with respect to the earlies detected photon. For this aim, the photons detected earlier than 10% of the IRF peak were excluded from the IRF curve, the first temporal data point () was considered as the zero time (top time-axis in Fig. 6), and each DTOF was shifted by .
Fig. 6.
(a-c) The IRF corresponding to each laser and DTOFs obtained from media with similar optical properties (of about an average value of and ) obtained from liquid phantoms with different glycerol concentrations. (d-f) The values were obtained from a time gate with 100 ps width centered at different TOFs, for each emitting module. is the temporal difference between 10% of IRF maximum at its rising edge and IRF peak, defined for each module separately. The negative time values indicated in the bottom time-axes represent the TOF of the photons detected earlier than the IRF peak.
A time gate with 100 ps width centered at different TOFs (from 100 ps to 1.1 ns with respect to the location of the IRF peak) was utilized to provide TOF-resolved ACF for each medium. The values corresponding to the achieved TOF-resolved autocorrelation curves are compared between the laser modules in Fig. 6(d-f). As expected, is constant for media with different dynamics, however the trend of changes across TOF became smoother for the medium comprising slower particles (with higher glycerol concentration).
The TOF-resolved intensity autocorrelation curves were fitted by the theoretical model (Eq. (5)). The resulting ACF decays, are shown in Fig. 7(a-c) for each module. As indicated, the standard deviation of the estimated decays increases for late TOFs, at which a limited photon number is available. The results obtained for the LDH module, Fig. 7(a), clearly show a linear regression for ACF decay as a function of TOF, as predicted by DWS theory [31,32]. While this trend cannot be seen at early TOFs using Ti:Sapphire and VisIR modules. Due to applying short SDS and broad IRF generated by these lasers, the early time gates are affected by less diffusing photons combined with the influence of IRF, which is challenging to disentangle. This trend was observed in another study employing iNIRS technique [43].
Fig. 7.
The time-gated ACF decay was estimated for different time gates (a-c). Time zero is set to IRF maximum for the bottom time-axis while the red axis located on top of the sub-figures present TOF with respect to a point located at 10% of the DTOF maximum on its rising edge (). The corresponding for each medium was calculated based on time zero located at IRF max (d-f), and time zero at IRF edge (g-i).
As explained earlier, the ACF decay depends on the reduced scattering coefficient () of the medium, , and an average value of TOF representing the location of the applied time gate. Determination of the absolute value of TOF is challenging and strongly depends on IRF. Conventionally, the IRF peak is considered as the time zero [15], while in other studies, a certain level of IRF was introduced as the reference point [20]. Moreover, to obtain a constant level of over TOF, as expected for homogeneous media, we fit a linear model to the ACF decays acquired from time gates centered above 200 ps and follows a linear trend [20]. Then, the corrected ACF decays were obtained by subtracting each datapoint () from the estimated intercept. Finally, the of the phantoms was calculated based on both approaches of time zero quantification. By considering the time zero on the rising edge of the IRF (before IRF peak), the absolute value of TOF for each time gate is increased which reduces the value (Fig. 7).
3.3. In vivo measurements
Figure 8 reports the results obtained from cuff occlusion measurements carried out on three healthy subjects. The rBFI changes are shown for a 100 ps time gate width centered at 240 ps, 390 ps, and 540 ps (in respect to the IRF maximum), called early, intermediate, and late time gates, respectively. First, we estimated the BFI from every 5 s collection time, then to obtain rBFI, the absolute values were normalized to the average value of the baseline (the first 2 min of the measurement). The time-gated rBFIs obtained from each subject were compared across the employed emitting modules in Fig. 8. Although a similar trend and the hyperemia peak are observed in all experiments, the post-occlusive peak amplitudes are different for different subjects. This effect may be caused by the short breaks between repetitions of the experiment. These results show the feasibility of detecting the dynamic changes in the tissue with 5 s temporal resolution by using LDH laser, which generates lower illumination power than the other employed emitting modules. In order to compare the hyperemic responses obtained using each emitting module, the resulting rBFI changes were averaged over all three subjects. Then the mean value of hyperemic overshoot was quantified. The values presented in Table 2 show that Ti:Sapphire and VisIR lasers can reveal higher flow values after deflating the cuff.
Fig. 8.
Relative blood flow index (rBFI) obtained by employed lasers are shown during cuff occlusion measurements on three healthy adult humans’ forearm. Each row is corresponding to one of the participants, and each color represents the results of one of the time gates, including early (red), intermediate (blue), and late (green) centered at 240, 390, and 540 ps, respectively. For this analysis, the IRF peak was considered as the time zero.
Table 2. Responses in the forearm arterial cuff occlusion measurements. Relative BFI hyperemic overshoot averaged over three healthy subjects are compared between three time gates, using different laser modules.
| Laser name | Time gate position | Hyperemic overshoot |
|---|---|---|
| Early | 1.6 | |
| LDH | Intermediate | 1.7 |
| Late | 1.4 | |
|
| ||
| Early | 2.8 | |
| Ti:Sapphire | Intermediate | 3.8 |
| Late | 2.8 | |
|
| ||
| Early | 2.7 | |
| VisIR | Intermediate | 3.0 |
| Late | 3.5 | |
4. Discussion
In this work, we systematically characterized and examined three picosecond pulsed lasers for application in time-domain diffuse correction spectroscopy, TD-DCS. For each emitting module, the coherence length, measurement error induced by noise, and other parameters such as IRF, ACF decay trend over TOF, and time gate limits, were systematically analyzed based on phantom and in vivo measurements. Three emitting modules based on a custom-made Ti:Sapphire, LDH-P-C-N-760, and VisIR-765-HP "STED" lasers were utilized and compared.
The measured emission spectrum of the lasers demonstrated a similar shape of Ti:Sapphire and LDH lasers spectrum with bandwidths <0.1 nm, while the VisIR laser spectrum is 3.8 times higher. The spectral widths reported in Table 1 present the upper limits since the jitter of the spectrometers limited measurement accuracy. An interferometric measurement is required to measure the spectrum and the corresponding coherence length of the lasers accurately. By assuming a Gaussian profile of the emitter spectrum, we estimate a coherence length of about 6 mm for LDH and Ti:Sapphire lasers and 1.6 mm for VisIR laser.
To assess the coherence between the detected photons traveled through similar path-lengths, we quantified for four time gates with widths of 50, 100, 200, and 400 ps centered at different TOFs. The measurements were carried out on a homogeneous liquid phantom at interoptode separations of 10 and 15 mm (Fig. 3). The results reveal different trends of over TOF for each emitting module. The Ti:Sapphire laser provides a decreasing trend of [15], in which a maximum value around 0.45 is achieved by a narrow time gate containing early arriving photons. In contrast, the maximum value of provided by diode lasers (LDH and VisIR) is lower than 0.3 and obtained around the DTOF peak. Due to the limited coherence length of the lasers, by increasing the time gate width the ratio of the number of coherent photons to the total number of gated photons decreases, which influences the coherence parameter [14]. As shown in Fig. 3(a,b), the values for time gates centered at early to middle TOFs, slightly decrease by increasing the time gate width from 50 to 200 ps, while VisIR laser present significant changes by broadening the time gate width, Fig. 3(c), which is likely because of its lower coherence length than the other sources. The standard deviation, obtained from five repetitions, illustrates higher errors for narrow time gates, late TOFs, and larger SDS due to the drop of photon counts. Also, by increasing interoptode separation from 10 to 15 mm, the values decrease slightly. Therefore, a fixed 100 ps width time gate provides a balance between value and the noise contribution, at 10 mm SDS.
We used this configuration to quantify the noise contribution to the intensity autocorrelation function based on the contrast-to-noise ratio at different count rate levels. The results indicate that the CNR is proportional to the values and decays to 0.1 at late TOFs, which are more sensitive to the changes in flow in deep layers of the medium [44].
As described in the raw data processing section, the moving scatterer weighed, the Brownian diffusion coefficient () or BFI, is derived from the decay of the theoretical model of electric-field ACF fitted to the experimentally obtained ACF curve. Hence, standard deviation of ACF decay reflects the estimation error of the BFI. Typically, the estimation error grows significantly with photon counts reduction. A low number of detected photons is typically acquired at late TOFs, at large interoptode distances.
In order to improve the quantification of the , or BFI, in the TD-DCS technique, two parameters, including the linearity of ACF decay rate over TOF and determination of the time zero play critical roles. To obtain a certain level of at different depths of homogeneous media, we employed the strategy proposed by us recently [20]. The time-gated ACF decay obtained from fitting the theoretical model to the experimentally acquired curves, is modeled by a linear equation, yielding a slope and intercept. Then, subtracting the ACF decay from the intercept generates a corrected value of used to calculate the . In phantom experiments, we evaluated the time-gated ACF trend obtained using a 100 ps width time gate centered at different TOFs, with 10 mm SDS for homogeneous liquid media with different viscosities. The results illustrate a linear trend of ACF decay for LDH laser, while Ti:Sapphire and VisIR are incapable of providing such a linear regression. This ACF decay deviation from a linear pattern may be caused by the broad IRF which leads to increase in the BFI estimation error [21,22]. Furthermore, the BFI calculation desires accurate knowledge of the photon traveling time through the sample, which is quantified with respect to the time zero. We compared absolute values based on determining the time zero at the IRF peak or 10% of the IRF maximum on its rising edge. Positioning the time zero earlier than the IRF peak, e.g. at 10% of the IRF peak, leads to a reduction of the values by increasing the estimated TOF value of the time-gated photons. Hence, accurate quantification of the time zero is one of the key requirements in TD-DCS applications, specifically for emitting modules producing IRF with large time-to-peak, such as Ti:Sapphire and VisIR.
The results obtained with the use of Ti:Sapphire laser presented in Fig. 7 (middle column) reveal two crucial effects. First, time gate positioning with respect to the IRF peak narrows the path-length-resolved flow quantification to a limited range from 0.2 to 0.6 ns, particularly for the phantom with 0% glycerol concentration (Fig. 7(e)). In contrast, allocating zero time at 10% of IRF maximum extends these limits from 0.4 to 1 ns and yields high CNR in the early part. The upper limit of these ranges is limited by the broadening of the standard deviation of the estimated . Second, an appropriate estimation of was obtained using the time gates with low value of (), which were located close to the upper limit of the mentioned range. LDH and VisIR lasers also presented an appropriate value at TOF = 800 ps with respect to the time zero adjusted at 10% of IRF maximum, although the values were 0.13 and 0.1, respectively. These results show the sub-optimal value of about 0.1.
Furthermore, a particular time gate centered at an absolute TOF value cannot contain photons propagated through a specific path-length because the absolute values of TOF depend on the IRF broadening. For instance, a time gate centered at 800 ps (in respect to 10% of IRF peak on its rising edge) covers another range of TOFs with respect to the DTOF peak. Besides, because the wide IRF leads to expanding of the DTOF, a constant width of the time gate selects more coherent photons from the laser for broader IRF, provided that the spectral bandwidths of the sources are similar.
The capability of each emitting module to reveal blood flow changes was assessed by the cuff occlusion experiment. The rBFI corresponding to three time gates, with 100 ps width, was quantified using each laser with 5 s temporal resolution. Although the LDH laser illumination power was 60% lower than the other two light sources, a similar blood flow variation was achieved. To obtain a better temporal resolution, higher illumination power, satisfying the exposure skin limits, can be applied using lasers operating at longer wavelengths [24]. The employed time gates allow to distinguish photons propagating through particular range of path-lengths in the medium. In layered media, such as biological tissues, the early time gates may allow to probe the blood flow changes in superficial layers and the late time gates are more sensitive to the changes in flow appearing in deeper layers [44]. This advantage of the TD approach to separate between extra- and intra-cerebral tissues was highlighted in multiple TD-NIRS studies [45–47]. However, no significant difference between time gates were observed during the occlusion measurement. This effect is likely caused due to employing short SDS and thin superficial (skin and adipose) layers of the probed tissues. Here, the mean value of the forearm superficial layer thickness, averaged over all three subjects, was estimated at 4.6 mm; while in an adult human, the thickness of extra-cerebral layers varies from 1 to 2 cm, depending on the subject [48,49]. In order to distinguish the influence of different layers, employing more advanced data processing [20] or utilizing time-gated detectors [16,26] is required.
5. Conclusions
By systematic characterization of three pulsed lasers providing limited coherence lengths and different IRF shapes, we assessed the performance of these light sources in TD-DCS applications. Although a light source with a high coherence length, narrow IRF, and sufficient illumination power perfectly satisfy the conditions required for TD-DCS, the near-infrared laser sources that have been employed in this technology provide relatively short coherence length and relatively broad IRF. In this study, we showed that IRF broadening yields a higher BFI quantification error than the limited coherence length. IRF broadening produces uncertainty in the absolute magnitude of TOF and causes a deviation from the ACF decay linear growth trend over TOFs, which ultimately leads to inconsistencies of the measured data with the theoretical model. This limitation could be tackled by including the laser pulse shape into the model, yet at the expenses of a less straightforward interpretation.
We found that the LDH-P-C-N-760 diode laser is less affected by the IRF broadening effects, although it provides a limited optical power; therefore, this module offers an appropriate configuration for laboratory studies. While for clinical applications, further photon-counting optimization is required. In contrast, the VisIR-765-HP "STED" laser module and the custom-made Ti:Sapphire laser used in this study generate sufficient count rates, but the results obtained using these modules are significantly influenced by the IRF-related effects. The Ti:Sapphire laser provides a high correlation between the photons traveled across short paths from the source to the detector. In the present study, the Ti:Sapphire laser configuration was tailored to yield powerful, narrowband and stable pulses, with a relatively long pulse duration. As a consequence of this work, an optimization of the IRF could be rather preferred. In terms of correlation loss of the injected photon to the sample, the VisIR laser generates a large emission spectrum bandwidth, which leads to the shortest coherence length. The results show that all lasers provide low CNR at late time gates due to the loss of coherence caused by increasing the path-lengths.
Performance assessment of the lasers was carried out on the homogeneous phantoms and during an arterial occlusion on the forearm muscles of three healthy adult humans. We noted that all employed lasers enable to reveal the dynamic changes in scattering media. In order to evaluate the efficiency of the lasers for monitoring blood flow changes of the human brain cortex, further investigations on layered media are required. Besides, to fulfill the conditions of bedside studies, other parameters such as the photons counting efficiency, instrument size, portability, and ambient temperature influence need to be considered.
Overall, our study proposes a metrics to assess the performances of TD-DCS systems in an objective and quantitative way. This effort, joined with other multi-laboratory exercises could set the basis for internationally agreed protocols for laboratory validation of TD-DCS instruments, following the path of what is pursued for instance in Diffuse Optics [50] or Photoacoustics [51].
Acknowledgement
We thank PicoQuant for their support. We also acknowledge Dr. Michał Karpiński and Ali Golestani at the University of Warsaw and Dr. Gianluca Galzerano at Politecnico di Milano for their assistance in measuring lasers emission spectrums.
Funding
Horizon 2020 Framework Programme10.13039/100010661 (BITMAP, Grant No. 675332, LASERLAB-EUROPE V 871124, LUCA project, Grant No. 688303); Narodowe Centrum Nauki10.13039/501100004281 (Preludium 2019/33/N/ST7/03024); Narodowe Centrum Nauki10.13039/501100004281 (Maestro 2016/22/A/ST2/00313); Centres de Recerca de Catalunya10.13039/100015439; Agència de Gestió d'Ajuts Universitaris i de Recerca10.13039/501100003030 (2017 SGR 1380); “Severo Ochoa” Programme for Centres of Excellence in R&D10.13039/100017199 (CEX2019-000910-S); “la Caixa” Foundation10.13039/100010434 (LlumMedBcn); Ministerio de Economía y Competitividad10.13039/501100003329 (PHOTOMETABO); Fundación Cellex10.13039/100008050.
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Boas D. A., Campbell L. E., Yodh A. G., “Scattering and imaging with diffusing temporal field correlations,” Phys. Rev. Lett. 75(9), 1855–1858 (1995). 10.1103/PhysRevLett.75.1855 [DOI] [PubMed] [Google Scholar]
- 2.Boas D. A., Yodh A. G., “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A 14(1), 192–215 (1997). 10.1364/JOSAA.14.000192 [DOI] [Google Scholar]
- 3.Durduran T., Choe R., Baker W. B., Yodh A. G., “Diffuse optics for tissue monitoring and tomography,” Rep. Prog. Phys. 73(7), 076701 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Buckley E. M., Parthasarathy A. B., Grant P. E., Yodh A. G., Franceschini M. A., “Diffuse correlation spectroscopy for measurement of cerebral blood flow: future prospects,” Neurophotonics 1(1), 011009 (2014). 10.1117/1.NPh.1.1.011009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sathialingam E., Lee S. Y., Sanders B., Park J., McCracken C. E., Bryan L., Buckley E. M., “Small separation diffuse correlation spectroscopy for measurement of cerebral blood flow in rodents,” Biomed. Opt. Express 9(11), 5719–5734 (2018). 10.1364/BOE.9.005719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shang Y., Chen L., Toborek M., Yu G., “Diffuse optical monitoring of repeated cerebral ischemia in mice,” Opt. Express 19(21), 20301–20315 (2011). 10.1364/OE.19.020301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Durduran T., Zhou C., Edlow B. L., Yu G., Choe R., Kim M. N., Cucchiara B. L., Putt M. E., Shah Q., Kasner S. E., Greenberg J. H., Yodh A. G., Detre J. A., “Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients,” Opt. Express 17(5), 3884–3902 (2009). 10.1364/OE.17.003884 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yu G., Durduran T., Lech G., Zhou C., Chance B., Mohler E. R., Yodh A. G., “Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies,” J. Biomed. Opt. 10(2), 024027 (2005). 10.1117/1.1884603 [DOI] [PubMed] [Google Scholar]
- 9.Durduran T., Choe R., Yu G., Zhou C., Tchou J. C., Czerniecki B. J., Yodh A. G., “Diffuse optical measurement of blood flow in breast tumors,” Opt. Lett. 30(21), 2915–2917 (2005). 10.1364/OL.30.002915 [DOI] [PubMed] [Google Scholar]
- 10.Yazdi H. S., O’Sullivan T. D., Leproux A., Hill B., Durkin A., Telep S., Lam J., Yazdi S. S., Police A. M., Carroll R. M., Combs F. J., Strömberg T., Yodh A. G., Tromberg B. J., “Mapping breast cancer blood flow index, composition, and metabolism in a human subject using combined diffuse optical spectroscopic imaging and diffuse correlation spectroscopy,” J. Biomed. Opt. 22(4), 045003 (2017). 10.1117/1.JBO.22.4.045003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Durduran T., Zhou C., Buckley E. M., Kim M. N., Yu G., Choe R., Gaynor J. W., Spray T. L., Durning S. M., Mason S. E., Montenegro L. M., Nicolson S. C., Zimmerman R. A., Putt M. E., Wang J., Greenberg J. H., Detre J. A., Yodh A. G., Licht D. J., “Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects,” J. Biomed. Opt. 15(3), 037004 (2010). 10.1117/1.3425884 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ruesch A., Yang J., Schmitt S., Acharya D., Smith M. A., Kainerstorfer J. M., “Estimating intracranial pressure using pulsatile cerebral blood flow measured with diffuse correlation spectroscopy,” Biomed. Opt. Express 11(3), 1462–1476 (2020). 10.1364/BOE.386612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Milej D., Shahid M., Abdalmalak A., Rajaram A., Diop M., Lawrence K. S., “Characterizing dynamic cerebral vascular reactivity using a hybrid system combining time-resolved near-infrared and diffuse correlation spectroscopy,” Biomed. Opt. Express 11(8), 4571–4585 (2020). 10.1364/BOE.392113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sutin J., Zimmerman B., Tyulmankov D., Tamborini D., Wu K. C., Selb J., Gulinatti A., Rech I., Tosi A., Boas D. A., Franceschini M. A., “Time-domain diffuse correlation spectroscopy,” Optica 3(9), 1006–1013 (2016). 10.1364/OPTICA.3.001006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pagliazzi M., Sekar S. K. V., Colombo L., Martinenghi E., Minnema J., Erdmann R., Contini D., Dalla Mora A., Torricelli A., Pifferi A., Durduran T., “Time domain diffuse correlation spectroscopy with a high coherence pulsed source: in vivo and phantom results,” Biomed. Opt. Express 8(11), 5311–5325 (2017). 10.1364/BOE.8.005311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pagliazzi M., Sekar S. K. V., Di Sieno L., Colombo L., Durduran T., Contini D., Torricelli A., Pifferi A., Dalla Mora A., “In vivo time-gated diffuse correlation spectroscopy at quasi-null source-detector separation,” Opt. Lett. 43(11), 2450–2453 (2018). 10.1364/OL.43.002450 [DOI] [PubMed] [Google Scholar]
- 17.Samaei S., Sawosz P., Gerega A., Liebert A., “Time-resolved diffuse correlation spectroscopy based on commercial laser module,” in Optical Tomography and Spectroscopy (Optical Society of America, 2018), pp. OTu2D—-3. [Google Scholar]
- 18.Tamborini D., Stephens K. A., Wu M. M., Farzam P., Siegel A. M., Shatrovoy O., Blackwell M., Boas D. A., Carp S. A., Franceschini M. A., “Portable system for time-domain diffuse correlation spectroscopy,” IEEE Trans. Biomed. Eng. 66(11), 3014–3025 (2019). 10.1109/TBME.2019.2899762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li J., Qiu L., Poon C.-S., Sunar U., “Analytical models for time-domain diffuse correlation spectroscopy for multi-layer and heterogeneous turbid media,” Biomed. Opt. Express 8(12), 5518–5532 (2017). 10.1364/BOE.8.005518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Samaei S., Sawosz P., Kacprzak M.., Pastuszak Ż., Borycki D., Liebert A., “Time-domain diffuse correlation spectroscopy (TD-DCS) for noninvasive, depth-dependent blood flow quantification in human tissue in vivo,” Sci. Rep. 11(1), 1817 (2021). 10.1038/s41598-021-81448-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cheng X., Tamborini D., Carp S. A., Shatrovoy O., Zimmerman B., Tyulmankov D., Siegel A., Blackwell M., Franceschini M. A., Boas D. A., “Time domain diffuse correlation spectroscopy: modeling the effects of laser coherence length and instrument response function,” Opt. Lett. 43(12), 2756–2759 (2018). 10.1364/OL.43.002756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Colombo L., Pagliazzi M., Sekar S. K. V., Contini D., Dalla Mora A., Spinelli L., Torricelli A., Durduran T., Pifferi A., “Effects of the instrument response function and the gate width in time-domain diffuse correlation spectroscopy: model and validations,” Neurophotonics 6(03), 1 (2019). 10.1117/1.NPh.6.3.035001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Colombo L., Pagliazzi M., Sekar S. K. V., Contini D., Durduran T., Pifferi A., “In vivo time-domain diffuse correlation spectroscopy above the water absorption peak,” Opt. Lett. 45(13), 3377–3380 (2020). 10.1364/OL.392355 [DOI] [PubMed] [Google Scholar]
- 24.Carp S. A., Tamborini D., Mazumder D., Wu K.-C., Robinson M. B., Stephens K. A., Shatrovoy O., Lue N., Ozana N., Blackwell M. H., Franceschini M. A., “Diffuse correlation spectroscopy measurements of blood flow using 1064 nm light,” J. Biomed. Opt. 25(09), 097003 (2020). 10.1117/1.JBO.25.9.097003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Borycki D., Kholiqov O., Srinivasan V. J., “Reflectance-mode interferometric near-infrared spectroscopy quantifies brain absorption, scattering, and blood flow index in vivo,” Opt. Lett. 42(3), 591–594 (2017). 10.1364/OL.42.000591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pagliazzi M., Colombo L., Vidal-Rosas E. E., Dragojević T., Parfentyeva V., Culver J. P., Sekar S. K. V., Di Sieno L., Contini D., Torricelli A., Pifferi A., Dalla Mora A., Durduran T., “Time resolved speckle contrast optical spectroscopy at quasi-null source-detector separation for non-invasive measurement of microvascular blood flow,” Biomed. Opt. Express 12(3), 1499–1511 (2021). 10.1364/BOE.418882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liebert A., Wabnitz H., Grosenick D., Macdonald R., “Fiber dispersion in time domain measurements compromising the accuracy of determination of optical properties of strongly scattering media,” J. Biomed. Opt. 8(3), 512–516 (2003). 10.1117/1.1578088 [DOI] [PubMed] [Google Scholar]
- 28.Bigio I. J., Fantini S., Quantitative Biomedical Optics: Theory, Methods, and Applications (Cambridge University Press, 2016). [Google Scholar]
- 29.Siegert A. J. F., On the Fluctuations In Signals Returned by Many Independently Moving Scatterers (Radiation Laboratory, Massachusetts Institute of Technology, 1943). [Google Scholar]
- 30.Lemieux P.-A., Durian D. J., “Investigating non-Gaussian scattering processes by using nth-order intensity correlation functions,” J. Opt. Soc. Am. A 16(7), 1651–1664 (1999). 10.1364/JOSAA.16.001651 [DOI] [Google Scholar]
- 31.Pine D. J., Weitz D. A., Chaikin P. M., Herbolzheimer E., “Diffusing wave spectroscopy,” Phys. Rev. Lett. 60(12), 1134–1137 (1988). 10.1103/PhysRevLett.60.1134 [DOI] [PubMed] [Google Scholar]
- 32.Yodh A., Kaplan P., Pine D., “Pulsed diffusing-wave spectroscopy: High resolution through nonlinear optical gating,” Phys. Rev. B 42(7), 4744–4747 (1990). 10.1103/PhysRevB.42.4744 [DOI] [PubMed] [Google Scholar]
- 33.Zerbini P. E., Vanoli M., Rizzolo A., Grassi M., de Azevedo Pimentel R. M., Spinelli L., Torricelli A., “Optical properties, ethylene production and softening in mango fruit,” Postharvest Biol. Technol. 101, 58–65 (2015). 10.1016/j.postharvbio.2014.11.008 [DOI] [Google Scholar]
- 34.Liebert A., Wabnitz H., Grosenick D., Möller M., Macdonald R., Rinneberg H., “Evaluation of optical properties of highly scattering media by moments of distributions of times of flight of photons,” Appl. Opt. 42(28), 5785–5792 (2003). 10.1364/AO.42.005785 [DOI] [PubMed] [Google Scholar]
- 35.Van Staveren H. J., Moes C. J., van Marie J., Prahl S. A., Van Gemert M. J., “Light scattering in lntralipid-10% in the wavelength range of 400–1100 nm,” Appl. Opt. 30(31), 4507–4514 (1991). 10.1364/AO.30.004507 [DOI] [PubMed] [Google Scholar]
- 36.Choe R., Diffuse Optical Tomography and Spectroscopy of Breast Cancer and Fetal Brain (University of Pennsylvania, 2005). [Google Scholar]
- 37.Szkulmowski M., Wojtkowski M., “Averaging techniques for OCT imaging,” Opt. Express 21(8), 9757–9773 (2013). 10.1364/OE.21.009757 [DOI] [PubMed] [Google Scholar]
- 38.Cortese L., Presti G. L., Pagliazzi M., Contini D., Dalla Mora A., Pifferi A., Sekar S. K. V., Spinelli L., Taroni P., Zanoletti M., Weigel U. M., de Fraguier S., Nguyen-Dihn A., Rosinski B., Durduran T., “Liquid phantoms for near-infrared and diffuse correlation spectroscopies with tunable optical and dynamic properties,” Biomed. Opt. Express 9(5), 2068–2080 (2018). 10.1364/BOE.9.002068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Qiu L., Cheng H., Torricelli A., Li J., “Using a simulation approach to optimize time-domain diffuse correlation spectroscopy measurement on human head,” Neurophotonics 5(02), 1 (2018). 10.1117/1.NPh.5.2.025007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Patterson M. S., Chance B., Wilson B. C., “Time resolved reflectance and transmittance for the noninvasive measurement of tissue optical properties,” Appl. Opt. 28(12), 2331–2336 (1989). 10.1364/AO.28.002331 [DOI] [PubMed] [Google Scholar]
- 41.Zhou C., Yu G., Furuya D., Greenberg J. H., Yodh A. G., Durduran T., “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt. Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 42.Qiu L., Zhang T., Huang W., Sun W., Wu X., Sun H., Lin F., Li J., “Time domain diffuse correlation spectroscopy for detecting human brain function: optimize system on real experimental conditions by simulation method,” IEEE Photonics Journal 13, 3700109 (2021). 10.1109/JPHOT.2021.3089635 [DOI] [Google Scholar]
- 43.Kholiqov O., Zhou W., Zhang T., Du Le V., Srinivasan V. J., “Time-of-flight resolved light field fluctuations reveal deep human tissue physiology,” Nat. Commun. 11(1), 391 (2020). 10.1038/s41467-019-14228-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wabnitz H., Contini D., Spinelli L., Torricelli A., Liebert A., “Depth-selective data analysis for time-domain fNIRS: moments vs. time windows,” Biomed. Opt. Express 11(8), 4224–4243 (2020). 10.1364/BOE.396585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lange F., Tachtsidis I., “Clinical brain monitoring with time domain NIRS: a review and future perspectives,” Appl. Sci. 9(8), 1612 (2019). 10.3390/app9081612 [DOI] [Google Scholar]
- 46.Lange F., Peyrin F., Montcel B., “Broadband time-resolved multi-channel functional near-infrared spectroscopy system to monitor in vivo physiological changes of human brain activity,” Appl. Opt. 57(22), 6417–6429 (2018). 10.1364/AO.57.006417 [DOI] [PubMed] [Google Scholar]
- 47.Elliott J. T., Milej D., Gerega A., Weigl W., Diop M., Morrison L. B., Lee T.-Y., Liebert A., Lawrence K. S., “Variance of time-of-flight distribution is sensitive to cerebral blood flow as demonstrated by icg bolus-tracking measurements in adult pigs,” Biomed. Opt. Express 4(2), 206–218 (2013). 10.1364/BOE.4.000206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Strangman G., Franceschini M. A., Boas D. A., “Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters,” NeuroImage 18(4), 865–879 (2003). 10.1016/S1053-8119(03)00021-1 [DOI] [PubMed] [Google Scholar]
- 49.Sawosz P., Wojtkiewicz S., Kacprzak M., Weigl W., Borowska-Solonynko A., Krajewski P., Bejm K., Milej D., Ciszek B., Maniewski R., “Human skull translucency: post mortem studies,” Biomed. Opt. Express 7(12), 5010–5020 (2016). 10.1364/BOE.7.005010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wabnitz H., Jelzow A., Mazurenka M., Steinkellner O., Macdonald R., Milej D., Żołek N., Kacprzak Michałand Sawosz P., Maniewski R., Liebert A., Magazov S., Hebden J. C., Martelli F., Di Ninni P., Zaccanti G., Torricelli A., Contini D., Re R., Zucchelli L. M., Spinelli L., Cubeddu R., Pifferi A., “Performance assessment of time-domain optical brain imagers, part 2: nEUROPt protocol,” J. Biomed. Opt. 19(8), 086012 (2014). 10.1117/1.JBO.19.8.086012 [DOI] [PubMed] [Google Scholar]
- 51.Bohndiek S., “Addressing photoacoustics standards,” Nat. Photonics 13(5), 298 (2019). 10.1038/s41566-019-0417-3 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.