Abstract
Biomedical images contain a large volume of sensor measurements, which can reveal the descriptors of the disease under investigation. Computer-based analysis of such measurements helps detect the disease, and thereby swiftly aid medical professionals to choose adequate therapy. In this paper, we propose a robust deep learning ensemble framework known as COVID Fuzzy Ensemble Network, or COFE-Net. This strategy is proposed for the task of COVID-19 screening from chest X-rays (CXR) and CT Scans, as a part of Computer-Aided Detection (CADe) for medical practitioners. We leverage the strategy of Transfer Learning for Convolutional Neural Networks (CNNs) widely adopted in recent literature, and further propose an efficient ensemble network for their combination. The principles of fuzzy logic have been leveraged to combine the measured decision scores generated by three state-of-the-art CNNs – Inception V3, Inception ResNet V2 and DenseNet 201 – through the Choquet fuzzy integral. Experimental results support the efficacy of our approach over empirical ensembling, as the fuzzy ensembling strategy for biomedical measurement consists of dynamic refactoring of the classifier ensemble weights on the fly, based upon the confidence scores for coalitions of inputs. This is the chief advantage of our biomedical measurement strategy over others as other methods do not adjust to the multiple generated measurements dynamically unlike ours.Impressive results on multiple datasets demonstrate the effectiveness of the proposed method. The source code of our proposed method is made available at: https://github.com/theavicaster/covid-cade-ensemble.
Keywords: COVID-19 detection, COFE-Net, Deep learning, Fuzzy integral, Ensemble, Classifier fusion, Chest X-Ray, CT Scan, Biomedical measurement
1. Introduction
The rapid spread of the Novel Coronavirus disease (COVID-19) has been a cause for great concern ever since it first emerged in Wuhan, China in 2019. It has resulted in a global pandemic situation and served as a catalyst to the disruption of normal life worldwide. COVID-19 or SARS-CoV-2 is a severe acute respiratory syndrome, the typical symptoms of which include breathlessness, fever, weakness, cough and cold, and loss of smell and taste. The virus has infected over 176 million people worldwide as of the 15th of June 2021, with over 3.8 million of them succumbing to the disease. An SIR model-based investigation about the propagation of the disease has been carried out by Saxena et al. in [1].
The primary problem of the COVID-19 disease is the high incubation period of the virus ranging from few days to up to multiple weeks, and in some cases, we come across asymptomatic patients as well. Due to this, the person acts as an active carrier of the disease, spreading it to other people in their vicinity unknowingly during this period. The applications of technology, such as proposed in the works [2], [3], [4], [5] for monitoring, biomedical imaging and early detection of disease have had a positive impact on the medical field. Applications of research such as the work [6] have helped in proper social distancing measures. Though conventional detection methods like Reverse Transcription Polymerase Chain Reaction (RT-PCR) from a nasopharyngeal swab has proved to be highly effective [7], the time taken by such methods is high and there are quite a few false positives as in the results of the work [8]. Hence, Computer Aided Detection (CADe) has been looked into as an alternative and viable solution.
CADe is a sub-field of the Biomedical Image Analysis domain, which is one of rapidly growing interdisciplinary research fields that includes biology, engineering and medicine. It is concerned with measurements of the human body on macroscopic and microscopic scales. The core part of this research field is the application of image processing methodologies in order to solve various medical problems of the human bodies. As biomedical images contain important information about the anatomical structure of the affected body parts, it would be extremely useful for proper detection, thus it assists the medical experts for better treatment of the patients.
Generally, medical experts analyse such images manually and apply their experience to understand the severity of the disease. However, it can be easily understood that such manual analysis of these images by the medical professionals is limited owing to differences in interpersonal interpretation capability among others, which make this analysis a subjective matter. On the contrary, computer-based automated investigation of biomedical images favours objective analysis, thus leading to the better diagnosis of the patients. Such systems can make the diagnosis more economical and less time-consuming which is the one of the basic needs of the developing nations.
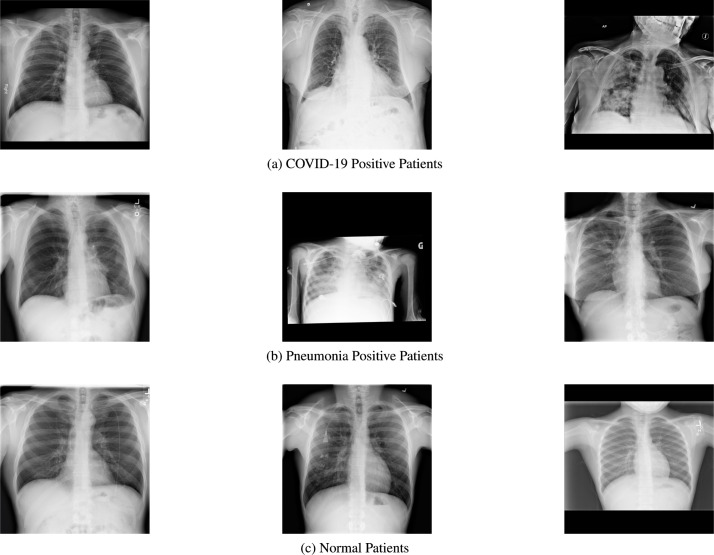
It is notable that in recent years, CADe has proved to be very successful for biomedical purposes. It has been used for detection of pulmonary disorders, coronary artery disease, Alzheimer’s disease and other such diseases. For COVID-19, CADe based methods focus on analysing the Chest X-ray (CXR) or chest Computed Tomography (CT) Scan images for detecting the presence of COVID-19. The sample CXR images for COVID-19, pneumonia and normal patients are shown in Fig. 1. More recently, alternative modalities such as Scattergram images [9] have also found success in COVID-19 CADe.
Fig. 1.
Sample Images of chest X-rays for all three classes in the COVID-X dataset.
Deep learning has shown rapid improvement in CADe based treatment in various fields, the latest being COVID-19. Quite a few attempts have been made to develop a robust system capable of efficiently detecting COVID-19 in a person such as in the works [10], [11], [12], [13], [14], [15] Most of these have utilized deep learning due to its high efficiency in recent years. Specifically speaking, Convolutional Neural Networks (CNNs) have been used in most cases due to the fact that they have obtained great success in recent years for classifying radiological images. Further, deep CNNs also do not need to be fed handcrafted features using feature engineering due to which they are preferred over conventional machine learning classifiers. They have also proved to be more effective in image classification in general than most other methods due to which most researchers resort to it for classification purposes for any category of images.
1.1. Motivation
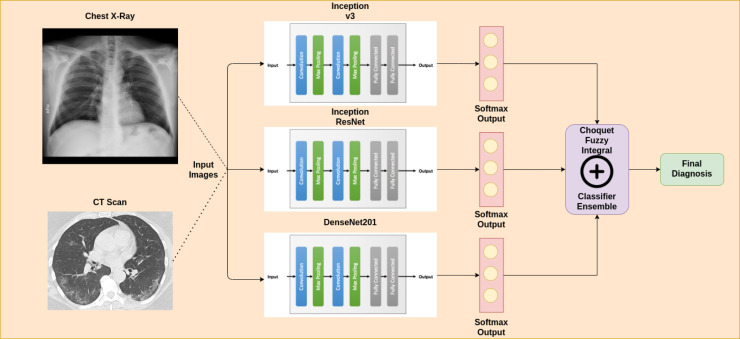
In this paper, we propose a CADe framework which benefits from the combined prediction abilities of CNN models. The entire steps of the proposed work are summarized in Fig. 2.
Fig. 2.
Schematic diagram of our proposed methodology which consists of: (I) Preprocessing input biomedical images to conform to expected input of standard CNN architectures, (II) Classification using three CNNs leveraging Transfer Learning, and (III) Ensemble of classifiers using Choquet fuzzy integral to yield prediction, available for medical practitioners.
Initially, we process the acquired images to be of uniform shape. This is necessary to harness the standard CNN architectures as feature extractors. A large body of methods have investigated the use of transfer learning for CNN classifiers. We employ three such state-of-the-art CNN architectures to generate decision scores based on the processed inputs.
Owing to the stochastic learning process of deep learning models, the decision scores generated by CNNs contain a degree of uncertainty. Each of the constituent models converges at a particular local minimum of the loss function used, as a result of the particular gradient descent algorithm used for training. The imperfectly converged models, as well as noises in the sampled observations upon which they are trained lead to the uncertainty in the predictions. To counter this, we rely on the principles of fuzzy logic to harness this degree of uncertainty and use it effectively to generate our final predictions. This is done by an efficient ensembling strategy which uses fuzzy logic principles to combine the results of the individual classifiers weighing them in accordance with their scores. Fuzzy logic performs exceptionally well in situations wherein decisions are made upon imprecise information. We investigate the Choquet integral for the classifier ensemble through fuzzy integrals, which works as a generalization of previously explored empirical schemes. It additionally supports conditioning the weightage of each classifier at inference based upon the decision scores of prior classifiers in the ensemble process. Specifically, it caters to the fact that the biomedical images may contain crucial information which is too specific to be detected by a particular CNN of the network, which is important for other details.
1.2. Contributions
We have chosen a unique combination of three CNN based classifiers such that the outputs complement each other appropriately while generating decision scores upon CXRs or CT Scans. Transfer learning is used to reduce training time as well as increase the efficiency of the networks. An ensemble method is employed using an efficient strategy based on the Choquet Fuzzy Integral method, and the performance obtained is compared with empirical ensemble strategies. We have achieved impressive performance on multiple COVID-19 image datasets through the ensemble framework, wherein the result achieved is beyond the reach of the individual classifiers. Appreciable performance on multiple datasets in varied fields of medical imaging using a variety of metrics along with a detailed ablation study, K-fold cross validation results, and a comparative study with other methods demonstrate the robustness of the network. Overall, the method is an unique combination of both new as well as a few existing research topics which generates desirable results and mostly outperforms its predecessors.
2. Related work
Among the recently proposed CADe methods for COVID-19, there are two sources of medical images — CXRs and CT scans. The authors of [16] had utilized an ensembling approach via majority vote on classical machine learning models, using texture features extracted from the X-ray images. A hierarchical classification methodology for the multiple class problem had been utilized.
CNN based classifiers have been a popular choice for CADe in recent literature. In the work [17], the authors had adapted the Darknet-19 CNN architecture from YOLO object detection to work on X-ray scans, with evaluation of activation maps generated in the training process by an expert radiologist. In the work [18], the authors leveraged a CNN based architecture where the design of the network was explored through generative synthesis, a machine-driven exploration strategy.
The principle of transfer learning has been extensively explored when utilizing CNNs. It is useful for the application of deep learning in various domains, as in the work [19]. The authors of [20] had utilized a transfer learning based approach by harnessing the architecture and saved weights of state-of-the-art CNN classifiers on the ImageNet benchmark. In the study [21], the authors had investigated a large number of state-of-the-art CNN models with transfer learning along with image augmentation to enhance the limited number of X-ray samples. In the work [22], the ResNet-50 architecture was fine-tuned by progressively resizing, and data augmentation techniques were utilized. In [23], an Xception architecture based CNN transfer learning method had been utilized. In [24], a hierarchical classification methodology for a multi-class approach had been utilized. This multi-stage cascaded disease classification also leveraged transfer learning using CNNs. In [25], transfer learning had been utilized via the SqueezeNet CNN architecture, along with Bayesian optimization and data augmentation.
In the work [26], VGG architecture based CNNs with transfer learning had been ensembled with the empirical late fusion strategy of stacking. In the work [27], a capsule-based network had been used, a similar approach to CNNs, however including a “routing by agreement” component which was utilized to combine different capsules and identify spatial relations. Transfer learning was utilized on an X-ray based dataset. The authors of [28] proposed an ensemble approach exploring several empirical fusion schemes upon transfer learning based CNNs which were pruned for optimal hyperparameters.
Fuzzy logic is a natural choice for the ensemble of classifiers, given the uncertainty of decision scores from each of the learners. The principles of fuzzy measures and fuzzy integrals were first introduced in the work [29]. Building on those ideas, the authors of [30], introduced -measures. These state that the sum of all interactions of sources is 1, allowing the efficient calculation of . In the study [31], the authors had introduced the concept of the Choquet integral as a non-linear aggregation in the form of the generalization of product and addition rules, two empirical rules for classifier ensembles.
The concept of fuzzy integrals has been used to solve a variety of pattern recognition problems across various domains including human action recognition [32].
2.1. Research gaps
The existing supervised classification algorithms using machine learning, such as used in the work [16], are unable to harness the data-rich image modalities as effectively as the deep learning strategies such as the CNN. This is because in conventional machine learning, the features mostly need to be handcrafted and fed to the model, whereas in deep learning, the features are automatically extracted by the network such that its purpose is best suited. Thus, the handcrafted features are mostly not as efficient as those extracted by the deep learning architectures, which are delineated by the ability to learn complex representations from the image data, without any feature engineering by the researchers. The ensemble strategy used in the classical models, however, can also be enhanced by the proposed fuzzy ensemble framework in such cases where class probabilities are generated by the models.
While multiple works [20], [21], [23], [24], [25], [26], [27], [28], [33] have utilized transfer learning on standard CNN architectures for CADe, most of them do not harness complementary constituent base classifiers for the ensemble. Moreover, the ensemble strategies used do not support the dynamic refactoring of weights at inference time, and are mostly static which affects performance to an extent. The dynamic refactoring using the principles of fuzzy logic as introduced in the work [29] have been utilized as part of the proposed framework.
3. Proposed method
We approach the problem of COVID-19 CADe from biomedical images as a multi-class classification setting. The classifiers used in our approach are state-of-the-art CNNs, which are further supported by leveraging transfer learning to utilize the knowledge of existing pre-trained models. Besides, the principles of fuzzy logic have been used as a classifier combination technique, specifically based upon the Choquet fuzzy integral.
3.1. CNN classifiers
In this paper, the pre-trained convolutional blocks and the weights of some standard CNN architectures are utilized, followed by a deep learning based classifier which is trained end-to-end. The training phase involves fine-tuning the convolutional feature extractors, and training the classifier which is accelerated by the saved weights of the convolutional layers. This strategy has been followed to leverage the effective convolutional feature extractors with knowledge mined from the ImageNet dataset, as well as the reduced computational complexity leading to faster training.
We utilize the strategy of transfer learning to fine-tune pre-trained CNN models which were originally trained on the task of ImageNet Large Scale Visual Recognition Challenge (ILSVRC) dataset, to work on COVID-19 detection from CXRs. Thus, owing to the large size of the ImageNet dataset, the classifier is well-trained to recognize certain low-level features from the biomedical images even before being trained on them. This is also helpful when the dataset of the necessary domain is of limited size, as the knowledge from other domains upon which the networks are already trained on can be transferred to overcome the limitations of data in terms of size.
The CNN models are originally trained on the ImageNet dataset. However, the CXRs used in this study are of varying dimensions, while ImageNet input images are of the dimension 224 × 224. Subsequently, it is necessary to resize the images to be of a compatible dimension. Hence, at the boundaries of the images, black borders are added to ensure that they conform to a square input.
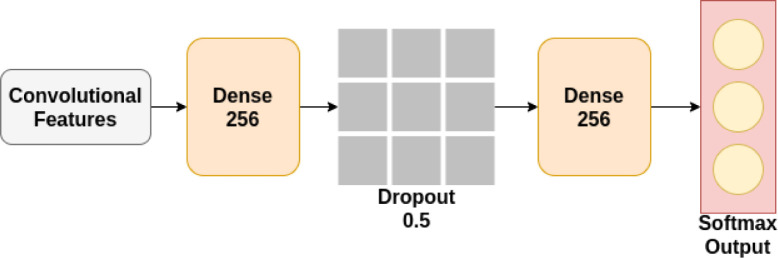
The same architecture of the original model has been adopted, except the layers following the convolutional layers. The weights of the convolutional layers are frozen, and additional layers are added after the feature extractors. The block diagram of the layers following the feature extractors is shown in Fig. 3.
Fig. 3.
Proposed classification network following state-of-the-art CNN architectures.
The last layer of each of the CNN models comprises of the Softmax activation function, which is defined by the following formula:
| (1) |
The output of this layer represents a probability distribution over the predicted output classes, which we refer to as the confidence score generated by the classifier.
An overview of each of the classifiers used in the present work has been provided in the upcoming subsections.
3.1.1. Inception V3
The inception module was proposed by the authors of [34] in 2014. This first version involves using multiple filter sizes on the same convolutional level, hence increasing the width of the network. The idea behind this was to negate the effect of the size of the object in question and improve the efficiency of the localization of information. It also includes an extra 1 × 1 convolution for dimensionality reduction. The GoogLeNet architecture proposed in the same paper includes nine such inception modules.
Inception V2 and V3 were proposed in the work [35]. Inception V2 includes certain enhancements to improve the computational speed of the network such as factorization of layers and expansion of the filter banks to make the network wider instead of deeper. Inception v3 uses RMSProp Optimizer, batch normalization in the auxiliary classifiers and label smoothing as well to improve performance of the network. For our purpose, we use this version of Inception (i.e., Inception V3) while using the SGD optimizer. The architecture of our Inception classifier consists of 11 separate inception modules stacked linearly, each of which consists of four separate networks at the first level. Each network consists of a series of convolutional, batch normalization and pooling layers of varying sizes. As mentioned before, the sizes of the filters for the layers in concern are appropriately factored and 1 × 1 convolutions are added. Factorization such as breaking up a filter into a and filter helps in reducing the time taken by the network and improves the performance of the network by a great margin. However, by altering the dimensions of a network drastically, crucial information may be lost. To handle this, the filter banks in the network are expanded so that the representational bottleneck is removed and the network is further wider than deeper. The four separate networks are then concatenated to get a single output which is then fed into the next module. The output from the final module gives the result.
3.1.2. Inception ResNet V2
Inspired by the performance of the ResNet, researchers came up with a hybrid model that took into account both the Inception and the ResNet models. Thus, Inception-ResNet was proposed in the work [36]. Inception-ResNet involves residual connections that feed the output of the convolutional layer to the input. It also includes explicit reduction blocks that are used to change the height and width of the grid.
In Inception ResNet V2, inception modules are used and we add residual connections that combine the convolution output of the inception module to the input. For this to work, the two of these must have the same dimensions. Hence 1 × 1 convolutions are used after the original convolutions to match the depths of the two. Pooling is replaced by residual connections, and the pooling is performed by the residual blocks as and when required. The residual activations are scaled appropriately to ensure that the network does not die out. The stem and hyperparameter settings are in line with Inception ResNet V2 as mentioned in the original paper.
3.1.3. DenseNet 201
DenseNet was proposed in the work [37] as an advancement over traditional CNNs. In conventional models, subsequent layers are connected by just one connection from its preceding layer in a feedforward fashion. DenseNet, however, exploits the outputs of all previous layers and uses them as input to generate the output for the current layer. This eliminates the vanishing gradient problem to a large extent while facilitates easier flow of information among the layers of the network and hence, the network needs fewer parameters to train.
For our purpose, we use the version DenseNet 201 where 201 indicates the number of layers in the network. The architecture starts off with conventional convolution and pooling layers followed by three sequences of dense blocks and transition layers. This is followed by a dense block and classification layer which gives us the output. As mentioned previously, in a dense block, each layer receives inputs from all previous layers. The difference with its counterparts lies in the number of convolutional layers in the third and fourth dense blocks. Overall, there are 201 layers in the network.
3.2. Fuzzy integral based classifier fusion
The fuzzy integral has obtained considerable success in the process of combining the classifiers’ outputs in various pattern recognition problems [32]. Fuzzy integrals exploit the decision scores obtained from individual classifiers as means to effectively produce a final output. The effectiveness comes as a result of the output being a set of confidence scores instead of singleton values. These scores are subsequently being combined with some measures for each classifier, with the measures assigned beforehand according to prior results. The combination process also allows a dynamic refactoring of weights for each classifier, dependent upon the scores.
As per the work reported in [29], the fuzzy measure concerned in our case lies in the range . Formally, a fuzzy measure is a real valued set function.
Each of the constituent CNN classifiers is responsible for generating a distinct confidence score. If the confidence scores are given by with N denoting the total number of scores, and , we can infer that the fuzzy measure is a function , with , . As a matter of fact, the following formula holds monotonically:
| (2) |
The identification of fuzzy measures as per the classic approach is a learning problem that scales exponentially with respect to the parameter , the number of information sources.
The concept of a specific type of measure is presented in the work [30]. It is known as the Sugeno fuzzy- measure with an additional characteristic that if , there exists , where —
| (3) |
From the previous definitions, we can find the value of by solving the following equation —
| (4) |
where, in our case, as each model generates a set of scores. So is the real root of a quadratic equation which is .
Hence, there is a need to identify only fuzzy measures instead of , as can be used to generate fuzzy measures for all coalitions of the inputs through Eq. (2). The reduction in the search space offered by Sugeno fuzzy- measures enables experimental determination of measures to be a computationally feasible strategy.
The Choquet integral described in the study [31] can be utilized to implement all linear algebraic combinations such as sum and product to be used as a generalized combination of empirical ensemble strategies such as average and multiplication. It is a form of a non-linear aggregation operation. Its performance is dependent on the choice of fuzzy measures. Inferring from the trivial definition of integration operator, it can be expanded as
| (5) |
where, the set of scores is permuted to such that
| (6) |
and is the subset of the highest scores in given by Sugeno fuzzy- measures. is used to generate in Algorithm 1.
Choquet integral utilizes both the fuzzy weight assigned to a classifier score along with the confidence of the score itself. It can be inferred that depends upon . Algorithm 1 entails many decisions in the entire process based on the different confidence scores, leading to a sensitive and exhaustive decision making process based on the coalitions of input scores which is proven to be much more effective than normal softmax probabilities. The time complexity of the process is , with representing the number of classifiers and representing the number of classes.
Among empirical ensemble based methods, the unweighted averaging scheme is the most commonly used. This has the natural advantage of reducing the variance of CNN classifiers, as deep learning based stochastic methods have high variance and low bias. However, when the ensemble network consists of heterogeneous learners such as in our case, even if the classifiers have a comparable performance, the unweighted averaging scheme is vulnerable to the situation in which a weak learner is given higher weightage, or when an overconfident candidate leads to incorrect predictions.
The weighted average ensemble strategy is another empirical strategy, wherein the weights for each learner is determined experimentally. This allows a degree of adaptive combination of learners, such as the case in which a weaker learner might be good at predicting certain classes.
However, the determination of the weights in this strategy is a one-time process. There is no opportunity to fine-tune or update these weights at the inference time, hence this strategy is not dynamic, unlike the principle of fuzzy fusion. To be specific, the fuzzy fusion allows fine-tuning of these weights for each classifier on the fly, and does so on the basis of the predictions for each individual sample of data. Subsets or coalitions of multiple classifier predictions are processed with their corresponding fuzzy measures at intermediate stages of the ensemble strategy. Thus, there is a scope for further refinement even after the fuzzy measures have been determined, unlike the weights in typical averaging methods.
4. Results and analysis
We have performed several experiments upon multiple datasets which demonstrate the robustness of our proposed method. In this section, we discuss empirical details about our method and interpret the results which we have obtained.
4.1. Data description
The proposed method is used upon four medical imaging datasets. The detail description of these datasets, used in the present work, are highlighted in the following subsections.
4.1.1. COVID-X (CXRs)
The database, namely COVID-X, introduced in the work [18], has been utilized in this paper. To the best of our knowledge, this is the largest open access COVID-19 X-ray dataset which is currently available, consisting of CXR images. This dataset has been generated by merging five different repositories of chest X-ray scans. It consists of three different classes of scans — COVID-19 positive patients, pneumonia infected patients, and normal patients. The distribution of data used in this current work is shown in Table 1. We have utilized the train-test split as per the labels provided by the authors.
Table 1.
Class-wise distribution of CXR samples in the COVID-X dataset.
| Phase | COVID-19 | Pneumonia | Normal | Total |
|---|---|---|---|---|
| Train | 468 | 5458 | 7966 | 13892 |
| Test | 100 | 594 | 885 | 1579 |
4.1.2. COVID-19 Radiography Database (CXRs)
We have used the database introduced in the work [21], called COVID-19 Radiography Database on Kaggle in this paper. The COVID-19 X-ray dataset is a balanced dataset, with the three classes comprising of COVID-19 positive patients, viral pneumonia infected patients, and normal patients. There are 1200 COVID-19, 1345 Viral Pneumonia and 1342 normal samples in this dataset, with a total of 3886 samples. We have utilized a 90-10 train-test split upon this dataset, to use the same split as other recent methods.
4.1.3. SARS-COV-2 CT Scan Dataset
We have utilized the dataset shared by the authors of the work [38], namely the SARS-COV-2 CT Scan Dataset on Kaggle. This dataset comprises of CT Scans of two categories of Brazilian patients — COVID-19 infected and non-infected patients. There are 1252 COVID-19 samples, and 1230 non COVID-19 samples in this dataset, with a total of 2482 samples. We have utilized both a 70-30 train-test split as well as a 5-fold cross validation split where each fold consists of 20% of the samples.
4.1.4. Montgomery Dataset (CXRs)
We have evaluated the proposed ensemble method upon the problem of Tuberculosis detection from CXRs as an additional test to evaluate the performance on a related biomedical imaging domain. The Montgomery Dataset shared by the authors of the work [39] has been utilized. This dataset comprises of Tuberculosis positive patients, and non affected patients. There are 58 Tuberculosis samples and 80 normal samples, with a total of 139 samples in this dataset. We have used a 80-20 train-test split to compare with recent methods.
4.2. Performance metrics
For evaluation of performance from our experiments, we have used a variety of performance metrics. These metrics are defined briefly as follows. In the mathematical formulas given below, denotes True Positive, denotes False Negative, denotes True Negative, and denotes False Negative.
-
•Accuracy — Here, accuracy is defined by the number of samples correctly classified out of the total number of samples expressed as a percentage. Mathematically,
(7) -
•Precision — Precision of a class denotes the number of samples of that class which are correctly classified out of the total number of samples which are classified as to belong to that class. Mathematically,
(8) -
•Recall — Recall of a class denotes the number of correctly classified samples of that class which are correctly classified out of the total number of samples which actually belong to that class. Mathematically, for a class denoted by class label ,
(9) -
•F1-Score — F1-Score is the harmonic mean of precision and recall. Mathematically,
(10) -
•Specificity — Specificity is denoted by the number of correct negative predictions out of the total number of negative samples. It is also known as the True Negative Rate. Mathematically,
(11) -
•False Positive Rate (FPR) — False Positive Rate is the number of incorrect positive predictions out of the total number of negative samples. Mathematically,
(12) -
•Area Under the Curve (AUC) — The AUC is a measure of the region under the Receiver Operator Characteristic (ROC) curve for binary classification. It measures the ability of the classifier to distinguish between classes. Mathematically,
(13) -
•Matthew’s Correlation Coefficient (MCC) — The MCC, also known as phi coefficient, is an evaluation metric that measures the difference between the actual values and predicted values. It is balanced performance metric which works well even when the classes are of different sizes, as the coefficient considers all four categories of prediction. It is equivalent to the chi-square statistic for a 2 × 2 contingency table. Mathematically,
(14)
4.3. Training configuration
In the transfer learning stage, all the CNN models are trained using the stochastic gradient descent algorithm having the momentum value as 0.9 and the initial learning rate as 0.01. The batch size is experimentally fixed to be . The models are trained till saturation of accuracy, with training continuing to a maximum of 50 epochs in the case of the DenseNet 201 model. The learning rate is decreased on plateau of performance by a factor of 0.7.
4.4. Choice of constituent learners
We have initially trained a large number of state-of-the-art CNN models to evaluate which architecture would be the best fit for the medical imaging classification task under consideration. Our experimental results, as shown in Table 2, illustrates that the DenseNet 201 architecture achieves the highest performance. Hence this model has been included in the ensemble.
Table 2.
Comparison of base learners on the SARS-COV 2 CT Scan Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | AUC (%) | MCC (%) | McNemar’s Test -value |
|---|---|---|---|---|---|---|---|---|---|
| DenseNet 201 | 98.79 | 98.38 | 99.18 | 98.78 | 98.40 | 1.59 | 98.79 | 97.58 | – |
| Inception v3 | 97.18 | 97.02 | 97.28 | 98.92 | 97.07 | 2.92 | 97.18 | 94.36 | 0.0247 |
| Inception ResNet v2 | 97.58 | 97.30 | 97.83 | 97.56 | 97.34 | 2.65 | 97.58 | 95.16 | 0.0323 |
| ResNet 152 v2 | 96.24 | 96.20 | 96.20 | 96.20 | 96.27 | 3.72 | 96.24 | 92.48 | 0.0085 |
| EfficientNet B7 | 97.44 | 98.88 | 95.93 | 97.38 | 98.93 | 1.06 | 97.43 | 94.93 | 0.0441 |
| Xception | 97.18 | 98.06 | 96.20 | 97.12 | 98.13 | 1.86 | 97.17 | 94.37 | 0.0247 |
| VGG 19 | 97.71 | 97.82 | 97.56 | 97.69 | 97.87 | 2.12 | 97.71 | 95.43 | 0.05330 |
We have performed a non-parametric statistical hypothesis test, the McNemar’s test [40], to analyse the performance of the CNN architectures, compared to the DenseNet 201 architecture. The null hypothesis in this statistical test is that the different classifiers have the same error rate based upon the predictions made upon the test set. Table 2 shows the results of McNemar’s test on the SARS COV-2 CT Scan dataset. A lower -value indicates that the distribution of the predictions made by the classifiers are dissimilar, and hence complementary.
We have further included the Inception v3 architecture within the ensemble as it shows significantly high performance, while showing a small -value when compared to DenseNet201 as observed in Table 2. Moreover, the Inception ResNet v2 architecture is also included within the ensemble framework as it also achieves impressive performance, while being statistically verified to be dissimilar to the chosen DenseNet 201 architecture. It is to be noted that even if the -value obtained by the ResNet152 v2 architecture is lower than Inception ResNet v2, the former model achieves much superior performance in terms of other metrics such as accuracy and F1-Score, which is why we have chosen it to be the final member of the ensemble.
The confusion matrices generated by the constituent classifiers, namely Inception v3, Inception ResNet v2, and DenseNet 201 are shown in Tables 3, Table 4, Table 5 respectively. It can be seen from the predictions made upon the validation set that the classifiers offer differing performance metrics. The source of errors for the classifiers are different, as upon certain samples one classifier makes the right prediction, while failing upon other samples which another classifier correctly classifies.
Table 3.
Confusion matrix for Inception V3 on SARS-COV 2 CT Scan Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 365 |
11 |
|
| 10 | 359 | ||
Table 4.
Confusion matrix for Inception ResNet v2 on SARS-COV 2 CT Scan Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 366 |
10 |
|
| 8 | 361 | ||
Table 5.
Confusion matrix for DenseNet 201 on SARS-COV 2 CT Scan Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 370 |
6 |
|
| 3 | 366 | ||
Our next experiment compares the distribution of the predictions made by the constituent classifiers to that of the proposed ensemble method. The null hypothesis in this case is that the distribution of the predictions made by the ensemble and that made by the constituents has the same error rate. To reject the null hypothesis, the -value in McNemar’s test should be below a certain threshold, which we have chosen as 5%. According to Table 6, for every case, the -value is below 0.05. Thus, the null hypothesis is rejected for all the cases which verifies that the proposed ensemble framework captures the complementary information supplied by the considered classifiers. This is a contributory factor to the superior predictions of the proposed method, which is dissimilar to any of the contributing models.
Table 6.
McNemar’s test on the SARS COV-2 CT Scan Dataset compared to ensemble model.
| CNN Model | McNemar’s Test -value |
|---|---|
| Inception v3 | 0.0360 |
| Inception ResNet v2 | 0.0442 |
| DenseNet 201 | 0.0483 |
To confirm the dissimilarity among the decision scores generated by the three constituent classifiers, we use KL divergence, also known as relative entropy. It is an asymmetrical measure of dissimilarities between two probability distributions. For distributions and on same probability space , we have KL divergence from to as
| (15) |
As , we have a symmetrical measure known as JS divergence derived from the KL divergence. It is given as
| (16) |
where, . KL and JS divergences among the different scores of the CNN classifiers on SARS COV-2 CT Scan Dataset are shown in Table 7.
Table 7.
KL and JS divergences among CNN classifiers on SARS COV-2 CT Scan Dataset.
| Distribution | Distribution | ||
|---|---|---|---|
| Inception V3 | DenseNet 201 | 0.3452 | 0.1020 |
| DenseNet 201 | Inception V3 | 0.2202 | |
| Inception ResNet v2 | DenseNet 201 | 0.3245 | 0.1262 |
| DenseNet 201 | Inception ResNet v2 | 0.2506 | |
| Inception V3 | Inception ResNet v2 | 0.3330 | 0.0983 |
| Inception ResNet v2 | Inception V3 | 0.3100 | |
4.5. Comparison of Fuzzy ensemble
Table 8, Table 9 show the choice of fuzzy measures which are experimentally determined for the ensemble strategy in our method for the COVID-X dataset. The fuzzy measure is a real valued set function for each confidence score, and it is integral to the performance of the proposed method. The other empirical fusion strategies compared are unweighted average, weighted average, Hadamard product or element-wise multiplication, and maximum. Table 10 highlights the advantage offered by fuzzy integral based ensembling over empirical fusion strategies through superior performance.
Table 8.
Configuration for fuzzy ensemble on the 3-class classification problem on the COVID-X Dataset.
| CNN Model | Accuracy (%) | Fuzzy Measure |
|---|---|---|
| Inception v3 | 95.06 | 0.038 |
| Inception ResNet v2 | 94.62 | 0.015 |
| DenseNet 201 | 95.88 | 0.074 |
Table 9.
Configuration for fuzzy ensemble on the 2-class classification problem on the COVID-X Dataset.
| CNN Model | Accuracy (%) | Fuzzy Measure |
|---|---|---|
| Inception v3 | 99.36 | 0.030 |
| Inception ResNet v2 | 99.36 | 0.043 |
| DenseNet 201 | 99.36 | 0.026 |
Table 10.
Comparison with empirical ensemble methods on the COVID-X Dataset.
| Ensemble Method | Accuracy (%) 3-Class | Accuracy (%) 2-Class |
|---|---|---|
| Maximum | 94.68 | 99.36 |
| Multiplication | 95.22 | 99.36 |
| Average | 95.87 | 99.41 |
| Weighted Average | 96.20 | 99.46 |
| Fuzzy | 96.39 | 99.49 |
From Table 10, it is to be noted that the dynamic assignment of weights using the fuzzy strategy yields better results than other methods. This is reflective of the fact that our method can adjust the weights in the ensemble strategy on the fly according to the confidence of the individual classifiers as opposed to the other methods which are not capable of doing so. This justifies the better performance for the Fuzzy ensemble.
4.6. Performance
We have evaluated the proposed method on multiple datasets and reported multiple metrics for our experiments.
4.6.1. COVID-X CXR dataset
The confusion matrices generated by the prediction of the proposed method for 3-class and 2-class classification problems are shown in Table 11, Table 12 respectively.
Table 11.
Confusion matrix for 3-class classification on COVID-X.
| Predicted |
||||
|---|---|---|---|---|
| 95 |
5 |
0 |
||
| True | 0 |
870 |
15 |
|
| 2 | 35 | 557 | ||
Table 12.
Confusion Matrix for 2-class classification on COVID-X dataset.
| Predicted |
|||
|---|---|---|---|
| True | 93 |
7 |
|
| 1 | 1478 | ||
Table 13, Table 14 show the class-wise performance of the proposed method.
Table 13.
Performance Metrics for 3-class classification on COVIDx dataset.
| Metric (%) | COVID-19 | Normal | Pneumonia | Overall |
|---|---|---|---|---|
| Accuracy | 99.56 | 96.51 | 96.70 | 96.39 |
| Precision | 97.94 | 95.60 | 97.38 | 96.97 |
| Recall | 95.00 | 98.30 | 93.77 | 95.69 |
| F1-Score | 96.44 | 96.93 | 95.54 | 96.30 |
| Specificity | 99.86 | 94.24 | 98.47 | 97.52 |
| FPR | 0.135 | 5.764 | 1.523 | 2.474 |
| AUC | 97.43 | 96.27 | 96.12 | – |
| MCC | 96.22 | 92.95 | 92.97 | 93.31 |
Table 14.
Performance Metrics for 2-Class classification on COVIDx dataset.
| Metric (%) | COVID-19 | Non COVID-19 | Overall |
|---|---|---|---|
| Accuracy | 99.49 | 99.49 | 99.49 |
| Precision | 98.94 | 99.52 | 99.23 |
| Recall | 93.00 | 99.93 | 96.46 |
| F1-Score | 95.88 | 99.73 | 97.80 |
| Specificity | 93.00 | 99.93 | 96.46 |
| FPR | 0.068 | 7.00 | 3.53 |
| AUC | 96.46 | 96.46 | – |
| MCC | 95.66 | 95.66 | 95.66 |
From the results, we note that our method classifies most of the samples correctly as demonstrated by the high accuracy of our method. We further note that the precision is especially high for the COVID-19 class which proves that it is very highly likely that the patients detected positive for COVID-19 indeed have the disease. The other performance metrics indicate good performance as well which, combined with the overall high accuracy, denote the robustness of our method.
4.6.2. COVID-19 Radiography Database
The confusion matrix generated by the predictions of the proposed method upon the COVID-19 Radiography Database is shown in Table 15. The performance metrics of the proposed method is shown in Table 16.
Table 15.
Confusion matrix for classification on COVID-19 Radiography Database.
| Predicted |
||||
|---|---|---|---|---|
| 120 |
0 |
0 |
||
| True | 0 |
133 |
1 |
|
| 0 | 1 | 133 | ||
Table 16.
Performance Metrics for Classification on COVID-19 Radiography Database.
| Metric (%) | COVID-19 | Normal | Viral Pneumonia | Overall |
|---|---|---|---|---|
| Accuracy | 100.00 | 99.46 | 99.46 | 99.49 |
| Precision | 100.00 | 99.25 | 99.25 | 99.50 |
| Recall | 100.00 | 99.25 | 99.25 | 99.50 |
| F1-Score | 100.00 | 99.25 | 99.25 | 99.50 |
| Specificity | 100.00 | 99.61 | 99.61 | 99.74 |
| FPR | 0.00 | 0.394 | 0.394 | 0.262 |
| AUC | 100.00 | 99.43 | 99.43 | – |
| MCC | 100.00 | 98.86 | 98.86 | 99.22 |
Upon this dataset, the proposed method have achieved exemplary performance. In particular, not a single COVID-19 sample has been misclassified, and there are only two cases where there is a confusion between the Normal and Viral Pneumonia classes. We see that the ensemble strategy is also successful in distinguishing between COVID-19 and Viral Pneumonia, which is a difficult task as these are both of viral origin. The exceptional results are manifested through the extremely low error rate for all three of the classes in this dataset.
4.6.3. SARS-COV 2 CT Scan Dataset
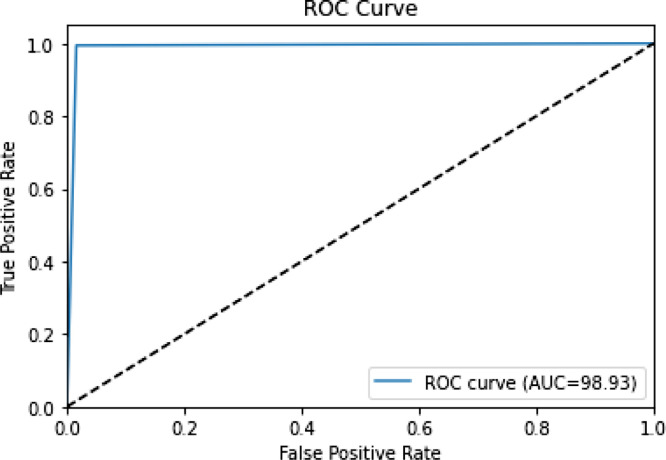
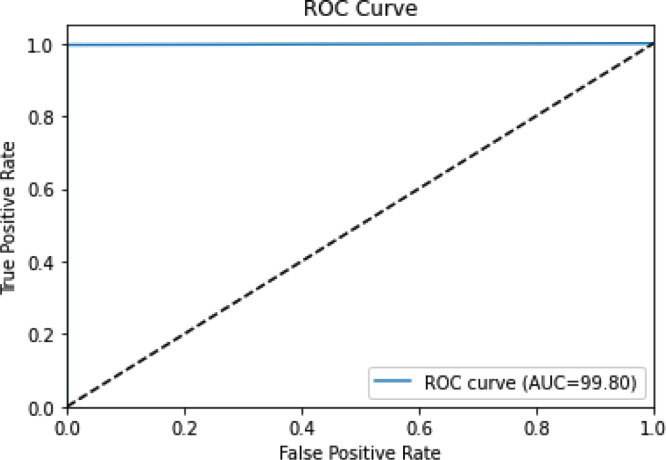
The confusion matrix generated by the predictions of the proposed method upon the SARS-COV 2 CT Scan dataset is shown in Table 17. The performance metrics of our ensemble method along with the constituent base learners are depicted in Table 18. The ROC curve generated by our method is shown in Fig. 4.
Table 17.
Confusion matrix for classification on SARS-COV 2 CT Scan Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 370 |
6 |
|
| 2 | 367 | ||
Table 18.
Performance metrics upon SARS-COV 2 CT Scan Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| COFE-Net | 98.93 | 98.40 | 99.46 | 98.92 | 98.40 | 1.59 | 98.93 | 97.86 |
| Inception V3 | 97.18 | 97.02 | 97.28 | 98.92 | 97.07 | 2.92 | 97.18 | 94.36 |
| Inception ResNet V2 | 97.58 | 97.30 | 97.83 | 97.56 | 97.34 | 2.65 | 97.58 | 95.16 |
| DenseNet 201 | 98.79 | 98.38 | 99.18 | 98.78 | 98.40 | 1.59 | 98.79 | 97.58 |
Fig. 4.
ROC Curve for SARS-COV 2 CT Scan Dataset.
We note that along with the high classification accuracy achieved, the proposed method yields good performance on the rest of the metrics as well, which experimentally validates the robustness of the approach.
4.6.4. Montgomery Dataset
The confusion matrix generated by the predictions of the proposed method on the Montgomery Dataset are shown within Table 19. Table 20 highlights the impressive performance metrics achieved by the method.
Table 19.
Confusion matrix for classification on the Montgomery Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 16 |
0 |
|
| 1 | 11 | ||
Table 20.
Performance Metrics on the Montgomery Dataset.
| Metric (%) | Normal | Tuberculosis | Overall |
|---|---|---|---|
| Accuracy | 96.43 | 96.43 | 96.43 |
| Precision | 94.11 | 100.00 | 97.06 |
| Recall | 100.00 | 91.67 | 95.83 |
| F1-Score | 96.97 | 95.65 | 96.31 |
| Specificity | 91.67 | 100.00 | 95.83 |
| FPR | 8.333 | 0.000 | 4.167 |
| AUC | 95.83 | 95.83 | – |
| MCC | 92.88 | 92.88 | 92.88 |
It can be noted that the ensemble strategy in the present work produces extremely sound results upon this related biomedical imaging domain. Only one sample upon the test set has been misclassified. Hence, the proposed method is successful for multiple classification problems and can be adapted for any requisite purposes by the users.
4.7. Ablation study
We have performed an ablation study to investigate the relative contribution of the different architectural components in the proposed method. Along with the individual constituent learners, we have also considered the ensemble of the pairs of classifiers. The performance metrics obtained from these experiments are shown in Table 21
Table 21.
Results of the ablation study upon SARS-COV 2 CT Scan Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| Inception V3 | 97.18 | 97.02 | 97.28 | 98.92 | 97.07 | 2.92 | 97.18 | 94.36 |
| Inception ResNet V2 | 97.58 | 97.30 | 97.83 | 97.56 | 97.34 | 2.65 | 97.58 | 95.16 |
| DenseNet 201 | 98.79 | 98.38 | 99.18 | 98.78 | 98.40 | 1.59 | 98.79 | 97.58 |
| Inception V3 and Inception ResNet V2 | 97.71 | 96.56 | 98.91 | 97.72 | 96.54 | 3.457 | 97.72 | 95.46 |
| Inception V3 and DenseNet 201 | 98.79 | 98.38 | 99.18 | 98.78 | 98.40 | 1.595 | 98.79 | 97.58 |
| Inception ResNet V2 and DenseNet 201 | 98.79 | 98.64 | 98.91 | 98.78 | 98.67 | 1.329 | 98.79 | 97.58 |
| Ensemble of all three | 98.93 | 98.40 | 99.46 | 98.92 | 98.40 | 1.59 | 98.93 | 97.86 |
It can be noted that on the SARS COV-2 CT Scan Dataset, the choice of a complementary classifier as a pair with DenseNet 201 has not significantly boosted the performance as compared to a singular classifier. However, when the ensemble of three classifiers is taken, the Choquet integral algorithm is able to run for an additional iteration, which results in superior results and increases the performance of the proposed method.
Further results from the ablation study on the COVID-X dataset are presented in Table 22, Table 23. Owing to the larger scale of this dataset, the results herein are more representative of our method. The efficacy of using all three classifiers is demonstrated Through these results.
Table 22.
Results of the ablation study for three-class classification upon COVID-X Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | MCC (%) |
|---|---|---|---|---|---|---|---|
| Inception V3 | 95.06 | 96.77 | 94.01 | 95.30 | 95.50 | 3.491 | 90.86 |
| Inception ResNet V2 | 97.58 | 93.07 | 91.81 | 92.42 | 96.59 | 3.41 | 90.05 |
| DenseNet 201 | 95.88 | 96.03 | 95.02 | 95.50 | 97.22 | 2.77 | 92.38 |
| Inception V3 and Inception ResNet V2 | 95.95 | 94.88 | 94.42 | 94.65 | 97.44 | 2.557 | 92.50 |
| Inception V3 and DenseNet 201 | 96.07 | 96.76 | 95.15 | 95.92 | 97.30 | 2.700 | 92.73 |
| Inception ResNet V2 and DenseNet 201 | 96.20 | 95.28 | 94.36 | 94.81 | 97.60 | 2.393 | 92.96 |
| Ensemble of all three | 96.39 | 96.97 | 95.69 | 96.30 | 97.52 | 2.474 | 93.31 |
Table 23.
Results of the ablation study for two-class classification upon COVID-X Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| Inception V3 | 99.36 | 98.67 | 95.93 | 97.25 | 95.93 | 4.06 | 95.93 | 94.56 |
| Inception ResNet V2 | 99.36 | 99.15 | 95.46 | 97.22 | 95.46 | 4.53 | 95.46 | 94.56 |
| DenseNet 201 | 99.36 | 98.67 | 95.93 | 97.25 | 95.93 | 4.06 | 95.93 | 94.56 |
| Inception V3 and Inception ResNet V2 | 99.36 | 99.15 | 95.46 | 97.22 | 95.46 | 4.534 | 95.46 | 94.54 |
| Inception V3 and DenseNet 201 | 99.43 | 98.71 | 96.43 | 97.54 | 96.43 | 3.56 | 96.43 | 95.11 |
| Inception ResNet V2 and DenseNet 201 | 99.43 | 99.19 | 95.96 | 97.51 | 95.96 | 4.03 | 95.96 | 95.10 |
| Ensemble of all three | 99.49 | 99.23 | 96.46 | 97.80 | 96.46 | 3.53 | 96.46 | 95.66 |
4.8. K-Fold cross validation
We have performed the K-Fold cross validation to verify the robustness of the proposed method. We have prepared 5 folds from the SARS COV-2 CT Scan dataset. Each fold consists of 20% of the samples from the dataset. It has been ensured that each fold contains an equivalent proportion of the two classes, i.e stratified K-Fold cross validation has been followed. The results of this experiment are shown in Table 24. The ROC curve obtained for the first fold is shown in Fig. 5 while the corresponding confusion matrix is in Table 25.
Table 24.
K-Fold performance metrics upon SARS-COV 2 CT Scan Dataset.
| Fold Number | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | FPR (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 99.80 | 100.00 | 99.59 | 99.79 | 100.00 | 0.000 | 99.79 | 99.59 |
| 2 | 99.60 | 100.00 | 99.19 | 99.59 | 100.00 | 0.000 | 99.59 | 99.20 |
| 3 | 99.79 | 99.59 | 100.00 | 99.79 | 99.60 | 0.0040 | 99.80 | 99.59 |
| 4 | 99.59 | 99.19 | 100.00 | 99.59 | 99.20 | 0.0079 | 99.60 | 99.35 |
| 5 | 99.60 | 98.38 | 99.60 | 99.60 | 99.60 | 0.0040 | 99.60 | 99.49 |
| Average | 99.68 | 98.38 | 99.68 | 99.68 | 99.68 | 0.0032 | 99.68 | 99.44 |
Fig. 5.
ROC curve for first fold on SARS-COV 2 CT Scan Dataset.
Table 25.
Confusion matrix for first fold on SARS COV-2 CT Scan Dataset.
| Predicted |
|||
|---|---|---|---|
| True | 250 |
0 |
|
| 1 | 244 | ||
As evident from our results, we achieve high performance across each of the folds. Hence, our proposed method is not prone to overfitting, and the results achieved are extremely sound.
4.9. Comparison with some past methods
The proposed method in the present work has been compared with multiple other high performing methods which have been recently published.
4.9.1. COVID-X
Table 26 shows comparison with other methods that use the same dataset from [18] as the proposed work. Table 27, Table 28 show comparison with methods on other COVID-19 CXR datasets for the multi-class and binary classification problems.
Table 26.
Comparison with state-of-the-art methods for COVID-19 CADe on the COVID-X dataset [18].
| Method | Data Distribution | Accuracy (%) |
|---|---|---|
| COVID-Net [18] | 358 COVID-19, 5538 Pneumonia, 8066 Normal | 93.3 |
| COVID-ResNet [22] | 68 COVID-19, 1591 Pneumonia, 1203 Normal | 96.23 |
| COVID-CAPS [27] | Not specified | 98.3 |
| COVIDiagnosis-Net [25] | 76 COVID-19, 4290 Pneumonia, 1583 Normal | 98.26 |
| COFE-Net | 568 COVID-19, 6052 Pneumonia, 8851 Normal | 96.39 |
| COFE-Net | 568 COVID-19, 14903 nonCOVID-19 | 99.49 |
Table 27.
Comparison with state-of-the-art methods for COVID-19 CADe on multi-class classification.
| Method | Data Distribution | Accuracy (%) |
|---|---|---|
| Transfer Learning Dataset 1 [20] | 224 COVID-19, 700 Pneumonia, 504 Normal | 93.48 |
| Transfer Learning Dataset 2 [20] | 224 COVID-19, 714 Pneumonia, 504 Normal | 94.72 |
| Majority Voting ML [16] | 782 COVID-19, 782 Pneumonia, 782 Normal | 93.41 |
| DenseNet201 [21] | 423 COVID-19, 1485 Pneumonia, 1579 Normal | 97.94 |
| Cascaded CNNs [24] | 69 COVID-19, 79 Bact. Pneumonia, 79 Viral Pneumonia, 79 Normal | 99.9 |
| CoroNet Dataset 1 [23] | 284 COVID-19, 657 Pneumonia, 310 Normal | 95.0 |
| CoroNet Dataset 2 [23] | 157 COVID-19, 500 Pneumonia, 500 Normal | 90.21 |
| Stacked VGG Ensemble [26] | 219 COVID-19, 1345 Pneumonia, 1341 Normal | 97.4 |
| Pruned Weighted Average [28] | 313 COVID-19, 8792 Pneumonia, 7595 Normal | 99.01 |
| COFE-Net | 568 COVID-19, 6052 Pneumonia, 8851 Normal | 96.39 |
Table 28.
Comparison with state-of-the-art methods for COVID-19 CADe on binary-class classification.
| Method | Data Distribution | Accuracy (%) |
|---|---|---|
| Transfer Learning Dataset 1 [20] | 224 COVID-19, 1204 nonCOVID-19 | 98.75 |
| Transfer Learning Dataset 2 [20] | 224 COVID-19, 1214 nonCOVID-19 | 96.78 |
| DenseNet201 [21] | 423 COVID-19, 3064 nonCOVID-19 | 99.70 |
| CoroNet Dataset 1 [23] | 284 COVID-19, 967 nonCOVID-19 | 99.0 |
| DarkCovidNet [17] | 127 COVID-19, 500 nonCOVID-19 | 98.08 |
| Majority Voting ML [16] | 782 COVID-19, 1564 nonCOVID-19 | 98.06 |
| Stacked VGG Ensemble [26] | 219 COVID-19, 2686 nonCOVID-19 | 99.48 |
| Class Decomposition [41] | 116 COVID-19, 80 nonCOVID-19 | 97.35 |
| COFE-Net | 568 COVID-19, 14903 nonCOVID-19 | 99.49 |
The COVID-X dataset is comprised of five different open source datasets which are continuously updated. The number of samples in the data distribution used in the current work is larger than any of the compared methods, as it is more updated.
From the comparison, we note that for methods which have been reported using the same as well as different datasets, the proposed method outperforms most of the other methods. For multi-class classification, we note that there are very few state-of-the-art methods that are able to outperform the proposed method and the margin for that is small. It must be noted that due to the lack of a standardized benchmark dataset, past methods cannot be directly compared. Even so, the proposed method has been validated to achieve impressive performance with a considerably larger number of CXR samples than all compared methods. For binary-class classification, the proposed method outperforms all state-of-the-art methods and achieves an extremely sound accuracy. Overall, we can safely comment that the results are extremely competitive and the proposed method is technically sound and robust.
4.9.2. COVID-19 Radiography Database
Table 29 shows the comparison with state-of-the-art methods upon the COVID-19 Radiography Database. The proposed method exceeds the performance of competing methods by a margin of greater than 1% accuracy, which is a significant gain. Hence, the method in the present work can be said to be superior to all the methods which have validated their experiments upon this dataset.
Table 29.
Comparison with state-of-the-art methods on the COVID-19 Radiography Database.
4.9.3. SARS-COV-2 CT scans
The present work has been compared with seven different high performing methods on the SARS-COV 2 CT Scan dataset, and has exceeded them in performance by a considerable margin. Table 30 shows comparison of these methods with the current work. Specifically, the proposed method achieves a higher F1-score compared to the previous state-of-the-art method by a margin of greater than 2%, which is an essential increase when considering the nature of the classification problem.
Table 30.
Comparison with state-of-the-art methods on the SARS-COV 2 CT Scan Dataset.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) |
|---|---|---|---|---|---|
| xDNN [44] | 88.60 | 89.70 | 88.60 | 89.15 | – |
| Transfer Learning [45] | 94.04 | 95.00 | 94.00 | 94.50 | 95.86 |
| Bi-stage FS [13] | 95.32 | 95.30 | 95.30 | 95.30 | – |
| DenseNet 201 [46] | 96.25 | 96.29 | 96.29 | 96.29 | 96.21 |
| KarNet [47] | 97.00 | 95.00 | 98.00 | 97.00 | 95.00 |
| Gabor Ensemble [48] | 97.40 | 99.10 | 95.50 | 97.30 | – |
| COFE-Net | 98.93 | 98.40 | 99.46 | 98.92 | 98.40 |
4.9.4. Montgomery dataset
Table 31 shows the comparison of the proposed method with other recent strategies upon the Montgomery dataset. The ensemble strategy in the proposed method has shown appreciable performance on this dataset while outperforming most recent methods in terms of classification accuracy. With larger samples sizes for training, there is more variance in the classifiers, so the ensemble performance of our method is expected to increase upon larger datasets.
Table 31.
Comparison with state-of-the-art methods on the Montgomery Dataset.
4.10. Error analysis
While the proposed ensemble strategy in the present work is able to achieve results which are beyond the reach of the constituent classifiers, there are certain sample images upon which the strategy fails. Some of these sources of errors and their probable causes are discussed in this section.
Fig. 6 displays a sample CT scan image which was misclassified as COVID-19 positive. It is to be noted that unlike other CT scan images, this sample image is of a very high contrast, and subsequently very few distinguishing features can be found within the lobes. Hence, the CNN feature extractors are not able to gather useful information so the proposed strategy failed on this anomalous sample.
Fig. 6.
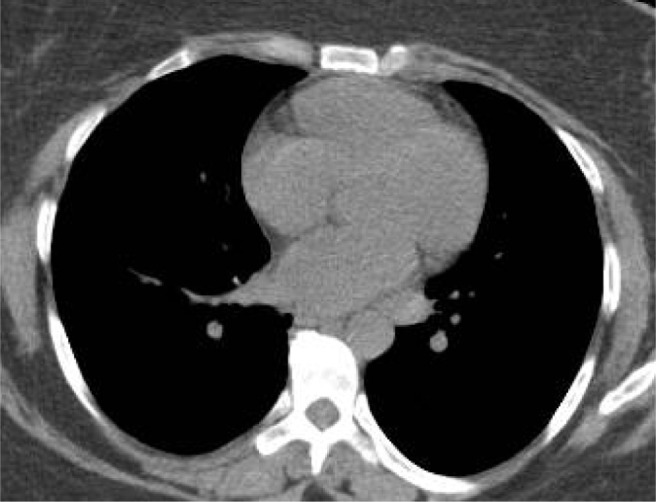
Misclassified CT Scan sample with true class non COVID-19.
Fig. 7 displays a sample CT scan image which was misclassified as COVID-19 negative. Upon visual inspection, it is to be noted that this sample lacks the characteristic ground glass opacity which is a major distinguishing feature in COVID-19. Hence it is possible that the models were not able to concentrate about the specific local features within each lobe, and instead only utilized the lack of the common distinguishing feature to make a prediction.
Fig. 7.
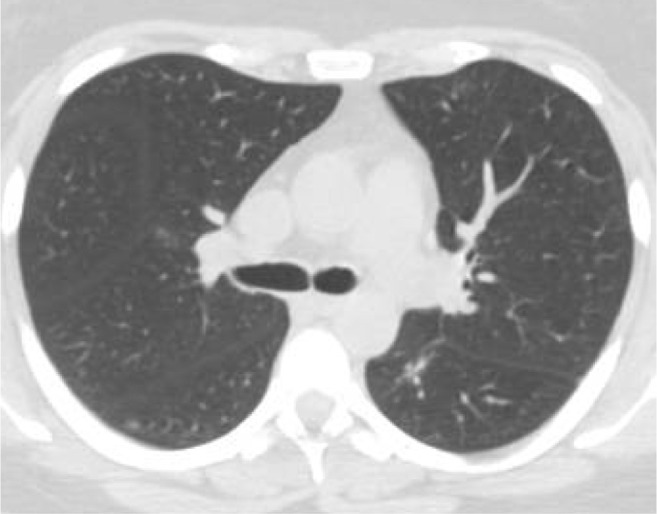
Misclassified CT Scan sample with true class COVID-19.
Fig. 8 displays a sample CXR image which was misclassified as Normal. It can be noted that there are certain occlusions along the sternum of the patient which might be a contributory factor to the misclassification.
Fig. 8.
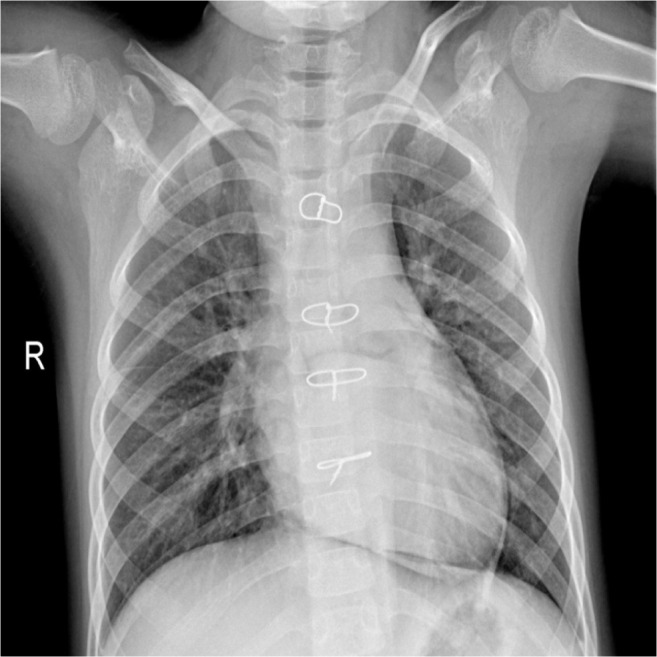
Misclassified CXR sample with true class Viral Pneumonia.
5. Conclusion
This paper has addressed the problem of screening of COVID-19 CXRs and CT scans, hence providing a computer-assisted prediction upon biomedical measurements. Initially, transfer learning upon complementary state-of-the-art CNNs has been utilized to generate decision scores from the medical images. Next, a fuzzy ensemble framework through the Choquet integral has been used to combine decision scores of CNNs through an adaptive combination strategy depending upon the confidence of each decision score. Results upon multiple COVID-19 datasets highlight the superior performance over empirical ensemble methods. The proposed framework can be utilized to enhance the predictive power of the existing methods, which by large do not follow a classifier fusion approach. The fuzzy integral based ensemble strategy we have utilized is sensitive to the dynamic measurements of the confidence of each classifier in the ensemble. This is in contrast to other traditionally used strategies which are not sensitive and flexible to the generated measurements at runtime.
While we experimentally verify our approach upon CXR and CT scan samples for COVID-19, pneumonia, and tuberculosis diseases, it is to be noted that the proposed framework is a robust detection system for any form of biomedical measurements. In fact, using other measurements such as MRI scans would also be a viable input for the proposed ensemble framework. Furthermore, the fuzzy integral based confidence aggregation is an ensemble strategy which is sensitive to the confidence of individual classifiers at runtime. This sensitivity to dynamic measurements is another desirable characteristic which makes the proposed framework suitable for not only biomedical imaging, but also other domains of measurement from sensor data, wherein ensemble learning may find use.
To summarize, this paper proposes an ensemble network, known as COFE-Net, of three CNN-based classifiers, which are chosen to be complimentary through various parameters and experiments, for COVID-19 Detection. The results from the complimentary set of classifiers are fused using a fuzzy ensembling strategy using the Choquet Integral Method which dynamically assigns weights to the component CNNs based on the confidence scores of their predictions. Exhaustive experimentation on a variety of datasets using various metrics prove the robustness of our method and it outperforms the state-of-the-art in the domain on most occasions. It obtains an accuracy of 96.39% for 3-class classification and 99.49% for 2-class classification on the COVIDx dataset and performs appreciably well on most datasets in the domain. Additionally, it also performs well on the Montgomery dataset for Tuberculosis detection as well with an accuracy of 96.43% which proves that our method can adapt to other field of medical imaging as well.
The proposed method has some limitations. These include the empirical determination of fuzzy measures, which is the basis of the fuzzy combination mechanism. Although the use of the Sugeno fuzzy- measure has highly reduced the search space, it is still a time consuming process to experimentally identify the optimal measurements. Another limitation of the proposed method is that the CNN classifiers involved utilize globally extracted features from the whole input images, while the distinguishing elements may be concentrated in a specific part of the image.
Going forward, we would like to use an attention mechanism to improve the focus on the affected lung regions in the image so that more accurate features can be extracted. We would also like to extend this method to other areas of healthcare where it can make an impact to help the biomedical community at large.
CRediT authorship contribution statement
Avinandan Banerjee: Software, Methodology, Formal analysis, Writing – original draft. Rajdeep Bhattacharya: Data curation, Software, Methodology, Writing – original draft. Vikrant Bhateja: Writing – review & editing, Resources, Visualization, Project administration. Pawan Kumar Singh: Conceptualization, Validation, Resources, Data curation, Writing – review & editing, Supervision. Aime’ Lay-Ekuakille: Investigation, Supervision, Funding acquisition. Ram Sarkar: Investigation, Supervision, Project administration.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
We would like to thank the Centre for Microprocessor Applications for Training, Education and Research (CMATER) research laboratory of the Computer Science and Engineering Department, Jadavpur University, Kolkata, India for providing us the infrastructural support.
References
- 1.Saxena R., Jadeja M., Bhateja V. Propagation analysis of COVID-19: An SIR model-based investigation of the pandemic. Arab. J. Sci. Eng. 2021:1–13. doi: 10.1007/s13369-021-05904-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lay-Ekuakille A., Chiffi C., Celesti A., Rahman M.Z.U., Singh S.P. Infrared monitoring of oxygenation process generated by robotic verticalization in bedridden people. IEEE Sens. J. 2021;21 doi: 10.1109/JSEN.2021.3068670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Conversano F., Franchini R., Lay-Ekuakille A., Casciaro S. In vitro evaluation and theoretical modeling of the dissolution behavior of a microbubble contrast agent for ultrasound imaging. IEEE Sens. J. 2011;12:496–503. [Google Scholar]
- 4.Alarifi A., Alwadain A. Computer-aided cancer classification system using a hybrid level-set image segmentation. Measurement. 2019;148 [Google Scholar]
- 5.Pal B., Bhateja V., Johri A., Pal D., Satapathy S.C. Smart Computing Techniques and Applications. Springer; 2021. Glaucoma detection using morphological filters and GLCM features; pp. 627–635. [Google Scholar]
- 6.Loey M., Manogaran G., Taha M.H.N., Khalifa N.E.M. A hybrid deep transfer learning model with machine learning methods for face mask detection in the era of the COVID-19 pandemic. Measurement. 2021;167 doi: 10.1016/j.measurement.2020.108288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ezhilan M., Suresh I., Nesakumar N. SARS-CoV, MERS-CoV and SARS-CoV-2: A diagnostic challenge. Measurement. 2021;168 doi: 10.1016/j.measurement.2020.108335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., Tao Q., Sun Z., Xia L. Correlation of chest CT and RT-PCR testing in coronavirus disease 2019 (COVID-19) in China: a report of 1014 cases. Radiology. 2020 doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tuncer S.A., Ayyıldız H., Kalaycı M., Tuncer T. Scat-NET: COVID-19 diagnosis with a CNN model using scattergram images. Comput. Biol. Med. 2021 doi: 10.1016/j.compbiomed.2021.104579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goel T., Murugan R., Mirjalili S., Chakrabartty D.K. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2020:1–16. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sahlol A.T., Yousri D., Ewees A.A., Al-Qaness M.A., Damasevicius R., Abd Elaziz M. COVID-19 image classification using deep features and fractional-order marine predators algorithm. Sci. Rep. 2020;10:1–15. doi: 10.1038/s41598-020-71294-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liang W., Yao J., Chen A., Lv Q., Zanin M., Liu J., Wong S., Li Y., Lu J., Liang H., et al. Early triage of critically ill COVID-19 patients using deep learning. Nature Commun. 2020;11:1–7. doi: 10.1038/s41467-020-17280-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sen S., Saha S., Chatterjee S., Mirjalili S., Sarkar R. A bi-stage feature selection approach for COVID-19 prediction using chest CT images. Appl. Intell. 2021:1–16. doi: 10.1007/s10489-021-02292-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kundu R., Basak H., Singh P.K., Ahmadian A., Ferrara M., Sarkar R. Fuzzy rank-based fusion of CNN models using Gompertz function for screening COVID-19 CT-scans. Sci. Rep. 2021;11:1–12. doi: 10.1038/s41598-021-93658-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kundu R., Singh P.K., Ferrara M., Ahmadian A., Sarkar R. Et-NET: an ensemble of transfer learning models for prediction of COVID-19 infection through chest CT-scan images. Multimedia Tools Appl. 2021:1–20. doi: 10.1007/s11042-021-11319-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chandra T.B., Verma K., Singh B.K., Jain D., Netam S.S. Coronavirus disease (COVID-19) detection in chest X-Ray images using majority voting based classifier ensemble. Expert Syst. Appl. 2020;165 doi: 10.1016/j.eswa.2020.113909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Acharya U.R. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang L., Lin Z.Q., Wong A. Covid-net: A tailored deep convolutional neural network design for detection of covid-19 cases from chest x-ray images. Sci. Rep. 2020;10:1–12. doi: 10.1038/s41598-020-76550-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chakraborty S., Mondal R., Singh P.K., Sarkar R., Bhattacharjee D. Transfer learning with fine tuning for human action recognition from still images. Multimedia Tools Appl. 2021;80:20547–20578. [Google Scholar]
- 20.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020:1. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chowdhury M.E., Rahman T., Khandakar A., Mazhar R., Kadir M.A., Mahbub Z.B., Islam K.R., Khan M.S., Iqbal A., Al Emadi N., et al. Can AI help in screening viral and COVID-19 pneumonia? IEEE Access. 2020;8:132665–132676. [Google Scholar]
- 22.Farooq M., Hafeez A. 2020. Covid-resnet: A deep learning framework for screening of covid19 from radiographs. ArXiv Preprint ArXiv:2003.14395 (2020) [Google Scholar]
- 23.Khan A.I., Shah J.L., Bhat M.M. Coronet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020 doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Karar M.E., Hemdan E.E.-D., Shouman M.A. Cascaded deep learning classifiers for computer-aided diagnosis of COVID-19 and pneumonia diseases in X-ray scans. Complex Intell. Syst. 2020:1–13. doi: 10.1007/s40747-020-00199-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ucar F., Korkmaz D. COVIDiagnosis-net: Deep Bayes-SqueezeNet based diagnostic of the coronavirus disease 2019 (COVID-19) from X-Ray images. Med. Hypotheses. 2020 doi: 10.1016/j.mehy.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Boddeda R., Deepak V S., Patel S.A., et al. 2020. A novel strategy for COVID-19 classification from chest X-ray images using deep stacked-ensembles. ArXiv Preprint ArXiv:2010.05690 (2020) [Google Scholar]
- 27.Afshar P., Heidarian S., Naderkhani F., Oikonomou A., Plataniotis K.N., Mohammadi A. Covid-caps: A capsule network-based framework for identification of covid-19 cases from x-ray images. Pattern Recognit. Lett. 2020;138:638–643. doi: 10.1016/j.patrec.2020.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rajaraman S., Siegelman J., Alderson P.O., Folio L.S., Folio L.R., Antani S.K. Iteratively pruned deep learning ensembles for COVID-19 detection in chest X-rays. IEEE Access. 2020;8:115041–115050. doi: 10.1109/ACCESS.2020.3003810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sugeno M. Readings in Fuzzy Sets for Intelligent Systems. Elsevier; 1993. Fuzzy measures and fuzzy integrals—a survey; pp. 251–257. [Google Scholar]
- 30.Tahani H., Keller J.M. Information fusion in computer vision using the fuzzy integral. IEEE Trans. Syst. Man Cybern. 1990;20:733–741. [Google Scholar]
- 31.Murofushi T., Sugeno M. An interpretation of fuzzy measures and the Choquet integral as an integral with respect to a fuzzy measure. Fuzzy Sets and Systems. 1989;29:201–227. [Google Scholar]
- 32.Banerjee A., Singh P.K., Sarkar R. Fuzzy integral based CNN classifier fusion for 3D skeleton action recognition. IEEE Transactions on Circuits and Systems for Video Technology (2020) 2020 [Google Scholar]
- 33.Das S., Roy S.D., Malakar S., Velásquez J.D., Sarkar R. Bi-level prediction model for screening COVID-19 patients using chest X-Ray images. Big Data Research. 2021;25 [Google Scholar]
- 34.C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, A. Rabinovich, Going deeper with convolutions, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 1–9.
- 35.C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, Z. Wojna, Rethinking the inception architecture for computer vision, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 2818–2826.
- 36.C. Szegedy, S. Ioffe, V. Vanhoucke, A.A. Alemi, Inception-v4, inception-resnet and the impact of residual connections on learning, in: Thirty-First AAAI Conference on Artificial Intelligence, 2017.
- 37.G. Huang, Z. Liu, L. Van Der Maaten, K.Q. Weinberger, Densely connected convolutional networks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 4700–4708.
- 38.Angelov P., Almeida Soares E. 2020. SARS-CoV-2 CT-scan dataset: A large dataset of real patients CT scans for SARS-CoV-2 identification. MedRxiv (2020) [Google Scholar]
- 39.Jaeger S., Candemir S., Antani S., Wáng Y.-X.J., Lu P.-X., Thoma G. Two public chest X-ray datasets for computer-aided screening of pulmonary diseases. Quant. Imag. Med. Surg. 2014;4:475. doi: 10.3978/j.issn.2223-4292.2014.11.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Singh P.K., Sarkar R., Nasipuri M. Significance of non-parametric statistical tests for comparison of classifiers over multiple datasets. Int. J. Comput. Sci. Math. 2016;7:410–442. [Google Scholar]
- 41.Abbas A., Abdelsamea M.M., Gaber M.M. Classification of COVID-19 in chest X-ray images using DeTraC deep convolutional neural network. Appl. Intell. 2021;51:854–864. doi: 10.1007/s10489-020-01829-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Taresh M.M., Zhu N., Ali T.A.A., Hameed A.S., Mutar M.L. Transfer learning to detect COVID-19 automatically from X-Ray images using convolutional neural networks. Int. J. Biomed. Imaging. 2020;2021 doi: 10.1155/2021/8828404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pham T.D. Classification of COVID-19 chest X-rays with deep learning: new models or fine tuning? Health Inform. Sci. Syst. 2021;9:1–11. doi: 10.1007/s13755-020-00135-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Angelov P., Soares E. 2020. Explainable-by-design approach for covid-19 classification via ct-scan. MedRxiv (2020) [Google Scholar]
- 45.Panwar H., Gupta P., Siddiqui M.K., Morales-Menendez R., Bhardwaj P., Singh V. A deep learning and grad-CAM based color visualization approach for fast detection of COVID-19 cases using chest X-ray and CT-Scan images. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jaiswal A., Gianchandani N., Singh D., Kumar V., Kaur M. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020:1–8. doi: 10.1080/07391102.2020.1788642. [DOI] [PubMed] [Google Scholar]
- 47.Halder A., Datta B. COVID-19 detection from Lung CT-scan images using transfer learning approach. Mach. Learn. Sci. Technol. 2021 [Google Scholar]
- 48.Horry M.J., Chakraborty S., Pradhan B., Fallahpoor M., Hossein C., Paul M. 2021. Systematic investigation into generalization of COVID-19 CT deep learning models with gabor ensemble for lung involvement scoring. ArXiv Preprint ArXiv:2105.15094 (2021) [Google Scholar]
- 49.Xie Y., Wu Z., Han X., Wang H., Wu Y., Cui L., Feng J., Zhu Z., Chen Z. Computer-aided system for the detection of multicategory pulmonary tuberculosis in radiographs. J. Health. Eng. 2020;2020 doi: 10.1155/2020/9205082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Win K.Y., Maneerat N., Hamamoto K., Sreng S. Hybrid learning of hand-crafted and deep-activated features using particle swarm optimization and optimized support vector machine for tuberculosis screening. Appl. Sci. 2020;10:5749. [Google Scholar]
- 51.Ayaz M., Shaukat F., Raja G. Ensemble learning based automatic detection of tuberculosis in chest X-ray images using hybrid feature descriptors. Phys. Eng. Sci. Med. 2021;44:183–194. doi: 10.1007/s13246-020-00966-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tasci E., Uluturk C., Ugur A. A voting-based ensemble deep learning method focusing on image augmentation and preprocessing variations for tuberculosis detection. Neural Comput. Appl. 2021:1–15. doi: 10.1007/s00521-021-06177-2. [DOI] [PMC free article] [PubMed] [Google Scholar]