Mathematical modeling of Erk activity waves in regenerating zebrafish scales

Abstract

Erk signaling regulates cellular decisions in many biological contexts. Recently, we have reported a series of Erk activity traveling waves that coordinate regeneration of osteoblast tissue in zebrafish scales. These waves originate from a central source region, propagate as expanding rings, and impart cell growth, thus controlling tissue morphogenesis. Here, we present a minimal reaction-diffusion model for Erk activity waves. The model considers three components: Erk, a diffusible Erk activator, and an Erk inhibitor. Erk stimulates both its activator and inhibitor, forming a positive and negative feedback loop, respectively. Our model shows that this system can be excitable and propagate Erk activity waves. Waves originate from a pulsatile source that is modeled by adding a localized basal production of the activator, which turns the source region from an excitable to an oscillatory state. As Erk activity periodically rises in the source, it can trigger an excitable wave that travels across the entire tissue. Analysis of the model finds that positive feedback controls the properties of the traveling wavefront and that negative feedback controls the duration of Erk activity peak and the period of Erk activity waves. The geometrical properties of the waves facilitate constraints on the effective diffusivity of the activator, indicating that waves are an efficient mechanism to transfer growth factor signaling rapidly across a large tissue.

Significance

Signaling waves are a possible mechanism of spatiotemporal organization of multicellular tissues. We have recently shown that waves of activity of the kinase Erk control osteoblast regeneration in adult zebrafish scales. Here, we present a detailed characterization of a mathematical model of these signaling waves. We show that a source region poised in an oscillatory state can broadcast traveling waves of Erk activity in the surrounding excitable tissue. The dynamics of the source control the number and frequency of waves. Geometrical arguments support the notion that excitable Erk waves are an effective mechanism to transport growth factor signaling across a large regenerating tissue.

Introduction

The proper function of multicellular systems requires tight coordination of their cellular components. Coordination across tissues is often provided by nonuniformly distributed signaling molecules (1, 2, 3). In the classic “morphogen gradient” model, a certain information-carrying molecule, the morphogen, is distributed in a graded manner across the tissue, and cell behaviors are instructed differentially by morphogen local concentration or its dynamics (3, 4, 5). These morphogens can be transcription factors, as in the case of Bicoid in Drosophila embryos, or extracellular ligands that bind to a transmembrane receptor and activate signaling cascades. In a simple model of gradient formation, morphogen molecules are produced in a localized source, diffuse in the extracellular space, and are absorbed or processed (“degraded”) by cells on a characteristic timescale. Under these conditions, a gradient would form, characterized by an exponential decay profile with a length scale equal to the square root of diffusivity divided by degradation rate. Although morphogen gradients can form quickly in small tissues, it might be difficult to establish such diffusion gradients spanning large tissues, as the time needed to distribute molecules by diffusion scales with the square of the distance. Moreover, the time needed for morphogen concentration to approach its equilibrium value can vary significantly across the gradient (6), suggesting that for large tissue, a static morphogen gradient might be difficult to generate and/or maintain. As a consequence, although several examples of morphogen gradients have been described in embryonic tissues of size of 10–100 μm, the role or mechanism of establishment of these gradients in larger tissues of order of a millimeter or longer remains poorly understood (7). Active transport, for example, through specialized cytonemes (8,9), can provide faster morphogen spreading. Alternatively, coupling diffusion with positive feedback can transport information across large spatial scales by generating waves (10, 11, 12, 13). Waves can propagate quickly across a tissue and maintain their intensity, providing efficient information transport (14,15). Thus, waves are an alternative mechanism to morphogen gradients for the regulation of cellular dynamics in large tissues.

Signaling waves might be particularly important in the control of adult tissue regeneration, i.e., the process through which tissues regain their functional form after injury. Tissue regeneration requires precise control of cellular dynamics across a wide range of temporal and spatial scales (16). Many pathways that are important during development are reactivated in regeneration (17), but it is unclear how these signals are coordinated across the large spatial dimensions of adult regenerating tissues. Extracellular signal-regulated kinase (Erk) is a signaling component that has been implicated in many developmental contexts, including regeneration (18, 19, 20). Several feedback systems confer on Erk activity a variety of dynamic behaviors, which can lead to different outcomes in a context-dependent manner (21,22). Understanding how these feedback mechanisms are explored in different biological processes is likely to reveal important regulatory principles. In particular, it has been shown that Erk oscillations can be transmitted to nearby cells and propagate as waves, thereby coordinating cellular dynamics across multiple cells (23, 24, 25, 26, 27). For example, in response to a wound in the mouse skin, epithelial cells collectively migrate toward the wound (25,28). This process is recapitulated in wound assays of MDCK cell cultures, in which it has been extensively studied. Cells most proximal to the wound first move toward the injury site, inducing stretching forces on the neighboring cells (24,29, 30, 31). This mechanical deformation likely triggers activation of a disintegrin and metalloprotease 17 (ADAM17), which in turn drives the release of membrane-tethered epidermal growth factor (EGF), signaling to neighboring cells through the EGF receptor (EGFR) (24). ERK activation through the EGFR signaling cascade induces cell contraction in follower cells. Contraction in these cells exerts stretching forces on the next follower cells, prompting another round of ERK activation. This positive feedback loop between mechanical forces and ERK activation (24) can result in traveling waves. It has been proposed that the coupling of forces and ERK activity facilitates long-range order and migration in the direction of the wound (32), whereas mechanical forces alone would tend to lose directionality and strength while spreading across a tissue (33,34).

Recently, we have reported Erk activity waves in vivo in regenerating osteoblast tissue in zebrafish scales (35). These waves have properties of reaction-diffusion waves in an excitable medium. Here, we present a detailed characterization of a mathematical model of Erk activity propagation in zebrafish scales. Our model shows that coupling a localized oscillatory source region with a surrounding excitable tissue can generate periodic excitable waves. Thus, our model suggests that tuning the dynamic properties of the source region is a simple strategy to control wave generation and, ultimately, tissue growth.

Materials and methods

Experimental data

Experimental data were published in (35). Experimental data collection and analysis were described in (35).

Numerical solutions of the model

The numerical solution of the presented mathematical model and analysis were performed with custom MATLAB (The MathWorks, Natick, MA) 2019b software. The system of partial differential equations was simulated using the finite differences method (36). In the standard simulation, the simulation domain is a 1090 μm × 1090 μm square. Absorbing boundary conditions are set at the domain edge. A circle with a radius of 520 μm, centered in the simulation domain, is the scale region. Erk activity and the inhibitor concentration are set to 0 outside the scale region. Because a gap of at least 25 μm exists between the edge of the scale region and the domain edge and the activator degradation length is 7 μm, boundary conditions do not majorly affect system dynamics in the scale region. In the standard simulation, the activator source region is a small off-center circle with a radius of 40 μm. The standard time step is 0.01 h, and the spatial coordinates were discretized using a square lattice with grid size of 5 μm. The initial condition is that all chemical species are set to 0. Parameters (Table 1) were chosen to generate waves with properties (peak speed, frequency, Erk activation and inactivation time) that are compatible with experimental observations. For parameter sensitivity analysis (Figs. 2 and 5) and to reduce confounding effects because of wave curvature, we used a domain geometry that generates planar waves. Thus, in this case the simulations domain is a 10 μm × 1000 μm rectangle with a 10 μm × 50 μm rectangular source region at one end. Reflecting boundary conditions are used for the activator diffusion at the domain edges. Velocity was calculated by measuring the time required for the planar wave to travel 20 μm, starting from when a wave was 130 μm away from the source region. The analysis was limited to parameters that generate dynamics compatible to those observed in vivo (i.e., each source oscillation generates a traveling wave reaching the edge of the tissue). A source oscillation event was scored when active Erk in the source reached transiently a prominence above 0.2 (the “prominence” is the Erk active fraction at any given time minus the baseline Erk active fraction). A wave reaching the edge event was scored 500 μm from the source when active Erk reached transiently a prominence above 0.2. Wave period was calculated by the duration between successive peaks in the excited region, 150 μm away from the source region. Wave width was calculated as full width half-maximum when the wave peak was ∼900 μm from the source region. Wave period, velocity, and width were calculated exclusively for parameter sets that led to the formation of a stable wave at every oscillation of the source region as it is seen experimentally.

Table 1.

Parameters of the standard simulation

Parameter	Value	Description
α1	12.6 h−1	maximal Erk activation rate
β	0.35	Erk activation AC50
γ1	15.4 h−1	Erk inhibitor-dependent inactivation rate
γe	0.14 h−1	Erk autonomous inactivation rate
α2	0.112 h−1 (at the source); 0 (outside the source)	activator deposition rate
α3	3.9 h−1	Erk-dependent activator production rate
γ2	11.8 h−1	activator degradation rate
D	566 μm2 h−1	activator diffusion constant
γ3	0.14 h−1	inhibitor timescale separation
α4	0.5	inhibitor Erk-dependent production rate

Note that to fully nondimensionalize the equations of the mathematical model, we would need to specify the concentration of total Erk [E_T]. We lack experimental data on this parameter; however, experiments in different cell types argue for values in the range of [E_T] ∼0.1–1 μM (37). Notice that these parameters are slightly different from those of (35), as we found that by rescaling all time-dependent parameters, we could tune α₂ to obtain any wave frequency seen experimentally.

Figure 2.

Parameter analysis and sensitivity. Wave speed and period varying the parameters of the model: D (A), α₁ (B), β (C), γ_e (D), α₃ (E), γ₂ (F), α₄ (G), γ₃ (H), and α₂ (I) individually and covarying α₁/β (J), α₃/α₄ (K), and α₃/γ₂ (L). Parameters are expressed relative to the reference value in our standard simulation (see Table 1). Predicted dependencies in (A) and (J) are plotted as dashed black curves: (A) v = v₀D^1/2, where v₀ = 11 μm/h is velocity for the standard set of parameters and D is expressed in relative units; (J) β = α₁^1/2. Wave speed and period are calculated for regions of parameter space that feature periodic persistent waves. Orange box: parameters that affect mainly wave speed. Blue box: parameters that affect mainly wave period. Please note that γ₁ and α₄ together determine the action of the inhibitor by controlling its activity toward Erk and its levels, respectively. Thus, the dependencies of the wave period and speed on those parameters are identical, and the plot for γ₁ was omitted. To see this figure in color, go online.

Figure 5.

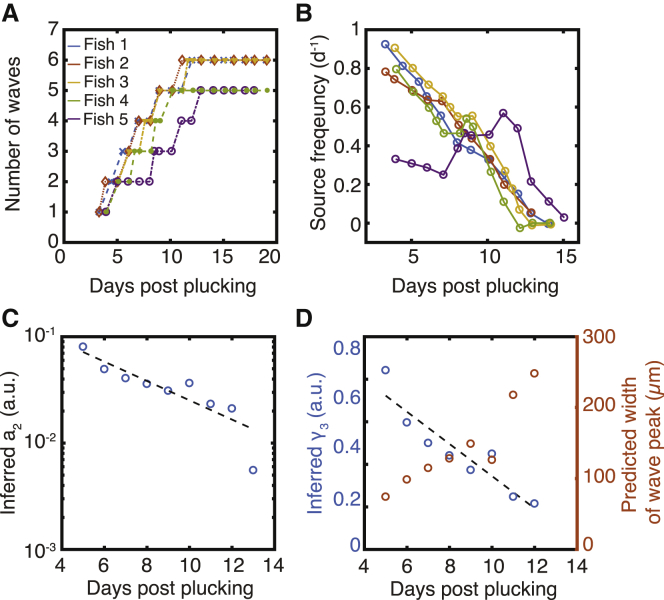
Effects of parameter changes on wave frequency. (A and B) Number of in vivo waves (A, panel adapted from (35)) and wave frequency (B) over the course of scale regeneration. (C) Inference of α₂ from experimentally measured wave frequency. Dashed line: exponential fit α₂ = α₂(0)e^−rt with α₂(0) = (0.20 ± 0.05) and r = (0.21 ± 0.04) d⁻¹. (D) Inference of γ₃ and wave width over time. Dashed line: linear fit γ₃ = γ₃(0) + rt with γ₃(0) = (1.1 ± 0.1) and r = (−3.2 ± 0.6)10⁻³ h⁻¹. Inferred parameter values are relative to the values in the standard simulation. To see this figure in color, go online.

The oscillatory deposition model was similar to the standard simulation, but the activator deposition at the source α₂ varied over time as a periodic Gaussian pulse:

$${\alpha }_2\left(t\right)=\frac{a}{s{\left(2\pi \right)}^{1/2}}exp\left(-\frac{{\left(tmodT-\phi \right)}^2}{2s^2}\right),$$

with amplitude a, standard deviation s, oscillation period T, and oscillation phase φ. mod indicates the modulus function, that is, the remainder of the division of t by T. The oscillation period is set to 24.3 h to match the period of source oscillation in the constant deposition model. The oscillation phase is chosen as half the period. The standard deviation of the temporal oscillation was chosen to be 1 h to approximately match the activation and inactivation time of the wave. The Gaussian peak amplitude was 2.8, calculated so that the total amount of activator deposited by the source over one oscillation period is approximately equal in the two models. To simulate treatment with an Erk inhibitor (Fig. 3 D), α₁ was set to 0 for 10 h and then set back to its standard value. The time elapsed until the formation of the next wave was calculated as the time from the end of the treatment to that of the formation of a local maximum of Erk activity in the source region. In the model including inhibitor diffusion (Fig. 3 F), inhibitor diffusion was treated in the same way as activator diffusion. To determine whether stationary waves formed, simulations were performed for at least 200 h of simulated time.

Figure 3.

Variations in model type and assumptions. (A and B) Erk activity as a function of time in two models of wave generation at the source region. Dashed lines indicate the boundary of the source region. The standard model with a constant (A) or oscillatory (B) activator deposition in the source region is shown. (C and D) In silico Erk inhibition and recovery experiment. Pharmacological inhibition is implemented in our model by setting α₁ to 0 for the duration of the treatment. (E and F) Alternative wave propagation model in which the Erk inhibitor diffuses. (E) Example of stationary pattern established after 200 h of simulation time. (F) Wave peak speed as a function of activator and inhibitor diffusion constants relative to value of the activator diffusion constant in the standard simulation. Scale bars, 250 μm. To see this figure in color, go online.

To calculate the velocity of Erk activity waves as a function of radial distance (Fig. 4 A) and to minimize the effect of the source on wave propagation, a 6 μm radius source region was used. To measure the minimal radius of the source excited region that can generate traveling waves (Fig. 4 D), the source activator production α₂ was set to 0, and a certain concentration of activator was deposited in a circle of 10 μm radius at the onset of the simulation; each simulation was performed for 50 h of simulation time. At each time step, the excited region was calculated by testing for each grid point (grid size, 1 μm) if it reached the region of the phase space in which an excitation occurs (in a simulation with null diffusion). The total excited region is the set of points that reached the excitation region at a certain moment during the simulation.

Figure 4.

Consequences of activator diffusion constant and effects of curvature on wave propagation. (A) Schematics of activator gradient established by simple diffusion alone. (B and C) Activator gradient formation by simple diffusion (B) versus excitable wave propagation (C). (D) Wave speed as a function of radial distance from the source. (E) Definitions of wave profile characteristics. (F) Radius of the excited region for different initial activator amounts. Initial activator concentrations higher than ∼0.36 E_T induced an excited radius above 45 μm and triggered wave propagation. To see this figure in color, go online.

In the model of activator simple diffusion (Fig. 4 G), all model parameters were set to 0, except α₂ and D.

In Fig. 5 B, the experimental wave frequency was measured by smoothening the number of waves as a function of time and calculating its numerical derivative. Values of α₂ and γ₃ relative to the value in the standard simulation were inferred using the predictions of Fig. 2. The simulation code is available at https://github.com/lhaydene26/Hayden_modelingErkWaves2021.

Results

A three-component excitable system generates Erk activity waves

Zebrafish scales are millimeter-sized bone disks that form a protective skeletal array on the body of the fish (38). The scale bone is covered by a monolayer of osteoblasts that secrete bone matrix. After scale loss, a new osteoblast pool regenerates and reforms the bone. The osteoblast tissue forms first by differentiation of an unknown progenitor, then osteoblasts proliferate and finally increase in size without cell division (cell hypertrophy) (35,39,40). This latter hypertrophic phase is coordinated by repeated waves of Erk activity, which can be visualized using a transgenic biosensor expressed specifically in osteoblasts (Fig. 1 A; (35)). Using image analysis methods, we were able to map Erk activity in the entire osteoblast population of regenerating scales—see Fig. 1 A and (35). This approach revealed repeated Erk activity waves that originate from a central source region and propagate outward as expanding rings (Fig. 1 A; (35)). These waves move at a speed on the order of 10 μm/h and cross the entire scale in a few days; Erk is activated in 3 h and deactivated in 5 h, thus generating a peak 50–100 μm wide (35). The dynamic properties of the central source region suggest that it could be a dynamic system operating in an oscillatory regime, whereas the rest of the scale would be excitable. An excitable system is a nonlinear system that displays small responses to small stimuli but undergoes a large excursion in the phase space in response to perturbations above a certain threshold (42,43). Multiple excitable units can be coupled by diffusion and generate waves. Compatible with this idea, we found that wave initiation and propagation depend on fibroblast growth factor receptor (Fgfr) signaling, which is activated by extracellular diffusible ligands of the fibroblast growth factor family (Fgfs) (35). Thus, Fgfs are candidates for propagating Erk activity from one cell to the next. To form an excitable system that can sustain a wave, Erk active cells need to produce or stimulate Fgfs, thus generating a positive feedback loop. In addition, cells at high Erk activity switch off after a certain time, indicating that one or multiple Erk inhibitors are activated in Erk active cells, generating a negative feedback loop. Thus, the minimal components of the proposed model are Erk itself, an Erk activator, and an Erk inhibitor. In our model, the activator can diffuse in the extracellular space, whereas the Erk kinase and its inhibitor are confined within each cell. We use a coarse-grained continuum approach and describe the extracellular movement of the Erk activator by simple diffusion (Fig. 1 B). These assumptions lead to the following model for Erk activity:

$$\begin{array}{c}\frac{\partial \left[E\right]}{\partial t}=\frac{{\alpha }_1{\left[A\right]}^2}{{\beta }^2+{\left[A\right]}^2}\left(E_T-\left[E\right]\right)-\left[E\right]\left({\gamma }_1\left[I\right]+{\gamma }_e\right)\\ \frac{\partial \left[A\right]}{\partial t}={\alpha }_2+{\alpha }_3\left[E\right]-{\gamma }_2\left[A\right]+D{\nabla }^2\left[A\right]\\ \frac{\partial \left[I\right]}{\partial t}={\gamma }_3\left({\alpha }_4\left[E\right]-\left[I\right]\right)\end{array}$$

where [E], [A], and [I] represent the concentrations of active Erk, diffusible activator, and inhibitor, respectively. For simplicity, reaction terms are described according to the law of mass action with the exception of the rate of Erk activation by the activator, expressed as a Hill function of the activator concentration (a nonlinearity in the positive feedback regulation between the activator and Erk is needed for the system to be excitable; similar results may be obtained with other nonlinear terms in the positive feedback loop). In the model, α₁ is the Erk activation rate at saturating activator, β is the AC₅₀ of Erk activation by the activator, E_T is the mass-conserved sum of active and inactive Erk, γ₁ is the Erk inactivation rate by the inhibitor I, γ_e is the Erk autonomous inactivation rate, α₂ is the activator production rate, α₃ is the Erk-dependent activator production rate, γ₂ is the autonomous activator degradation rate, D is the diffusion constant of the activator, γ₃α₄ is the inhibitor production rate, and γ₃ is the inhibitor autonomous degradation rate. By nondimensionalizing the concentrations [E], [A], and [I] by dividing by the total amount of Erk E_T, we obtain the equations (brackets are omitted):

$$\begin{array}{c}\frac{\partial E}{\partial t}=\frac{{\alpha }_1{A}^2}{{\tilde{\beta }}^2+A^2}\left(1-E\right)-E\left({\tilde{\gamma }}_{1}I+{\gamma }_e\right)\\ \frac{\partial A}{\partial t}=\widetilde{{\alpha }_2}+{\alpha }_{3}E-{\gamma }_{2}A+D{\nabla }^{2}A\\ \frac{\partial I}{\partial t}={\gamma }_3\left({\alpha }_{4}E-I\right)\end{array}$$

where $\tilde{\beta }$ = β/E_T, $\widetilde{{\gamma }_1}$ = γ₁E_T, and $\widetilde{{\alpha }_2}$ = α₂/E_T. For the sake of simplicity, we omit the tilde signs from $\tilde{\beta }$, $\widetilde{{\gamma }_1}$, and $\widetilde{{\alpha }_2}$ hereafter. To tune the system to an oscillatory state in the source region (Fig. 1 C), instead of an excitable state, we introduced in that region a constant term of production of the activator α₂. This term can be interpreted as a basal activator production by osteoblasts in the source region or a contribution from an external cellular pool. This term is null in the excitable region. Numerical solutions of the previous equations demonstrate that the system can generate traveling waves of Erk activity (Fig. 1 D). As expected, linear stability analysis shows that with the chosen set of parameters, the source region oscillates (limit cycle, Fig. 1 E), whereas outside the source region, the system is excitable (Fig. 1 F). Thus, oscillations of activator levels (and Erk activity) in the source trigger the propagation of excitable waves. The features of the excitable wave can be understood through the following arguments (10). The leading edge of the wave (inhibitor levels low) can be approximated with a bistable system, with stable fixed points at high and low Erk activity (Fig. 1 G). Activator diffusion triggers excitations in the tissue in front of the leading edge. In that region, the system will leave the basin of attraction of the low Erk activity state and move toward the high Erk activity state. At the same time, the accumulating active Erk triggers the production of its own inhibitor. As the inhibitor accumulates, the level of active Erk decreases until the system resets to a state of low Erk activity. The system cannot be excited again until the inhibitor has substantially degraded (refractory period). Thus, our analysis points to a simple dynamical picture for Erk waves in scale regeneration.

Figure 1.

Model formulation and stability analysis. (A) Erk activity in regenerating scales in vivo, measured using an Erk kinase translocation reporter (Erk KTR). The Erk KTR sensor provides a proxy of Erk activity through measurement of its subcellular localization. The sensor contains both a nuclear localization signal and a nuclear export signal and preferentially localizes to the nucleus when unphosphorylated and to the cytoplasm when phosphorylated (41). Thus, a readout of Erk activity at cellular resolution is calculated by measuring the ratio of nuclear and cytoplasmic Erk KTR signals. The data shown were imaged and analyzed in (35). hpp, hours post plucking. (B) Schematics of theoretical model including a diffusible extracellular activator, Erk, and an inhibitor of Erk. Arrows between chemical species indicate feedback. (C) Numerical simulation of the dynamical system in the source region when diffusion is null. (D) Numerical simulation of the reaction-diffusion dynamical system. (E and F) Stability analysis of the system when diffusion is null. E: source region; F: outside the source region. Curves indicate pairwise intersections between nullcline surfaces. (G) Leading edge fixed-point analysis: nullclines in the leading edge of the wave, where the inhibitor is taken to be 0. Circles: fixed points at 4 h from simulation start (stability is indicated). Scale bars, 250 μm. a.u., arbitrary unit. To see this figure in color, go online.

To understand which parameters control wave properties, namely wave frequency and speed, we performed a parameter sensitivity analysis by varying a single parameter at a time. The phenomenology of source oscillation and wave propagation can change while varying parameters. For example, for some parameter variations, damped waves originate from the source or the source or excitable region is locked in a high or low Erk activity state (Fig. S1). However, in our in vivo observations, each oscillation of the source corresponded to the generation of a wave reaching the edge of the tissue. Therefore, we limited our analysis to parameter values that generate a phenomenology that corresponds to these observations (see Materials and methods for details). We found that waves with a well-defined speed and frequency are generated in a wide region of the parameter space, with some parameters having broader ranges than others. As the parameters are varied outside this range, stable waves are replaced either by unstable pulses that lose amplitude over time or by a stable propagating front of high Erk activity, indicating the establishment of a bistable system (Fig. 2).

The theory of chemical waves predicts that the speed of the wave is determined by the activator diffusion constant D and by the timescale of activation τ via v ∼(D/τ)^1/2 (10, 11, 12). As predicted, the speed of Erk activity waves scales as the square root of the diffusion constant (Fig. 2 A). Furthermore, our analysis demonstrates that parameters controlling the activator-Erk positive feedback loop have a larger impact on wave speed than its frequency (Fig. 2, B–F). This can be intuitively understood by the fact that the positive feedback loop between Erk and its activator dominates in the leading edge, i.e., where the inhibitor concentration is low. However, parameters controlling inhibitor dynamics mainly impact wave frequency as they control the duration of the refractory period and thus the intrinsic minimal lag time between subsequent excitation events. An interesting exception is the rate of deposition of the activator at the source (α₂), which controls the period of oscillation of the source. When the period imparted by α₂ is longer than the intrinsic oscillation period of the excitable region (Fig. 2, G and H), this period imparted by α₂ will determine the tempo of wave generation (Fig. 2 I). However, when the oscillation period at the source is shorter than the intrinsic oscillation period of the excitable system, this latter intrinsic oscillation period will limit the rate of wave generation.

Sensitivity analysis also indicates that several parameters have a similar impact on wave speed and frequency, and this codependency is strengthened by changing two parameters simultaneously (Fig. 2, J–L). For some of these parameters, this codependency is intuitive. For example, the speed of the Erk wave is controlled by the dynamics of the leading edge at concentration A ≪ β; therefore, the term controlling Erk activation by the activator effectively reduces to α₁/β², which indeed captures the codependency between the two parameters (Fig. 2 J). This analysis suggests that although our model has several parameters that are not known experimentally, the emergent properties of the system belong to a few general scenarios. Furthermore, parameter values are constrained by the dynamic features of Erk oscillations and waves.

The dynamic properties of the source region can impact how wave generation responds to perturbations

In the proposed model, the Erk activator is deposited in the source region, forcing it to an oscillatory regime (Fig. 3 A). In an alternative model, external activator deposition may be intrinsically oscillatory (Fig. 3 B). In principle, these two different scenarios could be distinguished experimentally by pharmacological inhibition of Erk. In this experiment, Erk activity would be temporarily impaired using a pharmacological inhibitor; then this pharmacological inhibitor would be washed away, and the recovery of the system would be monitored. When the inhibitor is washed out, there would be a delay before the system recovers and another wave is generated (Fig. 3 C). The constant deposition model predicts a constant delay in wave onset determined by the time needed for the activator to build up in the source region and trigger the positive feedback loop. By contrast, the oscillatory deposition model predicts a variable delay that depends on the phase of the deposition oscillation at the time of pharmacological inhibitor washout (Fig. 3 D). Thus, experiments that analyze how new waves arise after perturbations of Erk activity could provide insights on the dynamic properties of the source. However, we note that this analysis may be complicated by potential additional feedback mechanisms between the rate of production of the activator and its downstream activity.

Analysis of the effects of diffusion argue for waves as an effective mechanism to transfer information

The diffusivity of ligands in vivo is context dependent because of the complex microscopic details of ligand movement, and a wide range of different values have been observed for ligands of the Fgf family (7). Our experimental data on the speed of Erk waves (v = 10 μm/h) and the typical timescale of Erk activation (τ = 3 h) allow us to estimate the effective diffusion constant of the signal propagating Erk waves as D ∼v²τ ∼0.1 μm²/s (35). To further strengthen the evidence toward a small diffusion constant, we consider the possibility that an alternative model could generate the slow waves seen experimentally but for larger values of the diffusion constant of the activator. In particular, we tested whether a faster activator diffusion would be compatible with our experimental observations in a model in which the Erk inhibitor could also diffuse extracellularly (Fig. 3, E and F). However, we found that allowing the inhibitor to diffuse slows waves down only minorly (Fig. 3 F). In addition, waves are replaced by stationary patterns at high inhibitor diffusion (Fig. 3 E). We conclude that simply adding a diffusing inhibitor to our model does not allow higher values of the activator diffusion constant, given the experimentally observed wave speed.

To understand the physical implications of the low value of inferred diffusivity, we tested the ability of a diffusible morphogen (Fig. 4 A) to propagate a signal across a domain of size similar to a regenerating adult zebrafish scale in a timescale like that of scale regeneration (35). To that end, we simulated the dynamics of an undegradable/unprocessed diffusible morphogen produced at the source. We found that for D ≈ 0.1 μm²/s, it takes on the order of weeks to achieve a significant morphogen concentration across the domain (Fig. 4 B), whereas the wave mechanism in our model forms and propagates a wave across the same distance in just a couple days (Fig. 4 C). Thus, we conclude that for values of the diffusion constant of the activator similar to the ones we estimated, morphogen gradients established by diffusion are, in principle, not well suited to coordinate cellular dynamics on the observed timescales.

The effects of the geometry of the source on wave propagation

Wave geometry impacts the speed of excitable wave propagation according to the relationship v = v_p + DK for normal and planar velocity v and v_p, respectively, and curvature K (11,44). K is negative for wavefronts that curve away from the propagation direction. This relationship predicts that circular stable waves have a minimal radius. This critical radius is estimated to be R_c ≈ D/v_p ≈ 45 μm in our system. However, in simulations, we can observe wave propagation even when the source region is smaller than the critical radius (Figs. 1 D and 3, A and B). We hypothesize that this is because of the fact that diffusion generates a larger profile of baseline activator concentration surrounding the source, thus an “effective source region.” The radius of this effective source region would be larger than that of the source by the order of magnitude of the activator diffusion length, $\sqrt{D\tau }.$ Compatibly with this idea, the initial spatially inhomogeneous profile of activator triggers the system excitation at different times, thus resulting in a high apparent speed of the Erk activity peak in and around the source (Fig. 4 D). Thus, it is the size of this effective source region, and not the size of the source domain (i.e., when activator deposition α₂ > 0), that determines whether a wave can propagate outward. To test this idea, we varied the amount of an initial pool of activator in the source region and tested system dynamics in the absence of additional activator production at the source (α₂ = 0; Fig. 4 E). Depending on the initial concentration of activator, regions of different sizes were excited; for small initial activator amounts, small regions were excited, and when regions larger than the critical radius R_c ≈ D/v_p ≈ 45 μm were activated, then the entire scale eventually reached excitation (Fig. 4 F). Thus, our results support the notion that Erk activity waves can propagate only when their radius of curvature is above a certain threshold. These results further argue against a value of the diffusion constant much larger than D ≈ 0.1 μm²/s, as for such values the effective source region would be significantly larger and occupy a large fraction, if not the entirety, of the scale tissue.

A change in activator deposition can control wave frequency during regeneration

During regeneration of zebrafish scales in vivo, wave generation starts with a frequency of ∼1 wave per day and slows down over time until it stops (Fig. 5, A and B). Wave frequency directly controls the rate at which scales grow over the timescale of regeneration (35). Our parameter analysis suggests that a change over time of the rate of deposition of the activator in the source region (α₂) could explain this phenomenology (Fig. 2 H). Alternatively, a change over time in the rate of degradation of the inhibitor γ₃ could reduce the frequency of wave generation (Fig. 2 I). We combined experimental data with the numerical predictions to infer how these two parameters would have to vary to explain the experimentally observed change in frequency. We found that an approximately exponential decrease of the activator deposition rate at the source over time (α₂) would be sufficient to explain wave generation dynamics (Fig. 5 C). Thus, reducing the amount of activator delivered to the regenerating scale could be a mechanism to control the duration of regeneration and thus the size of the regenerated scale. This exponential reduction of activator deposition could be achieved, for example, if the activator at the source was deposited by a pool of cells, each independently switching to a nondepositing state with a constant probability. Importantly, α₂ controls only the dynamic of the source region, whereas the geometrical properties of the traveling excitable waves would be unaltered. Conversely, a reduction in the timescale of separation between Erk and the inhibitor (γ₃) could explain the slowing of wave frequency but would result in an increase in wave width (Fig. 5 D). This can be understood by noting that for smaller γ₃, the time required to extinguish Erk increases, and thus, the width of the traveling Erk activity peak increases. Therefore, our results argue that the mechanism for controlling the duration of scale regeneration can be distinguished experimentally by monitoring waves throughout regeneration.

Discussion

Waves can propagate stable signals across large tissues. We have recently reported that periodic waves of Erk activity, originating from a common source, control osteoblast regeneration in the zebrafish scale (35). This work provides a rare example of a source region emitting repeated and coherent signals traveling across an entire growing and developing tissue. Here, we provide a mathematical model of Erk activity wave propagation in an excitable medium. At the core of this mechanism is an oscillatory source region, whose cellular nature and molecular regulation remain to be discovered. Once Erk activity is turned on in the source region, an excitable wave can travel across the rest of the tissue. Excitability requires positive and negative feedback mechanisms. Our analysis of the dependency of wave properties on model parameters supports the notion that the positive feedback between Erk and its activator controls the speed of the traveling wave. Conversely, the negative feedback between Erk and its inhibitor impacts the period of Erk excitable oscillations with little impact on wave speed. The periodic and repetitive nature of the wave is also controlled by the properties of the source region. Scenarios in which the ligand is continuously or periodically produced in the source region are both compatible with the observed repetitive nature of the waves. However, the two scenarios make different predictions on when a new wave would appear after inhibition of Fgf or Erk signaling. Future experiments should focus on discovering the nature and dynamic properties of the source region and how Erk oscillatory activity is controlled in such regions. In particular, it will be important to discover whether the source region is created by interactions with other tissues, e.g., the vasculature or dermis, or whether cells in the source region become specified by a self-organized mechanism that locks them in an oscillatory Erk regime, thus making them act as pacemakers.

Erk activity waves in scale regeneration present features that are different from many previously observed examples of Erk activity propagation. In scale regeneration, Erk activity propagates as a stable wave, with a constant amplitude. Similar long-distance (several hundred microns) traveling waves have recently been discovered in the morphogenesis of the murine cochlear duct (27). By contrast, in homeostatic mouse epidermis, ERK activity waves feature damped propagation up to ∼50 μm and have a lifetime of ∼30 min (25). In the epithelium of Drosophila tracheal placodes, waves propagate comparable distances over the course of about an hour (45). Similar to the case of scale regeneration, in wound-healing assays, ERK activity waves can propagate from the edge of the wound for hundreds of microns, typically up to 200 μm. However, the remaining tissue displays a multitude of more disorganized waves that travel shorter distances (<∼100 μm) (46). Less organized waves with origins influenced by noise are also seen in the activity of Cdk1 spanning the early Drosophila embryo to organize mitotic waves (47,48).

The directionality of cellular flows is a crucial feature differentiating Erk activity waves in osteoblast regeneration from those reported in other systems. Thus, in the mouse epidermis and cochlear duct and in cultured MDCK cells, tissue flow is retrograde to the direction of ERK activity waves (24, 25, 26, 27). Instead, in osteoblast regeneration, Erk activity triggers tissue growth and thus leads neighboring cells away from the expanding region (35). In fact, a retrograde flow in regenerating scales would move osteoblasts toward the central source region, arguably an undesirable feature for tissue growth. In the wound-healing assays and cochlear duct morphogenesis, cellular contractions precede ERK activation (24,27), whereas in our model, Erk activation triggers osteoblast hypertrophy and the corresponding cellular flows (35). These observations suggest a different relationship between Erk activity waves and tissue flows in osteoblast regeneration and other systems. The Erk waves in scale regeneration and in wound healing are also characterized by different timescales. For example, Erk activity waves in regeneration are slower than those observed in wound healing (5–10 μm/h vs. ∼60 μm/h) (24,25,28). This slower speed is accompanied by an overall slower oscillation of Erk activity in individual cells (∼10 h in osteoblast regeneration vs. ∼1 h seen in wound healing).

The slower dynamics and different flow patterns observed during osteoblast regeneration (35) argue for different mechanisms of wave propagation. In our experiments, Erk activates in ∼3 h, a timescale compatible with a reaction-diffusion mechanism involving the activation of gene expression. Consistently, inhibition of de novo protein synthesis decreases the speed of wave propagation (35). Notably, a similar timescale or speed of propagation has been observed in the Drosophila eye imaginal disks, where the role of a transcriptional positive feedback is well documented (49). In wound-healing assays, however, ERK activates in <1 h, which suggests that faster mechanisms are at play (24). Consistent with this scenario, a mechanochemical mechanism in which the cleavage of pro-growth factor signaling molecules is coupled with cell contraction has been proposed (24). Interestingly, ERK activity waves in murine cochlear duct morphogenesis have intermediate speeds and periods (∼25 μm/h and ∼3 h, respectively) and were proposed to originate from mechanochemical mechanisms similar to those of wound healing (27).

Collectively, these observations suggest that different molecular processes can control Erk activity waves and that these processes might be selected to match the relevant timescales of the biological process. Interestingly, Erk waves are dependent on different ligand families in different contexts. Waves in regenerating osteoblasts and in the cochlear duct are Fgf dependent, whereas waves in wound healing are EGF dependent (24,25). In the future, it would be interesting to determine whether and how the different mechanisms depend on different ligand and tissue properties.

The longer timescales of Erk oscillations also have implications on the possible mechanisms of the negative feedback that turns Erk activity off. Several negative feedback mechanisms exist that may regulate Erk. Some of these mechanisms involve phosphorylation by active Erk, which can, for example, desensitize the pathway (50). These mechanisms would likely operate on rapid timescales, and it is not obvious how they can be compatible with ∼10 h of Erk excitation. However, mechanisms of negative feedback that involve the transcriptional activation of Erk inhibitors, namely proteins belonging to the Spry and Dusp families, are likely compatible with the timescales observed experimentally. In agreement with this, we previously reported that spry and dusp transcripts are enhanced in Erk active cells (35).

The geometric features of Erk waves have interesting implications on the role of diffusion. If the diffusion constant is high, molecules quickly move away from the source region, and as a result, the system would require a high activator production to surpass the threshold to begin a wave. Moreover, a high diffusion constant is predicted to lead to wide waves and a more uniform-like Erk activation profile (35). Because a wave-like pattern of Erk activity is more conducive to regeneration than a wide activation of Erk (35), this further argues against a high value of the diffusion constant. Finally, the speed of a stable wavefront is negatively influenced by curvature-dependent effects. These theoretical arguments suggest that the diffusion constant must be on the order of 0.1 μm²/s, which implies that simple diffusion would take several weeks to form a gradient across the tissue. It will be important for future experiments to investigate the receptors and ligand(s), as well as the extracellular matrix, determining the properties of this system. In conclusion, we speculate that waves provide two important advantages in the regulation of scale regeneration: rapid delivery of growth factor signaling and stereotypical pulses of fixed amplitude eventually exciting all cells across the tissue. It is likely that excitable waves will emerge as a general principle of coordination of cell behaviors across large regenerating tissues.

Author contributions

L.D.H., K.D.P., A.D., and S.D. designed research. L.D.H. and A.D. performed numerical simulations. L.D.H., A.D., and S.D. analyzed the numerical and experimental data. L.D.H., A.D., and S.D. contributed analytical tools. L.D.H., A.D., and S.D. wrote the manuscript with comments from K.D.P.

Editor: Stanislav Shvartsman.