Abstract
Controlling magnon densities in magnetic materials enables driving spin transport in magnonic devices. We demonstrate the creation of large, out-of-equilibrium magnon densities in a thin-film magnetic insulator via microwave excitation of coherent spin waves and subsequent multimagnon scattering. We image both the coherent spin waves and the resulting incoherent magnon gas using scanning-probe magnetometry based on electron spins in diamond. We find that the gas extends unidirectionally over hundreds of micrometers from the excitation stripline. Surprisingly, the gas density far exceeds that expected for a boson system following a Bose–Einstein distribution with a maximum value of the chemical potential. We characterize the momentum distribution of the gas by measuring the nanoscale spatial decay of the magnetic stray fields. Our results show that driving coherent spin waves leads to a strong out-of-equilibrium occupation of the spin-wave band, opening new possibilities for controlling spin transport and magnetic dynamics in target directions.
Keywords: Magnon gas, Spin waves, Yttrium iron garnet, Scanning-probe magnetometry, Nitrogen-vacancy centers, Spin relaxometry
Spin waves are collective, wave-like precessions of spins in magnetically ordered materials. Magnons are the bosonic excitations of the spin-wave modes. The ability to control the number of magnons occupying the spin-wave energy band is important for driving spin transport in spin-wave devices such as magnon transistors.1−4 In addition, the generation of large magnon densities can trigger phenomena such as magnetic phase transitions,5 magnon condensation,6−8 and domain-wall motion.9−12 As such, several methods to control magnon densities have been developed, with key methods including spin pumping based on the spin-Hall effect,1,2,13,14 in which magnons are created by sending an electric current through heavy-metal electrodes, and microwave driving of ferromagnetic resonance (FMR)15−18 via metallic electrodes deposited onto the magnetic films.
Here, we demonstrate how the excitation of coherent, traveling spin-wave modes in a thin-film magnetic insulator can be used to generate a high-density, out-of-equilibrium magnon gas unidirectionally with respect to an excitation stripline. We characterize this process using scanning-probe magnetometry based on spins in diamond, a technique which enables probing magnons in thin-film magnets at microwave frequencies by detecting their magnetic stray fields.17,19−21 We find that the magnon gas has an unexpectedly high density that far exceeds the density expected for a magnon gas following a Bose–Einstein distribution with the maximum possible value of the chemical potential,22 opening new opportunities for creating and manipulating magnon condensates.6−8,23 We further characterize the gas by probing its momentum distribution through distance-dependent measurements of the stray-field magnetic noise it creates. The observed nanoscale spatial decay lengths reveal the presence of large-wavenumber magnons in the gas and underscore the need for nanometer proximity enabled by our scanning-probe magnetometer.
Our scanning-probe magnetometer is based on nitrogen-vacancy (NV) ensembles embedded in the tip of a diamond probe (Figure 1a)24 (Supporting Information Notes 1–3). The electron spins associated with the NV centers act as magnetic-field sensors that we read out via their spin dependent photoluminescence.20 We use the NV sensors to locally characterize the magnetic stray fields generated by spin waves in a 235 nm-thick film of yttrium iron garnet (YIG),25 a magnetic insulator with record long spin-wave lifetimes.26 We employ two measurement modalities to shed light on the interaction between coherently driven spin waves and the resulting out-of-equilibrium magnon gas at higher frequencies: in the first, we measure the coherent NV-spin rotation rate (Rabi frequency) to image the coherent spin waves excited by the stripline. In the second, we drive coherent spin waves with frequencies near the bottom of the spin-wave band while we measure the NV spin relaxation rates at frequencies hundreds of MHz above the drive frequency to characterize the local density of the magnon gas.
Figure 1.
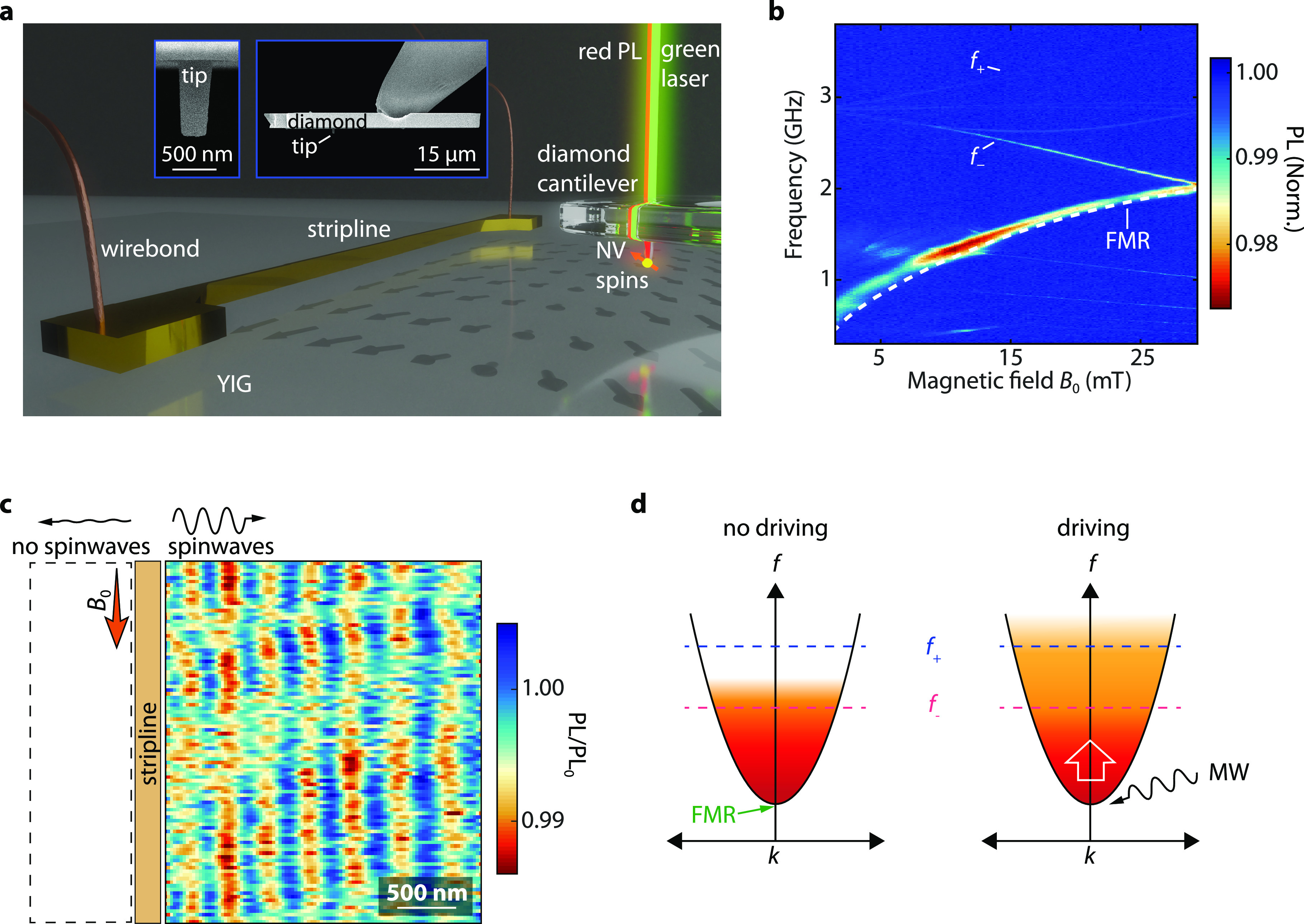
Detecting coherent spin
waves and incoherent magnon densities using
NV spins in diamond. (a) A diamond cantilever, with NVs implanted
∼20 nm below the tip surface, is mounted in an AFM setup and
used for probing the stray field of spin waves that are excited by
a gold stripline. The NV spins are initialized using a green laser
and read out via spin-dependent photoluminescence (PL). Insets: scanning
electron micrographs of diamond cantilever and tip. (b) Normalized
NV photoluminescence vs external field B0 and microwave drive frequency. The ESR frequencies (f±) of the NV family that is most aligned with B0 are labeled. The strong PL response close
to the ferromagnetic resonance (FMR) is a result of the process depicted
in (d). The FMR is calculated as 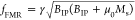 , where
γ = 28 GHz/T, μ0 = 4π × 10–7 H/m, Ms = 1.42 × 105 A/m, and BIP is the in-plane magnetic
field component (Supporting Information Note 4). (c) Spatial map
of the normalized NV ESR PL showing a coherent spin wave excited unidirectionally
(to the right) by applying a microwave current at f– through the stripline. On the left of the stripline
there is no detectable spin-wave signal. The film is magnetized along
the stripline direction by a magnetic field B0 (orange arrow), which is set to a low value (B0 ≈ 0 mT) in this measurement. At each pixel, the
measured PL under microwave driving is normalized to that without
microwave driving (PL0). The image is low-pass filtered
to reduce pixel-by-pixel noise. (d) Sketch of the spin-wave dispersion
(black line) and its occupation by magnons (color gradient). Without
microwave driving (left), only thermally excited magnons are present.
Microwave (MW) driving near the FMR frequency (oscillating arrow in
right panel) increases the magnon density, which can be detected via
the increased stray-field noise at the NV ESR frequencies (f±).
, where
γ = 28 GHz/T, μ0 = 4π × 10–7 H/m, Ms = 1.42 × 105 A/m, and BIP is the in-plane magnetic
field component (Supporting Information Note 4). (c) Spatial map
of the normalized NV ESR PL showing a coherent spin wave excited unidirectionally
(to the right) by applying a microwave current at f– through the stripline. On the left of the stripline
there is no detectable spin-wave signal. The film is magnetized along
the stripline direction by a magnetic field B0 (orange arrow), which is set to a low value (B0 ≈ 0 mT) in this measurement. At each pixel, the
measured PL under microwave driving is normalized to that without
microwave driving (PL0). The image is low-pass filtered
to reduce pixel-by-pixel noise. (d) Sketch of the spin-wave dispersion
(black line) and its occupation by magnons (color gradient). Without
microwave driving (left), only thermally excited magnons are present.
Microwave (MW) driving near the FMR frequency (oscillating arrow in
right panel) increases the magnon density, which can be detected via
the increased stray-field noise at the NV ESR frequencies (f±).
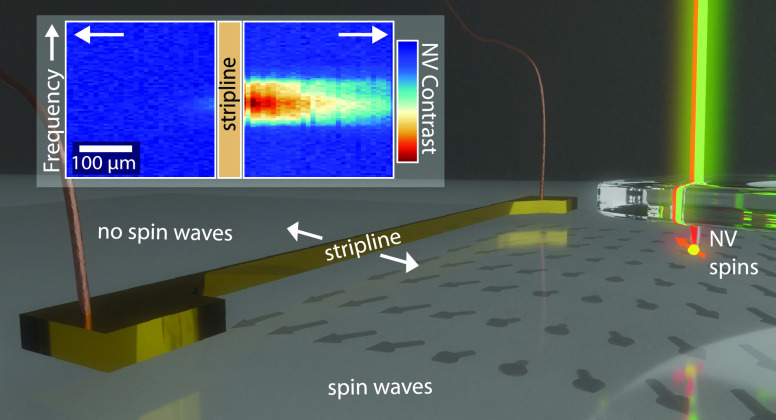
We reveal the directionality of the coherent spin waves launched by the stripline by spatially mapping the contrast of the f– ESR transition (Figure 1c). At B0 ≈ 0, this transition is resonant with spin waves of wavelength ∼500 nm, as expected from the known spin-wave dispersion (Supporting Information Note 5). On the right-hand side of the stripline, we observe a spatial standing-wave pattern in the ESR contrast that results from the interference between the direct field of the stripline and the stray fields of the spin waves launched by the stripline.21 In contrast, we do not observe a spin-wave signal to the left of the stripline. This directionality is characteristic of coherent spin waves traveling perpendicularly to the magnetization and results from the handedness of the stripline field and the precessional motion of the spins.27
In addition to the narrow lines of reduced photoluminescence indicating the NV ESR frequencies (Figure 1b), we observe a broad band of photoluminescence reduction close to the expected ferromagnetic resonance (FMR) frequency of our YIG film that is detuned from the NV ESR transitions. A similar off-resonant NV response was observed previously17−19,25,28−30 and has been attributed to the driving of a uniform FMR mode and subsequent multimagnon scattering. The scattering processes lead to an increased magnon density at the NV ESR frequencies, causing NV spin relaxation17,18 (Figure 1d). However, in contrast with the uniform nature of the FMR mode, we observe that the signal strength depends strongly on the detection location with respect to the stripline (Figure 2a): on the right-hand side, we observe a much stronger response than on the left, up to distances 300 μm away from the stripline. This asymmetry shows that directional spin waves excited by the stripline, such as those in Figure 1c, underlie the increased magnon densities at the NV ESR frequencies (Figure 2b).
Figure 2.
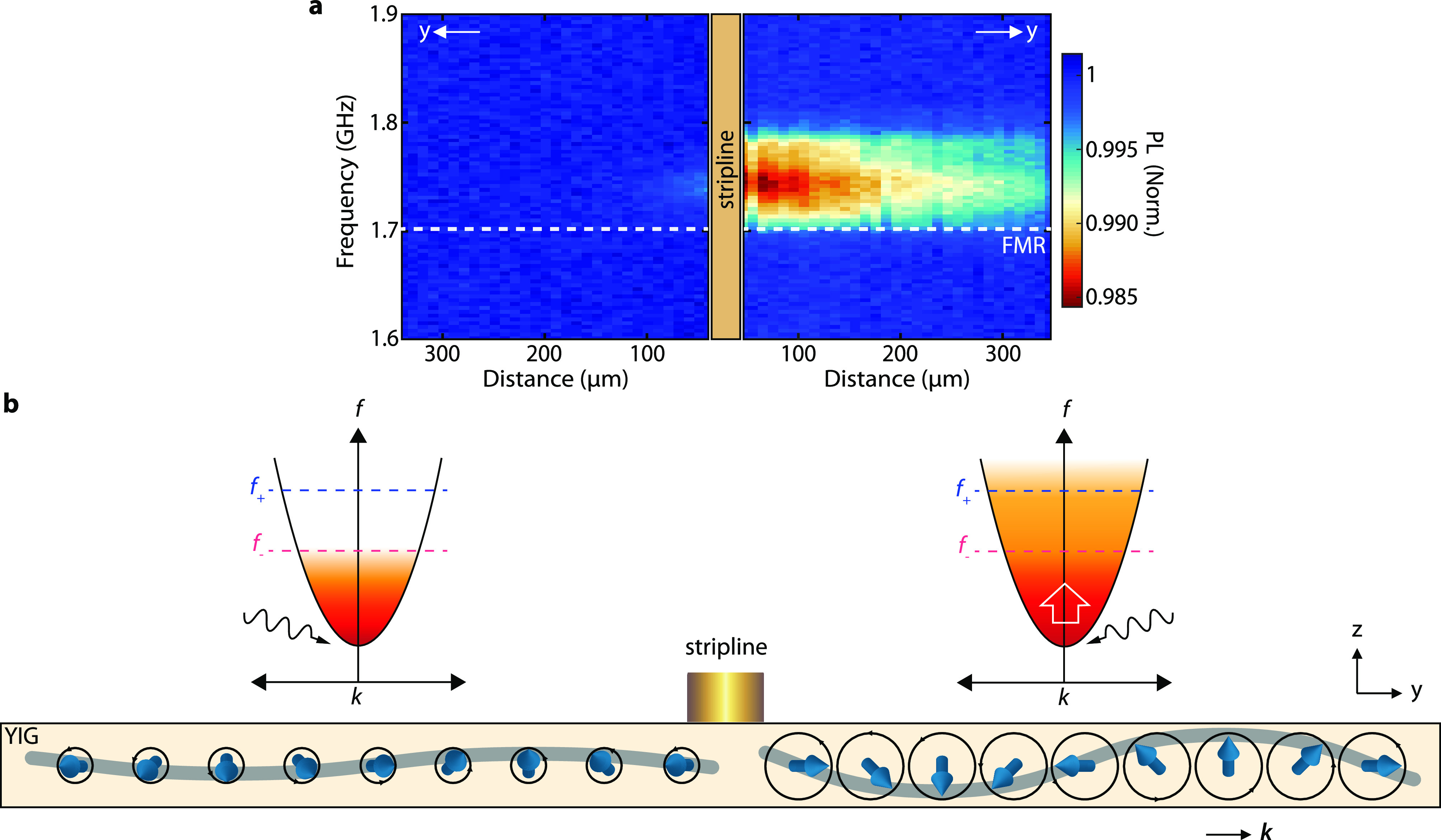
Unidirectional excitation of an out-of-equilibrium magnon gas by microwave driving near the ferromagnetic resonance. (a) One-dimensional spatial maps of the NV photoluminescence (PL) as a function of the frequency of a microwave drive current in the stripline. The microwave current excites directional coherent spin waves (traveling to the right in the image) at near-FMR frequencies. The decrease in NV photoluminescence is a result of incoherent magnons generated at the NV ESR frequencies via multimagnon scattering (see schematics in (b)). An external magnetic field B0 = 20 mT magnetizes the film along the stripline direction. The NV ESR frequencies at this field can be seen in Figure 1b. (b) Schematic of the directional excitation of a coherent spin wave by the microwave stripline and the accompanying out-of-equilibrium occupation of the spin-wave band that arises through multimagnon scattering. The coherent spin waves are depicted as a collective wave-like precession of the spins in the film (blue arrows). The increased excitation efficiency for right-propagating spin waves results in larger spin-wave amplitudes on the right-hand side (gray lines). The spin-wave band is schematically depicted by a parabolic dispersion. The microwave field that drives the coherent spin waves is indicated by the oscillating arrow. The out-of-equilibrium occupation of the spin-wave band is indicated by the color gradient (as in Figure 1d). The NV detection frequencies f± are indicated by dashed lines.
Next, we study the density of the magnon gas created via the driving
of directional spin waves. Magnons can redistribute over the spin-wave
band through magnon–magnon interactions and lead to an equilibrated
occupation described by a Rayleigh-Jeans distribution7 with chemical potential μ:23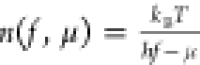 (which is the high-temperature
limit of
the Bose–Einstein distribution, appropriate for our room-temperature
measurements); here kB is Boltzmann’s
constant, T is the temperature, h is Planck’s constant, and f is the probe
frequency. To study whether the magnon gas (Figure 2a) is described by this distribution we monitor
the magnon density at the f– ESR
frequency while driving directional spin waves. To determine which
drive frequency yields the strongest NV response, we first characterize
the NV photoluminescence while sweeping the frequency and power of
the microwave drive field (Figure 3a). Then, we apply the microwave drive at a frequency
near the frequency of maximum response and characterize the increase
in magnon density at the f– ESR
frequency by measuring the NV relaxation rate Γ– between the 0 and the −1 spin states (Figure 3b,c) (Supporting Information Note 6). Under the near-FMR driving, f– frequency magnons are added to the magnon gas as the scattering
products of magnon–magnon interactions, resulting in an enhanced
Γ–. We measure Γ– at
several drive frequencies (Figure 3d), as the location of maximum NV response changes
slightly with drive power (Figure 3a). For all drive frequencies, we observe a strong
increase in the relaxation rate for increasing drive power, reaching
up to ∼60 times its equilibrium value. Consistent with previous
observations,17 this process is strongly
nonlinear, as can be seen from the threshold power required to increase
the relaxation rate at the higher drive frequencies.
(which is the high-temperature
limit of
the Bose–Einstein distribution, appropriate for our room-temperature
measurements); here kB is Boltzmann’s
constant, T is the temperature, h is Planck’s constant, and f is the probe
frequency. To study whether the magnon gas (Figure 2a) is described by this distribution we monitor
the magnon density at the f– ESR
frequency while driving directional spin waves. To determine which
drive frequency yields the strongest NV response, we first characterize
the NV photoluminescence while sweeping the frequency and power of
the microwave drive field (Figure 3a). Then, we apply the microwave drive at a frequency
near the frequency of maximum response and characterize the increase
in magnon density at the f– ESR
frequency by measuring the NV relaxation rate Γ– between the 0 and the −1 spin states (Figure 3b,c) (Supporting Information Note 6). Under the near-FMR driving, f– frequency magnons are added to the magnon gas as the scattering
products of magnon–magnon interactions, resulting in an enhanced
Γ–. We measure Γ– at
several drive frequencies (Figure 3d), as the location of maximum NV response changes
slightly with drive power (Figure 3a). For all drive frequencies, we observe a strong
increase in the relaxation rate for increasing drive power, reaching
up to ∼60 times its equilibrium value. Consistent with previous
observations,17 this process is strongly
nonlinear, as can be seen from the threshold power required to increase
the relaxation rate at the higher drive frequencies.
Figure 3.
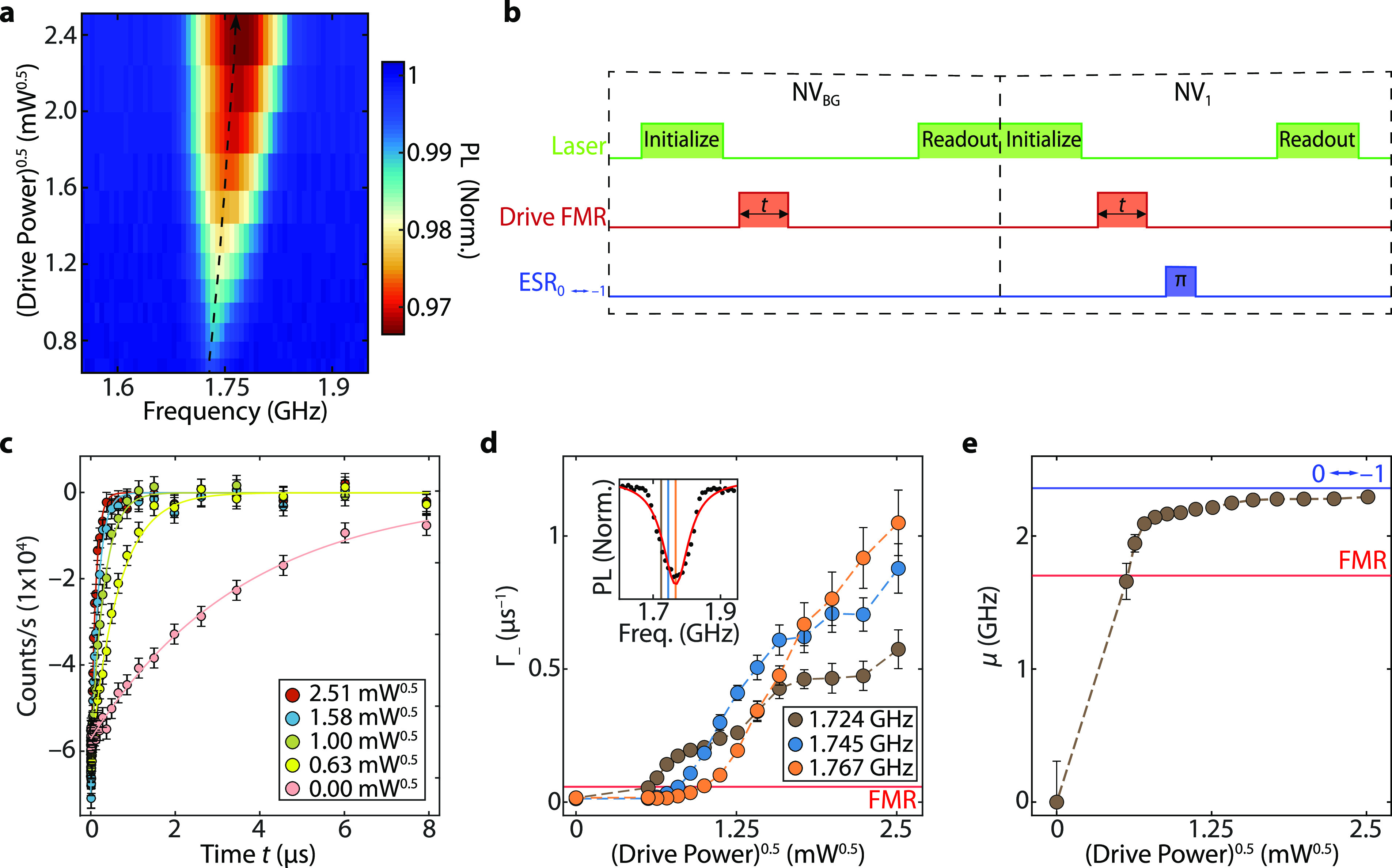
Characterizing the density of the magnon gas under near-FMR driving using NV relaxometry. (a) Normalized NV photoluminescence (PL) versus microwave drive frequency and the square root of the power, which is linear with the amplitude of the applied microwave field. The maximum contrast shifts with drive power (dashed black line). (b) Measurement sequence to characterize the magnon density at the f– NV ESR frequency: a 2 μs laser pulse prepares the NV spins in |0⟩. A variable-duration microwave pulse (red) causes an out-of-equilibrium magnon density that induces NV spin relaxation. Two sequences are performed, with and without a microwave π-pulse. The π-pulse at the f– ESR frequency switches the |0⟩ and |−1⟩ populations of the target NV spins. The final spin state is characterized by measuring the PL during the first 600 ns of a green laser pulse. The PL difference between the two sequences enables the extraction of the |0⟩ ↔ |−1⟩ relaxation rate of the target NV spins assuming negligible |0⟩ ↔ |+1⟩ relaxation (Supporting Information Note 6). (c) Relaxation rate measurement of the PL difference between the two sequences versus duration of the spin-wave drive pulse (see (b)), for different drive powers. B0 = 20 mT. Filled circles: data. Solid lines: fits to Ae–2Γ–t, where A is an offset and Γ– the |0⟩ ↔ |−1⟩ relaxation rate. The error bars represent uncertainties stemming from photon shot noise. (d) Γ– versus the square root of the drive power for three near-FMR drive frequencies, extracted from measurements as in (b). The red line labeled “FMR” indicates the maximum rate for a system described by a chemical potential that saturates at the bottom of the spin-wave band. Error bars determined from fits. Inset: Normalized NV PL versus microwave drive frequency at 2.51 mW0.5 microwave power (see (c)). The vertical lines indicate the drive frequencies used for the measurements in the main panel. (e) Effective chemical potential as a function of the square root of the drive power. Blue line: ESR transition frequency (2.359 GHz). Red line: Calculated FMR frequency (1.702 GHz).
If the magnon density is described by the Rayleigh–Jeans distribution, then we can determine the chemical potential by measuring the NV relaxation rates using18
| 1 |
where Γ–(0) is the relaxation rate in the absence of microwave driving and Γ–(μ) is the relaxation rate measured at a raised chemical potential caused by driving coherent spin waves. A key characteristic of the chemical potential for a bosonic system is that its maximum value is set by the bottom of the energy band,18,22 which in our system is located about 400 MHz below the FMR (at 20 mT) as can be calculated from the spin-wave dispersion (Supporting Information Note 5). Using eq 1 to calculate the chemical potential from the measured NV relaxation rates (Figure 3d), we find values far above the FMR, thereby exceeding this maximum (Figure 3e). We therefore conclude that the magnon gas created by near-FMR driving cannot be described by the Rayleigh–Jeans distribution with a finite chemical potential. Presumably, the magnon density is instead concentrated in a finite frequency range near the bottom of the spin-wave band that includes our detection (ESR) frequency. The strong increase in magnon density, compared to that observed in thinner YIG films,18 might be related to the lower threshold power needed for triggering nonlinear spin-wave responses in thicker magnetic films.30 Spectroscopic techniques such as Brillouin Light Scattering7,31 could shed further light on the spectral characteristics of the out-of-equilibrium magnon gas.
The Rayleigh–Jeans distribution describes an equal population of the spin-waves mode at a given frequency (i.e., the Rayleigh–Jeans occupation factor does not depend on the wavevector of the mode). We now study whether the spatial frequency content of the magnon gas created by near-FMR driving can be distinguished from that corresponding to a Rayleigh-Jeans occupation via distance-dependent measurements of the NV relaxation rate. To do so, we measure the spatial decay of the spin-wave stray fields away from the film, which is determined by the spatial frequencies (wavenumbers) of the magnons that generate the fields.32 We observe the stray fields associated with the incoherent magnon gas decay much more rapidly with increasing NV-film distance than the stray fields generated by the coherently driven spin waves at the NV ESR frequency (Figure 4a). To quantify this difference, we first characterize the decay of the stray field BSW of a coherent spin wave with a single, well-defined wavenumber kSW that we excite by applying a microwave drive resonant with the f– NV ESR frequency using the stripline. The amplitude of this field decays exponentially with distance d according to21
| 2 |
Figure 4.
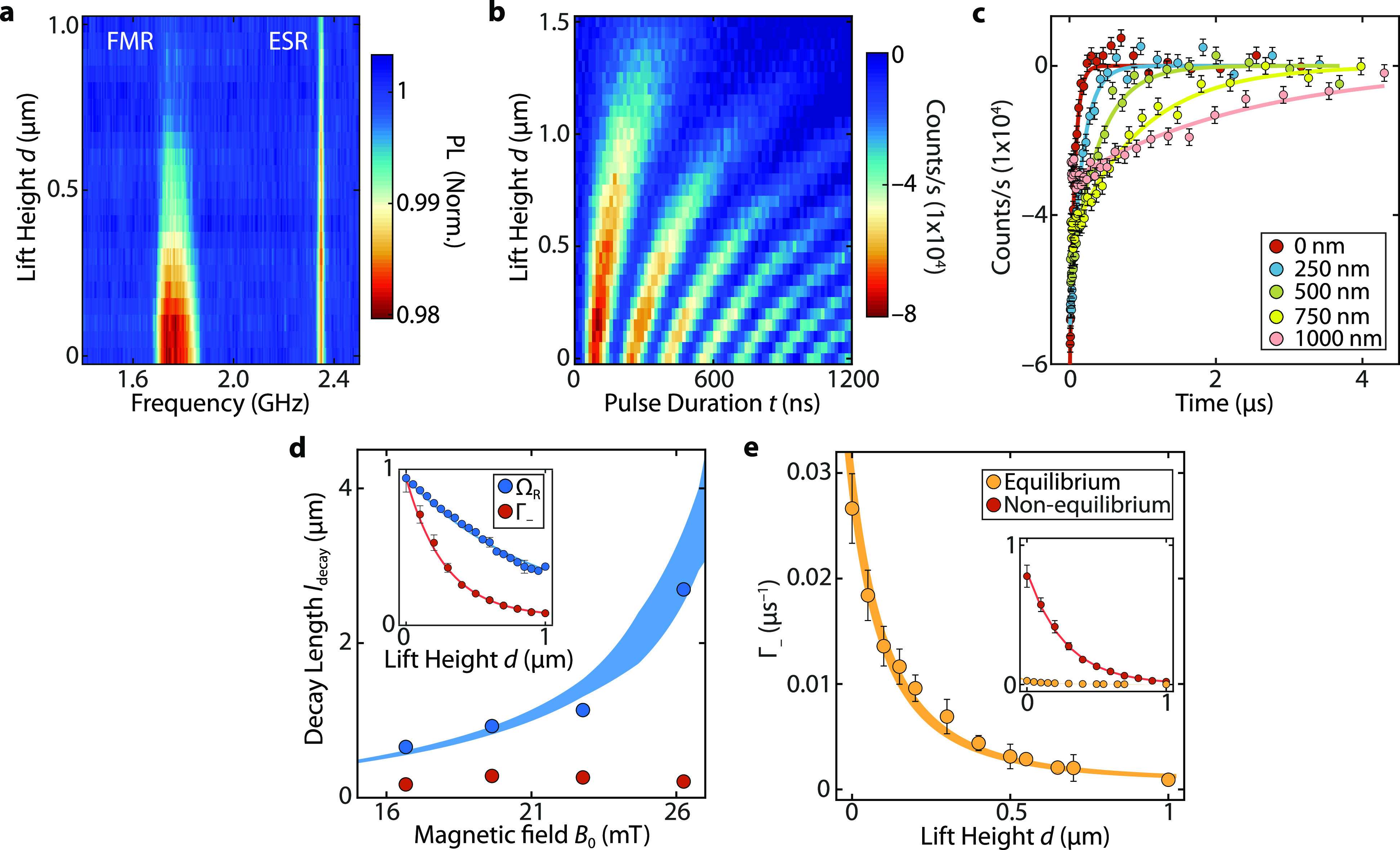
Characterizing the wavenumber content of the equilibrium and out-of-equilibrium magnon gases. (a) Normalized NV photoluminescence (PL) vs tip lift height d and microwave drive frequency, measured at ∼150 μm to the right of the stripline. The decay of the signal for increasing lift height is caused by the decay of the spin-wave stray fields driving the NV spins. The tip touches the sample at 0 μm. (b) Coherent NV spin rotations (Rabi oscillations) vs lift height d. The rotations are driven by a coherent spin-wave pulse of varying durations launched by the stripline at the f– ESR frequency at B0 = 20 mT. The measurement was performed at 37 μm to the right of the stripline. (c) NV spin relaxation measurements for different tip lift heights. B0 = 20 mT. Filled circles: data. Solid lines: fits to PL = Ae–2Γ–t. (d) Measured spatial decay length of the stray field of the driven coherent spin waves (blue circles) and of the out-of-equilibrium magnon gas (red circles) vs B0. The blue band indicates the expected decay length for a coherent spin wave that is resonant with the NV ESR frequency, determined by calculating the spin-wavelength from the spin-wave dispersion while considering an uncertainty of ±10 nm in film thickness,21 the ±1.8° uncertainty in the angle between the diamond cantilever and the YIG surface, and the uncertainty in the angle of B0 (Supporting Information Note 4). Inset: Spatial decay of the NV Rabi frequency (ΩR) when the Rabi oscillations are driven via coherent spin waves (blue circles) and of the NV relaxation rate (Γ–) caused by the out-of-equilibrium magnon gas (red circles) at B0 = 20 mT. Solid lines: fits to Ae–d/ldecay. (e) NV relaxation rate vs lift height d without microwave drive (orange circles). Orange line: calculation for an equilibrium occupation of the spin-wave band. The width of the line considers the uncertainties discussed in (e). Inset: Comparison of the spatial decay of the NV relaxation rates without (as in the main panel, orange circles) and with microwave drive (as in inset in (d), red circles) near the FMR. B0 = 20 mT. Red line: fit to Γ– = Ae–d/ldecay). The two lines possess a similar decay constant.
Because the excitation frequency is resonant with the NV ESR frequency, the field BSW drives coherent NV spin rotations (Rabi oscillations) with a rotation rate (Rabi frequency) that is proportional to the stray-field amplitude:21 ΩRabi ∝ BSW.
To quantify the decay length, we measure the NV Rabi
frequency
ΩRabi as a function of the tip–sample distance
(Figure 4b). By fitting
the spatial decay using 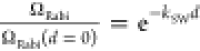 , we extract wavenumber, kSW, of the
spin waves and the corresponding decay length, ldecay, which ranges between ∼0.65 and
2.7 μm depending on the external field B0 (Figure 4d,
blue dots). We find a good agreement with the wavenumber calculated
from the spin-wave dispersion (Figure 4d, blue filled area; Supporting Information Note 5), demonstrating the power of height-dependent
measurements for determining spatial frequencies.
, we extract wavenumber, kSW, of the
spin waves and the corresponding decay length, ldecay, which ranges between ∼0.65 and
2.7 μm depending on the external field B0 (Figure 4d,
blue dots). We find a good agreement with the wavenumber calculated
from the spin-wave dispersion (Figure 4d, blue filled area; Supporting Information Note 5), demonstrating the power of height-dependent
measurements for determining spatial frequencies.
We find that
the stray fields of the out of-equilibrium magnon
gas, generated upon driving near the FMR, decay on a much shorter
length scale, i.e., ∼280 nm at B0 = 20 mT (Figure 4a). To quantify the corresponding decay length, we measure the NV
relaxation rate Γ– at different tip–sample
distances d (Figure 4c). By fitting the spatial decay of the relaxation
rate using an exponential approximation 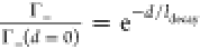 , we observe that the decay length ldecay is below 1 μm over the entire range
of B0 (Figure 4d, red dots). This short decay length contrasts
with that measured for the coherent spin waves (Figure 4d, blue dots), reflecting the additional
presence of large-wavenumber magnons in the incoherent magnon gas.
, we observe that the decay length ldecay is below 1 μm over the entire range
of B0 (Figure 4d, red dots). This short decay length contrasts
with that measured for the coherent spin waves (Figure 4d, blue dots), reflecting the additional
presence of large-wavenumber magnons in the incoherent magnon gas.
To examine if this is different for a magnon gas in equilibrium, we compare the NV relaxation rates measured in the absence of microwave driving to a calculation of the stray-field noise generated by a magnon gas in thermal equilibrium with zero chemical potential (Figure 4e). This calculation is based on a model32 that assumes a Rayleigh–Jeans occupation of the spin-wave band and calculates the stray-field noise at the NV ESR frequency by summing the contributions of all spin-wave modes at this frequency (Supporting Information Note 5 and Figure 4e, orange line). This model was recently demonstrated to accurately describe the stray-field noise of thin magnetic films.32 We find a quantitative match with the measured equilibrium NV relaxation rate Γ–(μ = 0) if we assume a 0.28 ± 0.03 μm distance offset of the NV centers at zero tip-lift height (Figure 4e). This offset is larger than the NV implantation depth of ∼20 nm, which could be caused by small particles picked up by the tip during scanning. We compare the measured relaxation rate under near-FMR driving to the same model scaled by a prefactor to account for the larger magnon occupation under near-FMR driving. Because the rate (Figure 4e) is well described by this model, we conclude that the spatial frequency content of the incoherent magnon gas cannot be distinguished from a homogeneous k-space occupation such as that expected for a Rayleigh-Jeans distribution. Furthermore, the calculations confirm that the spatial decay length should not depend strongly on the external field B0 (Supporting Information Note 5), consistent with the measurements shown in Figure 4d.
We have shown that coherent spin waves enable the generation of a high-density magnon gas unidirectionally with respect to an excitation stripline. The threshold power required to trigger this process underscores the nonlinearity of the underlying magnon scattering. From the more than 10-fold increase of the stray-field noise under near-FMR driving, probed via relaxometry measurements of our sensor spin, we conclude that the resulting magnon gas cannot be described by a Rayleigh–Jeans occupation of the spin-wave band. We demonstrate that the spatial decay length of the spin-wave stray fields contains valuable information about the spatial frequencies of the spin waves generating the fields. The observed submicrometer spatial decay lengths of the stray fields generated by the out-of-equilibrium magnon gas indicate the presence of large wavenumber magnons and highlights the need for proximal sensors such as the scanning-probe NV magnetometer. Further controlling the directionality of the excited coherent spin waves by, e.g., shaping stripline geometries and/or tuning the direction of the magnetic external field could enable delivering high-density magnon gases to target locations in a magnetic film or device. Targeted delivery of high-density magnon gases provides new opportunities for controlling spin transport and for triggering magnetic phenomena such as phase transitions,5 magnon condensation,6−8 and spin-wave-induced domain-wall motion.9−12
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c02654.
Experimental and theoretical details on the YIG sample, the measurement setup, the fabrication of the scanning tip, the calibration of the external magnetic field magnitude and direction, the theoretical computation of the NV relaxation rate induced by thermal magnons, and the NV relaxation rate measurement (PDF)
Author Contributions
B.G.S, S.K., A.J.K., and T.v.d.S. conceived and designed the experiments and realized the imaging setup. B.G.S., S.K., and A.J.K performed the experiments. B.G.S., S.K., T.v.d.S., and H.L. analyzed and modeled the experimental results with contributions of I.B. and J.J.C. I.B. fabricated the stripline on the YIG sample. B.G.S, M.R, N.d.J., and H.v.d.B. fabricated the diamond cantilevers. B.G.S., S.K., and T.v.d.S. wrote the manuscript with contributions from all coauthors.
Author Contributions
⊥ (B.G.S. and S.K.) These authors contributed equally to this work.
This work was supported by the Dutch Research Council (NWO) through the NWO Projectruimte grant 680.91.115 and the Kavli Institute of Nanoscience Delft.
The authors declare no competing financial interest.
Notes
All data contained in the figures will be made available at zenodo.org upon publication with the identifier 10.5281/zenodo.5266548. Additional data related to this paper may be requested from the authors.
Supplementary Material
References
- Cornelissen L.; Liu J.; Duine R.; Youssef J. B.; Van Wees B. Long-Distance Transport of Magnon Spin Information in a Magnetic Insulator at Room Temperature. Nat. Phys. 2015, 11 (12), 1022–1026. 10.1038/nphys3465. [DOI] [Google Scholar]
- Cornelissen L.; Liu J.; Van Wees B.; Duine R. Spin-Current-Controlled Modulation of the Magnon Spin Conductance in a Three-Terminal Magnon Transistor. Phys. Rev. Lett. 2018, 120 (9), 097702. 10.1103/PhysRevLett.120.097702. [DOI] [PubMed] [Google Scholar]
- Wimmer T.; Althammer M.; Liensberger L.; Vlietstra N.; Geprägs S.; Weiler M.; Gross R.; Huebl H. Spin Transport in a Magnetic Insulator with Zero Effective Damping. Phys. Rev. Lett. 2019, 123 (25), 257201. 10.1103/PhysRevLett.123.257201. [DOI] [PubMed] [Google Scholar]
- Chumak A. V.; Serga A. A.; Hillebrands B. Magnon Transistor for All-Magnon Data Processing. Nat. Commun. 2014, 5 (1), 4700. 10.1038/ncomms5700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nan T.; Lee Y.; Zhuang S.; Hu Z.; Clarkson J. D.; Wang X.; Ko C.; Choe H.; Chen Z.; Budil D.; et al. Electric-Field Control of Spin Dynamics During Magnetic Phase Transitions. Science Advances 2020, 6 (40), eabd2613. 10.1126/sciadv.abd2613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider M.; Brächer T.; Breitbach D.; Lauer V.; Pirro P.; Bozhko D. A.; Musiienko-Shmarova H. Y.; Heinz B.; Wang Q.; Meyer T.; et al. Bose–Einstein Condensation of Quasiparticles by Rapid Cooling. Nat. Nanotechnol. 2020, 15 (6), 457–461. 10.1038/s41565-020-0671-z. [DOI] [PubMed] [Google Scholar]
- Demokritov S. O.; Demidov V. E.; Dzyapko O.; Melkov G. A.; Serga A. A.; Hillebrands B.; Slavin A. N. Bose–Einstein Condensation of Quasi-Equilibrium Magnons at Room Temperature under Pumping. Nature 2006, 443 (7110), 430–433. 10.1038/nature05117. [DOI] [PubMed] [Google Scholar]
- Demokritov S.; Demidov V.; Dzyapko O.; Melkov G.; Slavin A. Quantum Coherence Due to Bose–Einstein Condensation of Parametrically Driven Magnons. New J. Phys. 2008, 10 (4), 045029. 10.1088/1367-2630/10/4/045029. [DOI] [Google Scholar]
- Kim S. K.; Tserkovnyak Y.; Tchernyshyov O. Propulsion of a Domain Wall in an Antiferromagnet by Magnons. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90 (10), 104406. 10.1103/PhysRevB.90.104406. [DOI] [Google Scholar]
- Shen P.; Tserkovnyak Y.; Kim S. K. Driving a Magnetized Domain Wall in an Antiferromagnet by Magnons. J. Appl. Phys. 2020, 127 (22), 223905. 10.1063/5.0006038. [DOI] [Google Scholar]
- Chang L.-J.; Liu Y.-F.; Kao M.-Y.; Tsai L.-Z.; Liang J.-Z.; Lee S.-F. Ferromagnetic Domain Walls as Spin Wave Filters and the Interplay between Domain Walls and Spin Waves. Sci. Rep. 2018, 8 (1), 3910. 10.1038/s41598-018-22272-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W.; Albert M.; Beg M.; Bisotti M.-A.; Chernyshenko D.; Cortés-Ortuño D.; Hawke I.; Fangohr H. Magnon-Driven Domain-Wall Motion with the Dzyaloshinskii-Moriya Interaction. Phys. Rev. Lett. 2015, 114 (8), 087203. 10.1103/PhysRevLett.114.087203. [DOI] [PubMed] [Google Scholar]
- Kajiwara Y.; Harii K.; Takahashi S.; Ohe J.-i.; Uchida K.; Mizuguchi M.; Umezawa H.; Kawai H.; Ando K.; Takanashi K.; et al. Transmission of Electrical Signals by Spin-Wave Interconversion in a Magnetic Insulator. Nature 2010, 464 (7286), 262–266. 10.1038/nature08876. [DOI] [PubMed] [Google Scholar]
- Schneider M.; Breitbach D.; Serha R.; Wang Q.; Serga A. A.; Slavin A. N.; Tiberkevich V. S.; Heinz B.; Lägel B.; Brächer T.. Control of the Bose–Einstein Condensation of Magnons by the Spin-Hall Effect. arXiv, 2021, 2102.134812021. https://arxiv.org/abs/2102.13481 (accessed May 1, 2021). [DOI] [PubMed]
- Wettling W.; Wilber W.; Kabos P.; Patton C. Light Scattering from Parallel-Pump Instabilities in Yttrium Iron Garnet. Phys. Rev. Lett. 1983, 51 (18), 1680. 10.1103/PhysRevLett.51.1680. [DOI] [Google Scholar]
- Bauer H. G.; Majchrak P.; Kachel T.; Back C. H.; Woltersdorf G. Nonlinear Spin-Wave Excitations at Low Magnetic Bias Fields. Nat. Commun. 2015, 6 (1), 8274. 10.1038/ncomms9274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullian B. A.; Thabt A. M.; Gray B. A.; Melendez A. L.; Wolf M. S.; Safonov V. L.; Pelekhov D. V.; Bhallamudi V. P.; Page M. R.; Hammel P. C. Broadband Multi-Magnon Relaxometry Using a Quantum Spin Sensor for High Frequency Ferromagnetic Dynamics Sensing. Nat. Commun. 2020, 11 (1), 5229. 10.1038/s41467-020-19121-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du C.; Van der Sar T.; Zhou T. X.; Upadhyaya P.; Casola F.; Zhang H.; Onbasli M. C.; Ross C. A.; Walsworth R. L.; Tserkovnyak Y.; et al. Control and Local Measurement of the Spin Chemical Potential in a Magnetic Insulator. Science 2017, 357 (6347), 195–198. 10.1126/science.aak9611. [DOI] [PubMed] [Google Scholar]
- Van der Sar T.; Casola F.; Walsworth R.; Yacoby A. Nanometre-Scale Probing of Spin Waves Using Single Electron Spins. Nat. Commun. 2015, 6 (1), 7886. 10.1038/ncomms8886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casola F.; Van Der Sar T.; Yacoby A. Probing Condensed Matter Physics with Magnetometry Based on Nitrogen-Vacancy Centres in Diamond. Nature Reviews Materials 2018, 3 (1), 17088. 10.1038/natrevmats.2017.88. [DOI] [Google Scholar]
- Bertelli I.; Carmiggelt J. J.; Yu T.; Simon B. G.; Pothoven C. C.; Bauer G. E.; Blanter Y. M.; Aarts J.; Van Der Sar T. Magnetic Resonance Imaging of Spin-Wave Transport and Interference in a Magnetic Insulator. Science Advances 2020, 6 (46), eabd3556. 10.1126/sciadv.abd3556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitaevskii L.; Stringari S.. Bose–Einstein Condensation and Superfluidity; Oxford University Press: 2016; pp 15–19. [Google Scholar]
- Demidov V.; Dzyapko O.; Demokritov S.; Melkov G.; Slavin A. Thermalization of a Parametrically Driven Magnon Gas Leading to Bose–Einstein Condensation. Phys. Rev. Lett. 2007, 99 (3), 037205. 10.1103/PhysRevLett.99.037205. [DOI] [PubMed] [Google Scholar]
- Maletinsky P.; Hong S.; Grinolds M. S.; Hausmann B.; Lukin M. D.; Walsworth R. L.; Loncar M.; Yacoby A. A Robust Scanning Diamond Sensor for Nanoscale Imaging with Single Nitrogen-Vacancy Centres. Nat. Nanotechnol. 2012, 7 (5), 320–324. 10.1038/nnano.2012.50. [DOI] [PubMed] [Google Scholar]
- Wang X.; Xiao Y.; Liu C.; Lee-Wong E.; McLaughlin N. J.; Wang H.; Wu M.; Wang H.; Fullerton E. E.; Du C. R. Electrical Control of Coherent Spin Rotation of a Single-Spin Qubit. npj Quantum Information 2020, 6 (1), 78. 10.1038/s41534-020-00308-8. [DOI] [Google Scholar]
- Serga A.; Chumak A.; Hillebrands B. Yig Magnonics. J. Phys. D: Appl. Phys. 2010, 43 (26), 264002. 10.1088/0022-3727/43/26/264002. [DOI] [Google Scholar]
- Yu T.; Blanter Y. M.; Bauer G. E. Chiral Pumping of Spin Waves. Phys. Rev. Lett. 2019, 123 (24), 247202. 10.1103/PhysRevLett.123.247202. [DOI] [PubMed] [Google Scholar]
- Wolfe C. S.; Bhallamudi V. P.; Wang H. L.; Du C. H.; Manuilov S.; Teeling-Smith R.; Berger A.; Adur R.; Yang F.; Hammel P. C. Off-Resonant Manipulation of Spins in Diamond Via Precessing Magnetization of a Proximal Ferromagnet. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89 (18), 180406. 10.1103/PhysRevB.89.180406. [DOI] [Google Scholar]
- Wolfe C.; Manuilov S.; Purser C.; Teeling-Smith R.; Dubs C.; Hammel P.; Bhallamudi V. Spatially Resolved Detection of Complex Ferromagnetic Dynamics Using Optically Detected Nitrogen-Vacancy Spins. Appl. Phys. Lett. 2016, 108 (23), 232409. 10.1063/1.4953108. [DOI] [Google Scholar]
- Lee-Wong E.; Xue R.; Ye F.; Kreisel A.; van Der Sar T.; Yacoby A.; Du C. R. Nanoscale Detection of Magnon Excitations with Variable Wavevectors through a Quantum Spin Sensor. Nano Lett. 2020, 20 (5), 3284–3290. 10.1021/acs.nanolett.0c00085. [DOI] [PubMed] [Google Scholar]
- Kabos P.; Wiese G.; Patton C. E. Measurement of Spin Wave Instability Magnon Distributions for Subsidiary Absorption in Yttrium Iron Garnet Films by Brillouin Light Scattering. Phys. Rev. Lett. 1994, 72 (13), 2093–2096. 10.1103/PhysRevLett.72.2093. [DOI] [PubMed] [Google Scholar]
- Rustagi A.; Bertelli I.; Van Der Sar T.; Upadhyaya P. Sensing Chiral Magnetic Noise Via Quantum Impurity Relaxometry. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 102 (22), 220403. 10.1103/PhysRevB.102.220403. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.