Technical Note: Dose prediction for radiation therapy using feature‐based losses and One Cycle Learning

Abstract

Purpose

To present the technical details of the runner‐up model in the open knowledge‐based planning (OpenKBP) challenge for the dose–volume histogram (DVH) stream. The model was designed to ensure simple and reproducible training, without the necessity of costly advanced generative adversarial network (GAN) techniques.

Methods

The model was developed based on the OpenKBP challenge dataset, consisting of 200 and 40 head‐and‐neck patients for training and validation, respectively. The final model is a U‐Net with additional ResNet blocks between up‐ and down convolutions. The results were obtained by training the model with AdamW with the One Cycle scheduler. The loss function is a combination of the L1 loss with a feature loss, which uses a pretrained video classifier as a feature extractor. The performance was evaluated on another 100 patients in the OpenKBP test dataset. The DVH metrics of the test data were evaluated, where $D_{0.1cc}$, and $D_{\mathit{mean}}$ were calculated for the organs at risk (OARs) and $D_{1\%}$, $D_{95\%}$, and $D_{99\%}$ were computed for the target structures. DVH metric differences between predicted and true dose are reported in percentage.

Results

The model achieved 2nd and 4th place in the DVH and dose stream of the OpenKBP challenge, respectively. The dose and DVH score were 2.62 ± 1.10 and 1.52 ± 1.06, respectively. Mean dose differences for the different structures and DVH parameters were within ±1%.

Conclusion

This straightforward approach produced excellent results. It incorporated One Cycle Learning, ResNet, and feature‐based losses, which are common computer vision techniques.

1. INTRODUCTION

Treatment techniques in radiation therapy have become more complex and time consuming. As a result, there is demand for automating the planning process to provide fast and reliable treatment plans with consistent plan quality. A promising method to help creating these plans is deep learning, which has been used to predict dose distributions for various body sites. ¹ , ² , ³ Unfortunately, most models are developed and tested on private datasets, which makes it difficult to compare the methods. The open knowledge‐based planning (OpenKBP) challenge provided a platform with a dataset of intensity modulated radiation therapy treatment plans to make a quantitative comparison of these models possible. ⁴ This technical note provides detailed information on the first runner‐up model in the dose–volume histogram (DVH) stream of the OpenKBP challenge. Recent dose prediction models have utilized generative adversarial networks (GANs) to improve conversion performance. ¹ , ³ However, despite the fact that GANs resulted in great success for many different applications, the technique still suffers from shortcomings like vanishing gradients and mode collapse. This makes GANs difficult to train and requires an extensive hyperparameter search for optimal performance. Because of this we focused our work on alternative techniques which include learning rate scheduling, ⁵ advanced nonlinear activation functions, ⁶ and neural network based feature cost functions ⁷ to make predictions more accurate and reproducible during testing.

The baseline U‐Net model has been used for dose prediction within a GAN architecture that was based on pix2pix. ¹ , ⁸ Even though various GAN techniques (e.g., conditional GANs, ¹ , ⁸ spectral normalization, ⁹ attention‐gated convolutions ¹⁰ ) help to improve performance, the hyperparameter search is difficult as there are many hyperparameters. Multiple research groups demonstrated that a simple model like the U‐Net or pretrained ResNet classifiers can be trained without the requirement of GAN training and still perform well in the head and neck region. ² , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ Most of the studies utilized the mean squared error loss function for optimization, which does not capture geometric representations of the volume. DVH parameters for these studies ranged from 3 to 5% of the mean or median value relative to the prescribed dose, which is similar to values reported for commercially available systems. ¹⁶ , ¹⁷ However, the results of published studies are difficult to compare due to different datasets and non‐standardized evaluation procedures.

In this study, the focus was to use robust training techniques which do not rely on GAN methods. For example, fast.ai is a library that uses One Cycle Learning Scheduling which is a method that overcomes warm‐up problems of the Adam optimizer, to efficiently train models without GAN techniques. ⁵ , ¹⁸

Additionally, optimizers have been studied extensively in the past years which has resulted in a large variety of methods. AdamW, for example, combines the Adam optimizer with decoupled weight decay regularization to prevent overfitting. ¹⁹

Another important factor for neural networks is the choice of the activation function. Many new activation functions have been developed in an effort to replace the popular ReLU activation function, which is non‐differentiable at zero and results in no gradient flow if the input value is below zero. One of these new activation functions is Mish, which does not saturate and is everywhere differentiable and demonstrated improved accuracy by 1–2% for image classification and object detection. ⁶

Lastly, many new loss functions have been developed that incorporate feature loss metrics, which are extracted via pretrained models. ⁷ Feature losses were already successfully applied for denoising images like low‐ dose CT, tomography, and optical coherence tomography. ²⁰ , ²¹ , ²² , ²³ A previous study of Ngyuen et al. demonstrated good results when a DVH based loss was included for dose prediction in the pelvic region which highlights the necessity of domain specific loss functions. ²⁴

2. MATERIALS AND METHODS

2.1. Datasets

The OpenKBP provided a preprocessed dataset with 200, 40, and 100 patients for training, validation, and testing, respectively. All patients included a CT, structure sets for organs at risk (OAR) and target volumes (with up to three dose levels), as well as corresponding dose distributions. All volumes are represented as 128 × 128 × 128 matrix with a variable voxel resolution of about $3.5\times 3.5\times 2m{m}^3$.

2.2. Baseline model

The baseline model was the U‐Net implementation of the pix2pix model. ⁸ However, three major changes were made to that baseline model: (a) three‐dimensional (3D) convolutions were used instead of two‐dimensional convolutions, (b) instance normalization with affine transformations instead of batch normalization, and (c) a sigmoid output function instead of a tanh.

The model input consisted of the challenge data as a concatenated 4D volume. CT and dose distribution values were clipped and divided by 4000 and 100, respectively, to bring the voxel values into the interval between [0, 1]. An illustration of the final model can be found in Fig. 1 and the code for the model is available at https://github.com/junyanz/pytorch‐CycleGAN‐and‐pix2pix.

Fig. 1.

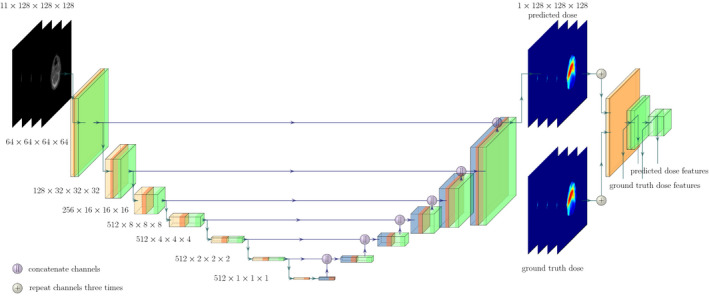
The final U‐Net model with ResNet blocks (green), 4 × 4 convolutions (orange) and transposed convolutions (blue). Purple dots represent the feature map concatenation. Note that the blocks represent the output of the respective operations given by the color. On the right side of the predicted dose, the pre‐trained ResNet model can be seen where the feature outputs are extracted from different depths for the predicted and the ground truth dose distribution. Please note that the ResNet blocks of the U‐Net and the pre‐trained classifier differ in architecture.

2.3. Hyperparameter search

All different configurations of the parameters were tracked using the weights and biases service (Weights&Biases Software wandb.com, CA, USA) to allow for fast and easy evaluation. Starting from the baseline model, the following hyperparameters were adapted:

• Activation function: Set to Mish for all convolutions, except for the output of the network.

• ResNet blocks: Between the up‐ and down‐sampling blocks a ResNet block was included with a bottleneck. Feature size was reduced to 64 with a 1 × 1 convolution, followed by a 3 × 3 convolution with 64 features, and a last 1 × 1 convolution increasing the feature size to the initial one. The convolution blocks follow the form of convolution, normalization, and activation where the activation is skipped for the final convolution.

• Masking: To increase the information density, the error calculation was limited to the external contour.

• Loss function: For training, the L1 metric was used as a baseline. Furthermore, a feature based loss was implemented which extracted high higher‐order information with a pre‐trained model. Since the data is three dimensional, the pre‐trained ResNet3D for video classification was utilized for feature extraction. ²⁵ This pre‐trained model was taken from torchvision. ²⁶ To fit the input criteria of the classifier, the predicted dose output and the ground truth dose were repeated three times to fill the red‐green‐blue (RGB) channels. Features were extracted from different depths of the model, where the single block outputs were used which are called, for example, stem, layer1, layer2 as can be seen in Table I. For more information, please see the original paper ²⁵ or the torchvision implementation. ²⁶ The model outputs can be seen as dimensionality reduction of the input dose matrix into a lower dimension matrix. By passing the ground truth and the prediction through the model the output features can be compared by a distance measure (see Fig. 1). The overall loss function is then given as:

  $$L=\lambda \frac{1}{m}{\Vert x‐y\Vert }_1+\sum _{i=1}^n\frac{1}{m}{\lambda }_{F,i}{\Vert F^{[i]}(x)‐F^{[i]}(y)\Vert }_1$$ (1)

  where F(·) is the pre‐trained model, m is the number of voxels considered in the comparison, [i] denotes the last layer positions of the the different blocks specified above, and x,y are the ground truth and predicted dose distributions, respectively. λ and ${\lambda }_{F,i}$ are weighting factors where λ was set to 100 for all experiments and ${\lambda }_{F,i}$ to 1.

Table I.

Convolution operations in the ResNet3D. All layers use batch normalization and ReLU. The encoder number for F gives the integer output position of the formula.

Encoder number F	Layer name	Output size	Convolution layers
$F^0$	stem	64 × 128 × 64 × 64	3 × 7 × 7, 64, stride 1 × 2 × 2
$F^1$	layer1	64 × 128 × 64 × 64	$\left[\begin{array}{c}3\times 3\times 3,64\\ 3\times 3\times 3,64\end{array}\right]\times 2$
$F^2$	layer2	128 × 64 × 32 × 32	$\left[\begin{array}{c}3\times 3\times 3,128\\ 3\times 3\times 3,128\end{array}\right]\times 2$

2.4. Model training

The maximum learning rate was defined with the learning rate finder which resulted in ${10}^{‐3}$ for all different configurations. The models were trained using AdamW with a weight decay of ${10}^{‐4}$ and ${\beta }_1$ and ${\beta }_2$ values of 0.5 and 0.999, respectively. The One Cycle Learning rate schedule was applied over a training time of 200 epochs. Additionally, data augmentation was performed including transversal flips with orientation consistency, and random translations of the image volume along all three coordinate axes. The algorithm was implemented using Pytorch Lightning with Pytorch.

2.5. Evaluation

The model performance was tracked with the dose score which is the mean absolute error of the predicted dose distribution inside of the external contour as well as the DVH score which is the mean absolute error of five predefined DVH metrics ($D_{0.1cc}$, $D_{\mathit{mean}}$, $D_{1\%}$, $D_{95\%}$, and $D_{99\%}$). The mean and standard deviation of the dose and DVH score over all patients are reported. Improvements are given via the difference to the means of the baseline model for the dose and DVH score. The best performing model was chosen by the lowest dose and DVH score of the validation dataset.

The dose and DVH score were computed and reported for the test dataset for the best performing model. All relative DVH metric differences are additionally reported for the test dataset, where $D_{0.1cc}$ and $D_{\mathit{mean}}$ are computed for the OARs and $D_{1\%}$, $D_{95\%}$ and $D_{99\%}$ are computed for the target structures. The dose differences for the single structures are given as:

$$\mathrm{\Delta }D=\frac{D_{\mathit{pred}}‐D_{\mathit{true}}}{70Gy}\times 100$$ (2)

where $D_{\mathit{pred}}$ and $D_{\mathit{true}}$ are the predicted and ground truth dose metric, respectively.

3. RESULTS

The baseline model yielded relatively good starting scores for both dose and DVH, which were further improved by the proposed methods (see Table II). The final model that performed best used ResNet blocks, Mish activation functions, mask guided loss metrics, and the first convolution block (stem) of the feature loss.

Table II.

Dose and dose‐volume histogram (DVH) scores for the different hyperparameter settings and their mean differences to the baseline model (Δ) for the validation dataset. The highest difference is shown in bold.

	Dose score	Δ	DVH score	Δ
Baseline	2.651 ± 0.849	–	1.666 ± 0.853	–
+ ResNet blocks	2.548 ± 0.796	0.103	1.617 ± 0.759	0.049
+ Mish	2.534 ± 0.796	0.117	1.611 ± 0.777	0.055
+ Masking	2.530 ± 0.747	0.121	1.607 ± 0.789	0.059
+ Feature loss	2.503 ± 0.738	0.148	1.563 ± 0.790	0.103

This configuration resulted in a dose score of 2.62 ± 1.10 ($4\mathit{th}$ place in dose stream) and a DVH score of 1.52 ± 1.06. (2nd place in DVH stream) on the test set of 100 patients. By omitting one patient of the test dataset, which was identified to include a wrong PTV label, the final dose score and the DVH score could be improved to 2.58 ± 1.04 and 1.43 ± 0.53, respectively.

Figure 2 shows the percentage dose difference between the predicted and ground truth DVH metric. The medians of all parameters were distributed between −1.2% and 0.9%. The inter‐quartile ranges were also within −4% and 3%. In total, there were 61 outliers across all DVH metrics, however, only 16% outliers were observed that had a dose difference > ± 10%.

Fig. 2.

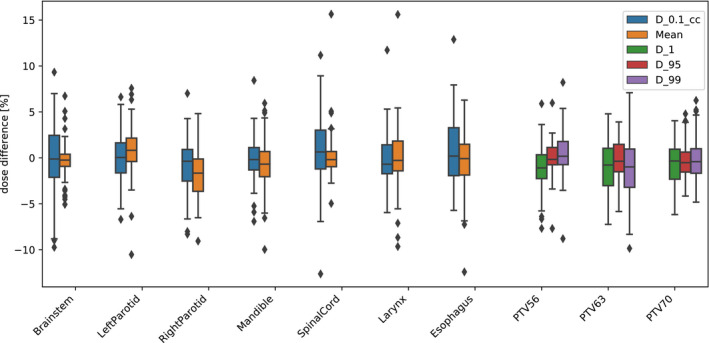
The colored dose parameters for the test dataset for all organs at risks and target structures. The boxes indicate median and interquartile range (IQR) and the whiskers extend to 1.5 times the IQR. Outliers are denoted by diamonds.

4. DISCUSSION AND CONCLUSION

The initial U‐Net baseline model trained with AdamW and One Cycle Learning resulted already in good results. We observed that training the model for 100 epochs is efficient as the validation loss improved only slightly by increasing the epochs to 200. Two of the main effects of One Cycle Learning are the adaptive changing of the learning rate and the momentum, which were recently shown to be a key component for improving optimization. ²⁷ Additionally, instance normalization with affine transformations was applied because initial experiments with batch normalization showed worse results during validation due to memory dependent small batch size (n = 1).

The modifications to the baseline model affected the dose and DVH score differently. The use of ResNet blocks and masking resulted in much better dose score (improvement of 0.103 and 0.121, respectively). However, the feature loss helped to improve the DVH score by 0.103 and consequently the DVH metrics further, even though the dose score changed only slightly. The model’s feature extraction network learned from non‐medical RGB video data, which are not representative for dose distributions. Still the model seems to provide useful information to improve model performance. Using the first layer of the pre‐trained model resulted in the best performance and including one additional layer output (layer1) resulted in a similar dose score but a worse DVH score value. Models trained with this feature loss technique would likely benefit if the corresponding classifier was pre‐trained on medical images specific to the task at hand. This should be further investigated as great success was achieved by using feature‐ based losses not only in this study but also in other fields of application.

There are many other promising techniques from the field of computer vision that could be explored. For example, transfer learning with 3D models was successfully used for classification of medical data. ²⁸ Similarly, the model could be adapted to be used as a pre‐trained encoder part of a U‐Net, as it is performed by the fast.ai library. ¹⁸ Unfortunately, these kind of experiments were excluded due to memory and time constrains.

Changing the activation function also slightly improved the performance as can be seen in Table II. Since the Mish implementation was done in native pytorch, memory requirements were sub‐optimal and high compared to ReLU based activation functions. The entire implementation used to obtain the training results in wandb as well as the link to the wandb report can be found at this github repository.

In conclusion, this straightforward approach resulted in good results for dose predictions, with only common computer vision techniques and without the necessity of complicated training methods (e.g., GANs).