Abstract
Identifying local adaptation in bottlenecked species is essential for conservation management. Selection detection methods have an important role in species management plans, assessments of adaptive capacity, and looking for responses to climate change. Yet, the allele frequency changes exploited in selection detection methods are similar to those caused by the strong neutral genetic drift expected during a bottleneck. Consequently, it is often unclear what accuracy selection detection methods have across bottlenecked populations. In this study, simulations were used to explore if signals of selection could be confidently distinguished from genetic drift across 23 bottlenecked and reintroduced populations of Alpine ibex (Capra ibex). The meticulously recorded demographic history of the Alpine ibex was used to generate comprehensive simulated SNP data. The simulated SNPs were then used to benchmark the confidence we could place in outliers identified in empirical Alpine ibex RADseq derived SNP data. Within the simulated data set, the false positive rates were high for all selection detection methods (F ST outlier scans and Genetic‐Environment Association analyses) but fell substantially when two or more methods were combined. True positive rates were consistently low and became negligible with increased stringency. Despite finding many outlier loci in the empirical Alpine ibex SNPs, none could be distinguished from genetic drift‐driven false positives. Unfortunately, the low true positive rate also prevents the exclusion of recent local adaptation within the Alpine ibex. The baselines and stringent approach outlined here should be applied to other bottlenecked species to ensure the risk of false positive, or negative, signals of selection are accounted for in conservation management plans.
Keywords: bottleneck, conservation, evolutionary management, outlier, reintroduction
1. INTRODUCTION
Identification of recent responses to selection, or local adaptation, is of great interest to evolutionary and conservation biologists. Insights gained from recent adaptive changes can facilitate our understanding of evolutionary processes (Whitlock & Lotterhos, 2015a), and also have applied or practical importance to conservation biologists. Characterizing intraspecific adaptive differences is often necessary for species management plans (e.g., Robertson et al., 2014) and may offer insight into long‐term extinction risk, particularly if a population or species is no longer able to respond to selection (Frankham et al., 2010). Within reintroduced populations specifically, optimized source populations can be chosen for translocations or establishing new populations if local adaptations are known (Flanagan et al., 2018). The sudden environmental change experienced when founder individuals are released in new locations may also fuel rapid adaptive change that is important to consider in future management (e.g., Reznick et al., 2004; Stockwell et al., 2003). This new conservation mindset where evolutionary processes are considered in species management, is known as “evolutionary” or “adaptive” conservation management (Hoffmann et al., 2015). The long‐term success of evolutionary conservation management requires accurate assessments of the evolutionary processes in bottlenecked populations and thus, it is important to evaluate the analytical biases and limitations of selection detection methods in nonequilibrium populations.
The increase accessibility of genome‐wide SNP data has driven a resurgence of studies scanning for selection at the genomic level in wild populations (e.g., Gasterosteus aculeatus, Hohenlohe et al., 2010; Peromyscus maniculatus, Linnen et al., 2013; Sarcophilus harrisii, Epstein et al., 2016; Oncorhynchus clarkii henshawi, Amish et al., 2019). F ST‐based selection detection methods are widely used to detect recent intraspecific selective responses by scanning for unusually high values of F ST (“outlier” loci), which are assumed to be driven directly or indirectly (i.e., hitchhiking) by positive selection (Fay & Wu, 2000; Lewontin & Krakauer, 1973). Popularity of selection detection studies has fuelled analytical methods that identify selective responses using environmental clines (Coop et al., 2010; De Mita et al., 2013). Referred to as Genetic‐Environment Association analyses or “GEA” analyses, these methods identify alleles that display repeated associations with an environmental variable due to local adaptation (Hoban et al., 2016; Lotterhos & Whitlock, 2015).
The degree to which currently available selection detection methods successfully accommodate unusual, or more complex demographic histories, is still being tested. This information is essential to ensure accuracy because violations of demographic assumptions can fuel elevated rates of false signals of selection, where neutral loci are falsely identified as outliers. This can arise, for example, from unaccounted variance in the distribution of F ST due to shared history and relatedness of populations (Excoffier et al., 2009; Robertson, 1975a, 1975b).
Recent population bottlenecks and reintroductions pose particularly severe challenges for selection detection, because they are associated with high or complex patterns of interpopulation relatedness (Frankham et al., 2010). Furthermore, the random allele frequency changes caused by the strong genetic drift inherent in a bottleneck can lead to large allele‐frequency differences between populations (Kimura, 1955a, 1955b). Genetic drift can therefore create outlier‐like loci that can easily be mistaken as loci under selection and will increase the false positive rate of selection detection methods in bottlenecked populations (Foll & Gaggiotti, 2008; Hofer et al., 2009; Klopfstein et al., 2006; Lotterhos & Whitlock, 2014; Nielsen et al., 2007). Such false signals have previously hampered selection scans in bottlenecked species, including humans (Sabeti, 2006).
Examination of selection detection accuracy in bottlenecked populations is limited. Foll and Gaggiotti (2008) examined the effects of including a subset of populations that are bottlenecked in a selection detection analysis. It was recommended to remove bottlenecked populations due to the increase in false positives (Foll & Gaggiotti, 2008). The effects of historical bottlenecks (thousands of generations prior) were also examined using simulated populations of Peromyscus spp. (Poh et al., 2014) and Haemorhous mexicanus (Shultz et al., 2016), where the false positive rate often exceeded selection detection power. Nevertheless, selection detection analyses have since been applied to bottlenecked populations (e.g Amish et al., 2019; Funk et al., 2016; Pilot et al., 2014), and will probably continue to be applied, because of the conservation management need to identify intraspecific adaptive differences. It is therefore essential that we expand our understanding of bottleneck effects on selection detection accuracy.
The Alpine ibex (Capra ibex) is a recently bottlenecked and reintroduced species with a demographic history that is virtually unparalleled in recorded detail (Biebach & Keller, 2009). Historically spread throughout the European Alps, the species was overhunted and underwent a prolonged decline starting in the 16th century that resulted in its extirpation from virtually all of its range. Only a single population of an estimated 100 individuals survived this crash in the Gran Paradiso region of Northern Italy. Royal protection in the 19th century enabled the population to grow to 3,000–5,000 individuals. Reintroductions have facilitated its successful reestablishment from France to Eastern Austria (Toïgo et al., 2020).
Reintroductions of Alpine ibex from the Gran Paradiso region into Switzerland began in 1906. Detailed demographic records were kept as part of this reintroduction programme. Information that was recorded included the origin of founder individuals (often coming from previously reintroduced populations, Figure 1), the number and sex of founders, and the year an individual was moved. In addition, annual census records of the number of animals alive in spring were collected for the majority of reintroduced populations (Biebach & Keller, 2009; Stuwe & Grodinsky, 1987; Stuwe & Neivergelt, 1991). This reintroduction programme was very successful, to date more than 17,000 Alpine ibex are present in the Swiss Alps (BAFU, 2015; Brambilla et al., 2020; Shackleton & Group ISCI, 1997).
FIGURE 1.
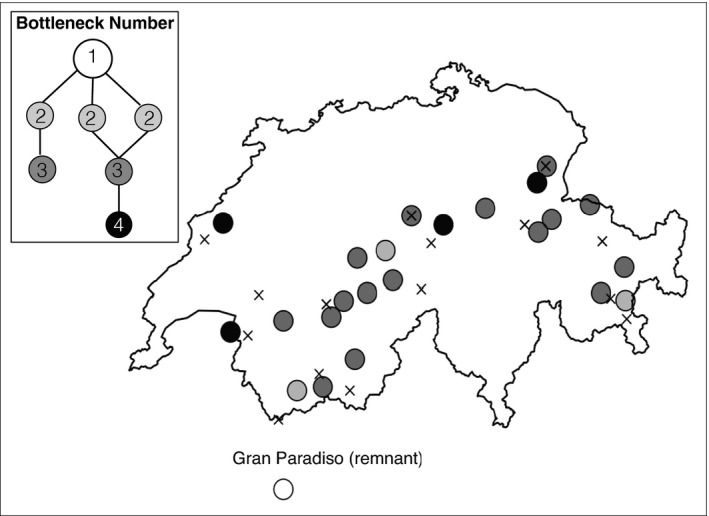
The 23 Alpine ibex focal populations and a simplified representation of the reintroduction history in Switzerland equating to the effective bottleneck number each population experienced (top left panel). All Swiss populations descend from the Gran Paradiso national park in Northern Italy (open circle), which is included in the figure but was excluded from the selection detection analysis. Reintroductions in Switzerland often used founder individuals from previously established reintroduced populations. As a result, many populations have experienced several serial bottlenecks. Within this figure, each circle represents a Swiss Alpine ibex focal population and the circle's shading indicates the number of bottlenecks each population experienced. Marked by a cross are the weather stations used to estimate the local environment experienced by each population. Details about founder populations can be found in Biebach and Keller (2009)
Across the reintroduced Swiss range there are considerable differences in local environmental conditions known to impact Alpine ibex recruitment. Mean winter snow depth in particular, has been shown to have an effect at both the Gran Paradiso source population and across Swiss reintroduced populations (Grøtan et al., 2007; Jacobsen & Provenzale, 2004). In Gran Paradiso, a mean winter snow depth of 126 cm was estimated (Jacobsen & Provenzale, 2004) but this can exceed 277 cm in the reintroduced range. Reintroductions into “deep snow” locations could have produced sudden shifts in the selective environment. Such sudden environmental shifts have previously been shown to fuel rapid adaptive change in other species and may have done so in the Alpine ibex (e.g Reznick et al., 2004; Stockwell et al., 2003).
In this study, we utilized the detailed Swiss Alpine ibex reintroduction records to create a comprehensive simulated SNP data set through individual‐based forward simulations. We then examined the performance of different selection detection methods by quantifying both the observed true and false positive rates and the composition of outlier loci. This information was coupled with selection scans on an empirical Alpine ibex restriction site associated DNA sequencing (RADseq) data set, and used to guide the confidence we could place in any outliers detected in these reintroduced populations. This provided insight into the accuracy, or rather lack‐there‐of, expected within species with complex histories of bottlenecks and reintroductions. The detection thresholds and methods outlined here can be used as a guideline to help avoid erroneous signals of selection in other species with similar histories. Furthermore, these results also highlight the high risk of failing to identify ongoing selection or existing local adaptation in bottlenecked species.
2. MATERIALS AND METHODS
2.1. RAD sequencing
The focal populations used in this study are shown in Figure 1. To apply selection detection methods to an empirical data set from a bottlenecked species, we used the published RADseq data set from Leigh et al. (2018) and Grossen et al., (2017). This consists of 304 Alpine ibex from 23 reintroduced populations (Figure 1). We used only variants called by GATK (Poplin et al., 2017; see Leigh et al., 2018 for a discussion of variant caller effects). After SNP filtering (described in section S1) a sample of 213 individuals remained (sample size in Table 1). For selection detection all singletons were removed and SNPs within 1 kb were randomly thinned using vcftools (vcftools; Danecek et al., 2011), which resulted in a final data set of 12,695 SNPs. After exclusion of individuals from the Gran Paradiso, 5225 SNPs remained. The Gran Paradiso was removed as it represents the ancestral population and violates the assumption that pairs of populations share an ancestor in the past with non‐zero independent drift arising in each since founding (Coop et al., 2010; Günther & Coop, 2013; Nicholson et al., 2002).
TABLE 1.
The populations included in the simulations and sequenced with RADseq (note: neither wilderness park was sequenced as these are captive populations). The number of samples included in the selection detection analyses and estimated means of key environmental parameters from the weather stations in Figure 1 are shown. Also shown is the simulated environmental optimum. Positive and negative values of the simulated optimums were based on the relative difference in snow depth between each population and the Gran Paradiso population. An optimum of zero was used for the burn‐in
| Population | Sample size used in selection scan | Real winter snow depth (cm) | Real summer precipitation (mm) | Simulated optimum |
|---|---|---|---|---|
| Gran Paradiso | NA | 115 | 2.8 | 0 |
| Wilderness Park Peter and Paul | NA | NA | NA | –2 |
| Wilderness Park Interlaken Harder | NA | NA | NA | –2 |
| Graue Hoerner | 7 | 28 | 5.0 | –2 |
| Albris | 11 | 120 | 5.3 | 0 |
| Brienzer‐Rothorn | 10 | NA | 4.8 | 0 |
| Schwarmoench | 9 | 27 | 4.2 | –2 |
| Wetterhorn | 10 | 185 | 4.7 | 0 |
| Mont Pleureur | 10 | NA | 5.2 | –2 |
| Justistal | 9 | NA | 4.8 | 0 |
| Gross Lohner | 10 | 28 | 4.2 | –2 |
| Alpstein | 10 | 266 | 7.2 | 2 |
| Val Bever | 6 | 30 | 2.6 | –2 |
| Crap da Flem | 10 | 27 | 5.0 | –2 |
| Flueela | 9 | 145 | 4.2 | 0 |
| Wittenberg | 10 | NA | 3.3 | 0 |
| Arolla | 10 | 20 | 2.4 | –2 |
| Bire‐Oeschinen | 10 | 27 | 4.2 | –2 |
| Creux du Van | 9 | NA | 3.8 | 0 |
| Pilatus | 9 | NA | 4.8 | 0 |
| Fluebrig | 10 | 27 | 5.0 | –2 |
| Weisshorn | 7 | 34 | 2.1 | –2 |
| Oberbauenstock | 10 | 18 | 5.0 | –2 |
| Falknis | 9 | 145 | 4.4 | 0 |
| Tanay | 8 | 1 | 3.2 | –2 |
| Churfirsten | 10 | 277 | 7.5 | 2 |
2.2. Simulating the Alpine ibex history
Simulated SNP data sets were generated using forward time simulations in Nemo (version 2.3.51; Guillaume & Rougemont, 2006) and used to assess the expected accuracy of each selection detection methods when applied to bottlenecked and reintroduced species. Details of the simulations can be found in Supporting Information S2.
Briefly, in each simulation the Gran Paradiso source population and all 23 Swiss populations sampled for RADseq were simulated (Figure 1). In order to accurately simulate the Swiss populations, an additional two populations (zoos known as “Wilderness Park Peter and Paul” and “Wilderness Park Interlaken Harder” Biebach & Keller, 2009) that were founder sources for the focal populations were also simulated. Therefore, 26 populations were simulated in total. The reintroduction history and population sizes were informed by detailed records, census data and the Alpine ibex species biology. No migration beyond recorded translocations was allowed because unassisted natural migration has been not yet been detected between populations (Aeschbacher et al., 2013).
Ten replicate simulations of the Alpine ibex reintroduction history were conducted for each of three genetic architectures: (a) neutral SNPs only, (b) 30 loci under selection, and (c) 120 loci under selection. In all architectures, each individual had 30 chromosomes (linkage groups) of 10 M (Morgan) each with 60,000 neutral loci. SNPs were evenly distributed and recombined at a rate of 5 × 10−5. This created a genome similar in size and structure to that of the goat (Bickhart et al., 2017; Guillaume & Rougemont, 2006). This also ensured several thousand SNPs were polymorphic after the bottleneck and generated the same chromosome number and a similar level of linkage disequilibrium to that in the RADseq data set as evaluated by the r 2 values between final polymorphic SNPs in vcftools.
In the architectures with selection, the loci under selection were diallelic QTL contributing additively to a quantitative trait. The 30 or 120 QTL loci were equally spread among the neutral loci and a loci under selection was found on each chromosome. Four QTL positions were used for each chromosome, they were positioned 3.33 M apart and 0.5 cM from the start on each chromosome. For the architecture with 30 QTL loci under selection one position was used per chromosomes and all four were used for the architecture with 120 QTL loci. Polygenic architectures were chosen because they are more often the subjects of selection in natural scenarios and thus increased the biological realism of our simulations (Pritchard et al., 2010; Burke et al., 2010; Timpson et al., 2018; Barghi et al., 2020). Furthermore, a monogenic trait with a single locus of large effect would probably have been fixed early on in our reintroduction programme and thus would have been undetectable by our selection detection methods.
We simulated phenotypic selection on the quantitative trait with a Gaussian fitness surface where the trait optimum value varies among populations depending on an environmental variable (snow cover). The trait optimum value during the burn‐in was held at zero (in the “Gran Paradiso” reference population) to maintain alleles of both negative and positive effect. To generate post‐reintroduction selection across the 30 or 120 QTL, the trait optimum in reintroduced populations was varied to either zero, –2 or +2. Values reflected observed real world snow conditions relative to the Gran Paradiso, for example those with a higher average snow depth than the Gran Paradiso had a value of +2 and those with a lower average snow depth had a value of –2. An environmental optimum value of ±2 was chosen in conjunction with QTL allelic values and phenotypic variances to generate a biologically realistic strengths of selection at QTL loci (detailed below). Snow conditions were chosen as they are a strong candidate real‐world selection pressure, specifically they have previously been shown to affect Alpine ibex population dynamics and vary dramatically across sites (detailed in Supporting Information S2, S3 and Table 1) (Jacobsen et al., 2004; Grøtan et al., 2008). The effects of snow are not linear and appear to be most severe in deep snow winters (>180–200 cm average winter snow depth Jacobsen et al., 2004), snow conditions were thus simplified to relative differences from the Gran Paradiso to make simulations manageable and maintain a more stable strength of selection at QTL loci (Table 1).
The strength of selection at each locus was determined by the size of its contribution to the trait. For the architecture where 30 diploid loci were under selection: six loci had large contributions to each trait (allelic value, a = ±0.1), and 24 were divided equally into four categories of lesser effect (a = ±0.08, ±0.04, ±0.02, ±0.01). A maximum trait value of ±3 was therefore achievable. For the architecture where 120 loci were under selection, the division of loci remained identical except for the loci of smallest effect. Specifically, 96 loci were of minor effect (± 0.01) and 24 were equally divided amongst the remaining allelic values (±0.1, ±0.08, ±0.04, ±0.02, six of each value in total). A maximum trait value of ±4.8 was achievable. Selection coefficients (s) equalled 0.027 (a = ±0.1), 0.022 (a = ±0.08), 0.012 (a = ±0.04), 0.007 (a = ±0.02) and 0.004 (a = ±0.01) in both architectures. Selection coefficients are for each individual locus in an allelic values category. Coefficients were calculated according to Bürger (2000) using the phenotypic variance (Vp) of 0.047 (120 loci under selection) or 0.035 (30 loci under selection), as well as a selection variance (ω2) of 7.5. This generated two biologically realistic trait architectures and realistic strengths of selection.
In each simulation, neutral loci and loci under selection were allowed to reach mutation‐selection‐drift equilibrium during a burnin of 10,000 generations in a single population that represented the Gran Paradiso. After this time, a bottleneck and the reintroduction history were applied. The simulated genotypes from the final generation were used to evaluate the expected accuracy of different selection detection methods, and only polymorphic SNPs were included in the simulated data from this time point. To mimic the available RADseq data, 10 simulated individuals were randomly chosen from each of the 23 populations that were sequenced with RADseq, 6000 polymorphic loci were then taken for each individual including all polymorphic selected loci and a subset of randomly selected neutral loci. 20% of genotypes were randomly set to “missing” due to missing data in the RADseq genotypes and singletons were removed (vcftools; Danecek et al., 2011). PGDspider (version: 2.0.9.2; Lischer & Excoffier, 2012) and custom scripts were used to convert Nemo output into input for the selection analyses.
2.3. Screens for signals of positive selection
Selection detection analyses were conducted for both the empirical Alpine ibex RADseq data and simulated data sets. This enables us to quantify the confidence we could place in any empirical outliers. To detect signatures of selection, Bayenv 2.0 (Günther & Coop, 2013), Baypass 2.1 (Gautier, 2015a), and OutFLANK (Whitlock & Lotterhos, 2015a) were used (following Leigh et al., 2018). These three programmes were chosen as they have been shown to have high accuracy in species with complex patterns of population relatedness (Gautier, 2015a; Günther & Coop, 2013; Lotterhos & Whitlock, 2014; Whitlock & Lotterhos, 2015a). Bayenv 2.0 and Baypass2.1 utilize a modified F ST ‐like statistic called XTX that is corrected for shared population history (Gautier, 2015a; Günther & Coop, 2013). Outflank utilizes an F ST statistic called F’ ST, a metric based on Wright's F ST statistic without corrections for a finite sample size (Whitlock & Lotterhos, 2015a). These three methods are hereafter referred to as F ST ‐like approaches. Bayenv 2.0 and Baypass2.1 also detect selection using GEA selection scans (as in Hoban et al., 2016).
Selection detection programme conditions are detailed in Leigh et al., (2018). Briefly, the estimation of covariance matrix and subsequent selection scan in Bayenv 2.0 were run independently three times with 2 × 105 Markov‐Chain‐Monte‐Carlo (MCMC) iterations (Blair et al., 2014). SNPs were considered putatively under selection for the GEA method, if the Bayes factor (BF) value exceeded 3 and the Spearman's Rho value was in the top and bottom 2.5% of all SNPs across the three runs. This threshold was chosen because it suggests high support for a SNP being under selection and that the trend is not due to a single outlier population (Günther & Coop, 2013; Nadeau et al., 2016). The F ST ‐like approach SNPs had to have XTX value among the top 100 ranking SNPs across all three runs (Günther & Coop, 2013).
Baypass2.1 was run three times for each data set with 20 pilot runs of 1000 MCMC iterations and 5000 MCMC iterations for the burnin (default conditions). For the GEA analysis we used the Auxillary model and consider a locus to be under selection when it had a 10 x log10 Bayes factor (db) greater than 4.7 for all three replicates (Gautier, 2015a). This value is equivalent to the threshold of a BF of 3 used in Bayenv 2.0. For the F ST ‐like approach, XTX outliers were determined following the best‐practice tutorial accompanying Baypass2.1 (Gautier, 2015b). This uses trained‐simulations to find the 99% threshold for XTX values for each data set, outliers were those loci in the top 1% for all three Baypass runs (Gautier, 2015b).
In OutFLANK, outlier SNPs were identified following the best practice tutorial (default settings, Whitlock & Lotterhos, 2015b). To be considered an outlier, a SNP had to have a Q‐value of <0.05 (Storey & Tibshirani, 2003; Whitlock & Lotterhos, 2015a), as well as a heterozygosity >10% (Whitlock & Lotterhos, 2015b).
Loci identified across multiple programmes as outliers were also compared. Loci identified as outliers across two programs were called “double positives” those found by all three programmes were called “triple positives.” To account for the different signals the F ST ‐like and GEA approaches look for, the outliers identified by the two methods in Bayenv 2.0 and Baypass2.1 were not combined into a single set. Thus, we had double and triple positive F ST ‐like outliers, and double positive GEA outliers. For the triple positive GEA outliers, the GEA outliers from Bayenv 2.0 and Baypass2.1 were overlapped with the F ST ‐like outliers from OutFLANK because OutFLANK does not use a GEA approach.
All environmental data used in the GEA analyses were obtained from MeteoSwiss (Switzerland). For each population, data from the closest meteorological station available (Figure 1, Section S2 and S3, Table S1) were used to obtain averages since a population was founded, or since records began. The environmental variables in the analyses were divided across winter and summer and included air temperature (°C), daily precipitation (mm), and snow depth measures (cm). Further details are available in the Supporting Information (Section S2 and S3). Since the simulations were intended to mimic real Alpine ibex populations, the corresponding weather data were included as environmental covariates in the Bayenv 2.0 and Baypass2.1 analyses of the simulated data. In addition, each simulated population's simulated environmental optimum was also included as an environmental covariate in the analysis of the simulated data (Table 1).
2.4. Evaluating method accuracy with simulations
The simulated genotype data were used to estimate the true or false negative and positive rates of each selection detection method. When examining loci flagged as putatively under selection, a true positive was considered to be a simulated locus under selection that was correctly identified. A false positive was considered to be a simulated neutral locus that was wrongly identified as being under selection. The proportion of all loci identified by a method as under selection that were true positives, hence indeed under selection (the true discovery rate), was used as a metric of the method's accuracy and reliability of selection detection. To place the results in the context of other simulation studies, the true positive rate, false positive rate, the false discovery rate, and false negative rate, were also calculated. All metrics are defined in Table 2 for ease of reference. All values displayed are the averages across 10 simulated data sets for each genetic architecture and are relative only to the number of polymorphic QTL loci and neutral loci in the final SNP set.
TABLE 2.
Definitions of each metric used to assess a selection detection method's accuracy with the simulated data
| Accuracy metric | Definition | Equationa | |
|---|---|---|---|
| True discovery rate | The proportion of all simulated loci identified as outliers that were actually under selection (i.e., QTL loci) |
|
|
| True positive rate | The proportion of loci under selection (i.e., QTL loci) correctly identified as an outlier |
|
|
| False positive rate | The number of neutral loci incorrectly identified as under selection (false positive outliers) divided by the number of retained polymorphic neutral SNPs |
|
|
| False discovery rate | The proportion of outlier SNPs that were false positives (i.e., simulated neutral loci) (Lotterhos & Whitlock, 2014) |
|
|
| False negative rate | The proportion of polymorphic QTLs that were not identified as outliers (and thus not identified as under selection) |
|
Osel, outer loci truly under selection; Onet, false positive neutral outlier loci; Totalsel, total number of polymorphic loci under selection; Totalnet, total number of polymorphic neutral loci.
3. RESULTS
In this study, we generated empirical RADseq (5225 SNPs) and simulated SNP data (retaining 6000 SNPs) for the Alpine ibex. Bayenv 2.0, Baypass2.1, and OutFLANK were then used to identify loci putatively under selection in these data sets. The simulated data provided an estimate of the selection detection accuracy of these three popular tools in the empirical Alpine ibex data set. Low true discovery rates were identified for all selection detection methods (detailed below), preventing us from confidently distinguishing selection from false positive outliers in the Alpine ibex RADseq data.
3.1. Alpine ibex RADseq data and signals of selection
Each selection detection method identified outliers in the Alpine ibex RADseq data set. Between two and 172 loci were found to be putatively under selection by the different selection detection methods (Figure 2a). However, only 14 loci in total were identified as double positives and no locus was identified as a triple positive. The highest number loci (n = 12) were double positive Bayenv Baypass GEA outliers. The double positive Bayenv and Baypass F ST ‐like approach and double positive Bayenv and Outflank F ST‐like approach each only identified one locus. As detailed below, this is within the range of drift‐driven false positives expected under all simulated genetic architectures.
FIGURE 2.
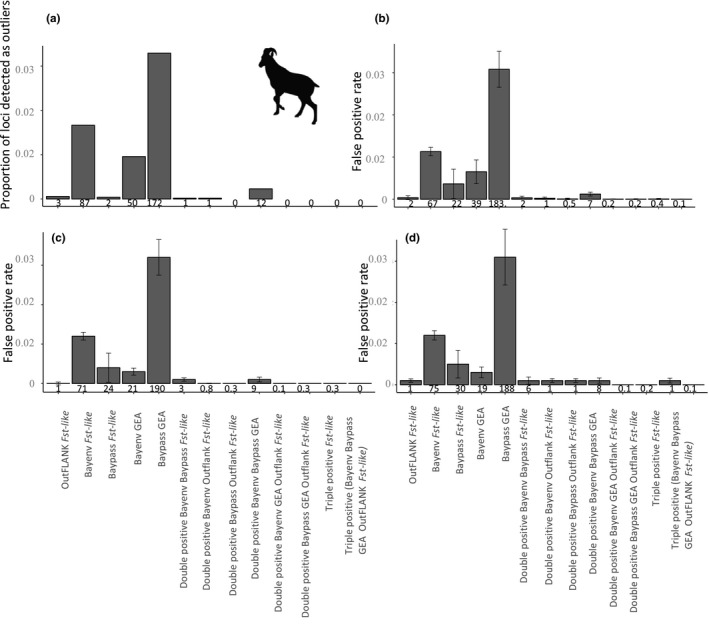
(a) The proportion of SNPs detected by each selection detection method as outliers in the Alpine ibex RADseq SNP set. The absolute number is below each bar. (b) The false positive rate from the fully neutral simulations, (c) 30 QTL loci and (d) 120 QTL loci. Below each bar for b–d is the average number of outlier loci identified
3.2. Evaluating expected selection detection accuracy
Analyses of simulated data revealed a very low selection detection accuracy under the Alpine ibex demography, regardless of the genetic architecture simulated. Figure 2b shows the false positive rates for the neutral only simulations, Figure 2c,d show the false positive rate for the two architectures with selection and Figure 3 the true and false discovery rates (i.e., the composition of loci identified as outliers) for the simulations with loci under selection. The false negative rates are shown in Figure 4.
FIGURE 3.

The true and false discovery rate of different selection detection methods for (a) the architecture with 30 loci under selection (six loci per selection coefficient “s”) and (b) the architecture with 120 loci under selection (96 loci at 0.004, six loci for each remaining value). Each bar shows the average composition of loci identified as outliers using each selection detection method, at the bottom of the bar is the average number of outliers across 10 replicate simulations. Replicates where no loci exceeded the significance threshold were excluded from the figure
FIGURE 4.
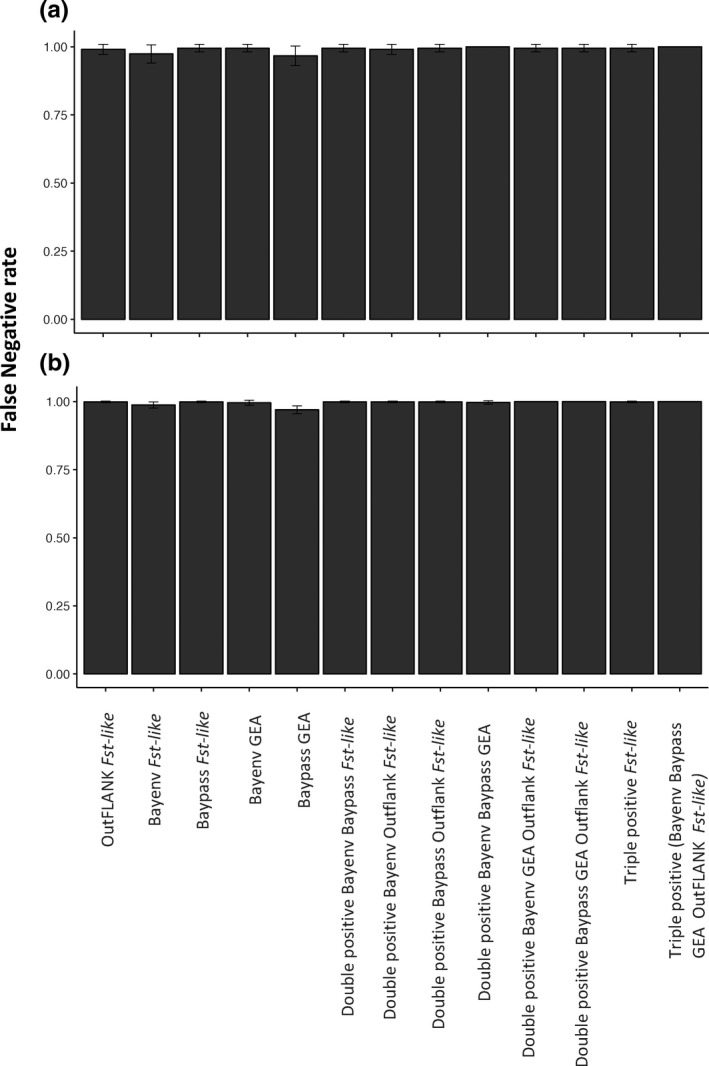
The mean false negative rate for (a) 30 QTL loci under selection and (b) 120 QTL loci under selection. The true positive rate is the inverse of the false negative rate
For all simulation types, each individual selection detection method had a high number of false positives and a considerable false negative rate (Figure 3). The false positives rate did decrease substantially (<0.001) for the double and triple positive methods, but this was at the expense of the false negative rate increasing (Figure 4). Greater variability in accuracy is seen for the architecture with 30 loci under selection than 120 loci under selection. Specifically, the true discovery rate does occasionally reach 1.0 (see Figure 3). However, as shown by the false negative rate (Figure 4), this does not reflect high accuracy of these methods but stochastic chance. Virtually all simulations had no outliers exceed this threshold, but a single simulation had 1 true positive locus, leading to a mean true discovery rate of 1.
In the simulations with selection, the allelic values and hence the strength of selection experienced by each QTL locus, were not equal. The loci with allelic values of 0.1 or 0.08 were under much stronger selection (s = 0.027, 0.022) relative to those with allelic values of 0.04, 0.02 or 0.01 (s = 0.012, 0.007, 0.004). Consequently, the signal of selection and therefore the true positive rate may be unequal across loci under selection. Table 3 shows the average allele frequency change of loci under selection, this can be considered a rough proxy for the signal of selection visible at a locus. As expected due to the strength of selection, loci under the strongest selection were often at extreme allele frequencies after the burn‐in and before the bottleneck (Figures S1 and S2). Consequently, such loci were fixed more frequently over the course of our simulations and thus more likely to be excluded from selection detection analysis. Nevertheless, loci under a selection pressure of >0.022 were the most likely to be identified as outliers in the architecture with 30 loci under selection. Those under weaker selection (0.004) were most likely to be identified as outliers in the architecture with 120 loci under selection, but this was because they were by far the most common in this architecture and their abundance drives this trend.
TABLE 3.
Mean absolute allele frequency change for loci under selection ± the standard error. Shown in brackets is the percentage of loci that remain polymorphic in at least one population at the end of the simulations. Values are calculated from immediately after the burnin using the values from the simulated Gran Paradiso population, relative to the frequency across all simulated populations in final generation. Loci fixed after the burnin were excluded from the values
| Locus type | Average allele frequency change (percentage polymorphic) | |
|---|---|---|
| 30 loci under selection | 120 loci under selection | |
| 0.01 | 0.086 ± 0.071 (93%) | 0.087 ± 0.079 (86%) |
| 0.02 | 0.095 ± 0.082 (94%) | 0.093 ± 0.078 (93%) |
| 0.04 | 0.067 ± 0.067 (77%) | 0.088 ± 0.078 (83%) |
| 0.08 | 0.043 ± 0.058 (48%) | 0.045 ± 0.060 (49%) |
| 0.1 | 0.031 ± 0.034 (44%) | 0.016 ± 0.022 (23%) |
4. DISCUSSION
In this study the accuracy of selection detection methods was assessed for the Alpine ibex, a species with a complex history of bottlenecks and reintroductions. We generated comprehensive simulations that followed the species’ recorded population history. Three genetic architectures were simulated: neutral loci only, 30 loci under selection, and 120 loci under selection. The simulated data revealed a low selection detection accuracy for each individual selection detection method. Improved accuracy was possible when only considering outliers identified by multiple methods, though this came at the expense of an increased false negative rate. This made it impossible to adjust our thresholds as we were either faced with a high proportion of false positives, or rarely identified ongoing selection. While candidate outlier loci could be identified in the Alpine ibex RADseq data set, the simulation results indicate they cannot be confidently considered as under selection. Importantly, the low true positive rate also prevents us from confidently concluding the absence of recent adaptation in the populations, posing significant challenges for the evolutionary management of this species. Nevertheless, identifying false positive outliers and concluding two populations are separate evolutionary significant units has a number of costly consequences for conservation management. Until more accurate selection detection methods are found, the stringent approach and criteria outlined here should be applied to other bottlenecked species to offer an indication of the confidence that we can place in outlier loci.
4.1. Screen for selection with Alpine ibex RADseq data
In the Alpine ibex RADseq data set 14 loci were identified as under selection using the double positive approach but no loci were triple positives. Based on our simulations, a proportion of <0.04 of loci identified by the double positive approach are likely to be true positives. This extremely low proportion indicates that these putatively selected loci in the Alpine ibex cannot confidently be distinguished from false positives. They should be viewed with extreme caution because many may be the consequence of the historical bottleneck and genetic drift‐driven false signals of selection. Consequently, these loci were not explored further, according to the recommendations from previous studies with low selection detection power (e.g., Shultz et al., 2016). Interestingly, the significant environmental correlations found in the GEA outliers were related to environmental variables known to have recruitment effects and to vary dramatically across the reintroduced range. Despite biologically realistic explanations, the expected high rates of false positives prevent us from making any confident conclusions about local adaptation in the Alpine ibex in this study. Furthermore, the size and nature of this species make the functional validation that was used in Peromyscus spp. impossible (Poh et al., 2014). Although it is likely some adaptation may be occurring in Alpine ibex, these candidate outliers and those found in other bottlenecked species, must be confirmed when more accurate selection methods for bottleneck population are identified in the future.
4.2. Simulated data and selection detection accuracy
Alpine ibex have experienced several profound and serial population bottlenecks. Given this extreme history, genome‐wide drift effects are highly likely and a high false positive rate was expected for selection detection methods applied to this data (Kimura, 1955a, 1955b; Lotterhos & Whitlock, 2014). The simulations of the Alpine ibex demography confirmed this, revealing an expected false positive rate of up to 0.03 and a false discovery rate often exceeding 0.99 of all outliers. These values mean that up to 3% of all neutral loci in a data set are identified incorrectly as outliers and that over 99% of loci identified as outliers can be false positive neutral loci. This accuracy was considerably less than that found for nonbottlenecked populations and for scans where a single population is bottlenecked (e.g., 0.1 false positive rate, Foll & Gaggiotti, 2008). However, the low accuracy is similar to studies where more ancient bottlenecks were simulated (e.g., 0.03–0.41 false positive rate, Poh et al., 2014; 0.05–0.30, Shultz et al., 2016). Importantly, increasing stringency to a double or triple positive approach did improve the false positive rate in the Alpine ibex data. This suggests that the double or triple overlap approaches may offer some improved power in bottlenecked populations, and their accuracy should be assessed for more simple bottleneck scenarios. However, this approach increases the already high risk of being too stringent and removing all loci under selection (high false negative rate), which must also be taken in to account when applying this method.
A low true positive rate was identified for all simulated loci under selection. To generate a biologically realistic trait, the majority of loci simulated were of small or moderate effect and it has been previously demonstrated that many selection detection methods struggle to identify such loci, regardless of demographic history (e.g., Biswas & Akey, 2006; Kalsson & Moen, 2010; Kemper et al., 2014; Lotterhos & Whitlock, 2015; Narum & Hess, 2011). This is particularly pronounced for loci contributing to polygenic traits such as ours (Berg & Coop, 2014; Kemper et al., 2014). However, in this study, loci under comparable selection coefficients were identified much less frequently than expected based on previous studies. Specifically, in our study, loci with a selection coefficient below 0.012 were rarely identified by the double or triple positive method. However, Lotterhos and Whitlock (2015) found a true positive rate of at least 0.11 for loci under a weaker selection coefficient of 0.005, with two or more selection detection methods. Our true positive rate for loci of the largest effect was also lower than seen previously, for example for the Bayenv GEA we found a 0.04 true positive rate, while previous studies have found 0.58–1 across multiple demographic scenarios (Coop et al., 2010; De Mita et al., 2013; Lotterhos & Whitlock, 2015).
The lower accuracy found here is probably driven by a combination of factors, including the intrinsic characteristics of bottlenecked populations. Specifically, the swamping of true positives with drift‐driven false positives (which will increase the false discovery and false positive rate), as well as the lower effective population size of a bottlenecked species. A lower effective population size will reduce the efficacy of selection (Frankham et al., 2010). This in turn limits detectable signals of selection. Though 17 000 Alpine ibex are now present in the Alps, population connectivity is low and contemporary population sizes are often in the hundreds. Effective population sizes range from ~900 to as low as 20 (Biebach & Keller, 2009). While the strength of selection at loci with an allelic value of 0.1 or 0.8 (s > 0.02) was sufficient to theoretically elicit a response even in the smallest simulated populations (s > 1/2Ne, Frankham et al., 2010), loci of the smallest effect will not overpower drift unless the effective population size exceeds 125 individuals and the census size of three of our simulated populations fell below this threshold. The reduced efficacy of selection in our smallest populations must disrupt signals of selection at loci under weak selection, and contribute to the low true positive rate observed for these loci.
Furthermore, loci under stronger selection were more often at extreme allele frequencies after the burnin (i.e., preceding any bottleneck) and their rare alleles were easily lost during the bottlenecks or during the shifts in selection pressures. Many of these loci had to be subsequently excluded from selection scans due to their fixation across all populations, exacerbating our difficulty in identifying selection. This also constrained the QTL architecture that we could simulate, for example a single locus of large effect would have fixed early on in the simulations and have been impossible to detect. These issues are probably common to selection scans on bottlenecked species where selection is long acting (i.e., continuous before and during a bottleneck). Accordingly, the true positive rate is similar to that found in other bottlenecked species (e.g., Poh et al., 2014). This is highly problematic for adaptive population management, because long standing adaptive differences are often exactly what we are trying to conserve. This result does suggest that greater success may be had when looking for signals of post‐bottleneck adaptation, for example when scanning for rapid post‐reintroduction adaptation to a novel environmental variable or adaptation to a new disease. To circumvent the reduced accuracy due to fixation of selected alleles, future studies should explore if any increase in power is obtained through using prebottleneck samples for SNP ascertainment.
4.3. Future selection detection evaluations
Future studies screening for adaptation in bottlenecked species should focus on selection detection methods less reliant on F ST (e.g., LFMM Frichot et al., 2013; time series approach, Brüniche‐Olsen et al., 2016; RDA Forester et al., 2018), and explore if sufficient power can be gained by more densely sampling the genome with whole genome resequencing and the selection methods this allows (Lowry et al., 2017). For studies interested in examining multiple naturally bottlenecked populations (i.e., not reintroduced species) exploiting museum and collection specimens could also be used to circumvent major genetic drift driven false positives by offering pre‐bottleneck allele frequencies. This will also characterize the historical polymorphic SNPs and help avoid the high false negative rate we observed from the fixation of sites under selection.
Evaluation of these suggestions is beyond the scope of this study, but we would recommend their accuracy in bottlenecked populations is explored. We would note that researchers should also explore the effects of genotype imputation if using LMFF and RDA analyses on RADseq or low coverage resequencing data (Forester et al., 2018; Frichot et al., 2013). An exploration of the effect of measurement error in environmental variables would also be of great value to the selection detection community at large.
While many species do not have the detailed history of the Alpine ibex, it is important that we fully exploit other species that do, to provide a range of potential selection detection accuracies. For species with more limited data, evaluating softwares with simplified bottleneck scenarios or a rough estimation of population history will always be informative. At minimum, this offers a guide for the range in accuracy expected and the uncertainty to incorporate into management plans. A difficulty arises if there is no information about recent population history, in such scenarios a first step should be to infer this (e.g., structure: Pritchard et al., 2000; and fastsimcoal2: Excoffier et al., 2013) and then simulate across the range of likely histories. Though time‐consuming this basic information will also be necessary to correctly use or interpret many selection detection methods. At the very least, an array of simplified histories could be used to give a rough range of potential accuracies for different selection detection methods (e.g., Adrion et al., 2020), but this should be avoided by species‐specific studies seeking to apply their results directly to management plans.
4.4. Conclusions
Overall, for populations like the Alpine ibex with a history of extreme population bottlenecks (and notably, serial founding events as well as complex reintroductions) the selection detection methods explored here have a considerably reduced accuracy relative to other demographic histories. Based on these results, loci identified as under selection in similar bottlenecked populations using GEA or F ST outlier methods should be viewed with caution, particularly those based on single selection detection methods. Unfortunately for bottlenecked species, the high false positive rate is also coupled with a high false negative rate. Therefore, if selective responses are not identified in bottlenecked populations, this cannot be considered evidence for an absence of responses to selection pressures or an absence of local adaptation. This unfortunate lack of power is highly problematic for effective adaptive population management and it is vital this uncertainty is now incorporated into management plans. Alongside this, the costs of concluding two populations as separate ESUs based on erroneous outliers must be evaluated. The criteria and approach outlined here, may offer other studies on bottlenecked species an approach and baseline on which to gauge their confidence in any outliers identified and adjust management plans accordingly. In the future, the accuracy of selection detection methods less reliant on F ST, such as those exploiting temporal samples, as well as use of more dense marker data, should be evaluated across bottlenecked scenarios. Despite the high false positive rate expected, it is important to see if these approaches offer greater power and if they can better facilitate conservation management.
AUTHOR CONTRIBUTIONS
D.M.L. performed the selection detection analysis, simulations and wrote the manuscript. T.G. supported the selection detection analysis and commented on the manuscript. C.G. supported the sequence data generation, commented on the manuscript and simulations. F.G. supported writing the simulation scripts and designing the genetic architecture of the QTL traits.
Supporting information
Supplementary Material
ACKNOWLEDGEMENTS
This project was funded by a University of Zurich’s Research Priority Program “Evolution in Action” grant to Lukas F Keller and Andreas Wagner. We would like thank them both for their support throughout this project. We would also like to thank the European Science Foundation for funding a Short Visit Grant to DML and TG to establish the collaboration. We would like to thank the ETH’s Genetic Diversity Center and BSSE for their help generating the RADseq data. We would also like to thank Glauco Camenisch, Kasia Sluzek and Iris Biebach for their help during the project.
Leigh, D. M. , Lischer, H. E. L. , Guillaume, F. , Grossen, C. , & Günther, T. (2021). Disentangling adaptation from drift in bottlenecked and reintroduced populations of Alpine ibex. Molecular Ecology Resources, 21, 2350–2363. 10.1111/1755-0998.13442
The bulk of this work was carried out while DML and HELL were at are the Department of Evolutionary Biology and Environmental Studies, University of Zurich, CH‐8057, Zurich, Switzerland.
DATA AVAILABILITY STATEMENT
Read data can be viewed on the short‐read archive, ncbi project number PRJNA422727: https://www.ncbi.nlm.nih.gov/bioproject/PRJNA422727. The Nemo ini files necessary to recreate the simulations have been made available at https://doi.org/10.5061/dryad.ns1rn8pt2. Custom conversation scripts for Nemo output files and to merge the output of Bayenv runs are accessible here https://bitbucket.org/HeidiLischer/ibex/src/. Sample mean coordinates have been included in Supporting Information.
REFERENCES
- Adrion, J. R. , Cole, C. B. , Dukler, N. , Galloway, J. G. , Gladstein, A. L. , Gower, G. , Kyriazis, C. C. , Ragsdale, A. P. , Tsambos, G. , Baumdicker, F. , Carlson, J. , Cartwright, R. A. , Durvasula, A. , Gronau, I. , Kim, B. Y. , McKenzie, P. , Messer, P. W. , Noskova, E. , Ortega‐Del Vecchyo, D. , … Kern, A. D. (2020). A community‐maintained standard library of population genetic models. Elife, 9, e54967. 10.7554/eLife.54967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aeschbacher, S. , Futschik, A. , & Beaumont, M. A. (2013). Approximate Bayesian computation for modular inference problems with many parameters: the example of migration rates. Molecular Ecology, 22(4), 987–1002. 10.1111/mec.12165 [DOI] [PubMed] [Google Scholar]
- Amish, S. J. , Ali, O. , Peacock, M. , Miller, M. , Robinson, M. , Smith, S. , & Neville, H. (2019). Assessing thermal adaptation using family‐based association and F ST outlier tests in a threatened trout species. Molecular Ecology, 28(10), 2573–2593. 10.1111/mec.15100 [DOI] [PubMed] [Google Scholar]
- BAFU (2015). Abschuss Steinbock, ganze Schweiz: 2000–2015. Retrieved from: www.wild.uzh.ch/jagdst/index.php [Google Scholar]
- Barghi, N. , Hermisson, J. , & Schlötterer, C. (2020). Polygenic adaptation: a unifying framework to understand positive selection. Nature Reviews Genetics, 21, 769–781. 10.1038/s41576-020-0250-z [DOI] [PubMed] [Google Scholar]
- Berg, J. J. , & Coop, G. (2014). A Population Genetic Signal of Polygenic Adaptation. PLoS Genetics, 10(8), 1–25. 10.1371/journal.pgen.1004412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickhart, D. M. , Rosen, B. D. , Koren, S. , Sayre, B. L. , Hastie, A. R. , Chan, S. , Lee, J. , Lam, E. T. , Liachko, I. , Sullivan, S. T. , Burton, J. N. , Huson, H. J. , Nystrom, J. C. , Kelley, C. M. , Hutchison, J. L. , Zhou, Y. , Sun, J. , Crisà, A. , Ponce de León, F. A. , … Smith, T. P. L. (2017). Single‐molecule sequencing and chromatin conformation capture enable de novo reference assembly of the domestic goat genome. Nature Genetics., 49, 643–650. 10.1038/ng.3802 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biebach, I. , & Keller, L. F. (2009). A strong genetic footprint of the re‐introduction history of Alpine ibex (Capra ibex ibex). Molecular Ecology., 18, 5046–5058. 10.1111/j.1365-294X.2009.04420.x [DOI] [PubMed] [Google Scholar]
- Biswas, S. , & Akey, J. M. (2006). Genomic insights into positive selection. Trends in Genetics, 22(8), 437–446. 10.1016/j.tig.2006.06.005 [DOI] [PubMed] [Google Scholar]
- Blair, L. M. , Granka, J. M. , & Feldman, M. W. (2014). On the stability of the Bayenv method in assessing human SNP‐environment associations. Hum Genomics, 8(1). 10.1186/1479-7364-8-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brambilla, A. , Hardenberg, A. V. , Nelli, L. , & Bassano, B. (2020). Distribution, status, and recent population dynamics of Alpine ibex Capra ibex in Europe. Mammal Review, 50(3), 267–277. 10.1111/mam.12194 [DOI] [Google Scholar]
- Brüniche‐Olsen, A. , Austin, J. J. , Jones, M. E. , Holland, B. R. , & Burridge, C. P. (2016). Detecting selection on temporal and spatial scales: A genomic time‐series assessment of selective responses to devil facial tumor disease. PLoS One, 11(3), 1–15. 10.1371/journal.pone.0147875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke, M. , Dunham, J. , Shahrestani, P. , Thornton, K. R. , Rose, M. R. , & Long, A. D. (2010). Genome‐wide analysis of a long‐term evolution experiment with Drosophila . Nature, 467, 587–590. 10.1038/nature09352 [DOI] [PubMed] [Google Scholar]
- Bürger, R. (2000). The mathematical theory of selection, recombination and mutation. John Wiley, Chichester, U.K. [Google Scholar]
- Coop, G. , Witonsky, D. , Rienzo, A. D. , & Pritchard, J. K. (2010). Using environmental correlations to identify loci underlying local adaptation. Genetics, 185(4), 1411–1423. 10.1534/genetics.110.114819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek, P. , Auton, A. , Abecasis, G. , Albers, C. A. , Banks, E. , DePristo, M. A. , Handsaker, R. E. , Lunter, G. , Marth, G. T. , Sherry, S. T. , McVean, G. , & Durbin, R. (2011). The variant call format and VCFtools. Bioinformatics, 27, 2156–2158. 10.1093/bioinformatics/btr330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Mita, S. , Thuillet, A. C. , Gay, L. , Ahmadi, N. , Manel, S. , Ronfort, J. , & Vigouroux, Y. (2013). Detecting selection along environmental gradients: Analysis of eight methods and their effectiveness for outbreeding and selfing populations. Molecular Ecology, 22(5), 1383–1399. 10.1111/mec.12182 [DOI] [PubMed] [Google Scholar]
- Epstein, B. , Jones, M. , Hamede, R. , Hendricks, S. , McCallum, H. , Murchison, E. P. , & Storfer, A. (2016). Rapid evolutionary response to a transmissible cancer in Tasmanian devils. Nature Communications, 7, 12684. 10.1038/ncomms12684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier, L. , Dupanloup, I. , Huerta‐Sánchez, E. , Sousa, V. C. , & Foll, M. (2013). Robust demographic inference from genomic and SNP data. PLOS Genetics, 9(10), e1003905.– 10.1371/journal.pgen.1003905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier, L. , Hofer, T. , & Foll, M. (2009). Detecting loci under selection in a hierarchically structured population. Heredity, 103(4), 285–298. 10.1038/hdy.2009.74 [DOI] [PubMed] [Google Scholar]
- Fay, J. C. , & Wu, C. I. (2000). Hitchhiking under positive Darwinian selection. Genetics, 155(3), 1405–1413. 10.1093/genetics/155.3.1405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan, S. P. , Forester, B. R. , Latch, E. K. , Aitken, S. N. , & Hoban, S. (2018). Guidelines for planning genomic assessment and monitoring of locally adaptive variation to inform species conservation. Evolutionary Applications, 11(7), 1035–1052. 10.1111/eva.12569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll, M. , & Gaggiotti, O. (2008). A genome‐scan method to identify selected loci appropriate for both dominant and codominant markers: A Bayesian perspective. Genetics, 180(2), 977–993. 10.1534/genetics.108.092221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forester, B. R. , Lasky, J. R. , Wagner, H. H. , & Urban, D. L. (2018). Comparing methods for detecting multilocus adaptation with multivariate genotype–environment associations. Molecular Ecolology, 27, 2215–2233. 10.1111/mec.14584 [DOI] [PubMed] [Google Scholar]
- Frankham, R. , Ballou, J. , & Brisco, D. (2010). Introduction to conservation genetics, 2nd ed. Cambridge University Press. [Google Scholar]
- Frichot, E. , Schoville, S. D. , Bouchard, G. , & François, O. (2013). Testing for associations between loci and environmental gradients using latent factor mixed models. Molecular Biology and Evolution, 30, 1687–1699. 10.1093/molbev/mst063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funk, W. C. , Lovich, R. E. , Hohenlohe, P. A. , Hofman, C. A. , Morrison, S. A. , Sillett, T. S. , & Andelt, W. F. (2016). Adaptive divergence despite strong genetic drift: genomic analysis of the evolutionary mechanisms causing genetic differentiation in the island fox (Urocyon littoralis). Molecular Ecology, 25(10), 2176–2194. 10.1111/mec.13605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier, M. (2015a). Genome‐wide scan for adaptive divergence and association with population‐specific covariates. Genetics, 201, 1555–1579. 10.1534/genetics.115.181453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier, M. (2015b). Baypass version 2.1 User Manual. Retrieved from: http://www1.montpellier.inra.fr/CBGP/software/baypass/index.html [Google Scholar]
- Grossen, C. , Biebach, I. , Angelone‐Alasaad, S. , Keller, L. F. , & Croll, D. (2017). Population genomics analyses of European ibex species show lower diversity and higher inbreeding in reintroduced populations. Evolutionary Applications., 11, 123–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grøtan, V. , Saether, B. E. , Filli, F. , & Engen, S. (2007). Effects of climate on population fluctuations of ibex. Global Change Biology, 14, 218–228. 10.1111/j.1365-2486.2007.01484 [DOI] [Google Scholar]
- Grøtan, V. , Saethar, B. –E. , Filli, F. , & Engen, S. (2008). Effects of climate on population fluctuations of ibex. Global Change Biology, 14, 218–228. 10.1111/j.1365-2486.2007.01484.x [DOI] [Google Scholar]
- Guillaume, F. , & Rougemont, J. (2006). Nemo: an evolutionary and population genetics programming framework. Bioinformatics, 22, 2556–2557. 10.1093/bioinformatics/btl415 [DOI] [PubMed] [Google Scholar]
- Günther, T. , & Coop, G. (2013). Robust identification of local adaptation from allele frequencies. Genetics, 195(1), 205–220. 10.1534/genetics.113.152462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann, A. , Griffin, P. , & Dillon, S. (2015). A framework for incorporating evolutionary genomics into biodiversity conservation and management. Clim Chang Responses, 2(1). 10.1186/s40665-014-000 [DOI] [Google Scholar]
- Hoban, S. , Kelley, J. L. , Lotterhos, K. E. , Antolin, M. F. , Bradburd, G. , Lowry, D. B. , Poss, M. L. , Reed, L. K. , Storfer, A. , & Whitlock, M. C. (2016). Finding the genomic basis of local adaptation: pitfalls, practical solutions, and future directions. The American Naturalist, 188(4), 379–397. 10.1086/688018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer, T. , Ray, N. , Wegmann, D. , & Excoffier, L. (2009). Large allele frequency differences between human continental groups are more likely to have occurred by drift during range expansions than by selection. Annals of Human Genetics, 73(1), 95–108. 10.1111/j.1469-1809.2008.00489.x [DOI] [PubMed] [Google Scholar]
- Hohenlohe, P. A. , Bassham, S. , Etter, P. D. , Stiffler, N. , Johnson, E. A. , & Cresko, W. A. (2010). Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genetics, 6(2), 10.1371/journal.pgen.1000862 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson, A. , & Provenzale, A. (2004). Climate forcing and density dependence in a mountain ungulate population. Ecology, 85, 1598–1610. 10.1890/02-0753 [DOI] [Google Scholar]
- Karlsson, S. , & Moen, T. (2010). The power to detect artificial selection acting on single loci in recently domesticated species. BMC Research Notes, 3, 232. 10.1186/1756-0500-3-232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemper, K. E. , Saxton, S. J. , Bolormaa, S. , Hayes, B. J. , & Goddard, M. E. (2014). Selection for complex traits leaves little or no classic signatures of selection. BMC Genomics, 15(1), 246. 10.1186/1471-2164-15-246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M. (1955a). Solution of a process of random genetic drift with a continuous model. Proceedings of the National Academy of Sciences of the United States of America, 41(3), 144–150. 10.1073/pnas.41.3.144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M. (1955b). Random Genetic Drift in Multi‐Allelic Locus. Evolution, 9(4), 419–435. 10.2307/2405476 [DOI] [Google Scholar]
- Klopfstein, S. , Currat, M. , & Excoffier, L. (2006). The fate of mutations surfing on the wave of a range expansion. Molecular Biology and Evolution, 23(3), 482–490. 10.1093/molbev/msj057 [DOI] [PubMed] [Google Scholar]
- Leigh, D. M. , Lischer, H. E. L. , Grossen, C. , & Keller, L. F. (2018). Batch effects in a multiyear sequencing study: False biological trends due to changes in read lengths. Molecular Ecology Resources, 18(4), 778–788. 10.1111/1755-0998.12779 [DOI] [PubMed] [Google Scholar]
- Lewontin, R. C. , & Krakauer, J. (1973). Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics, 74(1), 175–195. 10.1093/genetics/74.1.175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linnen, C. R. , Poh, Y. P. , Peterson, B. K. , Barrett, R. D. H. , Larson, J. G. , Jensen, J. D. , & Hoekstra, H. E. (2013). Adaptive evolution of multiple traits through multiple mutations at a single gene. Science, 339(6125), 1312–1316. 10.1126/science.1233213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lischer, H. E. L. , & Excoffier, L. (2012). PGDSpider: An automated data conversion tool for connecting population genetics and genomics programs. Bioinformatics, 28, 298–299. 10.1093/bioinformatics/btr642 [DOI] [PubMed] [Google Scholar]
- Lotterhos, K. E. , & Whitlock, M. C. (2014). Evaluation of demographic history and neutral parameterization on the performance of Fst outlier tests. Molecular Ecology, 23, 2178–2192. 10.1111/mec.12725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lotterhos, K. E. , & Whitlock, M. C. (2015). The relative power of genome scans to detect local adaptation depends on sampling design and statistical method. Molecular Ecology, 24(5), 1031–1046. 10.1111/mec.13100 [DOI] [PubMed] [Google Scholar]
- Lowry, D. B. , Hoban, S. , Kelley, J. L. , Lotterhos, K. E. , Reed, L. K. , Antolin, M. F. , & Storfer, A. (2017). Breaking RAD: An evaluation of the utility of restriction site‐associated DNA sequencing for genome scans of adaptation. Molecular Ecology Resources, 17(2), 142–152. 10.1111/1755-0998.12635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadeau, S. , Meirmans, P. G. , Aitken, S. N. , Ritland, K. , & Isabel, N. (2016). The challenge of separating signatures of local adaptation from those of isolation by distance and colonization history: The case of two white pines. Ecology and Evolution, 6(24), 8649–8664. 10.1002/ece3.2550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narum, S. R. , & Hess, J. E. (2011). Comparison of F(ST) outlier tests for SNP loci under selection. Molecular Ecology Resources, 11(Suppl 1), 184–194. 10.1111/j.1755-0998.2011.02987.x [DOI] [PubMed] [Google Scholar]
- Nicholson, G. , Smith, A. V. , Jonsson, F. , Gustafsson, Ó. , Stefansson, K. , & Donnelly, P. (2002). Assessing population differentiation and isolation from single‐nucleotide polymorphism data. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(4), 695–715. 10.1111/1467-9868.00357 [DOI] [Google Scholar]
- Nielsen, R. , Hellmann, I. , Hubisz, M. , Bustamante, C. , & Clark, A. G. (2007). Recent and ongoing selection in the human genome. Nature Reviews Genetics, 8(11), 857–868. 10.1038/nrg2187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilot, M. , Greco, C. , vonHoldt, B. M. , Jędrzejewska, B. , Randi, E. , Jędrzejewski, W. , Sidorovich, V. E. , Ostrander, E. A. , & Wayne, R. K. (2014). Genome‐wide signatures of population bottlenecks and diversifying selection in European wolves. Heredity, 112(4), 428–442. 10.1038/hdy.2013.122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poh, Y.‐P. , Domingues, V. S. , Hoekstra, H. E. , & Jensen, J. D. (2014). On the prospect of identifying adaptive loci in recently bottlenecked populations. PLoS One, 9(11), e110579. 10.1371/journal.pone.0110579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poplin, R. , Ruano‐Rubio, V. , DePristo, M. A. , Fennell, T. J. , Carneiro, M. O. , Van der Auwera, G. A. , Banks, E. (2017). Scaling accurate genetic variant discovery to tens of thousands of samples. bioRxiv.
- Pritchard, J. K. , Pickrell, J. K. , & Coop, G. (2010). The Genetics of human adaptation: Hard sweeps, soft sweeps, and polygenic adaptation. Current Biology, 20(4), R208–R215. 10.1016/j.cub.2009.11.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K. , Stephens, M. , & Donnelly, P. J. (2000). Inference of population structure using multilocus genotype data. Genetics, 155, 945–959. 10.1093/genetics/155.2.945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reznick, D. , Rodd, H. , & Nunney, L. (2004). Empirical evidence for rapid evolution. In Ferrière R., Dieckmann U., & Couvet D. (Eds.), Evolutionary conservation biology. Cambridge University Press. [Google Scholar]
- Robertson, A. (1975a). Gene frequency distributions as a test of selective neutrality. Genetics, 81(4), 775–785. 10.1093/genetics/81.4.775 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson, A. (1975b). Letters to the editors: Remarks on the Lewontin‐Krakauer test. Genetics, 80(2), 396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson, J. M. , Langin, K. M. , Scott Sillett, T. , Morrison, S. A. , Ghalambor, C. K. , & Funk, W. C. (2014). Identifying evolutionarily significant units and prioritizing populations for management on islands. Monographs of the Western North American Naturalist, 7(1), 397–411. 10.3398/042.007.0130 [DOI] [Google Scholar]
- Sabeti, P. C. (2006). Positive Natural Selection in the Human Lineage. Science, 312(5780), 1614–1620. 10.1126/science.1124309 [DOI] [PubMed] [Google Scholar]
- Shackleton, D. & Group ISCS (1997). Wild Sheep and Goats and their Relatives. Status Survey and Conservation Action Plan for Caprinae . IUCN. [Google Scholar]
- Shultz, A. J. , Baker, A. J. , Hill, G. E. , Nolan, P. M. , & Edwards, S. V. (2016). SNP s across time and space: Population genomic signatures of founder events and epizootics in the House Finch (Haemorhous Mexicanus) . Ecology and Evolution, 6(20), 7475–7489. 10.1002/ece3.2444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockwell, C. A. , Hendry, A. P. , & Kinnison, M. T. (2003). Contemporary evolution meets conservation biology. Trends in Ecology and Evolution, 18, 94–101. 10.1016/S0169-5347(02)00044-7 [DOI] [Google Scholar]
- Storey, J. D. , & Tibshirani, R. (2003). Statistical significance for genome‐wide studies. Proceedings of the National Academy of Sciences of the United States of America, 100(16), 9440–9445. 10.1073/pnas.1530509100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuwe, M. , & Grodinsky, C. (1987). Reproductive biology of captive Alpine ibex (Capra i. ibex). Zoo Biology, 6, 331–339. 10.1002/zoo.1430060407 [DOI] [Google Scholar]
- Stuwe, M. , & Nievergelt, B. (1991). Recovery of Alpine ibex from near extinction – the result of effective protection, captive breeding, and reintroductions. Applied Animal Behaviour Science, 29, 379–387. 10.1016/0168-1591(91)90262-V [DOI] [Google Scholar]
- Timpson, N. , Greenwood, C. , & Soranzo, N. (2018). Genetic architecture: the shape of the genetic contribution to human traits and disease. Nat Rev Genet, 19, 110–124. 10.1038/nrg.2017.101 [DOI] [PubMed] [Google Scholar]
- Toïgo, C. , Brambilla, A. , Grignolio, S. , & Pedrotti, L. (2020). Capra ibex. The IUCN Red List of Threatened Species 2020: e.T42397A161916377. 10.2305/IUCN.UK.2020-2.RLTS.T42397A161916377.en. Downloaded on 03 May 2021. [DOI]
- Whitlock, M. C. , & Lotterhos, K. E. (2015a). Reliable detection of loci responsible for local adaptation: inference of a null model through trimming the distribution of FST . The American Naturalist, 186(S1), S24–S36. 10.1086/682949 [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C. , & Lotterhos, K. E. (2015b). OutFLANK Finding Fst outliers with an inferred neutral distribution. Retrieved from https://github.com/whitlock/OutFLANK [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
Read data can be viewed on the short‐read archive, ncbi project number PRJNA422727: https://www.ncbi.nlm.nih.gov/bioproject/PRJNA422727. The Nemo ini files necessary to recreate the simulations have been made available at https://doi.org/10.5061/dryad.ns1rn8pt2. Custom conversation scripts for Nemo output files and to merge the output of Bayenv runs are accessible here https://bitbucket.org/HeidiLischer/ibex/src/. Sample mean coordinates have been included in Supporting Information.


