Molecular Electrostatic Potential and Noncovalent Interactions in Derivatives of Group 8 Elements

Abstract

This communication reports experimental and theoretical evidences of σ‐hole interactions in adducts between nitrogen or oxygen nucleophiles and tetroxides of osmium or other group 8 elements. Cocrystals between pyridine or pyridine N‐oxide derivatives and osmium tetroxide are characterized through various techniques and rationalized as σ‐hole interactions using DFT calculations and several other computational tools. We propose the term “osme bond” (OmB, Om=Fe, Ru, Os, (Hs)) for naming the noncovalent interactions wherein group 8 elements have the role of the electrophile. The word osme is the transcription of ὀσμή, the ancient Greek word for smell that was used to name the heaviest group 8 element in relation to the smoky odor of its tetroxide.

σ‐Hole interactions in adducts between nitrogen or oxygen nucleophiles and tetroxides of osmium or other group 8 elements are reported. Cocrystals between pyridine or pyridine N‐oxide derivatives and osmium tetroxide are characterized through various techniques including computational tools. We propose the term “osme bond” (OmB, Om=Fe, Ru, Os, (Hs)) for naming the noncovalent interactions wherein group 8 elements have the role of the electrophile.

The surface electrostatic potential of molecules is typically not uniform. Regions where it is positive can be present and they tend to act as the electrophilic sites in attractive interactions with regions in surrounding molecules where it is negative. A systematic rationalization of intermolecular interactions based on this mindset began in the 1990s when a region of most positive electrostatic potential, ^[1] the so called σ‐hole, ^[2] was found on the surface of halogen atoms in dihalogens and halocarbons and when soon after the resulting electrophilic character of halogens began to be exploited in supramolecular chemistry. ^[3] Analogous σ‐holes with positive electrostatic potential were successively identified on other elements of p‐block of the periodic table, for example, on elements of groups 14, ^[4] 15, ^[5] and 16. ^[6] The attractive interactions occurring between these positive holes and nucleophilic sites are now topics of intense research in fields as diverse as drug design, ^[7] catalysis, ^[8] and anion transport. ^[9]

While in some adducts involving d‐block elements a clear‐cut identification of the electropositive (i.e., electrophilic) and electronegative (i.e., nucleophilic) components is hardly possible, this identification is fairly straightforward for some other adducts wherein σ‐holes have been identified on metals. The understanding of resulting adducts as σ‐hole systems helps in recognizing the electronic basis of observed geometries. ^[10] For instance, the localization of positive σ‐holes on the group 11 metals in respective halides ^[11] allows for a rationalization of the geometry of the adducts formed with anions and lone‐pair possessing atoms.[ ¹¹ , ¹² , ¹³ ] An analogous rationalization based on σ‐holes has been suggested for the geometries of some adducts given by group 12 elements ^[14] and is proposed here for the geometries of cocrystals involving derivatives of group 8.

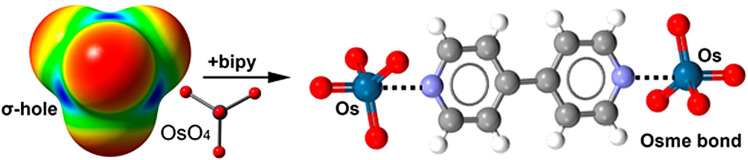
Specifically, we report that cocrystals have been obtained between osmium tetroxide and pyridine and pyridine N‐oxide derivatives (Figure 1). In these adducts short Os⋅⋅⋅O/N contacts ^[16] are present on the extension of one of O‐Os covalent bonds of OsO₄, consistent with the rationalization of these interactions as σ‐hole bondings. Calculation of the molecular electrostatic potential (MEP) surface of iron, ruthenium, and osmium tetroxides shows the presence of positive σ‐holes (Figure 2) at the regions of approach of the nucleophile. The quantum theory of “atoms‐in‐molecules” (QTAIM) combined with the noncovalent interaction plot (NCIplot) index analyses confirm the attractive nature of the Os⋅⋅⋅O/N short contacts and support crystallographic indications that these contacts are robust enough to drive the cocrystal formation.

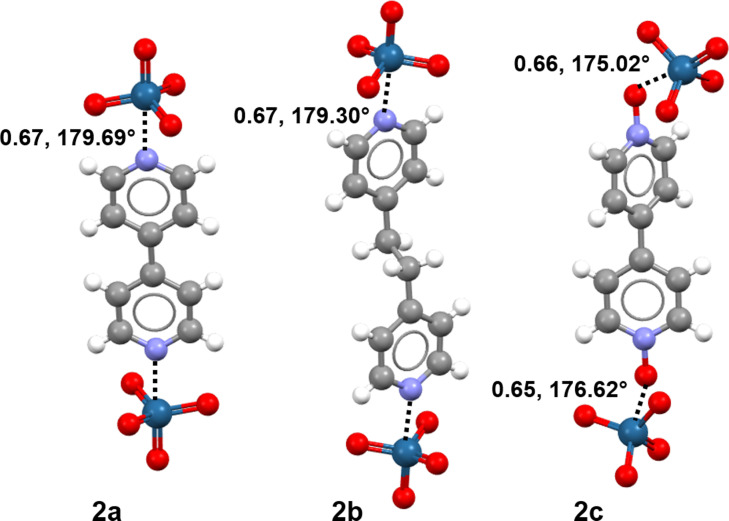
Figure 1.

Osme bonded adducts 2 a (left), 2 b (mid) and 2 c (right). OmBs are black dotted lines; Nc ^[15] and interaction angles are given. Color code: whitish, hydrogen; gray, carbon; blue, nitrogen; red, oxygen; navy, osmium.

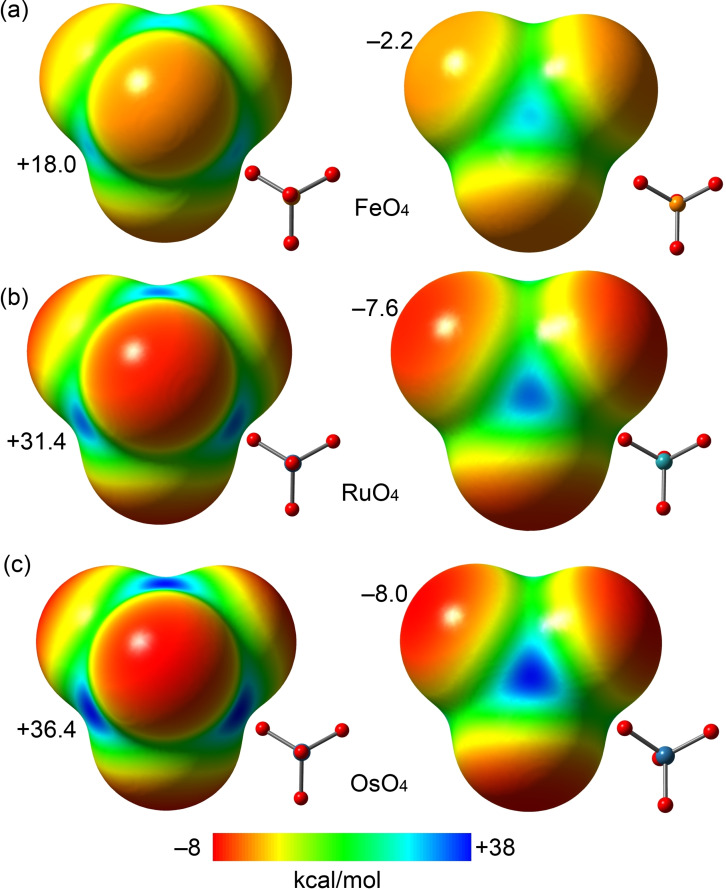
Figure 2.

MEP surfaces of FeO₄ (a), RuO₄ (b) and OsO₄ (c) at the PBE0‐D3/def2‐TZVP level of theory. Isosurface 0.001 a.u. The MEP maximum and minimum energies are indicated in kcal mol⁻¹.

σ‐Hole interactions are typically categorized referring to the group of the periodic table to which the atom at the electrophilic site belongs.[ ¹⁷ , ¹⁸ ] We propose that the term osme bond (OmB, Om=Fe, Ru, Os, (Hs)) is used for interactions described in this paper and for analogous interactions wherein group 8 elements are the electrophile (section S1.1). Osme is the transliteration of ὀσμή, the old Greek word for smell which was used by S. Tennant in 1803 to name osmium in relation to the smoky odor of OsO₄. ^[19]

The slow evaporation of a solution of OsO₄ and 4,4′‐bipyridine (1 a), 1,2‐di(pyridin‐4‐yl)ethane (1 b), [4,4′‐bipyridine] 1,1′‐dioxide (1 c), 1,3‐di(pyridin‐4‐yl)propane (1 d), 4‐methoxypyridine 1‐oxide (1 e), or isoquinoline 2‐oxide (1 f) affords brown cocrystals consisting in the osme bonded adducts 1 a⋅(OsO₄)₂ (2 a), 1 b⋅(OsO₄)₂ (2 b), 1 c⋅(OsO₄)₂ (2 c), 1 d⋅(OsO₄)₂ (2 d), 1 e⋅OsO₄ (2 e), or 1 f⋅OsO₄ (2 f). The formation of adducts between OsO₄ and nitrogen derivatives was observed since the early studies on olefin dihydroxylation via this reagent, ^[20] the first single crystal characterization of an adducts was reported in 1978, ^[21] and the interest in these adducts⋅(Table S25)[ ²² , ²³ , ²⁴ , ²⁵ ] grew in relation to the osmium‐catalyzed asymmetric dihydroxylation.

IR spectra of solid adducts 2 show the presence of absorptions of both 1 and OsO₄. Changes of bands frequencies and intensities in 2 with respect to pure 1 and OsO₄ indicate the presence of well‐defined chemical species rather than a mechanical mixture (Figures S1–S5). The νC‐H bands of pyridine rings (2850–3100 cm⁻¹ for pure 1) are blue‐shifted and become weaker on adducts 2 formation. These changes are similar to those observed when 1 give halogen bonded adducts ^[26] and suggest a decreased electron density at C−H groups on adducts 2 assembly, consistent with an n→σ* donation from N/O atoms to Os (see onwards). Also the pyridine breathing vibrations (1400–1600 cm⁻¹ region) are blue‐shifted in adducts 2, in analogy to other adducts wherein 1 are the nucleophiles. ^[27] The ν3 vibration for pure OsO₄ is at 960 cm⁻¹ in the gas phase and at 954 cm⁻¹ in CCl₄ solution. ^[28] It is at 930 cm⁻¹ for the hexamethylenetetramine⋅(OsO₄)₂ adduct in the solid and at 955 cm⁻¹ in CCl₄ solution. ^[29] Cocrystals 2 a–f show this vibration at 900–910 cm⁻¹ in the solid (consistent with non‐minor vibrational changes of OsO₄ on adducts formation) and at higher frequencies (e.g., at 942 cm⁻¹ for 2 a) in CHCl₃ solution, consistent with a partial dissociation of the adduct on dissolution. ^[30] Indeed, spectrophotometric studies showed that in solution the equilibrium between isolated OsO₄ and pyridine derivatives and the corresponding adducts is rapid even at low temperature ^[22] and equilibrium constants are extremely sensitive to steric effects. ^[31] The changes observed for the IR bands of pure components on adducts 2 formation agree well with DFT calculations, as discussed in the SI (S5.2, Figure S22).

¹³C and ¹⁵N solid state NMR (SSNMR) spectra of precursors 1 and cocrystals 2 are quite different and confirm the adducts formation. ¹⁵ N SSNMR signals of 2 are shifted upfield with respect to pure 1, consistent with electron density donation from N/O to Os on adducts formation. These shifts are similar to those shown by adducts wherein 1 interact with other electron acceptors. For instance, 1 a and 1 b show a shift of 31.7 and 41.7 ppm when osme bonded to OsO₄ (Figures S6–S9) and of 4.3 and 16.8 ppm when halogen bonded to 1,4‐diiodotetrafluorobenzene (1,4‐I₂‐C₆F₄). ^[32] The ¹⁵ N SSNMR signal of 1 c is at 282.0 and 280.9 ppm in 1 c⋅(OsO₄)₂, 269.1 ppm in 1 c⋅SbF_{3 ,} ^[33] 282.5 in 1 c⋅1,4‐I₂‐C₆F₄ , and 285.3 and 283.8 ppm in 1 c⋅(H₂O)₂ , (osme, pnictogen, halogen, and hydrogen bonded adducts, respectively) (Figures S10–S15). In experiments of competitive cocrystals formation, the self‐assembly of 1 c⋅SbF₃ prevails over the self‐assembly of 1 c⋅1,4‐I₂‐C₆F₄ which in turn prevails over the self‐assembly of 1 c⋅(H₂O)₂ . This suggests that the ¹⁵ N SSNMR chemical shift of 1 c in a cocrystal relates to the relative tendency of the self‐assembly of that cocrystal. We thus decided to test the hypothesis that the OmB might prevail over the hydrogen bond (HB) in identifying the modules involved in the formation of solid self‐assembled systems. Indeed, recrystallization of 1 c,e,f⋅(H₂O) _n (n=2–6) from CH₂Cl₂ affords oxides 1 c,e,f as hydrated species (Tables S19‐S24, Figure S21), while in the presence of OsO₄, the respective cocrystals 2 c,e,f are obtained exclusively.

Cocrystals 2 a–c afforded samples suitable for single crystal X‐ray analysis (Tables S1–S18, Figures S18–S20). The Os⋅⋅⋅N and Os⋅⋅⋅O interactions involving the pyridine nitrogen in 2 a,b and the pyridine oxide oxygen in 2 c are longer than typical Os‐N/O covalent bonds but remarkably shorter than the sum of the van der Waals radii of involved atoms. These contacts are by far the shortest interactions observed in the adducts, their normalized contacts (Nc) ^[15] are as small as 0.65–0.67 (Figure 1). It is thus reasonable to assume that the self‐assembly of cocrystals 2 a–c is largely driven by these OmBs. The structures reported in Scheme 1 can be assigned to adducts 2 d, 2 e, and 2 f considering ¹³C/¹⁵N SSNMR spectra (Figures S16,S17) and ¹H NMR spectra in solution where analyses in the presence of an internal standard established that the OsO₄ to 1 d,e,f ratio in these adducts is 2:1, 1:1, and 1:1, respectively. As typical for short σ‐hole interactions,[ ² , ³ , ⁴ , ⁵ , ⁶ , ¹⁷ , ¹⁸ ] the O‐Os⋅⋅⋅N/O angles are very close to 180°. Short and linear Os⋅⋅⋅N/O contacts are present also in X‐ray structures of other adducts between OsO₄ and nitrogen or oxygen containing compounds (Table S25).[ ²³ , ²⁴ , ²⁵ ] The tetrahedral geometry of pure OsO₄ is slightly distorted on OmB formation. While the geometry around osmium remains essentially tetrahedral (e.g., O‐Os‐O angles in 2 a span the range 101.5–117.7°), it becomes somewhat similar to a trigonal bipyramid, the incoming N or O atom occupying an apical position. A similar deformation from tetrahedral towards trigonal bipyramidal geometry is observed on formation of σ‐hole interactions involving tetravalent elements of group 14.[ ⁴ , ³⁴ ] An elongation of the covalent bond opposite to the incoming nucleophile is common for σ‐hole interactions,[ ³ , ⁴ ] and is usually rationalized as a consequence of the LP→σ* charge transfer. Such elongation is observed also in 2 a–c, e.g., in 2 b the Os−O bond opposite to the Os⋅⋅⋅N OmB is 171.2 pm while the mean value of the three other Os−O bonds is 169.2 pm and the mean Os−O bond in pure OsO₄ is 169.7 pm. ^[35] Computation affords analogous elongations (see onwards).

Scheme 1.

Structures of cocrystals 2 d–f.

To investigate the existence and intensity of σ‐holes in OsO₄ and analogous derivatives of other group 8 elements, the molecular electrostatic potential (MEP) surfaces of the OmO₄ species have been computed. Similar to OsO₄, RuO₄ forms adducts with derivatives containing lone pair donor atoms ^[36] while FeO₄ is an unknown compounds but it has been included for comparison purposes. Figure 2 shows the MEP surfaces of the three tetroxides studied herein; the same energetic scale and two different orientations are presented. Four symmetrically equivalent σ‐holes are observed opposite to the O‐Om bonds. The depth of the σ‐holes increases on going from Fe to Os, being significantly more intense for Ru and Os (+31.4 and +36.4 kcal mol⁻¹, respectively) than for Fe (+18.0 kcal mol⁻¹). The MEP minimum values in the three compounds are quite small, thus revealing the overall electrophilic nature of these molecules.

In order to analyze the ability of OmO₄ compounds to establish OmBs, six adducts have been fully optimized at the PBE0‐D3/def2‐TZVP level of theory. Acetonitrile and pyridine, two typical Lewis bases were used. The intermolecular interactions revealed by the combined QTAIM/NCIplot analysis are represented in Table 1 and Figure 3 (see S5.1). The OmBs are characterized in the six compounds by the corresponding bond critical points (CPs) and bond paths connecting N and Om atoms. The OmBs are also revealed by the NCIplot index analysis, showing isosurfaces located between the Om atoms and the Lewis bases. The NCIplot isosurfaces present different colors: green for both FeO₄ adducts, light blue for O₄Ru⋅⋅⋅NCCH₃ and O₄Os⋅⋅⋅NCCH₃ adducts, and dark blue for O₄Ru⋅⋅⋅NC₅H₅ and O₄Os⋅⋅⋅NC₅H₅, in line with the interaction energies that range from −2.2 to −11.4 kcal mol⁻¹. The interaction energies are in good agreement with the MEP values at the σ‐holes commented above and the relative basicity of acetonitrile and pyridine. For pyridine complexes with RuO₄ and OsO₄, a secondary C−H⋅⋅⋅O interaction is also observed characterized by a bond CP, bond path, and green NCIplot isosurface (weak interaction).

Table 1.

Interaction energies (ΔE, kcal mol⁻¹), equilibrium distances (pm) between N and Om atoms, and electron charge densities (ρ _r, a.u.) at the bond CPs connecting N and Om atoms for the adducts between OmO₄ (Om=Fe, Ru, Os) and acetonitrile or pyridine. The stabilization energies from the second order perturbation analysis E⁽²⁾ (kcal mol⁻¹) corresponding to the LP(N) → σ*(Om‐O) orbital donor‐acceptor interactions are also indicated.

Complex	ΔE	Distance [pm]	ρ r	LP(N)→σ*(Om‐O)
O4Fe⋅⋅⋅NCCH3	−2.2	340.7	0.0058	0.24
O4Fe⋅⋅⋅NC5H5	−3.7	327.9	0.0083	0.67
O4Ru⋅⋅⋅NCCH3	−3.6	325.1	0.0082	0.81
O4Ru⋅⋅⋅NC5H5	−7.6	270.5	0.0279	2.29
O4Os⋅⋅⋅NCCH3	−4.2	314.2	0.0109	1.89
O4Os⋅⋅⋅NC5H5	−11.4	251.3	0.0468	5.63

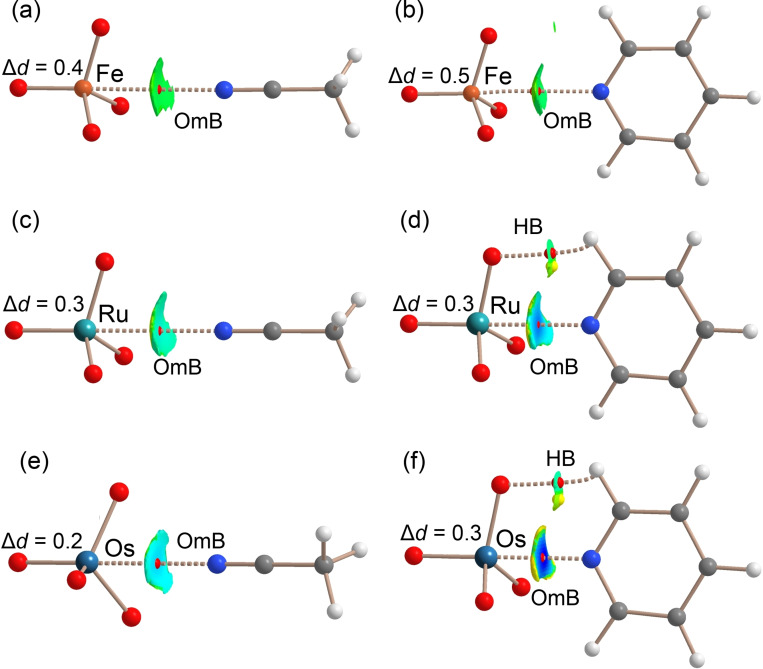
Figure 3.

a–f) PBE0‐D3/def2‐TZVP optimized geometries of six OmB complexes. QTAIM analysis: bond CPs in red and ring CPs in yellow. NCIPlot: |RGB| isosurface 0.4 a.u.; Color range 0.04 a.u. (red) ≤ (signλ ₂)ρ ≤ −0.04 a.u. (blue). Only the intermolecular interactions are shown. The computed Om‐O elongation (Δd, pm) upon complexation is given.

These adducts exhibit quite short Om⋅⋅⋅NC₅H₅ distances, especially in the OsO₄⋅⋅⋅NC₅H₅ adduct. In fact, for this system the NCIplot index shows that the outer part of the isosurface is yellow disclosing some N⋅⋅⋅O repulsion between the negative O atoms and the N atom of the Lewis base. The theoretical distance computed in the gas phase (251 pm) is in reasonable agreement with the experimental distances observed in cocrystals 2 a,b (≈240 pm).

Table 1 also summarizes the results from the natural bond orbital analysis applied to the adducts shown in Figure 3. In all cases we have found from modest to moderate orbital donor‐acceptor contributions, ranging from 0.24 to 5.63 kcal mol⁻¹, as a consequence of the electron donation from the nitrogen's lone pair to the antibonding σ* orbitals (Om‐O). The orbital contribution is very sensitive to the equilibrium distance. Consequently, for the weakest adduct O₄Fe⋅⋅⋅NCCH₃ with the longest equilibrium distance the contribution is around 10 % of the interaction energy. In sharp contrast, for the strongest adduct (O₄Os⋅⋅⋅NC₅H₅) the orbital contribution is approximately 50 % of the interaction energy. A similar behavior is obtained when computing the total orbital contribution using the EDA partition Scheme (sections S5.1, S5.3, Table S26, Figure S23). For all adducts, the distance of the O‐Om bond opposite to the electron donor atoms increases upon complexation, in line with the effect of filling the σ*(Om‐O) orbital.

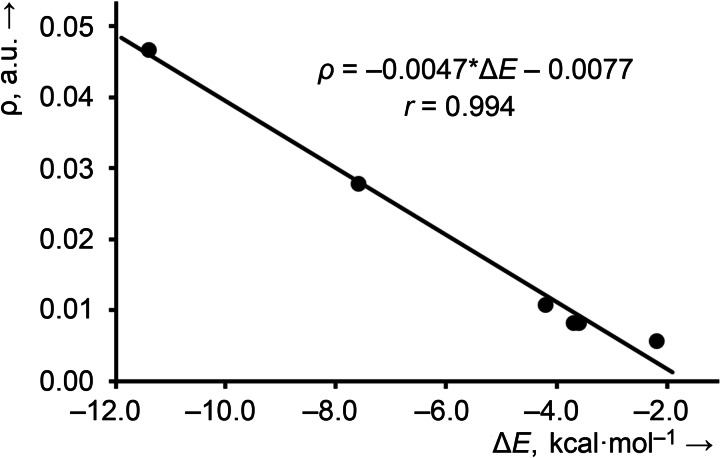
It is interesting to highlight that we have found a strong relationship (r=0.994) between the interaction energies and the values of the charge density at the bond CPs, as shown in Figure 4, thus suggesting that the value of ρ can be used as an energy predictor for OmBs. Similar relationships have been observed for other σ‐hole interactions like halogen, ^[37] chalcogen ^[38] and pnictogen bonds. ^[39]

Figure 4.

Regression plot of the interaction energy vs. the electron charge density at the bond CP of the OmB in the adducts shown in Figure 3.

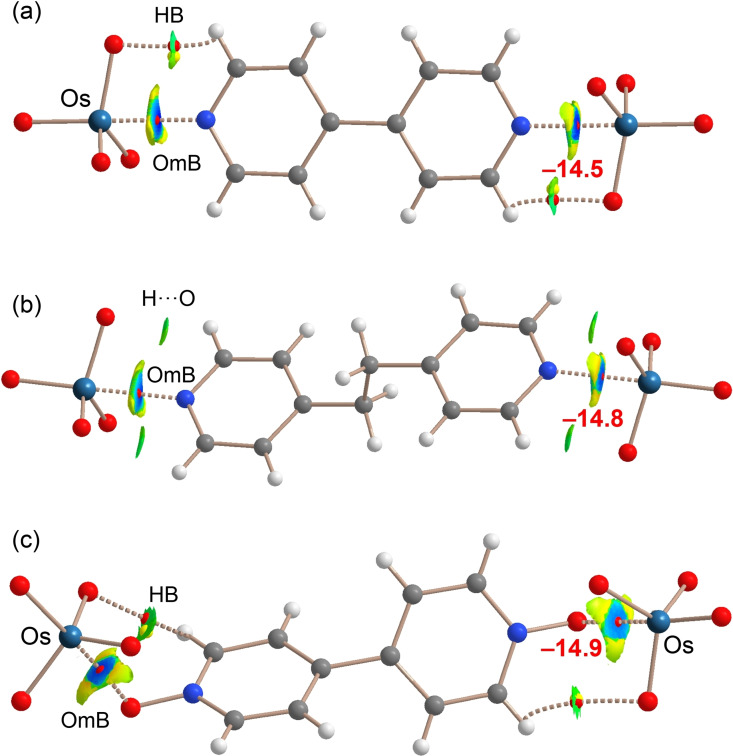
Similar QTAIM/NCIplot analyses (Figure 5) have been performed for the adducts characterized by X‐ray in order to prove that the experimentally observed short contacts are not crystal packing effects. In all systems 2 a–c the OmB is characterized by the corresponding bond CP and bond path connecting the N/O atom to the Os atom, thus confirming the attractive nature of the interaction. Also the C−H⋅⋅⋅O HBs found in the crystals of 2 a and 2 c are characterized by the corresponding bond CPs and bond paths (Figure 5 a,c). For 2 b, only the NCIplot index analysis reveals the existence of the C−H⋅⋅⋅O contacts (Figure 5 b). The NCIplot isosurfaces show that the Os⋅⋅⋅N/O interactions are strong (dark‐blue isosurface) in all adducts and also reveal the existence of N/O⋅⋅⋅O repulsion characterized by the yellow (weak repulsive) parts of the surfaces, consistent with the flattening at osmium observed on cocrystals formation. The short Os⋅⋅⋅N experimental distances can be explained by the fact that the MEP values at the O atoms are considerably smaller in absolute value than those at the σ‐holes, thus the O⋅⋅⋅N repulsion is much weaker than the Os⋅⋅⋅N attraction.

Figure 5.

Combined QTAIM/NCIplot analysis of adducts 2 a (a), 2 b (b) and 2 c (c). Bond CPs in red and ring CPs in yellow. NCIPlot: |RGB| isosurface 0.4 a.u.; Color range 0.04 a.u. (red) ≤ (signλ ₂)ρ ≤ −0.04 a.u. (blue). Only the intermolecular interactions are shown. In red the OmB energies estimated using the ρ values.

Finally, the interaction energies of the contacts have been estimated using the equation shown in Figure 4, their values are very similar in all adducts (−14.5 to −14.9 kcal mol⁻¹) (see also Table S27). These values agree well with the crystallographic short Os⋅⋅⋅N/O distances and the dark blue color of the NCIplot isosurfaces.

The MEPs of osmium imido derivatives OsO_4−n (=NR) _n were calculated (n=1–4, R=Me, t‐Bu, 1‐adamantyl) to assess how the electrostatic potential at the Os σ‐holes depend on the groups covalently bonded to Os (section S5.5, Figures S24–S26, Table S28). The σ‐holes opposite to nitrogen are less positive than opposite to oxygen and can become negative in polyimido derivatives (OsO_4−n (=NR) _n , n=2–4). Importantly, NCIplot analysis shows that OmB presence is not limited to OsO₄ adducts.

The crystallographic and computational results reported here consistently identify the net attractive interaction between tetroxides and imido‐oxides of group 8 elements and lone pair possessing atoms as a case of the wider set of the so named σ‐hole interactions. The name osme bond is proposed to categorize these noncovalent interactions in contrast to the metal‐ligand bond of classical coordination complexes. In competitive processes of cocrystal formation, the osme bond can prevail over the hydrogen bond in determining the composition of preferentially formed cocrystals. The tendency of OsO₄ to form adducts with lone pair donors (e.g., amine and pyridine derivatives) has been studied in relation to the asymmetric dihydroxylation of olefins by OsO₄. The results reported here may offer new insights on the correlation between the catalytic effect and the binding of OsO₄ to the nitrogen donor.[ ²⁴ , ²⁵ ]

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

A. Daolio, A. Pizzi, M. Calabrese, G. Terraneo, S. Bordignon, A. Frontera, G. Resnati, Angew. Chem. Int. Ed. 2021, 60, 20723.