Abstract
Interferometric synthetic aperture radar (InSAR) interferograms contain valuable information about the fault systems hidden beneath the surface of the Earth. In a new approach, we aim to fit InSAR ground deformation data using a distribution of multiple seismic point sources whose parameters are found by a genetic algorithm. The resulting source distribution could provide another useful tool in solving the difficult problem of accurately mapping earthquake faults. We apply the algorithm to an ALOS‐2 InSAR interferogram and perform a multifractal analysis on the resulting distribution, finding that it exhibits multifractal properties. We report first results and discuss advantages and disadvantages of this approach.
Keywords: genetic algorithm, InSAR, inversion, multifractal
Key Points
Inversion for seismic moment of point source distribution
Multifractal analysis of seismic moment distribution is performed
Seismic moment distribution exhibits multifractal properties
1. Introduction
Significant errors can occur in fault geometry and slip dislocation models as a result of fault surfaces not being well‐represented by simple planar or rectangular fault models. For this reason, it is necessary to utilize all of the tools available to improve estimates of fault geometry and location. One such tool is interferometric synthetic aperture radar (InSAR), which provides maps of surface deformation that contain valuable information about the complexity of the fault system giving rise to the image (Bürgmann et al., 2000). InSAR is a radar technique that uses a synthetic aperture radar (SAR) mounted on a satellite to image the same area at two different times, and uses those images to determine the differences in phase of the waves that return to the SAR. Since the wavelength of the electromagnetic waves emitted by the SAR is known, the phase difference between the images can be used to calculate their difference in line‐of‐sight distance to the satellite. The result is a map of the line‐of‐sight ground deformation of the imaged area that occurred between the times that the original SAR images were taken (Jet Propulsion Laboratory, California Institute of Technology, 2014). Despite being susceptible to different sources of error—such as orbital error (Fattahi & Amelung, 2014) and atmospheric uncertainty (Ding et al., 2008; Fattahi & Amelung, 2015)—InSAR is able to measure ground deformation to submillimeter accuracy if such effects are appropriately accounted for (Ferretti et al., 2007).
Previous work has been performed which aimed to invert the ground deformation contained in InSAR interferograms to find the geometry of faults that could cause the observed ground deformation. Such methods rely on having a model that depends on various parameters that can recreate the desired data set. For seismology, a commonly used model is Okada's analytical solutions for the surface deformation due to faults in an elastic half‐space, which can model ground deformation due to either point or finite rectangular seismic sources (Okada, 1985).
The inversion detailed in Bagnardi and Hooper (2018), for example, utilizes an Okada rectangular fault model described by nine parameters: length, width, depth, strike angle, dip angle, X‐ and Y‐coordinates, uniform slip in the strike direction and uniform slip in the dip direction (Bagnardi & Hooper, 2018). Their approach uses a Bayesian inversion to determine a posterior probability density function (PDF), which describes how well a set of parameters can explain a given data set based on their uncertainties and taking into account prior information in the form of a joint prior PDF. A Monte‐Carlo Markov Chain utilizing the Metropolis‐Hastings algorithm is then used to efficiently search the parameter space by taking steps in the prior PDF to get new sets of parameter values and comparing the likelihood of the new model to the previous step (Hastings, 1970). After an appropriate number of iterations, the sampling done by the algorithm approximates the desired posterior PDFs of each of the parameters, which can be used to estimate their most likely values. Jo et al. (2017) performed a different type of inversion for the 2014 South Napa earthquake for a similar set of parameters for a rectangular fault model (Jo et al., 2017). They used two separate inversions in their analysis, the first being a Monte‐Carlo simulation of 10,000 iterations to find the fault parameters. The second was a least squares inversion performed to find the slip distribution over the rectangular fault plane.
Aside from Monte‐Carlo methods, there are other analysis techniques that have been used to invert InSAR interferograms. Feng et al. (2013) utilized a method of inversion called multipeak particle swarm optimization (M‐PSO) to study the 2011 Burma earthquake (Feng et al., 2013). A PSO works by first defining a population (or swarm) of candidate solutions to a problem and then moving them throughout the parameter space to find the optimal solution. The particles move according to a “velocity” that is based on each particle's own best‐known position in the parameter space as well as the best‐known position of the other particles (Kennedy & Eberhart, 1995). Li et al. (2020) and Wen et al. (2016) also used a M‐PSO inversion in their analyses of the 2015 Pishan earthquake and the 2013 Lushan earthquake, respectively, while additionally adding a second inversion for the slip distribution on the fault plane (Li et al., 2020; Wen et al., 2016).
There have also been advances in specific aspects of the inversion, such as the slip distribution. Liu and Xu (2019) developed another method for the joint inversion of coseismic and postseismic fault slip from InSAR data called LogSIM, which uses a logarithmic model solved by a nonlinear least squares curve fitting function (Liu & Xu, 2019). Zhang et al. (2008) solved the slip distribution inverse problem with a model using triangular dislocation elements to more accurately model the three‐dimensional (3D) fault surface (Zhang et al., 2008). They solved the resulting inverse problem using a weighted damped least squares approach. G. Jiang et al. (2013) also performed an inversion utilizing a model made up of triangular dislocation elements, finding a solution using bounded variable least squares (G. Jiang et al., 2013). Fukahata and Wright (2008) aimed to improve the inversion of the slip distribution by treating the dip angle as a hyperparameter and estimating it using the Bayesian information criterion (Fukahata & Wright, 2008). This is followed by determining the slip distribution using maximum‐likelihood methods. Their work is continued in another study by Fukahata and Hashimoto (2016) who apply the same method to the 2016 Kumamoto earthquake (Fukahata & Hashimoto, 2016). Frietsch et al. (2019) extended the problem slightly, adding two new parameters for time‐shift to the centroid time and the compensated‐linear‐vector‐dipole (CLVD) component while also allowing for the parameters of multiple fault segments to be found at one time (Frietsch et al., 2019). This makes it possible for them to model a single event as multiple fault segments or model multiple separate events at the same time.
Finally, it should be noted that InSAR is not limited in usefulness to earthquake mechanism inversion, as shown by Peng et al. (2018) who used InSAR‐derived deformation data to invert the mechanism of subsidence of Line 3 of the Xi'an metro near Yuhuazhai (Peng et al., 2018). They found from their inversion of a flat lying sill model with distributed contractions—with a depth based on the average depth of local pumping wells—that the rapid subsidence could be explained by excessive groundwater extraction in the area.
Also note that the inversion of the focal mechanism of earthquakes can be done from a variety of sources other than InSAR data. A common method of inversion uses P‐wave first motion polarities, such as the analyses performed by Hicks et al. (2000) and Langet et al. (2020). If the number of seismic stations is too low to use first‐motion polarities a full waveform analysis can be performed to provide constraints on the focal mechanism. Examples of full waveform analysis are reported in Hicks et al. (2000) as well as Villegas et al. (2016). Efforts made to improve these analyses include work by Sokos and Zahradnik (2008) on the ISOLA software package, which can perform multi‐source inversions in addition to the typical single source inversions.
Though many previous inversions of InSAR data utilize a number of rectangular fault planes, it has been shown that fault surfaces are much more complex. Steps have been taken to fight this problem, Sahimi et al. (1993) performed an analysis of the fracture patterns in heterogeneous rocks and found “at large length scales, they are percolation fractals with a fractal dimension D1.9 and 2.5, in two‐dimensional (2D) and 3D, respectively.” This implies that fault surfaces cannot be completely represented by simple planar surfaces. Candela et al. (2012) studied fault surface roughness over nine decades of length scales from 50 to 50 and found that they could be characterized by an anisotropic self‐affine description. Bruhat et al. (2019) investigated the effect of surface roughness on surface displacement, finding that “slip distributions become increasingly more self‐affine, that is, containing more short wavelength fluctuations as compared to the self‐similar fault profiles, as roughness increases,” suggesting that fault roughness has a considerable effect on the behavior of faults and therefore our models must be improved to take such effects into account.
The complexity of earthquake modeling is not limited to the fault surfaces, as shown by the 2016 Kaikoura earthquake in New Zealand. This magnitude 7.8 earthquake was one of the largest recorded in New Zealand, and was found to have caused the rupture of at least 12 different faults, some separated by up to 15 km (Hamling et al., 2017). Hamling et al. (2017) also state, “The earthquake should motivate rethinking of certain seismic hazard models, which do not presently allow for this unusual complex rupture pattern.” Another complex earthquake sequence was that of the magnitude 7.3 Landers earthquake in 1992, around which occurred the magnitude 6.5 Big Bear earthquake and the magnitude 5.7 Little Skull Mountain earthquake, which were later determined to be separate events rather than mainshocks and aftershocks (Hauksson et al., 1993).
Due to the complex nature of faults, it is important to improve our models so that they can appropriately represent a wider range of behavior. In this study, a new approach that utilizes a model composed of a collection of seismic point sources is introduced. We choose point sources because their superposition can represent any possible physical surface as long as enough sources are utilized, providing much more freedom than simple rectangular models. A genetic algorithm is used to simultaneously find the parameters of the entire collection of point sources. As their name implies, genetic algorithms borrow their method of solving problems from genetics. A population of solutions to the problem is randomly generated, and these solutions are allowed to crossover and mutate until an ideal solution is found. A crossover operator is the genetic algorithm equivalent of parents giving birth to offspring that inherit their genes. In a traditional genetic algorithm, a solution is represented as an array of bits, and the crossover operator might be defined to swap certain bits between two “parent” solutions. The mutation operator randomly changes the value of one or more bits in a solution array, similar to what occurs during a long period of a species's evolution. A genetic algorithm also requires some form of “survival of the fittest,” which allows better solutions to be chosen to move forward during the execution of the algorithm. This is included in the algorithm as a cost function—more “fit” solutions to the problem are those who minimize the cost function or maximize some other desired measure of fitness (Kumar et al., 2010). In this study, we utilize what is known as a real‐coded genetic algorithm, in which the solutions are instead represented by a list of real‐valued parameters. This change in the form of the solutions necessitates a change in the genetic operators, which will be explained in the next section.
After fitting using the above‐mentioned algorithm, a multifractal analysis is performed on the resulting distribution of point sources. Multifractals are unique from monofractals in that they cannot be represented by a single fractal dimension, but rather require a spectrum of dimensions to characterize their properties (Rosenberg, 2020). Many systems in a wide variety of fields have been shown to have multifractal properties, from the distribution of soil particle sizes (Adolfo et al., 2001) to the behavior of financial markets (Z.‐Q. Jiang et al., 2019) as well as the structure of the universe (Jones et al., 1988). In studies of earthquakes, multifractal analysis has been applied to the distribution of earthquake locations in different regions. Some examples include a study of the 2001 Bhuj earthquake sequence by Aggarwal et al. (2017) and of the Taiwan seismic region by Hui et al. (2020). Similar analysis has also been applied to the results of coupled slider‐block models as reported by Tanaka (2014). In this study, specifically, we perform a multifractal analysis on the seismic moment distribution of a group of seismic point sources.
2. Genetic Algorithm
We begin by describing our genetic algorithm in more detail. As stated in the previous section, the solutions in a real‐coded genetic algorithm are represented as lists of real‐valued parameters. For the genetic algorithm used in this study, the solutions are a list of parameters that describe the locations and orientations of a number of seismic point sources. In particular, every point source has a parameter for each of the following: x‐coordinate, y‐coordinate, z‐coordinate, strike angle, dip angle, and seismic moment. The x‐, y‐, and z‐coordinate parameters define the location of the point source in 3D space—where z = 0 defines the ground's surface in the case of zero deformation. The strike angle and dip angle determine the orientation of the slipping fault represented by the point source. Strike angle determines the direction of the line created by the intersection of the fault plane and the ground's surface. The dip angle is the angle between the fault plane and the ground's surface. A diagram of the geometric parameters can be seen in Figure 1. In Okada's convention, the dip angle is restricted to lie within the range (Okada, 1985). The seismic moment of a point source represents a combination of the fault area and the amount that it slips. A solution will have parameters total, where n is the number of point sources the solution is composed of. These point sources give rise to surface deformation as defined by Okada's expressions for deformation due to shear and tensile faults in a half‐space (Okada, 1985). Our analysis utilizes these equations, which are included in Appendix A. The total deformation—the superposition of the deformation from all point sources—is compared to a desired surface deformation (the data), and the goal of the algorithm is to move and reorient the point sources until the model's surface deformation approximates that of the data. The specifics of the algorithm are discussed in the following paragraphs.
Figure 1.
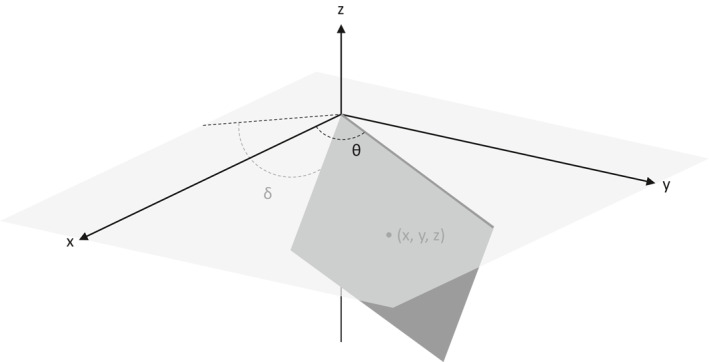
The definitions of the geometric parameters of the point sources used in this study. The source is represented as a rectangle to allow visualization of the strike and dip angles. In this figure, the point source would be located at the center of the rectangular surface, as indicated by the dot.
Given some ground deformation data in the form of ground coordinates and their corresponding deformations, the algorithm first determines the minimum and maximum x‐ and y‐values to use as limits when generating possible source distributions to fit the data. This restricts the allowed locations of the point sources to an area below the ground deformation. Then the algorithm generates a population of a user‐defined number of source distributions (models) containing a user‐defined number of sources with random locations and orientations within specified limits. It calculates each model's displacement field, which is the ground deformation resulting from a superposition of the ground deformation due to individual point sources in the model. Each model is compared to the input data, and the chi‐square value of each model is recorded. In this study, the chi‐square value for a given model is defined as:
| (1) |
where is the data value for the elevation of the ground at the point , is the model value for the elevation of the ground at the point and runs over all data points.
After the chi‐square of each model has been determined, pairs of models are selected to use as parents in the creation of the next generation of models. The models with lower are more likely to be selected as parents. Note that the same model cannot be both members of a pair, but can be present in more than one pair with another model. As each pair is selected, the member models are crossed to yield two more next‐generation models.
This study uses what is called a simulated binary crossover operator to generate new solutions based on the parent solutions (Deb & Agrawal, 1995). It is the real‐coded equivalent of the single‐point crossover operator of a binary genetic algorithm. The single‐point crossover operator crosses the parent solutions by picking a random point in one solution's bit array, and swaps the bits after that point between the two solutions. Simulated binary crossover uses a probability density function to imitate single‐point crossover for use in a real‐coded genetic algorithm. Simulated binary crossover works as follows:
Choose two parents and
Generate a random number
Calculate the parameter
where is the distribution index.
-
4.
Compute the child solutions using
The distribution index determines the width of the distribution used for generating children. Large values of tend to generate solutions closer to the parents, while smaller values generate solutions further away. The recommended value for , and the one used in this study, is (Deb & Agrawal, 1995). Pairs are selected and crossed until the next generation becomes equal in size to the original population of models.
Once the next generation has been created, there is a user‐defined chance for each model in the new generation to be mutated. The mutation operator, when applied to a model, gives each source in the model a user‐defined chance to be shifted from its original position, orientation and seismic moment. The amount of translation or rotation is determined by a Gaussian random number generator centered at the original value of the coordinate. For example, if the original strike angle of a source is , the Gaussian distribution used to select the new value has a mean value of . The amount of shift in the location and seismic moment is selected in a similar manner. The process of crossing to create new generations and mutation of the new generations is repeated until the user‐defined number of generations is reached. The overall process of the algorithm is pictured in Appendix C and Figure C1.
3. Applying the Algorithm to ALOS‐2 Data
The InSAR interferogram that is fit in this study was processed by Lindsey et al. (2015a) and was downloaded from the Nepal Earthquake ALOS‐2 InSAR website (Lindsey et al., 2015b). The particular one used is the combination of the ALOS2040533050‐150222 and ALOS2050883050‐150503 products, yielding an interferogram containing ground displacement between February 22, 2015 and May 3, 2015. This interferogram was chosen because it exhibits deformation due to a seismic event—in this case, the magnitude 7.8 earthquake that occurred on April 25, 2015, 36‐km east of Khudi, Nepal. The interferogram is a collection of points, each defined by their latitude, longitude and line‐of‐sight ground displacement. The line‐of‐sight displacement is converted to vertical displacement using the reported look angle of the satellite for each data point. To fit this interferogram, the data are binned into a 30‐by‐30 2D histogram to reduce the amount of computation time. The value of each bin is calculated as the average vertical displacement of each data point contained in that bin. After binning, the resulting pixels in latitude and longitude are mapped to the x‐y plane, in units of km, to allow comparison to the results of the algorithm. To further reduce computation time, the area of the interferogram being fit is reduced to pixels in the range and which contains the ground deformation of interest. For our analysis, only the vertical displacement of the ground was calculated and compared—the horizontal displacement was not considered.
When fitting this interferogram, the algorithm is set to use a population size of 2,000, with each solution in the population containing 513 seismic point sources arranged in a single‐layer 27 × 19 grid. The grid size is chosen such that point sources are placed in a square grid with 5 km side length below the significant ground deformation in the interferogram. Since the earthquake was a result of thrust faulting (United States Geological Survey, 2015), Okada's equations for dip‐slip faulting were used to calculate the ground deformation caused by each point source. For this run of the algorithm only the seismic moment of each point source was allowed to vary to reduce the computational complexity—each point source kept its location and orientation fixed during fitting. The strike angle, dip angle and depth of the point sources were chosen to be averages of the five sets of earthquake parameters reported in Lay et al. (2016) for the 2015 earthquake, held fixed at the values of 288.2, 6.06, and 18.8 km, respectively. The initial values of the point source seismic moments in the starting population are chosen from a uniform distribution in the range . The chance for a model to be chosen to mutate in a given generation was . If chosen to mutate, each source point in the model had a chance to have its seismic moment shifted up or down. After running until 500 successive generations passed with no improvement to the error between the best model and the data, the algorithm returned the model visible in Figure 2. The model is fully defined by its 513 values for each point source's seismic moment. The residuals between the model and data can be seen in Appendix B.
Figure 2.
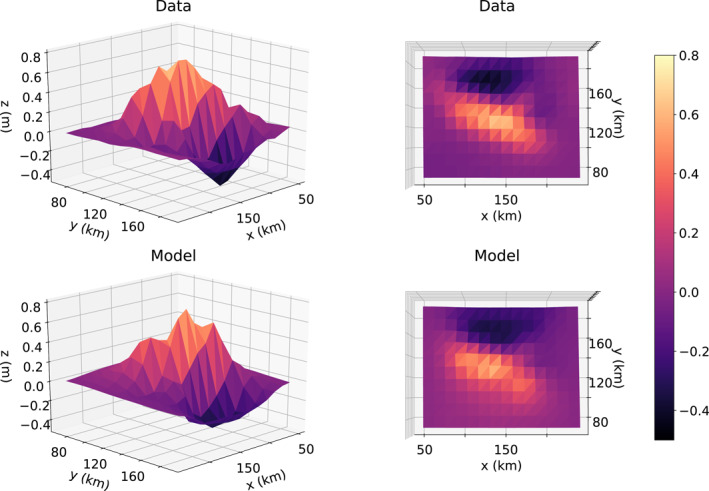
(Top left) Azimuthal view of the ALOS‐2 ground deformation data. (Top right) Top view of the ALOS‐2 ground deformation data. (Bottom left) Azimuthal view of the model generated by the algorithm. (Bottom right) Top view of the model generated by the algorithm.
4. Multifractal Analysis
We now turn to our multifractal analysis. Multifractals are more complicated than classic monofractals in that their behavior cannot be characterized by a single fractal dimension but rather requires a continuous spectrum of exponents to describe it (Rosenberg, 2020). The generally used method to analyze the spectrum of a multifractal is based on the box‐counting method. In this method, a grid of boxes is overlaid on the image (or distribution of points) in question and the amount of “mass” contained in each box is determined. A probability—as shown in Equation 2—is then calculated for each box of size , where is the mass contained in the ith box and the total mass in the image is calculated from Equation 3:
| (2) |
| (3) |
The partition function denoted by in Equation 4 is the sum of all of the box probabilities at box size raised to a power :
| (4) |
where is a moment order that can range from to and is used to distort the image to determine the generalized dimension of different regions of the image. The partition function is known to follow the relationship in Equation 5:
| (5) |
and from this relationship one can find the function —typically from the slopes of regression lines for versus at each Q value, as shown in Equation 6:
| (6) |
The relationship between and the generalized dimension is shown in Equation 7, which can be used to calculate :
| (7) |
The multifractal spectrum is a monotonically decreasing function which has several useful features. The general shape of the spectrum can be used to determine whether the system in question is nonfractal, monofractal or multifractal. Nonfractal and monofractal systems typically have little variation in as a function of , yielding flatter spectra than multifractal systems which tend to be sigmoidal in shape. The values of at the values are interpreted as the box‐counting dimension, the information dimension and the correlation dimension, respectively. These dimensions also follow the relationship (Rosenberg, 2020).
Another commonly used multifractal spectrum is versus , each of which can be found using equations reported by Chhabra and Jensen (1989):
| (8) |
| (9) |
where is given by:
| (10) |
and can be found using a similar method to that used to find . For each values, the slope of a regression line for the numerators of Equations 8 and 9 versus gives the value of and , respectively.
The multifractal spectra and resulting from our analysis on the 27 × 19 grid of point sources from Section 3 can be seen in Figure 3. In this particular case, the “mass” is taken to be the seismic moment of the point sources. To begin, a square centered at x = 150 km, y = 135 km with a side length of 135 km was defined to contain the point sources. This starting square was then subdivided into boxes—each side length . A set of five side length values were used along with Q values in the range to generate the spectra in Figure 3.
Figure 3.
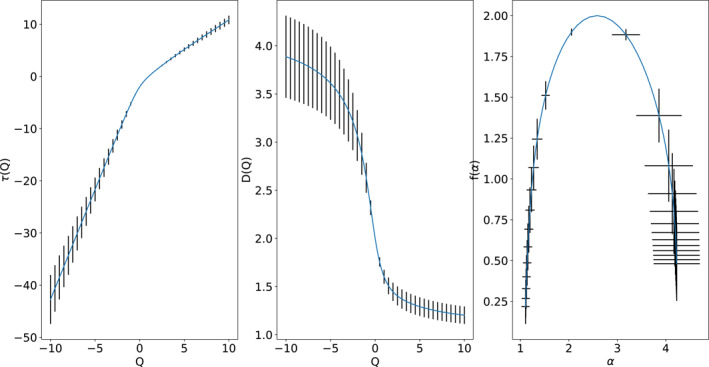
(left) The versus spectrum. (center) The versus spectrum. (right) The versus spectrum.
5. Discussion and Conclusion
When comparing the data to the resulting model in Figure 2, one can see that the basic shape of the data has been captured, but discrepancies exist if individual data points are compared. This is most likely a problem with the spread used when crossing and mutating the fit models. Since the spread of the parameters never changes, there comes a point where the error plateaus—further increases in fit accuracy require a decrease in the spread of the possible parameters. A larger initial spread is useful to widely search the parameter space for the appropriate fit and to prevent falling into a local minimum. However, a large spread also prevents the fit from settling to a more exact solution. Simply reducing the spread leads to an increase in the computation time, as more time will be required for the solutions to search the parameter space in smaller steps. Increasing the population size can help widen the initial search area, but this also increases the computation time. A possible fix for this problem is an adaptive algorithm that modifies the spread during calculation to more efficiently search the parameter space and reduce the spread when close to the optimum solution. One such algorithm is outlined in Deb et al. (2007). For this problem where only the seismic moments change, other methods are likely more efficient due to the equations being only linearly dependent on seismic moment. The genetic algorithm method would be more appropriate for scenarios in which the other parameters change, since the equations have nonlinear dependence on those parameters. Future work will allow various other parameters to change, fully exploring the strengths of the algorithm.
The spectrum shows a clear change in slope around Q = 0, indicating that the system of point sources exhibits multifractal properties (Mach et al., 1995). The spectrum contains the same information. Its sigmoidal shape also indicates that the system exhibits multifractal properties. Values of interest include the box‐counting dimension, the information dimension and the correlation dimension, which have values of 2, 1.602 0.072 and 1.446 0.095, respectively. Finally, the spectrum also reveals the multifractal properties of the system. While a nonfractal or monofractal spectrum would be very localized around a single value, a multifractal spectrum takes the shape of a curve over a wide range of values. This shape is seen in Figure 3c, further cementing the multifractality of the system in question.
The overall advantage of our genetic algorithm method described in this study lies in its ability to invert the parameters of many seismic sources simultaneously. Inversions of fault geometry are typically calculated for rectangular fault planes which may be separated into smaller elements. However, the effectiveness of this approach is limited for scenarios that are not accurately portrayed by planar surfaces. In our analysis, it is possible for the point sources to move independently, so in theory they can model any possible fault shape if an appropriate number of sources are used. The cost of this increased flexibility is an increase in the amount of computational complexity. The deformation caused by each source in a model must be calculated at every desired data point and their individual contributions must be summed to produce the total deformation field. This deformation field must be calculated for every model in the population for every generation that the genetic algorithm runs. For example, if you desire for a population of 500 models containing 15 sources each to run for 10,000 generations, you end up with 75,000,000 function evaluations for each data point you are fitting.
Future work with the algorithm could include a fit that allows more than just the seismic moment to vary. One possibility is a fit that uses a number of point sources with fixed seismic moment but allows their locations to vary. This could be done to see if the algorithm is able to provide new information on the 3D structure of earthquake faults. Another possibility is to perform many fits using a different number of point sources in each model, to shed light on how varying this parameter affects the overall fit. The likely greatest improvement to the algorithm would be the inclusion of data from multiple sources; for example, the joint inversion of GPS and InSAR data or a combination of ascending and descending InSAR images that provide both horizontal and vertical displacements. This would reduce the overall freedom of the solution and provide more reliable results. The results of the multifractal analysis could be expanded as well, particularly to a 3D multifractal analysis. A multi‐layer distribution of sources could be inverted to see how the multifractal properties are affected. To conclude, this study is meant more as a proof‐of‐concept for the method and the algorithm will be expanded in future iterations to include the above‐mentioned improvements.
Conflict of Interest
The authors declare no conflicts of interest relevant to this study.
Acknowledgments
C. Saylor and J. B. Rundle were supported by the National Aeronautics and Space Administration [grant number NNX17AI32G]. Portions of the research study by A. Donnellan were carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. The authors thank colleagues including Donald Turcotte for helpful discussions. The authors would also like to thank the anonymous referees for their comments that have substantially improved the manuscript.
Appendix A. Okada's Equations
A.1.
| (A1) |
for a point source located at (0,0,−d). The above parameters are defined by
For our purposes, the equations were slightly altered from this form to be written in terms of seismic moment, defined in Okada (1985) to be for dip‐slip sources. So in Equation A1, is replaced with .
Appendix B. Residuals Between Data and Models
B.1.
Figure B1.
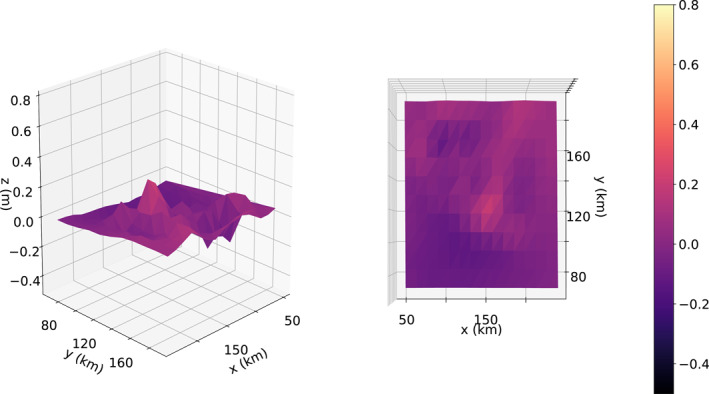
(left) Azimuthal view of the residuals between the ALOS‐2 ground deformation data and the corresponding model. (right) Top view of the residuals between the ALOS‐2 ground deformation data and the corresponding model.
Appendix C. Genetic Algorithm Flowchart
C.1.
Figure C1.
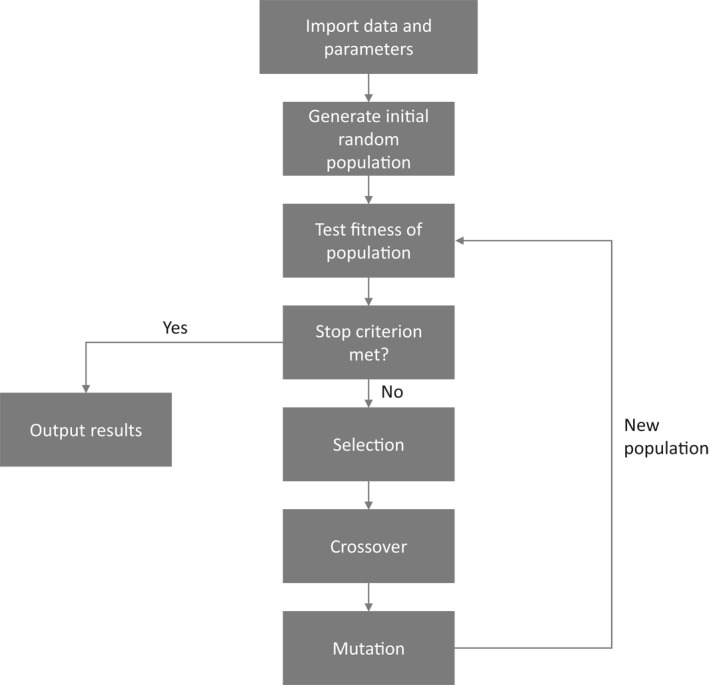
A flowchart detailing the general steps required of each iteration of the genetic algorithm. The selection, crossover and mutation portions of the process are explained in more detail in Section 2.
Saylor, C. , Rundle, J. B. , & Donnellan, A. (2021). Multifractal analysis of a seismic moment distribution obtained from InSAR inversion. Earth and Space Science, 8, e2020EA001433. 10.1029/2020EA001433
Data Availability Statement
The data used in this study were obtained from Lindsey et al. (2015b).
References
- Adolfo, P. , Giménez, D. , Bittelli, M. , Vaz, C. , & Flury, M. (2001). Multifractal characterization of soil particle‐size distributions. Soil Science Society of America Journal, 65, 1361–1367. 10.2136/sssaj2001.6551361x [DOI] [Google Scholar]
- Aggarwal, S. , Pasten, D. , & Khan, P. (2017). Multifractal analysis of 2001 Bhuj earthquake sequence in Gujarat, western India. Physica A: Statistical Mechanics and its Applications, 488, 177–186. 10.1016/j.physa.2017.06.022 [DOI] [Google Scholar]
- Bagnardi, M. , & Hooper, A. (2018). Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochemistry, Geophysics, Geosystems, 19(7), 2194–2211. 10.1029/2018GC007585 [DOI] [Google Scholar]
- Bruhat, L. , Klinger, Y. , Vallage, A. , & Dunham, E. M. (2019). Influence of fault roughness on surface displacement: From numerical simulations to coseismic slip distributions. Geophysical Journal International, 220(3), 1857–1877. 10.1093/gji/ggz545 [DOI] [Google Scholar]
- Bürgmann, R. , Rosen, P. A. , & Fielding, E. J. (2000). Synthetic aperture radar interferometry to measure earth’s surface topography and its deformation. Annual Review of Earth and Planetary Sciences, 28(1), 169–209. 10.1146/annurev.earth.28.1.169 [DOI] [Google Scholar]
- Candela, T. , Renard, F. , Klinger, Y. , Mair, K. , Schmittbuhl, J. , & Brodsky, E. E. (2012). Roughness of fault surfaces over nine decades of length scales. Journal of Geophysical Research, 117(B8). 10.1029/2011JB009041 [DOI] [Google Scholar]
- Chhabra, A. , & Jensen, R. V. (1989). Direct determination of the f(α) singularity spectrum. Physical Review Letters, 62, 1327–1330. 10.1103/PhysRevLett.62.1327 [DOI] [PubMed] [Google Scholar]
- Deb, K. , & Agrawal, R. (1995). Simulated binary crossover for continuous search space. Complex Systems, 9(2), 115–148. [Google Scholar]
- Deb, K. , Sindhya, K. , & Okabe, T. (2007). Self‐adaptive simulated binary crossover for real‐parameter optimization. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation (pp. 1187–1194). 10.1145/1276958.1277190 [DOI] [Google Scholar]
- Ding, X.‐L. , Li, Z.‐W. , Zhu, J.‐J. , Feng, G.‐C. , & Long, J.‐P. (2008). Atmospheric effects on InSAR measurements and their mitigation. Sensors, 8(9), 5426–5448. 10.3390/s8095426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fattahi, H. , & Amelung, F. (2014). InSAR uncertainty due to orbital errors. Geophysical Journal International, 199(1), 549–560. 10.1093/gji/ggu276 [DOI] [Google Scholar]
- Fattahi, H. , & Amelung, F. (2015). InSAR bias and uncertainty due to the systematic and stochastic tropospheric delay. Journal of Geophysical Research: Solid Earth, 120(12), 8758–8773. 10.1002/2015JB012419 [DOI] [Google Scholar]
- Feng, W. , Li, Z. , Elliott, J. R. , Fukushima, Y. , Hoey, T. , Singleton, A. , et al. (2013). The 2011 Mw 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophysical Journal International, 195(1), 650–660. 10.1093/gji/ggt254 [DOI] [Google Scholar]
- Ferretti, A. , Savio, G. , Barzaghi, R. , Borghi, A. , Musazzi, S. , Novali, F. , et al. (2007). Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Transactions on Geoscience and Remote Sensing, 45(5), 1142–1153. 10.1109/TGRS.2007.894440 [DOI] [Google Scholar]
- Frietsch, M. , Ferreira, A. M. G. , Funning, G. J. , & Weston, J. (2019). Multiple fault modelling combining seismic and geodetic data: The importance of simultaneous sub‐event inversions. Geophysical Journal International, 218, 958–976. 10.1093/gji/ggz205 [DOI] [Google Scholar]
- Fukahata, Y. , & Hashimoto, M. (2016). Simultaneous estimation of the dip angles and slip distribution on the faults of the 2016 Kumamoto earthquake through a weak nonlinear inversion of InSAR data. Earth Planets and Space, 68. 10.1186/s40623-016-0580-4 [DOI] [Google Scholar]
- Fukahata, Y. , & Wright, T. J. (2008). A non‐linear geodetic data inversion using ABIC for slip distribution on a fault with an unknown dip angle. Geophysical Journal International, 173, 353–364. 10.1111/j.1365-246X.2007.03713.x [DOI] [Google Scholar]
- Hamling, I. J. , Hreinsdóttir, S. , Clark, K. , Elliott, J. , Liang, C. , Fielding, E. , et al. (2017). Complex multifault rupture during the 2016 mw 7.8 Kaikoura earthquake, New Zealand. Science, 356(6334). 10.1126/science.aam7194 [DOI] [PubMed] [Google Scholar]
- Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and their applications. Biometrika, 57(1), 97–109. 10.1093/biomet/57.1.97 [DOI] [Google Scholar]
- Hauksson, E. , Jones, L. M. , Hutton, K. , & Eberhat‐Phillips, D. (1993). The 1992 landers earthquake sequence; seismological observations. Journal of Geophysical Research, 98(B11). 10.1029/93JB02384 [DOI] [Google Scholar]
- Hicks, E. , Bungum, H. , & Lindholm, C. (2000). Stress inversion of earthquake focal mechanism solutions from onshore and offshore Norway. Norsk Geologisk Tidsskrift, 80, 235–250. 10.1080/00291960051030545 [DOI] [Google Scholar]
- Hui, C. , Cheng, C. , Ning, L. , & Jing, Y. (2020). Multifractal characteristics of seismogenic systems and b values in the Taiwan seismic region. ISPRS International Journal of Geo‐Information, 9, 384. 10.3390/ijgi9060384 [DOI] [Google Scholar]
- Jet Propulsion Laboratory California Institute of Technology (2014). What is UAVSAR?. https://uavsar.jpl.nasa.gov/education/what-is-uavsar.html. (Accessed on 2020‐06‐16). [Google Scholar]
- Jiang, G. , Xu, C. , Wen, Y. , Liu, Y. , Yin, Z. , & Wang, J. (2013). Inversion for coseismic slip distribution of the 2010 Mw 6.9 Yushu Earthquake from InSAR data using angular dislocations. Geophysical Journal International, 194(2), 1011–1022. 10.1093/gji/ggt141 [DOI] [Google Scholar]
- Jiang, Z.‐Q. , Xie, W.‐J. , Zhou, W.‐X. , & Sornette, D. (2019). Multifractal analysis of financial markets: A review. Reports on Progress in Physics, 82(12), 125901. 10.1088/1361-6633/ab42fb [DOI] [PubMed] [Google Scholar]
- Jo, M.‐J. , Jung, H.‐S. , & Yun, S.‐H. (2017). Retrieving precise three‐dimensional deformation on the 2014 M 6.0 south Napa earthquake by joint inversion of multi‐sensor SAR. Scientific Reports, 7. 10.1038/s41598-017-06018-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones, B. , Martínez, V. , Saar, E. , & Einasto, J. (1988). Multifractal description of the large‐scale structure of the universe. The Astrophysical Journal, 332, L1–L5. 10.1086/185254 [DOI] [Google Scholar]
- Kennedy, J. , & Eberhart, R. (1995). Particle swarm optimization. In Proceedings of ICNN’95‐International Conference on Neural Networks (Vol. 4, pp. 1942–1948). [Google Scholar]
- Kumar, M. , Husain, M. , Upreti, N. , & Gupta, D. (2010). Genetic algorithm: Review and application. Journal of Information and Knowledge Management. [Google Scholar]
- Langet, N. , Goertz‐Allmann, B. , Oye, V. , Bauer, R. , Williams‐Stroud, S. , Dichiarante, A. , & Greenberg, S. (2020). Joint focal mechanism inversion using downhole and surface monitoring at the Decatur, Illinois, CO2 injection site. Bulletin of the Seismological Society of America, 110, 2168–2187. 10.1785/0120200075 [DOI] [Google Scholar]
- Lay, T. , Ye, L. , Koper, K. , & Kanamori, H. (2016). Assessment of teleseismically‐determined source parameters for the April 25, 2015 mw 7.9 Gorkha, Nepal earthquake and the May 12, 2015 mw 7.2 aftershock. Tectonophysics, 05, 714–715. 10.1016/j.tecto.2016.05.023 [DOI] [Google Scholar]
- Li, Z. , Wen, Y. , Zhang, P. , Liu, Y. , & Zhang, Y. (2020). Joint inversion of GPS, leveling, and InSAR data for the 2013 Lushan (China) earthquake and its seismic hazard implications. Remote Sensing, 12(4), 715. 10.3390/rs12040715 [DOI] [Google Scholar]
- Lindsey, E. O. , Natsuaki, R. , Xu, X. , Shimada, M. , Hashimoto, M. , Melgar, D. , & Sandwell, D. T. (2015a). Line‐of‐sight displacement from ALOS‐2 interferometry: Mw 7.8 Gorkha earthquake and mw 7.3 aftershock. Geophysical Research Letters, 42(16), 6655–6661. 10.1002/2015GL065385 [DOI] [Google Scholar]
- Lindsey, E. O. , Natsuaki, R. , Xu, X. , Shimada, M. , Hashimoto, M. , Melgar, D. , & Sandwell, D. T. (2015b). Nepal earthquake ALOS‐2 InSAR. https://topex.ucsd.edu/nepal/. (Accessed on 2020‐06‐09). [Google Scholar]
- Liu, X. , & Xu, W. (2019). Logarithmic model joint inversion method for coseismic and postseismic slip: Application to the 2017 mw 7.3 Sarpol Zaha¯b earthquake, Iran. Journal of Geophysical Research: Solid Earth, 124(11), 12034–12052. 10.1029/2019JB017953 [DOI] [Google Scholar]
- Mach, J. , Mas, F. , & Sagues, F. (1995). Two representations in multifractal analysis. Journal of Physics A: Mathematical and General, 28(19), 5607–5622. 10.1088/0305-4470/28/19/015 [DOI] [Google Scholar]
- Okada, Y. (1985). Surface deformation due to shear and tensile faults in a half‐space. Bulletin of the Seismological Society of America, 75(4), 1135–1154. 10.1785/bssa0750041135 [DOI] [Google Scholar]
- Peng, M. , Zhao, C. , Zhang, Q. , Zhang, J. , & Liu, Y. (2018). Ground subsidence monitoring with mt‐InSAR and mechanism inversion over Xi'an, China. ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XLII‐3, 1375–1380. 10.5194/isprs-archives-XLII-3-1375-2018 [DOI] [Google Scholar]
- Rosenberg, E. (2020). Fractal dimensions of networks. Springer Nature Switzerland AG. [Google Scholar]
- Sahimi, M. , Robertson, M. C. , & Sammis, C. G. (1993). Fractal distribution of earthquake hypocenters and its relation to fault patterns and percolation. Physical Review Letters, 70, 2186–2189. 10.1103/PhysRevLett.70.2186 [DOI] [PubMed] [Google Scholar]
- Sokos, E. N. , & Zahradnik, J. (2008). Isola a Fortran code and a Matlab GUI to perform multiple‐point source inversion of seismic data. Computers & Geosciences, 34(8), 967–977. 10.1016/j.cageo.2007.07.005 [DOI] [Google Scholar]
- Tanaka, A. (2014). Coupled stick‐slip simulation and multifractal analysis for earthquakes. Journal of Advanced Simulation in Science and Engineering, 1, 51–64. 10.15748/jasse.1.51 [DOI] [Google Scholar]
- United States Geological Survey (2015). M 7.8—26 km E of Khudi, Nepal. https://earthquake.usgs.gov/earthquakes/eventpage/us20002926/executive#general_summary. (Accessed on 2020‐06‐10). [Google Scholar]
- Villegas, R. J. , Zahradník, J. , Nacif, S. , Spagnotto, S. , Winocur, D. , & Leiva, M. F. (2016). Waveform inversion and focal mechanisms of two weak earthquakes in cordillera principal (Argentina) between 35 and 35.5 s. Journal of South American Earth Sciences, 71, 359–369. 10.1016/j.jsames.2015.12.001 [DOI] [Google Scholar]
- Wen, Y. , Xu, C. , Liu, Y. , & Jiang, G. (2016). Deformation and source parameters of the 2015 mw 6.5 earthquake in Pishan, western china, from sentinel‐1a and ALOS‐2 data. Remote Sensing, 8(2), 134. 10.3390/rs8020134 [DOI] [Google Scholar]
- Zhang, L. , Wu, J. C. , Ge, L. L. , Ding, X. L. , & Chen, Y. L. (2008). Determining fault slip distribution of the Chi‐Chi Taiwan earthquake with GPS and InSAR data using triangular dislocation elements. Journal of Geodynamics, 45(4–5), 163–168. 10.1016/j.jog.2007.10.003 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used in this study were obtained from Lindsey et al. (2015b).


