A multiscale analysis of early flower development in Arabidopsis provides an integrated view of molecular regulation and growth control

Abstract

We have analyzed the link between gene regulation and growth during the early stages of flower development in Arabidopsis. Starting from time-lapse images, we generated a 4-D atlas of early flower development including cell lineage, cellular growth rates and the expression patterns of regulatory genes. This information was introduced in MorphoNet, a web-based platform.

Using computational models, we found that the literature based molecular network only explained a minority of the gene expression patterns. This was substantially improved by adding regulatory hypotheses for individual genes. Correlating growth with the combinatorial expression of multiple regulators led to a set of hypotheses for the action of individual genes in morphogenesis. This identified the central factor LEAFY as a potential regulator of heterogeneous growth, which was supported by quantifying growth patterns in a leafy mutant. By providing an integrated view, this atlas should represent a fundamental step towards mechanistic models of flower development.

Introduction

The loss of function of many regulatory genes causes important perturbations in the growth patterns of multicellular organisms, which means that they directly or indirectly affect local growth parameters via the expression of other genes or physical cell properties. The regulatory networks and their dynamics have been extensively studied in a range of model species (e.g. Briggs et al., 2018; Chen et al., 2018; Wagner et al., 2018). This has been an active field of research, in particular with the advent of single cell sequencing methods, which can now be combined with molecular cell lineage tracking approaches (e.g. Cotterell et al., 2020; Frieda et al., 2017). However, there is often only a partial view of how growth is coordinated and as a result gene function is usually expressed in general terms such as organ identity or polarity, referring to their main mutant phenotype in a relatively abstract and qualitative manner. In addition, there are still many open questions regarding the regulatory network structures, and it is often impossible to test their coherence. An important first step towards addressing these problems is to integrate the existing information on gene expression, and to quantitatively correlate regulatory inputs, for example in the form of gene expression patterns, with the final output, i.e. shape changes during development (Coen et al., 2004; Whitewoods and Coen, 2017). This should then provide a solid basis for more mechanistic studies, involving also the regulation of biochemical interactions and biophysical aspects (Abad et al., 2017; Diaz de la Loza and Thompson, 2017; Pasakarnis et al., 2016; Thompson, 1917; Zhu and Roeder, 2020).

We address this question in the floral meristem (FM) of the model plant Arabidopsis, which generates four whorls of floral organs and is one of the best-characterized morphogenetic systems available (Blázquez et al., 2006; Bowman et al., 2012; Chen et al., 2018). The function of a range of key genes together with their domains of expression has mainly been studied on a one-by-one basis and their individual function, spatial expression and dynamics have been characterized (Fig. 1, supplemental table 1). Like the vegetative and inflorescence meristems, the floral meristem contains a population of stem cells, which are kept in an undifferentiated state by regulatory genes like SHOOTMERISTEMLESS (STM), WUSCHEL (WUS) and CLAVATA (CLV) 1-3 (Long and Barton, 2000; Lenhard and Laux, 2003; Mayer et al., 1998). Other genes, like AINTEGUMENTA and MONOPTEROS, have been more specifically associated with organ outgrowth (Krizek, 2009; Nole-Wilson and Krizek, 2006; Yamaguchi et al., 2013). During flower formation, yet another set of regulators, including PHAVOLUTA, PHABULOSA, ASYMMETRIC LEAVES1 and 2, FILAMENTOUS FLOWER and ETTIN, determines the abaxial/adaxial (dorso-ventral) polarity of the organs, i.e. the identity of the cells next to and further away from the shoot meristem (Emery et al., 2003; Iwakawa et al., 2007; Machida et al., 2015; Sawa et al., 1999a; McConnell et al., 2001; Sawa et al., 1999b; Sessions et al., 1997). The floral organs are separated by boundary domains characterized by the expression of notably the CUP SHAPED COTYLEDON (CUC) 1-3 genes (Aida et al., 1997; Hibara et al., 2006)). The spatial and temporal regulation also involves several hormones, including cytokinin and auxin (Besnard et al., 2014a; Reinhardt et al., 2003)). Cytokinin has been mainly associated with meristematic activity, whereas auxin is required for organ positioning and outgrowth. While the previous regulators can also be found in vegetative meristems, a major subnetwork, including the transcription factors LEAFY (LFY), APETALA (AP) 1-3, PISTILLATA (PI), AGAMOUS (AG) and SEPALLATA (SEP) 1-4, is involved in defining the type of organs to be produced (Blázquez et al., 2006; Krizek and Fletcher, 2005; Goto and Meyerowitz, 1994; Kaufmann et al., 2009; Ó’Maoiléidigh et al., 2014; Parcy et al., 1998; Pelaz et al., 2000; Wuest et al., 2012; Thomson and Wellmer, 2019).

Figure 1. Gene regulatory network proposed for flower patterning and morphogenesis.

Red and blue connections represent negative and positive regulations respectively. Color code indicates function in floral meristem development, floral organ identity (sepals, petals, stamens and carpels) and abaxial/adaxial organ polarity as described in the literature. The regulators in light blue characters are not recorded in the current version of the Atlas because there is not sufficient information on their expression patterns. For justification of interactions see table S1.

The general architecture of this network and parts thereof have been studied and models for molecular regulation have been proposed (e.g.: Sánchez-Corrales et al., 2010; La Rota et al., 2011; Chen et al., 2018). However, in spite of this extensive body of knowledge, our understanding of how the network orchestrates flower morphogenesis remains fragmentary. The coherence of the existing data needs to be tested, while a more integrated, multiscale view at the level of the whole system is missing. This not only implies a need for a better knowledge of how the network is behaving in time and space at cellular resolution. In addition, the network dynamics need to be correlated with growth patterns.

We used high-resolution time-lapse images to generate a comprehensive 4-D atlas of early flower development, including the expression patterns of 28 regulatory genes. This integrated view allowed us to test the coherence of the published data on molecular regulation. A quantitative correlation analysis between gene expression patterns and growth patterns then led us to propose a set of hypotheses for the combinatorial action of regulatory genes in patterning and morphogenesis. Hypotheses concerning the central regulator LEAFY were tested experimentally, which supported a role in growth control both during sepal initiation and organ boundary formation.

The results were made available in the form of an interactive web-based atlas using a dedicated online tool called ‘Morphonet’ (http://morphonet.org. Leggio et al., 2019) that can be accessed and further developed by the entire scientific community.

Results

High-resolution live imaging of flower development reveals consistency in shape and size

We used confocal microscopy to live image flower primordia from initiation to stage 4 when the sepals start to overlie the flower meristem and all four whorls have been specified (Smyth et al., 1990). This was done using a yellow fluorescent protein (YFP) targeted to the plasma membrane or using the membrane specific dye FM 4-64 (see Methods, (Fernandez et al., 2010; Willis et al., 2016)).

The development of six meristems (FM1-6) was recorded in a total of 50 3-D image-stacks, followed by cell segmentation and lineage tracking (Methods, Fig 2A, Fig S1). In flower meristems, cell division patterns are not fixed, in contrast to e.g., roots or hypocotyls (Montenegro-Johnson et al., 2015). It is, therefore, not straightforward to compute an average time course, including cell lineage information which is essential to study the correlation between cellular dynamics and gene expression. For this reason, we aimed to select a representative series for further analysis. To this end, we compared the shape of all 6 meristems during development. There is no obvious way to synchronise flower development and the geometrical shape of individual time points of one series does not exactly correspond to the time points of other series. To circumvent these problems, we applied a registration method to align and compare different acquisition sets using the surface of flower primordia, represented by a point cloud, as the overall shape measure (Methods, (Michelin et al., 2016) The quantitative assessment of the variability in shape and size of the flower primordia captured in sequences FM1-4 and FM6 illustrated that they go through similar developmental stages with consistent shapes and sizes (Fig. S3), while it was not possible to compare the shape of FM5 reliably with that of the other meristems (not shown). This motivated the choice of FM1, which had the highest temporal resolution and spanned floral development from initiation to stage 4, as a representative reference. To facilitate further analysis, this time series was added to the web-based browser MorphoNet (http://morphonet.org/, Methods, (Leggio et al., 2019)).

Figure 2. Cell lineage and gene expression patterns in reference series.

8 out of 18 timepoints of FM1 are shown. Times after first acquisition are indicated between brackets.

(A) Surface rendering of segmented images of time course 1 showing L1 layer cells.

(B) Rendering of gene expression patterns in the L1 layer of the initium, stage 1, stage 2, stage 3, and stage 4 time points. Each of the patterns are colored by a unique color and their corresponding codes are also given. Grey cells have not been annotated (no expression). Scale bars in A 20 μm

An integrated view of gene expression patterns provides a high-resolution spatiotemporal differentiation map of flower development

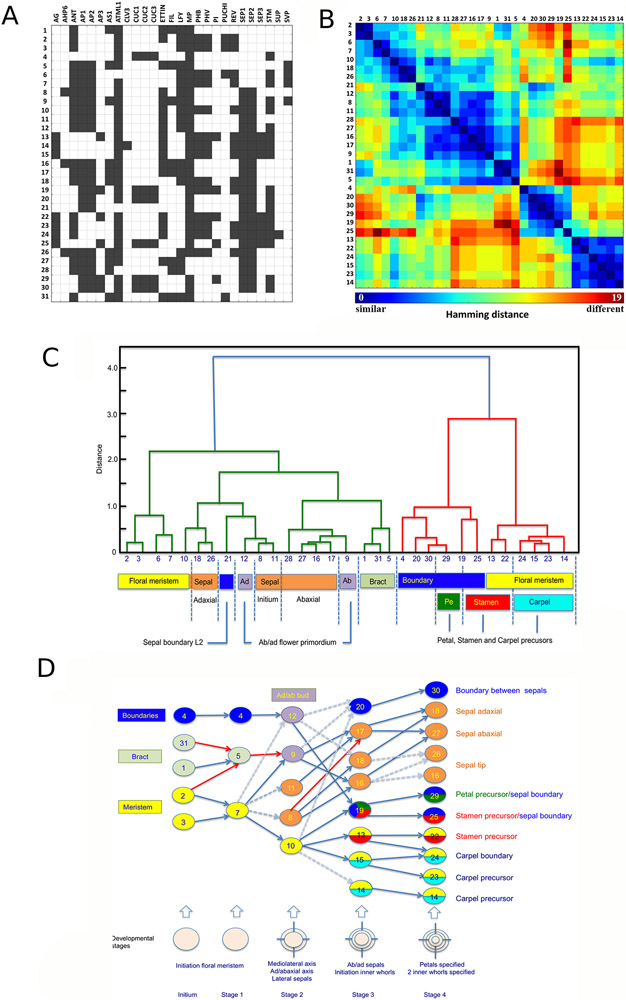
We next included the expression patterns of 28 important genes involved in floral meristem function, organ identity, organ outgrowth and organ polarity in the 4-D template (Fig. 1). For 21 genes, the often partial published information was complemented by our own results coming from RNA in situ hybridization or confocal live-imaging (Methods, for original data: https://doi.org/10.17863/CAM.61991 ). The collected patterns were integrated into the FM1 time course by manually annotating individual cells using the tools available via MorphoNet (Fig 2B, Methods, for justification of individual genes expression patterns see: https://doi.org/10.17863/CAM.61991). For this purpose, 5 distinct stages of development were chosen (as defined by (Smyth et al., 1990)): the initium stage (called here stage 0) and stage 1 to stage 4 (Fig 2B). We chose to perform a binary labelling, i.e., to indicate only the presence or absence of gene expression, given the predominant qualitative nature of the available expression data. The single gene expression patterns (‘gene patterns’) were then combined. We could thus identify cell groups that expressed unique gene combinations and corresponded to specific differentiation states, termed ‘cell states’. 28 cell states were present in both L1 and L2 (not taking into account the L1 marker ATML1) while states 6, 21 and 28 were L2-specific (Fig. 2B, 3A). We next conducted an exploratory data analysis using unsupervised hierarchical clustering, (Methods), to generate a cell state similarity map using Hamming distances, i.e., the number of gene expressions which differ between cell states, as the measure of similarity (Fig. 3B, C). The dendrogram revealed clusters of states, which formed different functional groups of cells through flower development (Fig. 3C, Supplemental Table 2). These included, for example, meristematic cells, boundary cells, as well as cells expressing genes defining polarity or organ primordia. Similarities in expression between alternative cell fates were identified at high resolution, e.g., connecting the boundary domain with the expression domains where petals and anthers are initiated (Fig 3C: boundary cluster, containing states 4, 20, 30, 19, 25 and 29). To investigate the temporal evolution or cell-differentiation paths of the cell states in the outer cell layer, we used the computed cell lineages and built a weighted directed cell state ‘transition graph’ where the nodes are the cell states (Fig. 3D, Methods). The graph reveals a core of ‘stem cells’ at the adaxial domain of the bud at stage 1 (State 7), providing all cell types of the flower at stage 4. This is similar to typical tree-like differentiation paths often described for mammalian development (Enver et al., 2009). Similarly, at stage 2, State 7 has split up in sepal ‘precursors’ and the central meristematic domain (State 10), which will give rise to all other states. However, the plasticity of plant cells is clearly represented where several cell types contribute to future stages. For example, sepal tip cells come from all cell states present at stages 0 and 1. Descendants of both bract (State 5) and SAM boundary cells (State 4) contribute to the same cell state at later stages, although being quite different in terms of their original expression patterns. It is important to note that both examples seem to reflect slightly fluctuating boundaries between the different domains causing cells to switch fate, showing that cell lineage alone cannot account for the observed patterns.

Figure 3. Identification and analysis of cell states.

(A) Matrix representing 32 combinatorial, binary expression patterns (referred to as ‘cell states’) of 28 genes. WUS, which is only expressed in internal tissues, is not represented. Each row corresponds to a particular state (state numbers are given on the left) and contains black (gene active) and white (gene inactive) squares. Names of the genes are given on top of each column. All states can also be found in the L2 (by excluding ATML1 expression). Note that the states 6, 21 and 28 are L2-specific.

(B) Hierarchical clustering of cell states using Hamming distances as the measure of similarity. The heat map (similarity matrix) corresponds to the Hamming distances and the columns and rows are the patterns.

(C) Individual clusters or combinations of clusters correspond to specific differentiation domains (organ identity for example) in the growing flower (color coded). Alternatively, the clusters can be assigned to more general ‘functional’ domains not specific for the flower (meristem, boundary domains).

(D) Temporal evolution of clusters and cell states. Color codes as in (C). Cell states with several colors have several identities. The graph combines ‘forward’ and ‘backward’ links. Forward links connect specific states at one time point to their descendant patterns in the next time with weights corresponding to the fractions of the daughter cells in each of the descendant patterns. Similarly, ‘backward’ links identify states at a previous time point from a current one. Arcs with blue arrows indicate the presence of corresponding arcs both in forward and reverse pattern transition graphs, dashed arrows indicate the presence of corresponding arcs in reverse pattern transition graph only, red arrows indicate the presence of corresponding arc forward patterns transition graph only (see also supplementary figures). The links whose weights were below a threshold of 20% were pruned.

Adding single regulatory hypotheses for individual genes substantially improves gene pattern predictions

We next examined alternative hypotheses to quantitatively explain these gene expression patterns (Fig. 4). We first analyzed the possibility of the patterns being driven mainly by the lineage, i.e. whether the gene expression at an earlier time point can be used to predict the expression at a later time point. This led to relatively good predictions at early and late stages but was less successful for transitions between intermediate stages (Fig. 4B-C), as measured by a Balanced Accuracy score (BAcc), combining the normalised false positive and false negative rates (Methods). This indicates that most regulatory interactions have an effect during the end of stage 2 and stage 3. For example, for over 75% of the genes we found a BAcc score larger than 0.75 (closer to a perfect pattern than to a random pattern) when following lineages from stage 0 to 1 or from 3 to 4, while this was only true for less than 20% of the genes when cells were followed from stage 2 to 3 (Fig. 4B-C). The result was highly variable between genes and also between individual time points for single genes (Fig. 4B).

Figure 4: Expected patterns vs predicted patterns from various models.

(A) Example of gene expression patterns at stage 4 (132h). Data from the template (top row) is compared with predicted patterns coming from: Following cell lineages from stage 3 (second row), Boolean regulatory model from literature network (Fig. 1, third row), and Boolean regulatory model where an additional regulatory arrow has been added as hypothesis (Table S4, fourth row). Numbers above the illustrations indicate the BAcc score. Below the illustrations either the selected combination of inputs (in the case of the literature based Boolean model) or the selected best hypothesis (in the case of the augmented literature Boolean model) is shown.

(B) BAcc score for all genes using the methods of lineage, literature network with randomised input (see Methods), literature network regulatory model (Fig. 1), and model with added hypotheses. Result of best hypothesis given for each Stage of flower development

(C) Average (and standard deviation) of BAcc score over all time points and genes for the same conditions as described in (B).

(D) Gene by gene comparison of BAcc scores between literature network (ref) and lineage (lin) at stage 4.

(E) Gene by gene comparison of BAcc scores between literature derived network (Fig 1) and after adding regulatory hypothesis (hyp) at stage 4.

We next tested whether the literature-derived network (Fig. 1) could account for the expression patterns of single genes. To do this, we modelled the gene regulatory network using a set of boolean rules combining activating and repressing inputs suggested by the literature and combined them in all possible ways using logical ‘AND’ and ‘OR’ rules (Methods). This produced a ranked list of alternative logical combinations for each gene regulation and the combination(s) with the best similarity with the gene expression pattern at hand were selected (Methods, Supplemental Table S3). For comparison, we also used the input regulatory arrows from the literature network but selected random genes as inputs (Fig. 4B-C, Methods). The literature-based regulatory network improved the ability to explain a number of gene expression patterns, in particular during the last two stages (BAcc increase of 0.22 on average for stage 3 and 4) compared to the randomized networks (Fig. 4B-C). Several genes, such as LFY and AG at all time points, AS1 at stages 1, 3-4, and FIL at stage 3 all map perfectly or almost perfectly on the expression patterns extracted from the literature, indicating that the regulation presented in the literature matches the patterns well for a subset of genes at certain time points (Fig. 4A-B). However, this is only true for a minority of genes in the network. While the literature network was, in average, always performing better than the randomized networks, it was only significant at the later stages 3 and 4 (p-values of 0.09, 0.19, 0.23 for stages 0, 1, 2, respectively compared to 0.04 and 0.008 at stages 3 and 4, respectively).

When comparing the literature-based regulatory predictions with lineage predictions, the literature-based regulation did not lead to significant improvements on average at any time point, and lineage even performed better at stage 4 (Fig. 4D, p-values 0.11, 0.44, 0.46, 0.02 at stages 1, 2, 3, 4, respectively). At stage 4 for example, the literature-based network only improved the predictions for a small number of genes such as LFY, AG, and SUP, while the patterns of ANT, the CUC genes, and SEP3 were better explained by lineage (Fig. 4A-D).

For a large subset of the genes the expression could not be reproduced using the regulatory interactions provided in the literature nor using lineages, indicating that the regulatory network is not complete. We therefore investigated how the addition or removal of single regulatory inputs changed the ability to predict the spatial pattern of each individual gene. This approach identifies the most plausible extra inputs required to generate the pattern. After testing all additional genes as activators or repressors and all possible logical combinations with the literature-suggested regulation, we identified the regulations leading to the best BAcc score for each gene (Methods, Table S4). This increased the predictability of the gene patterns significantly as compared to using the literature-proposed regulation (p-values 0.012, 0.003, 0.004, <10⁻³, <10⁻³ for timepoints at stages 0, 1, 2, 3 and 4 respectively; Fig. 4A-C, E), and improved the pattern for all but two genes (Fig. 4E).

In summary, our results show that the gene regulatory network provided by the scientific community only significantly improved the predictability of gene expression patterns compared to random interactions at late time points. Compared to cell lineage, the published network improved predictability for a small subset of the genes at specific stages of development only. Significant improvements in predictability were achieved for gene patterns by adding novel single interactions. When combined, the added hypotheses represent a plausible coherent mechanistic description of a gene regulatory network that can explain the gene patterns for early flower development.

Analyzing growth patterns reveals a transition to heterogeneous growth at stage 2.

We next investigated the control of growth during development. We therefore first computed the cellular properties. The distribution of cell sizes in this meristem was comparable to what was published in previous studies on Arabidopsis meristems (Fernandez et al., 2010; Gibson et al., 2006, 2011; Jackson et al., 2019; Willis et al., 2016) (not shown, but see http://morphonet.org/ for precise values) and the number of cell neighbors within the L1 (epidermal) and L2 (subepidermal) layers was in line with previous studies on plants and animals, (Lewis, 1926; Gibson et al., 2006, 2011; Jackson et al., 2019; Willis et al., 2016) (Not shown).

Using cell lineage information, we computed growth rates and growth anisotropy at cellular resolution (Fig. 5A, Fig S3A, Methods). Since absolute expansion rates can fluctuate considerably between individual flowers and throughout development (Figs. S1), we focused on relative growth rates and directions between consecutive time points. Relative differences in growth rate were particularly striking at stage 3 and 4, when the sepals start to grow out (Fig. 5A). The analysis of growth directions showed that cells start to grow anisotropically when the sepals are initiated. This was particularly evident on the abaxial side at stage 4, when these organs begin to cover the flower meristem (Fig S3).

Figure 5. Growth rate patterns identify a transition to heterogeneous growth at stage 2.

(A) Relative volumetric growth rates per hour of L1 cells, indicating how much the cells have grown. Color scale bar from nongrowing (black) to more rapidly growing cells (yellow/white) in relative growth rate per hour (h). L1 cells with positive, relative growth rates are displayed. Light grey cells are not taken into account.

(B) Distribution of growth rates (h⁻¹ vs number of cells) between different time points. Note that the number of cells followed between timepoints can differ, depending on the available, tracked lineage.

(C) and (D). Relative volumetric growth rates per hour of L1 cells between initium stage and stage 4 (C) and stage 2 and 4 (D). Color code on initium and stage 2 indicates how much the cells will grow. Color code on stage 4 how much the cells have grown. At 96h the cell lineage and increased growth rates of the sepals are already largely fixed. Two cells have not grown between stage 2 and 4, so their contribution must have been taken over by neighboring cells.

(E) Growth rates of combinatorial patterns or cell states, numbered as in Fig 2. Note that the growth rates were calculated from one point to the next point (forward), only the values of the last time point are calculated backwards (marked with *).

(F) Growth on the pattern transition graph calculated as the average of the backward and forward rates, except initium stage, only forward and stage 4 only backward (arrows colored as in Fig. 3).

(G) Current and future growth rates of different domains at stage 2 of flower development. Current growth rates are relatively homogeneous in state 10 (orange zone) vs the other states (8, 9, 11, 12, blue zone). However, the states in the blue zone will grow much more quickly afterwards, resulting in the outgrowth of the sepals.

Note: growth rates are taking into account both forward and backward rates (i.e. how much the cells have grown and how much they will grow). This is not the case for the first and last point, where resp only forward and backward growth is presented.

To know when this switch to heterogeneous growth can be first identified, we investigated growth over longer time scales. Considering the growth of cells from early stages (stages 0 and 1) onwards, no obvious spatial pattern of heterogeneity in the contribution to the final flower was found (Fig. 5B-C, Fig S4A).

This shows that at these early stages, the cells will produce a population of descendants of similar size at stage 4 or at least with no clear spatial correlation (Fig. 5C). However, at stage 2, although the flower bud is still close to a symmetric hemisphere (Figs. 2-3), cells have been committed to become fast or slow-growing at later stages (Fig. 5B, D), even if the growth rate at this time is quite homogeneous (Fig. 5A). The same observation was made for two other meristems with longer time series, FM2 and FM6 (Fig. S4 B,C).

We next examined the switch to heterogeneous growth using the state transition tree. The switch correlates with the division of the state transition tree at stage 2, where the central state 10 is defining the central parts of the flower and are highly disconnected from the sepal differentiation lineages (Fig. 3). To quantitatively compare the growth rates of different cell populations we introduced a ‘relative growth difference’ (RGD) defined as (g₁−g₂)/(g₁+g₂), where g₁ and g₂ are the median growth rates within the two populations (Methods).

At stage 2 cell states 8, 9, 11 and 12 grow at approximately the same rates as the neighboring domain (cell state 10) (RGD <0.13, p-values > 0.753, Fig. 5E and G). Still, when comparing the growth up until stage 4, the descendants of these four cell states grow much faster (RGD>0.19, p-value <0.001) and hence identify growth precursor states (Fig 5E-G). In particular, cell states 26 and 27 (RGD > 0.22, p-values <0.001 when compared with all other states) and their precursor states 16 and 17 (RGD > 0.1, p-values<0.003 when compared to states except 26 and 27) are fast-growing, identifying the central and abaxial side of the sepal (Figs. 3A and 5). By contrast, cell state 10 has descendant states that are all relatively slow-growing.

In conclusion, we identified a transition from a patterning phase with homogeneous growth at stage 2 to a growth phase, where in particular the sepal lineages increase their growth rates and anisotropy.

Exploring the genetic control of growth patterns

Whereas growth regulation is captured when using the cell state information, it is not trivial to determine the precise genes or gene combinations that provide the regulatory motif. Although all of the genes considered here are involved in growth regulation at some level, it is unknown where, when and to what extent they regulate growth rates and directions. To obtain further information on their roles, we next correlated the growth patterns with gene expression. A limited number of individual genes can be consistently connected to low or high relative growth rates (Fig. 6A). The gene expressed in cells with the highest median growth rate is AHP6 (RGD >0.07 and p-value < 0.001 when compared with all other genes). This gene has been linked to organ initiation (Besnard et al., 2014b), and is never connected to slowly growing cells. Conversely, CUC1-3 expressing cells are correlated with slow growth (RGD < 0.4, p-value < 0.003). By contrast, most expression domains show very broad distributions of growth rates indicating no instructive information and several genes have a double-peak distribution. Since the analysis of individual gene expression domains did not reveal any strong correlation, we therefore investigated growth correlations starting from pairwise comparisons of genes that had partial overlapping expression patterns (Fig. 6B, C). For a pair of genes, A and B, the idea was to see if the cells in the states expressing gene A were growing more slowly or more rapidly in the sub-set of states where they were co-expressed with gene B. This would identify gene B as having potentially a growth-promoting or inhibiting activity within the states where A is expressed. At floral stage 4, for example, STM identifies the slow-growing states 14, 22-24 within the ETTIN domain from the fast-growing states 16 and 27 (RGD = 0.36, Fig. 6B). Similarly, LFY identifies fast growing states within the AP1 domain (RGD = 0.36, Fig. 6B). This analysis was carried out for every gene combination and for every time point, which relates each individual gene expression pattern to all cell states where it has a differential expression (Fig. 6C, Figs. S5-6). The genes fell into three broad classes: those that were potentially growth-stimulating, those that were potentially growth-inhibiting and a set that apparently had mixed effects (Fig. 6C). This confirmed AHP6 and CUC1-3 as potentially growth-promoting and inhibiting, respectively (cf. Fig. 6A). In addition, genes with very wide growth rate distributions, such as ANT and LFY came up as potential growth-promoting regulators (Fig. 6C).

Figure 6. Correlating growth rates with gene function.

(A) Relative growth rates per hour in expression domains of individual genes.

(B) and (C): Correlating growth with gene function. The growth of cells expressing gene A and B is compared with the growth of those only expressing A. Two examples are given in (B) Within the ETTIN (gene A) expressing domain, the cells expressing STM (gene B) as well are growing more slowly; within the AP1 domain, the LFY cells are growing more quickly. (C). The results for all gene combinations. Values correspond to the RGD calculated using the median values of the growth distributions. Certain genes are mostly expressed in the more rapidly growing subdomains (e.g. LFY, AHP6, ANT) , others mostly in the slowly growing subdomains (e.g. SEP3, AG, CUC1-3). The darker blue the spots correspond to later time points.

In summary, apart from AHP6 and CUC1-3, individual genes could not consistently be connected to relative growth rates and do not seem to act as dominant growth regulators by themselves. However, correlating the pairwise expression patterns of all 28 genes with growth patterns, we were able to propose growth promoting and/or inhibiting activities for a majority of them. Given that we also identify the combination of genes active in these regions (Figs. S5-6), gene motifs for growth regulation are identified that can be included in mechanistic models.

With regard to the control of growth directions, the correlations with the individual gene expression patterns were not particularly informative. CLV3, PUCHI, SUP, SEP3 and SVP which showed low degrees of anisotropic growth (Fig. S3), but many other genes were expressed in domains with relatively wide distributions. Like for growth rates, the cell states defined much more distinct behaviors. The cell states of the forming sepal are growing most anisotropically as identified in the transition graph (Figs. S3D), where the abaxial cells of the developing sepal (cell state 27) were also growing slightly more anisotropically than the adaxial side (cell state 16). This puts the polarity genes, in particular FIL, forward as potential regulators of anisotropic growth. Early time points have relatively low anisotropies, and there is a transition at stage 2, where the whole lineage coming from cell state 10 has relatively more isotropic growth compared to the sepal structures (Fig. S3D).

Quantitative growth analysis confirms a role of LFY in the coordination of growth between specific domains.

Cells expressing LFY had one of the broadest growth distributions among all genes (Fig. 7A). Still, the more detailed analysis of the growth patterns described above, pointed at a prominent role in stimulating growth during early flower development. Whereas it is well known that LFY is required for the specification of floral organ identity, its precise role in organ outgrowth remains to be established and mainly a general role in auxin signalling and patterning has been proposed (Li et al., 2013; Parcy et al., 1998; Yamaguchi et al., 2014). To test whether LFY has a role in growth during early flower development, we live-imaged a number of flowers of the strong lfy-12 loss of function line (Fig 7A, Maizel and Weigel, 2004, original data available on: https://doi.org/10.17863/CAM.61991) during the formation of the four sepal-like organs, i.e. comparable to the stage 2 to 4 transitions in the wild type. In all three acquisitions, the organs in the medio-lateral position grew out first, while the adaxial and abaxial primordia followed later and the boundary regions between sepals were less pronounced. The last sepal-like organ to grow out was slightly misplaced in one of the series, suggesting the beginning of a spiralled phyllotaxis. To analyse how these morphological phenotypes relate to growth in cells where LFY is normally expressed, the relative growth rates in the different domains where LFY was identified as a potential growth promoter were subsequently compared in one of the time-series for stage 3 and 4 (Fig 7B, C; cf. Fig. 6). In the mutant, these were defined based on morphology (e.g., negative curvature for the boundary) and lineage. The differences in growth rates between these zones were reduced in the mutant compared to wild type at the equivalent of stage 4 (Fig 7B, C) supporting that LFY is positively contributing to local growth in early flower development. This was true for all zones identified (Fig 7C), and the cells in regions normally expressing LFY had consistently a higher reduction in growth rate compared to the regions where LFY is not expressed in wild type (Fig 7D). This was partially due to the delay in outgrowth of sepal-like organs in the adaxial and abaxial positions in lfy. Whereas the difference between the boundary zone and sepals was most clearly reduced (30% reduction in median RGD), the difference between the meristem center and the sepals was less affected (14% reduction in median RGD).

Fig 7. Comparison growth patterns in wildtype (wt) and lfy mutant (lfy).

(A) part of the time series of the lfy-12 mutant, equivalent to stage 2, 3 and 4 in WT. (B) Comparisons of growth rates between different equivalent regions in WT and lfy mutant at stage 4 (cf Fig 6). Blue and red histograms correspond to red and blue zones indicated in images. Combinations of regions are numbered 1-6.

(C) Plot integrating relative growth differences RGD: (median blue graph - median red graph)/(median blue graph + median red graph) in WT and lfy mutant combinations 1-6 at stage 4. The relative difference is consistently higher in WT indicating more heterogeneous growth.

(D) Plot showing medians lfy/ wt (blue median/blue median, red median/red median). In lfy, the medians of the blue and red histograms are systematically closer to each other than in wild type, hence the growth differential is reduced. Scale bars in A: 20 μm.

Discussion

We present here a detailed descriptive and quantitative model of early flower development. Integrating information at multiple scales, we have established a number of correlations which led us to propose an important set of testable hypotheses regarding the molecular regulatory network and its link to growth control. These hypotheses could not have been generated easily using other approaches.

Molecular network dynamics

Based on an extensive analysis of the expression patterns of 28 genes, we propose the existence of at least 31 cell states in the L1 and L2 layers, which mounts up to 60 by taking into account ATML1, expressed in the epidermal layer.

Even considering a simple, binary on/off regulation of gene expression, the patterns are so complex that the analysis of spatial gene regulation becomes impossible based on visual inspection only. We therefore developed a set of tools to analyze the structural dynamics of the molecular network in space and its capacity to predict the observed expression patterns. This indicated that the published interaction network is not complete. Importantly, the addition of a limited set of single regulatory hypotheses not identified during our literature search significantly improved the predictive power of the network. With these extra hypotheses, the coarse network structure and composition are in principle sufficient to explain the observed expression patterns. As a result, the proposed network can be a starting point for mechanistic gene regulatory models describing the developing patterns during early flower development. A complete set of testable hypotheses ranked by their effect on the predictive power of the model is given in tables S3 and S4. A set of 27 hypotheses that significantly improves the expression patterns is represented in Fig S7.

As a striking example, the predictions concerning AHP6 illustrate well the incomplete nature of the available data. AHP6 has been described as a direct target of MP (Besnard et al., 2014b). Whereas the data summarized in the atlas are compatible with the hypothesis that MP is required, the latter has a much broader expression pattern than AHP6, suggesting further regulation. The simple hypothesis that STM could act as an inhibitor of expression would substantially improve the predicted pattern. This is in contrast to the conclusion by Besnard et al (Besnard et al., 2014a) who observed a temporary co-expression of both genes and concluded that AHP6 was probably not repressed by STM. However, their observations are also compatible with the hypothesis that STM inhibits AHP6 above a certain threshold. In that case, the temporary overlap would correspond to the transition of cell state 7 to 8 or 9 to 16, when STM expression diminishes.

Novel hypotheses also resolve potential contradictions in the regulatory network model. The evidence so far suggests that the maximum levels of LFY and CUC, respectively involved in organ formation and the establishment of organ boundaries do not overlap (supplemental information). There are indications, however, that LFY directly activates CUC2 (Yamaguchi et al., 2014). Although this seems contradictory, several experiments indicate that during early stage 3, LFY is expressed in the future boundary region, but at a lower level than elsewhere in the developing flower (see justification of gene expression file at: https://doi.org/10.17863/CAM.61991). Likewise, CUC2 shows a broader expression pattern than just the boundary region, again at a weaker level. In parallel, the expression pattern of ANT, an upstream regulator of LFY, is much more complementary to CUC, and our hypothesis that ANT is a negative regulator of CUC would substantially enhance the coherence between the predicted and observed patterns (Fig. 6A). This then would lead us to propose the existence of an incoherent feedforward motif between ANT, LFY, CUC, where ANT positively regulates CUC via LFY together with the proposed negative direct regulation. This type of motif is common in biological regulation and can tune the level and timing of expression of the individual genes (Goentoro et al., 2009; Gruel et al., 2016).

Although our data suggest that lineage is a relatively good predictor for gene expression patterns during early stages of development (similar or better on average to the prediction capability of the literature network regulation), this is not the case later on. The cell state transition graph also illustrates that a particular cell state can have different origins This seems to reflect fluctuating boundaries between the different domains during the differentiation process, causing cells to switch fate. This is for example the case when sole of the boundary cells between the floral and inflorescence meristem are incorporated in the founder cells for the adaxial sepal. In contrast to what one could expect from a system where no cell movement occurs, plant lineage is not considered to be a major determinant of cell fate, i.e., gene expression patterns seem to depend largely on cell-cell communication systems such as hormone- and peptide-based signaling. This is well illustrated by the tonneau or trm mutants in Arabidopsis, where cell division patterns are severely perturbed, without major alterations in differentiation patterns (Schaefer et al., 2017; Traas et al., 1995). In the template used to construct the atlas, we also observed that several cells stopped growing, without any evident perturbation in the final shape, indicating that neighboring cells can take over, further illustrating the flexibility of the system.

Gene activity and growth control

A number of genes have been explicitly associated with growth control, in particular during organ outgrowth (Nole-Wilson et al., 2005; Yamaguchi et al., 2016; Besnard et al., 2014a) or in the slowly growing central zone (Schoof et al., 2000). When looking at the distribution of growth rates for each gene, this correlation was confirmed only for some cases: AHP6 is always expressed in rapidly growing cells during early organ formation, whereas the CUC, PUCHI and CLV3 genes (Chandler and Werr, 2017; Hibara et al., 2006; Lenhard and Laux, 2003) are active in the slowly growing domains of the flower. However, it was not possible to make such direct correlations for other genes supposed to control morphogenesis (Fig. 7A).

This is well illustrated by the auxin-regulated transcription factor MP and its downstream targets ANT and LFY which have been implicated together with AIL6 in flower morphogenesis (Elliott et al., 1996; Krizek, 2009; Nole-Wilson and Krizek, 2006; Nole-Wilson et al., 2005; Yamaguchi et al., 2013). There is convincing evidence that ANT is involved in the control of cell proliferation (Mizukami and Fischer, 2000; Nole-Wilson et al., 2005). It was therefore surprising that ANT expression patterns did not at first sight correlate with particular growth rates: they are expressed in both slowly and rapidly growing cells throughout development. We therefore carried out a more detailed analysis taking into account co-expression in the different cell states, which finally clearly indicated that ANT should indeed be considered as potentially growth-promoting (Fig. 6B). The precise function of LFY and MP in growth control is less well established. MP loss of function leads to reduced flower outgrowth suggesting it promotes growth, but we found that it was mainly expressed in more slowly growing subpopulations. This points at a broader role of MP and is in line with some observations that over-expression of MP can also lead to reduced organ growth (Hardtke and Berleth, 1998). LFY is one of the main regulators of floral organ initiation and identity. It has been mainly associated with patterning events, and might also be involved in promoting auxin signalling (Li et al., 2013; Parcy et al., 1998; Yamaguchi et al., 2014). Although the distribution of growth rates in the LFY domains was again very broad (Fig. 6A), the combinatorial analysis indicated one of the strongest correlations with rapid growth of all genes tested (Fig. 6C). We therefore quantitatively analysed the growth patterns in the strong lfy-12 loss of function mutant at a developmental stage equivalent to stage 3 and 4 in wild type plants. At the equivalent of stage 3 in the mutant, all four sepal-like organ primordia are marked by a local increase in auxin signalling, as revealed by the auxin inducible promoter DR5 (Yamaguchi et al., 2014), but we found that in particular organs in the abaxial and adaxial positions grow out later than the medio-lateral primordia, in contrast to the wild type. In addition, the differences in growth rates between the boundary and the adjacent zones is reduced, mainly when comparing stage 4 wild type flowers with an equivalent stage in lfy-12. The quantitative analysis, therefore, further supports the hypothesis that LFY is involved in coordinating cell expansion rates within specific subdomains, in particular to maintain sufficient growth rate differences between the sepals and sepal boundaries. The relative weak modifications in growth patterns might at first sight not seem significant. However, In terms of volume doubling times, the sepals in the wild type would achieve volume doubling two times faster than the boundary cells. In lfy-12 this would be reduced to 1,6 times faster. Since growth is exponential and doubling times are in the order of 24h, these changes have the potential to induce substantial changes in organ shape over a few days. We here only consider the effect of the lfy mutation on changes in geometry. While this is an essential first step, at lower scales the mutation affects a whole range of expression patterns of other genes (e.g. Parcy et al 1998; Li et al 2013). At this stage it is, therefore, not trivial to determine the direct or indirect effects of lfy-12 via downstream targets on changes in geometry. Further work should therefore focus on the precise role of LFY in the molecular network, including the analysis of spatial changes in gene expression caused by its mutation. This should be combined with the quantitative analysis of plant lines where downstream targets are mutated as well.

Conclusion

The integrated analysis of early flower development presented here suggests a number of further steps forward. The dataset can be easily extended by adding new expression patterns or expression gradients. By providing a dynamic template, it should be very useful in interpreting single cell sequencing efforts, which are precisely missing this type of detailed spatial information. The online atlas can also be enriched by information of different nature, including for instance cell polarity or mechanical properties. Other templates, coming from different time-series of wild type and mutants, can be added for further quantitative comparison as we show here for lfy. The ultimate aim would be to produce an artificial flower template using average behavior, or a collection of templates providing information on the variability existing in flower development. The atlas also provides an essential step towards the development of complex mechanistic models. Using the multiscale data of the atlas as input, it now becomes possible to compare quantitatively the results obtained in vivo with those coming from simulation where a large range of hypotheses can be tested in parallel, as we showed with boolean models here. Importantly, the interactive atlas is available online and provides a tool that can be used and further developed by the entire scientific community.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jan.Traas@ens-lyon.fr

Materials Availability

This study did not generate new unique reagents or biological materials.

Data and Code Availability

Confocal z-stacks, segmentation files, cell lineage information and in situ hybridisation images are available online (https://doi.org/10.17863/CAM.61991). A simplified manual for the use of MorphoNet can also be found there. Software scripts for reproducing the analyses performed here are available via the Sainsbury Laboratory gitlab repository (https://gitlab.com/slcu/teamhj/publications/refahi_etal_2019). All data is interactively minable via the MorphoNet ATLAS (http://www.morphonet.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

For this study and the reported results we either used Arabidopsis thaliana (Col-0) plants containing a modified Yellow Fluorescent Protein (YFP) that is acylated and localised to the cell membrane (Willis et al., 2016) or staining with FM4-64. lfy-12 (Columbia background, (Maizel and Weigel, 2004)) mutants were imaged after staining with FM4-64. Plants, grown in short days under standard conditions, were removed from soil soon after the transition to reproductive growth when the length of the inflorescence stem was less than 1 cm. These small plantlets, including roots, were carefully transferred into a plastic box containing molten, cooled 1% w/v agar supplemented with 2.2 grams l⁻¹ MS salts and Gamborg B5 vitamins.

METHOD DETAILS

Live imaging

Plants to be imaged were grown as described elsewhere in the Methods and then meristems were dissected to remove obstructing flowers, the box filled with water and then imaged using either a Zeiss LSM780 or LSM700 upright confocal microscope with a 20x or 40x water dipping objective. Confocal Z-stacks were taken of primordia and detector pixel format, slice interval and zoom were set so that each resulting voxel is less than 300 nm³, as specified in the data set provided online (https://doi.org/10.17863/CAM.61991). FM6 was imaged under different angles and merged. Time point 104h for FM1, was obtained merging two consecutive acquisitions to improve the image quality. Plants were transferred to the growth chamber between successive acquisitions.

Segmentation and lineage tracking

Z-stacks of 2D (x-y) optical sections of five primordia expressing YFP were collected (numbered as FM1-5). A sixth meristem (FM6) was imaged after staining with FM4-64.

The ImageJ registration plugin StackReg ((Willis et al., 2016; Thévenaz et al., 1998) was first applied to each Z-stack correcting misalignments between consecutive slices. During confocal imaging of primordia, the flowers moved upwards due to meristem growth and stem elongation which led to oversampling of confocal optical sections in z-direction and an artificially stretched primordium after 3D reconstruction. To correct this artefact, we first manually selected cells on the epidermal layer whose thickness were least affected by the movement in z-direction (whose anticlinal wall normal were pointing close to the x-y plane direction). We then computed the average cell thickness of the selected cells (L1_thickness). We then selected the epidermal cells whose thickness were the most affected by the movement (whose anticlinal wall normal were pointing close to the z-axis) and computed their thickness (L1s_thickness). To correct the artefact, we divided the voxel thickness by (L1s_thickness)/ L1_thickness. On a few time points, we also performed a rapid scan, where only two sections were made, to determine the height (in the Z-direction) of the flower bud as growth was negligible then (see also: (Willis et al., 2016)). These new estimations were close to the values calculated previously (<5%).

To quantify growth, we used the high throughput 4D (space + time) image segmentation and tracking pipeline that we previously developed (Willis et al., 2016). This 4D imaging pipeline allows precise quantification of cellular growth over multiple cellular generations using MARS-ALT (Fernandez et al., 2010). Using the collection of image stacks, we used a three-dimensional auto-seeded watershed algorithm (Fernandez et al., 2010) to segment the cells. The segmented images were manually checked for segmentation errors (over-segmentation, under-segmentation, missing cell, or shape error). For this purpose, we conducted a visual inspection of segmentation quality of two dimensional (x-y) optical sections by comparing the optical section obtained using a confocal microscope and corresponding segmentation. In case of segmentation error, the contours of the cells were corrected on 2D sections. Cell volumes were calculated by voxel counting and multiplying this count by the voxel volume.

To track mother-daughter cell lineages, we first performed an affine transformation followed by a nonlinear registration using a block-matching framework (Commowick et al., 2008; Malandain and Michelin, 2017; Michelin et al., 2016) between two successive confocal acquisitions which computed the deformation field between them. Using this deformation field, we used ALT (Automatic Lineage Tracking) (Fernandez et al., 2010) to compute cell lineages, between consecutive segmented time points. The mother-daughter pairings were further inspected for errors and manually corrected and validated for L1 and L2 layers, see Figs. 2 and S1.

Comparison of Floral Meristems

We used the surface of flower primordia, represented by a point cloud, as the overall shape to compare the six sets of acquisitions. Although they go through similar developmental stages, each primordium has different cell arrangements. Also, there is no obvious way to synchronise flower development and hence the geometrical shape of individual time points of one series do not exactly correspond to the time points of other series. Therefore, we first computed the spatial and temporal correspondence between the six time series by quantifying shape differences (Michelin et al., 2016). The method uses a rigid transformation based on the hypothesis that two primordia at the same developmental stage have similar size and global shape. Since the shape of the flower primordium does not change sufficiently during stage 1 and 2 for such a comparison, we examined the overall shape changes during stage 3 and 4, when the sepals grow out and more dramatic changes in geometry are observed. To facilitate comparison, the temporal resolution of each time course was first refined to one hour using a dedicated 3D image interpolation method (Malandain and Michelin, 2017).

Integration of the gene atlas into Morphonet and AtlasViewer

For online display and the introduction of expression patterns, Morphonet was used (http://www.morphonet.org). For access see supplemental information. Morphonet is a web-based interactive platform for visualization and sharing of complex morphological data and metadata (Leggio et al., 2019). Exploiting its Unity (https://unity.com) 3D visual engine, it offers a vast assortment of possible interactions with 2, 3 and 4D datasets. Through a flexible hierarchical representation of biological structures and dedicated formats for associated metadata, users can follow the dynamics of biological shapes, onto which associated quantitative and qualitative properties can be projected.

Cells are represented with meshes in Morphonet, and the meshes generated from the cell segmentation were converted to obj format and uploaded to Morphonet together with lineage information.

For the introduction of gene expression patterns, five time points were chosen (Fig. 3, (Smyth et al., 1990) corresponding to:

• the initium stage,

• stage 1 (the flower starts to bulge out),

• stage 2 (a globular bud is formed, separated from the inflorescence meristem),

• stage 3 (the ab- and adaxial sepals start to grow out)

• stage 4 (all sepals are clearly growing out and the four whorls have been specified).

The expression patterns of 28 genes were subsequently introduced. This was in short done as follows (see also Supplementary Information):

1. Collection of data from the literature. As many available image sets as possible were collected from the literature. This included GFP expression patterns and RNA in situ hybridizations.

2. Complete existing data with new data. We completed these data by our own RNA in situ hybridizations (for method see: (Ferrandiz and Sessions, 2008b, 2008a). For this purpose, we generated a further 60 sets of serial sections with the expression patterns of 20 genes (Original data available online (doi: provided upon acceptance), Supplementary Information).

3. Manual annotation of timepoints. To facilitate interpretation, we used a binary notation (i.e., genes are either on or off). Since often only 2D data in the form of sections were available and published 3D GFP data were usually partial, it was not possible to project directly the patterns automatically on the atlas. Instead, we used a manual protocol using the annotation tool in Morphonet by clicking on the individual cells. Cells potentially expressing a particular gene were identified by manually projecting sections of in situ hybridizations or confocal sections on the different time points of the atlas. Whenever possible, cell numbers were counted to estimate the size of the expression pattern. For each gene 2-4 datasets available in the literature were identified. We encountered three different cases:

   1. The patterns of the in situ hybridization and/or GFP were simple to interpret, and zones of expression could be unambiguously identified. In the absence of GFP patterns, the use of serial sections was crucial.
   2. There was a conflict between results obtained using GFP expression and in situ hybridizations. In that case, the in situ hybridization results were used.
   3. If information on both protein levels and RNA levels were available, the RNA pattern or promoter activity (in case of GFP construct) was retained.

4. The obtained patterns were subsequently refined using information of co-expression or based on information on mutual regulation (e.g., AG and AP1 mutually inhibit each other).

The references and images for each gene are summarized in: https://doi.org/10.17863/CAM.61991.

In addition, we integrated the four-dimensional gene expression data together with all segmented and tracked time courses in an open-source standalone software platform, called AtlasViewer (available at https://gitlab.com/slcu/teamHJ/publications/refahi_etal_2020/-/tree/master/atlasviewer/atlasviewer). The patterns were imported directly from Morphonet into AtlasViewer. Visualization of combination of gene expressions using AtlasViewer facilitated the identification and correction of annotation errors.

Cell states, clustering and transition graphs

After assigning expression values for the 27 genes to individual cells, this boolean element vector is used to define a cell state for each cell (Fig. 2B, Fig. 3). Similarities between cell states were calculated using the Hamming distance, i.e., the sum of the absolute differences between the vector elements (Fig. 4C). The states were clustered using hierarchical agglomerative clustering from SciPy package using Ward’s method, which uses Ward variance minimization algorithm, leading to a dendrogram. Manual flipping at the dendrogram nodes and identification of tissue structures were applied to generate the final graph (Fig. 3C).

To illustrate the evolution of cell states over time, cell lineages were used to generate a pattern transition graph whose vertices were cell states. An arrow connected two vertices if and only if any of the descendant cells of the source cell state acquired the target cell state at the next developmental stage. We then assigned weights to arrows as the number of descendant cells in a specific state divided by the total number of descendant cells. More precisely, let x → y be an arc of the transition graph, where x and y are cell states. The assigned weight, w, is defined as w = (#descendant cells of cells in pattern x in pattern y) / (#descendant cells of cells in pattern x), where # denotes number of cells. To extract the main structure of the pattern transition graph, we then pruned by keeping the arrows whose weight were equal or greater than a manually defined threshold of 0.2. However, in this representation the descendent patterns with a small number of cells are penalized. We therefore also computed a reverse pattern transition graph where arcs pointed from descendent patterns to their ancestors. For each arrow, x ← y, in the reverse transition graph, where x and y were cells states, we assigned a weight w’, defined as, w’= (#cells in pattern y whose ancestors are in pattern x) / (#cells of cells in pattern y). The weights were then used to prune the reverse transition graph by removing the arrows whose weight were below 0.2. The pruned transition graphs were then merged into a single transition graph, Figure 3D.

Cell growth and anisotropy rates and correlation analysis with gene expression and states

Assuming exponential growth of a cell of volume V, $\frac{dV}{dt}=kV$, with a constant relative growth rate we compute k from cell volumes and lineage information for a cell c at time point t_i, 0 ≤ i ≤ 4 ( index corresponding to the 5 developmental stages considered), as:

$$k_{c,t_i\to t_{i+1}}=(ln({\sum }_{d\in D_c}{V}_d)-ln(V_c))∕(t_{i+1}-t_i),$$

where V_c is the volume of the mother cell c, V_d is the volume of a daughter cell d, and D_c is the set of daughter cells of c at time point t_i+1.

Projection of computed values on time courses can be done either on the mother cell or on the daughter cells (e.g., Fig. 5C). Correlation analysis between the computed values and gene expression was done for cells expressing a specific gene in both forward (following all cells expressing a gene at one time point to the next) and backward (tracking all cells expressing a gene at a specific time backward in time). Similar correlation analysis is done for averaging cells within a specific cell state. When both forward and backward growth are available, the growth rate of a cell c at time point t_i was computed as the average of the two to quantify growth at a specific time:

$$g_r(c,t_i)=(k_{m,t_{i-1}\to t_i}+k_{c,t_i\to t_{i+1}})∕2,$$

where m is the mother cell of c. In the cases where only one was available, the reported values are for the first time point the forward growth calculation and for the last time point the backward growth calculation.

3D growth anisotropy was computed using cell and lineage information by identifying and matching key points on the cell and set of daughter cells’ surface. We define key points as the smallest set of points on the cell surface enveloping the cell (Convex Hull, calculated using Python bindings to QHull library, http://www.qhull.org/). The Convex Hulls of each cell and its daughter cells were centred and then mapped according to a nearest neighbour criterion. We then calculated the best (least-squares estimation) linear transformation A between the two hulls:

$$\overline{Y}=A\overline{X}+b,$$

where $\overline{X}$ is the collection of the selected points for a cell and $\overline{Y}$ the collection of corresponding points on the daughter cells’ surface.

The transformation was decomposed into three transformations, two rotations and an expansion using the Singular Value Decomposition (SVD):

$$A=DS{D}^T,$$

where D and D^T are the rotations and S is the expansion. The singular values of S(s₁, s₂, s₃) represent the length of the expansion along the axes. The anisotropy is then computed using these expansion lengths as the fractional anisotropy a:

$$a=\sqrt{\frac{3}{2}}\frac{\sqrt{(s_1-\widehat{s}{)}^2+(s_2-\widehat{s}{)}^2+(s_3-\widehat{s}{)}^2}}{\sqrt{{s_1}^2+{s_2}^2+{s_3}^2}}$$

where $\widehat{s}=(s_1+s_2+s_3)∕3$. The fractional anisotropy is a scalar value ranging from 0 (expansion was equal in all directions) to 1 (expansion was in only one direction). The anisotropy rate is the fractional anisotropy per hour.

Correlation analysis between growth anisotropy and gene expression and states, like in the case of growth rates, can be done in both forward and backward directions. When both are available the anisotropy rate at time point t_i, was calculated as the average of the forward anisotropy rate calculation from t_i to t_i+1 and the backward growth anisotropy rate calculation from t_i−1 to t_i.

Regulatory network analysis

We extracted the gene regulatory interactions, inhibition and activation, from the published literature based on the available data on direct binding on promoter regions and mutant analyses (Fig. 1).

Boolean regulatory terms

To analyse the regulatory network, we defined a subset of boolean rules combining the input arrows in the regulation network (i.e., repression and activation), and examined whether they could reproduce the spatial gene expression patterns of the Atlas. Since the input arrows indicate either positive (activation) or negative (repression) regulation, the corresponding boolean regulatory terms that we define have two sub-terms for activation and repression. We next define the types of terms used for the full regulatory term and the repression and activation sub-terms (for further details on network construction see (Moignard et al., 2015).

Regarding notation we assume we have a set of names where g₁, g₂, … ∈ Symb range over symbols representing gene names , ϵ, t, t ′ ∈ TExp range over (possibly empty) activation/repression terms, and r, r′ ∈ RExpr over full regulatory terms. We will give the following definitions using the ‘is defined as’ symbol (:: =) to separate the class being defined (e.g., regulatory expressions) with its definitions and the ‘alternative’ symbol (∣) to separate definitions in cases where there is more than one.

The class of regulatory interactions for each gene is defined as

$$r\colon\colon =t\wedge \neg t^{\prime },$$

where r ∈ RExpr is a full regulatory term for a gene including an activation term (t ∈ TExp) and a repression term (t′ ∈ TExp) combined by a logical and (∧) and logical not (¬).

Each term can be empty (ϵ), a gene name (g ∈ Symb syntactic case), or a combination of gene names with conjunction or disjunction, as described by

$$\begin{gathered} t\colon\colon =\epsilon \\ \mid g \\ \mid t^{\prime }\wedge g \\ \mid t^{\prime }\vee g, \end{gathered}$$

where ∨ represents a logical or.

We next define an evaluation function to evaluate the activation and repression terms to values in the set B = {T, F} (T for true, and F for false). Evaluation happens in a value environment providing values (True or False) for the gene names in the terms. To represent this context we use a sequence of gene name value bindings σ = g₁: b₁, ⋯ , g_n: b_n where g₁, ⋯ , g_n ∈ Symb(gene names) and b₁, ⋯ , b_n ∈ B (True or False representing expression or non-expression of the corresponding gene), where the gene names are required to be distinct. We will sometimes treat this context as a function with finite domain; for example, to obtain the value of g₁ in σ we wrote σ(g₁). The evaluation function [∣ ∣] : TExp → B in a value environment σ is then (per syntactic case):

$$\begin{gathered} [\mid ϵ\mid ]=F \\ [\mid g\mid ](\sigma )=\sigma (g) \\ [\mid t\wedge g\mid ](\sigma )=[\mid t\mid ](\sigma )\wedge [\mid g\mid ](\sigma ) \\ [\mid t\vee g\mid ](\sigma )=[\mid t\mid ](\sigma )\vee [\mid g\mid ](\sigma ), \end{gathered}$$

where t ∈ TExp, g ∈ Symb. For both TExp’s and RExpr’s evaluation functions, we assume that the given environments are well-formed, i.e., they contain mappings for all the gene names that appear in the expression being evaluated. Note that the above evaluation implies left association of expressions so, for example, the expression a ∧ b ∨ c is evaluated as (a ∧ b) ∨ c.

The evaluation function for the full regulatory term [∣ ∣] : RExpr → B is:

$$[\mid t\wedge \neg t^{\prime }\mid ](\sigma )=[\mid t\mid ](\sigma )\wedge \neg [\mid t^{\prime }\mid ](\sigma )$$

Two RExpr’s are semantically-equivalent if they contain the same gene names and given the same environment they evaluate to the same value.

Translating the gene regulatory network into boolean regulatory terms

Given a gene regulatory network, as in Fig. 1, for each gene we have a set of activators (positive regulation) and a set of repressors (negative regulation), but there is no information on how their inputs combine to control expression of their target gene. In order to see the most likely boolean regulatory term between the regulations, we enumerated all the possible TExpr’s for the activators, all the possible TExpr’s for the repressors, combined them into regulatory terms (RExpr’s) and scored them based on how well they agree with the expression data (Supplemental Table 2).

Given a set of input activators/repressors, {g₁, ⋯ , g_n} for a gene there are n! · 2ⁿ⁻¹possible TExp’s. For each permutation of the input genes (out of n! possible), we have a choice of disjunction or conjunction between them. For example, for 2 activator genes {g₁, g₂} we can generate the following terms: {g₁ ∧ g₂, g₁ ∨ g₂, g₂ ∧ g₁, g₂ ∨ g₁}. If we also had 2 repressors, then the number of terms becomes 16. While the number grows very quickly with n, we found that is not prohibitive for the number of genes we have here (n < 5).

Each cell in a tissue dataset implies a value environment; for example, if in a cell gene g₁ is on, gene g₂ is off, gene g₃ is off, and g₄ is off we get a value environment g₁: T, g₂: F, g₃: F, g₄ : F. We can then evaluate the generated boolean regulatory terms in this environment so for example for an expression for g₄=(g₁ ∧ g₂) ∧ ¬g₁ we can evaluate for that cell [∣ (g₁, ∧ g₂) ∧ ¬g₁∣](g₁: T, g₂: F, g₃: F, g₄ : F) = F, which (for this example cell) agrees with the actual value of g₄.

Hypothesis generation

In order to generate new hypotheses for each gene, we enumerated all possible changes in the form of single regulatory interactions between genes of the published gene regulatory network. Therefore, either existing single interactions were removed, or new ones were added. For each modified interaction, we generated all possible TExp’s and full regulatory terms as before.

Suppose we have a universe of genes G = {g₁, g₂, g₃, g₄}. Then, for a gene A with two activators (g₁, g₂) and one repressor g₄, the following set of regulatory interactions for that gene would be generated: {(acts=(g₁, g₂, g₃), reprs=(g₄))), (acts=(g₁, g₂)), reprs=(g₄, g₃)), (acts=(g₁), reprs=(g₄)), (acts=(g₂), reprs=(g₄)), (acts=(g₁, g₂), reprs=())}. Note that we only added inputs from genes that were not in the original network, whereas the gene g₃, could represent any other gene in the network not yet connected to gene A. For each set of inputs (activators and repressors) we then generated and scored regulatory terms as before.

Growth regulation

To examine the gene regulation of growth by the action of single genes, we examined the differences between the population of cells expressing a gene versus the population of cells not expressing the gene. Spatially this defines two regions, which can be described as boolean expressions for a gene, g, as g and ¬g. The RGD of a gene g was calculated as:

$$(m(g,T)-m(\neg g,T))∕(m(g,T)+m(\neg g,T))$$

where m(e, T) is the median growth rate of the cells in the regions defined by the expression, e, over a set of time points, T. The evaluation of an expression in a cell follows the procedure described in the ‘Boolean regulatory expressions’ section. The growth rate of a cell is, when possible, the average of backward and forward growth rates as described above.

In order to get a more fine-tuned understanding of growth gene regulation we extended our single-gene analysis to pairs of genes that are co-expressed. Each combination of co-expressed genes implicitly defines two regions (populations of cells) on the flower tissue at any time point. These two regions can be defined using boolean expressions as, g₁ ∧ g₂ (region where they are co-expressed) and g₁ ∧ ¬g₂ (region where only one of them is expressed). For each pair of co-expressed genes, the RGD at time point t_i (color maps in the heatmaps in Supp. Figs 11, 12, 13) was calculated as:

$$(m(g_1\wedge g_2,\{t_i\})-m(g_1\wedge \neg g_2,\{t_i\}))∕(m(g_1\wedge g_2,\{t_i\})+m(g_1\wedge \neg g_2,\{t_i\}))$$

In order to get the most common regional separation implied by gene pairs at a time point we grouped the pairs into categories (numbered annotations in the heatmaps in Supplemental Figures S5 and S6) defining the same regions. Two pairs of genes g₁, g₂ and g′₁, g′₂ define the same regions at tif the two boolean expressions they imply select the same set of cells:

$$[g_1\wedge g_2{]}_t=[g_1^{\prime }\wedge g_2^{\prime }{]}_t\text{and}[g_1\wedge \neg g_2{]}_t=[g_1^{\prime }\wedge \neg g_2^{\prime }{]}_t$$

In Supp. Figs 11, 12 and 13 we only display the groupings in the top 50% (by RGD) of the pairs at that time point up to a maximum of 6 groupings. Groupings are also sorted by RGD so the group with index 1 has the highest RGD and so on.

QUANTIFICATION AND STATISTICAL ANALYSIS

Pattern Evaluation

To score an expression pattern generated from cell lineage, the regulatory network of a particular gene (Fig. 1), or a boolean model including hypothesis for an entire tissue, we evaluate it for all the cells and calculate the Balanced Accuracy (BAcc) for its predictions. BAcc is defined as $\frac{1}{2}(TN∕N+TP∕P)$ where TN is the number of true negatives (# of cells where the expression evaluates to false and the actual value of that gene is false --- like the example above), TP is the number of true positives (#of cells where the expression evaluates to true and the actual value of the gene is true), P is the number of positives (#of cells where the value of the gene is true), and N is the number of negatives (# of cells where the value of the gene is false). We chose BAcc as measure since it also penalizes errors where only few cells have an expression (or opposite). We also tried alternative similarity measures, such as Mutual Information and % correct. This led to the same conclusions.

The scores and therefore the best expressions are not necessarily the same for the tissues at different timepoints (Supplemental Table S3). For each gene and each time point we merged and ranked the generated regulatory expressions for all the proposed interactions keeping only the ones that are within 10% of the best expression for that time point. Starting from the last time point going backwards we then identify expressions that appear near the top in more than one time point for a single coherent hypothesis.

Model comparison and random models

In order to establish a baseline for the comparison of RExpr’s generated by the hypotheses, the RExpr’s based on the reference network, and lineage prediction, we also constructed a random network with the same structure as the gene regulatory network in Fig. 1, where all the inputs are replaced with random inputs. For the results reported in the main text we generated 100 random RExpr’s per gene based on random inputs with the same numbers as they appear in the gene regulatory network (Fig. 1). These were then scored (using BAcc) per time point and averaged.

All the p-values reported in the main text are the result of a paired t-test between the scores of all the genes under the different models, e.g., lineage scores vs best hypothesis scores.

Quantification of growth differences

In order to examine growth regulation by gene expression we used Relative Growth Difference (RGD) to compare growth differences between populations of cells (defining regions on a tissue), defined as:

$$(r_1-r_2)∕(r_1+r_2),$$

where r₁ is the median growth rate of the first population of cells and r₂ is the median growth rates of the second population of cells. The RGD ranges from 0 to 1 except in some cases early on in development where it can be > 1 when one of the regions considered has a negative median growth rate.

Supplementary Material

Supplement

Figure S1 – Surface rendering of segmented images of time courses of FM2 - 6 (Related to Fig 1A)

Figure S2 - Approach for comparison of meristems (Related to Fig 2).

Figure S3 - Anisotropy rates (related to Fig 5)

Figure S4 - Growth rates between time points reveal predetermined patterns at stage 2 (related to Fig 5).

Figure S5 - Relative Growth Differences (RGDs) (related to Fig 6)

Figure S6 - Relative Growth Differences (RGD) (related to Fig 6).

Figure S7 - Hypotheses resulting from network analysis (related to figures 1 and 4).

Supplementary Table S1

Supplemental Table S1 - Justification gene interactions (related to Fig 1)

Supplementary Table S2

Supplemental Table S2 - List of cell states and clusters with the description of their identity (related to Figures 2 and 3).

Supplementary Table S3

Supplemental Table S3 - hypotheses from the literature (linked to Fig 1 and table S1).

Supplementary Table S4

Supplemental Table S4 - Summary of novel inputs and their effect for every gene at different time points (linked to Figure 1, 4 and S7):

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
FM 4-64 (membrane stain)	ThermoFisher Scientific	T3166
Propidium Iodide	Sigma-Aldrich	P4170
Deposited data
Confocal raw data (FM1-FM6 and lfy-12) and segmented data	University of Cambridge open data repository	DOI:https://doi.org/10.17863/CAM.61991
Experimental Models: Organisms/Strains
Arabidopsis Thaliana Col-0 with modified, acetylated Yellow Fluorescent Protein (YFP)	Willis et al (2016)	N/A
Arabidopsis Thaliana mutant lfy-12	Maizel and Weigel (2004)	Nottingham Arabidopsis Stock Centre (NASC)
Oligonucleotides
AG S	acggcgtaccaatcggagct
AG T7 AS	tgtaatacgactcactatagggcttacactaa ctggagagcgg
ANT S	atgaagtctttttgtgataa
ANT T7 AS	tgtaatacgactcactatagggctcaagaatc agcccaagcag
AP1 T7 AS	tgtaatacgactcactatagggctcatgcggc gaagcagccaa
AP1 S	atgggaaggggtagggttca
CUC1 S	atcgatgttgatgtgtttaa
CUC1 T7 AS	tgtaatacgactcactatagggctcagagagt aaacggccaca
CUC2 S	tgtaatacgactcactatagggctcagtagttc caaatacagt
CUC2 T7 AS	atggacattccgtattacca
FIL S	atgtctatgtcgtctatgtc
FIL T7 AS	tgtaatacgactcactatagggcttaataagg agtcacaccaa
REV S	atggagatggcggtggctaa
REV T7 AS	tgtaatacgactcactatagggctcacacaa aagaccagttta
AS2 S	atggcatcttcttcaacaaa
AS2 T7 AS	tgtaatacgactcactatagggctcaagacg gatcaacagtac
ETT S	atgggtggtttaatcgatct
ETT T7 AS	tgtaatacgactcactatagggcctagagag caatgtctagca
ANT S	ccagcatggaaggtggcaagcacgg
FIL S	gctccagctccagctcggtcctc
CUC2 S	cgaccatggcggagacagcc
ANT S	atgaagtctttttgtgataatgatgataat
CUC2 S	atggacattccgtattaccactacgaccat
FIL S	atgtctatgtcgtctatgtcctccccttcc
AP2 S	atgtgggatctaaacgacgcaccacaccaa
AP2 T7 AS	tgtaatacgactcactatagggctcaagaag gtctcatgagag
AP3 S	atggcgagagggaagatccagatcaagag g
AP3 T7 AS	tgtaatacgactcactatagggcttattcaaga agatggaagg
MP S	atgatggcttcattgtcttgtgttgaagac
MP T7 AS	tgtaatacgactcactatagggcttatgaaac agaagtcttaa
AS1 S	atgaaagagagacaacgttggagtggtgaa
AS1 T7 AS	tgtaatacgactcactatagggctcaggggc ggtctaatctgc
LFY S	atggatcctgaaggtttcacgagtggctta
LFY T7 AS	tgtaatacgactcactatagggcctagaaac gcaagtcgtcgc
AHP6 S	atgttggggttgggtgtggaccggcttcaa
AHP6 T7 AS	tgtaatacgactcactatagggcttacattgga tatctgactc
PHB S	atgatgatggtccattcgatgagcagagat
PHB T7 AS	tgtaatacgactcactatagggctcaaacga acgaccaattca
PHV S	atgatggctcatcactccatggacgataga
PHV T7 AS	tgtaatacgactcactatagggctcaaacaaacgaccaactaa
PI S	atgggtagaggaaagatcgagataaagacg
PI T7 AS	tgtaatacgactcactatagggctcaatcgatgaccaaagaca
SEP3 S	atgggaagagggagagtagaattgaagagg
SEP3 T7 AS	tgtaatacgactcactatagggctcaaatagagttggtgtcat
STM S	atggagagtggttccaacagcacttcttgt
STM T7 AS	tgtaatacgactcactatagggctcaaagcatggtggaggaga
ARF4 S	atggaatttgacttgaatactgagattgcg
ARF4 T7 AS	tgtaatacgactcactatagggcctaaaccctagtgattgtag
WUS S	atggagccgccacagcatcagcatcatcat
WUS T7 AS	tgtaatacgactcactatagggcctagttcagacgtagctcaa
Software and Algorithms
MARS-ALT (cell segmentation–automated lineage tracking)	(Fernandez et al., 2010)	https://www.quantitative-plant.org/software/mars-alt
StackReg ImageJ plugin	(Willis et al., 2016) (Thévenaz et al., 1998)	https://github.com/fiji-BIG/StackReg/blob/master/src/main/java/StackReg_.java
Spatio-temporal registration and interpolation of microscopy images	(Michelin et al., 2016) (Malandain and Michelin, 2017)	N/A
MorphoNet	(Leggio et al., 2019)	https://morphonet.org/
AtlasViewer	N/A	https://gitlab.com/slcu/teamHJ/publications/refahi_etal_2020/-/tree/master/atlasviewer/atlasviewer
Scipy	(Virtanen et al., 2020a, 2020b)	RRID:SCR_008058
IPython	(Perez and Granger, 2007)	RRID:SCR_001658
QHull Convex hull algorithm	(Barber et al., 1996)	http://qhull.org/
Mypy (optional type checking for Python)	http://mypy-lang.org/	N/A