A Robust and Unified Framework for Estimating Heritability in Twin Studies using Generalized Estimating Equations

Summary

The ‘heritability’ of a phenotype measures the proportion of trait variance due to genetic factors in a population. In the past 50 years, studies with monozygotic and dizygotic twins have estimated heritability for 17,804 traits¹; thus twin studies are popular for estimating heritability. Researchers are often interested in estimating heritability for non-normally distributed outcomes such as binary, counts, skewed or heavy-tailed continuous traits. In these settings, the traditional normal ACE model (NACE) and Falconer’s method can produce poor coverage of the true heritability. Therefore, we propose a robust generalized estimating equations (GEE2) framework for estimating the heritability of non-normally distributed outcomes. The traditional NACE and Falconer’s method are derived within this unified GEE2 framework, which additionally provides robust standard errors. Although the traditional Falconer’s method cannot adjust for covariates, the corresponding ‘GEE2-Falconer’ can incorporate mean and variance-level covariate effects (e.g. let heritability vary by sex or age). Given a non-normally distributed outcome, the GEE2 models are shown to attain better coverage of the true heritability compared to traditional methods. Finally, a scenario is demonstrated where NACE produces biased estimates of heritability while Falconer remains unbiased. Therefore, we recommend GEE2-Falconer for estimating the heritability of non-normally distributed outcomes in twin studies.

1 ∣. INTRODUCTION

Twins and family studies have proven to be powerful instruments for understanding the inheritance of complex phenotypes.² The ‘inheritance’ or ‘heritability’ of a quantitative trait measures the proportion of total trait variance due to genetic factors in a given population. The accurate estimation of heritability is important, as it gives us a basic understanding of the genetic vs. environmental contribution to developing a particular human trait or disease. See^3,4 for a review of various concepts and methods for estimating heritability. In this paper, we focus on the twin ACE model^2,5,1 which compares the resemblance among monozygotic (MZ) and dizygotic (DZ) twins in order to estimate heritability. Specifically, the trait covariance of each twin pair is partitioned into additive genetic (A), common shared family environment (C), and non-shared environmental (E) variance components. The parameters of this twin ACE model are estimated using simple method of moment estimators called ‘Falconer’s equations’^5,1,6, structural equation models (SEM)^2,5, or likelihood based approaches assuming normality of the trait; henceforth referred to as the ‘normal ACE model’ or “NACE”.^7,8,9,10.

Although commonly used to estimate heritability in twin studies, the NACE model assumes the trait is normally distributed, and results in Section 3 demonstrate that when the assumption of normality is violated, the NACE model can lead to poor coverage of the true heritability parameter. Moreover, the NACE model assumes the ACE variance parameters are equal for both MZ and DZ twin types, an assumption that is often criticized for twin studies.⁵ For example, several studies have reported apparent sibling contrast effects in analyses of twin resemblance, which could produce higher DZ than MZ variance.¹¹ As an alternative to NACE, one can use Falconer’s distribution-free method of moment estimators.^6,5 Unlike the NACE model, Falconer’s method allows the ACE variance parameters to differ between MZs and DZs and only assumes the proportion of total variance explained by genetic and environmental effects to be the same for both twin types. In doing so, Falconer’s method makes less stringent assumptions about the twin population. In Section 3.3, we demonstrate that Falconer’s method can generate valid estimates of heritability when the ACE variance parameters differ between MZ and DZ twins, while NACE is biased in such settings.

Researchers are often interested in estimating heritability for highly non-normal traits such as binary, discrete counts, and skewed or heavy-tailed continuous data. Moreover, often the trait of interest doesn’t appear to follow any standard parametric distribution (see Figure 2 for examples). Existing approaches to estimating heritability for non-normal traits include generalized linear mixed effect models.^12,13,14 Recently Kirkpatrick and Neale¹⁵ developed three parametric models for estimating ACE variance components in count phenotypes. However, in practice, the estimation and inferences from these models may be sensitive to departures from the parametric distributional assumptions. In addition, often one will fit several different parametric models and then use model selection criteria to pick the ‘best fitting’ parametric model. This may lead to biased results if the model selection procedure is not accounted for while conducting inferences.¹ Thus a more flexible semi-parametric (or non-parametric) approach to estimating heritability may be desirable for non-normally distributed outcomes, which we attempt to develop in this paper.

FIGURE 2.

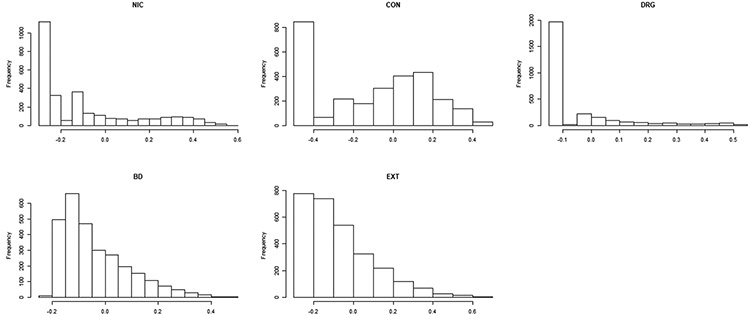
Histograms of 5 substance-abuse traits from the Minnesota Center for Twin and Family Research study. For each trait, there were 936 MZ and 478 DZ twin pairs.

Nicotine (NIC): composite measure of nicotine use and dependence; Alcohol Consumption (CON): composite of measures of alcohol use frequency and quantity; Illicit Drugs (DRG): composite of frequency of use of 11 different drug classes and DSM symptoms of drug dependence; Behavioral Disinhibition (BD): composite of measures non-substance use behavioral disinhibition including symptoms of conduct disorder and aggression; Externalizing Factor (EXT): a composite measure of all five previous traits

In summary, we propose a robust, unified framework for estimating heritability in twin studies using second-order generalized estimating equations (“GEE2”). The semi-parametric GEE2 models require only the first two moments to be correctly specified, and thus can be used to estimate heritability in a wide variety of phenotypes, without explicitly modeling the underlying true parametric distribution. We show that two traditional methods for estimating heritability (NACE and Falconer’s method) can both be fit within the GEE2 framework, which additionally provides robust standard errors. Although the traditional Falconer’s method cannot directly adjust for covariates, we show that the corresponding GEE2 version (‘GEE2-Falconer’) can accommodate covariate effects for both mean and variance-level parameters (e.g. let heritability vary by sex or age). Given a non-normal trait, we show that the robust GEE2 models produce significantly better coverage rates of the true heritability compared to the traditional NACE and Falconer’s methods. Finally, we demonstrate that if the ACE variance parameters differ between MZ and DZ twins, then the NACE produces biased estimates of heritability, while Falconer’s method remains unbiased under weaker assumptions and therefore should be preferred. All methods are compared via simulations and with an application to the Minnesota Center for Twin and Family Research study.¹⁶

2 ∣. METHODS

An outline of the Methods section is as follows: in Sections 2.1-2.2, we review the traditional NACE and Falconer’s method for estimating heritability in twin studies. Then in Section 2.3 we develop robust GEE2 versions of both models, and show how the GEE2 framework can allow heritability to vary as a function of covariates (e.g. sex or age).

For all methods, assume a study with N_MZ and N_DZ pairs of monozygotic and dizygotic twins, and let N = N_MZ + N_DZ be the total number of twin pairs. Let y_z = (y_z1, y_z2)^⊤ be a quantitative response measured on both twins (1 and 2) for a given twin pair, with zygosity “z” equal to “MZ” or “DZ”; and ${\mathit{x}}_z^{⊺}$ is a 2 × P matrix of P covariates for both twins. Then the twin ACE model for a given pair of twins of type z is defined as:

$${\mathit{y}}_z={\mathit{x}}_z^{⊺}\beta +{\mathit{A}}_z+{\mathit{C}}_z+{\mathit{E}}_z,$$ (1)

where $\mathbb{E}({\mathit{y}}_z)={\mathit{x}}_z^{⊺}\beta$ and cov(y_z) = Σ_z = cov(A_z)+cov(C_z)+cov(E_z). The ACE random effects are defined to have the following mean and covariance structures:

$${\mathit{A}}_z\sim (0,{\sigma }_{A_z}^2{\mathbf{K}}_z),{\mathit{C}}_z\sim (0,{\sigma }_{C_z}^2\mathbf{J}),{\mathit{E}}_z\sim (0,{\sigma }_{E_z}^2\mathbf{I})$$

where I is a 2×2 identity matrix, J is a 2×2 matrix of ones, and ${\mathbf{K}}_z=\left[\begin{array}{cc}\hfill 1\hfill & \hfill w_z\hfill \\ \hfill w_z\hfill & \hfill 1\hfill \end{array}\right]$ is the “genomic relationship matrix”. Note w_z = 1 for MZ twins and w_z = 0.5 for DZ twins, since MZ twins share 100% of their inherited genome while DZ twins share only 50% on average. The parameters ${\sigma }_{A_z}^2$, ${\sigma }_{C_z}^2$, and ${\sigma }_{E_z}^2$ represent additive genetic, shared and non-shared variance parameters for twin type z. The primary interest for this ‘ACE’ model is to estimate heritability, which is defined as the proportion of total trait variance due to additive genetic effects:

$$h^2=\frac{{\sigma }_{A_{MZ}}^2}{{\sigma }_{A_{MZ}}^2+{\sigma }_{C_{MZ}}^2+{\sigma }_{E_{MZ}}^2}=\frac{{\sigma }_{A_{DZ}}^2}{{\sigma }_{A_{DZ}}^2+{\sigma }_{C_{DZ}}^2+{\sigma }_{E_{DZ}}^2}$$

Often we are also interested in estimating the proportion of trait variance due to shared environmental effects:

$$c^2=\frac{{\sigma }_{C_{MZ}}^2}{{\sigma }_{A_{MZ}}^2+{\sigma }_{C_{MZ}}^2+{\sigma }_{E_{MZ}}^2}=\frac{{\sigma }_{C_{DZ}}^2}{{\sigma }_{A_{DZ}}^2+{\sigma }_{C_{DZ}}^2+{\sigma }_{E_{DZ}}^2}$$

Finally, the proportion of trait variance due to non-shared environmental effects is defined as: e² = 1 − h² − c². Note that equation (1) allows distinct variance parameters for the different twin types (z = “MZ” or “DZ”). However, all these distinct variance parameters are not estimable in a standard twin study with MZ and DZ twins. Hence the different methods to estimate heritability make certain assumptions about the underlying MZ, DZ populations to generate a valid identifiable model. Below we describe two such common approaches to estimate heritability.

Without loss of generality, for the remainder of this paper we assume the response is centered such that $\mathbb{E}({\mathit{y}}_z)=0$. Given that our primary focus in on variance parameters, fixing the mean equal to zero will greatly simplify formulas and thus help build intuitive connections between the various models considered in this paper. However, in practice, both the NACE and GEE2 models described below can incorporate both mean and variance-level covariate effects.

2.1 ∣. Normal ACE Model for Twin Studies

The NACE model assumes the random effects are normally distributed such that y_z has the following log-likelihood function:

$$\log \left(f({\mathit{y}}_z\mid \alpha )\right)=-0.5\left(\log (\mid {\Sigma }_z\mid )\right)+{\mathit{y}}_z^{⊺}{\Sigma }_z^{-1}{\mathit{y}}_z+2\log (2\pi ),$$

where ${\Sigma }_z=\left[\begin{array}{cc}\hfill {\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2\hfill & \hfill w_z{\sigma }_A^2+{\sigma }_C^2\hfill \\ \hfill w_z{\sigma }_A^2+{\sigma }_C^2\hfill & \hfill {\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2\hfill \end{array}\right]$ and $\alpha =({\sigma }_A^2,{\sigma }_C^2,{\sigma }_E^2)$. The NACE makes a few simplifying assumptions to the model in equation (1), such as ${\sigma }_{A_z}^2={\sigma }_A^2$, ${\sigma }_{C_z}^2={\sigma }_C^2$ and ${\sigma }_{E_z}^2={\sigma }_E^2$. Hence under the NACE model, $\text{cov}({\mathit{y}}_z)={\Sigma }_z={\sigma }_A^2{\mathbf{K}}_z+{\sigma }_C^2\mathbf{J}+{\sigma }_E^2\mathbf{I}$, for z = “MZ” or “DZ”. The parameters of interest are jointly estimated over the MZ and DZ families. See^7,8,9,10 for a review of the NACE model.

For a given twin pair, the estimating equations for α can be derived as:

$$\mathit{u}(\alpha {)}_{\text{NACE}}=\frac{\partial }{\partial \alpha }logf({\mathit{y}}_z\mid \alpha )={\left(\frac{\partial }{\partial {\sigma }_A^2}logf,\frac{\partial }{\partial {\sigma }_C^2}logf,\frac{\partial }{\partial {\sigma }_E^2}logf\right)}^{⊺}=0$$

Assuming the multivariate-normal distribution log f(y_z∣α) is correct, then under the regularity conditions of maximum likelihood estimation¹⁷:

$$\begin{gathered} \sqrt{N}(\widehat{\alpha }-\alpha )\stackrel{D}{\to }MVN(0,{\mathit{V}}^{-1}),\mathit{V}=-\mathbb{E}\left(\frac{{\partial }^2}{\partial \alpha \partial {\alpha }^{⊺}}\log f({\mathit{y}}_z\mid \alpha )\right), \\ \widehat{Cov}(\widehat{\alpha })=\frac{1}{N}{\widehat{\mathit{V}}}^{-1}=\frac{1}{N}{\left[\frac{-1}{N}\sum _1^N\frac{{\partial }^2}{\partial \alpha \partial {\alpha }^{⊺}}logf({\mathit{y}}_z\mid \alpha )\right]}_{\alpha =\widehat{\alpha }}^{-1} \end{gathered}$$ (2)

where the summation in $\widehat{Cov}(\widehat{\alpha })$ is taken with respect to all N twin pairs. After obtaining $\widehat{\alpha }$ and $\widehat{Cov}(\widehat{\alpha })$, we used the delta-method to construct approximate Wald tests and 95% confidence intervals for h² and c² (e.g. ${\widehat{h}}^2\pm 1.96\widehat{\text{SE}}({\widehat{h}}^2)$). It is worth noting that if the assumed multivariate-normal likelihood function is misspecified (as is often the case in practice), then in general, equation (2) will not hold. Finally, we used the twinlm() function from the mets R package¹⁸ to implement the NACE model.

2.2 ∣. Falconer’s Method of Moment Estimators

“Falconer’s equations” use method of moments to estimate heritability in twin studies.^6,5 Falconer’s estimators for h² and c² are defined as:

$${\widehat{h}}_{Falc}^2=2(r_{MZ}-r_{DZ}),{\widehat{c}}_{Falc}^2=2r_{DZ}-r_{MZ},$$ (3)

where r_MZ and r_DZ are Pearson’s sample correlation coefficients for the MZ and DZ twins respectively. Following the notation of equation (1), Falconer’s estimators are derived as follows:

$$\begin{gathered} {\rho }_{MZ}=Corr({\mathit{y}}_{M{Z}_1},{\mathit{y}}_{M{Z}_2})=\frac{Co{v}_{MZ}}{Var({\mathit{y}}_{MZ})}=\frac{{\sigma }_{A_{MZ}}^2+{\sigma }_{C_{MZ}}^2}{{\sigma }_{A_{MZ}}^2+{\sigma }_{C_{MZ}}^2+{\sigma }_{E_{MZ}}^2}=h^2+c^2 \\ {\rho }_{DZ}=Corr({\mathit{y}}_{D{Z}_1},y_{D{Z}_2})=\frac{Co{v}_{DZ}}{Var({\mathit{y}}_{DZ})}=\frac{0.5{\sigma }_{A_{DZ}}^2+{\sigma }_{C_{DZ}}^2}{{\sigma }_{A_{DZ}}^2+{\sigma }_{C_{DZ}}^2+{\sigma }_{E_{DZ}}^2}=0.5h^2+c^2 \\ \Rightarrow 2({\rho }_{MZ}-{\rho }_{DZ})=h^2,2{\rho }_{DZ}-{\rho }_{MZ}=c^2, \end{gathered}$$

where ρ_MZ and ρ_DZ are the population correlation coefficients between MZ and DZ twins respectively, and V ar(y_z) is the variance of both twins for a given zygosity type z. Unlike the NACE, Falconer’s method only requires the variance proportions (h², c², e²) to be equal for both MZ and DZ twins, but allows the magnitude of the ACE variance components $({\sigma }_{A_z}^2,{\sigma }_{C_z}^2,{\sigma }_{E_z}^2)$ to differ between MZs and DZs. In Section 3.3, we demonstrate that when the population variance differs between MZ and DZ twins (but the proportions h², c², e² are equal between twins), then NACE produces biased estimates of heritability while Falconer’s method remains unbiased.

However, Falconer’s approach is often criticized for being unable to directly adjust for covariates and there is no straightforward way to estimate the standard errors of the estimators. One could potentially derive the standard errors of the estimators based on asymptotic results of Pearson’s sample correlation coefficient¹⁹:

$$\begin{gathered} \widehat{SE}({\widehat{h}}_{Falc}^2)\approx \sqrt{4\left(\widehat{Var}(r_{MZ})+\widehat{Var}(r_{DZ})\right)}=\sqrt{4\left(\frac{(1-r_{MZ}^2{)}^2}{N_{MZ}}+\frac{(1-r_{DZ}^2{)}^2}{N_{DZ}}\right)} \\ \widehat{SE}({\widehat{c}}_{Falc}^2)\approx \sqrt{4\widehat{Var}(r_{DZ})+\widehat{Var}(r_{MZ})}=\sqrt{4\left(\frac{(1-r_{DZ}^2{)}^2}{N_{DZ}}\right)+\frac{(1-r_{MZ}^2{)}^2}{N_{MZ}}} \end{gathered}$$

Then using the estimated standard errors, we can construct approximate 95% Wald-type confidence intervals for h² and c². However, we demonstrate through simulations that the aforementioned standard errors can produce poor coverage rates of the true heritability parameter. On the otherhand, our proposed GEE2-Falconer approach gives robust standard error estimates for the estimated heritability parameter. Additionally, although the traditional Falconer’s method cannot adjust for covariate effects, we show that the GEE2 version of Falconer’s method can incorporate covariate effects for both mean and variance-level parameters.

In the following section, we develop a unified framework for fitting both the NACE and Falconer’s methods using a “GEE2” approach. Our proposed approach provides the flexibility to adjust for covariates (in both mean or variance-level parameters) and can accommodate inference of heritability for non-normal traits by generating robust standard error estimates.

2.3 ∣. GEE2 ACE Model for Twin Studies

Liang and Zeger²⁰ originally proposed the “GEE1” estimating equations which allow valid large-sample estimation and inferences on first order moment parameters (e.g. mean-level parameters “β”), while allowing all higher-order moments to be misspecified. The essential assumption of GEE1 is that the trait is some member of the linear exponential family with only the first-moment structure required to be correctly specified, e.g. $\mathbb{E}({\mathit{y}}_z)={\mathit{x}}_z^{⊺}\beta$ (or $g^{-1}({\mathit{x}}_z^{⊺}\beta )$ if using a link function).

However, in applications where one is interested in conducting inference on both mean and variance-level parameters, GEE1 is no longer applicable. Prentice and Zhao²¹ extended GEE1 by proposing the “GEE2” estimating equations which allow for valid inference on both mean and variance level-parameters with minimal distributional assumptions. The key assumption of GEE2 is that y is a member of the quadratic exponential family with the first two moments correctly specified (i.e. $\mathbb{E}({\mathit{y}}_z)$ and Cov(y_z)); while all higher-order moments are allowed to be misspecified. If the aforementioned assumptions of GEE2 are satisfied, then GEE2 can consistently jointly estimate both mean-level parameters (β) and variance-level parameters (α), as well as provide valid Wald tests and confidence intervals for all parameters. See^21,22,23 for a complete review of GEE2. We show that both the NACE and Falconer’s method can be fit within a unified GEE2 framework.

2.3.1 ∣. GEE2-NACE

We will first derive the NACE model under GEE2 framework, where we use the same notation and assumptions from Section 2.1 (e.g. assume the individual ACE variance component parameters are the same for both MZ and DZ twins). Let the outcome for a given pair of twins y_z = (y_z1, y_z2) be an arbitrary member of the quadratic exponential family with mean parameters (β) and variance parameters (α):

$$f({\mathit{y}}_z\mid \beta ,\alpha )=\text{exp}\left\{h(\beta ,\alpha {)}^{⊺}{\mathit{y}}_z+c(\beta ,\alpha )+d({\mathit{y}}_z)+{\mathit{y}}_z^{⊺}\mathbf{D}(\beta ,\alpha ){\mathit{y}}_z\right\}$$

Without loss of generality, assume β = 0 is fixed, and let $\alpha =({\sigma }_A^2,{\sigma }_C^2,{\sigma }_E^2)$ be the variance parameters. Then define Γ_z and γ_z to be the population and sample variances in the following vectorized form ${\Gamma }_z=({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2,{\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2,w_z{\sigma }_A^2+{\sigma }_C^2{)}^{⊺}$ and ${\gamma }_z=(y_{z_1}^2,y_{z_2}^2,y_{z_1}{y}_{z_2}{)}^{⊺}$. Define f_z = γ_z − Γ_z. Then Prentice and Zhao²¹ derived the following estimating equations assuming y_z belongs to the quadratic exponential family:

$$u_z(\alpha )={\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathbf{f}}_z=0,\text{where}{\mathit{D}}_z=\left[\frac{\partial {\Gamma }_z}{\partial {\alpha }^{⊺}}\right],{\Omega }_z=[Cov({\gamma }_z)]$$ (4)

Note that Ω_z is the “working covariance structure” of the sample covariance vector γ_z. Recall from GEE2 theory that only $\mathbb{E}({\mathit{y}}_z)$ and Cov(y_z) = Σ_z are required to be correctly specified, whereas the working covariance structure Ω_z is allowed to be misspecified and one can still obtain valid inference for both mean and variance parameters (β, α) in large samples. The “normal working covariance”²¹ for the GEE2-NACE model is defined as:

$${\Omega }_{z,Norm}=\left[\begin{array}{ccc}\hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2{)}^2\hfill & \hfill 2(w_z{\sigma }_A^2+{\sigma }_C^2{)}^2\hfill & \hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2)(w_z{\sigma }_A^2+{\sigma }_C^2)\hfill \\ \hfill 2(w_z{\sigma }_A^2+{\sigma }_C^2{)}^2\hfill & \hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2{)}^2\hfill & \hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2)(w_z{\sigma }_A^2+{\sigma }_C^2)\hfill \\ \hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2)(w_z{\sigma }_A^2+{\sigma }_C^2)\hfill & \hfill 2({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2)(w_z{\sigma }_A^2+{\sigma }_C^2)\hfill & \hfill (w_z{\sigma }_A^2+{\sigma }_C^2{)}^2+({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2{)}^2\hfill \end{array}\right]$$

Put simply, the normal working covariance assumes that all moments of y_z follow a multivariate normal distribution. Given an initial estimate α₀, a modified Newton-Raphson algorithm is used to iteratively update the estimator as follows²¹:

$${\alpha }_u={\alpha }_0+{\left\{(\sum _1^N{\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathit{D}}_z{)}^{-1}(\sum _1^N{\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathbf{f}}_z)\right\}}_{\alpha ={\alpha }_0}.$$ (5)

Next, the following robust estimator for $Cov(\widehat{\alpha })$ is used²¹:

$$\widehat{Cov}(\widehat{\alpha })=N^{-2}{\Psi }^{-1}{\phantom{\mid }\left(\sum _1^N{\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathbf{f}}_z{\mathbf{f}}_z^{⊺}{\Omega }_z^{-1}{\mathit{D}}_z\right){\Psi }^{-1}\mid }_{\alpha =\widehat{\alpha }}\text{where}\Psi =N^{-1}\sum _1^N{\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathit{D}}_z$$ (6)

Then robust standard errors for $\widehat{\alpha }$ can be obtained by taking the square-root of the diagonal of $\widehat{Cov}(\widehat{\alpha })$. Note that $\frac{1}{N}{\Psi }^{-1}$ is the “model-based” variance of $\widehat{\alpha }$, derived from the implied likelihood function which follows the quadratic exponential family. In general, this model-based variance estimator is incorrect when the implied likelihood function is misspecified. The inside “empirical-variance” term $\left({\sum }_1^N{\mathit{D}}_z^{⊺}{\Omega }_z^{-1}{\mathbf{f}}_z{\mathbf{f}}_z^{⊺}{\Omega }_z^{-1}{\mathit{D}}_z\right)$ is a consistent nonparametric estimator of the true variance of $\widehat{\alpha }$. The reason these standard errors are “robust” is because although we allow Ω_z = Cov(γ_z) to be misspecified when estimating $\widehat{\alpha }$, the standard errors “correct” this by using a consistent nonparametric estimator of Cov(γ_z) through the inside-term ${\mathbf{f}}_z{\mathbf{f}}_z^{⊺}=({\gamma }_z-{\Gamma }_z)({\gamma }_z-{\Gamma }_z{)}^{⊺}$. In contrast, the standard errors for the traditional NACE model are completely determined by the multivariate normal likelihood function, which if misspecified, can lead to poor coverage rates of the true variance parameters.

Note in Supplemental Material Section 2, the estimating equations for the NACE and GEE2-NACE models are derived and shown to be identical, thus both models will produce identical point estimates (with perhaps slight differences due to different software implementations). However, we show through simulations that the GEE2-NACE model, which uses robust standard errors, provides a better coverage rate of the true heritability parameter given a non-normally distributed outcome.

Lastly, it is possible to allow the ACE variance components to differ as a function of covariates. For example, suppose one wants to allow the ACE variance components to vary as a function of sex. Then for a given twin pair, we can redefine the ACE variance components as follows:

$$g({\sigma }_A^2)=a_0+a_{1}Sex,g({\sigma }_C^2)=c_0+c_{1}Sex,g({\sigma }_E^2)=e_0+e_{1}Sex$$

where g(.) is a specified link function (e.g. identity or log-link), and Sex represents the sex of a given twin pair. Note that we assume both twins within a given pair have the same sex, thus we do not allow for the case of mixed-gender DZ twins. Now our new variance parameters of interest are: α = (a₀, a₁, c₀, c₁, e₀, e₁), and equations (5-6) can be used to obtain the estimates and standard errors. Finally, the heritabilities for males and females are defined as:

$$h_{Male}^2=\frac{g^{-1}(a_0+a_1)}{g^{-1}(a_0+a_1)+g^{-1}(c_0+c_1)+g^{-1}(e_0+e_1)},h_{Female}^2=\frac{g^{-1}(a_0)}{g^{-1}(a_0)+g^{-1}(c_0)+g^{-1}(e_0)}$$

Note that c² and e² for males and females would be defined similarly. The delta-method is used to obtain the final standard errors for ${\widehat{h}}_{Male}^2$, ${\widehat{h}}_{Female}^2$. This framework can easily be extended to account for other covariate effects as long as the covariate takes on the same values within a given twin pair (e.g. age or family-level covariates). Accounting for ACE covariate effects with covariates that differ within a given twin pair is left for future work.

2.3.2 ∣. GEE2-Falconer

We now derive the GEE2 version of Falconer’s method. Recall from Section 2.2 that Falconer’s estimators allow the MZ and DZ population variance parameters to differ. Thus in deriving GEE2-Falconer, we assume a covariance matrix with two distinct parameters for MZ and DZ population variances $({\sigma }_{MZ}^2,{\sigma }_{DZ}^2)$ and two distinct correlation parameters (ρ_MZ, ρ_DZ). Thus this approach provides a more flexible way of estimating heritability compared to NACE model which requires the MZ and DZ variance parameters to be the same. Then define the following quantities which will allow us to fit Falconer’s method within the same GEE2-framework presented in Section 2.3.1:

$$\begin{gathered} Cov({\mathit{y}}_z)=\left[\begin{array}{cc}\hfill {\sigma }_z^2\hfill & \hfill {\sigma }_z^2{\rho }_z\hfill \\ \hfill {\sigma }_z^2{\rho }_z\hfill & \hfill {\sigma }_z^2\hfill \end{array}\right](\text{population trait covariance},z=\text{MZ or DZ}) \\ g({\sigma }_z^2)=v_0+v_{1}z(g\text{is identity or log-link}) \\ h({\rho }_z)=p_0+p_{1}z(h\text{is identity or Fisher}’\text{s Z-transformation}) \\ \alpha =(v_0,v_1,p_0,p_1)(\text{parameters to estimate}) \\ {\Gamma }_z=({\sigma }_z^2,{\sigma }_z^2,{\sigma }_z^2{\rho }_z)(\text{population covariance matrix in vectorized form}) \\ {\gamma }_z=(y_{z_1}^2,y_{z_2}^2,y_{z_1}{y}_{z_2})(\text{sample covariance matrix in vectorized form}) \\ {\Omega }_z={\mathbf{I}}_2(\text{Identity matrix}) \end{gathered}$$

The above implies that ${\sigma }_{MZ}^2=g^{-1}(v_0+v_1)$, ${\sigma }_{DZ}^2=g^{-1}(v_0)$, ρ_MZ = h⁻¹(p₀ + p₁), ρ_DZ = h⁻¹(p₀). Equations (5-6) can be used to obtain $\widehat{\alpha }$ and $\widehat{Cov}(\widehat{\alpha })$ respectively, which then can be plugged in to get ${\widehat{\rho }}_{MZ}$, ${\widehat{\rho }}_{DZ}$, which then are plugged into Falconer’s equations (3) to get ${\widehat{h}}^2$, ${\widehat{c}}^2$. The delta-method is used to obtain the final standard errors and Wald-type confidence intervals for h², c².

Recall that Ω_z = Cov(γ_z) encodes all assumptions about higher-order moments. Falconer’s estimators only use information from the first two moments thus ignoring all higher-order moments. Therefore we set Ω_z = I₂ so that Ω effectively drops out of equation (5) which is used to obtain the GEE2-Falconer point estimates.

Lastly, we show how GEE2-Falconer can allow heritability to vary as a function of covariates. For example, suppose we want to allow heritability to vary as a function of sex. Then define:

$$\begin{gathered} g({\sigma }_z^2)=v_0+v_{1}z+v_{2}Sex+v_{3}Sex\ast z \\ h({\rho }_z)=p_0+p_{1}z+p_{2}Sex+p_{3}Sex\ast z \end{gathered}$$

where the new parameters of interest are α = (v₀, v₁, v₂, v₃, p₀, p₁, p₂, p₃). Notice that unlike GEE2-NACE, GEE2-Falconer requires covariate-zygosity interactions when allowing h², c² to vary as a function of covariates. These interaction terms allow the variance and covariance parameters to differ between MZ and DZ twins (we found through simulations that ignoring the interaction terms could lead to under-coverage of the true h², results not shown). In contrast, the NACE model assumes all variance components are the same between MZ and DZ twins. Again, we can use equations (5-6) to obtain estimates and robust standard errors for α.

Then one can obtain sex-specific estimates of h², c² as follows:

$$\begin{gathered} {\widehat{\rho }}_{MZ,Male}=g^{-1}({\widehat{p}}_0+{\widehat{p}}_1+{\widehat{p}}_2+{\widehat{p}}_3),{\widehat{\rho }}_{DZ,Male}=g^{-1}({\widehat{p}}_0+{\widehat{p}}_2) \\ {\widehat{\rho }}_{MZ,Female}=g^{-1}({\widehat{p}}_0+{\widehat{p}}_1),{\widehat{\rho }}_{DZ,Female}=g^{-1}({\widehat{p}}_0) \\ {\widehat{h}}_{Male}^2=2({\widehat{\rho }}_{MZ,Male}-{\widehat{\rho }}_{DZ,Male}),{\widehat{c}}_{Male}^2=2{\widehat{\rho }}_{DZ,Male}-{\widehat{\rho }}_{MZ,Male} \\ {\widehat{h}}_{Female}^2=2({\widehat{\rho }}_{MZ,Female}-{\widehat{\rho }}_{DZ,Female}),{\widehat{c}}_{Female}^2=2{\widehat{\rho }}_{DZ,Female}-{\widehat{\rho }}_{MZ,Female} \end{gathered}$$

More generally: to estimate the heritability $h_{\mathit{x}}^2$ for a particular combination of covariates “x”, simply plug ${\widehat{\rho }}_{MZ,\mathit{x}}$, ${\widehat{\rho }}_{DZ,\mathit{x}}$ into Falconer’s equations (3) and use the delta-method with $\widehat{Cov}(\widehat{\alpha })$ to get the final standard errors for ${\widehat{h}}_{\mathit{x}}^2$, ${\widehat{c}}_{\mathit{x}}^2$.

3 ∣. RESULTS

In Sections 3.1-3.6, we compare the following ACE models via simulations and application to the Minnesota Center for Twin and Family Research study: the normal ACE model (“NACE”), Falconer’s simple moment estimators (“Falconer”), and robust GEE2 versions of both models (“GEE2-NACE” and “GEE2-Falconer” respectively).

3.1 ∣. Estimating Heritability for a Heavy-Tailed Continuous Trait

Assume the outcome for a given twin pair follows a centered heavy-tailed multivariate t-distribution:

$$\begin{gathered} {\mathit{y}}_z=(y_{z_1},y_{z_2})\sim f({\mathit{y}}_z)=\frac{\Gamma (\frac{v+2}{2})}{\Gamma (\frac{v}{2})v\pi \mid {\Sigma }_z{\mid }^{1∕2}}[1+\frac{1}{v}{\mathit{y}}_z^{⊺}{\Sigma }_z^{-1}{\mathit{y}}_z{]}^{\frac{-(v+2)}{2}} \\ {\Sigma }_z=\left[\begin{array}{cc}\hfill {\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2\hfill & \hfill w_z{\sigma }_A^2+{\sigma }_C^2\hfill \\ \hfill w_z{\sigma }_A^2+{\sigma }_C^2\hfill & \hfill {\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2\hfill \end{array}\right] \end{gathered}$$ (7)

Then with ${\sigma }_A^2=0.5$, ${\sigma }_C^2=0.3$, ${\sigma }_E^2=0.2$, and v = 4.5, we simulate 1000 datasets according to (7), each with 700 MZ and 700 DZ twin pairs. Among the various models, we are interested in comparing the the following metrics of h² and c² across 1000 simulated datasets: the average point estimate, the standard deviation of the estimates (i.e. the “true standard error”), the average estimated standard error, and the confidence interval coverage rate (i.e. the proportion of all 1000 confidence intervals that contain the true parameter value).

From Table 1, we see the traditional NACE model has poor coverage for both h² and c² (less than 75%), whereas GEE2-NACE attains coverage much closer to the nominal rate of 95%. Notice that GEE2-NACE produces identical point estimates to the normal NACE, however, GEE2-NACE produces larger and more trustworthy standard errors. Table 1 clearly shows that the average estimated SE’s for the NACE significantly underestimate the true SE’s; whereas the average estimated SE’s for GEE2-NACE match up very well with the true SE’s. The reason the NACE estimated standard errors are incorrect is because they are based on Fisher’s Information matrix which is determined by the assumed likelihood function (normal) which is misspecified (the true likelihood is a heavy-tailed t-distribution). In contrast, GEE2-NACE uses robust sandwich standard errors that provide significantly better coverage of the true variance parameters.

TABLE 1.

Heavy-tailed trait simulation: mean point estimates $({\overline{h}}^2,{\overline{c}}^2)$, true standard errors “S E” (standard deviation of estimates across all simulated datasets), mean estimated standard errors $(\overline{SE})$, and 95% confidence interval coverage rates of h² = 0.5 and c² = 0.3 across 1000 simulated datasets

Model	${\overline{h}}^2(SE,\overline{SE})$	${\overline{c}}^2(SE,\overline{SE})$	Coverage (h2, c2)
NACE	0.50 (0.10, 0.05)	0.30 (0.09, 0.05)	(0.74, 0.74)
GEE2-NACE	0.50 (0.10, 0.09)	0.30 (0.09, 0.08)	(0.95, 0.94)
Falconer	0.50 (0.10, 0.04)	0.30 (0.09, 0.04)	(0.58, 0.60)
GEE2-Falconer	0.50 (0.10, 0.10)	0.30 (0.09, 0.09)	(0.95, 0.95)

Notice that GEE2-Falconer and Falconer’s method produce identical point estimates, however, GEE2-Falconer uses robust standard errors and thus attains significantly better coverage of the true heritability compared to Falconer’s method. A key point is that although the GEE2 models do not attempt to model the true parametric distribution of the trait (heavy-tailed t), they can nevertheless still attain approximately correct coverage rates of the true heritability parameter.

3.2 ∣. Estimating Heritability for Right-Skewed Over-Dispersed Count Data

For a given pair of twins, let ${\mathit{y}}_z=(y_{z_1},y_{z_2})\sim bLGP({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2,\lambda )$, where bLGP(.) is the bivariate Lagrangian Poisson distribution with dispersion parameter λ ∈ (−1, 1). Following Kirkpatrick and Neale¹⁵, we can use the RMKdiscrete R package²⁴ to simulate from the bLGP distribution as follows:

$$\begin{gathered} \text{For MZ twins:} \\ \begin{array}{c}{Q}_0\sim LGP({\sigma }_A^2+{\sigma }_C^2,\lambda )\hfill \\ Q_1,Q_2\sim LGP({\sigma }_E^2,\lambda )\hfill \\ Y_1=Q_0+Q_1\text{and}{Y}_2=Q_0+Q_2\hfill \\ \Rightarrow Y_1,Y_2\sim bLGP({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2,\lambda )\hfill \end{array} \\ \text{For DZ twins:} \\ \begin{array}{c}{Q}_0\sim LGP(0.5{\sigma }_A^2+{\sigma }_C^2,\lambda )\hfill \\ Q_1,Q_2\sim LGP(0.5{\sigma }_A^2+{\sigma }_E^2,\lambda )\hfill \\ Y_1=Q_0+Q_1\text{and}{Y}_2=Q_0+Q_2\hfill \\ \Rightarrow Y_1,Y_2\sim bLGP({\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2,\lambda )\hfill \end{array} \end{gathered}$$

where LGP(.) and bLGP(.) are the univariate and bivariate lagrangian poisson distributions respectively. Then we have the following distributional properties¹⁵: $\mathbb{E}(y_{z_1})=\mathbb{E}(y_{z_2})=\frac{{\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2}{1-\lambda }$, $Var(y_{z_1})=Var(y_{z_1})=\frac{{\sigma }_A^2+{\sigma }_C^2+{\sigma }_E^2}{(1-\lambda {)}^3}$, $Cov(y_{M{Z}_1},y_{M{Z}_2})=\frac{{\sigma }_A^2+{\sigma }_C^2}{(1-\lambda {)}^3}$, $Cov(y_{D{Z}_1},y_{D{Z}_2})=\frac{0.5{\sigma }_A^2+{\sigma }_C^2}{(1-\lambda {)}^3}$.

However, note that the above construction of the bivariate lagrangian poisson distribution may be invalid when λ < 0 (under-dispersion), but will hold when λ > 0 (over-dispersion).¹⁵ In contrast, our GEE2 ACE models work for both underdispersed or overdispersed count data. Nevertheless, we will only consider the case of over-dispersed count data with λ = 0.35, ${\sigma }_A^2=0.5$, ${\sigma }_C^2=0.3$, and ${\sigma }_E^2=0.2$. One-thousand datasets were simulated, each with 700 MZ twin pairs and 700 DZ twin pairs.

Notice from Table 2 that the same patterns from Section 3.1 hold. GEE2-NACE has significantly better coverage rates and more accurate estimated standard errors compared to the traditional NACE. The same result holds for GEE2-Falconer compared to Falconer’s method. Again, the main problem is that the average estimated standard errors for the NACE and Falconer’s method are significantly less than their true standard errors, thus yielding coverage rates much less than the nominal rate of 95%. In contrast, the robust GEE2-NACE and GEE2-Falconer models produce much more accurate standard errors and coverage rates closer to the nominal level. A key point is that although the GEE2 models do not attempt to model the true parametric distribution of the trait (Lagrangian Poisson), they can nevertheless still attain approximately correct coverage rates of the true heritability parameter.

TABLE 2.

Right-skewed over-dispersed count trait simulation: mean point estimates $({\overline{h}}^2,{\overline{c}}^2)$, true standard errors “S E” (standard deviation of estimates across all simulated datasets), mean estimated standard errors $(\overline{SE})$, and 95% confidence interval coverage rates of h² = 0.5 and c² = 0.3 across 1000 simulated datasets, each with 700 MZ and 700 DZ twin pairs.

Model	${\overline{h}}^2(SE,\overline{SE})$	${\overline{c}}^2(SE,\overline{SE})$	Coverage (h2, c2)
NACE	0.50 (0.11, 0.05)	0.30 (0.10, 0.05)	(0.63, 0.67)
GEE2-NACE	0.50 (0.11, 0.11)	0.30 (0.10, 0.10)	(0.95, 0.94)
Falconer	0.50 (0.11, 0.04)	0.30 (0.10, 0.04)	(0.54, 0.55)
GEE2-Falconer	0.50 (0.11, 0.12)	0.30 (0.10, 0.10)	(0.95, 0.94)

To get a better sense of how sample size affects the GEE2 estimators of heritability, Table 3 reports results using the same LGP simulation settings except now the number of MZ and DZ twin pairs is varied from 50 to 400 pairs each. Again, in all scenarios, the GEE2 average estimated standard errors more closely match the true standard errors and the coverage rates are much closer to 95% compared to the traditional NACE and Falconer methods. However, with sample sizes less than 400 MZ and 400 DZ pairs, the coverage rate for the true heritability drops below the nominal rate, but is nevertheless still substantially better than the non-GEE2 models. The drop in coverage may be due to the poor performance of GEE-type standard errors in smaller sample sizes, as well as the fact that twin studies generally need large sample sizes for accurate inference of heritability to begin with - see the Discussion section for more details.

TABLE 3.

Right-skewed over-dispersed count trait simulation with varying sample size: "Npairs" is the number of MZ and DZ twin pairs (e.g. Npairs=50 means there were 50 MZ twin pairs and 50 DZ twin pairs). The number outside parentheses is the mean estimate of heritability $({\overline{h}}^2)$ across 1000 simulation replicates. Numbers inside parentheses: true standard errors (standard deviation of heritability estimates across all simulated datasets), mean estimated standard error, and 95% confidence interval coverage rate of h² = 0.5.

Npairs	NACE	GEE2-NACE	Falconer	GEE2-Falconer
50	0.48 (0.29, 0.14, 0.62)	0.51 (0.40, 0.33, 0.90)	0.50 (0.39, 0.16, 0.55)	0.51 (0.40, 0.33, 0.88)
100	0.49 (0.25, 0.11, 0.62)	0.50 (0.29, 0.27, 0.91)	0.50 (0.29, 0.11, 0.54)	0.50 (0.30, 0.26, 0.92)
200	0.50 (0.20, 0.09, 0.64)	0.51 (0.21, 0.20, 0.93)	0.51 (0.21, 0.08, 0.53)	0.51 (0.22, 0.20, 0.91)
400	0.50 (0.15, 0.07, 0.63)	0.51 (0.15, 0.15, 0.95)	0.50 (0.15, 0.06, 0.53)	0.50 (0.15, 0.15, 0.94)

Lastly, we wanted to investigate the performance of the GEE2 heritability estimators given an unequal number of MZ and DZ twins. For a normally distributed outcome, both^25,26 suggest that an unequal number of MZ and DZ twins results in less power to detect significant genetic effects (i.e. wider confidence intervals for heritability), unless the heritability is large (>50%).²⁵ Using the same simulation parameters for the right-skewed over-dispersed count outcome, except now with a total of 1000 twin pairs, we varied the ratio of MZ to DZ twins from 4:1, 3:2, 1:1, 2:3, and 1:4 (1000 simulation replicates per ratio setting). The results are given in Supplemental Table S1. Overall, the standard errors are relatively similar in the first four scenarios (ratio of MZ to DZ twins of 4:1, 3:2, 1:1, and 2:3), but tend to become slightly larger as the ratio deviates from 1. The standard errors are largest when there are many more DZ twins than MZ twins (1:4 scenario, 200 MZ pairs and 800 DZ pairs). Similar to^25,26, as the ratio of MZ to DZ twins moves further away from 1, GEE2-based confidence intervals for heritability may become slightly larger, especially if there are many more DZ than MZ twins.

3.3 ∣. Scenario where the NACE Twin model is Biased, but Falconer’s Method Remains Unbiased

Recall from Section 2.2 that Falconer’s method allows the ACE variance parameters to differ between MZ and DZ twins, as long as the variance proportions (h², c², e²) are the same in MZ and DZ twins. In contrast, the NACE approach makes a stronger assumption that the individual variance components $({\sigma }_A^2,{\sigma }_C^2,{\sigma }_E^2)$ are equal for both MZ and DZ twins. In the existing literature for the twin NACE model, researchers have made no comments on how to address the scenario where the ${\sigma }_A^2$, ${\sigma }_C^2$, ${\sigma }_E^2$ variance components differ between MZ and DZ twins.^7,8,9,10 Additionally, the assumption of equal variance parameters between MZ and DZ twins is a common criticism of twin studies.⁵ For example, there is some evidence that MZ twins are treated more similarly by their parents compared to DZ twins⁵: this may result in MZ twins having smaller shared family environmental variance $({\sigma }_C^2)$ compared to DZ twins. "Sibling contrast effects" can also lead to DZ twins having larger variance.¹¹ Thus it would be beneficial to have methods for estimating heritability that are less sensitive to the assumption of equal variances between MZ and DZ twins (e.g. Falconer’s method).

A simulation study was performed where the MZ variance parameters were less than the DZ variance parameters by a constant scaling factor "τ", while the variance proportions (h², c², e²) were equal for both twin types. The trait was simulated from a bivariate normal distribution with:

$$\begin{gathered} Var(y_{DZ})={\sigma }_{A_{DZ}}^2+{\sigma }_{C_{DZ}}^2+{\sigma }_{E_{DZ}}^2=.5+.3+.2=1 \\ Var(y_{MZ})=\tau \ast Var(y_{DZ}),\tau =0.5\text{to}1,\text{increments of}0.1 \end{gathered}$$

Notice the ratio of the total MZ variance to DZ variance (τ) ranges from 0.5 times less to 1 (equal). For each value of the variance scaling factor τ, 1000 datasets were simulated each with N_MZ = N_DZ = 700 pairs. From Figure 1, as the MZ variance becomes smaller relative to the DZ variance, the NACE heritability estimator becomes more biased, while Falconer’s method remains unbiased. The maximum bias (overestimation by 53.4%) occurs at τ = 0.5, with substantial bias (9.6%) still remaining for τ = 0.9.

FIGURE 1.

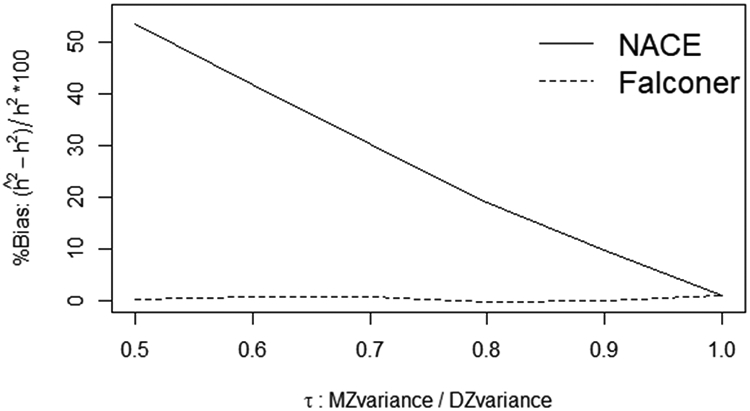
NACE is biased given unequal MZ and DZ variance while Falconer’s method remains unbiased

Although not discussed in the literature^7,8,9,10, we found that transforming the outcome by separately scaling the MZ and DZ variances each to 1 removed the bias (while combining MZ,DZ twins together and then scaling the variance to 1 does not remove the bias), results not shown. However, when interested in allowing heritability to differ by multiple covariates (especially continuous covariates), it is unclear how one should scale the outcome to remove this bias. Thus Falconer’s method (and GEE2-Falconer) may be preferred since it requires no data transformations/scaling to remain unbiased in this setting.

3.4 ∣. Allowing Heritability to vary as a Function of Sex

Here the ACE variance components are allowed to differ by sex. Following the notation and assumptions of Sections 2.1 and 2.3.1, let a₀ = 0.3, a₁ = 0.3, c₀ = 0.4, c₁ = −0.2, e₀ = 0.3, and e₁ = −0.1. This implies that for males: ${\sigma }_A^2=0.6$, ${\sigma }_C^2=0.2$, E = 0.2 and for females: ${\sigma }_A^2=0.3$, ${\sigma }_C^2=0.4$, ${\sigma }_E^2=0.3$. Two sample size scenarios were considered: 450 pairs in each of the following categories: MZ males, MZ females, DZ males, and DZ females; and only 100 pairs in each category. For each of the two sample size scenarios, 1000 datasets were simulated. "NACE-S" and "Falconer-S" refer to the traditional NACE and Falconer models except fit stratified by sex. The results in Table 4 indicate that the average estimated standard errors for the GEE2 models match up well with the corresponding true standard errors, thus approximately achieving the correct coverage rates for the sex-specific heritability parameters.

TABLE 4.

Simulation allowing heritability (h²) to vary by sex: average point estimates $({\overline{h}}_{Male}^2,{\overline{h}}_{Female}^2)$ across 1000 simulated datasets. In parentheses: true standard error (standard deviation of estimates across all datasets), average estimated standard error, and 95% confidence interval coverage rate. NACE-S and Falconer-S are the traditional NACE/Falconer methods except fit stratified by sex. "Npairs" is the number of twin pairs in each category: MZ male, MZ female, DZ male and DZ female.

Npairs	Model	${\overline{h}}_{Male}^2=0.60$	${\overline{h}}_{Female}^2=0.30$
450	NACE-S	0.60 (0.07, 0.07, 0.95)	0.30 (0.07, 0.07, 0.95)
	GEE2-NACE	0.60 (0.07, 0.07, 0.96)	0.30 (0.07, 0.07, 0.94)
	Falconer-S	0.60 (0.08, 0.06, 0.84)	0.30 (0.08, 0.06, 0.83)
	GEE2-Falconer	0.60 (0.08, 0.08, 0.96)	0.30 (0.08, 0.08, 0.95)
100	NACE-S	0.59 (0.14, 0.13, 0.90)	0.31 (0.15, 0.15, 0.96)
	GEE2NACE	0.59 (0.15, 0.14, 0.92)	0.31 (0.15, 0.14, 0.94)
	Falconer-S	0.60 (0.17, 0.12, 0.82)	0.31 (0.18, 0.12, 0.82)
	GEE2-Falconer	0.60 (0.17, 0.16, 0.92)	0.31 (0.17, 0.17, 0.95)

Lastly, for a normally distributed trait, there does not appear to be any efficiency gain when jointly estimating heritability for both sexes in GEE2-NACE and GEE2-Falconer compared to NACE-S and Falconer-S which are fit separately to each sex. However, as shown in Sections 3.1-3.2, if the trait is non-normally distributed, then the GEE2 models should be preferred for their more robust confidence intervals.

3.5 ∣. Estimating Heritability for a Normally Distributed Trait with varying Sample Size

Assuming the outcome from each twin pair follows a bivariate normal distribution, we want to compare the size of the standard errors from the GEE2 and traditional methods, across a range of sample sizes. The normal NACE model should have the smallest standard errors here (since the model is correctly specified), and it is of interest to see how much larger the GEE2-NACE and GEE2-Falconer standard errors are. The outcome was simulated such that h² = 0.5, c² = 0.3, and e² = 0.2. The range of sample sizes considered were 50 MZ and 50 DZ pairs to 400 pairs each. From Table 5, notice for Npairs=50 that the average estimated standard error for the GEE2-NACE heritability estimator is larger by 0.01 (5.6%) compared to the NACE model, while GEE2-Falconer is larger by 0.04 (22.2%). For Npairs ≥100, there is no difference between NACE and GEE2-NACE, however, the average estimated standard errors of GEE2-Falconer are still larger by 0.02 (15.4%, Npairs=100), 0.01 (10%, Npairs=200) and 0.01(14.3%, Npairs=400).

TABLE 5.

Estimating heritability for a normally distributed trait with varying sample size: "Npairs" is the number of MZ and DZ twin pairs (e.g. Npairs=50 means there were 50 MZ twin pairs and 50 DZ twin pairs). In each setting, the average estimated heritability (outside the parentheses) is reported across 1000 simulated datasets. In parentheses: true standard error (standard deviation of estimates across all simulation replicates), average estimated standard error, and 95% confidence interval coverage rate. The true h² = 0.5, c² = 0.3, e² = 0.2.

Npairs	NACE	GEE2-NACE	Falconer	GEE2-Falconer
50	0.50 (0.18, 0.18, 0.89)	0.50 (0.19, 0.19, 0.92)	0.51 (0.23, 0.16, 0.82)	0.51 (0.23, 0.22, 0.93)
100	0.50 (0.14, 0.13, 0.94)	0.50 (0.14, 0.13, 0.94)	0.50 (0.16, 0.11, 0.84)	0.50 (0.16, 0.15, 0.95)
200	0.50 (0.10, 0.10, 0.95)	0.50 (0.10, 0.10, 0.95)	0.50 (0.11, 0.08, 0.84)	0.50 (0.11, 0.11, 0.94)
400	0.50 (0.07, 0.07, 0.94)	0.50 (0.07, 0.07, 0.94)	0.50 (0.08, 0.06, 0.83)	0.50 (0.08, 0.08, 0.94)

3.6 ∣. Minnesota Center for Twin and Family Research Study (MCTFR)

The Minnesota Center for Twin and Family Research study (MCTFR)^27,16 contains 8,405 subjects clustered into 4-member families (each with 2 parents and 2 twins, either MZ or DZ). The overall goal of the study is to explore the genetic and environmental factors of substance abuse disorders. We consider five composite quantitative clinical phenotypes¹⁶, which were derived using a hierarchical factor analytic approach.²⁸ These five phenotypes are: 1) Nicotine (NIC): composite measure of nicotine use and dependence, 2) Alcohol Consumption (CON): composite of measures of alcohol use frequency and quantity, 3) Illicit Drugs (DRG): composite of frequency of use of 11 different drug classes and DSM symptoms of drug dependence, 4) Behavioral Disinhibition (BD): composite of measures non-substance use behavioral disinhibition including symptoms of conduct disorder and aggression, and 5) Externalizing Factor (EXT): a composite measure of all four previous traits.

We considered a total of 936 MZ and 478 DZ twin pairs for each phenotype (all twins with non-missing phenotype data, parent data was not included). See Figure 2 for the histograms of each phenotype; notice that all five phenotypes appear very right-skewed, non-normal, and do not appear to follow any standard parametric distributions. However, as long as the trait can be approximated by a member of the quadratic exponential family with the first two moments correctly specified, then it is not necessary to try and model the true parametric distribution of these traits, rather one can simply use GEE2 which produces a robust confidence interval of heritability. Note that the five substance abuse traits considered here were only measured once on each twin, when the twin cohort had a median age of 17.8 years (standard deviation=0.7, min.= 16.6, max.=21). Later in Section 3.6.1 we consider a longitudinal measure of alcohol use. Lastly, for all five substance abuse traits, first an ordinary linear model was fit to regress out the effects of several covariates: Sex, Age, and the top 5 principle components; then the residuals were used as the new response for fitting the ACE models. Although the NACE and GEE2 models can directly adjust for covariate effects, the original Falconer’s method cannot. Thus in order to present a fair comparison between all models, the trait covariate-adjusted residuals were used as the outcome for all models. As a sensitivity analysis (results not shown), we compared h², c² estimates and standard errors between GEE2-Falconer when using the trait covariate-adjusted residuals compared to the original outcome while directly adjusting for the covariates in the mean function of the model. The results were nearly identical, differing by at most 0.01 units.

The results from Table 6 indicate several patterns. First, notice that GEE2-NACE and NACE model produce identical point estimates, however, GEE2-NACE produces larger and probably more trustworthy standard errors (as shown throughout all of simulations). Similarly, GEE2-Falconer and Falconer’s method produce identical point estimates, although the standard errors for GEE2-Falconer are likely more accurate (as shown throughout all simulations). Interestingly, Falconer’s method (and GEE2-Falconer) consistently produce smaller estimates of heritability compared to NACE (and GEE2-NACE). Recall that the NACE model assumes the population variances are equal between MZ and DZ twins, whereas Falconer’s method allows them to differ. Note that the ratio of the MZ to DZ sample variance for the five substance abuse traits is 0.95, 0.99, 0.89, 0.97, and 0.96 respectively. The fact that the observed sample variances differ between MZ and DZ twins (by at most 11%) may explain why the NACE and Falconer’s method produce different point estimates of heritability in Table 6 (with a maximum difference of 8% for DRG).

TABLE 6.

Minnesota Center for Twin and Family Research study: point estimates and standard errors (in parentheses) for 5 substance-abuse traits

Trait	Model	h 2	c 2
NIC	NACE	0.53 (0.07)	0.19 (0.07)
	GEE2-NACE	0.53 (0.10)	0.19 (0.09)
	Falconer	0.48 (0.05)	0.24 (0.05)
	GEE2-Falconer	0.49 (0.10)	0.23 (0.09)
CON	NACE	0.44 (0.06)	0.29 (0.06)
	GEE2-NACE	0.44 (0.09)	0.29 (0.08)
	Falconer	0.40 (0.05)	0.32 (0.05)
	GEE2-Falconer	0.40 (0.09)	0.32 (0.08)
DRG	NACE	0.50 (0.07)	0.20 (0.07)
	GEE2-NACE	0.50 (0.13)	0.20 (0.12)
	Falconer	0.42 (0.06)	0.26 (0.05)
	GEE2-Falconer	0.42 (0.12)	0.26 (0.11)
BD	NACE	0.67 (0.07)	0.08 (0.07)
	GEE2-NACE	0.67 (0.09)	0.08 (0.09)
	Falconer	0.63 (0.06)	0.12 (0.05)
	GEE2-Falconer	0.63 (0.09)	0.12 (0.09)
EXT	NACE	0.60 (0.06)	0.18 (0.06)
	GEE2-NACE	0.60 (0.09)	0.18 (0.09)
	Falconer	0.55 (0.05)	0.23 (0.05)
	GEE2-Falconer	0.55 (0.09)	0.22 (0.08)

Nicotine (NIC): composite measure of nicotine use and dependence; Alcohol Consumption (CON): composite of measures of alcohol use frequency and quantity; Illicit Drugs (DRG): composite of frequency of use of 11 different drug classes and DSM symptoms of drug dependence; Behavioral Disinhibition (BD): composite of measures non-substance use behavioral disinhibition including symptoms of conduct disorder and aggression; Externalizing Factor (EXT): a composite measure of all five previous traits

3.6.1 ∣. Allow h², c², e² to vary as a Non-linear Function of Age in a Longitudinal Study

The MCTFR is a longitudinal study in which data was collected from the same cohort of twins at five different time periods: ages 11, 17, 20, 24, and 29. The five quantitative phenotypes in Table 6 were only available around age 17, however, additional phenotypes related to “alcoholism” were available at multiple time points (but not all time periods). The GEE2-Falconer model was used to jointly model the h², c², e² parameters from ages 17-29 for a count phenotype measure of alcohol use (values range from 0 to 5, larger values indicate greater alcohol use). See Supplemental Figure S1 for a histogram of the longitudinal alcohol phenotype.

The GEE2-Falconer model was fit as described in Section 2.3.2, with the following modification to allow the h², c², e² parameters to vary as a 2nd-degree polynomial function of age:

$$\begin{gathered} g({\sigma }_z^2)=v_0+v_{1}z+v_{2}Age+v_{3}Ag{e}^2+v_{4}Age\ast z+v_{5}Ag{e}^2\ast z \\ h({\rho }_z)=p_0+p_{1}z+p_{2}Age+p_{3}Ag{e}^2+p_{4}Age\ast z+p_{5}Ag{e}^2\ast z \end{gathered}$$ (8)

where Age is the age of a given twin pair, and Age² = (Age − mean(Age))² is the squared centered age of a given twin pair. Recall from Section 2.3.2 that covariate-zygosity interaction terms are necessary when incorporating ACE covariate effects for GEE2-Falconer. The interaction terms allow the correlations and ACE covariate effects to differ between MZ and DZ twins. For example, to estimate the heritability at age 17, the relevant covariate values are plugged into equation (8) to get ${\widehat{\rho }}_{M{Z}_{17}}$, ${\widehat{\rho }}_{D{Z}_{17}}$, then ${\widehat{h}}_{17}^2=2({\widehat{\rho }}_{M{Z}_{17}}-{\widehat{\rho }}_{D{Z}_{17}})$.

Although it’s straightforward to apply equations (4) and (6) in a cross-sectional study, it’s challenging to extend these to handle repeated measures in a longitudinal study. Equation (8) models the correlation between a pair of twins’ measures within a single time period, but treats the correlation across time periods or age groups (e.g. the correlation between a twin’s outcome at Age 17 and Age 29) as independent. In order to account for the correlation across time periods, we propose using the "cluster-bootstrap"²⁹ when calculating standard errors and confidence intervals for h², c², e², rather than equation (6). For the cluster-bootstrap, a single twin pair and all of its repeated measures are treated as a "cluster." These clusters are then resampled with replacement of size N (where N is the total number of clusters) and equal probability of selection. The model is then refit to the resulting bootstrap sample and h², c², e², are re-estimated. This process was repeated 5000 times. The bootstrap 95% CIs are then calculated as the 2.5th and 97.5th percentiles of the bootstrap distributions of a given statistic. Bootstrap standard errors can be estimated as the standard deviation of the bootstrap distribution.

Figure 3 displays the point estimates and cluster-bootstrap 95% percentile confidence intervals for h², c², e² at Ages 17-29. Notice that the non-shared environmental effect (e²) increases over time, while the shared environmental effect (c²) decreases. The genetic effect (h²) on the Alcohol Use trait remained relatively stable across the four time periods. Wald tests were used to check if h², c², e² significantly changed from ages 17 to 29 (e.g. ${\mathrm{H}}_0:h_{29}^2-h_{17}^2=0$, $\text{wald-stat}=({\widehat{h}}_{29}^2-{\widehat{h}}_{17}^2)∕\widehat{\text{SE}}{}_{boot}$, where $\widehat{\text{SE}}{}_{boot}$ is estimated as the standard deviation of the bootstrap distribution of the numerator) and produced the following p-values respectively: 0.76, 0.066, and < 0.0001. Intuitively, these results may mean that as the twins age and become more independent, their non-shared environmental experiences have a greater influence on their alcohol use, whereas the effect of their shared-family environment decreases.

FIGURE 3.

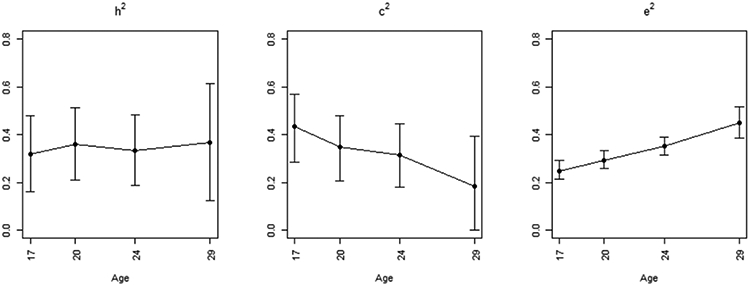
GEE2-Falconer model with h², c², e² allowed to vary as a non-linear function of Age (with 95% confidence intervals) for a longitudinal alcohol use trait from the Minnesota Center for Twin and Family Research study. There were 611 MZ and 341 DZ twin pairs with the outcome measured at all ages 17, 20, 24, and 29.

h², c², e²: proportion of total trait variance due to additive genetic effects, common shared environmental effects, and unique non-shared environmental effects respectively

Lastly, two more points are worth highlighting from the results in Supplemental Table S2. Jointly modeling the Alcohol Use trait at all four time periods usually resulted in smaller standard errors compared to fitting separate univariate GEE2 models at each time period. Interestingly, the cluster-bootstrap standard errors (which account for a twin pair’s correlation within each time period and across time periods) were nearly identical to the sandwhich standard errors that ignore the correlation between a twin pair’s outcome over time; although the cluster-bootstrap standard errors were consistently slightly larger.

4 ∣. DISCUSSION

Twin studies have proven to be powerful instruments in quantifying the genetic and environmental factors of complex phenotypes.^2,1 In practice, the normal ACE model (“NACE”)^7,8 and Falconer’s moment estimators^6,5 are popular methods for estimating heritability in twin studies. We’ve shown that both models can be fit within a unified second-order generalized estimating equations framework (“GEE2”), which provides robust standard errors and can incorporate covariate effects for both mean and variance parameters (e.g. let heritability vary by sex or age as done in Sections 3.4 and 3.6.1). It’s worth emphasizing that the original version of Falconer’s method⁶ cannot directly adjust for covariate effects, whereas our GEE2-Falconer model can.

Researchers are often interested in estimating heritability for non-normal phenotypes (e.g. counts, binary, skewed or heavy-tailed continuous data). When interested in fitting an ACE model to a non-normal phenotype, one option is to try and parametrically model the true distribution.^15,13,14,12 However, inferences on the variance components may be sensitive to departures from parametric distributional assumptions. Our simulations indicate that when the parametric distributional assumption is incorrect, Wald-type confidence intervals for the ACE variance parameters may significantly differ from the nominal rate. In addition, we’ve shown that as long as the trait can be approximated by a member of the quadratic exponential family, then it is not necessary to try and fit the true parametric distribution; rather one can simply use GEE2 which provides a robust confidence interval for the true heritability. The GEE2 model requires only the first two moments (i.e. mean and variance structures) to be correct, all other moments are allowed to be misspecified. In contrast, parametric models assume all moments (i.e. the likelihood function) are correct, and may lead to poor coverage rates when assumptions fail.

In Section 3.3, we demonstrated an important scenario where NACE produces biased estimates of heritability, while Falconer’s method remains unbiased. Specifically, the NACE assumes that the ACE variance components are equal for both MZ and DZ twins (e.g. ${\sigma }_{A_{MZ}}^2={\sigma }_{A_{DZ}}^2$); whereas Falconer’s method allows the variance components to differ between twins, and only assumes the variance proportions are the same for both twin types (e.g. $h_{MZ}^2=h_{DZ}^2$). A recent meta-analysis¹ of all twin studies performed in the last 50 years demonstrated that NACE and Falconer’s methods can produce substantially different estimates of heritability in practice (see their Supp. Figures 9-10 and Supp. Section 5.7). Our results highlight one possible explanation for these differences: if the magnitude of the ACE variance parameters differs between MZ and DZ twins (a common criticism of twin studies⁵), then the NACE will produce biased estimates of heritability, while Falconer’s method remains unbiased under weaker assumptions. Additionally, although far from solving the problem, this potential NACE-bias could be one of many factors contributing to the “missing heritability phenomena” where several authors have suggested that twin/family studies may be overestimating heritability.^30,31,32 Figure 1 shows that as the DZ trait-variance becomes larger than the MZ variance (which can happen due to sibling contrast effects¹¹), then NACE over-estimates heritability. As discussed in Section 3.3, one possible solution to remove the NACE bias is to first separately scale the MZ and DZ variances to 1. However, when interested in allowing heritability to differ by multiple covariates (especially continuous covariates), it is unclear how one should scale the outcome to remove this bias. Thus Falconer’s method (and GEE2-Falconer) may be preferred since it remains unbiased under weaker assumptions without requiring any data transformations/scaling.

In practice, the large twin study meta-analysis of Polderman et al¹ found that in the top 8 countries with the most number of twin studies, the average number of twin pairs per study ranged from 579 to 2,104 with 5/8 of these countries all averaging >1000 twin pairs per study. Only 2 countries in the top 20 had an average sample size <100 twin pairs per study (71 and 83 respectively). Nevertheless, further research improving the small-sample performance of GEE2-heritability estimators may be warranted, such as using cluster-bootstrap based confidence intervals. ²⁹

Another area for future work is "model-selection" for GEE2-based twin models. For example, what mean-level covariate effects should be included, should one use GEE2-NACE or GEE2-Falconer (we recommend the later due to the potential bias of GEE2-NACE demonstrated in Section 3.3), and what covariates should one allow heritability to differ by. Several information criteria have been proposed for model selection in GEE-type models.^33,34,35 It would be interesting to try extending these methods to the GEE2-NACE and GEE2-Falconer twin models, especially for deciding which covariates affect heritability.

Although this paper focuses on the ACE model, all models considered can be extended to fit the “ADE” twin model, where “D” stands for genetic dominance effects. In practice, researchers typically fit an ACE model if r_DZ > 0.5r_MZ, and an ADE model when r_DZ < 0.5r_MZ.⁵ However, we chose to focus on the ACE model for several reasons: 1) both^36,4 found that ignoring shared environmental effects lead to greater bias in estimated heritability compared to ignoring dominance or epistatic genetic effects. 2) Assuming the true model is ACDE, Wang et al ⁸ proved that ${\widehat{\sigma }}_A^2$ from a working ACE model is a consistent estimator of ${\sigma }_A^2+1.5{\sigma }_D^2$; while ${\widehat{\sigma }}_A^2$ from a working ADE model is a consistent estimator of ${\sigma }_A^2+3{\sigma }_C^2$. Notice the working ACE model estimate of ${\sigma }_A^2$ only reflects genetic effects (both additive and dominant), while the working ADE model estimate of ${\sigma }_A^2$ is confounded/biased by shared environmental effects. Thus if the goal is to estimate heritability (the proportion of trait variance due to genetic effects), then the working ACE model seems preferable to the working ADE model under model misspecification. 3) The Minnesota Center for Twin and Family Research study (Section 3.6) focused on substance abuse disorder traits, which have been shown to have substantial shared family environmental effects.¹

Lastly, although it is straightforward to use equations (4,6) to estimate heritability in a cross-sectional study, there are several challenges in extending these to estimating heritability in a longitudinal study with repeated measures. For example, the application in Section 3.6.1 had 4 repeated measures on each twin, for a total of 8 correlated measures within each twin pair. We proposed a simplified approach that treated the correlation between a twin’s repeated measures over time as independent, and accounted for this correlation when making inferences within a single time period by using the cluster-bootstrap.²⁹ However, further research should be conducted in using GEE2 to jointly estimate heritability in longitudinal studies.

In summary, we’ve shown that given non-normal data, the traditional normal NACE or Falconer’s method may significantly undercover the true heritability parameter. In contrast, the proposed GEE2 models can obtain valid inference for the heritability of a wide variety of outcomes, such as: normal, binary, counts, and heavy-tailed or skewed continuous traits. The GEE2 framework requires only the first two moments (i.e. mean and variance structures) to be correctly specified, while all higher-order moments are allowed to be modeled incorrectly. We showed that both the traditional NACE and Falconer’s methods can be fit within a unified GEE2 framework which provides robust standard errors and can incorporate covariate effects in mean and variance-level parameters (e.g. let heritability vary as a function of age or sex). It is important to note that the traditional Falconer’s method⁶ cannot directly adjust for covariate effects whereas our GEE2-Falconer model can. Finally, we demonstrated that if the ACE variance parameters differ between MZ and DZ twins, then the standard NACE produces biased estimates of heritability, while Falconer’s method still produces unbiased estimates under weaker assumptions. Therefore, we recommend GEE2-Falconer for estimating the heritability of non-normally distributed outcomes in future twin studies.