Abstract
The aim of this study was to develop a multistate model for overall survival (OS) analysis, based on parametric hazard functions and combined with an investigation of predictors derived from a longitudinal tumor size model on the transition hazards. Different states – stable disease, tumor response, progression, second‐line treatment, and death following docetaxel treatment initiation (stable state) in patients with HER2‐negative breast cancer (n = 183) were used in model building. Past changes in tumor size prospectively predicts the probability of state changes. The hazard of death after progression was lower for subjects who had longer treatment response (i.e., longer time‐to‐progression). Young age increased the probability of receiving second‐line treatment. The developed multistate model adequately described the transitions between different states and jointly the overall event and survival data. The multistate model allows for simultaneous estimation of transition rates along with their tumor model derived metrics. The metrics were evaluated in a prospective manner so not to cause immortal time bias. Investigation of predictors and characterization of the time to develop response, the duration of response, the progression‐free survival, and the OS can be performed in a single multistate modeling exercise. This modeling approach can be applied to other cancer types and therapies to provide a better understanding of efficacy of drug and characterizing different states, thereby facilitating early clinical interventions to improve anticancer therapy.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
In traditional overall survival (OS) analysis, a single hazard function is applied to the survival data in the presence of competing events, such as death due to non‐cancer causes and censoring. This could lead to a biased estimation of the hazard. Moreover, immortal time bias originating from a failure to adequately account for time‐dependent predictors in the OS model can be a major issue.
WHAT QUESTION DID THIS STUDY ADDRESS?
The intermediate events prior to OS time might contain accompanying information on disease status and hazard of death. A multistate model could be a way of characterizing the intermediate events and evaluation of predictors that are specific to the transition, and jointly describing the survival data. Different states – stable disease, tumor response, progression, second‐line treatment, and death following docetaxel treatment in patients with HER2‐negative breast cancer were used in model building.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
The developed multistate model operated by parametric hazard functions, estimates the transition hazards of intermediate events, and allows investigation of predictors derived from a longitudinal tumor size model. Past changes in tumor size prospectively predicts the probability of state changes the hazard of death after progression was lower for subjects who had longer time‐to‐progression. The developed multistate model adequately described the transitions between different states and jointly the survival data.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
Investigation of predictors and characterization of the time to develop response, the duration of response, the progression‐free survival, and the OS can be performed in a single multistate modeling exercise. This modeling approach can be applied to other cancer types and therapies to provide a better understanding of efficacy of drug and characterizing different states, thereby facilitating early clinical interventions to improve anticancer therapy.
INTRODUCTION
Modeling of longitudinal tumor size (TS) data to establish exposure‐response‐outcome relationships has been increasingly applied to facilitate trial design and the go/no‐go decision making in oncology clinical trials. 1 , 2 Time to event (TTE) models allow investigation of the association between various covariates and long‐term clinical end points, such as progression‐free survival (PFS) and overall survival (OS). The developed TS‐TTE models have the potential to predict PFS/OS of a similar population (i.e., same indication and end points), for example, utilizing results from phase II, and simulating event distributions in phase III trials. In a randomized clinical trial, the efficacy of new molecule is characterized into different response categories by the response evaluation criteria in solid tumors (RECIST), 3 , 4 which is based on the change in sum of longest diameters (SLDs). The TS is typically only recorded until disease progression because later to that, patients receive a different treatment or a sequential line of cancer therapy. The survival data comprise, however, the full duration of the time from enrollment into the clinical trial to the event of death or censor (end of trial or loss of follow‐up). Therefore, the existing TTE modeling approach where estimation of a single survival function to OS data has problems. The model predicted tumor size (or biomarker) is typically extrapolated until OS time during survival analysis, 5 , 6 , 7 leading to not accounting the effect of the sequential therapy. Immortal time bias originating from a failure to adequately account for time‐dependent covariates in the TTE model can be a major issue. For example, using “depth of tumor response” as a covariate on survival may introduce bias as a substantial decrease takes considerable time to achieve. 8 Thus, only the individual surviving for considerable time will have a large decrease in TS. Multistate models could be a way of addressing these issues and describe the hazard over time correctly.
In traditional survival analysis, a single hazard function is applied to the survival data in the presence of competing events, such as death due to non‐cancer causes and censoring. This could lead to a biased estimation of the hazard. Moreover, the intermediate events prior to OS time might contain accompanying information on disease status and hazard of death, for example, the RECIST assessment of progressive disease from stable disease/partial response may indicate an increase in the risk of death. Multistate models have been recommended and has been increasingly used for such data. 9 , 10 , 11 For the analysis of survival data, Beyer et al. 12 developed a multistate model, where the transition hazards of intermediate events were modeled using semiparametric models with a treatment arm as a binary covariate. The implementation of multistate models in a nonlinear mixed effect (NLME) modeling framework would allow NLME‐derived covariate evaluation. 13 NLME implementation could also allow for random effects 14 or mixture models to be incorporated into the description of the data. This investigation gives an example of the latter. In an NLME framework, the tumor model derived predictors can be evaluated to be transition‐dependent, and could more reliably predict different states (for example, time to response and duration of response) and survival. The aim of this study was to develop a multistate model operated by parametric hazard functions using data from docetaxel treated patients with HER2‐negative breast cancer, while allowing investigation of predictors derived from the longitudinal TS model on the transition hazards.
METHODS
Data
The tumor data (SLD) were available from the docetaxel (control) arm of the phase III AVADO trial where the efficacy and safety of combining bevacizumab with docetaxel were investigated in patients with HER2‐negative metastatic breast cancer (ClinicalTrials.gov Identifier: NCT00333775). 15 In the docetaxel arm (n = 241), three patients did not receive therapy, 21 patients either received one dose of bevacizumab (n = 7) or started bevacizumab before disease progression (n = 14) and 34 patients did not have a measurable target lesion at baseline. 15 Therefore, these 58 patients were not included in the multistate modeling, hence, the study data consisted of 183 patients with HER2‐negative metastatic breast cancer. The subjects were women with a median age of 55 years (range 29–83 years). Patients received docetaxel 100 mg/m2 infused over 1 h on day 1 of each 3‐week cycle. The SLD were evaluated from computed tomography scans every 9 weeks during the first 36 weeks and thereafter every 12 weeks; median follow‐up was 32 weeks (range 6–160 weeks). The TS response was evaluated according to RECIST version 1.0 3 (i.e., up to 10 lesions/patient were followed during the trial). Because individual lesion and metastatic organ data were available, the tumor SLD were re‐created as per the RECIST version 1.1 criteria, 4 which consider measurements of up to five lesions/individual but not more than two lesions/organ. The AVADO trial was conducted according to the Declaration of Helsinki, the Good Clinical Practice guidelines of the International Conference on Harmonization, and the laws and regulations of the countries involved. The protocol was approved by local ethics committees and written informed consent was obtained from all patients before the screening.
Tumor model
A tumor growth inhibition (TGI) model was applied to describe the change in SLD over time. 16 In this model, the tumor was best described to grow exponentially with a first‐order rate constant (kGROW). The tumor size shrinkage during treatment was explained by drug exposure, the drug‐specific cell kill rate constant (kSHR), and the emergence of resistance to the treatment (LAMBDA) (Equation 1). As docetaxel concentrations were not available, a population K‐pharmacodynamic (PD) modeling 17 approach (Equation 2), where the K‐PD parameter represents the elimination rate constant in K‐PD model, was used along with the TGI model to describe the docetaxel exposure over time (. Interindividual variability was tested on all parameters.
| (1) |
| (2) |
where IBASE, model estimated baseline SLD for individual I; TS(t), tumor time course; DOSE, the docetaxel dose, is the tumor growth rate; cell kill rate constant; LAMBDA, resistance parameter; , docetaxel exposure over time; K‐PD, the elimination rate constant.
Multistate model
Depending on the patient‐level tumor response and OS event data, subjects had the possibility to transfer among five different states. The states considered were stable disease (S1, time = 0 state), tumor response (S2, >= 30% decrease in SLD from baseline), progressive disease (S3, >= 20% increase in SLD from tumor nadir or appearance of new lesions or progression of nontarget lesions), initiated second‐line treatment (S4) and death (S5). At baseline, all individuals were assigned in the stable disease state and during the study and follow‐up period, after progression they could transfer to other states, as shown in Figure 1. In contrast to RECIST response evaluation, in multistate model if a tumor response (>= 30% decrease in SLD from baseline, stable →response) was observed, then the subject cannot move back to stable state (response →stable) even if it is later observed that the %decrease in SLD from baseline is less than 30%, or the %increase in SLD from baseline is less than 20%.
FIGURE 1.
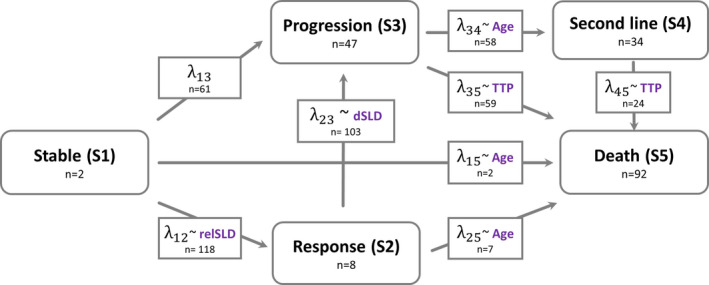
The multistate model describing different states in patients with HER2‐negative breast cancer treated with docetaxel. The represents the transition intensities between each state and the n along with is the number of observed transitions from state i to state j. The n along with different states are the number of clinical outcomes at the end of study. The metric in the dotted box indicating the associated predictor of the transition intensities in the final multistate model. relSLD, relative change from baseline; dSLD, change in SLD between previous two measurements; TTP, time to progression; Age, age in years
A multistate model, 13 where the transition rates () between each state were estimated, was developed to describe the observed events (Equations (3), (4), (5), (6), (7)). The transition intensity () was evaluated with different hazard distributions (Exponential and Weibull) and selected based on the likelihood ratio test.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Where Si‐j, different states; transition intensities between state i (Si) and state j (Sj) and Si‐j0, the initial conditions for the state.
The hazard of death from second‐line treatment () was set to be the same as the hazard for progression to death () if it was not statistically different from . A mixture model with two subpopulations was evaluated on , where the first population received second‐line treatment after disease progression and the second population did not receive second‐line therapy (i.e., . The investigated predictors on transition rates included baseline variables: age, Eastern Cooperative Oncology Group (ECOG) score at enrollment, TS, total number of lesions, number of metastatic sites involved, as well as post‐baseline model‐based tumor dynamic estimates: relative change in SLD from baseline to the present SLD, relative change in SLD between two previous measurements (dSLD), relative change in SLD from tumor nadir (defined as the lowest SLD up until the present time point) to the present SLD, tumor growth rate , and rate of appearance of resistance (LAMBDA. Both past‐observed and model‐predicted tumor dynamic metrics at time of transitions were evaluated as predictors of transition rate. Additionally, reason(s) of disease progression (>= 20% increase in SLD from tumor nadir or appearance of new lesions or progression of nontarget lesions), number of new lesions, and time to progression were investigated on . The predictors were investigated using proportional hazards model with a baseline transition rate of for example, predictor on transition rate stable to decrease () for individual would be:
| (8) |
where is the value of for individual I; is the population median value of ; is the coefficient of the effect of on , and represents the hazard ratio associated with covariate .
In traditional survival analysis, the predictors have most often been evaluated sequentially but in some cases as a joint model. 18 The metrics derived from a tumor model, for example, tumor growth rate ( or time‐to‐regrowth (TTG), has been computed based on all collected tumor data. In a sequential or joint model, the computed or TTG information is treated as baseline covariate (i.e., as it is available at time 0). This does not recognize that data relevant for its estimation largely is obtained after start of therapy. Whereas joint models with estimated time‐varying predictors (e.g., tumor time‐course [SLDt]) to some extent account for the immortal time bias, they are typically estimated based on all the tumor data, including the future tumor data. Thus, a tumor‐OS joint modeling does not completely eliminate such bias. 19 In the current analysis, the post‐baseline time‐varying predictors were investigated in a way that the future tumor observations would not influence the present predictions of transition rates. Thus, in contrast to the standard use of population pharmacokinetic (PK)PD models where all data contribute to defining individual parameters, only observations up to time t was used to make predictions beyond time t for each individual parameter. As a consequence, the tumor dynamic model parameters for an individual will change over time as more observations become available. The derivation of the model predicted metrics on‐fly using a joint tumor‐multistate model or using the PPP&D approach 18 could not be applied here, as the estimates are based on all available data. The proseval tool from PSN 20 was used for deriving tumor dynamic model parameters (, , and model predicted tumor change) with successive increase in number of tumor measurements and these metrics were available to the multistate model through the input dataset.
Model development and evaluation
Population models were developed using the nonlinear mixed‐effect modeling (NONMEN) software (version 7.4.4). 21 Model development was assisted by Pirana (version 2.9.9) for run management, the Perl‐speaks‐NONMEM (PsN) toolkit for handling NONMEM run commands, R (version 3.6), and Xpose (version 4.1) for model diagnostics and graphical analysis. 22 The objective function value (OFV; −2 log‐likelihood) and graphical diagnostics were used in the evaluation of model performance. A randomization test (randtest tool in PsN 20 ) was performed to determine actual significance levels and an OFV decrease of 5.17 (p < 0.05) was considered as significant for the addition of one parameter (1 degree of freedom) while testing predictors in the multistate model. An increase in OFV of 18.9 (p < 0.001) was used while testing (decrease in 1 degree of freedom). Parameter uncertainties were derived using the sampling importance resampling (SIR) 23 tool in PsN (tumor model) or R matrix (multistate model). Visual predictive checks (VPCs) for the tumor model and Kaplan–Meier VPCs for the multistate model were used for evaluating the predictive performance of the models. In the tumor model VPC, the simulated tumor data that is greater than 20% increase in SLD from tumor nadir along with at least 5 mm absolute size increase in SLD were censored (RECIST ‐ Progressive Disease based on target lesions 4 ). The final multistate model was evaluated using the case deletion diagnostics (CCD) tool in PsN 20 to identify any potential influential individual of estimated parameters/covariate effects.
To investigate if the final multistate model can be applied in a prospective manner to predict hazard of death over time for each individual, the “individual dynamic prediction” methods suggested by Desmée et al. 24 was used. The individual dynamic predictors include, time‐dependent Brier score (BS; Equation 9) and the time‐dependent area under the receiver operating characteristic (ROC) curve (AUC) metric (Equation 10). 24 , 25 The methods proposed by Desmée et al. 24 for assessing dynamic predictions and calculation of BS and AUC were here applied to the tumor‐multistate model implemented in NONMEM. The individuals’ data until landmark time (s) were used for deriving a posteriori distribution, from this distribution, 200 samples were drawn to compute the predicted hazard of death for each individual in the prediction window (t). In NONMEM, the SAEM estimation method along with ETASAMPLES argument was used for obtaining 200 samples from the conditional distribution. 25 The landmark times (s) considered were 0, 3, 6, 9, 12, and 18 months and prediction windows (t) until 36 months.
| (9) |
| (10) |
| (11) |
Where model predicted probability of death for subject i in interval s to s+t given individual survival to time s; , brier score based on the final multistate model; , brier score based on the base model without any covariates.
The time‐dependent AUC was calculated using timeROC R package and BS function (R script) by Blanche et al. 26 To account for censoring bias, the inverse probability of censoring weighting approach 27 , 28 , 29 was applied in both BS and AUC calculations. Because the number of events and number of subjects alive at that landmark time are different, scaled BS (sBS; Equation 11) was used for comparing different landmark times. 30 The sBS calculates the relative improvement from the base model in predicting individuals’ hazard of death over time in the final multistate model, whereas the AUC score shows the how well the final model distinguishes patients of low and high risk of death.
RESULTS
Tumor model
The tumor data consisted of 903 observations and the median SLD at time of enrollment (SLD0) was 56 mm (range, 10–221). OS data were collected for a median of 108 weeks (range, 12–160 weeks) after the start of docetaxel treatment. Ninety‐two patients (51%) had death event and the median time to death was 50 weeks (range, 13–145). The main characteristics of the study population are summarized in Table 1. The TGI model described the longitudinal SLD adequately and the parameter estimates in the final tumor model are provided in Table 2. The typical (k GROW) was estimated as 0.00576 week−1 (i.e., a tumor doubling time of ~ 2.3 years [doubling time = ln(2)/kGROW]). The interindividual variability was significant on all parameters, and kGROW was associated with a large interindividual variability (IIV; 126 coefficient of variation percentage [CV%]). The predictive performance was adequate from the VPC diagnostics (Figure S1) and the parameter uncertainties were less than 48% relative standard error (Table 2). The case deletion diagnostics did not identify any influential individuals of the parameter estimates (Figure S2a).
TABLE 1.
Summary of patients’ characteristics and data
| Characteristics | Median | Range |
|---|---|---|
| Total number of patients, n | 183 | ‐ |
| Age, years | 54 | 29–83 |
| Sum of longest diameters at baseline, mm | 56 | 10–221 |
| Tumor follow‐up, weeks | 35 | 6–160 |
| ECOG score at baseline, 0/1 (n) | 108/75 | ‐ |
| New lesion appearance (yes), n | 121 | 68% |
| Time of new lesion appearance, weeks | 34 | 6 – 111 |
| Overall survival time, weeks | 108 | 13–160 |
| Death events, n | 92 | 51% |
| Time to death, weeks | 50 | 13–145 |
Abbreviation: ECOG, Eastern Cooperative Oncology Group.
TABLE 2.
Parameter estimates and their uncertainty in the final tumor model
| Parameter | Description | Estimated value (RSE a ) | Interindividual variability CV% (RSE) |
|---|---|---|---|
| kGROW | Tumor growth rate (week−1) | 0.00576 (37) | 126 (15) |
| LAMBDA | Rate of resistance appearance (week−1) | 0.0703 (26) | 46 (18) |
| kSHR | Docetaxel specific cell kill rate (week−1) | 0.000809 (43) | 48 (16) |
| IBASE | Baseline tumor size (mm) | 58.9 (9) | 77 (11) |
| KPD | Parameter relating drug elimination in KPD model (week−1) | 0.66 (48) | 22 (19) |
| RUV b | Residual unexplained variability | 22% (7) | ‐ |
Abbreviations: CV%, coefficient of variation percentage; RSE, relative standard error.
Proportional residual error model.
Obtained from Sampling Importance Resampling (SIR).
Multistate model
The multistate data consisted of 961 observations that includes 720 post baseline tumor measurements, 58 second line and deaths (92)/censor (91) events. There were 432 transitions between each event (Figure 1). The multistate model operated by parametric hazard functions was developed to successfully characterize the different events in patients with HER2‐negative breast cancer treated with docetaxel. In the final model, the transition hazard λ12 (stable to response state) was decreasing with time, indicating that the probability of observing response state diminished over time. The past observed relative change from baseline SLD was predictive of λ12; every 10% reduction in SLD from baseline increased transition rate by 90%. The longer a patient stayed in the stable state the hazard of progression (λ13) became higher (i.e., λ13 increased with time). No covariates were significant in predicting λ13.
A constant hazard function described the transition from tumor response to progressive disease (λ23) and every 10% increase in the past observed SLD between the two previous measurements increased the hazard by 15%. A mixture model with two subpopulations best described the transition from progressive disease to second‐line (λ34), where 45% of disease progressors (pop‐1) received second‐line treatment within 6 weeks after disease progression and remaining 55% (pop‐2) did not receive second‐line treatment. Age was a significant predictor for the probability to receive second‐line treatment (i.e., younger patients had higher chance to receive second‐line therapy after disease progression than older patients).
The hazard of death from the second‐line treatment state was similar to the hazard for death from the state of progression and the parameter could be shared for the two transitions (λ45 = λ35) and was best described using a constant hazard function. The hazard of death was lower for subjects who had longer treatment response durations (i.e., longer time‐to‐progression). The baseline covariates and tumor model parameters ( or ) were not predictive of any transition rate. The model predicted tumor dynamics did not retain level of significance once the observed SLD changes at the previous tumor measurement were included in the model. The estimated hazard of death from stable disease (λ15) and tumor response (λ25) was estimated to be close to 0, and hence the hazards were fixed to Gompertz‐Makeham distribution 31 to allow for a hazard no lower than the expected age‐specific hazard.
The final parameters and their uncertainties are given in Table 3. The VPCs showed good predictive performance of the final model (proportions in different states, Figure 2 and Kaplan–Meier VPC Figure S3). The case deletion diagnostics results demonstrated no influential individuals that drive the parameter estimates and estimated covariate effects (Figure S2b).
TABLE 3.
Parameter estimates and their uncertainty in the final multistate model
| Parameter | Description | Transition | Estimated value | Hazard ratio a | RSE b | |
|---|---|---|---|---|---|---|
| Scale_12 | Scale and shape parameter in Weibull distribution for c | Stable →Response | 0.0348 | ‐ | 18 | |
| Shape_12 | 0.316 | ‐ | 15 | |||
| Scale_13 | Scale and shape parameter in Weibull distribution for c | Stable →Progression | 0.0206 | ‐ | 10 | |
| Shape_13 | 1.99 | ‐ | 14 | |||
|
|
Exponential distribution (week−1) | Response →Progression | 0.0372 | ‐ | 10 | |
| PPOP1 | Proportion of population receiving second line PPOP1 | ‐ | 0.445 | ‐ | 11 | |
| _POP1 c | Exponential distribution (week−1) | Progression →Second line | 0.171 | ‐ | 17 | |
| _POP2 | Fixed parameter | ‐ | 0.001 | ‐ | ||
|
|
Exponential distribution (week−1) | Progression →Death | 0.050 | ‐ | 23 | |
|
|
Coefficient of the effect of past change in SLD from baseline d on | −6.42 | 1.90 for every 10% decrease in SLD from baseline | 16 | ||
|
|
Coefficient of the effect of time to progression on | −0.0477 | 0.95 for every extra week from median TTP of 35weeks | 16 | ||
|
|
Coefficient of the effect of past change in SLDm on | 1.36 | 1.14 for every 10% increase in dSLD | 34 | ||
|
|
Coefficient of the effect of age on PPOP1 | −0.0512 | 1.05 for every one year less from median Age of 54years | 40 |
Abbreviation: SLD, sum of longest diameter.
Hazard ratio = ; for CHB, = −0.1 (10% decrease); for TTP, = (36–35) = 1 (week); for dSLD, = 0.1 (10% increase); for AGE, = (53–54) = −1 (year) and is corresponding coefficient of effect.
Obtained from NONMEM R‐matrix.
, is the transition intensities.
Past observed SLD derived metrics.
FIGURE 2.
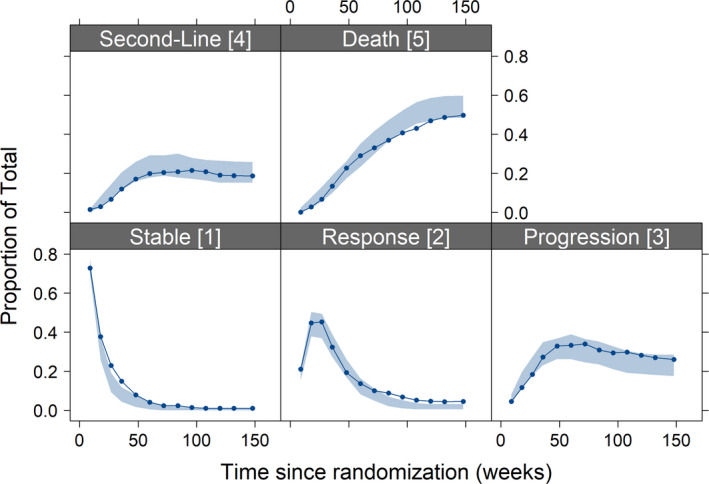
Visual predictive checks of the final multistate model. The sold line represents the observed data and blue shaded area is 95% confidence interval from 200 simulations
The sBS (Equation 11) showed that the final multistate model improved 5–26% in the accuracy of predicting survival at an individual level compared to the base model (Figure 3) along with a systematic increase in the AUC values (Table S1). For early predictions, a landmark time of s = 3 months was useful, and the BS was 0.19 (sBS = 0.29, ~30% improvement compared to base model) but with a smaller discrimination value (AUC = 0.19). The landmark time of s = 6 months provided best overall score for all prediction windows, when both BS (sBS ~0.2) and AUC metric (~ 0.25) were considered. The sBS for landmark time t = 0 was 0, indicating with only baseline information, the base model and full model perform similarly. The AUC values for s = 9 months were slightly better than the AUC for s = 6 months, however, the sBS was less than 0.15. The AUC improved (0.27 to 0.68) with a longer landmark times, whereas the sBS marginally affected by landmark time greater than 6 months.
FIGURE 3.
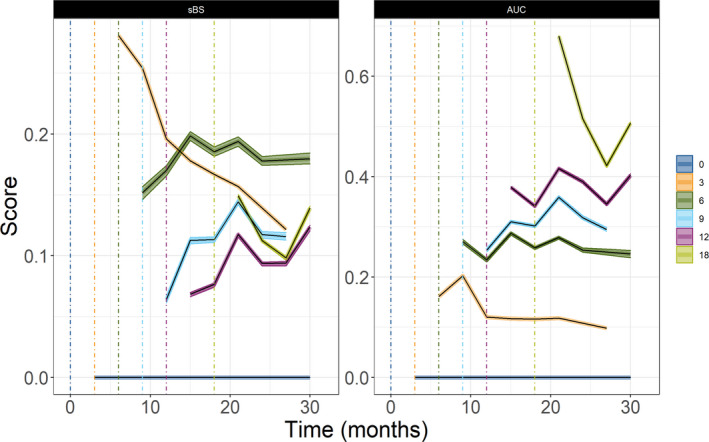
The 95% confidence interval around median scaled Brier score (sBS) (left panel) and time dependent area under the curve for different landmark times in months (0 [blue], 3 [yellow], 6 [green], 9 [light blue], 12 [purple], and 18 [light green]). There is no improvement at landmark time t = 0, and sBS = 0
DISCUSSION
Herein, a multistate model was developed to characterize the different intermediate events as per RECIST response status and jointly describing the survival data. The developed multistate model allows for simultaneous estimation of transition rates along with their tumor model derived predictors and their effect on transition rates. Changes in tumor SLD were predictive of treatment response and progression, whereas the duration of response or time to progression was predictive of hazard of death after progression.
Various metrics derived from longitudinal models (e.g., tumor or biomarker model) have been identified as predictors of OS. 2 , 5 , 6 , 7 , 16 , 30 , 32 , 33 , 34 In contrast to traditional tumor‐OS analysis, the multistate model framework is quite flexible model for describing the hazard of death with time and the metrics are investigated as predictors of the intermediate events. The intermediate events jointly described the hazard of death. In the current analysis, a large decrease in the relative change from baseline and an increase tumor size change from the previous two measurements were associated with a high transition rate of λ12 and λ23, respectively. The metrics were evaluated in a prospective manner so that there will not be immortal time bias.
The hazard of death after progression was higher for patients who had early disease progression (shorter time to progression). Time to progression is a similar predictor to a frequently identified predictor of OS – time to re‐growth (TTG). 2 , 16 , 35 , 36 , 37 , 38 Time to re‐growth is the time to achieve tumor nadir and calculated from model parameters. Time to progression is defined as an increase of greater than or equal to 30% in SLD from tumor nadir or identification of new lesions, or increase in nontarget lesions, and could be a different time than model derived TTG. The hazard of death from second‐line treatment and from progression was not statistically different. However, depending on the cancer type and treatments the hazard could vary between patients who received second‐line treatment compared to patients who did not receive treatment. A multistate model could be used to investigate the hazard of death associated with second‐line treatment and simulate the OS associated with the primary therapies (clinical trial regimens) without the confounding effect of second‐line treatment to provide a fair comparison of control versus treatment groups.
The multistate model could give detailed information compared to traditional TS‐OS analysis. This single framework allows investigation of predictors and characterization of time to tumor response, duration of response, PFS and OS (Figure S3). From the developed multistate model herein for docetaxel therapy in patients with HER2‐negative metastatic breast cancer, the median time to docetaxel response was 12 weeks (Figure S3a; i.e., after 4 cycles of docetaxel therapy). Median duration of response (time in response state) was 26 weeks, and this could be interpreted as the median time to develop resistance to therapy and tumor regrowth (Figure S3b).
Traditionally, tumor shrinkage (response) or growth is evaluated as an early marker of efficacy of an anticancer therapy. In clinical trials involving newer therapies like immunotherapies and regimens involving multiple molecules, identifying the proportion of responders at an early stage as compared to a clinical trial with cytotoxic therapy could be challenging. 39 Moreover, when patients are allowed to switch to secondary therapies, regardless of whether secondary therapies consisting of drugs are from the same class 40 or a chemotherapy cocktail, the traditional survival analysis becomes weaker to identify any treatment benefit of the new treatment. Beyer et al. 12 demonstrated the application of multistate models in oncology trials. Furthermore, the multistate model can be used to predict the probability of intermediate events (states) for a future clinical trial population. In drug development, forecasts of study populations’ treatment response trajectory and prediction of time to disease progression/OS is very valuable information that could help in the optimization of the trial.
Multistate models can also be used for optimizing treatment at an individual level. The BSs showed that data collected until 3 months is enough to get good individual predictions up until 9 months (s = 3 months, t = 6 months) and if data until 6 months (s = 6 months) is used in the multistate model, individuals’ hazards of death were predicted accurately for the first 2 years. The forecasts from the multistate model using varying amount of follow‐up data of a representative individual from the study population is given in Figure 4. The multistate model forecasts that at the first scheduled post baseline measurement (12 weeks), there is an ~ 40% probability to observe response state (i.e., >30% decrease in tumor size from baseline; Figure 4a). The patient had an initial treatment effect (Figure 4b), however, at the second visit (at 24 weeks), the decrease in tumor size was not as high as what was observed at the first visit (at 12 weeks), and the multistate model predicts around 30% risk of disease progression at the next scheduled visit, at week 36 (Figure 4c). After being assessed as progressive disease, and initiation of second‐line therapy, the increase in hazard of death with time was forecasted reasonably by the model framework (Figure 4d–f). The prediction of treatment benefit duration and early identification of patients at higher risk of disease progression would guide early clinical interventions to enhanced benefits for patients.
FIGURE 4.
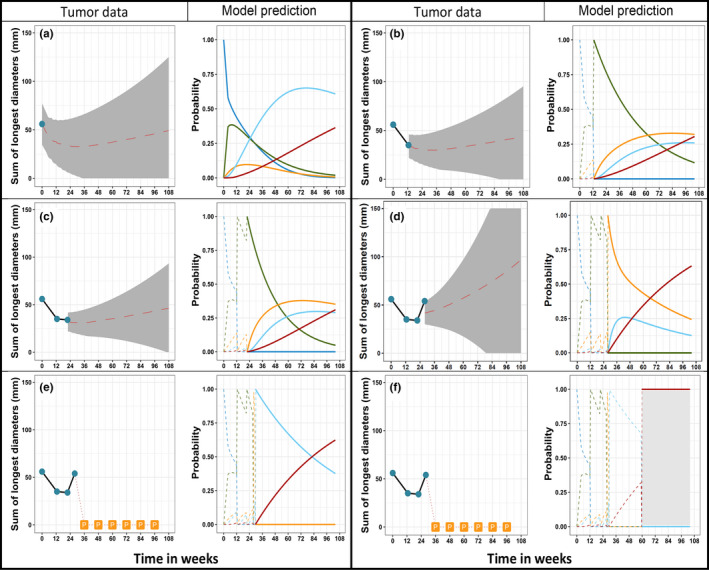
Multistate model forecasted tumor size, intermediate events, and hazard of death of an individual. In each panel (a–f), left subpanel shows observed tumor data (cyan dots) along with model predicted tumor time course, grey shaded area represents 95% confidence interval around the predicted median (dashed red line) time course. The loss of tumor follow‐up after disease progression is noted with “P” in panels e and f. The solid lines in the right subpanel shows the forecasted probability with time for stable (blue), response (green), progression (orange), second line (light blue), and death (red). The dashed lines in the right panel show the past transitions
There were 34 patients out of 58 excluded subjects who had no measurable target lesion at baseline but received docetaxel until disease progression, whereas the remaining 24 patients had received bevacizumab before disease progression. These 24 patients were not considered for inclusion in the analysis because of treatment crossover. When 34 patients (who received docetaxel until disease progression) were included in the analysis, they had a longer “stable state” before they had disease progression, compared to the other patients, whereas the uncertainty of λ12 and λ13 increased. Moreover, these individuals could not be included in the tumor modeling and should be excluded during investigation of tumor model derived metrics as predictor of transition intensities thus they were not included in the final analysis. There were five patients who had stable disease after an observed response state (<30% decrease from baseline and <20% increase from nadir). In the multistate model, these patients were allowed to continue in the response state with the assumption that they have the same risk of death and progression as that of response to progression/death. Moreover, this assumption will not influence the PFS and OS derived from the multistate model.
CONCLUSION
The developed multistate model adequately described the transitions between different possible states in patients with HER2‐negative metastatic cancer treated with docetaxel. The model jointly characterized the overall outcome events in the data, including both PFS and OS. The multistate model allows for simultaneous estimation of transition rates along with their tumor model derived predictors. The investigation of predictors and the characterization of time to develop response, duration of response, PFS, and OS can be performed in a single multistate modeling exercise. This modeling approach can be applied to other cancer types and therapies to provide a better understanding of efficacy of drug and characterizing different states, thereby facilitating early clinical interventions to improve anticancer therapy.
CONFLICT OF INTEREST
R.B., U.B., and J.Y.J, are employees of Roche/Genentech. L.E.F. and M.O.K. has acted as paid consultants to Genentech. S.M.K. declared no conflict of interest.
AUTHOR CONTRIBUTIONS
S.M.K., L.E.F., R.B., U.B., J.Y.J., and M.O.K. wrote the manuscript. S.M.K., L.E.F., R.B., U.B., J.Y.J., and M.O.K. designed the research. S.M.K. performed the research. S.M.K,, L.E.F., R.B., U.B,, J.Y.J,, and M.O.K analyzed the data.
DISCLAIMER
As Deputy‐Editor‐in‐Chief of CPT: Pharmacometrics & Systems Pharmacology, Lena E. Friberg was not involved in the review or decision process for this paper.
Supporting information
Fig S1‐S3
Table S1
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by the Swedish Cancer Society and Genentech Inc., San Francisco, CA.
Krishnan SM, Friberg LE, Bruno R, Beyer U, Jin JY, Karlsson MO. Multistate model for pharmacometric analyses of overall survival in HER2‐negative breast cancer patients treated with docetaxel. CPT Pharmacometrics Syst Pharmacol. 2021;10:1255–1266. 10.1002/psp4.12693
Funding information
This work was supported by the Swedish Cancer Society and Genentech Inc., San Francisco, CA.
REFERENCES
- 1. Bender BC, Schindler E, Friberg LE. Population pharmacokinetic‐pharmacodynamic modelling in oncology: A tool for predicting clinical response. Br J Clin Pharmacol. 2015;79:56‐71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bruno R, Bottino D, de Alwis DP, et al. Progress and opportunities to advance clinical cancer therapeutics using tumor dynamic models. Clin Cancer Res. 2020;26:1787‐1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Therasse P, Arbuck SG, Eisenhauer EA, et al. New guidelines to evaluate the response to treatment in solid tumors. J Natl Cancer Inst. 2000;92:205‐216. [DOI] [PubMed] [Google Scholar]
- 4. Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: Revised RECIST guideline (version 1.1). Eur J Cancer. 2009;45:228‐247. [DOI] [PubMed] [Google Scholar]
- 5. Ahansson EK, Ma G, Amantea MA, et al. PKPD modeling of predictors for adverse effects and overall survival in sunitinib‐treated patients with GIST. CPT Pharmacometrics Syst. Pharmacol. 2013;2:e85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Schindler E, Krishnan SM, Mathijssen R, Ruggiero A, Schiavon G, Friberg LE. Pharmacometric modeling of liver metastases’ diameter, volume, and density and their relation to clinical outcome in imatinib‐treated patients with gastrointestinal stromal tumors. CPT Pharmacometrics Syst. Pharmacol. 2017;6:449‐457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Netterberg I, Bruno R, Chen Y‐C, et al. Tumor time‐course predicts overall survival in non‐small cell lung cancer patients treated with atezolizumab: dependency on follow‐up time. CPT Pharmacometrics Syst. Pharmacol. 2020;9:115‐123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Anderson JR, Cain KC, Gelber RD. Analysis of survival by tumor response and other comparisons of time‐to‐event by outcome variables. J Clin Oncol. 2008;26:3913‐3915. [DOI] [PubMed] [Google Scholar]
- 9. Broët P, de la Rochefordière A, Scholl SM, et al. Analyzing prognostic factors in breast cancer using a multistate model. Breast Cancer Res Treat. 1999;54:83‐89. [DOI] [PubMed] [Google Scholar]
- 10. Proctor T, Schumacher M. Analysing adverse events by time‐to‐event models: the CLEOPATRA study. Pharm Stat. 2016;15:306‐314. [DOI] [PubMed] [Google Scholar]
- 11. Putter H, Fiocco M, Gekus RB. Tutorial in biostatistics: Competing risk and multi‐state models. Stat Med. 2007;26:2389‐2430. [DOI] [PubMed] [Google Scholar]
- 12. Beyer U, Dejardin D, Meller M, Rufibach K, Burger HU. A multistate model for early decision‐making in oncology. Biometrical J. 2020;62:550‐567. [DOI] [PubMed] [Google Scholar]
- 13. Ibrahim MMA, de Mello VD , Uusitupa M, Kjellson MC. Competing risks analysis of the Finnish diabetes prevention study. PAGE 28 Abstr 9033. www.page‐meeting.org/?abstract=9033.
- 14. Karlsson MO, Schoemaker RC, Kemp B, et al. A pharmacodynamic Markov mixed‐effects model for the effect of temazepam on sleep. Clin Pharmacol Ther. 2000;68:175‐188. [DOI] [PubMed] [Google Scholar]
- 15. Miles DW, Chan A, Dirix LY, et al. Phase III study of bevacizumab plus docetaxel compared with placebo plus docetaxel for the first‐line treatment of human epidermal growth factor receptor 2‐negative metastatic breast cancer. J Clin Oncol. 2010;28:3239‐3247. [DOI] [PubMed] [Google Scholar]
- 16. Claret L, Girard P, Hoff PM, et al. Model‐based prediction of phase III overall survival in colorectal cancer on the basis of phase II tumor dynamics. J Clin Oncol. 2009;27:4103‐4108. [DOI] [PubMed] [Google Scholar]
- 17. Jacqmin P, Snoeck E, van Schaick EA , et al. Modelling response time profiles in the absence of drug concentrations: Definition and performance evaluation of the K‐PD model. J Pharmacokinet Pharmacodyn. 2007;34:57‐85. [DOI] [PubMed] [Google Scholar]
- 18. Zhang L, Beal SL, Sheiner LB. Simultaneous vs. sequential analysis for population PK/PD data II: Robustness of methods. J Pharmacokinet Pharmacodyn. 2003;30:405‐416. [DOI] [PubMed] [Google Scholar]
- 19. Krishnan S, Friberg L. Accuracy in the estimation of the hazard in simultaneous and sequential estimation approaches of tumor size and overall survival (OS) modeling. PAGE 27 Abstr 8740. www.page‐meeting.org/?abstract=8740.
- 20. Nordgren R, Freiberga S, Ueckert S, Yngman G, Karlsson M. PsN: An open source toolkit for non‐linear mixed effects modelling. 2016. https://uupharmacometrics.github.io/PsN/.
- 21. Beal S, Sheiner L, Boeckmann A, Bauer R. NONMEM 7.4 users guides (ICON plc, Gaithersburg, MD, 1989–2018). Icon Dev. Solut. 2018. https://nonmem.iconplc.com/nonmem743/guides.
- 22. Keizer RJ, Karlsson MO, Hooker A. Modeling and simulation workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst. Pharmacol. 2013;2:e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Dosne A‐G, Bergstrand M, Harling K, Karlsson MO. Improving the estimation of parameter uncertainty distributions in nonlinear mixed effects models using sampling importance resampling. J Pharmacokinet Pharmacodyn. 2016;43:583‐596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Desmée S, Mentré F, Veyrat‐Follet C, Sébastien B, Guedj J. Nonlinear joint models for individual dynamic prediction of risk of death using Hamiltonian Monte Carlo: Application to metastatic prostate cancer. BMC Med Res Methodol. 2017;17:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Riglet F, Mentre F, Veyrat‐Follet C, Bertrand J. Bayesian individual dynamic predictions with uncertainty of longitudinal biomarkers and risks of survival events in a joint modelling framework: a comparison between Stan, Monolix, and NONMEM. AAPS J. 2020;22:1‐11. [DOI] [PubMed] [Google Scholar]
- 26. Blanche P, Proust‐Lima C, Loubère L, et al. Quantifying and comparing dynamic predictive accuracy of joint models for longitudinal marker and time‐to‐event in presence of censoring and competing risks: Comparing Dynamic Predictive Accuracy of Joint Models. Biometrics. 2015;71(1):102–113. [DOI] [PubMed] [Google Scholar]
- 27. Gerds TA, Schumacher M. Consistent estimation of the expected brier score in general survival models with right‐censored event times. Biometrical J. 2006;48:1029‐1040. [DOI] [PubMed] [Google Scholar]
- 28. Blanche P, Latouche A, Viallon V. Time‐dependent AUC with right‐censored data: a survey study. arXiv.org preprint. http://arxiv.org/abs/1210.6805.
- 29. Blanche P, Dartigues JF, Jacqmin‐Gadda H. Estimating and comparing time‐dependent areas under receiver operating characteristic curves for censored event times with competing risks. Stat Med. 2013;32:5381‐5397. [DOI] [PubMed] [Google Scholar]
- 30. Tardivon C, Desmée S, Kerioui M, et al. Association between tumor size kinetics and survival in patients with urothelial carcinoma treated with atezolizumab: implication for patient follow‐up. Clin Pharmacol Ther. 2019;106:810‐820. [DOI] [PubMed] [Google Scholar]
- 31. Missov TI, Lenart A. Gompertz‐Makeham life expectancies: Expressions and applications. Theor Popul Biol. 2013;90:29‐35. [DOI] [PubMed] [Google Scholar]
- 32. Schindler E, Amantea MA, Karlsson MO, Friberg LE. PK‐PD modeling of individual lesion FDG‐PET response to predict overall survival in patients with sunitinib‐treated gastrointestinal stromal tumor. CPT Pharmacometrics Syst Pharmacol. 2016;5:173‐181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Schindler E, Amantea MA, Karlsson MO, Friberg LE. A pharmacometric framework for axitinib exposure, efficacy, and safety in metastatic renal cell carcinoma patients. CPT Pharmacometrics Syst Pharmacol. 2017;6:373‐382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Bruno R, Mercier F, Claret L. Evaluation of tumor size response metrics to predict survival in oncology clinical trials. Clin Pharmacol Ther. 2014;95:386‐393. [DOI] [PubMed] [Google Scholar]
- 35. Claret L, Gupta M, Han K, et al. Prediction of overall survival or progression free survival by disease control rate at week 8 is independent of ethnicity: Western versus Chinese patients with first‐line non‐small cell lung cancer treated with chemotherapy with or without bevacizumab. J Clin Pharmacol. 2014;54:253‐257. [DOI] [PubMed] [Google Scholar]
- 36. Claret L, Lu J‐F, Bruno R, Hsu C‐P, Hei Y‐J, Sun Y‐N. Simulations using a drug‐disease modeling framework and phase II data predict phase III survival outcome in first‐line nonsmall‐cell lung cancer. Clin Pharmacol Ther. 2012;92:631‐634. [DOI] [PubMed] [Google Scholar]
- 37. Bruno R, Lindbom L, Schaedeli Stark F, et al. Simulations to assess phase II noninferiority trials of different doses of capecitabine in combination with docetaxel for metastatic breast cancer. CPT Pharmacometrics Syst. Pharmacol. 2012;1:e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Stein A, Bellmunt J, Escudier B, et al. Survival prediction in everolimus‐treated patients with metastatic renal cell carcinoma incorporating tumor burden response in the RECORD‐1 trial. Eur Urol. 2012;64:994‐1002. [DOI] [PubMed] [Google Scholar]
- 39. Hegde PS, Chen DS. Top 10 challenges in cancer immunotherapy. Immunity. 2020;52:17‐35. [DOI] [PubMed] [Google Scholar]
- 40. Ribas A, Kefford R, Marshall MA, et al. Phase III randomized clinical trial comparing tremelimumab with standard‐of‐care chemotherapy in patients with advanced melanoma. J Clin Oncol. 2013;31:616‐622. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1‐S3
Table S1
Supplementary Material


