Highlights
-
•
A new algorithm, ALL-Net, is introduced to improve MS lesion segmentation.
-
•
ALL-Net integrates anatomical coordinate information into the neural network.
-
•
ALL-Net integrates lesion-wise loss function to improve small lesion detection.
-
•
ALL-Net is robust to both small- and large-scale MS lesion datasets.
Keywords: Multiple sclerosis, Convolutional neural network, Lesion segmentation, MRI, Deep learning
Abstract
Accurate detection and segmentation of multiple sclerosis (MS) brain lesions on magnetic resonance images are important for disease diagnosis and treatment. This is a challenging task as lesions vary greatly in size, shape, location, and image contrast. The objective of our study was to develop an algorithm based on deep convolutional neural network integrated with anatomic information and lesion-wise loss function (ALL-Net) for fast and accurate automated segmentation of MS lesions. Distance transformation mapping was used to construct a convolutional module that encoded lesion-specific anatomical information. To overcome the lesion size imbalance during network training and improve the detection of small lesions, a lesion-wise loss function was developed in which individual lesions were modeled as spheres of equal size. On the ISBI-2015 longitudinal MS lesion segmentation challenge dataset (19 subjects in total), ALL-Net achieved an overall score of 93.32 and was amongst the top performing methods. On the larger Cornell MS dataset (176 subjects in total), ALL-Net significantly improved both voxel-wise metrics (Dice improvement of 3.9% to 35.3% with p-values ranging from p < 0.01 to p < 0.0001, and AUC of voxel-wise precision-recall curve improvement of 2.1% to 29.8%) and lesion-wise metrics (lesion-wise F1 score improvement of 12.6% to 29.8% with all p-values p < 0.0001, and AUC of lesion-wise ROC curve improvement of 1.4% to 20.0%) compared to leading publicly available MS lesion segmentation tools.
1. Introduction
Multiple sclerosis (MS) is a chronic inflammatory demyelinating disorder of the central nervous system with progressive axonal and neuronal loss (Haider et al., 2016, McDonald, 2000). MS has been a leading cause of long-term non-traumatic disability in young adults (Dobson and Giovannoni, 2019). Magnetic resonance imaging (MRI) is the standard imaging technique for detecting new MS lesions and monitoring lesion load, which provides useful information for diagnosing and informing medical treatment (Filippi et al., 2016).
MS lesions can be visually detected and segmented on MR images by human experts, but the process is time-consuming, tedious, and prone to intra- and inter-reader variability (Carass et al., 2017). Numerous automated lesion segmentation algorithms have been developed to address this problem, which can be categorized as unsupervised or supervised. Unsupervised algorithms, including geometry constrained iterative threshold adjusting (Codella et al., 2008), atlas-based topology preserving anatomic segmentation (Shiee et al., 2010), probabilistic classification growth lesion segmentation tool (Schmidt et al., 2012), or dictionary learning sparse coding (Weiss et al., 2013), rely on carefully selected image features or brain tissue priors and can be useful but often have limited detection accuracy and slow speed.
Supervised algorithms, especially those based on deep convolutional neural networks (CNNs), have emerged as more powerful alternatives to unsupervised methods. In recent years, CNNs have found promising applications in medical imaging segmentation, including brain tumor segmentation (Kamnitsas et al., 2017), myocardium segmentation (Ma et al., 2021), white matter hyperintensity segmentation (Zhang et al., 2021c), and MS lesion segmentation (Zhang et al., 2019a, Aslani et al., 2019). Most existing CNN methods for MS lesion segmentation can be categorized into one of the following three classes: patch-based, 2D slice-based, and 3D volume-based. Patch-based models suffer from repeated computation and insufficient contextual information. Cascaded architecture (Valverde et al., 2017) and densely-connected network (Huang et al., 2017) with asymmetric loss (Hashemi et al., 2018) are patch-based algorithms that have achieved good performance on the ISBI-2015 MS Lesion Segmentation Challenge dataset (denoted as ISBI-2015 dataset) (Carass et al., 2017), but fall behind recently developed fully convolutional network based models (Long et al., 2015, Ronneberger et al., 2015). Slice-based methods, such as Multi-branch network (Aslani et al., 2019) and Tiramisu network with numerous layers (Zhang et al., 2019a), offer improvements over patch-based methods by balancing training efficiency and utilizing contextual information. 3D volume-based CNN models, in which 3D spatially invariant convolution kernels are used to extract the image features, can dramatically reduce redundant computations compared to patch-based methods, and have richer contextual information compared to 2D slice-based methods. These methods include the U-Net like encoder-decoder network (Brosch et al., 2016, Çiçek et al., 2016), multi-dimensional gated recurrent units (Andermatt et al., 2017), recurrent slice-wise attention network (Zhang et al., 2019b), gated-attention networks (Hou et al., 2019, Oktay et al., 2018), and folded attention network (Zhang et al., 2021b).
Yet, the accuracy of CNN based automated MS lesion segmentation remains limited. We have identified three possible factors to be addressed in this study. First, CNN methods have not explicitly integrated brain anatomical coordinate information for MS lesion segmentation, though prior work (McKinley et al., 2021) has implicitly integrated anatomical information by jointly segmenting brain structures and MS lesions. CNNs can extract features well, but struggle to perceive the voxel position in the brain (Islam et al., 2019, Kayhan and Gemert, 2020, Liu et al., 2018) due to the spatial-invariant convolution. Second, prior work utilized voxel-wise loss functions for network training which regard all voxels as equally important; the imbalance between lesions of different sizes could lead to misdetection of smaller lesions. Third, the three publicly available MS lesion datasets (MICCAI 2008 (Styner et al., 2008), MICCAI 2016 (Commowick et al., 2016), and ISBI-2015 (Carass et al., 2017)) are relatively small, and evaluations on more extensive datasets are lacking (Danelakis et al., 2018).
The objective of this study was to integrate Anatomical information and Lesion-wise Loss function into neural network (ALL-Net) to overcome the shortcomings of existing CNN algorithms for MS lesion segmentation. We proposed an anatomical convolutional module that can efficiently encode anatomical structure information and a lesion-wise loss function to improve detection on the lesion level. In addition to the ISBI-2015 dataset, ALL-Net was compared to state-of-the-art algorithms on a larger in-house dataset of 176 MS patients.
2. Materials and methods
2.1. MRI image datasets
The proposed MS lesion segmentation algorithm was evaluated on the publicly available ISBI-2015 dataset released as part of the Longitudinal White Matter Lesion Segmentation of Multiple Sclerosis Challenge during the 2015 International Symposium on Biomedical Imaging (ISBI) (Carass et al., 2017), and also on a larger in-house Cornell MS dataset. The ISBI-2015 training dataset consists of whole-brain 3T MR images with T1-weighted (T1W), T2-weighted (T2W), proton density-weighted (PDW), and T2W fluid attenuated inversion recovery (FLAIR) contrast acquired on Philips scanners (Philips Medical Systems, Best, the Netherlands), as well as binary lesion masks traced independently by two expert readers for five patients, four of whom had four longitudinal scans, and the remaining patient had five scans. The ISBI-2015 testing dataset includes MR images for 14 patients, ten of whom had four scans, three had five scans, and one had six scans. The ground-truth lesion masks were not provided for the testing dataset. The performance evaluation metrics were described in details in (Carass et al., 2017) and obtained by submitting the predicted binary lesion mask at https://smart-stats-tools.org/lesion-challenge.
The cross-sectional Cornell MS dataset consists of 176 MS patients enrolled in an ongoing prospective database for MS research (see Table 1 for demographics and clinical information). The database was approved by the local Institutional Review Board and written informed consent was obtained from all patients prior to entry into the database. Imaging was performed on 3T Magnetom Skyra scanners (Siemens Medical Solutions USA, Malvern, PA, USA) using a product twenty-channel head/neck coil. The standardized scanning protocol consisted of sagittal 3D T1W MPRAGE sequence (Repetition Time (TR)/Echo Time (TE)/Inversion Time (TI) = 2300/2.3/900 ms, flip angle (FA) = 8°, GRAPPA parallel imaging factor (R) = 2, voxel size = 1.0 × 1.0 × 1.0 mm3), axial 2D T2W turbo spin echo sequence (TR/TE = 5840/93 ms, FA = 90°, turbo factor = 18, R = 2, voxel size = 0.5 × 0.5 × 3 mm3) and sagittal 3D fat-saturated T2W FLAIR sequence (TR/TE/TI = 8500/391/2500 ms, FA = 90°, turbo factor = 278, R = 3, voxel size = 1.0 × 1.0 × 1.0 mm3). T1W and T2W images were linearly co-registered to the FLAIR space using the FMRIB's Linear Image Registration Tool (FLIRT) command (Smith et al., 2004). Ground-truth binary lesion masks were also provided for all subjects. These masks were obtained by segmenting the FLAIR image using the LST-LPA algorithm in the LST toolbox version 3.0.0 (www.statisticalmodelling.de/lst.html) (Schmidt, 2017), followed by manual editing if necessary, and finalized by the consensus of two expert readers.
Table 1.
Demographic and clinical information of the Cornell MS dataset.
| Number of Subjects | 176 |
|---|---|
| Gender (count (%)) | |
| Female | 127 (72.16%) |
| Male | 49 (27.84%) |
| Race (count (%)) | |
| White | 132 (75.00%) |
| Asian | 7 (3.98%) |
| Black or African American | 29 (16.48%) |
| Hispanic | 1 (0.57%) |
| More than one race | 2 (1.14%) |
| Other | 4 (2.27%) |
| Unknown or not reported | 1 (0.57%) |
| Disease subtype (count (%)) | |
| RRMS | 163 (92.61%) |
| SPMS | 5 (2.84%) |
| CIS | 8 (4.55%) |
| Disease duration* (mean ± STD) | 10.69 ± 7.37 |
| Age (mean ± STD) | 42.89 ± 10.39 |
| EDSS (mean ± STD) | 1.41 ± 1.65 |
| Treatment duration (mean ± STD) | 8.16 ± 5.84 |
Reported for 173 patients with available data.
2.2. ALL-Net MS lesion segmentation algorithm
2.2.1. Overall framework
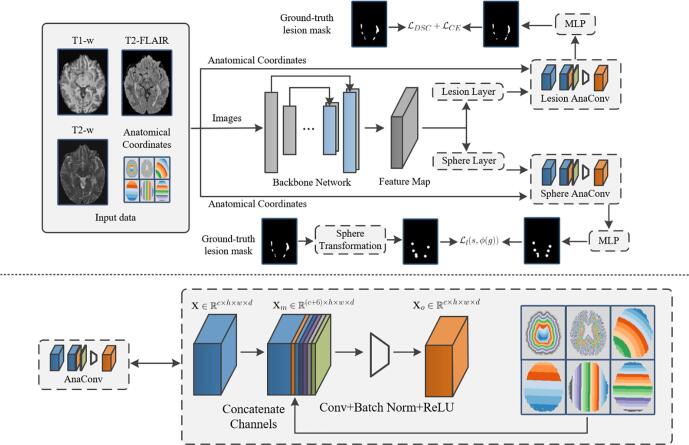
The proposed ALL-Net framework (Fig. 1) consists of three parts: an encoder-decoder structured backbone network, two Anatomical Convolutional (AnaConv) modules (defined in the section below) and associated convolutional layers, and traditional region-based loss as well as the Lesion-wise Loss (LesLoss) modules. In the first stage, multi-modal images (T1W, T2W, FLAIR) are fed into the backbone network for voxel-wise feature extraction. The obtained feature map is then fed into two different convolution layers to extract lesion- and sphere-specific features. Each feature map goes through an AnaConv module, followed by a multi-layer perceptron (MLP) (efficiently implemented by 1x1x1 convolutional kernels) to obtain the final prediction map.
Fig. 1.
Schematic of the proposed ALL-Net algorithm for MS lesion segmentation. The upper panel shows the overall framework which consists of three parts: an encoder-decoder structured backbone CNN network (3D U-Net in our implementation), two Anatomic Convolutional (AnaConv) modules for encoding anatomical information such as voxel coordinate and distance from the CSF and brain boundaries, and the traditional region-based loss (Dice loss and BCE loss) as well as the proposed lesion-wise loss (LesLoss) modules. The backbone network extracts voxel-wise features from the input multi-modal images (T1W, T2W, and FLAIR in Cornell MS dataset), the feature map of which will be used to predict the lesion mask and lesion spheres. The lower panel shows the details of the AnaConv module, which maps an input feature tensor ( is the number of channels in the feature tensor, and denote the size the of the image) to a new feature tensor by concatenating the anatomical coordinates and performing a common convolutional layer on .
2.3. Anatomical convolutional (AnaConv) module
Anatomical Convolution (AnaConv) is a neural network module that utilizes the anatomical location of each voxel obtained from the input T1W image to guide network training and inference by means of a feature fusion convolutional layer (Fig. 1) for MS lesion segmentation. MS lesions have a predilection for forming in the periventricular area (Filippi et al., 2019), and this unique spatial pattern can provide a useful anatomical prior to improve segmentation performance. In this study, two spatial coordinates were calculated for each brain voxel: 1) 3D voxel coordinates and distance to the origin mapped from the MNI space (Grabner et al., 2006) to the patient space, which were obtained by linearly aligning the MNI space to the native T1W image using FMRIB's Linear Image Registration Tool (FLIRT) command (Smith et al., 2004); 2) Distance to the nearest boundary voxel of CSF filled structures such as the ventricles and the pial surface, and distance to the nearest boundary voxel of the whole brain, calculated by first obtaining brain tissue segmentation (GM, WM, and CSF) using FMRIB's Automated Segmentation Tool (FAST) command (Smith et al., 2004), followed by smoothing and hole filling of the volumetric tissue masks by means of morphological opening and closing operations, and applying distance transformation mapping (Danielsson, 1980) to the filtered masks. Both coordinates are defined in the individual patient space and not in the MNI space and therefore change with the subject’s head size. To integrate the derived anatomical location information into network training, we used the computationally efficient CoordConv method (Liu et al., 2018) that augments the input of a common convolutional layer with extra coordinate and distance channels. The implemented AnaConv consists of two commonly used operations, a concatenation of a feature tensor and a coordinate tensor through the channel dimension and a common convolutional layer with convolution, batch normalization (Ioffe and Szegedy, 2015) and rectified linear unit (ReLU) as the activation function (Fig. 1).
2.4. Lesion-wise loss (LesLoss) module
Commonly used voxel-wise loss functions such as binary cross-entropy (BCE), Dice loss (Milletari et al., 2016), or Tversky loss (Hashemi et al., 2018) assign equal importance to every voxel, which implies that the cost of misclassifying a small lesion (missed or false positive lesion) is similar to that of correctly detecting but slightly under- or over-segmenting a large lesion. In clinical practice, however, misdetection of lesions as small as 3 voxels in diameter can have an important consequence on MS diagnosis (Thompson et al., 2018, Filippi et al., 2016). To improve detection on the lesion level in agreement with the clinical need, we proposed a Lesion-wise Loss (LesLoss) module which enforces lesion-wise learning, as opposed to voxel-wise learning, by modeling all lesions as spheres with a fixed size in the loss function. During early testing, the algorithm was found to be insensitive to the choice of the sphere diameter throughout the range of 8–20 mm, and consequently a 10 mm diameter was chosen in the final implementation. The sphere transformation turns individual lesions regardless of their size and shape into fixed size spheres, therefore assigning equal weights to all lesions during network training. This helps to prevent misdetection of lesions with smaller volumes.
Our approach was based on (Zhang et al., 2021a) which generalizes the voxel-wise loss function into a geometric loss function as follows:
| (1) |
Here is the spatial domain of an input 3D image, is the summation notation, is the spatial position vector, is the output probability map, is the value of at position , is the ground-truth binary lesion mask, and is the value of at position . Eq. 1 combines the volumetric () and geometric () correlations in a single formula, and traditional region-based and boundary-aware loss functions can be represented using the formula by specifying and (more details of the instantiations can be found in (Zhang et al., 2021a)). In this work, we proposed a geometric transformation to reduce lesions to spheres with a fixed size to be used as geometric constraints in Eq.1 as follows: 1) Use a 3x3x3 template filled with ones and the depth-first search method to find spatial-connected components; 2) Compute the mass center for each of the connected components; 3) Draw spherical masks with a fixed radius centered on the computed mass centers. If two spheres overlap, the union of their masks will be used (Fig. 2). This transformation involves indifferentiable operations, and thus differs from Eq.1 where both ground-truth map and predicted probability map can undergo the transformation process. Our lesion-wise loss only transforms the ground-truth map and uses a deep neural network to predict the probability map of spheres directly. Accordingly, Eq.1 was modified as follows:
| (2) |
Fig. 2.
Example of spherical lesion transformation for the proposed LesLoss function. The Les loss groups the voxel-wise binary lesion mask (a) into separate lesions based on spatial connectivity (b) and then transforms them into spheres with a fixed diameter of 10 mm (c).
where denotes the lesion-wise sphere transformation. Letting the volumetric correlation function be and the normalization function be , the final lesion-wise loss function is as follows:
| (3) |
Where is the natural logarithm function, is a factor to balance the importance of foreground (sphere) and background (non-sphere) voxels, and is a focusing factor (Lin et al., 2017) to balance the importance of misclassified voxels that are easy or difficult to train (difficulty is determined by the probability). We followed previous work (Lin et al., 2017) and set and .
2.5. Network implementation and inference details
For the ISBI-2015 dataset, the backbone network architecture for ALL-Net was the same as that of Tiramisu (Zhang et al., 2019a), a top-performing algorithm on the leaderboard of the ISBI-2015 challenge. ALL-Net was implemented in Python using a PyTorch library (Paszke et al., 2019) on a computer equipped with four Nvidia Titan Xp GPUs. ALL-Net was trained on 21 scans from 5 subjects and tested on 61 scans from 21 subjects. The original multi-modal images were padded to the same size of 217x217x217 voxels for all subjects. Elastic deformation, random intensity shifting, and random scaling were used for data augmentation. The loss function used for network training was selected as the sum of LesLoss, BCE loss, and soft Dice loss (Milletari et al., 2016) (with equal weight). The Adam algorithm (Kingma and Ba, 2014) with an initial learning rate of 0.001 and a multi-step learning rate scheduler with milestones at 50%, 70%, and 90% of the total epochs were used to train the network weights. A batch size of twenty was used for training, and training stopped after 140 epochs. We used five random seeds to train five models and the final lesion segmentation mask was determined by majority voting.
The larger Cornell MS dataset, consisting of 176 scans from 176 subjects, was split into three subsets for model training (119), validation (18), and testing (39). For this experiment, the network was implemented in a similar fashion as that for the smaller ISBI-2015 dataset, with the notable exception that the backbone network was changed from 2D convolution as in Tiramisu (Zhang et al., 2019a) to 3D convolution as in (Zhang et al., 2021a). To lessen computer memory demand, images were randomly cropped to 128 × 128 × 48 voxels for training. For testing, the original image size was used. A batch size of four was used for training, and training was stopped after 70 epochs.
When we performed the network inference on the testing dataset, T1W images were first used to generate a six-channel 4D tensor (, where denotes the spatial size of the T1W image) including anatomical coordinates described at Section 2.2. For ISBI-2015 dataset, intensity-normalized PDW, T1W, T2W, and FLAIR images as well as the coordinate tensor were used as inputs to the network. For Cornell dataset, co-registered and intensity-normalized T1W, T2W and FLAIR images as well as the coordinate tensor were used as network inputs.
2.6. Data and code availability statement
The ISBI-2015 dataset is publicly available and can be requested at their website http://iacl.ece.jhu.edu/index.php?title=MSChallenge. The Cornell MS dataset is a private clinical dataset and cannot be made publicly available due to confidentiality. The code is available at https://github.com/tinymilky/ALL-Net.
2.7. Evaluation metrics
Evaluation metrics were based on those used in the ISBI-2015 challenge (Carass et al., 2017). Dice Similarity Coefficient (DSC), Precision, Sensitivity, and Voxel-wise F1 Score (V-F1) were used to measure the voxel-wise agreement between the ground-truth and the predicted binary lesion masks:
| (4) |
| (5) |
| (6) |
| (7) |
where denote the number of voxel-wise true positives, false positives, and false negatives, respectively.
Similar metrics were defined on the lesion level including lesion-wise true positive rate (LTPR), lesion-wise false positive rate (LFPR), and lesion-wise F1 score (L-F1) as follows:
| (8) |
| (9) |
| (10) |
where denotes the number of lesion-wise true positives (predicted lesions that overlap with the ground-truth mask), is the number of lesions in the ground-truth mask, is the number of false positive lesions (predicted lesions that do not overlap with the ground-truth lesion mask), and is the number of lesions in the prediction mask.
In addition, the following aggregate evaluation score originally proposed in the ISBI-2015 challenge was used:
| (11) |
where is number of samples, is a normalization factor considering the inter-rater variation and the number of samples, and VC is the Pearson’s correlation coefficient of the lesion volumes between the ground-truth and the prediction. The inter-rater variation was excluded from the aggregate score calculation (Eq. (12)) for the Cornell dataset.
2.8. Statistical analysis and ablation study
For the ISBI-2015 dataset, the proposed ALL-Net algorithm was compared with top algorithms on the leaderboard of the ISBI-2015 challenge including Tiramisu (Zhang et al., 2019a), GEO Loss (Zhang et al., 2021a), Low-precision Ensemble (Ma et al., 2021), Asymmetric Loss (Hashemi et al., 2018), Multi-Branch Network (Aslani et al., 2019), Cascaded Network (Valverde et al., 2017), Multi-view Network (Birenbaum and Greenspan, 2016), and Location-aware network (Ghafoorian et al., 2017), based on performance metrics reported in the literature or posted on the challenge website at https://smart-stats-tools.org/lesion-challenge.
For the Cornell MS dataset, ALL-Net was compared with the LST-LPA algorithm (Schmidt, 2017), U-Net (Çiçek et al., 2016), nn-Unet (Isensee et al., 2021) and Tiramisu (Huang et al., 2017, Zhang et al., 2019a) using evaluation metrics that were calculated based on the provided ground-truth lesion masks. Two-tailed paired t-tests were used to compare performance metrics of the proposed ALL-Net with other algorithms. Receiver operating characteristics (ROC) analysis was used to compare diagnostic detection accuracy of the algorithms at the lesion level. Precision-recall (PR) curves were used to compare overall performance of the algorithms at the voxel-level. We further performed an ablation study on this dataset to evaluate the effectiveness of each of the proposed modules. All CNN based algorithms used the same three input contrasts (T1W, T2W, FLAIR), and these methods were trained and validated the same way on the Cornell dataset. LST-LPA, which does not require parameter tuning and by design only requires FLAIR input, was included in our comparison because it is a popular open-source MS lesion segmentation tool.
To verify the effectiveness of each proposed module, we further conducted an ablation study using Cornell MS dataset. The ablation study consists of four model variants of the proposed ALL-Net: 1) The baseline network without AnaConv and LesLoss; 2) The baseline network with AnaConv but without LesLoss; 3) The baseline network without AnaConv but with LesLoss; 4) The baseline network with both AnaConv and LesLoss. The effectiveness of ALL-Net resolving the first and the second issue mentioned in introduction can be observed by comparing the performance between 1) and 2), and 1) and 3) respectively.
3. Results
3.1. ISBI-2015 challenge dataset
Table 2 summarizes the comparison of the proposed ALL-Net and state-of-the-art MS lesion segmentation algorithms on the ISBI-2015 testing dataset. The ALL-Net and the Tiramisu network achieved the best and second-best performance in overall Score respectively, where the ALL-Net reduced LFPR by an average of 21.3% (from 0.155 to 0.122) compared to the Tiramisu network while maintaining similar LTPR (0.533 vs. 0.540). In terms of voxel-wise metrics, nn-Unet achieved the best DSC 0.679, surpassing the second-best DSC 0.661 from Low-precision Ensemble model by 2.7%, and the Asymmetric Loss model achieved the best PPV 0.921, improving the second-best PPV 0.914 from the ALL-Net by 0.7%. In terms of lesion-wise metrics, the ALL-Net achieved the best L-F1 score 0.663, improving the second-best L-F1 score 0.659 from the Tiramisu network by 0.6% and representing the best tradeoff between LTPR and LFPR among all other methods. In terms of volume correlation, the ALL-Net and other algorithms achieved similar VC score around 0.86, while Multi-view model and Location-aware model are exceptionally lower. Fig. 3 shows two examples from the testing set of the ISBI-2015 dataset, demonstrating the ability of ALL-Net to capture small juxtacortical lesions better than LST-LPA and Tiramisu algorithms, and avoid over-segmenting WM hyperintensities close to the ventricles.
Table 2.
Performance comparison of the proposed ALL-Net and state-of-the-art MS lesion segmentation algorithms on the ISBI-2015 testing dataset (61 scans from 14 patients). Bolded and underlined numbers refer to metrics with the best and the second-best performance, respectively.
| Algorithms | Score | DSC | PPV | LFPR | LTPR | VC | L-F1 |
|---|---|---|---|---|---|---|---|
| ALL-Net (proposed) | 93.32 | 0.639 | 0.914 | 0.122 | 0.533 | 0.860 | 0.663 |
| Tiramisu (Zhang et al., 2019a) | 93.11 | 0.641 | 0.902 | 0.155 | 0.540 | 0.867 | 0.659 |
| nn-Unet (Isensee et al., 2021) | 92.87 | 0.679 | 0.847 | 0.159 | 0.523 | 0.865 | 0.645 |
| GEO Loss (Zhang et al., 2021a) | 92.73 | 0.643 | 0.887 | 0.132 | 0.480 | 0.854 | 0.618 |
| Low-precision Ensemble (Ma et al., 2021) | 92.55 | 0.661 | 0.838 | 0.151 | 0.491 | 0.854 | 0.622 |
| Asymmetric Loss (Hashemi et al., 2018) | 92.48 | 0.584 | 0.921 | 0.087 | 0.414 | 0.858 | 0.569 |
| Multi-Branch (Aslani et al., 2019) | 92.12 | 0.611 | 0.899 | 0.139 | 0.410 | 0.867 | 0.556 |
| Recurrent Gated Units (Andermatt et al., 2017) | 92.07 | 0.629 | 0.845 | 0.201 | 0.487 | 0.862 | 0.605 |
| Cascaded Network (Valverde et al., 2017) | 91.33 | 0.630 | 0.787 | 0.153 | 0.367 | 0.866 | 0.512 |
| Multi-View (Birenbaum and Greenspan, 2016) | 90.07 | 0.627 | 0.789 | 0.498 | 0.568 | 0.822 | 0.533 |
| Location-Aware (Ghafoorian et al., 2017) | 86.92 | 0.501 | 0.549 | 0.577 | 0.429 | 0.791 | 0.426 |
Fig. 3.
Comparison of MS lesion segmentation masks obtained with the proposed ALL-Net and previously developed LST-LPA and Tiramisu algorithms from two test subjects in the ISBI-2015 dataset. In the first subject (top row), all three algorithms captured periventricular lesions equally well. However, only ALL-Net correctly detected small juxtacortical lesions (orange arrows). In the second example (bottom row), LST-LPA tended to over-segment lesions, leading to false positives (yellow arrows), while CNN-based ALL-Net and Tiramisu algorithms provided better results with tighter segmentation masks. Note that the ground-truth lesion masks were not available in this dataset. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.2. Cornell MS dataset
Table 3 summarizes the comparison of the proposed ALL-Net and several existing MS lesion segmentation algorithms on the testing set of the Cornell MS dataset (with lesion volume ranging from 26 mm3 to 26976 mm3). ALL-Net achieved the best overall score with relative improvement of 19.4% (from 0.705 to 0.842) over LST-LPA, 5.9% (from 0.795 to 0.842) over U-Net, 4.7% (from 0.804 to 0.842) over Tiramisu, and 4.5% (from 0.804 to 0.842) over nn-Unet. ALL-Net achieved the best DSC score of 0.755, improving the second-best DSC score 0.727 from U-Net by 3.9%. ALL-Net also achieved the best voxel-wise metrics in terms of precision, sensitivity and V-F1 score. In terms of lesion-wise metrics, ALL-Net achieved the second best LFPR of 0.301, which is higher than the best LFPR of 0.248 by nn-Unet. U-Net achieved the best LTPR of 0.937, which was slightly better than the second-best LTPR of 0.926 obtained by the Tiramisu network. More importantly, ALL-Net achieved the best L-F1 score of 0.793, which is slightly higher than the second-best L-F1 score of 0.782 by nn-Unet and represents the best trade-off between LFPR and LTPR.
Table 3.
Performance comparison on the Cornell MS testing dataset (39 scans from 39 patients). Bolded and underlined numbers refer to the metrics with the best and the second-best performance, respectively.
| Methods | Score | DSC | LFPR | LTPR | Precision | Sensitivity | VC | L-F1 | V-F1 |
|---|---|---|---|---|---|---|---|---|---|
| ALL-Net (proposed) | 0.842 | 0.755 | 0.301 | 0.917 | 0.781 | 0.748 | 0.983 | 0.793 | 0.764 |
| LST-LPA (Schmidt et al., 2012) | 0.705 | 0.558 | 0.527 | 0.866 | 0.661 | 0.526 | 0.872 | 0.611 | 0.586 |
| U-Net (Çiçek et al., 2016) | 0.795 | 0.727 | 0.465 | 0.937 | 0.736 | 0.738 | 0.977 | 0.681 | 0.737 |
| Tiramisu (Zhang et al., 2019a) | 0.804 | 0.723 | 0.432 | 0.926 | 0.752 | 0.710 | 0.984 | 0.704 | 0.730 |
| nn-Unet (Isensee et al., 2021) | 0.806 | 0.697 | 0.248 | 0.813 | 0.696 | 0.719 | 0.963 | 0.782 | 0.707 |
The top panel of Fig. 4 shows an example from the testing set of the Cornell MS dataset, demonstrating improved lesion detection of the proposed algorithm. In addition, the lower panel of Fig. 4 shows another example from the testing set of the Cornell MS dataset, where our ALL-Net successfully detected a lesion that was under-segmented by human experts (the under-segmented example was shown to another human expert with multi-contrast images, and consensus was obtained that the under-segmented area should be considered as lesion).
Fig. 4.
Comparison of MS lesion segmentation masks obtained with the proposed ALL-Net and previously developed LST-LPA, U-Net, Tiramisu and nn-Unet algorithms from two test subjects in the Cornell MS dataset. Lesion masks traced by human experts are shown as ground-truth reference. Orange arrows indicate lesions under-segmented by the algorithms, yellow arrows indicate false positives, and the blue arrow indicates a region where humans made a mistake which was confirmed in repeated review. Overall, ALL-Net provided better segmentation results than competitive methods. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 5, Fig. 6 compare the ROC curve and the PR curve, respectively, for different algorithms when applied to the testing set of the Cornell MS dataset. The proposed ALL-Net provided higher AUC for both lesion-wise and voxel-wise detection than existing algorithms, indicating improved lesion detection and segmentation performance. Fig. 7 shows boxplots for comparison of different methods. The proposed ALL-Net surpassed the other methods with statistical significance in both voxel-wise (Dice improvement of 3.9% to 35.3% with p-values ranging from p < 0.01 to p < 0.0001) and lesion-wise metrics (lesion-wise F1 score improvement of 1.4% to 29.8% with all p-values p < 0.0001 except for nn-Unet).
Fig. 5.

Comparison of lesion-wise ROC curves for different MS lesion segmentation algorithms on the testing set of the Cornell MS dataset. (LFPR = lesion-wise false positive rate; LTPR = lesion-wise true positive rate).
Fig. 6.

Comparison of voxel-wise Precision-Recall curve for different MS lesion segmentation algorithms on the testing set of the Cornell MS dataset.
Fig. 7.
Performance comparison of tested models with all metrics evaluated on the testing set of the Cornell MS dataset. Statistical significance test between of our method and the other state-of-the-art methods were evaluated using a paired t-test. The threshold of the significance was , and the p-values in the figure are annotated as: * for p < 0.05, ** for p < 0.01, *** for p < 0.001, **** for p < 0.0001, and ns for non-significant.
3.3. Ablation study
Table 4 shows results of the ablation study on the Cornell MS dataset. Compared with the base network, adding either the AnaConv or LesLoss module improved voxel-wise metrics such as DSC and V-F1 score, and provided a better trade-off between LFPR and LTPR. Most importantly, the best segmentation performance was attained with the addition of both modules to the base network.
Table 4.
Performance comparison on the Cornell MS testing dataset (39 scans from 39 patients) among variants of the proposed ALL-Net algorithm. “Base” denotes the baseline network (from (Zhang et al., 2021a)), “Base + AnaConv” denotes the baseline network with AnaConv module, and “Base + LesLoss” denotes the baseline network with LesLoss. “ALL-Net” is the final network with integration of both AnaConv module and LesLoss. Bolded and underlined numbers refer to the metrics with the best and the second-best performance, respectively.
| Methods | Score | DSC | LFPR | LTPR | Precision | Sensitivity | VC | L-F1 | V-F1 |
|---|---|---|---|---|---|---|---|---|---|
| Base | 0.795 | 0.727 | 0.465 | 0.937 | 0.736 | 0.738 | 0.977 | 0.681 | 0.737 |
| Base + AnaConv | 0.819 | 0.750 | 0.384 | 0.928 | 0.749 | 0.769 | 0.984 | 0.740 | 0.759 |
| Base + LesLoss | 0.839 | 0.734 | 0.271 | 0.870 | 0.821 | 0.680 | 0.980 | 0.793 | 0.744 |
| ALL-Net | 0.842 | 0.755 | 0.301 | 0.917 | 0.781 | 0.748 | 0.983 | 0.793 | 0.764 |
4. Discussion
Our results obtained from the ISBI-2015 dataset and the larger Cornell MS dataset demonstrated that the proposed ALL-Net algorithm improved overall MS lesion segmentation performance (measured by the aggregate evaluation score) when compared to traditional algorithms such as LST-LPA (Schmidt et al., 2012) and state-of-the-art CNN algorithms including nn-Unet (Isensee et al., 2021) and Tiramisu (Zhang et al., 2019a). ALL-Net achieved these advantages through the addition of two new modules to integrate voxel position learning for encoding anatomical information and lesion-wise learning for better lesion localization with the deep convolutional neural network.
In addition to image contrast, contextual and anatomical information play important roles in MS lesion segmentation. As shown in Fig. 4, traditional segmentation methods often miss juxtacortical lesions and over-segment periventricular hyperintensities due to ambiguous image contrast in these regions. As MS lesions tend to occur more frequently in the periventricular area, lesion location can also introduce bias into network training, leading to suboptimal segmentation. ALL-Net utilizes location information including anatomical position mapped from MNI space to patient space, voxel distance to the brain boundaries, and voxel distance to the boundary of CSF filled structures such as the ventricles and the pial surface to overcome this bias and to provide more uniform lesion detection over the whole brain.
In this work, we introduced a lesion-wise loss (LesLoss) function which models lesions of various sizes as individual objects of equal importance. This shift in focus from voxel-wise to lesion-wise detection is important because MS diagnosis is based on the dissemination of new lesions in space and time. Recent object detection methods such as Corner-Net (Law and Deng, 2018) and Center-Net (Zhou et al., 2019) formulated the object detection problem as an image mapping problem, where the corners or centers of an object become the prediction targets, in replacing the traditional bounding-box prediction. GEO Loss (Zhang et al., 2021a) bridged the gap of designing loss functions between region-based volume and geometric transformation by introducing the GEO Loss function. Inspired by these works, we proposed the LesLoss function to enhance segmentation performance. As can be seen in the quantitative results, our method can effectively trade-off between LFPR and LTPR (with similar LTPR, we achieved better LFPR; with similar LFPR, we achieved better LTPR), resulting in a better lesion-wise detection accuracy. Examples shown in Fig. 3, Fig. 4, Fig. 5 demonstrate improved detection of small lesions without over-segmenting (i.e., introducing false positives) using the proposed lesion-wise approach.
3D convolution tends to provide better network performance than 2D convolution in MS segmentation task as it aggregates richer contextual information for network training. However, as the number of network weights greatly increases, this approach requires a much larger dataset to prevent overfitting. A key contribution of the present work is to demonstrate that a 3D CNN can significantly improve the MS lesion segmentation performance when trained on a larger training dataset. When using the backbone network from GEO Loss (Zhang et al., 2021a), 3D convolution-based, the best score we can obtain from the testing set of the ISBI-2015 dataset is 92.99. If the backbone network is changed to Tiramisu (Zhang et al., 2019a), which is 2D convolution based, the score goes up to 93.32. On the contrary, in the larger Cornell MS dataset, we also found that 3D models outperform 2D models. While it may be beneficial to adapt the original 2D Tiramisu network to a 3D convolution model on the Cornell dataset, the resulting densely connected network (Huang et al., 2017) consumes 7-times more GPU memory than a U-Net with VGG block (Simonyan, 2014) and therefore could not be implemented on our GPU. Furthermore, since the core feature of the Tiramisu network is the slice stacking technique, which is by nature a 2D network, it would be fair to respect the original design in our comparisons. Similar performance gain from 2D to 3D models was also observed with nn-Unet algorithm (Isensee et al., 2021) that automatically tunes its hyper-parameters.
In this study, when ALL-Net was trained on the Cornell dataset and applied to the ISBI-2015 dataset, we found that the overall score of 88.23 was lower than the top leaderboard score of 93.32 achieved by ALL-Net when it was both trained and tested on the ISBI-2015 dataset. This result was not unexpected as the deep learning literature has shown (e.g., (Valverde et al., 2019)) that the performance of CNNs tend to degrade substantially when applied to image data obtained with different acquisition parameters such as voxel size, pulse sequence, timing parameters, and scanner vendor, among others. Data harmonization approaches such as those reported in (Fortin et al., 2017) and (Dewey et al., 2019) might overcome this issue and will be explored in our future work.
One limitation of the study was the potential bias caused by the lesion mask annotation process. Because a fully manual segmentation of a large dataset like ours would be time-prohibitive, we have adopted a semiautomatic approach, in which an initial segmentation mask was obtained by the automated LST-LPA algorithm and further reviewed and edited, if necessary, by the human experts to obtain the final lesion mask. This approach may create unwanted bias in the ground truth masks as the readers could be influenced by the initial masks generated by LST-LPA. We should also note that the ground truth lesion masks for the Cornell dataset were delineated by two expert readers and are therefore subject to intra- and inter-rater reliability and can be less stringent than those obtained by the consensus of a much larger number of expert readers. Our algorithm was trained to mimic the performance of these two readers, and likely can be further improved by aggregating input from more readers. A DSC of 0.73 is reported (Carass et al., 2017) to assess the agreement between two human experts as a measure of the degree of overlap between segmentations; our proposed ALL-Net achieved a DSC of 0.755 on the Cornell MS dataset. This indicates that our ALL-Net has the potential to be a useful clinical tool.
According to the ISBI-2015 challenge (Carass et al., 2017), a score over 90 indicates that segmentation accuracy is similar to that of human experts. ALL-Net’s score 93.32 on the challenge dataset, in combination with its speed of processing a whole brain in less than one second, suggest that it can serve as a fully automated tool to aid in routine MS lesion segmentation. Although ALL-Net correctly detects 91.7% (see LTPR in Table 3) of lesions, about 30% (see LFPR in Table 3) detected lesions are false positives. Future work will be focused on further reducing the false positive rate to improve clinical translation.
MS lesions accumulate and may expand over-time leading to the development of large confluent lesions. Currently, our method cannot separate out the original individual lesions from a large confluence. To this end, we will build upon our LesLoss to simultaneously segment and separate these confluent lesions. Currently, LesLoss computes lesion centers based on spatial-separated connected components, but it is possible to extend LesLoss to compute lesion centers for individual lesions. The probability map of spheres obtained by LesLoss can be used to pick up peak points for identifying individual lesions.
In conclusion, the proposed ALL-Net algorithm with efficient encoding of anatomical information and a lesion-wise loss function improves MS lesion detection accuracy compared to state-of-the-art algorithms.
CRediT authorship contribution statement
Hang Zhang: Conceptualization, Methodology, Software, Writing – original draft. Jinwei Zhang: Software, Validation. Chao Li: Software, Validation. Elizabeth M. Sweeney: Statistical analysis, Supervision. Pascal Spincemaille: Writing - review & editing, Supervision. Thanh D. Nguyen: Data curation, Writing - review & editing, Supervision. Susan A. Gauthier: Data curation, Supervision. Yi Wang: Writing - review & editing, Supervision, Funding acquisition.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This research was supported in part by grants from the National Institute of Health (R01NS105144) and the National MS Society (RR-1602-07671).
References
- Andermatt, S., Pezold, S., Cattin, P.C., 2017. Automated segmentation of multiple sclerosis lesions using multi-dimensional gated recurrent units. International MICCAI Brainlesion Workshop. Springer, pp. 31-42.
- Aslani S., Dayan M., Storelli L., Filippi M., Murino V., Rocca M.A., Sona D. Multi-branch convolutional neural network for multiple sclerosis lesion segmentation. NeuroImage. 2019;196:1–15. doi: 10.1016/j.neuroimage.2019.03.068. [DOI] [PubMed] [Google Scholar]
- Birenbaum A., Greenspan H. Deep Learning and Data Labeling for Medical Applications. Springer; 2016. Longitudinal multiple sclerosis lesion segmentation using multi-view convolutional neural networks; pp. 58–67. [Google Scholar]
- Brosch T., Tang L.Y.W., Yoo Y., Li D.K.B., Traboulsee A., Tam R. Deep 3D convolutional encoder networks with shortcuts for multiscale feature integration applied to multiple sclerosis lesion segmentation. IEEE Trans. Med. Imag. 2016;35(5):1229–1239. doi: 10.1109/TMI.2016.2528821. [DOI] [PubMed] [Google Scholar]
- Carass A., Roy S., Jog A., Cuzzocreo J.L., Magrath E., Gherman A., Button J., Nguyen J., Prados F., Sudre C.H. Longitudinal multiple sclerosis lesion segmentation: resource and challenge. NeuroImage. 2017;148:77–102. doi: 10.1016/j.neuroimage.2016.12.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Çiçek Ö., Abdulkadir A., Lienkamp S.S., Brox T., Ronneberger O. International conference on medical image computing and computer-assisted intervention. Springer; 2016. 3D U-Net: learning dense volumetric segmentation from sparse annotation; pp. 424–432. [Google Scholar]
- Codella N.C., Weinsaft J.W., Cham M.D., Janik M., Prince M.R., Wang Y. Left ventricle: automated segmentation by using myocardial effusion threshold reduction and intravoxel computation at MR imaging. J Am. J. Neuroradiol. 2008;248:1004–1012. doi: 10.1148/radiol.2482072016. [DOI] [PubMed] [Google Scholar]
- Commowick O., Cervenansky F., Ameli R. MSSEG challenge proceedings: multiple sclerosis lesions segmentation challenge using a data management and processing infrastructure. Miccai. 2016 [Google Scholar]
- Danelakis A., Theoharis T., Verganelakis D.A., Graphics Survey of automated multiple sclerosis lesion segmentation techniques on magnetic resonance imaging. Computer. Med. Imag. 2018;70:83–100. doi: 10.1016/j.compmedimag.2018.10.002. [DOI] [PubMed] [Google Scholar]
- Danielsson Per-Erik. Euclidean distance mapping. Comput. Graph. Image Process. 1980;14:227–248. [Google Scholar]
- Dewey B.E., Zhao C., Reinhold J.C., Carass A., Fitzgerald K.C., Sotirchos E.S., Saidha S., Oh J., Pham D.L., Calabresi P.A. DeepHarmony: A deep learning approach to contrast harmonization across scanner changes. J. Magn. Reson. Imag. 2019;64:160–170. doi: 10.1016/j.mri.2019.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson R., Giovannoni G. Multiple sclerosis–a review. Eur. J. Neurol. 2019;26:27–40. doi: 10.1111/ene.13819. [DOI] [PubMed] [Google Scholar]
- Filippi M., Rocca M.A., Ciccarelli O., De Stefano N., Evangelou N., Kappos L., Rovira A., Sastre-Garriga J., Tintorè M., Frederiksen J.L. MRI criteria for the diagnosis of multiple sclerosis: MAGNIMS consensus guidelines. Lancet Neurol. 2016;15:292–303. doi: 10.1016/S1474-4422(15)00393-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filippi M., Preziosa P., Banwell B.L., Barkhof F., Ciccarelli O., De Stefano N., Geurts J.J., Paul F., Reich D.S., Toosy A.T. Assessment of lesions on magnetic resonance imaging in multiple sclerosis: practical guidelines. Brain. 2019;142:1858–1875. doi: 10.1093/brain/awz144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortin J.-P., Parker D., Tunç B., Watanabe T., Elliott M.A., Ruparel K., Roalf D.R., Satterthwaite T.D., Gur R.C., Gur R.E. Harmonization of multi-site diffusion tensor imaging data. J. Neuroimage. 2017;161:149–170. doi: 10.1016/j.neuroimage.2017.08.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghafoorian M., Karssemeijer N., Heskes T., Bergkamp M., Wissink J., Obels J., Keizer K., de Leeuw F.-E., van Ginneken B., Marchiori E. Deep multi-scale location-aware 3D convolutional neural networks for automated detection of lacunes of presumed vascular origin. NeuroImage Clin. 2017;14:391–399. doi: 10.1016/j.nicl.2017.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabner G., Janke A.L., Budge M.M., Smith D., Pruessner J., Collins D.L. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2006. Symmetric atlasing and model based segmentation: an application to the hippocampus in older adults; pp. 58–66. [DOI] [PubMed] [Google Scholar]
- Haider L., Zrzavy T., Hametner S., Höftberger R., Bagnato F., Grabner G., Trattnig S., Pfeifenbring S., Brück W., Lassmann H. The topograpy of demyelination and neurodegeneration in the multiple sclerosis brain. Brain. 2016;139:807–815. doi: 10.1093/brain/awv398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashemi S.R., Salehi S.S.M., Erdogmus D., Prabhu S.P., Warfield S.K., Gholipour A. Asymmetric loss functions and deep densely-connected networks for highly-imbalanced medical image segmentation: application to multiple sclerosis lesion detection. IEEE Access. 2018;7:1721–1735. doi: 10.1109/ACCESS.2018.2886371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou B., Kang G., Xu X., Hu C. 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) IEEE; 2019. Cross attention densely connected networks for multiple sclerosis lesion segmentation; pp. 2356–2361. [Google Scholar]
- Huang G., Liu Z., Van Der Maaten L., Weinberger K.Q. Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. Densely connected convolutional networks; pp. 4700–4708. [Google Scholar]
- Ioffe S., Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Int. Conf. Mach. Learn. PMLR. 2015:448–456. [Google Scholar]
- Isensee F., Jaeger P.F., Kohl S.A., Petersen J., Maier-Hein K.H. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. J .Nat. methods. 2021;18:203–211. doi: 10.1038/s41592-020-01008-z. [DOI] [PubMed] [Google Scholar]
- Islam, M.A., Jia, S., Bruce, N.D., 2019. How much Position Information Do Convolutional Neural Networks Encode? , International Conference on Learning Representations.
- Kamnitsas K., Ledig C., Newcombe V.F., Simpson J.P., Kane A.D., Menon D.K., Rueckert D., Glocker B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017;36:61–78. doi: 10.1016/j.media.2016.10.004. [DOI] [PubMed] [Google Scholar]
- Kayhan, O.S., Gemert, J.C.v., 2020. On translation invariance in cnns: Convolutional layers can exploit absolute spatial location. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 14274-14285.
- Kingma, D.P., Ba, J., 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
- Law H., Deng J. Proceedings of the European conference on computer vision (ECCV) 2018. Cornernet: Detecting objects as paired keypoints; pp. 734–750. [Google Scholar]
- Lin T.-Y., Goyal P., Girshick R., He K., Dollár P. Proceedings of the IEEE international conference on computer vision. 2017. Focal loss for dense object detection; pp. 2980–2988. [Google Scholar]
- Liu R., Lehman J., Molino P., Such F.P., Frank E., Sergeev A., Yosinski J. Proceedings of the 32nd International Conference on Neural Information Processing Systems. 2018. An intriguing failing of convolutional neural networks and the CoordConv solution; pp. 9628–9639. [Google Scholar]
- Long J., Shelhamer E., Darrell T. Proceedings of the IEEE conference on computer vision and pattern recognition. 2015. Fully convolutional networks for semantic segmentation; pp. 3431–3440. [Google Scholar]
- Ma T., Zhang H., Ong H., Vora A., Nguyen T.D., Gupta A., Wang Y., Sabuncu M.R. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. 2021. Ensembling low precision models for binary biomedical image segmentation; pp. 325–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald W.I. Relapse, remission, and progression in multiple sclerosis. Mass Medical Soc. 2000 doi: 10.1056/NEJM200011163432010. [DOI] [PubMed] [Google Scholar]
- McKinley R., Wepfer R., Aschwanden F., Grunder L., Muri R., Rummel C., Verma R., Weisstanner C., Reyes M., Salmen A. Simultaneous lesion and brain segmentation in multiple sclerosis using deep neural networks. J. Sci. Rep. 2021;11:1–11. doi: 10.1038/s41598-020-79925-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milletari, F., Navab, N., Ahmadi, S.-A., 2016. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 2016 fourth international conference on 3D vision (3DV). IEEE, pp. 565–571.
- Oktay, O., Schlemper, J., Folgoc, L.L., Lee, M., Heinrich, M., Misawa, K., Mori, K., McDonagh, S., Hammerla, N.Y., Kainz, B., 2018. Attention u-net: Learning where to look for the pancreas. arXiv preprint arXiv:1804.03999.
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., 2019. Pytorch: An imperative style, high-performance deep learning library. arXiv preprint arXiv:1912.01703.
- Ronneberger O., Fischer P., Brox T. International Conference on Medical image computing and computer-assisted intervention. Springer; 2015. U-net: Convolutional networks for biomedical image segmentation; pp. 234–241. [Google Scholar]
- Schmidt P., Gaser C., Arsic M., Buck D., Förschler A., Berthele A., Hoshi M., Ilg R., Schmid V.J., Zimmer C. An automated tool for detection of FLAIR-hyperintense white-matter lesions in multiple sclerosis. NeuroImage. 2012;59:3774–3783. doi: 10.1016/j.neuroimage.2011.11.032. [DOI] [PubMed] [Google Scholar]
- Schmidt, P., 2017. Bayesian inference for structured additive regression models for large-scale problems with applications to medical imaging.
- Shiee N., Bazin P.-L., Ozturk A., Reich D.S., Calabresi P.A., Pham D.L. A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions. NeuroImage. 2010;49:1524–1535. doi: 10.1016/j.neuroimage.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonyan, K., Zisserman, A.J.a.p.a., 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
- Smith S.M., Jenkinson M., Woolrich M.W., Beckmann C.F., Behrens T.E., Johansen-Berg H., Bannister P.R., De Luca M., Drobnjak I., Flitney D.E. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Styner M., Lee J., Chin B., Chin M., Commowick O., Tran H., Markovic-Plese S., Jewells V., Warfield S. 3D segmentation in the clinic: a grand challenge II: MS lesion segmentation. Midas J. 2008;2008:1–6. [Google Scholar]
- Thompson A.J., Banwell B.L., Barkhof F., Carroll W.M., Coetzee T., Comi G., Correale J., Fazekas F., Filippi M., Freedman M.S. Diagnosis of multiple sclerosis: 2017 revisions of the McDonald criteria. Lancet Neurol. 2018;17:162–173. doi: 10.1016/S1474-4422(17)30470-2. [DOI] [PubMed] [Google Scholar]
- Valverde S., Cabezas M., Roura E., González-Villà S., Pareto D., Vilanova J.C., Ramió-Torrentà L., Rovira À., Oliver A., Lladó X. Improving automated multiple sclerosis lesion segmentation with a cascaded 3D convolutional neural network approach. NeuroImage. 2017;155:159–168. doi: 10.1016/j.neuroimage.2017.04.034. [DOI] [PubMed] [Google Scholar]
- Valverde S., Salem M., Cabezas M., Pareto D., Vilanova J.C., Ramió-Torrentà L., Rovira À., Salvi J., Oliver A., Lladó X. One-shot domain adaptation in multiple sclerosis lesion segmentation using convolutional neural networks. J. NeuroImage Clin. 2019;21 doi: 10.1016/j.nicl.2018.101638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss N., Rueckert D., Rao A. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2013. Multiple sclerosis lesion segmentation using dictionary learning and sparse coding; pp. 735–742. [DOI] [PubMed] [Google Scholar]
- Zhang H., Valcarcel A.M., Bakshi R., Chu R., Bagnato F., Shinohara R.T., Hett K., Oguz I. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2019. Multiple sclerosis lesion segmentation with tiramisu and 2.5 d stacked slices; pp. 338–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H., Zhang J., Zhang Q., Kim J., Zhang S., Gauthier S.A., Spincemaille P., Nguyen T.D., Sabuncu M., Wang Y. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2019. RsaNet: Recurrent slice-wise attention network for multiple sclerosis lesion segmentation; pp. 411–419. [Google Scholar]
- Zhang H., Wang R., Zhang J., Li C., Yang G., Spincemaille P., Nguyen T.D., Wang Y. NeRD: Neural Representation of Distribution for Medical Image Segmentation. arXiv:2103.04020. 2021 [Google Scholar]
- Zhang H., Zhang J., Wang R., Zhang Q., Gauthier S.A., Spincemaille P., Nguyen T.D., Wang Y. 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) IEEE; 2021. Geometric Loss for Deep Multiple Sclerosis lesion Segmentation; pp. 24–28. [Google Scholar]
- Zhang H., Zhang J., Wang R., Zhang Q., Spincemaille P., Nguyen T.D., Wang Y. Efficient Folded Attention for Medical Image Reconstruction and Segmentation. Proc. AAAI Conf. Artif. Intell. 2021;35:10868–10876. [Google Scholar]
- Zhou, X., Wang, D., Krähenbühl, P., 2019. Objects as points. arXiv preprint arXiv:1904.07850.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The ISBI-2015 dataset is publicly available and can be requested at their website http://iacl.ece.jhu.edu/index.php?title=MSChallenge. The Cornell MS dataset is a private clinical dataset and cannot be made publicly available due to confidentiality. The code is available at https://github.com/tinymilky/ALL-Net.