Quantitative assessment of distant recurrence risk in early stage breast cancer using a nonlinear combination of pathological, clinical and imaging variables

Abstract

Use of genomic assays to determine distant recurrence risk in patients with early stage breast cancer has expanded and is now included in the American Joint Committee on Cancer staging manual. Algorithmic alternatives using standard clinical and pathology information may provide equivalent benefit in settings where genomic tests, such as OncotypeDx, are unavailable. We developed an artificial neural network (ANN) model to nonlinearly estimate risk of distant cancer recurrence. In addition to clinical and pathological variables, we enhanced our model using intraoperatively determined global mammographic breast density (MBD) and local breast density (LBD). LBD was measured with optical spectral imaging capable of sensing regional concentrations of tissue constituents. A cohort of 56 ER+ patients with an OncotypeDx score was evaluated. We demonstrated that combining MBD/LBD measurements with clinical and pathological variables improves distant recurrence risk prediction accuracy, with high correlation (r = 0.98) to the OncotypeDx recurrence score.

Graphical Abstract

1 |. INTRODUCTION

Over 250 000 breast cancers are diagnosed annually in the U.S. and an estimated 90% of these will be diagnosed at an early stage, where the disease remains confined to the breast and axillary lymph nodes [1]. Following diagnosis, 50%–75% of early-stage patients undergo breast conserving surgery (BCS) followed by whole-breast radiation therapy. A persistent challenge of BCS and all breast oncologic treatment is the presence of clinically occult tumor cells that cause relapse—local recurrence and/or distant metastasis [2]. Over the past 15 years, the risk of distant recurrence has decreased and long-term survival has improved. Survival improvements have primarily been attributed to improved adjuvant treatments, including chemotherapy, directed HER2/neu therapy for HER2/neu + disease and estrogen receptor blocking agents and aromatase inhibitors for endocrine-positive breast cancer. Use of the most appropriate adjuvant or neoadjuvant therapy for a patient to reduce distant recurrence risk is an example of precision medicine that can reduce mortality, morbidity associated with over-treatment and healthcare cost [3–6].

Predicting the need for adjuvant or neoadjuvant therapy has improved over the past 15 years with the use of genomic multigene assays. Genomic multigene assays originated with an analysis of prior clinical tissue and data, wherein long-term outcomes from patient treatments were known and could be correlated with identified multigene arrays. The OncotypeDx assay was developed using data from the National Surgical Adjuvant Breast and Bowel Project (NSABP), particularly the B-20 and B-14 studies, which demonstrated that, while adjuvant chemotherapy improved disease-free survival, not all ER+/node-negative tumors benefited from adjuvant chemotherapy [7–11]. Treatment decisions were modified in up to 30% of patients receiving a recurrence score, sparing patients with low-risk cancers unnecessary cytotoxic therapy [12–15].

The OncotypeDx recurrence score provides a numeric indicator of distant recurrence risk (1–100) that is used to categorically assign patients to low-risk (1–17), intermediate-risk (18–30) and high-risk (>30) groups [16]. Several review studies suggest a definite adjuvant chemotherapy benefit for node-negative patients in the high-risk group, but little to no benefit for those in the low-risk group [17–21]. For the intermediate-risk category, the recent TAILORx trial showed no significant association between chemotherapy and recurrence score, except for a significant benefit for chemotherapy for women less than 50 years old [22, 23]. Notably, the recent AJCC 8th Cancer Staging Manual suggested the use of genomics profiles or multigene panels in clinical decision-making, demonstrating the important connection between pathology and genomics. To address resource limitations in settings where a validated genomic test such as OncotypeDx is unavailable, efforts have been devoted to developing inexpensive algorithmic recurrence risk estimators that are based on correlations with standard clinical and pathological features. The rationale for using pathological features to provide recurrence predictions stems from the relationship between genetic markers in the OncotypeDx assay and cellular features determined using histopathology [24]. Categorical (low-/intermediate-/high-risk) and numeric (1–100) linear regression models have been reported that use combinations of pathological feature variables, though the Pearson correlation coefficients have not exceeded 0.7 [25–28]. One review [27], which used an independent data set as input to published linear models, found that strategically selected combinations of pathological variables could be used to generate a reliable OncotypeDx surrogate for high-risk patients. However, in the intermediate- and low-risk groups, the predictions were less reliable and were statistically unfit to safely replace the validated OncotypeDx recurrence score.

Other models have included imaging features from magnetic resonance (MR), ultrasound or mammography in an attempt to more accurately predict OncotypeDx scores. Multivariate logistic regression was used to identify pleomorphic calcifications on a mass in mammography images and posterior acoustic enhancement on a mass in ultrasound as features for accurately predicting OncotypeDx category [29]. Linear models using MR images [30–32] identified image features significantly correlating with OncotypeDx scores, and a nonlinear convolutional neural network showed an accuracy of 81% and specificity of 90% for a three-class prediction [33]. These models demonstrate the value of using image features for OncotypeDx score prediction in both linear and nonlinear models.

Patients with elevated mammographic breast density (MBD) are predisposed to local recurrence [34–37]. Features relating to breast density could thus improve prediction of recurrence risk. In a previous study, patients in the high mammographic density group experienced much greater risk of local disease recurrence than patients in the low-density group (10-year actuarial risks: 21% vs 5%; hazards ratio [HR], 5.7) [36]. In fact, previous studies have shown that tumorigenic signaling and cellular persistence is enhanced with increased collagen matrix stiffness and the nature of fiber matrix alignment within the breast [38–41]. Our group has previously developed a spectral imaging probe that can intraoperatively capture a measure of local breast density (LBD) for every square millimeter of a given breast tumor margin [35, 42]. While a clear association was established between LBD and surgical margin status—and thereby risk of local recurrence [34]—no association with distant recurrence risk has been established. Features related to breast density have yet to be explored in genomic assays or in models that include pathological and/or imaging inputs.

The use of artificial neural networks (ANN) for diagnostic purposes has become increasingly popular, with many clinical trials showing an increase in benefit to health care outcomes [43]. ANNs are an evolving branch of machine learning that seeks to leverage information processing methods similar to the human brain. ANNs incrementally learn from feature patterns characteristic of a natural phenomenon, effectively capturing all linear and nonlinear relationships between inputs and outputs. The diagnosis of cancer, cardiovascular disease and diabetes are some more popular uses for ANNs, since there are large data sets available for these diseases [44]. Applications of ANNs for these diseases include diagnosis of coronary artery disease, arrhythmias, distinguishing cancer types, cancer diagnosis, the extrapolation of glucose concentrations and measuring patient quality of life. A variety of inputs have been used in ANNs for cancer diagnosis, including demographic, oncologic, radiologic and biochemical data [44]. For breast cancer, the use of ANNs has focused mainly on the interpretation of mammographic images. A 3-layer ANN performed at a higher level than the averages of attending radiologists or residents when interpreting mammograms, with a resulting AUC of 0.95 [45]. Convolutional Neural Networks (CNNs) are similar to ANNs, but typically include a fully connected layer at the end of the network, as well as many convolutional layers. CNNs have also shown promise in the field of breast cancer diagnostics, particularly when images are included in the input. CNNs have been used to classify invasive ductal carcinoma breast cancer (AUC 0.99–1.00) [46], for evaluation of digital mammography to detect breast cancer (AUC 0.8490) [47], for detection of malignant soft tissue lesions in mammography (AUC 0.87–0.895) [48], and for breast cancer screening exam classification (AUC 0.895) [49]. Some limitations of CNNs in breast cancer imaging include inferior performance compared wth experienced radiologists [47], small sample sets [49], and degradation of performance between the training and testing data sets [48].

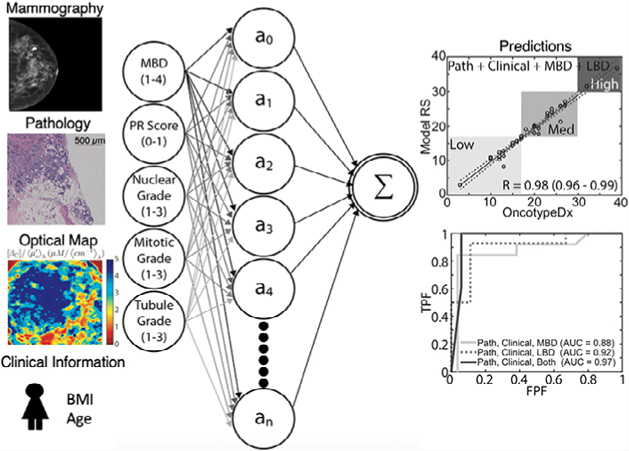
The goal of this study was to investigate the value of including global breast density measured using mammography and LBD measured using optical imaging for OncotypeDx score prediction. The relationships between composite pathological features (hormone receptor content, mitotic grade, nuclear grade, tubule formation grade), clinical features (body mass index [BMI], age) and imaging features (mammographic, optical breast density) and their influence on recurrence risk (local and distant), are likely complex and unstructured. Therefore, we developed a nonlinear ANN algorithm to predict risk of recurrence. We first demonstrated the improved effectiveness of the ANN model compared wth published linear models for OncotypeDx score prediction—particularly for patients in the low and intermediate risk categories, where linear models underperformed. Next, we demonstrated improved OncotypeDx score prediction for the ANN model when breast density information (MBD and LBD) was incorporated in addition to clinical and pathological information. Models using a combination of global and LBD outperformed models using either one alone.

2 |. MATERIALS AND METHODS

This study was performed in accordance with prospective clinical protocols approved by Duke University and The University of Wisconsin Institutional Review Boards (Pro00007857, Pro00028284). Patients over age 18 undergoing BCS granted written consent under the approved clinical protocol. For this study, 57 ER+, axillary lymph node-negative patients who underwent BCS, local optical tissue assessment and OncotypeDx testing were selected from the two institutions. The patient cohort was selected from a larger cohort of patients (n = 500) collected from November 2007 through March 2017. The eligibility criteria of this study were (a) patients undergoing a partial mastectomy for the treatment of an invasive or non-invasive breast malignancy; (b) subjects greater than 18 years of age; and (c) patients with a clinically detectable disease either by physical examination or radio-graphic studies. This group is representative of the general surgical population (mostly postmenopausal women with ER+ breast tumors). All subjects were recruited following the same eligibility criteria. For the investigation, we built two instruments that had identical specifications based on performance verification and placed at Duke University and at the University of Wisconsin-Madison [35, 42]. Patient variables and OncotypeDx recurrence scores were entered into a REDCap database at Duke University (n = 49) and the University of Wisconsin-Madison (n = 63). However, due to the stringent criteria (ER+ patients with an OncotypeDx test and negative margin that was imaged to obtain the LBD endpoints) used to select patients for this analysis, only 18 patients from the University of Wisconsin-Madison and 38 patients from Duke University were included in the analysis. Only consenting patients in whom optical images from pathologically confirmed negative margins (n = 56) were included in this study (no tumor within 2 mm of the edge).

The variables incorporated into this analysis can be categorized into clinical, pathological and imaging variable groups. The clinical characteristics recorded for each patient were BMI and age. Other clinical parameters such as menopausal status, prior surgeries and pregnancies were not used due to inconsistencies in reporting these parameters. The pathological features used included ER/PR levels as quantified by the Allred score; HER2 status; nuclear, mitotic and tubule formation grades; and tumor size. The combined Nottingham grade was also recorded; however, this parameter was used only in instances involving direct comparisons to previously developed predictive models. Similarly, the ER/PR “H-score,” which captures the percentage of cells presenting with weak, moderate, strong or no staining [28], was recorded for comparisons to published linear models. ER and PR expression was determined using standard immunohistochemistry where the percentage and intensity of nuclear staining of invasive tumor cells was used to calculate the composite Allred score and the H-score. Each patient had a positive ER status (AS >2). HER2 expression was categorized as negative, equivocal or positive using IHC combined with fluorescent in situ hybridization (FISH) as described by the American Society of Clinical Oncology guidelines. The imaging variables included MBD and LBD from breast tumor margins. For MBD, a single radiologist (MSS) re-read all breast mammograms to ensure consistency in scoring across patients recruited from Duke University and the University of Wisconsin, Madison. Each patient was assigned a value based on their presurgery mammogram: 1 (fatty), 2 (scattered fibroglandular), 3 (heterogeneously dense) or 4 (extremely dense). LBD information was collected using optical surrogates previously shown to correlate to radio-graphic breast density and disease specific subtypes in lumpectomy specimens [34, 35, 50, 51].

2.1 |. Optical imaging

Diffuse reflectance spectra were collected from excised breast tissue specimens from 106 tumor margins using an optical probe described previously [34, 35, 42]. We measured two negative margins in all tumor samples except six patients due to intraoperative time constraints. Specimen orientation for lumpectomies (partial mastectomies) was determined according to surgically-placed reference features, including a surgical wire inserted into the center of the tumor, colored sutures and surgical clips. Specimen faces were defined as the faces of a cube and labeled relative to the specimen orientation in situ; the six measurable faces are clinically referred to as the superior, inferior, posterior, anterior, medial or lateral margins.

Immediately following tissue resection, lumpectomy specimens underwent intraoperative mammography to verify removal of the tumor mass. The specimen was then placed onto the imaging device. Following orientation, a raster-scanning procedure was initiated and diffuse reflectance spectra were collected across the visible spectrum (λ = 420–700 nm). Most often, the specimen was then flipped to its opposing margin and the scan was performed on a second margin. All margins measured in the study were pathologically negative.

Tissue optical property maps were reconstructed post-measurement using an inverse Monte Carlo model as discussed previously [51–53]. Briefly, the spatial-spectral information was used to fingerprint the tissue by providing direct measures of the β-carotene concentration (a surrogate for fat content) relative to the amount of tissue light scattering (a surrogate for fibroglandular content). The optical image was then compressed to six total descriptor variables that encapsulate the local density landscape of the tumor margin (Figure 1). Compression of the image was achieved by first generating a cumulative distribution function (CDF) of the entire optical image. The CDF was then fit to a modified logistic function, yielding three descriptive fit parameters: A, which represents the left/right shift of the CDF; B, which represents the CDF skew; and C, a numeric offset. In addition to these three parameters, the means, medians and variances of the images were also used to fully capture the optical parameter distribution of the margin. The image compression technique is illustrated in Figure 1.

FIGURE 1.

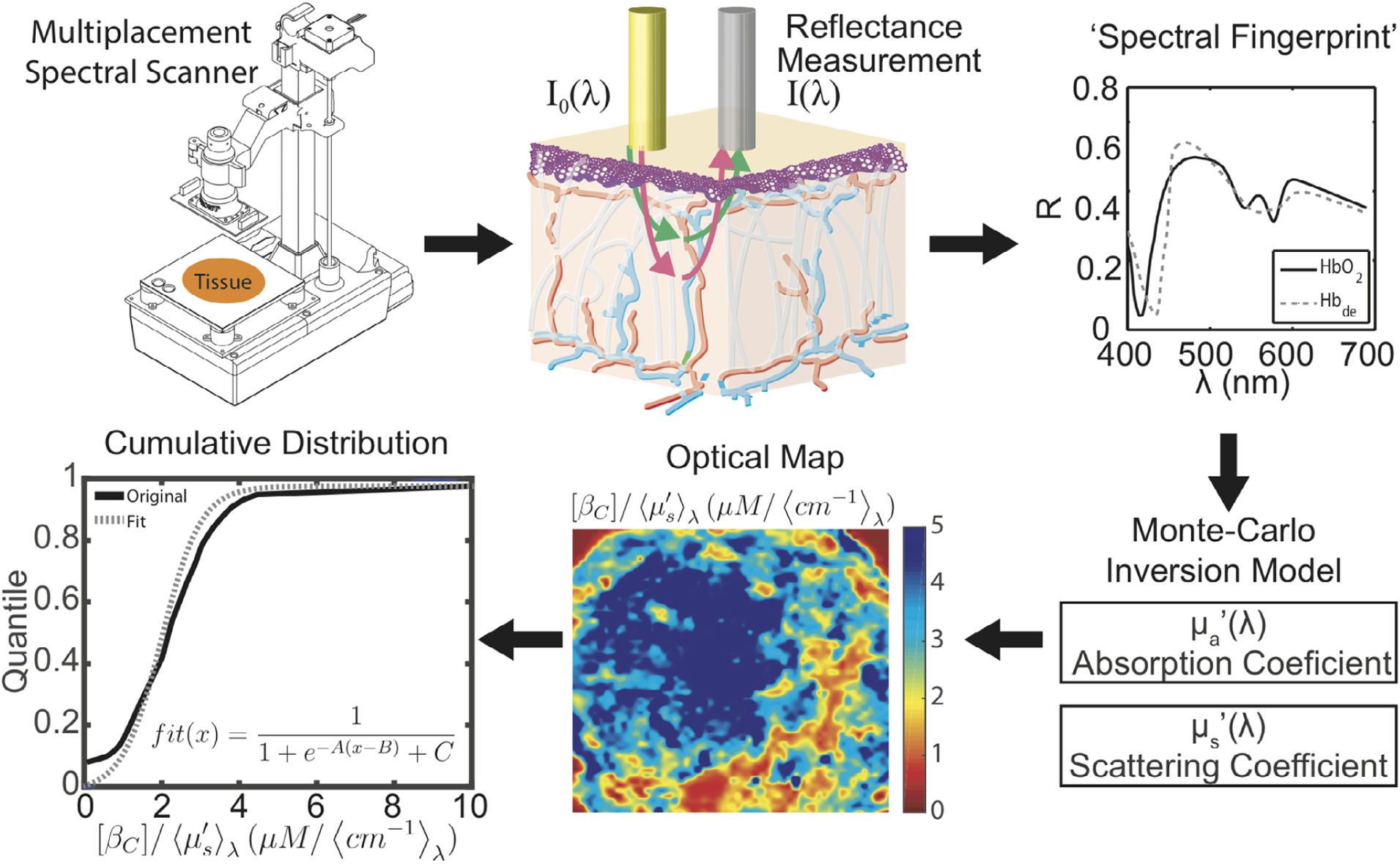
Microenvironment optical imaging. Clockwise: (1) Resected tissue specimens are placed on a scanning apparatus to capture spatial-spectral information (2, 3), which is processed using a Monte Carlo model to produce optical parameters (4). This process is repeated several times to capture the entire margin surface. When completed, the spatial distribution of the optical parameters is converted to a heat-map image (5). The cumulative distribution function (CDF) (6) is derived from this map, and the CDF is fit to a modified logistic function to obtain the optical parameter fit coefficients A, B and C

2.2 |. Nonlinear prediction model

The clinical, pathological and imaging variables were used in select combinations in a nonlinear ANN model to predict recurrence risk. A Machine Learning Toolbox in MATLAB 2017 was used to create the ANN used in this model. This toolbox contains apps and functions to create various architectures for neural networks. The sigmoid is the default activation function. Alternative activation functions were considered but were ultimately discarded as performance did not change significantly. The ANN model was constructed by using all pathology variables as a starting point and then systematically adding each additional variable to include all possible permutations. We investigated the effect of adding age and BMI individually (clinical endpoints), as well as each LBD variable (optical endpoints) and different combinations of these endpoints. The model was initially based on ~20 variables; therefore, the initial network was designed with 20 neurons. Performance was not statistically different when models with 10 and 30 were considered, so the model maintained the original choice of 20 neurons. The networks were constructed using 20 neurons or nodes, meaning a 20 × n coefficient matrix (where n is the number of variables) was used as variable input weights. The vector of weights corresponding to each node was determined using nonlinear backpropagation (Levenberg–Marquardt) to minimize the mean-square-error between an estimated OncotypeDx score and the true OncotypeDx score for the patient cohort. This model is diagrammed in Figure 2. The desired effect was to faithfully recreate the OncotypeDx score directly from learned patterns of input variables. This is in contrast to weighted coefficients used as scaling factors in linear regression. Indeed, this approach is nontraditional and unlike previously published models correlating input variables to the OncotypeDx score using linear regression [26–28]. While linear regression is easy to understand, the adaptive ability of the ANN model affords accuracy in what would traditionally be considered outlier circumstances, in which patients have uncommon combinations of scores. A common concern with any machine learning approach is model overfitting, which was overcome by randomly selecting 60% of the cohort to train the network and testing the network on the remaining 40% of the samples. The random sampling and training of the model were completed 1000 times. This increased the capacity of the model, because it was forced to fit a variety of functions. The weights from the 1000 fits were normally distributed about the mean, thus the mean weight was selected for the final model. The normal distribution of the weights indicates the model is not over-constrained or overfitted. The convergent network coefficients were then chosen as the trained network. Used in this manner, any combination of inputs can be trained to provide a single output score; in this case, the target score is the actual OncotypeDx recurrence score. Finally, the Pearson correlation coefficient (r) was calculated to indicate the accuracy of the predicted OncotypeDx recurrence scores when compared wth the true scores. Formally, r is the covariance of the predicted and true OncotypeDx scores divided by the product of their respective SD.

FIGURE 2.

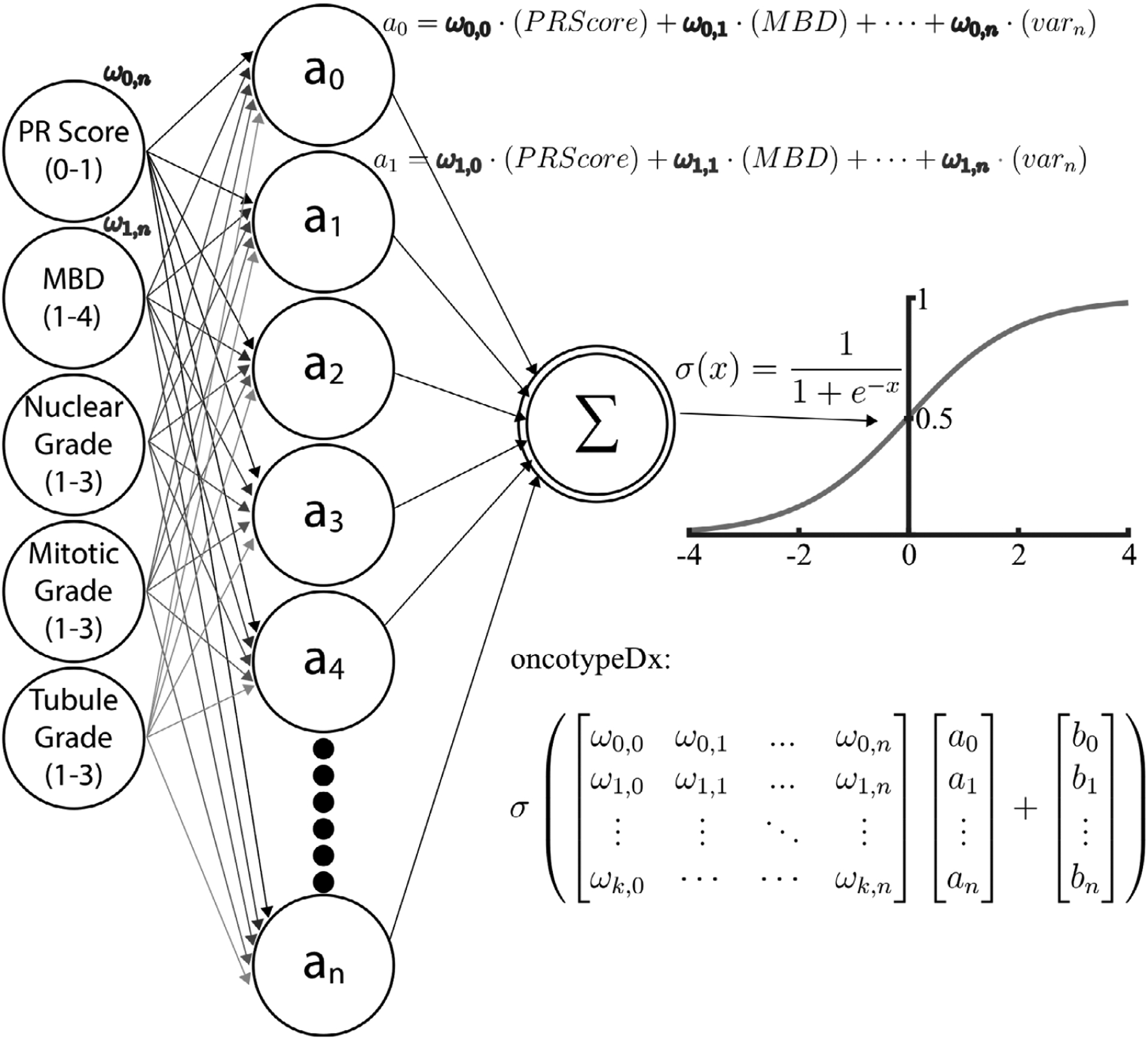
Artificial neural network model. From left to right: clinical, pathological and imaging variables were used as input nodes. Each of these nodes has an associated weighting matrix in which the coefficients represent the influence of that variable on a second, hidden layer of nodes. Finally, the second layer of nodes was summed and scaled by a sigmoid function that maps the output to the OncotypeDx score range of values (1–100)

Variable combinations were considered in a stepwise fashion. Although every possible combination of parameters could be attempted, we chose to start with the combination of the best three predictors and added the remaining parameters cumulatively, one at a time, keeping only those which improved estimates. Specifically, each possible set of three clinicopathological parameters was regressed against the true OncotypeDx score and parameters with correlation coefficients better than random chance were used in combination with the remaining parameters. In practice, this amounted to iteratively scoring each additional variable in combination with the current best performing set, in which case the best new set of variables was kept and this process continued for each remaining variable set. To eliminate random selection bias, the procedure was performed simultaneously with 10 branches containing less predictive, though similar accuracy, cumulative combination sets. This exercise was performed for pathological, clinical and imaging variables. Finally, variables were combined strategically across categories by removing subgroups accounting for the greatest variance of the true OncotypeDx score.

The correspondence of the true OncotypeDx recurrence score to the predicted score generated using clinical, pathological and imaging variables was assessed using parametric statistics, primarily the Pearson correlation coefficient. The normality of clinical variables was determined using the Shapiro–Wilk test. To assess the feasibility of safely using this algorithm in lieu of the OncotypeDx score, concordance between low-, medium- and high-risk classifications were assessed using weighted kappa statistics. Finally, receiver operating curves (ROCs) were generated to evaluate the sensitivity and specificity of classifying low- and medium-risk groups correctly, as this distinction is imperative for adoption of a low-cost alternative to the OncotypeDx score. Concordance of categorical risk classification between the OncotypeDx recurrence score and the ANN recurrence score was performed using the statistics toolbox in MATLAB, version 9.2.0.531146 (R2017a). The neural network was also developed in MATLAB R2017a using the machine learning toolbox.

3 |. RESULTS AND DISCUSSION

3.1 |. Distribution of pathological, clinical and imaging parameters of OncotypeDx patient cohort

Patient variables and OncotypeDx recurrence scores were obtained from the REDCap database at Duke University and the University of Wisconsin-Madison. Only consenting patients who had received LBD imaging (n = 56) were included in this study, where all tumor margins measured were negative (>2 mm). Patient information is detailed in Table 1. OncotypeDx scores ranged from 3 to 39 with an average of 19 ± 6.8 (SD); 28 patients were classified as low-risk, 26 as intermediate-risk and 2 as high-risk. The average patient age was 59 ± 9.8; average BMI was 29.6 ± 6.3. The average tumor size was 2 ± 1.2 cm. Analysis of pathology input parameter distributions conformed to the requirements of OncotypeDx assay eligibility: no patients had ER-tumors; 85% had an ER Allred score > 7, the remaining 15% had an ER Allred score of 2–7. Approximately 9% of patients had a negative progesterone receptor (PR) Allred score. Only one patient was HER2+, 40 were HER2- and 15 were equivocal as determined by immunohistochemistry (IHC). Most patients had a combined Nottingham score of either 1 (17 patients) or 2 (33), a nuclear grade of either 2 (35) or 3 (17), a mitotic grade of 1 (44) and a tubule formation grade of either 2 (20) or 3 (29). Only 3 patients had extremely dense breasts (MBD = 4), with 10 patients having mostly adipose breasts (MDB = 1), 25 having scattered fibrous breasts (MBD = 2) and 17 having heterogeneously dense breasts (MBD = 3). Though the models do not assume normal distributions for input parameters, the Nottingham, nuclear, mitotic and tubule formation grades were found to be normally distributed (Shapiro–Wilk test, P < .0001), indicating a non-biased patient cohort within the domain of ER positivity.

TABLE 1.

Patient demographics

OncotypeDx group	Variable type	Low (<18)	Intermediate (18–30)	High (>30)	Total
Patients (#)		28	26	2	56
Tumor size (cm)	Pathological	2.3 ± 1.4	1.8 ± 1.0	0.8 ± 0.2	2.0 ± 1.2
ER status (−/+)		0/28	0/25	0/2	0/55
PR status (−/+)		0/28	5/20	0/2	5/50
Combined Nottingham grade (1/2/3)		11/17/0	5/15/5	1/1/0	17/33/5
Nuclear grade (1/2/3)		1/22/5	3/13/10	0/0/2	4/35/17
Mitotic grade (1/2/3)		26/2/0	16/5/3	2/0/0	44/7/3
Tubule formation grade (1/2/3)		3/12/13	2/7/15	0/1/1	5/20/29
Age (avg. ± σ)	Clinical	58.0 ± 10.3	60.4 ± 8.7	56 ± 17	59.1 ± 9.8
BMI (avg. ± σ)		30 ± 6.3	28.9 ± 6.4	28.9 ± 5.2	29.6 ± 6.3
Mammographic density (MBD) (1/2/3/4)	Imaging	5/10/9/3	5/14/7/0	0/1/1/0	10/25/17/3

Note: Patient demographics by OncotypeDx risk group, subdivided based on clinical and pathology information.

Optical imaging surrogates for breast tissue morphology were normally distributed and correlated to the global MBD, reinforcing that optical imaging is measuring the fat-to-fibroglandular-content ratio. Figure 3 shows representative optical images with corresponding optical parameter distributions and summary variables, stratified by MBD. As MBD increases, the mean ratio of β-carotene and scattering decreases, causing the cumulative probability distribution (CDF) to shift to the left, captured as an increase in the A parameter. As MBD increases, the cumulative amount of fibroglandular content increases while fatty tissue decreases, resulting in increased tissue homogeneity, indicated as a narrower CDF and thus an increased slope. This effect is captured as an increase in the B parameter and can be thought of as microenvironment heterogeneity. The variance of the β-carotene-to-scattering ratio is also minimized in scattered fibroglandular tissue.

FIGURE 3.

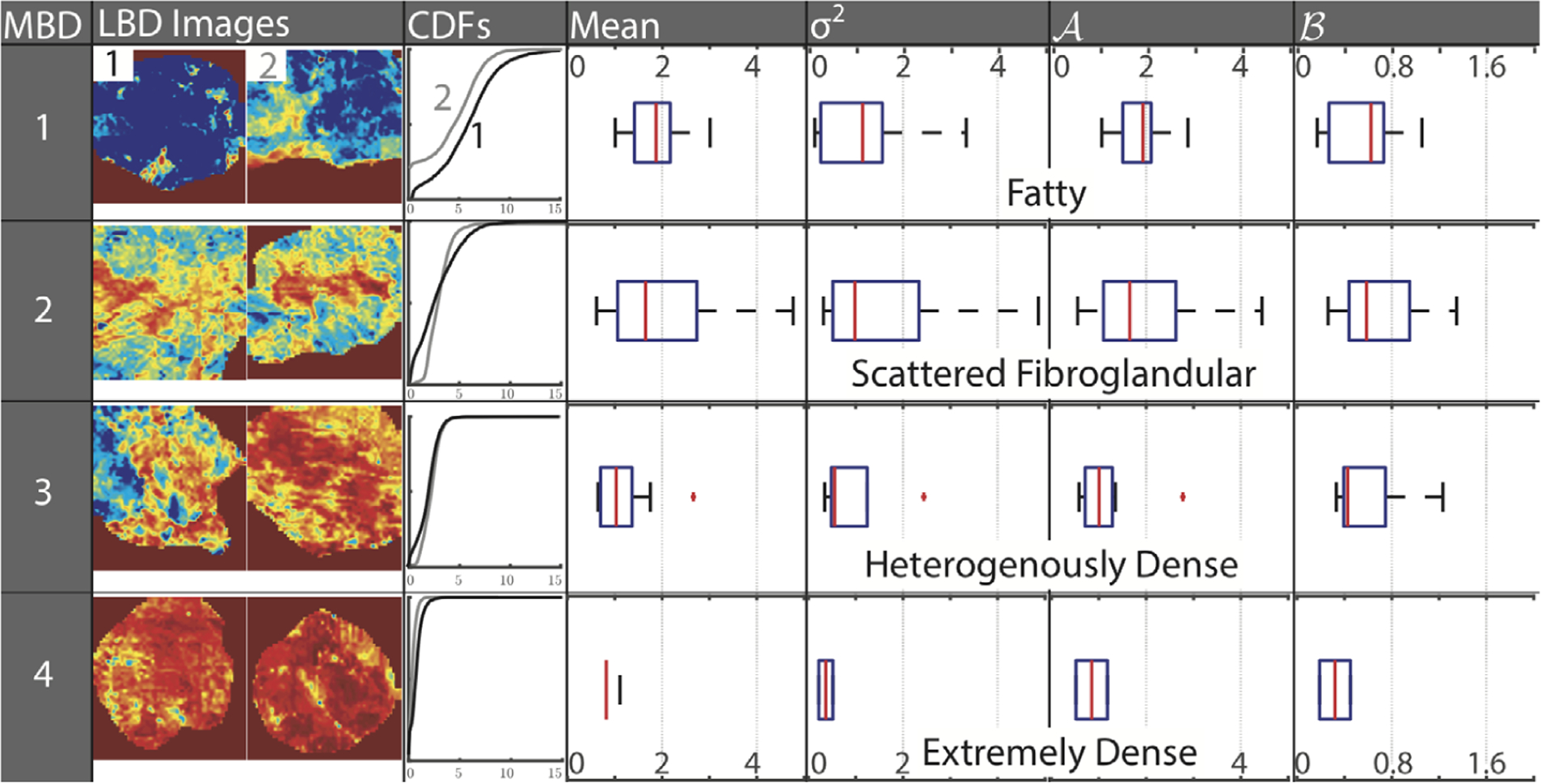
Optical imaging captures local density and heterogeneity reflected in mammographic breast density. Heat-map images of the ratio of β-carotene and scattering, a measure of local breast density (LBD), for increasing mammographic breast density (MBD), along with corresponding cumulative probability distributions (CDF). In each row, the CDF corresponding to the first image (labeled 1 in the top row) is represented by a black CDF curve, while the second image (labeled 2 in the top row) is represented by a gray curve. Optical trends corresponding to each MBD patient cohort are shown as box and whisker plots of the mean, variance (σ²), and the coefficients A and B of the CDF curve

3.2 |. Increased accuracy of the ANN model in predicting recurrence risk

Side-by-side comparison of the linear and ANN models revealed an impressive increase in prediction accuracy using the ANN model. The ANN model used the variables common to both of the previously published BCPS [26] and Magee [28] linear regression models: ER and PR status, nuclear grade, tubule grade and tumor size. We first evaluated the correlation between the predicted OncotypeDx recurrence score and the actual score using these two linear regression models with inputs from our data set. Correlation coefficients and variables used for each model are shown in Table 2. Regression lines and receiver operator curves (ROC) associated with the Magee₂, BCPS and ANN models are shown in Figure 4. We first evaluated the correlation between the predicted OncotypeDX recurrence score and the actual score using two published linear regression models using our data set. While the BCPS model uses the Nottingham score and the Magee₂, different cellular grades (mitotic, nuclear, tubule formation), these inputs are essentially describing the same features. The only input that is different is tumor size, which was included in the Magee₂ model. The Pearson correlation coefficient for the BCPS model using our data set (r = 0.44) was lower than the reported value (r = 0.65), likely due to the smaller sample size of our data set than in the previous study. Similarly, application of the Magee₂ equation to our data set resulted in a lower correlation coefficient than reported previously (r = 0.40 vs 0.66) [26, 28]. While the application of the BCPS and Magee₂ equation to our data set resulted in a lower correlation coefficient than reported previously [26, 28], the correlation coefficients were comparable between the models as was the case previously. Given that the BCPS model does not include tumor size, the ANN model was directly compared with the Magee₂ model as both use tumor size as one of the input variables. The ANN model outperformed the Magee₂ by a factor of 2 (correlation coefficient increased from 0.4 to 0.82). It should be noted that comparable correlation coefficients were achieved when the ANN model was tested either with nuclear grade and tubule grade or the Nottingham score.

TABLE 2.

Pathology inputs and resulting correlation coefficients of linear and ANN models

	Linear models		Nonlinear model ANN
	BCPS	Magee2
ERAS	✓	✓	✓
PRAS	✓	✓	✓
Nottingham score	x	✓	x
Nuclear grade	✓	x	✓
Tubule grade	✓	x	✓
Tumor size	x	✓	✓
r (95% CI) Literature	0.65 (N/A) [23]	0.66 (0.59–0.72) [25]	N/A
r (95% CI) Our data set	0.44 (0.19–0.63)	0.40 (0.15–0.61)	0.82 (0.71–0.89)

Note: Comparison of variables and goodness-of-fit for existing linear models to ANN model using data from Duke University and University of Wisconsin-Madison.

FIGURE 4.

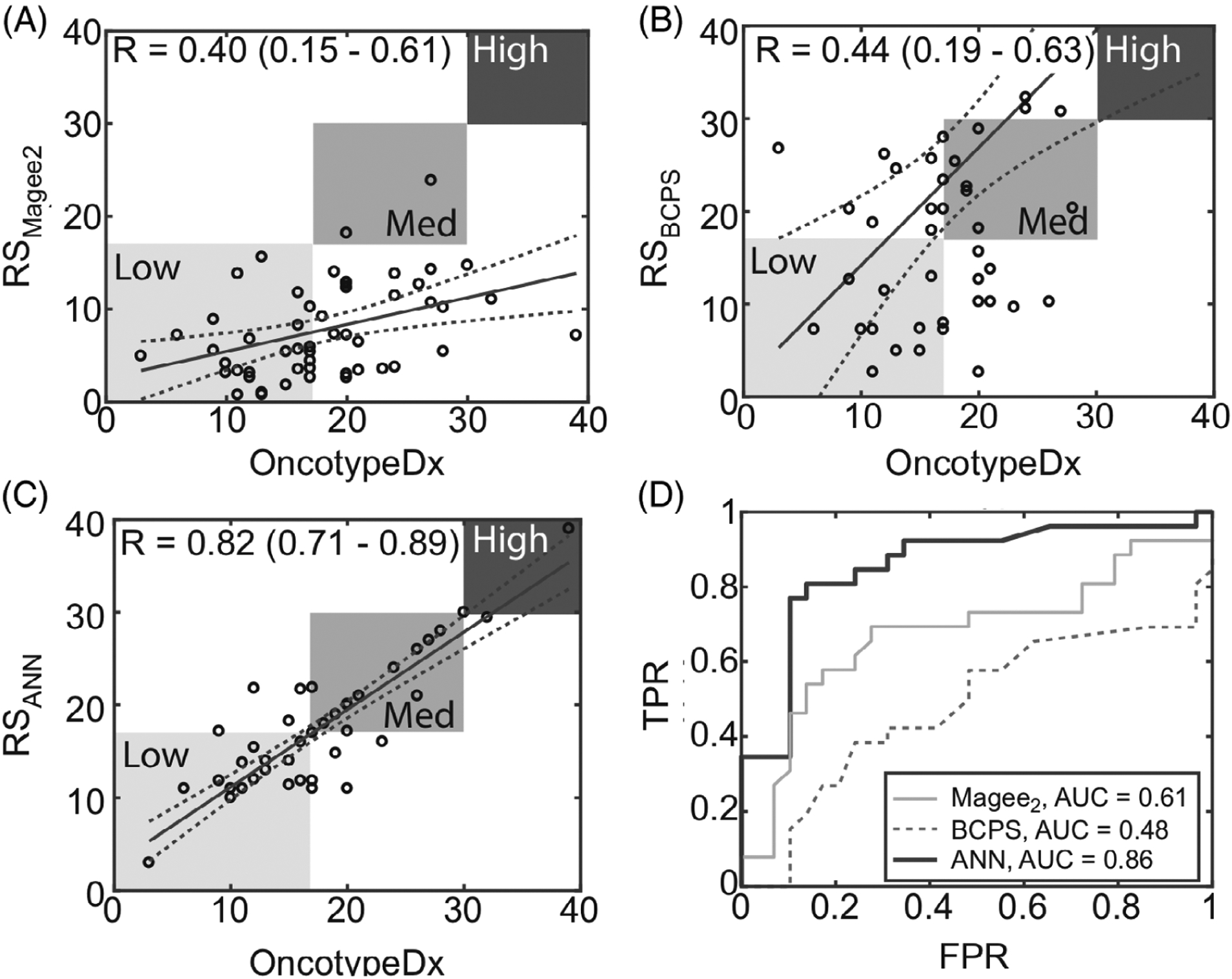
Correlation coefficients and performance of linear and ANN models based on pathology inputs. Regressions based on, A, the Magee₂ equation, B, the BCPS method and, C, the ANN model, incorporating only pathological features common to the BCPS and Magee₂ models. D, ROC curves for, A, B and, C for classification of low- vs intermediate-risk OncotypeDx recurrence scores

3.3 |. Enhancement of ANN model predictions with inclusion of patient clinical inputs

Using BMI combined with pathology improved correlations vs age combined with pathology (r = 0.88 [0.81–0.93] vs r = 0.86 [0.77–0.92]). The combination of both BMI and age with pathological features resulted in the highest correlation coefficient (r = 0.89 [0.82–0.94]). Figure 5 shows the regression lines associated with each of the clinical and pathological variable combinations.

FIGURE 5.

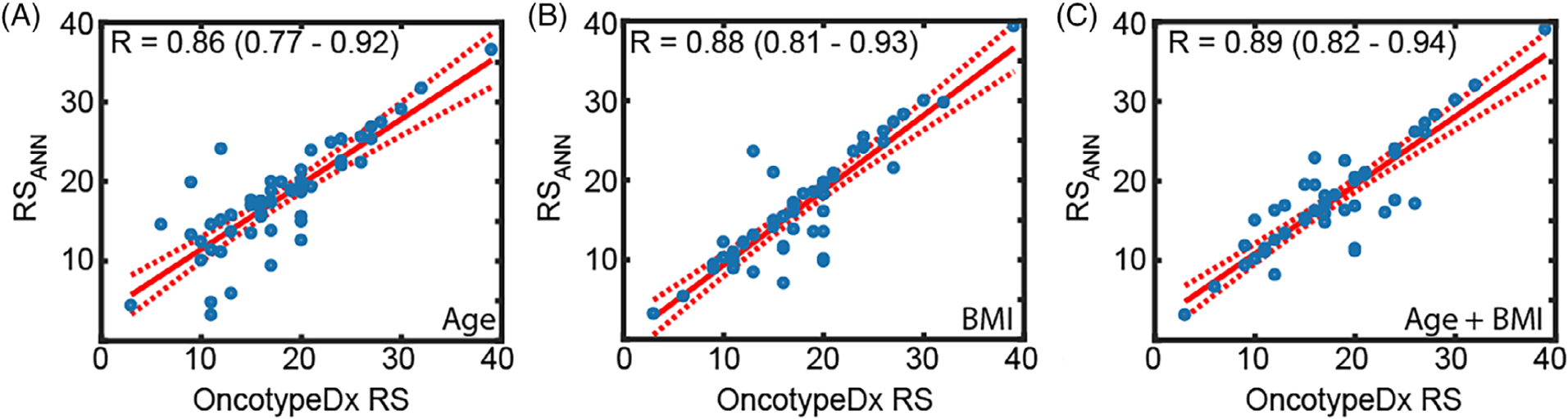
ANN model predictions for different combinations of clinical and pathology inputs. Regression lines associated with different inputs: A, patient age combined with pathology features, B, patient BMI combined with pathology features, and, C, both age and BMI combined with pathology features

Measures of MBD and LBD each independently improved correlation coefficients to above r = 0.90 (0.91 and 0.93, respectively) when combined with clinical and pathological features, suggesting the significance of breast density in recapitulating the true OncotypeDx score, as shown in Figure 6. Incorporating both variables in the model resulted in the highest correlation coefficient (r = 0.98 [0.96–0.99]). The predictive accuracy of including MBD from mammography, LBD from optical imaging and the combination of the two resulted in an area under the curve (AUC) of 0.88 to 0.97. Table 3 lists the variables used in each model and the respective risk prediction accuracy and AUC.

FIGURE 6.

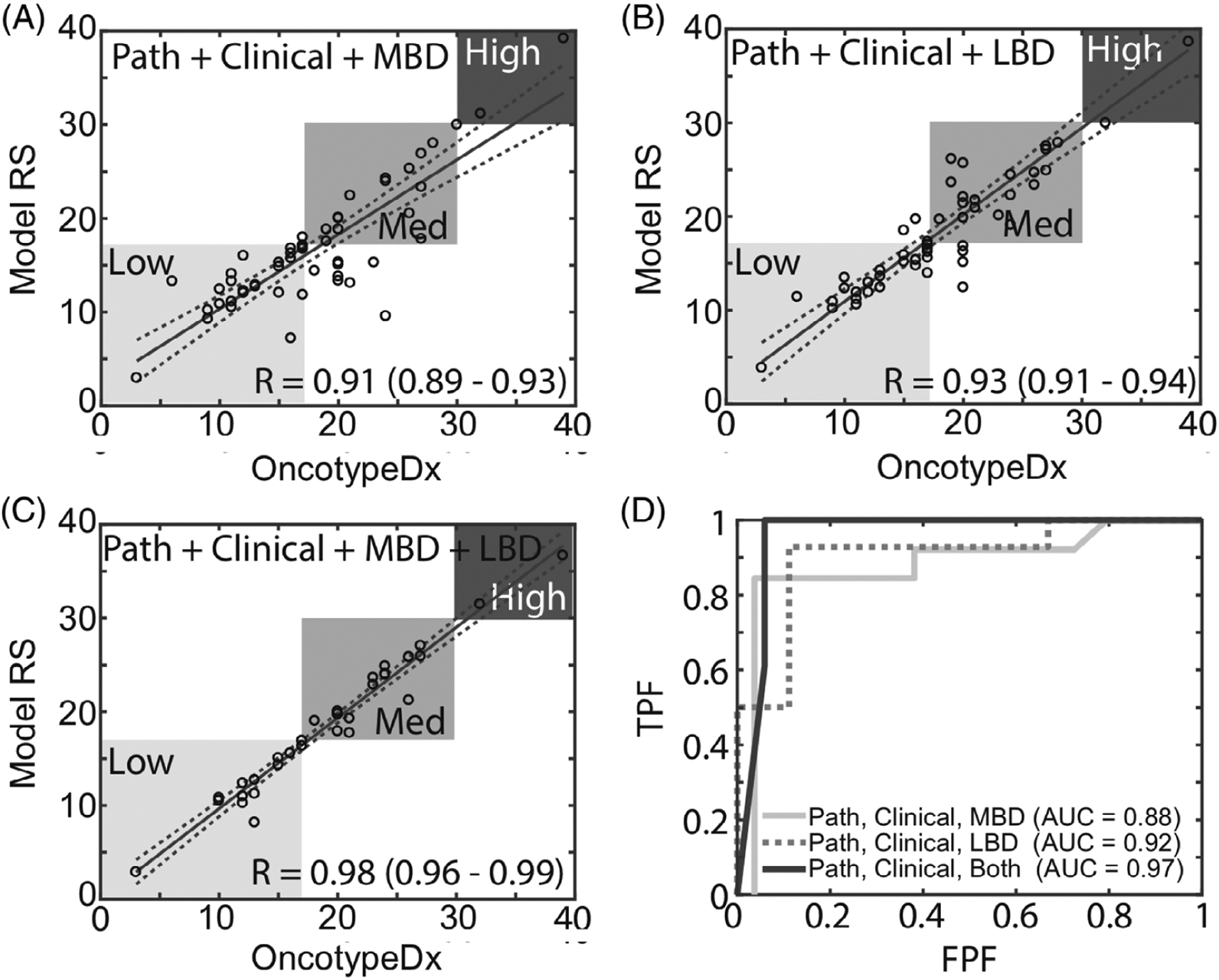
Improvement in prediction accuracy for the ANN model with inclusion of imaging parameters. Regression models based on, A, patient pathology, age, BMI and MBD; B, patient pathology, age, BMI and LBD; and A, patient pathology, age, BMI, MBD and LBD. D, ROC curves corresponding to panels A–C

TABLE 3.

Feature combinations and correlation coefficients

Features used	Variable type	Pathological + Clinical	Pathological + Clinical + MBD	Pathological + Clinical + LBD	Pathological + Clinical + MBD + Optical
Tumor size (cm)	Pathological	X	X	X	X
ER status (−/+)		X	X	X	X
PR status (−/+)		X	X	X	X
Combined Nottingham grade (1/2/3)		X	X	X	X
Nuclear grade (1/2/3)		X	X	X	X
Mitotic grade (1/2/3)		X	X	X	X
Tubule formation grade (1/2/3)		X	X	X	X
Age (avg. ± σ)	Clinical	X	X	X	X
BMI (avg. ± σ)		X	X	X	X
Mammographic density (MBD)	Imaging		X		X
Local breast density (LBD)				X	X
Risk prediction accuracy (r)		0.89	0.91	0.93	0.98
Area under the curve (AUC)		0.86	0.88	0.92	0.97

Note: Risk prediction accuracy for different combinations of clinical, pathological and optical features.

In previous studies, we demonstrated that LBD (essentially reflects adipose relative to fibro-glandular content) is correlated to global MBD [34, 35, 42, 50]. Because of the correlation between LBD and global MBD, comparable performance was achieved when either MBD or LBD was used in combination with the clinical and pathological variables (r = 0.91 and 0.93, respectively). However, with the addition of only LBD, variance in the correlation coefficients in the medium-risk category is higher than that for the low-risk category and the opposite is observed when only MBD is included. The variance in the correlation in the low-risk and medium-risk categories decreases when both MBD and LBD are included. For the case where the full combination of variables was used, only 2 of 56 patients were on the borderline of the low- and medium-risk groups. Only one of these patients would be classified incorrectly based on the selection of the threshold, thus the percentage of patients that would be classified incorrectly is less than 2%. This demonstrates that an algorithm combining pathological, clinical and imaging parameters is able to reliably predict OncotypeDx Scores. When either MBD or LBD are used on their own, the correlation of the predicted and actual OncotypeDx scores are not significant. To achieve improvement in the linear correlation coefficient, the confidence interval of these correlations and the corresponding AUC, all six variables LBD variables were needed.

In this work, we present an ANN model for predicting recurrence risk in early stage breast cancer patients undergoing breast conservation surgery using clinical, pathologic and imaging parameters as input. The ANN model is superior to published linear regression models using the same input variables. Other groups have reported C-index (AUC) of 0.85–0.89 using variables of age, tumor size, histologic tumor type, lymph-vascular invasion, grade and progesterone receptor status [25], 0.75 using the mammographic or sonographic imaging features [29] 0.68, 0.77–0.82 and 0.89–0.93 using MR imaging features [29, 30, 32, 54]. Furthermore, we demonstrated that MBD as well as LBD evaluated at the time of surgery using optical imaging significantly improves the accuracy of predicting recurrence risk. The addition of optical measures of LBD to a feature set that included MBD improved the correlation coefficient from r = 0.89 to 0.98, suggesting that the local morphological tumor landscape is associated with the risk of distant recurrence.

A review of the literature on predicting recurrence risk using algorithmic models and comparing with the OncotypeDx assay suggests that linear models cannot reliably predict low- and intermediate-risk OncotypeDx recurrence scores [26–28, 55]. The inability to distinguish low- and intermediate-risk patients using linear models suggests that the genomic OncotypeDx assay captures diagnostic information that is not available in standard clinicopathological parameters. The analysis presented here indicates a possible alternative: the OncotypeDx test may not capture more diagnostic information than standard clinicopathological endpoints, but instead, genomic profiles measured using the OncotypeDx assay may represent nonlinear, patternistic manifestations of these endpoints rather than direct correlations. Though this study does not prove this, the improvement in correlations of the nonlinear model vs linear models suggests this as a possibility. There are many examples within the literature that corroborate the diagnostic utility of patternistic models for capturing notoriously difficult-to-characterize pathophysiology; examples include the use of artificial intelligence to help radiologists diagnose breast cancer using mammography images [56], predict tumor drug response [57], understand tumor sensitivity to receptor inhibition [58] and detect early stage cervical cancer [59].

The distributions of pathological, clinical and optical parameters appear to follow normal distributions, suggesting that our 56-patient data set is representative of a typical ER+, node-negative patient cohort. A limitation of this study was the inability to compare the ANN model to many of the additional formulations of the Magee [28] equations, or to the handful of other linear models previously reported [28, 32, 55, 60–65], as these models rely on variables such as Ki-67 expression that are not consistently reported at our institutions. Application of the BCPS [26] and Magee₂ [28] models to our data set resulted in similar yet notably reduced correlation coefficients compared wth previously published or as verified by review articles with larger independent data sets. One plausible explanation for the deviation between our data set and those reported stems from the shortage of HER2/neu + patients in our study (n = 2). HER2/neu status has a large influence on the predicted OncotypeDx score for the linear models and typically accounts for >20% of the variance of the estimated score. This suggests that the data set used here deviates from the typical HER2 presentation, causing a circumstance in which the linear models would categorically fail to be reliable. The nonlinear adjustment of weighting coefficients prevents mis-classification of patients with outlier values for variables, as the weighting for that variable is inherently reduced via reference to known patterns. Many authors have reported that most HER2+ patients fall into the high-risk category [26–28, 60, 66]. Interestingly, some have suggested the alternative, that is, that assays used to determine HER2 status have poor agreement with the OncotypeDx assay. (In some cases, the concordance is a mere 40% [67].) Taken together, this suggests that the HER2 parameter introduces considerable uncertainty in recurrence risk models.

The work demonstrates that nonlinear models are superior to linear models and that Oncotype Dx prediction benefits from the addition of breast density, a variable that has not previously been explored. The addition of breast density (either LBD or MBD) improves both the correlation coefficient and confidence intervals, thereby improving AUC. Further, breast density quantified using two separate approaches (LBD or MBD) provides comparable improvements in the correlation coefficients and confidence intervals underscoring the benefit of breast density in the prediction of the Oncotype Dx scores. Further, MBD or information related to breast density obtained via other imaging modalities (for example, MRI) could also be used on larger retrospective data set of ER+, node negative patients for which optical breast density is not available. In previous studies, we validated the correspondence of LBD (obtained by optical imaging to measure surrogates corresponding to the amount of adipose tissue relative to the fibrous tissue content) to global MBD [34, 35, 42, 50]. The focus on breast density stems from an established link between density and increased risk of local recurrence and increased tumor aggressiveness [34, 37, 68, 69]. We hypothesized that these optical measures may also indirectly capture the morphology related to tumor invasiveness, and thus provide an additional indicator for distant recurrence risk. Indeed, the addition of LBD improved the nonlinear correlation coefficient from r = 0.89 to 0.98. The categorical predictive accuracy for the low-, medium- and high-risk groups was 100%.

These results suggest that the optically measured morphological landscape of the breast tumor margin directly captures the underlying tumor morphology, its corresponding microenvironment and possibly additional disease progenitors, faithfully reproducing recurrence risk estimates provided by the OncotypeDx recurrence score. In contrast, studies using MR imaging features have been unable to identify imaging features that accurately predict low- vs intermediate- and high-risk OncotypeDx score [70]. Further, studies acknowledge that the variability in acquisition parameters such as the magnetic field strength used in MRI scans has the potential to affect image quality [31–33], while the images in our data set were acquired using consistent settings on a single system.

However, our study does have limitations in applicability. The number of high-risk patients was limited (n = 2). Many other studies have also reported limited numbers of patients in the high-risk cohort [27, 29, 63, 70, 71]. Some of these studies have used random selection of patients in the low- and intermediate-risks groups to balance the data set for validation [30]; this was not done in this study due to the limited number of patients (n = 56). A limitation of this study is the small sample size. Accrual rates into the study were low because recruitment was limited to ER+ patients as these patients are the ones that undergo OncotypeDx testing, and additionally only a subset of these patients received the OncotypeDx test. Another reason for the small sample size was that the data set was restricted to negative surgical margins. That being said the studies to which we have compared our algorithm have comparable sample sizes, thus we can make meaningful comparisons to these other investigations [29, 63]. The greatest prediction accuracy achieved in this study requires the use of a novel optical spectroscopy system that would require non-trivial integration into a standard surgical suite once a breast tumor is removed. This system has not been applied to patients undergoing mastectomy and therefore its incorporation into assessment of tumor microenvironment in this patient population is untested. The optical imaging system is a non-commercial, research-grade instrument. A larger clinical trial in which the rapid use of this optical system is incorporated into a diverse population of patients with early-stage estrogen-positive patients undergoing both breast conservation and mastectomy is required to validate the ANN model. Furthermore, integration into standard clinical practice would require commercialization of the optical technology.

The ANN framework developed here represents a first step toward implementation of a low-cost, rapid alternative for predicting distant recurrence risk in breast cancer. Although no significant benefit of chemotherapy is found for patients with intermediate recurrence risk except for women less than 50 years old, chemotherapy is still a consideration for adjuvant treatment. Mis-classification of patients within the intermediate group could lead to unnecessary cytotoxic treatment of those in whom recurrence is unlikely, and the converse, a lack of treatment of those for whom chemotherapy would likely provide a survival benefit. With recent incorporation of genetic profiling in the AJCC staging system for breast cancer survival prediction, rapid assessment using the ANN model with existing clinicopathological variables together with optical assessment could provide prognostic information for a broader group of ER+ patients. Future investigation of this approach would include data sets that utilize other genomic tests from populations that are both ER+ and ER−, and an investigation into whether optical imaging could be used on core biopsy samples and resected breast conservation and mastectomy tissue.

Abbreviations:

ANN

artificial neural network

AUC

area under the curve

BCS

breast conserving surgery

BMI

body mass index

CDF

cumulative distribution function

ER

estrogen receptor

HR

hazards ratio

IHC

immunohistochemistry

LBD

local breast density

MBD

mammographic breast density

NSABP

national surgical adjuvant breast and bowel project

PR

progesterone receptor

ROC

receiver operating characteristic

DATA AVAILABILITY STATEMENT

Data are available upon request to the authors.