Abstract
Previous research has demonstrated the usefulness of hierarchical modeling for incorporating a flexible array of prior information in genetic association studies. When this prior information consists of estimates from association analyses of single-nucleotide polymorphisms (SNP)-intermediate or SNP-gene expression, a hierarchical model is equivalent to a 2-stage instrumental or transcriptome-wide association study (TWAS) analysis, respectively. We propose to extend our previous approach for the joint analysis of marginal summary statistics to incorporate prior information via a hierarchical model (hJAM). In this framework, the use of appropriate estimates as prior information yields an analysis similar to Mendelian randomization (MR) and TWAS approaches. hJAM is applicable to multiple correlated SNPs and intermediates to yield conditional estimates for the intermediates on the outcome, thus providing advantages over alternative approaches. We investigated the performance of hJAM in comparison with existing MR and TWAS approaches and demonstrated that hJAM yields an unbiased estimate, maintains correct type-I error, and has increased power across extensive simulations. We applied hJAM to 2 examples: estimating the causal effects of body mass index (GIANT Consortium) and type 2 diabetes (DIAGRAM data set, GERA Cohort, and UK Biobank) on myocardial infarction (UK Biobank) and estimating the causal effects of the expressions of the genes for nuclear casein kinase and cyclin dependent kinase substrate 1 and peptidase M20 domain containing 1 on the risk of prostate cancer (PRACTICAL and GTEx).
Keywords: hierarchical model, joint analysis of marginal summary statistics (JAM), Mendelian randomization, transcriptome-wide association studies
Abbreviations
- eQTL
expression quantitative trait loci
- GWAS
genome-wide association studies
- hJAM
hierarchical joint analysis of marginal summary statistics
- IVW MR
inverse-variance–weighted Mendelian randomization
- LD
linkage disequilibrium
- MVIVW MR
multivariable inverse-variance–weighted Mendelian randomization
- MR
Mendelian randomization
- NUCKS1
nuclear casein kinase and cyclin dependent kinase substrate 1
- PM20D1
peptidase M20 domain containing 1
- SNP
single-nucleotide polymorphism
- TWAS
transcriptome-wide association study
Instrumental variable analysis with genetic variants has been widely used as a general framework for estimating the causal effects of risk factors and gene expression on an outcome (Figure 1) (1–4). Within this framework using single-nucleotide polymorphisms (SNPs) as instrumental variables, the intermediates 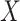 can be modifiable risk factors, expression of genes, or other potential intermediates such as methylation, metabolites, or proteomics. To be a valid instrumental variable and to yield an association of a risk factor, the genetic variants selected as the instruments must satisfy 3 assumptions: 1) they must not be associated with the outcome except through the intermediate; 2) they must be at least moderately associated with the intermediate; and 3) they must be independent of potential confounders of the association between the intermediate and the outcome (Figure 1). The violation of the first assumption results in a biased estimate due to pleiotropy. Weak instrument bias will be introduced if the second assumption is violated because the random error might mask the causal effect of the intermediate on the outcome (5). Previous work has demonstrated that weak instruments can lead to a large bias in estimators even though the first assumption is only slightly violated (6). Finally, the law of independent assortment of genetic variants within a homogeneous population or the ability to adequately control for potential confounding due to population structure, often leads genetic variants fulfilling the third assumption.
can be modifiable risk factors, expression of genes, or other potential intermediates such as methylation, metabolites, or proteomics. To be a valid instrumental variable and to yield an association of a risk factor, the genetic variants selected as the instruments must satisfy 3 assumptions: 1) they must not be associated with the outcome except through the intermediate; 2) they must be at least moderately associated with the intermediate; and 3) they must be independent of potential confounders of the association between the intermediate and the outcome (Figure 1). The violation of the first assumption results in a biased estimate due to pleiotropy. Weak instrument bias will be introduced if the second assumption is violated because the random error might mask the causal effect of the intermediate on the outcome (5). Previous work has demonstrated that weak instruments can lead to a large bias in estimators even though the first assumption is only slightly violated (6). Finally, the law of independent assortment of genetic variants within a homogeneous population or the ability to adequately control for potential confounding due to population structure, often leads genetic variants fulfilling the third assumption.
Figure 1.

The direct acyclic graph (DAG) for instrumental variable analysis with genetic variants. This DAG describes the framework for several approaches. Arrow denotes a causal effect in the direction of the arrow. The solid line refers to moderate or strong association and dashed line refers to uncertain association. Here,  denotes the whole set of single-nucleotide polymorphisms that we used in the analysis.
denotes the whole set of single-nucleotide polymorphisms that we used in the analysis.
Mendelian randomization (MR) and general transcriptome-wide association studies (TWAS) are the 2 major approaches within the instrumental variable analysis framework using genetic variants. MR approaches use a set of genetic variants as an instrumental variable set to estimate the association between modifiable risk factors and traits while TWAS, including the specific FUSION (7) and PrediXcan (8), use expression quantitative trait loci (eQTLs) to predict the gene expression and estimate the association between the predicted gene expressions and traits. For intermediates, MR studies focus on modifiable risk factors and TWAS target gene expression via eQTLs, loci that explain genetic variation in gene expression levels (9). As an alternative, TWAS approaches can be viewed as a weighted SNP approach in which the eQTL information is used to construct the weights. One advantage of using these tools is the ubiquity of publicly available genome-wide association studies (GWAS), such as UK Biobank (10), which enable researchers to initiate investigation of complex traits and diseases nearly immediately (11). The existing approaches differ in their strategies to combine the summary statistics of SNPs from GWAS or that of eQTLs from RNA sequencing data. The most widely used MR approach is inverse-variance–weighted MR (IVW MR) (12) which is similar to the fixed-effect meta-analysis, often constraining the intercept to be zero.
As a form of instrumental variable analysis, these approaches must fulfill all the caveats to yield valid estimates, and extensions exist to overcome some of these limitations. For example, MR approaches often include only the top genome-wide significant (P =  ) SNP estimates from a GWAS. However, the top SNPs might explain only a small proportion of the variance of the modifiable risk factor. In such cases, the instrument might not be strong enough to detect the true causal effect and result in bias. Of course, one solution is to increase the number of SNPs in the instrument set (13). However, such a solution could introduce pleiotropy, which is defined as the association between the genetic variants and the outcome that is not through the intermediates. Likewise, in TWAS analyses, pleiotropy might be present because of the potential existence of multifunctional genes, or if some cis-SNPs for the investigated gene are also associated with another gene that is associated with the trait (1, 14). For example, using the SNPs on the methylenetetrahydrofoloate reductase (MTHFR) gene as an instrument to explore the role of folate and homocysteine in the etiology of neural tube defects via a single-risk-factor MR, such as IVW MR, might not be appropriate because MTHFR has an effect on the etiology of neural tube defects through both folate and homocysteine (1). Potential solutions to pleiotropy include the MR-Egger method (15), which allows the intercept to be estimated as nonzero in the presence of pleiotropy. Alternatively, if multiple correlated intermediates are analyzed jointly, there is the potential for each intermediate to explain all or a portion of the pleiotropic effect, which thus relaxes the first assumption and allows the genetic variants to be associated with the outcome through multiple pathways or intermediates (16).
) SNP estimates from a GWAS. However, the top SNPs might explain only a small proportion of the variance of the modifiable risk factor. In such cases, the instrument might not be strong enough to detect the true causal effect and result in bias. Of course, one solution is to increase the number of SNPs in the instrument set (13). However, such a solution could introduce pleiotropy, which is defined as the association between the genetic variants and the outcome that is not through the intermediates. Likewise, in TWAS analyses, pleiotropy might be present because of the potential existence of multifunctional genes, or if some cis-SNPs for the investigated gene are also associated with another gene that is associated with the trait (1, 14). For example, using the SNPs on the methylenetetrahydrofoloate reductase (MTHFR) gene as an instrument to explore the role of folate and homocysteine in the etiology of neural tube defects via a single-risk-factor MR, such as IVW MR, might not be appropriate because MTHFR has an effect on the etiology of neural tube defects through both folate and homocysteine (1). Potential solutions to pleiotropy include the MR-Egger method (15), which allows the intercept to be estimated as nonzero in the presence of pleiotropy. Alternatively, if multiple correlated intermediates are analyzed jointly, there is the potential for each intermediate to explain all or a portion of the pleiotropic effect, which thus relaxes the first assumption and allows the genetic variants to be associated with the outcome through multiple pathways or intermediates (16).
In this work, we propose an approach that leverages the joint analysis of marginal summary statistics (17), a scalable algorithm designed to analyze published marginal summary statistics from GWAS under a joint multi-SNPs model to identify causal genetic variants for fine mapping. The marginal summary statistics refer to the univariate estimates of the SNPs from GWAS. Here, we extend joint analysis of marginal summary statistics with a hierarchical model (hJAM) to incorporate SNP-intermediate association estimates and unify the framework of MR and TWAS approaches when multiple intermediates and/or correlated SNPs exist. Overall, we demonstrate that hJAM yields an unbiased estimate, maintains a correct type-I error, and has increased power over other alternatives. The approach offers a flexible framework for these analyses with the ability to account for sharing of instruments (either in linkage disequilibrium (LD) or independent) and for the joint analysis of multiple intermediates.
METHODS
Unify the framework of Mendelian randomization and TWAS
Instrumental variable analysis with individual-level genotype data can be viewed as a 2-stage hierarchical model. Using linear regression, the first stage models the outcome as a function of the genetic variants:
 |
(1) |
Here, 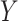 denotes a
denotes a  -length vector of a continuous outcome,
-length vector of a continuous outcome, 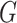 denotes an
denotes an  genotype matrix with
genotype matrix with 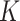 SNPs and n individuals and
SNPs and n individuals and  denotes the residuals. The second stage models the conditional estimates
denotes the residuals. The second stage models the conditional estimates  as a function of prior information (18–21),
as a function of prior information (18–21),  :
:
 |
(2) |
where 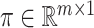 denotes the parameter of interest, the vector of causal effect estimates for the intermediates
denotes the parameter of interest, the vector of causal effect estimates for the intermediates 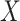 on outcome
on outcome 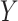 , and
, and  is the number of intermediates
is the number of intermediates  . We can join these 2-stage models into a single linear mixed model by substituting equation 2 into equation 1 (22):
. We can join these 2-stage models into a single linear mixed model by substituting equation 2 into equation 1 (22):
 |
(3) |
assuming there is no direct effect from the genetic variants to the outcome (i.e.,  ). The estimate of
). The estimate of  from equation 3 is equivalent to the result from the 2-stage least square regression, which is employed by PrediXcan (8) and others (7). The prior information
from equation 3 is equivalent to the result from the 2-stage least square regression, which is employed by PrediXcan (8) and others (7). The prior information  is the association estimates between the genetic variants and the intermediate and can be applied to impute the intermediate with the genetic variants:
is the association estimates between the genetic variants and the intermediate and can be applied to impute the intermediate with the genetic variants:
 |
(4) |
Note that equation 4 is the stage 2 in the 2-stage least square regression and that MR approaches with summary data are developed based on equation 2. One key aspect of the instrumental variable analysis with genetic variants is that the  matrix is computed from a separate data (i.e.,
matrix is computed from a separate data (i.e., 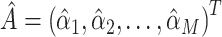 , where
, where  denotes the vector of association estimates between genetic variants and
denotes the vector of association estimates between genetic variants and  intermediate from external data). Two different
intermediate from external data). Two different  vectors have been used by previous methods. Marginal estimates
vectors have been used by previous methods. Marginal estimates 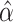 are widely employed by MR where marginal summary statistics from GWAS are being used (12, 16, 23). Here marginal estimates refer to the univariant estimates. Conditional estimates of
are widely employed by MR where marginal summary statistics from GWAS are being used (12, 16, 23). Here marginal estimates refer to the univariant estimates. Conditional estimates of  , which adjust for the correlations between genetic variants, can also be incorporated into the framework and are easily obtained from joint regression models with individual-level data. If only marginal summary statistics are available, one way to convert these estimates into conditional ones is incorporating the LD block among the SNPs using the joint analysis of marginal summary statistics approach (24). Alternatively, with individual-level data, a regularized estimate
, which adjust for the correlations between genetic variants, can also be incorporated into the framework and are easily obtained from joint regression models with individual-level data. If only marginal summary statistics are available, one way to convert these estimates into conditional ones is incorporating the LD block among the SNPs using the joint analysis of marginal summary statistics approach (24). Alternatively, with individual-level data, a regularized estimate 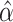 is obtained by applying regularized regression, such as those values reported in the PredictDB developed for PrediXcan (8). To model multiple intermediates, we construct an
is obtained by applying regularized regression, such as those values reported in the PredictDB developed for PrediXcan (8). To model multiple intermediates, we construct an  matrix by combining the vectors of association estimates of the SNPs on each intermediate,
matrix by combining the vectors of association estimates of the SNPs on each intermediate,  , into a matrix with the number of columns equal the number of intermediates (i.e.,
, into a matrix with the number of columns equal the number of intermediates (i.e.,  ):
):
 |
hJAM: hierarchical joint analysis of marginal summary statistics
We can employ the same hierarchical model with marginal summary data. Following Newcombe et al. (17), we use the marginal summary statistics, 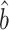 , which are obtained from a GWAS, and the minor allele frequency of the genetic variants,
, which are obtained from a GWAS, and the minor allele frequency of the genetic variants,  , to construct a vector
, to construct a vector  with the
with the 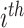 element,
element,  , for each genetic variant:
, for each genetic variant:
 |
assuming Hardy-Weinberg equilibrium. Each element represents the total trait burden for all risk alleles of SNP  present in the population. The minor allele frequency can be extracted from the same GWAS or using external populations such as the 1000 Genomes Project (25) as reference data. Using standard linear algebra, we can express the distribution of
present in the population. The minor allele frequency can be extracted from the same GWAS or using external populations such as the 1000 Genomes Project (25) as reference data. Using standard linear algebra, we can express the distribution of  as
as
 |
where 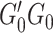 denotes the
denotes the 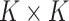 genotype variance-covariance from a centered reference genotype data set (e.g., 1000 Genomes Project (25)) to obtain the conditional association estimates of SNPs on the outcome,
genotype variance-covariance from a centered reference genotype data set (e.g., 1000 Genomes Project (25)) to obtain the conditional association estimates of SNPs on the outcome,  . The reference genotype data is centered by the mean to avoid an intercept term. Details are described in Newcombe et al. (17). To simplify the likelihood, we perform a Cholesky decomposition transformation
. The reference genotype data is centered by the mean to avoid an intercept term. Details are described in Newcombe et al. (17). To simplify the likelihood, we perform a Cholesky decomposition transformation  . Then we transform
. Then we transform  into
into  with the inverse of
with the inverse of 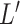 as
as  . When
. When  is positive semidefinite, we add a ridge term (i.e., a small positive element) on the diagonal to enforce it to be a positive definite matrix. The regularization term has a very small effect on the estimates while guaranteeing the invertibility of the
is positive semidefinite, we add a ridge term (i.e., a small positive element) on the diagonal to enforce it to be a positive definite matrix. The regularization term has a very small effect on the estimates while guaranteeing the invertibility of the 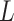 matrix. Then, the
matrix. Then, the  is a vector of independent statistics that can be expressed as
is a vector of independent statistics that can be expressed as
 |
(5) |
Similar to above, we then fit a hierarchical model by incorporating the second-stage model (equation 2) into equation 5 and construct the hJAM model as
 |
(6) |
assuming no association between the genetic variants and the outcome conditioning on the intermediates. Here,  denotes the causal effect estimate between the intermediate and outcome and is estimated using maximum likelihood, and the statistical significance is given by a Wald test. The estimate of
denotes the causal effect estimate between the intermediate and outcome and is estimated using maximum likelihood, and the statistical significance is given by a Wald test. The estimate of 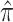 and corresponding variance are
and corresponding variance are
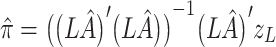 |
and
 |
Note that the number of genetic variants must be equal to or greater than the number of the intermediates. Egger-type approaches can be implemented in this framework by allowing an intercept in equation 6 by adding a column of ones to  matrix, which is analogue to MR-Egger regression (15).
matrix, which is analogue to MR-Egger regression (15).
Simulation settings
To assess the performance of hJAM, we performed an extensive set of simulation studies. For each simulation, we simulated an intermediate matrix  , an outcome vector
, an outcome vector  , and 3 standardized individual genotype matrices
, and 3 standardized individual genotype matrices  ,
,  , and
, and  .
. 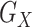 is the SNP-intermediate data used to obtain the
is the SNP-intermediate data used to obtain the  matrix,
matrix,  is the SNP-outcome data used to obtain the univariate
is the SNP-outcome data used to obtain the univariate  vectors, and
vectors, and 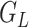 is the reference data with the LD structure between the SNPs. Each of the 3 standardized individual genotype matrices (
is the reference data with the LD structure between the SNPs. Each of the 3 standardized individual genotype matrices (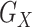 ,
,  , and
, and 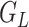 ) is composed of 2/3 SNP blocks (i.e.,
) is composed of 2/3 SNP blocks (i.e.,  ,
,  , and
, and 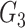 in Figure 2). Web Figure 1 shows the relationship between the
in Figure 2). Web Figure 1 shows the relationship between the 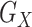 and the SNP blocks, which is the same as the relationship between
and the SNP blocks, which is the same as the relationship between  /
/ and the SNP blocks. Each SNP block contains 10 SNPs, in which we set 3 SNPs to be causal to the intermediate with
and the SNP blocks. Each SNP block contains 10 SNPs, in which we set 3 SNPs to be causal to the intermediate with  per SNP block. For each genotype matrix, we had 2 interblock relationships: no LD and moderate LD (
per SNP block. For each genotype matrix, we had 2 interblock relationships: no LD and moderate LD ( ). The minor allele frequency was sampled from a uniform distribution (0.05, 0.3). Sample size for each genotype data set was set to
). The minor allele frequency was sampled from a uniform distribution (0.05, 0.3). Sample size for each genotype data set was set to 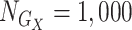 ,
,  , and
, and  , respectively. Without the loss of generality, we simulated 2 Xs and 4 scenarios representing different causal models for the 2 intermediates that are likely to be encountered in epidemiologic studies (Figure 2). For scenario A,
, respectively. Without the loss of generality, we simulated 2 Xs and 4 scenarios representing different causal models for the 2 intermediates that are likely to be encountered in epidemiologic studies (Figure 2). For scenario A, 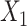 and
and  were independent. For scenarios B and D,
were independent. For scenarios B and D,  and
and  were correlated through a shared SNPs set
were correlated through a shared SNPs set 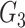 . The coefficient
. The coefficient  in the causal scenarios (Figure 2C and D) was simulated by
in the causal scenarios (Figure 2C and D) was simulated by  . These simulation scenarios are similar to those described in Sanderson et al. (26). To evaluate the robustness of different methods in terms of the reference set
. These simulation scenarios are similar to those described in Sanderson et al. (26). To evaluate the robustness of different methods in terms of the reference set  , we added a simulation where the LD of the
, we added a simulation where the LD of the  differs from
differs from  or
or  in scenario B (Figure 2B). We investigated the sensitivity of performance to scenarios with 1) lower heritability for the intermediates with
in scenario B (Figure 2B). We investigated the sensitivity of performance to scenarios with 1) lower heritability for the intermediates with  per SNP block and 2) scenarios with an unknown confounder simulated between the intermediates
per SNP block and 2) scenarios with an unknown confounder simulated between the intermediates 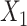 and the outcome
and the outcome 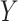 .
.
Figure 2.

Simulation scenarios of different relationships between X’s. A)  and
and 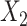 are independent. B)
are independent. B) 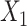 and
and  are correlated. C)
are correlated. C)  causes
causes 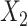 . D)
. D)  causes
causes 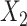 and is correlated. In the direct acyclic graph,
and is correlated. In the direct acyclic graph, 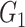 ,
,  , and
, and  represent 3 single-nucleotide polymorphism blocks that contribute to different intermediates. For example, in panel B,
represent 3 single-nucleotide polymorphism blocks that contribute to different intermediates. For example, in panel B, 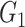 and
and 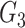 both contribute to
both contribute to 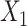 , and
, and  and
and 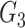 contribute to
contribute to  Taken together,
Taken together, 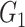 ,
,  , and
, and  compose each
compose each 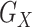 ,
,  , and
, and 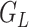 .
.
The primary objective was to estimate 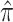 with each true
with each true 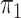 being set to null (
being set to null ( ) or a positive effect (
) or a positive effect ( ). To mimic applied applications and to ensure selection of at least 2 or more SNPs, a forward selection on
). To mimic applied applications and to ensure selection of at least 2 or more SNPs, a forward selection on  was performed to exclude the noninformative variants with a threshold
was performed to exclude the noninformative variants with a threshold  in the analysis step. All simulation analyses were performed in R (R Foundation for Statistical Computing, Vienna, Austria), version 3.4.0 (27). Results were calculated from 1,000 replications for each scenario. All tests were 1-sided with a type-I error of 0.05. We compared the performance of our approach with that of IVW MR (12), multivariate inverse-variance–weighted MR (MVIVW MR) (16), and S-PrediXcan (28) (see Web Appendix 1).
in the analysis step. All simulation analyses were performed in R (R Foundation for Statistical Computing, Vienna, Austria), version 3.4.0 (27). Results were calculated from 1,000 replications for each scenario. All tests were 1-sided with a type-I error of 0.05. We compared the performance of our approach with that of IVW MR (12), multivariate inverse-variance–weighted MR (MVIVW MR) (16), and S-PrediXcan (28) (see Web Appendix 1).
Data examples
To demonstrate hJAM on real data, we applied various methods to 2 examples: 1) for body mass index and type 2 diabetes on myocardial infarction and 2) gene expression and prostate cancer risk. Given that the study populations for both examples included individuals of European ancestry, we used the 503 European-ancestry subjects from the 1000 Genomes Project (25) as our reference data for the LD structure.
Causal effect of body mass index and type 2 diabetes on myocardial infarction.
Previous studies have shown that obesity (29, 30) and type 2 diabetes (31, 32) are 2 important risk factors for myocardial infarction. In addition, the association between obesity and type 2 diabetes is well-established (33, 34). A directed acyclic graph (DAG) shows the relationships between the 2 risk factors and myocardial infarction (Figure 3).
Figure 3.

Direct acyclic graph of the relationship between obesity, type 2 diabetes, and myocardial infarction. SNP, single-nucleotide polymorphism.
To estimate the causal effects of the 2 risk factors, we extracted the summary statistics for myocardial infarction, body mass index, and type 2 diabetes from, respectively, the UK Biobank (n = 459,324) (10); Genetic Investigation of Anthropometric Traits (GIANT) Consortium (n = 339,224) (35); and Diabetes Genetics Replication and Meta-analysis (DIAGRAM), Genetic Epidemiology Research on Aging (GERA), and UK Biobank (n = 659,316) (36). In total, 75 SNPs and 136 SNPs were identified as genome-wide significant for body mass index and type 2 diabetes. In this set of SNPs, there was 1 overlapping SNP in both the instrument sets for body mass index and type 2 diabetes (rs7903146,  ,
,  , and
, and  ). This SNP is a well-known type 2 diabetes–associated SNP and has been identified as a body mass index–associated hit in GIANT. Additionally, 4 correlated pairs of SNPs exist between the 2 sets (Web Table 1) (available at https://doi.org/10.1093/aje/kwaa287). We reoriented the association estimates of all SNPs but one (except the association estimate between the overlapping SNP rs7903146 and body mass index) to have a positive association, and we used MR-Egger regression (15) and hJAM-Egger to detect a potential directional pleiotropy bias.
). This SNP is a well-known type 2 diabetes–associated SNP and has been identified as a body mass index–associated hit in GIANT. Additionally, 4 correlated pairs of SNPs exist between the 2 sets (Web Table 1) (available at https://doi.org/10.1093/aje/kwaa287). We reoriented the association estimates of all SNPs but one (except the association estimate between the overlapping SNP rs7903146 and body mass index) to have a positive association, and we used MR-Egger regression (15) and hJAM-Egger to detect a potential directional pleiotropy bias.
Causal effect of PM20D1 and NUCKS1 on prostate cancer risk.
To further illustrate the benefit of hJAM, we next considered the gene–prostate cancer risk association of 2 genes on chromosome 1q32.1, for peptidase M20 domain containing 1 (PM20D10) and nuclear casein kinase and cyclin dependent kinase substrate 1 (NUCKS1). Both PM20D1 and NUCKS1 are protein-coding genes, and previous transcriptome studies have found a significant estimate of causal effect of both PM20D1 and NUCKS1 on the risk of prostate cancer among a European-ancestry population (37, 38). Due to the close proximity of the 2 genes along the genome, there is a potential for a univariate approach to result in biased estimates. To estimate the causal effects jointly, we applied hJAM to this research question.
We constructed the  matrix with 114 eQTL estimates with false discovery rate of <0.05 for the 2 genes from GTEx v7 (39). Among the 114 eQTLs, 1 locus has significant associations with both PM20D1 and NUCKS1. To limit the correlation between the eQTLs, we pruned the eQTLs by limiting the squared pairwise correlation coefficient
matrix with 114 eQTL estimates with false discovery rate of <0.05 for the 2 genes from GTEx v7 (39). Among the 114 eQTLs, 1 locus has significant associations with both PM20D1 and NUCKS1. To limit the correlation between the eQTLs, we pruned the eQTLs by limiting the squared pairwise correlation coefficient 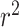 and using the magnitude of the eQTL association estimates on each gene as the priority criteria. The genome-wide summary statistics for the risk of prostate cancer were taken from a published GWAS including more than 140,000 European-ancestry men (40).
and using the magnitude of the eQTL association estimates on each gene as the priority criteria. The genome-wide summary statistics for the risk of prostate cancer were taken from a published GWAS including more than 140,000 European-ancestry men (40).
RESULTS
Simulation studies
Simulation results from the base scenario A, where 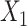 and
and 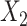 were independent, demonstrate that the estimates from most methods were unbiased (Figure 4). However, when IVW MR and MVIVW MR do not incorporate the LD structure, there is a slightly inflated type-I error under simulation scenarios with correlated SNPs (Figure 5). IVW MR with and without correlation had a less-precise estimate and lower power compared with the other methods in scenario A (Figures 4 and 5, Web Table 2). When a pleiotropic effect was simulated for each intermediate (scenarios B to D), the estimates from hJAM and MVIVW MR with LD were unbiased and had a correct type-I error for the corresponding intermediate (Figure 5). The estimates from MVIVW MR without LD were unbiased but showed an inflated type-I error due to a smaller estimated standard error in scenarios in which SNPs were correlated (Figures 4 and 5). IVW MR and S-PrediXcan had a biased estimate and an inflated type-I error regardless of the correlation structure of the SNPs in the presence of pleiotropy (Figure 5, Web Figure 2 and Web Table 3–5). The results for MVIVW MR and IVW MR reflect specification of the LD structure for the instruments when using the MedelianRandomization (41) package. Results without the LD structure showed poor performance as indicated by increased type-I errors.
were independent, demonstrate that the estimates from most methods were unbiased (Figure 4). However, when IVW MR and MVIVW MR do not incorporate the LD structure, there is a slightly inflated type-I error under simulation scenarios with correlated SNPs (Figure 5). IVW MR with and without correlation had a less-precise estimate and lower power compared with the other methods in scenario A (Figures 4 and 5, Web Table 2). When a pleiotropic effect was simulated for each intermediate (scenarios B to D), the estimates from hJAM and MVIVW MR with LD were unbiased and had a correct type-I error for the corresponding intermediate (Figure 5). The estimates from MVIVW MR without LD were unbiased but showed an inflated type-I error due to a smaller estimated standard error in scenarios in which SNPs were correlated (Figures 4 and 5). IVW MR and S-PrediXcan had a biased estimate and an inflated type-I error regardless of the correlation structure of the SNPs in the presence of pleiotropy (Figure 5, Web Figure 2 and Web Table 3–5). The results for MVIVW MR and IVW MR reflect specification of the LD structure for the instruments when using the MedelianRandomization (41) package. Results without the LD structure showed poor performance as indicated by increased type-I errors.
Figure 4.

Empirical power of the correlated single-nucleotide polymorphism scenarios across 1,000 replications. (A–D) 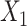 and
and  are independent. (E–H)
are independent. (E–H)  and
and  are correlated. (I–L)
are correlated. (I–L)  causes
causes  . (M–P)
. (M–P)  causes
causes  and is correlated. The black solid line refers to the default type-I error,
and is correlated. The black solid line refers to the default type-I error, 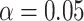 . In panels A, E, I, and M,
. In panels A, E, I, and M,  and
and 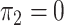 ; in panels B, F, J, and N,
; in panels B, F, J, and N, 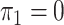 and
and  ; in panels C, G, K, and O,
; in panels C, G, K, and O,  and
and 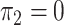 ; and in panels D, H, L, and P,
; and in panels D, H, L, and P,  and
and  . hJAM, hierarchical joint analysis of marginal summary statistics; IVW MR, inverse-variance–weighted Mendelian randomization; MVIVW MR, multivariable inverse-variance–weighted Mendelian randomization.
. hJAM, hierarchical joint analysis of marginal summary statistics; IVW MR, inverse-variance–weighted Mendelian randomization; MVIVW MR, multivariable inverse-variance–weighted Mendelian randomization.
Figure 5.

Average estimates and 95% confidence intervals of the correlated SNPs scenarios across 1,000 replications. (A–D)  and
and  are independent. (E–H)
are independent. (E–H)  and
and  are correlated. (I–L)
are correlated. (I–L) 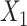 causes
causes  . (M–P)
. (M–P) 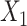 causes
causes  and correlated. The black solid line refers to the default type-I error,
and correlated. The black solid line refers to the default type-I error,  . In panels A, E, I and M,
. In panels A, E, I and M, 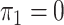 and
and 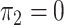 ; in panels B, F, J, and N,
; in panels B, F, J, and N, 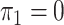 and
and  ; in panels C, G, K and O,
; in panels C, G, K and O,  and
and 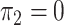 ; and in panels D, H, L, and P,
; and in panels D, H, L, and P,  and
and 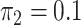 . hJAM, hierarchical joint analysis of marginal summary statistics; IVW MR, inverse-variance–weighted Mendelian randomization; MVIVW MR, multivariable inverse-variance–weighted Mendelian randomization.
. hJAM, hierarchical joint analysis of marginal summary statistics; IVW MR, inverse-variance–weighted Mendelian randomization; MVIVW MR, multivariable inverse-variance–weighted Mendelian randomization.
In addition, we found that the results from hJAM and MVIVW remained consistent even as the LD in the reference 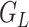 data differed from
data differed from  or
or  (Web Figure 3). For simulations with additional unknown confounders and
(Web Figure 3). For simulations with additional unknown confounders and  per SNP block, the results were consistent with the main simulation studies (Web Figures 4–5 and 6–7).
per SNP block, the results were consistent with the main simulation studies (Web Figures 4–5 and 6–7).
Data example 1: causal effect of body mass index and type 2 diabetes on myocardial infarction
Results for data example 1 are shown in Table 1. All methods suggested a significantly increasing risk of myocardial infarction with an increased body mass index and the presence of type 2 diabetes. This agrees with previous studies (29, 31). The magnitude of hJAM and MVIVW MR were similar while IVW MR and S-PrediXcan showed larger estimated values. The odds ratios from hJAM for the risk of myocardial infarction were 1.38 (95% confidence interval: 1.22, 1.56) and 1.16 (95% confidence interval: 1.12, 1.20) for per-1-unit increase in body mass index and having type 2 diabetes, respectively. MVIVW MR with LD had similar estimates with 1.37 (95% confidence interval: 1.22, 1.54) and 1.15 (95% confidence interval: 1.11, 1.19) for body mass index and having type 2 diabetes, respectively. The difference in estimates between the multivariate approaches and the univariate MR/TWAS approaches might be attributed to potential pleiotropy not accounted for in the analyses that do not model the intermediates jointly. When modeled jointly, results from hJAM-Egger and multivariate MR-Egger analyses both suggest that there was no residual pleiotropy detected when we incorporated both body mass index– and type 2 diabetes–associated instruments in the analysis ( and
and 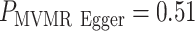 , respectively). In contrast, the MR-Egger approach applied univariately to type 2 diabetes resulted in a significant test for the intercept, suggesting the presence of pleiotropy, potentially due to association of some of the SNPs to the outcome via body mass index.
, respectively). In contrast, the MR-Egger approach applied univariately to type 2 diabetes resulted in a significant test for the intercept, suggesting the presence of pleiotropy, potentially due to association of some of the SNPs to the outcome via body mass index.
Table 1.
Causal Odds Ratios for Myocardial Infarction Per Unit of Body Mass Index and Having Type 2 Diabetesa
| Method | OR | 95% CI | P Value |
|---|---|---|---|
| Body Mass Index | |||
| hJAM | 1.38 | 1.22, 1.56 | 3.19 × 10−7 |
| MVIVW MR | 1.37 | 1.22, 1.54 | 1.94 × 10−7 |
| MVIVW MRb | 1.34 | 1.20, 1.49 | 1.65 × 10−7 |
| IVW MR | 1.54 | 1.32, 1.79 | 2.07 × 10−8 |
| IVW MRb | 1.53 | 1.32, 1.77 | 1.45 × 10−8 |
| S-PrediXcan | 1.66 | 1.58, 1.74 | 9.88 × 10−96 |
| MR-Egger interceptc | 0.01 | −0.01, 0.01 | 2.00 × 10−1 |
| Type 2 Diabetes | |||
| hJAM | 1.16 | 1.12, 1.20 | 4.12 × 10−11 |
| MVIVW MR | 1.15 | 1.11, 1.19 | 8.34 × 10−12 |
| MVIVW MRb | 1.16 | 1.11, 1.20 | 1.29 × 10−11 |
| IVW MR | 1.15 | 1.11, 1.20 | 1.77 × 10−14 |
| IVW MRb | 1.15 | 1.11, 1.20 | 1.98 × 10−14 |
| S-PrediXcan | 1.14 | 1.11, 1.16 | 9.43 × 10−109 |
| MR-Egger interceptc | 0.01 | 0, 0.01 | 0.017 |
Abbreviations: CI, confidence interval; hJAM, hierarchical joint analysis of marginal summary statistics; IVW MR, inverse-variance weighted Mendelian randomization; MR-Egger, Mendelian randomization with Egger regression; MVIVW MR, multivariable inverse-variance weighted Mendelian randomization; OR, odds ratio.
a Using data from multiple data sets (10, 35, 36).
b Without linkage disequilibrium adjustment.
c For MR-Egger intercept, we showed log odds ratio of the intercept and its 95% CI.
Data example 2: causal effect of PM20D1 and NUCKS1 on prostate cancer risk
Web Figure 8 displays forest plots of the odds ratios (95% confidence intervals) and P values of the estimates of the causal effects on the prostate cancer risk by each  cutoff (
cutoff (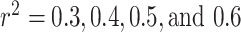 ) for LD pruning of SNPs for selection for the analysis. In general, all approaches show consistent estimates of causal effect across the various sets of SNPs included for analysis (from
) for LD pruning of SNPs for selection for the analysis. In general, all approaches show consistent estimates of causal effect across the various sets of SNPs included for analysis (from  to
to 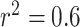 ), but the significance level is sensitive to the choice and number of SNPs selected. We observed that hJAM and MVIVW MR with LD yielded significant results for NUCKS1 with the pruning cutoffs
), but the significance level is sensitive to the choice and number of SNPs selected. We observed that hJAM and MVIVW MR with LD yielded significant results for NUCKS1 with the pruning cutoffs 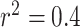 and
and  . Both of these approaches showed no significant causal effect of PM20D1 on the risk of prostate cancer regardless of the pruning cutoff used to select the SNPs. The univariate models, including IVW MR and S-PrediXcan, resulted in a significant positive causal effect estimate on prostate cancer risk for PM20D1 and NUCKS1. We consider the significance in the univariate models to be due to the correlation between the 2 genes and the LD between the eQTLs, which could be adjusted for by the hJAM and MVIVW MR with LD models.
. Both of these approaches showed no significant causal effect of PM20D1 on the risk of prostate cancer regardless of the pruning cutoff used to select the SNPs. The univariate models, including IVW MR and S-PrediXcan, resulted in a significant positive causal effect estimate on prostate cancer risk for PM20D1 and NUCKS1. We consider the significance in the univariate models to be due to the correlation between the 2 genes and the LD between the eQTLs, which could be adjusted for by the hJAM and MVIVW MR with LD models.
DISCUSSION
In this paper, we have proposed a 2-stage hierarchical model that unifies the framework of Mendelian randomization and transcriptome-wide association tools and can be applied to correlated instruments and multiple intermediates. We have implemented the method in an R package (hJAM) which is now available on the Comprehensive R Archive Network (https://cran.r-project.org/web/packages/hJAM/).
When only 1 intermediate or multiple independent intermediates is present, hJAM yields an equivalent estimate and standard error to alternative approaches (see Web Appendix 1). However, when intermediates are correlated, only MVIVW MR showed a comparable performance to that of hJAM under the independent SNPs scenarios. For the correlated-SNPs scenarios, when the LD structure is specified, the estimates of hJAM are empirically equivalent to MVIVW MR although the 2 approaches use slightly different weighted matrices: hJAM uses the adjusted variance-covariance matrix of SNPs from a reference panel while MVIVW MR uses an inverse-variance matrix. Nevertheless, we believe that the hJAM formulation offers several advantages in flexibility to specify the  matrix. As in TWAS, this matrix can specify eQTL estimates or, as in more classical MR approaches, it can specify SNP-intermediate associations. Moreover, it can incorporate other types of prior information, such as functional or genomic annotation or information from metabolomic studies (42). Inclusion of this type of annotation information can offer potential advantages for characterization of SNP effects as demonstrated in the hierarchical modeling context (18, 19, 43). In addition, the flexibility of hJAM not only allows for natural extensions such as hJAM-Egger but can also be applied to incorporate information from different ethnic groups or tissues to obtain an averaged causal effect estimate of the intermediate on the outcome across groups or tissues. In addition, optimal construction of the
matrix. As in TWAS, this matrix can specify eQTL estimates or, as in more classical MR approaches, it can specify SNP-intermediate associations. Moreover, it can incorporate other types of prior information, such as functional or genomic annotation or information from metabolomic studies (42). Inclusion of this type of annotation information can offer potential advantages for characterization of SNP effects as demonstrated in the hierarchical modeling context (18, 19, 43). In addition, the flexibility of hJAM not only allows for natural extensions such as hJAM-Egger but can also be applied to incorporate information from different ethnic groups or tissues to obtain an averaged causal effect estimate of the intermediate on the outcome across groups or tissues. In addition, optimal construction of the  matrix for high-dimensional data is an area that needs further investigation.
matrix for high-dimensional data is an area that needs further investigation.
Although hJAM provides an overall improvement over most existing MR methods, it is also susceptible to the caveats of these types of approaches. First, it might be subject to the bias in estimation due to unknown pleiotropy. hJAM-Egger, which is analogous to MR-Egger (15), showed a similar performance to the univariate MR-Egger regression with unbiased estimates under simulations in which the horizontal pleiotropy is balanced but biased estimates in the presence of unbalanced pleiotropy (results not shown) (15). hJAM-Egger can be applied as a sensitivity analysis of a multivariable framework MR analysis (44). Similar to MR-Egger, hJAM-Egger has to satisfy the “instrument strength independent of direct effect” (InSIDE) assumption. If InSIDE is violated, both the estimated intercept and corresponding variance will be influenced (44). An extension of the current hJAM approach could include variable selection to assess the pleiotropy assumption before incorporating the 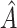 matrix into the model. Several approaches have been proposed, such as joint analysis of marginal summary statistics MR (45) and MR-presso (46). Second, the association estimates between the SNPs and the intermediates, and/or the causal effect of intermediates on the outcome, might include interactions or be nonlinear. One way to address the presence of interactions is to limit the use of summary data from stratified GWAS; however, it might attenuate the power due to a smaller sample size of the subset GWAS. For the presence of nonlinear relationships, potential approaches include modifying the 2-stage analysis by incorporating a nonlinear function in the second stage or more formally incorporating methods to investigate the shape of the exposure-outcome relationship, such as fractional polynomials or piecewise linear approaches (47).
matrix into the model. Several approaches have been proposed, such as joint analysis of marginal summary statistics MR (45) and MR-presso (46). Second, the association estimates between the SNPs and the intermediates, and/or the causal effect of intermediates on the outcome, might include interactions or be nonlinear. One way to address the presence of interactions is to limit the use of summary data from stratified GWAS; however, it might attenuate the power due to a smaller sample size of the subset GWAS. For the presence of nonlinear relationships, potential approaches include modifying the 2-stage analysis by incorporating a nonlinear function in the second stage or more formally incorporating methods to investigate the shape of the exposure-outcome relationship, such as fractional polynomials or piecewise linear approaches (47).
In applied applications, population structure could introduce potential difficulties for hJAM, as is similar for all MR and TWAS approaches using summary statistics. First, there is the reliance on the association statistics being unbiased due to potential confounding by population structure. This includes summary data for the SNP-intermediate associations in  matrix, as well as the marginal SNP–outcome association estimates that are required by the hJAM model. However, given that modern techniques to account for population structure are often sufficient (48, 49), this is a fair assumption. Additionally, to account for the correlation structure between SNPs, hJAM assumes that the LD structure estimated from the reference data is the same as the study data used to generate the summary statistics. Since hJAM and MVIVW MR incorporate the correlation structure of SNPs in slightly different weight matrices, there is the potential for this to affect these methods differently. However, in a limited set of simulations we found that both methods are fairly robust to scenarios in which the reference data and the association data have modest differences in LD structures.
matrix, as well as the marginal SNP–outcome association estimates that are required by the hJAM model. However, given that modern techniques to account for population structure are often sufficient (48, 49), this is a fair assumption. Additionally, to account for the correlation structure between SNPs, hJAM assumes that the LD structure estimated from the reference data is the same as the study data used to generate the summary statistics. Since hJAM and MVIVW MR incorporate the correlation structure of SNPs in slightly different weight matrices, there is the potential for this to affect these methods differently. However, in a limited set of simulations we found that both methods are fairly robust to scenarios in which the reference data and the association data have modest differences in LD structures.
In contrast to most current methods that rely on independent SNPs or analyze intermediates in isolation, we propose a 2-stage hierarchical model to jointly model summary statistics—hJAM—for correlated SNPs and multiple intermediates within Mendelian randomization and TWAS. As technology expands the potential use of these types of studies to proteomic, methylation, and metabolomic data, such flexible approaches will be needed to account for the potential increase in complexity in underlying relationships between factors.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Division of Biostatistics, Department of Preventive Medicine, Keck School of Medicine, University of Southern California, Los Angeles, California, United States (Lai Jiang, Shujing Xu, Nicholas Mancuso, David V. Conti); Center for Genetic Epidemiology, Keck School of Medicine, University of Southern California, Los Angeles, California, United States (Nicholas Mancuso, David V. Conti); Norris Comprehensive Cancer Center, University of Southern California, Los Angeles, California, United States (Nicholas Mancuso, David V. Conti); and MRC Biostatistics Unit, University of Cambridge, Cambridge, United Kingdom (Paul J. Newcombe).
This work was supported by the National Cancer Institute at the National Institutes of Health (grants P01CA196569, U19CA214253, and R01CA140561). P.J.N. was funded by the UK Medical Research Council (Unit Programme number MC_UU_00002/9) and also acknowledges support from the NIHR Cambridge Biomedical Research Centre.
The authors thank Drs. Duncan C. Thomas, William Gauderman, and Juan Pablo Lewinger for valuable discussions and comments throughout development.
Conflict of interest: none declared.
REFERENCES
- 1. Thomas DC, Conti DV. Commentary: the concept of ‘Mendelian randomization’. Int J Epidemiol. 2004;33(1):21–25. [DOI] [PubMed] [Google Scholar]
- 2. Didelez V, Sheehan N. Mendelian randomization as an instrumental variable approach to causal inference. Stat Methods Med Res. 2007;16(4):309–330. [DOI] [PubMed] [Google Scholar]
- 3. Greenland S. An introduction to instrumental variables for epidemiologists. Int J Epidemiol. 2000;29(4):722–729. [DOI] [PubMed] [Google Scholar]
- 4. McKeigue PM, Campbell H, Wild S, et al. Bayesian methods for instrumental variable analysis with genetic instruments (‘Mendelian randomization’): example with urate transporter SLC2A9 as an instrumental variable for effect of urate levels on metabolic syndrome. Int J Epidemiol. 2010;39(3):907–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Newhouse JP, McClellan M. Econometrics in outcomes research: the use of instrumental variables. Annu Rev Public Health. 1998;19:17–34. [DOI] [PubMed] [Google Scholar]
- 6. Martens EP, Pestman WR, Boer A, et al. Instrumental variables application and limitations. Epidemiology. 2006;17(3):260–267. [DOI] [PubMed] [Google Scholar]
- 7. Gusev A, Ko A, Shi H, et al. Integrative approaches for large-scale transcriptome-wide association studies. Nat Genet. 2016;48(3):245–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Gamazon ER, Wheeler HE, Shah KP, et al. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet. 2015;47(9):1091–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Nica AC, Dermitzakis ET. Expression quantitative trait loci: present and future. Philos Trans R Soc Lond B Biol Sci. 2013;368(1620):20120362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sudlow C, Gallacher J, Allen N, et al. UK Biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015;12(3):e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Burgess S, Davey Smith G. How humans can contribute to Mendelian randomization analyses. Int J Epidemiol. 2019;48(3):661–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Burgess S, Butterworth A, Thompson SG. Mendelian randomization analysis with multiple genetic variants using summarized data. Genet Epidemiol. 2013;37(7):658–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zheng J, Baird D, Borges MC, et al. Recent developments in Mendelian randomization studies. Curr Epidemiol Rep. 2017;4(4):330–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Smith GD, Ebrahim S. Mendelian randomization: prospects, potentials, and limitations. Int J Epidemiol. 2004;33(1):30–42. [DOI] [PubMed] [Google Scholar]
- 15. Bowden J, Davey Smith G, Burgess S. Mendelian randomization with invalid instruments: effect estimation and bias detection through Egger regression. Int J Epidemiol. 2015;44(2):512–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Burgess S, Thompson SG. Multivariable Mendelian randomization: the use of pleiotropic genetic variants to estimate causal effects. Am J Epidemiol. 2015;181(4):251–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Newcombe PJ, Conti DV, Richardson S. JAM: a scalable Bayesian framework for joint analysis of marginal SNP effects. Genet Epidemiol. 2016;40(3):188–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Conti DV, Witte JS. Hierarchical modeling of linkage disequilibrum: genetic structure and spatial relations. Am J Hum Genet. 2003;72(2):351–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lewinger JP, Conti DV, Baurley JW, et al. Hierarchical Bayes prioritization of marker associations from a genome-wide association scan for further investigation. Genet Epidemiol. 2007;31(8):871–882. [DOI] [PubMed] [Google Scholar]
- 20. Thomas DC, Conti DV, Baurley J, et al. Use of pathway information in molecular epidemiology. Hum Genomics. 2009;4(1):21–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Greenland S. Principles of multilevel modelling. Int J Epidemiol. 2000;29(1):158–167. [DOI] [PubMed] [Google Scholar]
- 22. Witte JS, Greenland S, Kim L-L, et al. Multilevel modeling in epidemiology with GLIMMIX. Epidemiology. 2000;11(6):684–688. [DOI] [PubMed] [Google Scholar]
- 23. Burgess S, Bowden J. Integrating summarized data from multiple genetic variants in Mendelian randomization: bias and coverage properties of inverse-variance weighted methods. arXiv. 2015. (doi: https://arxiv.org/abs/1512.04486). Accessed November 27, 2015.
- 24. Yang J, Ferreira T, Morris AP, et al. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat Genet. 2012;44(4):369–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Consortium GP . A global reference for human genetic variation. Nature. 2015;526(7571):68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Sanderson E, Davey Smith G, Windmeijer F, et al. An examination of multivariable Mendelian randomization in the single-sample and two-sample summary data settings. Int J Epidemiol. 2019;48(3):713–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. R Core Team . R: A language and environment for statistical computing. https://www.r-project.org/foundation/. Accessed March 19, 2021.
- 28. Barbeira AN, Dickinson SP, Bonazzola R, et al. Exploring the phenotypic consequences of tissue specific gene expression variation inferred from GWAS summary statistics. Nat Commun. 2018;9(1):1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Yusuf S, Hawken S, Ounpuu S, et al. Obesity and the risk of myocardial infarction in 27 000 participants from 52 countries: a case-control study. Lancet. 2005;366(9497):1640–1649. [DOI] [PubMed] [Google Scholar]
- 30. Lauer MS, Anderson KM, Kannel WB, et al. The impact of obesity on left ventricular mass and geometry: the Framingham Heart Study. JAMA. 1991;266(2):231–236. [PubMed] [Google Scholar]
- 31. Manson JE, Colditz GA, Stampfer MJ, et al. A prospective study of maturity-onset diabetes mellitus and risk of coronary heart disease and stroke in women. Arch Intern Med. 1991;151(6):1141–1147. [PubMed] [Google Scholar]
- 32. Barrett-Connor EL, Cohn BA, Wingard DL, et al. Why is diabetes mellitus a stronger risk factor for fatal ischemic heart disease in women than in men?: the Rancho Bernardo Study. JAMA. 1991;265(5):627–631. [PubMed] [Google Scholar]
- 33. Kahn SE, Hull RL, Utzschneider KM. Mechanisms linking obesity to insulin resistance and type 2 diabetes. Nature. 2006;444(7121):840–846. [DOI] [PubMed] [Google Scholar]
- 34. Group LAR . Long term effects of a lifestyle intervention on weight and cardiovascular risk factors in individuals with type 2 diabetes: four year results of the Look AHEAD trial. Arch Intern Med. 2010;170(17):1566–1575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Locke AE, Kahali B, Berndt SI, et al. Genetic studies of body mass index yield new insights for obesity biology. Nature. 2015;518(7538):197–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Xue A, Wu Y, Zhu Z, et al. Genome-wide association analyses identify 143 risk variants and putative regulatory mechanisms for type 2 diabetes. Nat Commun. 2018;9(1):2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wu L, Wang J, Cai Q, et al. Identification of novel susceptibility loci and genes for prostate cancer risk: a transcriptome-wide association study in over 140,000 European descendants. Cancer Res. 2019;79(13):3192–3204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Mancuso N, Gayther S, Gusev A, et al. Large-scale transcriptome-wide association study identifies new prostate cancer risk regions. Nat Commun. 2018;9(1):4079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Lonsdale J, Thomas J, Salvatore M, et al. The genotype-tissue expression (GTEx) project. Nat Genet. 2013;45(6):580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Schumacher FR, Al Olama AA, Berndt SI, et al. Association analyses of more than 140,000 men identify 63 new prostate cancer susceptibility loci. Nat Genet. 2018;50(7):928–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Yavorska OO, Burgess S. MendelianRandomization: an R package for performing Mendelian randomization analyses using summarized data. Int J Epidemiol. 2017;46(6):1734–1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Gusev A, Shi H, Kichaev G, et al. Atlas of prostate cancer heritability in European and African-American men pinpoints tissue-specific regulation. Nat Commun. 2016;7:10979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Chen GK, Witte JS. Enriching the analysis of genomewide association studies with hierarchical modeling. Am J Hum Genet. 2007;81(2):397–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Rees JM, Wood AM, Burgess S. Extending the MR-Egger method for multivariable Mendelian randomization to correct for both measured and unmeasured pleiotropy. Stat Med. 2017;36(29):4705–4718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Gkatzionis A, Burgess S, Conti D, et al. Bayesian variable selection with a pleiotropic loss function in Mendelian randomization. bioRxiv. 2019. (doi: 10.1101/593863). Accessed October 22, 2019. [DOI] [PMC free article] [PubMed]
- 46. Verbanck M, Chen CY, Neale B, et al. Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nat Genet. 2018;50(5):693–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Staley JR, Burgess S. Semiparametric methods for estimation of a nonlinear exposure-outcome relationship using instrumental variables with application to Mendelian randomization. Genet Epidemiol. 2017;41(4):341–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Price AL, Patterson NJ, Plenge RM, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–909. [DOI] [PubMed] [Google Scholar]
- 49. Runcie DE, Crawford L. Fast and flexible linear mixed models for genome-wide genetics. PLoS Genet. 2019;15(2):e1007978. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


