Abstract
13C kinetic isotope effects (KIEs) for the photoredox-promoted [2 + 2] cycloaddition of enones were determined in homocoupling and heterocoupling examples. The only significant KIEs were observed at the β carbon, indicating that Cβ─Cβ bond formation is irreversible. However, these KIEs were much lower than computational predictions, suggesting that product selectivity is determined in part by a step prior to Cβ─Cβ bond formation. The results are explained as arising from a competition between C─C bond formation and electron exchange between substrate alkenes. This idea is supported by a relatively small substituent effect on substrate selectivity. The possible rates for electron transfer and bond-forming steps are analyzed, and the competition appears plausible, particularly if the mechanism involves a complex between reduced and neutral enone molecules.
Graphical Abstract

INTRODUCTION
The mechanisms of photoredox-promoted reactions are intrinsically complex, involving a combination of photophysical steps, one or more electron-transfer steps leading to activated substrates, chemical conversions of radical ions, chain-transfer steps, and termination steps. Many aspects of these mechanisms are qualitatively understood from general chemical knowledge. In fact, a mechanistic understanding is often a key factor in the design and development of these reactions. However, the complexity of the mechanisms leaves some aspects undefined by either qualitative experimental studies or computational studies. The interplay of electron-transfer steps and chemical steps is particularly problematic, as electron-transfer steps are not readily tractable computationally and are often not directly accessible experimentally. We describe here a combined experimental and computational study of a photoredox-promoted cycloaddition that elucidates the importance of this interplay in selectivity.
A striking example of the synthetically valuable and complex photoredox reactions developed in recent years is the [2 + 2] cycloaddition of enones that occurs with visible light in the presence of RuII(bipy)3Cl2 (bipy = 2,2′-bipyridine) as a photosensitizer, as developed by Yoon and coworkers.1 The reaction is an extension of earlier work by Krische et al. on cathodic reduction of bis(enones),2 and the reaction is an example of the now broad class of cycloadditions of both anion radicals and cation radicals.3 Yoon et al. have recently extended these cycloadditions to enantioselective reactions by employing chiral europium Lewis acid complexes as cocatalysts.4
The basic photophysics of these reactions are well-known.5 The triplet excited state of the *Ru(bpy)32+ is rapidly formed after excitation, and it is both a reductant and an oxidant. In the presence of an amine, the triplet is reduced, and the resulting monovalent Ru(bpy)3+ is now a longer-lived strong reductant (E° = −1.33 V).6 The downhill transfer of an electron to a sufficiently electron-deficient enone such as phenyl propenyl ketone (E° = −1.26 V in the presence of LiClO4)7 may then occur to afford the radical anion of the substrate. It is at this point that the mechanism must first overcome a significant barrier, which for C─C bond formation is by the radical anion. The delayed reaction of a reactive intermediate is ripe for mechanistic complications, and the chemoselectivity and success versus failure of reactions may be expected to depend largely on the competition between traversal of the first large-barrier irreversible steps versus alternative reaction pathways. Such “selectivity-determining” steps can be interrogated by competition reactions, either using electronically differing substrates or using isotopically differing substrates in the measurement of kinetic isotope effects (KIEs). The results of such studies here are surprising and have implications toward the understanding and control of selectivity in these reactions.
RESULTS AND DISCUSSION
Experimental KIEs.
The photoredox-promoted dimerization of phenyl vinyl ketone (1) provided a simple example for study. Under the Yoon conditions (Figure 1) including RuII(bipy)3Cl2, LiBF4, and diisopropylethylamine in acetonitrile, the dimerization of 1 affords trans-disubstituted cyclobutane 2 cleanly in 89% yield as the sole cycloadduct. The 13C KIEs for the dimerization were studied at natural abundance by NMR methodology.8 Two independent reactions of 1 were taken to 85 and 60% conversion, and crude unreacted 1 was hydrogenated (H2/Pd/C) to propiophenone for final purification and analysis. The propiophenone was then analyzed by 13C NMR in comparison to propiophenone derived from the original 1 that had not been subjected to the reaction conditions. The changes in the isotopic composition in each position were determined relative to the para phenyl carbon as an “internal standard”, with the assumption that the isotopic fractionation in this position was negligible. From the percentage conversions and the changes in isotopic composition, the KIEs were calculated as previously described.8
Figure 1.
13C KIEs (k12/k13, 25 °C) for the dimerization of 1. In one case, the measurement was affected by an overlapping impurity, and the resulting KIE is marked with an asterisk (*).
The resulting KIEs are shown in Figure 1. KIEs measured in this way do not reflect a reaction’s “rate-limiting step”, a term not well-defined in a photochemical reaction. Rather, they reflect the first irreversible step undergone by the substrate. Because such steps determine which substrate molecules react, they may be referred to as selectivity-determining steps. Here, only the β-enone carbon exhibits a substantial 13C KIE, with the remaining carbons essentially within experimental error of unity. The qualitative interpretation of this observation is that the selectivity-determining step involves C─C bond formation at the β-enone carbons, as would fit with the reaction of a nominal enone radical anion (3−·) with a neutral enone (eq 1), as previously postulated by Krische/Bauld and by Yoon.
 |
(1) |
There is, however, a substantial limitation on this interpretation because the measured KIE will be the average of KIEs for two molecules of 1. This does not define the separate KIEs for each reactant; the observed 1.024 could result from the combination of values over a broad range, e.g., 1.023 and 1.025 or 1.000 and 1.048. As a consequence, the observed KIE cannot unambiguously define the selectivity-determining step for the enone radical anion 3−·.
To define the selectivity-determining step for each component in the cycloaddition, it was necessary to study an unsymmetrical reaction. Yoon and coworkers had previously reported the crossed cycloaddition of 1-phenyl-2-buten-1-one 5 with methyl vinyl ketone (6) to afford cycloadduct 7 in 84% yield. In this reaction, more conjugated 5 is more easily reduced, and it is expected to be the radical anion in the Cβ─Cβ bond-forming step, while unhindered 6 is a more reactive electrophile and is expected to be the neutral component in the reaction.
The determination of the KIEs for the reaction of 5 with 6 was more problematic than with the dimerization of 1. It was first found that the reaction required the use of an excess of 6 to proceed efficiently, and this precluded a measurement of the KIEs for 6. For 5, there was an overlap of olefinic and aromatic 13C NMR peaks that prevented a direct analysis of 5, so recovered unreacted 5 was hydrogenated to afford butyrophenone for the final purification and analysis. Even so, trace (1–3%) inseparable impurity peaks in the aromatic region of the 13C NMR the butyrophenone prevented the use of an aromatic peak as the internal standard for integrations. Instead, the terminal methyl group was used as the internal standard. The results from a total of five independent KIE determinations based on six measurements each are shown in Figure 2.
Figure 2.
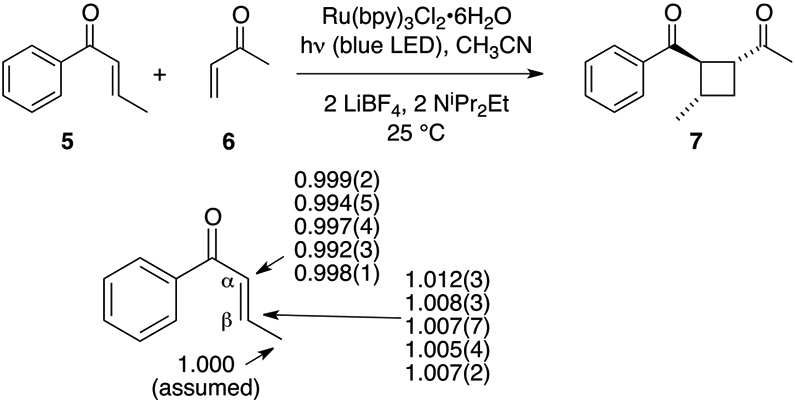
13C KIEs for the cycloaddition of 5 with 6 derived from five independent experiments with conversions from 66 to 92%.
The key observation is that the KIE for the β carbon of 5, at ~1.008, is much smaller than the composite KIE for 1. This value is sufficiently small that it could reflect a secondary 13C KIE. In other words, the KIE does not support Cβ─Cβ bond formation as the selectivity-determining step for the radical anion! A more quantitative interpretation of the KIE will be possible with the aid of computational studies.
The small β KIE for 5 in its reaction with 6 suggests that the KIE observed for the homocoupling of 1 results from the combination of a small KIE for the radical anion and a larger KIE for neutral 1 undergoing bond formation. This assumes that the mechanisms for the homo- and heterocouplings are identical. The observation of very different KIEs (e.g., 1.009 and 1.039, as a possibility) would be rather unusual if both 3−· and 1 were undergoing a selectivity-determining Cβ─Cβ bond-forming step. This fits with the idea that radical anion 1 has a separate selectivity-determining step prior to C─C bond formation. An alternative explanation will be considered below after the use of computations to evaluate the expected isotope effect for differing mechanistic scenarios.
Lithium Coordination.
Yoon reported that the photochemical [2 + 2] reactions require the presence of LiBF4, that an excess of the salt and diisopropylethylamine was required for high diastereoselectivity, and that lithium could not be successfully replaced with other cations. To explore the role of lithium coordination in these reactions, we examined its effect on the 13C chemical shifts of 5, 6, and diisopropylethylamine in CD3CN at concentrations similar to those in the reaction. Initial explorations using LiBF4 were complicated by the partial precipitation of LiF in the presence of amine, but it was found that LiClO4 was equally effective and stereoselective in the synthetic reactions, so LiClO4 was used for coordination studies. As LiClO4 is added to solutions containing the enones and amine, the carbonyl, alpha, and beta carbons of 5 and 6 shift downfield, upfield, and downfield, respectively, in a pattern and proportion that matches in direction the changes in the calculated chemical shifts for these carbons in going from the neutral structures to structures that are lithium-coordinated at their oxygen atoms (see the Supporting Information). Similarly, the alpha and beta carbons of diisopropylethylamine shift downfield and upfield, respectively, in line with predicted shift changes. No saturation of the shift changes could be observed in either case, with maximum shifts, in the presence of 8 equiv of LiClO4, of 2.2 ppm for the carbonyl carbon of 6 and 0.4 ppm for the amine alpha carbons. From this and the calculated shifts for lithium coordination, an order-of-magnitude estimate of the association constants for each is 1 M−1.
This is an extremely weak coordination, but the reaction conditions would contain significant amounts of lithium-coordinated reactants. Lithium coordination would make 5 a better electron acceptor and make 6 more electrophilic. It is uncertain whether both of these features are required for the success of the reaction, but it is notable that the electrochemical reactions of Krische/Bauld did not require added lithium salts. Unlike the photochemical reactions, the electrochemical reactions notably involve long-lived anion radicals that cannot readily be quenched by back electron transfer to the original donor.
Computational Method Selection.
To choose a DFT method suitable for the study of the experimental reactions, the model cycloaddition of 6 with the radical anion of 1-cyano-2-buten-1-one was studied using diverse combinations of DFT methods and basis sets (see the Supporting Information). The energetics of the transition states and intermediates along the cycloaddition pathway for the various computational methods were then compared with single-point energies obtained in CCSD(T)/aug-cc-pVDZ energies, and ωB97XD calculations employing a 6-311+G(d,p) basis set were chosen because they exhibited the lowest RMS error (1.4 kcal/mol across eight structures) among practical methods. Both PCM and SMD solvent models for acetonitrile were then employed for the exploration of the experimental mechanistic pathways in solution. For simple anionic structures, the two solvent models led to qualitatively similar results, while for structures containing lithium counterions and additional coordination, there were in cases significant differences, as will be noted. For structures of potential mechanistic relevance, the energies were corrected using DLPNO-CCSD(T)/aug-cc-pVTZ single-point calculations. The final energies reported here are a combination of the DLPNO potential energies and ωB97XD/PCM structures and free-energy corrections adjusted to a standard state concentration of 1 M (see the Supporting Information for details).
The lithium coordination studies described above provide one way to gauge the accuracy of the computational methods versus experimental observations. The free energy for coordination of 5 with a lithium ion in acetonitrile was calculated with the assumption that a “free” lithium ion in acetonitrile is coordinated by four solvent molecules and that 5 would replace one of these, giving rise to a Li(5)(MeCN)3 ion. The calculated free energies were −1.7 and −1.1 kcal/mol for the SMD and PCM solvent models, respectively, compared to the experimental value of 0 ± 1 kcal/mol.
Computational Pathways.
The potential involvement of the lithium ion and the amine in the mechanistic pathway complicates substantially computational exploration of these reactions. An additional complication is that several of the mechanistic models explored do not predict the correct major product for the reaction. Despite exhaustive effort on diverse systems including zero, one, or two lithium ions, zero to six solvent molecules, and zero to two amine molecules (see the Supporting Information), we ultimately concluded that computations alone could not adequately characterize the mechanism. Instead, we will use computations to aid in the interpretation of the experimental observations.
The important issues with regard to the computational explorations will be described here with reference to the simplified basic mechanisms of Figure 3. The effects of counterions, solvent, and amine will then be described as perturbations on these mechanisms. The initial Cβ─Cβ bond formation of 1 with its radical anion 3−· (Figure 3a) and of 6 with the radical anion of 5 (5−·) (Figure 3b) may occur by many transition state conformers (see the Supporting Information), but the lowest energy transition structures (TSs) invariably orient the olefinic units anti to each other, as in 8‡ and 12‡, and lead to Z configurations of the incipient enol radical and enolate anion moieties. The corresponding gauche TSs are energetically competitive in structures including lithium counterions, but in no case were they the lowest-energy TSs. The resulting distally oriented radical anions 4 and 13 must then undergo conformational interconversion (by TSs 9‡ and 14‡) to form gauche radical anions 10 and 15. These then undergo ring closure via TSs 11‡ and 16‡ to afford the closed radical anions of the trans products 2−· and 7−·. Since 2−· and 7−· would be expected to undergo exergonic electron transfers to the starting enones or other electron sinks in solution at a high rate, their formation would be irreversible as would passage over the highest-energy TSs 8‡ and 12‡.
Figure 3.

Simplified calculated mechanisms for (a) reactions of 1 with its radical anion 3−· and (b) of 6 with the radical anion of 5 (5−·). The relative free energies are DLPNO-CCSD(T)/aug-cc-pVTZ//ω-B97XD/PCM (acetonitrile) with a 1 M standard state in kcal/mol. Related structures including one or two lithium ions, varying explicit solvents, and one or two coordinating amines are shown in the Supporting Information.
After addition of one or two lithium ions to these parent structures, the energetically preferred structures invariably involve the chelation of a lithium ion by two oxygens. Since 11‡ and 16‡ cannot provide such chelation, these structures end up higher in energy than ring-closing TSs leading to the alternative cis product. Exhaustive attempts to locate a lower-energy TS for formation of the trans product were unsuccessful. In agreement with many similar observations of Yoon, we have confirmed that product 2 has trans stereochemistry by comparison of its melting point with the known values for the two stereoisomers.9 Clearly, the simple solvent model is computationally inadequate. In solution, solvent or amine molecules would specifically coordinate the lithium ions. A series of such structures were located and are presented in the Supporting Information. With a total of six acetonitrile molecules included, the preferred TS for ring closure was an analog of 11‡, leading to the correct trans product. This observation should not be overinterpreted in a positive sense; in solution, the actual ring closure would occur by an ensemble of structures that cannot be adequately represented by any single or small set of structures, so the calculations cannot be said to actually predict the trans product. The observation shows, however, that the general mechanism is consistent with the experimentally observed stereochemistry.
For the purpose at hand, the key question is the nature of the selectivity-determining step, that is, the first irreversible step undergone by each reactant. The experimental KIEs will be the ultimate arbiter on this question, but it should be clear that computations predict that the initial Cβ─Cβ bond formation is irreversible. In the absence of lithium ions, the highest barriers on the pathway from the enone radical anion to the product involve 8‡ and 12‡. Lithium ion coordination stabilizes the various anionic structures to different extents, but the Cβ─Cβ bond formation remains irreversible (see the Supporting Information).
Calculated KIEs: Disagreement with Experiments.
The diverse TSs obtained for the cycloaddition process were used to predict the 13C KIEs for the reaction from the scaled theoretical vibrational frequencies by the method of Bigeleisen and Mayer.10 Tunneling corrections based on a one-dimensional infinite parabolic barrier model were included in the predictions.11 KIE predictions done in this way have proven to be highly accurate, so long as the calculation accurately depicts the mechanism and transition state geometry.12
The resulting KIE predictions (Table 1) fit the qualitative expectation that carbons undergoing sigma-bond formation in the selectivity-determining step should exhibit substantial KIEs, that is, large at the β carbons for analogs of 8‡ and 12‡ and large at the α carbons for analogs of 11‡ and 16‡. The α carbons are predicted to exhibit a small 13C KIE for the Cβ─Cβ TSs, in line with observations in other additions to alkenes.13 The inverse 13C KIEs at the β positions for ring-closing TSs are also in line with previous observations and fit with the tighter potential energy well surrounding an sp3 carbon. Quantitatively, the predictions vary relatively little with the addition of lithium ions, or explicit solvation, or coordination of the lithium ions by amine or acetonitrile. This fits with the general observation that small changes in the calculation model or method lead to only modest changes in the predicted KIEs, so long as the mechanism is unchanged and the TS geometry does not change much.14
Table 1.
Predicted 13C KIEs (25 °C) for Transition Structures in the Cycloadditions of 1 with 3−· and of 6 with 5−·
| 1 + 3−· | 6 + 5−· | ||||
|---|---|---|---|---|---|
| α | β | α | β | ||
| Cβ─Cβ TSs (analogs of 8‡) | Cβ─Cβ TSs (analogs of 12‡) | ||||
| no Li+ | 1.011 | 1.034 | no Li+ | 1.005 | 1.031 |
| 1 Li+ | 1.008 | 1.033 | 1 Li+ | 1.006 | 1.033 |
| 2 Li+ | 1.004 | 1.033 | 1 Li+ + 2 MeCN | 1.006 | 1.034 |
| 2 Li+ gauche | 1.006 | 1.043 | 2 Li+ | 1.007 | 1.030 |
| 2 Li+ + 2 MeCN | 1.007 | 1.034 | 2 Li+ + 2 NMe3 | 1.006 | 1.029 |
| 2 Li+ + 2 NMe3 | 1.010 | 1.028 | |||
| ring-closing TSs (analogs of 11‡) | ring-closing TSs (analogs of 16‡) | ||||
| no Li+ | 1.035 | 0.990 | no Li+ | 1.042 | 0.992 |
| 1 Li+ | 1.041 | 0.990 | 1 Li+ | 1.040 | 0.992 |
| 2 Li+ | 1.041 | 0.990 | 2 Li+ | 1.037 | 0.992 |
| 2 Li+ + 2 NMe3 | 1.035 | 0.989 | 2 Li+ gauche | 1.045 | 0.991 |
| 2 Li+ + 4 MeCN | 1.035 | 0.989 | 2 Li+ + 2 NMe3 | 1.023 | 0.994 |
| 2 Li+ + 6 MeCN | 1.035 | 0.989 | 1 Li+ + 2 MeCN | 1.040 | 0.993 |
| Cβ─Cβ TSs non-Curtin–Hammett regime | Cβ─Cβ TSs non-Curtin–Hammett regime | ||||
| 1.002–1.006 | 1.014–1.022 | 1.000 | 1.000 | ||
| experimental | experimental | ||||
| 1.003 | 1.024 | 0.998 | 1.008 | ||
However, none of these predictions fit with experiments. For the Cβ─Cβ TSs, the predicted KIEs at the β carbon are all larger than those observed, particularly so in the reaction of 6 with 5−·. If Cβ─Cβ and ring closing were competitive as selectivity-determining steps, the β carbon KIE would go down, but the α carbon KIE would go up, and the agreement with experiment would in fact worsen. This fits with the computational finding that the ring-closing step has a lower barrier and should not be selectivity-determining. Our conclusion is that the experimental KIEs are inconsistent with a mechanism in which the selectivity is determined purely by C─C bond-forming steps.
An Alternative: Selectivity-Determining Electron Transfer.
An implicit assumption when considering TSs such as 8‡ or 12‡ as selectivity-determining is that the electron-transfer steps forming 3−· or 5−· have not themselves predestined particular molecules to react. In other words, it is assumed that the thermoneutral electron transfers between enone radical anions and their starting neutral counterparts (eq 2) are fast relative to the C─C bond-forming steps, or instead
 |
(2) |
 |
(3) |
that the deactivation of the radical anions by electron transfer with an amine cation radical (or any other electron acceptor) is faster than C─C bond formation. This may be viewed as a “Curtin–Hammett assumption”, the idea being that the selectivity is determined by the relative heights of competitive bond-forming transition states and not by the ease of formation of their precursors.
The Curtin–Hammett assumption breaks down, however, if these steps are kinetically competitive with the productforming steps. In the limit of slow electron exchange or deactivation of intermediate radical anions, the KIEs for 5 would be determined purely by the electron transfer, while the KIEs for 1 would be a 1:1 combination of electron-transfer KIEs for one molecule and Cβ─Cβ bond formation for the other.
KIEs for electron-transfer reactions can be complex when the electron transfer is intramolecular or thermoneutral, but they tend to approach the equilibrium isotope effect for endergonic reactions and unity for exergonic reactions. The calculated equilibrium isotope effect for electron transfer to 1 would be the largest at the carbonyl carbon (1.020), not in line with experiments. The electron transfer from the Ru(I) complex (Eox = −1.33 V versus SCE6) to lithium-coordinated 5 (Ered = −1.26 V versus SCE15) would be downhill by 1.6 kcal/mol. It would then be expected that the formation of the radical anion of 3−· and 5−· or their lithium-coordinated salts would be isotopically insensitive or nearly so. For the purpose of analysis, we will assume that the KIEs for the steps forming these intermediates are unity.
In the limiting case that there is no self-exchange electron transfer between 1 and 3−·, the observed KIEs for 1 would be an average of unity and the KIE from Table 1 for 1 + 3−· or in the range of 1.001–1.008 for Cα and 1.014–1.020 for Cβ. If there is no self-exchange between 5 and 5−·, the KIEs expected for 5 would simply be unity.
These limiting-model KIEs are substantially closer to experiments than those in Table 1, though now, the predicted KIEs are smaller than the experimental values instead of larger. A compromise mechanism in which electron transfer was competitive with Cβ─Cβ bond formation could readily account for the observed KIEs. The critical question for the remainder of this study is whether the possibility of competitive electron transfer and Cβ─Cβ bond formation can withstand logical and experimental scrutiny.
To start, the assumption of slow electron transfer is highly questionable. The self-exchange rates for aromatic radical anions in DMF have typical rate constants in the range of 108–109 M−1 s−1,16 while the calculated barriers associated with the Cβ─Cβ TSs (the analogs of 8‡ and 12‡) would lead to rate constants in the range of 104–106 M−1 s−1. Systems in which a high reorganization energy is associated with the self-exchange can exhibit lower rates for electron transfer, for example, in the self-exchange of cyclooctatetraene with its radical anion, but there is no reason to expect a high reorganization energy with simple enones and their radical anions.
However, the literature rates for electron transfers similar to that in eq 2) are fast relative to the C─C bond-forming steps, or instead that the deactivation of the radical anions by electron transfer with an a are most commonly measured using large counterions, such as tetraalkylammonium ions, that may be loosely bound or dissociated. The potential effects of tightly bound lithium ions may be more complex, in part because there are multiple possible mechanisms for the overall electron-transfer process.17 Within the possibilities discussed by Marcus,17a the most easily analyzed is an “electron transfer first” mechanism (eq 4) are fast relative to the C─C bond-
 |
(4) |
forming steps, or instead that the deactivation of the radical anions by electron transfer with an a) in which an electron transfer giving 17 + 5−· is followed by a separate discrete step transferring the counterion. We can estimate a lower bound for the barrier for this mechanism from calculations using a Marcus treatment. For this calculation, the ω-B97XD/PCM-calculated ΔG° for the electron transfer step is +9.9 kcal/mol. The internal reorganization energy λi for the electron transfer was estimated to be 11.5 kcal/mol based on the average of calculated reorganization energies for self-exchange of 5 with 5−· and self-exchange of 5-Li with 17 (10.9 and 12.1 kcal/mol, respectively, based on the ω-B97XD/PCM calculations). The external reorganization energy λo is more difficult to estimate, so we will simply ignore it to obtain a lower-bound ΔG‡ of 10.0 kcal/mol. This barrier would make electron transfer slow enough for plausible competition with Cβ─Cβ bond formation.
There are problems with this estimate of the electron-transfer barrier, two being that it assumes a mechanism that is often not the best choice and that it ignores the possibility of electron self-exchange between 5-Li and 17. It will be necessary to consider whether there is any other possible explanation for the low KIEs, but first, we consider whether other experimental observations can provide information on the rate of electron transfer versus C─C bond formation in these reactions.
Substituent Effect on Selectivity.
The relative reactivity of 5 versus p-Cl analog 18 was explored in a competition reaction. The idea of this experiment is that the relative rates of electron transfer versus C─C bond formation ought to have a significant effect on substrate selectivity. If the electron transfer between radical anions (eq 2) or their lithium-coordinated analogs (eq 4) is fast, then the competition ought to reflect the equilibrium distribution of the electron between substrates. If instead the electron transfer is slow or competitive with C─C bond formation, then the substrate selectivity should be decreased because the initial electron transfer from the strong reductant Ru(bpy)3+ should be fast.
 |
In the event, the relative rate for 18 versus 5 under the standard conditions was 2.5 ± 0.4:1. The relative rate decreased by ~15% when the reaction was diluted by a factor of four, but the uncertainty in the values did not allow a conclusion on whether this decrease was real. The chlorine-substituted analog was more reactive, but it was only moderately so. This observation can be evaluated from two perspectives. The first is electrochemical. The half-wave reduction potential for acetophenone versus p-chloroacetophenone differs by 0.16 V in acetonitrile,18 corresponding to 3.7 kcal/mol. This is likely to be an overestimate due to the anion-stabilizing effect of lithium coordination. The calculated free-energy change for the reaction of 5-Li + 18 going to 18-Li + 5 is 1.7 kcal/mol. If this reaction reaches equilibrium when radical anions are generated under the reaction conditions, then only 6% of the radical anions would be 5−·. The calculations predict that the barrier for the reaction of 18-Li with MVK is slightly lower than that for 5-Li (9.8 versus 10.2 kcal/mol, respectively), so the calculations predict a relative rate ratio of >30. The actual reaction is not as selective as would be expected for a purely rate-limiting C─C bond formation, which fits with the KIE observations.
The second perspective is that of a Hammett relationship. The experimental H/Cl difference is 2.5, and the Hammett sigma value of p-Cl is 0.23. This leads to a two-point estimate of 1.7 for the Hammett ρ value for the reaction. This is somewhat low. For comparison, the acidity of substituted acetophenones in DMSO has a ρ of 3.55.19 The latter value represents the effect of a full negative charge at equilibrium, while the relative reactivity of 5 and 18 is kinetic and reflects a partial charge at a transition state, so ρ would be expected to be lower here. However, for early transition states, as consistently calculated, most of the negative charge is retained, and a ρ that more closely approaches 3.55 might qualitatively be expected. The computationally predicted ρ assuming full electron equilibration and the 5-Li/18-Li reaction barriers is in fact +6.7. The lower observed ρ fits with the idea that the competition between reactants does not reflect full equilibration of the electrons between reactants, as fits with the observed KIEs.
An Alternative Mechanism.
The results so far suggest that electron transfer between reduced reactants occurs at a rate that is competitive with C─C bond formation. Such a competition would be predicted to give rise to KIEs that are in between those predicted for the Curtin–Hammett and non-Curtin–Hammett regimes in Table 1, which would be fully consistent with the experimental KIEs. While plausible, this mechanism requires a coincidence of similar barriers for independent processes, C─C bond formation and electron transfer, for two different reactions. We therefore considered whether an alternative mechanism that is less reliant on coincidence could be identified.
Previous work from Wiest et al. with Diels–Alder reactions of cation radicals had notably observed a similar set of results to that here, particularly finding that the experimental KIEs were much smaller than those predicted.20 That work faced the identical problem as here of having to account for the discrepancy. Based on kinetic modeling, it was suggested that the suppressed experimental KIEs could be accounted for by the importance of a diene–dienophile cation radical complex.
In an analogous way, we considered the possible role of alkene–alkene complexes in the present reactions. A minimal-complexity kinetic scheme allowing for this possibility is shown in eqs 5-8. This scheme is written with only a single lithium
| (5) |
| (6) |
| (7) |
| (8) |
ion in complex 20 and product 7-Li, but the inclusion of an extra lithium ion would make no essential difference. The real reaction would include both the chain-initiating formation of 5-Li and chain-termination steps, but these are inconsequential to the observed KIEs. Simulation of this scheme by numerical integration finds that the observed KIE does not exceed 90% of the intrinsic KIE (i.e., (KIEobs − 1)/(KIEint − 1) > 0.9) unless the rate constant for exchange kex exceeds the rate constant for C─C bond formation kCC by a factor of 250. If the rate constant for exchange was 1 × 108 M−1 s−1, then a kCC of approximately 106 s−1 would be consistent with the decreased observed KIEs as well as the calculated barriers. We have no direct evidence for the kinetic importance of 20 or related species, but they provide a plausible explanation for the observations.
CONCLUSIONS
The results here suggest that Cβ─Cβ bond formation in the photoredox-promoted [2 + 2] cycloaddition of enones is irreversible but kinetically competitive with electron transfer between the enones. This is supported by the observation of lower Cβ KIEs than would be expected if the C─C bond-forming step was fully product-determining and is consistent with a relatively small substituent effect on the selectivity for the cycloaddition. Whether the competition involves simple enone radical anions or alkene–alkene complexes is uncertain. It is notable that the competition between electron transfer and C─C bond formation has now been supported for both anion radical and cation radical reactions.20
This competition adds a potentially useful complication in the mechanism of photoredox-promoted reactions. That is, if the rates of key intermolecular steps can, as here, be competitive with electron-transfer rates between substrates, then it may be possible to engineer reactions in which the electron transfer is fully slow compared to the product-determining step. The challenge in this would be to lower electron-transfer rates. From a Marcus perspective, slower rates may be obtained from reaction conditions that increase the reorganization energy, either through changes to more polar solvent or changes in the associated counterion. The value of this possibility is that it may be possible to control the chemoselectivity of these reactions through the kinetics of the initial electron transfer, instead of having the reactive ion decided by equilibria. This suggests that there may be ways to influence or control chemoselectivity in these reactions.
EXPERIMENTAL SECTION
General Methods.
Diisopropylammonium trifluoroacetate was prepared by mixing equimolar amounts of diisopropylamine and trifluoroacetic acid in ether followed by filtration and vacuum drying. All other chemicals were commercially available. A Kessil H150B LED Grow Light (λmax = 423 and 454 nm, see the Supporting Information for an optical profile) was used as the blue LED. All photoreactions, unless otherwise noted, were carried out in ordinary Pyrex round-bottom flasks within a 6.5 in. × 10.5 in. cylindrical steel can as a light shield, with the blue LED clamped at the top of the can, making its distance to the solutions 8–10 inches. No additional light filter was used. A combination of a hot plate and an Optitherm reaction block was used for all heating of reactions.
Phenyl Vinyl Ketone (1).
By an adaptation of a literature procedure,21 a mixture of 10.12 g (83 mmol) of acetophenone, 10.50 g (333 mmol equiv of formaldehyde) of paraformaldehyde, 17.90 g (84 mmol) of diisopropylammonium trifluoroacetate, two drops of 1,4-cyclohexadiene, two drops of trifluoroacetic acid, and 100 mL of tetrahydrofuran was heated at 80 °C in a 250 mL pressure vessel overnight. The mixture was then concentrated on a rotary evaporator, and the residue was dissolved in 200 mL of diethyl ether and rinsed with 200 mL of 1 M HCl, 200 mL of 1 M NaOH, and 200 mL of brine. The organic layer was then dried (MgSO4) and concentrated on a rotary evaporator. The residue was chromatographed on multiple silica gel columns (initially 40 mm by 350 mm) using 5% ethyl acetate in hexanes to afford 3.71 g (34%) of 1 as a pale yellow liquid, contaminated with traces of hexanes and ethyl acetate.
4′-Chloro-1-phenylbut-2-en-1-one (18) Synthesis.
By an adaptation of a literature procedure,22 a mixture of 10.02 g (65 mmol) of 4-chloroacetophenone, 5.28 g (120 mmol) of acetaldehyde, two drops of 50% KOH solution, and 100 mL of methanol was stirred at 25 °C overnight. The reaction mixture was then concentrated on a rotary evaporator. The residue was dissolved in 150 mL of diethyl ether and washed sequentially with 2 × 150 mL of 1 M HCl and 2 × 150 mL of brine. The organic layer was then dried (MgSO4) and concentrated on a rotary evaporator. A few crystals of ZnCl2 were added into the residue, and it was vacuum-distillated (60 °C, 1.5 mmHg) to afford 0.56 g (4.8%) of 18 as a pale yellow liquid. The 1H NMR spectrum of 18 matches with the literature.23
Photodimerization of 1.
A mixture of 5.09 g (39 mmol) of freshly prepared 1, 7.09 g (76 mmol) of LiBF4, 9.78 g (76 mmol) of N,N-diisopropylethylamine, 1.0 g of mesitylene (internal standard), 1.42 g (1.9 mmol) of Ru(bpy)3Cl2·6H2O, and 400 mL of acetonitrile was irradiated under N2 by a blue LED at 25 °C. The reaction progress was monitored by 1H NMR analysis of aliquots versus the mesitylene internal standard until a conversion of 85% was reached. The reaction was then concentrated on a rotary evaporator, and the residue was dissolved in 200 mL of diethyl ether. The organic layer was washed by 200 mL of 1 M HCl and 200 mL of brine repeatedly until the aqueous layer is colorless. The organic layer was dried by MgSO4, filtered, and concentrated on a rotary evaporator. The residue was dissolved in 50 mL of diethyl ether, and 10 mg of palladium on carbon (5 wt % Pd/C) was added. The flask was connected to a balloon with H2 gas, and the reaction was monitored by 1H NMR until 100% conversion was reached. After completion, the reaction mixture was filtered and concentrated on a rotary evaporator. The residue was chromatographed through a 20 mm by 350 mm column packed with 300 mm height of silica gel using 12.5% ethyl acetate in hexanes to afford 0.23 g of colorless liquid propiophenone as KIE sample 1.
In an independent experiment, sample 2 was obtained by an analogous procedure to that described above, but the reaction was stopped at 60% conversion.
Compound 2 (clear crystals, mp 92.5–93.8 °C) is known,9 but its NMR spectra had not been reported: 1H NMR (CDCl3, 500 MHz): δ 7.98 (m, 4H), 7.56 (m, 2H), 7.46 (m, 4H), 4.57 (m, 2H), 2.38 (m, 4H). 13C{1H} NMR (CDCl3, 125 MHz): δ 199.6, 135.2, 133.2, 128.7, 128.6, 42.3, 22.9. HRMS (ESI) m/z: [M + Na]+ calcd for C18H16O2Na, 287.1048; found, 287.1038; [M + H]+ calcd for C18H17O2, 265.1229; found, 265.1220.
Photocycloaddition of 5 with 6.
Phenylbut-2-en-1-one (5, 5.04 g, 34 mmol), methyl vinyl ketone (6, 4.81 g, 68 mmol), Ru(bpy)3Cl2·6H2O (1.37 g, 1.7 mmol), LiBF4 (12.82 g, 137 mmol), N,N-diisopropylethylamine (8.80 g, 68 mmol), and mesitylene (1.01 g, 8.3 mmol) were dissolved in 400 mL of acetonitrile. The reaction was irradiated under N2 by a blue LED at 25 °C, and the reaction progress was monitored by 1H NMR until reaching 92% conversion; the reaction mixture was concentrated on a rotary evaporator. The residue was dissolved in 200 mL of diethyl ether, and the organic layer was washed with 200 mL of 1 M HCl and 200 mL of brine repeatedly until the aqueous layer became colorless. The organic layer was dried (MgSO4), filtered, and concentrated on a rotary evaporator. The residue was dissolved in 50 mL of diethyl ether, and 10 mg of palladium on carbon (5 wt % Pd/C) was added. The flask was connected to a balloon filled with H2 gas, and the reaction progress was monitored by 1H NMR until reaching 100% conversion. After completion, the reaction mixture was filtered and concentrated on a rotary evaporator. The residue was chromatographed on a 20 mm by 350 mm column packed with 300 mm height of silica gel using 12.5% ethyl acetate in hexanes to afford 0.26 g of colorless liquid butyrophenone as KIE sample 1.
By closely analogous procedures, KIE samples 2–5 were obtained with the reactions taken to 70, 73, 66, and 82% conversions, respectively.
Competition Reaction for the Substituent Effect.
A stock solution with 87 mg (0.60 mmol) of 5, 111 mg (0.61 mmol) of 18, and 18.3 mg of diphenylmethane (internal standard) was prepared, and the mixture was diluted with acetonitrile to 10.00 mL. A 2.0 mL aliquot of this solution was removed and diluted with acetonitrile to 8.00 mL solutions. This provided two 8 mL solutions with the latter four times as dilute as the former. A mixture of 210.4 mg (2.25 mmol) of LiBF4, 76.2 mg of 6, 23.8 mg (0.032 mmol) of Ru(bpy)3Cl2·6H2O, 18.3 mg of diphenylmethane (internal standard), 140.6 mg (1.08 mmol) of diisopropylethylamine, and 8 mL of acetonitrile was added to both solutions to make kinetics samples A and B.
The samples were irradiated side-by-side in identical tubes. During irradiation, 10-drop aliquots at 0, 10, 20, 30, 40, 50, 60, 90, 120, 180, and 240 min were taken. Each aliquot was added into a 2 mL CDCl3 solution and washed with distilled water twice. The organic layer was then dried and filtered into an NMR tube for kinetic measurements. As shown in Figure S5 in the Supporting Information, the product ratio of 19 to 7 was determined by the integration value of the middle peak from the two partially overlapping triplets from H on the α-carbon close to the aryl side. The integration ranges were kept the same across the series of spectra. The crude integration value was further divided by the total integral of 5, 7, 18, and 19. The results are shown in Table S1 in the Supporting Information.
Replicate data were obtained by an identical procedure, and the reported relative rate for 18/5 is based on the average of four results. The ratios obtained for the concentrated samples were 2.4 and 2.8, versus 2.2 and 2.3 for the dilute samples.
NMR Details for KIE Measurements.
NMR samples of 200 mg of recovered propiophenone or butyrophenone in 5 mm NMR tubes were filled to a constant height of 5 cm with CDCl3. The 13C NMR spectra were recorded at 125.7 MHz using inverse gated decoupling. The acquisitions used a 160 s (propiophenone) or a 125 s (butyrophenone) delay between calibrated π/2 pulses and a 7.55 s (for both propiophenone and butyrophenone) acquisition time to collect 524,288 points. Integrations were determined numerically using a macro. A zero-order baseline correction was generally applied, but to avoid any qualitative manipulation, no first-order or higher-order baseline was ever applied. The integration of the “internal standard” carbon (para in the case of propiophenone, methyl in the case of butyrophenone) was set at 1000, and the integrations of the other carbons are shown in Tables S3 and S4 in the Supporting Information. The NMR spectra for recovered materials were taken back-to-back with NMR spectra of the standard material from the same synthetic lot that had not been subjected to the reaction conditions, using the same NMR parameters, and the integrations for the standard materials are also shown in Tables S3 and S4 in the Supporting Information.
COMPUTATIONAL METHODS
The calculations of DFT structures, energies, and frequencies or CCSD(T) energies employed standard procedures in Gaussian 16.24 DLPNO-CCSD(T) energies were calculated using ORCA.25 Complete structures and energetics are provided in the Supporting Information. KIE calculations employed a modified version of the program QUIVER26 with frequencies scaled by 0.9614. No imaginary frequencies were found for minimum-energy structures, and all transition state structures exhibited exactly one imaginary frequency.
Supplementary Material
ACKNOWLEDGMENTS
We thank the NIH (Grant GM-45617) for financial support.
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.joc.1c00099.
Relevant spectra, results and details of the simulation of competition reactions, KIE results and calculations, NMR studies of lithium coordination, method validation studies, and calculated structures and energies (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).(a) Ischay MA; Anzovino ME; Du J; Yoon TP Efficient Visible Light Photocatalysis of [2+2] Enone cycloadditions. J. Am. Chem. Soc 2008, 130, 12886–12887. [DOI] [PubMed] [Google Scholar]; (b) Du J; Yoon TP Crossed Intermolecular [2+2] Cycloadditions of Acyclic Enones via Visible Light Photocatalysis. J. Am. Chem. Soc 2009, 131, 14604–14605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).(a) Felton GAN; Bauld NL Highly efficient, catalytic bis addition reactions of allyl phenyl sulfone to vinyl sulfones. Tetrahedron Lett. 2004, 45, 4841–4845. [Google Scholar]; (b) Yang J; Felton GAN; Bauld NL; Krische MJ Chemically induced anion radical cycloadditions: intramolecular cyclobutanation of bis(enones) via homogeneous electron transfer. J. Am. Chem. Soc 2004, 126, 1634–1635. [DOI] [PubMed] [Google Scholar]
- (3).((a)) For cycloaddition reactions via radical anion intermediates, see: (a) ref 2a 2b,.Hammerich O; Nielsen MF The Competition between the Dimerization of Radical Anions and their Reactions with Electrophiles. Acta Chem. Scand 1998, 52, 831–857.For cycloaddition reactions via radical cation intermediates, see: Redox-Tag Processes:(c) Okada Y; Chiba K Redox-tag processes: Intramolecular Electron Transfer and Its Broad Relationship to Redox Reactions in General. Chem. Rev 2018, 118, 4592–4630.
- (4).Du J; Skubi KL; Schultz DM; Yoon TP A Dual-Catalysis Approach to Enantioselective [2 + 2] Photocycloadditions Using Visible Light. Science 2014, 344, 392–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).(a) Kalyanasundaram K Photophysics, photochemistry and solar energy conversion with tris(bipyridyl)ruthenium(II) and its analogues. Coord. Chem. Rev 1982, 46, 159–244. [Google Scholar]; (b) Juris A; Balzani V; Barigelletti F; Campagna S; Belser P; von Zelewsky A Ru(II) polypyridine complexes: photophysics, photochemistry, eletrochemistry, and chemiluminescence. Coord. Chem. Rev 1988, 84, 85–277. [Google Scholar]
- (6).Prier CK; Rankic DA; MacMillan DWC Chem. Rev 2013, 113, 5322–5363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).(a) Huddleston RR; Krische MJ Enones as Latent Enolates in Catalytic Processes: Catalytic Cycloreduction, Cycloaddition, and Cycloisomerization. Synlett 2003, 0012–0021. [Google Scholar]; (b) Lee KN; Ngai M-Y Recent developments in transition-metal photoredox-catalysed reactions of carbonyl derivatives. Chem. Commun 2017, 53, 13093–13112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Singleton DA; Thomas AA High-Precision Simultaneous Determination of Multiple Small Kinetic Isotope Effects at Natural Abundance. J. Am. Chem. Soc 1995, 117, 9357–9358. [Google Scholar]
- (9).Ellingboe E; Fuson RC The 1,2-Dibenzoylcyclobutanes. J. Am. Chem. Soc 1934, 56, 1774–1777. [Google Scholar]
- (10).Bigeleisen J; Mayer MG Calculation of Equilibrium Constants for Isotopic Exchange Reactions. J. Chem. Phys 1947, 15, 261–267. [Google Scholar]
- (11).Bell RP The Tunnel Effect in Chemistry; Chapman & Hall: London, 1980; pp. 60–63. [Google Scholar]
- (12).Meyer MP; DelMonte AJ; Singleton DA Reinvestigation of the Isotope Effects for the Claisen and Aromatic Claisen Rearrangements. The Nature of the Claisen Transition States. J. Am. Chem. Soc 1999, 121, 10865–10874. [Google Scholar]
- (13).(a) Singleton DA; Nowlan DT; Jahed N; Matyjaszewski K Isotope Effects and the Mechanism of Atom Transfer Radical Polymerization. Macromolecules 2003, 36, 8609–8616. [Google Scholar]; (b) Plata RE; Singleton DA A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis-Hillman Reactions The Importance of Experimental Observations. J. Am. Chem. Soc 2015, 137, 3811–3826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Hirschi JS; Takeya T; Hang C; Singleton DA Transition-State Geometry Measurements from 13C Isotope Effects. The Experimental Transition State for the Epoxidation of Alkenes with Oxaziridines. J. Am. Chem. Soc 2009, 131, 2397–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Roh Y; Jang H-Y; Lynch V; Bauld NL; Krische MJ Anion Radical Chain Cycloaddition of Tethered Enones: Intramolecular Cyclobutanation and Diels–Alder Cycloaddition. Org. Lett 2002, 4, 611–613. [DOI] [PubMed] [Google Scholar]
- (16).(a) Eberson L; Shaik SS Electron-Transfer Reactions of Radical Anions: Do They Follow Outer- or Inner-Sphere Mechanisms? J. Am. Chem. Soc 1990, 112, 4484–4489. [Google Scholar]; (b) Larsen H; Pedersen SU; Pedersen JA; Lund H Self-exchange electron transfer rate constants and reorganization energies for some aromatic compounds in N,N-dimethylformamide determined by elect. J. Electroanal. Chem 1992, 331, 971–983. [Google Scholar]
- (17).(a) Marcus R A. Ion Pairing and Electron Transfer. J. Phys. Chem. B 1998, 102, 10071–10077. [Google Scholar]; (b) Savéant J-M Evidence for Concerted Pathways in Ion-Pairing Coupled Electron Transfers . J. Am. Chem. Soc 2008, 130, 4732–4741. [DOI] [PubMed] [Google Scholar]
- (18).Loutfy RO; Loutfy RO Correlation between the n,π* Triplet Energy of some Acetophenones and the Corresponding Electroreduction Potentials. Tetrahedron 1973, 29, 2251–2252. [Google Scholar]
- (19).Bordwell FG; Cornforth FJ Application of the Hammett Equation to Equilibrium Acidities of Meta- and Para-Substituted Acetophenones. J. Org. Chem 1978, 43, 1763–1768. [Google Scholar]
- (20).Saettel NJ; Wiest O; Singleton DA; Meyer MP Isotope Effects and the Mechanism of an Electron-Transfer-Catalyzed Diels-Alder Reaction. J. Am. Chem. Soc 2002, 124, 11552–11559. [DOI] [PubMed] [Google Scholar]
- (21).Bugarin A; Jones KD; Connell BT Efficient, Direct α-Methylenation of Carbonyls Mediated by Diisopropylammonium Trifluoroacetate. Chem. Commun 2010, 46, 1715–1717. [DOI] [PubMed] [Google Scholar]
- (22).Staudinger H; Bereza S Zur Kenntnis Der Ketene. Einwirkung von Diphenylketen Auf Chinone. Justus Liebigs Ann. Chem 1911, 380, 243–277. [Google Scholar]
- (23).Manjolinho F; Grünberg MF; Rodríguez N; Gooßen LJ Decarboxylative Allylation of Glyoxylic Acids with Diallyl Carbonate. Eur. J. Org. Chem 2012, 2012, 4680–4683. [Google Scholar]
- (24).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ Gaussian 16; Revision C.01, Gaussian, Inc.: Wallingford CT, 2016. [Google Scholar]
- (25).Neese F. Software update: The ORCA program system, version 4.0. Wiley Interdisciplinary Reviews: Computational Molecular Science; 2018, 8 (1) e1327. [Google Scholar]
- (26).Saunders M; Laidig KE; Wolfsberg M Theoretical calculation of equilibrium isotope effects using ab initio force constants: application to NMR isotope perturbation studies. J. Am. Chem. Soc 1989, 111, 8989. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



