Stock market comovements: Evidence from the COVID-19 pandemic

Abstract

The COVID-19 pandemic shock has harmed the US and East Asian stock markets. Focusing on measuring the inherent correlation, this paper employs a GARCH-Copula CoVaR approach to address the debate on the extreme risk spillovers from the US to China, Japan, Hong Kong, and South Korea stock returns. The results show a large spillover effect from the US to East Asian stock markets. Compared to the tranquil period, these spillovers become stronger in the COVID-19 period. The findings show that indirect spillovers on the Chinese stock market are heavier than direct spillovers, and impacts deluge only via Hong Kong. The study contrasts spillover’ features of the US COVID-19 shock and the Chinese 2015 crisis. These findings provide useful support for policymakers and risk managers involved in the East Asian stock markets.

1. Introduction

During the recent global pandemic crisis, financial integration has increased the countries' vulnerability to financial crises originating elsewhere. In East Asia, the transmission of financial distress in the real economy evolved at record speed, with tighter credit standards and sagging confidence hitting business investment and household demand. The COVID-19 shock created a highly volatile period in the US stock market and seemed to be implicated in turmoils among East Asian countries. Investigating the risk contagion of the US stock market return to East Asian markets would be an interesting topic full of practical implications. The analysis of this issue can be used by policymakers in planning the recovery strategies from this crisis (Evgenidis, Tsagkanos, & Siriopoulos, 2017). While for investors, the results of this paper should provide additional information for the creation of a trading strategy able to outperform the market.

The drivers of contagion literature are multiple and have influenced the approaches used by the researchers to understand financial contagion. Siriopoulos et al. (2021) suggest that the increased bilateral trade exchange as a channel risk transmission, the effect of VIX, and the international uncertainty are determinants of the volatility of European stock markets. The authors' estimations show that about 34% of the volatility in European stock markets is due to the Chinese stock market, while 7% is due to international uncertainty, as measured by VIX. Their findings also support the view that COVID-19 is more like a systematic risk. They conclude that the European stock market faced two risk elements: the first is the transmission volatility from the Chinese stock market, and the second is the international uncertainty. Eichengreen et al. (1996) discussed various channels of contagion in foreign exchange markets, highlighting the role of trading linkages between countries and speculative attacks on the international competitiveness of the countries. Forbes and Rigobon (2002) discuss three different mechanisms of international shock propagation: (i) aggregate shocks which affect the economic fundamentals of more than one country; (ii) country-specific shocks which affect the economic fundamentals of other countries; (iii) shocks which are not explained by fundamentals and are categorized as pure contagion. Bekaert et al. (2011) examined six different categories of international information transmission channels: (i) international banking sector links at the country level; (ii) country-specific policy responses to the crisis; (iii) trade and financial linkages; (iv) information asymmetries and informational flows; (v) domestic macroeconomic fundamentals; (vi) “investor contagion” caused by herding behavior. They proposed an international three-factor model including the US factor, a global financial factor, and a domestic factor. Two hypotheses have been tested, first, ‘globalization hypothesis’, i.e. countries that are highly integrated globally, through trade and financial linkages, are more susceptible to the crisis shock and, second, “wake-up call’ hypothesis, which suggests that a crisis initially restricted to one market segment or country provides new information that may prompt investors to reassess the vulnerability of other market segments or countries, which spreads the crisis across markets and borders”.

COVID-19 can be considered a “black swan” event: a situation that has never previously occurred and which caused existing risk management models to fail to adequately evaluate the risk. While it is challenging to predict the scale of the economic consequences of the COVID-19 crisis, we believe that previous literature already contains some answers and approaches that can be used to analyze the financial effects of the current pandemic.

This study highlights three main causes for a potential contagion from the US stock market to East Asian countries. First, the COVID-19 pandemic has resulted in panic as well as the temporary closure of businesses in most economies with confirmed positive coronavirus cases. These reactions are bound to affect the performance of the businesses in these economies as well as their stock market dynamics. As long as the coronavirus is contagious and migrations exist, this virus is capable of affecting many economies of the world and their stock markets simultaneously. Second, the US economy has faced a serious shock, the recent oil price slump. The combination of these two problems, COVID-19 shock, and oil price slump, will likely initiate a long-term economic downturn and drive the US economy into the next recession. During the period from 24 February to 24 March, the US economic policy uncertainty as gauged by the news-based Economic Policy Uncertainty index has shown a jump going from 100 to 400. Third, possible reasons for contagion could also be explained in terms of the strong economic trade link between the USA and Asian economies and the problem of contagion is more macroeconomic than financial (Bauer et al., 2006). The adverse contagion effect of the COVID-19 is then aggravated through these strong economic relationships. In this study, the three causes of contagion from the US to East Asian stock markets seem to be fulfilled.

This paper focuses on the spillover effects and the patterns of time-varying correlations between the realized volatility of the US stock market and the realized volatility of stock market returns of four economies, namely China, Hong Kong, Japan, and South Korea. We recognize that the interdependency between markets that exists in all economies does not necessarily act as the mechanism vehicle for the contagion effect. The hypothesis in the literature of market contagion, which suggests that periods of financial crisis generate large return connectedness among stock markets drives the raising of our issue. Dealing with the contagion hypothesis of stock markets is not an easy task as highlighted in Pragidis et al. (2015). The authors examine the contagion effects during the Greek financial crisis and recognize that the rejection or acceptance of the contagion hypothesis is a very complicated task since there are several possible channels of contagion. Our paper shares a similar point of view and investigated perceived difficulty to deal with the contagion hypothesis. We mainly concentrate on the part of the literature that tests the hypothesis of contagion in a correlation framework and tries to correct some of the existing statistical issues.

Drawing on the above literature, this paper hypothesizes the presence of contagion effect of the US stock market to East Asian stock markets in the COVID-19 period. The build hypothesis is founded on the work of Philippas and Siriopoulos (2013) who distinguished between three types of contagion, the “wake-up-call” contagion in which the crisis initially restricted to one country, providing new information that prompts investors to reassess the default risk of other countries, the “shift” contagion that occurs when the normal cross-market channel intensifies after a crisis in one country with increased sensitivity to global risk factors instead of country-specific factors and, the “pure” contagion which covers any instance of contagion that is completely unrelated to the level of fundamentals. In our case, the US spillovers to East Asian countries may be driven by the first and the third types of contagion suggested by Philippas and Siriopoulos (2013).

This study aims to contribute to the still-developing debate regarding the causes of stock markets contagion by testing the dependence structure for a new data set of incidences of contagion. Much of the research thus far has focused on one financial market crisis of the past decade. By expanding the number of crisis events, the 2015 China crisis, and the US-COVID-19 shock, to be tested, this paper establishes a larger data set to interrogate. Therefore, our study innovates and contributes to filling some existing gaps in the literature in at least three dimensions. First, we introduce a novel comparison of the transmission of contagion by making a distinction between a direct and indirect contagion effect. If the stock market in economy A has linkages to the stock market in economy B, there may be spillovers in the stock market of economy B. Further, the stock market in economy C that is connected to the stock market in economy B, may be influenced by direct impacts from B or indirect influence by the policy from A. This study examines the direct effect of the US contagion on East Asia economies and also the indirect effect, for which the spillovers are transmitted via a channel country. For instance, this study determines that the US spillovers on the Chinese stock market deluge only via Hong Kong. Second, we use an extensive sample that covers all recent major economic events, including the China crisis (2015) and the US COVID-19 crisis (2019). The period of 2015–2020 is very significant for addressing the issue of spillover effect. In this period, there are two special crises: the 2015 Chinese stock market crash caused by deleveraging effects and the 2020 US stock market drop due to the COVID-19 shock. A major contribution of our study is to examine jointly the US COVID-19 shock and China 2015 crises. It is relevant to examine whether and how the effects of financial stress are transmitted to others and differ in times of financial instability. Therefore, our model can differentiate between different states of the economy (lower volatility/normal periods and higher volatility/turmoil periods), by allowing us to control for the asymmetric adjustment of the stock market's returns to its equilibrium value (Tsagkanos & Siriopoulos, 2015). In addition, we highlight and compare possible asymmetries in the long-run equilibrium mechanisms across different developed economies by employing our framework in five major world economies that have been largely affected by the recent pandemic diseases; these are, the US, China, Japan, Hong Kong, and South Korea. Third, the deficiency of previous studies is that it is difficult to accurately grasp the direction of risk diffusion in different periods and to depict the intensity of risk contagion constantly. Even though a strand of the literature has recently examined the impact of the COVID-19 medical shock on financial markets, the way causal links among stock markets shifted from the pre-COVID-19 tranquil period to the COVID-19 crisis one remains unexplored.

This study has the merit of performing a sound empirical examination employing a modified Iterative Cumulative Sum of Squares (ICSS) algorithm to detect underlying structural breaks in the unconditional variance of stock returns. The span of the periods of instability is decided according to the identified breaks. The dynamic Copula model can better describe the dynamic and asymmetric dependency structure, overcome the drawbacks of the traditional model, and obtain dynamic lower tail coefficients based on static lower tail coefficients, which can effectively depict the risk of infection over a long time (Granger & Lee, 1989). Such sound empirical specifications constitute an innovative approach of this study compared with previous studies. In terms of the modeling approach, our research is broadly linked to the studies of Shahzad et al. (2018) and Xiao (2020) who employed copula and CoVaR models to investigate the spillover effects, systemic and tail dependence risks of some stock markets indexes. We also employ multivariate copula to model the dependency structure of the East-Asian and the US stock markets. The dependency structures are used to identify risk spillovers (Adrian & Brunnermeier, 2016; Fang et al., 2021; Shahzad et al., 2021). The robustness of the spillover effect is verified through the bootstrap Kolmogorov-Smirnov (KS) test used by several scholars (Bernal et al., 2014; Reboredo & Ugolini, 2015). Based on these useful empirical results, we analyze the differences in the risk spillovers. In addition to the above-mentioned contribution to existing literature, this paper has chosen a key analysis period. Finally, to confirm our findings, we conduct robustness checks for our baseline results by plotting curves of the C-vine copula quantile regression.

Our empirical findings highlight greater downside spillover effects from the US to East Asian stock markets, particularly throughout the COVID-19 period. The conditional spillovers are significant and confirm strong links. Besides, the indirect spillover effect of the US stock market on the Chinese stock market is more significant than the direct spillover. We find a strong dependence of the Chinese stock market on the fluctuations in the US stock market, especially when China controls transactions in Hong Kong. The results offer important evidence on the differences in the risk spillovers. First, the Chinese stock market exerted direct and indirect spillovers to East Asian stock markets throughout the tranquil period. However, the direct contagions are reduced, and the indirect effects become insignificant during its period of instability. Second, the contagion of the US to East Asian stock markets is distinct from that of the Chinese market because of dependent structures with other stock markets, especially in indirect dependency during the tranquil period. In addition, the contagion of the US stock market to East Asia is exacerbated during the period of instability due to the COVID-19 shock. The extreme joint behavior of the series analyzed shows rather high tail dependence coefficients. We also document an asymmetric feature underlying these extreme comovements. Another striking feature is the generally higher coefficients observed in the lower tail dependences in comparison with those in the upper tail dependences. A Wald test is performed to analyze the tail symmetry hypothesis. We find that an asymmetric feature characterizes the tail dependence dynamics in each market.

This paper is organized as follows: Section 2 presents data and preliminary analysis. Section 3 introduces the GARCH-Copula-CoVaR model specifications. Section 4 analyzes and discusses the empirical findings, along with robustness checks. Section 5 concludes.

2. Data analysis

The selected stock markets for analysis include the Standard & Poor's Index (S&P 500, US), the Shanghai Shenzhen Index (CSI 300, China), the Hang Seng Index (HS, Hong Kong), the Nikkei Index (N225, Japan), and the KOSPI Composite Index (KS, South Korea). These stock indexes describe their market shifts. This data1 is sourced from Yahoo Finance, covering January 1, 2015–October 20, 2020.

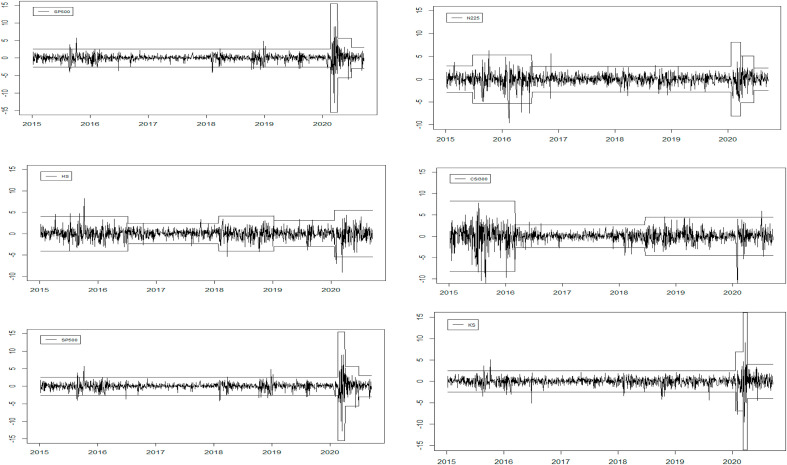
In Fig. 1 , the index returns reflect the volatile dynamics of the stock markets. In Table 1 , the underlying volatility structural points of stock markets are identified by the modified ICSS algorithm. During the 2015 period of instability in the Chinese stock market, the crisis occurred, and the CSI 300 Index slumped about 2000 points from 5353 to 3354 within three months. In this period, all stock markets presented an interval of intensive volatility, and the Japan and Hong Kong stock markets displayed stronger volatility groupings than the other stock markets. Moreover, the Hong Kong stock index exhibited the strongest co-movement over the stock market of China. In this respect, the high integration means that the stock market of China would affect neighbors’ Asian countries through Hong Kong. For the period of instability in the Chinese stock market, the COVID-19 outbreaks and panic of the pandemic spread across the globe. In this period, the US stock market crash exacerbated the collapse of other stock markets under the panic shocks. China was able to contain the rapid spread of infection, and its stock market rebounded from January 21, 2020, when the US stock market started to slump (Zehri, 2020b). However, the recovery only lasted for several days and stopped while the US stock market was crashing. Without a doubt, the Chinese stock market was susceptible to the risk contagion that the massive spillovers of the US stock market collapse caused. In this period of instability, the extreme sentiment overwhelmed all stock markets. Compared to the instability period of the Chinese stock market, this period indicated stronger and more expansive co-movement among stock markets. Based on the results of Table 1, the causality is tested, for the US stock market contagion, distinguishing a tranquil pre-crisis period (from January 2, 2019 to December 30, 2019) and a COVID-19 crisis period (from December 31, 2019 to June 30, 2020). For China, we distinguish a crisis period (from June 12, 2015 to February 6, 2016), and a tranquil pre-crisis period (from January 1, 2015 to June 10, 2015).

Fig. 1.

Total return indexes volatility.

Table 1.

Structural breaks in volatility.

	USA	China	Hong Kong	Japan	South Korea
	SP500	CSI300	HS	N225	KS
P1	2 Jan., 2015	5 Jan., 2015	5 Jan., 2015	4 Jan., 2015	4 Jan., 2015
	−2 Mar., 2016	−21 Feb., 2020	−9 Jul., 2016	−23 Jun., 2016	−20 Jan., 2020
P2	3 Mar., 2016	21 Feb., 2020	9 Jul., 2016	26 Jun., 2016	23 Jan., 2020
	−14 Jun., 2018	−6 Apr., 2020	−28 Jan., 2018	−12 Jul., 2016	−11 Mar., 2020
P3	14 Jun., 2018	7 Apr., 2020	29 Jan., 2018	13 Jul., 2016	12 Mar., 2020
	−18 Sept., 2020	−2 Jul., 2020	−7 Jan., 2019	−22 Jan., 2020	−9 Apr., 2020
P4			21 Jan., 2020	26 Mar., 2020
			−19 Sept., 2020	−18 Jun., 2020
P5				17 Jun., 2020
				−16 Sept., 2020

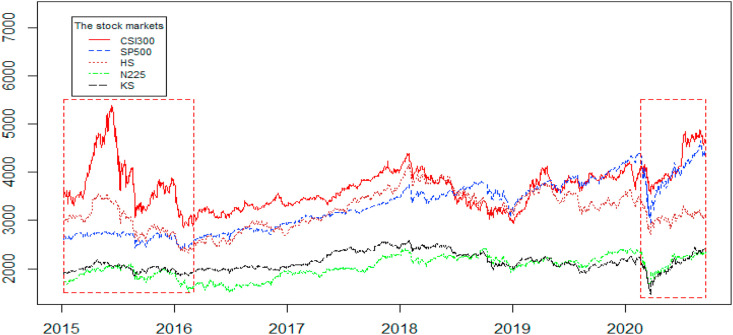
In Fig. 2 , two special periods are noted in terms of high volatility clustering (the Chinese and US stock markets drops). From a visual perspective, the tranquil period is more stable than the two special periods. As for relative comparison, the tranquil period and the COVID-19 period will be used in the empirical analysis.

Fig. 2.

Evolution of stock markets indices.

The left and right red frames represent periods surrounding the Chinese and US stock markets during the crisis, respectively. Assuming the spillover effect of Chinese stock markets on neighboring Asian countries is obvious, this paper focuses more on the US stock market collapse (during the COVID-19 period).

All stock markets indeed displayed strong co-movement during these two special periods. Regarding the period of instability in the US, all markets displayed two similar trends. The first trend is an abrupt fall that reflected the spread of panic contagion across stock markets. The second trend is a successive rebound that demonstrated that investor confidence recovered from the situation that was improved by a series of quantitative policies. These findings reflect the Chinese and the US stock market have strong contagion on the East Asian countries throughout their periods of instability. However, the corresponding effects would be different. Studying the dependence structure of different periods is important because risk management and investment strategy depend on underlying volatility, dependency, and contagion differences. The spillovers in the periods of instability have more meaningful policy implications due to the special features. Figs. 1 and 2 show volatile clustering and progress, which demonstrates that using a conditional variance model is appropriate.

Table 2 reports the linear dependency of the stock market indexes. The coefficients of correlation show differences between the two types of periods. The periods of instability exhibit special characteristics compared to the tranquil period. More specifically, the correlation of any market with the US during the tranquil period is over 0.35. However, we find the correlation of the Hong Kong market with the Chinese market is stronger than the Chinese market with other markets. This evidence demonstrates that the Hong Kong stock market is greater linked to the Chinese market. In the light of this finding, the extreme downside risk from the Chinese market would spill over to the other markets via Hong Kong. In addition, the correlations of other markets during the Chinese period of instability decreased, compared to the tranquil period. It may hint at the differences in the dependency structure during this special period. COVID-19 attacked almost all countries throughout the world and brought enormous shock.

Table 2.

Pearson correlation coefficients.

Correlation	CSI300	SP500	HS	N225	KS
The tranquil period
CSI300	1.0000	–	–	–	–
SP500	0.4013	1.0000	–	–	–
HS	0.5978	0.5792	1.0000	–	–
N225	0.3466	0.6123	0.5172	1.0000	–
KS	0.4068	0.7073	0.633	0.6071	1.0000
The COVID-19 period
CSI300	1.0000		–	–	–
SP500	0.6389	1.0000		–	–
HS	0.7139	0.5962	1.0000		–
N225	0.4821	0.6966	0.5546	1.0000
KS	0.6112	0.792	0.7098	0.7044	1.0000

Notes: Pearson's correlation coefficient reflects linear relationships of the markets.

3. A GARCH-copula-CoVaR approach

Value-at-Risk (VaR) is the most common and useful method to measure the risk of an individual institution in isolation. However, the VaR of a single institution cannot necessarily reflect systemic risk when the whole financial system stability is threatened. To emphasize systemic risk measurement, Adrian and Brunnermeier (2016) add the prefix “Co” to VaR risk measure, namely CoVaR, which represents conditional, contagion, or co-movement (Sun et al., 2020).

The GARCH model presented by Nelson (1991) catches irregular shocks to instability. We define the GARCH (1,1) model with structural breaks as follows:

$$r_t=\mu +\rho r_{t-1}+{\epsilon }_t,{\epsilon }_t=h_t{z}_t$$

$$\ln \left(h_t^2\right)=\omega +d_1{P}_1+\dots +d_n{P}_n+\alpha \left[\left|z_{t-1}\right|-E\left|z_{t-1}\right|\right]+\gamma z_{t-1}+\beta ln\left(h_{t-1}^2\right)$$

In this model, $\mu$ is mean and $h_t$ is conditional variance. $z_t$ is an autonomous random variable. $\alpha$ designate the magnitude impact that means a relevant impact on instability, and $\gamma$ determine the direction of effect that identifies unequal impacts on instability. Favorable shocks to instability are defined by the total of coefficients $\alpha$ + $\gamma$, conditional on the event that the innovation ${\epsilon }_t$ is bigger than zero or not; the harmful shocks, $\alpha$ - $\gamma ,$ alternatively. Following Ewing and Malik (2010) and Rapach and Strauss (2008), $P_1,\dots .,P_n$ are multiple dummy variables with the value ‘1’ when the variance process owns a structural change.

In this framework, the VaR at the quantile $\tau$ is defined as:

$$\text{P}\left(y\le Va{R}_{\tau }\right)=\tau$$

$$Va{r}_{\tau }^y={\text{F}}^{-1}\left(\tau \right)$$

The conditional VaR (CoVaR) of Y given X = x is given by:

$$F_{Y|X=x}\left(CoVa{R}_{\tau }^{y|x_1}\right)=P\left(Y\le CoVa{R}_{\tau }^{y|x_1}|X_1=x_1\right)$$

and the conditional copula quantile is defined as:

$$CoVa{R}_{\tau }^{y|x_1}=F_y^{-1}\left(C_{V|U_1}^{-1}\left(\tau |u_1\right)\right)$$

In this formula, $CoVa{R}_{\tau }^{y|x_1}$ is the quantile $\tau$ of the variable ‘y’ conditional on variable ‘x₁.’ The conditional copula quantile regression can be employed in measuring spillover effects as the explanatory variable has a crucial role in the CoVaR. The risk spillovers from one market to the other can be computed through the estimated conditional copula quantile equation. The risk spillovers measure how one market in crisis has a contagion effect on another.

In that case, the PIT of argument X ₁ is equal to a lower probability. The significance level of its VaR can represent the probability of its crisis. The corresponding conditional copula quantile formula is defined as:

$$CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(\beta \right)}=F_y^{-1}\left(C_{V|U_1}^{-1}\left(\tau |\beta \right)\right)$$

In this formula, $F_{x_1}^{-1}\left(\beta \right)$ is the inverse distribution function of X₁. The market X₁ is in a turmoil state if β takes ${\text{Fx}}_1\left({\text{VaR}}_{\mathrm{\beta }}^1\right)$. On the contrary, the market X₁ is in a normal state if β takes ${\text{Fx}}_1\left({\text{X}}_{0.5}^1\right)$, for ${\text{X}}_{0.5}^1$ is the median value of X₁.

To determine the contagion effects of one financial market on another we draw on the approach of Shahzad et al. (2018) and Xiao (2020). In these studies, relative spillover effects are measured as follow:

$$\Delta {\text{CoVaR}}_{\tau }^{y|x_1}=(CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(\beta \right)}-CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right)})/CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right)}$$

$$\Delta {\text{CoVaR}}_{\tau }^{y|x_1,x_2}=(CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(\beta \right),x_2}-CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right),x_2})/CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right),x_2}$$

We use the KS test, developed by Abadie (2002), to assess the occurrence of spillovers.

$$K{S}_m={\left(\frac{mn}{m+n}\right)}^{\frac{1}{2}}su{p}_x\left|F_m\left(x\right)-G_n\left(x\right)\right|$$

where $F_m\left(x\right)$ is the cumulative CoVaR distribution functions in an intense condition and $G_n\left(x\right)$ in regular condition. m and n are the two samples size.

To establish the presence of contagion across the institutions, the estimated ΔCoVaR could be compared for different pairs of financial institutions ‘y’ and ‘x₁’ or ‘x₂’. We then evaluate whether the stock market ‘y’ can affect the stock market ‘x₁’ and ‘x₂’, i.e, we test whether stock market contagion risk is statistically significant. Technically, this implies running a formal test of significance with null hypothesis H₀. We test the rejection of the following null hypothesis.

$$H_0^1:\Delta {\text{CoVaR}}_{\tau }^{y|x_1}=0$$

$$H_0^2:\Delta {\text{CoVaR}}_{\tau }^{y|x_1,x_2}=0$$

or,

$$H_0^1:CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(\beta \right)}=CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right)}$$

$$H_0^2:CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(\beta \right),x_2}=CoVa{R}_{\tau }^{y|x_1=F_{x_1}^{-1}\left(x_{0.5}^1\right),x_2}$$

The rejection of the null hypothesis, given by a very low p-value, indicates that a given “institution” y (i.e., the US stock market) generates contagion risks.

4. Results and discussion

4.1. Volatility of the return indexes

The GARCH (1,1) is used to examine the volatility of our five return indexes. The empirical estimation of the GARCH model with structural breaks is reported in Table 3 .

Table 3.

The estimated parameters.

	USA	China	Hong Kong	Japan	South Korea
	SP500	CSI300	HS	N225	KS
$\mu$	0.0393**	0.0398**	0.02778	0.0403	0.0183
	(0.0170)	(0.0192)	(0.0195)	(0.0306)	(0.0287)
$\rho$	−0.0799***	−0.0154	−0.0034	0.0195	−0.0194
	(0.0307)	(0.0292)	(0.1577)	(0.0241)	(0.0291)
$\omega {\times }^{10000}$	−0.0514***	0.1874***	0.0982***	0.0157	−0.1876***
	(0.0081)	(0.0627)	(0.0117)	(0.0359)	(0.0353)
$\alpha$	−0.3234***	−0.0856***	−0.1327***	−0.2078***	−0.1491***
	(0.0412)	(0.0193)	(0.0199)	(0.0195)	(0.0289)
$\beta$	0.8255***	0.7358***	0.8121***	0.7354***	0.5413***
	(0.0204)	(0.0297)	(0.0392)	(0.0307)	(0.0874)
$\gamma$	0.0931***	0.1529***	0.0594	0.0257	0.2205***
	(0.0118)	(0.0291)	(0.0399)	(0.0355)	(0.0421)
P1	0.2458***	−0.2907***	−0.1859***	0.1521***	0.2294***
	(0.0526)	(0.0617)	(0.0499)	(0.0397)	(1.7665)
P2	0.1419***	−0.2069***	0.0305	−0.0343*	1.7916***
	(0.0271)	(0.0322)	(0.0181)	(0.0216)	(0.4516)
P3	0.1549***	–	−0.2055***	0.2745***	0.4522***
	(0.0165)		(0.0409)	(0.0914)	(0.1093)
P4	–	–	0.1374***	0.1594***	–
			(0.0215)	(0.0514)
P5	–	–	–	−0.0878***	–
				(0.0246)
Q2(20)	11.631	9.9585	13.372	14.131	18.852
	[0.967]	[0.8734]	[0.9012]	[0.6985]	[0.5172]
ARCH (20)	0.4914	0.4125	0.7025	0.8257	0.9292
	[0.8791]	[0.9547]	[0.8269]	[0.6837]	[0.5492]
AIC	2.3944	3.3976	3.1082	2.9590	2.5809
BIC	2.3982	3.3877	3.1458	3.0004	2.6147
LL	−1588.673	−2412.363	−2124.827	−2037.975	−17.588
BDS	−1.1125	−0.1878	0.8245	0.5908	−0.8531
	[0.3175]	[0.8277]	[0.4575]	[0.5107]	[0.3295]

Notes: Lagrange Multiplier test for heteroskedasticity is the ARCH (20). Ljung-Box Q-statistics of order 20 is the Q² (20). The fitting of models is tested by the Akaike information criterion, Bayesian information criterion, and Log-likelihood noted AIC; BIC; and LL, respectively. *** **and *denote significance at 1%, 5% and 10%, respectively. The hypothesis that series are i.d.d is tested through the BDS test. Round brackets are used for the standard errors and square brackets for p values.

The parameter $\beta$ reflects volatility persistence. In general, $\beta$ is close to 1 but it decreases to some extent when the structural breaks are incorporated into the models. For all series, the parameter $\gamma$ is significant at 1% level for China, the US, and South Korea markets, which indicates the existence of leverage effect. One might even say, favorable shocks are bigger compared to unfavorable ones, reflecting the strong stimulation exerted by the fall in prices on stock markets. Structural breaks detected through the modified ICSS method are significant. The detected breakpoints indicate that the volatile dynamics of the stock markets vary with some financial events. The fitting quality of the models is verified according to the values of AIC, BIC, and LL. Likewise, there are no ARCH effects through the values of Q2 (20) and ARCH (20) tests. the filtered residuals are i.d.d based on the BDS test. All these diagnostic tests attest to the model specification robustness.

4.2. Volatility spillovers

Based on the PIT data, we estimated the dependency structure for the tranquil and the COVID-19 periods. The estimated copulas were selected according to the best AIC value. The pair copulas indicated unconditional and conditional dependency among stock markets. Correlation differences reported in Table 4 confirm the heterogeneity of the dependency structure during the two types of periods. The direct dependency in Table 4 is showing through only two indexes, for example, CSI300 HS displays a direct dependency of Hong Kong and China stock markets. The indirect dependency relates three indexes together, for example, CSI300 SP500|HS, show the indirect dependency of China and the US stock markets via Hong Kong. In other words, the transmission of contagion from China to the US passed through Hong Kong, the symbol ‘|’ refers to the indirect dependency.

Table 4.

Estimates for copula parameters.

Direct dependency					Indirect dependency
China spillover effect	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300
	HS	CSI300	N225	KS	SP500|HS	N225|HS	KS|HS
The tranquil period
Copula Name	T	Normal	Normal	Normal	C	C	C
Para1	0.59	0.34	0.32	0.36	0.06	0.03	0.07
	(0.02)	(0.02)	(0.02)	(0.02)	(0.03)	(0.02)	(0.03)
Para2	13.63	–	–	–	–	–	–
	(4.98)
Tau	0.43	0.27	0.23	0.26	0.02	0.02	0.03
AIC	−631.73	−197.05	−139.19	−220.2	−1337.55	−987.24	−1218.34
LL	−2.25	−087	−1.97	−1.75	−3.59	–	–
The 2015 crisis
China spillover effect	SP500	SP500	SP500	SP500	SP500	SP500	SP500
	HS	CSI300	N225	KS	CSI300|HS	HS|KS	KS|N225
Copula	Normal	Normal	Normal	Normal	C	Normal	Normal
Para1	0.59	0.36	0.36	0.29	−0.16	0.02	−0.04
	(0.03)	(0.03)	(0.04)	(0.04)	(0.09)	(0.07)	(0.04)
Para2	–	–	–	–	–	–	–
Tau	0.37	0.27	0.21	0.15	−0.05	0.02	−0.02
AIC	−107.84	−214.58	−28.4	−25.18	−238.03	−185.12	−201.68
LL	−0.61	-.27	−0.67	−0.85	−1.27	−5.12	−6.24

Direct dependency					Indirect dependency
US spillover effect	SP500	SP500	SP500	SP500	SP500	–	–
	HS	CSI300	N225	KS	CSI300|HS
The tranquil period
Copula Name	T	Normal	t	t	Normal	–	–
Para1	0.62	0.29	0.58	0.59	0.07	–	–
	(0.02)	(0.02)	(0.02)	(0.02)	(0.03)
Para2	13.23	–	12.46	7.84	–	–	–
	(5.61)		(4.51)	(2.36)
Tau	0.43	0.25	0.45	0.31	0.02	–	–
AIC	−624.73	−199.05	−597.99	−523.2	−1137.55	–	–
LL	−2.25	−087	−1.97	−1.75	−3.59	–	–
The COVID-19 period
US spillover effect	SP500	SP500	SP500	SP500	SP500	SP500	SP500
	HS	CSI300	N225	KS	CSI300|HS	HS|KS	KS|N225
Copula	Normal	Normal	t	RG	F	G	Normal
Para1	0.59	0.48	0.57	1.31	0.41	1.31	0.37
	(0.04)	(0.04)	(0.03)	(0.09)	(0.12)	(0.07)	(0.04)
Para2	–	–	6.17	–	–	–	–
			(3.51)
Tau	0.38	0.40	0.38	0.42	0.18	0.11	0.21
AIC	−61.84	−29.58	−65.4	−76.18	−124.03	−174.12	−184.68
LL	−0.61	-.27	−0.67	−0.85	−1.27	−5.12	−6.24

Notes: Copula Name: t: Student(t); N: Normal; F: Frank; C: Clayton; RG: Rotated Gumbel G: Gumbel. symmetric dependence is defined by Normal and Frank copulas, the other copulas for asymmetric dependence. Para₁ and Para₂ denote the evaluated copula parameters. Kendal's coefficient is presented by ‘Tau’. LL is the Log-Likelihood.

AIC is Akaike information criteria. the best copula fit is identified by lower values of AIC and LL.

Considering the tranquil period, we find a symmetric direct correlation of the Chinese stock market to the neighbors’ East Asian stock markets. In light of Kendal values, the dependency between the Hong Kong and Chinese markets is the strongest (0.43). In indirect dependency, the Chinese conditional on the Hong Kong market is positively correlated with the other markets. There exists an indirect link between the Chinese and the other markets through Hong Kong.

For the period of instability in the Chinese stock market, the direct structures are similar to the tranquil period. However, the indirect dependency of other stock markets and the Chinese market have changed these values from positive to negative or decreased them slightly. The evidence of the indirect dependency shows that the Chinese market is correlated with other East Asian markets through the Hong Kong market.

In another case, the estimated copulas for the tranquil period in the US market showed obvious differences compared to the tranquil period of the Chinese market. As for the direct correlation, the larger correlation values highlighted stronger dependency in extreme situations. In addition, the conditional copulas demonstrate that Hong Kong is a bridge linking the US market with the Chinese market. This finding is significantly different from the results of the tranquil period in China. The period of instability in the US market is very special because of the major crisis that occurred. Subsequently, the dependency structure among the stock markets changed under the huge risk shock, compared with the tranquil period. The estimated copulas show novel situations in terms of the dependency structure. In the direct case, the dependency of other markets on the US market is greater than in other periods according to Kendal's values. In this case, the finding is different from the instability of the Chinese market, as this period involves a more expansive and severe risk contagion. Furthermore, the indirect dependency structure indicates that the stock markets are interwoven. In this situation, the US market dependent on South Korea, Japan, and Hong Kong stock markets is correlated with Chinese, Hong Kong, and South Korea markets, respectively. In this period, their multivariate system became so complicated under the big shock. This case reflects the risk contagion caused by the extreme panic spreads across the global financial market. The risk spillovers in this period are massive. In the next section, we will compute risk spillovers based on these important dependency structures.

Following the copula model, CoVaR is used to evaluate the dependency relationships that may exist between stock markets. This approach has the merit to define the tail-dependence and intense contagion risk. The CoVaR has been broadly used in the economic and financial areas (Jian et al., 2018; Jin, 2018). We apply CoVaR to evaluate contagion from the US to East Asian stock markets returns. The ΔCoVaR is also an alternative measure used to detect eventual contagion risk. It measures the disparity among the VaR for East Asian stock market returns contingent on an intense shift of the US stock market returns and the VaR for East Asia contingent on a regular circumstance (mean values). The risk spillovers based on the estimated copulas are computed through the CoVaR approach. Table 5 reports the results of the CoVaR and ΔCoVaR across stock markets.

Table 5.

The BTKS tests of asymmetric risk spillover (CoVaR and ΔCoVaR measurements).

Direct dependency					Indirect dependency
China spillover effect	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300
	HS	SP500	N225	KS	SP500|HS	N225|HS	KS|HS
The tranquil period
CoVaR	−3.729	−2.4169	−2.1282	−2.2048	−1.2695	−1.7195	−1.4395
	(2.5121)	(2.5287)	(1.0984)	(1.4155)	(1.6543)	(1.1243)	(1.4243)
ΔCoVaR	1.2830	0.8619	0.4982	0.6458	0.3287	0.1487	0.3147
	(0.1541)	(0.0068)	(0.0065)	(0.0121)	(0.3154)	(0.0644)	(0.1846)
BTKS	0.4123	0.6854	0.5497	0.8733	0.1856	0.1486	0.3956
	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]
The 2015 crisis
	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300	CSI300
	HS	SP500	N225	KS	SP500|HS	N225|HS	KS|HS
CoVaR	−3.312	−2.2592	−3.4962	−1.708	−1.2071	−2.1192	−1.0463
	(0.4102)	(0.6126)	(11339)	(0.2956)	(1.8164)	(1.1535)	(0.6916)
ΔCoVaR	0.8743	0.5137	0.8137	0.2838	−0.2361	0.0255	−0.0512
	(0.0166)	(0.0254)	(0.0254)	(0.0017)	(0.3163)	(0.0242)	(0.692)
BTKS	0.9054	0.4251	0.5252	0.7731	0.0000	0.0155	0.7938
	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[1]	[0.8570]	[1]

Direct dependency					Indirect dependency
US spillover effect	SP500	SP500	SP500	SP500	SP500	–	–
	HS	CSI300	N225	KS	CSI300|HS
The tranquil period
CoVaR	−2.8229	−3.3169	−2.7382	−2.3188	−2.0955	–	–
	(0.7977)	(1.6287)	(1.1284)	(1.6155)	(1.1243)
ΔCoVaR	1.1130	0.6919	1.4995	1.1658	0.2051	–	–
	(0.0141)	(0.0197)	(0.0172)	(0.2025)	(0.1844)
BTKS	0.7033	0.395	0.7991	0.8733	0.2031	–	–
	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]
The COVID-19 period
	SP500	SP500	SP500	SP500	SP500	SP500	SP500
	HS	CSI300	N225	KS	CSI300|HS	HS|KS	KS|N225
CoVaR	−3.012	−6.8592	−2.7462	−1.818	−4.9271	−1.5692	−1.4563
	(0.3502)	(1.4326)	(0.6839)	(0.1956)	(1.7564)	(0.5735)	(0.3916)
ΔCoVaR	1.1243	1.1237	1.1937	1.6838	1.8561	0.4105	0.7562
	(0.0176)	(0.1454)	(0.0754)	(0.087)	(2.3163)	(0.0742)	(0.3052)
BTKS	0.9154	0.941	0.9252	0.8731	0.7157	0.4155	0.7938
	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]	[0.0000]

Notes: Table 5 reports the mean values of CoVaR and ΔCoVaR. In the round bracket, we display their standard deviation. BTKS tests the null hypothesis that CoVaR in the intense shift is equal to it in regular circumstances. The alternative hypothesis is: CoVaR in the intense shift is greater than it in the regular circumstances. In square brackets, we display the p-value. The figure is underlined if the CoVaR and ΔCoVaR are larger in the direct or indirect dependence. The figure is in bold if the ΔCoVaR is larger in the tranquil period or the instability period.

For the tranquil period, direct risk spillovers of China's highly volatile stock market are distinguishable from the indirect ones dependent on the Hong Kong market. This case is consistent with the estimated dependency degree evaluated by Kendal's coefficient in Table 4. At the same time, from this useful finding, it is evident that the spillover from the Chinese contingent on Hong Kong to the other markets is weaker, though the indirect spillovers still exist. On the other hand, the spillovers in the unstable period of the Chinese market display great discrepancy, compared to the tranquil period. In the direct aspect, the contagion of the Chinese market to other stock markets is weaker than the ones in the tranquil period, except for the spillover to Japan. The exception is attributed to the dependency structure described by the copula, in this case, a copula with a fatter tail. Due to the special circumstances of this period, the dependency structures of the Chinese and other markets have changed. The direct spillovers are over the indirect, and the latter is not all significant. Although the Chinese conditional on Hong Kong has positive spillover effects on the US, the conditional risk spillovers to Japan and South Korea are absent.

For the tranquil and unstable periods in the US stock market, the evidence on the dependency structure reported in Table 4 documented some special characteristics. Hence, the risk spillovers of the US to the other markets are distinct from the Chinese market. For the discrepancy on dependency systems, the spillovers in this context provide some novel findings. For the tranquil period in the US market, the extreme price drops only resulted in spillover effects on the Chinese market via Hong Kong, as the US and other markets are not indirectly correlated. In effect, the direct risk spillover of the US market to the Chinese market exceeds the corresponding indirect one, which is consistent with the dependency degree. For the period of instability in the US, the results show the spillovers of the US are stronger than corresponding values in the tranquil period.

Furthermore, the significant conditional spillovers also confirm that the stock markets are strongly correlated during this period. In addition, the indirect spillover of the US to the Chinese market is stronger than the direct spillover. This finding indicates that the Chinese are greatly affected by the black swan events of the US stock market when controlling for Hong Kong. All stock markets in this period are interwoven, and the dependency system of the stock markets has changed.

The empirical results for the tranquil and COVID-19 periods confirm the graphical proof. We found that CoVaR and ΔCoVaR mean values are close and standard deviations have equivalent extent. The CoVaR descriptive statistics computed through the copula approach also give the same results. The decrease in the CoVaR values highlights a rise in the spillover risk. The decrease is particularly shown for the direct dependency of the US to Hong Kong, China; and the indirect dependency on China via Hong Kong. This result is also confirmed by the estimates of the ΔCoVaR parameters. The positive sign of these estimates emphasizes identical shifts across stock markets returns.

4.3. Discussion

The acquired findings provide relevant proof of the distinctions in the risk spillovers. First, the Chinese stock market created direct and indirect contagion to other stock markets during the tranquil period. In contrast, the corresponding direct risk spillovers were weakened, and the indirect impacts became trivial throughout its period of instability. Second, the spillovers of the US market to other stock markets are different from the Chinese due to diverse dependency structures with other stock markets, particularly the indirect dependency during the tranquil period. Further, the risk spillover of the US stock market to other stock markets is aggravated during its period of instability due to the COVID-19 shock.

The dynamic volatility of stock markets is described well through conditional variance model. Motivated by Engle (1982) and Bollerslev (1986), extensive literature studies time-varying volatility of asset returns. In fact, volatility is asymmetric due to the stronger shock from bad news. However, the original GARCH model ignores this leverage effect because of its specifications. In further studies, more and more researchers consider asymmetric effects on volatility in financial markets and their studies provided new sights on asymmetric volatility (Campbell & Hentschel, 1992; Bollerslev et al., 2006; and; Ewing & Malik, 2016). In this paper, we employed an asymmetric GARCH model with structural breaks to identify high-volatility periods of the Chinese and the US stock markets. The results show that all fitting models are the best and no asymmetry effects are remaining. The fitting quality of the models is verified according to the values of AIC, BIC, and LL, and all the diagnostic tests attest to the model specification robustness.

According to the findings of this paper, financial investors need to understand how financial markets correlate and how country-specific shocks are transmitted to other markets because these factors affect their ability to hedge risk via international diversification. Despite the high correlation between the markets in periods of high volatility, U.S. investors can benefit largely by decreasing their holding on the U.S. market and investing abroad when the U.S. market undergoes a volatile period. The Asian investors will proceed similarly to the U.S. investors. A large benefit, in terms of risk reduction, for both the U.S. and Asian investors from international diversification in the periods of large market volatility and, more importantly, in the periods following jump events. Therefore, the identification of the jump events can be used as an important signal for portfolio reallocation (Asgharian & Nossman, 2011).

Understanding the impact of COVID-19 on financial markets therefore will be particularly important moving forward for investors and policymakers. Our findings are relevant for investors in the East Asian stock markets who hope to safeguard portfolios from the extreme movement in one market, which affects the stocks in other markets. During periods of instability, investors should carefully watch markets for co-movement and plan accordingly. Decisions should be made cautiously, and risks to portfolios must be carefully considered. Because COVID-19 is still a factor, the market continues to be unstable. Economic uncertainty could result in stunted growth or even a downturn. Inflation is on the rise, and China and the US will possibly implement policies to curb this inflation. If instituted, these policies could have a dramatic effect on the stock markets. Extreme caution should be exercised during this time due to the instability and the chance of another stock market crash. Extreme spillover is destructive to all markets. Investors in the Chinese stock market should proceed with caution when stock market crashes occur in either the East Asia or US markets, as these markets are interrelated. A stock market crash in China would be devastating due to their fragile, emerging market. The risk spillovers would create destructive results for the market (Zehri, 2020a).

Our results support the fact that the COVID-19 outbreak affects stock markets around the world. This pandemic has put the world economy at risk and has quickly spread in the American and Asian markets. The COVID-19 has affected the economic and social conditions in Asia. It has also affected the banking sector and weakened the trade flows. This paper will help policymakers and practitioners to enhance their knowledge of the existing approaches to contagion analysis and offers the conceptual framework that can be added used by various businesses around the world.

4.4. Robustness examination

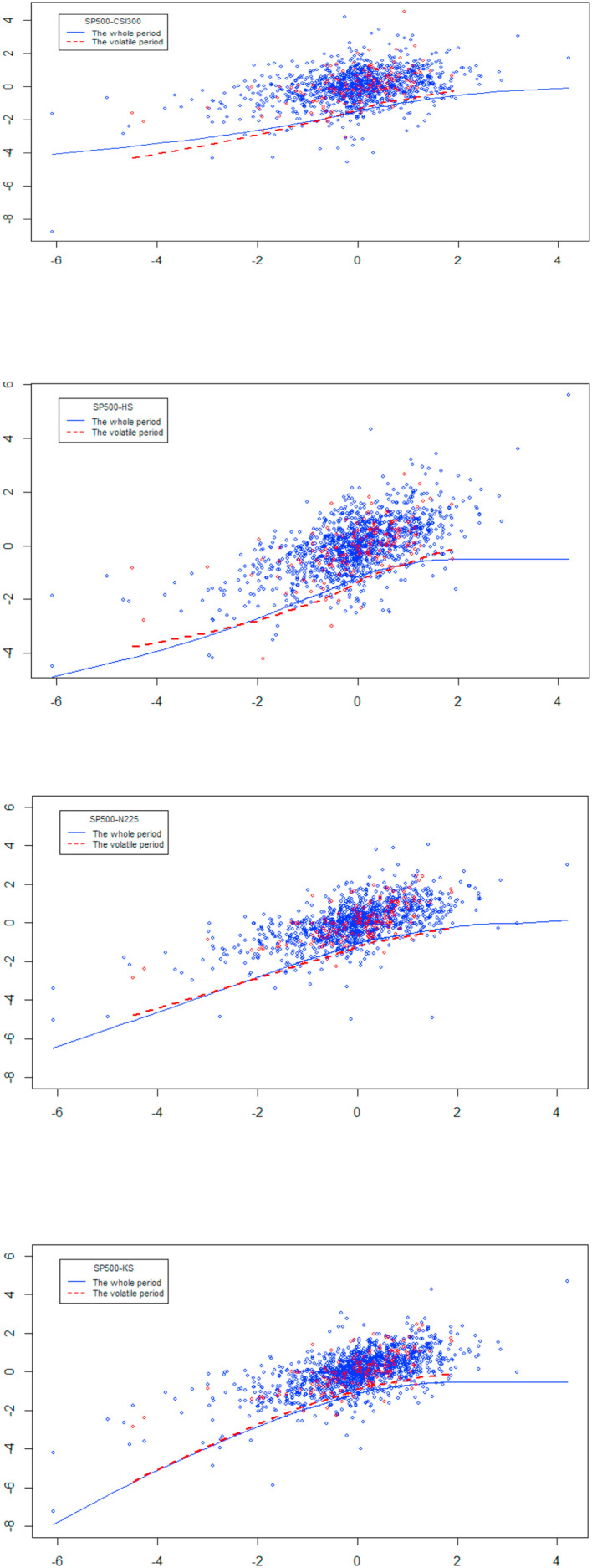
The Vine copula is an effective model in evaluating complicated relations among multidimensional variables. C-vine copula depicts a special correlation among multivariate situations where the dependency that one variable has with another is conditional on a connecting variable. To further understand dependency differences between the tranquil period and the high-volatility period, we plot fitting curves of the C-vine copula quantile regression of the stock markets on the US stock market spillover effect.

Fig. 3 illustrates the dynamic discrepancy between these periods at the 5% significance level. Blue dots in the plots represent the data from the tranquil period, and red dots are from the high-volatility period. The color of the fitting curves is in line with the dot specification. From a visional perspective, almost all of the fitting curves exert significant differences between the tranquil period and the high-volatility period. In particular, only the conditional regression of the Chinese on the US just has a fitting curve during the high-volatility period as the others lack corresponding conditional dependency captured by the C-vine copula. These results are consistent with the estimated copula in Table 4.

Fig. 3.

The quantile regression of the stock markets on the US.

5. Conclusion

This paper provides new understandings of the interdependence and spillover risk effects during times of instability using the empirical analysis of the US and East Asian stock markets indexes. The findings are obtained by implementing the modified ICSS algorithm to identify structural breaks in the stock markets. According to these jumps, we detected the unstable periods in the US and the Chinese stock markets. Subsequently, we used the copula approach to determine the multivariate dependency structures between these stock markets. Lastly, the risk spillovers of the US stock markets to the East Asian stock markets are estimated by the CoVaR approach.

The findings highlight greater downside spillover effects from the US to East Asian stock markets, particularly throughout the COVID-19 period. The conditional spillovers are significant and confirm the strong links between the US and East Asian stock markets. Besides, the indirect spillover effect of the US stock market on the Chinese stock market is more significant than the direct spillover.

The findings of this study raise important questions about the management of such pandemic crises. It is important to consider how catalysts and mechanisms related to contagion might be either exacerbated or dampened during COVID-19 or similar pandemics. This also concerns how pandemics such as COVID-19 might change the conditions for future financial contagion. The circumstances of COVID-19, alongside previous research, suggest a reconsideration of several catalysts and mechanisms of financial crises and subsequent contagion.

By extension, in the future, it is reasonable to expect that fears of pandemics, due to a discovery of new cases or a new disease, etc., will almost certainly lead to quick and severe global financial impacts. Future research will consider whether to regard these events as either extremely fast contagion or, alternatively, as simultaneities. In some ways, COVID-19 will leave the world less globalized with countries having greater aspirations to be able to close borders rapidly, but in other ways, COVID-19 will engender the world to become more keenly aware of the need to coordinate activity about preventions of global natural disasters. Preparations against pandemics will be seen as a global public good. Besides, the analysis of the dynamic, intensity, and direction of return and volatility spillovers can be extended to analyze the transmission of positive and negative shocks across markets and to the assessment of the predictive power of foreign information.

Regarding sharp declines in global domestic demand, future research will need to consider how this impacts the potentiality for financial and economic crises. Research shows that household credit booms take a prominent role in driving financial crises and recessions. How will a reduced domestic demand impact household credit booms? Certainly, there may be a considerable need for additional borrowing during economic crises. But will households be so shaken by COVID-19 as to permanently adjust personal savings rates? If so, how will this impact the potential for future financial contagion?

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

CRediT authorship contribution statement

Chokri Zehri: Conceptualization, Methodology, Software, Writing – original draft, Visualization, Investigation, An external expert in proofreading: .

Declaration of competing interest

The authors declare that they have no conflict of interest.