Ranking sets of morbidities using hypergraph centrality

Graphical abstract

Highlights

• •Multi-morbidity is increasingly common but poorly understood.
• •Hypergraphs allows for edges between more than two nodes.
• •Centrality can be calculated for hypergraphs, measuring node and edge importance.
• •Stroke and diabetes were the most central single conditions.
• •Diabetes and chronic pulmonary disease was the most central pair of diseases.

Abstract

Multi-morbidity, the health state of having two or more concurrent chronic conditions, is becoming more common as populations age, but is poorly understood. Identifying and understanding commonly occurring sets of diseases is important to inform clinical decisions to improve patient services and outcomes. Network analysis has been previously used to investigate multi-morbidity, but a classic application only allows for information on binary sets of diseases to contribute to the graph. We propose the use of hypergraphs, which allows for the incorporation of data on people with any number of conditions, and also allows us to obtain a quantitative understanding of the centrality, a measure of how well connected items in the network are to each other, of both single diseases and sets of conditions. Using this framework we illustrate its application with the set of conditions described in the Charlson morbidity index using data extracted from routinely collected population-scale, patient level electronic health records (EHR) for a cohort of adults in Wales, UK. Stroke and diabetes were found to be the most central single conditions. Sets of diseases featuring diabetes; diabetes with Chronic Pulmonary Disease, Renal Disease, Congestive Heart Failure and Cancer were the most central pairs of diseases. We investigated the differences between results obtained from the hypergraph and a classic binary graph and found that the centrality of diseases such as paraplegia, which are connected strongly to a single other disease is exaggerated in binary graphs compared to hypergraphs. The measure of centrality is derived from the weighting metrics calculated for disease sets and further investigation is needed to better understand the effect of the metric used in identifying the clinical significance and ranked centrality of grouped diseases. These initial results indicate that hypergraphs can be used as a valuable tool for analysing previously poorly understood relationships and information available in EHR data.

Multi-morbidity, also known as Multiple Long Term Conditions (MLTC), is the coexistence of two or more chronic health conditions in the same individual, and is increasing due to improvements in survival for acute conditions and people living longer [1]. In recent years, there has been a growing interest in multi-morbidity due to the realisation that it poses considerable challenges to health care systems that were designed to care for individuals with single conditions [2]. Of specific interest in our study is establishing a robust framework for identifying diseases or sets of chronic diseases that have an inordinate effect on the health outcomes of people that have them, and therefore providing evidence to support the design and implementation of appropriate care pathways to mitigate that extra risk.

As multi-morbidity has become increasingly studied, attention has been focused on developing statistical methods for analysing the phenomenon, in particular for finding sets of diseases that are more or less prevalent than would be expected from random chance in large scale Electronic Health Record (EHR) data [3]. For example, cluster analysis [4], latent class analysis [5], [6], deep learning [7], multi state models [8] and association rule analysis have all been explored as a means to understand multi-morbidity. A further alternative that has been previously explored is network analysis [9]. Network analysis uses available data to construct a mathematical object called a graph, in which relationships between elements in one set of objects (known as “nodes” or “vertices”) define elements of a second set of objects (called “edges” or “links”). Network analysis has been used previously to examine systems in geographical information science [10] and more recently to analyse social networks [11].

In applications to multi-morbidity, the nodes represent distinct diseases or conditions, and the links identify pairwise disease clusters observed in a population cohort. This approach is reported in a growing number of papers using network analysis to examine multi-morbidity using data from Korea [12], Nova Scotia [13], Ireland [14], Spain [15], the United States [16], [17] and Australia [9]. These studies used network analysis to investigate how prevalence of diseases varied in people of different sexes, people aged 50 years or older and with various index conditions. This previous work has shown that network analysis can be an important tool in the investigation of multiple health conditions and how they affect patient outcomes.

The simplest application of network analysis is to relate nodes to other nodes in binary relationships, represented by edges with a single node at each end, with no implied directionality. For example, in the analysis of social networks, nodes would represent people on social media platforms and edges would represent “friends.” There are several generalisations that have been developed. Firstly, adding directionality to the edges (creating a directed graph) which may be used, for example, to model citations in scientific literature with papers represented by nodes and directed edges indicating a paper cites another. Secondly, one may permit graph edges to carry information about the strength of relationships between nodes (a weighted graph); one example in a geographical network uses edge weights to represent the distance between towns or cities; in multi-morbidity, weights can reflect the numbers in a cohort with the observed disease cluster.

A limitation of previous graph based approaches is that each edge in a classic graph can only connect to two nodes. This means that information on the relationship between three or more diseases is lost in this construction, which may lead to interactions between sets of more than two diseases not being explored. This is a major limitation for multi-morbidity, since we are often directly interested in exploring multiple co-occurring conditions, not just pairs. For example, people with three or more diseases may be disproportionately at risk of mortality or serious clinical complications and therefore should not be omitted from analyses of multi-morbidity. This observation leads to the investigation of a generalisation to classic graphs called hypergraphs, where edges may connect to any number of nodes allowing for the quantification of relationships between any number of diseases. Hypergraphs are capable of representing many different types of data, and they include the set of all classic graphs since hypergraphs permit binary edges. Much of the mathematical formalism used to analyse classic graphs can directly or with straightforward generalisation be used to analyse hypergraphs. To the best of our knowledge, the application of hypergraphs to multimorbidity has not previously been explored.

In our study we aimed to establish the efficacy and feasibility of using hypergraphs in the analysis of routinely collected, large scale data to investigate multi-morbidity clusters. In this paper, we present the construction of multi-morbidity graphs where diseases are represented as nodes, and the edges connecting nodes represent a weighted measure of the number of people that have all diseases connected to the edge. Furthermore, we use centrality metrics to determine the most “central” single disease and sets of diseases in the population. Here, centrality is a quantitative analysis of a graph that measures how strongly connected a node is to other nodes in the graph. Different centrality measures have different interpretations, but for this analysis we will use the eigenvector centrality. This measure attempts to quantify the influence a node has within the graph, and is large for nodes that are connected to other nodes that are themselves highly central. Using this hypergraph formalism, we can see which diseases and sets of diseases co-occur most with others. This provides benefit over current methods which may discard information on interactions between more than two diseases.

1. Background

1.1. Matrix representation of a hypergraph

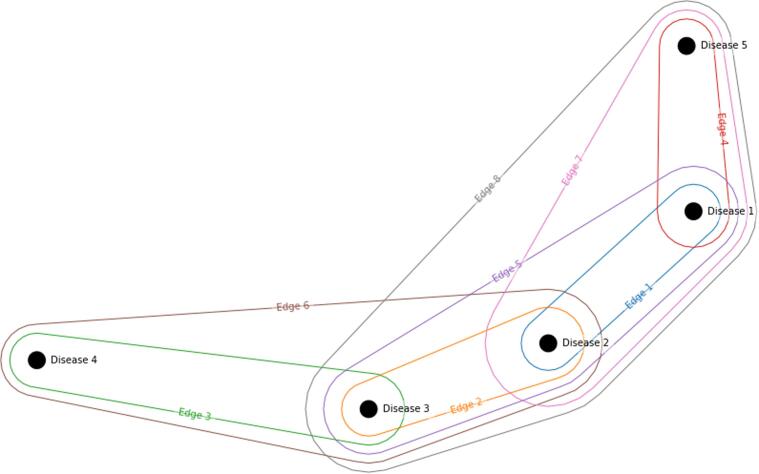
A weighted hypergraph $\mathcal{H}$ is a collection of objects $(\mathcal{N},\mathcal{E},{\mathcal{W}}_N,{\mathcal{W}}_E)$ known as nodes $\mathcal{N}$, edges $\mathcal{E}$ and weights ${\mathcal{W}}_N$ and ${\mathcal{W}}_E$. The set $\mathcal{N}$ contains nodes $\left\{v_0,v_1,\dots ,v_n\right\}$, the set $\mathcal{E}$ is the set of edges and is the power set of $\mathcal{N}$ such that subsets have two or more elements (since we disallow self edges). The sets ${\mathcal{W}}_N$ and ${\mathcal{W}}_E$ are the sets of weights. In contrast to a classic graph, a hypergraphs edges can connect to any number of nodes. Fig. 1 represents a simple example of a hypergraph representing a morbidity index consisting of $n=5$ nodes (diseases) with $m=8$ edges (disease clusters):

Fig. 1.

An example of a hypergraph, with five nodes and eight edges. Note that this is for illustrative purposes, and not all possible sets of diseases (edges) are represented.

We note that if we were considering a classic graph, all information carried by edges five, six, seven and eight would be lost, because these edges involve three or more nodes.

A useful representation of an (unweighted) hypergraph is the incidence matrix M which is a $n\times m$ matrix where n is the number of nodes and m is the number of edges. Each edge is represented by a column of the incidence matrix and each node is represented by a row. Elements of the matrix equal to one indicates an edge is connected to a node, whilst a zero indicates there is no connection. The incidence matrix can be considered a fundamental representation of the hypergraph, as there is a one-to-one correspondence between hypergraphs and their incidence matrices. The incidence matrix M for the above hypergraph is:

$$M=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right)$$ (1)

One may use the incidence matrix to compute the adjacency matrix of the graph, which directly quantifies the strength of connections between nodes and can in turn be used to compute useful derived measures such as centrality. The adjacency matrix is related to the incidence matrix by:

$$A=M^{T}M-D_n$$ (2)

where A is a square $n\times n$ matrix and $D_n$ is known as the node degree matrix, which has the node degree (or the valency), the number of edges the node is connected to, on the diagonal and zeros elsewhere. Subtracting its diagonal from the node degree matrix ensures the adjacency matrix has zeros on the diagonal, reflecting the idea that nodes have no connections to themselves. The adjacency matrix for the incidence matrix M given above is:

$$A=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 3\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 3\hfill \\ \hfill 3\hfill & \hfill 0\hfill & \hfill 3\hfill & \hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 3\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 3\hfill & \hfill 2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$ (3)

Note the adjacency matrix is symmetric with non-negative real elements $a_{\mathit{ij}}$, in which $a_{\mathit{ij}}$ represents the number of edges that connect nodes i and j. For example, $a_{15}=a_{51}=3$, indicating diseases 1 and 5 are connected by 3 edges - edges four, seven and eight as in Fig. 1 and the incidence matrix. Also note that this formalism would be identical for a classic graph, the only additional constraint being that columns would be limited to having only two ones in them, since edges are only allowed to connect to two nodes.

1.2. Edge weights

In our construction we assign weights to the edges of the graph, which represents a measure of how many people have the diseases that are connected to the edge. This information is contained in the weight matrix W, a diagonal $m\times m$ matrix with entries representing the weight of the corresponding edge; without loss of too much generality, we will assume the weights are non-negative. Including W in the definition of the graph modifies the expression for the adjacency matrix to

$$A=M^T{W}_{E}M-D_n$$ (4)

We note that including weights in a graph construction provides a high degree of flexibility and choice. Depending on the research question, we may be interested in a measure of the number of people with all diseases in the edge (as is the case here) but we could equally choose the weights to represent another measure relating the diseases. Furthermore, there are an infinite choice of ways we can quantify the number of people with all diseases in the edge. This flexibility can be seen as both a benefit and a disadvantage as it allows one to construct a graph with specific research questions in mind, but weighting schemes may have as yet poorly understood biases that may affect results.

For investigations into multi-morbidty and coincident diseases, the weighting scheme used should be some quantification of the number of people with all of the conditions represented by the edge, and as such is a problem of overlapping sets. There are infinite ways this quantification could be achieved, and while discussions of metrics quantifying the overlap of two sets have been previously performed [18], there is little literature on the overlap of more than two sets [19]. In this paper we use the overlap coefficient that has been generalised to apply to any number of sets to weight the edges, the number of people with all diseases in the set divided by the minimum number of people with one of the diseases:

$$w_E=\frac{\left|X_0\cap X_1\cap \dots \cap X_n\right|}{\min \left(\left|X_0\right|,\left|X_1\right|,\dots ,\left|X_n\right|\right)}$$ (5)

where $\left|X_i\right|$ is the number of people with disease $X_i$.

As described above, in a hypergraph several edges can contribute to each adjacency matrix element. This is not the case in a classic graph. Edges must terminate at two nodes, as such it is not possible to have two distinct edges that connect to the same nodes, and each edge contributes to exactly two elements of the adjacency matrix (since the adjacency matrix is symmetric). One must be more careful when interpreting the adjacency matrices of hypergraphs, because the adjacency matrix for nodes cannot be used to distinguish between one very highly weighted edge and a set of edges with large weights. In our research we require the hypergraph to have no self-edges and the weights representing the strength of relationships between diseases to be non-negative.

1.3. Eigenvector centrality

As discussed above, graphs can be analysed using centrality metrics. In this analysis we will use the eigenvector centrality. The eigenvector centrality is related to, but differs from, the degree (valency) of nodes in a graph. A high eigenvector centrality means that a node is connected to many nodes who themselves are connected to many nodes, and is therefore a powerful measure of centrality. Google’s PageRank is closely related to eigenvector centrality [20]. To compute the eigenvector centrality, we compute the eigenvectors of the adjacency matrix. In general there are up to $\dim (A)$ eigenvalues and eigenvectors of A, but since the weights of the network are positive real numbers the eigenvector corresponding to the largest eigenvalue will have all positive entries by the Perron-Frobenius theorem [21]. The elements of this eigenvector can be interpreted as a measure of centrality of each of the nodes. The interpretation of eigenvector centrality for hypergraphs is very similar to the interpretation for classic binary graphs. A minor difference is that more than one edge can contribute to each element of the adjacency matrix in a hypergraph which is not the case for binary graphs. The adjacency matrix therefore represents the overall weight between pairs of nodes and is no longer a fundamental representation of the hypergraph (since different incidence matrices could lead to the same adjacency matrix).

1.4. The dual hypergraph and the weighted resultant dual graph

Since a hypergraph removes the limitation on the number of nodes that can be connected to a single edge, there is no limit on the number of non-zero entries in each column of the incidence matrix (just as there is no limit on the number of non-zero entries in each row). Consider the transpose of the incidence matrix $M^T$. This is the incidence matrix of the dual hypergraph ${\mathcal{H}}^{\ast }$ which has m nodes and n edges, where the edges of the hypergraph $\mathcal{H}$ have become the nodes of ${\mathcal{H}}^{\ast }$ and vice versa. The adjacency matrix of the (unweighted) dual hypergraph ${\mathcal{H}}^{\ast }$ is $A^{\ast }={\mathit{MM}}^T-D_e$ where $D_e$ is the edge degree matrix, defined analogously with the node degree matrix above.

This symmetry between a hypergraph and its dual is not present for a classic graph, and it enables us to compute the centralities of $\mathcal{H}$ and ${\mathcal{H}}^{\ast }$ separately to obtain a quantitative understanding of the centrality of both the nodes representing single diseases and the edges representing sets of conditions.

For a weighted hypergraph, the adjacency matrix of the dual hypergraph $A^{\ast }={\mathit{MW}}_N{M}^T-D_e$ where $W_N$ is a $n\times n$ matrix with node weights on the diagonal. These weights are not related to the edge weights described above and are properties of the nodes, i.e. the single diseases, rather than the coincidence of sets of diseases. We choose the node weights to be the crude prevalence of the disease represented by the node, i.e. $w_N=\frac{\left|X\right|}{P}$ where $\left|X\right|$ is the number of people with the disease and P is the total population. Note the dual hypergraph does not depend on the prevalence of the sets of disease, only the prevalence of the single diseases. To avoid this limitation of the dual hypergraph we define the adjacency matrix of the weighted resultant dual graph as:

$$A_W^{\ast }=\sqrt{W_E}\left({\mathit{MW}}_N{M}^T-D_e\right)\sqrt{W_E}$$ (6)

where we use the fact that $W_E$ is diagonal so $W_E=W_E^T$ and $\sqrt{W_E}=\mathrm{diag}\left(\sqrt{w_1},\sqrt{w_2},\dots ,\sqrt{w_m}\right)$. Calculating the eigenvector centrality of this weighted resultant dual graph will provide a measure of centrality of the edges of the original hypergraph whilst taking both the node and edge weights into account. We could also calculate the weighted resultant graph related to the (non-dual) adjacency matrix in order to weight the results by the disease prevalence. We do not feel this is necessary as we are primarily interested in the most important diseases due to their coincidence with other diseases rather than their overall prevalence.

1.5. The bipartite representation of the hypergraph

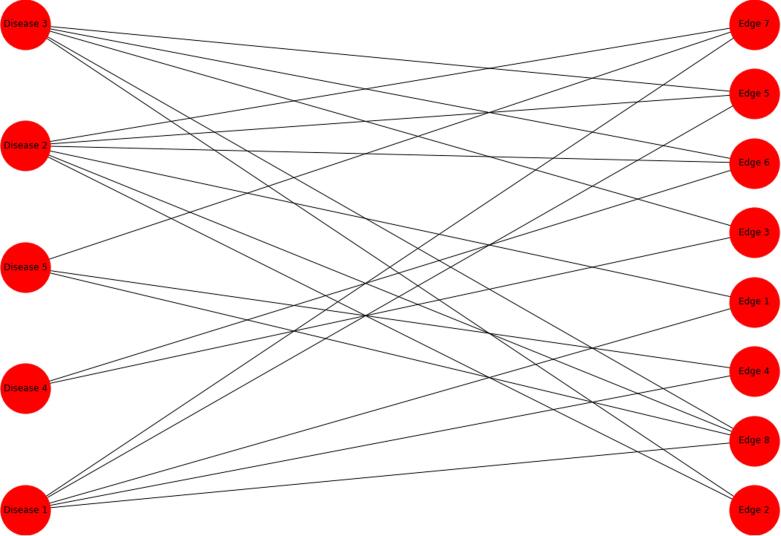
A hypergraph can be represented by a bipartite graph, which is a graph with the additional constraint that nodes have a binary partition label, and edges can only connect objects whose labels are different. The nodes and edges in the hypergraph become nodes in the bipartite graph with the partition label determining whether the object in the hypergraph was a node or an edge. Investigating the centrality of this bipartite graph allows for the quantification of the importance of individual diseases and sets of diseases together (since the atomic entities are both the nodes and edges of the original hypergraph). We will only translate the edge weights of the hypergraph to the bipartite graph; edge weights can unabiguously be attached to the new edges of the bipartite graph such that the weight of hyperedge $w_i$ is applied to all new edges of the bipartite graph that connect to the $i^{\mathrm{th}}$ hyperedge node of the bipartite graph. Note that by construction, the edges of the bipartite network cannot connect to nodes which both represent edges or both represent nodes. For example, the hypergraph above can be represented as a bipartite network (Fig. 2).

Fig. 2.

The bipartite graph resulting from the hypergraph defined in the incidence matrix above.

We note that there are three options to choose from when calculating centrality (the original hypergraph, the dual hypergraph and the bipartite representation of the hypergraph), in contrast to the classic binary graph where there was no such seeming ambiguity. This is an additional advantage of the hypergraph construction which gives one the option to calculate the centrality of nodes (which in this paper represents single diseases), hyperedges (sets of diseases) or both nodes and hyperedges together (single diseases and sets of diseases togther).

In the context of multi-morbidity, when considering the centralities of nodes in the dual hypergraph, the set of diseases with the largest centrality is the set of diseases that is most strongly connected to other sets of diseases, and is not necessarily an indication of how strongly connected the diseases are within the set. One must look at centralities of both the hypergraph and the dual hypergraph (or alternatively, the bipartite representation of the hypergraph) to form a complete picture of the centrality of diseases and sets of diseases.

1.6. Summary

In summary, hypergraphs allow for edges that connect more than two nodes. This leads to a symmetry between nodes and edges of the hypergraph, since edges can connect to any number of nodes and nodes can connect to any number of edges. The dual hypergraph ${\mathcal{H}}^{\ast }$ is an alternative representation of the data in the hypergraph $\mathcal{H}$, with the edges of $\mathcal{H}$ becoming the nodes of ${\mathcal{H}}^{\ast }$. Furthermore, one can express the hypergraph $\mathcal{H}$ as a bipartite (classical) graph $\mathcal{G}$, where the nodes and edges of $\mathcal{H}$ become nodes of $\mathcal{G}$. These changes in representation are very powerful, because they allow one to calculate node centralities separately for each representation. The most central single disease is given by calculating the centrality of $\mathcal{H}$, the most central sets of two or more diseases by calculating the centrality of ${\mathcal{H}}^{\ast }$ and the most central disease or set of diseases (i.e. a set of one or more diseases) by calculating the centrality of $\mathcal{G}$. Using centrality as a proxy for importance, this allows us to quantitatively evaluate the most important single diseases, set of two or more diseases or set of any number of diseases based on how well connected they are to other nodes.

2. Methods

2.1. Data

The analysis described here uses EHR data made available for research within the privacy protecting Trusted Research Environment, the Secure Anonymised Information Linkage (SAIL) Databank [22], [23], which contains all secondary care inpatient records from hospitals in Wales and records from approximately 85% of primary care practices [24] since 1998.

2.2. Variables

Clinical records from primary and secondary care were interrogated for codes relating to conditions defined by the Charlson comorbidity index (omitting HIV/AIDS status, which was not included in this study due to it being redacted by the original data providers before data is provided to SAIL as it was classed on the highly sensitive list by NHS Wales in 2008). There are 16 labels in the Charlson definition [25], [26], [27], but three related sets of diseases; (i) cancer, lymphoma and leukaemia and metastatic cancer, (ii) diabetes and diabetes with complication and (iii) mild and severe liver disease which were combined into three single conditions as they are by their nature closely related and would induce pseudoclustering. A person was regarded to have the condition if they had any occurrences between 1st January 2005 and 31st December 2019. See the discussion below for a more in depth analysis of the limitations of this construction and how it can be improved upon.

2.3. Participants

The cohort used has been described previously [28]. Briefly, all people living in Wales on 1st January 2000 and aged 20 years or older were included in the baseline cohort. Age was defined as the age at cohort exit, i.e., the age at death or the age of the individual on 31st December 2019. Any diagnosis of disease defined by the Charlson comorbidity index recorded prior to 31st December 2019 was considered indicative that the person had the disease.

2.4. Analysis

Hypergraphs were constructed for the cohort as a whole, and for age stratified sub-cohorts to investigate how the centrality of diseases changes by age group. The hyperedge weighting function used was the overlap coefficient, generalised to any number of diseases as defined in Eq. 5. The node weighting function used was the crude prevalence:

$$w=\frac{\left|X\right|}{P}$$ (7)

where $\left|X\right|$ is the number of people with disease X and P is the total population. Eigenvector centrality was used to quantify the centrality of the nodes. Centrality was calulated for the hypergraph, the dual hypergraph (to find most central sets of diseases) and the bipartite graph representation of the hypergraph (to find the most central single diseases and sets of diseases together). To demonstrate the importance of expanding the graph construction to include sets of three or more diseases we have constructed the equivalent classic network using only binary edges weighted by the overlap coefficient and compared node centralities. All analysis was performed using Python version 3.7.9 and numpy version 1.19.2 [29].

3. Results

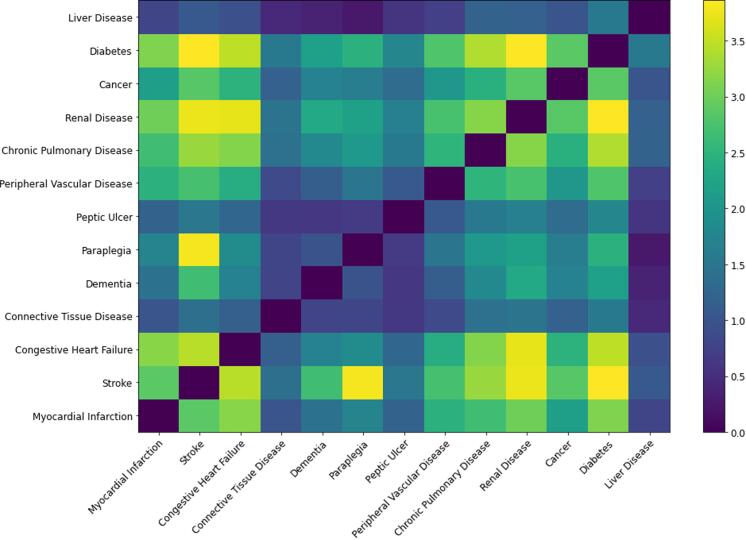
There were 2,178,938 people in the cohort, who were diagnosed with 2,918,569 conditions (including people who had no record of morbidity as defined by the Charlson index). Some 1,313,219 (60.3%) individuals had at least one condition and 755,421 (34.7%) had more than one condition diagnosed, meeting the definition of multi-morbid within this index. Table 1 shows the number of individuals, number of males and percentage of males in the population with each of the Charlson diseases. There are 13 Charlson conditions in this comparison and with the constraints listed above there are 8,177 possible hyperedges in the hypergraph. The adjacency matrix for hypernodes calculated from the incidence matrix is shown schematically in Fig. 3 with more yellow colourings indicating larger weights and more blue colourings indicating smaller weights.

Table 1.

The number of people, males and percentage of males in the cohort with each of the Charlson diseases.

	Counts	Counts (males)	Percentage (males)
Chronic Pulmonary Disease	566829	266536	47.02
Cancer	451604	220316	48.79
Diabetes	400753	206352	51.49
Stroke	276731	133058	48.08
Renal Disease	263994	122643	46.46
Congestive Heart Failure	212040	105239	49.63
Myocardial Infarction	182310	111377	61.09
Dementia	131831	48708	36.95
Peripheral Vascular Disease	125345	76774	61.25
Connective Tissue Disease	121572	40349	33.19
Peptic Ulcer	99241	57309	57.75
Paraplegia	54267	26997	49.75
Liver Disease	32052	18255	56.95

Fig. 3.

A heatmap illustrating the elements of the adjacency matrix of the hypergraph. Note that despite the overlap coefficient being bounded in the range [0,1] the values in the adjacency matrix can be greater than one. This is because each element in the adjacency matrix is the sum of overlap coefficients for each edge containing the two conditions.

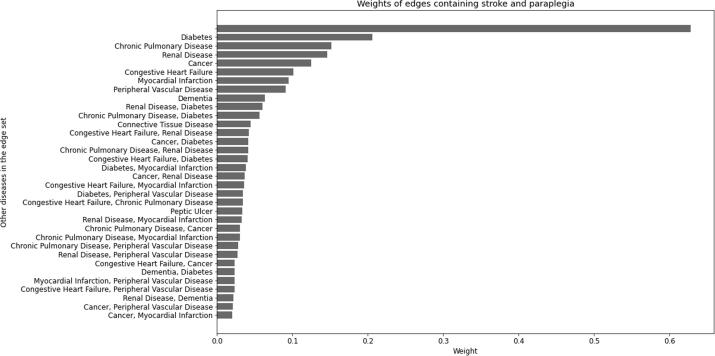
The node adjacency matrix for a hypergraph indicates the resultant weight between hypernodes. Recall that each element of this adjacency matrix has a contribution from each hyperedge that contains the nodes indicated by the row and column, and hyperedges involving more than two nodes will contribute to more than one adjacency matrix element. For example, the largest resultant weight between hypernodes is between stroke and paraplegia, which will contain contributions from all hyperedges of the form $\left\{\dots ,\mathrm{Stroke},\dots ,\mathrm{Paraplegia},\dots \right\}$ (see Fig. 4 for a bar chart illustrating the edges containing stroke and paraplegia with the largest weights, all of which contribute to the $(\mathrm{Stroke},\mathrm{Paraplegia})$ element of the adjacency matrix shown in Fig. 3).

Fig. 4.

The edge weights that contribute to the (stroke, paraplegia) element of the adjacency matrix. The labels are the additional diseases that are included in the edge, so the first and largest bar with no label is the weight of the (stroke, paraplegia) edge, the second is the (stroke, paraplegia, diabetes) edge, etc.

One can identify influential diseases qualitatively by looking at all values in a row of the adjacency matrix heatmap. For example, diabetes and renal disease appear to be influential while liver disease and connective tissue disease are less influential. The eigenvector centralities for the hypergraph adjacency matrix are shown in Table 2 (left). The “classical” binary graph derived from the same data is a much simpler object, since there are 78 possible binary edges in a graph of 13 nodes. The table of eigenvector centralities for the nodes of the binary graph is shown in Table 2 (right).

Table 2.

Left: The centrality measures of the hypergraph (single diseases). Right: The centrality measures of the “classical” binary graph.

Node	Centrality	Node	Centrality
Stroke	0.3641	Stroke	0.4532
Diabetes	0.3604	Diabetes	0.3962
Renal Disease	0.3536	Paraplegia	0.3866
Congestive Heart Failure	0.3280	Renal Disease	0.3009
Chronic Pulmonary Disease	0.3205	Congestive Heart Failure	0.2925
Myocardial Infarction	0.2952	Chronic Pulmonary Disease	0.2565
Cancer	0.2785	Myocardial Infarction	0.2361
Peripheral Vascular Disease	0.2675	Dementia	0.2307
Paraplegia	0.2408	Peripheral Vascular Disease	0.2274
Dementia	0.2120	Cancer	0.2169
Peptic Ulcer	0.1633	Liver Disease	0.1184
Connective Tissue Disease	0.1481	Peptic Ulcer	0.1173
Liver Disease	0.1202	Connective Tissue Disease	0.1037

Table 3 contains eigenvector centralities for the 20 largest centralities of the dual hypergraph, representing importance of sets of diseases. We note the most central sets of diseases are sets of two or three diseases, which may be an artefact of the chosen weighting metric.

Table 3.

The centrality measures of the resultant dual hypergraph (sets of diseases)

Edge	Eigenvector Centrality
Chronic Pulmonary Disease, Diabetes	0.1350
Renal Disease, Diabetes	0.1247
Congestive Heart Failure, Diabetes	0.1152
Cancer, Diabetes	0.1150
Myocardial Infarction, Diabetes	0.1141
Stroke, Diabetes	0.1124
Peripheral Vascular Disease, Diabetes	0.1109
Diabetes, Liver Disease	0.1078
Paraplegia, Diabetes	0.1043
Dementia, Diabetes	0.1038
Congestive Heart Failure, Chronic Pulmonary Disease, Diabetes	0.1007
Peptic Ulcer, Diabetes	0.0980
Connective Tissue Disease, Diabetes	0.0955
Stroke, Paraplegia, Diabetes	0.0943
Peripheral Vascular Disease, Chronic Pulmonary Disease, Diabetes	0.0921
Myocardial Infarction, Chronic Pulmonary Disease, Diabetes	0.0913
Chronic Pulmonary Disease, Renal Disease, Diabetes	0.0898
Stroke, Chronic Pulmonary Disease, Diabetes	0.0851
Congestive Heart Failure, Renal Disease, Diabetes	0.0839
Chronic Pulmonary Disease, Diabetes, Liver Disease	0.0830

The eigenvector centralies for the bipartite representation of the hypergraph containing both single diseases and sets of diseases is in Table 4. As before, sets with few diseases dominate the list of most important disease sets.

Table 4.

The centrality measures of the bipartite representation of the hypergraph (single diseases and sets of diseases).

Node	Eigenvector centrality
Diabetes	0.9248
Stroke	0.9169
Renal Disease	0.5976
Stroke, Paraplegia	0.5937
Paraplegia	0.5656
Congestive Heart Failure	0.5184
Chronic Pulmonary Disease	0.4523
Myocardial Infarction	0.3607
Stroke, Diabetes	0.3493
Renal Disease, Diabetes	0.3235
Congestive Heart Failure, Diabetes	0.3218
Cancer	0.3218
Peripheral Vascular Disease	0.3177
Stroke, Paraplegia, Diabetes	0.3169
Dementia	0.2845
Paraplegia, Diabetes	0.2829
Myocardial Infarction, Diabetes	0.2814
Stroke, Dementia	0.2708
Peripheral Vascular Disease, Diabetes	0.2621
Congestive Heart Failure, Renal Disease	0.2471

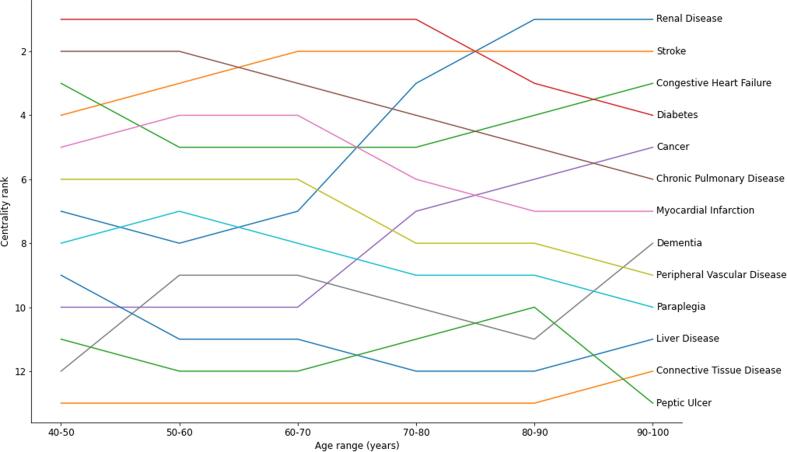
Stratifying the cohort by age and constructing a graph for each age band allows for the evaluation of the most central single disease as a function of age (Fig. 5).

Fig. 5.

The centrality rank of the diseases in the Charlson index, stratified by 10 year age bands.

4. Discussion

In this paper, we have described the use of hypergraphs for analysing multi-morbidity, which improves upon previous work involving classic network analysis (where edges are limited to being connected to two nodes). The method includes information on people with two or more conditions and can be used to quantitatively rank single diseases and sets of diseases both separately and together, which is essential for the understanding of multi-morbidity in a modern setting since people commonly have more than two chronic conditions that require services from multiple health care professionals and specialities. Aetiology and care of single chronic diseases is generally quite well understood nowadays, but as people are increasingly being diagnosed with multiple chronic health conditions it is important to develop methods for identifying sets of diseases that may or may not occur together at a rate that is different than would be expected by chance.

We have considered our cohort of people at a single time point and calculated the eigenvector centralities of: the “classical” binary graph; nodes in the hypergraph; nodes in the dual hypergraph (equivalently, edges in the hypergraph); and nodes in the bipartite representation of the hypergraph (which are the nodes and edges of the hypergraph). We found the most central single disease when considering people of all ages was stroke, followed by diabetes. The most central sets of diseases all feature diabetes, likely because of the high prevalence of the disease compared to other morbidities considered. The five most central sets of diseases were diabetes with COPD, renal disease, congestive heart failure, cancer and myocardial infarction. The associations between diabetes and cardiovascular disorders are expected as they are known to be complications of diabetes. The association between diabetes and cancer and COPD may be due to lifestyle factors causing both conditions in the same sub-population. Comparing the centrality results of the hypergraph with the classic graph, the most notable difference is that paraplegia is more central to the classic graph than the hypergraph. This has occurred because paraplegia is strongly connected to stroke but is not very strongly connected to other nodes (strokes in the brain or spinal cord may cause paraplegia or be an infrequent complication of aortic surgery [30]) and therefore hyperedges connecting three or more diseases including paraplegia have small weights. When the effect of all hyperedges is taken into account in the adjacency matrix, resultant relationships between most other pairs of nodes are enhanced more than relationships between paraplegia and other nodes. Neglecting to include sets of three or more diseases tends to exaggerate the effect of nodes that are strongly connected to other single nodes on the overall graph. In the hypergraph construction stroke is the most central single disease while paraplegia is the 9th most central. This indicates that the fraction of people that have a stroke that also have paraplegia is low compared to the number of people that have paraplegia that also had a stroke (since stroke is commonly coincident with other diseases that paraplegia is not commonly coincident with). This example therefore shows the additional value of using hypergraphs over traditional methods because the additional information captured in the hyperedge weights makes a difference to the calculated results.

The eigenvector centrality provides a method with which to quantify how strongly connected nodes are to other nodes in the graph and represents a measure of how strongly connected the nodes and edges are to other nodes and edges, i.e. diseases and sets of diseases with high centrality means they are commonly coincident with other diseases or sets of diseases. We note that eigenvector centrality is difficult to interpret as an absolute measure. It is not clear whether a node with an eigenvector centrality that is twice as large as some other node is twice as important, and for this reason we have investigated the ranking of nodes by their eigenvector centrality in addition to their absolute value.

The most central diseases for all people are observed to be consistently high in the centrality rankings for people of different age groups. Despite being the most central condition for people of all ages, stroke is not the most central disease for any ten year age band, although it is never ranked less than fourth most central. Somewhat surprisingly, the centrality of most diseases in the Charlson index do not change much for different age groups (with some notable exceptions, for example, renal disease and cancer become more central as age increases and peripheral vascular disease and chronic pulmonary disease become less central as age increases). We believe this result is a consequence of exactly what is being measured with centrality. Our graph construction does not take overall prevalence of diseases into account, so despite stroke and diabetes being comparatively more common in older people than younger people, they are still diseases which are most likely to co-occur with other conditions regardless of age. It is possible to include the prevalence of single diseases in the graph construction using node weights, and one could construct a similar object to what we have termed the Weighted Resultant Dual Graph for the original hypergraph, including node weights. Furthermore, our chosen study design only includes people if they are at least 18 years old at on 1st January 2000, and takes their age to be their age on the 30th December 2019 or their age at death. This means people surviving to the end of the study must be at least 38 years old. Conversely, the increase in centrality of cancer in older ages is likely due to cancers becoming more prevalent in older age groups and are known to be strongly associated with chronic conditions and underlying lifestyle risk factors [31]. We further note that there is considerable variation in the rank of some diseases (for example, peptic ulcer, renal disease and dementia) as a function of age group, and is likely due to the relatively small numbers of people that were multi-morbid with these conditions. This observation may also be due to our exploratory study design, which considers people to have a disease if they were diagnosed at any time during the study period.

5. Conclusion and future work

We have demonstrated the application of hypergraphs to the problem of examining multi-morbidity, and constructed a hypergraph for a relatively simple set of diseases for a large cohort of people. We believe there is potential for this technique to be used for identifying new commonly occuring disease sets. This would require the analysis of datasets with a larger number of diseases, including rare diseases which suggests some avenues for future study. Firstly, it will be important to investigate improvements in computational techniques and optimisations to improve the utility of results and help offset the combinatorial explosion of edges that occurs as the number of diseases under consideration increases. Our current implementation does not account for uncertainties in the estimated graph weights and while in principle it is relatively simple to calculate uncertainties for the adjacency matrix, the uncertainties in the eigenvector centrality might require an iterative perturbative approach that would add work to an already challenging computational problem. A possible simplification is the use of the apriori algorithm to limit the diseases and sets of diseases to only ones that meet a chosen prevalence threshold may be fruitful, but one still potentially loses information with this approach, particularly for diseases that affect small numbers that may be disproportionately important to quality of life or healthcare utilisation statistics. Secondly, there are important generalisations that could improve the utility of hypergraphs. For example, a directed graph allows for the investigation of whether the order of diseases acquired affected the relationships between diseases and sets of diseases (as one would expect it would). Furthermore, in this exploratory paper we have not applied any corrections for demographic variables such as age, sex and socioeconomic status. It is possible to apply these corrections in principle by adding nodes to the graph that represent these variables, or by stratifying these variables and constructing separate graphs for each stratum. Finally, the time evolution of the cohort itself could be captured by constructing a graph at several time points and observing the change in relative disease centrality, similarly to how we have approached the effect of age in this work.

Of crucial importance to future work on this topic is the weighting scheme that is used. There are infinite possibilities to choose from, and each has its own bias. Furthermore, the choice of weighting has been shown to have a significant effect on results when using the same data [17]. There has been some effort to understand different ways to quantify the overlap of two sets and their biases [32], [33], for example, it is well understood that the lift, a commonly used measure of the overlap of two sets in frequent item-set analysis and network analysis of diseases, overestimates the relative importance of rarer diseases. To date there has been less need for an exercise examining the biases in the overlap of more than two sets [19]. The number of sets is an additional factor that could cause biases in any overlap metric, in addition to possibilities present for the overlap of two sets. It is usually a simple matter to generalise a binary overlap function, but it is not clear whether the understood biases would persist in the same way for more than two sets and also how any bias in the weighting function would depend on the number of sets. A study similar to [32] is very important to inform future decisions regarding weighting of hypergraphs for multi-morbidity research. When implementing this method in practice, it is of paramount importance to select the weighting scheme such that any biases in the analysis are minimised, and as such the results are robust.

CRediT authorship contribution statement

James Rafferty: Methodology, Software, Formal analysis, Writing – original draft. Alan Watkins: Writing – review & editing. Jane Lyons: Data Curation, Writing – review & editing. Ronan A. Lyons: Funding acquisition, Writing – review & editing. Ashley Akbari: Writing – review & editing. Niels Peek: Funding acquisition, Writing – review & editing. Farideh Jalali-najafabad: Writing – review & editing. Thamer Ba Dhafari: Writing – review & editing. Alexander Pate: Writing – review & editing. Glen P. Martin: Writing – review & editing. Rowena Bailey: Project administration, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.