Nonlinear growth and mathematical modelling of COVID-19 in some African countries with the Atangana–Baleanu fractional derivative

Abstract

We analyse the time-series evolution of the cumulative number of confirmed cases of COVID-19, the novel coronavirus disease, for some African countries. We propose a mathematical model, incorporating non-pharmaceutical interventions to unravel the disease transmission dynamics. Analysis of the stability of the model’s steady states was carried out, and the reproduction number ${\mathcal{R}}_0$, a vital key for flattening the time-evolution of COVID-19 cases, was obtained by means of the next generation matrix technique. By dividing the time evolution of the pandemic for the cumulative number of confirmed infected cases into different regimes or intervals, hereafter referred to as phases, numerical simulations were performed to fit the proposed model to the cumulative number of confirmed infections for different phases of COVID-19 during its first wave. The estimated ${\mathcal{R}}_0$ declined from 2.452–9.179 during the first phase of the infection to 1.374–2.417 in the last phase. Using the Atangana–Baleanu fractional derivative, a fractional COVID-19 model is proposed and numerical simulations performed to establish the dependence of the disease dynamics on the order of the fractional derivatives. An elasticity and sensitivity analysis of ${\mathcal{R}}_0$ was carried out to determine the most significant parameters for combating the disease outbreak. These were found to be the effective disease transmission rate, the disease diagnosis or case detection rate, the proportion of susceptible individuals taking precautions, and the disease infection rate. Our results show that if the disease infection rate is less than 0.082/day, then ${\mathcal{R}}_0$ is always less than 1; and if at least 55.29% of the susceptible population take precautions such as regular hand washing with soap, use of sanitizers, and the wearing of face masks, then the reproduction number ${\mathcal{R}}_0$ remains below unity irrespective of the disease infection rate. Keeping ${\mathcal{R}}_0$ values below unity leads to a decrease in COVID-19 prevalence.

1. Introduction

Towards the end of December 2019, the infectious Coronavirus disease known as COVID-19 was first detected in Wuhan, the capital city of the Hubei province in China. Caused by the severe acute respiratory syndrome coronavirus SARS-CoV-2 [1], COVID-19 has caused a global health emergency. The World Health Organization (WHO) declared it to be a public health emergency of international concern on 30 January 2020 [2], and as a pandemic on 11 March 2020 [3]. By 15 June 2020, the outbreak had infected around 7.8 million people globally with total fatalities of around 430,000 people. Following Africa’s first case recorded in Egypt on 14 February 2020, there had been over 246,636 confirmed cases with over 6571 deaths by 16 June 2020. COVID-19 is a rapidly spreading contagious zoonotic disease with symptoms that manifest after an incubation period of approximately 5 days following infection. Symptoms are highly variable, but range from fever, dry cough, and fatigue to less common ones like aches, sore throat, conjunctivitis, diarrhoea, and loss of smell and taste. Because efficient vaccination is not yet widely available, and there are few validated medications for treatment, COVID-19 control strategies employed by government agencies are still largely dominated by non-pharmaceutical interventions such as social distancing, wearing of face masks, regular washing of hands with soap, and use of hand sanitizer. However, the efficacy of these control strategies are not yet well-quantified, and their effectiveness is likely to change as new COVID-19 mutants take the stage.

Infectious disease modelling is a very active scientific research field. The activity is motivated, in part, by the need to gain deeper insight into disease dynamics in order to predict the trend of an epidemic outbreak, through being able to validate and test the effectiveness of control measures proposed to check the spread of the disease [4]. In recent years, mathematical modelling has been playing a key role in understanding the dynamics of infectious diseases and their control measures. It has recently been applied to study, for example Ebola [5], [6], [7], [8], [9], Dengue fever [10], [11], [12], [13], [14], Zika virus [15], [16], [17], [18], [19], [20], and Tuberculosis [21], [22], [23], [24]. Research on comprehending and predicting the trend of COVID-19 has been focused mainly on Europe [25], [26], [27], [28], [29], [30], Asia [31], [32], [33], [34], [35], [36], [37], and the Americas [38], [39] due partly to the degree of spread and impact on these continents. However, a few research papers have appeared on cases in Africa, and in Nigeria in particular [40], [41], [42], [43], while earlier, Gilbert et al. [44] evaluated the vulnerability and preparedness of the African continent against the risk of importing the disease. The importance of investigating the dynamics of COVID-19 in Africa can hardly be overemphasized, not only for the sake of Africa itself, but also because the people of the African continent are constantly visiting or migrating to other continents in the pursuit of further education, business, or other bilateral purposes; thereby creating a high risk of spreading the disease, as already witnessed and reported. Moreover, the investigation of COVID-19 dynamics will provide reliable information to decision-makers on the implementation of possible strategies and control measures aimed at stemming the spread of the pandemic [42], [43]. Recently, Manchein et al. [45] analysed the growth of the cumulative number of confirmed infected cases of COVID-19 up to March 27, 2020, from countries of Asia, Europe, North America, and South America using the power-law: $\alpha +\beta t^{\mu }$, where $\alpha$ is a deviation accounting for the uncertainty in the observed values. They found values of $\alpha$, $\beta$ and $\mu$ for nine countries of Asia, Europe, North America, and South America and employed a distance correlation to show that the power-law curves between the countries are statistically highly correlated [45]; but African countries were not considered.

Inspired by the work of Manchein et al. [45], this present paper analyses the time-series evolution of COVID-19 for 6 African countries: Egypt, Ethiopia, Kenya, Nigeria, Senegal and South Africa. A modified SEIR model with integer order derivatives is proposed, incorporating some non-pharmaceutical interventions, to estimate the reproduction number of the infection in the various countries, and also to highlight the effectiveness of the interventions in flattening the time-evolution of new COVID-19 cases. In addition, a fractional order equivalent is considered using the Atangana–Baleanu derivative [46]. This derivative is to be preferred over other fractional derivatives, such as the Caputo and Caputo–Fabrizio, because of its non-singular and non-local kernel. It has already found numerous applications in diverse models arising in science, engineering and medicine [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58].

The paper is organized as follows: in Section 2, we carry out an analysis of data collected for the countries to be studied. In Section 3, the model and its basic dynamical properties are presented. Section 4 provides a qualitative analysis of the model, including a determination of the stability properties of the equilibrium points based on the next generation matrix method [59], [60] employed in obtaining the reproduction number. Numerical simulations, elasticity and sensitivity analysis, and fractional numerical simulations, are presented in Sections 5, 6, 7, respectively. The work is summarized and conclusions drawn in Section 8. Appendix providing details of the numerical scheme used for solution of the fractional derivative model.

2. Data analysis

The data for the countries to be analysed were collected from the daily situation reports published by the World Health Organization (WHO) [61]. The choice of countries to be analysed was made so as to ensure geographical spread, as well as relatively high population densities. Nigeria and Senegal were chosen in the West Africa zone, Ethiopia and Kenya in East Africa, Egypt in North Africa and South Africa in Southern Africa (Fig. 1). Fig. 2 shows the cumulative number of confirmed infected COVID-19 cases as a function of days since first case was recorded up till 20th June 2020 for the selected countries. Note that the values on the horizontal and vertical axes are different for each country due to the different levels of disease progression and different inception dates. The black-continuous and the blue-dashed curves in Fig. 2 represent respectively the cubic function, ${\alpha }_0+{\alpha }_{1}t+{\alpha }_2{t}^2+{\alpha }_3{t}^3$ and the power law function, ${\beta }_1{t}^{{\beta }_2}$ that was fitted to the time-series. Numerical values of the fitted parameters ${\alpha }_i$, ${\beta }_i$, $i=1,2,3$ for the cubic and power law equation for each country are given in Table 1. It is clear that the cubic equation fits best to the actual data for the cumulative number of confirmed cases in comparison with the power law equation of Manchein et al. [45]. However, the results of the cubic and power law fitting were comparable during the early stages of disease progression for all the countries. It is noteworthy that the fitted cubic equation for each country is such that there exists no maximum point for the curve beyond $t>25$ days. Such a maximum point would correspond to a time when a maximum in the cumulative number of infections is being approached so that the curve begins to flatten. The fact that no maximum value is approached reduces the usefulness of the cubic equation for investigating future dynamics of the pandemic and possible actions needed to flatten the curve of disease progression. Nevertheless, it can be adopted as a tool for forecasting the expected number of new infections.

Fig. 1.

Map of Africa showing the locations of the countries studied and the corresponding numbers of confirmed cases (NOC) and numbers of deaths (NOD) due to COVID-19 [61].

Fig. 2.

Cumulative number of confirmed infected cases by COVID-19 as a function of time from inception (first case) for South Africa, Egypt, Nigeria, Senegal, Ethiopia and Kenya. The black-continuous and the blue-dashed curves represent respectively the functions ${\alpha }_0+{\alpha }_{1}t+{\alpha }_2{t}^2+{\alpha }_3{t}^3$ and ${\beta }_1{t}^{{\beta }_2}$ that fit the actual time-series represented by the red dots. The parameters ${\alpha }_i$, ${\beta }_i$, $i=1,2,3$ for each country are described in Table 1.

Table 1.

Parameters of the cubic and power-law fitting curves.

Country	${\alpha }_0$	${\alpha }_1$	${\alpha }_2$	${\alpha }_3$	${\beta }_1$	${\beta }_2$
South Africa	−4223.492	671.706	−21.445	0.214	0.072	2.875
Egypt	−1911.406	258.244	−7.608	0.070	0.001	3.522
Nigeria	186.931	−14.660	−0.324	0.017	0.002	3.260
Senegal	226.162	−28.806	0.739	−0.000196	0.062	2.365
Ethiopia	−299.237	51.666	−1.771	0.017	0.092	2.046
Kenya	−155.907	28.809	−0.903	0.011	0.133	2.142

The cubic equation was used to predict the expected cumulative number of confirmed infected cases from June 21 to June 30 with Root Mean Square Error (RMSE) and Mean Percentage Error (MPE) used as performance indicators for the prediction (Table 2):

$$\text{RMSE}={\left[\frac{1}{n}\sum _1^n{\left(\text{Est.}-\text{Obs.}\right)}^2\right]}^{1/2},$$

$$\text{MPE}=\frac{1}{n}\sum _1^n{\left(\frac{\text{Est.}-\text{Obs.}}{\text{Obs.}}\times 100\right)}^2,$$

where $Obs$. and $Est$. are, respectively, the observed and estimated values of the cumulative number of confirmed infected cases and $n$ is the number of observations used. In general, the lower the RMSE and MPE, the better the model. A positive MPE value indicates overestimation in calculated values, while a negative MPE value indicate underestimation. From Table 2, we observe that the lowest and highest RMSE were obtained for Ethiopia and South Africa respectively and the MPEs obtained were of magnitude between $1.022\text{\%–}4.290\text{\%}$ of the actual cumulative number of confirmed infected cases.

Table 2.

Performance indicator for the cubic equation.

South Africa		Egypt		Nigeria
RMSE	MPE $\text{\%}$	RMSE	MPE $\text{\%}$	RMSE	MPE $\text{\%}$
6488.75	−3.005	2616.93	2.716	335.16	1.022
Senegal		Ethiopia		Kenya
RMSE	MPE $\text{\%}$	RMSE	MPE $\text{\%}$	RMSE	MPE $\text{\%}$
279.72	3.047	276.00	2.806	324.42	4.290

3. Model formulation

Here, we propose a new epidemiological model for the COVID-19 epidemic. The proposed model is an extended form of the well-known Susceptible Exposed Infected Recovered (SEIR) compartmental model that takes into account some features such as quarantine, isolation and asymptomatic infections, commonly employed in epidemiological studies of communicable diseases such as, Ebola, Zika, COVID-19, etc [62], [63], [64]. An asymptomatic transmission refers to transmission of the virus through a person, who does not develop any symptoms despite having been infected. The model contains seven epidemiological compartments namely: Susceptible $S\left(t\right)$, Exposed $E\left(t\right)$, Infected $I\left(t\right)$, Asymptomatic $I_A\left(t\right)$, Quarantined $Q\left(t\right)$, Hospitalized $H\left(t\right)$ and Recovered $R\left(t\right)$. The complete flow chart of the interactions between different classes of the proposed model is shown in Fig. 3. The susceptible population $S\left(t\right)$ represents the totality of the entire population that is at risk of being infected with the virus. This population is assumed to be increasing at a constant rate $\Omega$. The increase is not a net increase because $\mu$ is the natural death rate common to all the classes of the population. Exposure and transmission of the virus to the susceptible population involves the action of individuals in the infected class $I\left(t\right)$ and the asymptomatic class $I_A\left(t\right)$. We assume that the infected class consists of people that develop symptoms while the asymptomatic class $I_A\left(t\right)$ involves people that are without symptoms and therefore unaware of their positive COVID-19 status. $\beta$ denotes the rate of disease transmission with $\alpha$ representing a measure of the relative (reduced) effectiveness of individuals in the asymptomatic class as disease spreaders. The spread of the disease to the susceptible population can be controlled by several precautionary measures such as use of soap and sanitizers, lockdown, social distancing and use of face masks and other Personal Protective Equipment (PPE). We assume that $h$ $(0<h<1)$ represents the portion of the population that maintains these precautions with the disease only transmitted to $(1-h)$ portion of the susceptible population. $\theta$ is the infection rate for the model with $p\theta$ and $(1-p)\theta$ the portions of the exposed class $E\left(t\right)$ that go into the infected class $I\left(t\right)$ and asymptomatic class $I_A\left(t\right)$, respectively. The quarantine class $Q\left(t\right)$ involves the quarantining of exposed individuals usually through contact tracing, at a rate ${\eta }_1$ and people who develop symptoms in quarantine are also hospitalized at a rate ${\rho }_1$. As the current procedure in most African countries is to limit testing mostly to people who develop COVID-19 symptoms, we assume that the infectious and symptomatic class $I\left(t\right)$ are tested at a rate ${\eta }_2$ (diagnosis or detection rate of infected symptomatic individuals) and moved into the hospitalized class $H\left(t\right)$. Also, quarantined individuals who develop symptoms are moved to the hospitalized class $H\left(t\right)$ at a rate ${\rho }_1$ while those who do not develop symptoms after $1/{\rho }_2$ days are back into the susceptible population. Let ${\delta }_1$ and ${\delta }_2$ be respectively, the recovery rate of the isolated/hospitalized infected population $H\left(t\right)$ and untreated asymptomatic population $I_A\left(t\right)$ into the recovered population $R\left(t\right)$. ${\gamma }_1$ and ${\gamma }_2$ denote the COVID-19 induced death from the hospitalized and asymptomatic class, respectively with ${\gamma }_2$ usually very small compared to ${\gamma }_1$. $\mu$ is the natural death rate common to all the classes of the population. We assume, based on current scientific evidence, that the COVID-19 deceased are not infectious, and that individuals develop antibodies and become immune to the disease once they are recovered.

Fig. 3.

Flowchart of the COVID-19 Africa model (1).

On the basis of the above assumptions, the nonlinear system of differential equations describing the COVID-19 model used to analysed data from African countries can be written mathematically as:

$$\frac{dS}{dt}=\Omega -\beta (1-h)SI-\alpha \beta (1-h)S{I}_A+{\rho }_{2}Q-\mu S=f_1(S,E,I,I_A,Q,H,R),$$

$$\frac{dE}{dt}=\beta (1-h)SI+\alpha \beta (1-h)S{I}_A-\theta E-{\eta }_{1}E-\mu E=f_2(S,E,I,I_A,Q,H,R),$$

$$\frac{dI}{dt}=p\theta E-{\eta }_{2}I-\mu I=f_3(S,E,I,I_A,Q,H,R)$$

$$\frac{d{I}_A}{dt}=(1-p)\theta E-{\delta }_2{I}_A-{\gamma }_2{I}_A-\mu I_A=f_4(S,E,I,I_A,Q,H,R),$$

$$\frac{dQ}{dt}={\eta }_{1}E-{\rho }_{1}Q-{\rho }_{2}Q-\mu Q=f_5(S,E,I,I_A,Q,H,R),$$

$$\frac{dH}{dt}={\eta }_{2}I-{\delta }_{1}H-{\gamma }_{1}H+{\rho }_{1}Q-\mu H=f_6(S,E,I,I_A,Q,H,R),$$

$$\frac{dR}{dt}={\delta }_{1}H+{\delta }_2{I}_A-\mu R=f_7(S,E,I,I_A,Q,H,R),$$ (1)

with the initial conditions $S\left(0\right)>0$, $E\left(0\right)\ge 0$, $I\left(0\right)>0$, $I_A\left(0\right)\ge 0$, $Q\left(0\right)\ge 0$, $H\left(0\right)\ge 0$ and $R\left(0\right)\ge 0$. At every instant of time, the quantity $D\left(t\right)={\gamma }_{1}H\left(t\right)+{\gamma }_2{I}_A\left(t\right)$ represents the number of deaths caused by the disease at time $t$ while $C\left(t\right)={\eta }_{2}I\left(t\right)+{\rho }_{1}Q\left(t\right)+{\delta }_{1}H\left(t\right)$ represents the total number of confirmed COVID-19 cases at time $t$. Furthermore, let the total size of the population be $N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+I_A\left(t\right)+Q\left(t\right)+H\left(t\right)+R\left(t\right)$. Definitions of the model parameters (1) are presented in Table 3.

Table 3.

Description and unit of model parameters.

Parameter	Description	Unit
$\Omega$	Constant population growth rate	Persons day−1
$\mu$	Natural population death rate	day−1
$\beta$	Effective disease transmission rate	Persons−1 day−1
$\alpha$	Relative infectiousness of class $I_A$ with respect to $I$	dimensionless
$h$	Portion of $S\left(t\right)$ taking precautionary measures	dimensionless
$\theta$	Infection rate (1/Incubation Period)	day−1
$p$	Proportion of symptomatic infections	dimensionless
${\eta }_1$	Quarantine rate of exposed individuals	day−1
${\eta }_2$	Diagnosis or case detection rate	day−1
${\delta }_1$	Recovery rate of isolated/hospitalized individuals	${\text{day}}^{-1}$
${\delta }_2$	Recovery rate of the untreated asymptomatic	${\text{day}}^{-1}$
${\rho }_1$	Isolation rate of individuals from class $Q$ to class $H$	${\text{day}}^{-1}$
${\rho }_2$	Transition rate from class $Q$ to class $S$	${\text{day}}^{-1}$
${\gamma }_1$, ${\gamma }_2$	COVID-19 death rate	${\text{day}}^{-1}$

4. Qualitative analysis of the system

4.1. Positivity of the solutions

Theorem 1

If$S\left(0\right)\ge 0$,$E\left(0\right)\ge 0$,$I\left(0\right)\ge 0$,$I_A\left(0\right)\ge 0$,$Q\left(0\right)\ge 0$,$H\left(0\right)\ge 0$and$R\left(0\right)\ge 0$, then the solutions of system (1) ; $S\left(t\right)$ , $E\left(t\right)$ , $I\left(t\right)$ , $I_A\left(t\right)$ , $Q\left(t\right)$ , $H\left(t\right)$ and $R\left(t\right)$ are positive for all $t>0$ .

Proof

From the first equation of system (1), we have

$$\frac{dS}{dt}=\Omega +{\rho }_{2}Q\left(t\right)-S\left(t\right)\left[\beta (1-h)I\left(t\right)+\alpha \beta (1-h)I_A\left(t\right)+\mu \right]=\Omega +{\rho }_{2}Q\left(t\right)-P_1\left(t\right)S\left(t\right),$$ (2)

where $P_1\left(t\right)=\beta (1-h)I\left(t\right)+\alpha \beta (1-h)I_A\left(t\right)+\mu$. From Eq.  (2), we have

$$\frac{dS}{dt}{e}^{{\int }_0^t{P}_1\left(\tau \right)d\tau }+P_1\left(t\right)S\left(t\right)e^{{\int }_0^t{P}_1\left(\tau \right)d\tau }=\left[\Omega +{\rho }_{2}Q\left(t\right)\right]e^{{\int }_0^t{P}_1\left(\tau \right)d\tau },$$

$$\frac{d}{dt}\left(S\left(t\right)e^{{\int }_0^t{P}_1\left(\tau \right)d\tau }\right)=\left[\Omega +{\rho }_{2}Q\left(t\right)\right]e^{{\int }_0^t{P}_1\left(\tau \right)d\tau },$$

$$S\left(t\right)e^{{\int }_0^t{P}_1\left(\tau \right)d\tau }-S\left(0\right)={\int }_0^t\left[\Omega +{\rho }_{2}Q\left(t\right)\right]e^{{\int }_0^t{P}_1\left(\tau \right)d\tau }dt,$$

$$S\left(t\right)=S\left(0\right)e^{-{\int }_0^t{P}_1\left(\tau \right)d\tau }+e^{-{\int }_0^t{P}_1\left(\tau \right)d\tau }{\int }_0^t\left[\Omega +{\rho }_{2}Q\left(t\right)\right]e^{{\int }_0^t{P}_1\left(\tau \right)d\tau }dt\ge 0.$$ (3)

Eq.  (3) means that the solution of system (1) for $S\left(t\right)$ is positive. Similar expression for $E\left(t\right)$, $I\left(t\right)$, $I_A\left(t\right)$, $Q\left(t\right)$, $H\left(t\right)$ and $R\left(t\right)$ can be obtained from system (1) as

$$E\left(t\right)=E\left(0\right)e^{-P_{2}t}+e^{-P_{2}t}\beta (1-h){\int }_0^t\left[S\left(t\right)I\left(t\right)+\alpha S\left(t\right)I_A\left(t\right)\right]e^{P_{2}t}dt\ge 0,$$ (4)

$$I\left(t\right)=I\left(0\right)e^{-(\mu +{\eta }_2)t}+e^{-(\mu +{\eta }_2)t}p\theta {\int }_0^{t}E\left(t\right)e^{(\mu +{\eta }_2)t}dt\ge 0,$$ (5)

$$I_A\left(t\right)=I_A\left(0\right)e^{-P_{3}t}+e^{-P_{3}t}(1-p)\theta {\int }_0^{t}E\left(t\right)e^{P_{3}t}dt\ge 0,$$ (6)

$$Q\left(t\right)=Q\left(0\right)e^{-(\mu +{\rho }_1+{\rho }_2)t}+e^{-(\mu +{\rho }_1+{\rho }_2)t}{\eta }_1{\int }_0^{t}E\left(t\right)e^{(\mu +{\delta }_2+{\gamma }_2)t}dt\ge 0,$$ (7)

$$H\left(t\right)=H\left(0\right)e^{-P_{4}t}+e^{-P_{4}t}{\int }_0^t\left[{\eta }_{2}I\left(t\right)+{\rho }_{1}Q\left(t\right)\right]e^{P_{4}t}dt\ge 0,$$ (8)

$$R\left(t\right)=R\left(0\right)e^{-\mu t}+e^{-\mu t}{\int }_0^t\left[{\delta }_{1}H\left(t\right)+{\delta }_2{I}_A\left(t\right)\right]e^{\mu t}dt\ge 0,$$ (9)

where $P_2=\mu +\theta +{\eta }_1$, $P_3=\mu +{\delta }_2+{\gamma }_2$ and $P_4=\mu +{\delta }_1+{\gamma }_1$. Therefore, we can say that $S\left(0\right)\ge 0$, $E\left(0\right)\ge 0$, $I\left(0\right)\ge 0$, $I_A\left(0\right)\ge 0$, $Q\left(0\right)\ge 0$, $H\left(0\right)\ge 0$ and $R\left(0\right)\ge 0$ for all $t>0$. This completes the proof.

4.2. Boundedness of the system

Theorem 2

All solutions of system (1) that initiate in ${\Re }_{+}^7$ are bounded uniformly in the region $\chi =\{(S,E,I,I_A,Q,H,R)\in {\Re }_{+}^7:0\le S+E+I+I_A+Q+H+R\le \Omega /\mu \}$ .

Proof

Let $(S\left(t\right),E\left(t\right),I\left(t\right),I_A\left(t\right),Q\left(t\right),H\left(t\right),R\left(t\right))$ be any solution of system (1) with any given non-negative initial condition. Also, let $N\left(0\right)=S\left(0\right)+E\left(0\right)+I\left(0\right)+I_A\left(0\right)+Q\left(0\right)+H\left(0\right)+R\left(0\right)>0$. Then

$$\frac{dN}{dt}=\Omega -\mu (S+E+I+I_A+Q+H+R)-{\gamma }_{1}H-{\gamma }_2{I}_A\le \Omega -\mu N.$$ (10)

Thus, by the differential inequality theory [65], we obtain

$$N\le N\left(0\right)e^{-\mu t}+{\int }_0^t{e}^{-\mu (t-x)}\Omega dx,$$

$$N\le N\left(0\right)e^{-\mu t}+\frac{\Omega }{\mu }\left(1-e^{-\mu t}\right).$$

It thus follows that, for $t\to \infty$,

$$0\le N\left(t\right)\le \frac{\Omega }{\mu }.$$ (11)

This implies that, $\chi$ is positively invariant so that all solutions of (1) with initial conditions in ${\Re }_{+}^7$ are confined in $\chi$.

Furthermore, the interacting functions $f_i(S,E,I,I_A,Q,H,R),i=1-7$ of the system (1) are continuous and have continuous partial derivatives on ${\Re }_{+}^7$. Hence, they are Lipschitzian on ${\Re }_{+}^7$. Additionally, Theorem 2 implies that the solutions of Eq. (1) with initial conditions in ${\Re }_{+}^7$ are uniformly bounded. Therefore, the initial value problem (IVP) is well posed.

4.3. Basic reproduction number

Here, we employ the next generation matrix technique to determine the basic reproduction number ${\mathcal{R}}_0$, representing the number of secondary infections caused by a single infected individual in the entire duration of their infection [59], [60]. The classes which are directly involved in the spread of disease are $E$, $I$, $I_A$ and $Q$. Therefore, from the system equation (1), we obtain the reduced system:

$$\frac{dE}{dt}=\beta (1-h)SI+\alpha \beta (1-h)S{I}_A-\theta E-{\eta }_{1}E-\mu E,$$

$$\frac{dI}{dt}=p\theta E-{\eta }_{2}I-\mu I,$$

$$\frac{d{I}_A}{dt}=(1-p)\theta E-{\delta }_2{I}_A-{\gamma }_2{I}_A-\mu I_A,$$

$$\frac{dQ}{dt}={\eta }_{1}E-{\rho }_{1}Q-{\rho }_{2}Q-\mu Q.$$ (12)

In compact matrix form, system (1) can be written as:

$$\frac{d\mathbf{X}}{dt}=\mathcal{F}\left(\mathbf{X}\right)-\mathcal{V}\left(\mathbf{X}\right),$$ (13)

where $\mathbf{X}={\left(E,I,I_A,Q\right)}^T$,

$$\mathcal{F}=\left(\begin{array}{c}\hfill \beta (1-h)SI+\alpha \beta (1-h)S{I}_A\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$$

and

$$\mathcal{V}=\left(\begin{array}{c}\hfill \theta E+{\eta }_{1}E+\mu E\hfill \\ \hfill -p\theta E+{\eta }_{2}I+\mu I\hfill \\ \hfill -(1-p)\theta E+{\delta }_2{I}_A+{\gamma }_2{I}_A+\mu I_A\hfill \\ \hfill -{\eta }_{1}E+{\rho }_{1}Q+{\rho }_{2}Q+\mu Q\hfill \end{array}\right).$$

In epidemiology, the matrix $\mathcal{F}$ is referred to as the matrix of new infections and $\mathcal{V}$ is the transfer matrix of individuals between compartments. The transition matrices $V$ and $F$ are obtained from the partial derivatives of $\mathcal{V}$ and $\mathcal{F}$ with respect to $E$, $I$, $I_A$ and $Q$, evaluated at the disease-free equilibrium $X_0={\left(\Omega /\mu ,0,0,0\right)}^T$.

$$F=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \frac{\Omega }{\mu }\beta (1-h)\hfill & \hfill \frac{\Omega }{\mu }\alpha \beta (1-h)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),$$

$$V=\left(\begin{array}{cccc}\hfill \mu +\theta +{\eta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -p\theta \hfill & \hfill \mu +{\eta }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -(1-p)\theta \hfill & \hfill 0\hfill & \hfill \mu +{\delta }_2+{\gamma }_2\hfill & \hfill 0\hfill \\ \hfill -{\eta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mu +{\rho }_1+{\rho }_2\hfill \end{array}\right).$$

We define the next generation matrix by $F{V}^{-1}$, where the reproduction number ${\mathcal{R}}_0$ is given by the spectral radius of $F{V}^{-1}$ [60].

$${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)=\frac{(1-h)\beta \theta \Omega }{\mu (\mu +\theta +{\eta }_1)}\left[\frac{p}{\mu +{\eta }_2}+\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}\right].$$ (14)

The reproduction number ${\mathcal{R}}_0$ obtained for the model is the sum of two other reproduction numbers ${\mathcal{R}}_0^A$ and ${\mathcal{R}}_0^B$, where

$${\mathcal{R}}_0^A=\frac{(1-h)\beta \theta \Omega p}{\mu (\mu +\theta +{\eta }_1)(\mu +{\eta }_2)},$$

$${\mathcal{R}}_0^B=\frac{(1-h)\beta \theta \Omega (1-p)\alpha }{\mu (\mu +\theta +{\eta }_1)(\mu +{\delta }_2+{\gamma }_2)}.$$ (15)

${\mathcal{R}}_0^A$ represents the number of secondary infections caused by an infected individual during their time spent in the infected population. It is a measure of the number of the $(1-h)\Omega /\mu$ susceptible population that are infected by $\theta p$ people in the infected group with a bilinear transmission rate $\beta$, with $1/(\mu +{\eta }_2)$ being the time an infected individual remains in the infected group and $1/(\mu +\theta +{\eta }_1)$ being the time an individual remains in the exposed group. ${\mathcal{R}}_0^B$ represents the number of secondary infections because of an asymptomatic individual during their time spent in the asymptotic group. It represents the number of the $(1-h)\Omega /\mu$ susceptible population that are infected by $(1-p)\theta$ people in the asymptomatic group with an enhanced transmission rate $\alpha \beta$ with $1/(\mu +{\delta }_2+{\gamma }_2)$ being the time an individual remains in the asymptomatic group.

4.4. Equilibria of the system

The equilibrium points of the model system (1) are obtained by setting the interacting functions $f_i(S,E,I,I_A,Q,R),i=1-7=0$. The disease-free equilibrium is given by $X_0(\Omega /\mu ,0,0,0,0,0,0)$, while the endemic equilibrium is given by $X_1(S^{\ast },E^{\ast },I^{\ast },I_A^{\ast },Q^{\ast },H^{\ast },R^{\ast })$, where

$$S^{\ast }=\frac{\Omega }{\mu {\mathcal{R}}_0},E^{\ast }=\frac{\Omega ({\mathcal{R}}_0-1)}{{\mathcal{R}}_0\left[(\mu +\theta +{\eta }_1)-{\Delta }_1\right]},$$

$$I^{\ast }=\frac{p\theta }{\mu +{\eta }_2}{E}^{\ast },I_A^{\ast }=\frac{(1-p)\theta }{\mu +{\delta }_2+{\gamma }_2}{E}^{\ast },$$

$$Q^{\ast }=\frac{{\eta }_1}{\mu +{\rho }_1+{\rho }_2}{E}^{\ast },H^{\ast }=\frac{1}{\mu +{\delta }_1+{\gamma }_1}{\Delta }_2{E}^{\ast },$$

$$R^{\ast }=\frac{1}{\mu }\left[\frac{{\delta }_1}{\mu +{\delta }_1+{\gamma }_1}{\Delta }_2+\frac{{\delta }_2(1-p)\theta }{\mu +{\delta }_2+{\gamma }_2}\right]E^{\ast };$$

with ${\Delta }_1={\rho }_2{\eta }_1/(\mu +{\rho }_1+{\rho }_2)$ and ${\Delta }_2=\left(\frac{{\eta }_{2}p\theta }{\mu +{\eta }_2}+\frac{{\rho }_1{\eta }_1}{\mu +{\rho }_1+{\rho }_2}\right)$. We find that the disease-free equilibrium $X_0$ always exists, whereas, the endemic equilibrium $X_1$ is only feasible if ${\mathcal{R}}_0>1$ and $(\mu +\theta +{\eta }_1)>{\Delta }_1$.

4.5. Local stability analysis

Here, we discuss the local asymptotic stability criteria of the equilibria of system (1) by evaluating the Jacobian or community matrix and the resulting characteristic equation. We then examine the signs of the eigenvalues based on the Routh–Hurwitz conditions and/or Descartes rule of sign. It is easy to show that the Jacobian of system (1) is given as:

$$J=\left(\begin{array}{ccccccc}\hfill -{\Delta }_2-\mu \hfill & \hfill 0\hfill & \hfill {\Delta }_3\hfill & \hfill {\Delta }_4\hfill & \hfill {\rho }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\Delta }_2\hfill & \hfill {\Delta }_5\hfill & \hfill -{\Delta }_3\hfill & \hfill -{\Delta }_4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill p\theta \hfill & \hfill -\mu -{\eta }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill (1-p)\theta \hfill & \hfill 0\hfill & \hfill {\Delta }_6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\eta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\Delta }_7\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\eta }_2\hfill & \hfill 0\hfill & \hfill {\rho }_1\hfill & \hfill {\Delta }_8\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\delta }_2\hfill & \hfill 0\hfill & \hfill {\delta }_1\hfill & \hfill -\mu \hfill \end{array}\right),$$ (16)

where ${\Delta }_2=(1-h)\beta I+(1-h)\alpha \beta I_A$, ${\Delta }_3=-(1-h)\beta S$, ${\Delta }_4=-(1-h)\alpha \beta S$, ${\Delta }_5=-\mu -\theta -{\eta }_1$, ${\Delta }_6=-\mu -{\delta }_2-{\gamma }_2$, ${\Delta }_7=-\mu -{\rho }_1-{\rho }_2$ and ${\Delta }_8=-\mu -{\delta }_1-{\gamma }_1$.

Theorem 3

The disease-free equilibrium $X_0\left(\Omega /\mu ,0,0,0,0,0,0\right)$ is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$ .

Proof

The Jacobian matrix of system (1) evaluated at the disease-free equilibrium, $X_0$ is given by

$$J_{X_0}=\left(\begin{array}{ccccccc}\hfill {\omega }_1\hfill & \hfill 0\hfill & \hfill {\omega }_2\hfill & \hfill {\omega }_3\hfill & \hfill {\omega }_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_5\hfill & \hfill -{\omega }_2\hfill & \hfill -{\omega }_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_6\hfill & \hfill {\omega }_7\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_8\hfill & \hfill 0\hfill & \hfill {\omega }_9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_{10}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{12}\hfill & \hfill 0\hfill & \hfill {\omega }_{13}\hfill & \hfill {\omega }_{14}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{15}\hfill & \hfill 0\hfill & \hfill {\omega }_{16}\hfill & \hfill {\omega }_{17}\hfill \end{array}\right),$$ (17)

where, ${\omega }_1=-\mu$, ${\omega }_2=-(1-h)\beta \Omega /\mu$, ${\omega }_3=-(1-h)\alpha \beta \Omega /\mu$, ${\omega }_4={\rho }_2$, ${\omega }_5=-\mu -\theta -{\eta }_1$, ${\omega }_6=p\theta$, ${\omega }_7=-\mu -{\eta }_2$, ${\omega }_8=(1-p)\theta$, ${\omega }_9=-\mu -{\delta }_2-{\gamma }_2$, ${\omega }_{10}={\eta }_1$, ${\omega }_{11}=-\mu -{\rho }_1-{\rho }_2$, ${\omega }_{12}={\eta }_2$, ${\omega }_{13}={\rho }_1$, ${\omega }_{14}=-\mu -{\delta }_1-{\gamma }_1$, ${\omega }_{15}={\delta }_2$, ${\omega }_{16}={\delta }_1$ and ${\omega }_{17}=-\mu$. The characteristic equation of model system (1) evaluated at the disease free equilibrium point, $X_0$, is given by

$$(\lambda -{\omega }_1)(\lambda -{\omega }_{11})(\lambda -{\omega }_{14})(\lambda -{\omega }_{17})({\lambda }^3+A{\lambda }^2+B\lambda +C)=0,$$ (18)

where, $A=-{\omega }_5-{\omega }_7-{\omega }_9$, $B={\omega }_2{\omega }_6+{\omega }_5{\omega }_7+{\omega }_3{\omega }_8+{\omega }_5{\omega }_9+{\omega }_7{\omega }_9$ and $C=-{\omega }_3{\omega }_7{\omega }_8-{\omega }_2{\omega }_6{\omega }_9-{\omega }_5{\omega }_7{\omega }_9$. It is clear from Eq. (18) that the four eigenvalues, ${\omega }_1$, ${\omega }_{11}$, ${\omega }_{14}$ and ${\omega }_{17}$ have negative values and the remaining eigenvalues can be easily obtained by finding the roots of the cubic polynomial in Eq. (18). Applying the Routh–Hurwitz criteria on the cubic polynomial in (18) requires that $A>0$, $C>0$ and $AB>C$ for the other three eigenvalues to be negative or have negative real parts.

$$A=-{\omega }_5-{\omega }_7-{\omega }_9=3\mu +\theta +{\eta }_1+{\eta }_2+{\delta }_2+{\gamma }_2>0,$$

$$C=-{\omega }_3{\omega }_7{\omega }_8-{\omega }_2{\omega }_6{\omega }_9-{\omega }_5{\omega }_7{\omega }_9=(\mu +\theta +{\eta }_1)(\mu +{\eta }_2)(\mu +{\delta }_2+{\gamma }_2)(1-{\mathcal{R}}_0),$$

$$AB=(-{\omega }_5-{\omega }_7-{\omega }_9)({\omega }_2{\omega }_6+{\omega }_5{\omega }_7+{\omega }_3{\omega }_8+{\omega }_5{\omega }_9+{\omega }_7{\omega }_9)={(\mu +{\eta }_2)}^2(\mu +{\delta }_2+{\gamma }_2)+(\mu +{\eta }_2){(\mu +{\delta }_2+{\gamma }_2)}^2+(\mu +\theta +{\eta }_1)(\mu +{\eta }_2)(\mu +{\delta }_2+{\gamma }_2)+{(\mu +\theta +{\eta }_1)}^2(\mu +{\eta }_2)(1-{\mathcal{R}}_0^A)+{(\mu +{\eta }_2)}^2(\mu +\theta +{\eta }_1)(1-{\mathcal{R}}_0^A)+(\mu +\theta +{\eta }_1)(\mu +{\eta }_2)(\mu +{\delta }_2+{\gamma }_2)(1-{\mathcal{R}}_0^A)+{(\mu +\theta +{\eta }_1)}^2(\mu +{\delta }_2+{\gamma }_2)(1-{\mathcal{R}}_0^B)+(\mu +\theta +{\eta }_1)(\mu +{\eta }_2)(\mu +{\delta }_2+{\gamma }_2)(1-{\mathcal{R}}_0^B)+(\mu +\theta +{\eta }_1){(\mu +{\delta }_2+{\gamma }_2)}^2(1-{\mathcal{R}}_0^B)>C.$$

Hence, the Routh–Hurwitz criterion is satisfied if, ${\mathcal{R}}_0<1$ and we may conclude that the COVID-19 model (1) is locally asymptotically stable at the free equilibrium point, $X_0$.

Theorem 4

The disease-endemic equilibrium $X_1(S^{\ast },E^{\ast },I^{\ast },I_A^{\ast },Q^{\ast },H^{\ast },R^{\ast })$ is locally asymptotically stable, if ${\mathcal{R}}_0>1$ and ${\delta }_2+{\gamma }_2-{\eta }_2>0$ and unstable otherwise.

Proof

The Jacobian matrix of system (1) evaluated at the endemic equilibrium, $X_1$ is given by

$$J_{X_1}=\left(\begin{array}{ccccccc}\hfill {\omega }_1\hfill & \hfill 0\hfill & \hfill {\omega }_2\hfill & \hfill {\omega }_3\hfill & \hfill {\omega }_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\omega }_5\hfill & \hfill {\omega }_6\hfill & \hfill -{\omega }_2\hfill & \hfill -{\omega }_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_7\hfill & \hfill {\omega }_8\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_9\hfill & \hfill 0\hfill & \hfill {\omega }_{10}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{13}\hfill & \hfill 0\hfill & \hfill {\omega }_{14}\hfill & \hfill {\omega }_{15}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{16}\hfill & \hfill 0\hfill & \hfill {\omega }_{17}\hfill & \hfill {\omega }_{18}\hfill \end{array}\right),$$ (19)

where,

$${\omega }_1=-\mu ({\mathcal{R}}_0-1)\left(\frac{{\omega }_6{\omega }_{12}}{{\omega }_6{\omega }_{12}-{\omega }_4{\omega }_{11}}\right)-\mu ,{\omega }_2=-(1-h)\beta \Omega /\left(\mu {\mathcal{R}}_0\right),$$

$${\omega }_3=-(1-h)\alpha \beta \Omega /\left(\mu {\mathcal{R}}_0\right),{\omega }_4={\rho }_2,{\omega }_5=\mu ({\mathcal{R}}_0-1)\left(\frac{{\omega }_6{\omega }_{12}}{{\omega }_6{\omega }_{12}-{\omega }_4{\omega }_{11}}\right),$$

$${\omega }_6=-\mu -\theta -{\eta }_1,{\omega }_7=p\theta ,{\omega }_8=-\mu -{\eta }_2,{\omega }_9=(1-p)\theta ,$$

$${\omega }_{10}=-\mu -{\delta }_2-{\gamma }_2,{\omega }_{11}={\eta }_1,{\omega }_{12}=-\mu -{\rho }_1-{\rho }_2,{\omega }_{13}={\eta }_2,$$

$${\omega }_{14}={\rho }_1,{\omega }_{15}=-\mu -{\delta }_1-{\gamma }_1,{\omega }_{16}={\delta }_2,{\omega }_{17}={\delta }_1,\text{and}{\omega }_{18}=-\mu .$$

The characteristic equation of system (1) evaluated at the disease-endemic equilibrium, $X_1$, is given by

$$(\lambda -{\omega }_{15})(\lambda -{\omega }_{18})(a_5{\lambda }^5+a_4{\lambda }^4+a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0)=0,$$ (20)

where

$$a_0={\omega }_5{\omega }_8{\omega }_{10}(-{\omega }_4{\omega }_{11}+{\omega }_6{\omega }_{12}),$$

$$a_1=-{\omega }_5\left({\omega }_8{\omega }_{10}{\omega }_{12}+{\omega }_6{\omega }_8{\omega }_{10}+({\omega }_8+{\omega }_{10})(-{\omega }_4{\omega }_{11}+{\omega }_6{\omega }_{12})\right)+\frac{{\omega }_{12}}{{\omega }_8}\left({\omega }_8+{\omega }_{13}\right)\left({\omega }_2{\omega }_7({\omega }_8-{\omega }_{10})+{\omega }_8^2({\omega }_6+{\omega }_{10})\right),$$

$$a_2=-{\omega }_8({\omega }_6+{\omega }_{10})\left({\omega }_8+{\omega }_{13}\right)-{\omega }_{12}\left({\omega }_8+{\omega }_{13}\right)({\omega }_6+{\omega }_8+{\omega }_{10})-{\omega }_8{\omega }_{12}({\omega }_6+{\omega }_{10})+{\omega }_5\left({\omega }_8{\omega }_{10}+({\omega }_6+{\omega }_{12})({\omega }_8+{\omega }_{10})\right)+{\omega }_5(-{\omega }_4{\omega }_{11}+{\omega }_6{\omega }_{12})-\frac{{\omega }_2{\omega }_7}{{\omega }_8}({\omega }_8-{\omega }_{10})\left({\omega }_8+{\omega }_{12}+{\omega }_{13}\right),$$

$$a_3={\omega }_8^2+{\omega }_{10}{\omega }_{12}-{\omega }_5({\omega }_6+{\omega }_8+{\omega }_{10}+{\omega }_{12})+{\omega }_6(2{\omega }_8+{\omega }_{12}+{\omega }_{13})+\left({\omega }_8+{\omega }_{13}\right)({\omega }_{10}+{\omega }_{12})+{\omega }_8({\omega }_{10}+{\omega }_{12}+{\omega }_{13})+\frac{{\omega }_2{\omega }_7}{{\omega }_8}({\omega }_8-{\omega }_{10}),$$

$$a_4=-{\omega }_1-{\omega }_6-{\omega }_8-{\omega }_{10}-{\omega }_{12}>0,$$

$$a_5=1>0.$$

It is clear from Eq. (20) that the two eigenvalues, ${\omega }_{15}$ and ${\omega }_{18}$ are negative, and that the remaining five eigenvalues are roots of the quintic polynomial in (20). Using ${\mathcal{R}}_0>1$, ${\omega }_8-{\omega }_{10}={\delta }_2+{\gamma }_2-{\eta }_2>0$ and $-{\omega }_4{\omega }_{11}+{\omega }_6{\omega }_{12}>0$ guaranteed by the feasibility condition $(\mu +\theta +{\eta }_1)>{\Delta }_1$ of the endemic equilibrium, we observe that $a_i,i=1-5>0$. By employing the Descartes’ rule of signs, we find that the number of positive eigenvalues of the quintic polynomial given in Eq. (20) is equal to the number of sign-changes from $a_5$ to $a_1$, which equals zero. Hence, the system (1) is locally asymptotically stable if ${\mathcal{R}}_0>1$ and ${\delta }_2+{\gamma }_2-{\eta }_2>0$.

4.6. Global stability analysis

Theorem 5

The disease-free equilibrium $X_0\left(\Omega /\mu ,0,0,0,0,0,0\right)$ is globally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$ .

Proof

Consider the Lyapunov function $L(E,I)={\kappa }_{1}E+{\kappa }_{2}I$, where ${\kappa }_1$ and ${\kappa }_2$ are non-negative parameters. It is easy to see that $L(E,I)\in C^1$. Also, $L_{X_0}(E,I)=0$ and it is positive definite $\forall$ $(S,E,I,I_A,Q,H,R)\in {\Re }_{+}^7$.

$$\frac{dL}{dt}={\kappa }_1\dot{E}+{\kappa }_2\dot{I}.$$ (21)

Replacing $\dot{E}$ and $\dot{I}$, from system (1) into Eq. (21) yields

$$\frac{dL}{dt}={\kappa }_1\beta (1-h)SI+{\kappa }_2\alpha \beta (1-h)S{I}_A-{\kappa }_2(\mu +{\eta }_2)I-({\kappa }_1(\mu +\theta +{\eta }_1)-{\kappa }_{2}p\theta )E.$$ (22)

Choosing ${\kappa }_1=p\theta$, ${\kappa }_2=(\mu +\theta +{\eta }_1)$ and plugging $S=\Omega /\mu$ and $I_A=0$, we have

$$\frac{dL}{dt}=\left[\beta (1-h)\frac{\Omega }{\mu }p\theta -(\mu +{\eta }_2)(\mu +\theta +{\eta }_1)\right]I=(\mu +{\eta }_2)(\mu +\theta +{\eta }_1)({\mathcal{R}}_0^A-1)I.$$ (23)

Since ${\mathcal{R}}_0^A<1$ follows from ${\mathcal{R}}_0<1$, therefore, it is clear that $dL/dt<0$, when ${\mathcal{R}}_0<1$ and also $dL/dt=0$, if $I=0$. Hence, by LaSalle’s Invariance principle [66], [67], the disease-free equilibrium $X_0$ is globally asymptotically stable.

Theorem 6

If ${\mathcal{R}}_0>1$ , then there exist a disease-endemic equilibrium $X_1$ and it is globally asymptotically stable in the interior of $\chi$ .

Proof

Given that ${\mathcal{R}}_0>1$, then the existence and local asymptotic stability of the disease-endemic equilibrium is guaranteed. Consider the Lyapunov function

$$L(E,I,I_A,Q,H)=E-E^{\ast }-E^{\ast }ln\left(\frac{E}{E^{\ast }}\right)+I-I^{\ast }-I^{\ast }ln\left(\frac{I}{I^{\ast }}\right)+I_A-I_A^{\ast }-I_A^{\ast }ln\left(\frac{I_A}{I_A^{\ast }}\right)+Q-Q^{\ast }-Q^{\ast }ln\left(\frac{Q}{Q^{\ast }}\right)+H-H^{\ast }-H^{\ast }ln\left(\frac{H}{H^{\ast }}\right).$$ (24)

The time derivative of $L$ is given by

$$\dot{L}=\left(1-\frac{E^{\ast }}{E}\right)\dot{E}+\left(1-\frac{I^{\ast }}{I}\right)\dot{I}+\left(1-\frac{I_A^{\ast }}{I_A}\right)\dot{I_A}+\left(1-\frac{Q^{\ast }}{Q}\right)\dot{Q}+\left(1-\frac{H^{\ast }}{H}\right)\dot{H}=\left(1-\frac{E^{\ast }}{E}\right)\left[\beta (1-h)SI+\alpha \beta (1-h)S{I}_A-(\mu +\theta +{\eta }_1)E\right]+\left(1-\frac{I^{\ast }}{I}\right)\left[p\theta E-(\mu +{\eta }_2)I\right]+\left(1-\frac{I_A^{\ast }}{I_A}\right)\left[(1-p)\theta E-(\mu +{\gamma }_2+{\delta }_2)I_A\right]+\left(1-\frac{Q^{\ast }}{Q}\right)\left[{\eta }_{1}E-(\mu +{\rho }_1+{\rho }_2)Q\right]+\left(1-\frac{H^{\ast }}{H}\right)\left[{\eta }_{2}I+{\rho }_{1}Q-(\mu +{\gamma }_1+{\delta }_1)H\right].$$ (25)

However, at the endemic state, we have

$$\beta (1-h)S^{\ast }{I}^{\ast }+\alpha \beta (1-h)S^{\ast }{I}_A^{\ast }=(\mu +\theta +{\eta }_1)E^{\ast },p\theta E^{\ast }=(\mu +{\eta }_2)I^{\ast }(1-p)\theta E^{\ast }=(\mu +{\gamma }_2+{\delta }_2)I_A^{\ast },{\eta }_1{E}^{\ast }=(\mu +{\rho }_1+{\rho }_2)Q^{\ast },{\eta }_2{I}^{\ast }+{\rho }_1{Q}^{\ast }=(\mu +{\gamma }_1+{\delta }_1)H^{\ast }.$$ (26)

Then using Eq. (26) in Eq. (25), we have

$$\dot{L}=\beta (1-h)SI\left(1-\frac{E^{\ast }}{E}\right)+\beta (1-h)S^{\ast }{I}^{\ast }\left(1-\frac{E}{E^{\ast }}\right)+\alpha \beta (1-h)S{I}_A\left(1-\frac{E^{\ast }}{E}\right)+\alpha \beta (1-h)S^{\ast }{I}_A^{\ast }\left(1-\frac{E}{E^{\ast }}\right)+p\theta E\left(1-\frac{I^{\ast }}{I}\right)+p\theta E^{\ast }\left(1-\frac{I}{I^{\ast }}\right)+(1-p)\theta E\left(1-\frac{I_A^{\ast }}{I_A}\right)+(1-p)\theta E^{\ast }\left(1-\frac{I_A}{I_A^{\ast }}\right)+{\eta }_{1}E\left(1-\frac{Q^{\ast }}{Q}\right)+{\eta }_1{E}^{\ast }\left(1-\frac{Q}{Q^{\ast }}\right)+{\eta }_{2}I\left(1-\frac{H^{\ast }}{H}\right)+{\eta }_2{I}^{\ast }\left(1-\frac{H}{H^{\ast }}\right)+{\rho }_{1}Q\left(1-\frac{H^{\ast }}{H}\right)+{\rho }_1{Q}^{\ast }\left(1-\frac{H}{H^{\ast }}\right).$$ (27)

Since $E\le E^{\ast }$, $I\le I^{\ast }$, $I_A\le I_A^{\ast }$, $Q\le Q^{\ast }$ and $H\le H^{\ast }$, then Eq. (27) becomes

$$\dot{L}\le \beta (1-h)S^{\ast }{I}^{\ast }\left(2-\frac{E^{\ast }}{E}-\frac{E}{E^{\ast }}\right)+\alpha \beta (1-h)S^{\ast }{I}_A^{\ast }\left(2-\frac{E^{\ast }}{E}-\frac{E}{E^{\ast }}\right)+p\theta E^{\ast }\left(2-\frac{I^{\ast }}{I}-\frac{I}{I^{\ast }}\right)+(1-p)\theta E^{\ast }\left(2-\frac{I_A^{\ast }}{I_A}-\frac{I_A}{I_A^{\ast }}\right)+{\eta }_1{E}^{\ast }\left(2-\frac{Q^{\ast }}{Q}-\frac{Q}{Q^{\ast }}\right)+{\eta }_2{I}^{\ast }\left(2-\frac{H^{\ast }}{H}-\frac{H}{H^{\ast }}\right)+{\rho }_1{Q}^{\ast }\left(2-\frac{H^{\ast }}{H}-\frac{H}{H^{\ast }}\right).$$ (28)

It follows from arithmetic–geometric inequality that

$$\left(2-\frac{E^{\ast }}{E}-\frac{E}{E^{\ast }}\right)\le 0,\left(2-\frac{I^{\ast }}{I}-\frac{I}{I^{\ast }}\right)\le 0,\left(2-\frac{I_A^{\ast }}{I_A}-\frac{I_A}{I_A^{\ast }}\right)\le 0,$$

$$\left(2-\frac{Q^{\ast }}{Q}-\frac{Q}{Q^{\ast }}\right)\le 0,\left(2-\frac{H^{\ast }}{H}-\frac{H}{H^{\ast }}\right)\le 0.$$ (29)

Therefore, $\dot{L}\le 0$ and also $\dot{L}=0$, only if $E=E^{\ast }$, $I=I^{\ast }$, $I_A=I_A^{\ast }$, $Q=Q^{\ast }$ and $H=H^{\ast }$. Hence, by LaSalle’s Invariance principle [66], [67], the endemic equilibrium $X_1$ is globally asymptotically stable.

5. Numerical simulations

We now carry out numerical simulations to compare our proposed COVID-19 Africa model (1) to the data for cumulative number of confirmed infected cases obtained from the World Health Organization (WHO) [61] for South Africa, Egypt, Nigeria, Senegal, Ethiopia and Kenya. The starting point of our simulation will be a day before the index case was recorded in each country. The demographical parameters $\Omega$ and $\mu$ are estimated from the total population size ($N_0$) and life expectancy (L.E.) data obtained from the 2018 United Nations data bank [68]. For example, Nigeria has a life expectancy of 54.332 years with population size estimate of $200,963,599$. Hence, the average death rate, ($\mu$), used for the simulation will be $1/(54.332\times 365)=5.04\times 10^{-5}$/day with constant population growth rate, $\Omega =\mu N_0=10,128.57$. We assume that the proportion of new infections that are symptomatic, ($p$), is 60% and the portion of the susceptible population taking precautionary measures, ($h$), is 30% for all the countries except 40% used for South Africa and Egypt [69], [70]. The relative infectiousness of the asymptomatic class, ($\alpha$), is set to 0.5 [40], [71]. It is assumed that individuals in quarantine, either develop symptoms after an average of 7 days and are moved to isolation/hospitalization at a rate ${\rho }_1=(1/7)=0.143$/day or are released from quarantine, after an average of 14 days without developing symptoms, into the susceptible population at a rate ${\rho }_2=(1/14)=0.0714$/day. The average remission time is set to 14 days and 7 days for individuals in the hospitalized and asymptomatic classes respectively. Hence, the recovery rates ${\delta }_1=0.0714$/day and ${\delta }_2=0.143$/day were used in the model simulations. The COVID-19-induced death rates (${\gamma }_1$, ${\gamma }_2$) are estimated from the percentage of case fatalities recorded. The remaining parameters, the effective disease transmission rate ($\beta$), infection rate ($\theta$), quarantine rate of exposed individuals (${\eta }_1$) and diagnosis/case detection rate (${\eta }_2$) are obtained from fitting the model to the data using the NonlinearModelFit function in Mathematica. Table 4 gives the values of the parameters used in the simulations. The following values of the initial conditions were also used for all the simulated countries: $S\left(0\right)=N_0$, $E\left(0\right)=0$, $I\left(0\right)=1$, $I_A\left(0\right)=0$, $Q\left(0\right)=0$, $H\left(0\right)=0$ and $R\left(0\right)=0$. Moreover, the simulations and parameter estimations were performed such that new initial conditions and new values of fitting parameters were obtained whenever the percentage daily increase in cases was more than 30%. This approach divided the time evolution of the pandemic for the cumulative number of confirmed infected cases into different regimes or intervals, which we refer to as phases. (Note that this definition of phase is quite distinct from an interval of constant conditions determined by e.g. a particular “Tier” or level of lockdown restrictions as used in the UK.) South Africa, Egypt, Nigeria and Kenya all have two phases of the infection, and Senegal has three phases, while Ethiopia has only one phase of the infection. Table 5 gives the estimated values of the parameters $\beta$, $\theta$, ${\eta }_1$ and ${\eta }_2$, as well as the calculated reproduction number ${\mathcal{R}}_0$ for the different phases of the infection for all the countries. Fig. 4 gives the results of the numerical simulations for the different phases of the infection for all the countries. From Fig. 4, we observe that our model (1) was well-fitted to the actual data for cumulative number of confirmed infected cases for all the countries, with values of ${\mathcal{R}}_0$ between 1.374 and 9.179 and ${\mathcal{R}}_0$ highest during the first phase of the infection for all the countries. The observed decrease in the ${\mathcal{R}}_0$ values beyond the first phase may be due to the impact of the strict lockdown measure and other preventive policies enforced by the authorities.

Table 4.

Parameters used for numerical simulation.

Parameters	South Africa	Egypt	Nigeria	Senegal	Ethiopia	Kenya	Status
L.E.	63.857	71.825	54.332	67.665	66.240	66.342	[68]
$N_0$	$58,558,270$	$100,388,073$	$200,963,599$	$16,296,364$	$112,078,730$	$52,573,973$	[68]
$\mu$	$4.290\times 10^{-5}$	$3.814\times 10^{-5}$	$5.040\times 10^{-5}$	$4.049\times 10^{-5}$	$4.136\times 10^{-5}$	$4.130\times 10^{-5}$	${(365L.E.)}^{-1}$
$\Omega$	2512.389	3829.249	10128.565	659.833	4635.643	2171.148	$\mu N_0$
$\alpha$	0.5	0.5	0.5	0.5	0.5	0.5	Assumed
$h$	0.4	0.4	0.3	0.3	0.3	0.3	Assumed
$p$	0.6	0.6	0.6	0.6	0.6	0.6	Assumed
${\delta }_1$	0.0714	0.0714	0.0714	0.0714	0.0714	0.0714	$1/14$
${\delta }_2$	0.143	0.143	0.143	0.143	0.143	0.143	$1/7$
${\rho }_1$	0.143	0.143	0.143	0.143	0.143	0.143	$1/7$
${\rho }_2$	0.0714	0.0714	0.0714	0.0714	0.0714	0.0714	$1/14$
${\gamma }_1$	0.02	0.039	0.021	0.014	0.016	0.027	Assumed
${\gamma }_2$	0.005	0.0098	0.005	0.004	0.004	0.007	Assumed

Table 5.

Fitted parameters for different phases of the infection.

Countries	Phase	$\beta$	$\theta$	${\eta }_1$	${\eta }_2$	${\mathcal{R}}_0$
South Africa	1	$7.663\times 10^{-8}$	0.226	0.487	0.072	8.290
	2	$5.268\times 10^{-8}$	0.0095	0.035	0.073	3.794
Egypt	1	$1.426\times 10^{-8}$	0.243	0.073	0.079	5.906
	2	$4.385\times 10^{-9}$	0.246	0.059	0.083	1.825
Nigeria	1	$5.201\times 10^{-9}$	0.264	0.058	0.153	3.162
	2	$2.509\times 10^{-9}$	0.438	0.124	0.165	1.374
Senegal	1	$1.284\times 10^{-7}$	0.252	0.200	0.078	7.409
	2	$3.478\times 10^{-8}$	0.362	0.329	0.107	1.453
	3	$4.429\times 10^{-8}$	0.234	0.478	0.071	1.623
Ethiopia	1	$1.016\times 10^{-8}$	0.258	0.538	0.074	2.452
	2	$2.121\times 10^{-8}$	0.130	0.350	0.287	1.559
Kenya	1	$4.249\times 10^{-8}$	0.240	0.106	0.084	9.179
	2	$9.998\times 10^{-9}$	0.064	0.028	0.074	2.417

Fig. 4.

Cumulative number of confirmed infected cases by COVID-19 as a function of time for South Africa, Egypt, Nigeria, Senegal, Ethiopia and Kenya. The black dots corresponds to the real data while the blue continuous line represents the simulation from model (1).

6. Elasticity and sensitivity analysis of ${\mathcal{R}}_0$

Here, we analyse the elasticity and sensitivity of the reproduction number, ${\mathcal{R}}_0$. Sensitivity analysis is a well known technique for identifying the critical parameters or inputs of a model and quantifying their importance relative to one another [58]. For the purpose of elasticity and sensitivity analysis, we used data from Nigeria as a case study. The baseline values and ranges of the system parameters used here are given in Table 6.

Table 6.

Baseline values and ranges of the system parameters.

Parameter	Baseline value	Range
$\Omega$	10128.565 ${\text{day}}^{-1}$	$\left[10000,10200\right]$${\text{day}}^{-1}$
$\mu$	$5.040\times 10^{-5}$${\text{day}}^{-1}$	$\left[4.8\times 10^{-5},5.2\times 10^{-5}\right]$${\text{day}}^{-1}$
$\beta$	$2.509\times 10^{-9}$${\text{day}}^{-1}$	$\left[1\times 10^{-9},4\times 10^{-9}\right]$${\text{day}}^{-1}$
$\alpha$	0.5	$\left[0.3,0.7\right]$
$h$	0.3	$\left[0.2,0.5\right]$
$\theta$	0.438 ${\text{day}}^{-1}$	$\left[0.2,0.6\right]$${\text{day}}^{-1}$
$p$	0.6	$\left[0.4,0.75\right]$
${\eta }_1$	0.124 ${\text{day}}^{-1}$	$\left[0.05,0.2\right]$${\text{day}}^{-1}$
${\eta }_2$	0.165 ${\text{day}}^{-1}$	$\left[0.08,0.25\right]$${\text{day}}^{-1}$
${\delta }_2$	0.143 ${\text{day}}^{-1}$	$\left[0.05,0.2\right]$${\text{day}}^{-1}$
${\gamma }_2$	0.005 ${\text{day}}^{-1}$	$\left[0.0035,0.008\right]$${\text{day}}^{-1}$

In order to perform the elasticity analysis of ${\mathcal{R}}_0$, we first calculated the normalized forward sensitivity index. In general, the elasticity (normalized forward sensitivity index) of a variable, $u$, that depends differentiably on a parameter, $\phi$, is given as [72]:

$${\varpi }_{\phi }^u=\frac{\partial u}{\partial \phi }\times \frac{\phi }{u}.$$ (30)

A negative (or positive) sensitivity index indicates a decrease (or an increase) in the value of the parameter $\phi$ resulting in a decrease (or an increase) in the value of $u$. For, ${\mathcal{R}}_0$, we obtain the following:

$${\varpi }_{\Omega }^{{\mathcal{R}}_0}=1,{\varpi }_{\mu }^{{\mathcal{R}}_0}=-1-\frac{\mu }{\mu +\theta +{\eta }_1}-\frac{\mu \left(\frac{(1-p)\alpha }{{(\mu +{\delta }_2+{\gamma }_2)}^2}+\frac{p}{{(\mu +{\eta }_2)}^2}\right)}{\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}},{\varpi }_{\beta }^{{\mathcal{R}}_0}=1,$$

$${\varpi }_{\alpha }^{{\mathcal{R}}_0}=\frac{\alpha (1-p)(\mu +{\eta }_2)}{\alpha (1-p)(\mu +{\eta }_2)+p(\mu +{\delta }_2+{\gamma }_2)},{\varpi }_h^{{\mathcal{R}}_0}=\frac{h}{h-1},{\varpi }_{\theta }^{{\mathcal{R}}_0}=\frac{\mu +{\eta }_1}{\mu +\theta +{\eta }_1}.$$

$${\varpi }_p^{{\mathcal{R}}_0}=\frac{-\frac{p\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}}{\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}},{\varpi }_{{\eta }_1}^{{\mathcal{R}}_0}=\frac{-{\eta }_1}{\mu +\theta +{\eta }_1},{\varpi }_{{\eta }_2}^{{\mathcal{R}}_0}=\frac{-p{\eta }_2}{{(\mu +{\eta }_2)}^2\left(\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}\right)},$$

$${\varpi }_{{\delta }_2}^{{\mathcal{R}}_0}=\frac{-(1-p)\alpha {\delta }_2}{{(\mu +{\delta }_2+{\gamma }_2)}^2\left(\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}\right)},{\varpi }_{{\gamma }_2}^{{\mathcal{R}}_0}=\frac{-(1-p)\alpha {\gamma }_2}{{(\mu +{\delta }_2+{\gamma }_2)}^2\left(\frac{(1-p)\alpha }{\mu +{\delta }_2+{\gamma }_2}+\frac{p}{\mu +{\eta }_2}\right)}.$$

The elasticity or sensitivity index shows the influence of change in one parameter while keeping all other parameters constant. Note that the sensitivity indices of $\Omega$ and $\beta$ do not depend on any parameter value. Interestingly, the reproduction number ${\mathcal{R}}_0$ does not depend on the recovery rate of the hospitalized individuals (${\delta }_1$), or on the isolation rate of quarantined individuals (${\rho }_1$), or on the transition rate from quarantine class to susceptible class after quarantine (${\rho }_2$), or on the COVID-19-induced death rate of the hospitalized cases (${\gamma }_1$). We proceed to evaluate the above sensitivity indices using the baseline parameter values in Table 6. A plot showing the sensitivity indices for ${\mathcal{R}}_0$ with respect to its constituent parameters is presented in Fig. 5, from which we can state that ${\mathcal{R}}_0$ increases whenever $\Omega$, $\beta$ $\alpha$, $\theta$, or $p$ increase. On the other hand, whenever $\mu$, $h$, ${\eta }_1$, ${\eta }_2$, ${\delta }_2$ or ${\gamma }_2$ increase, then ${\mathcal{R}}_0$ decreases. For example, ${\varpi }_{\alpha }^{{\mathcal{R}}_0}=0.271$ implies that increasing $\alpha$ by 10% will increase ${\mathcal{R}}_0$ by 2.71%. Hence, a similar interpretation can be inferred for the remaining parameters in Table 6. Following the elasticity analysis, the most positive sensitivity index was obtained for $\beta$ with a 10% increase in $\beta$ leading to the same proportional increase in ${\mathcal{R}}_0$. Note that the same value of positive sensitivity index as $\beta$ was obtained for $\Omega$. However, $\Omega$ is a demographic variable that cannot be changed in the field. The controllable parameter with the most negative sensitivity index was ${\eta }_2$. With a 10% increase in ${\eta }_2$, a decrease of 7.29% in ${\mathcal{R}}_0$ was found. We observe that the most significant parameters are the effective disease transmission rate ($\beta$), the disease diagnosis or case detection rate (${\eta }_2$), and the proportion of susceptible individuals taking precautions ($h$). Therefore, we can conclude that efforts at controlling the disease should concentrate on decreasing the transmission rate through contact reduction via lockdown and social distancing measures. In addition, $h$ can be increased by encouraging social campaigns aimed at increasing the number of individuals taking precautionary measures such as regular hand washing with soap and use of sanitizers, use of face mask and other PPEs.

Fig. 5.

Plot showing sensitivity indices of ${\mathcal{R}}_0$ as a function of its constituent parameters.

For the sensitivity analysis of the reproduction number, ${\mathcal{R}}_0$, the Latin Hypercube Sampling (LHS) technique [73] was implemented for the parameters of the model. The correlation between ${\mathcal{R}}_0$ and the input parameter values obtained from 1000 simulations was quantified using Partial Rank Correlation Coefficients (PRCC). The sensitivity analysis results of ${\mathcal{R}}_0$, shown in Fig. 6 demonstrate that the parameters with the greatest influence on ${\mathcal{R}}_0$ are $\beta$, ${\eta }_2$, $h$, ${\delta }_2$, and $\theta$ in order of decreasing sensitivity. Clearly, the sensitivity analysis results are similar to those of the elasticity analysis, as the parameters $\beta$, ${\eta }_2$, and $h$, identified via sensitivity indices as being the most significant parameters, are also the most sensitive parameters. It is noteworthy that, though the demographic parameters, $\Omega$ and $\mu$ had sensitivity indices of $1$ and $-1$, respectively, the results of the sensitivity analysis shows that they have insignificant influence on ${\mathcal{R}}_0$ due to their very low PRCC values.

Fig. 6.

Plot of partial rank correlation coefficient showing the influence of input parameters on ${\mathcal{R}}_0$.

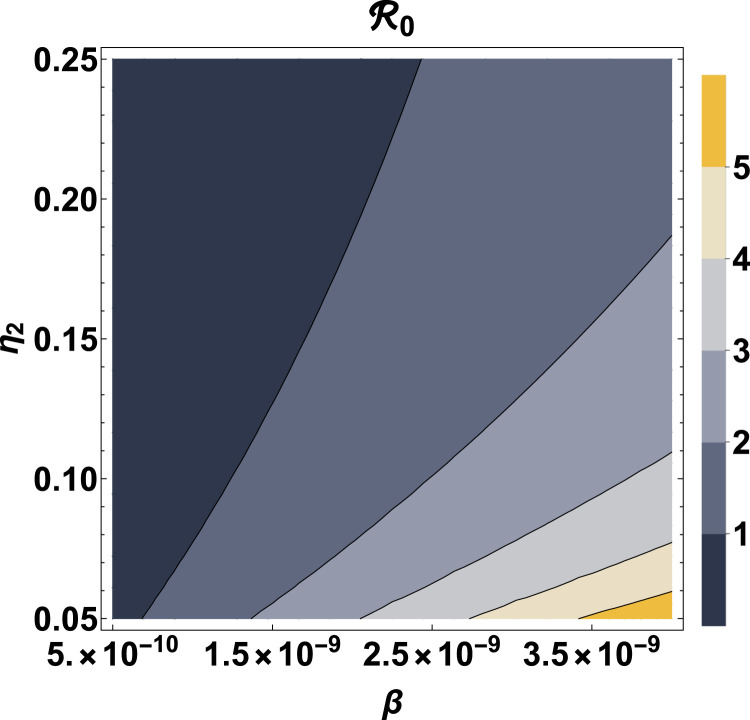
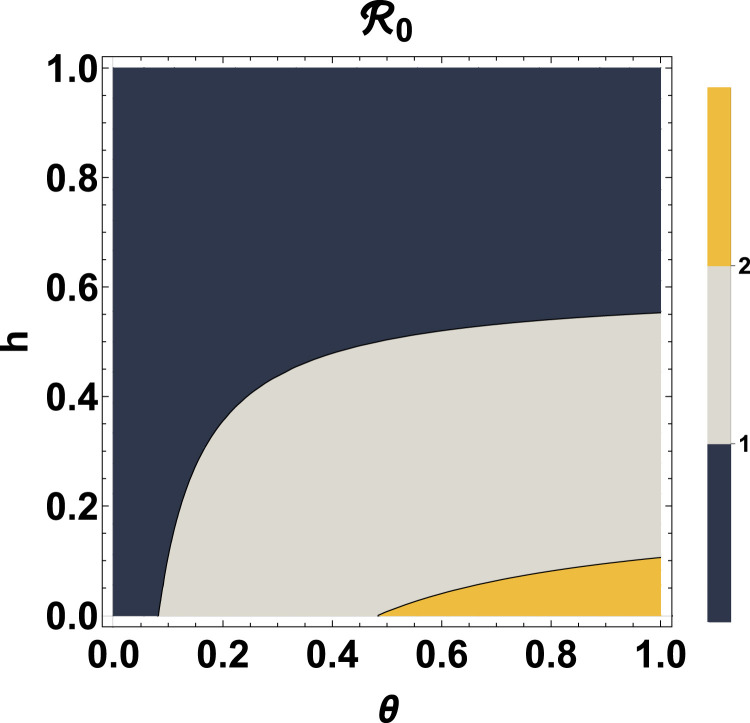
Fig. 7, Fig. 8 provide contour plots of the reproduction number ${\mathcal{R}}_0$ as a function of the parameter pairs $(\beta ,{\eta }_2)$ and $(\theta ,h)$, respectively. From Fig. 7, we observe that for an effective disease transmission rate, $\beta <6.839\times 10^{-10}$, ${\mathcal{R}}_0$ is always less than 1, indicating that, eventually the disease will die out in the population regardless of the value of the diagnosic or case detection rate (${\eta }_2$). For increase in the value of $\beta$, ${\mathcal{R}}_0$ can be kept under 1 by also increasing ${\eta }_2$. If $\beta >1.368\times 10^{-9}$ and ${\eta }_2<0.187$/day, then ${\mathcal{R}}_0>2$. Also, if $\beta >2.052\times 10^{-9}$ and ${\eta }_2<0.109$/day, then ${\mathcal{R}}_0>3$. Fig. 8 shows that if the disease infection rate, $\theta$ is less than 0.082/day, then ${\mathcal{R}}_0$ is always less than $1$ regardless of the proportion of susceptible individuals taking precautions ($h$). Another remarkable observation from Fig. 8 is that, if at least 55.29% of the susceptible population adheres to the prescribed precautions, such as regular hand washing with the use of soap, use of sanitizers and face masks, then the reproduction number ${\mathcal{R}}_0$ can be kept below unity regardless of the value of the disease infection rate. This result is in agreement with previous studies carried out for Lagos, Nigeria, where at least 55% of the population effectively making use of face masks while in public was recommended for the reproduction number of the disease to be brought below 1 [40]. Moreover, if less than 10.58% of the susceptible population take the prescribed precautions with a disease infection rate greater than 0.483, then ${\mathcal{R}}_0>2$.

Fig. 7.

Contour plot of ${\mathcal{R}}_0$ as a function of $\beta$ and ${\eta }_2$.

Fig. 8.

Contour plot of ${\mathcal{R}}_0$ as a function of $\theta$ and $h$.

Fig. 9 shows the influence of the variation in the model parameters on the progression of the number of active cases. The plots in Fig. 9 were obtained by simulating the model (1) numerically using different values of the system parameters, $\beta$, ${\eta }_2$, $\theta$ and $h$, while other parameters were kept constant. We observe that variations in the parameters have significant influence on the maximum of the infection and the number of days taken to reach this maximum. Notably, for an increase in the values of $\beta$ and $\theta$, there is a corresponding increase in the maximum infection in addition to this value being attained on a later day. For infection rates of 0.4, 0.5, 0.6 and 0.7, maxima of about 850,000, 750,000, 610,000 and 460,000 may be reached after about $280$, $310$, $350$ and $420$ days, respectively. For diagnostic or case detection rates of 0.10, 0.13, 0.16 and 0.18, maxima of about 1.5 million, $1$ million, 590,000 and 370,000 may be reached after about $220$, $280$, $370$ and $460$ days, respectively. If 15% of the susceptible population takes precautions, then the projection in Fig. 9 shows that the number of active cases may attain about 1.2 million by around the 240th day of the infection. Alternatively, with 35% of the population taking precautionary measures, then the number of active cases may reach around 320,000 by around the 510th day of the infection.

Fig. 9.

Figure showing the effect of the model parameters ($\beta$, ${\eta }_2$, $\theta$, $h$) on the number of active cases.

7. Fractional model with Atangana–Balenau derivative

Fractional models with the Atangana–Balenau fractional derivative provide more efficient results than the ordinary derivative models [46], [47], [51], [57], [74], [75], [76], [77], [78]. We begin here by defining the Atangana–Balenau fractional derivative and its integral.

Definition 7.1

Let $g\in H^1(a_1,a_2)$, $a_2>a_1$, $\sigma \in [0,1]$,. The Atangana–Balenau fractional derivative is then defined [46] as:

$${}_{a_1}^{ABC}{D}_t^{\sigma }g\left(t\right)=\frac{B\left(\sigma \right)}{1-\sigma }{\int }_{a_1}^t{g}^{\prime }\left(\zeta \right)E_{\sigma }\left[-\sigma \frac{{(t-\zeta )}^{\sigma }}{1-\sigma }\right]d\zeta ,$$ (31)

and the associated fractional integral of the Atangana–Balenau derivative is defined as [46]:

$${}_{a_1}^{ABC}{I}_t^{\sigma }g\left(t\right)=\frac{1-\sigma }{B\left(\sigma \right)}g\left(t\right)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_{a_1}^{t}g\left(\zeta \right){(t-\zeta )}^{\sigma -1}d\zeta ,$$ (32)

where $B\left(\sigma \right)$ is the normalization function satisfying $B\left(0\right)=B\left(1\right)=1$, and $E_{\sigma }(.)$ is the Mittag-Leffer function with one parameter.

Definition 7.2

The Mittag-Leffler function with one parameter is defined [46] as

$$E_{\sigma }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\sigma k+1)},\sigma >0,z\in \mathbf{C}.$$ (33)

We generalize the model (1) by applying the Atangana–Baleanu derivative and thus obtain the following fractional COVID-19 model for Africa:

$${}_0^{ABC}{D}_t^{\sigma }S=\Omega -\beta (1-h)SI-\alpha \beta (1-h)S{I}_A+{\rho }_{2}Q-\mu S=f_1(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }E=\beta (1-h)SI+\alpha \beta (1-h)S{I}_A-\theta E-{\eta }_{1}E-\mu E=f_2(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }I=p\theta E-{\eta }_{2}I-\mu I=f_3(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }{I}_A=(1-p)\theta E-{\delta }_2{I}_A-{\gamma }_2{I}_A-\mu I_A=f_4(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }Q={\eta }_{1}E-{\rho }_{1}Q-{\rho }_{2}Q-\mu Q=f_5(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }H={\eta }_{2}I-{\delta }_{1}H-{\gamma }_{1}H+{\rho }_{1}Q-\mu H=f_6(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }R={\delta }_{1}H+{\delta }_2{I}_A-\mu R=f_7(S,E,I,I_A,Q,H,R),$$ (34)

where $D_t^{\sigma }$ is the fractional derivative and $\sigma$ represents the fractional order parameter.

The numerical results for the fractional model (34) were obtained by following the procedure described in the Appendix in which the modified Adams–Bashforth scheme developed by Toufik and Atangana [78] was adopted. Readers are referred to some very recent applications of the modified Adams–Bashforth scheme [47], [48], [49], [79]. Fig. 10 shows the dependence of the number of active cases, infectious and symptomatic class, asymptomatic class and the hospitalized class from the fractional model (36) on the magnitude of the order of the fractional derivative, $\sigma$. Fig. 10 was obtained by using the initial conditions $S\left(0\right)=N_0$, $E\left(0\right)=0$, $I\left(0\right)=1$, $I_A\left(0\right)=0$, $Q\left(0\right)=0$, $H\left(0\right)=0$ and $R\left(0\right)=0$ and performing numerical simulation of the fractional model (36) using the modified Adams–Bashforth scheme (39)–(45) for $\sigma =1.0$, 0.95 and 0.9. The result shows that the magnitude of $\sigma$ has a marked impact on the day the maximum is reached, with a right shift in the time at which this happens as $\sigma$ decreases from 1.0. However, the order of the fractional derivative ($\sigma$) has only an insignificant effect on the projected peak numbers of active cases. Specifically, for $\sigma =1.0$, 0.95 and 0.9, the peak numbers of active cases were approximately 590,000, 570,000, 550,000 by about the 370th, 440th and 540th day after the first case of the infection was recorded, respectively. Hence, the order of the fractional derivative ($\sigma$) can be used as an effective delay variable for the peak of the infection.

Fig. 10.

The dynamics of the active cases, infectious and symptomatic class $I\left(t\right)$, asymptomatic class $I_A\left(t\right)$ and hospitalized class $H\left(t\right)$ of the fractional model (36) for different values of the order of the fractional derivative $\sigma$.

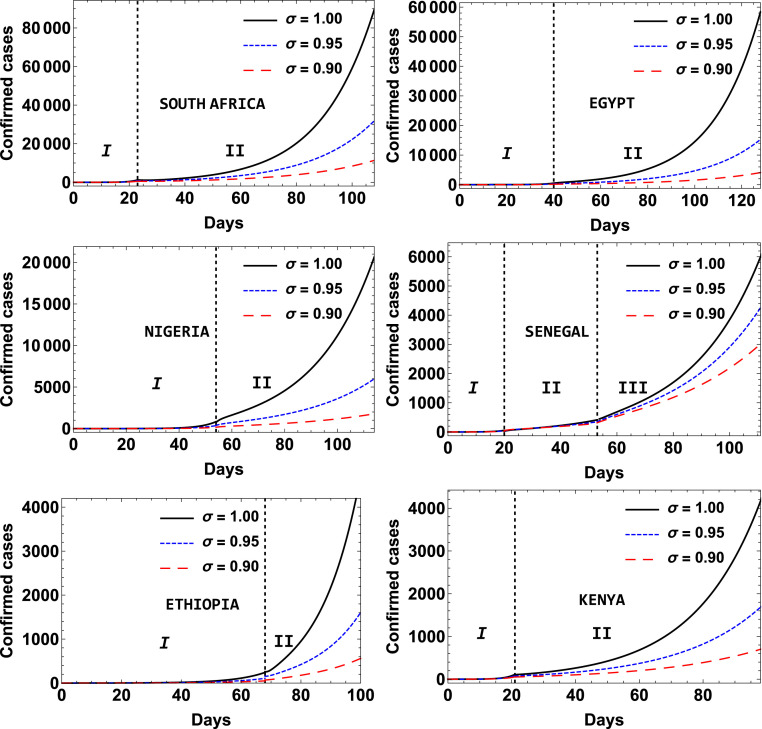
The results of the numerical simulations showing the effect of order of the fractional derivative $\sigma$ on the cumulative number of confirmed infected cases by COVID-19 for the different phases of the infection for all the countries is depicted in Fig. 11.

Fig. 11.

Effect of order of the fractional derivative $\sigma$ on the cumulative number of confirmed infected cases by COVID-19 as a function of time for South Africa, Egypt, Nigeria, Senegal, Ethiopia and Kenya.

The effective reproduction number ${\mathcal{R}}_e\left(t\right)$, defined as the actual average number of secondary cases per primary case at time $t$ (for $t>0$) is a useful time-varying threshold in epidemiology for measuring the trajectory and rate of spread of the disease at any point in time during the course of the epidemic. The effective reproduction number for Eq.  (1) is given by

$${\mathcal{R}}_e\left(t\right)={\mathcal{R}}_0\left(\frac{S\left(t\right)}{N\left(t\right)}\right).$$ (35)

Generally, the number of disease cases rises when ${\mathcal{R}}_e\left(t\right)>1$, attains a peak when ${\mathcal{R}}_e\left(t\right)=1$, and declines when ${\mathcal{R}}_e\left(t\right)<1$. For more details on the effective reproduction number, see Refs. [80], [81], [82]. Fig. 12, Fig. 13 gives an illustration of the effective reproduction number for the selected countries for different values of the order of the fractional derivative $\sigma$. As seen in Fig. 12, Fig. 13, the COVID-19 epidemic had an effective reproduction number that generally decreases with time for the different phases of the infection for all the countries. Also, the effective reproduction number falls more rapidly with time for $\sigma =1.00$ and least for $\sigma =0.95$. This observation is consistent with Fig. 10 which shows that the peak numbers of active cases was reached earliest for $\sigma =1.00$.

Fig. 12.

Evolution of the effective reproduction number ${\mathcal{R}}_e\left(t\right)$ with time for South Africa, Egypt and Nigeria for different values of the order of the fractional derivative $\sigma$.

Fig. 13.

Evolution of the effective reproduction number ${\mathcal{R}}_e\left(t\right)$ with time for Ethiopia, Kenya and Senegal for different values of the order of the fractional derivative $\sigma$.

8. Conclusion

In this paper, a mathematical model for the novel coronavirus (COVID-19) disease which incorporates some non-pharmaceutical interventions was proposed and used to investigate the transmission dynamics in selected African countries, namely, South Africa, Egypt, Nigeria, Senegal, Ethiopia and Kenya. The model contains seven epidemiological compartments namely: Susceptible $S\left(t\right)$, Exposed $E\left(t\right)$, Infected $I\left(t\right)$, Asymptomatic $I_A\left(t\right)$, Quarantine $Q\left(t\right)$, Hospitalized $H\left(t\right)$ and Recovered $R\left(t\right)$ and also takes into account some specific features of the COVID-19 epidemic such as quarantine, isolation and asymptomatic infections. We obtained the critical points, identified the disease-free states and the endemic states. The basic reproduction number, ${\mathcal{R}}_0$ was computed using the next generation matrix approach. Numerical simulations to fit the proposed model to the actual data for cumulative number of confirmed infected cases was performed for the different phases of the infection for all the countries, with values of ${\mathcal{R}}_0$ between 1.311 and 9.179 obtained. As expected, we observe that the condition ${\mathcal{R}}_0<1$ is necessary for the stability (or instability) of the disease-free(or endemic state). A fractional version of the model was introduced using the Atangana–Baleanu​ derivative and numerical simulations were performed for better understanding of the dependence of the dynamics of the disease on the order of the fractional derivative, $\sigma$. The result shows that the magnitude of $\sigma$ has a pronounced effect on the day the maximum is reached with a right shift observed in the time taken for the maximum to be attained as $\sigma$ decreases from 1.0. However, the order of the fractional derivative has insignificant effect on the projected peak number of active cases. Hence, $\sigma$ can be used as an effective delay variable for the peak of the infection. Elasticity and sensitivity analyses show that the most significant parameters are the effective disease transmission rate ($\beta$), disease diagnosis or case detection rate (${\eta }_2$), proportion of susceptible taking precautions ($h$) and the disease infection rate ($\theta$). If the disease infection rate, $\theta$ is less than 0.082/day, then ${\mathcal{R}}_0$ is always less than $1$ regardless of the proportion of susceptible taking precautions ($h$). Another remarkable inference from the study is that, if at least 55.29% of the susceptible population take precautions such regular hand washing with the use of soap, use of sanitizers and wearing of face masks, then, the reproduction number ${\mathcal{R}}_0$ can be kept below $1$ irrespective of the value of the disease infection rate. The most important practical conclusion is that efforts to control the disease should concentrate on decreasing the transmission rate by contact reduction, via lockdown and social distancing measures. In addition, $h$ can be increased by encouraging social campaigns aimed at increasing the number of individuals taking prescribed precautionary measures.

CRediT authorship contribution statement

O.T. Kolebaje: Methodology, Investigation, Writing – original draft. O.R. Vincent: Conceptualization, Software, Formal analysis. U.E. Vincent: Conceptualization, Validation, Writing – review & editing. P.V.E. McClintock: Supervision, Validation, review and editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data Availability

All data used for this study were obtained from the daily situation reports published by the World Health Organization (WHO) and are available at https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports. The codes used are available on request to replicate the results in this paper. The Appendix also provides information on our numerical scheme.

Appendix. Numerical scheme

We now describe the numerical procedure used for solution of the fractional model (34) by adopting the modified Adams–Bashforth scheme developed by Toufik and Atangana [78]. Some recent applications of the modified Adams–Bashforth scheme, include [47], [48], [49], [79]. Before applying the procedure in Toufik and Atangana [78], we write the fractional COVID-19 model (34) in the following form:

$${}_0^{ABC}{D}_t^{\sigma }S=f_1(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }E=f_2(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }I=f_3(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }{I}_A=f_4(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }Q=f_5(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }H=f_6(S,E,I,I_A,Q,H,R),$$

$${}_0^{ABC}{D}_t^{\sigma }R=f_7(S,E,I,I_A,Q,H,R).$$ (36)

Following the procedure in Toufik and Atangana [78], the fractional model can take the form:

$$S\left(t\right)-S\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_1(t,S)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_1(t,S){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$E\left(t\right)-E\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_2(t,E)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_2(t,E){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$I\left(t\right)-I\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_3(t,I)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_3(t,I){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$I_A\left(t\right)-I_A\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_4(t,I_A)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_4(t,I_A){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$Q\left(t\right)-Q\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_5(t,Q)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_5(t,Q){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$H\left(t\right)-H\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_6(t,H)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_6(t,H){(t-\zeta )}^{\sigma -1}d\zeta ,$$

$$R\left(t\right)-R\left(0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_7(t,R)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^t{f}_7(t,R){(t-\zeta )}^{\sigma -1}d\zeta ,$$ (37)

Using $t=t_{n+1}$, $n=0,1,2,\dots$, in (37), we obtain:

$$S\left(t_{n+1}\right)-S\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_1(t_n,S)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_1(t,S){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$E\left(t_{n+1}\right)-E\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_2(t_n,E)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_2(t,E){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$I\left(t_{n+1}\right)-I\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_3(t_n,I)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_3(t,I){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$I_A\left(t_{n+1}\right)-I_A\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_4(t_n,I_A)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_4(t,I_A){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$Q\left(t_{n+1}\right)-Q\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_5(t_n,Q)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_5(t,Q){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$H\left(t_{n+1}\right)-H\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_6(t_n,H)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_6(t,H){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$

$$R\left(t_{n+1}\right)-R\left(t_0\right)=\frac{1-\sigma }{B\left(\sigma \right)}{f}_7(t_n,R)+\frac{\sigma }{B\left(\sigma \right)\Gamma \left(\sigma \right)}\sum _{k=0}^n{\int }_{t_k}^{t_{k+1}}{f}_7(t,R){(t_{k+1}-\zeta )}^{\sigma -1}d\zeta ,$$ (38)

Employing the two-step Lagrange-polynomial approximation for the integral in (38), we obtain the following the numerical scheme for the fractional model (34):

$$S\left(t_{n+1}\right)=S\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_1(t_n,S)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_1(t_k,S)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_1(t_{k-1},S)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (39)

$$E\left(t_{n+1}\right)=E\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_2(t_n,E)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_2(t_k,E)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_2(t_{k-1},S)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (40)

$$I\left(t_{n+1}\right)=I\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_3(t_n,I)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_3(t_k,I)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_3(t_{k-1},I)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (41)

$$I_A\left(t_{n+1}\right)=I_A\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_4(t_n,I_A)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_4(t_k,I_A)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_4(t_{k-1},I_A)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (42)

$$Q\left(t_{n+1}\right)=Q\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_5(t_n,Q)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_5(t_k,Q)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_5(t_{k-1},Q)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (43)

$$H\left(t_{n+1}\right)=H\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_6(t_n,H)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_6(t_k,H)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_6(t_{k-1},H)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (44)

$$R\left(t_{n+1}\right)=R\left(t_0\right)+\frac{1-\sigma }{B\left(\sigma \right)}{f}_7(t_n,R)+\frac{\sigma }{B\left(\sigma \right)}\times \sum _{k=0}^n\left[\frac{{\varphi }^{\sigma }{f}_7(t_k,R)}{\Gamma (\sigma +2)}\left({(n+1-k)}^{\sigma }(n-k+2+\sigma )\right)\right)-\left({(n-k)}^{\sigma }(n-k+2+2\sigma )\right)-\frac{{\varphi }^{\sigma }{f}_7(t_{k-1},R)}{\Gamma (\sigma +2)}\left(\times \left({(n+1-k)}^{\sigma +1}-{(n-k)}^{\sigma }(n-k+1+\sigma )\right)\right],$$ (45)

where $\varphi =t_{n+1}-t_n$.