On the use of constrained reactive mixtures of solids to model finite deformation isothermal elastoplasticity and elastoplastic damage mechanics

Abstract

This study presents a framework for plasticity and elastoplastic damage mechanics by treating materials as reactive solids whose internal composition evolves in response to applied loading. Using the framework of constrained reactive mixtures, plastic deformation is accounted for by allowing loaded bonds within the material to break and reform in a stressed state. Bonds which break and reform represent a new generation with a new reference configuration, which is time-invariant and provided by constitutive assumption. The constitutive relation for the reference configuration of each generation may depend on the selection of a suitable yield measure. The choice of this measure and the resulting plastic flow conditions are constrained by the Clausius–Duhem inequality. We show that this framework remains consistent with classical plasticity approaches and principles. Verification of this reactive plasticity framework, which is implemented in the open source FEBio finite element software (febio.org), is performed against standard 2D and 3D benchmark problems. Damage is incorporated into this reactive framework by allowing loaded bonds to break permanently according to a suitable damage measure, where broken bonds can no longer store free energy. Validation is also demonstrated against experimental data for problems involving plasticity and plastic damage. This study demonstrates that it is possible to formulate simple elastoplasticity and elastoplastic damage models within a consistent framework which uses measures of material mass composition as theoretically observable state variables. This theoretical frame can be expanded in scope to account for more complex behaviors.

1. Introduction

In a reactive framework, a solid may be defined as a material whose bonds (e.g., chemical bonds, such as metallic bonds) may store strain energy. Any dissipation of stored energy occurs as a result of bond breakage, which represents a reaction that transforms intact bonds into either permanently broken bonds, or bonds reformed in a new reference configuration. When bonds break permanently, they are no longer able to store free energy upon loading and this reactive framework describes damage mechanics (Nims et al., 2016). In that case, it is typical to assume that not all bonds in an elemental region of the continuum break simultaneously; the fraction of bonds that remain intact may continue to store free energy, whereas the fraction of broken bonds represents the measure of damage (Nims et al., 2016). When bonds break and reform, the material response is no longer elastic and the reference configuration of the bonds’ reformed state determines alternative frameworks of reactive mechanics. For example, when loaded bonds break and reform into a stress-free state, the resulting material response is consistent with viscoelasticity, where the rate response is governed by the kinetics of bonds breaking and reforming (Ateshian, 2015).

This study is motivated by our interest in the mechanics of biological tissues, including growth mechanics, damage mechanics and fatigue failure. Modeling material responses using a reactive framework that depends on evolving composition is desirable in biomechanics, since many experimental methods exist to track their composition, including various imaging techniques and biochemical assays. In an effort to develop a reactive theory for fatigue failure of biological tissues, we find it necessary to validate this reactive mixture framework against the classic literature on metallic fatigue. To account for the significant plastic deformation which virtually always accompanies metallic fatigue, our first aim was to develop a compatible reactive mixture theory for plastic (permanent) deformation and damage. Thus, the purpose of this work is to present our finding that a reactive solid with bonds that break and reform can reproduce behaviors consistent with standard elastoplasticity and damage, thereby offering an alternative framework for these classical topics.

In this study we describe the mechanism by which loaded bonds break and reform into a stressed state. By restricting our analysis to isothermal processes, we demonstrate that the resulting response reproduces the classical framework of plasticity, when all bonds within an elemental region break simultaneously and reform into a stressed state. Then, elastoplastic damage occurs when a fraction of intact or reformed bonds breaks permanently in response to loading. The simplest constitutive assumption for plasticity is that all bonds within an elemental region break at the same yield threshold, which produces an elastic–perfectly plastic response; a more elaborate formulation would allow different bond types to break at different thresholds, or the same bond type to break over a range of thresholds described by a probability density function, or combinations thereof. In this paper we show that the phenomenon commonly described as plastic hardening may be modeled using multiple bond families within an elemental region, which exhibit distinct yielding thresholds. We also assume that the time constant for bond-breaking-and-reforming reactions is much shorter than the characteristic time of loading, which is effectively represented as an instantaneous bond reformation process.

In a reactive framework, bonds that break and reform are modeled as different mixture constituents and their evolving mass concentrations are governed by the axiom of mass balance, which is a first-order differential equation in the time variable. We can formulate constitutive relations to describe the mass supply to each constituent in the mass balance equations, which govern the bond kinetics. Since they are measures of composition, bond concentrations represent observable variables of state. In a reactive framework that allows new solid constituents to form as products of a reaction, the reference configuration of each solid product is postulated by constitutive assumption, based on the nature of bond reactions.

To describe bond breaking and reforming reactions we use the framework of constrained reactive mixtures (Humphrey and Rajagopal, 2002; Nims and Ateshian, 2017), which represents a specialization of the general theory of reactive mixtures originally formulated by Truesdell and Toupin (1960) and further elaborated by Kelly (1964) and Eringen and Ingram (1965). A constrained mixture represents a mixture of constituents that all share the same velocity but not necessarily the same reference configuration (Humphrey and Rajagopal, 2002). The specialization of mixture theory to constrained reactive mixtures was presented in our previous study of multi-generational growth mechanics (Ateshian and Ricken, 2010) and used in our presentation of reactive viscoelasticity (Ateshian, 2015) and reactive damage mechanics (Nims et al., 2016). A review of this framework may also be found in Nims and Ateshian (2017).

The basic concept of explicitly modeling plastic deformation as arising from some manner of internal configuration change has been reported previously in the biomechanics and plasticity literature. Rajagopal and coworkers (Rajagopal and Srinivasa, 1998a,b) have developed a consistent theoretical framework for a “multiconfigurational approach” to any manner of inelastic behavior, and applied this concept to diverse behaviors including viscoelasticity (Rajagopal and Srinivasa, 2004), polymer crystallization (Rao and Rajagopal, 2000), plasticity of polymeric networks (Rajagopal and Wineman, 1992; Muliana et al., 2016), load reversal in metals (Mollica et al., 2001), and anisotropic fluids (Rajagopal and Srinivasa, 2001). The basic concept in this work is the existence of any number of natural configurations for a material, with accompanying families of elastic response functions, each with their own natural configuration. Changes in the material’s microstructure lead to changes in the natural configuration and hence material response. Similarities to our approach may be found in many of these works. In particular, the study on plasticity of polymeric networks by Rajagopal and Wineman (1992) provides a physical explanation of network junctions breaking and reforming as a different network. Despite the conceptual similarities, the multiconfigurational approach relies upon altering the natural configuration of the material, whereas we present a reaction kinetics-based approach that creates new materials as products of a reaction.

Alternatively, the recent papers by Montáns and coworkers (Zhang and Montans, 2019; Nguyen et al., 2020) assemble nonlinear kinematic hardening behavior by superposing the response of N elastic–perfectly plastic “Prandtl devices”, remarkably similar to Section 4 of this work where a reactive mixture of multiple elastic–perfectly plastic bond families is used for the same purpose. In the biomechanics literature, a recent study on permanent deformation of crosslinked collagen appealed to crosslinks forming and dissociating, governed by reaction kinetics and a stretch-based criterion (Ban et al., 2018). Deformation was captured by relative deformation gradients evaluated from the deformation at the time a new crosslink formed. Safa et al. applied constrained reactive mixtures to inelasticity of fibrous soft tissues (Safa et al., 2019b) and used the model to evaluate plasticity and damage in tendon (Safa et al., 2019a). However, these authors did not attempt to treat metallic plasticity, and several elements of their presentation differ significantly from the present work.

In the following presentation, we frequently use terminology most familiar to researchers within the field of plasticity, invoking terms such as plastic strain and plastic deformation tensor to apply physical meaning to equations. It is important to understand, as we address further below, that our usage of these terms is based on analogy with classical theories and does not share a one-to-one correspondence. In particular, our framework does not employ plastic deformation or plastic strain as a state variable. Instead, a tensorial constitutive model relates the reference configuration of a newly-formed bond to the reference configuration of the undeformed material. Though this is conceptually similar to the plastic deformation gradient in standard theories, no evolution equation is postulated for this function of state in our framework. Additionally, though a plastic strain-like quantity may be extracted from this function of state for purposes of comparison to experimental and numerical results, this measure is not an observable variable in our framework. This point is emphasized here and later in our presentation, as it is well-understood today that plastic strain is ill-defined, physically ambiguous and non-observable, and does not represent a valid state variable (Naghdi, 1990; Rubin, 2001; Volokh, 2013).

This paper is structured as follows: In Section 2 we briefly review salient features of our constrained reactive mixture theory. Section 3 develops a formulation for reactive plasticity with a single bond family, producing elastic–perfectly plastic behavior. Section 4 extends the reactive plasticity framework to multiple coexisting bond families, allowing different families to yield at different thresholds. Results from this section also demonstrate that this model with multiple bond families produces kinematic hardening-like behavior consistent with the well-known Bauschinger effect (Skelton et al., 1997). Section 5 synthesizes our earlier work on reactive damage mechanics (Nims et al., 2016) with reactive plasticity to develop a thermodynamically consistent framework for elastoplastic damage mechanics. A finite element implementation is used in Section 6 to present results of verification and validation studies, with closure provided in the discussion, Section 7.

2. Elements of a constrained reactive mixture theory

2.1. Mixture kinematics

Consider a mixture of multiple constituents α. The motion of each constituent is given by χ^α (X^α, t), where X^α denotes a material point in the reference configuration of that constituent. At the current time t, various constituents α which occupy an elemental region with a spatial position x may have originated from distinct referential positions X^α. We often label a convenient constituent as the master constituent s (e.g., the oldest constituent in a reactive mixture with evolving composition) and call the reference configuration X^s the master reference configuration. All the referential mass densities and mass density supplies (see below) are evaluated relative to the master reference configuration X^s. The kinematics of each constituent α may be related to the kinematics of the master constituent s through

$$\mathbf{x}={\mathbf{\chi }}^s\left({\mathbf{X}}^s,t\right)={\mathbf{\chi }}^{\alpha }\left({\mathbf{X}}^{\alpha },t\right).$$ (2.1)

By definition, a mixture is constrained when the material time derivative of this relation in the material frame produces the same velocity v for all constituents. However, as detailed previously (Ateshian and Ricken, 2010; Nims and Ateshian, 2017), constituents may have distinct deformation gradients F^α = ∂χ^α/∂X^α. When a reaction converts a reactant α = a into a product α = b, these constituents may have distinct reference configurations. The deformation gradient of the master constituent F^s, which also serves as the total deformation gradient, may be related to the relative deformation gradient F^α of constituent α by applying the chain rule to Eq. (2.1), producing

$${\mathbf{F}}^s\left({\mathbf{X}}^s,t\right)=\frac{\partial {\mathbf{\chi }}^s\left({\mathbf{X}}^s,t\right)}{\partial {\mathbf{X}}^{\alpha }}\cdot \frac{\partial {\mathbf{X}}^{\alpha }\left({\mathbf{X}}^s\right)}{\partial {\mathbf{X}}^s}={\mathbf{F}}^{\alpha }\left({\mathbf{X}}^s,t\right)\cdot {\mathbf{F}}^{\alpha s}\left({\mathbf{X}}^s\right).$$ (2.2)

In this expression, F^αs (X^s) is the deformation gradient of α relative to s, which must be postulated by constitutive assumption. The relationship between X^α and X^s is time-invariant; consequently, F^αs is a time-invariant spatial mapping. It follows that only one deformation gradient represents an independent state variable in a constrained mixture framework, whereas all others are related to it via Eq. (2.2); any of the F^α’s may be selected, based on convenience. In Eq. (2.2) the spatio-temporal arguments have been written explicitly for clarity. These dependencies are implied in the forthcoming sections and henceforth those arguments may be selectively suppressed. Taking the determinant of Eq. (2.2) produces a relation between the volume ratios J^α = det F^α and J^s = det F^s,

$$J^s=J^{\alpha }{J}^{\alpha s},$$ (2.3)

where J^αs = det F^αs.

2.2. Mixture composition

Each constituent α has an apparent mass density ρ^α which may evolve due to deformation, or due to reactive processes which alter the mixture composition. Following Bowen (1969) and Ateshian (2007), we define the referential apparent mass density ${\rho }_r^{\alpha }$ of each constituent as

$${\rho }_r^{\alpha }=J^s{\rho }^{\alpha }.$$ (2.4)

Eq. (2.4) expresses the mass of constituent α per referential volume of the master constituent s; thus ${\rho }_r^{\alpha }$ may only evolve if the mass content changes via reactions, making it a suitable state variable for tracking composition in a reactive framework. The axiom of mass balance for each constituent α may be written as

$${\dot{\rho }}_r^{\alpha }={\widehat{\rho }}_r^{\alpha },$$ (2.5)

where the dot operator represents the material time derivative and ${\widehat{\rho }}_r^{\alpha }$ is the referential mass supply density for constituent α, representing the rate at which mass (per referential volume) is added to α due to reactions with all other mixture constituents (Ateshian and Ricken, 2010; Nims and Ateshian, 2017). A constitutive relation must be provided for ${\widehat{\rho }}_r^{\alpha }$ for various types of reactions. The mixture referential mass density ρ_r is given by

$${\rho }_r=\sum _{\alpha }{\rho }_r^{\alpha }.$$ (2.6)

This summation is carried out over all constituents. Since a constrained mixture of solid constituents represents a closed system, ρ_r remains constant over time. Taking the material time derivative of Eq. (2.6) and using Eq. (2.5) shows that the referential mass density supplies must satisfy

$$\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }=0.$$ (2.7)

2.3. Reaction kinetics

The referential mass densities are not constant, as any number of reactions between various mixture constituents may occur at any given time. These reactions may be triggered by changes in any of the state variables, such as those occurring in response to loading (typically, composition and strain). A forward reaction between a single reactant α = a and product α = b may be represented as

$${\mathcal{E}}^a\to {\mathcal{E}}^b,$$ (2.8)

where ${\mathcal{E}}^{\alpha }$ is the chemical or molecular species associated with α. For example, in metallic bonding where an electron cloud bonds neighboring metal ions, ${\mathcal{E}}^{\alpha }$ may refer to the metal species bonded by the metallic bond. We may interchangeably refer to constituent α as the species ${\mathcal{E}}^{\alpha }$ (whose referential mass density is ${\rho }_r^{\alpha }$ ) or the bonds α that store the specific free energy ψ^α of that molecular species. In our simplified treatment, the stoichiometric coefficient associated with each ${\mathcal{E}}^{\alpha }$ in Eq. (2.8) is unity (more general reactions are described in Nims and Ateshian (2017)). The stoichiometry of the reaction in Eq. (2.8) imposes constraints on ${\widehat{\rho }}_r^{\alpha }$. For each reaction we define a referential molar production rate ${\widehat{\zeta }}_r$ (units of moles per referential volume, per time), such that

$$\begin{gathered} {\widehat{\rho }}_r^a=-M^a{\widehat{\zeta }}_r \\ {\widehat{\rho }}_r^b=M^b{\widehat{\zeta }}_r, \end{gathered}$$ (2.9)

where M^α is the molar mass of ${\mathcal{E}}^{\alpha }$. These relations, which must satisfy the constraint of Eq. (2.7) (thus M^a = M^b), show that a constitutive relation is needed only for ${\widehat{\zeta }}_r$, from which relations for all ${\widehat{\rho }}_r^{\alpha }$ follow. This framework accommodates multiple simultaneous reactions, as ${\widehat{\rho }}_r^{\alpha }$ from each reaction may be summed to produce the total mass supply for each constituent.

2.4. Bond energy

The referential free energy density of the mixture is obtained as

$${\Psi }_r=\sum _{\alpha }{\rho }_r^{\alpha }{\psi }^{\alpha },$$ (2.10)

where ψ^α is the specific free energy of constituent α (e.g., the specific free energy stored in the deformable bonds associated with ${\mathcal{E}}^{\alpha }$ ). An important function of state which arises later in our treatment is the chemical potential of constituent α, given by

$${\mu }^{\alpha }=\frac{\partial {\Psi }_r}{\partial {\rho }_r^{\alpha }}.$$ (2.11)

2.5. Clausius–Duhem inequality

The axiom of entropy inequality for a constrained reactive mixture takes the form described by Truesdell and Toupin (1960) and named after Clausius and Duhem,

$$\rho \dot{\eta }+\mathrm{div}\frac{\mathbf{q}}{\theta }-\rho \frac{r}{\theta }⩾0,$$ (2.12)

where η is the mixture specific entropy, q is the heat flux, r is the specific radiative heat supply (positive for heat entering the continuum) and all constituents share the same temperature θ (Coleman and Noll, 1963; Ateshian and Ricken, 2010). Using the energy balance in Eq. (2.20) to eliminate r, we may multiply all terms by J^s to rewrite this inequality as

$$-\left({\dot{\Psi }}_r+H_r\dot{\theta }\right)+J^s\mathbf{T}:\mathbf{D}-\frac{J^s}{\theta }\mathbf{q}\cdot \mathrm{grad}\theta \ge 0,$$ (2.13)

where

$${\Psi }_r=E_r-\theta H_r$$ (2.14)

emerges naturally. In Eq. (2.13), H_r is the mixture referential entropy density, E_r is the mixture referential internal energy density, and D is the rate of deformation tensor (the symmetric part of grad v).

For the reactive elastoplasticity and damage framework presented in this study, the state variables are chosen to include $\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$ to account for deformation and evolving composition due to reactions. In particular, in our treatment we exclude the absolute temperature θ and its gradient grad θ from the list of state variables, because we want to examine an isothermal framework for elastoplasticity and damage, instead of a temperature-varying framework for thermo-elastoplasticity and damage. With these state variables, we apply the chain rule to ${\dot{\Psi }}_r={\dot{\Psi }}_r\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$ to reduce the Clausius–Duhem inequality for the mixture in Eq. (2.13) to the residual dissipation statement

$$\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }{\mu }^{\alpha }\le 0.$$ (2.15)

The Clausius–Duhem inequality also introduces the following constraints on our functions of state:

$$\mathbf{T}=\frac{1}{J^s}\frac{\partial {\Psi }_r}{\partial {\mathbf{F}}^s}\cdot {\left({\mathbf{F}}^s\right)}^T,$$ (2.16)

where T is the mixture Cauchy stress, and

$$H_r=0,\mathbf{q}=\mathbf{0}.$$ (2.17)

In other words, in an isothermal process, the entropy is zero and there can be no heat conduction.

In general, energy stored in trapped dislocations (the stored energy of cold work) cannot be removed by a purely mechanical process and must be fluxed out as thermal energy during heating (e.g., annealing) (Bever et al., 1973). Therefore, the isothermal framework presented here does not and cannot account for this specific phenomenon. Consequently, all the mechanical work done on the material during a purely inelastic process is dissipated (Section 2.6).

In the list of state variables $\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$, the only deformation measure is the total deformation gradient F^s, which is observable from a defined reference state; this represents what we may call the St. Venant approach familiar from elasticity. Given constitutive models for the functions of state F^αs, we may evaluate the relative elastic deformation gradients F^α via F^α = F^s ⋅ (F^αs)⁻¹. We may then alternatively list our state variables in the form $\left({\mathbf{F}}^{\alpha },{\rho }_r^{\alpha }\right)$. This alternative is consistent with arguments that suggest only elastic strain may be observed without knowing a material’s history and therefore it represents the only fundamental state variable for deformation (Eckart, 1948; Rubin, 2001; Volokh, 2013; Rajagopal and Srinivasa, 2015, 2016).

For a plasticity and damage framework, the Clausius–Duhem inequality in Eq. (2.15) implies that the sole dissipative process in reactive plasticity and damage results from the bond-breaking (-and-reforming) reactions. These reactions may proceed forward if and only if the residual dissipation statement is satisfied. The stress in this constrained reactive mixture, Eq. (2.16), is provided by the familiar hyperelastic relation (Ateshian and Ricken, 2010), with the understanding that Ψ_r in Eqs. (2.10)–(2.17) may vary with evolving ${\rho }_r^{\alpha }$, as per the mass balance equation in Eq. (2.5). Alternatively, by making use of Eq. (2.2), the mixture stress tensor may be written as

$$\mathbf{T}=\sum _{\alpha }{\mathbf{T}}^{\alpha },$$ (2.18)

where T^α is given by

$${\mathbf{T}}^{\alpha }={\rho }^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}\cdot {\left({\mathbf{F}}^{\alpha }\right)}^T.$$ (2.19)

2.6. Energy balance

The axiom of energy balance for a constrained mixture has the same form as that of a pure substance,

$${\dot{E}}_r=J^s(\mathbf{T}:\mathbf{D}-\mathrm{div}\mathbf{q})+{\rho }_{r}r.$$ (2.20)

In general, the internal energy is related to the free energy and entropy via E_r = Ψ_r + θH_r. Given the constraints of Eq. (2.17) imposed by the entropy inequality for our choice of state variables, and using the chain rule of differentiation when evaluating ${\dot{E}}_r={\dot{E}}_r\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$, it can be shown that the energy balance reduces to

$$0={\rho }_{r}r-\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }{\mu }^{\alpha }.$$ (2.21)

This relation informs us that isothermal conditions can be maintained during plasticity if the referential reactive power density ${\sum }_{\alpha }{\widehat{\rho }}_r^{\alpha }{\mu }^{\alpha }$ produced by plastic deformation and damage radiates out of the continuum such that ${\rho }_{r}r={\sum }_{\alpha }{\widehat{\rho }}_r^{\alpha }{\mu }^{\alpha }$. Of course, this phenomenon of radiation should be viewed as the hypothetical process needed to maintain an artificially-imposed isothermal plasticity and damage framework. A more elaborate framework of thermo-elastoplasticity and damage would explicitly account for variations in the temperature and its gradient, and the heat flux q.

3. Reactive elastic-perfect plasticity

This section describes a reactive framework in which all loaded bonds in an elemental region break and reform simultaneously into a stressed state with a new reference configuration, resulting in elastic–perfectly plastic behavior. The theory outlined here is similar to our presentation of multigenerational reactive viscoelasticity (Ateshian, 2015; Nims and Ateshian, 2017), although bonds now reform in a stressed, rather than stress-free, state. The aim is to show that constrained reactive mixtures can undergo permanent deformation, and under suitable assumptions reproduce classical elastic–perfectly plastic behavior. A notable feature of this work is that this is accomplished without recourse to plastic potentials, plastic relaxation stress tensors, or internal variable theory (Coleman and Gurtin, 1967; Simo, 1988, 1992).

Earlier work by Safa et al. (2019b) represented the first development of plastic behavior in a constrained reactive mixture framework; these authors introduced the concept of a “sliding bond” and allowed for constitutively-defined sliding rules. Though conceptually similar to the present work, Safa and co-workers were primarily interested in plasticity of biological tissues and hence did not seek to model classical plasticity (i.e., metallic plasticity), thus our treatment differs significantly from theirs. This development of a framework for reactive perfect plasticity anticipates the forthcoming Section 4 where we develop a reactive theory valid for elastoplasticity with so-called hardening, followed in Section 5 by reactive elastoplasticity coupled with damage mechanics.

3.1. Kinematics and kinetics of the yielding reaction

We first consider elastic–perfectly plastic behavior as the simplest case within which the new framework may be developed. In perfect plasticity, all bonds within an elemental region break and reform simultaneously. All bonds are initially intact prior to loading, with an initial referential mass density ρ_r. Consider a loaded bond in an elemental region which breaks and reforms into a new bond with a different reference configuration. Each time that a bond breaks and reforms, we may consider that the material associated with that reformed bond represents a constituent α as a new generation. Thus, bonds that break and reform at time t = u are denoted by α = u and called u–generation bonds. Similarly, bonds which break and reform at time t = υ are called υ–generation bonds and denoted by α = υ. In what follows, mixture constituents{s, u, υ} represent consecutive bond generations, with s representing intact (unyielded) bonds.

The reference configuration of species ${\mathcal{E}}^{\alpha }$ bonded by α–generation bonds is X^α. The earliest generation s (intact bonds) corresponds to t → −∞ and its reference configuration is the master reference configuration X^s. The deformation gradient of the α–generation is related to the master deformation gradient via Eq. (2.2). In that relation, F^αs represents the change in the reference configuration of the α–generation relative to the reference configuration of the s–generation; therefore, it defines the plastic deformation. Unlike the Kroner–Lee decomposition in classical plasticity where F^s is decomposed into elastic and plastic parts (Kroner, 1960; Lee, 1969), F^αs is not a hidden state variable in this formulation; it is a function of state postulated by constitutive assumption.

In the plastic regime, bonds may break and reform continuously as the deformation changes. When the u–generation breaks and reforms into the υ–generation, it is defined as a yielding reaction, ${\mathcal{E}}^u\to {\mathcal{E}}^v$. The mass density supplies for each generation satisfy the constraint of Eq. (2.7). In perfect plasticity, we assume that all bonds in an elemental region break and reform simultaneously, thus the apparent densities in consecutive generations satisfy

$$\begin{gathered} {\rho }_r^s=(1-H(t-u)){\rho }_r \\ {\rho }_r^u=(H(t-u)-H(t-v)){\rho }_r \\ {\rho }_r^v=H(t-v){\rho }_r, \end{gathered}$$ (3.1)

where H (⋅) is the Heaviside unit step function and ${\rho }_r={\sum }_{\alpha }{\rho }_r^{\alpha }$ according to Eq. (2.6). According to the axiom of mass balance, Eq. (2.5), it follows that the referential mass supplies are

$$\begin{gathered} {\widehat{\rho }}_r^s=-\delta (t-u){\rho }_r \\ {\widehat{\rho }}_r^u=(\delta (t-u)-\delta (t-v)){\rho }_r \\ {\widehat{\rho }}_r^v=\delta (t-v){\rho }_r \end{gathered}$$ (3.2)

where δ (⋅) is the Dirac delta function. It is apparent from Eqs. (3.1)–(3.2) that only one bond generation is extant at any given time. Consequently, each time the yielding reaction takes place the entire current mass of bonded species in an elemental volume breaks and reforms into a new generation.

3.2. Bond energy

By adopting the constitutive assumption that all bonds of a generation break simultaneously to reform into a new generation, it implies that the referential density ${\rho }_r^{\alpha }$ of generation α remains constant and equal to ρ_r over the lifetime of that generation; in particular, the lifetime of u–generation bonds is u ≤ t < υ. We now adopt the simplifying constitutive assumption that

$${\psi }^{\alpha }=\psi \left({\mathbf{F}}^{\alpha }\right).$$ (3.3)

In other words, ψ^α is not a function of any of the evolving referential mass densities ${\rho }_r^{\alpha }$, and ψ^α has the same functional form ψ for all generations α. The first of these assumptions is sensible since ${\rho }_r^{\alpha }={\rho }_r$ remains constant over the lifetime of generation α; as will become clearer below, the second assumption implies that the elastic response of the elastic–perfectly plastic material described here remains the same regardless of the magnitude of plastic flow. The mixture free energy density and stress are given by Eqs. (2.10) and (2.18)–(2.19), respectively.

Substituting Eq. (3.3) into Eq. (2.11) shows that the chemical potential of generation α is also equal to its specific free energy, μ^α = ψ (F^α), in this constitutive framework. In what follows, we may use μ^α, ψ^α, or ψ (F^α) interchangeably, depending upon which form offers more clarity. Using Eqs. (2.6) and (2.11), we may rewrite the heat supply as

$${\rho }_{r}r=\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }\psi \left({\mathbf{F}}^{\alpha }\right).$$ (3.4)

This equation is used below to further examine and quantify heat dissipation due to plastic deformation and damage.

3.3. Yield criterion

Consider that bonds of the α–generation yield based on a scalar yield measure Φ^α (U^α) (e.g., the von Mises stress), where U^α is the right stretch tensor from the polar decomposition F^α = R ⋅ U^α, and R is the rotation tensor, assumed to also be the rotation tensor of F^s. Thus, according to Eq. (2.2), U^s = U^α ⋅F^αs; from the invariance of U^s and U^α to orthogonal transformations, it follows that F^αs is also an invariant tensor. For a classical elastic–perfectly plastic response, we need to adopt the same functional form for the yield measure Φ^α over all generations α, i.e., Φ^α (U^α) = Φ (U^α). This assumption allows us to provide a method for determining F^αs for all generations based on conventional approaches (see Section 3.4.1).

Let the yield threshold for the α–generation be given by ${\Phi }_m^{\alpha }$, which represents the threshold value at which yielding begins.¹ In our treatment, we make the simplifying assumption that the yield threshold is a constant that remains the same for all generations α, ${\Phi }_m^{\alpha }={\Phi }_m$. For α–generation bonds, the yield criterion may thus be defined as

$$\phi \left({\mathbf{U}}^{\alpha }\right)=\Phi \left({\mathbf{U}}^{\alpha }\right)-{\Phi }_m\le 0,$$ (3.5)

where φ (U^α) represents the yield surface of α–generation bonds whose tensorial normal is

$${\mathbf{N}}^{\alpha }=\frac{\partial \phi }{\partial {\mathbf{U}}^{\alpha }}=\frac{\partial \Phi \left({\mathbf{U}}^{\alpha }\right)}{\partial {\mathbf{U}}^{\alpha }}.$$ (3.6)

This expression produces a symmetric tensorial normal N^α and ensures that rigid body rotations do not affect the tensorial normal. A frame-invariant normal is required when using N^α to formulate a constitutive relation for the function of state F^αs, as described in Section 3.4. When yield thresholds are formulated in stress space, the dependence on the deformation takes the form Φ = Φ (T^α (U^α)).

Unlike classical plasticity theory, in the current mixture-based framework it is not physically meaningful to seek a material time derivative of φ, since F^αs is a time-invariant mapping postulated constitutively (its material time derivative is strictly equal to zero). Furthermore, φ is a function of the stretch tensor U^α of whichever generation α is currently extant. Under the assumptions of the present theory, an incremental form of Eq. (3.5) may be used to formulate the plastic consistency condition. Using Eq. (3.5), it follows that

$$d\phi =\frac{\partial \phi }{\partial {\mathbf{U}}^{\alpha }}:d{\mathbf{U}}^{\alpha }={\mathbf{N}}^{\alpha }:d{\mathbf{U}}^{\alpha }.$$ (3.7)

The yield criterion of Eq. (3.5) presents the following alternatives: φ (U^α) < 0 if the state of deformation of the α–generation at the current time t ≥ α is below its yield threshold, or φ (U^α) = 0 at time t = α + dt and the deformation is receding from (dφ < 0), tangent to (dφ = 0), or advancing past (dφ > 0) the yield surface. A persistent state of tangency to the yield surface (the plastic consistency condition) implies that φ = 0 and dφ = 0. Thus, dφ > 0 only happens for the breaking u–generation at time υ = u + dt, where it signifies the current deformation state is not permissible, triggering bond breaking and reformation. To complete this argument, the increment dU^α which appears in Eq. (3.7) must be given by

$$d{\mathbf{U}}^u=\{\begin{array}{ccc}{\mathbf{U}}^u(u+dt)-{\mathbf{U}}^u(u)& d\phi <0& u-\text{generation}\text{does}\text{not}\text{break}\\ {\mathbf{U}}^u(v)-{\mathbf{U}}^u(u)& d\phi >0& u-\text{generation}\text{must}\text{break}\\ {\mathbf{U}}^v(v)-{\mathbf{U}}^u(u)& d\phi =0& u-\text{generation}\text{broke}\text{and}\text{reformed}\text{into}v-\text{generation,}\end{array}$$ (3.8)

for the u–generation. Upon breaking of the u–generation to form the υ–generation, the plastic consistency condition reduces from Eqs. (3.7)–(3.8) to

$${\mathbf{N}}^u(u):\left({\mathbf{U}}^v(v)-{\mathbf{U}}^u(u)\right)=0.$$ (3.9)

3.4. Normality condition and associated flow rule

3.4.1. Constitutive assumption for F^αs

We now provide a constitutive relation for the collection of mappings F^αs that is consistent with classical plasticity frameworks and validated against experimental evidence. On both theoretical (Simo, 1988; Khan and Huang, 1995; Xiao et al., 2006; Aretz, 2006; Bruhns, 2014) and exhaustive experimental (Hecker, 1976; Brown et al., 2003) grounds, it is known that plastic deformation in metals generally obeys the normality condition and an associated flow rule, which together constrain the increment in plastic deformation to lie normal to the yield surface in tensorial space. An associated flow rule signifies that the scalar potential whose derivative indicates the direction of plastic deformation is the yield criterion, and the normality condition represents the assumption of co-directionality of the plastic deformation increment and the yield surface normal. As pointed out by Lubliner (1986), symmetry considerations restrict such flow rules to a six-, rather than nine-, dimensional space (see e.g., Simo (1988), Khan and Huang (1995) and Xiao et al. (2006) for a review of the standard approach). Other investigators have argued that the plastic spin (and hence any plastic rotation) is indeterminate and thus may be neglected, producing irrotational plastic flow (Boyce et al., 1989; Dafalias, 1998). These conditions are consistent with our constitutive assumption that the rotation R should be the same for F^s and F^α whereas the yield surface normal N^α should be evaluated using the right stretch tensor of F^α according to Eq. (3.6).

To recover classical plasticity frameworks, the constitutive model adopted for F^αs in our treatment takes the recursive form

$${\left({\mathbf{F}}^{vs}\right)}^{-1}={\left({\mathbf{F}}^{us}\right)}^{-1}\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)$$ (3.10)

where

$${\widehat{\mathbf{N}}}^v=\frac{{\mathbf{N}}^v}{\sqrt{{\mathbf{N}}^v:{\mathbf{N}}^v}}$$ (3.11)

is the unit tensor along N^υ and λ is a non-dimensional scalar which may be determined analytically by using Eq. (3.7) and enforcing the plastic consistency condition dφ = 0. For the earliest yielded generation u, the preceding s–generation is in the elastic regime; therefore, F^us = I at the start of the recursive relation in Eq. (3.10). Eq. (3.10) satisfies frame indifference since F^αs and $\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v$ are invariant to orthogonal transformations.

To solve for λ, substitute Eq. (3.10) into the plastic consistency condition of Eq. (3.9) to produce

$$\lambda =\frac{{\mathbf{N}}^u(u):\left({\mathbf{U}}^u(v)-{\mathbf{U}}^u(u)\right)}{{\mathbf{N}}^u(u):\left({\mathbf{U}}^u(v)\cdot {\widehat{\mathbf{N}}}^v(v)\right)}$$ (3.12)

where

$${\mathbf{U}}^u(v)={\mathbf{U}}^s(v)\cdot {\left({\mathbf{F}}^{us}\right)}^{-1}$$ (3.13)

is often called the elastic predictor. It represents the elastic stretch tensor at t = υ if no further plastic yielding were to take place between t = u and t = υ. It has been used as an initial guess in predictor–corrector type algorithms (Simo, 1992). The expression for λ in Eq. (3.12) is an implicit relation, since N^υ depends on λ through U^υ. As this expression was derived based on an infinitesimal step size, we may further assume N^υ ≈ N^u and solve for λ directly. The solution of Eq. (3.12) remains valid for finite total deformation, provided every increment is infinitesimal. Since this is a fairly restrictive condition, a general numerical scheme is described in Section 3.4.2 below, which remains valid for finite step sizes, facilitating an efficient computational implementation of this finite deformation reactive plasticity framework.

The formulation in Eq. (3.10) implies the existence of a specific position vector X^υ for the newly formed bond, via the mapping F^υs = ∂X^υ/∂X^s according to Eq. (2.2). However, the evaluation of the function of state F^υs from Eq. (3.10) never requires an explicit evaluation of X^υ. Furthermore, since F^υs is a non-observable function of state that may be inhomogeneous across a domain, there is no value in attempting to back-calculate X^υ from F^υs since it does not represent an observable measure. This clarification is consistent with the concept first described by Eckart (1948) and expanded upon by others (Rubin, 2001; Rajagopal and Srinivasa, 2004; Sadik and Yavari, 2016, 2017; Goodbrake et al., 2021), namely that plastically deformed materials do not necessarily admit a globally stress-free state upon unloading.

3.4.2. Numerical algorithm

To handle finite step sizes in a numerical solution, we may use Newton’s method to iteratively solve for λ within each time step. Our starting point is the constitutive relation in Eq. (3.10), which may be pre-multiplied by U^s (υ) to read

$${\mathbf{U}}^v={\mathbf{U}}^u\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)$$ (3.14)

All the terms in this expression and for the remainder of this section are evaluated at time υ. During plastic flow, the condition φ (U^υ) = 0 must be enforced. A Taylor series expansion about the current iteration for λ yields

$$\phi +\frac{\partial \phi }{\partial {\mathbf{U}}^v}:\frac{\partial {\mathbf{U}}^v}{\partial \lambda }\Delta \lambda =0,$$ (3.15)

where Δλ represents an increment in the solution λ. Recognizing that $\partial {\mathbf{U}}^v/\partial \lambda =-{\mathbf{U}}^u\cdot {\widehat{\mathbf{N}}}^v$ from Eq. (3.14), the problem to solve becomes

$$\phi \left({\mathbf{U}}^v\right)-{\mathbf{N}}^v:\left({\mathbf{U}}^u\cdot {\widehat{\mathbf{N}}}^v\right)\Delta \lambda =0,$$ (3.16)

which leads to

$$\Delta \lambda =\sqrt{{\mathbf{N}}^v:{\mathbf{N}}^v}\frac{\phi \left({\mathbf{U}}^v\right)}{{\mathbf{N}}^v:\left({\mathbf{U}}^u\cdot {\mathbf{N}}^v\right)}.$$ (3.17)

The algorithm is initialized with a guess of λ₀ = 0, which corresponds to U^υ (υ) = U^u (υ), i.e., the elastic deformation is given by the elastic predictor and no further plastic deformation has occurred at this time step. λ is then updated at iteration n as λ_n ← λ_n−1 + Δλ until convergence is achieved.

As discussed further in Section 5.2, depending on the choice of the yield function Φ, the plastic deformation may need to be isochoric. To enforce such isochoric plastic deformation, we modify this derivation by letting det F^υs = J^υs = 1. Then, the mapping (F^υs)⁻¹ must be adjusted such that Eq. (3.10) becomes

$${\left({\mathbf{F}}^{vs}\right)}^{-1}=\xi {\left({\mathbf{F}}^{us}\right)}^{-1}\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right),$$ (3.18)

where

$$\xi ={\left(\det \left({\left({\mathbf{F}}^{us}\right)}^{-1}\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)\right)\right)}^{-1/3}.$$ (3.19)

Consequently, in our numerical algorithm, the starting point is now given by

$${\mathbf{U}}^v=\xi {\mathbf{U}}^u\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right).$$ (3.20)

In the Taylor series expansion, we now have

$$\begin{gathered} \frac{\partial {\mathbf{U}}^v}{\partial \lambda }=-\xi {\mathbf{U}}^u\cdot {\widehat{\mathbf{N}}}^v \\ +\frac{\xi }{3}\left({\left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)}^{-1}:{\widehat{\mathbf{N}}}^v\right){\mathbf{U}}^u\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right) \end{gathered}$$ (3.21)

Inserting Eq. (3.21) into Eq. (3.15) allows the Newton update to be identified as

$$\Delta \lambda =\frac{\phi \left({\mathbf{U}}^v\right)}{{\mathbf{N}}^v:\left(\xi {\mathbf{U}}^u\cdot {\widehat{\mathbf{N}}}^v-\frac{\xi }{3}{n}^v{\mathbf{U}}^u\cdot \left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)\right)},$$ (3.22)

where we defined

$$n^v\equiv {\left(\mathbf{I}-\lambda {\widehat{\mathbf{N}}}^v\right)}^{-1}:{\widehat{\mathbf{N}}}^v$$ (3.23)

Application of the update formula λ_n ← λ_n−1 + Δλ then proceeds as before.

3.4.3. Calculation of tensorial normal N^α

The tensorial normal N^α contains information about both the yield criterion and the elastic stress–strain relationship of the material, and is defined through Eq. (3.6). Here we derive an analytical expression for the normal tensor, given any yield measure Φ which is expressed in terms of the Cauchy stress. The definition of Eq. (3.6) may be expanded with the chain rule as

$${\mathbf{N}}^{\alpha }=\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}:\frac{\partial {\mathbf{T}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}:\frac{\partial {\mathbf{F}}^{\alpha }}{\partial {\mathbf{U}}^{\alpha }}$$ (3.24)

By pulling back to the material frame, it can be shown that

$$\frac{\partial {\mathbf{T}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}=\left({\mathit{C}}^{\alpha }+\mathbf{I}\oslash {\mathbf{T}}^{\alpha }+{\mathbf{T}}^{\alpha }⦸\mathbf{I}-{\mathbf{T}}^{\alpha }\otimes \mathbf{I}\right)\cdot {\left({\mathbf{F}}^{\alpha }\right)}^{-T},$$ (3.25)

where ${\mathit{C}}^{\alpha }$ is the spatial elasticity tensor for bond generation α and the tensor dyadic products ⨂,⊘,⦸, and ⊙ are defined in Eq. (A.1). Substituting Eq. (3.25) into Eq. (3.24) and grouping suitable terms provides the normal as

$${\mathbf{N}}^{\alpha }=\frac{1}{2}{\mathbf{R}}^T\cdot {\mathbf{M}}^{\alpha }\cdot \mathbf{R}\cdot {\left({\mathbf{U}}^{\alpha }\right)}^{-1}+\frac{1}{2}{\left({\mathbf{U}}^{\alpha }\right)}^{-1}\cdot {\mathbf{R}}^T\cdot {\left({\mathbf{M}}^{\alpha }\right)}^T\cdot \mathbf{R},$$ (3.26)

where

$${\mathbf{M}}^{\alpha }=\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}:{\mathit{C}}^{\alpha }+2\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}\cdot {\mathbf{T}}^{\alpha }-\left(\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}:{\mathbf{T}}^{\alpha }\right)\mathbf{I}.$$ (3.27)

Thus the tensorial normal may be calculated analytically as long as the derivative ∂Φ/∂T^α is provided. Details of the derivations leading to Eqs. (3.25)–(3.27) are provided in the Appendix.

For example, in the case where the yield measure is taken as the von Mises (effective) stress, Φ = σ_Y, differentiation shows that

$$\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}=\frac{3}{2{\sigma }_Y}\mathrm{dev}{\mathbf{T}}^{\alpha }.$$ (3.28)

Alternatively, if the yield measure is taken as the specific free energy, Φ = ψ, we may evaluate the normal directly as

$${\mathbf{N}}^{\alpha }=\frac{\partial \psi }{\partial {\mathbf{U}}^{\alpha }}=\frac{J^{\alpha }}{{\rho }_r}{\mathbf{R}}^T\cdot {\mathbf{T}}^{\alpha }\cdot \mathbf{R}\cdot {\left({\mathbf{U}}^{\alpha }\right)}^{-1},$$

where we have made use of Eq. (2.19).

3.4.4. Relationship to classical infinitesimal plasticity

Classical models of infinitesimal plasticity typically present the increment in the plastic strain as a function of the increment in the total strain, and the deviatoric stress, e.g., Δε^p = f (Δε, devσ) (Khan and Huang, 1995). Here, the finite deformation constitutive relation of Section 3.4.1 is reduced to the infinitesimal regime to examine the relationship between reactive and classical plasticity.

Under infinitesimal strains and rotations, F^α ≈ I + ε^α + ω where ε^α is the infinitesimal strain tensor and ω is the antisymmetric tensor such that R ≈ I+ω is the infinitesimal rotation tensor; similarly, U^α ≈ I+ε^α. Under these assumptions, Eqs. (3.10) and (3.12) reduce to

$$\Delta {\mathit{\epsilon }}^p=\frac{{\mathbf{N}}^u:\Delta \mathit{\epsilon }}{{\mathbf{N}}^u:{\mathbf{N}}^u}{\mathbf{N}}^u,$$ (3.30)

where Δε^p and Δε are increments in the plastic and total strain, respectively, defined by

$$\begin{gathered} \Delta {\mathit{\epsilon }}^p={\mathit{\epsilon }}^{vs}-{\mathit{\epsilon }}^{us} \\ \Delta \mathit{\epsilon }={\mathit{\epsilon }}^s(v)-{\mathit{\epsilon }}^s(u). \end{gathered}$$ (3.31)

Under the same assumptions, it can be shown that Eq. (3.27) reduces to ${\mathbf{M}}^{\alpha }=\left(\partial \Phi /\partial {\mathbf{T}}^{\alpha }\right):{\mathit{C}}^{\alpha }$ while Eq. (3.26) now produces N^α = M^α. When the yield measure is taken to be the von Mises stress, Φ = σ_Y, and the material is linear isotropic elastic, T^α = λ (tr ε^α)I+2Gε^α where λ and G are the Lamé constants, we find from Eq. (3.28) that N^u = (3G/σ_Y) dev T^u. Inserting this result into Eq. (3.30) and recalling that ${\sigma }_Y=\sqrt{\frac{3}{2}\mathrm{dev}{\mathbf{T}}^u:\mathrm{dev}{\mathbf{T}}^u}$ produces

$$\Delta {\mathit{\epsilon }}^p=\frac{3(\mathrm{dev}\mathit{\sigma }:\Delta \mathit{\epsilon })}{2{\sigma }_Y^2}\mathrm{dev}\mathit{\sigma },$$ (3.32)

where $\sigma \equiv {\mathbf{T}}^u$. Eq. (3.32) is identical to the classical Prandtl–Reuss constitutive relation for infinitesimal plasticity (Khan and Huang, 1995), demonstrating that our alternative reactive mixture framework does reduce to a familiar form in the limit of infinitesimal strains and rotations when the von Mises stress is adopted as the yield criterion.

3.5. Thermodynamics

3.5.1. Clausius–Duhem inequality

For bond reactions producing plastic behavior the residual dissipation constraint of Eq. (2.15) is equivalent to

$$-\delta (t-u)\left(\psi \left({\mathbf{F}}^s(t)\right)-\psi \left({\mathbf{F}}^u(t)\right)\right)-\delta (t-v)\left(\psi \left({\mathbf{F}}^u(t)\right)-\psi \left({\mathbf{F}}^v(t)\right)\right)\le 0,$$ (3.33)

where we have made use of Eqs. (3.2)–(3.3). Therefore, at t = υ, when u–generation bonds break and reform into υ–generation bonds, we must have

$$\psi \left({\mathbf{F}}^u(v)\right)\ge \psi \left({\mathbf{F}}^v(v)\right).$$ (3.34)

where F^u (υ) = R⋅U^u (υ) is related to the elastic predictor of Eq. (3.13). In other words, to satisfy the entropy inequality, the specific free energy of the breaking bond must be greater than that of the reforming bond at the time of the reaction. By definition, when plastic deformation is impending, F^u (υ) lies outside the yield surface whereas F^υ (υ) lies on the yield surface, causing u–generation bonds to break and reform into υ–generation bonds. Therefore, the yield criterion must be defined such that it satisfies this thermodynamic constraint. Using Eq. (2.2), we can also see that F^u (υ) = F^υ (υ)⋅F^υu, where F^υu = F^υs⋅(F^us)⁻¹ is the plastic deformation increment from u to υ. Thus, the thermodynamic constraint in Eq. (3.34) is entirely dependent on the constitutive model for the plastic deformation F^αs, which itself depends on the yield function φ, as illustrated in Section 3.3.

For example, for an isotropic linear elastic solid undergoing infinitesimal strains, its specific free energy is

$$\psi \left({\mathbf{\epsilon }}^{\alpha }\right)=\frac{K}{2{\rho }_r}{\left(\mathrm{tr}{\mathbf{\epsilon }}^{\alpha }\right)}^2+\frac{G}{{\rho }_r}\left(\mathrm{dev}{\mathbf{\epsilon }}^{\alpha }\right):\left(\mathrm{dev}{\mathbf{\epsilon }}^{\alpha }\right),$$ (3.35)

where K > 0 is the bulk modulus and G > 0 is the shear modulus. The yield surface for the von Mises criterion is defined by φ = 0, where

$$\phi \left({\mathbf{\epsilon }}^{\alpha }\right)=G\sqrt{6\left(\mathrm{dev}{\mathbf{\epsilon }}^{\alpha }\right):\left(\mathrm{dev}{\mathbf{\epsilon }}^{\alpha }\right)}-{\sigma }_Y.$$ (3.36)

From the definition of yielding (Section 3.3), we must have φ (ε^u (υ)) > 0 while φ (ε^υ (υ)) = 0 with an associated flow rule. Combining these relations produces

$$\frac{{\rho }_r}{G}\psi \left({\mathit{\epsilon }}^u(v)\right)-\frac{K}{2G}{\left(\mathrm{tr}{\mathit{\epsilon }}^u(v)\right)}^2>\frac{{\rho }_r}{G}\psi \left({\mathit{\epsilon }}^v(v)\right)-\frac{K}{2G}{\left(\mathrm{tr}{\mathit{\epsilon }}^v(v)\right)}^2.$$ (3.37)

Plastic deformation is isochoric in this case (tr ε^us = tr ε^υs = 0) due to the dual constitutive assumptions of an associated flow rule and the von Mises yield criterion, as can be verified by the fact that tr Δε^p = 0 in Eq. (3.32) (Section 3.4.4). Consequently, since ε^s (υ) = ε^u (υ) + ε^us = ε^υ (υ) + ε^υs, it follows that tr ε^u (υ) = tr ε^υ (υ) = tr ε^s (υ). Substituting this result into Eq. (3.37) shows that the Clausius–Duhem inequality constraint in Eq. (3.34) is automatically satisfied by our choice of the von Mises yield criterion with an associated flow rule.

3.5.2. Energy dissipation

Any free energy dissipated in the bond reaction will be converted to heat according to Eq. (3.4). When we substitute the mass supply densities of Eq. (3.2) into this relation, we find that the specific heat supply resulting from u–generation bonds breaking and reforming at time t = υ is

$$r(t)=\delta (t-v)\left(\psi \left({\mathbf{F}}^v(v)\right)-\psi \left({\mathbf{F}}^u(v)\right)\right).$$ (3.38)

Thus, over the duration u < t ≤ υ, the specific heat that has been released is ψ (F^υ (υ)) − ψ (F^u (υ)). According to the Clausius–Duhem constraint in Eq. (3.34), this quantity is negative, consistent with the fact that heat is leaving the continuum (exothermic reaction) to maintain it at constant temperature.

3.6. Discussion

The theory of reactive plasticity outlined in this section falls under the category of incremental theories of plasticity, in that the plastic deformation is path-dependent (in contrast to a deformation theory) (Khan and Huang, 1995). Under the reactive framework, the material response is dependent upon the composition of the bonds which comprise the material, and the bond compositions evolve during the course of loading. Classical theories of plasticity recognize that in terms of observable state variables, such as the deformation gradient F, the response of functions of state such as T = T(F) cannot be defined uniquely, leading to the introduction of hidden (internal) state variables which are non-observable. By postulating evolution equations for a suitable set of internal variables, following the procedure outlined by Coleman and Gurtin (1967), unique plastic behavior could be described.

In contrast, in the reactive mixture framework the mathematics produce a material response that depends only on observable state variables $\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$. This dependence emerges because the mixture is described in terms of referential bond mass densities ${\rho }_r^{\alpha }$, whose evolution is governed by mass balance. No state variables representing plastic strain-like quantities are involved. Our reactive mixture framework proposes that the mapping F^αs (X^s) that relates the reference configuration of generation α to the master reference configuration s is a function of state, for which a constitutive relation must be provided, such as that presented in Eq. (3.10). Like other functions of state, e.g., stress or heat flux, the constitutive model for the mapping F^αs (X^s) may be validated by measuring observable variables (e.g., surface traction for the stress, temperature gradient for the heat flux) and comparing those measurements to predictions that employ those constitutive models. In particular, the constitutive model for F^αs (X^s) may be validated by performing measurements of the deformation gradient F^s (X^s, t), as illustrated in several examples in Section 6 below, particularly in Section 6.5. Plastic strains reported in our presentation are non-observable functions of state rather than state variables.

As seen in Eqs. (2.16)–(2.19), our reactive formulation of plasticity recovers expressions for the stress, Eqs. (2.18)–(2.19), which are of the same form as for hyperelasticity. In contrast to theories labeled “hyper-elasto-plastic” (e.g., Wallin et al. (2003)), which propose hyperelastic (rather than hypo-elastic) behavior only prior to yield, the reactive theory described in this section achieves plastic deformation through familiar hyperelastic relations, by allowing bonds to break and reform with different reference configurations, such that the stress is always derived from the same strain energy potential by differentiating it with respect to elastic deformation. Our theory is not unique in this regard (Zhang and Montans, 2019; Nguyen et al., 2020), and this type of formulation does not imply improved performance, but in our view it offers a simpler set of equations and allows the numerical implementation to be achieved using a standard hyperelastic framework. Limitations to the present theory are addressed more thoroughly in Section 4, following development of a general theory of reactive elastoplasticity which includes hardening.

4. Reactive plasticity with kinematic “hardening”

The framework presented in Section 3 has only considered perfect plasticity, i.e., all the bonds yield when a single yield criterion is met. However, a wealth of experimental results show a more progressive yielding, rather than a sudden onset, and an increase in the stress with increasing plastic deformation, a phenomenon alternately termed strain hardening or work hardening (Khan and Huang, 1995). The simplest form of hardening is known as isotropic hardening, where the boundaries of the yield surface expand uniformly. For a reversal of load, isotropic hardening predicts yielding occurs when the change in load is twice the highest value reached before unloading. Classical plasticity allows the yield threshold to evolve as a function of the accumulated plastic strain for isotropic hardening (Khan and Huang, 1995); more modern theories shift the yield surface based upon constitutively-prescribed evolution equations for internal hardening variables (Henann and Anand, 2009). In our framework, this method would correspond to having distinct ${\Phi }_m^{\alpha }$ for each generation α, where ${\Phi }_m^{\alpha }={\Phi }_m^{\alpha }\left({\mathbf{U}}^{\alpha }\right)$. However, as noted previously, we hold ${\Phi }_m^{\alpha }$ constant across generations α.

Isotropic hardening cannot predict the Bauschinger effect demonstrated by real materials, where loading to yield in one direction changes the yield threshold in the reverse direction (Khan and Huang, 1995; Skelton et al., 1997). The hardening behavior that accounts for this effect is known as kinematic hardening; for a load reversal, it predicts yielding occurs when the change in load achieves twice the monotonic yield strength. The reactive framework can be extended to allow for kinematic hardening by introducing multiple families of bonds. Each bond family β may have its own yield function Φ_β and associated threshold Φ_mβ, and follows the elastic–perfectly plastic behavior for multiple generations outlined in Section 3. As will become evident below, the superposition of multiple bond families β in parallel naturally develops behavior consistent with kinematic hardening, as different bond families yield at different thresholds. This reactive framework is conceptually similar to a Masing-type model (Skelton et al., 1997) and recent studies considering superposition of elastic–perfectly plastic Prandtl devices (Zhang and Montans, 2019; Nguyen et al., 2020), with our bond families behaving like Masing elements or Prandtl devices, respectively, though details of the presentation differ significantly.

4.1. Notation

We consider multiple bond families β = 0, …, n_f −1, which may yield or get damaged under different criteria or thresholds, where each bond family may evolve over multiple generations α. We assume that there are no reactions between bonds of different families β. This framework requires us to update our notation to include a subscript β for suitable variables introduced in the presentation above. In particular, the reference configuration of generation α in bond family β is now denoted by ${\mathbf{X}}_{\beta }^{\alpha }$ and the corresponding deformation gradient is ${\mathbf{F}}_{\beta }^{\alpha }$. We assume that the specific free energy function of bond family β is ${\psi }_{\beta }\left({\mathbf{F}}_{\beta }^{\alpha }\right)$, which takes the same form for all generations α of that family, as before. The master reference configuration of all bond families remains X^s and the associated (total) deformation gradient is still F^s. Therefore, each bond family β requires a constitutive relation for the function of state ${\mathbf{F}}_{\beta }^{\alpha s}$ in the updated form of Eq. (2.2), such as that given in Eq. (3.10), where each term should now include a subscript β.

The referential mass density of bond family β is ρ_rβ, such that the mixture referential mass density is given by ${\rho }_r={\sum }_{\beta }{\rho }_{r\beta }$. The referential mass density of generation α in bond family β is ${\rho }_{r\beta }^{\alpha }$, which satisfies ${\sum }_{\alpha }{\rho }_{r\beta }^{\alpha }={\rho }_{r\beta }$, as per Eq. (2.6). For convenience, we define

$$w_{\beta }\equiv \frac{{\rho }_{r\beta }}{{\rho }_r},\sum _{\beta }{w}_{\beta }=1,$$ (4.1)

which represents the mass fraction of each bond family β within the constrained solid mixture, and

$$w_{\beta }^{\alpha }=\frac{{\rho }_{r\beta }^{\alpha }}{{\rho }_{r\beta }},\sum _{\alpha }{w}_{\beta }^{\alpha }=1,$$ (4.2)

which represents the mass fraction of each generation α within the bond family β. From these definitions, it follows that bond family mass fractions w_β are time-invariant, whereas generation mass fractions $w_{\beta }^{\alpha }$ evolve with bond-breaking-and-reforming reactions.

The mixture stress T is given by Eq. (2.16), where Ψ_r is now

$${\Psi }_r=\sum _{\beta }\sum _{\alpha }{\rho }_{r\beta }^{\alpha }{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^{\alpha }\right)={\rho }_r\sum _{\beta }{w}_{\beta }\sum _{\alpha }{w}_{\beta }^{\alpha }{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^{\alpha }\right).$$ (4.3)

It follows from Eq.(2.16) that the mixture stress may be expressed as the weighted sum of stresses T_β in each bond family,

$$\mathbf{T}=\sum _{\beta }{w}_{\beta }{\mathbf{T}}_{\beta },{\mathbf{T}}_{\beta }=\sum _{\alpha }{w}_{\beta }^{\alpha }{\mathbf{T}}_{\beta }^{\alpha },$$ (4.4)

where the stress in generation α of bond family β is

$${\mathbf{T}}_{\beta }^{\alpha }=\rho \frac{\partial {\psi }_{\beta }}{\partial {\mathbf{F}}_{\beta }^{\alpha }}\cdot {\left({\mathbf{F}}_{\beta }^{\alpha }\right)}^T.$$ (4.5)

Here, ${\mathbf{T}}_{\beta }^{\alpha }$ is the stress calculated under the assumption that the entire mixture consists of bonds only from family β in generation α. Similarly, T_β is the stress under the assumption that the entire mixture consists of bonds only from family β, accounting for contributions from all its generations α.

4.2. Theoretical formulation

4.2.1. Mixture composition and yielded bond fraction

To simplify the following presentation, we introduce the concept of yielded bonds, denoted by y, to represent bonds of the current extant generation in a plasticity formulation. The yielded bond fraction for each family β is given by

$$w_{\beta }^y=\sum _{\alpha \ne s}{w}_{\beta }^{\alpha }=1-w_{\beta }^s$$ (4.6)

where the summation runs over all possible yielded generations α ≠ s. In particular, at time t = u, Eq. (4.6) reduces to the statement $w_{\beta }^y=w_{\beta }^u$. We then define the relative deformation gradient of yielded bonds as ${\mathbf{F}}_{\beta }^y$, which equals ${\mathbf{F}}_{\beta }^{\alpha }$ for the extant generation α in family β. With these notational changes, we may write Eq. (2.8) in the equivalent form

$${\mathcal{E}}^s\to \underset{{\mathcal{E}}^y}{\underbrace{{\mathcal{E}}^u\to {\mathcal{E}}^v\to \dots }}.$$ (4.7)

We may also define the total fraction w^s of intact bonds in the mixture as $w^s={\sum }_{\beta }{w}_{\beta }{w}_{\beta }^s$, and the total fraction of yielded bonds as $w^y={\sum }_{\beta }{w}_{\beta }{w}_{\beta }^y=1-w^s$, such that w^s + w^y = 1.

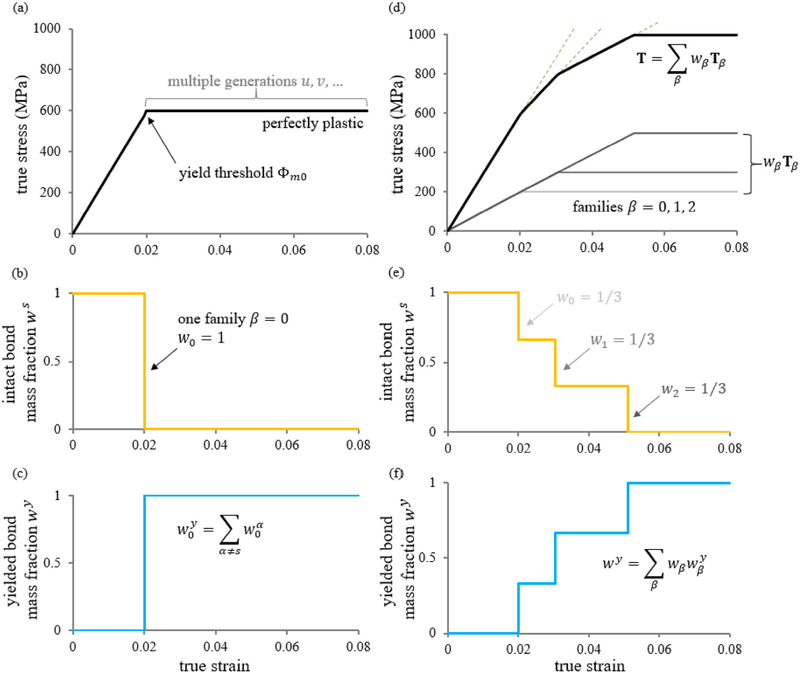
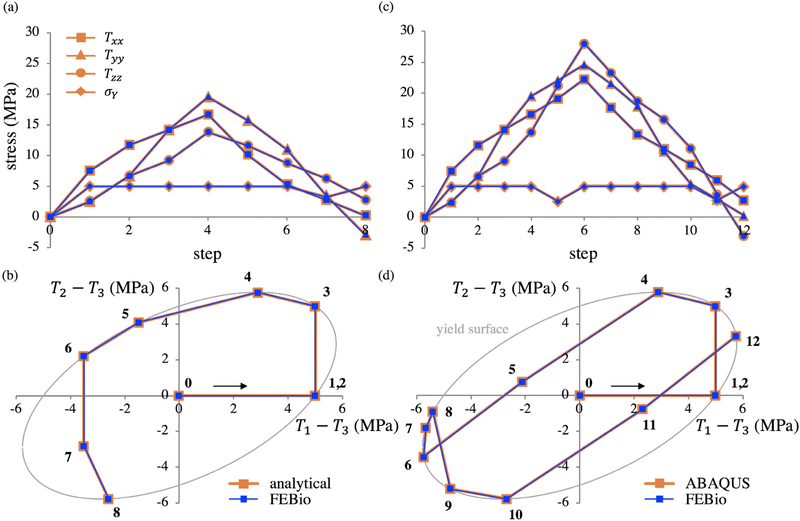
Let each bond family β exhibit an elastic–perfectly plastic response, following the model of Section 3. Once the yield threshold Φ_mβ is reached, all the intact bonds of that family yield at once, such that $w_{\beta }^s=0$ and $w_{\beta }^y=1$, as shown for the mixture stress response in Fig. 1a–c. Now consider that there are three bond families, β = 0, 1, 2 which are weighted evenly, w_β = 1/3∀β; also consider that ψ_β = ψ, implying that each bond family exhibits the same elastic response. The stress response for this illustrative example is shown in Fig. 1d–f. Though each bond family is elastic–perfectly plastic, their superposition develops “hardening”-like behavior. At the onset of yielding, when family β = 0 yields, its bond mass fractions are $w_0^s=0$ and $w_0^y=1$, implying that this entire family has yielded. However, since the family has a mass fraction w₀ = 1/3 in the solid mixture, two-thirds of the bonds in the mixture remain intact at this juncture, $1-w_0^s=2/3$. As subsequent families β yield, their bonds transition from intact to yielded generations in the same manner. Though the stress response in Fig. 1d is classically described as a “hardening” behavior, our reactive mixture framework proposes a different interpretation, namely that there are multiple elastic–perfectly plastic bond families in the material, each with a different threshold of yielding (Skelton et al., 1997; Zhang and Montans, 2019; Nguyen et al., 2020).

Fig. 1.

The phenomenon described as “kinematic hardening” in classical plasticity may be represented by the superposition of multiple elastic–perfectly plastic bond families with different yield thresholds. The elastic–perfectly plastic stress response of a single bond family β = 0 in the reactive framework is presented in (a), with the initial linear response contributed by the intact bonds s; upon yielding at the threshold Φ_m0, the perfectly plastic response consists of multiple generations of breaking and reforming bonds α = u, υ, …. The evolution of mass fractions $w_0^s$ of intact and $w_0^y$ of yielded bonds is presented in (b) and (c), respectively. The stress response obtained from the superposition of three bond families β = 0,1,2 is shown in (d), where each family occupies the same mass fraction in the mixture, $w_0=w_1=w_2=\frac{1}{3}$, reproducing the classical kinematic hardening behavior. Green dashed lines help indicate changes in slope due to yielding of each bond family. The corresponding mixture mass fractions of (e) intact bonds w^s, and (f) yielded bonds w^y = 1−w^s further illustrates the occurrence of each yielding reaction.

For each bond family β, the family mass fraction w_β, the functional forms of the specific strain energy ψ_β and yield function Φ_β, and the associated yield threshold Φ_mβ must be provided by constitutive assumption. The total number n_f of bond families must also be provided. The simplest approach, adopted in all the illustrations in this paper, is to assume that ψ_β and Φ_β have the same respective functional forms ψ and Φ for all bond families β, where ρ_rψ represents the strain energy density Ψ_r of the elastic response. Then, parameters n_f and {w_β, Φ_mβ}, β ∈ [0, n_f – 1] suffice to define an elastoplastic material which exhibits classical kinematic hardening behavior, for given functional forms ψ and Φ. The selection of the mass fraction and yield threshold for each family is a constitutive choice which should be guided by experimental data. The examples in Section 4.3 provide simple constitutive models for these various parameters which have the ability to match a variety of experimental data.

4.2.2. Reaction kinetics and thermodynamics

Reaction kinetics take the same form for each bond family β as for the single bond family in Section 3.1; in particular, in the expressions for Eqs. (3.1)–(3.2), substitute ${\rho }_{r\beta }^{\alpha }$ for ${\rho }_r^{\alpha }$ and ${\widehat{\rho }}_{r\beta }^{\alpha }$ for ${\widehat{\rho }}_r^{\alpha }$. As per Section 3.5.1, the Clausius–Duhem inequality places a constraint on the functional forms of the mappings ${\mathbf{F}}_{\beta }^{\alpha s}$, subject to constitutively provided yield measures Φ_β. Assuming that all bond families β share the same functional form Φ simplifies the effort to satisfy the inequality constraint for the entire mixture. It is further assumed that all bond families adopt the same constitutive model for plastic flow, i.e., the functional forms of the constitutive mappings ${\mathbf{F}}_{\beta }^{\alpha s}$ are identical.

The heat supply generated by bonds breaking and reforming in a mixture of multiple bond families β can be obtained from the general expression of Eq. (3.4) as

$${\rho }_{r}r=\sum _{\beta }\sum _{\alpha }{\widehat{\rho }}_{r\beta }^{\alpha }{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^{\alpha }\right).$$ (4.8)

Similarly, the specific heat supply resulting from u–generation bonds breaking and reforming at time t = υ is evaluated as per Eq. (3.38),

$$r(t)=\delta (t-v)\sum _{\beta }{w}_{\beta }\left({\psi }_{\beta }\left({\mathbf{F}}_{\beta }^v(v)\right)-{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^u(v)\right)\right),$$ (4.9)

where each bond family is weighted by its mixture mass fraction w_β. It is implicit in this expression that only those bond families that are yielding at time υ contribute to this expression. It follows that heat dissipation increases as more bond families start yielding.

4.3. Constitutive modeling of yield response

Here, we provide basic constitutive relations for the parameters {w_β, Φ_mβ}, β ∈ [0, n_f – 1] which define an elastoplastic material. We also demonstrate how these various parameters affect the uniaxial stress–strain response of a material. The example in Fig. 1d shows how superposition of multiple elastic–perfectly plastic bond families may create a hardening-like curve. In particular, we present a constitutive modeling framework that requires at most six scalar parameters, regardless of the value of n_f.

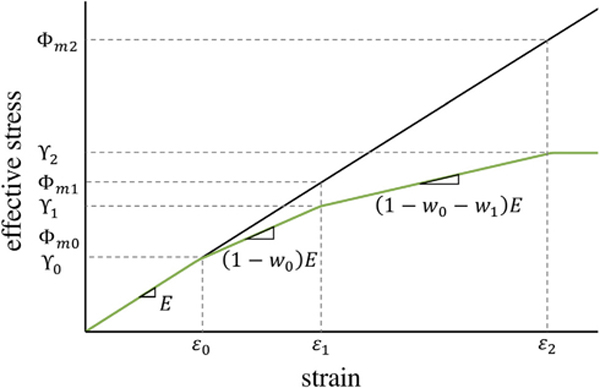
Since each family behaves elastically until it yields, a family’s yield threshold Φ_mβ is generally not the value recorded on a stress–strain curve when the slope changes (Fig. 2). That value may be called the apparent yield threshold ${\mathcal{Y}}_{\beta }$, which can be related to the true yield threshold Φ_mβ by assuming a linear elastic stress–strain relationship prior to yielding. For simplicity, we assume that ${\mathcal{Y}}_{\beta }$ values are evenly distributed between an initial yield threshold ${\mathcal{Y}}_0$ and a final yield threshold ${\mathcal{Y}}_{\text{max}}$, parameters which may be identified from a stress–strain curve (Fig. 3a–b). Beyond ${\mathcal{Y}}_{\text{max}}$, the material either behaves as if it is perfectly plastic (a scenario which may be valid around the ultimate strength, for example), or it transitions to a linear hardening regime. The constitutive model thus specifies

$$\begin{gathered} {\mathcal{Y}}_{\beta }={\mathcal{Y}}_0+\beta \frac{{\mathcal{Y}}_{\max }-{\mathcal{Y}}_0}{n_f-1},\beta =0,\dots ,n_f-1 \\ {\Phi }_{m\beta }={\Phi }_{m,\beta -1}+\frac{{\mathcal{Y}}_{\beta }-{\mathcal{Y}}_{\beta -1}}{1-{\sum }_{b=0}^{\beta -1}{w}_b},{\Phi }_{m0}={\mathcal{Y}}_0 \end{gathered}$$ (4.10)

The relationships between ${\mathcal{Y}}_{\beta }$ and Φ_mβ embodied in Eq. (4.10) are illustrated graphically in Fig. 2. Through this relationship, only the values of ${\mathcal{Y}}_0$ and ${\mathcal{Y}}_{\text{max}}$ must be specified, along with n_f.

Fig. 2.

Schematic stress–strain curve illustrating derivation of constitutive models for Φ_mβ. E is Young’s modulus of the elastic solid, 𝜀_β are the unknown yield strains for each bond family, ${\mathcal{Y}}_{\beta }$ are the effective yield thresholds for the global material, Φ_mβ are the true yield thresholds for each family, and w_β are the family mass fractions.

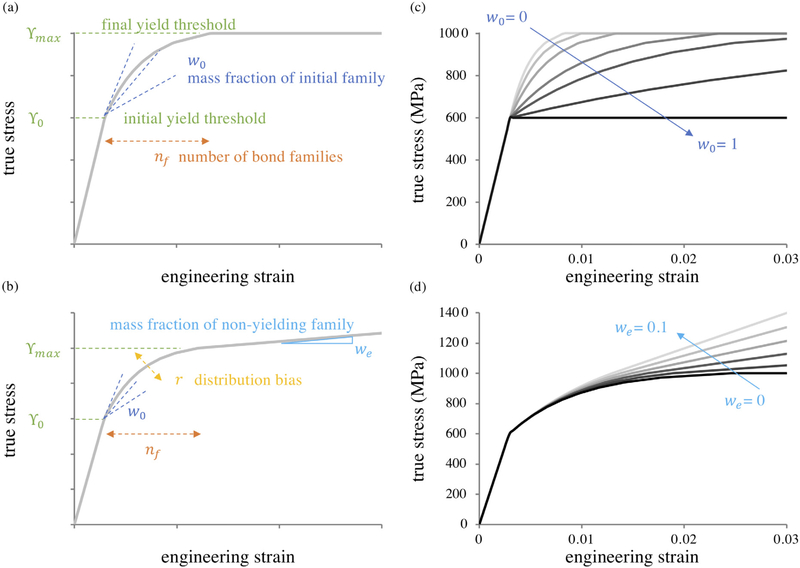
Fig. 3.

Modeling uniaxial stress–strain curves using the constitutive model for scalar bond family parameters given in Section 4.3. Identification of parameters on idealized stress–strain curves showing (a) a plateau in the stress, or (b) exhibiting a region of linear hardening. The yielding behavior is fully described by the set of parameters {n_f, ${\mathcal{Y}}_0$, ${\mathcal{Y}}_{\text{max}}$, w₀, w_e, r}. Parametric variations of (c) w₀ and (d) w_e illustrate their influence on the stress–strain response; other parameters are held fixed. In (c–d) n_f = 10, ${\mathcal{Y}}_0$ = 600 MPa, ${\mathcal{Y}}_{\text{max}}$ = 1000 MPa, and r = 1. In (c), w_e = 0 and in (d) w₀ = 0.75. For all cases, $\text{E}=200\text{GPa}$ and $\nu =0.33$.

The family mass fractions w_β govern the influence of each family on the overall material response. The simplest model for w_β involves specifying the mass fraction of the first yielding family w₀, which controls the slope of the initial post-yield response (Fig. 3a), and then evenly weighting the rest of the bond families, w_β = (1 − w₀) / (n_f – 1). However, in cases where the material transitions to a linear hardening regime, we can recover this behavior by adding one more bond family, β = n_f, that never yields, thus remaining elastic. The associated mass fraction w_β for β = n_f is called the elastic mass fraction and denoted w_e; a non-zero value for this parameter may be specified whenever we wish to include linear hardening behavior (Fig. 3b). Given initial and elastic mass fractions w₀ and w_e, the simplest constitutive assumption for the remaining w_β’s assumes the remaining mass is evenly divided, such that

$$w_{\beta }=\frac{1-w_e-w_0}{n_f-1},\beta \in \left[1,n_f-1\right].$$ (4.11)

The effect of the mass fraction parameters w₀ and w_e is explored parametrically in Fig. 3c and d, respectively. In general, most ductile materials have w₀ very close to unity, which provides hardening behavior over a finite strain range. As w₀ → 1 the stress–strain behavior approaches perfect plasticity. In contrast, when w_e = 0, the material response becomes perfectly plastic once the final yield threshold ${\mathcal{Y}}_{\text{max}}$ has been exceeded. As w_e increases, a region of linear hardening is seen on a plot of the true stress against strain. For most ductile materials, w_e is usually 0 or on the order of 0.001 (see the fits in Section 6).

It is also possible to refine the constitutive relations of Eqs. (4.10)–(4.11) by introducing a bias factor r, which allows a geometric progression for the apparent yield thresholds and family mass fractions, instead of uniform spacing. The bias factor r has the effect of modifying the shape of the hardening region between ${\mathcal{Y}}_0$ and ${\mathcal{Y}}_{\text{max}}$ (Fig. 3b). The modified constitutive relations for w_β and Φ_mβ take the form

$$\begin{gathered} c=\frac{1-r}{1-r^{n_f-1}}{\Phi }_{m0}={\mathcal{Y}}_0 \\ {\mathcal{Y}}_1={\mathcal{Y}}_0+c\left({\mathcal{Y}}_{\max }-{\mathcal{Y}}_0\right),{\Phi }_{m1}={\mathcal{Y}}_0+\frac{{\mathcal{Y}}_1-{\mathcal{Y}}_0}{1-w_0} \\ {\mathcal{Y}}_{\beta }={\mathcal{Y}}_{\beta -1}+r\left({\mathcal{Y}}_{\beta -1}-{\mathcal{Y}}_{\beta -2}\right),{\Phi }_{m\beta }={\Phi }_{m,\beta -1}+\frac{{\mathcal{Y}}_{\beta }-{\mathcal{Y}}_{\beta -1}}{1-{\sum }_{b=0}^{\beta -1}{w}_b} \end{gathered}$$ (4.12)

The mass fractions w_β are similarly biased, where w₀ and w_e are specified and

$$\begin{gathered} w_1=c\left(1-w_e-w_0\right) \\ {w}_{\beta }=w_{\beta -1}r \end{gathered}$$ (4.13)

The full set of parameters is then given by {n_f, ${\mathcal{Y}}_0$, ${\mathcal{Y}}_{\text{max}}$, w₀, w_e, r}. Setting r = 1 recovers the uniform distribution presented in Eqs. (4.10)–(4.11). Fig. 3a–b graphically describes the influence of each parameter on simplified stress–strain curves, showing how these parameters may be extracted from experimental data.

4.4. Discussion

We may consider some primary distinctions between reactive and classical formulations. The reactive constrained mixture framework for plasticity described above is fully hyperelastic in the sense that free energies and stresses are calculated from standard hyperelastic relationships as functions of elastic deformation only. It is only the breaking and reforming of bonds in a new reference configuration which produces plastic behavior through hyperelastic relations. A second distinction between reactive and classical frameworks arises in the definition of kinematic hardening. Classically, hardening is an expansion or shift of the material’s yield surface in response to the evolution of internal hardening variables, and thus directly corresponds to increasing resistance to plastic flow. Strictly speaking, it is the material’s response to plastic flow which is hardening, i.e., the concept of “hardening” is relative to perfect plasticity. In the reactive framework, so-called “hardening” behavior emerges due to progressively yielding bond families. Since a material described by reactive plasticity is hyperelastic, the term “hardening” does not accurately describe the material’s response. However, relative to the post-yield behavior of an elastic–perfectly plastic material, the response of a reactive elastoplastic material composed of multiple bond families may be considered “harder”, and it is in this sense that we say reactive plasticity recovers kinematic hardening behavior.

In this presentation, we have not attempted to model any cyclic plasticity effects, thus cyclic hardening and softening are behaviors which the present model does not capture (Chaboche, 1989). Developing kinematic hardening through the superposition of multiple non-interacting bond families also introduces a certain coarseness to the model (depending on the choice of n_f), although it would be possible in theory to extend the concept of multiple bond families to a continuous spectrum by following the method developed by Skelton et al. (1997). Furthermore, we have not made an effort to model isotropic hardening, though this is a relatively straightforward extension of the mixture framework which may be accomplished by allowing ${\Phi }_{m\beta }^{\alpha }$ to evolve with the deformation, i.e., each reformed α–generation would have ${\Phi }_{m\beta }^{\alpha }$ greater than the preceding generation, for family β.

It is also interesting to note striking similarities between this work and the cyclic hyperelasto-plasticity framework of Zhang and Montans (2019). Both theories are fully hyperelastic and only employ elastic state variables in flow equations, stresses, and free energy density. The present use of multiple bond families is also substantially similar in concept, if not practice, to those authors’ parallel assembly of so-called Prandtl devices. As also reported in their work, we have no need for explicit descriptions of backstress. Although our formulation is developed within the constrained reactive mixture framework and bears little operational resemblance to Zhang and Montans (2019), their success in applying a similar type of model to cyclic elastoplasticity with hardening suggests possible further expansion of the present framework.

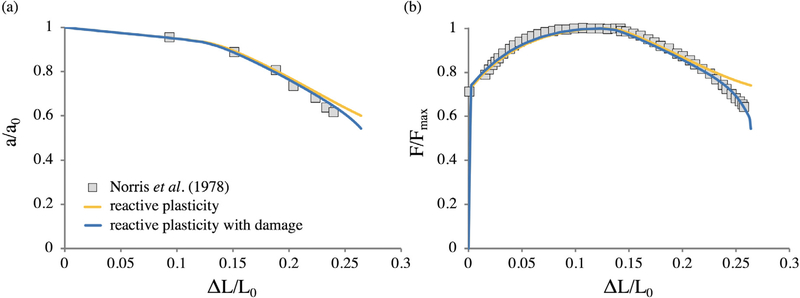
A validation of our model’s description of plastic deformation is deferred to Section 6.

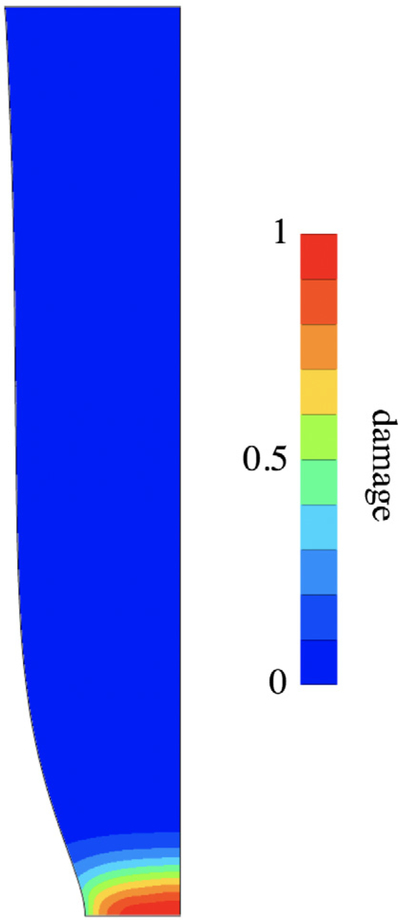
5. Reactive elastoplastic damage mechanics

Plastic deformation is often coupled with damage (Chow and Wang, 1987; Ju, 1989; Bonora, 1997), as the finite deformation and plastic flow of a loaded material typically induces some amount of failure. Within the constrained reactive mixture framework adopted in this study, damage is produced by bonds breaking permanently (Nims et al., 2016), which reduces the generation mass fractions $w_{\beta }^{\alpha }$. In this section, we assume that both intact and yielded bonds may become damaged. Damage to intact bonds may represent some initial damage value for a material with defects, or damage due to intermolecular failure of bonds that never yielded; we refer to this as elastic damage. Damage to yielded bonds represents plastic damage. The mechanism of damage and the failure measure may be different for these two types of bonds, particularly since a stress- or energy-based failure measure may not be appropriate for plastic damage. Recalling the discussion in Section 4.2.1, intact bonds belong to the s–generation which is present at t = −∞. Once yielding occurs, all successive generations of that family are labeled as yielded bonds y. This distinction is necessary so we can then distinguish between damage to intact bonds (elastic damage) and damage to yielded bonds (plastic damage), since intact bonds which get damaged never have the ability to yield. It is important to note that the nature of the plastic deformation described in the preceding section remains unchanged. Damage modifies the material behavior by reducing the fraction of bonds in various generations, which scales the response accordingly.

In a reactive constrained mixture framework, the insertion of damage into the reactive plasticity formulation is straightforward. Our framework for reactive damage was presented in an earlier study (Nims et al., 2016), though it may be viewed as a simpler version of the concepts presented here for reactive plasticity, since bonds break permanently in a damage reaction, thus requiring no function of state ${\mathbf{F}}_{\beta }^{\alpha s}$ to describe a reformed configuration. Furthermore, the specific free energy of broken bonds is zero. The scalar elastic damage criterion ${\Xi }_{\beta }^e\left({\mathbf{F}}^s\right)$ for bond family β is the analog to the yield criterion Φ_β for plasticity. As shown by Nims et al. (2016), the main contrast with reactive plasticity is that not all bonds in the family β break simultaneously at a single elastic damage threshold ${\Xi }_{m\beta }^e$. Instead, the fraction of broken bonds varies as a function of ${\Xi }_{\beta }^e\left({\mathbf{F}}^s\right)$, denoted by $F_{\beta }^e\left({\Xi }_{\beta }^e\right)$, such that $0\le F_{\beta }^e\left({\Xi }_{\beta }^e\right)\le 1$. Here, $F_{\beta }^e\left({\Xi }_{\beta }^e\right)$ is a function of state; it must be a monotonically increasing function of its argument to satisfy the Clausius–Duhem inequality (Nims et al., 2016). We may view $F_{\beta }^e$ as a cumulative distribution function (CDF), whose corresponding probability distribution function (PDF) represents the probability of damage at a particular value of ${\Xi }_{\beta }^e$. The mass fraction of broken bonds w^b is in fact equal to the damage variable D as defined in classical damage mechanics; however, it must be noted that w^b is a mass fraction governed by the axiom of mass balance, and therefore does not carry the same meaning in our theory as damage variables do in classical works.

5.1. Theoretical formulation

We first briefly sketch the structure of our elastoplastic damage theory for a single bond family β. Since each bond family in reactive plasticity yields all at once, we can easily split an elastoplastic damage theory into two parts to represent elastic and plastic damage regimes. Assume that the first yielding reaction for bond family β occurs at time t = u_β. Prior to this initial yielding, the damage behavior described by Nims et al. (2016) applies, and the material composition is generally a mixture of intact (α = s) and broken (α = b) bonds satisfying the reaction ${\mathcal{E}}^s\to {\mathcal{E}}^b$. The corresponding bond mass fractions satisfy $1=w_{\beta }^s+w_{\beta }^b$ and $w_{\beta }^y=0$, where $w_{\beta }^b=F_{\beta }^e\left({\Xi }_{\beta }^e\right)$ is the elastic damage in bond family β. At t = u_β, the remaining intact bonds $w_{\beta }^s=1-w_{\beta }^b$ all yield, following the reaction in Eq. (4.7). The family mass balance is then given as $1=w_{\beta }^y+w_{\beta }^b$, since $w_{\beta }^s=0$ after yielding.

For time t > u_β, yielded bonds may continue to yield, but they may also sustain damage according to the reaction ${\mathcal{E}}^y\to {\mathcal{E}}^b$, which reduces their mass fraction $w_{\beta }^y$. Following the classical literature, damage to yielded bonds may occur based on a measure of plastic strain (Section 5.1.4; Chow and Wang, 1987; Simo and Ju, 1989; Bonora, 1997), which is distinct from the measure of elastic damage. Therefore, we denote the plastic damage measure as ${\Xi }_{\beta }^p\left({\mathbf{F}}_{\beta }^{ys}\right)$ and its cumulative distribution function by $F_{\beta }^p\left({\Xi }_{\beta }^p\right)$. Only the remaining undamaged fraction $1-F_{\beta }^p\left({\Xi }_{\beta }^p\right)$ of yielded bonds may break and reform as the next yielded generation. As mentioned above, the modern understanding is that plastic strain is ill-defined and not a suitable state variable. It must be recognized that, just as ${\mathbf{F}}_{\beta }^{ys}$ is a constitutively-prescribed function of state and does not carry the meaning of a plastic deformation gradient, the plastic damage measure ${\Xi }_{\beta }^p$ derived from ${\mathbf{F}}_{\beta }^{ys}$ is also function of state. When we provide a precise form of ${\Xi }_{\beta }^p$ in Section 5.1.4, it is with the understanding that this quantity is called a plastic strain for convenience only.

When plastic deformation occurs simultaneously with damage, the mass fraction of each successive yielded generation will have decreased. The following treatment now considers the superposition of multiple plastic bond families, as described in Section 4.

5.1.1. Damage to intact bonds

We now adopt the simplifying assumption that the elastic damage measure is the same for all bond families β, ${\Xi }_{\beta }^e\equiv {\Xi }^e$. Furthermore, the associated CDF has the same functional form for all β, $F_{\beta }^e\equiv F^e$. At any given time t, there is a maximum value of Ξ^e that has been achieved over the past deformation history. This maximum value may be distinct for each bond family β, since intact bond families may yield at different values of F^s; it is thus denoted by ${\Xi }_{m\beta }^e$,

$${\Xi }_{m\beta }^e=\underset{-\infty <\tau \le t<u_{\beta }}{\max }{\Xi }^e\left({\mathbf{F}}^s(\tau )\right).$$ (5.1)

Any damage sustained by intact bonds reduces their mass fraction, such that

$$\{\begin{array}{l}{w}_{\beta }^s=1-F^e\left({\Xi }_{m\beta }^e\right)\hfill \\ w_{\beta }^y=0,t<u_{\beta },\hfill \\ w_{\beta }^b=F^e\left({\Xi }_{m\beta }^e\right)\hfill \end{array}$$ (5.2)

and hence the mass balance of Eq. (4.2) is satisfied. Since all remaining intact bonds yield at t = u_β and thus no intact bonds are left to sustain damage, $F^e\left({\Xi }_{m\beta }^e\right)$ remains constant when t ≥ u_β.

5.1.2. Damage to yielded bonds

At time t = u_β, the yield threshold Φ_mβ for family β is reached and all remaining intact bonds in family β yield such that

$$\{\begin{array}{l}{w}_{\beta }^s=0\hfill \\ w_{\beta }^y=1-F^e\left({\Xi }_{m\beta }^e\right),t=u_{\beta }.\hfill \\ w_{\beta }^b=F^e\left({\Xi }_{m\beta }^e\right)\hfill \end{array}$$ (5.3)

Once they have formed, yielded bonds may sustain plastic damage. Here also we adopt the simplifying assumption that the plastic damage measure has the same functional form for all bond families β, ${\Xi }_{\beta }^p\equiv {\Xi }^p$. The maximum value of Ξ^p experienced by family β up until the current time t is denoted ${\Xi }_{m\beta }^e$,

$${\Xi }_{m\beta }^p=\underset{u_{\beta }\le \tau <t}{\max }{\Xi }^p\left({\mathbf{F}}_{\beta }^y(\tau )\right).$$ (5.4)

For t > u_β, yielded bonds may continue to yield, breaking and reforming into successive generations. However, in contrast to Section 3, the mass fraction $w_{\beta }^y$ of yielded bonds in family β no longer remains constant over successive yield generations, due to the plastic damage reaction. Each time a yielded bond breaks and reforms into a new generation, $w_{\beta }^y$ is given by the undamaged fraction of yielded bonds,

$$\{\begin{array}{l}{w}_{\beta }^s=0\hfill \\ w_{\beta }^y=\left(1-F^p\left({\Xi }_{m\beta }^p\right)\right)\left(1-F^e\left({\Xi }_{m\beta }^e\right)\right),t>u_{\beta }.\hfill \\ w_{\beta }^b=F^e\left({\Xi }_{m\beta }^e\right)+F^p\left({\Xi }_{m\beta }^p\right)\left(1-F^e\left({\Xi }_{m\beta }^e\right)\right)\hfill \end{array}$$ (5.5)

Eqs. (5.2), (5.3), and (5.5) govern the temporal behavior of the bond species mass fractions.

5.1.3. Free energy density, stress, and damage

Recognizing that damaged (broken) bonds do not store free energy, the referential mixture free energy density in Eq. (4.3) may be rewritten as

$${\Psi }_r={\rho }_r\sum _{\beta }{w}_{\beta }\left(w_{\beta }^s{\psi }_{\beta }\left({\mathbf{F}}^s\right)+w_{\beta }^y{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^y\right)\right),$$ (5.6)

where the bond mass fractions $w_{\beta }^s$ and $w_{\beta }^y$ are given in Eqs. (5.2)–(5.5) prior to, during, and after yielding of each bond family β. Similarly, the mixture stress may be evaluated from Eq. (4.4) as

$$\mathbf{T}=\sum _{\beta }{w}_{\beta }\left(w_{\beta }^s{\mathbf{T}}_{\beta }^s\left({\mathbf{F}}^s\right)+w_{\beta }^y{\mathbf{T}}_{\beta }^y\left({\mathbf{F}}_{\beta }^y\right)\right),$$ (5.7)

where the stresses ${\mathbf{T}}_{\beta }^{\alpha }$ are given by the standard hyperelasticity relation of Eq. (4.5). These expressions may be simplified further when assuming that the functional form of ψ_β remains the same for all bond families β. Finally, the reactive mixture equivalent of the damage variable D may be evaluated for elastoplastic damage as the fraction of all bonds that are broken,

$$D=w^b=\sum _{\beta }{w}_{\beta }{w}_{\beta }^b.$$ (5.8)

5.1.4. Damage measures

For elastic damage, we propose to use the von Mises stress, which is the same functional measure proposed for plastic yielding; this implies that the functions Ξ^e and Φ have the same form. For plastic damage, experimental results show that during plastic flow damage is coupled with measures of plastic strain (Lemaitre and Desmorat, 2005), necessitating a strain-based plastic damage measure Ξ^p. For yielded bonds in a bond family β, we can use the constitutively-determined mapping ${\mathbf{F}}_{\beta }^{ys}$ to define plastic right Cauchy–Green and Lagrange strain tensors through

$$\begin{gathered} {\mathbf{C}}_{\beta }^{ys}={\left({\mathbf{F}}_{\beta }^{ys}\right)}^T\cdot {\mathbf{F}}_{\beta }^{ys} \\ {\mathbf{E}}_{\beta }^{ys}=\frac{1}{2}\left({\mathbf{C}}_{\beta }^{ys}-\mathbf{I}\right). \end{gathered}$$ (5.9)

One possible constitutive relation for Ξ^p, which remains valid for general deformations, is to set it equal to the effective plastic strain $e_{\beta }^p$ for the various bond families β,

$$e_{\beta }^p=\sqrt{\frac{2}{3}\mathrm{dev}{\mathbf{E}}_{\beta }^{ys}:\mathrm{dev}{\mathbf{E}}_{\beta }^{ys}}.$$ (5.10)

In a numerical implementation, the effective plastic strain $e_0^p$ of the first bond family to yield may be reported as the effective plastic strain in the entire material, for consistency with plastic strain measures in classical models of plasticity.

Quantities in this section do not represent plastic strains or plastic strain tensors, though we adopt the terminology due to similarities. Recall that the non-observable function of state ${\mathbf{F}}_{\beta }^{ys}={\mathbf{F}}_{\beta }^{ys}\left({\mathbf{F}}^s,{\rho }_{r\beta }^{\alpha }\right)$ is a time-invariant mapping providing the reference configuration of a yielded bond y with respect to the reference configuration of the master constituent s, for family β. The quantities ${\mathbf{C}}_{\beta }^{ys}$ and ${\mathbf{E}}_{\beta }^{ys}$ then also represent non-observable functions of state calculated as strain tensors. Consequently, $e_{\beta }^p$ is a measure of the relative motion of the reference configuration of bond family β, expressed as a scalar “strain”. Physically, this amounts to the modeling assumption that once the breaking-and-reforming process takes a bond family out of a local neighborhood centered about its original position, the bond begins to degrade with further breaking-and-reforming processes. That each of these quantities exists for every bond family β emphasizes the lack of any true or unique plastic strain measure in this framework.

5.1.5. Cumulative damage distribution functions

The final set of constitutive relations required to fully define an elastoplastic damage material are the two CDFs, $F^e\left({\Xi }_{m\beta }^e\right)$ and $F^p\left({\Xi }_{m\beta }^p\right)$. As shown by Nims et al. (2016), the only requirement imposed by the Clausius–Duhem inequality is that these be monotonically increasing functions. Whereas these CDFs may be characterized directly from experimental data, we illustrate our elastoplastic damage framework using a Weibull distribution of the form

$$F(\Xi )=1-\exp \left(-{\left(\frac{\Xi }{\kappa }\right)}^{\gamma }\right),$$ (5.11)

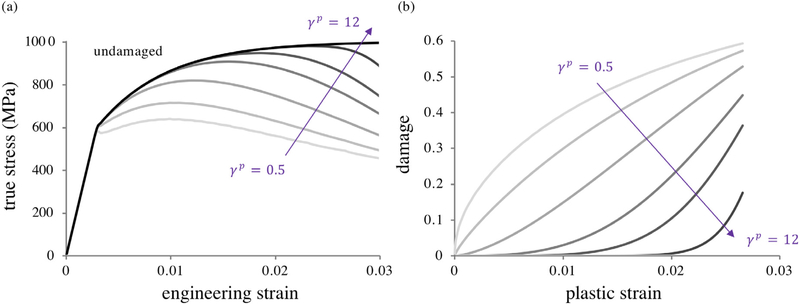
where κ (same units as Ξ) is the value of Ξ at which the fraction 1 − e⁻¹ of bonds have failed and the exponent γ (unitless) controls the slope of the response, such that F (Ξ) approaches a step function with a jump at Ξ = κ as γ → ∞. Therefore, each damage function has two free parameters κ and γ. Based on experimental evidence, we let Ξ^e be given by the von Mises (effective) stress, while Ξ^p is taken to be the effective plastic strain (Section 5.1.4). Fig. 4 shows the effect of the Weibull parameter γ^p on the stress–strain and damage–strain responses, with κ^p fixed. The damage response as a function of plastic strain is identically the prescribed CDF (Fig. 4b). The shape of the CDF changes from logarithmic-like to exponential as γ^p increases, demonstrating the ability of this formulation to recover a broad variety of experimentally measured damage–strain behaviors (Bonora, 1997).

Fig. 4.

Parametric study of the effect of the damage parameter γ^p for a Weibull distribution, with no intact damage taking place. (a) As γ^p increases, the onset of noticeable damage shifts to higher strains and becomes more rapid. (b) Plot of the damage variable $D=\sum _{\beta }{w}_{\beta }{F}^p\left({\Xi }_{m\beta }^p\right)$. The response becomes more nonlinear as γ^p deviates from unity. Other plasticity and damage parameters are n_f = 20, ${\mathcal{Y}}_0$ = 600 MPa, ${\mathcal{Y}}_{\text{max}}$ = 1000 MPa, w₀ = 0.75, w_e = 0, r = 1, and κ^p = 0.03.

5.2. Thermodynamics

The heat supply density generated by plastic yielding reactions $\left({\mathcal{E}}^s\to {\mathcal{E}}^y\right)$, and damage reactions ( ${\mathcal{E}}^s\to {\mathcal{E}}^b$ and ${\mathcal{E}}^y\to {\mathcal{E}}^b$ ), may be evaluated from Eq. (4.8), recalling that the specific free energy of broken bonds is zero,

$${\rho }_{r}r=\sum _{\beta }{\widehat{\rho }}_{r\beta }^s{\psi }_{\beta }\left({\mathbf{F}}^s\right)+{\widehat{\rho }}_{r\beta }^y{\psi }_{\beta }\left({\mathbf{F}}_{\beta }^y\right).$$ (5.12)

Here, ${\widehat{\rho }}_{r\beta }^s$ and ${\widehat{\rho }}_{r\beta }^y$ are obtained by summing the respective mass density supplies from each reaction. The yielding reaction supplies were given in Eq. (3.2) for a single bond family. To evaluate the mass density supplies ${\widehat{\rho }}_{r\beta }^{\alpha }$ for damage reactions, recognize that the mass balance Eq. (2.5) may be rewritten as ${\widehat{\rho }}_{r\beta }^{\alpha }={\rho }_{r\beta }{\dot{w}}_{\beta }^{\alpha }$. Thus, the contribution to the heat supply density from damage mechanics may be obtained by evaluating the material time derivatives of generation mass fractions $w_{\beta }^{\alpha }$ in Eqs. (5.2)–(5.5), for α = s and α = y. Since those relations involve the CDFs, we need to evaluate ${\dot{F}}^e\left({\Xi }_m^e\right)$ and ${\dot{F}}^p\left({\Xi }_{m\beta }^p\right)$, which are non-zero on the damage surface when the damage is increasing. In turn, these expressions require the evaluation of ${\dot{\Xi }}^e$ and ${\dot{\Xi }}^p$,

$${\dot{\Xi }}^e\left({\mathbf{F}}^s\right)=\frac{\partial {\Xi }^e}{\partial {\mathbf{F}}^s}:{\dot{\mathbf{F}}}^s,$$ (5.13)

and

$${\dot{\Xi }}^p\left({\mathbf{F}}_{\beta }^{ys}\right)=\frac{\partial {\Xi }^p}{\partial {\mathbf{F}}_{\beta }^{ys}}:\frac{{\mathbf{F}}_{\beta }^{vs}-{\mathbf{F}}_{\beta }^{us}}{v_{\beta }-u_{\beta }},$$ (5.14)

using an incremental form for consecutive yielding generations u and υ. Combining these relations, we find that

$$\begin{array}{l}{\widehat{\rho }}_{r\beta }^s=-\delta \left(t-u_{\beta }\right){\rho }_{r\beta }-\{\begin{array}{ll}{\rho }_{r\beta }{\dot{F}}^e\left({\Xi }_{m\beta }^e\right)\hfill & t<u_{\beta }\hfill \\ 0\hfill & t\ge u_{\beta }\hfill \end{array}\\ {\widehat{\rho }}_{r\beta }^y=\left(\delta \left(t-u_{\beta }\right)-\delta \left(t-v_{\beta }\right)\right){\rho }_{r\beta }\\ -\{\begin{array}{ll}0\hfill & t<u_{\beta }\hfill \\ {\rho }_{r\beta }{\dot{F}}^e\left({\Xi }_{m\beta }^e\right)\hfill & t=u_{\beta }\hfill \\ {\rho }_{r\beta }{\dot{F}}^p\left({\Xi }_{m\beta }^p\right)\left(1-F^e\left({\Xi }_{m\beta }^e\right)\right)+{\rho }_{r\beta }{\dot{F}}^e\left({\Xi }_{m\beta }^e\right)\left(1-F^p\left({\Xi }_{m\beta }^p\right)\right)\hfill & u_{\beta }<t<v_{\beta }.\hfill \end{array}\end{array}$$ (5.15)

5.3. Discussion

This section has presented a constrained reactive mixture theory for elastoplastic damage mechanics, using reaction kinetics to describe bonds which break and reform. Bonds which break permanently lead to damage, and both intact and yielded bonds may break. Yielded bonds break based on a measure which is derived from the constitutive model for F^αs and bears some resemblance to a classical scalar plastic strain. Since F^αs is not an observable kinematic variable but rather a function of state, this damage criterion is not kinematically based, despite its name. The constitutive freedom in the present model allows for a wide variety of damage behaviors to be modeled, using only simple scalar variables. Accordingly, our reactive framework does not need to develop tensorial damage potentials (such as Chow and Wang, 1987) or postulate damage evolution laws within an internal state variable framework (such as Simo and Ju, 1989), as the evolution of damage in our mixture model is given by the mass fraction of broken bonds, based on reaction kinetics governed by mass balance.

6. Verification and validation

6.1. Finite element implementation

The theoretical models discussed in Sections 3–5 were implemented in the custom, open source finite element code FEBio (www.febio.org; Maas et al., 2012) as material models “reactive plasticity” and “reactive plastic damage”. All finite element analyses below were performed using three-dimensional models and isoparametric eight-node hexahedral elements, unless otherwise specified. Due to its origins as a nonlinear finite deformation code designed for the biomechanics and biophysics communities (Maas et al., 2017), FEBio is built around a mixture theory framework (Ateshian and Humphrey, 2012; Ateshian et al., 2013, 2014), which greatly facilitated the implementation of the proposed models. Details of the numerical implementation can be found in the source code (github.com/febiosoftware/FEBio). Here, we mention that a secant method was employed to numerically calculate the consistent tangent matrix (Simo and Taylor, 1985). In contrast to the complexity involved with evaluating an analytical consistent tangent, the proposed secant method only requires seven stress evaluations (Miehe, 1996).

6.2. Constitutive models

6.2.1. Elasticity

The present theory treats materials which exhibit plasticity and plastic deformation as reactive solids. Due to the use of a purely hyperelastic framework, the theory places no further constraints upon the constitutive model for the underlying elastic solid beyond those familiar from hyperelasticity. However, for the purposes of verification and validation, a constitutive model must be selected. For the remainder of this presentation, all materials are modeled as isotropic compressible neo-Hookean solids, with a referential strain energy density function given by

$${\rho }_r\psi (\mathbf{F})=\frac{G}{2}\left(I_1-3\right)-G\ln J+\frac{\lambda }{2}{(\ln J)}^2,$$ (6.1)

with material constants G and λ. Here, J = det F, I₁ = tr C, and C = F^T ⋅F is the right Cauchy–Green tensor (Bonet and Wood, 1997). Young’s modulus E and Poisson’s ratio ν are related to G and λ via the standard relations E = 2G (1 + ν) and λ = 2Gν/(1 − 2ν). This finite deformation neo-Hookean model reduces to Hooke’s law for isotropic linear elasticity under infinitesimal strains. Unless specified otherwise, material properties E and ν for the models presented below were obtained from online reference tables (MatWeb; www.matweb.com).

6.2.2. Plasticity

For verification and validation problems, the plastic yield measure Φ was set to the von Mises (effective) stress σ_Y, as it is an experimentally-supported choice for isotropic, ductile materials (Khan and Huang, 1995). The distribution of bond families, the superposition of which is responsible for developing kinematic hardening, was governed by the constitutive relations outlined in Section 4.3. The parameters n_f, ${\mathcal{Y}}_0$, ${\mathcal{Y}}_{\text{max}}$, w₀, w_e, and r were obtained by fitting experimental data, under the assumption that each bond family represents an elastic–perfectly plastic material.

6.2.3. Damage

For simplicity, we assumed that intact bonds of all families share the same function $F^e\left({\Xi }_{m\beta }^e\right)$. We further assumed that all yielded bonds (every generation α ≠ s for every family β) sustain plastic damage in the same manner according to $F^e\left({\Xi }_{m\beta }^p\right)$. In what follows, we adopted Weibull distributions for both CDFs, as given in Eq. (5.11).

6.3. Fundamental benchmarks

The fundamental 2D and 3D plasticity benchmarks proposed by Becker (2001) were selected to verify the constitutive modeling behind reactive plasticity as well as the FEBio finite element implementation. Each benchmark is a single-element analysis with an elastic–perfectly plastic material (one bond family, β = 0). Following Becker, we used E = 250 GPa and ν = 0.25. The yield measure for perfect plasticity was set to ${\mathcal{Y}}_0$ = 5 MPa. For a perfectly plastic material with these specifications, n_f = r = w₀ = 1, w_e = 0, and ${\mathcal{Y}}_{\text{max}}$ does not play a role.

The 2D benchmark problem consisted of a 1mm×1mm square domain in the xy−plane (vertices ABCD counterclockwise starting from origin), subjected to prescribed displacements along x and y, and then returned to its original geometry. Fixed displacements were prescribed as u_x = 0 for line AD and u_y = 0 for line AB. Lines BC and CD had respective prescribed displacement histories u_x and u_y as given in Table 1. Since FEBio models only 3D geometries, a unit cube was used, fixing u_z = 0 on the positive and negative z−faces. The problem was solved in 8 steps, using a single isoparametric quadratic (20-node) hexahedral brick element. This fundamental 2D plasticity benchmark has an analytical solution available for the case of perfect plasticity with a von Mises yield criterion (Krieg and Krieg, 1977), which was used as the reference solution.

Table 1.

Loading history for fundamental 2D plasticity benchmark, R = 2.5 × 10⁻⁵ mm.

Step	1	2	3	4	5	6	7	8
ux	R	2R	2R	2R	R	0	0	0
uy	0	0	R	2R	2R	2R	R	0

The geometry of the fundamental 3D plasticity benchmark consisted of a 1mm×1mm×1mm cube with counter-clockwise vertices ABCD on the positive z−face and EFGH on the negative z−face. Fixed displacements u_x = 0, u_y = 0, and u_z = 0 were respectively prescribed on faces AEHD, ABFE, and ABCD. Faces BCGF, CDHG and EFGH had respective prescribed displacement histories u_x, u_y, and u_z as given in Table 2. The problem was solved in 12 steps. For this 3D benchmark an analytical solution was not available, thus the problem was also simulated in the commercial finite element code ABAQUS (www.simulia.com) whose results were used as the reference solution. For both analyses, a single isoparametric quadratic (20-node) hexahedral brick element was employed.

Table 2.

Loading history for fundamental 3D plasticity benchmark, R = 2.5 × 10⁻⁵ mm.

Step	1	2	3	4	5	6	7	8	9	10	11	12
ux	R	2R	2R	2R	2R	2R	R	0	0	0	0	0
uy	0	0	R	2R	2R	2R	2R	2R	R	0	0	0
uz	0	0	0	0	R	2R	2R	2R	2R	2R	R	0

Results for the fundamental benchmarks are summarized in Fig. 5. For both benchmarks, the normal stresses were equal to the principal stresses, T_xx = T₁, T_yy = T₂, T_zz = T₃. Exact agreement was found between the normal stresses and von Mises stresses calculated by FEBio’s implementation of reactive plasticity and the reference solutions. In addition, using a special projection (Becker, 2001), the stress paths may be followed on the yield surface by plotting them in the reduced $\overline{x}-\overline{y}$ plane, where $\overline{x}=T_1-T_3$ and $\overline{y}=T_2-T_3$. The reference stress paths agreed identically with those calculated by FEBio, establishing that reactive plasticity exactly obeys the normality condition. More fundamentally, both benchmarks had their displacement histories completely specified for all nodes. As a result, no equation solving was necessary during the analyses; therefore, only the constitutive models for plasticity within the finite element codes were tested.

Fig. 5.

Results for the fundamental 2D and 3D plasticity benchmarks examined in Section 6.3. Comparison of normal stresses and von Mises stress between the reference solution and FEBio, for (a) 2D and (c) 3D benchmarks. Stress paths plotted in the reduced plane, along with the von Mises yield surface, are shown for the reference and FEBio solutions, for (b) 2D, and (d) 3D benchmarks, demonstrating no violation of normality. The reference solution for the 2D benchmark was analytical (Krieg and Krieg, 1977), while the 3D reference solution was obtained with ABAQUS.

6.4. Multi-element multi-material benchmark

A multi-element, multi-material benchmark (Roberts et al., 1992) was used to examine the predictive ability of the constitutive modeling framework, and results were compared to an experimental study on composite panels (Atkins and Weinstein, 1970). The geometry of the multi-element panels is shown in Fig. 6a. In this benchmark, tensile tests were performed on four three-panel composites (Fig. 6b) which varied from entirely annealed mild steel to entirely annealed copper. The responses of the single material steel and copper panels were fitted to a reactive plasticity model to extract the material properties of these metals. The tensile responses of the multi-material panels (2/3 steel + 1/3 copper, 1/3 steel + 2/3 copper) were then predicted using the fitted material properties of steel and copper for the appropriate panels. Three isoparametric quadratic (20-node) hexahedral brick elements were used in FEBio to represent each composite. Material properties for annealed mild steel and annealed copper (E, ν, ${\mathcal{Y}}_0$ ) were obtained from online reference tables, and ${\mathcal{Y}}_0$ was slightly adjusted, as needed, to better fit the experimental data of Atkins and Weinstein (1970).

Fig. 6.

(a) Geometry and (b) multi-material composite panels for the multi-element multi-material benchmark of Section 6.4.

Reactive plasticity models were successfully fitted to steel and copper panels (Fig. 7, blue and orange curves, respectively). For annealed mild steel, the elastic properties were E = 205 GPa and ν = 0.29. Curve-fitting identified plasticity parameters n_f = 15, ${\mathcal{Y}}_0$ = 220 MPa, ${\mathcal{Y}}_{\text{max}}$ = 490 MPa, w₀ = 0.973, w_e = 0, and r = 1.² For annealed copper, material properties E = 120 GPa and ν = 0.34 were prescribed. By fitting the solid copper panel, plasticity parameters n_f = 15, ${\mathcal{Y}}_0$ = 60 MPa, ${\mathcal{Y}}_{\text{max}}$ = 288 MPa, w₀ = 0.988, w_e = 0, and r = 1 were obtained. (Online reference tables report ${\mathcal{Y}}_0$ = 69 MPa for copper.) The predicted responses of the multi-material panels were then observed to be in very close agreement with experimental results (Fig. 7, green and gray curves). This benchmark served to show that reactive plasticity can fit a variety of different material responses with simple scalar parameters. The successful prediction of experimental responses not used for extracting material properties served as a validation of the reactive plasticity framework.

Fig. 7.

Comparison between experimental and computational results for the multi-element multi-material benchmark of Section 6.4.

6.5. Volume change during plastic flow

The assumption of incompressible plastic flow has been thoroughly investigated experimentally (Bridgman, 1947, 1952). In a study by Spitzig et al. (1976), the authors measured the change in volume of unaged maraging steel during a tensile load-unload-reload cycle. In our validation analysis, the elastic properties of unaged maraging steel were taken to be E = 165 GPa and ν = 0.33. Then, the experimental stress–strain response provided by Spitzig et al. (1976) was successfully fitted to the reactive plasticity model, with n_f = 22, ${\mathcal{Y}}_0$ = 398 MPa, ${\mathcal{Y}}_{\text{max}}$ = 1010 MPa, w₀ = 0, w_e = 0, and r = 0.9 (Fig. 8a). The volume change experiment was then predicted, using those material properties. Here, we note that Spitzig et al. provided a curve of true stress vs. true strain for material characterization, and the true strain during the volume change experiment was close to the proportional limit. For these two reasons, we were able to simulate the experimental tests using a single-element model, as the true stress accounts for necking and, in the volume change experiment, any geometric effects due to necking were very unlikely to have occurred under such small strains.

Fig. 8.

Predicting volume change during plastic deformation (Section 6.5). (a) Material properties for unaged maraging steel were obtained by curve-fitting the experimental results, and (b) the resulting volume change during a separate load-unload-reload cycle was predicted using these material properties.

The predicted volume change during the load-unload-reload cycle was in close agreement with the experimental results (Fig. 8b). This finding served to further validate the implementation of the normality condition and the theoretical basis of the decomposition F^s = F^α ⋅ F^αs. Here again, a successful fit of the model to experimental data served as a necessary condition for model validation, whereas the ability to predict independent experimental measurements using those fitted properties served as a sufficient condition for validation.

6.6. Forging a ball bearing

Another validation of the reactive plasticity model considered forging a ball bearing by compressing a cylindrical billet between two dies with hemispherical sockets, as studied by Shih and Yang (1991). To validate our theory and implementation, we first fitted the reactive plasticity model to their material characterization study, then used these properties to predict the ball forming experiment. The material used in the experimental part of Shih and Yang (1991) was annealed aluminum 1100; its elastic material properties are E = 68 GPa and ν = 0.33. These authors performed material characterization using compression of cylindrical specimens between two flat, polished dies (Fig. 9a). The cylindrical specimens had a radius R_b = 5.08 mm and a height H = 13.843 mm. Due to symmetry considerations, a 3 degree wedge model was utilized, with frictionless contact between the cylindrical specimen and the rigid die. The reactive plasticity model, using the von Mises stress as the yield measure, was successfully fitted to experimental results (Fig. 9b), producing n_f = 18, ${\mathcal{Y}}_0$ = 63 MPa, ${\mathcal{Y}}_{\text{max}}$ = 112 MPa, w₀ = 0.994, and w_e = 0, with a bias r = 0.6. These material properties were then used to predict the results of the bearing forging experiment.

Fig. 9.

(a) Geometry and mesh for frictionless compression of a cylindrical billet, used for material characterization in Section 6.6. (b) Finite element fit to the experimental flow curve of Shih and Yang (1991), used to extract reactive plasticity parameters.

In bearing forging, the hemispherical socket of the die had a radius R = 7.938 mm, and the die was modeled as a rigid body. The cylindrical workpiece had a radius R_b = 12.4 mm and a height H = 18.171 mm. Due to symmetry, a 3 degree wedge model of one quarter of the geometry was employed. The geometry and initial mesh are shown in Fig. 10. The mesh was biased towards the initial contact point, and a butterfly mesh was used in this corner due to the extreme deformations during forging. The analysis began with the die socket in grazing contact with the corner of the annealed aluminum workpiece. The final die displacement was set to u_y = d, where d = −4.0005 mm in the symmetric model. As per Shih and Yang (1991), frictionless contact was assumed between the die surface and the workpiece, using our recently developed contact algorithm (Zimmerman and Ateshian, 2018). Though the contact analysis was computationally challenging, due to the die initially contacting the billet at a corner node, snapshots of the deformed mesh at several time points during the analysis show a clean response and good contact enforcement (Fig. 10). The small rib formed at the midsection of the bearing at the final displacement (Fig. 10, right) was also observed in pictures of forged bearings provided by Shih and Yang (1991). Quantitatively, the predicted reaction force on the die compared favorably to these authors’ experimental results (Fig. 11). The small deviation in the predicted slope of the response around the vertical displacement of 7.5 mm may have occurred because friction was neglected in the model.

Fig. 10.

Initial geometry and mesh (left) for the example of forging a ball bearing in Section 6.6. Deformed mesh at the halfway point (center) and upon completion of forging (right). The butterfly mesh in the corner was employed to avoid element distortion due to large deformation at this location. In the right-most figure, the ridge around the bearing midsection is to be expected and can be seen in photographs of actual bearings forged by this process (Shih and Yang, 1991).

Fig. 11.

Die force–displacement curve predicted by FEBio with reactive plasticity compared to experimental measurements (Shih and Yang, 1991), for the bearing forging example in Section 6.6.

6.7. Upsetting of a cylindrical billet

The latter half of the study by Shih and Yang (1991) also considered the classic example of upsetting a cylindrical billet, using the same annealed aluminum 1100 material considered in the previous section (Section 6.6). In this example, the billet was mounted in a cylindrical socket, producing large deformations and rotations since isochoric plastic flow produces barreling. The radius of the billet was R_b = 6.096 mm and the height was H = 18.288 mm. Both ends of the billet were firmly seated in a socket h = 1.27 mm deep in the corresponding die (Fig. 12, left). The top surface of the die was displaced u_y = d. Due to symmetry, a 3 degree wedge model of one quarter of the geometry was considered for the finite element model; the applied displacement was d = −3.81 mm on this symmetric model. Tied contact was applied between the billet and the die socket, representing the experimental boundary conditions, and the die was modeled as a rigid body. Material properties for the annealed aluminum 1100 were taken from Section 6.6.

Fig. 12.

(a) Initial (left) and final deformed geometry and mesh (middle) for the example of upsetting a cylindrical billet considered in Section 6.7. The deformed mesh shows very large rotations. (b) Contour plot of effective plastic strain $e_0^p$ at the final configuration, which compares favorably to the computational results of Shih and Yang (1991).

The final deformed mesh presents significant lateral bulging and large rotations (Fig. 12a). A contour plot of the effective plastic strain at the end of the analysis (Fig. 12b) agrees with that reported by Shih and Yang (1991). The predicted axial upsetting force is also in close agreement with the experimental results (Fig. 13). These two examples (upsetting of a billet, and forging of a ball bearing in Section 6.6) were both analyzed using material properties obtained by fitting results from a third mechanical test. Thus, the agreement between results predicted by reactive plasticity and those directly measured from experiments validates the ability of reactive plasticity to accurately simulate material behavior in a variety of finite deformation and finite rotation tests. This type of validation argues in favor of reactive plasticity effectively capturing the underlying physics of plastic deformation.

Fig. 13.

Die force–displacement curve predicted by FEBio with reactive plasticity, compared to experimental results recorded by Shih and Yang (1991) for the upsetting of a cylindrical billet presented in Section 6.7.

6.8. Simultaneous fitting of stress–strain and damage–strain data

As a necessary condition for validating the reactive constrained mixture framework for elastoplastic damage (Section 5), our model should be able to couple experimental stress–strain data with experimental measurements of material damage in a consistent way. In this example we used experimental data for Al2024-T3 to demonstrate this process. By measuring the damaged modulus of a tensile specimen of Al2024-T3, Chow and Wang (1987) obtained a curve of the damage as a function of strain. A plot of the engineering stress versus engineering strain for Al2024-T3 was obtained from a recent study on material characterization methods (Pourhassan et al., 2017). The elastic properties of Al2024-T3 were taken to be E = 73 GPa and ν = 0.3. Using a single-element model, successful fits to both sets of experimental data were obtained with the reactive elastoplastic damage model. The plasticity parameters were identified as n_f = 15, ${\mathcal{Y}}_0$ = 330 MPa, ${\mathcal{Y}}_{\text{max}}$ = 489 MPa, w₀ = 0.97, w_e = 0, and r = 1 (Fig. 14a). To account for plastic damage, the yielded bonds were allowed to sustain failure according to a Weibull distribution, with the plastic damage measure taken to be the effective plastic strain $e_{\beta }^p$. The Weibull parameters κ^p = 7.95 and γ^p = 0.65 were obtained from the damage–strain curve (Fig. 14b).

Fig. 14.

Simultaneous fitting of (a) experimental stress–strain, and (b) damage–strain results for Al2024-T3 (Section 6.8).

The ability to simultaneously fit different data sets from two separate studies on the same material lends credence to the proposed coupling between plastic deformation and damage. However, it is important to point out that a simple single-element model was used in this analysis, which corresponds to simply numerically solving the governing equations without taking any geometric effects into account, such as necking. Therefore the purpose of this example was to illustrate the way in which plasticity and damage parameters interact in a coupled formulation, rather than to explicitly replicate the underlying experiments. A full direct validation of coupled effects is often difficult to perform due to incomplete details in the data sets found in the literature.

6.9. Uniaxial tension of a cylindrical bar

Uniaxial tension of a cylindrical bar is a classic experiment demonstrating plastic deformation and complex necking behavior, and has been frequently used as a finite element validation problem (such as Simo and Hughes (2006)). In this example, we used reactive plasticity to replicate the experimental study of Norris Jr et al. (1978) and demonstrate the ability of the present model to capture geometric and mechanical effects of necking instability. We then extended this validation by incorporating elastoplastic damage, to model the physics of coupled plasticity and damage during necking and subsequent failure of a tensile specimen.

The material considered by these authors was A-533 Grade B class 1 nuclear pressure vessel steel, with elastic properties E = 206.9 GPa and ν = 0.29. An experimentally-derived flow curve was provided specifically for sample 2499R of that study, which was also the only sample tested at room temperature (Norris Jr et al., 1978); the analysis in this section specifically attempted to predict data from that sample. Its yield threshold was reported to be ${\mathcal{Y}}_0$ = 458 MPa. As the effective plastic strain increased, there was necessarily some uncertainty in the experimental flow curve provided by these authors, as it was based upon an attempt to correct for necking behavior (Norris Jr et al., 1978). The material properties for reactive plasticity (without damage) were successfully fitted to that flow curve (yellow curve in Fig. 15a), producing plasticity parameters n_f = 10, ${\mathcal{Y}}_{\text{max}}$ = 730 MPa, w₀ = 0.985, w_e = 0.00072, and r = 1, with ${\mathcal{Y}}_0$ given above.

Fig. 15.

(a) Flow curve adopted by Norris Jr et al. (1978) to model uniaxial tension of a cylindrical bar (Section 6.9), compared to reactive plasticity fits with and without damage. (b) Damage curves as a function of effective plastic strain $e_0^p$ for the reactive plasticity models presented in (a). To produce their curve, Norris et al. had to use correction factors to extrapolate experimental data beyond the onset of necking.

However, as is evident from Fig. 15a, it remained unclear from the reported range of experimental data how long the material would continue hardening before becoming damaged, since necking is a prelude to failure of tensile specimens. In our second analysis of this data set, we adopted the same plasticity parameters but allowed yielded bonds to also get damaged; the resulting fit (blue curve in Fig. 15a) produced Weibull damage parameters κ^p = 3.3 and γ^p = 3; damage to intact bonds was not considered in this analysis. The resulting damage curves as a function of plastic strain are shown in Fig. 15b.

The description of the uniaxial tension problem by Norris Jr et al. (1978) does not provide dimensions of the entire specimen, only the reduced section modeled in their computational study; as a consequence, we had to adopt the same dimensions. The tensile specimen is a bar with radius a₀ = 6.415 mm. The total length of their model was H = 53.34 mm, with a gage length of 2L₀ = 50.8 mm. An axial elongation u_y = 13.3335 mm was prescribed. Due to symmetry considerations, a 3 degree wedge model of one quarter of the bar was considered in our analysis (Fig. 16a); consequently, the prescribed displacement in the finite element model was halved. A fine biased mesh containing 4800 elements was utilized to capture the necking and post-yield behavior. Simulations were performed using reactive plasticity and reactive plasticity with damage, to contrast plasticity and damage against a standard elastoplastic analysis.

Fig. 16.

(a) Initial geometry and mesh for the example of uniaxial tension of a circular bar considered in Section 6.9. Contour plots show (b) the effective plastic strain $e_0^p$ and (c) the effective stress at the end of the analysis for plastic (“intact”) and elastoplastic damage (“damage”) models.

Contour plots of the effective plastic strain and effective stress in the bar for both material models are presented in Fig. 16b–c. The effective stress in the bar modeled without any damage compares very favorably to the results of Simo and Hughes (2006), where this problem was used as a finite element validation. In our elastoplastic damage model, it was clear that the damage was highly localized to the region of most significant necking (Fig. 17). When comparing the two material models in the present study, there was more plastic deformation in the damaged bar, and the stresses were significantly lower. Although not strongly evident visually in Fig. 16, greater necking occurred in the bar modeled with damage (yellow and blue curves in Fig. 18a).

Fig. 17.

Contour plot showing the spatial distribution of damage at the end of the uniaxial tension analysis of Section 6.9, for the material model incorporating reactive plasticity with damage.

Fig. 18.

Finite element model and experimental data (Norris Jr et al., 1978) for (a) normalized neck radius and (b) applied load as a function of gage strain, for both undamaged and damaged elastoplastic material models (Section 6.9).

Over the duration of the experiment, Norris et al. measured the current bar radius a at the necking region, the change in length 2ΔL of the gage region, and the reaction force F. Plots of the normalized radius a/a₀ and normalized force F/F_max as a function of the engineering gage strain ΔL/L₀ are shown in Fig. 18. Reactive plasticity was able to provide a close prediction of the experimental data up until ΔL/L₀ ≈ 0.22, at which point the increasing hardening due to the contribution of w_e (the minute fraction of unyielded elastic bonds) led the model to diverge. However, the addition of damage allowed the model to provide a much improved prediction of the necking and force responses. In addition, the sharp drop in the force response predicted by the plastic damage model at the end of the analysis heralded impending fracture (also evident in the damage contour plot in Fig. 17). This example served as a successful validation of the reactive elastoplastic damage model, due to the wealth of experimental data available from the study of Norris Jr et al. (1978).

7. Discussion

This study presented a framework for plasticity and elastoplastic damage mechanics by treating such materials as reactive solids whose internal composition evolves in response to applied loading. Using the framework of constrained reactive mixtures, plastic deformation was accounted for by allowing loaded bonds (e.g., metallic bonds) within the material to break and reform in a stressed state with a new reference configuration, as presented in Section 3. This concept was adopted from the literature on biological tissues and fibrous networks where it has proven successful (Ban et al., 2018; Safa et al., 2019b). The concept of plastic behavior occurring due to configurational changes in materials is not a novel theory within the broader mechanics literature (Rajagopal and Wineman, 1992; Rajagopal and Srinivasa, 1998a,b), where these philosophically similar approaches have increasingly been applied to a broad spectrum of inelastic material responses (Rao and Rajagopal, 2000; Mollica et al., 2001; Muliana et al., 2016; Rajagopal and Srinivasa, 2016; Zhang and Montans, 2019). Though our work was biologically motivated and operationally distinct from these prior works, it falls within this established school of thought and offers an alternative method for modeling plasticity and damage. Rather than considering multiple natural configurations of a material, as in the multiconfigurational approach of Rajagopal and coworkers, within the present work bonds which break and reform represent a new generation and hence a new material with a new reference configuration. This new reference configuration is time-invariant and provided by constitutive assumption, a significant departure from the classical Kroner–Lee approach (Kroner, 1960; Lee, 1969). There is freedom in postulating the new reference configuration; however, when modeling plasticity, the constitutive relation for the reference configuration of each generation may depend on the selection of a suitable yield measure Φ, as described in Sections 3.3–3.4. The choice of Φ and the resulting plastic flow conditions are constrained by the Clausius–Duhem inequality, as illustrated in Section 3.5.1.

Importantly, the reactive framework proposed in this study can be formulated to remain consistent with classical plasticity approaches and principles. For example, in Section 3.4 we demonstrated how our framework could adopt the constitutive assumption of normality, though it should be emphasized that the theory is not restricted to this assumption. The mass content of the chemical species whose bonds are breaking and reforming may be tracked using scalar state variables which are in principle observable, a departure from the classical internal state variable framework (Coleman and Gurtin, 1967). The ability to formulate a framework for dissipative material responses using observable state variables should not be surprising, given that the prior damage mechanics literature has proposed a number of methods for characterizing damage from experiments, despite the fact that internal state variable theory implies that such measures are not observable. This apparent contradiction suggests that the internal state variable framework is not a unique method for modeling such dissipative processes. In reactive mixtures, mass composition measures are theoretically observable, even if experimental methods available today are not yet able to detect some of the state variables appearing in this framework. A theoretical model structured in this manner has all evolution equations provided by fundamental balance axioms, notably the axiom of mass balance which includes a function of state for the mass density supply, and thereby obviates the need to provide alternative evolution equations for internal variables. In this study, we have demonstrated that this reactive constrained mixture framework can recover elastoplastic and damage behaviors using only scalar state variables representing the referential mass densities ${\rho }_r^{\alpha }$. A consequence of this approach is that complex elastoplastic behavior was obtained without the use of explicit backstress tensors or plastic potentials, a feature also seen in the similar recent studies by Montáns and coworkers (Zhang and Montans, 2019; Nguyen et al., 2020).

Kinematic hardening-like behavior was shown to emerge through a simple superposition of multiple bond families which is akin to a Masing-type model (Skelton et al., 1997; Zhang and Montans, 2019; Nguyen et al., 2020), as described in Section 4; though it was not demonstrated in this study, further incorporating isotropic hardening would be a straightforward extension of the presented model. A coupled theory of elastoplastic damage was then developed in Section 5 by synthesizing our previous work on reactive damage mechanics (Nims et al., 2016) with the constrained reactive mixture model of elastoplasticity developed in Section 4. In reactive damage mechanics, damage emerges due to bonds which break permanently and do not reform. Consequently, the theory discussed in Section 5 involved no further state variables beyond accounting for the mass content of broken bonds via ${\rho }_r^b$; furthermore, a putative evolution equation for the damage variable D was not postulated but rather emerged by satisfying the fundamental axiom of mass balance. This had the benefit of resulting in a conceptually cleaner and simpler framework, especially with regard to heat dissipation and enforcement of the Clausius–Duhem inequality. The seamless incorporation of damage into the elastoplastic model shows the agility of the mixture framework. When the material response is governed by reaction kinetics, developing more coupled behaviors is relatively straightforward, as one only needs to sum the mass supply terms governing each response. This framework can easily be extended to account for more complex behaviors, such as thermoelasticity, thermo-elastoplasticity and damage, and elastoplastic damage with fatigue. We may address these more elaborate frameworks in future studies. In an upcoming study, we will demonstrate how this reactive framework may be applied to the modeling of fatigue failure, by incorporating an energy-based, loading-history-dependent reaction that transforms intact and yielded bonds into fatigued bonds.

Despite the alternative approach of the present theory, it was shown in Section 3.4.4 that reactive plasticity reduces identically to the classical Prandtl–Reuss theory of infinitesimal plasticity, given appropriate and relevant assumptions. The ability to recover a thoroughly-understood classical framework in the limit of infinitesimal strains and rotations emphasizes that although the mathematics and conceptual formulation may differ, the underlying physical description of plastic behavior embodied in our reactive model is the same. We reported similar recovery of classical frameworks in our previous reactive viscoelasticity (Ateshian, 2015; Nims and Ateshian, 2017) and damage (Nims et al., 2016) studies.

The elastoplasticity and elastoplastic damage theories developed in this study were implemented into the free, open-source finite element software FEBio and thoroughly verified and validated in Section 6. Verification was completed against two fundamental benchmarks which included both analytical and standard computational (ABAQUS) solutions (Section 6.3). Due to the alternative approach of this study, a thorough validation effort against experimental data was then undertaken. Validation was performed using a fundamental two-pronged approach: (1) The necessary condition to validate a theoretical model is that it fits experimental data; (2) the sufficient condition is the ability to predict experimental results which were not used to inform the model, under specific testing conditions. A simple multi-material model was first used to demonstrate the predictive ability of constitutive models (Sections Section 6.4), before considering more complex 3D geometries. In Sections 6.6–6.7 we predicted the reaction forces required for finite deformation forming problems and produced agreement with experimental results.

In Section 6.8 we demonstrated that independent measurements of the plastic and damage responses of a material may be fitted simultaneously within our framework, though we could not find additional experimental responses in the literature for that material, preventing us from reporting an additional prediction. Finally, in Section 6.9 we reported the canonical example of uniaxial tension, both with and without damage, and recovered experimentally-observed behavior. In this thorough series of validation problems, confidence in both the fitting and predictive abilities of the reactive theory has been established. Here, we must point out that our current FEBio implementation of a local damage mechanics model exhibits mesh dependence, as is well recognized in the finite element literature (Borst et al., 1993; Samal et al., 2008). Future work may remove this limitation by implementing a nonlocal formulation to introduce a characteristic length scale into the numerical implementation (Pijaudier-Cabot and Bažant, 1987; Bažant and Jirásek, 2002).

This study demonstrated that it is possible to formulate simple elastoplasticity and elastoplastic damage models within a consistent framework which uses measures of material mass composition as theoretically observable state variables, representing an addition to the established biomechanics (Ban et al., 2018; Safa et al., 2019b) and plasticity (Rajagopal and Wineman, 1992; Rajagopal and Srinivasa, 1998a,b) literature that introduced the concept of modeling plasticity through configurational change. The present work has been specialized to plasticity and damage in metals, but the underlying formulation offers a valid method to describe plasticity and damage in any material, given the ability to define necessary constructs for the material such as a yield threshold and criterion. Through an approach centered upon reaction kinetics, this theoretical frame can be expanded in scope to account for more complex behaviors. The present formulation represents an extension of previous seminal work applying constrained reactive mixtures (Humphrey and Rajagopal, 2002) to growth and remodeling mechanics, which we utilized for similar applications (Ateshian and Ricken, 2010; Nims and Ateshian, 2017), then extended to viscoelasticity (Ateshian, 2015; Nims and Ateshian, 2017), and damage mechanics (Nims et al., 2016). Our immediate future work will be directed towards further extending these concepts to model fatigue mechanics.

Appendix. Derivation of the tensorial normal N^α

The derivation that follows makes extensive use of the tensorial products ⨂, ⊘, ⦸ and ⨀, defined using Cartesian components such that

$$\begin{gathered} {\left(\mathbf{A}\otimes \mathbf{B}\right)}_{ijkl}=A_{ij}{B}_{kl}{\left(\mathbf{A}⦸\mathbf{B}\right)}_{ijkl}=A_{il}{B}_{jk} \\ {\left(\mathbf{A}\oslash \mathbf{B}\right)}_{ijkl}=A_{ik}{B}_{jl}{\left(\mathbf{A}\odot \mathbf{B}\right)}_{ijkl}=\frac{1}{2}\left(A_{ik}{B}_{jl}+A_{il}{B}_{jk}\right). \end{gathered}$$ (A.1)

The first term on the right hand side of Eq. (3.24) is determined by the specific functional form of Φ. The last term is found by using the polar decomposition F^α = R ⋅ U^α and assuming R is independent of U^α, producing

$$\frac{\partial {\mathbf{F}}^{\alpha }}{\partial {\mathbf{U}}^{\alpha }}=\mathbf{R}\odot \mathbf{I}.$$ (A.2)

The remaining stiffness-like term ∂T^α/∂F^α may be evaluated by first pulling the Cauchy stress back to the material frame through the standard relation T^α = (J^α)⁻¹F^α ⋅S^α ⋅(F^α)^T, where S^α is the second Piola–Kirchhoff stress, then carrying out the differentiation, producing the unwieldy expression

$$\begin{gathered} \frac{\partial {\mathbf{T}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}={\left(J^{\alpha }\right)}^{-1}[-{\mathbf{F}}^{\alpha }\cdot {\mathbf{S}}^{\alpha }\cdot {\left({\mathbf{F}}^{\alpha }\right)}^T\otimes {\left({\mathbf{F}}^{\alpha }\right)}^{-T}+\mathbf{I}\oslash \left({\mathbf{F}}^{\alpha }\cdot {\mathbf{S}}^{\alpha }\right)+\left({\mathbf{F}}^{\alpha }\cdot {\mathbf{S}}^{\alpha }\right)⦸\mathbf{I} \\ +{\mathbf{F}}^{\alpha }\oslash {\mathbf{F}}^{\alpha }:{\mathbf{C}}^{\alpha }:\frac{1}{2}\left({\left({\mathbf{F}}^{\alpha }\right)}^T\oslash {\left({\mathbf{F}}^{\alpha }\right)}^T+{\left({\mathbf{F}}^{\alpha }\right)}^T⦸{\left({\mathbf{F}}^{\alpha }\right)}^T\right)\cdot {\left({\mathbf{F}}^{\alpha }\right)}^{-T}]. \end{gathered}$$ (A.3)

Here, ${ℂ}^{\alpha }$ is the material elasticity tensor for bond generation α, and we have needed the following useful derivatives:

$$\begin{gathered} \frac{\partial {\left(J^{\alpha }\right)}^{-1}}{\partial {\mathbf{F}}^{\alpha }}=-{\left(J^{\alpha }\right)}^{-1}{\left({\mathbf{F}}^{\alpha }\right)}^{-T}\frac{\partial {\mathbf{S}}^{\alpha }}{\partial {\mathbf{E}}^{\alpha }}={ℂ}^{\alpha } \\ \frac{\partial {\mathbf{F}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}=\mathbf{I}\oslash \mathbf{I}\frac{\partial {\mathbf{E}}^{\alpha }}{\partial {\mathbf{C}}^{\alpha }}=\frac{1}{2}\mathbf{I}\odot \mathbf{I} \\ \frac{\partial {\mathbf{S}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}=\frac{\partial {\mathbf{S}}^{\alpha }}{\partial {\mathbf{E}}^{\alpha }}:\frac{\partial {\mathbf{E}}^{\alpha }}{\partial {\mathbf{C}}^{\alpha }}:\frac{\partial {\mathbf{C}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}\frac{\partial {\mathbf{C}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}={\left({\mathbf{F}}^{\alpha }\right)}^T\oslash \mathbf{I}+\mathbf{I}⦸{\left({\mathbf{F}}^{\alpha }\right)}^T, \end{gathered}$$ (A.4)

where ${\mathbf{E}}^{\alpha }=\frac{1}{2}\left({\mathbf{C}}^{\alpha }-\mathbf{I}\right)$ is the Green–Lagrange strain tensor and C^α = (F^α)^T ⋅ F^α is the right Cauchy–Green tensor. Eq. (A.3) can now be manipulated to only include the Cauchy stress and spatial elasticity tensor, where we recognize ${\mathit{C}}^{\alpha }={\left(J^{\alpha }\right)}^{-1}\left({\mathbf{F}}^{\alpha }\oslash {\mathbf{F}}^{\alpha }\right):{ℂ}^{\alpha }:\left({\left({\mathbf{F}}^{\alpha }\right)}^T\oslash {\left({\mathbf{F}}^{\alpha }\right)}^T\right)$. By factoring out a post-multiplied (F^α)^−T term, the compact form of Eq. (3.25) is obtained.

Making use of Eq. (3.25) and performing the first contraction in Eq. (3.24) is straightforward and directly yields

$$\frac{\partial \Phi }{\partial {\mathbf{T}}^{\alpha }}:\frac{\partial {\mathbf{T}}^{\alpha }}{\partial {\mathbf{F}}^{\alpha }}={\mathbf{M}}^{\alpha }\cdot {\left({\mathbf{F}}^{\alpha }\right)}^{-T},$$ (A.5)

where M^α emerges naturally and is given by Eq. (3.27). Finally, the tensorial normal N^α may be evaluated by inserting Eqs. (A.2) and (A.5) into Eq. (3.24),

$$\begin{gathered} {\mathbf{N}}^{\alpha }=\left({\mathbf{M}}^{\alpha }\cdot {\left({\mathbf{F}}^{\alpha }\right)}^{-T}\right):\mathbf{R}\odot \mathbf{I} \\ =\frac{1}{2}{\mathbf{R}}^T\cdot {\mathbf{M}}^{\alpha }\cdot {\left({\mathbf{F}}^{\alpha }\right)}^{-T}+\frac{1}{2}{\left({\mathbf{F}}^{\alpha }\right)}^{-1}\cdot {\left({\mathbf{M}}^{\alpha }\right)}^T\cdot \mathbf{R} \\ =\frac{1}{2}{\mathbf{R}}^T\cdot {\mathbf{M}}^{\alpha }\cdot \mathbf{R}\cdot {\left({\mathbf{U}}^{\alpha }\right)}^{-1}+\frac{1}{2}{\left({\mathbf{U}}^{\alpha }\right)}^{-1}\cdot {\mathbf{R}}^T\cdot {\left({\mathbf{M}}^{\alpha }\right)}^T\cdot \mathbf{R}. \end{gathered}$$