Abstract
本文提出一种基于Wasserstein Gan的无监督单模配准方法。与现有的基于深度学习的单模配准方法不同，本文的方法完成训练不需要Ground truth和预设的相似性度量指标。本文方法的主要结构包括生成网络和判别网络。首先，生成网络输入固定图像（正例图像）和浮动图像并提取图像间潜在的形变场，通过插值方式预测配准图像（负例图像）；然后，判别网络交替输入正例图像和负例图像，判断图像间的相似性，并将判断结果作为损失函数反馈，进而驱动网络参数更新；最后，通过对抗训练，生成网络预测的配准图像能欺骗判别网络，网络收敛。实验中随机选取30例LPBA40脑部数据集、25例EMPIRE10肺部数据集和15例ACDC心脏数据集用作训练数据集，然后将剩下的10例LPBA40脑部数据集、5例EMPIRE10肺部数据集和5例ACDC心脏数据集用作测试数据集。配准结果与Affine算法、Demons算法、SyN算法和VoxelMorph算法对比。实验结果显示，本研究算法的DICE系数（DSC）和归一化相关系数（NCC）评价指标均是最高，表明本文方法的配准精度高于Affine算法、Demons算法、SyN算法和目前无监督的SOTA算法VoxelMorph。
Keywords: 无监督, Wasserstein Gan, 单模配准, 对抗训练
Abstract
We propose an unsupervised unimodal registration method based on Wasserstein Gan. Different from the existing registration methods based on deep learning, the proposed method can finish training without ground truth or preset similarity metrics. The network is composed of a generation network and a discrimination network. The generation network extracts the potential deformation fields between fixed images (positive images) and moving images, and predicts the registered images (negative images) by interpolation; the discrimination network then judges the similarity between the positive images and negative images that are input alternately, and feeds back the judgment result as a loss function to drive the network parameter update. Finally, through adversarial training, the registration image generated by the generation network deceives the discrimination network and the network converges. In the experiment, we randomly selected 30 cases of LPBA40 brain dataset, 25 cases of EMPIRE10 lung dataset and 15 cases of ACDC heart dataset as the training datasets, with 10 cases of LPBA40 brain dataset, 5 cases of EMPIRE10 lung dataset and 5 cases of ACDC heart dataset as the test datasets. The results of registration were compared with those obtained using Affine algorithm, Demons algorithm, SyN algorithm and VoxelMorph algorithm. The DICE coefficient (DSC) and the normalized correlation coefficient (NCC) evaluation index of the proposed algorithm were the highest, indicating a better registration accuracy of our method than Affine algorithm, Demons algorithm, SyN algorithm and the current unsupervised SOTA algorithm VoxelMorph.
Keywords: unsupervised, Wasserstein Gan, unimodal registration, adversarial training
在临床应用中，精确地完成术前图像和术中图像的配准是准确定位病灶与手术成功的关键。传统的配准方法包括使用b-spline的Elastix[1]、光流模型Demons[2]和标准对称归一化SyN算法[3]等通过参数或非参数的迭代优化建立待配准图像间的空间变换函数，但这些方法需要进行高维的数值优化，导致配准速度慢，计算成本高。而基于深度学习的配准方法研究思路主要有两个：基于卷积神经网络优化策略的配准方法[4-5]；基于卷积神经网络直接估计配准变换参数的方法[6-8]。基于卷积神经网络优化策略的配准方法虽然能提高配准指标，但是未考虑待配准图像中存在的噪声和伪影，训练中难以保证导数能平滑地优化，导致很难获得良好对齐的图像。基于卷积神经网络直接估计配准变换参数的方法包括基于CNN回归配准方法和基于CNN端到端配准方法。基于CNN回归配准方法通过训练CNN回归器来估计待配准图像间潜在的变换参数[7]，这种方法虽然能解决速度慢、捕获范围小的问题，但不足之处是不能应用到形变图像配准中。目前，基于CNN端到端配准方法主要分为有监督的和无监督的配准方法。有监督的配准方法在训练中使用Ground truth惩罚网络输出和期望输出之间的差异[9-11]，但这种方法受到Grouth truth标签数据短缺的限制，导致实际可用性变差。而无监督的配准方法旨在没有金标准的情况下，通过优化配准图像和目标图像间预设的相似性度量指标完成训练[13, 16]；如将可微分的STN网络插入到CNN中的VoxelMorph算法[14, 15]。这种无监督配准方法的不足之处是面对不同的配准目的，最终难以确定一个最有效的相似性度量指标，可能导致配准效果变差。
医学图像配准过程中，个体解剖图像与标准图谱之间出现较大形变和复杂形变是不可避免的，这种现象会增加配准难度，导致很难获得病灶区域全面的形变特征。受生成对抗网络能利用密度比估计最大化数据分布的概率密度[17]，从而能显著提高网络特征提取能力的启发，若能在无监督配准策略的前提下，用对抗相似性替代预设的相似性度量指标完成配准图像和标准图谱间的相似性判断，算法能更加精确地进行特征值提取、特征值差异对比，进而完成较大形变和复杂形变的配准；此外，训练中还会因为病理样本数据不足、病理样本数据不均衡问题导致网络出现过拟合现象，但生成对抗网络[18]强大的图像生成能力，可以帮助解决训练样本不足的问题。
因此，本文提出一种基于Wasserstein Gan[19]的无监督单模配准方法。该方法首先利用生成网络完成图像配准，以便向判别网络提供输入（作为负例图像），然后判别网络负责判断输入图像间的相似性，并向训练中的网络提供反馈信息，进而更新优化网络参数，驱动生成网络训练。最后为了避免生成对抗训练中常出现的梯度消失或爆炸的现象，设置梯度惩罚函数[20]，提高训练的稳定性。
1. 方法
实验采用对抗训练完成单模的2D医学图像配准，网络架构总体分为两部分：生成网络、判别网络。鉴于卷积神经网络强大的特征提取能力，两个主要的网络模块都基于卷积神经网络设计。生成网络主要的任务是获取固定图像和浮动图像间潜在的准形变场ϕ，利用配准形变场预测出负例图像（预测配准图像）。判别网络主要的任务是判断输入网络中图像对的相似性，并将相似性判断结果以损失函数的形式反馈。
实验中生成网络以一对固定图像和浮动图像作为输入（图 1），图像对经过命名为Unet_S网络输出配准形变场，STN网络将配准形变场和浮动图像作为输入，采用线性插值方式对浮动图像进行扭曲，输出预测配准图像（作为负例图像）。对生成网络进行训练，能最大化固定图像和浮动图像的相似性，获得更加理想的配准形变场，输出更优的预测配准图像。判别网络将固定图像作为正例图像、预测配准图像作为负例图像交替地输入网络，输出对输入图像拟合的Wasserstein距离，通过计算图像间Wasserstein距离的差值判断图像对的相似性，进而替代预设的相似性度量指标。为了判别网络能更好地区分正例图像和负例图像，我们需要对判别网络进行大量训练，进而拟合出更加精确的Wasserstein距离。
1.
网络结构
Network structure.
1.1. 网络细节
网络的主要结构包括生成网络和判别网络，生成网络的主要结构又包括Unet_S、STN（图 1）。
1.1.1. Unet_S网络
Unet_S网络采用与Voxelmorph算法[16, 17]中相同的U_net[9]结构（图 2）。Unet_S网络将两个单通道灰度图像（固定图像和浮动图像）拼接成一个两通道的灰度图作为生成网络的输入，输出是3通道的配准形变场。编码阶段采用2D卷积运算，卷积核大小为3×3，步长为2，每个卷积层后面都连接参数为0.2的LeakyReLU层；每次编码过后，图像的尺寸缩小一半，分辨率降低。解码阶段，交替使用upsample2D层、卷积层、Skip Connection层。Skip Connection层将编码层学习的特征传递到解码层，解码器使用upsample2D层恢复图像的尺寸和分辨率。
2.
Unet_S网络结构
Unet_S network structure.
1.1.2. STN网络
STN网络以配准形变场和浮动图像作为网络输入，通过线性插值的方式对浮动图像进行扭曲得到预测配准图像，预测配准图像将作为判别网络输入的负例图像。预测配准图像中的每一个像素点位置的计算公式如下：
 |
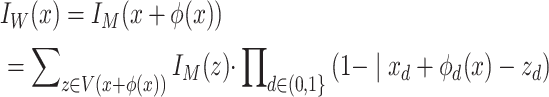1 |
其中IW是预测配准图像，x是IW中的像素点坐标位置，IM是浮动图像，
是
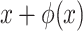的邻域，d是图像的迭代计算维度。
1.1.3. 判别网络
判别网络结构（图 3），网络的输入是正例图像或负例图像，输出是拟合图像的Wasserstein距离。由于判别网络的任务不再是分类而是回归，所以去掉sigmoid层。每层都采用2D卷积运算，每个2D卷积层的卷积核的大小为4×4，步长为2，填充大小为2，每个卷积层后都添加LayerNorm层和参数为0.2的ReLU激活层。
3.
判别网络结构
Discriminator network structure.
1.2. 损失函数
1.2.1. 判别网络损失
判别网络负责判断输入的正例图像和负例图像的相似性。对于输入的每一张正例图像都期望判别网络给出一个极大的Wasserstein值，每一张负例图像都期望给出一个极小的Wasserstein值，判别网络通过最大化正例图像和负例图像Wasserstein距离的差值[即最小化公式（2）的值]实现优化。同时为了防止训练过程中出现梯度消失或爆炸的现象，加入梯度惩罚函数L(GP)[20]。判别网络损失函数定义如下：
 |
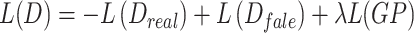2 |
其中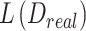
是判别网络对正例图像拟合的Wasserstein距离，
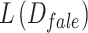是判别网络对负例图像拟合的Wasserstein距离，L(GP) 是梯度惩罚函数，λ是梯度惩罚参数。
 |
3 |
 |
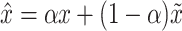4 |
其中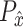
是在正例图像样本和负例图像样本连线上的随机样本分布，
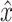对应随机样本中像素点位置，x对应正例图像中像素点位置，
对应负例图像中像素点位置，α是一个[0, 1]的随机数。
 |
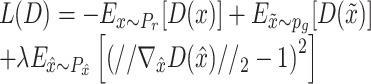5 |
其中Pr和x对应正例图像的样本分布和像素点位置，Pg和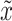
对应负例图像的样本分布和像素点位置，
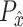和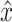
对应随机样本的样本分布和像素点位置。
1.2.2. 生成网络损失
生成网络的目的是使预测的负例图像尽可能地与正例图像相似，需要最小化负例图像的Wasserstein值。相似性损失函数定义如下：
 |
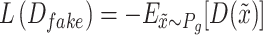6 |
其中Pg是负例图像的样本分布，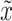
对应负例图像中像素点位置。
为了获得平滑的配准形变场ϕ，设置形变场平滑惩罚函数。函数定义如下：
 |
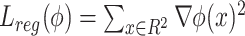7 |
其中R2是图像中所有的像素点，x对应像素点的位置。
连接公式(5)和公式(6)，生成网络的损失函数定义如下：
 |
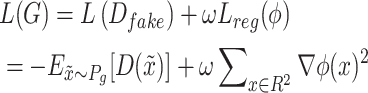8 |
其中ω是正则化参数，ϕ是形变场。
1.3. 对抗训练
对抗训练中采用交替训练的方式，训练过程如下：（1）向判别网络中输入固定图像（作为正例图像）学习图像特征；（2）向判别网络中输入预测配准图像（作为负例图像）学习图像特征；（3）向生成网络中输入固定图像和浮动图像获得一个尽可能与固定图像相似的预测配准图像。循环执行如上操作直至网络收敛。
2. 实验
2.1. 比较方法和算法指标
医学图像配准质量的评估指标虽然没有金标准，但是目前常用的指标有DICE相似性系数（DSC）、TRE、均方差（MSE）、归一化相似性系数（NCC）、互信息（MI）等。其中单模配准评价指标有DICE、TRE、MSE、NCC等；多模配准评价指标有DICE、TRE、MI等。而目前主流的单模配评价指标是DICE和TRE。
作为单模图像配准实验，我们将DICE相似性系数（DSC）和归一化相似性系数（NCC）作为最主要的评价指标，配准时间作为辅助指标。算法的实验结果将与传统算法的实验结果和先进算法的实验结果用颜色叠加图和轮廓图做可视化展示。
2.1.1. 对比方法
（1）Affine：基于仿射变换的传统配准方法；（2）Demons：一种依靠图像灰度值驱动配准的光流场模型；（3）SyN：一种采用互相关相似性度量的对称归一化方法，实现于公共的ANTs配准软件包；（4）VoxelMorph：基于CNN的无监督形变医学图像配准方法，使用均方差（MSE）或互相关（CC）作为相似性度量指标。
2.1.2. 算法指标
Dice相似性系数（DSC）是配准后图像Mask中的兴趣区域（ROI）与固定图像Mask中的兴趣区域的重合程度。值的范围为0~1，配准效果越好，值越接近1，配准效果越差，值越接近0。
 |
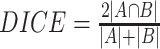9 |
其中A、B分别是固定图像和浮动图像（或配准后图像）Mask中兴趣区域的面积，A∩B表示两个图像Mask中兴趣区域重叠部分的面积。
归一化相似性系数（NCC）表示配准图像和固定图像的相关程度，其值的范围是-1~1。若值为-1，表示两幅图像完全不相关；若值为1，表示两幅图像的相关程度非常高。
 |
10 |
其中xi和yi是配准图像和固定图像中的第i个像素的灰度值，xm和ym是配准图像和固定图像的平均灰度值。
2.2. 实验数据
本次实验使用的数据集包括LPBA40、Evaluation Methods for Pulmonary Image Registration 2010（EMPIRE10）、Automated Cardiac Diagnosis challenge（ACDC）公共数据集。其中，数据集LPBA40包含40对3D的MRI脑部图像和专家标记的脑部Mask标签；EMPIRE10包含了30对3D的CT肺部图像和医学专家用分割方法获得的肺部Mask标签；ACDC数据集包含150名患者的4D（3D+T）MRI心脏数据和专家标记的心脏Mask标签。
实验中随机选取30对3D的LPBA40图像和25对3D的EMPIRE10图像作为制作训练集的图像对，将剩下的10对3D的LPBA40图像和5对3D的EMPIRE10图像作为制作测试集的图像对；把选取好的3D图像对通过重采样的方式处理成192×192×n的大小，将重采样后的3D图像沿着深度的方向切割为n张192×192大小的2D图像。通过Simard网格形变方法对切割后的2D图像进行随机形变，把形变前的2D图像作为固定图像，形变后的2D图像作为浮动图像。其中图像的形变强度由形变参数β决定，参数越大，形变效果越明显，β的范围是150~250。对于4D的ACDC数据集，随机选取时序ED=1（舒张末期）和ES=15（收缩末期）的15对3D图像作为制作训练集的图像对，将剩下的5对作为制作测试集的图像对；将选取好的3D图像对通过重采样的方式处理成192×192×n的大小，将重采样后的3D图像沿着深度的方向切割为n张192×192大小的2D图像；将切割后的ED=1的2D图像作为固定图像和ES=15的2D图像作为浮动图像。
2.3. 实验设置
实验网络采用Pytorch作为基本框架，使用NVIDIA Tesla K40C GPU训练网络。训练中使用Adam优化算法，初始学习率默认为0.001，调整间隔（step_size）默认为100，调整倍数(gamma)默认为0.90，batch_size默认为1，epochs默认为2000，每个epoch中的steps默认为100。训练过程中，配准形变场的正则化参数ω默认为1000，梯度惩罚系数λ默认为10。
2.4. 实验结果
为验证实验算法的可行性，我们将Simard模拟形变数据集（EMPIRE10、LPBA40）和真实形变数据集（ACDC）在网络上训练，Simard模拟形变实验结果见图 4~5，真实形变实验结果见图 6~7。表 1提供所有算法在LPBA40、EMPIRE10、ACDC测试集上的DICE均值和NCC均值。对比表 1中所有算法，本文算法的DICE均值和NCC均值最高，表明本研究方法在Simard模拟形变实验和真实形变实验中都能学习到平滑的配准形变场，获得高质量的预测配准图像。表 2提供所有算法在LPBA40、EMPIRE10、ACDC测试集上配准消耗时间的平均值。对比表 2提供的数据，分析得出基于深度学习的配准算法（VoxelMoprh算法和本文算法）在图像配准上消耗的时间比传统配准方法（Affine算法、Demons算法、SyN算法）少；由于本研究算法的网络结构更复杂，超参数更多，增加了计算成本，所以配准消耗的时间多于VoxelMorph算法，但依然低于Affine算法、Demons算法、SyN算法。
4.
EMPIRE10（β=250）数据集实验结果的颜色叠加图
Color overlap of experimental results of EMPIRE10 dataset (β=250). A: Fixed Image; B: Moving Image; C-G: After registration usingAffine; Demons; SyN; VoxelMorph; Ours.
5.
Simard形变实验的DICE平均值
DICE average value in Simard deformation experiment.
6.
ACDC数据集实验结果的轮廓图
Contour of experimental results of ACDC dataset. A: Fixed Image; B: Moving Image; C-G: After registration usingAffine, Demons, SyN, VoxelMorph, Ours.
7.
ACDC数据集中ROI的DICE值箱形图
DICE boxplot of ROI fromACDC dataset.
1.
LPBA40, EMPIRE10和ACDC测试集的DICE平均值和NCC平均值
DICE average and NCC average in LPBA40, EMPIRE10 andACDC test datasets
| Indicators | Data base | β/ROI | Affine | Demons | SyN | VoxelMorph | Ours |
| DICE | LPBA40 | 150 | 0.9651 | 0.9835 | 0.9851 | 0.9892 | 0.9905 |
| 200 | 0.9602 | 0.9802 | 0.9847 | 0.9889 | 0.9899 | ||
| 250 | 0.9527 | 0.9756 | 0.9833 | 0.9886 | 0.9898 | ||
| 150 | 0.9612 | 0.9842 | 0.9862 | 0.9888 | 0.9910 | ||
| EMPIRE10 | 200 | 0.9504 | 0.9802 | 0.9849 | 0.9877 | 0.9908 | |
| 250 | 0.9380 | 0.9756 | 0.9800 | 0.9869 | 0.9904 | ||
| ACDC | Ventriculus sinister | 0.7113 | 0.7508 | 0.7853 | 0.8530 | 0.8791 | |
| Ventriculus dexter | 0.6636 | 0.7296 | 0.7798 | 0.9230 | 0.9309 | ||
| Myocardium | 0.4757 | 0.5304 | 0.6474 | 0.6039 | 0.6665 | ||
| Whole heart | 0.8820 | 0.9016 | 0.9228 | 0.9280 | 0.9470 | ||
| LPBA40 | 150 | 0.9632 | 0.9856 | 0.9896 | 0.9923 | 0.9955 | |
| 200 | 0.9528 | 0.9809 | 0.9887 | 0.9917 | 0.9930 | ||
| 250 | 0.9384 | 0.9767 | 0.9867 | 0.9909 | 0.9923 | ||
| NCC | 150 | 0.8986 | 0.9534 | 0.9710 | 0.9915 | 0.9953 | |
| EMPIRE10 | 200 | 0.8563 | 0.9335 | 0.9552 | 0.9904 | 0.9934 | |
| 250 | 0.8204 | 0.9053 | 0.9381 | 0.9898 | 0.9921 | ||
| ACDC | Whole heart | 0.8360 | 0.8809 | 0.9131 | 0.9694 | 0.9832 |
2.
LPBA40, EMPIRE10和ACDC测试集配准时间的平均值
Average registration time in LPBA40, EMPIRE10, ACDC test datasets
| Times (s) | Database | Affine | Demons | SyN | VoxelMorph | Ours |
| LPBA40 | 107.5962/- | 10.1764/- | 118.6548/- | 3.6859/0.2448 | 5.3986/0.2856 | |
| CPU/GPU | EMPIRE10 | 110.6952/- | 10.6514/- | 119.5684/- | 3.8864/0.2569 | 5.5953/0.2907 |
| ACDC | 111.5811/- | 12.6765/- | 122.3309/- | 4.3833/0.2924 | 5.8766/0.3498 |
EMPIRE10（β =250）实验结果的颜色叠加图显示（图 4），绿色伪影是配准后的图像，红色伪影是固定图像。当两幅图像完全一致时，叠加图中不会出现绿色伪影或红色伪影，特别是放大框中形变强度较大的左侧肺门区域（包括左肺动脉、支气管、肺动脉分支部位）。
所有Simard模拟形变实验（形变参数β变化范围150，200，250）DICE均值结果图显示，所有算法在不同形变强度下配准精度的变化趋势（图 5）。
真实形变数据集ACDC实验结果的轮廓图显示（图 6），绿色区域是配准结果上对应的兴趣区域面积，红色区域是固定图像上对应的兴趣区域面积，当两幅图像上的兴趣区域完全一致时，绿色区域会将红色区域完全覆盖。特别的，每行从左到右的兴趣区域分别是左心室、心肌壁和右心室。
ACDC数据集中各兴趣区域（ROI）DICE值的箱型图展示了所有算法在数据集ACDC各兴趣区域（ROI）上配准精度的离散程度（图 7）。
3. 讨论
在EMPIRE10数据集实验结果的颜色叠加图中，对比Affine算法、Demons算法、SyN算法的结果，其肺部边框呈现出红色伪影，表明这3种传统配准方法不能较好地对齐形变较小的肺部外边框，不如VoxelmMorph算法和本文算法。VoxelMorph算法虽然能较好对齐肺部外边框，但在放大区域中，肺动脉分支部位出现较明显地红色和绿色伪影，表明VoxelMorph算法在形变较大的左侧肺门区域的配准效果不如本文的算法。
DICE均值结果显示了无论在肺部的CT图像（EMPIRE10）还是在脑部的MRI图像（LPBA40）中，随着形变参数β从150增大到250，传统的配准方法（Affine算法、Demons算法、SyN算法）的配准精度都发生了明显的下降，而基于深度学习的配准方法（VoxelMorph算法、本文算法）的配准精度变化不大，较稳定。
本研究结果显示，对于较大形变的左心室区域，Affine算法、Demons算法、SyN算法都不能准确地对齐兴趣区域，VoxelMorph算法虽然能对齐兴趣区域，但是在局部边缘的配准效果不如本研究的算法。在较小形变的右心室区域，除Affine算法，其余的算法都对齐了兴趣区域，但在边缘的配准效果和平滑程度上，Demons算法、SyN算法、VoxelMorph算法都不如本研究提出的算法。对于心肌壁区域的配准，本研究的算法和SyN算法比Affine算法、Demons算法、VoxelMorph算法能较明显地对齐兴趣区域，但在局部边缘和整体的平滑程度上，SyN算法呈现的效果不如本研究的算法。
DICE值箱型图显示了无论在大形变区域还在小形变区域，本文算法配准精度的离散程度低于其他算法（Affine算法、Demons算法、SyN算法、VoxelMorph算法）。表明本研究的方法在训练中稳定性更好，泛化性更高，配准精度不会因为兴趣区域的变化而出现明显的波动现象。
对比以上算法的实验结果，Affine算法仅仅通过优化特征点的仿射变换矩阵实现配准，而较大的形变使优化得到的仿射变换矩阵不再精确，导致大形变的配准效果差。Demons算法仅依靠图像的灰度值驱动配准，忽视了图像结构的变化，而较大的形变不仅使图像的灰度值发生了变化还使得图像的拓扑结构也发生明显变化。SyN算法虽然能最大化图像空间内的互相关信息，但是较大的形变使得图像的微分同构的可逆性变差，所以这3种算法在大形变图像配准时的效果比Balakrishnan和本研究提出的方法差。Balakrishnan等[14, 15]提出的算法在处理较大的形变时，由于较大的形变使图像的局部空间也发生明显变化，使用预设的相似性度量指标不能再精确地计算固定图像和配准图像局部的差异性，导致算法处理局部形变的能力不如本研究算法。本研究提出的算法与需要大量的计算时间和资源的传统配准方法不同，本研究的方法通过卷积神经网络提取的高层特征，直接获取更加接近真实形变的配准形变场，避免了多次迭代优化操作，提高配准速率，同时也提高了配准精度。与有监督的配准方法不同，本文提出无监督的学习策略避免了Ground truth的需求，提高网络实用性。Wasserstein Gan的引入使得相似性度量基于判别网络实现[19]，不再需要预设的相似性度量指标，增强了局部形变的处理能力。采用对抗训练的方式可以解决医学数据集样本不足和分布不均匀的问题，同时能增强对抗训练样本的多样性，以提高训练的稳定性和配准精度。
综上所述，本研究提出一种基于Wasserstein Gan的无监督单模配准方法，该方法采用对抗训练的方式提取精度高的、区分度强的深度卷积特征，基于该特征学习的形变场更接近真实的形变场，所以对大形变的处理效果更好。通过定性和定量分析，与Affine算法、Demons算法、SyN算法、VoxelMorph算法相比，本研究的算法能精确地完成大形变的2维医学图像进行配准。
Biography
陈宇，在读硕士研究生，E-mail: 2508696630@qq.com
Funding Statement
国家自然科学基金（82174534）
Supported by National Natural Science Foundation of China (82174534)
Contributor Information
陈 宇 (Yu CHEN), Email: 2508696630@qq.com.
邹 茂扬 (Maoyang ZOU), Email: zoumy@cuit.edu.cn.
References
- 1.Klein S, Staring M, Murphy K, et al. Elastix: A toolbox for intensitybased medical image registration. http://elastix.isi.uu.nl/download/ElastixArticleIEEETMIpreprint.pdf. IEEE Transac Med Imag. 2009;29(1):196–205. doi: 10.1109/TMI.2009.2035616. [Klein S, Staring M, Murphy K, et al. Elastix: A toolbox for intensitybased medical image registration[J]. IEEE Transac Med Imag, 2009, 29(1): 196-205.] [DOI] [PubMed] [Google Scholar]
- 2.Thirion JP. Image matching as diffusion process: an analogy with maxwell's demons. http://hal.inria.fr/inria-00615088/file/thirion-media-1998.pdf. Med ImagAnaly. 1998;2(3):243–60. doi: 10.1016/s1361-8415(98)80022-4. [Thirion JP. Image matching as diffusion process: an analogy with maxwell's demons[J]. Med ImagAnaly, 1998, 2(3): 243-60.] [DOI] [PubMed] [Google Scholar]
- 3.Avants BB, Epstein CL, Grossman M, et al. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [Avants BB, Epstein CL, Grossman M, et al. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain[J]. Med Image Anal, 2008, 12(1): 26-41.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cheng X, Zhang L, Zheng Y. Deep similarity learning for multimodal medical images. Comp Method Biomech Biomed Engin. 2018;76:125–32. [Cheng X, Zhang L, Zheng Y. Deep similarity learning for multimodal medical images[J]. Comp Method Biomech Biomed Engin, 2018, 76: 125-32.] [Google Scholar]
- 5.Haskins G, Kruecker J, Kruger U, et al. Learning deep similarity metric for 3D MR-TRUS image registration. Int J Comput Assist Radiol Surg. 2019;14(3):417–25. doi: 10.1007/s11548-018-1875-7. [Haskins G, Kruecker J, Kruger U, et al. Learning deep similarity metric for 3D MR-TRUS image registration[J]. Int J Comput Assist Radiol Surg, 2019, 14(3): 417-25.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Salehi M, Khan S, Erdogmus D, et al. Real-time deep pose estimation with geodesic loss for image-to-template rigid registration[EB/OL]. 2018. <a href="https://arxiv.org/abs/1803.05982" target="_blank">https://arxiv.org/abs/1803.05982</a>.
- 7.Shun M, Wang ZJ, Rui L. A CNN regression approach for real-time 2D/3D registration. IEEE Trans Med Imaging. 2016;35(5):1352–63. doi: 10.1109/TMI.2016.2521800. [Shun M, Wang ZJ, Rui L. A CNN regression approach for real-time 2D/3D registration[J]. IEEE Trans Med Imaging, 2016, 35(5): 1352- 63.] [DOI] [PubMed] [Google Scholar]
- 8.Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation[J]//Med Image Comput Comput Assist Interv, 2015. DOI: <a href="http://dx.doi.org/10.1007/978-3-319-24574-4_28" target="_blank">10.1007/978-3-319-24574-4_28</a>.
- 9.Cao X, Yang J, Zhang J, et al. Deformable image registration using a cue-aware deep regression network. IEEE Trans Biomed Eng. 2018;65(9):1900–11. doi: 10.1109/TBME.2018.2822826. [Cao X, Yang J, Zhang J, et al. Deformable image registration using a cue-aware deep regression network[J]. IEEE Trans Biomed Eng, 2018, 65(9): 1900-11.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu C, Ma L, Lu Z, et al. Multimodal medical image registration via common representations learning and differentiable geometric constraints. http://ieeexplore.ieee.org/document/8666210/ Electron Lett. 2019;52(31):1205–11. [Liu C, Ma L, Lu Z, et al. Multimodal medical image registration via common representations learning and differentiable geometric constraints[J]. Electron Lett, 2019, 52(31): 1205-11.] [Google Scholar]
- 11.Fan J, Cao X, Yap PT, et al. BIRNet: Brain image registration using dual-supervised fully convolutional networks. Med Image Anal. 2019;54:193–206. doi: 10.1016/j.media.2019.03.006. [Fan J, Cao X, Yap PT, et al. BIRNet: Brain image registration using dual-supervised fully convolutional networks[J]. Med Image Anal, 2019, 54: 193-206.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hu Y, Modat M, Gibson E, et al. Weakly-supervised convolutional neural networks for multimodal image registration. Med Image Anal. 2018;49:1–13. doi: 10.1016/j.media.2018.07.002. [Hu Y, Modat M, Gibson E, et al. Weakly-supervised convolutional neural networks for multimodal image registration[J]. Med Image Anal, 2018, 49: 1-13.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim B, Kim J, Lee JG, et al. Unsupervised deformable image registration using cycle-consistent CNN[C]//Med Image Comput Comput Assist Interv MICCAI, 2019. DOI: <a href="http://dx.doi.org/10.1007/978-3-030-32226-7_19" target="_blank">10.1007/978-3-030-32226-7_19</a>.
- 14.Balakrishnan G, Zhao A, Sabuncu MR, et al. An unsupervised learning model for deformable medical image registration[EB/OL]. 2018. <a href="https://arxiv.org/abs/1802.02604" target="_blank">https://arxiv.org/abs/1802.02604</a>.
- 15.Balakrishnan G, Zhao A, Sabuncu MR, et al. VoxelMorph: a learning framework for deformable medical image registration. http://www.onacademic.com/detail/journal_1000041625840099_e319.html. IEEE Transact Med Imag. 2019:1788–800. doi: 10.1109/TMI.2019.2897538. [Balakrishnan G, Zhao A, Sabuncu MR, et al. VoxelMorph: a learning framework for deformable medical image registration[J]. IEEE Transact Med Imag, 2019: 1788-800.] [DOI] [PubMed] [Google Scholar]
- 16.Lu Z, Yang G, Hua T, et al. Unsupervised three-dimensional image registration using a cycle convolutional neural network[C]// 2019 IEEE International Conference on Image Processing (ICIP). IEEE, 2019.
- 17.Isola P, Zhu JY, Zhou T, et al. Image-to-Image translation with conditional adversarial networks[C]// IEEE Conference on Computer Vision & Pattern Recognition. IEEE, 2016.
- 18.Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Nets. MIT Press. 2014 [Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Nets[J]. MIT Press, 2014.] [Google Scholar]
- 19.Arjovsky M, Chintala S, Bottou L. Wasserstein GAN[EB/OL]. 2017. <a href="https://arxiv.org/abs/1701.07875" target="_blank">https://arxiv.org/abs/1701.07875</a>.
- 20.Gulrajani I, Ahmed F, Arjovsky M, et al. Improved Training of Wasserstein GANs[J]. 2017, 12: 5767-77.