Abstract
The longest common consecutive subsequences (LCCS) play a vital role in revealing the biological relationships between DNA/RNA sequences especially the newly discovered ones such as COVID-19. FLAT is a Fragmented local aligner technique which is an accelerated version of the local pairwise sequence alignment algorithm based on meta-heuristic algorithms. The performance of FLAT needs to be enhanced since the huge length of biological sequences leads to trapping in local optima. This paper introduces a modified version of FLAT based on improving the performance of the BA algorithm by integration with particle swarm optimization (PSO) algorithm based on a novel infection mechanism. The proposed algorithm, named BPINF, depends on finding the best-explored solution using BA operators which can infect the agents during the exploitation phase using PSO operators to move toward it instead of moving toward the best-exploited solution. Hence, moving the solutions toward the two best solutions increase the diversity of generated solutions and avoids trapping in local optima. The infection can be propagated through the agents where each infected agent can transfer the infection to other non-infected agents which enhances the diversification of generated solutions. FLAT using the proposed technique (BPINF) was validated to detect LCCS between a set of real biological sequences with huge lengths besides COVID-19 and other well-known viruses. The performance of BPINF was compared to the enhanced versions of BA in the literature and the relevant studies of FLAT. It has a preponderance to find the LCCS with the highest percentage (88%) which is better than other state-of-the-art methods.
Keywords: Longest common consecutive subsequence (LCCS), COVID-19, Computaional Biology, Meta-heuristics, BA algorithm
Nomenclature
Acronyms
- ALO
Ant Lion Optimizer
- ANNs
Artificial Neural Networks
- BA
Bat Optimization Algorithm
- BFA
Bacterial Foraging Algorithm
- BPINF
BA-PSO hybrid technique with infection mechanism
- DE
Differential Evolution
- CSA
Cuckoo Search Algorithm
- FLAT
Fast Local Aligner Technique
- GA
Genetic Algorithms
- GSA
Gravitational Search Algorithm
- GWO
Grey Wolf Optimization
- IMO
Ions Motion Optimization
- IWO
Invasive Weed Optimization
- LBBA
Leader-Based BA Algorithm
- LCCS
Longest Common Consecutive Subsequences
- MA
Meta-heuristic Algorithm
- NFL
No-Free-Lunch Theorem
- PSO
Particle Swarm Optimization
- SCA
Sine Cosine Algorithm
- SW
Smith-Waterman
- TS
Tabu search
- WOA
Whale Optimization Algorithm
1. Introduction
Sequence alignment is one of the important tasks in bioinformatics which is used to measure the similarity and relationships between biological and genomic sequences. Sequence alignment operation is used as an essential step with other biological analysis processes such as phylogenetic tree construction (Feng & Doolittle, 1990), assembly of DNA fragments (L. Li & Khuri, 2004), protein structure prediction (Morshedian et al., 2019, Xiong, 2006), and drug design (Xiong, 2006). The local sequence alignment is a specific alignment operation that aims to discover the longest common consecutive subsequences (LCCS) between two biological sequences. Hence, LCCS can help biologists to reveal the common features between the considered sequences. The contemporary worldwide circumstances resulting from COVID-19 spreading out (Zu et al., 2020) motivate researchers in diverse fields to recruit their tools to participate in such pandemic control efforts. Local alignment can be employed for seeking biological databases to detect probable LCCS between COVID-19 and other known viruses. Such findings aim to improve the knowledge of the nature of this emerging virus and hence to help the specialists in vaccination and drug design fields.
From the Computer Science side, the problem of LCCS has been solved using the historical Smith-Waterman (SW) alignment algorithm (Smith & Waterman, 1981). It can detect the exact LCCS between two sequences since it is based on a dynamic programming approach (Cormen, 2009). However, the time complexity of SW algorithm, which is , where is the length of the input sequences, ceases the direct application of such technique for extreme length sequences. For example, the sequence of COVID-19 has a length of more than 7000 bp (Shereen, Khan, Kazmi, Bashir, & Siddique, 2020).
The recently presented Fast Local Aligner Technique (FLAT) in (Issa, Hassanien, Oliva, et al., 2018) can accelerate the process of LCCS detection. It aims to find a near-exact LCCS in a reasonable time. In FLAT, the input sequences are divided into short fragments, which can be (individually) aligned iteratively using SW algorithm. Thus the operational time of SW algorithm will be highly degraded. Meta-heuristic Algorithms (MAs) are employed for looking for the best locations of fragment cut in input sequences. Sequences with huge lengths still introduce a challenge facing the application of FLAT where the working MA may get trapped in local optima regions (Issa and Elaziz, 2020, Issa et al., 2018). Early convergence during the search process results in poor performance of FLAT.
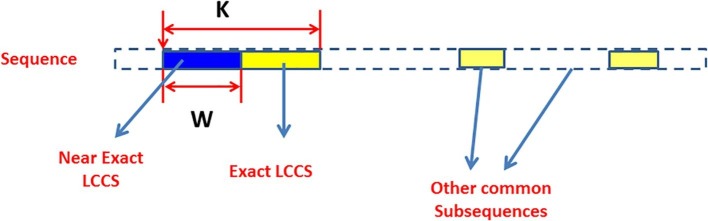
As shown in Fig. 1 , a sequence may have many subsequences (which are represented in yellow-filled rectangles) but the desired one is the exact LCCS with length (K).
Fig. 1.
The near-exact LCCS versus the exact LCCS (Issa et al., 2018).
FLAT can be used to find the near-exact LCCS, which is part of the exact one. As shown in Fig. 1, the blue-filled rectangle with length (W) is part of the exact LCCS with length (K). Hence, the development of FLAT aims to two points:
-
1-
To find a common subsequence around the exact LCCS, not around other common subsequences.
-
2-
Increasing the length of near-exact LCCS with length (W) to cover a high percentage of the exact LCCS with length (K).
FLAT is categorized as a discrete optimization problem where MA is used for choosing the positions at which the fragments to be cut. The positions lie in the range [1,L] where L is the length of the sequence. Hence, the positions are integer numbers 1, 2, 3,…, L. The discrete nature of FLAT problem requires specific adaptation for the continuous optimization algorithms such as Particle Swarm Optimization (PSO) (Kennedy, 1995) and Bat Algorithm (BA) (Yang, 2010) when working in the problem.
Therefore, this paper is mainly devoted to improving the performance of FLAT via more clever MA when applied to recent sequences such as the protein of COVID-19. The key entry of handling the entrapment in local optima regions is to apply a more balanced exploration/exploitation search strategy. On the other hand, previous related studies to FLAT application (Issa and Elaziz, 2020, Issa et al., 2018) suggested that hybrid MA can be more effective than single optimizers for such complex problems (e.g., the product of the length of input sequences is up to 21,000,000). In this context, the No-Free-Lunch (NFL) theorem (Wolpert & Macready, 1997) that states that no one MA can solve all optimization problems with the same efficiency opens a window for developing new algorithms that can both improve the efficiency of existing ones and achieve better results for emerging problems.
In this work, a novel hybrid technique is developed based on PSO (Kennedy, 1995) and BA (Yang, 2010). PSO, which is among the historical MAs is an efficient optimization technique for diverse applications (Zahid, Hasan, Khan, & Ullah, 2015). As well, the superiority of BA in processing optimization problems with huge search space has been proven in many areas such as structure optimization (Hasançebi, Teke, & Pekcan, 2013), training Artificial Neural Networks (ANNs) (Jaddi, Abdullah, & Hamdan, 2015), DC wheel motor problem (Bora, Coelho, & Lebensztajn, 2012), load frequency control (Elsisi, Soliman, Aboelela, & Mansour, 2016), and other problems in the literature (Yang & He, 2013).
The combination between PSO and BA is taking place in the light of a novel infection propagation mechanism. The proposed technique, named BPINF, implements the movement strategy of BA to explore the input biological sequences to detect the candidate fragments with LCCS, in the first phase. In the second phase, the movements of the population are updated based on the operators of PSO to enhance the exploitation of the search space. The first-best solution in the first phase carries an infection that may transfer to other solutions during the exploitation phase. Using distance-based criteria, the first-best solution will infect nearby ones while far solutions may be infected with some probability. In the case of non-infection, the agents update their movement based on PSO’s operators toward the second-best solution. Moreover, the infected agents can be recovered and get attracted to the second-best solution.
Thus, the proposed technique can generate more diverse solutions based on the novel infection mechanism among solutions which hopefully can overcome the early entrapment in local optima when handling biological sequences with huge lengths.
The extensive experimental work in the paper shows that the proposed BPINF can improve the performance of FLAT when applied to many datasets with the variant product of lengths between 25,000 and 21,000,000. BPINF is impartially compared to other known hybrid techniques in literature such as integrated PSO with Ions Motion Optimization (IMO-PSO) (Issa & Abd Elaziz, 2020), Adaptive Sine Cosine Optimization (ASCA-PSO) [9], BA-Cuckoo Search Algorithm (CSA) (Shehab, Khader, Laouchedi, & Alomari, 2019), BA-Differential Evolutionary (DE) (Yildizdan & Baykan, 2020) and two different versions of BA-PSO (Ferdowsi et al., 2019, Manoj et al., 2016). Moreover, the protein of COVID-19 is investigated against other five viruses, and the LCCS results are reported for many hybrid techniques, as well as the standard SW algorithm. Later simulation figures out that BPINF can achieve a near-score to that one of SW algorithm in most examined datasets. This supports the motivation of this paper regarding the enhancement of FLAT, in particular for newly emerged biological sequences with huge length.
The main contributions of this work can be summarized as follows:
-
1-
A novel integrated scheme between BA and PSO algorithms is presented which is based on an infection mechanism for enhancing the performance of FLAT.
-
2-
FLAT using the proposed hybrid mechanism was tested on real biological sequences in impartial comparison with other techniques in the literature.
-
3-
FLAT performance is examined on biological sequences with a challenging dimension that is up to 21,000,000 of product length.
-
4-
The findings of this work are directed at detecting the LCCS between the recent COVID-19 and the other five viruses to verify the performance of the proposed technique.
The rest of the paper is organized as follows: Section 2 introduces the related literature review to current work. Section 3 introduces a brief explanation of FLAT, besides the basic versions of each of PSO and BA. Section 4 illustrates the characteristics of the proposed technique (BPINF) for FLAT. Section 5 presents the results of testing the FLAT version using BPINF on biological sequences. The proposed technique is verified to detect the LCCS between the COVID-19 virus and other known diseases in Section 6. Finally, Section 6 concludes the presented work and provides future research directions.
2. Literature review
This section sheds light on the related literature work to the developed MAs and applied techniques in the current paper. First, some relevant applications of BA in medical and bioinformatics fields are illustrated, besides different versions and modifications of the algorithm. After that, the trails of accelerating the SW algorithm are discussed, as well as the previous related studies that implemented FLAT. Finally, various hybrid MAs are mentioned with a summary of the hybridization methodology and applications.
BA was used in many medical and bioinformatics applications such as gene selection in a cancer classification (Al-Betar, Alomari, & Abu-Romman, 2020) where the algorithm was developed based on a new operator called Triz. It showed notable superiority for gene selection when tested on a dataset of Ten cancer benchmarks.
BA was applied to optimize the parameters of a least square support vector machine (SVM) for disease classification in (Jiang, Li, Liao, & Jiang, 2019). This work developed BA to avoid premature convergence and avoiding trapping in local optima by calling chaotic functions for population initialization and using a decreasing weight parameter. The validation of this algorithm in (J. L. Jiang et al., 2019) was performed on a Hear disease (Statlog) and Breast cancer dataset. Besides, many other applications made use of BA, such as MR brain image segmentation (Alagarsamy, Kamatchi, Govindaraj, Zhang, & Thiyagarajan, 2019), human diseases prediction (Enireddy et al., 2021), and pathological brain detection (Lu, Wang, & Zhang, 2020).
In (Shehab et al., 2019), BA was merged with CSA (BA-CSA) to speed up CSA's convergence but avoiding early stuck in local optima. For each search step of an agent of CSA, updating equations of BA algorithm was applied, and new solutions survive only in case of better fitness. In (Dao et al., 2019), BA was hybrid with the Ant Lion algorithm (ALA) where the updating operators of ALA were embedded into the updating equations of BA. A leader-based BA algorithm (LBBA) was a developed BA based on using several micro-bats as a leader instead of only one best solution to influence the other agents (Neto, Pinto, Marcato, da Silva, & Fernandes, 2019). The best solution or one of the leader's solutions is used for influencing other randomly selected agents. This developed version of the BA was validated on the mobile robot localization problem.
Moreover, DE was merged with BA (Yildizdan & Baykan, 2020) where the updating mechanism of BA was modified to depend not only on the best solution but also on the other agents in the population. This helps in decelerating the convergence towards early found local optima solutions, hence, increasing the population's diversity. This work tried to achieve the balance between exploration of BA and exploitation of DE. In (Alihodzic & Tuba, 2014), another trial of merging BA with DE was proposed where the crossover and mutation operators of DE were modified, besides new pulse rate and loudness functions were embedded. The performance of the developed BA-DE version in (Alihodzic & Tuba, 2014) was validated on five mathematical benchmark functions.
In (Pravesjit, 2016), the BA algorithm was developed by embedding the reproduction step of the Genetic Algorithm (GA) to clone each agent of the BA algorithm. Also, PSO was merged with GA (Garg, 2016) where the mutation and crossover operators of GA were embedded into the PSO update procedure. A hybrid algorithm of BA and Invasive Weed Optimization (IWO) algorithm was introduced in (Yue & Zhang, 2019), where IWO was applied to enhance the local search. The balance between exploration and exploitation was suggested based on a novel inertia weight depending on Lagrange interpolation.
In addition, there were many trials for enhancing the PSO algorithm (Kennedy, 1995) to make use of its exploitation’s efficiency. In (Şenel, Gökçe, Yüksel, & Yiğit, 2019), PSO was merged with the Grey Wolf Optimization (GWO) algorithm to gain the benefit of better exploitation of PSO and better exploration of GWO. The agents are processed using the updating mechanism of PSO and for each particle, there is a small probability to update it using GWO's updating strategy.
PSO was combined with Gravitational Search Algorithm (GSA) (Eappen & Shankar, 2020) and the hybridization aims to balance between exploitation and exploration for the efficient spectrum of energy sensing in cognitive radio network in 5G heterogeneous network. In (Trivedi, Jangir, Kumar, Jangir, & Totlani, 2018), PSO was hybrid with Whale Optimization Algorithm (WOA) to achieve balance between exploration and exploitation, and the developed algorithm was validated on some mathematical benchmark functions.
In (Issa et al., 2018), a two-layer ASCA-PSO was presented as a hybrid adaptive SCA with PSO. The bottom layer divides the agents into groups which are updated using SCA’s updating strategy and the best agent of each group is assigned to the top layer where updating strategy of PSO is working. ASCA-PSO was validated on mathematical benchmark functions, then it is applied to enhance the performance of biological sequence local alignment (Cohen, 2004).
Moreover, PSO was combined with the IMO algorithm (Issa & Abd Elaziz, 2020) to enhance the performance of locating the longest common subsequences of biological sequences and it was validated on COVID-19 datasets. The developed PSO-IMO algorithm consists of the execution of the two algorithms in a serial manner where the IMO is used for exploring the search space while PSO is used to intensify the explored solution founded.
The cooperation between BA and PSO was considered in some previous studies. In (Manoj et al., 2016), an improved version of BA using PSO was proposed to enhance the image registration process for the diagnosis of medical images.
Also, in (Yadav, Sharma, & Gupta, 2015) a hybrid mechanism of BA and PSO was proposed for optimization of the location of UPFC in electrical power systems. In (Manoj et al., 2016) and (Yadav et al., 2015), BA and PSO were executed in a serial manner where the solutions were explored by BA for some iterations, and then PSO intensifies the best solution so far. Besides, BA was integrated with PSO to optimize the labyrinth spillway (Ferdowsi et al., 2019). The population was divided into two groups (one group for each algorithm) executed in parallel. After each specified number of iterations, some search agents with the worst fitness of each algorithm get replaced by that one with the best fitness of the other algorithm.
Various research studies have pointed out the superiority of hybrid MAs over single optimizers to address complex optimization applications. Table 1 introduces a gentle summary of some hybrid MAs that involve BA and PSO. It is noticed that the hybridization between BA and PSO received a notable interest in literature (Ferdowsi et al., 2019, Manoj et al., 2016, Yadav et al., 2015). PSO has been called, as well, for integration with other algorithms in different applications such as (Abd-Elazim and Ali, 2013, Issa and Elaziz, 2020, Issa et al., 2018; S. Jiang et al., 2014, Shen et al., 2008, Yadav et al., 2015) which reflects its effective exploitation capabilities.
Table 1.
Summary of some BA-based and PSO-based hybrid techniques.
| Ref. | Technique | Hybridization methodology | Application |
|---|---|---|---|
| (Issa et al., 2018) | ASCA-PSO* | PSO exploits the regions around solutions found by SCA | LCCS between biological sequences |
| (Issa & Abd Elaziz, 2020) | IMO-PSO* | IMO starts exploring the search space then PSO refines the found solutions (exploitation phase) | LCCS between biological sequences |
| (Shehab et al., 2019) | BA-CSA | BA update procedure is applied to agents of CSA where new solutions survive if fitness improves | Global numerical optimization |
| (Yildizdan & Baykan, 2020) | BA-DE | The population is updated randomly using improved BA or DE mechanism to improve both exploration and exploitation | Global numerical optimization |
| (Manoj et al., 2016) | BA-PSO | PSO operators are applied to BA solutions in the exploitation phase | ANN training for Enhancement of image registration process of the diagnosis of medical images |
| (Ferdowsi et al., 2019) | BA-PSO | Swap and update mechanism is applied where best solutions of one algorithm replace worst solutions in the other one | Design of the labyrinth spillway geometry |
| (Yadav et al., 2015) | BA-PSO | Non satisfied solutions in the PSO population are updated using BA operators | Location of unified power flow controller in power systems |
| (Abd-Elazim & Ali, 2013) | PSO-BFA | PSO is applied as a mutation operator for BFA individuals | Design of power systems stabilizers in multimachine power systems |
| (Shen et al., 2008) | PSO-TS | TS works as a local improvement procedure for PSO solutions | Tumor classification using gene expression data |
| (Jiang et al., 2014) | PSO-GSA | Each updates its position with the contribution of both algorithms (co-evolutionary technique) | Economic emission load dispatch problems |
| (Dao et al., 2020) | BA-ALO | Updating operators of ALO were embedded into the updating equations of BA | Global numerical optimization |
| (Neto et al., 2019) | BA-LBBA | One of many micro-bats is assigned as a leader instead of only one best solution to influence the other agents of LBBA | The mobile robot localization problem |
| (Garg, 2016) | PSO-GA | Balancing exploration and exploitation is achieved via incorporating the crossover and mutation operators within PSO | Solving constrained optimization problems |
*Studies which implement the FLAT technique.
SW algorithm (Smith & Waterman, 1981) aims to find the accurate LCCS between pair of biological sequence while Neeldemean-Wunch global sequence alignment algorithm aims to find the whole alignment between two sequences (Issa et al., 2018, Needleman and Wunsch, 1970). Various trials have been devoted to accelerate the SW algorithm such as (Zahid et al., 2015), a fast version of this algorithm was proposed based on dividing the two sequences into two portions and each portion is again divided into two sub-portions until reaching the minimum length of sub-portions. Every two sub-portions of the two sequences were aligned and if the score passed some certain threshold then the length of sub-portions is increased and the alignment process is repeated. The limitation of this technique is ignoring the affine gap penalty when estimating the alignment score which affects the alignment accuracy. Also, hardware accelerators were used to accelerate the execution of the SW algorithm in a parallel manner, such as using a graphical processing unit (GPU) (Ahmed et al., 2019, Elloumi et al., 2013, Khajeh-Saeed et al., 2010, Mohamed Issa et al., 2017, Zou et al., 2019). Moreover, the field-programmable gate array (FPGA) was used to speed up the SW algorithm (Benkrid et al., 2009, Di Tucci et al., 2017, Issa et al., 2012, Li et al., 2007, Yamaguchi et al., 2011). The high cost of needed hardware accelerators (GPUs and FPGAs) is one drawback in the latter approach.
FLAT is a so-recent technique for solving the sequence alignment problem. It was first developed based on ASCA-PSO in (Issa et al., 2018). ASCA-PSO was developed to enhance the exploitation (performing the search process in a narrow region in the search space) capabilities of SCA with the benefit of the efficient search mechanism of PSO. Besides, IMO-PSO [10] was developed to enhance FLAT's performance. FLAT-ASCA-PSO finds the near exact LCCS with a percent of 77% of the length of the exact LCCS, while FLAT-IMO-PSO produced a percent 81%. The main limitation of these FLAT methods was their poor performance when FLAT was executed on biological sequences that have a product of lengths up to 21,000,000. The reason for this degradation in FLAT's performance using ASCA-PSO and IMO-PSO is the extreme length of sequences which leads the algorithms to be trapped in local optima.
This detailed literature review reveals the gaps of current techniques to solve the LCCS problem for biological sequences. The exact method of SW is time inefficient, and its hardware-based implementations seem expensive in the case of huge length sequences. FLAT is a promising stochastic technique that can report a near-optimal result in a reasonable time but may suffer from the premature convergence of applied optimizers which leads to performance degradation. On the other side, BA gained popularity in bioinformatics problems, but it was applied for neither sequence alignment nor FLAT in past research studies. Furthermore, newly discovered biological sequences such as the protein of COVID-19 with huge length require that FLAT should be incorporated by efficient optimization algorithms. For challenging optimization problems, such as listed in Table 1, hybrid techniques seem to outperform single optimizers. According to the aforementioned discussion, the current paper introduces a hybrid version of BA and PSO using a novel infection mechanism to improve FLAT performance. Such a combination aims to enhance the capabilities of both techniques in tackling the problem search space. The newly developed technique, namely BPINF, helps FLAT to report better results than previous techniques such as (Issa and Elaziz, 2020, Issa et al., 2018) for both sequences of standard biological datasets and the protein of COVID-19.
3. Preliminaries
In this section, the description of the FLAT procedure for the detection of LCCS between a pair of sequences is presented. As well as, the procedure of the standard version of each of BA and PSO algorithms is illustrated.
3.1. Flat
Sequence alignment is considered one of the frequently addressed problems in bioinformatics. It aims to determine the regions of similarities between genomic sequences like DNA, RNA, and protein. Such similarity between aligned sequences expresses the corresponding similarity in their function, their secondary and tertiary structure [46, 47]. Other operations like DNA fragment assembly [12] and construction of phylogenetic trees [11] can also make use of sequence alignment.
In particular, local pairwise alignment between two sequences depends on gap insertion incorrect places to achieve high scores [48]. The famous SW technique [14] can solve the problem deterministically. It follows a dynamic programming approach where, after filling a scores matrix, the optimal solution can be found. For large sequences, the later technique is expected to exhaust huge computational time rather than memory. Fragmentation was employed to two huge length sequences to extract many shorter length fragments, then applying the SW algorithm becomes more time-efficient.
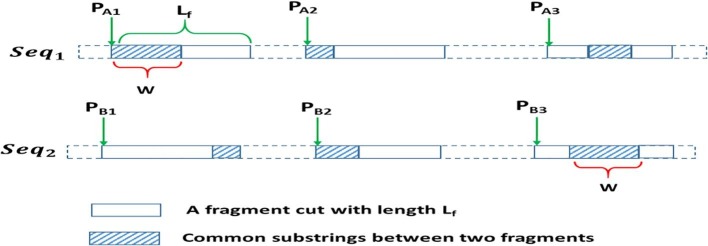
Let A and B denote two sequences of length , each of them is divided into several fragments with a length . Applying the SW algorithm can perform the alignment over the fragments and report the LCCS with length . Fig. 2 shows a simplified example of the fragmentation of two sequences into shorter-length ones, where Seq1 and Seq2 are the input two strings. After fragmentation into three fragments (i.e., substrings) with fragment length, the LCCS is found with length .
Fig. 2.
A simplified example of FLAT (Issa et al., 2018).
Using stochastic optimization such as MAs involves pointing search agents toward the position of the discovered LCCS. The defined fitness function in Eq. (1) (Issa et al., 2018) is called to evaluate the determined alignments during the search process.
| (1) |
where A and B are the aligned sequences, denotes the length of aligned sequences, and denotes the index. According to implementing the SW algorithm, the FLAT time complexity is where and represent the maximum number of iterations and population size of the applied optimizer, resp. Algorithm 1 presents a pseudo-code of FLAT.
| Algorithm 1: The procedure of FLAT | |
|---|---|
| 1: | Input: two sequences with length and . |
| 2: | Output: LCCS between Seq1 and Seq2 |
| 3: | Set the parameters: fragment length , search agent size , and number of iterations |
| 4: | Initialize a random population where each agent marks two positions, one in each sequence, in the range (1, length ( or )) |
| 5: | While hasn’t been reached yet |
| 6: | Apply the SW algorithm to every two fragments pointed out by each agent. |
| 7: | Evaluate solutions using Eq. (1) |
| 8: | Move positions of search agents using the update procedure of applied optimizer toward the location of fragments where LCCS is found. |
| 9: | End While |
3.2. BA algorithm
The main characteristics of the echolocation process of micro-bats motivated Yang (Yang, 2010) to design the basic version of BA. During flying to search for prey, bats tend to change position and velocity. The emitted echolocation pulses, which is their tool to detect barriers and preys, have a varying frequency (or varying wavelength) and loudness value. Also, the pulse emission rate can be adapted according to the proximity of the prey. Bat position represents the problem under study solution while remaining properties are called for search and update operations. In a population of BA, the th individual updates its position using Eq. (2) (Yang, 2010):
| (2) |
where is bat velocity, and is the current iteration index. Bat velocity is evolving during the search process according to the distance between the current solution and the global best one and the frequency as given by Eq. (3) and Eq. (4) (Yang, 2010):
| (3) |
| (4) |
where and determine the band of allowable frequencies, while is a randomly generated number. To improve exploitation capabilities, BA involves applying a random walk to generate a local solution around each individual using Eq. (5) (Yang, 2010).
| (5) |
where is a random value and represents the mean loudness factor of all individuals in the current population. The loudness factor is updated using Eq. (6) (Yang, 2010).
| (6) |
where is a predetermined parameter, as well as an initial value . The pulse emission rate, shown in Eq. (7), is employed to control the convergence of solutions. The initial value of pulse emission is .
| (7) |
where is a constant. Thus, as the search proceeds, the best bat becomes closer to the prey, and it is supposed to stop emitting any sound when catching it, i.e., and as . The main procedure of the BA appears in Fig. 3 .
Fig. 3.
Main procedure of BA algorithm (Yang, 2010).
3.3. PSO algorithm
The social behavior of particle swarms such as birds and fish schools was the basis of the applied mechanism in PSO. In the swarm, every individual has its position and velocity, which are dynamically updated. The distances between the current individual position and each of the best position along search history and the global best position are used to update the velocity. Then, according to changing velocity, the new position is determined.
Let and denote the th particle position and velocity in the current population, resp. Then the update mechanism of PSO is given by Eq. (8) (Kennedy, 1995).
| (8) |
The velocity update is commonly adjusted by an inertia factor as shown in Eq. (9) (Kennedy, 1995):
| (9) |
where , , and are two constants that control particle acceleration, and are two randomly generated numbers in [0,1], denotes the global best position so far and is the best historical position of the particle. Moreover, the inertia factor is decreased using Eq. (10) for convergence purposes.
| (10) |
where and denote current iteration and the total number of iterations, resp., while and are the initial and final values of inertia, resp. Fig. 4 introduces the main procedure of PSO.
Fig. 4.
Main procedure of the PSO algorithm (Kennedy, 1995).
4. The proposed hybrid method between BA and PSO based on infection technique (BPINF) for FLAT
The proposed method, named BPINF, integrates BA and PSO algorithms so that search agents can be updated using BA's operators for efficient exploration of the search space, whilst PSO’s update mechanism can improve the exploitation task of the search space. Hence, this integration tends to enhance both capabilities, the exploitation of BA and the exploration of PSO algorithms. The main problem when implementing FLAT based on this integration is that the agents are early trapped into local optima during applying PSO algorithm (due to the huge length of sequences). So that, an infection mechanism is proposed to avoid this drawback. In the next subsections, the inspiration of the developed BPINF technique besides its mathematical model is introduced in Section 3.1, then the framework of BPINF for implementing FLAT is discussed in Section 3.2.
4.1. Inspiration and mathematical model
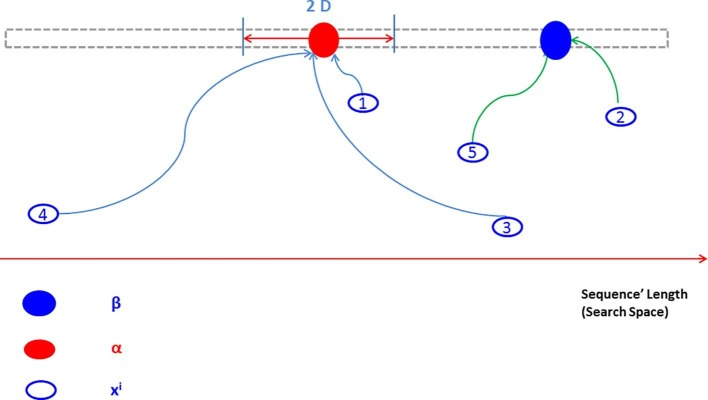
The infection is defined as the infestation of body tissues by disease-causing agents which cause an illness due to infection and is called infection disease (Aljamali, Jawad, & Alsabri, 2020). The infection can be transferred with a high probability from one organism to other if two organisms being nearby in the distance. Based on this concept, the entrapment in local optima when updating the search agents using PSO operators can hopefully be avoided. The agents simulate the organisms, and the search space is the distances between organisms. Changing the way of movement of an agent simulates the infection. The infection mechanism simulates the infection process where the first best solution () is considered as an infection carrier. This infection can spread out through some/all agents; thus the infected agents are moved toward () based on PSO's updating strategy instead of moving toward the second-best agent ().
The agents get infected from () will be moved toward it based on the following conditions:
-
-
If the agent has a position that lies within a specified neighborhood () around (i.e., in the range from () to ()).
-
-
Otherwise, the agent will be infected based on a random criterion (generating a random value bigger than a user-specified infection parameter (Inf_rate)).
If the previous conditions cannot be achieved, then the agent can be updated by moving toward the second-best solution (), and in this case, the agent is considered as non-infected.
For clarifying these concepts, Fig. 5 describes the operation of the infection mechanism. Five agents are represented in blue-empty circles (numbered as 1, 2, 3, 4, and 5), and is represented in the blue-filled circle, while is represented in a red-filled circle. As seen in the figure, the circle which lies in the boundary of around , gets infected, and thus it has to update its position toward the red-filled circle . Whereas the solutions which are represented in circle 3 and circle 4 lie out of the range of infection distance from (). Hence, they may be get infected too, according to the stochastic criteria (rand > Inf_rate), where rand is a randomly generated number in [0,1]. Circle 2 and circle 5 are not infected hence the movement of each of them will be updated toward the best solution ().
Fig. 5.
An explanation of updating agents based on the proposed infection mechanism in BPINF.
The infection can be propagated through the agents where the user-specified parameter () controls the propagation intensiveness. The parameter () also follows stochastic criteria in order to determine carrying the infection to another agent. While the (Inf_Rate) controls the chance of an agent if being infected or not based on stochastic criteria, in case of the agent is not located in the infection boundary around the agent (). The propagation of infection is simulated by transferring the infection from an infected agent i to other three non-infected agents (are chosen randomly from the population) to update their movements toward the infection carrier . The number of three agents is chosen experimentally as a tradeoff between enhancing the quality of solutions and keeping the execution time reasonable.
The infected agents can be recovered (then moving toward ) according to another stochastic criterion controlled by the parameter (). The recovery increases the possibility of producing more diverse solutions. This mechanism of integration aims to release more diversification of solutions due to the infection mechanism for updating agents toward two agents (the and best solutions). Besides, spreading the infection between the agents also increases the avoidance of local optima and convergence to the optimal solutions.
Regarding the mathematical model of BPINF, during the exploration phase (i.e., BA execution), the agents are updated based on Eq. (2) to Eq. (7). In the exploitation phase (i.e., execution of PSO), the infected agents follow Eq. (11) and Eq. (12)
| (11) |
| (12) |
where is the current position of agent i, is the first best solution, is the best solution achieved by agent i, is the speed of agent i and , and are predetermined constants.
For propagation of infection through agents, Eq. (13) and Eq. (14) are used assuming the chosen agent is j then it will move toward the infection carrier agent i if a stochastic criterion is satisfied.
| (13) |
| (14) |
where is the position of the current agent who carries infection to agent j, and are the speed of the infection carrier and the infected agents, respectively.
For the non-infected agents, Eq. (15) and Eq. (16) can be used for updating their positions:
| (15) |
| (16) |
where is the current position of agent i, is the second-best solution, is the best solution achieved by agent i, is the speed of agent i, and , , and are predetermined constants.
4.2. FLAT based on the developed BPINF technique
The proposed BPINF technique is applied to enhance FLAT to align huge sequences. In the previous studies (Issa and Elaziz, 2020, Issa et al., 2018), employing FLAT has achieved a score of 77% of the exact LCCS which gives a strong motivation to present the current work. Algorithm (2) describes the details of the BPINF algorithm for implementing FLAT. It accepts two biological sequences (SeqA and SeqB) as inputs and the required output is the near-exact LCCS between the two sequences. The solution of each search agent points to two positions (one in SeqA and the other in SeqB) where these positions represent the cut starting location of a fragment with length (LF).
In line 2, agents (, ) are initialized with two random positions, one in SeqA and the other in SeqB. The positions lie in the range from 1 to (Length (SeqA or SeqB) - LF), where LF represents the length of the cut fragments. Each agent cuts two fragments (one in each sequence) starting from the positions () such as indicated in line 3.
Each pair of fragments is aligned using the SW algorithm (Smith & Waterman, 1981), as in line 4. Then, the fitness of each solution is computed based on Eq. (1), and the first-best () and the second-best () solutions can be determined by sorting the fitness descendingly as in line 5.
In lines 7–8, if the exploration phase is performed during the first half of iterations (), the agents are updated based on the strategy of BA using Eq. (2) to Eq. (7). For exploitation (i.e., ), the search agents are updated based on the PSO's updating strategy and the infection mechanism. For each agent, the infection conditions are checked as stated in line 11 based on the following conditions :
-
-
If the agent has a position that lies within a specified neighborhood () around (i.e., in the range from () to ()), see line 12.
-
-
Otherwise, the agent still has some chance to get infected based on a stochastic criterion as described in line 14.
To mark infected agents, an infection array that has a size of population size (Infection (i), ) is used. The array Infection is binary-valued 1/0 to refer to infected/non-infected agents, resp. Then, all agents are updated according to their status (infected or non-infected), where the infected agents are updated based on Eq. (11) and Eq. (12) by moving toward the first best solution () as described in line 21. If the agent is infected, there is a possibility of infecting the other three agents that have been chosen randomly (line 24) based on stochastic criteria (rand () > Spread_Rate). The parameter Spread_Rate is tuned practically in order to achieve the highest performance. Line 25 shows the updating of agents during infection propagation through population using Eq. (13) and Eq. (14). For infected agents, the recovery conditions (rand () > Recovery_Rate) can be applied, which recover the infected agents to the non-infected status as described in line 28.
In line 33, the non-infected agents are updated based on Eq. (15) and Eq. (16) by moving toward the best solution (). Once search termination, each agent points to two positions in the aligned sequences; hence fragments are cut to be aligned using the SW algorithm. The length of near-exact LCCS for each agent can be computed as in line 37. In line 40, the near-exact LCCS pointed by the first best solution (), and its length are reported as the best-found solution. For more clarification, Fig. 6 shows the procedure of implementing the FLAT based on the proposed BPINF.
| Algorithm 2: The proposed BPINF algorithm for implementing FLAT |
|---|
| 1: Input SeqA and SeqB; initialize the parameters: , , Inf_Rate, Spreed_Rate, Recovery_Rate |
| 2: Initialize the population () with () search agents, each (), , locates two positions one in SeqA and the other in SeqB such that (Length (SeqA or SeqB) - LF) |
| 3: Cut two fragments starting from the positions of () in the two sequences (SeqA and |
| SeqB) |
| 4: Apply SW algorithm on each pair of fragments of each search agent (), . |
| 5: Compute the alignment score (length of near-exact LCCS found) for each search agent based on Eq. (1). |
| 6: While (tT) |
| 7: Update the first () and second () best solutions from the population () based on the alignment score. |
| 8: If (tT) |
| 9: Update each solution () based on BA's operator using Eqs. (2) - (6). |
| 10: Else |
| 11: Check the infection conditions for each solution (): |
| 12: IF () |
| 13: Infection () = 1 |
| 14: Else IF (rand () > Inf_Rate) |
| 15: Infection () = 1 |
| 16: Else |
| 17: Infection () = 0 |
| 18: End IF |
| 19: For |
| 20: IF Infection () = 1 |
| 21: Update the solution () toward () based on Eqs. (11) - (12). |
| 22: For(propagate the infection through three agents) |
| 23: Select randomly one solution () , |
| 24: IF (rand () > Spread_Rate): |
| 25: Update the solution () toward () according to Eqs. (13) - (14). |
| 26: Infection () = 1 |
| 27: End IF |
| 28: IF (rand () > Recovery_Rate): Infection () = 0 End IF |
| 30: End For |
| 31: IF (rand () > Recovery_Rate): Infection () = 0 End IF |
| 32: Else |
| 33: Update the solution () toward () based on Eq. (15) - (16) |
| 34: End IF |
| 35: End For |
| 36: End IF |
| 37: Cut two fragments starting from the positions of () in the two sequences (SeqA and SeqB) |
| Compute the alignment score for the search agents based on Eq. (1). |
| 38: ; |
| 39: End While |
| 40: Output the near-exact LCCS pointed by the first best solution () and its length. |
FLAT based on BPINF has a time complexity where is the total number of iterations, represents the length of the cut fragment, is the population size of the working algorithm, and is the execution time for updating one agent of BA population, and is the execution time for updating one agent of PSO population, as well as the updating the movement of three other agents of PSO in case of spreading out the infection.
Fig. 6.
The flow charts of BPINF for FLAT.
5. Experimental results and discussion
This section presents the performance evaluation of FLAT based on the proposed technique (BPINF) against the standard BA (Yang, 2010) and other techniques in the literature such as ASCA-PSO (Issa et al., 2018), SCA (Mirjalili, 2016), IMO-PSO (Issa & Abd Elaziz, 2020), BA-DE (Yildizdan & Baykan, 2020) and BA-CSA (Shehab et al., 2019). The integrated versions of BA and PSO algorithms in (Manoj et al., 2016) and (Ferdowsi et al., 2019), namely BA-PSO-1 and BA-PSO-2, resp., are reimplemented for purposes of comparison. BPINF performance is evaluated using a set of pairs of real viruses protein sequences datasets gathered from the National Center for Biotechnology Information (NCBI). The pairs of sequences have a product length ranges from 250,000 to 21,000,000.
In this application, it is more meaningful to refer to the product of the sequence's length as a distinguished parameter instead of each individual sequence length (the sequences don’t have the same length). In this work, the range of sequence's length gets increased compared to the previous versions of FLAT (ASCA-PSO (Issa et al., 2018) and IMO-PSO (Issa & Abd Elaziz, 2020)) where the product of sequence’s length reached 9,000,000. The exact LCCS of each pair of sequences over different product lengths are determined by SW algorithm (Smith & Waterman, 1981), and it is used as a reference in the experimental tests.
The evaluation metrics that are applied for characterizing the performance of examined algorithms through the experimental tests are illustrated as follows:
-
1-
The percentage of similarity (%) between the reported near-exact LCCS' length (W) and the exact LCCS' length (K), see Fig. 1.
-
2-
The standard deviation of the numerical results.
-
3-
The statistical analysis using the Wilcoxon test (Gehan, 1965).
-
4-
The execution time.
The implementations of FLAT based on various MAs are coded under MATLAB environment using a computer machine with a multiprocessor CORE-I3 (2.14 GHz per processor) and 4 GB RAM. The length of a fragment being cut at each position is 50 residues for FLAT versions. Table 2 shows the settings of various parameters of all implemented Mas in the tests. These parameters are tuned practically where certain adjustments are held in order to find the most useful value for each parameter. The population size is tuned experimentally to produce the best performance according to the product of sequences' length (), where and represent the length of the aligned sequences, as shown in Table 3 . The maximum number of iterations is set to 30.
Table 2.
The settings of parameters of various examined MAs.
| Algorithm | Parameter | Value | |
|---|---|---|---|
| SW alignment | Match | +1.0 | |
| ge | −0.5 | ||
| go | −1.0 | ||
| FLAT | SCA | A | 2.2 |
| ASCA-PSO | W | 0.25 | |
| C1, C2 | 0.5 | ||
| A | 2.0 | ||
| BA | A0 | 0.8 | |
| F_min | 5.0 | ||
| F_max | 20 | ||
| Α | 0.95 | ||
| Γ | 2 | ||
| BPINF, BA-PSO-1, BA-PSO-2, BA-CSA and BA-DE | A0 | 0.8 | |
| F_min | 5.0 | ||
| F_max | 20 | ||
| Α | 0.95 | ||
| Γ | 2 | ||
| W | 0.25 | ||
| C1, C2 | 0.5 | ||
| Inf_Rate | 0.30 | ||
| Spread_Rate | 0.70 | ||
| Recovery_Rate | 0.30 | ||
| D | 25 | ||
Table 3.
Average LCCS similarity percentage (%) measured by FLAT for compared optimizers.
| PSO | IMO | IMO-PSO | SCA | ASCA-PSO | BA | BA-PSO-1 | BA-PSO-2 | BA-DE | BA-CSA | BPINF | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 250,000 | 40 | 53 | 50 | 87 | 56 | 89 | 39 | 73 | 71 | 81 | 78 | 92 |
| 350,000 | 40 | 52 | 53 | 87 | 55 | 89 | 36 | 75 | 73 | 78 | 75 | 92 |
| 550,000 | 100 | 54 | 58 | 88 | 58 | 85 | 37 | 71 | 70 | 79 | 76 | 90 |
| 750,000 | 120 | 51 | 56 | 91 | 55 | 86 | 34 | 69 | 72 | 77 | 74 | 91 |
| 1,000,000 | 150 | 52 | 51 | 88 | 56 | 82 | 34 | 68 | 74 | 76 | 73 | 90 |
| 1,400,000 | 180 | 48 | 48 | 85 | 50 | 78 | 36 | 70 | 69 | 70 | 65 | 92 |
| 1,800,000 | 200 | 45 | 52 | 84 | 48 | 80 | 35 | 62 | 68 | 67 | 65 | 89 |
| 2,200,000 | 240 | 46 | 47 | 81 | 49 | 78 | 34 | 63 | 67 | 69 | 64 | 91 |
| 2,600,000 | 400 | 39 | 43 | 84 | 44 | 76 | 33 | 58 | 62 | 61 | 56 | 90 |
| 3,000,000 | 400 | 38 | 41 | 87 | 41 | 80 | 32 | 55 | 60 | 62 | 59 | 90 |
| 4,000,000 | 450 | 42 | 44 | 86 | 44 | 75 | 33 | 52 | 61 | 58 | 54 | 91 |
| 5,000,000 | 450 | 43 | 45 | 84 | 45 | 78 | 34 | 53 | 59 | 59 | 56 | 90 |
| 6,000,000 | 450 | 45 | 39 | 89 | 46 | 74 | 34 | 63 | 60 | 60 | 58 | 88 |
| 7,000,000 | 500 | 40 | 38 | 81 | 43 | 75 | 35 | 65 | 62 | 56 | 52 | 87 |
| 8,000,000 | 700 | 39 | 39 | 84 | 40 | 73 | 33 | 64 | 61 | 52 | 47 | 84 |
| 9,000,000 | 900 | 36 | 37 | 75 | 38 | 74 | 34 | 60 | 57 | 50 | 43 | 85 |
| 11,000,000 | 1000 | 36 | 33 | 80 | 39 | 71 | 36 | 50 | 56 | 51 | 46 | 81 |
| 13,000,000 | 1300 | 32 | 30 | 70 | 36 | 70 | 31 | 53 | 57 | 47 | 41 | 81 |
| 15,000,000 | 1600 | 27 | 31 | 71 | 32 | 71 | 28 | 45 | 50 | 42 | 38 | 78 |
| 18,000,000 | 1900 | 31 | 29 | 68 | 34 | 69 | 29 | 42 | 47 | 44 | 38 | 79 |
| 21,000,000 | 2200 | 29 | 28 | 65 | 30 | 70 | 26 | 38 | 48 | 39 | 33 | 80 |
Table 3 shows the percentage of similarity (%) using FLAT based on BPINF (30 independent runs) against the relevant algorithms in the literature. The first column shows the product of lengths of sequences that ranges from 250,000 to 21000000. In Table 3, the first column shows the product of aligned sequences (), and the second column shows the corresponding agent size required to align the two sequences using FLAT. The population size differs across the lengths as the sequence length increases. Search space becomes more complicated as sequence length gets longer; thus population size should be increased in order to efficiently seek such emerging search space. The suitable population size with respect to the length of sequences is chosen practically after trying many values for BPINF-based FLAT. Notice that the choice of population size bears a tradeoff between the execution time and the quality of results. For each sequence length, there is a limit for increasing the number of agents to keep execution time below the corresponding one taken by the SW algorithm. As shown in Table 3, BPINF-based FLAT achieves the highest percentage over the whole range of the product of sequences length (especially for huge-length sequences), and the average percentage reaches 88% for all examined sequences.
While FLAT based on each of IMO-PSO and ASCA-PSO achieves an average percentage of 82% and 78%, resp. Using BA-PSO-1 and BA-PSO-2, FLAT can achieve 60% and 63%, resp., and using BA-CSA and BA-DE, the percentage only reaches 57% and 61%, resp. FLAT based on standard algorithms such as IMO, SCA and BA achieve an average percentage of 43%, 45%, and 34%, resp. These results reflect the efficiency of BPINF for finding near-exact LCCS using FLAT by avoiding early trapping in local optima for a sequence with a huge length.
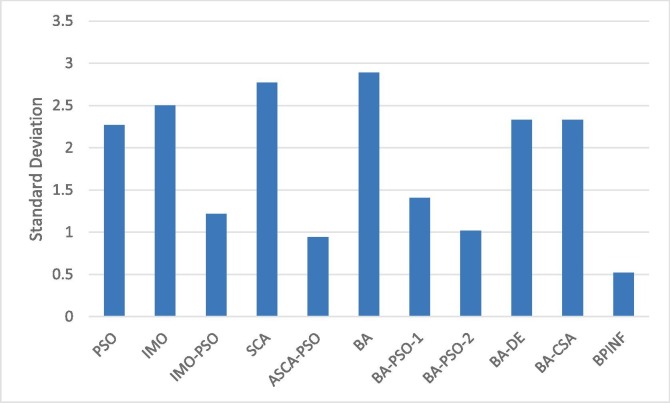
Table 4 shows the standard deviation of 30 individual runs of the FLAT based on various algorithms over various sequences length. As shown, FLAT based on BPINF has the lowest standard deviation in comparison to the other versions (see Fig. 7 ). The highest standard deviation is reported by IMO, SCA, and BA, while other algorithms have less standard deviations but are still higher than that one of BPINF. Moreover, the standard deviation of BPINF is for all examined datasets that gives a positive indicator of the robustness and precision of such a developed version of FLAT.
Table 4.
Standard deviation of LCCS similarity percentage measured by FLAT for compared optimizers.
| PSO | IMO | IMO-PSO | SCA | ASCA-PSO | BA | BA-PSO-1 | BA-PSO-2 | BA-DE | BA-CSA | BPINF | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 250,000 | 2.24 | 2.28 | 1.28 | 3.52 | 0.90 | 3.64 | 0.64 | 0.37 | 0.89 | 0.89 | 0.56 |
| 350,000 | 1.52 | 1.79 | 1.00 | 1.96 | 0.75 | 2.08 | 1.65 | 0.33 | 2.31 | 2.31 | 0.75 |
| 550,000 | 2.57 | 2.64 | 1.28 | 1.76 | 1.01 | 1.88 | 0.85 | 0.66 | 1.19 | 1.19 | 0.32 |
| 750,000 | 2.27 | 2.41 | 0.77 | 2.70 | 0.94 | 2.82 | 0.95 | 1.13 | 1.33 | 1.33 | 0.19 |
| 1,000,000 | 2.93 | 3.12 | 1.11 | 4.48 | 1.15 | 4.60 | 2.49 | 0.92 | 3.73 | 3.73 | 0.75 |
| 1,400,000 | 1.58 | 1.59 | 0.85 | 3.92 | 0.69 | 4.04 | 0.77 | 0.14 | 1.15 | 1.15 | 0.39 |
| 1,800,000 | 2.09 | 2.41 | 1.12 | 2.05 | 0.94 | 2.17 | 1.29 | 1.46 | 1.93 | 1.93 | 0.50 |
| 2,200,000 | 1.77 | 2.22 | 0.79 | 2.26 | 0.88 | 2.38 | 1.43 | 1.08 | 2.14 | 2.14 | 0.58 |
| 2,600,000 | 1.89 | 2.32 | 1.47 | 1.58 | 0.91 | 1.70 | 1.11 | 0.95 | 1.80 | 1.80 | 0.35 |
| 3,000,000 | 1.59 | 1.91 | 0.96 | 2.90 | 0.79 | 3.02 | 0.96 | 0.87 | 1.56 | 1.56 | 0.69 |
| 4,000,000 | 4.31 | 4.45 | 1.31 | 9.22 | 1.55 | 9.34 | 2.73 | 2.49 | 4.44 | 4.44 | 0.86 |
| 5,000,000 | 2.07 | 2.32 | 1.49 | 3.12 | 0.91 | 3.24 | 4.12 | 0.79 | 6.71 | 6.71 | 0.18 |
| 6,000,000 | 2.53 | 2.67 | 1.10 | 1.18 | 1.01 | 1.30 | 1.01 | 1.56 | 1.64 | 1.64 | 0.35 |
| 7,000,000 | 3.55 | 3.72 | 1.27 | 1.35 | 1.33 | 1.47 | 0.84 | 0.44 | 1.36 | 1.36 | 0.43 |
| 8,000,000 | 0.75 | 1.02 | 0.92 | 2.35 | 0.52 | 2.47 | 1.65 | 0.09 | 2.68 | 2.68 | 0.67 |
| 9,000,000 | 5.51 | 5.91 | 2.35 | 2.83 | 1.99 | 2.95 | 1.38 | 4.11 | 2.24 | 2.24 | 0.79 |
| 11,000,000 | 1.4 | 1.79 | 1.00 | 1.79 | 0.75 | 1.91 | 0.48 | 0.49 | 2.75 | 2.75 | 0.90 |
| 13,000,000 | 1.61 | 1.95 | 1.13 | 1.91 | 0.8 | 2.03 | 1.62 | 0.52 | 2.30 | 2.30 | 0.61 |
| 15,000,000 | 1.2 | 1.35 | 1.50 | 1.35 | 0.62 | 1.47 | 1.02 | 0.98 | 2.33 | 2.33 | 0.31 |
| 18,000,000 | 2.08 | 2.20 | 1.31 | 3.39 | 0.88 | 3.51 | 1.92 | 1.06 | 2.70 | 2.70 | 0.56 |
| 21,000,000 | 2.14 | 2.47 | 1.51 | 2.59 | 0.43 | 2.71 | 0.64 | 0.92 | 1.70 | 1.70 | 0.23 |
Fig. 7.
Average standard deviation of BPINF-based FLAT versus other examined versions.
Table 5 shows the results (-value) of the Wilcoxon test (Gehan, 1965) for evaluating the quality of solutions produced by BPINF-based FLAT compared to other related MAs. FLAT based on BPINF runs for 30 trials, and these results were compared with each other algorithm using the Wilcoxon test. As shown in Table 5, the -value of all comparisons is below 0.05, which indicates there is a significant superiority of the performance of BPINF.
Table 5.
Wilcoxon test results for the numerical results of various FLAT versions against BPINF.
| PSO | IMO | IMO-PSO | SCA | ASCA-PSO | BA | BA-DE | BA-CSA | BA-PSO-1 | BA-PSO-2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 250,000 | 4.0E-06 | 2.5E-05 | 2.8E-07 | 7.7E-06 | 3.9E-07 | 2.1E-06 | 2.0E-06 | 1.3E-05 | 2.5E-06 | 3.5E-05 |
| 350,000 | 1.4E-06 | 3.2E-06 | 1.8E-06 | 4.7E-06 | 2.3E-06 | 2.6E-06 | 1.6E-07 | 1.5E-06 | 2.9E-07 | 1.9E-06 |
| 550,000 | 8.5E-07 | 4.6E-05 | 1.0E-06 | 5.8E-06 | 8.0E-08 | 2.2E-06 | 3.2E-07 | 3.1E-05 | 2.5E-06 | 3.4E-05 |
| 750,000 | 5.5E-06 | 2.9E-06 | 5.5E-07 | 1.1E-05 | 3.8E-08 | 1.7E-06 | 3.5E-05 | 2.0E-05 | 7.7E-05 | 6.6E-05 |
| 1,000,000 | 1.2E-05 | 4.1E-07 | 2.6E-07 | 2.3E-05 | 2.4E-07 | 1.5E-06 | 5.1E-06 | 3.9E-07 | 7.0E-06 | 4.1E-07 |
| 1,400,000 | 6.2E-06 | 3.2E-06 | 5.9E-06 | 1.3E-05 | 2.4E-06 | 9.5E-06 | 1.6E-06 | 2.2E-05 | 3.5 E-06 | 2.3E-05 |
| 1,800,000 | 9.1E-07 | 4.5E-06 | 8.1E-07 | 1.5E-06 | 3.5E-07 | 1.2E-06 | 2.2E-07 | 4.5E-05 | 4.2E-07 | 5.6E-05 |
| 2,200,000 | 1.3E-06 | 1.0E-05 | 1.0E-08 | 1.9E-06 | 1.3E-07 | 1.2E-06 | 1.7E-04 | 2.8E-06 | 3.3E-04 | 4.6E-06 |
| 2,600,000 | 4.7E-06 | 3.8E-05 | 2.5E-06 | 2.8E-05 | 1.2E-06 | 2.9E-06 | 4.8E-05 | 2.6E-04 | 7.1E-05 | 6.2E-04 |
| 3,000,000 | 5.2E-07 | 1.4E-06 | 1.4E-07 | 1.4E-06 | 1.5E-07 | 1.2E-06 | 2.5E-05 | 2.0E-07 | 7.0E-05 | 5.0E-07 |
| 4,000,000 | 1.0E-05 | 1.5E-06 | 1.2E-06 | 1.4E-05 | 3.3E-07 | 1.3E-06 | 2.2E-07 | 6.9E-05 | 7.0E-06 | 7.1E-05 |
| 5,000,000 | 1.1E-06 | 9.5E-06 | 1.8E-06 | 2.4E-06 | 9.7E-07 | 1.9E-06 | 3.0E-04 | 2.3E-07 | 3.5E-04 | 6.3E-07 |
| 6,000,000 | 6.3E-05 | 7.7E-05 | 3.4E-07 | 8.0E-05 | 1.8E-08 | 5.1E-07 | 2.9E-05 | 3.9E-05 | 7.0E-05 | 4.5E-05 |
| 7,000,000 | 9.1E-07 | 1.8E-06 | 1.3E-07 | 1.2E-06 | 4.9E-07 | 1.2E-06 | 3.2E-06 | 5.0E-07 | 7.0E-06 | 5.3E-07 |
| 8,000,000 | 6.0E-07 | 5.6E-07 | 3.4E-07 | 2.3E-06 | 2.1E-08 | 4.5E-07 | 1.2E-05 | 4.4E-04 | 6.0E-05 | 5.3E-04 |
| 9,000,000 | 6.5E-06 | 5.9E-06 | 4.0E-08 | 8.4E-05 | 4.7E-07 | 1.4E-06 | 7.3E-07 | 1.4E-05 | 3.7E-06 | 4.3E-05 |
| 11,000,000 | 6.9E-07 | 3.5 E-06 | 8.5E-06 | 2.2E-06 | 5.1E-06 | 1.3E-05 | 9.5E-07 | 2.2E-06 | 2.1E-06 | 2.4E-06 |
| 13,000,000 | 2.3E-07 | 4.0E-07 | 2.8E-07 | 2.7E-07 | 4.0E-07 | 2.5E-06 | 1.8E-08 | 1.7E-05 | 3.5E-06 | 3.2E-05 |
| 15,000,000 | 6.2E-06 | 3.3E-04 | 3.8E-07 | 1.5E-05 | 8.9E-08 | 3.9E-07 | 3.5E-07 | 4.9E-04 | 4.3E-06 | 5.3E-04 |
| 18,000,000 | 6.0E-07 | 1.6E-06 | 9.8E-06 | 1.4E-06 | 5.3E-06 | 2.8E-05 | 2.8E-06 | 1.8E-05 | 5.3E-06 | 4.3E-05 |
| 21,000,000 | 3.2E-06 | 1.8E-06 | 1.0E-07 | 1.7E-05 | 4.5E-08 | 1.4E-07 | 9.3E-07 | 1.3E-04 | 1.6E-06 | 2.3E-04 |
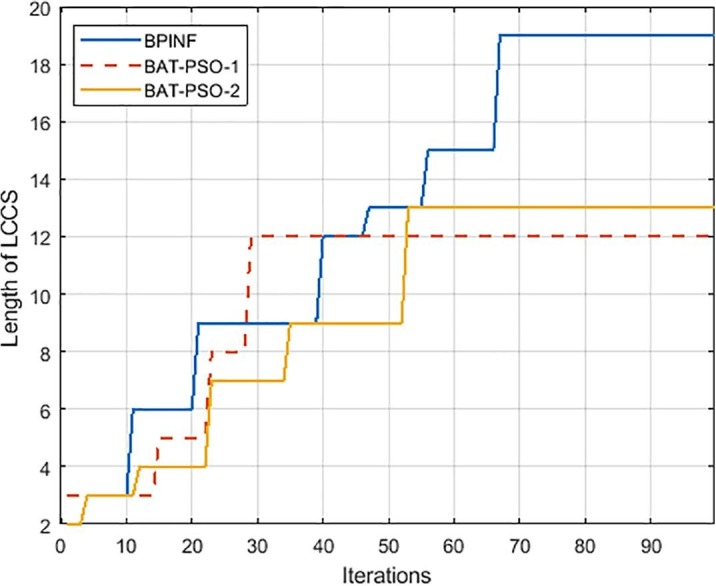
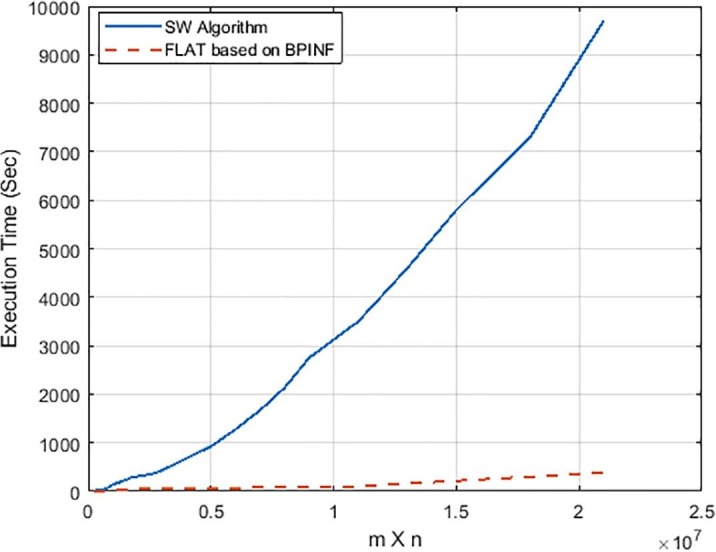
Fig. 8 shows the convergence curve of BPINF versus BA-PSO-1 and BA-PSO-2. As shown in Fig. 8, BPINF is able to avoid entrapment in local optima in the time that the other two algorithms converged early. The speedup of FLAT using BPINF is measured and compared against that of the standard SW algorithm (Smith & Waterman, 1981) as in Fig. 9 . There is a notable speedup of performing the local alignment process between a pair of sequences using BPINF-based FLAT over that one of SW. Fig. 10 shows the comparison of the execution time of PBINF versus that of other algorithms over various sequence lengths.
Fig. 8.
Convergence curve of BPINF.
Fig. 9.
The execution time of FLAT using BPINF technique against SW for variable lengths.
Fig. 10.
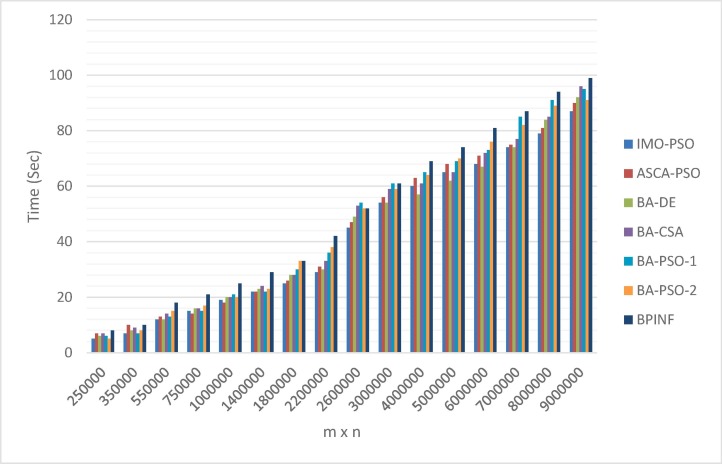
The execution time of FLAT using BPINF technique versus other algorithms.
5.1. Sensitivity analysis of BPINF parameters
This subsection demonstrates the impact of different BPINF parameters on its performance. BPINF's main parameters are loudness factor (), pulse emission rate (), weight inertia (), infection rate (), infection propagation rate (), recovery rate (), population size and the maximum number of iterations. The sensitivity analysis tests are performed by trying different values for each parameter over a reasonable range for a subset of the datasets. Each parameter under test is assigned three values while the best settings for other parameters are fixed.
Loudness factor is an important parameter of BA (see Eq. (6)). It controls the search process where it decreases by increasing the iterations until reaching approximately zero by search termination. represents the initial loudness in Eq. (6) and has a great influence on the value of loudness through the rest of the iterations. Table 6 shows the influence of on the performance of BPINF for a set of sequences that have a product that ranges from 3,000,000 to 8000000. Three values (0.1, 0.6, and 0.8) are examined for this parameter. The performance is worst at ( = 0.1) while it increases as increasing (which may be justified by improving search space exploration), until reaching the best performance at ( = 0.8).
Table 6.
Results of conducted sensitivity analysis of the BPINF parameters.
|
Performance of Parameters |
||||||
|---|---|---|---|---|---|---|
|
Loudness (Ao) |
Pulse Rate Emission (ro) |
|||||
| Ao = 0.1 | Ao = 0.6 | Ao = 0.8 | ro = 0.1 | ro = 0.5 | ro = 0.8 | |
| 3,000,000 | 65 | 85 | 90 | 90 | 82 | 78 |
| 4,000,000 | 73 | 82 | 91 | 91 | 79 | 76 |
| 5,000,000 | 68 | 84 | 90 | 90 | 78 | 78 |
| 6,000,000 | 63 | 80 | 88 | 88 | 81 | 72 |
| 7,000,000 | 60 | 83 | 87 | 87 | 76 | 74 |
| 8,000,000 | 61 | 81 | 84 | 84 | 78 | 73 |
| Weight Inertia (w) | Inf_rate | |||||
| w = 0.2 | w = 0.5 | w = 0.9 | 0.1 | 0.3 | 0.9 | |
| 3,000,000 | 90 | 75 | 60 | 79 | 90 | 60 |
| 4,000,000 | 91 | 73 | 65 | 77 | 91 | 59 |
| 5,000,000 | 90 | 69 | 63 | 74 | 90 | 57 |
| 6,000,000 | 88 | 63 | 61 | 71 | 88 | 61 |
| 7,000,000 | 87 | 68 | 59 | 65 | 87 | 62 |
| 8,000,000 | 84 | 72 | 60 | 62 | 84 | 58 |
| Spread_rate | Recovery_rate | |||||
| 0.3 | 0.7 | 0.9 | 0.1 | 0.3 | 0.8 | |
| 3,000,000 | 89 | 90 | 72 | 82 | 90 | 68 |
| 4,000,000 | 90 | 91 | 81 | 75 | 91 | 72 |
| 5,000,000 | 87 | 90 | 73 | 77 | 90 | 66 |
| 6,000,000 | 83 | 88 | 79 | 79 | 88 | 69 |
| 7,000,000 | 86 | 87 | 74 | 76 | 87 | 71 |
| 8,000,000 | 83 | 84 | 72 | 73 | 84 | 67 |
| Population Size | Iteration | |||||
| 100 | 400 | 800 | 10 | 30 | 60 | |
| 3,000,000 | 43 | 90 | 91 | 62 | 90 | 90 |
| 4,000,000 | 39 | 86 | 90 | 69 | 91 | 91 |
| 5,000,000 | 41 | 84 | 89 | 65 | 90 | 90 |
| 6,000,000 | 37 | 85 | 91 | 69 | 88 | 88 |
| 7,000,000 | 34 | 74 | 88 | 59 | 87 | 87 |
| 8,000,000 | 32 | 69 | 86 | 63 | 84 | 84 |
The pulse emission rate () which is described in Eq. (7), decays as the search proceeds. represents the initial pulse emission rate and three values of (0.1, 0.5, and 0.8) are used to test its influence on the performance of BPINF. In Table 6 ( = 0.1) delivers the best performance while the performance was decreasing when increasing .
The weight inertia () mentioned in Eq. (9) is used in updating the movement of the agents according to the PSO strategy. It controls the influence of the velocity of the previous iteration on the new velocity in the current iteration. The allowable range of is from 0.2 to 0.9 (Kennedy, 1995). Three values of (0.25, 0.5, and 0.9) are examined to test the influence of on performance. Table 6 shows the results of changing where small values lead to better performance over large values. The best performance is reported at (w = 0.2) using experimental tunning.
The infection rate () BPINF is employed for controlling the degree of infection through population conditioned to a boundary of () around the first best solution (). Table 6 presents the impact of this parameter on BPINF performance. A small value of leads to better performance than higher ones. which is located in the range from 0.25 to 0.35, can produce acceptable performance; however, based on the experimental tuning, the best performance is registered at ( = 0.3).
The spread rate () controls the propagation of the infection through the agents where three randomly chosen agents can be additionally infected. Three values of (0.3, 0.7, and 0.9) are examined. In Table 6, the best choice of is 0.7 using the experimental tunning, where the range from 0.6 to 0.8 produces acceptable performance. Raising the value of up to 0.9 negatively impacts the performance due to the small probability of generating a random number that exceeds 0.9.
The recovery rate parameter () controls the recovery operation of infected agents so that it can be updated conventionally toward the second-best solution (). In Table 6, for small values such as (), it can produce better performance than for higher value (). Conversely, the small value of as the probability of recovery may lead to a weak exploration phase, and hence falling into local optima. So that, choosing the value of at (0.3) provides a balanced compromise for the sake of achieving a satisfying quality of solutions.
For the population size, different values such as (100, 400, and 800) are used in order to test the influence on the performance of BPINF. In Table 6, the population size (1 0 0) produced a lower performance than that one reported by larger size, which is an obvious result. However, for relatively small-length sequences, increasing population size over 100 is not suggested in order to keep the execution time of FLAT at reasonable limits. Furthermore, the number of exhausted search iterations is examined at the values (10, 30, and 60). For a value of (10) BPINF performance is the lowest. However, as the number of iterations is increased, the performance is increased as well but gets saturated at some limit. In Table 6, increasing the total number of iterations from (30) to (60) does not improve the BPINF perfomance.
6. BPINF-based FLAT for COVID-19
The promising numerical results of BPINF, when applied to operate FLAT for some conventional datasets, pave the way to examine such a procedure for investigating the newly discovered sequences like the protein of COVID-19 virus. BPINF-based FLAT is evaluated to detect the LCCS between the protein of COVID-19 virus, and a set of diseases were gathered from NCBI such as (1) Middle East respiratory syndrome coronavirus (MERS-CoV), (2) Hepatitis B, (3) Severe acute respiratory syndrome coronavirus (SARS-CoV), (4) Dengue virus and (5) Cowbox virus. Table 7 shows the results of FLAT based on BPINF when looking for LCCS in comparison of SW algorithm (Smith & Waterman, 1981) and the other relevant FLAT versions. The column score presents the length of the detected near-exact LCCS for each technique besides the exact LCCS that can be found by the exact SW algorithm.
Table 7.
Detecting the LCCS between COVID-19 virus with other viruses with FLAT using BPINF and other versions.
| Virus Protein Name | Technique | Score | LCCS | |
|---|---|---|---|---|
| 1 | MERS-CoV | SW | 5 | CVYSV |
| SCA | 3 | LAT | ||
| ASCA-PSO | 3 | QVL | ||
| IMO | 2 | NR | ||
| IMO-PSO | 3 | LSA | ||
| BA | 2 | HT | ||
| BA-DE | 3 | YSV | ||
| BA-CSA | 4 | LEGN | ||
| BA-PSO-1 | 3 | NRA | ||
| BA-PSO-2 | 4 | LPTG | ||
| BPINF | 5 | QVLSA | ||
| 2 | Hepatitis B | SW | 5 | SIFSR |
| SCA | 5 | SIFSR | ||
| ASCA-PSO | 5 | SILSP | ||
| IMO-PSO | 3 | LSP | ||
| IMO | 3 | ILS | ||
| BA | 3 | IGD | ||
| BA-DE | 4 | SIFS | ||
| BA-CSA | 4 | IGD | ||
| BA-PSO-1 | 3 | FSR | ||
| BA-PSO-2 | 4 | IGDA | ||
| BPINF | 5 | SIFSR | ||
| 3 | SARS-CoV | SW | 280 | SGFRKMAFPSGKVEGCMVQVTCGTTTLNGLWLDDVVYCPRHVICTSEDMLNPNYEDLLIRKSNHNFLVQAGNVQLRVIGHSMQNCVLKLKVDTANPKTPKYKFVRIQPGQTFSVLACYNGSPSGVYQCAMRPNFTIKGSFLNGSCGSVGFNIDYDCVSFCYMHHMELPTGVHAGTDLEGNFYGPFVDRQTAQAAGTDTTITVNVLAWLYAAVINGDRWFLNRFTTTLNDFNLVAMKYNYEPLTQDHVDILGPLSAQTGIAVLDMCASLKELLQNGMNGRTILGSALLEDEFTPFDVVRQCSGVTFQ |
| SCA | 12 | TIKGSFLNGSCG | ||
| ASCA-PSO | 30 | YNYEPLTQDHVDILGPLSAQTGIAVLDMCA | ||
| IMO-PSO | 23 | SALLEDEFTPFDVVRQCSGVTFQ | ||
| IMO | 18 | EGCMVQVTCGTTTLNGLW | ||
| BA | 11 | TIKGSFLNGSC | ||
| BA-DE | 15 | EDMLNPNYEDLLIRK | ||
| BA-CSA | 16 | GTTTLNGLWLDDTVYC | ||
| BA-PSO-1 | 14 | SGFRKMAFPSGKVE | ||
| BA-PSO-2 | 16 | FTPFDVVRQCSGVTFQ | ||
| BPINF | 30 | SGFRKMAFPSGKVEGCMVQVTCGTTTLNGL | ||
| 4 | Dengue virus | SW | 5 | IVTCA |
| SCA | 4 | LTGY | ||
| ASCA-PSO | 5 | SGNLL | ||
| IMO | 3 | VLV | ||
| IMO-PSO | 4 | FLNG | ||
| BA | 4 | FDGS | ||
| BA-DE | 4 | FDGS | ||
| BA-CSA | 4 | TLVT | ||
| BA-PSO-1 | 3 | TLV | ||
| BA-PSO-2 | 4 | SGNL | ||
| BPINF | 5 | ETLVT | ||
| 5 | Cowbox virus | SW | 5 | QAIAS |
| SCA | 4 | IKRS | ||
| ASCA-PSO | 5 | SVRVV | ||
| IMO-PSO | 4 | IKRS | ||
| IMO | 3 | VDS | ||
| BA | 2 | VN | ||
| BA-DE | 3 | RVV | ||
| BA-CSA | 4 | VDSA | ||
| BA-PSO-1 | 3 | QVT | ||
| BA-PSO-2 | 4 | VNAS | ||
| BPINF | 5 | SVRVV | ||
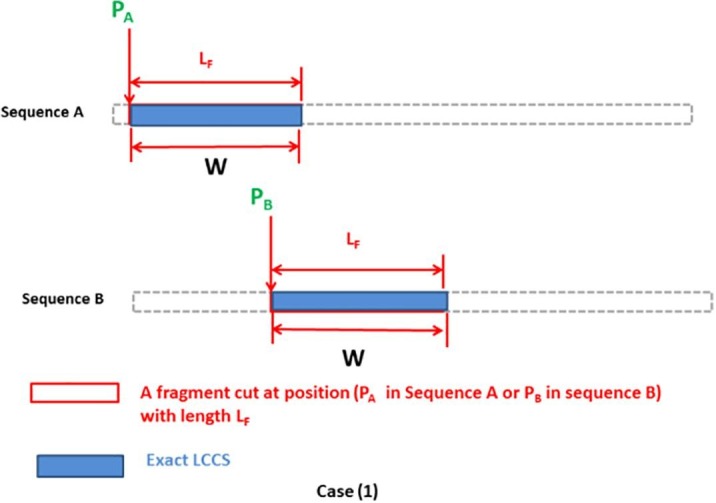
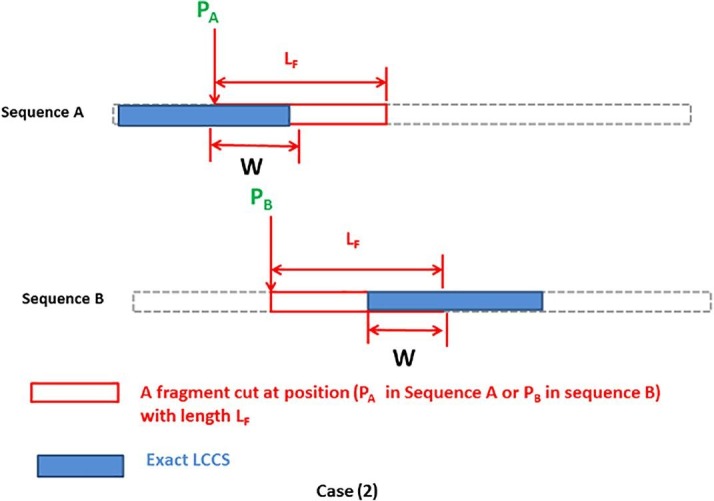
In Table 7, FLAT using BPINF can achieve a high percentage of the exact LCCS found by the SW algorithm while other algorithms report lower-percentage solutions. The sequences may have many common subsequences with different lengths; however, the objective is to find the longest one (LCCS) or as high a percentage of it as possible. The 1st disease (MERS-CoV), 4th disease (Dengue virus), and 5th disease (Cowbox virus) have many LCCS with 5 residues, and BPINF is able to find one of such LCCS. ASCA-PSO and IMO-PSO achieve a percentage of exact LCCS but with a lower length, while the rest of the algorithms of comparison fail to find a portion of the exact LCCS. For the 3rd disease (SARS-CoV), the exact LCCS has a length of 280 residues, and BPINF succeeded in achieving the highest portion of it (30 residues), where the fragment size used in the experimental tests is 50 residues. Besides, it is noticed from Table 6 that the length of found near-exact LCCS has different lengths. Such results are sensitive to the positions of the fragments cut, such as in cases (1), (2) illustrated in Fig. 10, Fig. 11 .
Fig. 11.
Case of finding the exact LCCS.
For case (1) in Fig. 10, the agent points to the start of the exact LCCS (the blue-filled rectangle) with positions (PA) in sequence (A) and position (PB) in sequence (B). The two fragments are cut with length () which is equal to the length of the exact LCCS. Hence when the two cut fragments are aligned the maximum possible LCCS with length () can be found using FLAT (Fig. 12 ).
Fig. 12.
Case of finding portions of the exact LCCS.
This case is rarely occurred due to the following reasons:
-
•
It is impossible to guess the length of exact LCCS from the very beginning, and thus one user could assign it as the length of the cut fragment (). Besides, the length of LCCS is variable for different sequences.
-
•
In case of much increasing , the execution time of FLAT will enormously increase which affects the main advantage of using FLAT that is processing a reasonable execution time. Hence, the parameter setting represents a tradeoff between the quality of found near-exact LCCS and the execution time.
-
•
Pointing to the start of the exact LCCs by search agents is quite difficult where the positions of agents are updated based on random criteria. That means that if (PA) points to the start of exact LCCS in sequence (A), there is still a high probability that (PB) does not point to the start of exact LCCS in sequence (B).
In case (2), the positions (PA) and (PB) point to some positions that differ from the start of the exact LCCS but are still close to it. Hence, the percentage of cutting part of one exact LCCS by the cut fragments (depends on LF starting from the cutting positions) will determine the length of the reported near-exact LCCS by an optimizer. Moreover, the length of the near-exact LCCS (W) is shorter than that one in the case (1). The main reason for such issue is the stochastic nature of MAs when updating the positions of search agents, as well as the predetermined length of cut fragments which is a critical parameter for FLAT.
The main merits of BPINF-based FLAT can be summarized as follows:
-
1-
Detecting near-exact LCCS with an average similarity percentage of 88% with the exact LCCS that can be found by SW for a product of sequence length up to 21,000,000. While the rates of FLAT using ASCA-PSO and IMO-PSO are 78% and 82%, resp.
-
2-
The proposed infection propagation mechanism is able to reduce the chances of trapping in local optima, which is reflected in the behavior of BPINF when applied for FLAT in comparison of both conventional MAs and recent related hybrid techniques to the same problem.
However, the proposed approach still suffer from the following listed limitations:
-
1-
Despite, BPINF-based FLAT is able to achieve high performance by finding 88% (on average) of the exact LCCS for tested sequences with a product of the length of 21,000,000, but the performance is expected to degrade for longer sequences.
-
2-
The fragment length (LF) was tuned practically to be (50) residues in order to keep the balance between the execution time and the quality of solutions. Such length value may be considered limited when compared to the real length of existing LCCS. Hence, the fragment length needs to be tuned in a more clever way so that a satisfying performance can be reached in a reasonable time.
-
3-
The developed infection mechanism of BPINF propagates infection through agents, which adds execution time overhead. As the population grows, which is a need to face extreme sequence length, then the number of infected agents needs to be increased too in order to maximize the benefit of such mechanism. In other words, the number of infected agents is better to get increased as population size increases. But this modification for the proposed BPINF will be stuck with the aim of reducing the execution time as possible to meet the goals of operating FLAT.
7. Conclusions and future research directions
This work presents an enhancement for FLAT based on a novel integration mechanism between BA and PSO algorithms. The integration mechanism is based on updating the positions of search agents using BA operators to first explore the input sequences to find the best region that may have the longest common subsequences. After exploration, the first and second-best solutions are reported and the exploitation phase starts to move the agents using PSO operator. In the proposed mechanism (BPINF), during the exploitation, some agents are infected toward the first best solution, while the non-infected agents are moved toward the second-best solution. The infection is transferred according to the current distance of the position of an agent to the first-best solution. Besides, each infected agent can transfer the infection to the other three agents in order to propagate the infection through the population. The main merit of the BPINF is increasing the diversity of generated solutions which maximizing the chance to avoid early trapping in local optima during the search. The infected agents can be recovered based on some stochastic criteria, which also helps to increase the diversity of generated solutions. The performance of FLAT based on BPINF is evaluated on a real protein sequence that has a various range of sequence lengths (have a product of lengths from 250,000 to 21,000,000). The BPINF shows outstanding performance for detecting near-exact LCCS in comparison to other versions of FLAT based on ASCA-PSO, IMO-PSO, BA-PSO-1, BA-PSO-2, BA-DE, BA-CSA, and SCA. Besides, the small standard deviation, relative to other versions of FLAT, shows the high robustness and precision of the proposed technique. The developed technique shows usefulness for investigating newly discovered biological sequences such as the protein of COVID-19. Results of LCCS detection between COVID-19 and the other five viruses are available using BPINF-based FLAT.
The findings of current research give a great motivation to continue investigating the recently discovered genetic strains of COVID-19. Moreover, it is interesting to implement a faster version of BPINF-based FLAT using a GPU accelerator. In the later environment, the critical parameters such as population size, fragment length, and infection rate can be adapted in the more wider window to efficiently seek search space of huge sequences without losing the advantage of limited execution time (i.e., reasonable execution time in comparison of the time taken by the standard SW algorithm).
Funding
The authors declare that there is no funding associated with this project.
CRediT authorship contribution statement
Mohamed Issa: Conceptualization, Methodology, Data curation, Software, Validation, Writing – original draft. Ahmed M. Helmi: Software, Validation, Writing – review & editing, Writing – original draft. Ammar H. Elsheikh: Data curation, Software, Validation. Mohamed Abd Elaziz: Conceptualization, Methodology, Writing – original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abd-Elazim S.M., Ali E.S. A hybrid particle swarm optimization and bacterial foraging for optimal power system stabilizers design. International Journal of Electrical Power & Energy Systems. 2013;46:334–341. [Google Scholar]
- Ahmed N., Lévy J., Ren S., Mushtaq H., Bertels K., Al-Ars Z. GASAL2: A GPU accelerated sequence alignment library for high-throughput NGS data. BMC bioinformatics. 2019;20(1):520. doi: 10.1186/s12859-019-3086-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Betar M.A., Alomari O.A., Abu-Romman S.M. A TRIZ-inspired bat algorithm for gene selection in cancer classification. Genomics. 2020;112(1):114–126. doi: 10.1016/j.ygeno.2019.09.015. [DOI] [PubMed] [Google Scholar]
- Alagarsamy S., Kamatchi K., Govindaraj V., Zhang Y.-D., Thiyagarajan A. Multi-channeled MR brain image segmentation: A new automated approach combining BAT and clustering technique for better identification of heterogeneous tumors. Biocybernetics and Biomedical Engineering. 2019;39(4):1005–1035. [Google Scholar]
- Alihodzic A., Tuba M. Paper presented at the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation. 2014. Improved hybridized bat algorithm for global numerical optimization. [Google Scholar]
- Aljamali, N. M., Jawad, A. M., & Alsabri, I. K. A. (2020). Public Health in Hospitals. 1 First Edition, 2020, Eliva Press, ISBN: 9798636352129.
- Benkrid K., Liu Y., Benkrid A. A highly parameterized and efficient FPGA-based skeleton for pairwise biological sequence alignment. IEEE Transactions on Very Large Scale Integration (VLSI) Systems. 2009;17(4):561–570. [Google Scholar]
- Bora T.C., Coelho L.d.S., Lebensztajn L. Bat-inspired optimization approach for the brushless DC wheel motor problem. IEEE Transactions on magnetics. 2012;48(2):947–950. [Google Scholar]
- Cohen J. Bioinformatics—an introduction for computer scientists. ACM Computing Surveys (CSUR) 2004;36(2):122–158. [Google Scholar]
- Cormen T.H. MIT press; 2009. Introduction to algorithms. [Google Scholar]
- Dao T.-K., Chu S.-C., Pan J.-S., Ngo T.-G., Nguyen T.-D., Tran H.-T. Paper presented at the International Conference on Genetic and Evolutionary Computing. 2019. An Improved Bat Algorithm Based on Hybrid with Ant Lion Optimizer. [Google Scholar]
- Dao T.-K., Chu S.-C., Pan J.-S., Nguyen T., Ngo T., Nguyen T., Tran H. An Improved Bat Algorithm Based on Hybrid with Ant Lion Optimizer. Advances in Intelligent Systems and Computing. 2020;1107:50–60. [Google Scholar]
- Di Tucci, L., O'Brien, K., Blott, M., & Santambrogio, M. D. (2017). Architectural optimizations for high performance and energy efficient Smith-Waterman implementation on FPGAs using OpenCL. Paper presented at the Design, Automation & Test in Europe Conference & Exhibition (DATE), 2017.
- Eappen G., Shankar T. Hybrid PSO-GSA for energy efficient spectrum sensing in cognitive radio network. Physical Communication. 2020;40:101091. doi: 10.1016/j.phycom.2020.101091. [DOI] [Google Scholar]
- Elloumi M., Issa M.A.S., Mokaddem A. In: Biological Knowledge Discovery Handbook. Elloumi M., Zomaya A.Y., editors. John Wiley & Sons, Inc.; Hoboken, New Jersey: 2013. A. Accelerating Pairwise Alignment Algorithms by Using Graphics Processor Units; pp. 969–980. [DOI] [Google Scholar]
- Elsisi M., Soliman M., Aboelela M.A.S., Mansour W. Bat inspired algorithm based optimal design of model predictive load frequency control. International Journal of Electrical Power & Energy Systems. 2016;83:426–433. [Google Scholar]
- Enireddy V., Anitha R., Vallinayagam S., Maridurai T., Sathish T., Balakrishnan E. Prediction of human diseases using optimized clustering techniques. Materials Today: Proceedings. 2021 [Google Scholar]
- Feng D.-F., Doolittle R.F. [23] Progressive alignment and phylogenetic tree construction of protein sequences. Methods in enzymology. 1990;183:375–387. doi: 10.1016/0076-6879(90)83025-5. [DOI] [PubMed] [Google Scholar]
- Ferdowsi A., Farzin S., Mousavi S.-F., Karami H. Hybrid Bat & Particle Swarm Algorithm for optimization of labyrinth spillway based on half & quarter round crest shapes. Flow Measurement and Instrumentation. 2019;66:209–217. [Google Scholar]
- Garg H. A hybrid PSO-GA algorithm for constrained optimization problems. Applied Mathematics and Computation. 2016;274:292–305. [Google Scholar]
- Gehan E.A. A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika. 1965;52(1-2):203–224. [PubMed] [Google Scholar]
- Hasançebi O., Teke T., Pekcan O. A bat-inspired algorithm for structural optimization. Computers & Structures. 2013;128:77–90. [Google Scholar]
- Issa M., Elaziz M.A. Analyzing COVID-19 virus based on enhanced fragmented biological Local Aligner using improved Ions Motion Optimization algorithm. Applied Soft Computing. 2020;96:106683. doi: 10.1016/j.asoc.2020.106683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Issa M., Abo Bakr H., Mansour Alzohairy A., Zeidan I. Gene-Tracer: Algorithm tracing genes modification from ancestors through offsprings. International Journal of Computer Applications. 2012;52(19):11–14. [Google Scholar]
- Issa M., Hassanien A.E., Helmi A., Ziedan I., Alzohairy A. Paper presented at the International Conference on Advanced Machine Learning Technologies and Applications. 2018. Pairwise Global Sequence Alignment Using Sine-Cosine Optimization Algorithm. [Google Scholar]
- Issa M., Hassanien A.E., Oliva D., Helmi A., Ziedan I., Alzohairy A. ASCA-PSO: Adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment. Expert Systems with Applications. 2018;99:56–70. [Google Scholar]
- Jaddi N.S., Abdullah S., Hamdan A.R. Optimization of neural network model using modified bat-inspired algorithm. Applied Soft Computing. 2015;37:71–86. [Google Scholar]
- Jiang J.L., Li S.Y., Liao M.L., Jiang Y. Application in Disease Classification based on KPCA-IBA-LSSVM. Procedia Computer Science. 2019;154:109–116. [Google Scholar]
- Jiang S., Ji Z., Shen Y. A novel hybrid particle swarm optimization and gravitational search algorithm for solving economic emission load dispatch problems with various practical constraints. International Journal of Electrical Power & Energy Systems. 2014;55:628–644. [Google Scholar]
- Kennedy Particle swarm optimization. Neural Networks. 1995 [Google Scholar]
- Khajeh-Saeed A., Poole S., Blair Perot J. Acceleration of the Smith-Waterman algorithm using single and multiple graphics processors. Journal of Computational Physics. 2010;229(11):4247–4258. [Google Scholar]
- Li I.T., Shum W., Truong K. 160-fold acceleration of the Smith-Waterman algorithm using a field programmable gate array (FPGA) BMC bioinformatics. 2007;8(1):185. doi: 10.1186/1471-2105-8-185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L., Khuri S. Paper presented at the METMBS. 2004. A Comparison of DNA Fragment Assembly Algorithms. [Google Scholar]
- Lu S.-Y., Wang S.-H., Zhang Y.-D. A classification method for brain MRI via MobileNet and feedforward network with random weights. Pattern Recognition Letters. 2020;140:252–260. [Google Scholar]
- Manoj S., Ranjitha S., Suresh H. Paper presented at the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT) 2016. Hybrid BAT-PSO optimization techniques for image registration. [Google Scholar]
- Mirjalili S. SCA: A sine cosine algorithm for solving optimization problems. Knowledge-Based Systems. 2016;96:120–133. [Google Scholar]
- Mohamed Issa A.H., Ziedan I., Alzohairy A. Maximizing Occupancy of GPU for Fast Scanning Biological Database Using Sequence Alignment. Journal OF Applied Sciences Research. 2017;13(6) [Google Scholar]
- Morshedian A., Razmara J., Lotfi S. A novel approach for protein structure prediction based on an estimation of distribution algorithm. Soft Computing. 2019;23(13):4777–4788. [Google Scholar]
- Needleman S.B., Wunsch C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of molecular biology. 1970;48(3):443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- Neto W.A., Pinto M.F., Marcato A.L., da Silva I.C., Fernandes D.d.A. Mobile robot localization based on the novel leader-based bat algorithm. Journal of Control, Automation and Electrical Systems. 2019;30(3):337–346. [Google Scholar]
- Pravesjit S. A hybrid bat algorithm with natural-inspired algorithms for continuous optimization problem. Artificial Life and Robotics. 2016;21(1):112–119. [Google Scholar]
- Şenel F.A., Gökçe F., Yüksel A.S., Yiğit T. A novel hybrid PSO–GWO algorithm for optimization problems. Engineering with Computers. 2019;35(4):1359–1373. [Google Scholar]
- Shehab M., Khader A.T., Laouchedi M., Alomari O.A. Hybridizing cuckoo search algorithm with bat algorithm for global numerical optimization. The Journal of Supercomputing. 2019;75(5):2395–2422. [Google Scholar]
- Shen Q., Shi W.-M., Kong W. Hybrid particle swarm optimization and tabu search approach for selecting genes for tumor classification using gene expression data. Computational Biology and Chemistry. 2008;32(1):53–60. doi: 10.1016/j.compbiolchem.2007.10.001. [DOI] [PubMed] [Google Scholar]
- Shereen M.A., Khan S., Kazmi A., Bashir N., Siddique R. COVID-19 infection: Origin, transmission, and characteristics of human coronaviruses. Journal of advanced research. 2020;24:91–98. doi: 10.1016/j.jare.2020.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith T.F., Waterman M.S. Identification of common molecular subsequences. Journal of molecular biology. 1981;147(1):195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- Trivedi I.N., Jangir P., Kumar A., Jangir N., Totlani R. Springer; 2018. A novel hybrid PSO–WOA algorithm for global numerical functions optimization Advances in computer and computational sciences; pp. 53–60. [Google Scholar]
- Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation. 1997;1(1):67–82. [Google Scholar]
- Xiong J. Cambridge University Press; 2006. Essential bioinformatics. [Google Scholar]
- Yadav P., Sharma P.R., Gupta S.K. Bat search algorithm based hybrid PSO approaches to optimize the location of UPFC in power system. International Journal on Electrical Engineering and Informatics. 2015;7(3):475–488. [Google Scholar]
- Yamaguchi Y., Tsoi H.K., Luk W. Paper presented at the International Symposium on Applied Reconfigurable Computing. 2011. Fpga-based smith-waterman algorithm: Analysis and novel design. [Google Scholar]
- Yang, X.-S. (2010). A new metaheuristic bat-inspired algorithm Nature inspired cooperative strategies for optimization (NICSO 2010) (pp. 65-74): Springer.
- Yang X.-S., He X. Bat algorithm: Literature review and applications. International Journal of Bio-Inspired Computation. 2013;5(3):141–149. [Google Scholar]
- Yildizdan G., Baykan Ö.K. A novel modified bat algorithm hybridizing by differential evolution algorithm. Expert Systems with Applications. 2020;141:112949. doi: 10.1016/j.eswa.2019.112949. [DOI] [Google Scholar]
- Yue X., Zhang H. Improved hybrid bat algorithm with invasive weed and its application in image segmentation. Arabian Journal for Science and Engineering. 2019;44(11):9221–9234. [Google Scholar]
- Zahid S.K., Hasan L., Khan A.A., Ullah S. Paper presented at the 2015 Third International Conference on Digital Information, Networking, and Wireless Communications (DINWC) 2015. A novel structure of the Smith-Waterman Algorithm for efficient sequence alignment. [Google Scholar]
- Zou H., Tang S., Yu C., Fu H., Li Y., Tang W. Asw: Accelerating Smith-Waterman algorithm on coupled CPU–GPU architecture. International Journal of Parallel Programming. 2019;47(3):388–402. [Google Scholar]
- Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. (COVID-19): A perspective from China. Radiology. 2020;296(2):E15–E25. doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]